Generalized Arithmetic Staircase Graphs and Their Total Edge Irregularity Strengths
Abstract
1. Introduction
2. Results
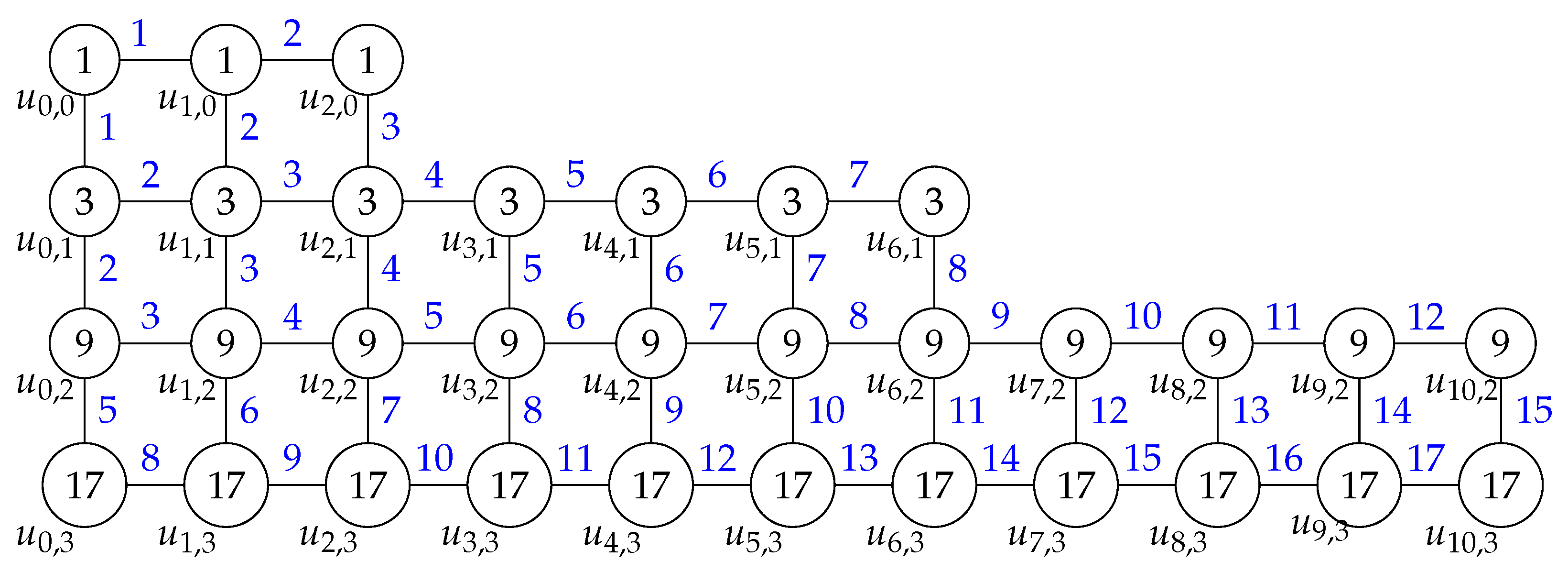
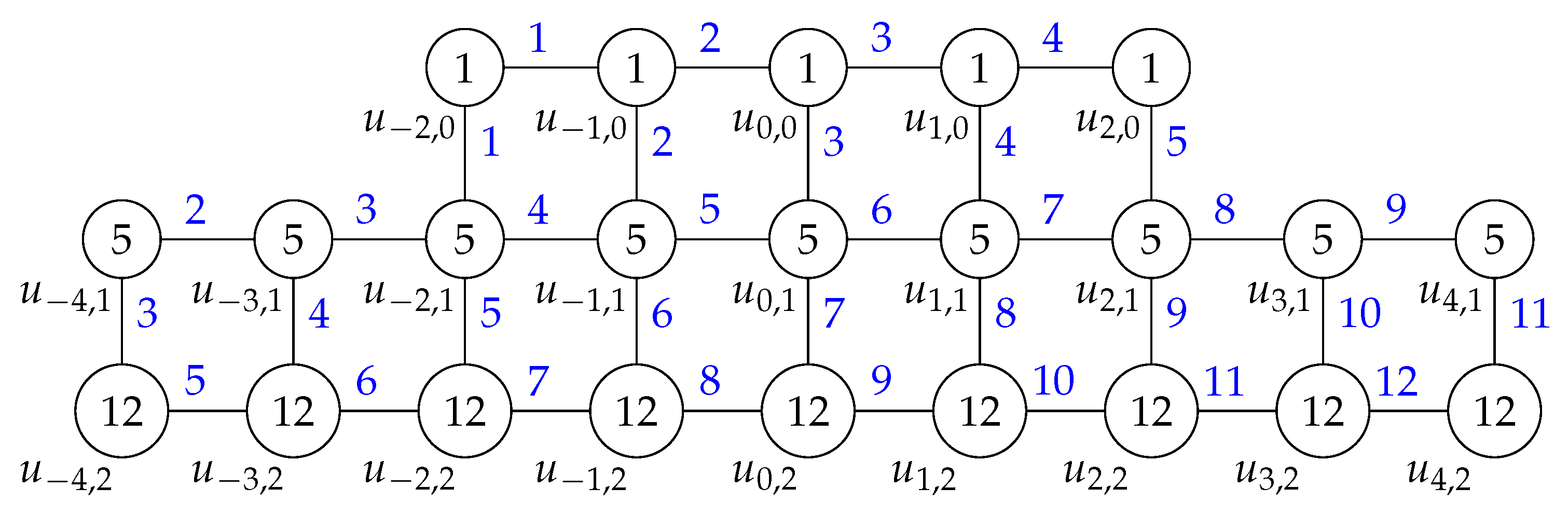
2.1. Generalized Arithmetic Staircase Graph
- (i)
- CaseThe vertex and edge labels are given as follows
vertex and edge label i and j - (ii)
- CaseThe vertex labels are
and the edge labels arevertex label i and j edge label , . From the labeling , it is easy to check that the weights of ’s edges constitute numbers from 3 up to . Thus, we complete the proof.
- (i)
- CaseThe vertex and edge labels are
vertex and edge label i and j . - (ii)
- CaseWe label the vertices as follows
and for the edges, we give labels in the following wayvertex label i and j
with .edge label , Based on the definition of the labeling , the edge weights of vary from 3 up to .
- (i)
- CaseThe vertex and edge labels are
vertex and edge label i and j - (ii)
- CaseThe vertices are labeled in the following way
and the edge labels are as followsvertex label i and j
withedge label , With respect to the labeling , the weights of ’s edges are varying from 3 up to .
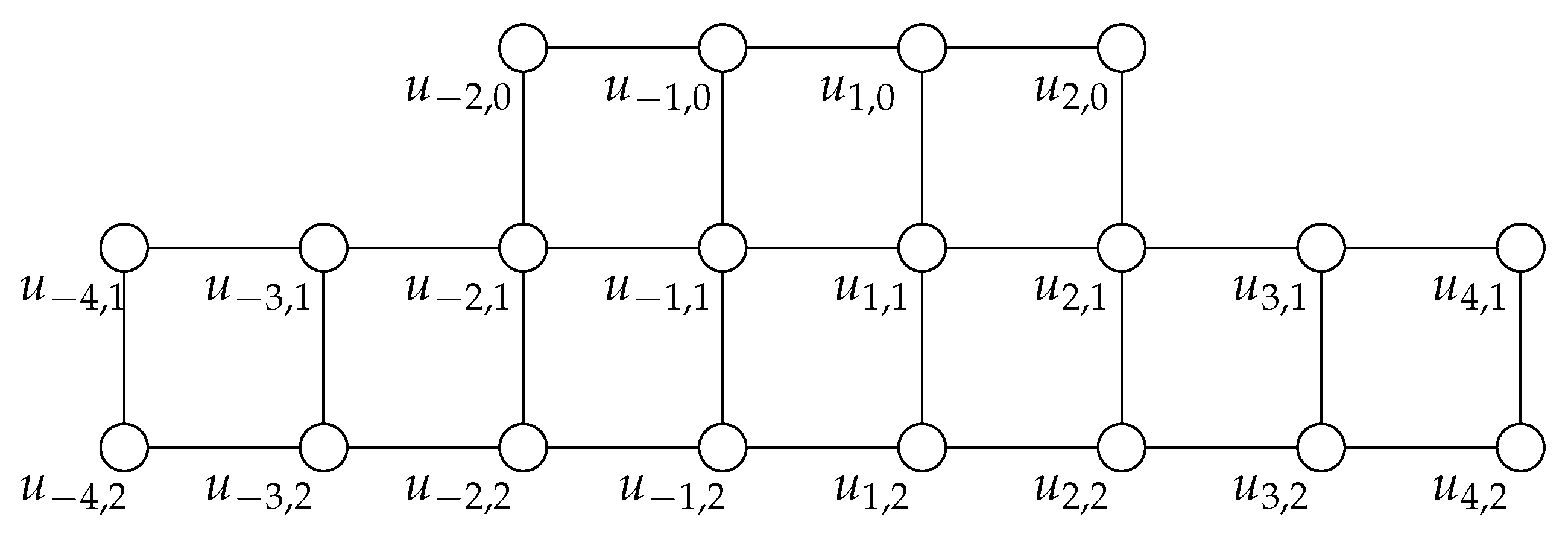
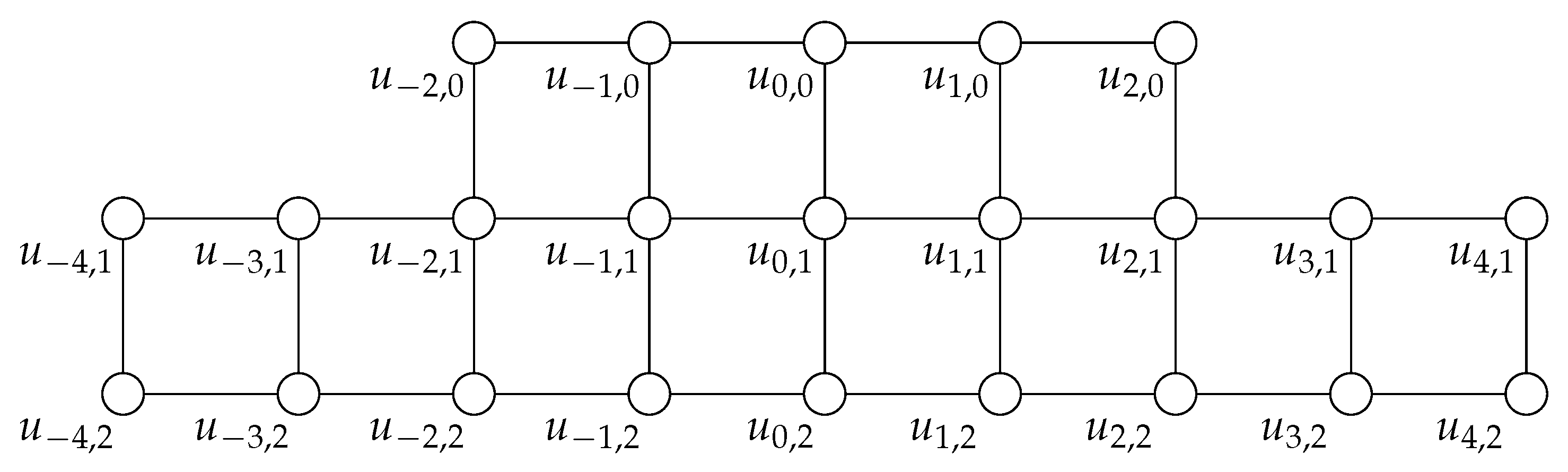
2.2. Generalized Arithmetic Double-Staircase Graph
| edge | i and j |
| . | |
| edge | i and j |
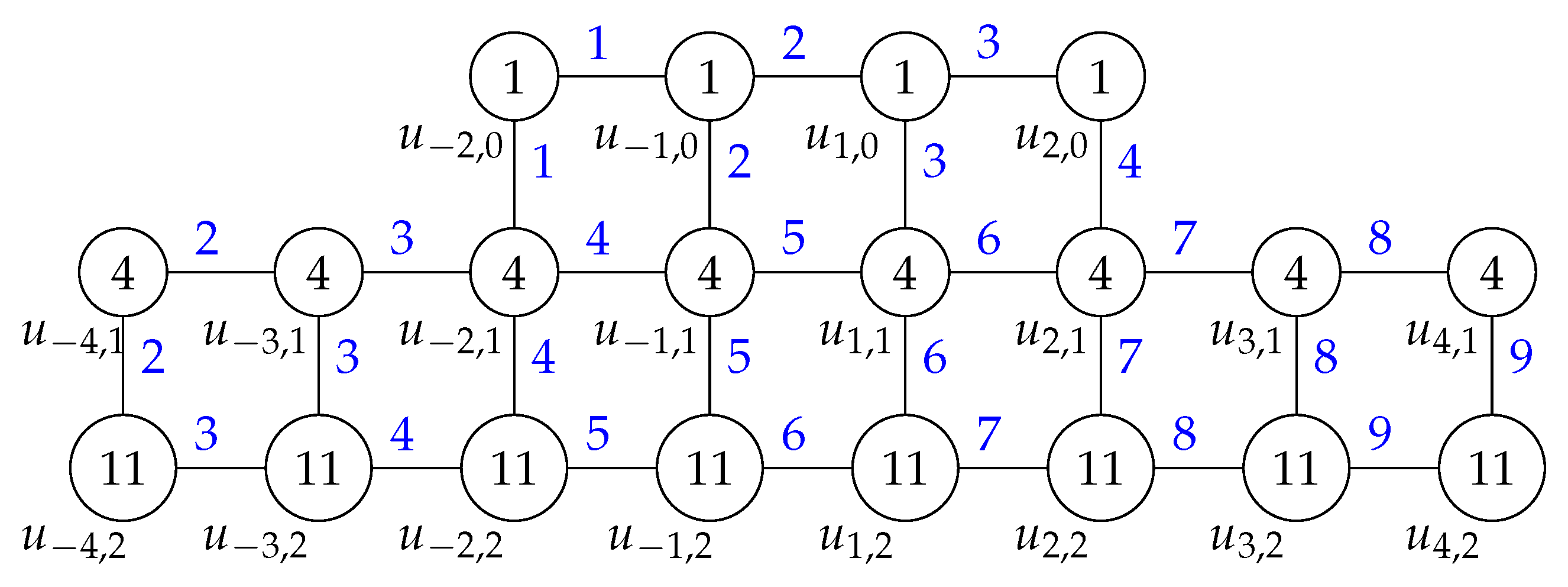
- (i)
- CaseThe labels of the vertices and the edges are
vertex and edge label i and j - (ii)
- CaseThe vertex labels are
vertex label i and j . The edge labels are
with . With respect to the labeling , it is easy to see that all edges in have different weights.edge label
- (i)
- CaseFor a odd, the vertices and the edges are labeled in the following manner:
vertex and edge label i and j For a even, the labels of the vertices and the edges arevertex and edge label i and j - (ii)
- CaseFor a odd, the vertex labels are
vertex label i and j For a even, the vertex labels arevertex label i and j For a odd, the edge labels are as follows
with .edge label For a even, the edge labels are
with .edge label
- (i)
- CaseFor a odd, the vertex and edge labels are
vertex and edge label i and j For a even, the labels of the vertices and edges arevertex and edge label i and j - (ii)
- CaseFor a odd, the vertices are labeled as the following
vertex label i and j For a even, the vertex labels are given as followsvertex label i and j For a odd, the edge labels are as follows
with .edge label For a even, the edge labels are
with .edge label
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Juan, J.S.-T.; Chen, Y.-C.; Lin, C.-H.; Chen, S.-C. Efficient Approaches to the Mixture Distance Problem. Algorithms 2020, 13, 314. [Google Scholar] [CrossRef]
- Cherkashin, D.; Kulikov, A.; Raigorodskii, A. On the Chromatic Numbers of Small-Dimensional Euclidean Spaces. Discret. Appl. Math. 2018, 243, 125–131. [Google Scholar] [CrossRef]
- Jäntschi, L. The Eigenproblem Translated for Alignment of Molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef]
- Bobu, A.V.; Kupriyanov, A.É.; Raigorodskii, A.M. A Generalization of Kneser Graphs. Math. Notes 2020, 107, 392–403. [Google Scholar] [CrossRef]
- Jordán, C.; Murillo-Arcila, M.; Torregrosa, J.R. The STEM Methodology and Graph Theory: Some Practical Examples. Mathematics 2021, 9, 3110. [Google Scholar] [CrossRef]
- Werner, F. Graph-Theoretic Problems and Their New Applications. Mathematics 2020, 8, 445. [Google Scholar] [CrossRef]
- Angelini, P.; Eades, P.; Hong, S.-H.; Klein, K.; Kobourov, S.; Liotta, G.; Navarra, A.; Tappini, A. Graph Planarity by Replacing Cliques with Paths. Algorithms 2020, 13, 194. [Google Scholar] [CrossRef]
- Tomescu, M.A.; Jäntschi, L.; Rotaru, D.I. Figures of Graph Partitioning by Counting, Sequence and Layer Matrices. Mathematics 2021, 9, 1419. [Google Scholar] [CrossRef]
- Gallian, J.A. A Dynamic Survey of Graph Labelling. Electron. J. Comb. 2021, 1, DS6. [Google Scholar]
- Su, J.; Wang, H.; Yao, B. Matching-Type Image-Labelings of Trees. Mathematics 2021, 9, 1393. [Google Scholar] [CrossRef]
- Marr, A.; Simanjuntak, R. D-Magic Oriented Graph. Symmetry 2021, 13, 2261. [Google Scholar] [CrossRef]
- Nada, S.; Elrokh, A.; Elsakhawi, E.A.; Sabra, D.E. The Corona between Cycles and Paths. J. Egypt. Math. Soc. 2017, 25, 111–118. [Google Scholar] [CrossRef]
- Lozano, A.; Mora, M.; Seara, C. Antimagic Labelings of Caterpillars. Appl. Math. Comput. 2019, 347, 734–740. [Google Scholar]
- Simanjuntak, R.; Nadeak, T.; Yasin, F.; Wijaya, K.; Hinding, N.; Sugeng, K.A. Another Antimagic Conjecture. Symmetry 2021, 13, 2071. [Google Scholar] [CrossRef]
- Yang, H.; Siddiqui, M.K.; Ibrahim, M.; Ahmad, S.; Ahmad, A. Computing the Irregularity Strength of Planar Graphs. Mathematics 2018, 6, 150. [Google Scholar] [CrossRef]
- Bača, M.; Jendrol, S.; Miller, M.; Ryan, J. On irregular total labellings. Discrete Math. 2007, 307, 1378–1388. [Google Scholar] [CrossRef]
- Ivančo, J.; Jendrol, S. The Total Edge Irregularity Strength of Trees. Discuss. Math. Graph Theory 2006, 26, 449–456. [Google Scholar] [CrossRef]
- Jendrol, S.; Miskuf, J.; Sotak, R. Total Edge Irregularity Strength of Complete Graphs and Complete Bipartite Graphs. Discret. Math. 2010, 310, 400–407. [Google Scholar] [CrossRef]
- Ahmad, A.; Siddiqui, M.K.; Ibrahim, M.; Asif, M. On the Total Irregularity Strength of Generalized Petersen Graph. Math. Rep. 2016, 18, 197–204. [Google Scholar]
- Naeem, M.; Siddiqui, M.K. Total Irregularity Strength of Isomorphic Copies of Generalized Petersen Graph. Discret. Math. Algorithms Appl. 2017, 9, 1750071. [Google Scholar] [CrossRef]
- Ahmad, A.; Bača, M.; Bashir, Y.; Siddiqui, M.K. Total Edge Irregularity Strength of Strong Product of Two Paths. Ars Combinatoria 2012, 106, 449–459. [Google Scholar]
- Pfender, F. Total Edge Irregularity Strength of Large Graphs. Discrete Math. 2012, 312, 229–237. [Google Scholar] [CrossRef][Green Version]
- Al-Mushayt, O.; Ahmad, A.; Siddiqui, M.K. On the Total Edge Irregularity Strength of Hexagonal Grid Graphs. Australas. J. Comb. 2012, 53, 263–271. [Google Scholar]
- Rajasingh, I.; Arockiamary, S.T. Total Edge Irregularity Strength of Series Parallel Graphs. Int. J. Pure Appl. Math. 2015, 99, 11–21. [Google Scholar] [CrossRef][Green Version]
- Ramdani, R.; Salman, A.N.M. On the Total Irregularity Strength of Some Cartesian Product Graphs. AKCE Int. J. Graphs Comb. 2013, 10, 199–209. [Google Scholar]
- Bača, M.; Siddiqui, M.K. Total Edge Irregularity Strength of Generalized Prism. Appl. Math. Comput. 2014, 235, 168–173. [Google Scholar] [CrossRef]
- Rosyida, I.; Indriati, D. Computing Total Edge Irregularity Strength of Some n-Uniform Cactus Chain Graphs and Related Chain Graphs. Indones. J. Comb. 2020, 4, 53–75. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Afzal, D.; Faisal, M.R. Total Edge Irregularity Strength of Accordion Graphs. J. Comb. Optim. 2017, 34, 534–544. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Ahmad, A.; Nadeem, M.F.; Bashir, Y. Total Edge Irregularity Strength of the Disjoint Union of Sun Graphs. Int. J. Math. Soft Comput. 2013, 3, 21–27. [Google Scholar] [CrossRef]
- Susanti, Y.; Puspitasari, Y.I.; Khotimah, H. On Total Edge Irregularity Strength of Staircase Graphs and Related Graphs. Iran. J. Math. Sci. Inform. 2020, 15, 1–13. [Google Scholar] [CrossRef]
- Susanti, Y.; Haq, M.A. On the Total Edge Irregularity Strength of Odd and Even Staircase Graphs. Preprints 2022, 2022080259. [Google Scholar] [CrossRef]

| a | b | n | s | a | b | n | s |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 1 | 1 | 4 | 9 | 200 | 150 |
| 1 | 3 | 3 | 2 | 7 | 4 | 200 | 163 |
| 1 | 3 | 100 | 82 | 10 | 11 | 1225 | 1000 |
| 1 | 5 | 120 | 98 | 15 | 15 | 1300 | 1061 |
| 2 | 3 | 130 | 106 | 20 | 20 | 2450 | 2000 |
| 2 | 7 | 135 | 110 | 50 | 23 | 6125 | 5001 |
| 3 | 3 | 2 | 2 | 100 | 100 | 12250 | 10,002 |
| 3 | 3 | 150 | 122 | 200 | 1000 | 14,600 | 11,921 |
| 4 | 2 | 1 | 1 | 1000 | 1400 | 15,000 | 12,247 |
| 4 | 2 | 2 | 1 | 10,000 | 2000 | 1,000,000 | 816,470 |
| a | b | n | t | a | b | n | t |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 3 | 2 | 20 | 50 | 3700 | 3021 |
| 2 | 5 | 5 | 4 | 20 | 100 | 3700 | 3021 |
| 3 | 4 | 2 | 2 | 50 | 60 | 7000 | 5715 |
| 4 | 2 | 2 | 1 | 60 | 4 | 1000 | 815 |
| 4 | 2 | 20 | 16 | 80 | 40 | 500 | 408 |
| 4 | 9 | 200 | 163 | 100 | 100 | 12,250 | 10,002 |
| 7 | 4 | 200 | 163 | 200 | 500 | 14,600 | 11,921 |
| 10 | 10 | 135 | 110 | 2000 | 2000 | 1000 | 816 |
| 10 | 11 | 1225 | 1000 | 2000 | 5000 | 1000 | 816 |
| 15 | 15 | 1300 | 1061 | 10,000 | 2000 | 1,000,000 | 816,496 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Susanti, Y.; Wahyuni, S.; Sutjijana, A.; Sutopo, S.; Ernanto, I. Generalized Arithmetic Staircase Graphs and Their Total Edge Irregularity Strengths. Symmetry 2022, 14, 1853. https://doi.org/10.3390/sym14091853
Susanti Y, Wahyuni S, Sutjijana A, Sutopo S, Ernanto I. Generalized Arithmetic Staircase Graphs and Their Total Edge Irregularity Strengths. Symmetry. 2022; 14(9):1853. https://doi.org/10.3390/sym14091853
Chicago/Turabian StyleSusanti, Yeni, Sri Wahyuni, Aluysius Sutjijana, Sutopo Sutopo, and Iwan Ernanto. 2022. "Generalized Arithmetic Staircase Graphs and Their Total Edge Irregularity Strengths" Symmetry 14, no. 9: 1853. https://doi.org/10.3390/sym14091853
APA StyleSusanti, Y., Wahyuni, S., Sutjijana, A., Sutopo, S., & Ernanto, I. (2022). Generalized Arithmetic Staircase Graphs and Their Total Edge Irregularity Strengths. Symmetry, 14(9), 1853. https://doi.org/10.3390/sym14091853









