Abstract
In this article, we apply the double ARA–Sumudu transformation (DARA-ST) to the nonlocal fractional Caputo derivative operator. We achieve interesting results and implement them to solve certain classes of fractional partial differential equations (FPDEs). Several physical applications are discussed and analyzed, such as telegraph, Klein–Gordon and Fokker–Planck equations. The new technique with DARA-ST is efficient and accurate in examining exact solutions of FPDEs. In order to show the applicability of the presented method, some numerical examples and figures are illustrated. A symmetry analysis is used to verify the results.
1. Introduction
The fractional calculus generalizes the operations of differentiation and integration to noninteger orders. The fractional calculus has become an important tool for the study of some physical phenomena, engineering and science, such as electromagnetics, viscoelasticity, fluid mechanics, electrochemistry, biological population models, optics and signal processing. Furthermore, fractional calculus processes have become one of the most useful approaches in a variety of applied sciences to deal with certain properties of (long) memory effects. There are many definitions of fractional derivatives, such as Riemann–Liouville, Caputo, Caputo–Fabrizio, Atangana–Baleanu, conformable and the generalized fractional derivative [1,2,3,4,5,6].
Fractional partial differential equations appear in various applications of science, such as chemistry, physics, engineering and mathematics, which is why researchers have established many techniques for solving such equations such as the homotopy perturbation method, variation iteration method, Adomian decomposition method, finite difference method and others [7,8,9,10,11,12,13,14,15].
A new approach in this area has recently emerged, including combining some previous methods with integral transforms, such as Laplace transform, Sumudu transform, Elzaki transform and ARA transform. These composites generated some new methods, such as Laplace decomposition method, Laplace variation iteration method, Sumudu decomposition method, Sumudu homotopy perturbation method, Elzaki variation iteration method, Elzaki project differential transform method, Elzaki homotopy perturbation method, Elzaki decomposition method, ARA residual power series method, etc. [16,17,18,19,20,21,22,23,24]. The previous methods can be implemented to solve linear and nonlinear FPDEs.
The method of double integral transforms is a hot topic in recent research, and it basically depends on applying a single transformation twice on functions of two variables or applying two different transformations on the same function. This new approach is a powerful tool for solving PDEs. Although double integral transformations, their properties and theorems are recent studies, they have attracted the interest of many mathematicians. Therefore, many researchers have studied new combinations, such as double Laplace transform, double Sumudu transform, double Elzaki transform, double Laplace-Sumudu transform and others [25,26,27,28,29,30,31,32].
Sumudu and ARA integral transformations are efficient tools for solving FDPEs [33,34,35], these transformations can be combined with other iteration methods to solve nonlinear problems.
Recently, a new combination between ARA transform and Sumudu transform was introduced in [35] and it is given by
where is a continuous function of two variables and .
In this article, we implement DARA-ST to solve families of FPDEs of the form
with the initial conditions (ICs)
and the boundary conditions (BCs)
where and are real constants, and are the fractional Caputo’s derivatives with respect to and , respectively, is a linear operator and is the source function.
The main motivation of the present study is to expand the applications of DARA-ST by using it to solve FPDEs. We show the efficiency of the proposed method by applying the DARA-ST to several interesting applications to obtain the exact solutions and analyze the results. The novelty of this work arises from the establishment of a new simple formula for solving PDEs of fractional orders. The simplicity and applicability of this new formula is illustrated by handling some applications, where we use the new approach to solve some important FPDEs.
This article is organized as follows: in the next two sections, we present some basic definitions and theorems related to our work. A new algorithm for solving families of FPDEs using DARA-ST is presented in Section 4. Several examples are given in Section 5 to demonstrate the proposed technique. We illustrate the numerical evaluations of the results in Section 6. Finally, our results are discussed in Section 7.
2. Sumudu and ARA Transformations
In this section, we introduce the definition of Sumudu and ARA transforms with some properties.
Definition 1
[33]. Sumudu transform of the function is defined as
Definition 2
[34]. ARA transform of order of the function is given by
and the ARA transform of the function of order one is defined as
For simplicity, let us denote by .
Theorem 1
[33]. (The sufficient condition for the existence of Sumudu transform).
If the functionis a piecewise continuous in every finite intervaland satisfies
then Sumudu transform exists for all.
Theorem 2
[34]. (The sufficient condition for the existence of ARA transform).
If the functionis a piecewise continuous in every finite intervaland satisfies
then ARA transform exists for all.
Table 1 presents the fundamental properties of ARA and Sumudu transforms.

Table 1.
ARA and Sumudu transforms for some functions.
3. Basic Definitions and Theorems of DARA-ST
In this section, we present the definition of DARA-ST of functions of two variables and the existence conditions and some basic properties of the new double transform are introduced.
Basic Definitions
Definition 3
[35]. The DARA-ST of the continuous function of two variables and is given by
provided the integral exists.
Clearly, the DARA-ST is linear, since
where and are constants.
The inverse DARA-ST is given by
Definition 4.
The Caputo derivatives of ordersandof the functionwith respect toand, respectively, are given by
Definition 5.
The Mittag-Leffler function is defined by
The single ARA transform of takes the value
The single Sumudu transform of takes the value
Definition 6.
A functiondefined onis called a function of exponential ordersandasand, ifsuch thatand, we have
Table 2 illustrates the values of DARA-ST for some basic functions.

Table 2.
DARA-ST for some functions [35].
Theorem 3
[35]. (Existence condition). Let be a continuous function on the region . If is exponential orders and , then DARA-ST of exists, for and .
Proof of Theorem 1.
The DARA-ST definition yields that
The proof is completed. □
Theorem 4
(Derivative properties) [35]. If , then
- i.
- ii.
- iii.
- iv.
- v.
Theorem 5
[35]. (Convolution theorem).
Ifand, then
where
4. Algorithm of DARA-ST Method
In this section, we present the technique of using DARA-ST to solve families of FPDEs. In order to achieve our goal, we have to calculate DARA-ST for the nonlocal Caputo fractional derivative in the following lemma.
4.1. DARA-ST of Fractional Derivatives
Lemma 1.
The DARA-ST for Caputo fractional derivatives can expressed as
- i.
- ii.
Proof of Lemma 1.
i. Applying DARA-ST on , we obtain
from the definition of the convolution, we have
Using the convolution property of ARA transform in Table 1, we obtain
Applying the derivative property of ARA transform in Table 1, we obtain
After simple computations, we obtain
ii. Applying DARA-ST on , we obtain
from the definition of the convolutions, we have
Using the convolution property of Sumudu transform in Table 1, we obtain
Applying the derivative property of Sumudu transform in Table 1, we obtain
After simple computations, we obtain
□.
4.2. Solving FPDEs by DARA-ST
In this section, we apply DARA-ST to obtain solutions of some FPDEs. We consider the initial boundary value problems (1)–(3). To obtain the solution by the new approach, we apply DARA-ST on both sides of Equation (1), to obtain
which implies
Furthermore, we apply the single ARA transform to the ICs (3), and the single Sumudu transform to the BCs (2), to obtain
Simplifying Equation (4), and substituting the values in Equations (5) and (6), we have
Running the inverse DARA-ST, on both sides of Equation (7), we obtain
which is the solution of the target problem.
5. Illustrative Examples
In this section, we introduce some famous PDEs in mathematical physics such as Reaction–diffusion, advection–diffusion, telegraph equation, wave equation, Klein–Gordon and Fokker–Planck, we apply the new double transform on these equations and use it to obtain the solution of these problems and we implement the obtained formula in Equation (8) to solve FPDEs, to handle these problems using the new approach. The main goal here is to illustrate the applicability and ease of use of the new double transform.
5.1. Fractional Reaction–Diffusion Equation
Consider the fractional reaction–diffusion equation
with the IC
and the BCs
Applying the single ARA transform on in Equation (10), we obtain
Applying the single Sumudu transform on and in Equation (11), we obtain
Substituting , , , and the functions in the general formula in Equation (8), after simple computations, we obtain
Example 1.
Consider the heat diffusion equation
with the IC
and the BCs
Solution.
Putting , , and in Equation (12), we obtain the solution of (13) as follows
Figure 1 represent the solution of the heat diffusion Equation (13) with the IC (14) and the BCs (15).
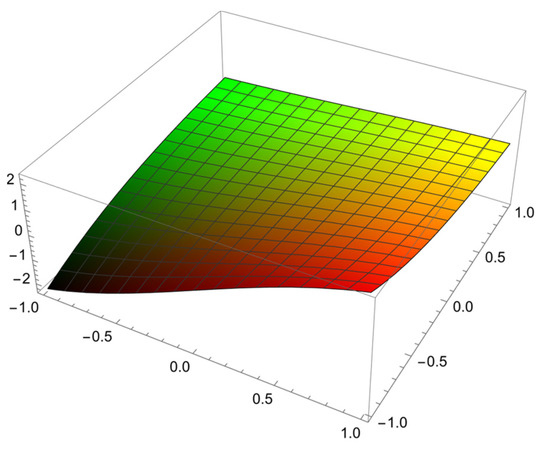
Figure 1.
The surface graph of the solution for the heat diffusion equation at for the problem in Example 1.
5.2. Fractional Advection–Diffusion Equation
Consider the fractional advection–diffusion equation
with the IC
and the BCs
Applying the single ARA transform on in Equation (17), we obtain
Applying the single Sumudu transform on and in Equation (18), we obtain
Substituting , , , and the functions , , in the general formula in Equation (8) and after simple computations, we obtain
Example 2.
Consider the fractional advection–diffusion equation
with the IC
and the BCs
Solution.
Putting , and in Equation (19), we obtain the solution of (20) as follows
Figure 2 represent the solution of the advection–diffusion Equation (20) with the IC (21) and the BCs (22).
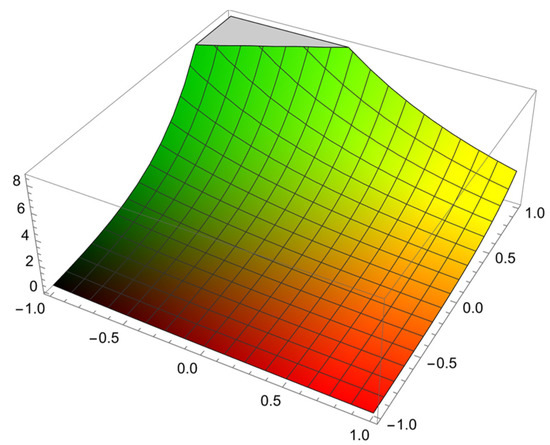
Figure 2.
The surface graph of the solution for the advection–diffusion equation at for the problem in Example 2.
5.3. Fractional Telegraph Equation
Consider the fractional telegraph equation
with the ICs
and the BCs
Applying the single ARA transform on and in Equation (24), we obtain
Applying the single Sumudu transform on and in Equation (25), we obtain
Substituting , , , and the functions , , , in the general formula in Equation (8) and after simple computations, we obtain
Example 3.
Consider the telegraph equation
with the ICs
and the BCs
Solution.
Putting , , , and in Equation (26), we obtain the solution of (27) as follows
Figure 3 represent the solution of the telegraph Equation (27) with the ICs (28) and the BCs (29).
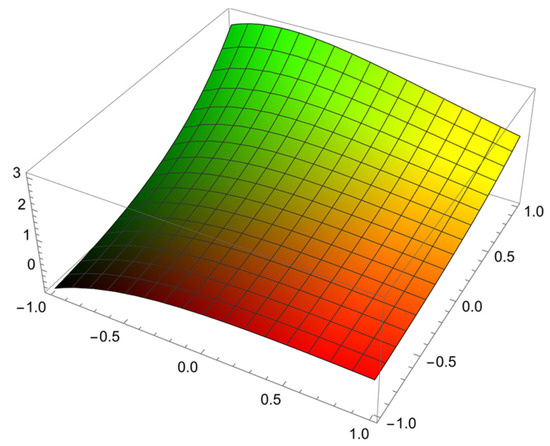
Figure 3.
The surface graph of the solution for the telegraph equation at for the problem in Example 3.
5.4. Fractional Wave Equation
Consider the fractional wave equation
with the ICs
and the BCs
Applying the single ARA transform on and in Equation (31), we obtain
Applying the single Sumudu transform on and in Equation (32), we obtain
Substituting , , , , and the functions , , , in the general formula in Equation (8) and after simple computations, we obtain
5.5. Fractional Klein–Gordon Equation
Consider the fractional Klein–Gordon equation
with the ICs
and the BCs
Applying the single ARA transform on and in Equation (35), we obtain
Applying the single Sumudu transform on and in Equation (36), we obtain
Substituting , , and the functions , , , in the general formula in Equation (8) and after simple computations, we obtain
Example 4.
Consider the fractional Klein–Gordon equation
with the ICs
and the BCs
Solution.
Putting 2, , , , , in Equation (37), we obtain
Figure 4 represent the solution of the Klein–Gordon (38) with the ICs (39) and the BCs (40).
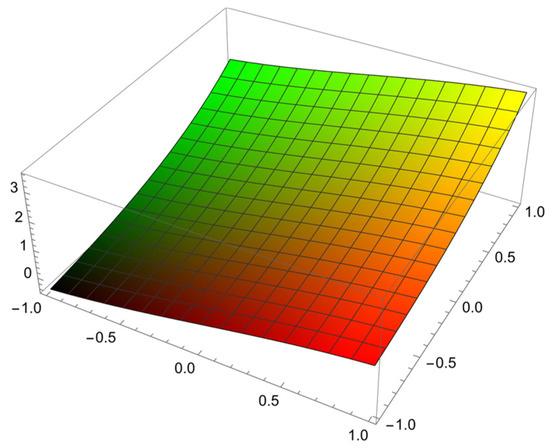
Figure 4.
The surface graph of the solution for the Klein–Gordon equation at for the problem in Example 4.
5.6. Fractional Fokker–Planck Equation
Consider the fractional Fokker–Planck equation
with the IC
and the BCs
Applying the single ARA transform on in Equation (43), we obtain
Applying the single Sumudu transform on and in Equation (44), we obtain
Substituting , , 1, and the functions , , in the general formula in Equation (8) and after simple computations, we obtain
Example 5.
Consider the fractional Fokker–Planck equation
with the IC
and the BCs
Solution.
Putting , , in Equation (45), we obtain the solution of (46) as follows
Figure 5 represent the solution of the Fokker–Planck (46) with the IC (47) and the BCs (48).
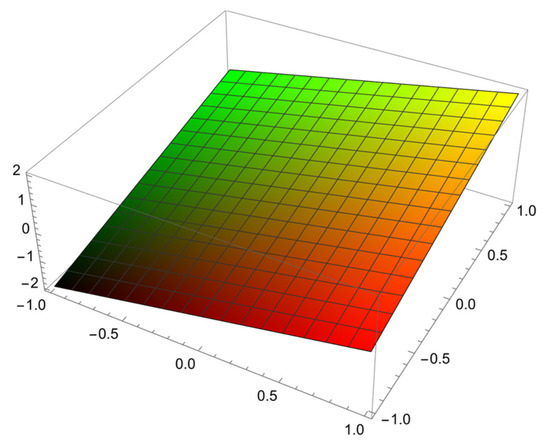
Figure 5.
The surface graph of the solution for the Fokker–Planck equation at for the problem in Example 5.
6. Numerical Simulations
In this section, we illustrate the numerical evaluation of the solutions obtained by solving the given FPDEs. We also discuss the numerical behavior of the results when solving FPDEs, then we compare it with the solution of the equation of integer order.
The solutions of Examples 1, 2 and 5 are simply computed when . We examine the numerical solutions of different values of and . As a result, we notice that, with choosing different values of , the obtained fractional solutions are in coordination with the closed form of the solution when , as illustrated in Figure 6. Moreover, it clearly implies that as approaches 1, the obtained solutions of the FPDEs approach the exact solutions obtained in the integer case.
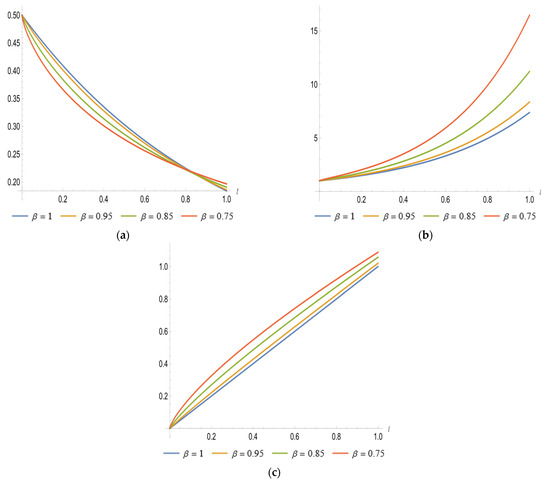
Figure 6.
(a) Plots of the exact solution when and different values of and of Examples 1. (b) Plots of the exact solution when and different values of and of Examples 2. (c) Plots of the exact solution when and different values of and of Examples 5.
The solution of Example 3 when and the solution of Example 4 when are simply computed. We examine the numerical solutions of different values of in Example 3 and in Example 4. As a result, we note that, with choosing different values of and , the obtained fractional solutions are in coordination with the closed forms of the solutions when and , as illustrated in Figure 7.
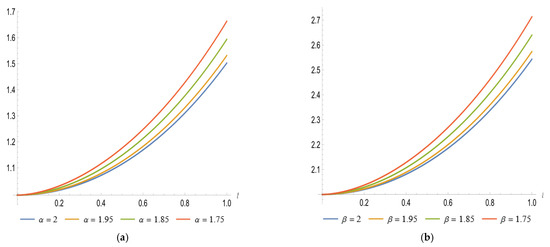
Figure 7.
(a) Plots of the exact solution when and different values of and of Example 3. (b) Plots of the exact solution when and different values of and of Example 4.
Moreover, we mention that as and approach the close integer orders, the obtained solutions of the FPDEs approach the exact solutions in the integer case.
7. Conclusions
In this research, DARA-ST is applied to the Caputo fractional derivative to obtain a new interesting formula, that is implemented to solve families of FPDEs. We have presented a new method to obtain exact solutions of these equations. We show the reliability and efficiency of the proposed method by presenting some interesting physical applications. In the future, we will pair DARA-ST with some iteration methods to solve nonlinear FPDEs, such as nonlinear telegraph equation, nonlinear wave equation, nonlinear Klein–Gordon and nonlinear Fokker–Planck. In addition, researchers can use new definitions of FC such as the generalized fractional derivative and others to search and obtain new results on transformations.
Author Contributions
Data curation, R.S., A.B., R.K. and A.Q.; Formal analysis, A.B., R.S., A.Q. and R.K.; Investigation, A.B., R.S., A.Q. and R.K.; Methodology, A.B., R.S., A.Q. and R.K.; Project administration, A.Q., R.S., R.K. and A.B.; Resources, A.B., R.S., R.K. and A.Q.; Writing—Original draft, A.Q., R.S., R.K. and A.B.; Writing—Review and editing, A.Q., A.B., R.S. and R.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their gratitude to the dear referees, who wish to remain anonymous, and the editor for their helpful suggestions, which improved the final version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Agarwal, P.; Agarwal, R.P.; Ruzhansky, M. Special Functions and Analysis of Differential Equations; Chapman and Hall: London, UK; CRC: New York, NY, USA, 2020. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Algahtani, O.J.J. Comparing the Atangana–Baleanu and Caputo–Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals. Nonlinear Dyn. Complex. 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abu-Shady, M.; Kaabar, M.K. A Novel Computational Tool for the Fractional-Order Special Functions Arising from Modeling Scientific Phenomena via Abu-Shady–Kaabar Fractional Derivative. Comput. Math. Methods Med. 2022, 2022, 2138775. [Google Scholar] [CrossRef] [PubMed]
- Constanda, C. Solution Techniques for Elementary Partial Differential Equations; Chapman and Hall: London, UK; CRC: New York, NY, USA, 2002. [Google Scholar]
- Tyn Myint, U. Partial Differential Equations of Mathematical Physics; Courier Dover Publications: New York, NY, USA, 1980. [Google Scholar]
- Qin, H.; Li, D.; Zhang, Z. A novel scheme to capture the initial dramatic evolutions of nonlinear subdiffusion equations. J. Sci. Comput. 2021, 89, 65. [Google Scholar] [CrossRef]
- Ziane, D.; Hamdi Cherif, M. A new analytical solution of Klein–Gordon equation with local fractional derivative. Asian-Eur. J Math. 2021, 14, 2150029. [Google Scholar] [CrossRef]
- Li, D.; Sun, W.; Wu, C. A novel numerical approach to time-fractional parabolic equations with nonsmooth solutions. Numer. Math. Theor. Meth. Appl. 2021, 14, 355–376–376. [Google Scholar]
- Burqan, A.; Saadeh, R.; Qazza, A. ARA-Residual Power Series Method for Solving Partial Fractional Differential Equations. Alex. Eng. J. 2022, 62, 47–62. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Agarwal, R.P.; Shah, R.; Ababneh, O.Y.; Weera, W. A Reliable Way to Deal with Fractional-Order Equations That Describe the Unsteady Flow of a Polytropic Gas. Mathematics 2022, 10, 2293. [Google Scholar] [CrossRef]
- Zhou, S.-S.; Areshi, M.; Agarwal, P.; Shah, N.A.; Chung, J.D.; Nonlaopon, K. Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations. Symmetry 2021, 13, 939. [Google Scholar] [CrossRef]
- Sunarto, A.; Agarwal, P.; Chew, J.V.L.; Sulaiman, J. Approximation Solution of the Fractional Parabolic Partial Differential Equation by the Half-Sweep and Preconditioned Relaxation. Symmetry 2021, 13, 1005. [Google Scholar] [CrossRef]
- Widder, V. The Laplace Transform; Princeton University Press: Princeton, NJ, USA, 1941. [Google Scholar]
- Bochner, S.; Chandrasekharan, K. Fourier Transforms; Princeton University Press: London, UK, 1949. [Google Scholar]
- Qazza, A.; Burqan, A.; Saadeh, R. A New Attractive Method in Solving Families of Fractional Differential Equations by a New Transform. Mathematics 2021, 9, 3039. [Google Scholar] [CrossRef]
- Elzaki, T.M. The new integral transform “Elzaki transform”. Glob. J. Pure Appl. Math. 2011, 7, 57. [Google Scholar]
- Atangana, A.; Kiliçman, A. A novel integral operator transform and its application to some FODE and FPDE with some kind of singularities. Math. Probl. Eng. 2013, 2013, 531984. [Google Scholar] [CrossRef]
- Srivastava, H.; Luo, M.; Raina, R. A new integral transform and its applications. Acta Math. Sci. 2015, 35B, 1386. [Google Scholar] [CrossRef]
- Barnes, B. Polynomial integral transform for solving differential Equations. Eur. J. Pure Appl. Math. 2016, 9, 140. [Google Scholar]
- Kiliçman, A.; Eltayeb, H. Some Remarks on the Sumudu and Laplace Transforms and Applications to Differential Equations. Int. Sch. Res. Not. 2012, 2012, 13. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Karaballi, A.A. Sumudu transform fundamental properties investigations and applications. Int. J. Stoch. Anal. 2006, 2006, 231. [Google Scholar] [CrossRef]
- Debnath, L. The double Laplace transforms and their properties with applications to functional, integral and partial differential equations. Int. J. Appl. Comput. Math. 2016, 2, 223. [Google Scholar] [CrossRef]
- Dhunde, R.R.; Waghmare, G.L. Double Laplace transform method in mathematical physics. Int. J. Eng. Res. Technol. 2017, 7, 14. [Google Scholar]
- Alfaqeih, S.; Misirli, E. On double Shehu transform and its properties with applications. Int. J. Anal. Appl. 2020, 18, 381. [Google Scholar]
- Ganie, J.A.; Ahmad, A.; Jain, R. Basic analogue of double Sumudu transform and its applicability in population dynamics. Asian J. Math. Stat. 2018, 11, 12. [Google Scholar] [CrossRef][Green Version]
- Idrees, M.I.; Ahmed, Z.; Awais, M.; Perveen, Z. On the convergence of double Elzaki transform. Int. J. Adv. Appl. Sci. 2018, 5, 19. [Google Scholar] [CrossRef]
- Ahmed, S.; Elzaki, T.; Elbadri, M.; Mohamed, M.Z. Solution of partial differential equations by new double integral transform (Laplace—Sumudu transform). Ain Shams Eng. J. 2021, 12, 4045. [Google Scholar] [CrossRef]
- Ahmed, S.A.; Qazza, A.; Saadeh, R. Exact Solutions of Nonlinear Partial Differential Equations via the New Double Integral Transform Combined with Iterative Method. Axioms 2022, 11, 247. [Google Scholar] [CrossRef]
- Kiliçman, A.; Gadain, H.E. An application of double Laplace transform and double Sumudu transform. Lobachevskii J. Math. 2009, 30, 214–223. [Google Scholar] [CrossRef]
- Watugala, G.K. Sumudu transform: A new integral transform to solve differential equations and control engineering problems. Int. J. Math. Edu. Sci. Technol. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. A new integral transform: ARA transform and its properties and applications. Symmetry 2020, 12, 925. [Google Scholar] [CrossRef]
- Saadeh, R.; Qazza, A.; Burqan, A. On the Double ARA-Sumudu Transform with Applications. Mathematics 2022, 10, 2581. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).