Abstract
The energy and mass transition through Newtonian hybrid nanofluid flow comprised of copper Cu and aluminum oxide (Al2O3) nanoparticles (nps) over an extended surface has been reported. The thermal and velocity slip conditions are also considered. Such a type of physical problems mostly occurs in symmetrical phenomena and are applicable in physics, engineering, applied mathematics, and computer science. For desired outputs, the fluid flow has been studied under the consequences of the Darcy effect, thermophoresis diffusion and Brownian motion, heat absorption, viscous dissipation, and thermal radiation. An inclined magnetic field is applied to fluid flow to regulate the flow stream. Hybrid nanofluid is created by the dispensation of Cu and Al2O3 nps in the base fluid (water). For this purpose, the flow dynamics have been designed as a system of nonlinear PDEs, which are simplified to a system of dimensionless ODEs through resemblance substitution. The parametric continuation method is used to resolve the obtained set of dimensionless differential equations. It has been noticed that the consequences of heat absorption and thermal radiation boost the energy transmission rate; however, the effect of suction constraint and Darcy–Forchhemier significantly diminished the heat transference rate of hybrid nanofluids. Furthermore, the dispersion of Cu and Al2O3 nps in the base fluid remarkably magnifies the velocity and energy transmission rate.
1. Introduction
The analysis of the energy and mass communication through hybrid nanoliquid (hnf) across a vertical stretching surface has several implementations in various fields of biomedicine and industries [1]. Hamad et al. [2] used a mathematical approach to investigate the remarkable features of 2D Walters-B nanoliquid flows across a vertically stretching surface in which the substrate contains motile microbes. It was established that the viscoelastic component diminishes the mobility of the nanoliquid flow, but the velocity ratio factor greatly elevates the acceleration of the fluid. Wakif [3] developed a new method for estimating the steady hydromagnetic radiative flows of viscous fluids across a stretchy sheet that is non-uniformly elongating and has a nonhomogeneous thickness. Gangadhar et al. [4] presented a numerical analysis to examine the steady, 2D flow and heat transmission over an elongating sheet with varying suction/injection effects in the presence of Newtonian heating and a magnetic field. Algehyne et al. [5] studied the bioconvection that results from the micropolar fluid flow containing movable nanomaterials and microbes along a permeable vertical moving substrate. It was found that the energy transformation curve greatly improves when the Eckert number, Hartmann number, and heat absorption/generation. Gautam et al. [6] scrutinized the effects of binary reaction on the MHD 2D Williamson nano liquid’s flow on an extending sheet with varying thickness immersed in a Darcy permeable medium. It was found that the rising trend of reaction rate variables rises the surface heat flux while lessening the mass flux. Rasool et al. [7] performed a numerical evaluation of MHD nanofluid flows in a Darcy permeable medium with a Riga pattern implanted diagonally. It was noted that the frictional component at the stretching sheet is strengthened by Lorentz’s forces and Darcy–Forchheimer’s. Zaib et al. [8] inspected the effects of entropy formation on Williamson nano liquid’s stagnation point flow across a movable sheet. Asjad et al. [9] discussed the continuous flow of a hybrid nanoliquid that conducts an electric effect through a thin, impermeable stretchy sheet. The velocity curve has been found to improve when velocity power index and Hall current are present while decreasing when nanoparticle quantities and sheet thickness are present. Algehyne et al. [10] analyzed a critical viewpoint on the kinematics of water and aluminum based nanofluid across slippery circular geometries (for example, a hemispheric) related to the linear straining movement of the asymmetrical boundaries.
Relative to the traditional fluids employed for energy transference, such as water, ethylene glycol, oil, and nanofluids, hybrid nanocomposites operate well in terms of heat transport. Hybrid nanoliquids are effective at freezing areas with a vast range of temperatures and a variety of thermal activities. Hybrid nanofluids are a novel type of nanomaterials that are often created by disseminating two distinct forms of nps in conventional fluids [11,12,13]. Applications of hybrid nanocomposites in the fields of refrigeration, ventilation, heating, air conditioning, heat pipes, heat exchangers, coolants in metalworking and production, microelectronics, the auto sector, turbine cooling, transistor cooling, nuclear device, biomedicine, aircraft, and defense are among the foremost domains of study [14,15,16]. Reddy et al. [17,18] regulated the pulsatile hybrid nanoliquid circulation in a laterally porous irregular tube. It was found that as the ratios of body force variables are increased, the blood flow drops. Additionally, the blood circulation is faster for CuO nanoliquid than hybrid nanoliquid; nevertheless, for a smaller valuation of the frequency factor, the situation is precisely the contrary. Sun et al. [19] have developed the parametric analysis for the flow of the Darcy–Forchheimer CuO hybrid nanoliquid over a porous rotational disc using the parametric continuation method. Hybrid nanoliquid including copper (Cu) and aluminum oxide (Al2O3) nano particulates, where the viscosity and thermal conductivity vary non-uniformly with the volume percentage [20], studied the convective flow and energy transmission of various nanofluids. With a rise in Cu nanocomposites, the streams of Cu-C2H6O (copper-ethylene glycol) base nanoliquids showed the best improvement in the heat transference rate. Al-Mubaddel et al. [21] examined a hybrid ferrofluid flow through a heated, irregular, extensible cylinder at a 3D stagnation point with the impact of slip parameters and variable diameter. Alsallami et al. [22] have performed a numerical analysis of the nanoliquid flow under the effects of thermophoresis, Brownian motion, and thermal radiation on a warmed revolving surface. It was thought that the radiation and Prandtl number impact increased the frequency of heat transfer. Shahsavar et al. [23] considered the impact of magnetic flux and the Hall effect on hybrid nanoliquid flow on a gyrating disk’s top. Their goal was to upsurge the efficiency of energy transport for use in engineering and industry. Ashraf et al. [24] used the generalized differential quadrature methodology to quantitatively investigate the peristaltic transport of magnetite Fe3O4 nanocrystals in blood-based ferrofluid.
The exploration of the electromagnetic characteristics and dynamics of electrically conducting fluids is known as magneto-fluid dynamics (MHD). These magneto fluids, which include plasmas, salt water, liquid metals, and electrolytes, are a few illustrations. Hannes Alfvén founded the concept of MHD in 1970. The core idea driving MHD is that electromagnets can cause current flow in conducting fluids that are flowing, which polarizes the flow and modifies the magnetic field [25,26,27]. Ramaiah et al. [28] discussed the consequences of energy exchange in addition to the mass phenomena of an MHD Maxwell fluid in rotating flow across a vertical stretchable sheet. It was found that a solute’s percentage in a compound depends on both the rotational constants and the activation energy. Riaz et al. [29] examined the dimensionless model of magnetic properties in a nanoliquid flow using basic symmetry when applied to a movable preheated vertical surface that is either flowing or static with the surface. Zeeshan et al. [30], Chen et al. [31], and Abbas et al. [32] investigated the MHD nanoliquids flow across two simultaneous vertical plates in a permeable media made of carbon nanotubes derived from engine oil. When relative to engine-oil MWCNTs, it is observed that the energy contour of the engine-oil SWCNTs significantly rises.
In the current investigation, we are analyzing the dynamics of Newtonian hybrid nanoliquid containing Cu and Al2O3 nanoparticles over an extending vertical surface with thermal and partial slip conditions. No such study and analysis have been found in the literature. The fluid flow has been studied under the consequences of the Darcy effect, thermophoresis diffusion and Brownian motion, heat absorption, viscous dissipation, and thermal radiation. An inclined magnetic field is applied to fluid flow to regulate the flow stream. Hybrid nanofluid is synthesized by the dispensation of Cu and Al2O3 nps in the blood. The PCM approach is used to resolve the obtained set of dimensionless differential equations.
2. Mathematical Formulation
The energy and mass transmission through two-dimension electrically conducting Darcy–Forchheimer Newtonian hybrid nanofluid flow across an extending sheet is considered. The consequences of thermal and velocity slip on the hybrid nanoliquid flow are also considered. An inclined magnetic strength is employed in the flow field as appeared in Figure 1. Here, the non-uniform inertia constraint stated as is the permeable media. The Cu and Al2O3 nps are dispersed into the base fluid for hybrid composition. and present the mass and energy of nanofluid, while and show the surrounding mass and energy. The basic equations are written as [33]:
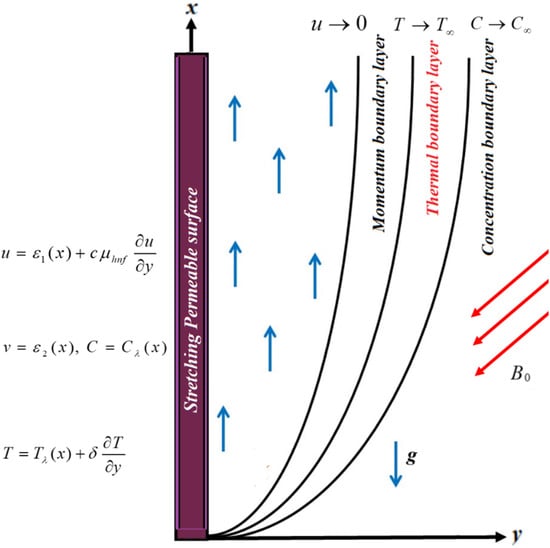
Figure 1.
The hybrid nanoliquid flow over a stretching sheet.
The u and v are the velocity terms in the x, y direction. Here, is the no-slip conditions, while , , and are the sheet stretching velocity, velocity slip, and thermal slip, respectively. and signify the initial velocity and thermal slip, and is the heat absorption constant, while is the suction/injection effect. The term in Equation (4) denotes the modified Arrhenius equation in which Ea is the activation energy, is the reaction rate, is the Boltzmann constant, and n is the fitted rate constant, which generally lies in the range .
The radiative heat flux is inscribed as [33]:
By executing Taylor’s series and disregarding the higher order term:
By putting Equation (5) in Equation (3), we have:
The initial and boundary conditions are [33]:
The experimental values of Cu, Al2O3, and blood are described in Table 1. In Table 2, the bf and hnf characterize the base fluid and hybrid nanofluid. represent the nano particulates volume fraction. is the electrical conductivity, is the heat capacitance, and is the thermal conductivity of the hybrid nanoliquid.

Table 1.
The tentative numerical values of Cu, Al2O3, and water [34].

Table 2.
The mathematical model for the hybrid nanoliquid [35].
The similarity variables are [33]:
By putting Equation (10) in Equations (1)–(4):
The transmute conditions are:
Here, M, , Tb, Sc, Nt, K, Re, Ec, Ha, and L is the magnetic term, non-dimensional coordinate, thermal radiation, Schmidt number, chemical reaction, Reynold number, Eckert number, heat source, and velocity slip, respectively, while, Gr, S, , Fr, Pr, Nb, and E are the Grashof number, injection/suction, porosity term, Forchheimer term, Brownian motion, and activation energy, respectively.
The physical interest quantities are revealed as:
where , , and are the surface heat flux, wall shear stress, and wall mass flux.
The non-dimensional form of Equation (16) is:
3. Numerical Solution
The fundamental steps involved in the PCM solution methodology, while dealing with the system of ODEs (11–13), are the following [36,37]:
- Step 1: Convert BVP to first order
By putting (18) in Equations (11)–(14), we obtain:
The transform conditions are:
- Step 2: Introducing parameter p:
- Step 3: Apply Cauchy Principal and Discretized Equations (23)–(25).
After discretization, the obtained set of equations is computed through the MATLAB code of PCM.
4. Results and Discussion
This segment assesses the physical scenario behind each table and Figure. The following observations have been noted while keeping all the parameters’ values as and .
- Velocity Profile :
Figure 2a–d revealed the outlines of fluid velocity versus the upshot of Forchhemier number Fr, magnetic field M, suction effect +S, and injection −S, respectively. Figure 2a presents the relation of velocity curve versus the Forchheimer parameter Fr for both cases, no-slip and slip conditions of the hybrid nanoliquid. The rising values of Fr lessen the velocity outline. Physically, the increment of Fr produced inertial drag force, which is a barrier to the velocity field ; hence as a result, the velocity profile decelerates. Figure 2b expresses the exhibition of velocity contour versus the magnetic constraint M. It was noted that with the rising values of M, the velocity profile declines, because the Lorentz force created due to magnetic flux resists the fluid velocity. Figure 2c,d are drafted to indicate the impact of and on the velocity outline. Both illustrate a contradictory performance versus velocity curve. The kinetic viscosity has an inverse relation with the suction/injection parameters, so the rising effect of S diminishes the viscosity of the fluid and vice versa. Furthermore, physically the suction effect also resists the fluid field; as a result, such a scenario has been observed in Figure 2c,d.
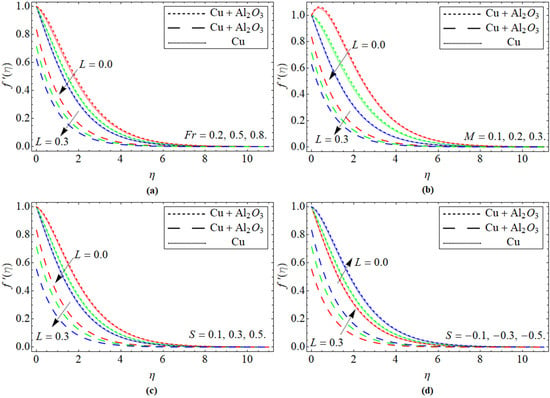
Figure 2.
Velocity profile versus the upshot of (a) Forchhemier number Fr, (b) magnetic field M, (c) suction effect +S, and (d) injection −S.
- Energy Profile :
Figure 3a–d exemplified the demonstration of energy profile versus the upshot of suction term +S, injection −S, Nt, and Nb, respectively. Figure 3a,b are drawn to display the upshot of suction and injection constraints on the energy profile . For mounting values of the energy curve is reduced, while it augments with the effects of the injunction parameter. As discussed earlier, the kinetic viscosity has an inverse relation with the suction/injection parameters, so the rising effect of S diminishes the viscosity of the fluid and vice versa. Furthermore, physically, the suction/injection effect also resists the fluid field, and that fractional force produces an additional heat, which enhances the energy contour as detected in Figure 3a,b. Figure 3c is calculated to observe the nature of Nt on the energy profile. It is noted that the energy curve boosts with the flourishing values of Nt. The temperature change occurred due to the upshot of Nt, which causes the reduction in kinetic viscosity of the fluid, and as a result, energy contour augments . Figure 3d is drawn to reveal the consequences of Nb versus the temperature outline . The molecular diffusion enhances with the rising effect of Nb, while the kinetic viscosity of fluid declines with the influence of Brownian motion, as a result, the energy contour augments .
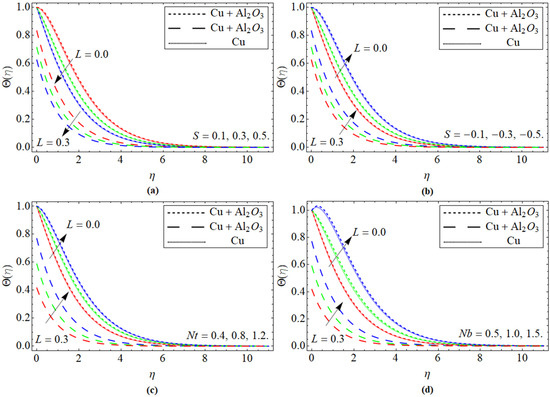
Figure 3.
Energy profile versus the upshot of (a) suction +S, (b) injection −S, (c) thermophoresis Nt, and (d) Brownian motion Nb.
Figure 4a reveals the relation of the magnetic effect M versus the energy outline . It can be realized that the growing values of M augment the . Physically, the enhancement of M fashions a resistance force (Lorentz Force), which opposes the flow path, and that resistive effect also generates heat; as a result, the energy contour boosts.
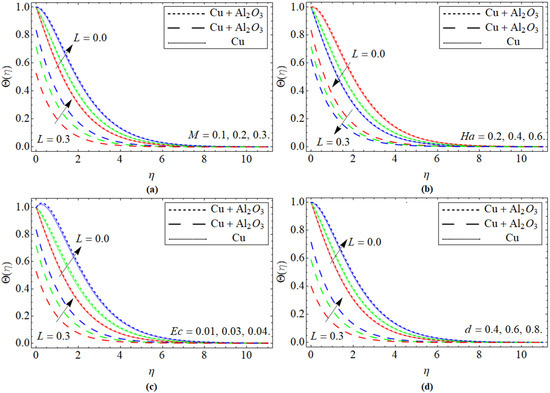
Figure 4.
Energy profile versus the upshot of (a) magnetic field, (b) heat source term, (c) Eckert number, and (d) thermal slip factor d.
Figure 4b illustrates the influence of heat source Ha on the energy outline . It is noticed that the energy contour decreases with the upshot of Ha. Physically, the improving worth of Ha suggestively rises the heat capacity of the fluid, and thus energy contour drops. Figure 4c shows the relation of energy contour versus Ec. It can be perceived that the augmentation in Ec drops the . Physically, Ec is the relation between kinetic energy and enthalpy generation; therefore, the influence of Ec diminishes the viscous fluid stresses by decoding kinetic energy to internal energy, as a result, the energy field becomes improved. The upshot of the thermal slip factor d versus is presented in Figure 4d.
- Concentration Profile:
Figure 5a–e displays the nature of the mass profile versus the upshot of Schmidt number Sc, chemical reaction Kr, Nt, Nb, and Arrhenius activation energy E, respectively. Figure 5a displays that the growing values of the number Sc weakens the concentration field. The molecular diffusion declines, while the kinetic viscosity of fluid augments with the upshot of Sc, which results in the diminution of mass profile. Figure 5b represents the nature of concentration gradients as a function versus chemical reaction. It is revealed that the cumulative trend of the chemical reaction factor lessens the concentration contour.
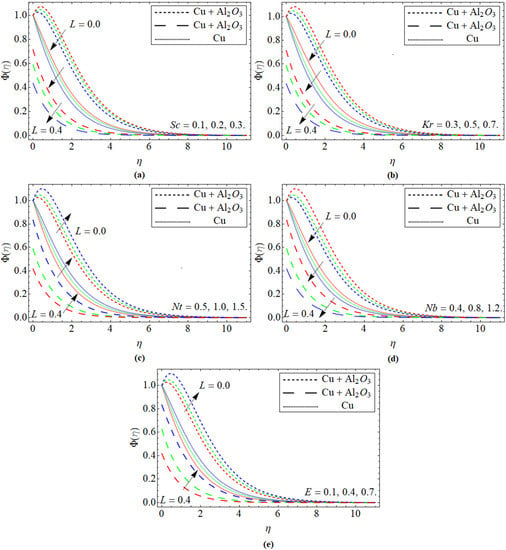
Figure 5.
Mass profile versus the upshot of (a) Schmidt number Sc, (b) chemical reaction Kr, (c) thermophoresis Nt, (d) Brownian motion Nb, and (e) activation energy E.
Figure 5c,d are drafted to elaborate on the behavior of Nt and Nb on the mass transmission profile. From Figure 5c,d, it is observed that the mass contour is enhanced due to the rising tendency of Nt, while it decreases with the influence of Nb. Figure 5e reveals that the mass curve significantly boosts with the influence of Arrhenius activation energy.
Figure 6 expresses the percentage relative valuation between nanoliquid (Cu or Al2O3) and hybrid nanoliquid (Cu + Al2O3) for both energy and velocity profiles. It can be observed that as compared to nanofluids, the hybrid nanofluid has a remarkable capability of energy transmission.
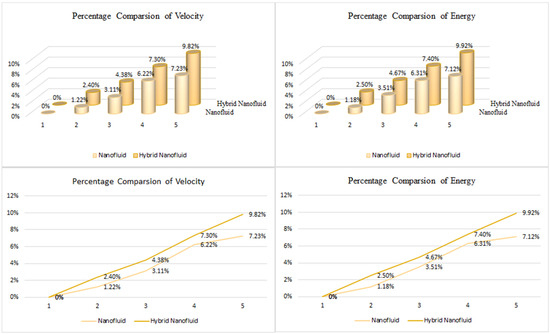
Figure 6.
Percentage comparison between nanoliquid and hybrid nanoliquid.
Table 3, Table 4 and Table 5 exhibit the relative statistical assessment between hybrid and simple nanoliquid for skin friction , Nusselt number , and Sherwood number , respectively. In both cases, slip and non-slip phenomena have been studied for analysis. It is observed from Figure 3 that the rising credit of magnetic effect and Grashof number enhances the drag force. Figure 4 reports that the flourishing values of Brownian motion and thermophoresis effect diminish the Nusselt number. On other hand, the Sherwood magnifies with the increment of Schmidt number and chemical reaction. Table 5 also presents the comparison of present outcomes with another numerical technique bv4c package for the validity purpose of the results. Both the methods show the best settlement with each other, so it can be perceived that the results are reliable and accurate. Table 6 expressed the comparative analysis of present work with the existing literature. It can be observed that the present outcomes are reliable and accurate.

Table 3.
Numerical outputs of Skin friction for slip and no-slip conditions.

Table 4.
Numerical outputs of Nusselt number for slip, , and no-slip, , conditions.

Table 5.
Comparative analysis of Sherwood number for no-slip conditions between PCM and bvp4c package.

Table 6.
Comparative analysis of present work with the existing literature.
5. Conclusions
The present analysis reported the energy and mass conversion through Newtonian hybrid nanoliquid flow consisting of Cu and Al2O3 nps over an extended surface. The thermal and velocity slip conditions are also considered. Hybrid nanofluid is created by the inclusion of Cu and Al2O3 nps in the water. The key findings are:
- The velocity contour of a hybrid nanofluid is diminished by enriching the magnetic field’s angle and effect while boosting the energy profile
- The velocity and energy profiles enhance by the intensification of injection constraint, while the Darcy–Forchheimer impact and suction term have an opposite influence on both outlines.
- The thermal profile of hybrid nanofluid increased by rising the thermal effects, heat source, and viscous dissipation, while diminished by varying the thermal slip factor.
- Heat absorption and thermal radiation contributions boost the energy transmission rate, and the thermal slip factor increases the thermal profile.
- The dispersion of Cu and Al2O3 nps in the base fluid remarkably magnifies the velocity and energy transmission rate, which is the most tremendous property of Cu and Al2O3 nps, used for biomedical and industrial applications.
Author Contributions
Conceptualization, M.B.; Data curation, I.H.; Formal analysis, I.H., M.F.Y., M.E.G. and W.W.; Funding acquisition, W.W.; Investigation, M.E.G., M.B. and W.W.; Methodology, I.H., M.F.Y., M.E.G., M.B. and A.A.; Software, M.F.Y. and M.E.G.; Supervision, I.H.; Validation, A.A.; Visualization, A.A. and W.W.; Writing—original draft, M.B.; Writing—review and editing, I.H., A.A. and W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (grant number B05F640092).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that supports the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Cartesian coordinate (m) | Components of velocity | ||
| T | Temperature (k) | Stretching velocity | |
| Exponential temperature | Angle | ||
| C | Slip velocity factor | Thermal slip factor | |
| Heat source | Suction velocity | ||
| Kinematic viscosity | Dynamic viscosity | ||
| Density | Electrical conductivity | ||
| Magnetic field | Thermal diffusivity | ||
| Heat capacity | Thermal conductivity | ||
| Porosity parameter | Ambient temperature | ||
| Fr | Forchhemier term | Gr | Grashof number |
| S | Suction/injection | d | Thermal slip |
| L | Velocity slip | Ec | Eckert number |
| Pr | Prandtl number | Re | Reynold number |
| M | Magnetic factor | Ra | Radiation factor |
| Ha | Heat absorption | f | Velocity profile |
References
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Hamad, N.H.; Wakif, A.; Alshehri, A. Towards the dynamics of a radiative-reactive magnetized viscoelastic nanofluid involving gyrotactic microorganisms and flowing over a vertical stretching sheet under multiple convective and stratification constraints. Waves Random Complex Media 2022, 1–31. [Google Scholar] [CrossRef]
- Wakif, A. A novel numerical procedure for simulating steady MHD convective flows of radiative Casson fluids over a horizontal stretching sheet with irregular geometry under the combined influence of temperature-dependent viscosity and thermal conductivity. Math. Probl. Eng. 2020, 2020, 1675350. [Google Scholar] [CrossRef]
- Gangadhar, K.; Kannan, T.; Jayalakshmi, P. Magnetohydrodynamic micropolar nanofluid past a permeable stretching/shrinking sheet with Newtonian heating. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4379–4391. [Google Scholar] [CrossRef]
- Lakshmi Devi, G.; Niranjan, H. The Novelty of Thermo-Diffusion and Diffusion-Thermo, Slip, Temperature and Concentration Boundary Conditions on Magneto–Chemically Reactive Fluid Flow Past a Vertical Plate with Radiation. Symmetry 2022, 14, 1496. [Google Scholar] [CrossRef]
- Gautam, A.K.; Verma, A.K.; Bhattacharyya, K.; Mukhopadhyay, S.; Chamkha, A.J. Impacts of activation energy and binary chemical reaction on MHD flow of Williamson nanofluid in Darcy–Forchheimer porous medium: A case of expanding sheet of variable thickness. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Rasool, G.; Shah, N.A.; El-Zahar, E.R.; Wakif, A. Numerical investigation of EMHD nanofluid flows over a convectively heated riga pattern positioned horizontally in a Darcy-Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Zaib, A.; Abelman, S.; Chamkha, A.J.; Rashidi, M.M. Entropy generation in a Williamson nanofluid near a stagnation point over a moving plate with binary chemical reaction and activation energy. Heat Transf. Res. 2018, 49, 1131–1149. [Google Scholar] [CrossRef]
- Asjad, M.I.; Sarwar, N.; Ali, B.; Hussain, S.; Sitthiwirattham, T.; Reunsumrit, J. Impact of Bioconvection and Chemical Reaction on MHD Nanofluid Flow Due to Exponential Stretching Sheet. Symmetry 2021, 13, 2334. [Google Scholar] [CrossRef]
- Algehyne, E.A.; Wakif, A.; Rasool, G.; Saeed, A.; Ghouli, Z. Significance of Darcy-Forchheimer and Lorentz forces on radiative alumina-water nanofluid flows over a slippery curved geometry under multiple convective constraints: A renovated Buongiorno’s model with validated thermophysical correlations. Waves Random Complex Media 2022, 1–30. [Google Scholar] [CrossRef]
- Alharbi, K.A.M.; Ahmed, A.E.-S.; Ould Sidi, M.; Ahammad, N.A.; Mohamed, A.; El-Shorbagy, M.A.; Bilal, M.; Marzouki, R. Computational valuation of darcy ternary-hybrid nanofluid flow across an extending cylinder with induction effects. Micromachines 2022, 13, 588. [Google Scholar] [CrossRef] [PubMed]
- Bilal, M.; Ahmed, A.E.-S.; El-Nabulsi, R.A.; Ahammad, N.A.; Alharbi, K.A.M.; Elkotb, M.A.; Anukool, W.; SA, Z.A. Numerical Analysis of an Unsteady, Electroviscous, Ternary Hybrid Nanofluid Flow with Chemical Reaction and Activation Energy across Parallel Plates. Micromachines 2022, 13, 874. [Google Scholar] [CrossRef] [PubMed]
- Alhowaity, A.; Hamam, H.; Bilal, M.; Ali, A. Numerical study of Williamson hybrid nanofluid flow with thermal characteristics past over an extending surface. Heat Transf. 2022. [Google Scholar] [CrossRef]
- Reddy, S.; Basha, H.T.; Duraisamy, P. Entropy generation for peristaltic flow of gold-blood nanofluid driven by electrokinetic force in a microchannel. Eur. Phys. J. Spec. Top. 2022, 231, 2409–2423. Available online: https://link.springer.com/article/10.1140/epjs/s11734-021-00379-4 (accessed on 14 July 2022). [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG),(40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Gangadhar, K.; Bhargavi, D.N.; Kannan, T.; Venkata Subba Rao, M.; Chamkha, A.J. Transverse MHD flow of Al2O3-Cu/H2O hybrid nanofluid with active radiation: A novel hybrid model. Math. Methods Appl. Sci. 2020. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/mma.6671 (accessed on 14 July 2022). [CrossRef]
- Reddy, S.; Raju, C.; Gunakala, S.R.; Basha, H.T.; Yook, S.-J. Bio-magnetic pulsatile CuO− Fe3O4 hybrid nanofluid flow in a vertical irregular channel in a suspension of body acceleration. Int. Commun. Heat Mass Transf. 2022, 135, 106151. [Google Scholar] [CrossRef]
- Wahidunnisa, L.; Suneetha, S.; Reddy, S.; Reddy, P.B.A. Comparative study on electromagnetohydrodynamic single-wall carbon nanotube–water dusty nanofluid in the presence of radiation and Ohmic heating. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 235, 950–958. [Google Scholar] [CrossRef]
- Sun, T.-C.; DarAssi, M.H.; Bilal, M.; Khan, M.A. The study of Darcy-Forchheimer hybrid nanofluid flow with the thermal slip and dissipation effect using parametric continuation approach over a rotating disk. Waves Random Complex Media 2022, 1–14. [Google Scholar] [CrossRef]
- Nayak, M.; Wakif, A.; Animasaun, I.; Alaoui, M. Numerical differential quadrature examination of steady mixed convection nanofluid flows over an isothermal thin needle conveying metallic and metallic oxide nanomaterials: A comparative investigation. Arab. J. Sci. Eng. 2020, 45, 5331–5346. [Google Scholar] [CrossRef]
- Al-Mubaddel, F.S.; Allehiany, F.; Nofal, T.A.; Alam, M.M.; Ali, A.; Asamoah, J.K.K. Rheological Model for Generalized Energy and Mass Transfer through Hybrid Nanofluid Flow Comprised of Magnetized Cobalt Ferrite Nanoparticles. J. Nanomater. 2022, 2022, 7120982. [Google Scholar] [CrossRef]
- Alsallami, S.A.; Zahir, H.; Muhammad, T.; Hayat, A.U.; Khan, M.R.; Ali, A. Numerical simulation of Marangoni Maxwell nanofluid flow with Arrhenius activation energy and entropy anatomization over a rotating disk. Waves Random Complex Media 2022, 1–19. [Google Scholar] [CrossRef]
- Shahsavar Goldanlou, A.; Badri, M.; Heidarshenas, B.; Hussein, A.K.; Rostami, S.; Safdari Shadloo, M. Numerical investigation on forced hybrid nanofluid flow and heat transfer inside a three-dimensional annulus equipped with hot and cold rods: Using symmetry simulation. Symmetry 2020, 12, 1873. [Google Scholar] [CrossRef]
- Ashraf, M.U.; Qasim, M.; Wakif, A.; Afridi, M.I.; Animasaun, I.L. A generalized differential quadrature algorithm for simulating magnetohydrodynamic peristaltic flow of blood-based nanofluid containing magnetite nanoparticles: A physiological application. Numer. Methods Partial. Differ. Equ. 2022, 38, 666–692. [Google Scholar] [CrossRef]
- Wakif, A.; Chamkha, A.; Animasaun, I.; Zaydan, M.; Waqas, H.; Sehaqui, R. Novel physical insights into the thermodynamic irreversibilities within dissipative EMHD fluid flows past over a moving horizontal riga plate in the coexistence of wall suction and joule heating effects: A comprehensive numerical investigation. Arab. J. Sci. Eng. 2020, 45, 9423–9438. [Google Scholar] [CrossRef]
- Zaydan, M.; Wakif, A.; Animasaun, I.; Khan, U.; Baleanu, D.; Sehaqui, R. Significances of blowing and suction processes on the occurrence of thermo-magneto-convection phenomenon in a narrow nanofluidic medium: A revised Buongiorno’s nanofluid model. Case Stud. Therm. Eng. 2020, 22, 100726. [Google Scholar] [CrossRef]
- Rehman, A.; Saeed, A.; Bilal, M. Analytical study of three-dimensional MHD hybrid nanofluid flow along with thermal characteristics and radiative solar energy. Waves Random Complex Media 2022, 1–15. [Google Scholar] [CrossRef]
- Ramaiah, K.D.; Kotha, G.; Thangavelu, K. MHD rotating flow of a Maxwell fluid with Arrhenius activation energy and non-Fourier heat flux model. Heat Transf. 2020, 49, 2209–2227. [Google Scholar] [CrossRef]
- Riaz, M.B.; Rehman, A.U.; Awrejcewicz, J.; Jarad, F. Double diffusive magneto-free-convection flow of Oldroyd-B fluid over a vertical plate with heat and mass flux. Symmetry 2022, 14, 209. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Atif, M.; Ellahi, R.; Sait, S.M. Electromagnetic flow of SWCNT/MWCNT suspensions in two immiscible water-and engine-oil-based newtonian fluids through porous media. Symmetry 2022, 14, 406. [Google Scholar] [CrossRef]
- Chen, L.; Abbas, M.A.; Khudair, W.S.; Sun, B. Analytical Solution for the MHD Flow of Non-Newtonian Fluids between Two Coaxial Cylinders. Symmetry 2022, 14, 953. [Google Scholar] [CrossRef]
- Abbas, N.; Shatanawi, W.; Abodayeh, K. Computational Analysis of MHD Nonlinear Radiation Casson Hybrid Nanofluid Flow at Vertical Stretching Sheet. Symmetry 2022, 14, 1494. [Google Scholar] [CrossRef]
- Hussain, S.M. Dynamics of ethylene glycol-based graphene and molybdenum disulfide hybrid nanofluid over a stretchable surface with slip conditions. Sci. Rep. 2022, 12, 1751. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Raza, A.; Khan, S.U.; Ijaz Khan, M.; Ayadi, M.; El-Shorbagy, M.; Alshehri, N.A.; Wang, F.; Malik, M. Prabhakar fractional simulations for hybrid nanofluid with aluminum oxide, titanium oxide and copper nanoparticles along with blood base fluid. Waves Random Complex Media 2022, 1–20. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation of solar system equipped with innovative turbulator and hybrid nanofluid. Sol. Energy Mater. Sol. Cells 2022, 243, 111786. [Google Scholar] [CrossRef]
- Berezowski, M. The application of the parametric continuation method for determining steady state diagrams in chemical engineering. Chem. Eng. Sci. 2010, 65, 5411–5414. [Google Scholar] [CrossRef]
- Shuaib, M.; Shah, R.A.; Bilal, M. Variable thickness flow over a rotating disk under the influence of variable magnetic field: An application to parametric continuation method. Adv. Mech. Eng. 2020, 12, 1687814020936385. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).