Abstract
Two polytypic modifications of new non-centrosymmetric iodate Rb3Sc(IO3)6 are synthesized hydrothermally. Their structures demonstrate different degrees of ordering and are solved in the same space group, Pc, with differing choice of b-axis: either 20 or 40 Å is selected from the same diffraction data, measured on crystals with better ordering. The difference in NLO properties of two polytypes is disclosed. Topology–symmetry analysis of separated blocks and layers allowed determination of local symmetry corresponding to mirror plane m, which defines strong optical nonlinearity. Layer alternation indicates a polytypic nature of Rb, Sc-iodate and its similarity to K, In- and K, Sc-nonlinear-optical iodate crystals, space group Fdd2, belonging to the proposed common family A3M(IO3)6 (A = K, Rb; M = Sc, In), whose properties are explained on a symmetry basis for every known member. Hypothetical structural variant is predicted; structural disorder and crystal growth conditions are discussed as factors affecting properties.
1. Introduction
Iodates comprise inorganic compounds possessing trigonal umbrella-like [IO3]-anionic groups in which the I5+ non-bonded lone pair makes the fourth’s vertex-completing umbrella up to a tetrahedron. Within the group, this geometry corresponds to a strong polar distribution of the electron density. When the local environment and the asymmetric coordination of the groups are aligned unequally, relative to center of symmetry in a crystal structure, they yield a polar material [1]. Non-centrosymmetric compounds, especially polar materials, attract great interest due to their nonlinear optical, ferroelectric, piezoelectric and magnetic properties. Various metal iodates have been intensively explored in the last decades in a search of new materials, and the results are summarized in reviews on structures and properties in corresponding material science considerations [2]. Recently, metal iodates with large optical second-order nonlinearity have been studied [3]. Umbrella-like iodate groups (IO3) usually exist in isolated positions; however, different condensed anions have been also discovered, for example, in [4].
Successful searches for new phases may be produced on the basis of a deep understanding of the fundamental structural features responsible for properties, especially symmetry. An important tool is the topology–symmetry analysis of the OD theory of structures [5] that deals with families of structures with order (O) and disorder (D) features. Some basal definitions, as well as the formation of ordered and disordered structures, are given in [6], in which a successful explanation of structure–properties relationships using this approach was developed for Ba(OH)(IO3).
2. Materials and Methods
The hydrothermal synthesis method is widely used in the search for new iodates. The experiments are carried out at different temperature intervals, pressures and reagent concentrations. Single crystals of new iodate Rb3Sc(IO3)6 were obtained in our experiments under hydrothermal conditions from a mixture of chemically pure Sc2O3 (0.5 g, 3.7 mmol), I2O5 (3 g, 9 mmol) and Rb2CO3 (2 g, 8.7 mmol). All reagents were dissolved in 10 mL of distilled water shared equally for two experiments. For synthesis of Rb3Sc(IO3)6 in the first experiment using a large autoclave, 5 mL of water solution was loaded into a Teflon-lined stainless steel pressure vessel with a 20 mL capacity; the fill factor of the autoclave was 25%. For testing reproducibility of synthesis of Rb3Sc(IO3)6, the second experiment was undertaken in a smaller autoclave with the same reagents in the same proportions as in the first experiment with the addition of 5 mL of the dissolved mixture in a 7 mL capacity autoclave of, in order to produce a fill factor as high as 80%. Both synthetic experiments were carried out at a temperature of 270 °C over 5 days. Final cooling after synthesis to room temperature was done in 24 h. The grown crystals were isolated by filtration of the stock solution and washed with hot water. Note that both experiments were carried out from the same solutions and under the same conditions; the only difference was the pressure, which correlates with the filling factor of the autoclave.
Morphological separation of new crystals was done using an optical microscope with ×32 magnification (Stereoscopic microskope MBC1, Optical Factory, Lytkarino, Moscow, 1971, USSR). Transparent colorless flattened crystals with habitus similar to hexagons were found in crystallization products in the first experiment. The crystals presented in the experiment were well-faceted and sufficiently large, with sizes up to 1 mm, and obviously identical to each other. The yield of the experiment was close to ~90%. In the second experiment, crystals were similar to the first: colorless, well-faceted, but significantly smaller and more isometrically shaped, but with the same yield; see Figure 1.

Figure 1.
Bulk crystals of Rb3Sc(IO3)6. Left are crystals from first experiment, right—from second experiment.
Elemental analysis was carried out on crystal surfaces using a Jeol JSM-6480LV scanning electronic microscope combined with WDX analysis. The test revealed the presence of Rb, Sc and I for crystals in both experiments.
The crystals obtained in the course of both series of hydrothermal synthesis showed PXRD patterns which were close each to other (Figure S1a,b). After crystal structure determination (see below), a theoretical powder pattern (Figure S1c,d) for both polytypes was calculated based on a.cif file using the STOE XPow program [7]. The simulated pattern matches well with the experimentally registered one and with the iodate investigated earlier: K3Sc(IO3)6 (see Section 3 below).
Second harmonic generation measurement was carried out on the crystalline samples according to the Kurtz and Perry scheme [8] using the Minilite-I YAG: a Nd laser operating at Q-switched mode, at the repetition rate of 10 Hz and at wavelength λω = 1.064 mcm. The incident beam peak power was about 0.1 MW on a spot 5 mm in diameter on the surface of the sample. Measurements of light with doubled frequency at 0.532 mcm were performed in the reflection mode, which allowed the exclusion of the influence of powder thickness on SHG output. A standard α-SiO2 powder sample with 5 mcm grain size was used as a reference.
Powder samples for the SHG were prepared from crystals of both aforementioned experiments obtained under various conditions in hydrothermal synthesis (see description above). After grinding, the powders were separated with sieves according to a main grain size of 30–100 mcm, except for the finest powder. The last fraction was prepared by prolonged grinding of powders in alcohol until a suspension was formed. This fraction from 5 mcm grains after drying was used for quantitative comparison of their SHG activity with α-quarts standard. For both experiments, the dependence of SHG response on grain size is typical for phase-matching materials [9]. Stronger SHG was observed in the first experiment (Figure 2) as the grains become larger: evidence for better conditions for phase-matching in a more-ordered structure (see below). Nevertheless, fundamental optical nonlinearities of both experiments are almost equal, as it follows from SHG in the smallest size fractions. The intensity Q = I2ω/I2ω (SiO2) of optical second harmonic generation (SHG) in thin powder with grains of size l = 5 mcm is almost the same (Q = 15 and 17 in I2ω(SiO2)-units correspondingly for both experiments). According to the simplified relation from [9]:
this SHG output may be related with space-averaged effective second-order nonlinear optical coefficient for both experiments, <deff> ≈ 1.5 pm/V, which allows referring both experiments to A class, after Kurtz [8].
<deff> ≈ 0.365 pm/V[I2ω/I2ω (SiO2)]½
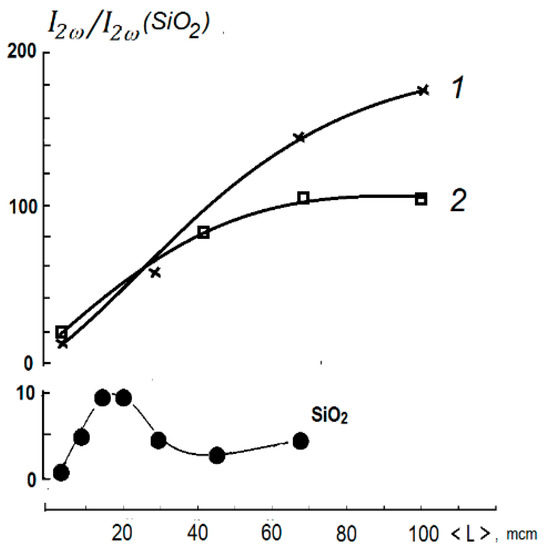
Figure 2.
Powder SHG response of two experiments of Rb3Sc(IO3)6 in comparison with a-quartz in dependence on main grain size in the powders. Curve 1—first experiment with well-shaped larger flattened crystals; curve 2—second experiment with smaller isometric crystals.
The unit cells were determined on single crystals using an XCalibur S diffractometer equipped with a CCD area detector (ω scanning mode) and graphite-monochromatic Mo Kα radiation source (λ = 0.71073 Å). The pre-experiment shows unit cells similar to K3In(IO3)6 [10] and K3Sc(IO3)6 [11] investigated recently. Small colorless transparent crystals with sizes of 0.283 mm × 0.250 mm × 0.102 mm and of 0.225 mm × 0.125 mm × 0.05 mm were selected from the crystals of the first and second experiment, respectively, for single-crystal X-ray study (Figure 3). The diffraction experiments were carried out on the same diffractometer. The data were integrated using the CrysAlis Pro Agilent Technologies software [12] and corrected for the Lorentz and polarization factors. The refined unit-cell parameters changed to monoclinic ones, comparable to known orthorhombic structures, and allowed indexing with two unit-cell parameters which differ in the size of the b-axis: 20 Å for the first experiment and 40 Å for the second experiment.

Figure 3.
Images of crystals used in diffraction experiments from hydrothermal experiments: first experiment (left) and second experiment (right), colorless transparent flattened crystal have sizes of 0.283 mm × 0.250 mm × 0.102 mm (left) and 0.225 mm × 0.125 mm × 0.05 mm (right).
The topology–symmetry analysis of OD theory was carried out in accordance with the basal principles, as well as our experience in the study of structural families.
3. Results and Discussion
3.1. Rb3Sc(IO3)6 Iodate Structures
3.1.1. Crystal Structure Rb3Sc(IO3)6, Experiment 1, b = 20 Å
A structural model of a new iodate was determined by the direct methods using SHELXS [13] on the basis of experimental data obtained on crystals from the first experiment indexed in monoclinic cell a = 7.1147(1), b = 20.1463(3), c = 7.0991(1) Å, which has not been previously defined and is not in the CCDC (ICSD) data base. This unit cell correlates with the known orthorhombic (Fdd2 [10,11]) with the choice of two F-vectors as the a,c-axis of the new monoclinic cell (Figure 4). Indexing of our data in “orthorhombic” cells leads to bad Rint between equivalents, the absence of the F-lattice, the presence of only the C-lattice and one angle deviation from 90°; thus, again, a monoclinic symmetry in pseudo-orthorhombic axes (a = 8.3901(2), b = 11.4700(3), c = 40.265(1) Å, β = 89.909(3)°) is determined. The connection of the cells indicated the connection of the new monoclinic and previously studied orthorhombic structures. Doubling of the monoclinic b-axis up to 40.3039(8) Å was found in our data due to additional significantly weaker satellite reflections thanks to visualization of the reciprocal lattice in the CrysAlis program and control “by hand” of F2 hkl and σ (F2 hkl) correlation. Obviously, crystals with a cell of 20 Å predominated in the first experiment. The morphology of crystals correlates with unit cells with flattening perpendicular to large axis b-mon (a-orth) and β-angle close to 60° (pseudo-hexagonal habitus).
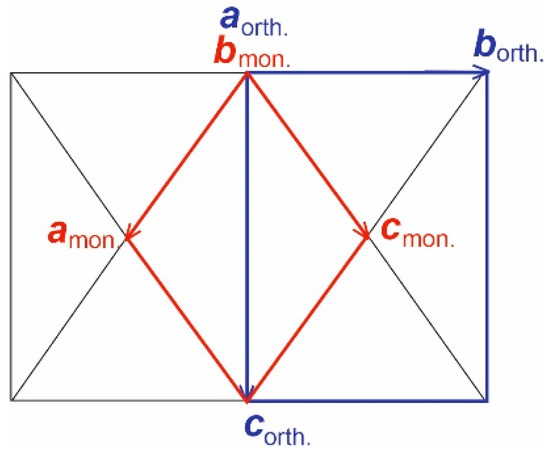
Figure 4.
Monoclinic P-lattice (red) selected from the orthorhombic F-lattice (blue).
The structural solution was started using the prevailing strong reflections in the smaller unit cell (20 Å). Suggested by the CrysAlis program, space group P2/c did not pass because of its strong SHG signal. Between the two acentric groups Pc and P2, the first was true and allowed us to solve the structure in SHELXS [13] by direct methods. Initially, six heavy atoms, and then four additional ones, were identified as I, Rb and Sc atoms, in accordance with heights of peaks and the composition of crystals. The remaining O atoms were obtained in difference Fourier synthesis, completed cation coordination and significantly improved the R-factor after being introduced into the model. All six I atoms were coordinated in an umbrella-like by oxygen on distances typical for (IO3)-groups, Sc atoms were coordinated octahedrally, Rb atoms have large distances with O atoms and all oxygen atoms participated in I–O bonding and, thus, were O2−. The model was neutral based on Pauling’s balance of valences. The resulting chemical formula is Rb3Sc(IO3)6, Z = 2. Absorption correction that was necessary to take into account was done using numerical Gaussian integration over a multifaceted crystal model [14]. The refinement of the model in SHELXL [13] gave satisfactory atomic displacement parameters, interatomic distances and R-factor. According to the Flack parameter, a racemic twin in the crystal has been introduced by a matrix −100/0–10/00–1 that lowered R-factor; the twin component was 0.436.
The structural model was finally refined using the least squares procedure in anisotropic approximation of the atomic displacements for all the atoms, correction of anomalous scattering and with the refinement of a weighting scheme using SHELXL [13]. Crystallographic data, atomic coordinates and selected bonds are presented in Table 1, Tables S1 and S2. CCDC (ICSD) 2186415 contains crystallographic data for this structure. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif (accessed on 8 July 2022). All illustrations were produced using ATOMS [15] and CORELDRAW programs.

Table 1.
Crystal data and structure refinement for Rb3Sc(IO3)6, Experiment 1, with b = 20 Å and b = 40 Å 1.
3.1.2. Crystal Structure Rb3Sc(IO3), Experiment 1, b = 40 Å
The structural model for the structure in large the monoclinic cell with b = 40.3039(3) Å was also solved by direct methods in SHELXS [13] on the basis of all experimental reflections registered for the crystal from the first experiment. The space group chosen in the structure solution was the same, Pc, in analogue with the previous structure and after unsuccessful attempts to use Pa and Pm. A half of the structure was easily received and was equal to the previous model with b = 20.1463(3) Å. It presents so-called “family structure” and is the simplest common part. A central part of the doubled unit cell appeared only in a series of approximations and differ in some atomic positions from the previous one; thus, b-axis doubling by translation was broken. The refinement of the large structure with the anisotropic displacement only for Rb atoms, and introducing, again, a racemic twin (twin component 0.54), converted the R-factor to a higher value than for the structural model with b = 20 Å (Table 1, Tables S3 and S4) because of the polytypic nature of the crystal. It is connected with some disorder and strong correlations in the refinement. Atomic displacement parameters and interatomic distances corresponded to standard counterparts. The CCDC (ICSD) 2186468 contains crystallographic data for this compound. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif (accessed on 8 July 2022). The correlation between structures will be discussed below.
3.1.3. Crystal Structure Rb3Sc(IO3), Experiment 2, b = 40 Å
As we mentioned before, crystals from the second experiment have, in pre-experiment and in full experiment, a large b-axis with 40 Å in the unit cell. The space group suggested by CrysAlis, Pm, did not fit and Pc was chosen, in analogue with the previous large structure from first experiment. A part of the structure corresponding to the 20 Å variant was, again, simply found by direct methods in SHELXS, was ordered, equal to previous case and possessed standard interatomic distances. However, the central part of the structure has chaotic distribution of atoms giving only R~15% (Figure S2, Table S5). An attempt to insert an ordered model of the central part taken from the first experiment in space group Pc, or using other symmetries of layer multiplication, failed. This indicated significant structural disorder in the crystal from the second experiment compared to the first experiment, and it was not possible to finish the structural model for the crystal from the second experiment.
3.2. Comparison of New Monoclinic Rb3Sc(IO3)6 Polytypes with Each Other and with the Orthorhombic K3In(IO3)6 and K3Sc(IO3)6 Using Topology–Symmetry Analysis; Structure–Properties Relation
The Rb3Sc(IO3)6 structure with 20 Å has sufficient regular Sc octahedra with standard average Sc–O distances 2.109 Å (Table S2), umbrella-like iodate groups (IO3) with average I–O 1.82 Å and large Rb polyhedra with a high coordination number (CN): Rb1 CN = 8, average Rb1-O 3.00 Å, Rb2 CN = 9, average Rb2-O 3.19 Å and Rb3 CN = 8, average Rb3-O 2.98 Å. They may be approximated as distorted square prisms (Rb1, Rb3) and trigonal prisms (Rb2 for 3.15 Å distance) combined in triples along common edges. The Rb3Sc(IO3)6 structure with 40 Å has the same polyhedra (Table S4); however, distance deviations are higher. Isolated blocks [Sc(IO3)6]3− as the most stabile structural units are joint in resulting in a sufficient flexible framework by large Rb ions in equal manner for both structures.
The crystal chemical analysis determined that the proposed family of structures A3M(IO3)6 (A = K, Rb; M = Sc, In) had common structural features. The first member of the family K3In(IO3)6 crystal structure was solved in orthorhombic symmetry, known as the Fdd2 space group [10]. An isolated [In(IO3)6]3− anion was selected as a basal unit or fundamental building block. It consisted of a central octahedron with a six (IO3)-groups attached to its six vertices. Similar structural units were previously found in compounds with trigonal (space group R-3), hexagonal polar (P63) and triclinic (P-1) symmetry. Their chemical formulas are very similar and, taking into account hetero-valence substitutions, may be written as A2M4+(IO3)6 with A = Li, Na, K, Rb, Cs or Tl, and M = Ti, Zr, Ge, Pt or A3M3+(IO3)6; A = Na, K, Rb or Cs; M = In, Sc, Fe3+. Stereo-active lone pairs of electrons are aligned along the c-axis for the structures Li2Ti(IO3)6 and Na2Ti(IO3)6 in the P63 space group, providing second-order optical nonlinearity [16], although the hexagonal distribution of blocks is not presented in the family A3M(IO3)6 (A = K, Rb; M = Sc, In).
Optical nonlinearity was also found in K3In(IO3)6 and was explained by orientation of iodate lone pair anions along a single crystallographic axis 2 in the polar space group Fdd2 (Figure 1b in [10]). Detailed analysis of the block symmetry in K3In(IO3)6 allows us to derive a local mirror plane perpendicular to the axis 2, which gives a pseudo-inversion center and local point group 2/m for the block (Figure 5a,b). The absence of pronounced polarity, along with the compensation of iodate lone pair dipole moments because of block symmetry, explains a weaker nonlinear optical signal despite the polar space group. It is not a seldom case and is characteristic, for example, of Ba(OH)(IO3) [6].
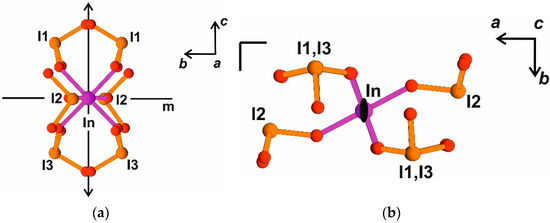
Figure 5.
[In(IO3)6]3− block in K3In(IO3)6 crystal structure, local symmetry elements: pseudo-mirror plane m and twofold axis 2 are shown. (a) bc projection, here and after ball-stick presentation is used for (IO3)-groups and In(Sc) atoms; (b) ab projection.
A new monoclinic structure Rb3Sc(IO3)6 possessing a block similar to K3In(IO3)6 is considered; however, its topology fundamentally differs and demonstrates absence of inversion with the only mirror plane m. Polar direction is in the plane and corresponds to diagonal ac [101] (Figure 6a); absence of inversion is visualized also on Figure 6b compared with Figure 5b.
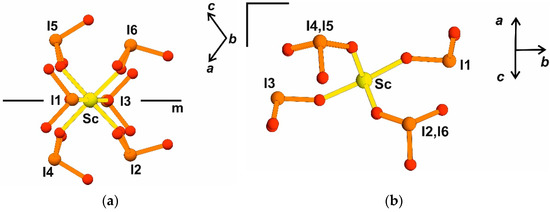
Figure 6.
[Sc(IO3)6] 3−block in Rb3Sc(IO3)6 crystal structure, local symmetry element: pseudo-mirror plane m is shown (a) ac projection along monoclinic axis; (b) diagonal ac projection in the same view as in Figure 3b.
A similar block was found in the crystal structure K3Sc(IO3)6 [10], space group Fdd2. In contrast to K3In(IO3)6, the structure demonstrates disorder up to the statistical distribution of (IO3)-groups, giving zig-zag trimers with the alternation of (IO3) and (I2O5) [10] due to the splitting of I2 and I3 atomic positions (Figure 7). The comparison of the block found in the monoclinic structure of Rb3Sc(IO3)6 (Figure 6a) with the disordered block in K3Sc(IO3)6 (Figure 7) allows us to suggest polar configuration in K,Sc-iodate, similar to Rb,Sc-iodate, by choosing one of the pairs of disordered I2 and I3 atoms: only I3B and I2B in the left side on Figure 7 and only I3A and I2A in the right side with the keeping of the local mirror plane m, or vice versa. The second-order optical nonlinearity in Rb3Sc(IO3)6 may be attributed to lone pairs’ polar ordering as in K3Sc(IO3)6, though many features of this ordering are quite different (crystal systems, unit cells, space groups).
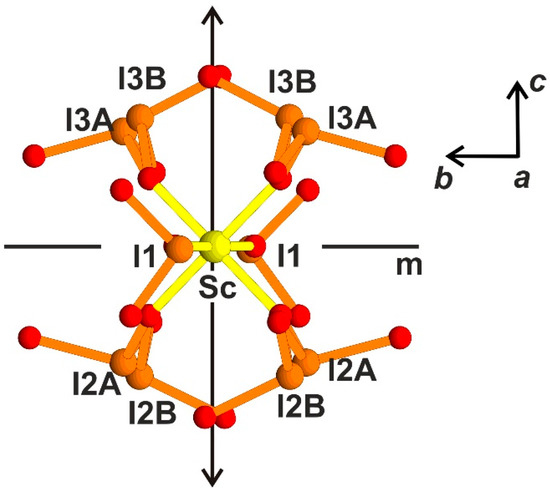
Figure 7.
[Sc(IO3)6]3− disordered block in K3Sc(IO3)6 crystal structure, local symmetry elements: pseudo-mirror plane m and twofold axis 2 are shown, bc projection, choosing of I3B and I2b in the left side and I3A and I2A in the right side provides polarity.
The described blocks are multiplied by diamond d-glades parallel to ac and bc in orthorhombic structures, and by c-glade (correlates with one of d-glade) parallel to the ac-plane in monoclinic structures. The blocks with the triples of Rb atoms are organized in “layers” parallel to ac of symmetry Pm, which is out of space group Pc (Figure 8a) as a local symmetry. Layer alternation along large b-axis and the monoclinic structure with 20 Å is shown on the Figure 8b. Every layer is multiplied to the next one by c-glade of space group Pc with resulting two layers along b-axis in the unit cell; polar direction in every layer corresponds to a [101] vector, and lies inside layers despite layer multiplication happening in a non-polar way. It was described in OD theory as a special case (category Ib [5]). The structure with the doubled unit cell of 40 Å (Figure 8c) possesses, already, four layers in the unit cell. Two layer pairs, namely L4−L1 and L2−L3, are multiplied by real c-glades of the space group; other pairs L1−L2 and L3−L4 are multiplied by pseudo-c-glade; the difference is shown in Figure 6c. Analysis of structure in the large unit cell demonstrates some disorder for the central part of the structure (layers L2−L3), which gives doubling of the b-axis. It is necessary to emphasize that, in the first experiment, predominate crystals with a structure corresponding to axis b = 20 Å.
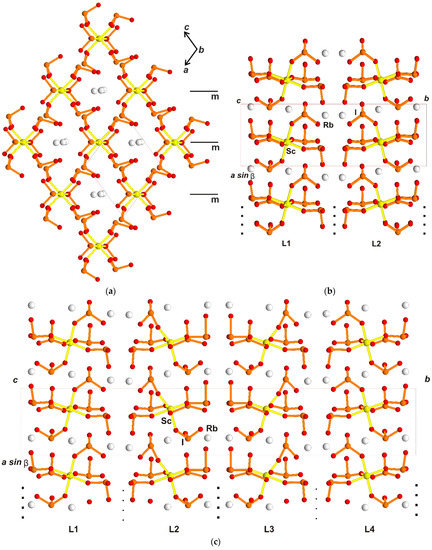
Figure 8.
Rb3Sc(IO3)6 crystal structure, (a) ac projection of the one layer, local symmetry element: pseudo-mirror plane m is shown; (b) structure with b = 20 Å, projection along c-axis, c-glades of the space group as multiplying symmetry elements are shown; (c) structure with b = 40 Å in the same projection along c-axis, multiplying symmetry elements: c-glades of the space group are shown by bold dots and pseudo-c-glades are shown by simple dots.
There are four layers in both orthorhombic structures similar to those described for the new monoclinic one with the equally large parameter ~40 Å. This confirms similarity and the polytypic nature of the structures of the proposed family A3M(IO)6 (A = K, Rb; M = Sc, In). Polytypes in structural families demonstrate the largest parameters along directions of layer alternation for more complicated members. For SiC polytypes, this direction may reach 100 or 200 Å. Indeed, this direction corresponds to structural disorder.
Structural data for K3In(IO3)6 shows that symmetry of one layer is consistent with the derived symmetry of block A2/m (P2/m in monoclinic axes), and differs from the space group of the structure Fdd2 (Figure 9). However, it is pseudo-symmetrical and gives some deviation of inversion. Multiplication here is by d-glades of the space group of the structure. In the K3Sc(IO3)6 structure, the layers are similar; however, it is possible to lower their symmetry by choosing a special order in (IO3)-group orientation with the resulting polarity (Figure 7). The local symmetry of a layer is denoted in OD theory as λ PO (partial operation), and symmetry of layer multiplication is denoted as σ PO. Depending on layer symmetry, the layer and the resulting whole structure may be polar (τ) or non-polar (ρ) [5].
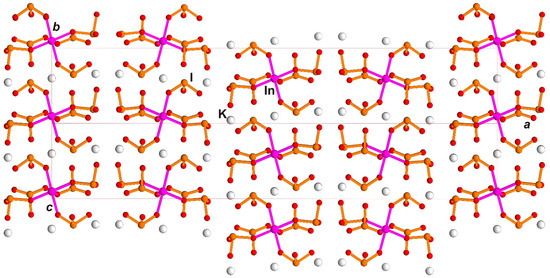
Figure 9.
K3In(IO3)6 crystal structure in diagonal bc projection similar to Rb3Sc(IO3)6 projection on Figure 8c.
The Rb, Sc-iodate structure with b = 20 Å is the simplest two-layer variant of currently known polytypes. We may suppose the possibility to synthesize single-layer polytypes in this family, which will possess the same a,c-axes and two times less b-axis, equal to ~10 Å, with space group Pm. Such hypothetic compounds will obey good optical nonlinearity and will be fully ordered. The polytypic nature of similar families is usually accompanied by structural disorder and is pronounced strongly in our second experiment. Multiplied symmetry element σ PO may be presented here by another glade, not only c or d, but, for example, a or m. It is possible to assume existence of such members of this family, in which the absence of a regular alternation of σ PO between basal layer pairs will lead to disordered structures.
4. Conclusions
Crystals of two polytypes of new iodate Rb3Sc(IO3)6 synthesized hydrothermally demonstrate strong optical nonlinearity and phase-matchable properties in SHG from a Nd laser. Both polytype structures were solved in two monoclinic unit cells with b-axis equal to 20 and 40 Å chosen from the same diffraction data using a single crystal from our first experiment. The crystal from our second experiment has a monoclinic cell with 40 Å; the structure demonstrates significant disorder and it was not possible to finish it. Due to the conditions of their formation in either experiment, the crystals possess stronger or weaker SHG activity, depending on the ordering of their structures. Structure with smaller unit cells—“family structure”—is completely ordered, but the structure with larger unit cell has some disorder in the first experiment. All the crystals from the second higher-pressure experiment have a large unit cell and higher disorder compared with crystals from the first lower-pressure experiment. The polarity of the new structures is determined by symmetry of the block-layer units, resulting in the final polar group of the whole structure, which explains the properties. Apparently, a noticeable contribution to the optical nonlinearity comes from the polar-oriented IO3-groups, as it takes place in many iodates. Contribution of large Rb ions or Sc ions does not seem to play a self-dependent crucial role because of sufficient symmetric surrounding of these ions with oxygen atoms.
Topology–symmetry analysis allowed us to reveal the similarity of new crystals with the known orthorhombic K3In(IO3)6 and K3Sc(IO3)6. Deviation from orthorhombic symmetry for Rb3Sc(IO3)6 is most likely determined by large Rb-alkali metal in the composition compared to K3Sc(IO3)6. Three mentioned compounds currently represent the family of nonlinear optical crystals A3M(IO3)6 (A = K, Rb; M = Sc, In), although it is also possible to further expand this family due to the discovery of new polytype members with different compositions and structures. The proposed polytypic family has clear features of disorder, and the SHG signal is higher for the new Rb, Sc-crystals in the first experiment, where the ordered structure with 20 Å predominates, and is weaker for the crystals in the second experiment, in which there is strong disorder in half of the unit cell because of disorder of layer conjugation. Detailed topology–symmetry analysis of block-layer symmetry allowed the explanation of nonlinear optical activities for every member: less pronounced for K3In(IO3)6, pronounced for K3Sc(IO3)6 because of order–disorder application and pronounced in Rb3Sc(IO3)6 due to polarity inside the layers. Simultaneous growth of several members is known for polytypes. Unfortunately, no “pure” or “family structure” of 20 Å was synthesized as well as for the predicted simplest 10 Å polytype. More stable crystallization conditions with lower pressure and smaller crystallization rate often favor formation of more perfect crystals with ordered structure. This way is promising to produce new members of the family with high optical nonlinearity. Topology–symmetry analysis and control on order–disorder processes during crystal structure formation seems fruitful for discovering and the explanation of structure–properties relations in this and other structural families.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/sym14081699/s1, Tables S1–S5, Figure S1a–d, Figure S2.
Author Contributions
Conceptualization, E.B. and O.D.; methodology, E.B., S.S. and O.D.; software, O.R., E.B.; investigation, O.R., A.V. and S.S.; resources, O.D., A.V., S.S. and E.B.; writing—original draft preparation, O.R., E.B., O.D. and S.S.; writing—review and editing, E.B. and S.S.; visualization, O.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
CCDC (ICSD) 2186415 and 2186468 contain crystallographic data for this paper. These data can be obtained free of charge via www.ccdc.cam.ac.uk/data_request/cif (accessed on 8 July 2022).
Acknowledgments
The authors are grateful to Natalie Zubkova for her aid in collection of experimental diffraction, to the Laboratory of local methods of materials investigation, and to Vasilij Yapaskurt, geological faculty, MSU, for determination of compositions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nguyen, S.D.; Yeon, J.; Kim, S.H.; Halasyamani, P.S. BiO(IO3): A New Polar Iodate that Exhibits an Aurivillius-Type (Bi2O2)2+ Layer and a Large SHG Response. J. Am. Chem. Soc. 2011, 133, 12422–12425. [Google Scholar] [CrossRef]
- Mao, J.-G.; Sun, C.-F.; Yang, B.-P. Structures and properties of functional metal iodates. Sci. China Chem. 2011, 54, 911–922. [Google Scholar] [CrossRef]
- Hu, C.-L.; Mao, J.-G. Recent advances on second-order NLO/materials based on metal iodates. Coord. Chem. Rev. 2015, 288, 1–17. [Google Scholar] [CrossRef]
- Mao, F.-F.; Hu, C.-L.; Chen, J.; Wu, B.-L.; Mao, J.-G. HBa2.5(IO3)6(I2O5) and HBa(IO3)(I4O11): Explorations of second-order nonlinear optical materials in the alkali-earth polyiodate system. Inorg. Chem. 2019, 58, 3982–3989. [Google Scholar] [CrossRef]
- Dornberger-Schiff, K. Grundzuege einer Theory der OD-strukturen aus Schichten. Abh. Deutsch. Akad. Wiss. Berlin 1964, 3, 89. [Google Scholar]
- Reutova, O.; Belokoneva, E.; Volkov, A.; Dimitrova, O. Structure-properties relation in two iodate families studied by topology-symmetry analysis of OD theory. Symmetry 2021, 13, 1477. [Google Scholar] [CrossRef]
- WinXPow; Stoe&CIE GmbH: Darmstadt, Germany, 2002.
- Kurtz, S.K.; Perry, T.T. A Powder Technique for the Evaluation of Nonlinear Optical Materials. J. Appl. Phys. 1968, 39, 3798–3813. [Google Scholar] [CrossRef]
- Beskorovaynaya, D.A.; Deyneko, D.V.; Baryshnikova, O.V.; Stefanovich, S.Y.; Lazoryak, B.I. Optical Non-Linearity Tuning in Ca8-xPbxMBi(VO4)7 Whitlockite-Type Systems. J. Alloys Compd. 2016, 674, 323–330. [Google Scholar] [CrossRef]
- Liu, X.; Li, G.; Hu, Y.; Yang, M.; Kong, X.; Shi, Z.; Feng, S. Hydrothermal synthesis and crystal structure of polar and nonpolar compounds in indium iodate family. Cryst. Growth Des. 2008, 8, 2453–2457. [Google Scholar] [CrossRef]
- Vagourdi, E.M.; Zhang, W.; Denisova, K.; Lemmens, P.; Halasyamani, P.S.; Johnsson, M. Synthesis and characterization of two new second harmonic generation active iodates: K3Sc(IO3)6 and KSc(IO3)3Cl. ACS Omega 2020, 5, 5235–5240. [Google Scholar] [CrossRef] [PubMed]
- Agilent Technologies. CrysAlisPro Software System, version 1.171.3735; Agilent Technologies UK Ltd.: Oxford, UK, 2014. [Google Scholar]
- Sheldrick, G.M. SHELXL-97, a Program for Crystal Structure Refinement; SHELXS-97, a Program for Automatic Solution of Crystal Structures; University of Goettingen: Goettingen, Germany, 1997. [Google Scholar]
- CrysAlisPro, version 1.171.3946; Rigaku Oxford Diffraction: Oxford, UK, 2018.
- Dowty, E. Atoms 3.2—A Computer Program for Displaying Atomic Structures; Shape Software: Kingpost, TN, USA, 1995; p. 37663. [Google Scholar]
- Chang, H.Y.; Kim, S.H.; Ok, K.M.; Halasyamani, P.S. Polar or nonpolar? A+ cation polarity control in A2Ti(IO3)6 (A = Li, Na, K, Rb, Cs, Tl). J. Am. Chem. Soc. 2009, 131, 6865–6873. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).