Analytical Study of Fractional Epidemic Model via Natural Transform Homotopy Analysis Method
Abstract
:1. Introduction
2. Integral Transform Techniques
3. Fractional Epidemic Model
- The recruitment of individuals increases the size of the susceptible group at a constant rate .
- The childbirth rate and natural mortality rate of individuals are indicated by parameters and , respectively.
- A susceptible individual is infected over numerous contacts with infected individuals via the given term , where the contact rate is the disease transmission coefficient.
- Transmission from an asymptotic infected individual to a susceptible individual can take place in the form , where is a transmissibility multiple of to ; if , no transmissibility multiple will exist and thus vanish, and if , then a transmissibility multiple will exist.
- The parameter is the proportion of asymptotic infections. The parameters and respectively indicate the transmission rate after the incubation period and joining classes and .
- Individuals in the symptomatic group and asymptomatic group are removed at recovery rates of and and are added to the recovered compartment.
- A susceptible individual will be infected after interaction with the reservoir or the seafood place or market class through the term given by , where is the disease transmission coefficient from to . and individuals transmit the virus to the reservoir or the seafood place or market class at constant rates of and , respectively.
4. Methodology of the Proposed Method
5. Solution of the Fractional Epidemiological Model (FEM) via NTHAM
6. Solution via LHPM
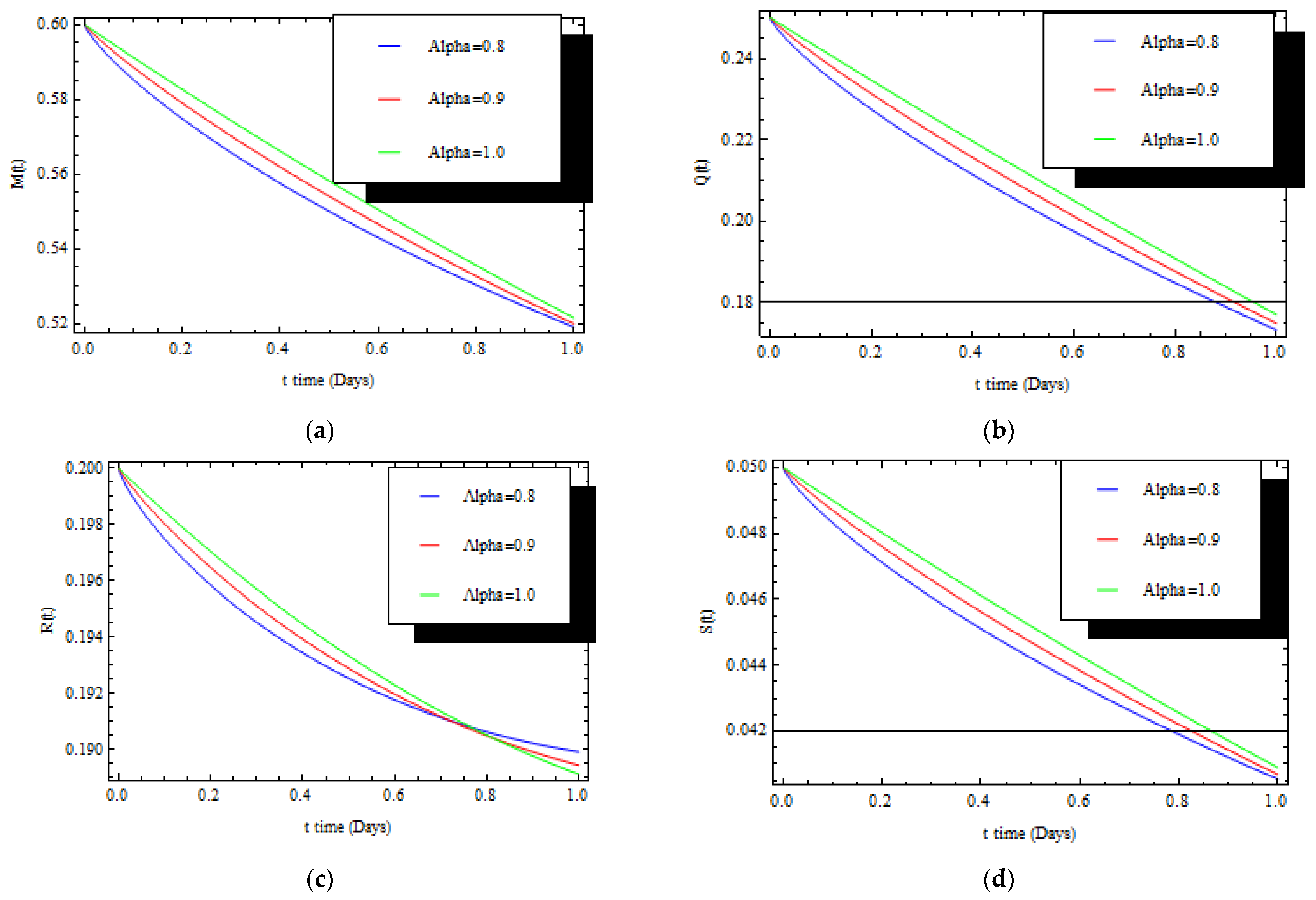
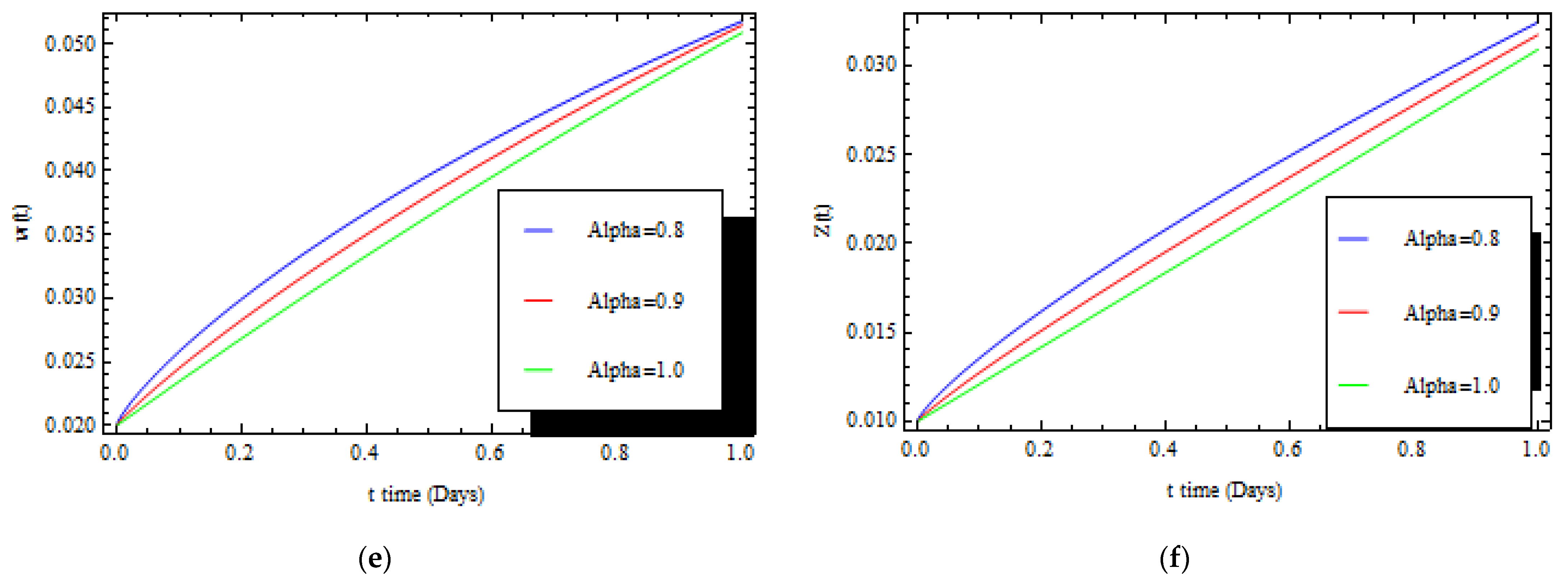
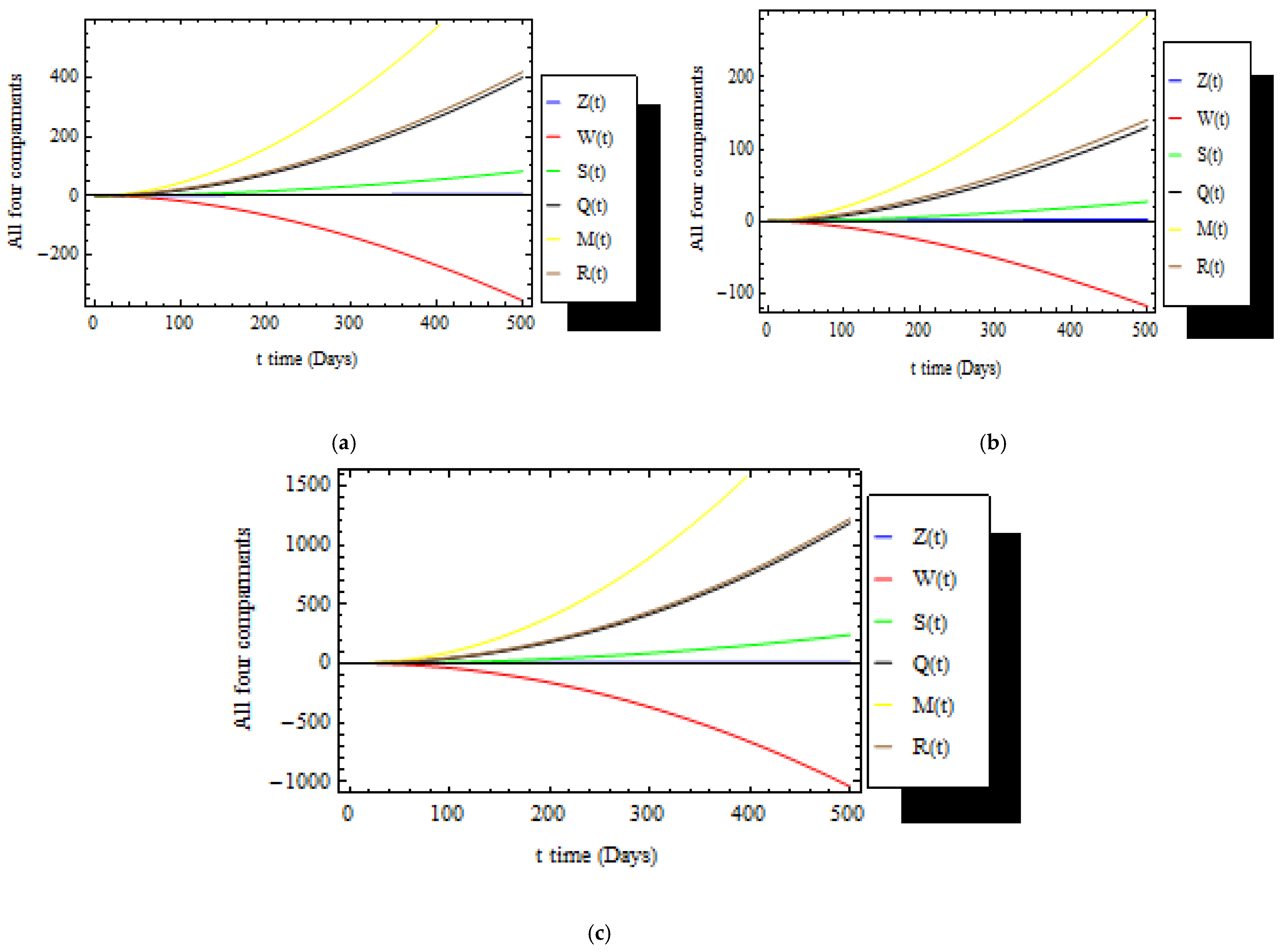
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Breuer, F.; Driesch, V.D. Mathematical Epidemiology; Springer: New York, NY, USA, 2008; p. 415. [Google Scholar]
- Ma, Z.; Li, J. Dynamic Modeling and Analysis of Epidemics; World Scientific: Singapore, 2009; p. 513. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An introduction; Springer: New York, NY, USA, 2002; p. 576. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. 1927, 115, 700–721. [Google Scholar]
- Talaee, M.; Shabibi, M.; Gilani, A.; Rezapour, S. On the existence of solutions for a pointwise defined multi-singular integro-differential equation with integral boundary condition. Adv. Diff. Equ. 2020, 2020, 41. [Google Scholar] [CrossRef]
- Angstmann, C.N.; Henry, B.N.; McGann, A.V. A fractional order recovery SIR model from a stochastic process. Bull. Math. Biol. 2016, 78, 468–499. [Google Scholar] [CrossRef] [PubMed]
- Angstmann, C.N.; Henry, B.I.; McGann, A.V. A fractional-order infectivity and recovery SIR model. Fractal Fract. 2017, 1, 11. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, S. A new fractional modelling on susceptible-infected-recovered equations with constant vaccination rate. Nonlinear Eng. 2014, 3, 11–19. [Google Scholar] [CrossRef]
- El-Saka, H.A.A. The fractional-order SIS epidemic model with variable population size. J. Egypt. Math. Soc. 2014, 22, 50–54. [Google Scholar] [CrossRef]
- Ozalp, N.; Demirrci, E. A fractional order SEIR model with vertical transmission. Math. Comput. Model. 2011, 54, 1–6. [Google Scholar] [CrossRef]
- AL-Smadi, M.H.; Gumah, G.N. On the homotopy analysis method for fractional SEIR epidemic model. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 3809–3820. [Google Scholar] [CrossRef]
- Casagrandi, R.; Bolzoni, L.; Levin, S.; Andreasen, V. The SIRC model for influenza A. Math. Biosci. 2006, 200, 152–169. [Google Scholar] [CrossRef]
- Lin, Q.; Zhao, S.; Gao, D.; Lou, Y.; Yang, S.; Musa, S.S.; Wangb, M.H.; Cai, Y.; Wang, W.; Yang, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Xia, S.; Ying, T.; Lu, L. A novel coronavirus (2019-nCoV) causing pneumonia-associated respiratory syndrome. Cell. Mol. Immunol. 2020, 17, 554. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Baskonus, H.M.; Prakasha, D.J.; Kumar, P. A new study of unreported cases of 2019-nCOV epidemic outbreaks. Chaos Solitons Fractals 2020, 138, 109929. [Google Scholar] [CrossRef]
- Liu, Z.; Magal, P.; Seydi, O.; Webb, G. Understanding Unreported Cases in the COVID-19 Epidemic Outbreak in Wuhan, China, and the Importance of Major Public Health Interventions. Biology 2020, 9, 50. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ahmed, S.; Ullah, A.; Shah, K.; Alrabaiah, H.; Arafan, M. Mathematical analysis of SRID model of COVID-19 with Caputo fractional derivative based on real data. Results Phys. 2021, 21, 103772. [Google Scholar] [CrossRef] [PubMed]
- Makinde, O.D. Adomian decomposition approach to a SIR epidemic model with constant vaccination strategy. Appl. Math. Comput. 2007, 184, 842–848. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new algorithm for calculating Adomain polynomials for nonlinear operators. Appl. Math. Comput. 2000, 111, 53–62. [Google Scholar]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Khan, M.; Gondal, M.A. New modified Laplace decomposition algorithm for Blasius flow equation. Adv. Res. Sci. Comput. 2010, 2, 35–43. [Google Scholar]
- Khan, Y. An efficient modification of the Laplace decomposition method for nonlinear equations. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 1373–1376. [Google Scholar] [CrossRef]
- Rida, S.Z.; Arafa, A.A.M.; Gaber, Y.A. Solution of the fractional epidemic model by L-ADM. J. Fract. Calc. Appl. 2016, 7, 189–195. [Google Scholar]
- Liao, S.J. Beyond Perturbation: Introduction to Homotopy Analysis Method; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S.J. Approximate solution technique not depending on small parameters: A special example. Int. J. Nonlinear Mech. 1995, 30, 371–380. [Google Scholar] [CrossRef]
- El-Tawil, M.A.; Huseen, S.N. The q-homotopy analysis method (q-HAM). Int. J. Appl. Math. Mech. 2012, 8, 51–75. [Google Scholar]
- El-Tawil, M.A.; Huseen, S.N. On convergence of the q-homotopy analysis method. Int. J. Contemp. Math. Sci. 2013, 8, 481–497. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013119. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abedl-Rahim, H.R.; Abdel-Aty, A.; Kharabsheh, R.; Alharbi, W.; Abdel-Aty, M. An analytical solution for fractional oscillator in a resisting medium. Chaos Solitons Fractals 2020, 130, 109395. [Google Scholar] [CrossRef]
- Ismail, G.M.; Abedl-Rahim, H.R.; Ahmad, H.; Chu, Y.M. Fractional residual power series method for the analytical and approximate studies of fractional physical phenomena. Open Phys. 2020, 18, 799–805. [Google Scholar] [CrossRef]
- Yadav, S.; Kumar, D.; Singh, G.; Bleanu, D. Analysis and dynamics of fractional order COVID-19 model with memory effect with. Results Phys. 2021, 24, 104017. [Google Scholar] [CrossRef]
- Bleanu, D.; Mohammad, H.; Rezapour, S. A fractional differential equation model for the COVID-19 transmission by using Caputo-Fabrizio derivative. Adv. Diff. Equ. Phys. 2020, 299, 1–27. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Baleanu, D.; Aydogn, S.M.; Mohammadi, H.; Rezapour, S. On modelling of epidemic childhood diseases with the Caputo-Fabrizio derivative by using the Laplace Adomian decomposition method. Alex. Eng. J. 2020, 59, 3029–3039. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Mustafa, S.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Diffusion Equations by Natural Transform Decomposition Method. Entropy 2019, 21, 557. [Google Scholar] [CrossRef]
- Alotaibi, H.; Abo-Dahab, S.M.; Abdlrahim, H.R.; Kilany, A.A. Fractional calculus of thermoelastic of P-waves reflection under influence of gravity and electromagnetic field. Fractals 2020, 8, 2040037. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kumar, S. New treatment of fractional Fornberg-Whitham equation via Laplace transform. Ain Shams Eng. J. 2013, 4, 557–562. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; p. 198. [Google Scholar]
- Mittag-Leffler, G. Sur la Nouvelle Fonction Eα(x). C. R. Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel Fractional differential equations. Prog. Fract. Diff. Appl. 2015, 2, 73–85. [Google Scholar]
- Mainardi, F.; Rionero, S.; Ruggeeri, T. On the Initial Value Problem for the Fractional Diffusion-Wave Equation in Waves and Stability Continuous Media; World Scientific: Singapore, 1994; Volume 23, pp. 246–251. [Google Scholar]
- Wiman, A. Über den Fundamentalsatz in der Teorie der Funktionen. Acta Math. 1905, 29, 191–201. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus; its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Babakhani, A.; Daftardar-Gejj, V. On calculus of local fractional derivative. J. Math. Anal. Appl. 2002, 270, 66–79. [Google Scholar] [CrossRef]
- Hemeda, A.A.; Eladdad, E.E.; Lairje, A. Local fractional analytical methods for solving wave equations with local fractional derivative. Math. Meth. Appl. Sci. 2018, 41, 2515–2529. [Google Scholar] [CrossRef]
- Tarasov, V.E. Local fractional derivatives of differentiable functions are integer-order derivatives or zero. Int. J. Appl. Comput. Math. 2016, 2, 195–201. [Google Scholar] [CrossRef]
- Kolwankar, K.M.; Gangal, A.D. Holder exponents of irregular singles and local fractional derivatives. Pramana J. Phys. 1997, 48, 49–68. [Google Scholar] [CrossRef]
- Georgiev, S.G. Fractional Dynamic Calculus and Fractional Dynamic Equations on Time Scales; Springer International Publishing: Sofia, Bulgaria, 2018. [Google Scholar]
- Chen, W.; Liang, Y. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Ca, W.; Chen, W.; Xu, W. The fractal derivative wave equation: Application to clinical amplitude/velocity reconstruction imaging. J. Acoust. Soc. Am. 2018, 143, 1559–1566. [Google Scholar] [CrossRef] [PubMed]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. New derivatives on the fractal subset of real-line. Entropy 2016, 18, 1. [Google Scholar] [CrossRef]
- Allwright, A.; Atangana, A. Fractal advection-dispersion equation for groundwater transport in fractured aquifers with self-similarities. Eur. Phys. J. Plus 2018, 48, 133. [Google Scholar] [CrossRef]
- Hu, Z.; Tu, X. A new discrete economic model involving generalized fractal derivative. Adv. Differ. Equ. 2015, 2015, 1–11. [Google Scholar] [CrossRef]
- Sintunavarat, W.; Turab, A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-fractional operator. Math. Comput. Simul. 2022, 198, 65–84. [Google Scholar] [CrossRef]
- Perez, J.E.S.; Francisco, J.; Aguilar, G.; Baleanu, D.; Tchier, F.; Ragoub, L. Anti-synchronization of chaotic systems using a fractional conformable derivative with power law. Math. Meth. Appl. Sci. 2021, 44, 8286–8301. [Google Scholar] [CrossRef]
- Rezapour, S.; Souid, M.S.; Bouazza, Z.; Hussain, A.; Etemad, S. On the Fractional Variable Order Thermostat Model: Existence Theory on Cones via Piece-Wise Constant Functions. J. Funct. Space 2022, 2020, 8053620. [Google Scholar] [CrossRef]
- Watugala, G.K. Sumudu transform-a new integral transform to solve differential equations and control engineering problems. Math. Eng. Ind. 1993, 24, 35–43. [Google Scholar] [CrossRef]
- Eltayeb, H.; Kılıçman, A. Application of Sumudu Decomposition Method to Solve Nonlinear System of Partial Differential Equations. Abstr. Appl. Anal. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Karaballi, A.A.; Kalla, S.L. Analytical investigations of the Sumudu transform and applications to integral production equations. Math. Probl. Eng. 2003, 2003, 103–118. [Google Scholar] [CrossRef]
- Katatbeh, Q.D.; Belgacem, F.B.M. Applications of the Sumudu transform to fractional differential equations. Nonlinear Stud. 2011, 18, 99–112. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform-properties and applications. NUST. J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Silambarasan, R.; Belgacem, F.B.M. Applications of the natural transform to Maxwell’s equation. Prog. Electromagn. Res. Symp. Proc. 2011, 899–902. [Google Scholar] [CrossRef]
- Al-Omari, S.K.Q. On the applications of natural transform. Int. J. Pure Appl. Math. 2013, 85, 729–744. [Google Scholar] [CrossRef]
- Bulut, H.; Baskonus, H.M.; Belgacem, F.B.M. The analytical solution of some fractional ordinary differential equations by the Sumudu transform method. Abstr. Appl. Anal. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Loonker, D.; Banerji, P.K. Natural transform for distribution and Boehmian spaces. Math. Eng. Sci. Aerosp. 2013, 4, 69–76. [Google Scholar]
- Loonker, D.; Banerji, P.K. Natural transform and solution of integral equations for distribution spaces. Am. J. Math. Sci. 2013, 3, 65–72. [Google Scholar]
- Loonker, D.; Banerji, P.K. Applications of natural transform to differential equations. J. Indian Acad. Math. 2013, 35, 151–158. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R.F.M. Theory of natural transform. Math. Eng. Sci. Aerosp. 2012, 3, 99–124. [Google Scholar]
- Baskonus, H.M.; Bulut, H.; Pandir, Y. The natural transform decomposition method for linear and nonlinear partial differential equations. Math. Eng. Sci. Aerosp. 2014, 5, 111–126. [Google Scholar]
- Chen, T.; Rui, J.; Wang, Q.; Zhao, Z.; Cui, J.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdl-Rahim, H.R.; Zayed, M.; Ismail, G.M. Analytical Study of Fractional Epidemic Model via Natural Transform Homotopy Analysis Method. Symmetry 2022, 14, 1695. https://doi.org/10.3390/sym14081695
Abdl-Rahim HR, Zayed M, Ismail GM. Analytical Study of Fractional Epidemic Model via Natural Transform Homotopy Analysis Method. Symmetry. 2022; 14(8):1695. https://doi.org/10.3390/sym14081695
Chicago/Turabian StyleAbdl-Rahim, Hamdy R., Mohra Zayed, and Gamal M. Ismail. 2022. "Analytical Study of Fractional Epidemic Model via Natural Transform Homotopy Analysis Method" Symmetry 14, no. 8: 1695. https://doi.org/10.3390/sym14081695
APA StyleAbdl-Rahim, H. R., Zayed, M., & Ismail, G. M. (2022). Analytical Study of Fractional Epidemic Model via Natural Transform Homotopy Analysis Method. Symmetry, 14(8), 1695. https://doi.org/10.3390/sym14081695





