Extremal Structure on Revised Edge-Szeged Index with Respect to Tricyclic Graphs

Tongkun Qu; Shengjin Ji

doi:10.3390/sym14081646

and

School of Mathematics and Statistics, Shandong University of Technology, Zibo 255000, China

^*

Author to whom correspondence should be addressed.

Symmetry2022, 14(8), 1646;https://doi.org/10.3390/sym14081646

This article belongs to the Special Issue Symmetry in Graph and Hypergraph Theory

Version Notes

Order Reprints

Abstract

For a given graph G,

S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})

is the revised edge-Szeged index of G, where

m_{u} (e)

and

m_{v} (e)

are the number of edges of G lying closer to vertex u than to vertex v and the number of edges of G lying closer to vertex v than to vertex u, respectively, and

m_{0} (e)

is the number of edges equidistant to u and v. In this paper, we identify the lower bound of the revised edge-Szeged index among all tricyclic graphs and also characterize the extremal structure of graphs that attain the bound.

Keywords:

Wiener index; revised Szeged index; revised edge-Szeged index; tricyclic graphs

MSC:

05C92; 05C12; 05C35; 05C38; 05C75; 05C76

1. Introduction

All graphs considered in this paper are finite, undirected, and simple. The molecular topological index is constructed from the molecular graph mapping, which has applications in physics, chemistry, and network theory. There are relationships between topological indices and some physical properties or some chemical properties. There are nearly a thousand kinds of topological indices that have been proposed since the Wiener index appeared in 1947. The Wiener index is one of the most important chemical topological indexes. For

u, v \in V (G)

,

d (u, v)

denotes the distance between u and v in G. The Wiener index of graph G is defined as follows:

W (G) = \sum_{{u, v} \subseteq V (G)} d (u, v) .

It has been extensively studied, see [1,2,3,4]. The properties and applications of topological indices have been reported in [5,6,7,8,9,10,11,12,13,14,15,16]. Let

e = u v

be an edge of G and define three subsets of

V (G)

as follows:

\begin{matrix} N_{u} (e) = {w \in V (G) : d (u, w) < d (v, w)}, \\ N_{v} (e) = {w \in V (G) : d (u, w) > d (v, w)}, \\ N_{0} (e) = {w \in V (G) : d (u, w) = d (v, w)} . \end{matrix}

Evidently,

N_{u} (e), N_{v} (e), N_{0} (e)

consists of a partition of vertices set V(G) with respect to e. The number of vertices of

N_{u} (e), N_{v} (e), N_{0} (e)

are denoted by

n_{u} (e), n_{v} (e), n_{0} (e)

, respectively. Note that

n_{u} (e) + n_{v} (e) + n_{0} (e) = n

for

| G | = n

. In particular, G is bipartite implies that

n_{0} (e) = 0

holds for each edge

e \in E (G)

; so,

n_{u} (e) + n_{v} (e) = n

.

When T is a tree, the Wiener index has the following formula

W (T) = \sum_{e = u v \in E (T)} n_{u} (e) n_{v} (e) .

Motivated by the above formula, Gutman produced a new graph invariant named the Szeged index and defined it by

S_{z} (G) = \sum_{e = u v \in E (G)} n_{u} (e) n_{v} (e),

where G is an arbitrary graph, not necessarily connected. Randić discovered that Gutman did not consider the contributions of these vertices, which are equidistant to u and v. Thus, he conceived a correctional version of the Szeged index and named it the revised Szeged index. The revised Szeged index of a connected graph G is defined as

S_{z^{*}} (G) = \sum_{e = u v \in E (G)} (n_{u} (e) + \frac{n_{0} (e)}{2}) (n_{v} (e) + \frac{n_{0} (e)}{2}) .

In addition, for a connected graph G, it is well known that

S z^{*} (G) \geq S z (G) \geq W (G)

.

Let an edge

e = u v \in E (G)

; the distance between the edge e and the vertex x, denoted by

d (e, x)

, is defined as

d (e, x) = m i n {d (u, x), d (v, x)}

. Similarly,

M_{0} (e)

is the set of edges equidistant from u and v,

M_{u} (e)

is the set of edges whose distance to vertex u is smaller than the distance to vertex v, and

M_{v} (e)

is the set of edges closer to v than u. The number of edges of

M_{0} (e), M_{u} (e), M_{v} (e)

are marked as

m_{0} (e), m_{u} (e), m_{v} (e)

, respectively. Thus, the edge-Szeged index [17] and the revised edge-Szeged index [18] of G are defined below:

S z_{e} (G) = \sum_{e = u v \in E (G)} m_{u} (e) m_{v} (e),

S z_{e}^{*} (G) = \sum_{e = u v \in E (G)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) .

The results of the edge-Szeged index can be found in [19,20,21,22]. In [7,10,18], the authors determined the maximum values regarding the revised edge-Szeged index for unicyclic graphs, bicyclic graphs, and tricyclic graphs, respectively. In addition, Ref. [9] determined unicyclic graphs with the minimum value of the revised edge-Szeged index. Ref. [23] identified those graphs having the minimum value of the revised edge-Szeged index among all bicyclic graphs. Motivated by these results, we study the revised edge-Szeged index on tricyclic graphs. In this paper, we obtain a lower bound of the revised edge-Szeged index for connected tricyclic graphs.

2. Preliminaries

In the section, we will present some notations and results. If a graph H is obtained by getting rid of as many pendants of G as possible, we say that H is the brace of G. All braces of tricyclic graphs are shown in Figure 1. Let

B_{m}

be the set of tricyclic graphs of order m and

B_{m}^{i}

be the set whose element contains

α_{i}

as its brace for

i = 1, 2, \dots, 15

. Clearly,

B_{m} = \cup_{i = 1}^{15} B_{m}^{i}

. For convenience, let

B_{1} = \cup_{i = 5}^{15} B_{m}^{i}

. We call an edge

e = u v

a pendant edge if

d (u) \geq 3

and

d (v) = 1

.

G ≅ G_{1} \cdot G_{2}

is the graph obtained by fusing two vertices as a new vertex from

G_{1}

and

G_{2}

, respectively, and name it w. w is the fusing vertex of G. Clearly, w is a cut vertex of G. For every

e = u v \in E (G_{1})

, w belongs to one of the three sets

N_{u} (e), N_{v} (e), N_{0} (e)

. Since every path from

u (or v)

to each vertex in

V (G_{2})

is via w, all edges of

G_{2}

must be contained in one of the three sets

M_{u} (e), M_{v} (e), M_{0} (e)

(they are similar to w). Therefore, the contribution of

G_{2}

to the item

(m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})

completely relies on the number of the edges in

G_{2}

; in other words, changing the structure of

G_{2}

cannot alter the value of

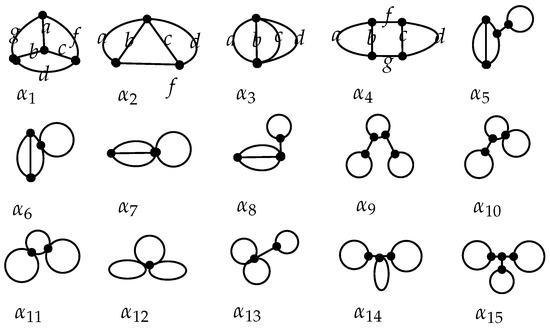
\sum_{e = u v \in E (G_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2})

.

Figure 1. The braces in

B_{m}

.

Dong et al. [18] acquired the lower bound of the revised edge-Szeged index among all unicyclic graphs with size m.

Theorem 1.

Suppose G is a unicyclic graph with size m. Then,

S z_{e}^{*} (G) \geq \{\begin{matrix} \frac{1}{2} m^{2} + \frac{23}{4} m - 15, & m \geq 15, \\ \frac{3}{4} m^{2} + \frac{5}{4} m - \frac{15}{4}, & m \leq 15 \end{matrix}

with equality, if and only if

G ≅ S_{m, 3}

for

m \leq 14

,

G ≅ S_{m, 3}

,

S_{m, 4}

for

m = 15

, and

G ≅ S_{m, 4}

for

m \geq 16

.

Soon after, Liu et al. [23] showed the lower bound of bicyclic graphs with the revised edge-Szeged index.

Theorem 2.

Let G be a connected bicyclic graph with size m. Then,

S z_{e}^{*} (G) \geq \{\begin{matrix} \frac{1}{2} m^{2} + \frac{47}{4} m - 30, & if m \geq 17, and^{'} =^{'} holds iff G ≅ A_{1}, \\ \frac{3}{4} m^{2} + \frac{29}{4} m - \frac{99}{4}, & if 13 \leq m \leq 16, and^{'} =^{'} holds iff G ≅ A_{2}, \\ m^{2} + \frac{11}{4} m - \frac{15}{2}, & if 7 \leq m \leq 12, and^{'} =^{'} holds iff G ≅ A_{3}, \\ 45, & if m = 6, and^{'} =^{'} holds iff G ≅ A_{3}, A_{0}, \\ \frac{121}{4}, & if m = 5, and^{'} =^{'} holds iff G ≅ A_{3} . \end{matrix}

In this paper, for tricyclic graphs, the minimum value of

S z_{e}^{*}

is determined.

Theorem 3.

Let G be a connected tricyclic graph of size m. Then,

S z_{e}^{*} (G) \geq \{\begin{matrix} \frac{1}{2} m^{2} + \frac{71}{4} m - 45, & if m \geq 16, and^{'} =^{'} holds iff G ≅ A_{4}, \\ \frac{3}{4} m^{2} + \frac{53}{4} m - \frac{159}{4}, & if 12 \leq m \leq 15, and^{'} =^{'} holds iff G ≅ A_{5}, \\ m^{2} + \frac{35}{4} m - \frac{57}{2}, & if 11 \leq m \leq 12, and^{'} =^{'} holds iff G ≅ A_{6}, \\ \frac{5}{4} m^{2} + \frac{23}{4} m - \frac{51}{2}, & if m \leq 10, and^{'} =^{'} holds iff G ≅ B_{1} . \end{matrix}

By

m_{u} (e) + m_{v} (e) + m_{0} (e) = m

, we have an equivalent formula of the revised edge-Szeged index.

\begin{matrix} S z_{e}^{*} (G) & = \sum_{e = u v \in E (G)} (m_{u} (e) + m_{0} (e)) (m_{v} (e) + m_{0} (e)) \\ = \sum_{e = u v \in E (G)} (\frac{m + m_{u} (e) - m_{v} (e)}{2}) (\frac{m - m_{u} (e) + m_{v} (e)}{2}) \\ = \sum_{e = u v \in E (G)} \frac{m^{2} - {(m_{u} (e) - m_{v} (e))}^{2}}{4} \\ = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e = u v \in E (G)} {(m_{u} (e) - m_{v} (e))}^{2} . \end{matrix}

(1)

For brevity, let

δ (e) = | m_{u} (e) - m_{v} (e) |

. Equation (1) is rewritten as

S z_{e}^{*} (G) = \frac{m^{3}}{4} - \frac{1}{4} \sum_{e \in E} δ {(e)}^{2} .

(2)

Based on the property of pendant edge, we have the following two elementary results. Graphs are shown in Figure 2.

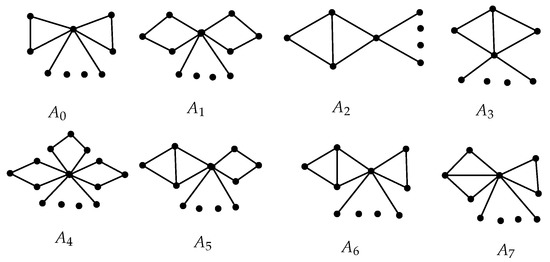
Figure 2. The graphs are used in Theorem 2 and Theorem 3.

Lemma 1.

Let

e \in E (G)

. Then,

δ (e) \leq m - 1

with equality, if and only if e is a pendant edge.

Lemma 2.

Let

G_{2}

be a connected graph of size m. Then,

S z_{e}^{*} (G_{1} \cdot S_{m}) < S z_{e}^{*} (G_{1} \cdot G_{2}),

where the fusing vertex of

G_{1} \cdot S_{m}

is the center vertex of

S_{m}

.

3. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 5}^{15} B_{m}^{i}$

In this section, we identify a lower bound of

S z_{e}^{*} (G)

on

B_{1} = ⋃_{i = 5}^{15} B_{m}^{i}

. Before listing the proof, some preparations are necessary. The next conclusion holds due to Theorem 1.

Lemma 3.

Let

H_{1}

be a connected graph and

H_{2}

be a unicyclic graph with

| E (H_{1}) | = m_{1}

, and

| E (H_{2}) | = m_{2}

. Then,

S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3})

for

m_{1} + m_{2} \leq 14

,

S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 3}) = S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4})

for

m = 15

, and

S z_{e}^{*} (H_{1} \cdot H_{2}) \geq S z_{e}^{*} (H_{1} \cdot S_{m_{2}, 4})

for

m_{1} + m_{2} \geq 16

, where the fusing vertex of

H_{1} \cdot S_{m_{2}, 3} (or H_{1} \cdot S_{m_{2}, 4})

is the center vertex of

S_{m_{2}, 3} (or S_{m_{2}, 4})

.

By means of Theorem 2 and the above result, the next two conclusions are obtained. Note that the fusing vertex of

H_{1} \cdot S_{m_{2}, 3} (or H_{1} \cdot S_{m_{2}, 4})

is the center vertex of

S_{m_{2}, 3} (or S_{m_{2}, 4})

.

Lemma 4.

Let G be a tricyclic graph on order

(m \leq 14)

and H be a bicyclic graph on order

m_{1} \leq m - 3

. If

G = H \cdot S_{m_{2}, 3}

. Then

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{2} \cdot S_{m_{2}, 3})

for

13 \leq m \leq 14

and equality holds only if

H ≅ A_{2}

,

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{3} \cdot S_{m_{2}, 3})

for

m \leq 12

and equality holds only if

H ≅ A_{3}

.

Lemma 5.

Let G be a tricyclic graph on order

m \geq 16

and H be a bicyclic graph on order

m_{1} \leq m - 4

. If

G = H \cdot S_{m_{2}, 4}

, then

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{1} \cdot S_{m_{2}, 4})

for

m \geq 17

with equality, only if

H ≅ A_{1}

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{2} \cdot S_{m_{2}, 4})

for

m = 16

with equality, only if

H ≅ A_{2}

. In particular,

S z_{e}^{*} (A_{2} \cdot S_{m_{2}, 4}) = S z_{e}^{*} (A_{2} \cdot S_{m_{2}, 3})

for

m = 15

.

We now exhibit the proof of Lemma 5.

Proof.

Assume that

m_{1} + m_{2} \geq 17

.

S z_{e}^{*} (A_{1}) \leq S z_{e}^{*} (H)

by Theorem 2. The fusing vertex of

A_{1} \cdot S_{m_{2}, 4}

is the center of

S_{m_{2}, 4}

, and we have

\begin{matrix} S z_{e}^{*} (H \cdot S_{m_{2}, 4}) & = \sum_{e = u v \in E (H \cdot S_{m_{2}, 4})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e = u v \in E (H)} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ + \sum_{e = u v \in E (S_{m_{2}, 4})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = S z_{e}^{*} (H \cdot S_{m_{2}}) - \frac{1}{2} (m_{2} - 1) (m - \frac{1}{2}) \\ + \sum_{e = u v \in E (S_{m_{2}, 4})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ \geq S z_{e}^{*} (A_{1} \cdot S_{m_{2}}) - \frac{1}{2} (m_{2} - 1) (m - \frac{1}{2}) \\ + \sum_{e = u v \in E (S_{m_{2}, 4})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = \sum_{e = u v \in E (A_{1})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ + \sum_{e = u v \in E (S_{m_{2}, 4})} (m_{u} (e) + \frac{m_{0} (e)}{2}) (m_{v} (e) + \frac{m_{0} (e)}{2}) \\ = S z_{e}^{*} (A_{1} \cdot S_{m_{2}, 4}) . \end{matrix}

In the same way, we obtain

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{2} \cdot S_{m_{2}, 4})

for

15 \leq m \leq 16

. □

Theorem 4.

Let

G \in

B_{1}

with m edges. Then,

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{4}) = \frac{1}{2} m^{2} + \frac{71}{4} m - 45

for

m \geq 17

,

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{5})

for

m = 16

,

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{6})

for

13 \leq m \leq 14

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{7})

for

m \leq 12

. In particular,

S z_{e}^{*} (G) \geq S z_{e}^{*} (A_{5}) = S z_{e}^{*} (A_{6})

for

m = 15

.

Proof.

Suppose G belongs to

B_{1}

, and it contains some

α_{i} (i = 5, 6, \cdot \cdot \cdot, 15)

as its brace. It is clear to find a vertex

x \in V (G)

such that

G = H_{1} \cdot H_{2}

with

V (H_{1}) \cap V (H_{2}) = x

and

| H_{1} | + | H_{2} | = m - 1

, where

H_{1}

is a bicyclic subgraph of G, and

H_{2}

is an unicyclic subgraph of G. By means of Lemma 3, we have

S z_{e}^{*} (G) \geq S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 4})

for

m \geq 16

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 3})

for

m \leq 14

. In particular,

S z_{e}^{*} (G) \geq S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 4}) = S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 3})

for

m = 15

.

For

m \geq 15

, from Lemma 5, we deduce that

\begin{matrix} S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 4}) & \geq S z_{e}^{*} (A_{1} \cdot S_{| H_{2} |, 4}) = S z_{e}^{*} (A_{4}) for m \geq 17, \\ S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 4}) & \geq S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 4}) = S z_{e}^{*} (A_{5}) for m = 16, \end{matrix}

S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 4}) \geq S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 4}) = S z_{e}^{*} (A_{5})

, and

S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 3}) \geq S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 3}) = S z_{e}^{*} (A_{6})

for

m = 15

.

Thus, we deduce that

S z_{e}^{*} (A_{5}) = S z_{e}^{*} (A_{6})

by

S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 4}) = S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 3})

for

m = 15

.

For

m \leq 14

, Lemma 4 results in

\begin{matrix} S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 3}) & \geq S z_{e}^{*} (A_{2} \cdot S_{| H_{2} |, 3}) = S z_{e}^{*} (A_{6}) for 13 \leq m \leq 14, \\ S z_{e}^{*} (H_{1} \cdot S_{| H_{2} |, 3}) & \geq S z_{e}^{*} (A_{3} \cdot S_{| H_{2} |, 3}) = S z_{e}^{*} (A_{7}) for m \leq 12 . \end{matrix}

Thus, the proof is finished. □

4. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 1}^{4} B_{m}^{i}$

In this section, we will present the lower bound of

S z_{e}^{*} (G)

on

\cup_{i = 1}^{4} B_{m}^{i}

. If

G \in B_{m}^{i} (i = 1, 2, 3, 4)

, then, it has a subgraph

α_{i}

. Obviously,

α_{i} (i = 1, 2, 3, 4)

is 2-connected. In view of Equation (2), in order to determine the minimum

S z_{e}^{*} (G)

, it is sufficient to to ensure

\sum_{e \in E (G)} δ {(e)}^{2}

is as large as possible. Thus, we assume that the all vertices of G outside its brace are pendant edges. Let

G_{i}, G_{j} \in B_{m}

with edge sets

E_{i}

and

E_{j}

, respectively. From Equation (2),

S z_{e}^{*} (G_{i}) - S z_{e}^{*} (G_{j}) = \sum_{e \in E_{i}} δ {(e)}^{2} - \sum_{e \in E_{j}} δ {(e)}^{2}

. For the sake of brevity, let

t_{i, j} = \sum_{e \in E_{i}} δ {(e)}^{2} - \sum_{e \in E_{j}} δ {(e)}^{2}

. Before showing the main result of the section, we need some preparation. Graphs are shown in Figure 3.

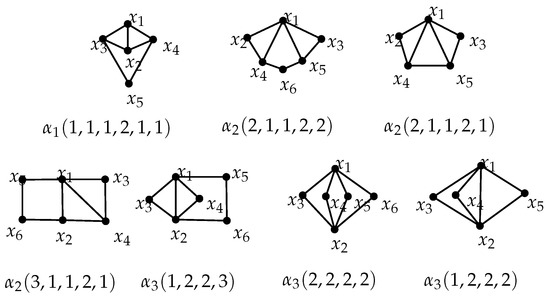
Figure 3. Labeling the vertices of some braces.

Lemma 6.

Suppose G is a tricyclic graph and contains a brace

α_{1} (1, 1, 1, 2, 1, 1)

. Then,

S z_{e}^{*} (G) \geq S z_{e}^{*} (B_{2})

for

m \geq 20

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (B_{3})

for

8 \leq m \leq 19

. Moreover,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{1}

with a brace

α_{1} (1, 1, 1, 2, 1, 1)

. Let

x_{1}, x_{2}, x_{3}, x_{4}, x_{5}

be the five vertices of

α_{1}

, as shown in Figure 3, and

l_{i}

be the number of pendants connecting to

x_{i}

. Assume that

l_{1} + l_{3} \geq l_{2} + l_{4} \geq 1

, let

G_{1}

be the graph obtained from

G_{0}

by deleting the pendant vertices of

x_{2}

and

x_{4}

and adding them to

x_{1}

and

x_{3}

, respectively. We hence have

\begin{matrix} t_{1, 0} & = {(l_{1} + l_{2} - l_{3} - l_{4} - l_{5})}^{2} - {(l_{1} + l_{4} - l_{3} - l_{5})}^{2} + {(l_{3} + l_{4} + l_{5} + 2 - 3)}^{2} \\ - {(l_{2} + l_{4} + 3 - l_{3} - l_{5} - 2)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} - l_{5})}^{2} - {(l_{1} + l_{3} - l_{4} - l_{5})}^{2} \\ + {(l_{3} + l_{4} + 3 - l_{5} - 2)}^{2} - {(l_{2} + l_{3} + 3 - l_{4} - l_{5} - 2)}^{2} + {(l_{1} + l_{2})}^{2} - {(l_{1} - l_{2})}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + 3 - l_{5} - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + 3 - l_{4} - l_{5} - 1)}^{2} \\ + {(l_{1} + l_{2} + 3 - l_{3} - l_{4} - l_{5} - 1)}^{2} - {(l_{1} + l_{2} + l_{4} + 3 - l_{3} - l_{5} - 1)}^{2} \\ = 8 l_{1} l_{2} - 4 l_{2} + 24 l_{3} l_{4} > 0 . \end{matrix}

Let

G_{2}

be the graph from

G_{1}

by shifting the pendant vertices of

x_{5}

to

x_{3}

. Then, we deduce that

\begin{matrix} t_{2, 1} & = {(l_{1} - l_{3} - l_{5})}^{2} - {(l_{1} - l_{3} - l_{5})}^{2} + {(l_{1} + l_{3} + l_{5})}^{2} - {(l_{1} + l_{3} - l_{5})}^{2} \\ + {(3 - l_{3} - l_{5} - 2)}^{2} - {(3 - l_{3} - l_{5} - 2)}^{2} + {(l_{3} + l_{5} + 3 - 2)}^{2} - {(l_{3} + 3 - l_{5} - 2)}^{2} \\ + l_{1}^{2} - l_{1}^{2} + {(l_{1} + l_{3} + l_{5} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - l_{5} - 1)}^{2} \\ + {(l_{1} + 3 - l_{3} - l_{5} - 1)}^{2} - {(l_{1} + 3 - l_{3} - l_{5} - 1)}^{2} \\ = 8 l_{1} l_{5} + 12 l_{3} l_{5} + 12 l_{5} > 0 . \end{matrix}

If

l_{3} > 0

, let

G_{3}

be the graph obtained from

G_{2}

by switching

l_{1}

pendant vertices from

x_{1}

to

x_{3}

. Thus, we verify that

\begin{matrix} t_{3, 2} & = {(l_{1} + l_{3})}^{2} - {(l_{3} - l_{1})}^{2} + {(l_{1} + l_{3})}^{2} - {(l_{1} + l_{3})}^{2} + {(l_{1} + l_{3} + 2 - 3)}^{2} \\ - {(l_{3} + 2 - 3)}^{2} + {(l_{1} + l_{3} + 3 - 2)}^{2} - {(l_{3} + 3 - 2)}^{2} + {(2 - 2)}^{2} - l_{1}^{2} \\ + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} + {(l_{1} + l_{3} + 1 - 3)}^{2} - {(l_{3} + 1 - l_{1} - 3)}^{2} \\ = l_{1}^{2} + 12 l_{1} l_{3} - 8 l_{1} > 0 . \end{matrix}

Combining Equation (2) with the above three relations, we show that

S z_{e}^{*} (G_{0}) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2}) > S z_{e}^{*} (G_{3})

,

G_{3} ≅ B_{3}

. Clearly,

G_{2} ≅ B_{2}

for

l_{3} = 0

. Observe that

S z_{e}^{*} (B_{2}) = m^{2} + \frac{47}{4} m - \frac{190}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45,

S z_{e}^{*} (B_{3}) = \frac{5}{4} m^{2} + \frac{23}{4} m - \frac{102}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Hence, the result holds. □

Graphs are shown in Figure 4.

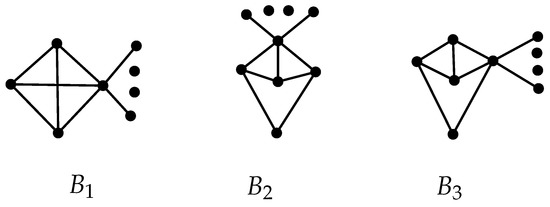
Figure 4. The graphs used in Lemma 6 and Theorem 5.

Lemma 7.

Suppose G includes the brace

α_{2} (3, 1, 1, 2, 1)

. Then,

S z_{e}^{*} (G) \geq S z_{e}^{*} (C_{4})

with equality only if

G ≅ C_{4}

. Moreover,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Let

G (= G_{0}) \in B_{m}^{2}

with a brace

α_{2} (3, 1, 1, 2, 1)

. Label the six vertices

α_{2} (3, 1, 1, 2, 1)

x_{1}, x_{2}, \dots, x_{6}

, as shown in Figure 3.

l_{i}

denotes the number of pendant vertices connecting to

x_{i}

for

i = 1, 2, \dots, 6

. Let

G_{1}

denote the graph obtained from

G_{0}

by deleting the pendant vertices of

x_{5}

and

x_{6}

and adding them to

x_{1}

. If

l_{3} + l_{4} \geq 1

, let

G_{2}

denote the graph obtained from

G_{1}

by moving the pendant vertices of

x_{3}

and

x_{4}

to

x_{1}

and

x_{2}

, respectively. Thus, we obtain

\begin{matrix} t_{1, 0} & = {(l_{1} + l_{3} + l_{5} + l_{6} + 3 - 2 - l_{2})}^{2} - {(l_{1} + l_{3} + l_{5} + 3 - l_{2} - l_{6} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1 - l_{5} - l_{6})}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1 - l_{5} - l_{6})}^{2} \\ + {(l_{1} + l_{3} + l_{5} + l_{6} + 3 - 2 - l_{2})}^{2} - {(l_{1} + l_{3} + l_{5} + 3 - l_{2} - 2 - l_{6})}^{2} \\ + {(l_{1} + l_{2} + l_{5} + l_{6} + 5 - 1 - l_{3} - l_{4})}^{2} - {(l_{1} + l_{2} + l_{5} + l_{6} + 5 - 1 - l_{3} - l_{4})}^{2} \\ + {(l_{4} + l_{2} + 3 - 1 - l_{3})}^{2} - {(l_{2} + l_{4} + l_{6} + 3 - l_{3} - 1)}^{2} + {(l_{3} + l_{4} + 2 - 3 - l_{2})}^{2} \\ - {(l_{2} + l_{6} + 3 - l_{3} - l_{4} - 2)}^{2} + {(l_{1} + l_{5} + l_{6} + 4 - 2 - l_{4})}^{2} - {(l_{1} + l_{5} + 4 - l_{4} - 2)}^{2} \\ = 18 l_{1} l_{6} + 20 l_{3} l_{6} + 10 l_{5} l_{6} + 38 l_{6} + 8 l_{1} l_{5} + 8 l_{2} l_{5} + 8 l_{3} l_{5} + 8 l_{4} l_{5} + 32 l_{5} + 6 l_{4} l_{6} > 0, \end{matrix}

\begin{matrix} t_{2, 1} & = {(l_{1} + l_{2} + l_{3} + l_{4} + 2 - 3)}^{2} - {(l_{1} + l_{3} + 3 - l_{2} - 2)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1)}^{2} \\ - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + 2 - 3)}^{2} - {(l_{1} + l_{3} + 3 - l_{2} - 2)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1)}^{2} \\ - {(l_{1} + l_{2} + 5 - l_{3} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + 3 - 1)}^{2} - {(l_{2} + l_{4} + 3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + 3 - 2)}^{2} - {(l_{2} + 3 - l_{3} - l_{4} - 2)}^{2} + {(4 - 2)}^{2} - {(l_{1} + 4 - l_{4} - 2)}^{2} \\ = l_{1}^{2} + 2 l_{4}^{2} - 6 l_{1} + 20 l_{3} + 12 l_{4} + 12 l_{1} l_{2} + 20 l_{2} l_{3} + 10 l_{2} l_{4} + 12 l_{1} l_{4} + 10 l_{3} l_{4} + 8 l_{1} l_{3} > 0 . \end{matrix}

For

l_{1} > 0

,

G_{3}

denotes the graph from

G_{2}

by switching all pendant vertices from

x_{1}

to

x_{2}

. So, we have

\begin{matrix} t_{3, 2} & = {(l_{1} + l_{2} + 2 - 3)}^{2} - {(3 + l_{1} - 2 - l_{2})}^{2} + {(l_{1} + l_{2} + 5 - 1)}^{2} - {(l_{1} + l_{2} + 5 - 1)}^{2} \\ + {(l_{1} + l_{2} + 5 - 1)}^{2} - {(l_{1} + l_{2} + 5 - 1)}^{2} + {(l_{1} + l_{2} + 2 - 3)}^{2} - {(l_{2} + 2 - l_{1} - 3)}^{2} \\ + {(l_{1} + l_{2} + 5 - 1)}^{2} - {(l_{1} + l_{2} + 5 - 1)}^{2} + {(l_{1} + l_{2} + 3 - 1)}^{2} - {(l_{2} + 3 - 1)}^{2} \\ + {(l_{1} + l_{2} + 3 - 2)}^{2} - {(l_{2} + 3 - 2)}^{2} + {(4 - 2)}^{2} - {(l_{1} + 4 - 2)}^{2} \\ = 3 l_{1}^{2} + 2 l_{1} + 12 l_{1} l_{2} > 0 . \end{matrix}

The above three relations with Equation (2) infer that

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2}) > S z_{e}^{*} (G_{3})

. Clearly,

G_{3} ≅ C_{4}

, and

S z_{e}^{*} (C_{4}) = \frac{3}{4} m^{2} + \frac{69}{4} m - \frac{291}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Hence, we finish the proof. □

Graphs are shown in Figure 5.

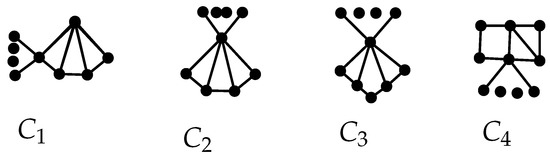
Figure 5. The graphs used in Lemmas 7–9 and Theorem 6.

Lemma 8.

If G has the brace

α_{2} (2, 1, 1, 2, 2)

, then

S z_{e}^{*} (G) \geq S z_{e}^{*} (C_{3})

, and

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{2}

with a brace

α_{2} (2, 1, 1, 2, 2)

. The six vertices of

α_{2} (2, 1, 1, 2, 2)

are labeled as

x_{1}, x_{2}, \dots, x_{6}

, see Figure 3. Let

l_{i}

denote the number of pendent vertices connecting to

x_{i}

. For

l_{6} > 0

, the new graph

G_{1}

is from

G_{0}

by attaching

l_{6}

pendant vertices to

x_{1}

from

x_{6}

. It is deduced that

\begin{matrix} t_{1, 0} & = {(5 + l_{1} + l_{3} + l_{5} + l_{6} - 1 - l_{2})}^{2} - {(5 + l_{3} + l_{5} + l_{1} - 1 - l_{2})}^{2} \\ + {(5 + l_{2} + l_{1} + l_{6} + l_{4} - l_{3} - 1)}^{2} - {(5 + l_{1} + l_{2} + l_{4} - l_{3} - 1)}^{2} \\ + {(4 + l_{3} + l_{1} + l_{6} + l_{5} - 2 - l_{4})}^{2} - {(4 + l_{1} + l_{3} + l_{5} - l_{4} - l_{6} - 2)}^{2} \\ + {(4 + l_{1} + l_{6} + l_{2} + l_{4} - l_{5} - 2)}^{2} - {(4 + l_{1} + l_{2} + l_{4} + l_{4} - l_{5} - l_{6} - 2)}^{2} \\ + {(4 + l_{4} + l_{2} + l_{1} + l_{6} - 2 - l_{5})}^{2} - {(4 + l_{1} + l_{2} + l_{4} - l_{5} - l_{6} - 2)}^{2} \\ + {(4 + l_{3} + l_{5} + l_{1} - 2 - l_{4})}^{2} - {(4 + l_{1} + l_{3} + l_{5} - l_{4} - l_{6} - 2)}^{2} \\ + {(1 + l_{2} - 3 - l_{4})}^{2} - {(l_{2} + 1 - l_{4} - l_{6} - 3)}^{2} \\ + {(l_{3} + 1 - l_{5} - 3)}^{2} - {(l_{3} + 1 - l_{5} - l_{6} - 3)}^{2} \\ = 24 l_{6} + 20 l_{1} l_{6} + 10 l_{2} l_{6} + 9 l_{3} l_{6} > 0 . \end{matrix}

For

l_{2} + l_{4} \geq l_{3} + l_{5} \geq 1

, let

G_{2}

denote the graph from

G_{1}

by shifting the pendant vertices from

x_{3}

and

x_{5}

to

x_{2}

and

x_{4}

, respectively. We deduce that

\begin{matrix} t_{2, 1} & = {(l_{2} + l_{3} + 1 - l_{1} - 5)}^{2} - {(l_{1} + 5 + l_{5} + l_{3} - l_{2} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + 5 - 1)}^{2} \\ - {(l_{1} + l_{2} + l_{4} + 5 - l_{3} - 1)}^{2} + {(l_{1} + 4 - l_{4} - l_{5} - 2)}^{2} - {(l_{1} + 4 + l_{3} + l_{5} - l_{4} - 2)}^{2} \\ + {(4 + l_{1} + l_{2} + l_{3} + l_{4} + l_{5} - 2)}^{2} - {(4 + l_{1} + l_{2} + l_{4} - 2 - l_{5})}^{2} + {(l_{2} + l_{3} + 1 - l_{4} - l_{5} - 3)}^{2} \\ - {(l_{2} + 1 - l_{4} - 3)}^{2} + {(3 - 1)}^{2} - {(l_{3} + 1 - l_{5} - 3)}^{2} + {(4 + l_{1} + l_{2} + l_{3} + l_{4} + l_{5} - 2)}^{2} \\ - {(4 + l_{1} + l_{2} + l_{4} - 2 - l_{5})}^{2} + {(4 + l_{1} - 2 - l_{4} - l_{5})}^{2} - {(l_{5} + 4 + l_{3} + l_{1} - 2 - l_{4})}^{2} \\ = 14 l_{2} l_{3} + 10 l_{3} l_{4} + 10 l_{2} l_{5} + 20 l_{4} l_{5} > 0 . \end{matrix}

Now, assume that

l_{2} + l_{4} \geq 1

, and

l_{3} = l_{5} = 0

. Let

G_{3}

be the graph obtained from

G_{2}

by transferring all pendant vertices from

x_{2}

and

x_{4}

to

x_{1}

.

\begin{matrix} t_{3, 2} & = {(5 + l_{1} + l_{2} + l_{4} - 1)}^{2} - {(5 + l_{1} - 1 - l_{2})}^{2} + {(5 + l_{1} + l_{2} + l_{4} - 1)}^{2} - {(5 + l_{1} - 1 - l_{2})}^{2} \\ + {(4 + l_{1} + l_{2} + l_{4} - 2)}^{2} - {(4 + l_{1} - l_{4} - 2)}^{2} + {(4 + l_{1} + l_{2} + l_{4} - 2)}^{2} - {(l_{1} + l_{2} + l_{4} + 4 - 2)}^{2} \\ + {(1 - 3)}^{2} - {(l_{2} + 1 - l_{4} - 3)}^{2} + {(1 - 3)}^{2} - {(1 - 3)}^{2} + {(l_{1} + l_{2} + l_{4} + 4 - 2)}^{2} \\ - {(l_{1} + l_{2} + l_{4} + 4 - 2)}^{2} + {(4 + l_{1} + l_{2} + l_{4} - 2)}^{2} - {(4 + l_{1} - 2 - l_{4})}^{2} \\ = l_{2}^{2} + l_{4}^{2} + 12 l_{2} + 12 l_{4} + 4 l_{1} l_{2} + 8 l_{1} l_{4} + 6 l_{2} l_{4} > 0 . \end{matrix}

The above relations together with Equation (2) imply that

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2}) > S z_{e}^{*} (G_{3}) .

Observe that

G_{3} ≅ C_{3}

, and

S z_{e}^{*} (C_{3}) = m^{2} + \frac{47}{4} m - 44 > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Consequently, the proof is obtained. □

Lemma 9.

If G includes a brace

α_{2} (2, 1, 1, 2, 1)

, then

S z_{e}^{*} (G) \geq S z_{e}^{*} (C_{1})

for

m \geq 19

,

S z_{e}^{*} (G) \geq S z_{e}^{*} (C_{2})

for

8 \leq m \leq 17

, and

S z_{e}^{*} (C_{1}) = S z_{e}^{*} (C_{2})

for

m = 18

. Moreover,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{2}

with a brace

α_{2} (2, 1, 1, 2, 1)

. We label the five vertices of

α_{2} (2, 1, 1, 2, 1)

as

x_{1}, x_{2}, x_{3}, x_{4}, x_{5}

(see, Figure 3) and denote

l_{i}

the number of pendant vertices connecting to

x_{i}

. Assume that

l_{2} + l_{4} \geq l_{3} + l_{5} \geq 1

by symmetry, let

G_{1}

denote the graph obtained from

G_{0}

by shifting the pendant vertices from

x_{3}

and

x_{5}

to

x_{2}

and

x_{4}

, respectively. We obtain

\begin{matrix} t_{1, 0} & = {(l_{2} + l_{3} + 1 - l_{1} - 4)}^{2} - {(l_{1} + l_{3} + l_{5} + 4 - l_{2} - 1)}^{2} + {(1 + l_{2} + l_{3} - 3 - l_{4} - l_{5})}^{2} \\ - {(l_{2} + 1 - l_{4} - l_{5} - 3)}^{2} + {(l_{1} + 3 - l_{4} - l_{5} - 2)}^{2} - {(l_{1} + l_{3} + 3 - l_{4} - 2)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + 3 - 3)}^{2} - {(l_{2} + l_{4} + 3 - l_{5} - l_{3} - 3)}^{2} + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + 4 - 1)}^{2} \\ - {(l_{1} + l_{2} + l_{4} + 4 - l_{3} - 1)}^{2} + {(l_{4} + l_{5} + 3 - 1)}^{2} - {(l_{4} + l_{5} + 3 - 1 - l_{3})}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 3 - 2)}^{2} - {(l_{1} + l_{2} + 3 - l_{5} - 2)}^{2} \\ = 16 l_{2} l_{3} + 10 l_{4} l_{3} + 10 l_{2} l_{5} + 8 l_{4} l_{5} > 0 . \end{matrix}

For

l_{4} \geq 1

, let

G_{2}

be the graph obtained from

G_{1}

by deleting pendant vertices of

x_{4}

and adding them to

x_{1}

. Then, we arrive at

\begin{matrix} t_{2, 1} & = {(l_{1} + l_{4} + 4 - l_{2} - 1)}^{2} - {(4 + l_{1} - 1 - l_{2})}^{2} + {(l_{1} + l_{4} + 3 - 2)}^{2} - {(l_{1} + 3 - l_{4} - 2)}^{2} \\ + {(l_{1} + l_{2} + l_{4} + 3 - 2)}^{2} - {(l_{1} + l_{2} + 3 - 2)}^{2} + {(l_{1} + l_{2} + l_{4} + 4 - 1)}^{2} - {(l_{1} + l_{2} + l_{4} + 4 - 1)}^{2} \\ + {(l_{2} + 1 - 3)}^{2} - {(l_{2} + 1 - 3 - l_{4})}^{2} + {(l_{2} + 3 - 3)}^{2} - {(l_{2} + l_{4} + 3 - 3)}^{2} + {(3 - 1)}^{2} - {(l_{4} + 3 - 1)}^{2} \\ = l_{4}^{2} + 8 l_{1} l_{4} + 4 l_{4} + 4 l_{2} l_{4} > 0 . \end{matrix}

For

l_{2} > 0

,

l_{1} \geq l_{2} - 2

, let

G_{3}

be the graph obtained from

G_{2}

by moving the pendant vertices from

x_{2}

to

x_{1}

. Thus, we obtain

\begin{matrix} t_{3, 2} & = {(l_{1} + l_{2} + 4 - 1)}^{2} - {(4 + l_{1} - 1 - l_{2})}^{2} + {(l_{1} + l_{2} + 3 - 2)}^{2} - {(l_{1} + 3 - 2)}^{2} \\ + {(l_{1} + l_{2} + 3 - 2)}^{2} - {(l_{1} + l_{2} + 3 - 2)}^{2} + {(l_{1} + l_{2} + 4 - 1)}^{2} - {(l_{1} + l_{2} + 4 - 1)}^{2} \\ + {(1 - 3)}^{2} - {(l_{2} + 1 - 3)}^{2} + {(3 - 3)}^{2} - {(l_{2} + 3 - 3)}^{2} + {(3 - 1)}^{2} - {(3 - 1)}^{2} \\ = 6 l_{1} l_{2} + 18 l_{2} - l_{2}^{2} > 0 . \end{matrix}

For

l_{1} > 0

,

l_{1} \leq l_{2} - 3

, let

G_{4}

be the graph obtained from

G_{2}

by shifting the pendant vertices from

x_{1}

to

x_{2}

. We deduce that

\begin{matrix} t_{4, 2} & = {(l_{1} + l_{2} + 1 - 4)}^{2} - {(4 + l_{1} - 1 - l_{2})}^{2} + {(3 - 2)}^{2} - {(l_{1} + 3 - 2)}^{2} + {(3 - 1)}^{2} - {(3 - 1)}^{2} \\ + {(l_{1} + l_{2} + 3 - 2)}^{2} - {(l_{1} + l_{2} + 3 - 2)}^{2} + {(l_{1} + l_{2} + 4 - 1)}^{2} - {(l_{1} + l_{2} + 4 - 1)}^{2} \\ + {(l_{1} + l_{2} + 1 - 3)}^{2} - {(l_{2} + 1 - 3)}^{2} + {(l_{1} + l_{2} + 3 - 3)}^{2} - {(l_{2} + 3 - 3)}^{2} \\ = l_{1}^{2} + 8 l_{1} l_{2} - 18 l_{1} > 0 . \end{matrix}

The four relations with Equation (2) infer that

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2}) > S z_{e}^{*} (G_{3})

(or

S z_{e}^{*} (G_{4})

), where

G_{3} ≅ C_{2}

for

l_{1} \geq l_{2} - 2

, and

G_{4} ≅ C_{1}

for

l_{1} \leq l_{2} - 3

. Clearly,

S z_{e}^{*} (C_{1}) = \frac{3}{4} m^{2} + \frac{75}{4} m - \frac{357}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45,

S z_{e}^{*} (C_{2}) = \frac{5}{4} m^{2} + \frac{25}{4} m - \frac{105}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Hence, the result holds. □

Lemma 10.

If G has a brace

α_{3} (2, 2, 2, 2)

, then

S z_{e}^{*} (G) \geq S z_{e}^{*} (D_{1})

with equality only if

G ≅ D_{1}

. Furthermore,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{3}

with a brace

α_{3} (2, 2, 2, 2)

.

x_{1}, x_{2}, \dots, x_{6}

denote the six vertices of

α_{3} (2, 2, 2, 2)

with

d (x_{1}) = d (x_{2}) = 4

and

d (x_{i}) = 2

for

3 \leq i \leq 6

, see Figure 3. Let

l_{i}

be the number of pendant vertices connecting to

x_{i}

. Assume that

l_{3} \geq l_{4} \geq l_{5} \geq l_{6}

by symmetry. For

l_{4} + l_{5} + l_{6} \geq 1

, let

G_{1}

denote the graph, which is obtained from G by deleting all pendant vertices of

x_{i} (i \geq 4)

and adding them to

x_{3}

. Thus, we verify that

\begin{matrix} t_{1, 0} & = {(l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 1 - l_{1} - 3)}^{2} - {(l_{1} + l_{4} + l_{5} + l_{6} + 3 - l_{2} - l_{3} - 1)}^{2} \\ + {(1 + l_{1} + l_{3} + l_{4} + l_{5} + l_{6} - 3 - l_{2})}^{2} - {(l_{2} + l_{4} + l_{5} + l_{6} + 3 - l_{1} - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{2} - 1)}^{2} - {(l_{1} + l_{3} + l_{5} + l_{6} + 3 - l_{4} - l_{2} - 1)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{1} - 1)}^{2} - {(l_{2} + l_{3} + l_{5} + l_{6} + 3 - l_{1} - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{2} - 1)}^{2} - {(l_{1} + l_{3} + l_{4} + l_{6} + 3 - l_{2} - l_{5} - 1)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{1} - 1)}^{2} - {(l_{2} + l_{3} + l_{4} + l_{6} + 3 - 1 - l_{1} - l_{5})}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{2} - 1)}^{2} - {(l_{1} + l_{3} + l_{4} + l_{5} + 3 - l_{6} - l_{2} - 1)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 3 - l_{1} - 1)}^{2} - {(l_{2} + l_{3} + l_{4} + l_{5} + 3 - l_{1} - l_{6} - 1)}^{2} \\ = 16 l_{3} l_{4} + 16 l_{3} l_{5} + 16 l_{3} l_{6} + 16 l_{4} l_{5} + 16 l_{4} l_{6} + 16 l_{5} l_{6} > 0 . \end{matrix}

For

l_{1} + l_{2} \geq 1

, let

G_{2}

be the graph obtained from

G_{1}

by shifting the pendant vertices from

x_{i} (i \leq 2)

to

x_{3}

. Then, we have that

\begin{matrix} t_{2, 1} & = {(l_{1} + l_{2} + l_{3} + 1 - 3)}^{2} - {(l_{2} + l_{3} + 1 - l_{1} - 3)}^{2} + {(l_{1} + l_{2} + l_{3} + 1 - 3)}^{2} \\ - {(l_{2} + 3 - l_{1} - l_{3} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - l_{2} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{2} + l_{3} + 3 - l_{1} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} \\ - {(l_{1} + l_{3} + 3 - l_{2} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{2} + l_{3} + 3 - l_{1} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - l_{2} - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} \\ - {(l_{2} + l_{3} + 3 - l_{1} - 1)}^{2} \\ = 32 l_{1} l_{2} + 16 l_{1} l_{3} + 8 l_{2} l_{3} + 16 l_{1} + 16 l_{2} > 0 . \end{matrix}

The two relations with Equation (2) result in

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2})

, and

G_{2} ≅ D_{1}

. Furthermore,

S z_{e}^{*} (D_{1}) = \frac{1}{2} m^{2} + \frac{95}{4} m - 102 > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Thus, we complete the proof. □

Graphs are shown in Figure 6.

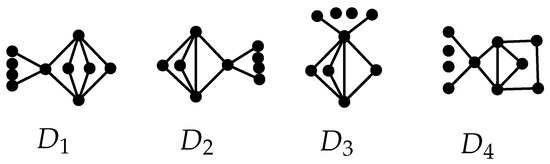
Figure 6. The graphs used in Lemmas 10–12 and Theorem 7.

Lemma 11.

Suppose G contains a brace

α_{3} (1, 2, 2, 2)

. Then,

S z_{e}^{*} (G) \geq S z_{e}^{*} (D_{2})

for

m = 8

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (D_{3})

for

m \geq 10

,

S z_{e}^{*} (D_{2}) = S z_{e}^{*} (D_{3})

for

m = 9

. In addition,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{3}

with a brace

α_{3} (1, 2, 2, 2)

. We label the vertices of

α_{3} (1, 2, 2, 2)

as

x_{1}, x_{2}, x_{3}, x_{4}, x_{5}

with

d (x_{1}) = d (x_{2}) = 4

and

d (x_{i}) = 2

for

i = 3, 4, 5

and denote

l_{i}

the number of pendant vertices connecting to

x_{i}

. Assume that

l_{3} \geq l_{4} \geq l_{5}

by symmetry. For

l_{4} + l_{5} \geq 1

, let

G_{1}

denote the graph obtained from

G_{0}

by shifting the pendant vertices from

x_{i} (i \geq 4)

to

x_{3}

. Thus, we obtain

\begin{matrix} t_{1, 0} & = {(l_{3} + l_{4} + l_{5} + 1 - l_{1} - 3)}^{2} - {(l_{1} + l_{4} + l_{5} + 3 - l_{3} - 1)}^{2} \\ + {(1 + l_{3} + l_{4} + l_{5} - 3 - l_{2})}^{2} - {(l_{2} + l_{4} + l_{5} + 3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + 3 - 1)}^{2} - {(l_{1} + l_{3} + l_{5} + 3 - l_{4} - 1)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + 3 - 1)}^{2} - {(l_{2} + l_{3} + l_{5} + 3 - l_{4} - 1)}^{2} \\ + {(l_{1} + 3 - l_{2} - 3)}^{2} - {(l_{1} + 3 - l_{2} - 3)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + 3 - 1)}^{2} - {(l_{1} + l_{3} + l_{4} + 3 - 1 - l_{5})}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + 3 - 1)}^{2} - {(l_{2} + l_{3} + l_{4} + 3 - l_{5} - 1)}^{2} \\ = 2 l_{2} l_{4} + 2 l_{2} l_{5} + 16 l_{3} l_{4} + 16 l_{3} l_{5} + 16 l_{4} l_{5} > 0 . \end{matrix}

For

l_{2} \geq 1

, let

G_{2}

be the graph obtained from

G_{1}

by shifting the pendant vertices from

x_{2}

to

x_{1}

. Then, we have

\begin{matrix} t_{2, 1} & = {(l_{1} + l_{2} + 3 - 1 - l_{3})}^{2} - {(l_{1} + 3 - l_{3} - 1)}^{2} + {(l_{3} + 1 - 3)}^{2} - {(l_{2} + 3 - l_{3} - 1)}^{2} \\ + {(l_{1} + l_{2} + 3 - 3)}^{2} - {(l_{1} + 3 - l_{2} - 3)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} \\ + {(l_{3} + 3 - 1)}^{2} - {(l_{2} + l_{3} + 3 - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} \\ + {(l_{3} + 3 - 1)}^{2} - {(l_{2} + l_{3} + 3 - 1)}^{2} \\ = 2 l_{2}^{2} + 10 l_{1} l_{2} + 4 l_{2} l_{3} + 8 l_{2} > 0 . \end{matrix}

Note that

G_{2} ≅ D_{2}

for

l_{1} = 0

,

l_{3} > 0

, and

G_{2} ≅ D_{3}

for

l_{1} > 0

,

l_{3} = 0

. Assume that

l_{1} > 0

,

l_{3} > 0

.

G_{3}

is the graph from

G_{2}

by switching the pendant vertics from

x_{1}

to

x_{3}

. Then, we have

\begin{matrix} t_{3, 2} & = {(l_{1} + l_{3} + 1 - 3)}^{2} - {(l_{1} + 3 - l_{3} - 1)}^{2} + {(l_{1} + l_{3} + 1 - 3)}^{2} - {(l_{3} + 1 - 3)}^{2} \\ + {(3 - 3)}^{2} - {(l_{1} + 3 - 3)}^{2} + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} \\ + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{3} + 3 - 1)}^{2} + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{1} + l_{3} + 3 - 1)}^{2} \\ + {(l_{1} + l_{3} + 3 - 1)}^{2} - {(l_{3} + 3 - 1)}^{2} \\ = 2 l_{1}^{2} + 10 l_{1} l_{3} - 4 l_{1} > 0 . \end{matrix}

The above relations, combined with Equation (2), infer that

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2}) > S z_{e}^{*} (G_{3})

. Observe that

S z_{e}^{*} (G_{3}) ≅ D_{2}

. Furthermore, we deduce that

S z_{e}^{*} (D_{2}) = \frac{3}{4} m^{2} + \frac{61}{4} m - \frac{255}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45,

S z_{e}^{*} (D_{3}) = \frac{5}{4} m^{2} + \frac{29}{4} m - \frac{129}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Hence, the conclusion holds. □

Lemma 12.

Suppose G includes the subgraph

α_{3} (1, 2, 2, 3)

. Then

S z_{e}^{*} (G) \geq S z_{e}^{*} (D_{4})

.

Proof.

Suppose

G (= G_{0}) \in B_{m}^{3}

with a brace

α_{3} (1, 2, 2, 3)

. We label the vertices of

α_{3} (1, 2, 2, 3)

as

x_{1}, x_{2}, \dots, x_{6}

with

d (x_{1}) = d (x_{2}) = 4

and

d (x_{i}) = 2

for

3 \leq i \leq 5

.

l_{i}

denotes the number of pendant vertices connecting to

x_{i}

. Assume that

l_{4} + l_{5} + l_{6} \geq 1

, and let

G_{1}

denote the graph from

G_{0}

by transferring the pendant vertices from

x_{i} (i \geq 4)

to

x_{3}

. From the two graphs, we deduce that

\begin{matrix} t_{1, 0} & = {(l_{1} + 4 - l_{3} - l_{4} - l_{5} - l_{6} - 1)}^{2} - {(l_{1} + l_{4} + l_{5} + 4 - l_{3} - 1)}^{2} \\ + {(1 + l_{3} + l_{4} + l_{5} + l_{6} - 4 - l_{2})}^{2} - {(l_{2} + l_{4} + l_{6} + 4 - l_{3} - 1)}^{2} \\ + {(l_{1} + 3 - l_{2} - 3)}^{2} - {(l_{1} + l_{5} + 3 - l_{2} - l_{6} - 3)}^{2} \\ + {(l_{1} + l_{3} + l_{4} + l_{5} + l_{6} + 4 - 1)}^{2} - {(l_{1} + l_{3} + l_{5} + 4 - l_{4} - 1)}^{2} \\ + {(l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 4 - 1)}^{2} - {(l_{2} + l_{3} + l_{6} + 4 - l_{4} - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1 - l_{5} - l_{6})}^{2} \\ + {(l_{1} + l_{2} + l_{3} + l_{4} + l_{5} + l_{6} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + l_{4} + 5 - 1 - l_{5} - l_{6})}^{2} \\ + {(l_{1} + 3 - l_{2} - 3)}^{2} - {(l_{1} + l_{5} + 3 - l_{2} - l_{6} - 3)}^{2} \\ = 12 l_{1} l_{6} + 12 l_{5} l_{6} + 12 l_{2} l_{5} + 16 l_{3} l_{5} + 16 l_{4} l_{5} + 16 l_{3} l_{6} + 16 l_{4} l_{6} + 16 l_{3} l_{4} + 20 l_{5} + 20 l_{6} + 24 l_{4} > 0 . \end{matrix}

For

l_{1} + l_{2} \geq 1

, let

G_{2}

be the graph obtained from

G_{1}

by deleting the pendant vertices of

x_{i} (i \leq 2)

and adding them to

x_{3}

. We deduce that

\begin{matrix} t_{2, 1} & = {(l_{1} + l_{2} + l_{3} + 1 - 4)}^{2} - {(l_{3} + 1 - l_{1} - 4)}^{2} + {(l_{1} + l_{2} + l_{3} + 1 - 4)}^{2} - {(l_{3} + 1 - l_{2} - 4)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 4 - 1)}^{2} - {(l_{1} + l_{3} + 4 - 1)}^{2} + {(l_{1} + l_{2} + l_{3} + 4 - 1)}^{2} - {(l_{2} + l_{3} + 4 - 1)}^{2} \\ + {(3 - 3)}^{2} - {(l_{1} + 3 - l_{2} - 3)}^{2} + {(l_{1} + l_{2} + l_{3} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + 5 - 1)}^{2} \\ + {(l_{1} + l_{2} + l_{3} + 5 - 1)}^{2} - {(l_{1} + l_{2} + l_{3} + 5 - 1)}^{2} + {(3 - 3)}^{2} - {(l_{1} + 3 - l_{2} - 3)}^{2} \\ = 12 l_{1} l_{2} + 8 l_{1} l_{3} + 8 l_{2} l_{3} + 12 l_{1} + 12 l_{2} > 0 . \end{matrix}

Combining Equation (2) and the above two relations, we infer that

S z_{e}^{*} (G) > S z_{e}^{*} (G_{1}) > S z_{e}^{*} (G_{2})

and

G_{2} ≅ D_{4}

. Clearly,

S z_{e}^{*} (D_{4}) = m^{2} + \frac{63}{4} m - \frac{316}{4} > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Hence, the proof is complete. □

Graphs are shown in Figure 7.

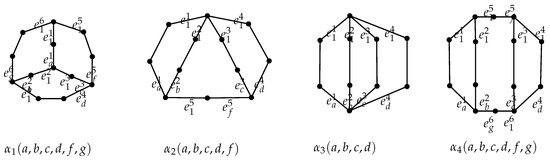
Figure 7. Labeling some edges in the four braces

α_{i} (i = 1, 2, 3, 4)

.

Theorem 5.

Let

G \in G_{m}^{1}

with m edges. Wee have

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

for

m \geq 15

, and

S z_{e}^{*} (G) \geq S z_{e}^{*} (B_{1})

for

m \leq 14

.

Proof.

Suppose

G \in G_{m}^{1}

; then, G has brace

α_{1} (a, b, c, d, f, g)

, as shown in Figure 2. In order to deduce the conclusion, it is sufficient to show

\sum_{e \in E (G)} δ {(e)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

from Equation (2).

Case 1.

α_{1}

has at least three paths with lengths no less than 2.

Subcase 1.1 The three paths enclose a cycle. Assume that the three paths are

P (a), P (b),

and

P (g)

by the symmetry of

α_{1}

. Choose the nine edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{b}^{2}, e_{c}^{3}, e_{d}^{4}, e_{f}^{5}, e_{1}^{6}, e_{g}^{6}

, see Figure 7, and count the value

δ (e)

of the nine edges, respectively. Evidently, they are no less than

m - 7

. It follows that

\sum_{e \in E} δ {(e)}^{2} \leq 9 {(m - 7)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 1.2 The three paths consist of a new path. Assume that the three paths are

P (a), P (b),

and

P (d)

by the symmetry of

α_{1}

. Choose the nine edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{b}^{2}, e_{c}^{3}, e_{1}^{4}, e_{d}^{4}, e_{f}^{5}, e_{1}^{6}

, see Figure 7. Thus, we deduce that

\sum_{e \in E} δ {(e)}^{2} \leq 2 {(m - 6)}^{2} + 4 {(m - 7)}^{2} + 2 {(m - 8)}^{2} + {(m - 9)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 1.3 The three paths share a common vertex. Assume that the three paths are

P (a), P (b),

and

P (c)

by the symmetry of

α_{1}

. Choose the nine edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{b}^{2}, e_{1}^{3}, e_{c}^{3}, e_{1}^{4}, e_{f}^{5}, e_{1}^{6}

, see Figure 7, and count the value

δ (e)

of the nine edges. In fact, they are no less than

m - 7

, which brings about

\sum_{e \in E} δ {(e)}^{2} \leq 3 {(m - 7)}^{2} + 3 {(m - 8)}^{2} + 3 {(m - 9)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Case 2.

α_{1}

contains just two paths with lengths no less than 2.

Subcase 2.1 The two paths belong to the same cycle in

α_{1}

. Assume that the two paths are

P (a), P (b)

by the symmetry of

α_{1}

. Choose eight edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{b}^{2}, e_{1}^{3}, e_{1}^{4}, e_{1}^{5}, e_{1}^{6}

, see Figure 7, and count the

δ (e)

of these edges. Thus, we obtain

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 6)}^{2} + 3 {(m - 7)}^{2} + {(m - 8)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 2.2 The two paths belong to two distinct cycles in

α_{1}

.

In the same way as subcase 2.1, we also verify that

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 5)}^{2} + 4 {(m - 8)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Case 3.

α_{1}

just possesses one path with length no less than 2.

By symmetry, assume the path is

P (d)

with

d \geq 2

. We claim that

d = 2

(If not,

d \geq 3

, we obtain

\sum_{e \in E} δ {(e)}^{2} \leq 6 {(m - 8)}^{2} + 2 {(m - 5)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

). It follows from Lemma 6 that

S z_{e}^{*} (G) \geq S z_{e}^{*} (B_{2})

(or

B_{3}

)

> \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

Case 4. The six paths with length one.

Notice that

α_{1} ≅ K_{4}

. Denote its vertices as

x_{1}, x_{2}, x_{3}, x_{4}

and

l_{i}

the number of

x_{i}

’s pendant vertices. Let

G_{1}

be the graph from

G (= G_{0})

by shifting the pendant vertices from the other three vertices to

x_{1}

. We obtain

t_{1, 0} = 3 {(l_{1} + l_{2} + l_{3} + l_{4})}^{2} - {(l_{1} - l_{2})}^{2} - {(l_{1} - l_{3})}^{2} - {(l_{1} - l_{4})}^{2} - {(l_{2} - l_{3})}^{2} - {(l_{2} - l_{4})}^{2} - {(l_{3} - l_{4})}^{2} = 8 (l_{1} l_{2} + l_{1} l_{3} + l_{1} l_{4} + l_{2} l_{3} + l_{2} l_{4} + l_{3} l_{4}) > 0 .

By Equation (2),

S z_{e}^{*} (G) \geq S z_{e}^{*} (G_{1}) = S z_{e}^{*} (B_{1}) = \frac{5}{4} m^{2} + \frac{23}{4} m - \frac{51}{2} .

In addition,

S z_{e}^{*} (B_{1}) < \frac{1}{2} m^{2} + \frac{71}{4} m - 45

for

m \leq 14

, and

S z_{e}^{*} (B_{1}) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

otherwise. □

Theorem 6.

Let

G \in G_{m}^{2}

with m edges. Then,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G \in G_{m}^{2}

, which implies G has the subgraph

α_{2} (a, b, c, d, f)

as its brace. For symmetry, assume that

a, d \geq 2

. From Equation (2), it is sufficient to confirm that

\sum_{e \in E (G)} δ {(e)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

. We will divide the process into four cases to verify the conclusion.

Case 1.

a, d \geq 3 .

Subcase 1.1.

b = c = f = 1 .

Selecting nine edges

e_{1}^{1}, e_{2}^{1}, e_{a}^{1}, e_{1}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}, e_{1}^{5}

in

α_{2}

, see Figure 7, we deduce that

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 4)}^{2} + 4 {(m - 7)}^{2} + {(m - 9)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 1.2. At least one of

b, c, f

is more than 1. If

b \geq 2 (c \geq 2)

, we choose 10 edges

e_{1}^{1}, e_{2}^{1}, e_{a}^{1}, e_{1}^{2}, e_{b}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}, e_{1}^{5}

, as shown in Figure 7, and deduce

\sum_{e \in E} δ {(e)}^{2} \leq 2 {(m - 4)}^{2} + {(m - 5)}^{2} + 2 {(m - 6)}^{2} + 2 {(m - 8)}^{2} + 3 {(m - 9)}^{2} + (m - 10) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

If

f \geq 2

, choose 10 edges

e_{1}^{1}, e_{2}^{1}, e_{a}^{1}, e_{1}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}, e_{1}^{5}, e_{f}^{5}

, see Figure 7. Thus, we verify that

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 4)}^{2} + 6 {(m - 7)}^{2} + (m - 10) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Case 2.

a \geq 3

,

d = 2

.

Subcase 2.1.

a \geq 4

,

d = 2

, and

b = c = f = 1

. We choose 9 edges

e_{1}^{1}, e_{2}^{1}, e_{3}^{1}, e_{a}^{1}, e_{1}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{1}^{5}

, as shown in Figure 7, and count

δ (e)

of these edges. Thus, we have

\sum_{e \in E} δ {(e)}^{2} \leq {(m - 4)}^{2} + 2 {(m - 5)}^{2} + {(m - 6)}^{2} + 2 {(m - 7)}^{2} + 3 {(m - 8)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 2.2.

a = 3, d = 2

, and

b = c = f = 1 .

The subcase is confirmed by Lemma 6.

Subcase 2.3

a \geq 3, d = 2

, and at least one of

b, c, f

is more than 1. The proof of Subcase 2.3 is similar to Subcase 2.1.

Case 3.

a = d = 2

.

Subcase 3.1. At least one of three numbers

b, c, f

is more than one. If

b \geq 2

(or

c \geq 2

), we choose

e_{1}^{1}, e_{2}^{1}, e_{1}^{2}, e_{b}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{1}^{5}

(see Figure 7) and deduce that

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 5)}^{2} + 4 {(m - 7)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

If

f \geq 3

, we choose

e_{1}^{1}, e_{2}^{1}, e_{1}^{2}, e_{1}^{3}, e_{1}^{4}, e_{2}^{4}, e_{1}^{5}, e_{2}^{5}, e_{f}^{5}

(see Figure 7) and show that

\sum_{e \in E} δ {(e)}^{2} \leq 2 {(m - 5)}^{2} + 2 {(m - 6)}^{2} + 4 {(m - 7)}^{2} + {(m - 9)}^{2} + {(m - 9)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

. If

f = 2

, Lemma 8 means that

S z_{e}^{*} (G) \geq S z_{e}^{*} (C_{3}) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Subcase 3.2 $b = c = f = 1$ .

Applying Lemma 9, we have

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Thus, we confirm the conclusion. □

Theorem 7.

Let

G \in G_{m}^{3}

with m edges. Then,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Since

G \in G_{m}^{3}

, then there is some

α_{3} (a, b, c, d)

as its brace. Without loss of generality, suppose

1 \leq a \leq b \leq c \leq d

. We now divide this into three cases to show the result.

Case 1.

3 \leq a \leq b \leq c \leq d

.

Choose the 12 edges

e_{1}^{1}, e_{2}^{1}, e_{a}^{1}, e_{1}^{2}, e_{2}^{2}, e_{b}^{2}, e_{1}^{3}, e_{2}^{3}, e_{c}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}

(see Figure 7). We deduce that

\sum_{e \in E} δ {(e)}^{2} \leq 8 {(m - 8)}^{2} + 4 {(m - 12)}^{2} + (m - 12) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Case 2.

a = 2

.

Subcase 2.1.

3 \leq b \leq c \leq d

. We choose the 11 edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{2}^{2}, e_{b}^{2}, e_{1}^{3}, e_{2}^{3}, e_{c}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}

(see Figure 7) and show that

\sum_{e \in E} δ {(e)}^{2} \leq 2 {(m - 9)}^{2} + 6 {(m - 7)}^{2} + 3 {(m - 11)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

.

Subcase 2.2.

b = c = d = 2

. The subcase can be verified by Lemma 10.

Case 3.

a = 1 .

Subcase 3.1.

3 \leq b \leq c \leq d

. We deduce that

\sum_{e \in E} δ {(e)}^{2} \leq 6 {(m - 4)}^{2} + 4 {(m - 10)}^{2} + (m - 10) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

, through selecting the 10 edges

e_{1}^{1}, e_{1}^{2}, e_{2}^{2}, e_{b}^{2}, e_{1}^{3}, e_{2}^{3},

e_{c}^{3}, e_{1}^{4}, e_{2}^{4}, e_{d}^{4}

(see Figure 7) in

α_{3}

and figuring out their

δ (e)

.

Subcase 3.2.

b = 2, 3 \leq c \leq d

. The proof of Subcase 3.2 is similar to that of Subcase 3.1. So, the process is omitted here.

Subcase 3.3.

b = c = 2, d \geq 3

. If

d \geq 4

, we choose 9 edges

e_{1}^{1}, e_{1}^{2}, e_{2}^{2}, e_{1}^{3}, e_{2}^{3}, e_{1}^{4}, e_{2}^{4}, e_{3}^{4}, e_{d}^{4}

(see Figure 7) in

α_{3}

and count

δ (e)

of these edges. We deduce that

\sum_{e \in E} δ {(e)}^{2} \leq {(m - 9)}^{2} + 2 {(m - 5)}^{2} + 2 {(m - 7)}^{2} + 4 {(m - 6)}^{2} + (m - 9) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

). We now assume that

d = 3

. The assertion holds from Lemma 12.

Subcase 3.4.

b = c = d = 2

.

The subcase is verified through Lemma 11.

Together with the above discussion, we complete the proof. □

Theorem 8.

Let

G \in G_{m}^{4}

with m edges. Then,

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45

.

Proof.

Suppose

G \in G_{m}^{4}

. Clearly, G has a subgraph

α_{4}

. We choose 8 edges

e_{1}^{1}, e_{a}^{1}, e_{1}^{2}, e_{c}^{3}, e_{1}^{4}, e_{d}^{4}, e_{1}^{5}, e_{1}^{6}

(see Figure 7) and count

δ (e)

of these edges. We show that

\sum_{e \in E} δ {(e)}^{2} \leq 4 {(m - 5)}^{2} + 4 {(m - 8)}^{2} + (m - 8) {(m - 1)}^{2} < m^{3} - 2 m^{2} - 71 m + 180

. Combined with Equation (2),

S z_{e}^{*} (G) > \frac{1}{2} m^{2} + \frac{71}{4} m - 45 .

□

Theorems 4–8 imply Theorem 3.

5. Conclusions

The upper bound of the revised edge-Szeged index on tricyclic graphs was obtained by Liu et al. [7]. This work motivated us to further research these graphs to obtain a sharp lower bound and thereby characterize all graphs that meet the bound with the utilization of the graph operation and asymmetry of graphs. The result completes the extremal value study of tricyclic graphs and enriches the conclusions on the revised edge-Szeged index.

Author Contributions

All authors contriuted to the paper. All authors have read and agreed to the published version of the manuscript.

Funding

Shengjin Ji and Tongkun Qu are supported by Shandong Provincial Natural Science Foundation of China (No. ZR2019MA012).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors thank the reviewers for providing helpful comments and suggestions to improve this paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

Dobrynin, A.; Entringer, R.; Gutman, I. Wienner index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
Gutman, I.; Klavžar, S.; Mohar, B. Fifty Years of the Winner Index. MATCH Commun. Math. Comput. Chem. 1997, 35, 1–259. [Google Scholar]
Gutman, I.; Yeh, Y.; Lee, S.; Luo, Y. Some recent results in the theory of the Winner number. Indian J. Chem. 1993, 32A, 651–661. [Google Scholar]
Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
Aouchiche, M.; Hansen, P. On a conjecture about the Szeged index. Eur. J. Combin. 2010, 31, 1662–1666. [Google Scholar] [CrossRef]
Azari, M. Some variants of the Szeged index under rooted product of graphs. Miskolc Math. Notes 2016, 17, 761–775. [Google Scholar] [CrossRef]
Chen, L.; Li, X.; Liu, M. Tricyclic graphs with maximal revised Szeged index. Discr. Appl. Math. 2014, 177, 71–79. [Google Scholar] [CrossRef]
Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
Khadikar, P.; Karmarkar, S.; Agrawal, V.; Singh, J.; Shrivastava, A.; Lukovits, I.; Diudea, M. Szeged index-Applications for drug modeling. Lett. Drug Des. Disc. 2005, 2, 606–624. [Google Scholar] [CrossRef]
Li, X.; Liu, M. Bicyclic graphs with maximal revised Szeged index. Discr. Appl. Math. 2013, 161, 2527–2531. [Google Scholar] [CrossRef]
Marin, M.; Othman, M.; Abbas, I. An Extension of the Domain of Influence Theorem for Generalized Thermoelasticity of Anisotropic Material with Voids. J. Comput. Theor. Nanosci. 2015, 12, 1594–1598. [Google Scholar] [CrossRef]
Pisanski, T.; Randič, M. Use of the Szeged index and the revised Szeged index for measuring network bipartivity. Discr. Appl. Math. 2010, 158, 1936–1944. [Google Scholar] [CrossRef]
Simić, S.; Gutman, I.; Baltić, V. Some graphs with extremal Szeged index. Math. Slovaca 2000, 50, 1–15. [Google Scholar]
Wang, S. On extremal cacti with respect to the Szeged index. Appl. Math. Comput. 2017, 309, 85–92. [Google Scholar] [CrossRef]
Xing, R.; Zhou, B. On the revised Szeged index. Discr. Appl. Math. 2011, 159, 69–78. [Google Scholar] [CrossRef][Green Version]
Žerovnik, J. Szeged index of symmetric graphs. J. Chem. Inf. Comput. Sci. 1999, 39, 77–80. [Google Scholar] [CrossRef]
Gutman, I.; Ashrafi, A. The edge version of the Szeged index. Croat. Chem. Acta 2008, 81, 263–266. [Google Scholar]
Dong, H.; Zhou, B.; Trinajstić, C. A novel version of the edge-Szeged index. Croat. Chem. Acta 2011, 84, 543–545. [Google Scholar] [CrossRef]
Cai, X.; Zhou, B. Edge Szeged index of Unicyclic graphs. MATCH Commun. Math. Comput. Chem. 2010, 63, 133–144. [Google Scholar]
Khalifeh, M.; Yousefi-Azari, H.; Ashrafi, A.; Gutman, I. The edge Szeged index of product graphs. Croat. Chem. Acta 2008, 81, 277–281. [Google Scholar]
Tranik, N. The edge-Szeged index and the PI index of benzenoid systems in linear time. MATCH Commun. Math. Comput. Chem. 2017, 77, 393–406. [Google Scholar]
Vukičević, D. Note on the graphs with the greatest edge Szeged index. MATCH Commun. Math. Comput. Chem. 2009, 61, 673–681. [Google Scholar]
Liu, M.; Ji, S. Bicyclic graphs with minimal revised edge Szeged index. 2022; submitted. [Google Scholar]

Figure 1. The braces in

B_{m}

.

Figure 2. The graphs are used in Theorem 2 and Theorem 3.

Figure 3. Labeling the vertices of some braces.

Figure 4. The graphs used in Lemma 6 and Theorem 5.

Figure 5. The graphs used in Lemmas 7–9 and Theorem 6.

Figure 6. The graphs used in Lemmas 10–12 and Theorem 7.

Figure 7. Labeling some edges in the four braces

α_{i} (i = 1, 2, 3, 4)

.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Extremal Structure on Revised Edge-Szeged Index with Respect to Tricyclic Graphs

Abstract

1. Introduction

2. Preliminaries

3. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 5}^{15} B_{m}^{i}$

4. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 1}^{4} B_{m}^{i}$

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics

Extremal Structure on Revised Edge-Szeged Index with Respect to Tricyclic Graphs

Abstract

1. Introduction

2. Preliminaries

3. Lower Bound of Sz e * ( G ) on ∪ i = 5 15 B m i

4. Lower Bound of Sz e * ( G ) on ∪ i = 1 4 B m i

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Article Metrics

Citations

Article Access Statistics

3. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 5}^{15} B_{m}^{i}$

4. Lower Bound of ${Sz}_{e}^{*} (G)$ on $\cup_{i = 1}^{4} B_{m}^{i}$