Analytical Properties of Degenerate Genocchi Polynomials of the Second Kind and Some of Their Applications
Abstract
1. Introduction
2. Degenerate Genocchi Polynomials of the Second Kind
3. Degenerate Genocchi Polynomials of the Second Kind Attached with Dirichlet Character
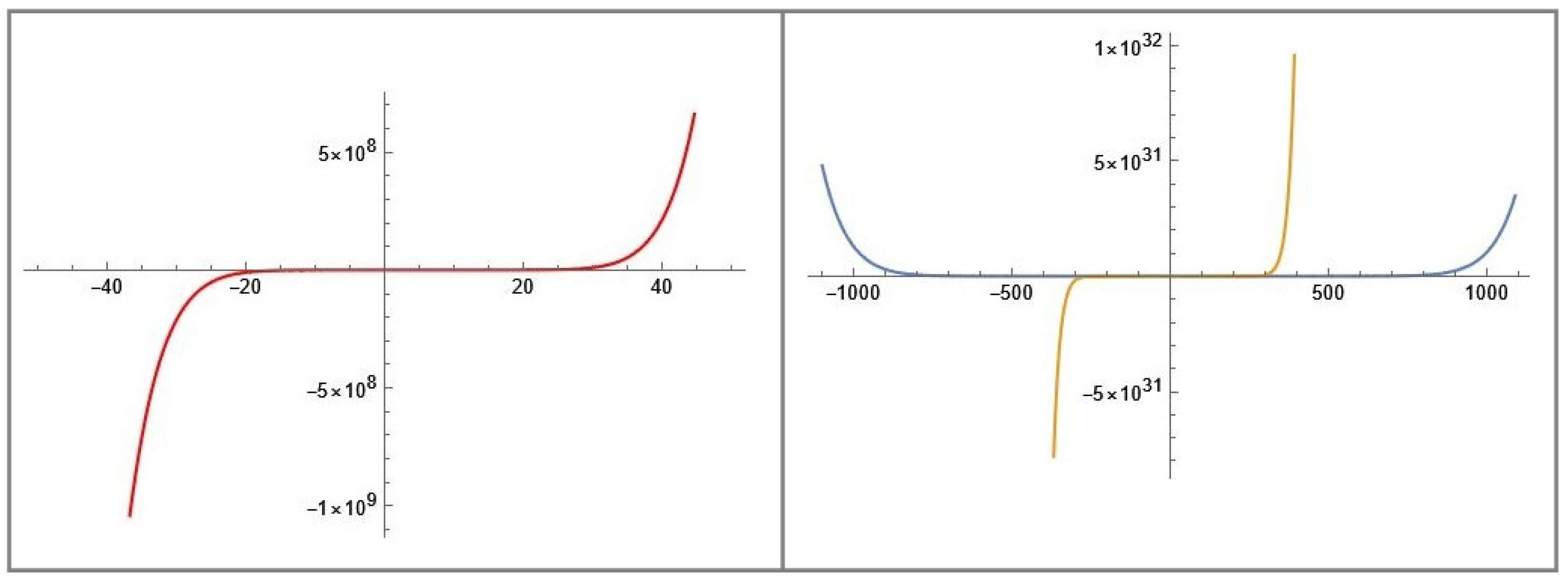
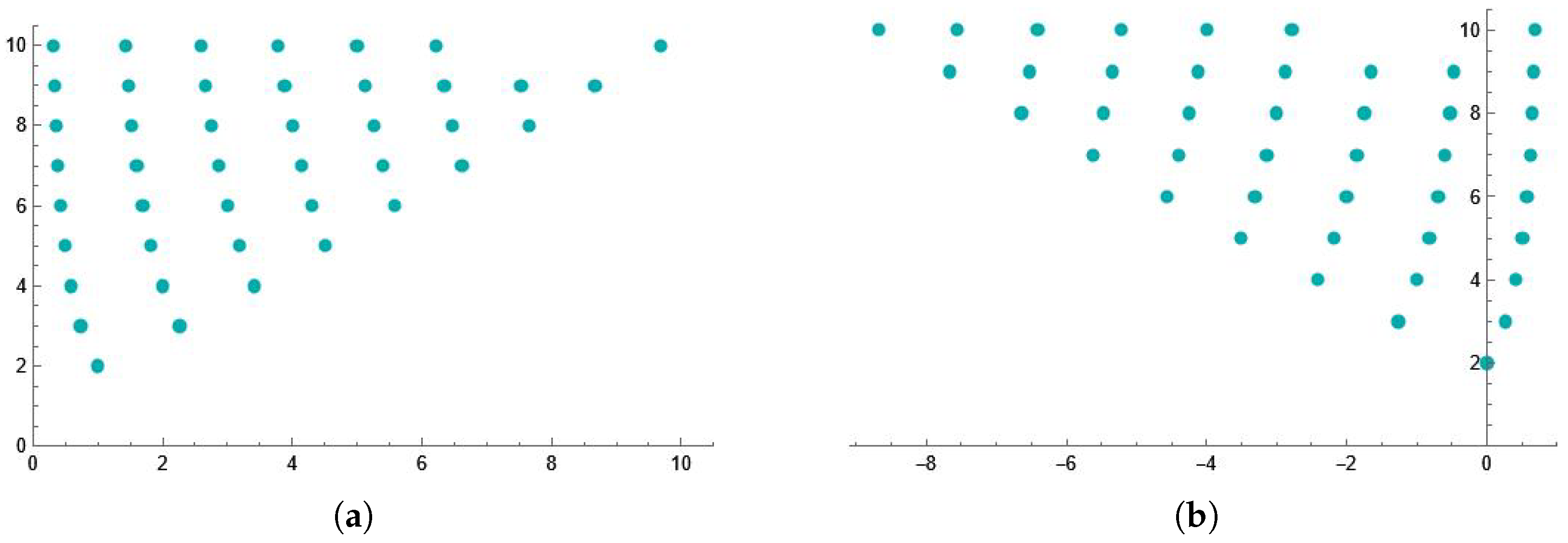
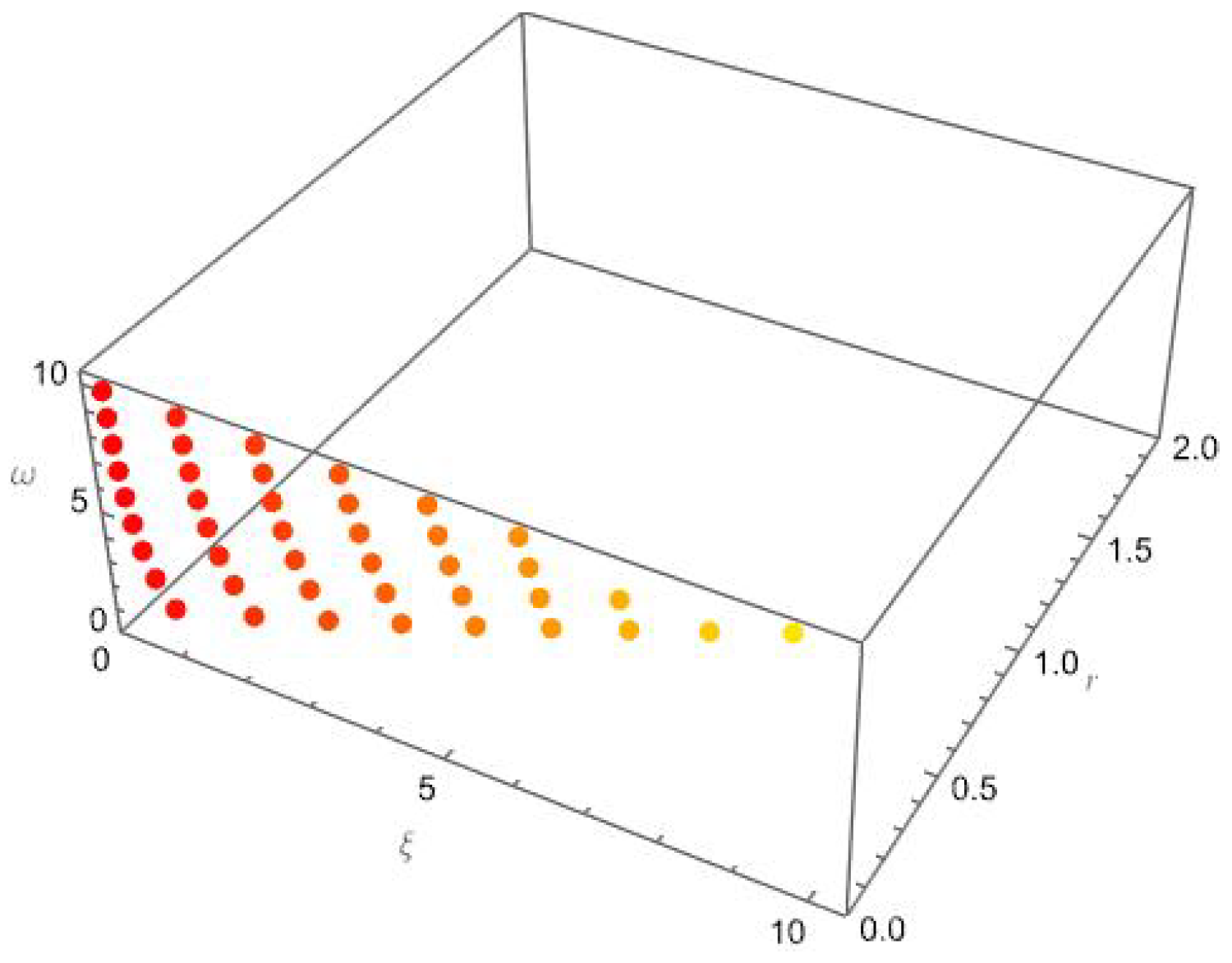
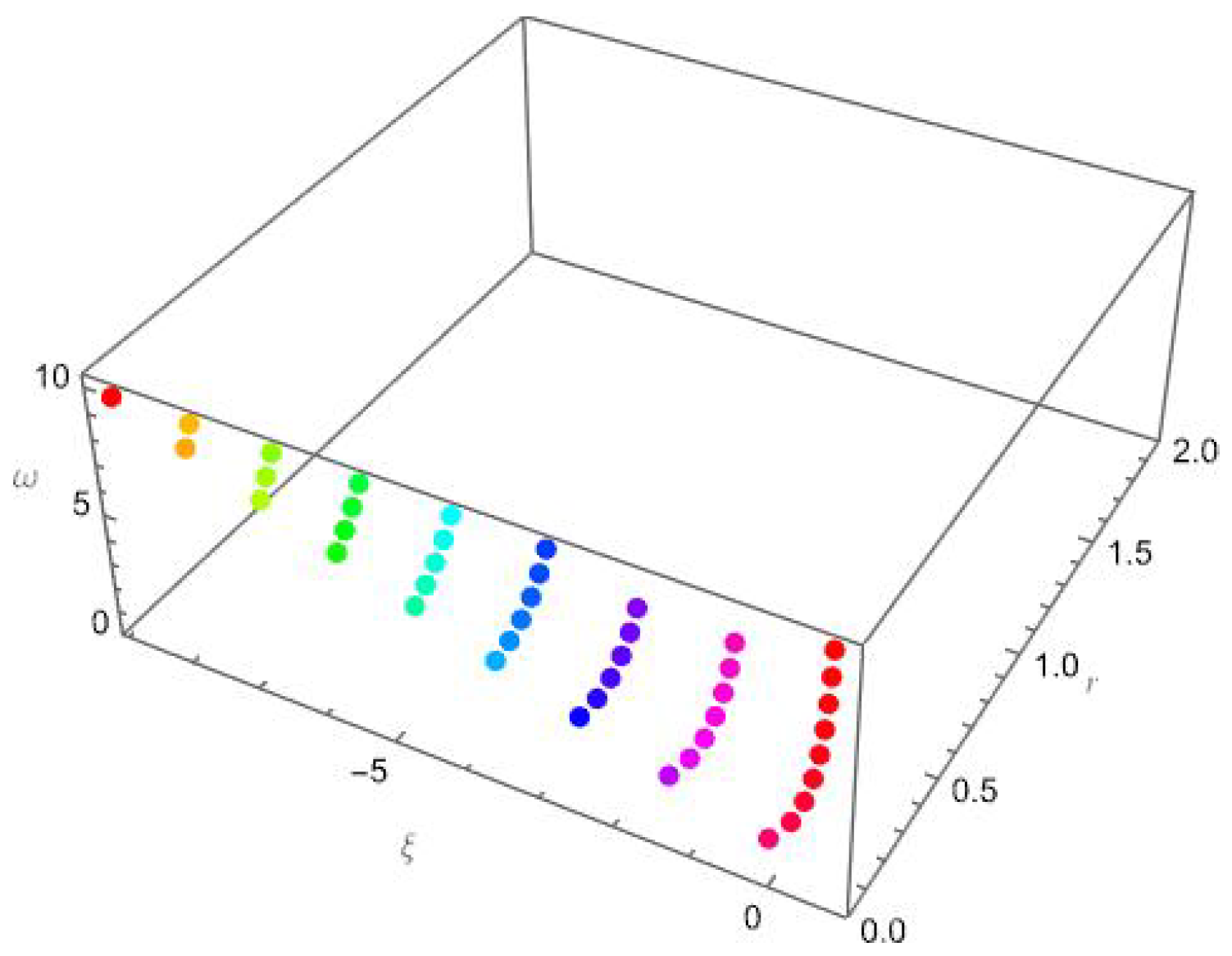
4. Computational Values and Graphical Representations of Degenerate Genocchi Polynomials of the Second Kind
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carlitz, L. Degenerate Stirling Bernoulli and Eulerian numbers. Util. Math. 1979, 15, 51–88. [Google Scholar]
- Carlitz, L. A degenerate Staud-Clausen theorem. Arch. Math. 1956, 7, 28–33. [Google Scholar] [CrossRef]
- Kim, T.; Seo, J.J. Degenerate Bernoulli numbers and polynomials of the second kind. Int. J. Math. Anal. 2015, 9, 1269–1278. [Google Scholar] [CrossRef][Green Version]
- Sharma, S.K.; Khan, W.A.; Araci, S.; Ahmed, S.S. New type of degenerate Daehee polynomials of the second kind. Adv. Differ. Equ. 2020, 2020, 428. [Google Scholar] [CrossRef]
- Sharma, S.K.; Khan, W.A.; Araci, S.; Ahmed, S.S. New construction of type 2 of degenerate central Fubini polynomials with their certain properties. Adv. Differ. Equ. 2020, 2020, 587. [Google Scholar] [CrossRef]
- Khan, W.A.; Araci, S.; Acikgoz, M.; Haroon, H. A new class of partially degenerate Hermite-Genocchi polynomials. J. Nonlinear Sci. Appl. 2017, 10, 5072–5081. [Google Scholar] [CrossRef]
- Khan, W.A.; Acikgoz, M.; Duran, U. Note on the type 2 degenerate multi-poly-Euler polynomials. Symmetry 2020, 12, 1691. [Google Scholar] [CrossRef]
- Khan, W.A. A note on q-analogue of degenerate Catalan numbers associated with p-adic Integral on . Symmetry 2022, 14, 1119. [Google Scholar] [CrossRef]
- Araci, S.; Acikgoz, M. A note on the Frobenius-Euler numbers and polynomials associated with Bernstein polynomials. Adv. Stud. Contemp. Math. (Kyngshang) 2012, 22, 399–406. [Google Scholar]
- Haroon, H.; Khan, W.A. Degenerate Bernoulli numbers and polynomials associated with degenerate Hermite polynomials. Commun. Korean Math. Soc. 2018, 33, 651–669. [Google Scholar]
- Kim, T. Symmetry of power sum polynomials and multivariate fermionic p-adic invariant integral on . Russ. J. Math. Phys. 2009, 16, 93–96. [Google Scholar] [CrossRef]
- Lim, D. Some identities of degenerate Genocchi polynomials. Bull. Korean Math. Soc. 2016, 53, 569–579. [Google Scholar] [CrossRef]
- Jang, L.-C.; Kwon, H.I.; Lee, J.G.; Ryoo, C.S. On the generalized partially degenerate Genocchi polynomials. Glob. J. Pure Appl. Math. 2015, 11, 4789–4799. [Google Scholar]
- Maryam, S.A.; Khan, W.A. New type of degenerate Changhee-Genocchi polynomials. Axioms, 2022; accepted. [Google Scholar]
| 2 | 1 |
| 3 | , |
| 4 | , 2, |
| 5 | , , , |
| 6 | , , 3, , |
| 7 | , , , , , |
| 8 | , , , 4, , , |
| 9 | , , , , , , |
| , | |
| 10 | , , , , 5, , |
| , , |
| 2 | 0 |
| 3 | , |
| 4 | , , |
| 5 | , , , |
| 6 | , , , , |
| 7 | , , , , , |
| 8 | , , , , , , |
| 9 | , , , , , , |
| , | |
| 10 | , , , , , , |
| , , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, W.A.; Alatawi, M.S. Analytical Properties of Degenerate Genocchi Polynomials of the Second Kind and Some of Their Applications. Symmetry 2022, 14, 1500. https://doi.org/10.3390/sym14081500
Khan WA, Alatawi MS. Analytical Properties of Degenerate Genocchi Polynomials of the Second Kind and Some of Their Applications. Symmetry. 2022; 14(8):1500. https://doi.org/10.3390/sym14081500
Chicago/Turabian StyleKhan, Waseem Ahmad, and Maryam Salem Alatawi. 2022. "Analytical Properties of Degenerate Genocchi Polynomials of the Second Kind and Some of Their Applications" Symmetry 14, no. 8: 1500. https://doi.org/10.3390/sym14081500
APA StyleKhan, W. A., & Alatawi, M. S. (2022). Analytical Properties of Degenerate Genocchi Polynomials of the Second Kind and Some of Their Applications. Symmetry, 14(8), 1500. https://doi.org/10.3390/sym14081500






