Multivariate Symmetric Interpolating Dual Multiwavelet Frames

Abstract

The construction of symmetric multiwavelets in the multivariate case with useful in applications properties is a challenging task, mainly due to the complexity of the matrix extension problem. Nevertheless, for the interpolating case, a general technique can be developed. For an appropriate pair of symmetry group $\mathcal{H}$ and matrix dilation M and for a given $\mathcal{H}$-symmetric interpolating refinable matrix mask, a method for the construction of $\mathcal{H}$-symmetric dual refinable matrix masks with a preassigned order of sum rule is suggested. Wavelet matrix masks are constructed using a certain explicit matrix extension algorithm, and their symmetry properties are studied via its polyphase components. The resulting multiwavelet systems form dual multiwavelet frames, where wavelet functions have symmetry properties, preassigned order of vanishing moments and preassigned order of the balancing property. Several examples are presented.

1. Introduction

Wavelet systems are widely used in applied mathematics for signal analysis and synthesis, compression tasks, data preprocessing and feature extraction for neural networks and so on in a large number of applications (see, for example, [1,2,3,4,5,6]). The symmetry property is among the most desirable features for wavelets. Multiwavelets are a natural generalization of usual wavelets (see, for example, [7,8,9] for the pioneering works and [10] for the comprehensive treatment of the subject). Their construction is more flexible since multiwavelets can provide similar to usual wavelets properties but with shorter support or even provide incompatible for usual wavelets properties. For instance, in [11], examples of univariate refinable function vectors with dilation factor $M=2$, which are interpolating, orthonormal, continuous and with compact support simultaneously, were constructed. The paper is devoted to the construction of symmetric multiwavelet systems in the multivariate case with several other useful properties such that desirable number of vanishing moments and high order of the balancing property.

Let us briefly highlight current investigations on the problem of the construction of symmetric multiwavelets. In the univariate case, general methods for the construction of orthogonal and biorthogonal multiwavelets with symmetry were suggested in [12,13]. In the multivariate case, the development of the analogous general methods is a much more difficult task, due to the complexity of the matrix extension problem (see Section 4 for details). General results related to the multivariate extension principle for multiwavelets can be found, for example, in [14,15,16] and the references therein. The symmetry properties of wavelets for the multivariate case can be defined using the notion of symmetry groups (for details see Section 2 and also, for example, [17]). For a simple symmetry group $\mathcal{H}=\{I_d,-I_d\},$ symmetric multiwavelet systems based on lifting scheme were constructed in [18]. Additionally, for the same symmetry group, the construction of symmetric multiwavelet frames as a symmetrization of some multiwavelet frames was suggested in [19]. For a class of appropriate (in some natural sense) symmetry groups $\mathcal{H}$, a numerical method for the construction of interpolating refinable function vectors and their duals with the $\mathcal{H}$-symmetry property, based on solving certain linear systems of equations, was given in [20]. Additionally, a method for getting multiwavelets was suggested in [20], but there were no proofs concerning the properties of the obtained multiwavelet systems, such as symmetry and vanishing moments. A family of symmetric dual multiwavelet frames obtained by convolving scalar wavelets with multiwavelets from [20] in a Kronecker type manner was produced in [21]. To the best of the author’s knowledge, no other approaches related to the construction of symmetric multiwavelets in the multivariate case were suggested.

The results of the paper propose a method for the construction of dual multiwavelet frames, starting from symmetric interpolating refinable function vector in the multivariate case. The construction starts from a pair of appropriate symmetry group $\mathcal{H}$ and matrix dilation M (there are some restrictions on the choice of this pair in the interpolating case, see Section 3 for details). The initial symmetric interpolating matrix mask can be constructed using several methods developed in [20] or [22] (see also [23]). Any preassigned order of the sum rule can be provided for the matrix mask (this property is related to approximation properties of the resulting multiwavelet system). Next, a symmetric dual matrix mask is constructed in two steps. Firstly, a dual matrix mask is constructed using the algorithm in [24]. Further, a symmetrization step is completed. Again, any preassigned order of sum rule can be provided for the dual matrix mask. Finally, the matrix extension principle is used for the construction of wavelet matrix masks. The main point here is to extend two known blocks of rows with trigonometric polynomials up to square matrices of trigonometric polynomials such that the columns of these matrices are biorthogonal. Generally speaking, multivariate matrix extension is not a simple process. However, in the interpolating case, matrix extension can be done explicitly and the symmetry properties for wavelet functions can be provided.

The paper is organized as follows. In Section 2, basic notations and definitions are given, including the description of the action of a symmetry group on a set of digits, which is a key point in the description of symmetry properties for wavelet functions and their masks. Section 3 is devoted to the facts related to the construction of $\mathcal{H}$-symmetric refinable matrix masks with a desirable order of sum rule. This is the starting point in the construction of multiwavelets. In Section 4.1, the construction of $\mathcal{H}$-symmetric dual matrix masks with a desirable order of sum rule is presented. Section 4.2 describes the construction of dual multiwavelet systems with symmetry properties. In Section 4.3, the order of vanishing moments and the balancing property of the obtained multiwavelets are discussed together with some other aspects. In Section 5, several examples are presented.

2. Basic Notations and Definitions

For $x,y\in {\mathbb{R}}^d$, their inner product is denoted by $(x,y):= x_1{y}_1+ \dots +x_d{y}_d$, $x\ge y$ means that $x_j\ge y_j$ for $j=1,\dots ,d$, $\mathbf{0}=(0,\dots ,0)\in {\mathbb{R}}^d$, ${\mathbb{Z}}_{+}^d:=\{x\in {\mathbb{Z}}^d: x\ge \mathbf{0}\}.$ If $\alpha ,\beta \in {\mathbb{Z}}_{+}^d$, $a,b\in {\mathbb{R}}^d$, we set $\left[\alpha \right]={\displaystyle \sum _{j=1}^d}{\alpha }_j$, $\alpha !={\displaystyle \prod _{j=1}^d}{\alpha }_j!$, $\left(\genfrac{}{}{0pt}{}{\beta }{\alpha }\right)=\frac{\alpha !}{\beta !(\alpha -\beta )!}$, $a^b={\displaystyle \prod _{j=1}^d}{a}_j^{b_j}$, $D^{\alpha }f=\frac{{\partial }^{\left[\alpha \right]}f}{\partial x^{\alpha }},$ ${\delta }_{ab}$ is the Kronecker delta. For $n\in \mathbb{N}$, ${\mathsf{\Delta }}_n := \{\alpha : \alpha \in {\mathbb{Z}}_{+}^d, \left[\alpha \right]<n\}.$ For $\beta \in {\mathbb{Z}}_{+}^d$, ${\square }_{\beta }:=\{\alpha :\alpha \in {\mathbb{Z}}_{+}^d, \alpha \le \beta \}.$ The cardinality of a finite set $\mathcal{H}$ is denoted by $\#\mathcal{H}$. The (i,j)-th element of matrix M is denoted by ${\left[M\right]}_{i,j}$ The i-th column of matrix M is denoted by ${\left[M\right]}^i$. ${\ell }_0\left({\mathbb{Z}}^d\right)$ denotes the set of sequences on ${\mathbb{Z}}^d$ with finitely many non-zero elements.

An integer $d\times d$ matrix M is called a dilation matrix if the eigenvalues of M are greater than 1 in absolute value. $M^{*}={\overline{M}}^T$, $I_d$ denotes the $d\times d$ identity matrix, $m=|detM|.$ A complete set of representatives of ${\mathbb{Z}}^d/M{\mathbb{Z}}^d$ is denoted by $D\left(M\right)=\{s_1,\dots ,s_m\}$. An element of $D\left(M\right)$ is called a digit, $D\left(M\right)$ is called the set of digits (see, for example, [25] Section 2.2). We assume that $s_1=\mathbf{0}.$ The coset corresponding to digit $s\in D\left(M\right)$ is denoted by $⟨s⟩$, i.e., $⟨s⟩=s+M{\mathbb{Z}}^d.$ By $\mathcal{D}:=\{⟨s_1⟩,\dots ,⟨s_m⟩\}$, we denote the set of cosets. The set of digits will be frequently used as the index set for some objects, so we assume that the digits are ordered somehow such that the first digit is $s=\mathbf{0}$.

The Fourier transform of a function $f\in L_1\left({\mathbb{R}}^d\right)$ is $\widehat{f}\left(\xi \right)={\int }_{{\mathbb{R}}^d}f\left(x\right)e^{-2\pi i(x,\xi )} dx,$ $\xi \in {\mathbb{R}}^d.$ This notion can be naturally extended to $L_2\left({\mathbb{R}}^d\right)$ and to tempered distributions. For a column vector of functions $\mathsf{\Phi }={({\phi }_1,\dots ,{\phi }_r)}^T$, we set $\widehat{\mathsf{\Phi }}:={({\widehat{\phi }}_1,\dots ,{\widehat{\phi }}_r)}^T$, if applicable.

Additionally, the following lemma, which can be proved by direct computations, will be useful.

Lemma 1.

Let A be a $d\times d$ invertible real-valued matrix, $n\in \mathbb{N},$ $a,b\in {\mathbb{R}}^d.$ For any sufficiently smooth functions f and g defined on ${\mathbb{R}}^d$, the following statements are equivalent

1. 

$D^{\alpha }f\left(x\right){|}_{x=a}=D^{\alpha }g\left(x\right){|}_{x=a}$ for all $\alpha \in {\mathsf{\Delta }}_n$,

2. 

$D^{\alpha }\left(f\left(A^{*}x\right)\right){|}_{x=M^{*-1}a}=D^{\alpha }\left(g\left(A^{*}x\right)\right){|}_{x=M^{*-1}a}$ for all $\alpha \in {\mathsf{\Delta }}_n$,

3. 

$D^{\alpha }\left(f\left(x\right)e^{2\pi i(b,x)}\right){|}_{x=a}=D^{\alpha }\left(g\left(x\right)e^{2\pi i(b,x)}\right){|}_{x=a}$ for all $\alpha \in {\mathsf{\Delta }}_n$.

Action of a Symmetry Group on a Set of Digits

A finite set $\mathcal{H}$ of $d\times d$ unimodular matrices (i.e., integer matrices with determinant equal to $\pm 1$) is a symmetry group with respect to the dilation matrix M, if $\mathcal{H}$ forms a group under the matrix multiplication and $M^{-1}EM\in \mathcal{H}$ for all $E\in \mathcal{H}.$ In what follows, we assume that $\mathcal{H}$ is a symmetry group with respect to some fixed dilation matrix M.

A function $f:{\mathbb{R}}^d\to \mathbb{C}$ is called $\mathcal{H}$-symmetric with respect to the center $c_f\in {\mathbb{R}}^d$, if

$$f(E(·-c_f)+c_f)=f\hspace{1em}\forall E\in \mathcal{H}.$$

For trigonometric polynomials, we use a slightly different definition, which is compatible with the above definition of symmetric functions, if we are dealing with compactly supported refinable functions.

A trigonometric polynomial $t\left(\xi \right)={\sum }_{k\in {\mathbb{Z}}^d}{h}_k{e}^{2\pi i(k,\xi )},$ $h_k\in \mathbb{C},$ is $\mathcal{H}$-symmetric with respect to the center $c\in {\mathbb{R}}^d$, if

$$t\left(E^{*}\xi \right)=e^{2\pi i(Ec-c,\xi )}t\left(\xi \right)\hspace{1em}\forall E\in \mathcal{H},$$

(1)

where $Ec-c\in {\mathbb{Z}}^d$ for all $E\in \mathcal{H}.$ Condition (1) is equivalent to the fact that $h_{Ek}=h_{k+Ec-c}$ $\forall k\in {\mathbb{Z}}^d$ and $\forall E\in \mathcal{H}.$ We say that $c\in {\mathbb{R}}^d$ is an appropriate symmetry center for $\mathcal{H}$, if $Ec-c\in {\mathbb{Z}}^d$ for all $E\in \mathcal{H}$.

It can be checked that for any $E\in \mathcal{H}$, for any coset $⟨s⟩\in \mathcal{D}$ and any appropriate symmetry center $c\in {\mathbb{R}}^d$ for $\mathcal{H}$, there exists a unique $⟨q⟩\in \mathcal{D}$ such that $E⟨s⟩=⟨q⟩+c-Ec$. This fact allows us to define a group action on the set $\mathcal{D}$ by the group $\mathcal{H}$ (associated with the symmetry center c) as follows (for details see, for example, [26,27])

$$E[⟨s⟩]:=⟨q⟩,$$

where $⟨q⟩$ is such that $⟨q⟩=E⟨s⟩-(c-Ec).$

Further, we need some notions and results from group theory (see, for example, [28]). The orbit of $⟨s⟩\in \mathcal{D}$ is $\mathcal{H}[⟨s⟩]=\left\{E\right[⟨s⟩],E\in \mathcal{H}\}$. Clearly, $\mathcal{H}[⟨s⟩]\subset \mathcal{D}$ and two orbits are either equal or disjoint. Denote by $\mathsf{\Lambda }$ the set of representatives from each orbit, then $\mathcal{D}={\cup }_{⟨s⟩\in \mathsf{\Lambda }}\mathcal{H}\left[⟨s⟩\right].$ For convenience, redenote the elements of the set $\mathsf{\Lambda }$ by $⟨s_{p,1}⟩,$ where $p=1,\dots ,\#\mathsf{\Lambda },$ such that $s_{1,1}=\mathbf{0}.$

For a fixed index $p=1,\dots ,\#\mathsf{\Lambda },$ the stabilizer of $⟨s_{p,1}⟩$ is denoted by ${\mathcal{H}}_p:=\{F\in \mathcal{H}:F\left[⟨s_{p,1}⟩\right]=⟨s_{p,1}⟩\}.$ Note that ${\mathcal{H}}_p\subset \mathcal{H}$ and ${\mathcal{H}}_p$ is a subgroup of $\mathcal{H}.$ A left coset of $\mathcal{H}$ by subgroup ${\mathcal{H}}_p$ is a set $E{\mathcal{H}}_p$ where $E\in \mathcal{H}$. Any two left cosets are either coincide or disjoint. $\mathcal{H}/{\mathcal{H}}_p$ denotes the set of left cosets of $\mathcal{H}$ by ${\mathcal{H}}_p$.

Let ${\mathcal{E}}_p$ be a set of representatives of $\mathcal{H}/{\mathcal{H}}_p,$ ${\mathcal{E}}_p\subset \mathcal{H}.$ Then $\mathcal{H}={\bigcup }_{E\in {\mathcal{E}}_p}E{\mathcal{H}}_p$. Thus, the orbit $\mathcal{H}\left[⟨s_{p,1}⟩\right]$ can be represented as

$$\mathcal{H}\left[⟨s_{p,1}⟩\right]=\bigcup _{E\in {\mathcal{E}}_p}E\left[⟨s_{p,1}⟩\right].$$

For a fixed index p, matrices of the set ${\mathcal{E}}_p$ will be denoted by $E^{\left(i\right)}$, $i=1,\dots ,\#{\mathcal{E}}_p.$ We assume that $E^{\left(1\right)}=I_d.$ Define

$$s_{p,i}:=E^{\left(i\right)}{s}_{p,1}-(c-E^{\left(i\right)}c), i=1,\dots ,\#{\mathcal{E}}_p.$$

Then $E^{\left(i\right)}\left[⟨s_{p,1}⟩\right]=⟨s_{p,i}⟩$ and the elements of the orbit $\mathcal{H}\left[⟨s_{p,1}⟩\right]$ are $⟨s_{p,i}⟩,$ where $i=1,\dots ,\#{\mathcal{E}}_p.$ This redefined after the division by orbits set of digits is called to be associated with the symmetry center c and is denoted by $D(M,c)=\{s_{p,i},\hspace{1em}\hspace{1em}p=1,\dots ,\#\mathsf{\Lambda },\hspace{1em}\hspace{1em}i=1,\dots ,\#{\mathcal{E}}_p\}$.

For fixed $p=1,\dots ,\#\mathsf{\Lambda }$, by the Lagrange’s theorem $\#\mathcal{H}=\#{\mathcal{H}}_p·\#{\mathcal{E}}_p$ and for each matrix K in $\mathcal{H}$, there exist unique matrices $E\in {\mathcal{E}}_p$ and $F\in {\mathcal{H}}_p$ such that $K=EF.$ The sets ${\mathcal{E}}_p,$ ${\mathcal{H}}_p$ can be considered the "coordinate axes" of the symmetry group $\mathcal{H}$ (for each $p,$ these “coordinate axes” of $\mathcal{H}$ can be different).

Fix index $p=1,\dots ,\#\mathsf{\Lambda }$. For a matrix $K\in \mathcal{H}$ consider $K\left[⟨s_{p,i}⟩\right]$. There exist matrices $E^{\left(i\right)}\in {\mathcal{E}}_p$ and $F\in {\mathcal{H}}_p$ such that $K=E^{\left(i\right)}F$. Then $K\left[⟨s_{p,1}⟩\right]=E^{\left(i\right)}F\left[⟨s_{p,1}⟩\right]=⟨s_{p,i}⟩$. Next, since $K\left[⟨s_{p,i}⟩\right]=K{E}^{\left(i\right)}\left[⟨s_{p,1}⟩\right],$ there exist matrices $E^{\left(j\right(i,K\left)\right)}\in {\mathcal{E}}_p$ and $F\in {\mathcal{H}}_p$ such that $K{E}^{\left(i\right)}=E^{\left(j\right(i,K\left)\right)}F$. Then $K\left[⟨s_{p,i}⟩\right]=E^{\left(j\right(i,K\left)\right)}F\left[⟨s_{p,1}⟩\right]=⟨s_{p,j(i,K)}⟩$. Here the notation $j(·,K)$ means the map from the set of indices $\{1,\dots ,\#{\mathcal{E}}_p\}$ to itself and the index $j(i,K)$ is uniquely determined by index i and matrix $K\in \mathcal{H}$ for a fixed index $p.$ Additionally, by $r_{p,i}^K$, we denote a special vector from ${\mathbb{Z}}^d$ such that

$$K{s}_{p,i}=s_{p,j(i,K)}+M{r}_{p,i}^K+c-Ec.$$

For convenience, a brief summary of notations related to the action of symmetry group on the set of cosets $\mathcal{D}$ is presented in Table 1.

Table 1. Summary of notations.

Notation	Comments
$⟨s⟩:=s+M{\mathbb{Z}}^d$	the coset corresponding to digit $s\in D\left(M\right)$
$\mathcal{D}:={\mathbb{Z}}^d/M{\mathbb{Z}}^d$	the set of cosets
$E[⟨s⟩]:=E⟨s⟩-(c-Ec)$	action of a matrix $E\in \mathcal{H}$ on the coset $⟨s⟩$
$\mathcal{H}[⟨s⟩]:=\left\{E\right[⟨s⟩],E\in \mathcal{H}\}$	the orbit of $⟨s⟩\in \mathcal{D}$
$\mathsf{\Lambda }:={\left\{⟨s_{p,1}⟩\right\}}_{p=1,\dots ,\#\mathsf{\Lambda }}$	the set of representatives from each orbit
${\mathcal{H}}_p:=\{F\in \mathcal{H}:F\left[⟨s_{p,1}⟩\right]=⟨s_{p,1}⟩\}$	the stabilizer of $⟨s_{p,1}⟩$
${\mathcal{E}}_p$ is such that $\mathcal{H}={\mathcal{E}}_p{\mathcal{H}}_p$	the set of representatives of $\mathcal{H}/{\mathcal{H}}_p$
$⟨s_{p,i}⟩:=E^{\left(i\right)}\left[⟨s_{p,1}⟩\right]$, $i=1,\dots ,\#{\mathcal{E}}_p,$	the elements of the orbit $\mathcal{H}\left[⟨s_{p,1}⟩\right]$, $E^{\left(i\right)}\in {\mathcal{E}}_p$, $E^{\left(1\right)}=I_d$.
$j(i,K)$ is such that $K{E}^{\left(i\right)}=E^{\left(j\right(i,K\left)\right)}F$	index $j(i,K)$ is uniquely defined by i and K
	for $K\in \mathcal{H}$, $E^{\left(i\right)}\in {\mathcal{E}}_p$, $F\in {\mathcal{H}}_p$ for fixed p.
$r_{p,i}^K=M^{-1}(K{s}_{p,i}-s_{p,j(i,K)}+Ec-c)$	a special vector in ${\mathbb{R}}^d$

3. Symmetric Refinable Function Vectors

Consider compactly supported functions ${\phi }_{\nu }:{\mathbb{R}}^d\to \mathbb{C}$, $\nu =1,\dots ,r,$ and denote $\mathsf{\Phi }:={({\phi }_1,\dots ,{\phi }_r)}^T$. $\mathsf{\Phi }$ is called a refinable function vector if it satisfies a refinement equation

$$\mathsf{\Phi }\left(x\right)=m\sum _{k\in {\mathbb{Z}}^d}A\left(k\right)\mathsf{\Phi }(Mx+k),$$

(2)

where a finitely supported sequence of matrices $A={\left\{A\left(k\right)\right\}}_{k\in {\mathbb{Z}}^d}\in {\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{r\times r}$ is called a mask with multiplicityr. The symbol of sequence $A\in {\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{r\times r}$ is defined by

$$\widehat{A}\left(\xi \right)=\sum _{k\in {\mathbb{Z}}^d}A\left(k\right)e^{2\pi i(k,\xi )}, \xi \in {\mathbb{R}}^d,$$

i.e., $\widehat{A}$ is a matrix of trigonometric polynomials, which we will call a matrix mask. If the Fourier transform is applicable, the refinement Equation (2) can be equivalently written as

$$\widehat{\mathsf{\Phi }}\left(\xi \right)=\widehat{A}\left(M^{*-1}\xi \right)\widehat{\mathsf{\Phi }}\left(M^{*-1}\xi \right),\hspace{1em}\xi \in {\mathbb{R}}^d.$$

(3)

It is known ([29] Proposition 1) that the compactly supported distributional solution of the refinement equation is unique (up to multiplication by a constant), when matrix mask $\widehat{A}\left(\xi \right)$ consists of trigonometric polynomials and matrix $\widehat{A}\left(\mathbf{0}\right)$ has only one eigenvalue equal to 1 and others are less than 1 in absolute value.

A refinable function vector $\mathsf{\Phi }={({\phi }_1,\dots ,{\phi }_r)}^T$ is $\mathcal{H}$-symmetric with respect to the row of centers $C:=(c_1,\dots ,c_r),$ $c_{\nu }\in {\mathbb{R}}^d,$ $\nu =1,\dots ,r$, if each function ${\phi }_{\nu }$ is $\mathcal{H}$-symmetric with respect to the center $c_{\nu }$. To define the $\mathcal{H}$-symmetry property for matrix masks, we need an additional notation. Suppose $E\in \mathcal{H}$ and denote

$${\mathcal{S}}_C\left[E\right]\left(\xi \right):=\mathrm{diag}(e^{2\pi i(E{c}_1,\xi )},\dots ,e^{2\pi i(E{c}_r,\xi )}),\hspace{1em}\xi \in {\mathbb{R}}^d.$$

The obvious properties of ${\mathcal{S}}_C\left[E\right]$ are ${\left({\mathcal{S}}_C\left[E\right]\right)}^{-1}={\mathcal{S}}_C[-E]$, ${\mathcal{S}}_C[E+F]={\mathcal{S}}_C\left[E\right]·{\mathcal{S}}_C\left[F\right]$, ${\mathcal{S}}_C\left[E\right]\left(F^{*}\xi \right)={\mathcal{S}}_C\left[FE\right]\left(\xi \right)$. Then the $\mathcal{H}$-symmetry property of $\mathsf{\Phi }$ in terms of the Fourier transform can be written as

$$\widehat{\mathsf{\Phi }}\left(E^{*}\xi \right)=S_C[E-I_d]\left(\xi \right)\widehat{\mathsf{\Phi }}\left(\xi \right)\hspace{1em}\forall E\in \mathcal{H}.$$

Together with the refinable Equation (3) this yields that $\forall E\in \mathcal{H}$

$$\widehat{\mathsf{\Phi }}\left(M^{*}{E}^{*}\xi \right)=\widehat{A}\left(E^{*}\xi \right)\widehat{\mathsf{\Phi }}\left(E^{*}\xi \right)=\widehat{A}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\widehat{\mathsf{\Phi }}\left(\xi \right).$$

On the other hand, since $M^{-1}EM\in \mathcal{H}$, we can write

$$\begin{array}{cc}\hfill \widehat{\mathsf{\Phi }}\left(M^{*}{E}^{*}\xi \right)=\widehat{\mathsf{\Phi }}\left({\left(M^{-1}EM\right)}^{*}{M}^{*}\xi \right)& ={\mathcal{S}}_C[M^{-1}EM-I_d]\left(M^{*}\xi \right)\widehat{\mathsf{\Phi }}\left(M^{*}\xi \right)\hfill \\ \hfill & ={\mathcal{S}}_C[EM-M]\left(\xi \right)\widehat{A}\left(\xi \right)\widehat{\mathsf{\Phi }}\left(\xi \right).\hfill \end{array}$$

This is the motivation for the definition of symmetric matrix masks. We say that matrix mask $\widehat{A}$ is $\mathcal{H}$-symmetric with respect to the row of centers $C=(c_1,\dots ,c_r)$, if

$$\widehat{A}\left(E^{*}\xi \right)={\mathcal{S}}_C[EM-M]\left(\xi \right)\widehat{A}\left(\xi \right){\mathcal{S}}_C[I_d-E]\left(\xi \right)\hspace{1em}\forall E\in \mathcal{H}.$$

(4)

Or, equivalently, the $(\nu ,\mu )-$ th element of the matrix mask $\widehat{A}\left(\xi \right)$ is $\mathcal{H}$-symmetric with respect to the center $M{c}_{\nu }-c_{\mu }$, since

$${\left[\widehat{A}\left(E^{*}\xi \right)\right]}_{\nu ,\mu }={\left[\widehat{A}\left(\xi \right)\right]}_{\nu ,\mu }{e}^{2\pi i(E(M{c}_{\nu }-c_{\mu })-(M{c}_{\nu }-c_{\mu }),\xi )}\hspace{1em}\forall E\in \mathcal{H}.$$

Of course, it should be provided that $E(M{c}_{\nu }-c_{\mu })-(M{c}_{\nu }-c_{\mu })\in {\mathbb{Z}}^d$. But we require a little more. Namely, we say that the row of centers $C=(c_1,\dots ,c_r)$ is appropriate for $\mathcal{H}$, if $E{c}_{\nu }-c_{\nu }\in {\mathbb{Z}}^d$ for all $E\in \mathcal{H}$, $\nu =1,\dots ,r.$ A connection between the $\mathcal{H}$-symmetry of refinable function vector and its matrix mask is stated in the following theorem (see [20,22]).

Theorem 1.

Let $C=(c_1,\dots ,c_r)$ be an appropriate row of centers for $\mathcal{H}$. Suppose $\mathsf{\Phi }={({\phi }_1,\dots ,{\phi }_r)}^T$ is the unique compactly supported solution of the refinement equation with matrix mask $\widehat{A}$ and the multi-integer shifts of refinable function vector Φ are linearly independent. Then Φ is $\mathcal{H}$-symmetric with respect to the row of centers C if and only if matrix mask $\widehat{A}$ is $\mathcal{H}$-symmetric with respect to the row of centers $C.$

Here, the linear independence of the multi-integer shifts of $\mathsf{\Phi }$ means that the synthesis operator ${\mathcal{T}}_{\mathsf{\Phi }}$ is injective, where ${\mathcal{T}}_{\mathsf{\Phi }}$ is defined on ${(\ell \left({\mathbb{Z}}^d\right))}^{1\times r}$ as follows ${\mathcal{T}}_{\mathsf{\Phi }}a={\displaystyle \sum _{\nu =1}^r}{\displaystyle \sum _{k\in {\mathbb{Z}}^d}}{a}^{\left(\nu \right)}\left(k\right){\phi }_{\nu }(·+k)$ for $a=(a^{\left(1\right)},\dots ,a^{(r})\in {(\ell \left({\mathbb{Z}}^d\right))}^{1\times r}$.

Let $n\in \mathbb{N},$ $\widehat{A}$ be a matrix mask. We say that $\widehat{A}$ obeys sum rule of order n (with respect to the dilation matrix M) if there exist a $1\times r$ row of functions $y:{\mathbb{R}}^d\to {\mathbb{C}}^{1\times r}$ such that $y\left(\mathbf{0}\right)\ne 0$,

$$D^{\beta }\left[y\left(M^{*}\xi \right)\widehat{A}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}=D^{\beta }y\left(\xi \right){|}_{\xi =\mathbf{0}},\hspace{1em} \forall \beta \in {\mathsf{\Delta }}_n$$

(5)

and

$$D^{\beta }\left[y\left(M^{*}\xi \right)\widehat{A}(\xi +M^{*-1}q)\right]{|}_{\xi =\mathbf{0}}=0,\hspace{1em} \forall \beta \in {\mathsf{\Delta }}_n,\hspace{1em} \forall q\in D\left(M^{*}\right)\backslash \left\{\mathbf{0}\right\}.$$

(6)

In fact, to formulate and check these conditions, we only need to know the derivatives of y at the origin up to the order n. However, in the paper, it is more convenient to write and apply these conditions using the row of functions y.

A matrix mask $\widehat{A}$ with sum rule of order n implies the accuracy of order n for the corresponding refinable function vector $\mathsf{\Phi }$, which means that polynomials up to order n lies in the shift-invariant space generated by functions ${\phi }_1,\dots ,{\phi }_r$. In more details, suppose that $\mathsf{\Phi }$ is a refinable vector of compactly supported distributions related to matrix mask $\widehat{A}$ and the sequences ${\left\{{\widehat{\phi }}_{\nu }(M^{*-1}q+k)\right\}}_{k\in {\mathbb{Z}}^d},$ $\nu =1,\dots ,r$, are linearly independent for all $q\in D\left(M^{*}\right).$ Then the accuracy of order n for $\mathsf{\Phi }$ is equivalent to the sum rule conditions of order n for $\widehat{A}$ (see ([24] Theorem 2.4) for details). Note that the above conditions about linear independence will be valid if, for example, the multi-integer shifts of $\mathsf{\Phi }$ are linearly independent, since this fact is equivalent to for examplelinear independence of the sequences ${\left\{{\widehat{\phi }}_{\nu }(\xi +k)\right\}}_{k\in {\mathbb{Z}}^d}$, $\nu =1,\dots ,r$, for all $\xi \in {\mathbb{R}}^d$ (see, for example, ([30] Theorem 5.1)). The order of accuracy of $\mathsf{\Phi }$ is related to the approximation order of the corresponding shift-invariant space (see, for example, [31]).

The polyphase component of the mask A corresponding to the digit $s\in D\left(M\right)$ is a sequence $A_s\in {\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{r\times r}$ defined by

$$A_s\left(k\right):=\frac{1}{\sqrt{m}}A(Mk+s),\hspace{1em}k\in {\mathbb{Z}}^d.$$

The polyphase representation of the matrix mask $\widehat{A}$ is

$$\widehat{A}\left(\xi \right)=\frac{1}{\sqrt{m}}\sum _{s\in D\left(M\right)}{e}^{2\pi i(s,\xi )}{\widehat{A}}_s\left(M^{*}\xi \right).$$

(7)

However, it is more convenient to use another partition for the polyphase components. Consider the $\nu$-th column of $\widehat{A}$ and place the columns of its polyphase components into a matrix $\widehat{A^{\left(\nu \right)}}$ for $\nu =1,\dots ,r.$ In other words, the $\nu$-th column of ${\widehat{A}}_s$ is the column with index s in the matrix $\widehat{A^{\left(\nu \right)}}$, i.e. ${\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}^s:={\left[\widehat{A_s}\left(\xi \right)\right]}^{\nu }$ for $\nu =1,\dots ,r,$ $s\in D\left(M\right).$ We call these matrices $\widehat{A^{\left(\nu \right)}}$, $\nu =1,\dots ,r,$ the modified polyphase components of $\widehat{A}$. Note that the following representation is valid

$${\left[\widehat{A}\left(\xi \right)\right]}^{\nu }=\frac{1}{\sqrt{m}}\sum _{s\in D\left(M\right)}{\left[\widehat{A^{\left(\nu \right)}}\left(M^{*}\xi \right)\right]}^s{e}^{2\pi i(s,\xi )},\hspace{1em}\nu =1,\dots ,r.$$

(8)

3.1. Symmetry of the Polyphase Components

Next, we need to reformulate the $\mathcal{H}$-symmetry conditions of a matrix mask in terms of its modified polyphase components. Let us fix an appropriate row of symmetry centers $C=(c_1,\dots ,c_r)$ for the symmetry group $\mathcal{H}.$ Suppose $\widehat{A}$ is an $\mathcal{H}$-symmetric matrix mask, i.e., (4) is valid. Consider this condition by columns:

$${\left[\widehat{A}\left(E^{*}\xi \right)\right]}^{\nu }={\mathcal{S}}_C[M^{-1}EM-I_d]\left(M^{*}\xi \right){\left[\widehat{A}\left(\xi \right)\right]}^{\nu }{e}^{2\pi i(c_{\nu }-E{c}_{\nu },\xi )}\hspace{1em}\forall E\in \mathcal{H},$$

where ${\left[\widehat{A}\right]}^{\nu }$ is the $\nu$-th column of matrix $\widehat{A}$, $\nu =1,\dots ,r$. Note that the certain columns of matrix mask $\widehat{A}$ turn out to be mutually symmetric and this can be described. Recall that matrix $\widehat{A^{\left(\nu \right)}}$ contains the polyphase components of the column ${\left[\widehat{A}\right]}^{\nu }$. It is convenient to index the columns of modified polyphase component $\widehat{A^{\left(\nu \right)}}$ using the digits, while digits are indexed according to their division by orbits with respect to the group action $E[⟨s⟩]:=⟨q⟩,$ where $⟨q⟩$ is such that $⟨q⟩=E⟨s⟩+E{c}_{\nu }-c_{\nu }.$ The corresponding notation for set of digits associated with the symmetry center $c_{\nu }$ is the following:

$$D(M,c_{\nu })=\{s_{p,i}^{\left(\nu \right)},\hspace{1em}p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },\hspace{1em}i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}\}.$$

The “coordinate axes” for $\mathcal{H}$ will be denoted by ${\mathcal{H}}_p^{\left(\nu \right)},$ ${\mathcal{E}}_p^{\left(\nu \right)}.$ Additionally, later we have to deal with several columns of matrix mask $\widehat{A}$ at the same moment, so it will be convenient to use notation $s_{p^{\left(\nu \right)},i^{\left(\nu \right)}}^{\left(\nu \right)}$ for digits from $D(M,c_{\nu })$.

Lemma 2.

A matrix mask $\widehat{A}$ is $\mathcal{H}$-symmetric with respect to the appropriate row of centers $C=(c_1,\dots ,c_r)$ if, and only if, for any fixed $\nu =1,\dots ,r$ and for each $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu }$ the columns ${\left[A^{\left(\nu \right)}\left(\xi \right)\right]}^{(p,i)}$, $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$ satisfy

$${\left[\widehat{A^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)\right]}^{(p,i)}={\mathcal{S}}_C[M^{-1}KM-I_d]\left(\xi \right){\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}^{(p,j)}{e}^{2\pi i(-r_{p,i}^{K,\left(\nu \right)},\xi )}\hspace{1em}\forall K\in \mathcal{H},$$

(9)

where j is such that $K{E}^{\left(i\right)}=E^{\left(j\right)}F$ for matrices $E^{\left(i\right)},E^{\left(j\right)}\in {\mathcal{E}}_p^{\left(\nu \right)}$ and $F\in {\mathcal{H}}_p^{\left(\nu \right)}$, $r_{p,i}^{K,\left(\nu \right)}\in {\mathbb{Z}}^d$ is such that

$$K{s}_{p,i}^{\left(\nu \right)}=s_{p,j}^{\left(\nu \right)}+M{r}_{p,i}^{K,\left(\nu \right)}+c_{\nu }-K{c}_{\nu }.$$

(10)

Proof. 

Suppose $\widehat{A}$ is H-symmetric with respect to the appropriate vector of centers $C=(c_1,\dots ,c_r)$. Let us fix $\nu =1,\dots ,r.$ Then by (7) and (10) we obtain for the $\nu$-th column of $\widehat{A}$ and $K\in H$ that

$$\begin{array}{cc}\hfill {\left[\widehat{A}\left(K^{*}\xi \right)\right]}^{\nu }=& \frac{1}{\sqrt{m}}\sum _{p=1}^{\#{\mathsf{\Lambda }}_{\nu }}\sum _{i=1}^{\#{\mathcal{E}}_p^{\left(\nu \right)}}{\left[A^{\left(\nu \right)}\left(M^{*}{K}^{*}\xi \right)\right]}^{(p,i)}{e}^{2\pi i(K{s}_{p,i},\xi )}\hfill \\ \hfill =& \frac{1}{\sqrt{m}}{e}^{2\pi i(c_{\nu }-K{c}_{\nu },\xi )}\sum _{p=1}^{\#{\mathsf{\Lambda }}_{\nu }}\sum _{i=1}^{\#{\mathcal{E}}_p^{\left(\nu \right)}}{\left[A^{\left(\nu \right)}\left(M^{*}{K}^{*}\xi \right)\right]}^{(p,i)}{e}^{2\pi i(M{r}_{p,i}^{K,\left(\nu \right)},\xi )}{e}^{2\pi i(s_{p,j}^{\left(\nu \right)},\xi )},\hfill \end{array}$$

where index j is connected with i by $j=j(i,K)$, i.e., j is such that $K{E}^{\left(i\right)}=E^{\left(j\right)}F$ for matrices $E^{\left(i\right)},E^{\left(j\right)}\in {\mathcal{E}}_p^{\left(\nu \right)}$ and $F\in {\mathcal{H}}_p^{\left(\nu \right)}$. On the other hand, we have

$$\begin{array}{cc}\hfill {\mathcal{S}}_C& (M^{-1}KM-I_d)\left(M^{*}\xi \right){\left[\widehat{A}\left(\xi \right)\right]}^{\nu }{e}^{2\pi i(c_{\nu }-K{c}_{\nu },\xi )}\hfill \\ \hfill =& \frac{1}{\sqrt{m}}{e}^{2\pi i(c_{\nu }-K{c}_{\nu },\xi )}\sum _{p=1}^{\#{\mathsf{\Lambda }}_{\nu }}\sum _{j=1}^{\#{\mathcal{E}}_p^{\left(\nu \right)}}{\mathcal{S}}_C(M^{-1}KM-I_d)\left(M^{*}\xi \right){\left[A^{\left(\nu \right)}\left(M^{*}\xi \right)\right]}^{(p,j)}{e}^{2\pi i(s_{p,j},\xi )}.\hfill \end{array}$$

Since the polyphase representation is unique with respect to the chosen set of digits $D(M,c_{\nu })$, we obtain (9). The converse statement can be proved by the analogous straightforward computations. □

In particular, for a fixed $\nu =1,\dots ,r$ and $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu }$ for any $F\in {\mathcal{H}}_p^{\left(\nu \right)}$ we obtain

$${\left[\widehat{A^{\left(\nu \right)}}\left({\left(M^{-1}FM\right)}^{*}\xi \right)\right]}^{(p,1)}={\mathcal{S}}_C[M^{-1}FM-I_d]\left(\xi \right){\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}^{(p,1)}{e}^{2\pi i(-r_{p,1}^{F,\left(\nu \right)},\xi )},$$

(11)

where $r_{p,1}^{F,\left(\nu \right)}=M^{-1}F(c_{\nu }+s_{p,1}^{\left(\nu \right)})-M^{-1}(c_{\nu }+s_{p,1}^{\left(\nu \right)}).$ This leads to the fact that matrix element ${\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}_{k,(p,1)}$ is $M^{-1}{\mathcal{H}}_p^{\left(\nu \right)}M-$ symmetric with respect to the center $c_k-M^{-1}(c_{\nu }+s_{p,1}^{\left(\nu \right)}),$ $k=1,\dots ,r.$ Additionally, by the choice of $s_{p,i}^{\left(\nu \right)}$, we obtain

$${\left[\widehat{A^{\left(\nu \right)}}\left({\left(M^{-1}{E}^{\left(i\right)}M\right)}^{*}\xi \right)\right]}^{(p,1)}={\mathcal{S}}_C(M^{-1}{E}^{\left(i\right)}M-I_d)\left(\xi \right){\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}^{(p,i)},$$

(12)

for $E^{\left(i\right)}\in {\mathcal{E}}_p^{\left(\nu \right)}$, $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}.$ By direct computations, it can be checked that matrix element ${\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}_{k,(p,i)}$ is $M^{-1}{\mathcal{H}}_{p,i}^{\left(\nu \right)}M-$ symmetric with respect to the center $c_k-M^{-1}(c_{\nu }+s_{p,i}^{\left(\nu \right)}),$ $k=1,\dots ,r.$ Here ${\mathcal{H}}_{p,i}^{\left(\nu \right)}$ is a conjugate subgroup to ${\mathcal{H}}_p^{\left(\nu \right)}$ by matrix $E^{\left(i\right)}$, namely ${\mathcal{H}}_{p,i}^{\left(\nu \right)}:=E^{\left(i\right)}{\mathcal{H}}_p^{\left(\nu \right)}{\left(E^{\left(i\right)}\right)}^{-1},$ where $E^{\left(i\right)}\in {\mathcal{E}}_p^{\left(\nu \right)}$, $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}.$

3.2. Interpolating Refinable Function Vector

A refinable function vector $\mathsf{\Phi }={({\phi }_1,\dots ,{\phi }_r)}^T$ is called interpolating, if multiplicity r is equal to $m=|detM|$, all components of $\mathsf{\Phi }$ are continuous functions with compact support and

$${\phi }_i\left(M^{-1}k\right)={\delta }_{s_i,k}\hspace{1em}\forall i=1,\dots ,m,\hspace{1em}\forall k\in {\mathbb{Z}}^d.$$

(13)

Since $r=m$, we can associate ${\phi }_i$ with corresponding digit $s_i$ and we can index functions ${\phi }_i$ using digits. Condition (13) can be rewritten as

$${\phi }_s\left(M^{-1}k\right)={\delta }_{s,k}\hspace{1em}\forall s\in D\left(M\right),\hspace{1em}\forall k\in {\mathbb{Z}}^d.$$

(14)

Or, since any $k\in {\mathbb{Z}}^d$ can be represented as $k=Ml+q$ for some $l\in {\mathbb{Z}}^d,$ $q\in D\left(M\right),$ condition (14) is equivalent to

$${\phi }_s(l+M^{-1}q)={\delta }_{l,\mathbf{0}}{\delta }_{s,q}\hspace{1em}\forall q\in D\left(M\right),\hspace{1em}\forall l\in {\mathbb{Z}}^d.$$

(15)

An interpolating refinable function vectors related to Shannon-like sampling expansions

$$f\left(x\right)=\sum _{k\in {\mathbb{Z}}^d}\sum _{s\in D\left(M\right)}f(M^{-1}s-k){\phi }_s(x+k).$$

(16)

This expansion allows us to state that the multi-integer translates of $\mathsf{\Phi }$ are linearly independent. Indeed, if ${\mathcal{T}}_{\mathsf{\Phi }}$ is the synthesis operator of $\mathsf{\Phi }$, then ${\mathcal{T}}_{\mathsf{\Phi }}a=0$ for $a\in {(\ell \left({\mathbb{Z}}^d\right))}^{1\times r}$ implies that $a=\mathbf{0}$ by (16).

For an interpolating refinable function vector $\mathsf{\Phi }$ its matrix mask $\widehat{A}$ should have the following special form of the first column: ${\left[\widehat{A}\left(\xi \right)\right]}_{s,\mathbf{0}}=\frac{1}{m}{e}^{2\pi i(s,\xi )},$ for $s\in D\left(M\right)$. The following theorem states the details.

Theorem 2

([32] Theorem 2.1). Let Φ be a refinable function vector with matrix mask $A\in {\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{m\times m}$. Then Φ is interpolating refinable function vector if and only if

1. 

$(1,1,\dots ,1)\widehat{\mathsf{\Phi }}\left(\mathbf{0}\right)=1$;

2. 

${\nu }_{\infty }(A,M)>0$;

3. 

$(1,1,\dots ,1)\widehat{A}\left(\mathbf{0}\right)=(1,1,\dots ,1)$ and

$$\widehat{A}\left(\xi \right)=\left(\begin{array}{cccc}\frac{1}{m}& \widehat{a_{1,2}}\left(\xi \right)& \dots & \widehat{a_{1,m}}\left(\xi \right)\\ \frac{1}{m}{e}^{2\pi i(s_1,\xi )}& \widehat{a_{2,2}}\left(\xi \right)& \dots & \widehat{a_{2,m}}\left(\xi \right)\\ ⋮& ⋮& \dots & ⋮\\ \frac{1}{m}{e}^{2\pi i(s_m,\xi )}& \widehat{a_{m,2}}\left(\xi \right)& \dots & \widehat{a_{m,m}}\left(\xi \right)\end{array}\right),$$

(17)

where $\widehat{a_{i,j}}$ are some trigonometric polynomials, $s_i\in D\left(M\right)$.

The quantity ${\nu }_{\infty }(A,M)$ is related to $L_{\infty }$-smoothness exponent of a refinable function vector $\mathsf{\Phi }$ with dilation matrix M and matrix mask A (see [32] for details). Matrix mask $\widehat{A}$ in (17) is called an interpolating matrix mask.

Let us consider an $\mathcal{H}$-symmetric interpolating refinable function vector $\mathsf{\Phi }$ with the row of symmetry centers $C={\left\{c_s\right\}}_{s\in D\left(M\right)}.$ From the $\mathcal{H}$-symmetry property and (15) we have

$$1={\phi }_s\left(M^{-1}s\right)={\phi }_s(E{M}^{-1}s-E{c}_s+c_s)$$

for all $s\in D\left(M\right)$ and $E\in \mathcal{H}.$ Then

$$1={\phi }_s\left(M^{-1}(ME{M}^{-1}s-ME{c}_s+M{c}_s)\right)={\delta }_{s,ME{M}^{-1}s-ME{c}_s+M{c}_s}.$$

Hence $ME{M}^{-1}(s-M{c}_s)=s-M{c}_s$ for all $s\in D\left(M\right)$ and $E\in \mathcal{H}$. This condition will be satisfied, if $s=M{c}_s$ for all $s\in D\left(M\right)$. So, in the interpolating case the symmetry centers are defined by the digits.

By Theorem 1 for the $\mathcal{H}$-symmetric interpolating refinable function vector $\mathsf{\Phi }$ with matrix mask $\widehat{A}$ matrix elements ${\left[\widehat{A}\right]}_{s,q}$, $s,q\in D\left(M\right),$ are $\mathcal{H}$-symmetric with respect to the centers $M{c}_s-c_q$ or $s-M^{-1}q.$ Thus, the natural limitation on the symmetry centers for trigonometric polynomials gives the following restrictions

$$E(s-M^{-1}q)-(s-M^{-1}q)\in {\mathbb{Z}}^d\hspace{1em}\forall E\in \mathcal{H},\hspace{1em}\forall s,q\in D\left(M\right).$$

This is equivalent to

$$Eq-q\in M{\mathbb{Z}}^d\hspace{1em}\forall E\in \mathcal{H},\hspace{1em}\forall q\in D\left(M\right).$$

(18)

The latter condition reduces possible variants for the appropriate choice of symmetry groups $\mathcal{H}$ and dilation matrices M, i.e., (18) should be checked for a chosen pair $\mathcal{H}$ and M before the construction.

Additionally, note that if matrix mask $\widehat{A}$ of an interpolating refinable function obeys sum rule of order n, then y is not arbitrary. For instance, the appropriate choice is $y\left(\xi \right)=(1,e^{2\pi i(s_2,\xi )},\dots ,e^{2\pi i(s_m,\xi )})$ (see, for example, [33]).

Methods for the construction of $\mathcal{H}$-symmetric matrix masks with any preassigned order of sum rule were suggested in [20,22]. Additionally, the canonical form of matrix mask (see, for example, [34]) can be used for the construction of symmetric matrix masks starting from any appropriate refinable mask in the scalar case (see, e.g., [22] for details). For instance, any known interpolating symmetric refinable masks can be used (see, for example, [22,27,35,36,37] for examples of such masks and for methods of their construction). This provides the initial step in the construction of symmetric multiwavelets.

4. Extension Principle

A general scheme for the construction of compactly supported MRA-based wavelet systems was developed in [38] (the Mixed Extension Principle). This scheme is also applicable for the construction of multiwavelet systems.

Let $\mathsf{\Phi }$, $\tilde{\mathsf{\Phi }}$ be compactly supported refinable function vectors, which satisfy the refinement equation with matrix masks $\widehat{A},\widehat{\tilde{A}}$. For convenience, we use notations ${\widehat{B}}_1:=\widehat{A}$, $\widehat{{\tilde{B}}_1}:=\widehat{\tilde{A}}$. Assume that there exist $r\times r$ matrices of trigonometric polynomials ${\widehat{B}}_{\nu },$ $\widehat{{\tilde{B}}_{\nu }}$, $\nu =2,\dots ,u$, $u\ge m$, such that the following $u\times m$ matrices of $r\times r$ blocks

$$\mathcal{L}:={\left\{\widehat{B_{\nu }}(\xi +M^{*-1}q)\right\}}_{\nu =1,u}^{q\in D\left(M^{*}\right)},\hspace{1em}\tilde{\mathcal{L}}:={\left\{\widehat{{\tilde{B}}_{\nu }}(\xi +M^{*-1}q)\right\}}_{\nu =1,u}^{q\in D\left(M^{*}\right)}$$

(19)

satisfy

$${\mathcal{L}}^{*}\tilde{\mathcal{L}}\equiv I_{mr}.$$

(20)

Wavelet function vectors ${\mathsf{\Psi }}^{\left(\nu \right)}$, ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)},$ $\nu =2,\dots ,u$, are defined via its Fourier transforms

$$\widehat{{\mathsf{\Psi }}^{\left(\nu \right)}}\left(\xi \right)=\widehat{B_{\nu }}\left(M^{*-1}\xi \right)\widehat{\mathsf{\Phi }}\left(M^{*-1}\xi \right),\hspace{1em}\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(\xi \right)=\widehat{{\tilde{B}}_{\nu }}\left(M^{*-1}\xi \right)\widehat{\tilde{\mathsf{\Phi }}}\left(M^{*-1}\xi \right).$$

(21)

Then the set of the function vectors $\{\mathsf{\Phi },{\mathsf{\Psi }}^{\left(2\right)},\dots ,{\mathsf{\Psi }}^{\left(u\right)}\}$, $\{\tilde{\mathsf{\Phi }},{\tilde{\mathsf{\Psi }}}^{\left(2\right)},\dots ,{\tilde{\mathsf{\Psi }}}^{\left(u\right)}\}$ is said to be a compactly supported MRA-based dual multiwavelet system generated by the refinable function vectors $\mathsf{\Phi },\tilde{\mathsf{\Phi }}$ (or their matrix masks $\widehat{A},\widehat{\tilde{A}}$).

The set of function vectors $\{\mathsf{\Phi },{\mathsf{\Psi }}^{\left(2\right)},\dots ,{\mathsf{\Psi }}^{\left(u\right)}\}$ is a multiwavelet frame in $L_2\left({\mathbb{R}}^d\right)$, if there exist positive constants $C_1$ and $C_2$ such that

$$C_1{\parallel f\parallel }_{L_2\left({\mathbb{R}}^d\right)}^2\le \sum _{k\in {\mathbb{Z}}^d}\parallel ⟨f,{\mathsf{\Phi }}_{0k}⟩{\parallel }^2+\sum _{j=0}^{\infty }\sum _{\nu =2}^u\sum _{k\in {\mathbb{Z}}^d}\parallel ⟨f,{\mathsf{\Psi }}_{jk}^{\left(\nu \right)}⟩{\parallel }^2\le C_2{\parallel f\parallel }_{L_2\left({\mathbb{R}}^d\right)}^2,\hspace{1em}\forall f\in L_2\left({\mathbb{R}}^d\right).$$

Here, ${\mathsf{\Psi }}_{jk}^{\left(\nu \right)}=m^{j/2}{\mathsf{\Psi }}^{\left(\nu \right)}(M^j·+k)$ and $⟨f,\mathsf{\Phi }⟩=(⟨f,{\phi }_1⟩,\dots ,⟨f,{\phi }_r⟩)$. We say that a pair of sets $\{\mathsf{\Phi },{\mathsf{\Psi }}^{\left(2\right)},\dots ,{\mathsf{\Psi }}^{\left(u\right)}\}$ and $\{\tilde{\mathsf{\Phi }},{\tilde{\mathsf{\Psi }}}^{\left(2\right)},\dots ,{\tilde{\mathsf{\Psi }}}^{\left(u\right)}\}$ is a dual multiwavelet frame in $L_2\left({\mathbb{R}}^d\right)$, if each set is a multiwavelet frame in $L_2\left({\mathbb{R}}^d\right)$ and

$$f=\sum _{k\in {\mathbb{Z}}^d}⟨f,{\tilde{\mathsf{\Phi }}}_{0k}⟩{\mathsf{\Phi }}_{0k}+\sum _{j=0}^{\infty }\sum _{\nu =2}^u\sum _{k\in {\mathbb{Z}}^d}⟨f,{\tilde{\mathsf{\Psi }}}_{jk}^{\left(\nu \right)}⟩{\mathsf{\Psi }}_{jk}^{\left(\nu \right)},$$

where the series converge unconditionally.

It is known (see, for example, ([15] Theorem 2.1)) that compactly supported MRA-based dual multiwavelet system $\{\mathsf{\Phi },{\mathsf{\Psi }}^{\left(2\right)},\dots ,{\mathsf{\Psi }}^{\left(u\right)}\}$, $\{\tilde{\mathsf{\Phi }},{\tilde{\mathsf{\Psi }}}^{\left(2\right)},\dots ,{\tilde{\mathsf{\Psi }}}^{\left(u\right)}\}$ is a dual multiwavelet frame in $L_2\left({\mathbb{R}}^d\right)$ if $\mathsf{\Phi },\tilde{\mathsf{\Phi }}\in {\left(L_2\left({\mathbb{R}}^d\right)\right)}^{r\times 1}$, $\widehat{\mathsf{\Phi }}{\left(\mathbf{0}\right)}^{*}\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)=1$ and ${\mathsf{\Psi }}^{\left(\nu \right)}\left(\mathbf{0}\right)=\mathbf{0}$, ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}\left(\mathbf{0}\right)=\mathbf{0}$, $\nu =2,\dots ,u$ (i.e., all wavelet function vectors have vanishing moments at least of order 1).

Since wavelet matrix masks ${\widehat{B}}_{\nu }$, $\widehat{{\tilde{B}}_{\nu }}$ are matrices of trigonometric polynomials, then the wavelet function vectors ${\mathsf{\Psi }}^{\left(\nu \right)}$, ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$, $\nu =1,\dots ,u,$ are linear combinations of function vectors ${\mathsf{\Phi }}_{1k},$ ${\tilde{\mathsf{\Phi }}}_{1k}$, respectively. Therefore, wavelet functions in vectors ${\mathsf{\Psi }}^{\left(\nu \right)}$, ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$ also have compact support and they are in the same function space as functions from refinable function vectors.

For the realization of the extension principle starting from some initial symmetric matrix mask $\widehat{A}$, we need to construct symmetric dual matrix mask $\widehat{\tilde{A}}$ and we need to obtain symmetric wavelet matrix masks $\widehat{B_{\nu }},$ $\widehat{{\tilde{B}}_{\nu }}$ $\nu =2,\dots ,u,$ such that the equality (20) is valid. In this paper, we set $u=m$, i.e., the extended matrices $\mathcal{L}$ and $\tilde{\mathcal{L}}$ are square block matrices.

4.1. Symmetric Dual Matrix Mask

Firstly, we need to obtain a symmetric dual matrix mask. Let $\widehat{A}$ be a matrix mask. For a finitely supported sequence of matrices $\tilde{A}\in {\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{r\times r}$ its symbol $\widehat{\tilde{A}}$ is called a dual matrix mask for $\widehat{A}$, if

$$\sum _{q\in D\left(M^{*}\right)}\widehat{A}(\xi +M^{*-1}q)\widehat{\tilde{A}}{(\xi +M^{*-1}q)}^{*}=I_r.$$

(22)

A dual matrix mask for $\widehat{A}$ with preassigned order of sum rule can be constructed using the following result (see ([24] Theorem 3.4) for the constructive proof).

Theorem 3.

Let $\widehat{A}$ be a matrix mask such that $\widehat{A}$ has at least one dual matrix mask. Then for any $\tilde{n}\in \mathbb{N}$, there exists a dual matrix mask $\widehat{\tilde{A}}$ which obeys sum rule of order $\tilde{n}$.

Note that for the interpolating matrix mask $\widehat{A}$, at least one trivial dual matrix mask always exists (see Section 4.2). In order to provide the $\mathcal{H}$-symmetry property for the dual matrix mask $\widehat{\tilde{A}}$ we need several additional considerations. Let $\widehat{\tilde{A}}$ be a dual matrix mask, constructed by Theorem 3. Its symmetrization can be done as follows:

$${\widehat{\tilde{A}}}_{sym}\left(\xi \right):=\frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{\mathcal{S}}_C[M-EM]\left(\xi \right)\widehat{\tilde{A}}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right).$$

Below, we prove that ${\widehat{\tilde{A}}}_{sym}$, indeed, is a dual matrix mask for $\widehat{A}$ with the $\mathcal{H}$-symmetry property and with the same order of sum rule as $\widehat{\tilde{A}}$.

Theorem 4.

Matrix mask ${\widehat{\tilde{A}}}_{sym}$ is an $\mathcal{H}$-symmetric dual matrix mask for an $\mathcal{H}$-symmetric matrix mask $\widehat{A}$.

Proof. 

First, let us show that ${\widehat{\tilde{A}}}_{sym}$ is $\mathcal{H}$-symmetric with respect to the same row of centers C as the primal mask $\widehat{A}$. For $K\in \mathcal{H}$, consider

$$\begin{array}{cc}\hfill {\widehat{\tilde{A}}}_{sym}& \left(K^{*}\xi \right):=\frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{\mathcal{S}}_C[KM-KEM]\left(\xi \right)\widehat{\tilde{A}}\left(E^{*}{K}^{*}\xi \right){\mathcal{S}}_C[KE-K]\left(\xi \right)\hfill \\ \hfill =& \frac{1}{\#\mathcal{H}}{\mathcal{S}}_C[KM-M]\left(\xi \right)\sum _{E\in \mathcal{H}}{\mathcal{S}}_C[M-KEM]\left(\xi \right)\widehat{\tilde{A}}\left(E^{*}{K}^{*}\xi \right){\mathcal{S}}_C[KE-I_d]\left(\xi \right){\mathcal{S}}_C[I_d-K]\left(\xi \right)\hfill \\ \hfill =& {\mathcal{S}}_C[KM-M]\left(\xi \right){\widehat{\tilde{A}}}_{sym}\left(\xi \right){\mathcal{S}}_C[I_d-K]\left(\xi \right).\hfill \end{array}$$

Thus, ${\widehat{\tilde{A}}}_{sym}$ is $\mathcal{H}$-symmetric with respect to the same row of centers C. Next, we show that ${\widehat{\tilde{A}}}_{sym}$ is a dual matrix mask for $\widehat{A}$, i.e.,

$$\sum _{q\in D\left(M^{*}\right)}{\widehat{\tilde{A}}}_{sym}(\xi +M^{*-1}q)\widehat{A}{(\xi +M^{*-1}q)}^{*}=I_r.$$

(23)

Inserting the definition of ${\widehat{\tilde{A}}}_{sym}$ into the left-hand side of (23), using (4) for $\widehat{A}$ and the following equality

$${\mathcal{S}}_C[M-EM](\xi +M^{*-1}q)={\mathcal{S}}_C[I_d-M^{-1}EM](M^{*}\xi +q)={\mathcal{S}}_C[M-EM]\left(\xi \right),$$

(24)

the left-hand side of (23) is equal to

$$\frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}\sum _{q\in D\left(M^{*}\right)}{\mathcal{S}}_C[M-EM]\left(\xi \right)\widehat{\tilde{A}}(E^{*}\xi +E^{*}{M}^{*-1}q)\widehat{A}{(E^{*}\xi +E^{*}{M}^{*-1}q)}^{*}{\mathcal{S}}_C[M-EM]{\left(\xi \right)}^{*}.$$

It remains to note that the inner sum over $q\in D\left(M^{*}\right)$ can be rewritten as

$$\begin{array}{cc}\hfill \sum _{q\in D\left(M^{*}\right)}\widehat{\tilde{A}}& (E^{*}\xi +E^{*}{M}^{*-1}q)\widehat{A}{(E^{*}\xi +E^{*}{M}^{*-1}q)}^{*}=\hfill \\ \hfill & \sum _{q\in D\left(M^{*}\right)}\widehat{\tilde{A}}(E^{*}\xi +M^{*-1}{\left(M^{-1}EM\right)}^{*}q)\widehat{A}{(E^{*}\xi +M^{*-1}{\left(M^{-1}EM\right)}^{*}q)}^{*}=I_r,\hfill \end{array}$$

since $M^{-1}EM\in \mathcal{H}$ and ${\left(M^{-1}EM\right)}^{*}q=q^{new}+M^{*}k$ for some $q^{new}\in D\left(M^{*}\right)$, $k\in {\mathbb{Z}}^d$. Thus, if q is running over $D\left(M^{*}\right)$, i.e., over the complete set of representatives of ${\mathbb{Z}}^d/M^{*}{\mathbb{Z}}^d$, then ${\left(M^{-1}EM\right)}^{*}q$ is also running over the complete set of representatives of ${\mathbb{Z}}^d/M^{*}{\mathbb{Z}}^d$, but may be in another order and may be across some other representatives. Nevertheless, due to the periodicity of $\widehat{A}$ we get the equality $\widehat{A}(E^{*}\xi +M^{*-1}{\left(M^{-1}EM\right)}^{*}q)=\widehat{A}(E^{*}\xi +M^{*-1}{q}^{new})$ and the same for $\widehat{\tilde{A}}.$ Therefore, since $\widehat{\tilde{A}}$ is a dual matrix mask to $\widehat{A}$, then the right-hand side of the last formula is indeed equal to $I_r$. □

Next, we check the new dual matrix mask ${\widehat{\tilde{A}}}_{sym}$ has the same order of sum rule as the old dual matrix mask $\widehat{\tilde{A}}$. If the dual matrix mask obeys sum rule of order $\tilde{n}$, then Equations (5) and (6) for $\widehat{\tilde{A}}$ are valid with some row of trigonometric polynomials $\tilde{y}$. However, $\tilde{y}$ cannot be arbitrary. It is known that the derivatives $D^{\beta }\tilde{y}\left(\mathbf{0}\right)$ for $\beta \in {\mathsf{\Delta }}_n$ are uniquely defined (up to a multiplication by a constant) and can be found based on the equality (22). This fact is stated in Theorem 3.1 in [24]. In more details, $\tilde{y}$ should satisfy the following conditions:

$$D^{\beta }\left(\widehat{A}\left(M^{*-1}\xi \right){\tilde{y}}^{*}\left(M^{*-1}\xi \right)\right){|}_{\xi =\mathbf{0}}=D^{\beta }{\tilde{y}}^{*}\left(\mathbf{0}\right), \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}},$$

or equivalently

$$D^{\beta }\left(\widehat{A}\left(\xi \right){\tilde{y}}^{*}\left(\xi \right)\right){|}_{\xi =\mathbf{0}}=D^{\beta }{\tilde{y}}^{*}\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}}, \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}.$$

(25)

Theorem 5.

Let $\widehat{A}$ be an $\mathcal{H}$-symmetric matrix mask and let $\widehat{\tilde{A}}$ be its dual matrix mask with sum rule of order $\tilde{n}$. Then matrix mask ${\widehat{\tilde{A}}}_{sym}$ obeys sum rule of order $\tilde{n}$.

Proof. 

The fact that equality (25) is valid with symmetric matrix mask $\widehat{A}$ imposes some conditions on the choice of $\tilde{y}$. Indeed, from the one hand (25) can be rewritten as

$$D^{\beta }\left(\widehat{A}\left(E^{*}\xi \right)\tilde{y}{\left(E^{*}\xi \right)}^{*}\right){|}_{\xi =\mathbf{0}}=D^{\beta }\tilde{y}{\left(M^{*}{E}^{*}\xi \right)}^{*}{|}_{\xi =\mathbf{0}}, \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}$$

(26)

for $E\in \mathcal{H}$. On the other hand, by the $\mathcal{H}$-symmetry of $\widehat{A}$, we obtain

$$D^{\beta }\left({\mathcal{S}}_C[M-EM]\left(\xi \right)\widehat{A}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\tilde{y}{\left(\xi \right)}^{*}\right){|}_{\xi =\mathbf{0}}=D^{\beta }\tilde{y}{\left(M^{*}\xi \right)}^{*}{|}_{\xi =\mathbf{0}}, \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}.$$

Or by Lemma 1, the last equality is equivalent to

$$D^{\beta }\left(\widehat{A}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\tilde{y}{\left(\xi \right)}^{*}\right){|}_{\xi =\mathbf{0}}=D^{\beta }\left({\mathcal{S}}_C[EM-M]\left(\xi \right)\tilde{y}{\left(M^{*}\xi \right)}^{*}\right){|}_{\xi =\mathbf{0}}, \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}.$$

(27)

Comparing Equations (26) and (27) and using the fact that the derivatives of $\tilde{y}$ are uniquely defined by (25), we get that

$$D^{\beta }\tilde{y}{\left(E^{*}\xi \right)}^{*}{|}_{\xi =\mathbf{0}}=D^{\beta }\left({\mathcal{S}}_C[E-I_d]\left(\xi \right)\tilde{y}{\left(\xi \right)}^{*}\right){|}_{\xi =\mathbf{0}}.$$

Since only the derivatives of $\tilde{y}$ are needed, we can assume that

$$\tilde{y}\left(E^{*}\xi \right)=\tilde{y}\left(\xi \right){\mathcal{S}}_C[I_d-E]\left(\xi \right).$$

(28)

Next, show that ${\widehat{\tilde{A}}}_{sym}$ also obeys sum rule of order $\tilde{n}$ with the row of trigonometric polynomials $\tilde{y}$. Consider,

$$\begin{array}{cc}\hfill D^{\beta }\left(\tilde{y}\left(M^{*}\xi \right){\widehat{\tilde{A}}}_{sym}\left(\xi \right)\right){|}_{\xi =\mathbf{0}}& =\frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{D}^{\beta }\left(\tilde{y}\left(M^{*}\xi \right){\mathcal{S}}_C[M-EM]\left(\xi \right)\widehat{\tilde{A}}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\right){|}_{\xi =\mathbf{0}}\hfill \\ \hfill =& \frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{D}^{\beta }\left(\tilde{y}\left(M^{*}{E}^{*}\xi \right)\widehat{\tilde{A}}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\right){|}_{\xi =\mathbf{0}}\hfill \\ \hfill =& \frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{D}^{\beta }\left(\tilde{y}\left(E^{*}\xi \right){\mathcal{S}}_C[E-I_d]\left(\xi \right)\right){|}_{\xi =\mathbf{0}}=D^{\beta }\tilde{y}\left(\mathbf{0}\right).\hfill \end{array}$$

Next, for any $q\in D\left(M^{*}\right)\backslash \left\{\mathbf{0}\right\}$ conditions

$$D^{\beta }\left[\tilde{y}\left(M^{*}\xi \right)\widehat{\tilde{A}}(\xi +M^{*-1}q)\right]{|}_{\xi =\mathbf{0}}=0,\hspace{1em}\forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}$$

by Lemma 1 are equivalent to

$$D^{\beta }\left[\tilde{y}\left(M^{*}{E}^{*}\xi \right)\widehat{\tilde{A}}(E^{*}\xi +M^{*-1}q){\mathcal{S}}_C[E-I_d](\xi +M^{*-1}q)\right]{|}_{\xi =\mathbf{0}}=0, \forall \beta \in {\mathsf{\Delta }}_{\tilde{n}}.$$

(29)

Additionally, by (24) and (28) we have

$$\tilde{y}\left(M^{*}\xi \right){\mathcal{S}}_C[M-EM](\xi +M^{*-1}q)=\tilde{y}\left(M^{*}\xi \right){\mathcal{S}}_C[I_d-M^{-1}EM]\left(M^{*}\xi \right)=\tilde{y}\left(M^{*}{E}^{*}\xi \right).$$

Therefore, we obtain that

$$\begin{array}{cc}\hfill D^{\beta }& \left(\tilde{y}\left(M^{*}\xi \right){\widehat{\tilde{A}}}_{sym}(\xi +M^{*-1}q)\right){|}_{\xi =\mathbf{0}}\hfill \\ \hfill & =\frac{1}{\#\mathcal{H}}\sum _{E\in \mathcal{H}}{D}^{\beta }\left(\tilde{y}\left(M^{*}{E}^{*}\xi \right)\widehat{\tilde{A}}(E^{*}\xi +E^{*}{M}^{*-1}q){\mathcal{S}}_C[E-I_d](\xi +M^{*-1}q)\right){|}_{\xi =\mathbf{0}}=\mathbf{0}\hfill \end{array}$$

by the fact that $\widehat{\tilde{A}}(E^{*}\xi +E^{*}{M}^{*-1}q)=\widehat{\tilde{A}}(E^{*}\xi +M^{*-1}{\left(M^{-1}EM\right)}^{*}q)=\widehat{\tilde{A}}(E^{*}\xi +M^{*-1}{q}_{new})$, where $q_{new}\in D\left(M^{*}\right)\backslash \left\{\mathbf{0}\right\}$ is such that ${\left(M^{-1}EM\right)}^{*}q-q_{new}\in M^{*}{\mathbb{Z}}^d$ and, thus, (29) can be applied. □

4.2. Symmetric Wavelet Matrix Masks

Let $\mathcal{H}$ be a symmetry group with respect to the dilation matrix M, such that $Es-s\in M{\mathbb{Z}}^d$ for all $E\in \mathcal{H}$ and for all $s\in D\left(M\right)$. Let $\mathsf{\Phi }=({\phi }_1,\dots ,{\phi }_r)$, $r=m$, be an interpolating refinable function vector which is $\mathcal{H}$-symmetric with respect to the centers $c_s=M^{-1}s$, $s\in D\left(M\right).$ Let $\widehat{A}$ be the corresponding matrix mask. Then mask $\widehat{A}$ is also $\mathcal{H}$-symmetric, i.e., (4) is valid or the matrix element ${\left[\widehat{A}\right]}_{s,q}$ is $\mathcal{H}$-symmetric with respect to the center $M^{-1}q-s$, $s,q\in D\left(M\right).$ Let $\widehat{\tilde{A}}$ be an $\mathcal{H}$-symmetric dual matrix mask.

It is more convenient to write the process of matrix extension using the modified polyphase components. First, note that for the modified polyphase representation of each column of matrix mask $\widehat{A}$, we will use its own set of digits. Namely, for a fixed $\nu =1,\dots ,m$, consider the set of digits $D(M,c_{\nu })$ associated with the symmetry center $c_{\nu }$. In what follows, the modified polyphase components of the column $\nu$ of $\widehat{A}$ are defined using the set of digits $D(M,c_{\nu })$. The modified polyphase representation of ${\left[\widehat{A}\right]}^{\nu }$ defined in (8) can be alternatively written as

$${\left[\widehat{A}\left(\xi \right)\right]}^{\nu }=\widehat{A^{\left(\nu \right)}}\left(M^{*}\xi \right){\left[{\mathcal{P}}_{c_{\nu }}\right]}^1\left(\xi \right),$$

where ${\mathcal{P}}_{c_{\nu }}$ is the matrix defined by

$${\mathcal{P}}_{c_{\nu }}\left(\xi \right)=\frac{1}{\sqrt{m}}{\left\{e^{2\pi i(s,\xi +M^{*-1}q)}\right\}}_{s\in D(M,c_{\nu })}^{q\in D\left(M^{*}\right)}.$$

It is known that ${\mathcal{P}}_{c_{\nu }}$ is a unitary matrix, i.e., ${\mathcal{P}}_{c_{\nu }}\left(\xi \right){\mathcal{P}}_{c_{\nu }}^{*}\left(\xi \right)=I_m$. Denote by $\mathbb{P}$ a block-diagonal matrix $\mathrm{diag}\{{\mathcal{P}}_{c_1},\dots ,{\mathcal{P}}_{c_m}\}$. Clearly, $\mathbb{P}$ is also a unitary matrix. Let $e_1,\dots ,e_m$ be the standard basis in ${\mathbb{R}}^m$. Then

$$\widehat{A}\left(\xi \right)=\left(\widehat{A^{\left(1\right)}}\left(M^{*}\xi \right),\dots ,\widehat{A^{\left(m\right)}}\left(M^{*}\xi \right)\right)\mathbb{P}\left(\xi \right)\hspace{1em}(I_m\otimes e_1),$$

where $A\otimes B$ is the Kronecker product of matrices A and B.

Now, return to the extended matrices $\mathcal{L}$ and $\tilde{\mathcal{L}}$ defined in (19) with $u=m$. Since these matrices are square matrices, then ${\mathcal{L}}^{*}\tilde{\mathcal{L}}\equiv I_{m^2}$ is equivalent to $\mathcal{L}{\tilde{\mathcal{L}}}^{*}\equiv I_{m^2}$. Consider the first block row of matrix $\mathcal{L}$ and denote it by $T\left(\xi \right):={\left\{\widehat{A}(\xi +M^{*-1}q)\right\}}^{q\in D\left(M^{*}\right)}$. Additionally, denote the row of matrices $\widehat{A^{\left(\nu \right)}},$ $\nu =1,\dots ,m$, by $\mathcal{T}\left(\xi \right):=(\widehat{A^{\left(1\right)}}\left(M^{*}\xi \right),\dots ,\widehat{A^{\left(r\right)}}\left(M^{*}\xi \right)).$ These matrices are connected by $m^2\times m^2$ matrix $V:=\mathbb{P}(I_m\otimes e_1,\dots ,I_m\otimes e_m)$, i.e.,

$$T\left(\xi \right)=\mathcal{T}\left(\xi \right)V.$$

Lemma 3.

Let A and $\tilde{A}$ be in ${\left({\ell }_0\left({\mathbb{Z}}^d\right)\right)}^{r\times r}$. Define the rows $T,\tilde{T}$, $\mathcal{T},\tilde{\mathcal{T}}$ by

$$T\left(\xi \right)={\left\{\widehat{A}(\xi +M^{*-1}q)\right\}}^{q\in D\left(M^{*}\right)}, \tilde{T}\left(\xi \right)={\left\{\widehat{\tilde{A}}(\xi +M^{*-1}q)\right\}}^{q\in D\left(M^{*}\right)}$$

and $\mathcal{T}\left(\xi \right)={\left\{\widehat{A^{\left(\nu \right)}}\left(M^{*}\xi \right)\right\}}^{\nu =\overline{1,m}}$, $\tilde{\mathcal{T}}\left(\xi \right)={\left\{\widehat{{\tilde{A}}^{\left(\nu \right)}}\left(M^{*}\xi \right)\right\}}^{\nu =\overline{1,m}}$, where $\widehat{A^{\left(\nu \right)}}$ and $\widehat{{\tilde{A}}^{\left(\nu \right)}}$, $\nu =1,\dots ,m,$ are the modified polyphase components of $\widehat{A}$ and $\widehat{\tilde{A}}$, respectively. Then

$$\sum _{q\in D\left(M^{*}\right)}\widehat{A}(\xi +M^{*-1}q)\widehat{\tilde{A}}{(\xi +M^{*-1}q)}^{*}=\sum _{\nu =1}^m\widehat{A^{\left(\nu \right)}}\left(M^{*}\xi \right)\widehat{{\tilde{A}}^{\left(\nu \right)}}{\left(M^{*}\xi \right)}^{*}$$

or $T{\tilde{T}}^{*}=\mathcal{T}\hspace{1em}{\tilde{\mathcal{T}}}^{*}.$

Proof. 

Note that matrix V is a unitary matrix since it is a product of unitary matrices $\mathbb{P}$ and $(I_m\otimes e_1,\dots ,I_m\otimes e_m)$, where the latter matrix is just a rearrangement of columns of $I_{m^2}$. Hence $V{V}^{*}=I_{m^2}$ and

$$T{\tilde{T}}^{*}=\mathcal{T}V{V}^{*}{\tilde{\mathcal{T}}}^{*}=\mathcal{T}\hspace{1em}{\tilde{\mathcal{T}}}^{*}.$$

□

This lemma allows us to extend matrices $\mathcal{L}$ and $\tilde{\mathcal{L}}$ from the initial first block row in terms of the modified polyphase components. Consider the row of the modified polyphase components of matrix mask $\widehat{A}$. Due to Theorem 2 its first block has a special form: $(I_m,\widehat{A^{\left(2\right)}},\dots ,\widehat{A^{\left(m\right)}})$. This consideration easily implies the fact that interpolating matrix mask $\widehat{A}$ always has at least one dual matrix mask, since the row of the modified polyphase components of such dual matrix mask can be taken as $(I_m,{\mathbf{0}}_{m\times m},\dots ,{\mathbf{0}}_{m\times m})$. Denote $P:=(\widehat{A^{\left(2\right)}},\dots ,\widehat{A^{\left(m\right)}})$. Next, let $\widehat{\tilde{A}}$ be a dual matrix mask constructed in Section 4.1 and consider its row of the modified polyphase components. Denote $(\widehat{{\tilde{A}}^{\left(1\right)}},\tilde{P}):=(\widehat{{\tilde{A}}^{\left(1\right)}},\widehat{{\tilde{A}}^{\left(2\right)}},\dots ,\widehat{{\tilde{A}}^{\left(m\right)}})$. These two block rows of the modified polyphase components are biorthogonal by design. Starting from these rows, the required matrix extension up to square matrices can be done explicitly as follows

$$\mathcal{N}=\left(\begin{array}{cc}{I}_m& P\\ -{\tilde{P}}^{*}& I_{m(m-1)}-{\tilde{P}}^{*}P\end{array}\right), \tilde{\mathcal{N}}=\left(\begin{array}{cc}\widehat{{\tilde{A}}^{\left(1\right)}}& \tilde{P}\\ -P^{*}& I_{m(m-1)}\end{array}\right).$$

(30)

By direct computations, it can be checked that $\mathcal{N}{\tilde{\mathcal{N}}}^{*}=I_{mm}$. These matrices contain the modified polyphase components of all masks, and they can be transformed back into matrices $\mathcal{L},\tilde{\mathcal{L}}$ using the transformation matrix V. By Lemma 3, $\mathcal{N}{\tilde{\mathcal{N}}}^{*}=I_{m^2}$ is equivalent to $\mathcal{L}{\tilde{\mathcal{L}}}^{*}=I_{m^2}$. The next theorem describes the symmetry properties of the obtained by (30) wavelet matrix masks.

Theorem 6.

Let $\widehat{A}$ be an interpolating $\mathcal{H}$-symmetric matrix mask with respect to row of centers $C={\left\{c_s\right\}}_{s\in D\left(M\right)}$, where $c_s=-M^{-1}s$. Let $\widehat{\tilde{A}}$ be a dual $\mathcal{H}$-symmetric matrix mask with respect to the row of centers C. Let $\widehat{B_{\nu }}$, $\widehat{{\tilde{B}}_{\nu }}$, $\nu =2,\dots ,m$ be wavelet matrix masks, obtained via the matrix extension based on (30).

Then wavelet function vectors ${\mathsf{\Psi }}^{\left(\nu \right)}$ and ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$ contain wavelet functions, which are mutually symmetric in the following sense. For fixed $\nu =2,\dots ,m$ each wavelet function from the vector ${\mathsf{\Psi }}^{\left(\nu \right)}=({\psi }_1^{\left(\nu \right)},\dots ,{\psi }_m^{\left(\nu \right)})$ can be associated with a digit from $D(M,c_{\nu })$, i.e., $s_{(p,i)}^{\left(\nu \right)}$ can be associated with ${\psi }_{(p,i)}^{\left(\nu \right)}$, $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },$ $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$, same for ${\tilde{\mathsf{\Psi }}}^{(}\nu )$. Then for $K\in \mathcal{H}$

$$\widehat{{\psi }_{(p,i)}^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)=\widehat{{\psi }_{(p,j)}^{\left(\nu \right)}}\left(\xi \right)e^{2\pi i(r_{p,i}^{K,\left(\nu \right)},\xi )}, \widehat{{\tilde{\psi }}_{(p,i)}^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)=\widehat{{\tilde{\psi }}_{(p,j)}^{\left(\nu \right)}}\left(\xi \right)e^{2\pi i(r_{p,i}^{K,\left(\nu \right)},\xi )},$$

(31)

where j is such that $K\left[⟨s_{p,i}^{\left(\nu \right)}⟩\right]=⟨s_{p,j}^{\left(\nu \right)}⟩$ for the group action associated with the symmetry center $c_{\nu }$ and $r_{p,i}^{K,\left(\nu \right)}$ is defined in (10).

Proof. 

Let $\widehat{B_{\nu }^{\left(\mu \right)}}$ denote the modified polyphase component of $B_{\nu }$, namely, $\widehat{B_{\nu }^{\left(\mu \right)}}$ contains the polyphase components of the $\mu$-th column of matrix mask $\widehat{B_{\nu }}$. Additionally, let ${\widehat{B}}_1=\widehat{A}$ and $\widehat{{\tilde{B}}_1}=\widehat{\tilde{A}}$. Using these notations, the matrices in (30) can be written as

$$\mathcal{N}=\left(\begin{array}{cccc}\widehat{B_1^{\left(1\right)}}& \widehat{B_1^{\left(2\right)}}& \dots & \widehat{B_1^{\left(m\right)}}\\ \widehat{B_2^{\left(1\right)}}& \widehat{B_2^{\left(2\right)}}& \dots & \widehat{B_1^{\left(m\right)}}\\ ⋮& ⋮& \dots & ⋮\\ \widehat{B_m^{\left(1\right)}}& \widehat{B_m^{\left(2\right)}}& \dots & \widehat{B_m^{\left(m\right)}}\end{array}\right), \tilde{\mathcal{N}}=\left(\begin{array}{cccc}\widehat{{\tilde{B}}_1^{\left(1\right)}}& \widehat{{\tilde{B}}_1^{\left(2\right)}}& \dots & \widehat{{\tilde{B}}_1^{\left(m\right)}}\\ \widehat{{\tilde{B}}_2^{\left(1\right)}}& \widehat{{\tilde{B}}_2^{\left(2\right)}}& \dots & \widehat{{\tilde{B}}_2^{\left(m\right)}}\\ ⋮& ⋮& \dots & ⋮\\ \widehat{{\tilde{B}}_m^{\left(1\right)}}& \widehat{{\tilde{B}}_m^{\left(2\right)}}& \dots & \widehat{{\tilde{B}}_m^{\left(m\right)}}\end{array}\right).$$

Next, we check the symmetry properties of wavelet matrix masks and then show how these properties will reflect on wavelet function vectors.

Let us start with matrix $\tilde{\mathcal{N}}$. Fix $\nu =2,\dots ,m$ and the corresponding set of digits $D(M,c_{\nu })$. Consider block $\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}$ in matrix $\tilde{\mathcal{N}}$ and its elements ${\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(\xi \right)\right]}_{(p,i),l},$ here $l=1,\dots ,m,$ $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },$ $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$. By (30) ${\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(\xi \right)\right]}_{(p,i),l}=-\overline{{\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}_{l,(p,i)}}$. According to Lemma 2 for the column with index $(p,i)$ of matrix $\widehat{A^{\left(\nu \right)}}$, we have the following relation for $K\in \mathcal{H}$:

$${\left[\widehat{A^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)\right]}^{(p,i)}={\mathcal{S}}_C(M^{-1}KM-I_d)\left(\xi \right){\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}^{(p,j)}{e}^{2\pi i(-r_{p,i}^{K,\left(\nu \right)},\xi )},$$

where j is such that $K{E}^{\left(i\right)}=E^{\left(j\right)}F$ for matrices $E^{\left(i\right)},E^{\left(j\right)}\in {\mathcal{E}}_p^{\left(\nu \right)}$ and $F\in {\mathcal{H}}_p^{\left(\nu \right)}$, $r_{p,i}^{K,\left(\nu \right)}\in {\mathbb{Z}}^d$ is defined in (10). For the column elements, after applying the complex conjugation, we obtain

$$\overline{{\left[\widehat{A^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)\right]}_{l,(p,i)}}=e^{2\pi i(c_l-M^{-1}KM{c}_l,\xi )}\overline{{\left[\widehat{A^{\left(\nu \right)}}\left(\xi \right)\right]}_{l,(p,j)}}{e}^{2\pi i(r_{p,i}^{K,\left(\nu \right)},\xi )}.$$

Thus,

$${\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)\right]}_{(p,i),l}=e^{2\pi i(c_l-M^{-1}KM{c}_l,\xi )}{e}^{2\pi i(r_{p,i}^{K,\left(\nu \right)},\xi )}{\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(\xi \right)\right]}_{(p,j),l}.$$

Since $c_l=M^{-1}{s}_l$, then $e^{2\pi i(c_l-M^{-1}KM{c}_l,\xi )}=e^{2\pi i(s_l-K{s}_l,M^{*-1}\xi )}$. Hence, changing $M^{*-1}\xi$ by $\xi$, we can rewrite

$${\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(M^{*}{K}^{*}\xi \right)\right]}_{(p,i),l}\hspace{1em}{e}^{2\pi i(K{s}_l,\xi )}=e^{2\pi i(s_l,\xi )}{e}^{2\pi i(r_{p,i}^{K,\left(\nu \right)},M^{*}\xi )}{\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(M^{*}\xi \right)\right]}_{(p,j),l}.$$

(32)

Summing over $l=1,\dots ,m$ and using the modified polyphase representation, we can get the first column of the wavelet matrix mask $\widehat{{\tilde{B}}_{\nu }}$. Namely, since

$$\sum _{l=1}^m{\left[\widehat{{\tilde{B}}_{\nu }^{\left(1\right)}}\left(M^{*}\xi \right)\right]}_{(p,i),l}{e}^{2\pi i(s_l,\xi )}={\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,i),1},$$

then (32) implies that

$${\left[\widehat{{\tilde{B}}_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),1}=e^{2\pi i(K{c}_{\nu }-c_{\nu }+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,j),1},$$

(33)

where j is such that $K\left[⟨s_{p,i}^{\left(\nu \right)}⟩\right]=⟨s_{p,j}^{\left(\nu \right)}⟩$ with the group action associated with the symmetry center $c_{\nu }$ and (10) is used.

The other columns of wavelet matrix mask $\widehat{{\tilde{B}}_{\nu }},$ $\nu =2,\dots ,m$, are equal to ${\mathbf{0}}_{m\times 1}$ except the $\nu$-th column, since the corresponding block with the modified polyphase component $\widehat{{\tilde{B}}_{\nu }^{\left(\nu \right)}}\left(\xi \right)$ is equal to $I_m.$ Then $\nu$-th column of wavelet matrix mask $\widehat{{\tilde{B}}_{\nu }}$ contains elements ${\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,i),\nu }=e^{2\pi i(s_{p,i}^{\left(\nu \right)},\xi )}$, $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },$ $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$. It’s not hard to see that

$${\left[\widehat{{\tilde{B}}_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),\nu }=e^{2\pi i(K{s}_{p,i}^{\left(\nu \right)},\xi )}=e^{2\pi i(s_{p,j}^{\left(\nu \right)}+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}={\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,j),\nu }{e}^{2\pi i(K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}.$$

(34)

Overall, we obtain the following relation:

$${\left[\widehat{{\tilde{B}}_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),l}={\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,j),l}{e}^{2\pi i(K{c}_{\nu }-c_{\nu }-(K{c}_l-c_l)+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )},$$

(35)

which is true for $l=1$ by (33), since $c_1=M^{-1}{s}_1=\mathbf{0}$, and for $l=\nu$ by (34), and also for all other $l=2,\dots ,m,$ since the elements in the l-th column, $l\ne \nu$, are just zeros.

Next, let us obtain the analogous relations for wavelet matrix masks obtained from the matrix $\mathcal{N}$. The blocks ${\widehat{B}}_1^{\left(\nu \right)}$ obviously gives the result similar to (33), since the symmetry properties of the elements of the rows P and $\tilde{P}$ are the same. Therefore,

$${\left[\widehat{B_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),1}=e^{2\pi i(K{c}_{\nu }-c_{\nu }+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}{\left[\widehat{B_{\nu }}\left(\xi \right)\right]}_{(p,j),1},$$

where j is such that $K\left[⟨s_{p,i}^{\left(\nu \right)}⟩\right]=⟨s_{p,j}^{\left(\nu \right)}⟩$ with the group action associated with the symmetry center $c_{\nu }$.

Next, consider other blocks of matrix $\mathcal{N}$. Note that each block has the form $\widehat{B_{\nu }^{\left(\mu \right)}}={\delta }_{\nu ,\mu }{I}_m-{\widehat{{\tilde{A}}^{\left(\nu \right)}}}^{*}\widehat{A^{\left(\mu \right)}}$, $\nu ,\mu =2,\dots ,m$. Consider each block element-wise, where elements are indexed by double index as follows: the rows are indexed using $(p^{\left(\nu \right)},i^{\left(\nu \right)})$, i.e., using indexing of the digits in $D(M,c_{\nu })$ and the columns are indexed using $(p^{\left(\mu \right)},i^{\left(\mu \right)})$, i.e., using indexing of the digits in $D(M,c_{\mu })$. Using the symmetry properties of the modified polyphase components $\widehat{{\tilde{A}}^{\left(\nu \right)}}$ and $\widehat{A^{\left(\mu \right)}}$ from Lemma 2, we obtain

$$\begin{array}{cc}\hfill [\widehat{B_{\nu }^{\left(\mu \right)}}& \left(M^{*}{K}^{*}{M}^{*-1}\xi \right){]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),(p^{\left(\mu \right)},i^{\left(\mu \right)})}\hfill \\ & ={\delta }_{\nu ,\mu }{I}_m-\sum _{t=1}^m{\left[\overline{\widehat{{\tilde{A}}^{\left(\nu \right)}}\left(M^{*}{K}^{*}{M}^{*-1}\xi \right)}\right]}_{t,(p^{\left(\nu \right)},i^{\left(\nu \right)})}{\left[\widehat{A^{\left(\mu \right)}}\left(M^{*}{K}^{*}{M}^{*-1}\xi \right)\right]}_{t,(p^{\left(\mu \right)},i^{\left(\mu \right)})}\hfill \end{array}$$

$$\begin{array}{l}={\left[\widehat{B_{\nu }^{\left(\mu \right)}}\left(\xi \right)\right]}_{(p^{\left(\nu \right)},j^{\left(\nu \right)}),(p^{\left(\mu \right)},j^{\left(\mu \right)})}{e}^{2\pi i(r_{p,i}^{K,\left(\nu \right)}-r_{p,i}^{K,\left(\mu \right)},\xi )},\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\end{array}$$

(36)

where $j^{\left(\nu \right)}$ is such that is such that $K\left[⟨s_{p^{\left(\nu \right)},i^{\left(\nu \right)}}^{\left(\nu \right)}⟩\right]=⟨s_{p^{\left(\nu \right)},j^{\left(\nu \right)}}^{\left(\nu \right)}⟩$ with the group action associated with the symmetry center $c_{\nu }$ and $j^{\left(\mu \right)}$ such that $K\left[⟨s_{p^{\left(\mu \right)},i^{\left(\mu \right)}}^{\left(\mu \right)}⟩\right]=⟨s_{p^{\left(\mu \right)},j^{\left(\mu \right)}}^{\left(\mu \right)}⟩$ with the group action associated with the symmetry center $c_{\mu }$, $r_{p,i}^{K,\left(\mu \right)}$ is defined as

$$r_{p,i}^{K,\left(\mu \right)}=M^{-1}(K{s}_{p^{\left(\mu \right)},i^{\left(\mu \right)}}^{\left(\mu \right)}-s_{p^{\left(\mu \right)},j^{\left(\mu \right)}}^{\left(\mu \right)}+K{c}_{\mu }-c_{\mu })=$$

$$M^{-1}K{s}_{p^{\left(\mu \right)},i^{\left(\mu \right)}}^{\left(\mu \right)}-M^{-1}{s}_{p^{\left(\mu \right)},j^{\left(\mu \right)}}^{\left(\mu \right)}+M^{-1}(K{c}_{\mu }-c_{\mu })$$

and similar for $r_{p,i}^{K,\left(\nu \right)}$.

Next, consider the modified polyphase representation in order to obtain the elements from the $\mu$-th column of wavelet matrix mask $\widehat{B_{\nu }}$

$$\sum _{(p^{\left(\mu \right)},i^{\left(\mu \right)})}{\left[\widehat{B_{\nu }^{\left(\mu \right)}}\left(\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),(p^{\left(\mu \right)},i^{\left(\mu \right)})}{e}^{2\pi i(s_{p^{\left(\mu \right)},i^{\left(\mu \right)}}^{\left(\mu \right)},M^{*-1}\xi )}={\left[\widehat{B_{\nu }}\left(M^{*-1}\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),\mu },$$

where the sum is taken over all indices of digits $s_{p^{\left(\mu \right)},i^{\left(\mu \right)}}^{\left(\mu \right)}$ from $D(M,c_{\mu })$. Then relation (36) implies that

$${\left[\widehat{B_{\nu }}\left(K^{*}{M}^{*-1}\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),\mu }={\left[\widehat{B_{\nu }}\left(M^{*-1}\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),\mu }{e}^{2\pi i(r_{p,i}^{K,\left(\nu \right)}-M^{-1}(K{c}_{\mu }-c_{\mu }),\xi )}$$

or

$${\left[\widehat{B_{\nu }}\left(K^{*}\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),\mu }={\left[\widehat{B_{\nu }}\left(\xi \right)\right]}_{(p^{\left(\nu \right)},i^{\left(\nu \right)}),\mu }{e}^{2\pi i(M{r}_{p,i}^{K,\left(\nu \right)}-(K{c}_{\mu }-c_{\mu }),\xi )}.$$

(37)

This gives the required symmetry relation similar to (35).

Next, we check how the obtained symmetry relation for wavelet matrix masks will affect on wavelet function vectors. Recall that

$$\widehat{{\mathsf{\Psi }}^{\left(\nu \right)}}\left(M^{*}\xi \right)=\widehat{B_{\nu }}\left(\xi \right)\widehat{\mathsf{\Phi }}\left(\xi \right), \widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(M^{*}\xi \right)=\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\widehat{\tilde{\mathsf{\Phi }}}\left(\xi \right),$$

$\nu =2,\dots ,m.$

Since only two columns of $\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)$ are non-zero, then

$$\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(M^{*}\xi \right)={\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}^1{\widehat{\phi }}_1\left(\xi \right)+{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}^{\nu }{\widehat{\phi }}_{\nu }\left(\xi \right).$$

By default, $\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}=(\widehat{{\tilde{\psi }}_1^{\left(\nu \right)}},\dots ,\widehat{{\tilde{\psi }}_m^{\left(\nu \right)})}.$ However, it is more convenient, if wavelet functions are indexed in the same way as digits from $D(M,c_{\nu })$. Namely, consider $\widehat{{\tilde{\psi }}_{(p,i)}^{\left(\nu \right)}}$, where $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },$ $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$. Then for $K\in \mathcal{H}$ equality (35) implies that

$$\begin{array}{cc}\hfill \widehat{{\tilde{\psi }}_{(p,i)}^{\left(\nu \right)}}& \left(M^{*}{K}^{*}\xi \right)={\left[\widehat{{\tilde{B}}_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),1}{\widehat{\phi }}_1\left(K^{*}\xi \right)+{\left[\widehat{{\tilde{B}}_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),\nu }{\widehat{\phi }}_{\nu }\left(K^{*}\xi \right)\hfill \\ \hfill =& e^{2\pi i(K{c}_{\nu }-c_{\nu }+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,j),1}{\widehat{\phi }}_1\left(\xi \right)+{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}_{(p,j),\nu }{e}^{2\pi i(K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}{\widehat{\phi }}_{\nu }\left(\xi \right)e^{2\pi i(K{c}_{\nu }-c_{\nu },\xi )}\hfill \\ \hfill =& e^{2\pi i(K{c}_{\nu }-c_{\nu }+K{s}_{p,i}^{\left(\nu \right)}-s_{p,j}^{\left(\nu \right)},\xi )}\widehat{{\tilde{\psi }}_{(p,j)}^{\left(\nu \right)}}\left(M^{*}\xi \right).\hfill \end{array}$$

Or

$$\widehat{{\tilde{\psi }}_{(p,i)}^{\left(\nu \right)}}\left({\left(M^{-1}KM\right)}^{*}\xi \right)=\widehat{{\tilde{\psi }}_{(p,j)}^{\left(\nu \right)}}\left(\xi \right)e^{2\pi i(r_{p,i}^{K,\left(\nu \right)},\xi )},$$

where j is such that $K\left[⟨s_{p,i}^{\left(\nu \right)}⟩\right]=⟨s_{p,j}^{\left(\nu \right)}⟩$ with the group action associated with the symmetry center $c_{\nu }$. This means that functions of wavelet function vector ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$ are mutually symmetric with each other.

Similar relations can be established for wavelet functions in vector $\widehat{{\mathsf{\Psi }}^{\left(\nu \right)}}$. Fix $\widehat{{\psi }_{(p,i)}^{\left(\nu \right)}}$, where $p=1,\dots ,\#{\mathsf{\Lambda }}_{\nu },$ $i=1,\dots ,\#{\mathcal{E}}_p^{\left(\nu \right)}$. Then for $K\in \mathcal{H}$ equality (37) implies that

$$\begin{array}{cc}\hfill \widehat{{\psi }_{(p,i)}^{\left(\nu \right)}}\left(M^{*}{K}^{*}\xi \right)=& \sum _{\mu =1}^m{\left[\widehat{B_{\nu }}\left(K^{*}\xi \right)\right]}_{(p,i),\mu }{\widehat{\phi }}_{\mu }\left(K^{*}\xi \right)\hfill \\ \hfill =& \sum _{\mu =1}^m{\left[\widehat{B_{\nu }}\left(\xi \right)\right]}_{(p,j),\mu }{e}^{2\pi i(M{r}_{p,i}^{K,\left(\nu \right)}-(K{c}_{\mu }-c_{\mu }),\xi )}{\widehat{\phi }}_{\mu }\left(\xi \right)e^{2\pi i(K{c}_{\mu }-c_{\mu },\xi )}\hfill \\ \hfill =& e^{2\pi i(M{r}_{p,i}^{K,\left(\nu \right)},\xi )}\widehat{{\psi }_{(p,j)}^{\left(\nu \right)}}\left(M^{*}\xi \right),\hfill \end{array}$$

where j is such that $K\left[⟨s_{p,i}^{\left(\nu \right)}⟩\right]=⟨s_{p,j}^{\left(\nu \right)}⟩$ with the group action associated with the symmetry center $c_{\nu }$. □

Relations (31) describe the symmetry properties of the resulting wavelets. If the set of digits $D(M,c_{\nu })$ associated with symmetry center $c_{\nu }$ is such that all orbits contain only one element, i.e., $D(M,c_{\nu })=\{s_{p,1}^{\left(\nu \right)},p=1,\dots ,m\}$, then all wavelet functions are, indeed, $\mathcal{H}$-symmetric. If some orbit has more than one element, then the corresponding wavelet functions are mutually symmetric, which means that for some matrices $K\in \mathcal{H}$, one wavelet function transforms into another according to relations (31). For some symmetry groups, additional symmetrization step can be done, which helps to obtain truly $\mathcal{H}$-symmetric wavelets from mutually symmetric ones. The idea of this symmetrization step and details can be found in [27].

4.3. Further Details and Discussion

The above considerations give a method for the construction of compactly supported MRA-based dual multiwavelet system with symmetry properties. It remains to check that the obtained system of multiwavelets is, indeed, a dual multiwavelet frame. Recall that functions in vectors $\mathsf{\Phi }$ and $\tilde{\mathsf{\Phi }}$ should be in $L_2\left({\mathbb{R}}^d\right)$ and vanishing moments at least of order 1 for all wavelet functions should be provided. The fact that refinable functions belong to $L_2\left({\mathbb{R}}^d\right)$ can be checked after the construction of matrix masks. Moreover, it is known (see ([39] Theorem 2.2)) that if compactly supported refinable functions are in $L_2\left({\mathbb{R}}^d\right)$, then they are in $W_2^{\nu }\left({\mathbb{R}}^d\right)$ with some $\nu >0$. This value $\nu$ can be computed using the algorithm in [34]. Regarding the vanishing moments of wavelet functions, the following lemma, which is the generalization to the multivariate case of Theorem 2.1 in [40], will be helpful.

Lemma 4.

Let $\mathcal{L}$ and $\tilde{\mathcal{L}}$ be the matrices defined in (19) with $u=m$. Then $\widehat{B_1}$ obeys sum rule of order n with a row of functions y if and only if

$$D^{\alpha }\left[\widehat{y}\left(\xi \right)\widehat{{\tilde{B}}_{\nu }}{\left(\xi \right)}^{*}\right]{|}_{\xi =\mathbf{0}}={\delta }_{1,\nu }{D}^{\alpha }\widehat{y}\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}},\hspace{1em}\forall \alpha \in {\mathsf{\Delta }}_n,\hspace{1em}\nu =1,\dots ,m.$$

Proof. 

The sum rule condition of order n for matrix mask $\widehat{B_1}$ can be rewritten as follows

$$D^{\alpha }\left[y\left(M^{*}\xi \right)\widehat{B_1}(\xi +M^{*-1}{s}_j)\right]{|}_{\xi =\mathbf{0}}={\delta }_{1,j}{D}^{\alpha }y\left(\mathbf{0}\right),\hspace{1em}\forall j=1,\dots ,m.$$

(38)

Since $\mathcal{L}{\tilde{\mathcal{L}}}^{*}\equiv I_{mr}$ then

$$\sum _{j=1}^m\widehat{B_1}(\xi +M^{*-1}{s}_j){\left[\widehat{{\tilde{B}}_{\nu }}(\xi +M^{*-1}{s}_j)\right]}^{*}={\delta }_{1,\nu }{I}_r,\hspace{1em}\forall \nu =1,\dots ,m.$$

Multiplying the last equality from the left by the column vector $y\left(M^{*}\xi \right)$, we obtain

$$\sum _{j=1}^{m}y\left(M^{*}\xi \right)\widehat{B_1}(\xi +M^{*-1}{s}_j){\left[\widehat{{\tilde{B}}_{\nu }}(\xi +M^{*-1}{s}_j)\right]}^{*}={\delta }_{1,\nu }y\left(M^{*}\xi \right), \forall \nu =1,\dots ,m.$$

Taking the derivatives of order $\alpha \in {\mathsf{\Delta }}_n$ at the origin, we obtain

$$\begin{array}{cc}\hfill {\delta }_{1,\nu }& D^{\alpha }y\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}}\hfill \\ \hfill =& \sum _{j=1}^m\sum _{\beta \in {\square }_{\alpha }}\left(\genfrac{}{}{0pt}{}{\alpha }{\beta }\right)D^{\alpha -\beta }\left[y\left(M^{*}\xi \right)\widehat{B_1}(\xi +M^{*-1}{s}_j)\right]{|}_{\xi =\mathbf{0}}{D}^{\beta }{\left[\widehat{{\tilde{B}}_{\nu }}(\xi +M^{*-1}{s}_j)\right]}^{*}{|}_{\xi =\mathbf{0}}.\hfill \end{array}$$

By (38) and since $s_1=\mathbf{0}$ we obtain

$${\delta }_{1,\nu }{D}^{\alpha }y\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}}=\sum _{\beta \in {\square }_{\alpha }}\left(\genfrac{}{}{0pt}{}{\alpha }{\beta }\right)D^{\alpha -\beta }y\left(\xi \right){|}_{\xi =\mathbf{0}}{D}^{\beta }{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}^{*}{|}_{\xi =\mathbf{0}}.$$

Conversely, since $\mathcal{L}{\tilde{\mathcal{L}}}^{*}\equiv I_{mr}$ is equivalent to ${\tilde{\mathcal{L}}}^{*}\mathcal{L}\equiv I_{mr}$, then

$$\sum _{\nu =1}^m{\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}^{*}\widehat{B_{\nu }}(\xi +M^{*-1}q)={\delta }_{\mathbf{0},q}{I}_r, \forall q\in D\left(M^{*}\right).$$

Multiplying the last equality from the left by $y\left(\xi \right)$, we obtain

$$\sum _{\nu =1}^{m}y\left(\xi \right){\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\right]}^{*}\widehat{B_{\nu }}(\xi +M^{*-1}q)={\delta }_{\mathbf{0},q}y\left(\xi \right), \forall q\in D\left(M^{*}\right).$$

Taking the derivatives of order $\alpha \in {\mathsf{\Delta }}_n$ at the origin, we obtain

$$\begin{array}{c}\hfill \sum _{\nu =1}^m\sum _{\beta \in {\square }_{\alpha }}\left(\genfrac{}{}{0pt}{}{\alpha }{\beta }\right)D^{\beta }\left[y\left(\xi \right)\widehat{{\tilde{B}}_{\nu }}{\left(\xi \right)}^{*}\right]{|}_{\xi =\mathbf{0}}{D}^{\alpha -\beta }\widehat{B_{\nu }}(\xi +M^{*-1}q){|}_{\xi =\mathbf{0}}={\delta }_{\mathbf{0},q}{D}^{\alpha }y\left(\mathbf{0}\right),\\ \hfill \sum _{\beta \in {\square }_{\alpha }}\left(\genfrac{}{}{0pt}{}{\alpha }{\beta }\right)D^{\beta }y\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}}{D}^{\alpha -\beta }\widehat{{\tilde{B}}_1}(\xi +M^{*-1}q){|}_{\xi =\mathbf{0}}={\delta }_{\mathbf{0},q}{D}^{\alpha }y\left(\mathbf{0}\right),\end{array}$$

which is equivalent to sum rule condition of order n. □

This result allows us to check that MRA-based multiwavelets are provided with vanishing moments of order 1. Indeed, if the initial matrix mask $\widehat{A}={\widehat{B}}_1$ obeys sum rule at least of order 1, then Lemma 4 says that

$$y\left(\mathbf{0}\right)\widehat{{\tilde{B}}_1}{\left(\mathbf{0}\right)}^{*}=y\left(\mathbf{0}\right) \mathrm{and} y\left(\mathbf{0}\right)\widehat{{\tilde{B}}_{\nu }}{\left(\mathbf{0}\right)}^{*}=\mathbf{0},\hspace{1em}\nu =2,\dots ,m.$$

Note that $\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(\mathbf{0}\right)=\widehat{{\tilde{B}}_{\nu }}\left(\mathbf{0}\right)\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$ and $\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$ is the unique 1-eigenvector of $\widehat{{\tilde{B}}_1}\left(\mathbf{0}\right)$, therefore $\widehat{{\tilde{B}}_1}\left(\mathbf{0}\right)\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)=\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$. Hence, $\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$ is equal to $y{\left(\mathbf{0}\right)}^{*}$ up to a multiplication by a constant and $\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(\mathbf{0}\right)=\mathbf{0}.$ By duality, it is also true that $\widehat{{\mathsf{\Psi }}^{\left(\nu \right)}}\left(\mathbf{0}\right)=\mathbf{0}$, if the dual matrix mask obeys sum rule at least of order 1.

Moreover, in practice, dual wavelet function vectors ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$ are used for the analysis operations, and it is good to provide these functions with high order of vanishing moments. This is indeed the case, namely, the order of vanishing moments for ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$ is equal to n (i.e., equal to the order of sum rule of the initial matrix mask $\widehat{A}$). Note that by Lemma 4

$$D^{\alpha }\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)y^{*}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}=\mathbf{0},\hspace{1em}\forall \alpha \in {\mathsf{\Delta }}_n,\hspace{1em}\nu =2,\dots ,m.$$

We have to check that $D^{\alpha }{y}^{*}\left(\mathbf{0}\right)=D^{\alpha }\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$, since this equality provides vanishing moments for ${\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}$. Indeed, equalities

$$D^{\alpha }\left[\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(M^{*}\xi \right)\right]{|}_{\xi =\mathbf{0}}=D^{\alpha }\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)\widehat{\tilde{\mathsf{\Phi }}}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}=D^{\alpha }\left[\widehat{{\tilde{B}}_{\nu }}\left(\xi \right)y^{*}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}=\mathbf{0},\hspace{1em}\forall \alpha \in {\mathsf{\Delta }}_n,$$

$\nu =2,\dots ,m,$ imply that $D^{\alpha }\widehat{{\tilde{\mathsf{\Psi }}}^{\left(\nu \right)}}\left(\mathbf{0}\right)=\mathbf{0}$, $\forall \alpha \in {\mathsf{\Delta }}_n,$ $\nu =2,\dots ,m.$ By the refinement equation, it is true that

$$D^{\alpha }\widehat{\tilde{\mathsf{\Phi }}}\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}}=D^{\alpha }\left[\widehat{\tilde{A}}\left(\xi \right)\widehat{\tilde{\mathsf{\Phi }}}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}.$$

(39)

Note that by duality and by Equation (25), the derivatives of y at the origin are related with the derivatives of $\widehat{\tilde{A}}$ as follows

$$D^{\alpha }\left[\widehat{\tilde{A}}\left(\xi \right)y^{*}\left(\xi \right)\right]{|}_{\xi =\mathbf{0}}=D^{\alpha }\left[y^{*}\left(M^{*}\xi \right)\right]{|}_{\xi =\mathbf{0}},\hspace{1em}\forall \alpha \in {\mathsf{\Delta }}_n.$$

Since this relation defines the derivatives of y at the origin uniquely (up to a multiplication by a constant), then comparing it with (39), we obtain the required connection $D^{\alpha }{y}^{*}\left(\mathbf{0}\right)=D^{\alpha }\widehat{\tilde{\mathsf{\Phi }}}\left(\mathbf{0}\right)$.

It is also worth noting that the constructed symmetric multiwavelets have the balancing property. For a filter bank related to some wavelet system, the high number of vanishing moments for wavelets ${\tilde{\psi }}_{\nu }$ is equivalent to the same number of vanishing moment for the corresponding wavelet masks ${\tilde{b}}_{\nu }$. In practice, this means that during the analysis step of the discrete wavelet transform high frequency components of the input sequence vanish. For a multiwavelet filter bank $(\widehat{A},{\widehat{B}}_2,\dots ,{\widehat{B}}_r)$ and $(\widehat{\tilde{A}},\widehat{{\tilde{B}}_2},\dots ,\widehat{{\tilde{B}}_r})$, generally, this is not the case. This property should be provided specifically, and the related notion is called the balancing property. However, in the interpolating case, balancing order for the analysis filter bank $(\widehat{\tilde{A}},\widehat{{\tilde{B}}_2},\dots ,\widehat{{\tilde{B}}_r})$ is equal to the order of sum rule of matrix mask $\widehat{A}$. The necessary and sufficient conditions are stated in ([41] Proposition 3.1, Theorem 4.1) (see, also, ([16] Theorem 2.1)). The balancing property of order n is provided for the analysis filter bank $(\widehat{\tilde{A}},\widehat{{\tilde{B}}_2},\dots ,\widehat{{\tilde{B}}_r})$ if $y\left(\xi \right)={\left\{e^{2\pi i(M^{-1}s,\xi )}\right\}}_{s\in D\left(M\right)}$, and

$$D^{\alpha }\left[y\left(\xi \right)\widehat{{\tilde{B}}_{\nu }}{\left(\xi \right)}^{*}\right]{|}_{\xi =\mathbf{0}}=\mathbf{0},\hspace{1em}\alpha \in {\mathsf{\Delta }}_n,$$

$$D^{\alpha }\left[y\left(\xi \right)\widehat{\tilde{A}}{\left(\xi \right)}^{*}\right]{|}_{\xi =\mathbf{0}}=D^{\alpha }\widehat{y}\left(M^{*}\xi \right){|}_{\xi =\mathbf{0}},\hspace{1em}\alpha \in {\mathsf{\Delta }}_n.$$

For the interpolating matrix mask $\widehat{A}$, a vector of functions y is taken exactly as required. The last two conditions are true due to Lemma 4.

Next, we discuss several additional aspects. Let us compare the obtained results with the approach proposed in [20] for the same problem. In [20] the construction of matrix masks is done by transferring all required conditions into the form of systems of linear equations. The coefficients of initial matrix mask and dual matrix mask are obtained as a numerical solution of such systems. The existence of solution for any appropriate set of initial parameters is out of consideration. Wavelet matrix masks are obtained by an explicit procedure, but the study of their symmetry and approximation properties is not carried out. The approach proposed in the current paper describes the inner structure of symmetric matrix masks in terms of the modified polyphase components; coefficients of the matrix masks can be obtained even analytically, if needed. Additionally, the description of symmetry in terms of the modified polyphase components helps to study the symmetry properties of the obtained wavelet matrix masks.

In fact, the interpolating property leads to some limitations on the choice of a pair of appropriate symmetry group and dilation matrix (see condition (18)). Additionally, the interpolating property means that the number r of functions in refinable function vector is equal to $|detM|$, and the symmetry centers are defined by digits. On the other hand, in the non-interpolating case, general matrix extension with symmetry becomes a challenging problem. In the scalar case, several methods were developed (see, for example, [42,43,44] and the references therein). This is a question for future investigations, whether these methods can be modified for multiwavelets.

Finally, multivariate wavelet frames are successively used in applications related to signal processing and numerical solution of PDEs (for example, in [5] 2D multiwavelet transform is used in the iris biometric technique for person authentication, in [1] 2D multiwavelets are used for dimensionality reduction and features extraction in the algorithm of face recognition, in [21] 2D multiwavelets are applied to variational image denoising and in [4] 2D multiwavelets are used for the compression, analysis and assembly of hydrodynamic model data within Godunov-type solvers based on second-order discontinuous Galerkin methods). Mostly, 2D multiwavelets in the above-mentioned applications and in the literature are separable, i.e., they are obtained as a tensor product of 1D multiwavelets. However, there are several results that non-separable wavelets provide some advantages in certain applications compared to separable ones (see, for example, [45,46] for wavelet and [47] for multiwavelets). The proposed method for the construction of symmetric non-separable multiwavelets can help to obtain multiwavelets, which potentially can lead to improvements in the mentioned and other applications. We leave these problems for future research.

5. Examples

1. Consider simple symmetry group in ${\mathbb{R}}^2$: $\mathcal{H}=\{I_2,-I_2\}$ and quincunx dilation matrix $M=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$. The set of digits is $D\left(M\right)=\left\{\right(0,0),(1,0\left)\right\}$. Clearly, condition $Es-s\in M{\mathbb{Z}}^d$ is valid for all $E\in \mathcal{H}$ and $s\in D\left(M\right)$. For interpolating matrix mask the row of symmetry centers is $C=((0,0),(\frac{1}{2},\frac{1}{2}))$.

Consider matrix mask $\widehat{A}$ defined by

$$\widehat{A}\left(\xi \right)=\left(\begin{array}{cc}\frac{1}{2}& \frac{3}{16}+\frac{1}{16y}+\frac{3}{16xy}+\frac{1}{16x}\\ \frac{x}{2}& \frac{3x}{16}+\frac{x}{16y}+\frac{1}{16}+\frac{3}{16y}\end{array}\right).$$

Here (and below) $x=e^{2\pi i{\xi }_1}$, $y=e^{2\pi i{\xi }_2}$. This matrix mask is $\mathcal{H}$-symmetric with respect to the row of centers C. The matrix of symmetry centers for each matrix element is $\left(\begin{array}{cc}(0,0)& (-\frac{1}{2},-\frac{1}{2})\\ (1,0)& (\frac{1}{2},-\frac{1}{2})\end{array}\right)$. This matrix mask obeys the sum rule of order 2. Additionally, the eigenvalues of $\widehat{A}\left(\mathbf{0}\right)$ are 1 and 0. The Sobolev smoothness of the corresponding refinable functions here and below can be computed using algorithm developed in [34]. Here ${\phi }_i$, $i=1,2$, are at least in $W_2^{1.58411}\left({\mathbb{R}}^2\right).$ See Figure 1 for the graph of ${\phi }_1$ (note that ${\phi }_2$ is just a shifted copy of ${\phi }_1$). The dual matrix mask $\widehat{\tilde{A}}$ can be taken as follows:

$$\widehat{\tilde{A}}\left(\xi \right)=\left(\begin{array}{cc}-\frac{3}{32}yx-\frac{x}{32}+\frac{13}{16}-\frac{y}{32}-\frac{1}{32x}-\frac{1}{32y}-\frac{3}{32xy}& \frac{1}{4}+\frac{1}{4xy}\\ -\frac{3}{32}y{x}^2-\frac{x^2}{32}+\frac{13x}{16}-\frac{yx}{32}-\frac{x}{32y}-\frac{1}{32}-\frac{3}{32y}& \frac{x}{4}+\frac{1}{4y}\end{array}\right).$$

It is also $\mathcal{H}$-symmetric with respect to the same row of centers C and it obeys sum rule of order 1. The eigenvalues of $\widehat{\tilde{A}}\left(\mathbf{0}\right)$ are 1 and 0. The corresponding refinable functions are at least in $W_2^{0.10204}\left({\mathbb{R}}^2\right)$. After the matrix extension is obtained, the wavelet matrix masks are

$$\begin{gathered} {\widehat{B}}_2\left(\xi \right)=\left(\begin{array}{cc}-\frac{xy}{4}-\frac{1}{4}& -\frac{3}{32}yx-\frac{x}{32}+\frac{13}{16}-\frac{y}{32}-\frac{1}{32x}-\frac{1}{32y}-\frac{3}{32xy}\\ -\frac{y{x}^2}{4}-\frac{x}{4}& -\frac{3}{32}y{x}^2-\frac{x^2}{32}+\frac{13x}{16}-\frac{yx}{32}-\frac{x}{32y}-\frac{1}{32}-\frac{3}{32y}\end{array}\right), \\ \widehat{{\tilde{B}}_2}\left(\xi \right)=\left(\begin{array}{cc}-\frac{3}{16}yx-\frac{x}{16}-\frac{y}{16}-\frac{3}{16}& \frac{1}{2}\\ -\frac{3}{16}y{x}^2-\frac{x^2}{16}-\frac{yx}{16}-\frac{3x}{16}& \frac{x}{2}\end{array}\right). \end{gathered}$$

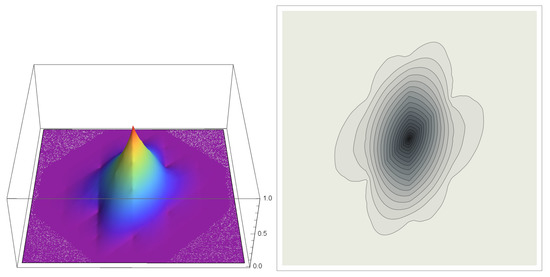
Figure 1. The 3D and contour plots of centrally symmetric refinable function ${\phi }_1$.

Note that in this case, the sets of digits associated with symmetry centers are: $D(M,c_1)=\{s_{1,1}^{\left(1\right)}=(0,0),s_{2,1}^{\left(1\right)}=(1,0)\}$ and $D(M,c_2)=\{s_{1,1}^{\left(2\right)}=(0,0),s_{2,1}^{\left(2\right)}=(1,0)\}$. This means that each trigonometric polynomial in wavelet matrix masks is $\mathcal{H}$-symmetric, which implies simple symmetry of the corresponding wavelets.

2. Consider axis symmetry group in ${\mathbb{R}}^2$:

$$\mathcal{H}=\left\{\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right),\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\right\}.$$

Let $M=\left(\begin{array}{cc}0& -1\\ 2& 0\end{array}\right)$. The set of digits is $D\left(M\right)=\left\{\right(0,0),(0,1\left)\right\}$. Clearly, condition $Es-s\in M{\mathbb{Z}}^d$ is valid for all $E\in \mathcal{H}$ and $s\in D\left(M\right)$. For interpolating matrix mask the row of symmetry centers is $C=((0,0),(\frac{1}{2},0))$.

Consider matrix mask $\widehat{A}$ defined by

$$\widehat{A}\left(\xi \right)=\left(\begin{array}{cc}\frac{1}{2}& \frac{1}{2}\left(\frac{1}{2}+\frac{1}{2x}\right)\\ \frac{y}{2}& \frac{1}{2}\left(\frac{y}{2}+\frac{y}{2x}\right)\end{array}\right).$$

Here (and below) $x=e^{2\pi i{\xi }_1}$, $y=e^{2\pi i{\xi }_2}$. This matrix mask is $\mathcal{H}$-symmetric with respect to the row of centers C. The matrix of symmetry centers for each matrix elements is $\left(\begin{array}{cc}(0,0)& (-\frac{1}{2},0)\\ (0,1)& (-\frac{1}{2},1)\end{array}\right)$. This matrix mask obeys sum rule of order 2. Also, the eigenvalues of $\widehat{A}\left(\mathbf{0}\right)$ are 1 and 0. The corresponding refinable functions are at least in $W_2^{1.5}\left({\mathbb{R}}^2\right).$ See Figure 2 for the graph of ${\phi }_1$ (note that ${\phi }_2$ is just a shifted copy of ${\phi }_1$). The dual matrix mask $\widehat{\tilde{A}}$ can be taken as follows

$$\widehat{\tilde{A}}\left(\xi \right)=\left(\begin{array}{cc}-\frac{x}{8}+\frac{3}{4}-\frac{1}{8x}& \frac{1}{4}+\frac{1}{4x}\\ \frac{3y}{4}-\frac{xy}{8}-\frac{y}{8x}& \frac{y}{4}+\frac{y}{4x}\end{array}\right).$$

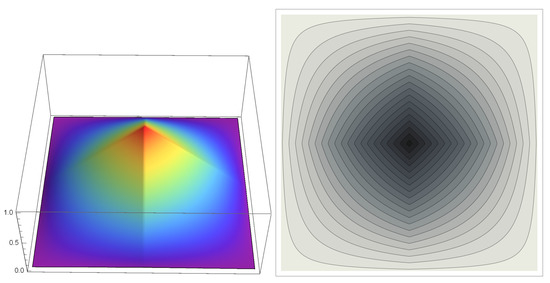
Figure 2. The 3D and contour plots of axially symmetric refinable function ${\phi }_1$.

It is also $\mathcal{H}$-symmetric with respect to the same row of centers C, and it obeys sum rule of order 2. Additionally, the eigenvalues of $\widehat{\tilde{A}}\left(\mathbf{0}\right)$ are 1 and 0. The corresponding dual refinable functions are at least in $W_2^{0.440765}\left({\mathbb{R}}^2\right).$ After the matrix extension is obtained, the wavelet matrix masks are

$${\widehat{B}}_2\left(\xi \right)=\left(\begin{array}{cc}-\frac{x}{4}-\frac{1}{4}& -\frac{x}{8}+\frac{3}{4}-\frac{1}{8x}\\ -\frac{xy}{4}-\frac{y}{4}& \frac{3y}{4}-\frac{xy}{8}-\frac{y}{8x}\end{array}\right), \widehat{{\tilde{B}}_2}\left(\xi \right)=\left(\begin{array}{cc}-\frac{x}{4}-\frac{1}{4}& \frac{1}{2}\\ -\frac{xy}{4}-\frac{y}{4}& \frac{y}{2}\end{array}\right).$$

Note that in this case, the sets of digits associated with symmetry centers are: $D(M,c_1)=\{s_{1,1}^{\left(1\right)}=(0,0),s_{2,1}^{\left(1\right)}=(0,1)\}$ and $D(M,c_2)=\{s_{1,1}^{\left(2\right)}=(0,0),s_{2,1}^{\left(2\right)}=(0,1)\}$. This means that each trigonometric polynomial in wavelet matrix masks is $\mathcal{H}$-symmetric, which implies axis symmetry of the corresponding wavelets.

3. Consider hexagonal abelian symmetry group

$$\mathcal{H}=\left\{I_2,\left(\begin{array}{cc}0& -1\\ 1& -1\end{array}\right),\left(\begin{array}{cc}-1& 1\\ -1& 0\end{array}\right)\right\}$$

and dilation matrix $M=\left(\begin{array}{cc}2& -1\\ 1& 1\end{array}\right).$ The set of digits are $D\left(M\right)=\left\{\right(0,0),(0,1),(1,1\left)\right\}$. It can be checked that $Es-s\in M{\mathbb{Z}}^d$ is valid for all $E\in \mathcal{H}$ and $s\in D\left(M\right)$. The row of symmetry centers for interpolating matrix mask is $C=\left\{\right(0,0),(1/3,2/3),(2/3,1/3\left)\right\}$.

Consider matrix mask $\widehat{A}$ defined by

$$\widehat{A}\left(\xi \right)=\left(\begin{array}{ccc}\frac{1}{3}& \frac{4}{27}+\frac{4}{27xy}+\frac{4}{27y}& \frac{1}{9}+\frac{1}{9xy}+\frac{1}{9x}\\ \frac{y}{3}& -\frac{xy}{81}+\frac{10y}{81}-\frac{y}{81x}+\frac{10}{81}+\frac{10}{81x}-\frac{1}{81xy}& \frac{y}{9}+\frac{y}{9x}+\frac{1}{9x}\\ \frac{xy}{3}& -\frac{2}{81}y{x}^2+\frac{8yx}{81}+\frac{8x}{81}-\frac{2y}{81}+\frac{8}{81}-\frac{2}{81y}& \frac{xy}{9}+\frac{y}{9}+\frac{1}{9}\end{array}\right).$$

Here (and below) $x=e^{2\pi i{\xi }_1}$, $y=e^{2\pi i{\xi }_2}$. This matrix mask is $\mathcal{H}$-symmetric with respect to the row of centers C. The matrix of symmetry centers for each matrix elements is $\left(\begin{array}{ccc}(0,0)& (-\frac{1}{3},-\frac{2}{3})& (-\frac{2}{3},-\frac{1}{3})\\ (0,1)& (-\frac{1}{3},\frac{1}{3})& (-\frac{2}{3},\frac{2}{3})\\ (1,1)& (\frac{2}{3},\frac{1}{3})& (\frac{1}{3},\frac{2}{3})\end{array}\right)$.

This matrix mask obeys the sum rule of order 2. Additionally, the eigenvalues of $\widehat{A}\left(\mathbf{0}\right)$ are 1, 0 and 0. The corresponding refinable functions are at least in $W_2^{1.6726}\left({\mathbb{R}}^2\right)$. See Figure 3, Figure 4 and Figure 5 for the graphs of ${\phi }_1$, ${\phi }_2$, ${\phi }_3$. The dual matrix mask $\widehat{\tilde{A}}$ can be taken as follows

$$\widehat{\tilde{A}}\left(\xi \right)=\left(\begin{array}{ccc}{a}_{1,1}\left(\xi \right)& \frac{1}{6}+\frac{1}{6xy}+\frac{1}{6y}& \frac{4}{27}+\frac{4}{27xy}+\frac{4}{27x}\\ y& 0& 0\\ a_{1,3}\left(\xi \right)& \frac{yx}{6}+\frac{x}{6}+\frac{1}{6}& \frac{x{y}^2}{27}+\frac{xy}{9}+\frac{y}{9}+\frac{x}{27}+\frac{1}{9}+\frac{1}{27x}\end{array}\right),$$

where

$$a_{1,1}\left(\xi \right)=-\frac{7}{81}yx-\frac{17x}{162}+\frac{17}{27}-\frac{17y}{162}-\frac{7}{81x}-\frac{7}{81y}-\frac{17}{162xy},$$

$$a_{1,3}\left(\xi \right)=-\frac{10}{81}y{x}^2-\frac{17y^2{x}^2}{162}+\frac{20yx}{27}-\frac{10y^{2}x}{81}-\frac{17x}{162}-\frac{10}{81}-\frac{17y}{162}.$$

It is also $\mathcal{H}$-symmetric with respect to the same row of centers C and it obeys sum rule of order 1. Additionally, the eigenvalues of $\widehat{\tilde{A}}\left(\mathbf{0}\right)$ are 1, $-\frac{1}{2}$ and 0. The corresponding dual refinable functions are at least in $W_2^{0.136994}\left({\mathbb{R}}^2\right).$ Again, the matrix extension allows us to construct wavelet matrix masks. For instance, dual wavelet masks are

$$\widehat{{\tilde{B}}_2}\left(\xi \right)=\left(\begin{array}{ccc}-\frac{8}{81}yx+\frac{x}{81}-\frac{4}{27}-\frac{10y}{81}+\frac{2}{81x}& \frac{1}{3}& 0\\ \frac{2x^2{y}^3}{81}-\frac{4x{y}^2}{27}-\frac{10x^2{y}^2}{81}-\frac{8xy}{81}+\frac{y}{81}& \frac{xy}{3}& 0\\ \frac{x{y}^3}{81}-\frac{4x{y}^2}{27}-\frac{8y^2}{81}+\frac{2xy}{81}-\frac{10y}{81}& \frac{y}{3}& 0\end{array}\right),$$

$$\widehat{{\tilde{B}}_3}\left(\xi \right)=\left(\begin{array}{ccc}-\frac{yx}{9}-\frac{x}{9}-\frac{1}{9}& 0& \frac{1}{3}\\ -\frac{y{x}^2}{9}-\frac{x^2}{9}-\frac{x}{9}& 0& \frac{x}{3}\\ -\frac{1}{9}{y}^2{x}^2-\frac{y{x}^2}{9}-\frac{yx}{9}& 0& \frac{xy}{3}\end{array}\right).$$

Analogously, primal wavelet masks can be obtained. Note that in this case the sets of digits associated with symmetry centers are: $D(M,c_1)=\{s_{1,1}^{\left(1\right)}=(0,0),s_{2,1}^{\left(1\right)}=(0,1),s_{3,1}^{\left(1\right)}=(1,1)\}$ and $D(M,c_2)=\{s_{1,1}^{\left(2\right)}=(0,0),s_{1,2}^{\left(2\right)}=(1,1),s_{1,3}^{\left(3\right)}=(0,1)\}$, $D(M,c_3)=\{s_{1,1}^{\left(2\right)}=(0,0),s_{1,2}^{\left(2\right)}=(1,0),s_{1,3}^{\left(3\right)}=(1,1)\}$. This means that trigonometric polynomials in columns of wavelet matrix masks are mutually symmetric, which implies mutual symmetry of the corresponding wavelets.

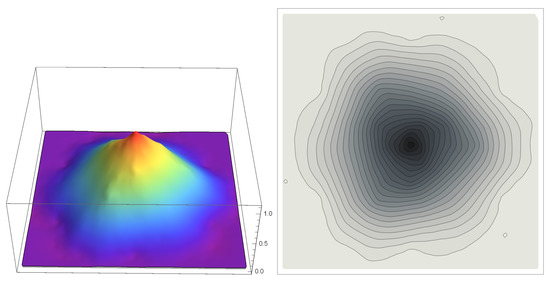
Figure 3. The 3D and contour plots on hexagonal lattice of hexagonally symmetric refinable function ${\phi }_1$.

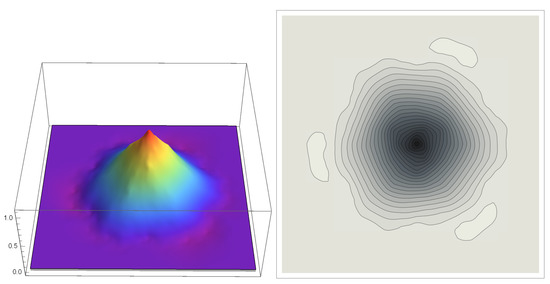
Figure 4. The 3D and contour plots on hexagonal lattice of hexagonally symmetric refinable function ${\phi }_2$.

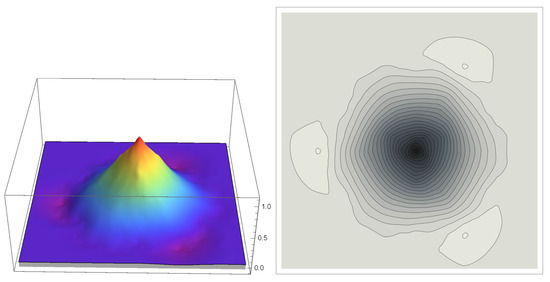
Figure 5. The 3D and contour plots on hexagonal lattice of hexagonally symmetric refinable function ${\phi }_3$.