Abstract
This paper presents a method for obtaining the shape and area of a sofa. The proposed approach is based on a discrete solution to the equation, which states the necessary conditions for the existence of envelopes. Based on provided examples, it was proved that the method can be used for deriving the solutions of the posed problem. The method offers an area calculation accuracy of .
MSC:
53A70
1. Introduction
The moving sofa problem was formulated for the first time by Moser [] as: "What is the largest area region which can be moved through a hallway of width one?". This is one of the unsolved mathematical problems []. The essence is to find such a shape of the maximum area that can be moved around a ninety-degree corner while a planar case is under consideration. The simplicity of the formulation of the problem, which allows anyone to understand it, and advanced calculation techniques used for analyses have retained the scientific interest of researchers until today.
One of the first proposed solutions was a sofa built from circular arcs and straight lines, the area of which was []. However, this solution was not optimal, as proved by Gerver [], who proposed a sofa with the area constructed from 18 analytically defined curves. This solution was probably the optimum one, though it has not yet been proven globally. Over the years, various attempts at designing other solutions have been made. The author in [] presented a shape similar to the shape of Gerver’s sofa obtained by the Monte Carlo method. Numerical analyses were also performed for an ambidextrous sofa []. Gerver’s sofa was modelled with the aid of Boolean operations performed for each discrete position of the hallway []. An improved upper bound for the optimal solution, which should now be within the interval , has recently been obtained []. Attempts were also made to describe this problem by means of variational analysis [].
The solution to the problem also found practical applications, i.e., while choosing the shape of a trolley moving around the corner [] or in mobile robot path planning—the so-called “piano movers” problem [,,].
The aim of this paper was to lay the foundation for further investigating the moving sofa problem. In particular, we sought to obtain such a mathematical model of sofa generation which could be used for searching the novel solutions of the problem or to prove that the Gerver’s solution truly is an optimal one. For this purpose, the method for obtaining the shape of the moving sofa is proposed. The method is based on discrete solutions to the equations, stating necessary conditions of the existence of envelopes [,,].
2. Sofa Generation
Fixed coordinate system h was established, in which the region of hallway is bounded by two curves parametrised as and (Figure 1).
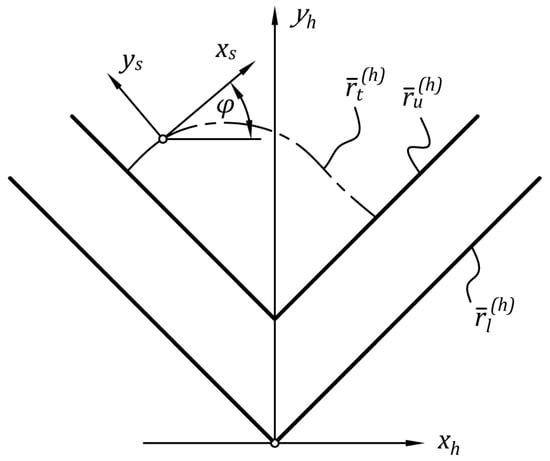
Figure 1.
Coordinate systems.
Position vectors of the upper and lower boundaries of the hallway are expressed by Equations (1) and (2):
where i are the hallway’s parameters. Moreover, coordinate system s connected with the sofa moves along the trajectory defined by a parametric curve in the form of and rotates by , where is the parameter of the path of movement. In order to express the hallway’s boundaries in the coordinate system connected with the sofa, we may use Equation (3)
where indexes u and l refer to the upper and lower boundaries of the hallway, respectively. Equation (3) describes one parameter family of curves with parameter . After transformation, we obtain (4) and (5):
The necessary condition for the existence of envelopes expressed as the perpendicularity of the vector normal and a derivative of the vector of a family of curves with respect to its parameter [] takes the form of:
By calculating the partial derivatives of expressions (4) and (5) and putting them into (6) and (7), we arrive at the envelope Equations (8) and (9):
wherein the upper sign stands for the right-hand side and the lower sign stands for the left-hand side. The solutions to Equations (8) and (9), with the assumption that , are parameters (10) and (11):
Taking into account the above results in Equations (4) and (5), we obtain the envelopes of the consecutive positions of the hallway boundaries in the sofa’s coordinate system (12) and (13):
The above equations stand while the derivatives and exist. Otherwise, as for point , the envelope can be represented by the curve defined as (14) (Appendix A, Theorem A1)
Assuming that the sofa’s path of movement and angle of rotation are given in a discrete way as a set of points , and , where , and taking finite differences quotients instead of derivatives, solutions to envelope Equations (10) and (11) can be expressed as (15) and (16):
Taking the above equations into (1) and (2), and subsequently into (4) and (5), the discrete representation of curves which bound the region of sofa (17) and (18) can be established:
Moreover, Equation (14) takes the discrete form (19)
Finally, it can be said that the region of sofa is , where it should be within the region limited by the initial and the final position of the hallway , where:
The shape of the sofa is obtained based on discrete curves bounding its region by means of standard curve intersection detection algorithms. The area of the sofa can be calculated as the area of a polygon with multiple numbers of sides; if the symmetrical case is considered (Appendix A, Theorem A2) in order to accelerate the calculations, they can be run for half of the sofa only.
3. Application of the Proposed Method
3.1. Gerver’s Solution
Generating the shape of the sofa proposed by Gerver [] starts by defining the path of movement and angle of rotation. This was accomplished by the discretisation of Equation (25) from study []. Therefore, values where were obtained. Subsequently, the path of the movement was transformed into the coordinate system used in the present study with the aid of Equation (21).
The results are presented in Figure 2a,b.
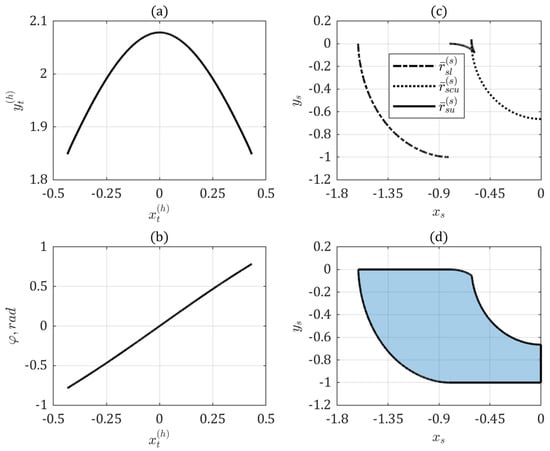
Figure 2.
Gerver’s sofa: (a) path of movement; (b) angle of rotation; (c) envelopes of hallway; and (d) shape of sofa.
The path of movement is symmetrical with respect to axis , while the angle of rotation is an odd function. Based on the above, according to Section 2, the envelopes of hallway (Figure 2c) were established for half of the sofa. Taking into account conditions (20), the shape of one half of the sofa was obtained (Figure 2d). The calculation time for was 2.65 s, and the resulting area of the sofa differs by only from the area obtained by Gerver: [].
3.2. Romik’s Solution
In order to arrive at the shape of sofa as proposed by Romik, its path of movement and angle of rotation were discretised based on Equation (47) from []. As in Section 3.1, they were transformed with the aid of Equation (21). The resulting path of the movement and rotation angle are shown on Figure 3a,b.
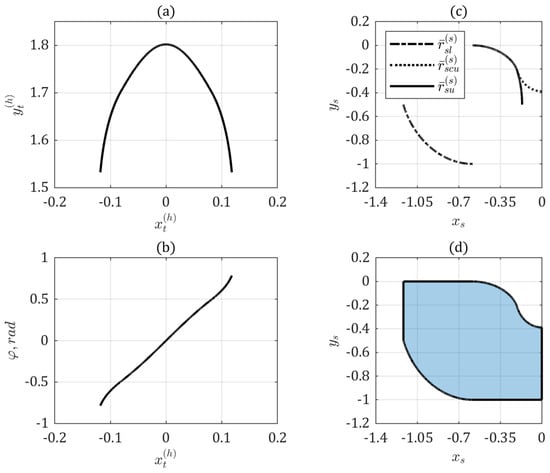
Figure 3.
Romik’s sofa: (a) path of movement; (b) angle of rotation; (c) envelopes of hallway; and (d) shape of sofa.
Since Romik’s solution is also symmetrical, calculations were limited to one half of the sofa. The envelopes of the hallway are shown in Figure 3c). Figure 3d presents the shape generated in this manner. To derive the ambidextrous sofa, an intersection with its reflection on either side of axis was performed (Figure 4).
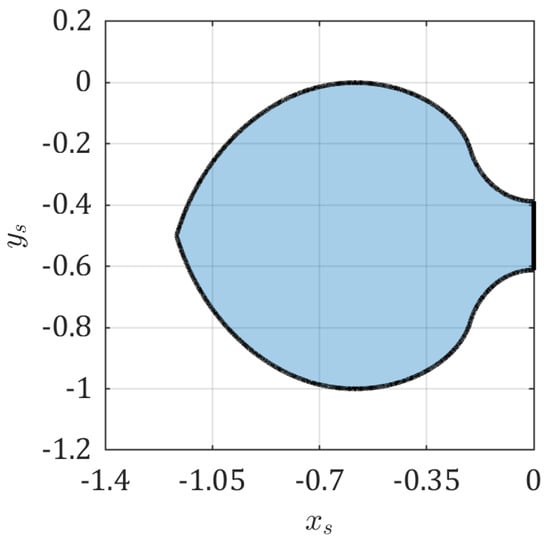
Figure 4.
Ambidextrous Romik’s sofa.
The area of the ambidextrous sofa generated with the aid of the proposed method is (for ) and differs by from Romik’s analytical solution [].
3.3. Asymmetrical Sofa
In order to demonstrate whether the proposed method is capable of generating a sofa of an asymmetric shape, the path of movement was defined by cubic spline interpolation over three points: , while the angle of the rotation was a linear function in the form of , as shown in Figure 5a,b. The envelopes of the hallway and the shape of the sofa are presented in Figure 5c,d. The area of the sofa amounts to and is smaller than in Gerver’s solution.
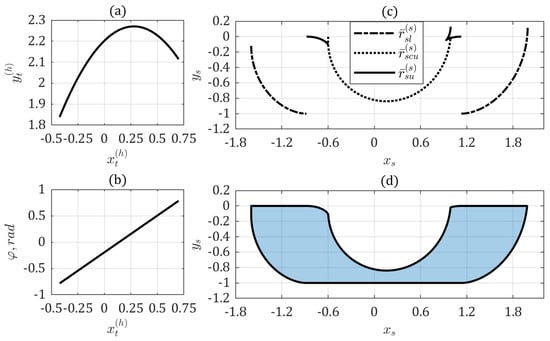
Figure 5.
Asymmetrical sofa: (a) path of movement; (b) angle of rotation; (c) envelopes of hallway; and (d) shape of sofa.
4. Conclusions
Based on the provided examples, it was concluded that the proposed method may be successfully used for generating sofas. The calculation accuracy defined as the difference between the analytically and numerically obtained areas is presented in Figure 6.
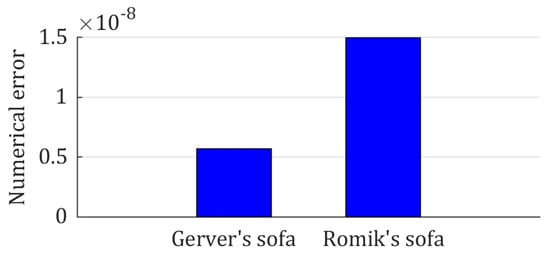
Figure 6.
Numerical error of area calculation.
It can be observed that the calculation error is small, therefore the method is considered as correct.
Moreover, the method could be used for designing a mathematical model in which functions of the path of movement and the angle of rotation are obtained in order to maximise the sofa’s area. Another potential application of the designed method is to prove that a truly optimal solution must be symmetrical. For that purpose, one can formulate a functional describing the area of the sofa and construct a proof that the extremum is only reached when the path of movement is symmetric and there is an odd parity of the angle of rotation (in other words, the sofa is symmetric, as can be seen in Theorem A2). One can try to achieve this by undermining, on the basis of the above assumptions, the system of Euler equations, which is a necessary condition for the existence of an extremum.
Nevertheless, the sofa with the maximum area is that proposed by Gerver; not only is it highly likely to be the optimal solution to the posed problem, but it is also possible to design a neat piece of furniture offering space for rather a large coffee table (Figure 7).
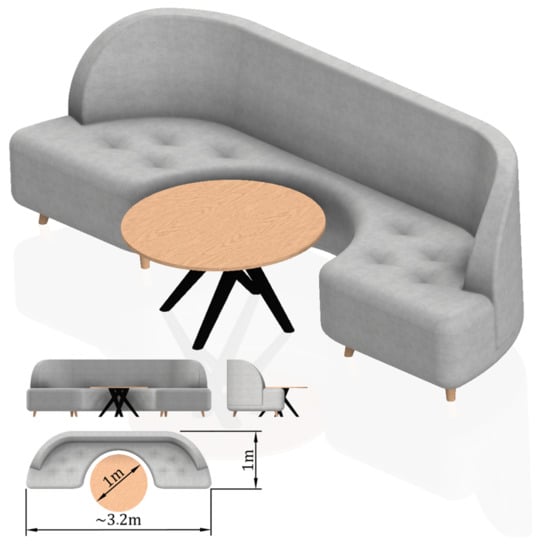
Figure 7.
A visualisation of the optimal design of the sofa.
Funding
This work was supported by the Rzeszów University of Technology.
Institutional Review Board Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Auxiliary Theorems
Theorem A1.
Proof.
While the case for is obvious, since it directly results from the necessary condition of envelope existence (6), it is problematic to determine the envelope when the derivative does not exist as in the case of point . It is assumed that the corner of curve (1) is rounded by a tangent circle with radius r, parametrised as follows . The above parametric form can be brought to an implicit one , wherein when , it defines point . The family of curves can be obtained using the parametric representation of a circle in Equation (4). After differentiation, the necessary condition for the existence of the envelope (6) takes the form of (A1)
Assuming that and the solution to Equation (A1) is . For an infinitesimal circle radius r, the above solution approaches zero, which can be expressed as . It follows that, for , the envelope of the family of curves (4) can indeed be represented by equation , which completes the proof. □
Theorem A2.
If the sofa’s path of movement is symmetrical along the axis and the rotation angle φ is an odd function of parameter , the sofa is symmetrical along axis.
Proof.
Assumptions regarding the symmetry of the path of movement and odd parity of the angle of rotation can be written out as . After differentiation with respect to the parameter, the following relations between derivatives can be obtained . Taking the above equalities into (10) and (11), and then into (12) and (13), the equalities can be obtained, where index R and L refers to the right- (upper sign) and left-hand side (lower sign) of sofa, respectively. Furthermore, the use of conditions supplied at the beginning of the proof in (14) leads to equality , which proves the thesis on the symmetry of the sofa. □
References
- Moser, L. Moving furniture through a hallway. SIAM Rev. 1966, 8, 381. [Google Scholar] [CrossRef]
- Croft, H.T.; Falconer, K.; Guy, R.K. Unsolved Problems in Geometry: Unsolved Problems in Intuitive Mathematics; Springer Science & Business Media: Berlin, Germany, 2012; Volume 2. [Google Scholar]
- Hammersley, J.M. On the enfeeblement of mathematical skills by modern mathematics and by similar soft intellectual trash in schools and universities. Educ. Stud. Math. 1968, 1, 17. [Google Scholar] [CrossRef][Green Version]
- Gerver, J.L. On Moving a Sofa Around a Corner. Geom. Dedicata 1992, 42, 267–283. [Google Scholar] [CrossRef]
- Wagner, N.R. The sofa problem. Am. Math. Mon. 1976, 83, 188–189. [Google Scholar] [CrossRef]
- Maruyama, K. An approximation method for solving the sofa problem. Int. J. Comput. Inf. Sci. 1973, 2, 29–48. [Google Scholar] [CrossRef][Green Version]
- Gibbs, P. A Computational Study of Sofas and Cars. Comput. Sci. 2014, 2, 1–5. [Google Scholar]
- Kallus, Y.; Romik, D. Improved upper bounds in the moving sofa problem. Adv. Math. 2018, 340, 960–982. [Google Scholar] [CrossRef]
- Song, N. A Variational Approach to the Moving Sofa Problem; Senior Project; Bard College: Annandale-On-Hudson, NY, USA, 2016. [Google Scholar]
- Gerd, E.; Henrik, E.; Kimmo, E. Moving a food trolley around a corner. Theor. Comput. Sci. 1998, 191, 193–203. [Google Scholar] [CrossRef][Green Version]
- Wilson, D.; Davenport, J.H.; England, M.; Bradford, R. A “piano movers” problem reformulated. In Proceedings of the 2013 15th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 23–26 September 2013; pp. 53–60. [Google Scholar]
- Schwartz, J.T.; Sharir, M. On the “piano movers” problem I. The case of a two-dimensional rigid polygonal body moving amidst polygonal barriers. Commun. Pure Appl. Math. 1983, 36, 345–398. [Google Scholar] [CrossRef]
- Maddila, S.; Yap, C.K. Moving a polygon around the corner in a corridor. In Proceedings of the Second Annual Symposium on Computational Geometry, Yorktown Heights, NY, USA, 2–4 June 1986; pp. 187–192. [Google Scholar]
- Litvin, F.L.; Fuentes, A. Gear Geometry and Applied Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Batsch, M. A novel method of obtaining honing tool profile for machining gears with profile modifications. J. Manuf. Sci. Eng. 2020, 142, 091004. [Google Scholar] [CrossRef]
- Polowniak, P.; Sobolak, M.; Marciniec, A. Mathematical model of the worm wheel tooth flank of a double-enveloping worm gear. Alex. Eng. J. 2021, 60, 3037–3046. [Google Scholar] [CrossRef]
- Romik, D. Differential Equations and Exact Solutions in the Moving Sofa Problem. Exp. Math. 2018, 27, 316–330. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).