Error Control Coding Algorithms in High Reliability Telemetry Systems

Abstract

In the oil and gas industry, in the process of drilling support (geosteering) and well telemetry, there is a problem of transmitting reliable information via wireless communication channels. The quality of such communication, as a rule, suffers due to the presence of errors caused by interference. As the depth of the well increases, the problem becomes more extensive. In order to solve the problem, it is proposed to choose noise-resistant coding in the system of residual classes. This system parallelizes the execution of arithmetic operations, has corrective abilities and organically adapts to the neural network basis of intelligent field management. At the same time, there are constraining factors for the mass application of the RNS; for example, difficulties in implementing non-modular procedures, forward and reverse coding, and some difficulties in identifying and correcting errors. That is why the task of improving the RNS seems relevant not only for oil and gas complexes, but also for any digital signal processing applications focused on intelligent neural network management on the basis of non-positional computing. The material of the article is limited to the study of the noise immunity of linear codes of the deduction system and the development of algorithms for detecting and correcting errors.

1. Introduction

Drilling of oil and gas wells in Russia at the present stage is mainly focused on maintaining the production level. In recent years, there has been a trend of moderate growth in the drilling market. At the same time, the volume of penetration at the level of 2016 (25.6 million m) will be restored no earlier than 2023, and the share of horizontal drilling will continue to increase to 44% by 2022. The analysis of drilling technology and methods of controlling the trajectory of directional wells shows that for effective control of the process of directional drilling, it is necessary to expand the informative base to ensure the transmission of reliable data based on the parameters of the drilling regime [1]. The information obtained from the bottom of the well in combination with the readings of the instruments at the mouth allows for effective monitoring and control of the parameters of the drilling mode. The solution of this urgent problem is possible when using navigation telesystems with processors with high-speed and reliable information processing capabilities.

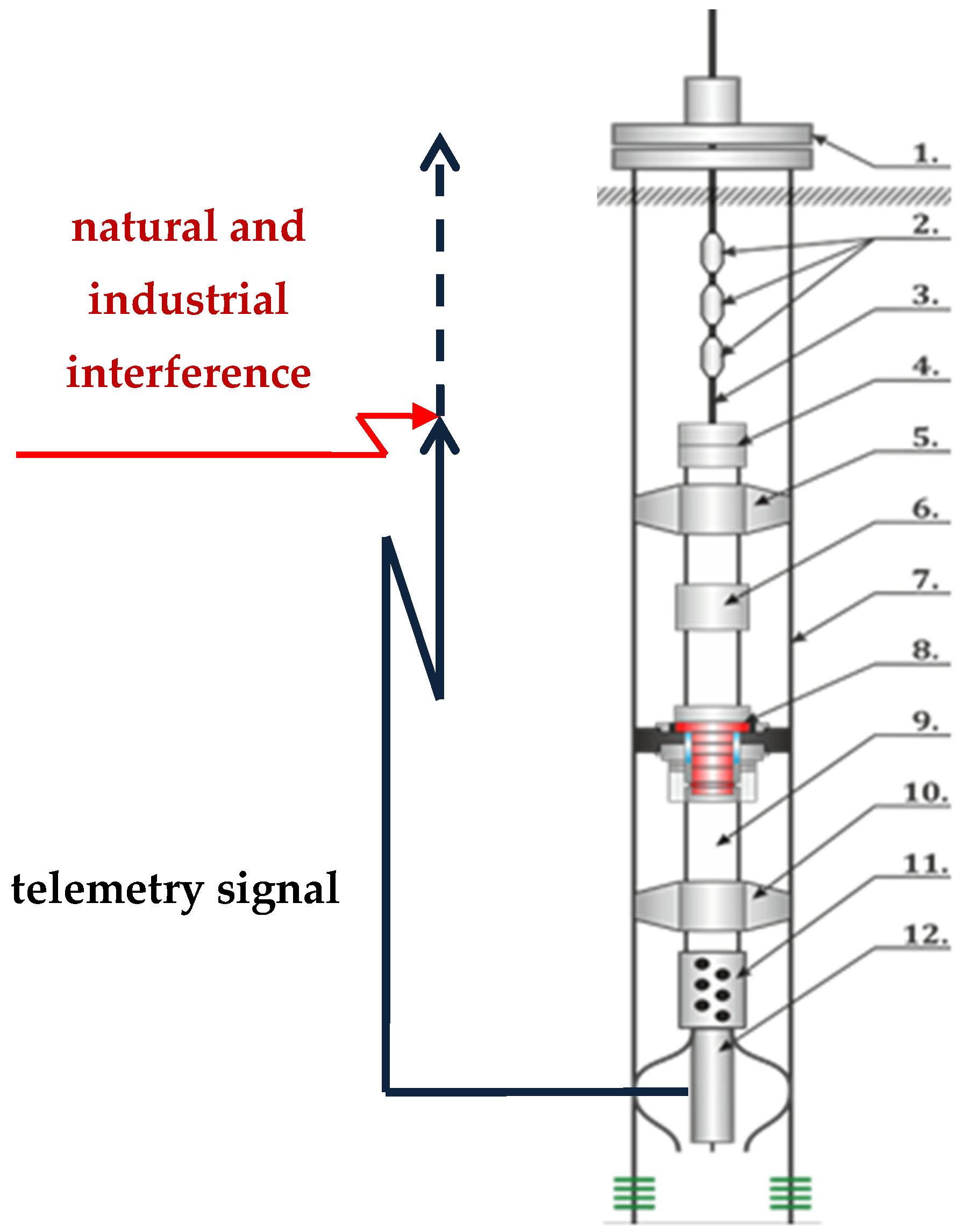
Similar tasks are also solved when developing wells that have already been drilled, which is when information about telemetry and geophysical research must also be processed and transmitted to control points with a high degree of reliability via a wireless communication channel during the entire inter-repair period, which can be from two to three years. The structure of the autonomous telemetry system, explaining the impossibility of organizing wired (cable) communication, is shown in Figure 1.

Thus, during construction, geonavigation and geophysical exploration of operated wells, one of the problems is a large amount of field information that needs to be transmitted from a great depth via wireless communication channels. Figure 1 shows that the use of wired cable communication in these cases is impossible due to the presence of a packer (No. 8). Therefore, the transmission of information can only be provided by an electromagnetic, acoustic or radio channel at low frequencies of transmission of packet messages. At the same time, an important role is played by ensuring the reliability of the received information [1,2,3].

As the main conditions for the transmission of telemetry formulated by oil and gas companies, the following are selected: high-speed processing of wide-range signals, low and ultra-low frequencies for transmitting packet messages from the well and adaptation to neural networks for subsequent integration into intelligent enterprise management systems [1].

In practice, the achievement of high reliability of information transmission, i.e., ensuring the reliability of its recovery at the receiving end of the transmission line, is ensured not so much by improving the technical means of information transmission as by using various methods of noise-resistant coding. This is explained by the fact that any possible increase in reliability is too expensive and sometimes requires the development of complex protective measures and hardware. The correctly chosen encoding method is able to provide the greatest resistance to possible accidental distortions [4,5,6,7]. To do this, special processing of the received information is carried out, which in turn assumes to eliminate the interference introduced into it, clear the signal from errors and achieve compliance with what was sent from the transmitting end of the line [8,9,10,11].

As a solution to the problem, the authors propose the use of coding in the system of residual classes. The choice of the encoding method is due to several reasons at once. Firstly, it is already the de facto existence of a neural network basis, with which a number system capable of parallelizing arithmetic operations is best combined; secondly, it meets the need for multiple high-speed processings of broadband packet information, dictated, as a special case, by the need to save power resources of autonomous equipment; thirdly, it meets the provision of fault tolerance due to code capable of detecting and correcting errors that occur.

It is generally accepted that of the known methods of encoding information in problems of ensuring high noise immunity (Reed–Muller, cyclic redundancy check (CRC), (Bose–Chowdhury–Hockingham (BCH), etc.), the code in the deduction system (the system of residual classes, RNS, built on the basis of the Chinese remainder theorem) and the Reed–Solomon code have the greatest appeal [12,13,14]. These codes are used with high efficiency in high-speed, digital signal processing algorithms with a large amount of computational operations, but the RNS is most organically combined with a neural network basis [15]. Computing structures developed specifically for the oil and gas industry based on the deduction system have proven themselves well in practice. Therefore, the task of ensuring high reliability of wireless communication channels for transmitting geonavigation information during drilling and about the state of wells in regard to a variety of geophysical and telemetric parameters based on the RNS is relevant for modern oil and gas complexes with intelligent control.

This article discusses the possibilities of correcting linear codes of the deduction system from the point of view of their suitability to ensure the noise immunity of transmitted telemetry signals by detecting and correcting the resulting distortions.

To this end, the authors formulated four statements and developed three error correction algorithms in the RNS which are largely capable of improving the reliability of wireless communication when transmitting downhole information.

2. Materials and Methods

It is known that among the correction codes, a special place is occupied by the non-positional system of deductions or residual classes (RNS) [16,17,18,19]. This is due to the fact that, firstly, the codes and the numbers being checked in it are represented in the form of residues (deductions), which makes it possible to consider such codes completely arithmetically, and secondly, in the RNS there is no significance of the order of digits in the number record.

The deduction system is a modular non-positional system for representing digits. In scientific circles, it is generally believed that this view is based on the Chinese remainder theorem, the calculations of Nicomachus from Gerasa, Euclid, and Euler, or even more ancient Aztec and Mayan calculus [5,6,7,8,9].

Nevertheless, the most famous extant work of the Chinese mathematician Sun Tzu (III century) is called the “Mathematical Treatise”. In this treatise the remainder theorem is formulated, according to which there is a unique non-negative solution modulo M.

This representation of numbers makes it possible to replace operations with large numbers A with operations with small numbers in the form of deductions (residues) (α₁, α₂,…, α_n) from division by the selected modules m_i. Thus, comparisons are obtained: A ≡ α₁(mod m₁), A ≡ α₂(mod m₂),…, A ≡ α_n(mod m_n). Therefore, any number A_k belonging to the set L can be represented in the deduction system by bases (or modules) M = [m₁, m₂, …, m_n], where M is the smallest common multiple of the natural numbers m₁, m₂, …, m_n, and L is the maximum length (number of terms) of the polynomial. If we multiply all the bases, we obtain the range of the system P_n = m₁ × m₂ ×, …, × m_n.

In the RNS, all basic arithmetic operations such as addition, subtraction, multiplication and division are performed in a component-by-component way, and the result is known in advance, is an integer and lies in the range [0, M − 1]. For example, the result of adding two numbers A ≡ α_n(mod m_n) and B ≡ β_n(mod m_n) is the number C ≡ c_n(mod m_n). Then,

c₁ ≡ (α₁ + β₁)(mod m₁);
    c₂ ≡ (α₂ + β₂)(mod m₂);
...
     c_n ≡ (α_n + β_n)(mod m_n).

Similarly, subtraction, multiplication and division are performed, but additional restrictions are imposed on division: it must be an integer, that is, the divisor must completely divide the divisible. The divisor must be mutually simple with all the modules of the basis.

As can be seen, computing operations not with integers but with their residues can significantly reduce machine time and provide the required accuracy, which has always attracted developers seeking high-speed digital signal processing. Operations on individual modules can be implemented using parallel and parallel pipeline architectures.

The following two systems are most often used in the RNS:

(1). An asymmetric system of non-negative deductions modulo m, consisting of the numbers 0, 1, 2, m − 1;

(2). A symmetric system of the smallest deductions in absolute value, consisting of numbers 0, ±1, ±2,..., ±(m − 1)/2 for an odd number m.

In order to ensure corrective abilities, redundancy is introduced into the deduction system. In addition to the information modules m₁, m₂, …, m_n, control bases m_n+1,…, m_n+k are also used [2,5,7,8].

Depending on the ratio between the values L, M and P_n, the correction codes in the RNS are divided into three main classes:

(1).

Non-linear codes (L = M = P_n);

(2).

Semi-linear codes (L < M < P_n);

(3).

Linear codes (L = M < P_n) [7].

Let us consider some general concepts for codes in the system of residual classes. Let the set L contain a set of such natural numbers in which if any two numbers A₁ and A₂ satisfy the requirement A₁, A₂ ∈ L, then any number A₃ between A₁ and A₂ also belongs to L, A₃ ∈ L.

In the works of [7,8], for error correction in the RNS, the possibilities of non-linear codes (R-codes) were investigated. They have good corrective abilities, as well as comparative ease of construction for any given minimum code distance. At the same time, it turned out that the technical implementation of the correction requires sufficiently large values of control bases (m_j > 40), which leads to a significant increase in hardware costs.

Unlike the R-code, in the linear L-code and the semi-linear RL-code, the bases are not mutually prime, i.e., integers have no common divisors except ±1.

In the correcting L-code, the sum, difference and product of any vectors are code words. In this case, no natural numbers can be matched with a non-code word. Correction of information by the L-code leads to a useful redundancy equivalent to redundancy. Therefore, from the point of view of ensuring the possibility of monitoring and correcting errors arising in the dynamics of the computational process, linear L-codes are the most attractive [5,7,8].

Taking this into account, the authors of this study investigated the noise immunity of linear codes (L-codes). This article presents the results of determining the necessary and sufficient conditions for the implementation of the developed algorithms for detecting and correcting errors in the deduction system.

3. Results

It is known [16,17,18,19,20] that the sum, difference and product of any linear code vectors are code words. In this case, no natural numbers can be matched to non-code words. It is shown in [3] that the correction of errors in the deduction system by means of L-codes leads to redundancy equivalent to redundancy. An important characteristic here is the concept of the minimum code distance d_min. In the usual ordered deduction system, d_min = k + 1. However, if the RNS is expanded by adding k modules and each module is larger than any information module, then the minimum code distance is automatically increased by k.

Let us examine two statements.

Statement 1.

The minimum distance d_min of the correcting L-code in the deduction system is equal to the minimum weight of non-zero code words.

It follows from the statement that the minimum code distance can be determined if the weights of the code words are already known.

Statement 2.

In order for the L-code to have a minimum distance d_min, it is necessary and sufficient that the degree of redundancy satisfies the ratio R = M^{d min−1}.

It turns out that the correction of arbitrary errors of information in the deduction system by means of L-codes leads to a large redundancy equivalent to conservation. At the same time, arbitrary distortions of the code word residues in the RNS correspond to the linear code with equal probability. Therefore, is it impractical to use linear codes for error correction? This is not quite true. It is further proved that the possibilities of L-codes can be significantly expanded by limiting the class of possible errors in individual code word deductions. To do this, it is only necessary to ensure that certain conditions are met [2,5].

Statement 3.

For any integer A = (α₁,α₂,…,α_n) in the system of deductions with modules m_i (i = 1,2,...,n) and for any pair of modules m_i and m_j, the condition must be met:

(α_i − α_j) ≡ 0(mod d_ij),

(1)

where d_ij = (m_i, m_j) is the largest common divisor of modules m_i, m_j, (i, j = 1,2,…n, i ≠ j).

To detect errors in the deduction by an arbitrary modulus m_i (I = 1, 2,…, n) of the number A = (α₁, α₂,…, α_n) specified in the deduction system with modules m₁, m₂,…, m_n, it is necessary that the module m_i has at least one that differs from one, a common divisor with the module m_j (i ≠ j).

Indeed, if we assume that the greatest common divisor of modules d_ij = (m_i, m_j) is defined for arbitrary modules of the residue system (i ≠ j), and the error occurred modulo m_i, i.e., ά_i = α_i + Δα_i, then the expression (ά_i − α_j) = 0(mod d_ij) is equivalent to the expression Δα_i(mod d_ij).

Since, in accordance with Statement 3, the condition (ά_i − α_j) = 0(mod d_ij) is satisfied, then we can assume that:

α_i + Δα_i = ά_i(mod m_i), and α_i + Δα_i = m × m_i + ά_i,

(2)

where m is the modulus of the deduction system, an integer.

The distorted deduction ά_i = α_i + Δα_i − m × m_iis determined from (1). Then we can write:

ά_i − α_j = [(α_i − α_j) + (m × k × d_ij) + Δα_i].

(3)

Since (α_i − α_j) ≡ 0(mod d_ij) and −m × k × d_ij ≡ 0(mod d_ij), where m_i = k × d_ij, k is a natural number, then (ά_i − α_j) ≡ Δα_i(mod d_ij).

This means that in the absence of common divisors (d_ij = 1) Δα_i ≡ 0(mod d_ij), which proves the necessary condition of Statement 3. The necessary condition may also be sufficient if the error is not a multiple of the divisor d_ij.

Indeed, (m × d_ij + α_ij) ≠ 0(mod × d_ij), where 0 < α_ij < d_i.

Statement 4.

To detect an error in the deduction by an arbitrary modulus m_i of the number A = (α₁, α₂,…, α_n) given in the system of residual classes, it is necessary and sufficient that the error Δα_i is not a multiple of the divisors d_ij and d_i = (d_i1, d_i2,…, d_in), where d_i is the largest common divisor of d_i1, d_i2,…, d_in, i ≠ j.

Proof. 

Calculate the values of α_ij, α_ik and α_jk. If the error occurred on the basis of m_i, then α_ik = 0, and α_ij ≠ 0 and α_ik ≠ 0. The number of different combinations of α_ij, α_ik is equal to (d_ij − 1) × (d_ik − 1), where (d_ij − 1) is the number of possible values of α_ij (α_ij ≠ 0), and (d_ik − 1) is the number of possible values of α_ik (α_ik ≠ 0). On the other hand, the number of possible error values based on m_i is m_i − 1 (Δα_i ≠ 0) minus the number of undetected errors. The number of undetected errors consists of the number of errors that are multiples of the divisor d_ik − K_dik and multiples of the divisor d_ij − K_dij. □

Thus, the number of possible values of detected errors is equal to m_i − 1 − (K_dik + K_dij − K_[dik,dij]).

To ensure that the number of combinations corresponds to the possible values of errors on the basis of mi, it is necessary to fulfill the condition:

(d_ij − 1) × (d_ik − 1) ≥ m_i − 1 − (K_dik + K_dij − K_[dik,dij]), which was required to be proved.

Taking into account the proven statement 4, it is possible to write a sufficient condition for correcting the error in the deduction α_i:

(d_ik − 1) × (d_ij − 1) > σ(Δα₁),

(4)

where σ(Δα₁) = (m_i − 1 − (K_dik + K_dij − K_[dik,dij]));

K_dik is the number of possible divisors of the error Δα_i on the basis of m_i, (i.e., the number of possible divisors m_i − 1), multiples of the value d_ik;

K_dij is the number of possible divisors of the error Δα_i on the basis of m_i, multiples of the value d_ij;

K_[dik,dij] is the number of possible error divisors Δα_i based on m_i, multiples of d_ik and d_ij.

Based on the results obtained in Statement 4, an error detection algorithm was developed in Algorithm 1.

Algorithm 1 Error detection

1. Check the deduction based on mi to determine the set of values1. Check the deduction based on mi to determine the set of values: α1 − α2 = α12(mod d12), α1 − α3 = α13(mod d13), … α1 − αn = α1n(mod d1n). (5) If α1i = 0(mod d1i), then the second deduction is checked, etc. 2. For the obtained values αij (i≠j), make a matrix |G| of the form: α12, α13,…, α1n α21, α23,…, α2n G =             … αn2, αn3,…, αnn−1. (6) When composing the matrix G, it is not necessary to identify the true numerical value αij. It is enough to present it in the form of: αij = 0, if αi − αj = 0(mod dij), (7) αij = 1, if αi − αj ≠ 0(mod dij) (8) 3. If the determinant of the matrix |G| is zero, then the number A = (α1, α2,…, αn) is correct, and if |G| ≠ 0, then the number A is incorrect.

Since α_i − α_j ≡ [d_ij − (α_j − α_i)]mod d_ij, then the determinant |G| cannot be found. It is enough to calculate the diagonal elements of the matrix G and add one value to α_n1, i.e., α₁₂, α₂₃, α₃₄, …, α_n−1 n, α_n1.

It is possible to check not only at which values α_ij the fact of the distortion of the code word is established, but also at which values the number of the distorted deduction is calculated.

Checking the validity of necessary and sufficient conditions for correcting one-time errors.

Suppose that in order to correct one-time errors by means of L-codes in a deduction by an arbitrary modulus m_i, the number A = (α₁, α₂,..., α_n), given in the deduction system with modules m₁, m₂,…, m_n, will be sufficient to satisfy the condition:

(d_ik − 1) × (d_ij − 1) ≥ m_i − 1 − (K_(dik) + K_(dij) − K_[dik,dij]),

(9)

where d_ik = (m_i, m_k), d_ij = (m_i, m_j);

K_(dik) is the number of divisors that are multiples of d_ik;

K_(dij) is the number of divisors that are multiples of d_ij;

K_[dik,dij] is the number of divisors that are multiples of the smallest common multiple of _[dik,dij] for i = j.

Indeed, if an error occurred modulo m_i when determining the values α_ij, α_ik, α_jk, then α_jk = 0, α_ij ≠ 0, α_jk ≠ 0 and the number of possible values of detected errors is (d_ij − 1) × (d_ikj − 1). Here, d_ij − 1 is the number of possible values of the value α_jk (α_jk ≠ 0).

At the same time, the number of possible errors modulo m_i is m_i − 1, (Δα_i ≠ 0) without taking into account the number of undetected errors. Here, the undetected errors include errors that are multiples of the divisor d_ik − K_(dik) and multiples of the divisor d_ij − K_(dij).

Therefore, the number of possible values of detected errors can be determined as follows:

m_i − 1 − (K_(dik) + K_(dij) − K_[dik,dij]).

(10)

In order to ensure that the number of combinations corresponds to the possible values of errors modulo, the condition must be met:

(d_ij − 1) × (d_ikj − 1) ≥ m_i − 1 − (K₍d_ik) + K₍d_ij) − K_[dik,dij]).

(11)

This proves the validity of condition (9). It is sufficient when different values of the errors Δα_i correspond to different values of the product α_jk × α_ij, and vice versa. It is then that there is an unambiguous mutual correspondence between the possible values of Δα_i and the values of the product α_jk × α_ij, which makes it possible to uniquely determine the magnitude of the error in Algorithm 2.

Algorithm 2 Correction of errors by an arbitrary module

1. Calculate the number of the distorted deduction, for which the values are determined in accordance with (4): α1 − α2 = α12(mod d12), α2 − α3 = α23(mod d23), … αn−1 − αn = αn−1(mod dn−1), αn − α1 = αn1(mod dn1). If all deductions are equal to αij = 0(mod dij), then the number A is correct. If an error occurred modulo mi, then αij ≠ 0 and αik ≠ 0, and this, in turn, means that the number being checked Á = (α1, α2,… άi,…, αn) is incorrect. 2. According to the values αij and αik, refer to the error constants storage table where the corresponding value Δαi is selected. 3. Make a correction of the number Á minus αi and obtain the correct number A = (α1, α2,…, αn).

In the reduced deduction system with the excluded modules for which an error occurred, it is possible to unambiguously represent the number A. It is only necessary, instead of determining the error values Δα_i by the values α_ij and α_ik, to directly calculate the values of the correct deduction α_i. Based on this, Algorithm 3 can be formulated.

Algorithm 3 Correction of errors

1. Calculation of deduction values α12, α23,…, αn1. 2. Determination of the number of the distorted deduction (for example, if an error occurred modulo mi, then this module is excluded, and the number A is represented by modules m1, m2,…, mn, i.e., A = (α1, α2,…, αi−1, αi+1,…, αn)). 3. Implementation of convolution (transformation) of the number A into a positional code. 4. Determination of the true value of the distorted remainder αi = A − [A/mi] mi, where [x] is an integer part not exceeding x.

The corrected number will look like:

A_corr = (α₁, α₂,…, α_i,…, α_n).

(12)

There are conditions under which it is possible to exclude some modules from the deduction system. Thus, if we imagine the modules of the original system of residual classes in the form:

m₁ = β₁₁(α₁₁), β₁₂(α₁₂), …, β_1ll(α_1l1);
m₂ = β₂₁(α₂₁), β₂₂(α₂₂), …, β_2ln(α_2ln);
…
m_n = β_n1(α_n1), β_n2(α_n2), …, β_nln(α_nln),
M = β₁(α₁), β₂(α₂), …, β_k(α_k),

(13)

then, in order to accurately determine the number A given in the deduction system with modules m₁, m₂…, m_n in the range [0, M), it is possible to exclude only those modules for which β_m, β_n = β_ijj, (m = 1, 2,…, k, i = 1, 2,…, n) and it is necessary that α_m ≥ α_ilj.

Thus, the necessary and sufficient conditions for error correction by the method of exclusion of the distorted module were investigated. Such conditions are the simultaneous fulfillment of equality and inequality:

β_m = β_ijj;

(14)

α_m ≥ α_ijj.

(15)

Example 1.

Let a residue system with four modules m₁ = 4, m₂ = 6, m₃ = 12, and m₄ = 18 be given. Moreover, M = [4, 6, 12, 18] = 36.

Let us represent the modules of the system in the canonical form:

m₁ = 2²; m₂ = 2 × 3, m₃ = 2² × 3, m₄ = 2 × 3², M = 2² × 3²

Obviously, the required modules are m₁, m₂, and m₃.

To check, let us compose the particular values:

M₁ = [6, 12, 18] = 36;

M₂ = [4, 12, 18] = 36;

M₃ = [4, 6, 18] = 36;

M₄ = [4, 6, 12] = 12.

As you can see, the particular value M₄ < 36, which confirms the correctness of de-terminating the excluded grounds from the specified system of residue related to L-codes.

Example 2.

Let us assume that when calculating the values (α_k − α_k+1)mod d_k k+1, α_i i−1 ≠ 0 and α_i i+1 ≠ 0 are obtained. In this case, the remaining values are equal to α_k k+1 = (α_k − α_k+1)mod d_k k+1 = 0.

In this case, the number Á = (α₁, α₂,… ά_i,…, α_n) is incorrect. The error is located at the base of m_i. For this example, you can determine the true value of the deduction Δα_i. To do this, you need to contact the block where the error constants are stored. After that, you can determine the true value of the deduction α_i corr = ά_i − Δα_i.

The number corrected in this way will be represented as:

A_corr = (α₁, α₂,…, α_i corr,…, α_n).

(16)

It should be noted that this method has a limitation. In order to complete the correction, a necessary condition is that the error Δα_i i is not simultaneously a multiple of two divisors d_i i−1 and d_i i+1.

4. Discussion

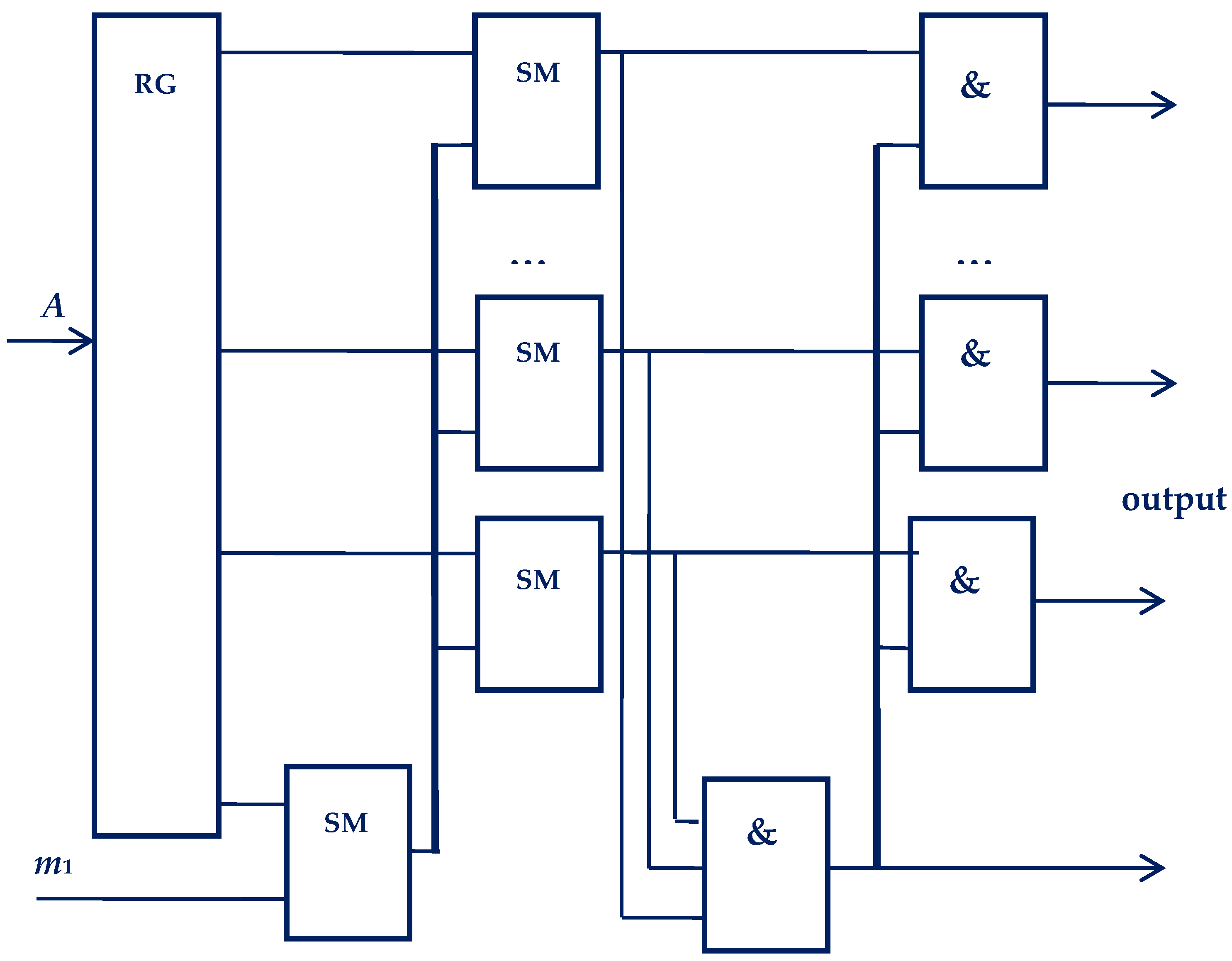
The results obtained as formulated above in four statements and in three algorithms are the theoretical basis for the synthesis of error detection and correction blocks. A variant of the device for error correction in the RNS is shown in Figure 2.

The device works as follows. Let us assume that the input of the device is supplied with a code already familiar to us in the RTS, with mutually pairwise simple bases m₁ = 4, m₂ = 6, and m₃ = 12. In this case, the code word table L = [4, 6, 12] = 12 it will look like this (

Table 1. Table of code numbers for the input sequence A_i on three bases.

Ai	Code Numbers
	m1	m2	m3
0000	00	000	0000
0001	01	001	0001
0010	10	010	0010
0011	11	011	0011
0100	00	100	0100
0101	01	101	0101
0110	10	000	0110
0111	11	001	0111
1000	00	010	1000
1001	01	011	1001
1010	10	100	1010
1011	11	101	1011

).

In this case, d₁₂ = (4, 6) = 2, d₂₃ = (6, 12) = 6, and d₃₁ = (4, 12) = 4; σ(Δα₁) = 2 in accordance with

Table 2. Correspondence table α₃₁ and α₁₂.

α31	α12 = 1
1	Δά1 = 1
2	-
3	Δά1 = 3

.

σ (Δα₂) = 3 (

Table 3. Correspondence table α₂₃ and α₁₂.

α31	α12 = 1
1	Δά2 = 5
2	-
3	Δά2 = 3
4	-
5	Δά2 = 1

) and σ(Δα₃) = 8 (

Table 4. Error table for α₃₁ and α₁₂.

α31	α23
	1	2	3	4	5
1	Δά3 = 7	-	Δά3 = 3	-	Δά3 = 11
2	-	Δά3 = 2	-	Δά3 = 10	-
3	Δά3 = 1	-	Δά3 = 9	-	Δά3 = 5

), where σ(Δα₁) = m_i − 1 − (K_d12 + K_d31 − K_[d12,d31]); σ(Δα₂) = m₂ − 1 − (K_d12 + K_d23 − K_[d12k,d23]); σ(Δα₃) = m₃ − 1 − (K_d23 + K_d31 − K_[d23,d31]).

Let it be necessary to determine the correctness of the number Á = (11, 100, 0111). Then the initial number Á is entered in the first and second registers. The first adder of the first group determines the value of ά₁ = m₁ − α₁ = 01, the second determines the value of ά₂ = m₂ − α₂ = 010, and the third determines the value of ά₃ = m₃ − α₃ = 0101. The first adder modulo d_ij determines the value of α₁₂ = (α₁ + ά₂)mod d₁₂, the second determines the value of α₂₃ = (α₂ + ά₃)mod d₂₃, and the third determines the value of α₃₁ = (α₃ + ά₁)mod d₁₃. Thus, from the outputs of the corresponding decoders, only the second switch receives the values α₁₂ = 1, α₂₃ = 3, according to which it determines the values of the error inverted modulo m₂, i.e., Δά₂ = 3. The last value through the second encoder in binary code goes to the first input of the second adder, and the second input of this adder is fed the value Δά₂ = α₂ + Δα₂ = 100. The adder of the second group determines the result of the operation (Δά₂ + ά₂)mod d₂ = (m₂ − Δα₂ + α₂ + Δα₂)mod m₂ = 001. The corrected number A = (11, 001, 0111) is sent to the output of the device.

The developed device has an applied value. It was developed to solve a specific problem and was designed to increase the noise immunity of downhole telemetry information transmitted over wireless communication channels. However, it should be noted that the prospective applicability of the presented algorithms and structures is much broader and is not limited only to the oil and gas industry.

It should be noted that the verification of the real increase in the noise immunity of the telemetric information using RNS linear correction codes has not yet been carried out. The problem of distortion of telemetry signals when transmitted to the earth’s surface via a wireless communication channel has not yet been solved. This is confirmed by attempts to introduce cable-free telemetry in wells equipped with rod-type deep-water pumps in the oil companies “Saratovneftegaz”, “Varioganneft” and “Ulianovskneft” in 2012–2014. Packers are installed in all the squares, preventing the organization of cable communication. The presence of a large amount of interference caused the noise of the received signals at a depth of 1200–1500 m and, as a result, caused the temporary cessation of work on the introduction of wireless telemetry technology. Since more than 75% of wells in Russia are accounted for by rod depth pumps, the scale of the problem speaks for itself.

In the future, a consistent development of coding theory is expected to continue the search for effective paradigms combining the corrective properties of the residual class system with a neural network basis and quantum computing.

This article may be useful to specialists in the field of digital signal processing, control error coding, radio communications, and oil and gas field development.

5. Conclusions

The article presented the results for determining the necessary and sufficient conditions for the implementation of the developed algorithms for detecting and correcting errors using linear L-codes of the deduction system. Four statements were formulated and proved, necessary and sufficient conditions were determined, three algorithms were developed and the principles of operation were explained on the example of a specific, developed device for detecting, localizing and correcting errors.

The main advantages of L-codes in the deduction system were proved, which consist of the simplicity of the procedures for detecting and localizing their location. It is concluded that by the simplicity of the decoding schemes, L-codes have no analogues in the conventional positional number system.

Thus, error correction methods in a system of residual classes with mutually pairwise simple bases make it relatively easy to implement an error detection and correction procedure, allowing you to localize an erroneous base and correct the remainder in just five conditional time cycles for any number of bases in the RNS.

Codes in the RNS with mutually pairwise simple bases should be used to create highly reliable and high-speed computing structures of digital signal processing, where the criterion of redundancy of the representation of code words does not have a determining value.