From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity
Abstract
1. Introduction
2. Theoretical Background to MOND
2.1. Spacetime Scale Invariance
2.2. Possible Fundamental Basis
2.3. Non-Relativistic Theories
Numerical Solvers
2.4. The External Field Effect (EFE)
The Two-Body Force Law
2.5. Modified Inertia
2.6. Relativistic Theories
2.7. Theoretical Uncertainties in the Missing Gravity Problem
3. Equilibrium Galaxy Dynamics
3.1. Disc Galaxies
3.1.1. Rotation Curves
3.1.2. Vertical Dynamics
3.2. Elliptical Galaxies and Dwarf Spheroidals
3.2.1. Velocity Dispersion
3.2.2. Rotation of a Sub-Dominant Component
3.3. Observational Signatures of the EFE
3.4. Strong Gravitational Lensing
3.5. Weak Gravitational Lensing
3.6. Implications for Alternatives to ΛCDM and MOND
4. Disc Galaxy Stability and Secular Evolution
4.1. Survival of Thin Disc Galaxies
4.2. Number of Spiral Arms
- The radial velocity dispersion ,
- Disc self-gravity, and
- Shear caused by differential rotation of the disc.
4.3. Bar Strength
4.4. Bar Fraction
4.5. Bar Pattern Speed
5. Interacting Galaxies and Satellite Planes
5.1. Tidal Stability
5.2. Tidal Streams and EFE-Induced Asymmetry
5.3. Polar Ring Galaxies
5.4. Shell Galaxies
5.5. Tidal Dwarf Galaxies (TDGs)
5.6. The Local Group Satellite Planes
5.7. Satellite Planes beyond the Local Group
6. Galaxy Groups
6.1. The Local Group and the NGC 3109 Association
6.2. M81 and Hickson Compact Groups
6.3. Binary Galaxies
6.4. Virial Analysis of Galaxy Groups
7. Galaxy Clusters
7.1. Internal Dynamics
7.2. Probing Structure Formation
8. Large-Scale Structure
8.1. The KBC Void and Hubble Tension
8.2. Other Anomalies in Large-Scale Structure
8.3. Cosmic Shear and the Matter Power Spectrum
9. Cosmological Context
9.1. Time Variation of
9.2. The HDM Model
9.2.1. At High Redshift
9.2.2. At Low Redshift
9.3. Towards a Relativistic Model
10. Comparing CDM and MOND with Observations
10.1. ΛCDM
10.2. MOND
10.3. Comparing the Models
10.4. Parallels with the Heliocentric Revolution
- All currently proposed models are surely wrong at some level, but it is still worthwhile to find a model which is more nearly correct as this would form a more reliable stepping stone to a more complete theory.
- At an early stage of development, the more realistic model will not be able to explain everything it seeks to explain.
- Even if both models are fully developed, the less realistic model will provide a better explanation of some observables, similarly to how a broken clock tells the correct time twice each day.
11. Future Tests of MOND
11.1. Galaxy Cluster Collision Velocities
11.2. Dynamically Old TDGs
11.3. Wide Binaries
11.3.1. Using the Velocity Distribution
11.3.2. Using the Acceleration of Proxima Centauri
11.4. Solar System Ephemerides
11.5. Spacecraft Tests
11.5.1. Within the Solar System
11.5.2. Beyond the Solar System
12. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gaia Collaboration. Gaia Early Data Release 3: Acceleration of the solar system from Gaia astrometry. Astronom. Astrophys. 2021, 649, A9. [Google Scholar] [CrossRef]
- Levenson, T. The Hunt for Vulcan…And How Albert Einstein Destroyed a Planet, Discovered Relativity, and Deciphered the Universe; Random House: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Einstein, A. Die Feldgleichungen der Gravitation. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin). 1915, pp. 844–847. Available online: https://articles.adsabs.harvard.edu/cgi-bin/get_file?pdfs/SPAW./1915/1915SPAW.......844E.pdf (accessed on 23 May 2022).
- Gravity Collaboration. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astronom. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef]
- Gravity Collaboration. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astronom. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef]
- Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. ApJL 2019, 875, L1. [Google Scholar] [CrossRef]
- Virgo & LIGO Collaborations. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Rowland, D.R. On claims that general relativity differs from Newtonian physics for self-gravitating dusts in the low velocity, weak field limit. Int. J. Mod. Phys. D 2015, 24, 1550065. [Google Scholar] [CrossRef]
- De Almeida, Á.O.F.; Piattella, O.F.; Rodrigues, D.C. A method for evaluating models that use galaxy rotation curves to derive the density profiles. Mont. Notices R. Astronom. Soc. 2016, 462, 2706–2714. [Google Scholar] [CrossRef][Green Version]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Kahn, F.D.; Woltjer, L. Intergalactic Matter and the Galaxy. Astrophys. J. 1959, 130, 705. [Google Scholar] [CrossRef]
- Faber, S.M.; Gallagher, J.S. Masses and mass-to-light ratios of galaxies. Annu. Rev. Astron. Astrophys. 1979, 17, 135–187. [Google Scholar] [CrossRef]
- Sanders, R.H. The Dark Matter Problem: A Historical Perspective; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Toomre, A. On the gravitational stability of a disk of stars. Astrophys. J. 1964, 139, 1217–1238. [Google Scholar] [CrossRef]
- Hohl, F. Numerical Experiments with a Disk of Stars. Astrophys. J. 1971, 168, 343. [Google Scholar] [CrossRef]
- Knox, R.A.; Hawkins, M.R.S.; Hambly, N.C. A survey for cool white dwarfs and the age of the Galactic disc. Mont. Notices R. Astronom. Soc. 1999, 306, 736–752. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Wilkinson, A. Dynamics of barred galaxies. Rep. Prog. Phys. 1993, 56, 173–256. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E. A Numerical Study of the Stability of Flattened Galaxies: Or, can Cold Galaxies Survive? Astrophys. J. 1973, 186, 467–480. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Peebles, P.J.E.; Yahil, A. The Size and Mass of Galaxies, and the Mass of the Universe. ApJL 1974, 193, L1. [Google Scholar] [CrossRef]
- White, S.D.M.; Rees, M.J. Core condensation in heavy halos: A two-stage theory for galaxy formation and clustering. Mont. Notices R. Astronom. Soc. 1978, 183, 341–358. [Google Scholar] [CrossRef]
- Carr, B. Baryonic Dark Matter. Annu. Rev. Astron. Astrophys. 1994, 32, 531–590. [Google Scholar] [CrossRef]
- Aubourg, E.; Bareyre, P.; Bréhin, S.; Gros, M.; Lachièze-Rey, M.; Laurent, B.; Lesquoy, E.; Magneville, C.; Milsztajn, A.; Moscoso, L.; et al. Evidence for gravitational microlensing by dark objects in the Galactic halo. Nature 1993, 365, 623–625. [Google Scholar] [CrossRef]
- Refsdal, S. On the possibility of determining the distances and masses of stars from the gravitational lens effect. Mont. Notices R. Astronom. Soc. 1966, 134, 315. [Google Scholar] [CrossRef]
- Paczynski, B. Gravitational microlensing by the galactic halo. Astrophys. J. 1986, 304, 1–5. [Google Scholar] [CrossRef]
- Tisserand, P.; Le Guillou, L.; Afonso, C.; Albert, J.N.; Andersen, J.; Ansari, R.; Aubourg, É.; Bareyre, P.; Beaulieu, J.P.; Charlot, X.; et al. Limits on the Macho content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. Astronom. Astrophys. 2007, 469, 387–404. [Google Scholar] [CrossRef]
- Alcock, C.; Allsman, R.A.; Alves, D.R.; Axelrod, T.S.; Becker, A.C.; Bennett, D.P.; Cook, K.H.; Dalal, N.; Drake, A.J.; Freeman, K.C.; et al. The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations. Astrophys. J. 2000, 542, 281–307. [Google Scholar] [CrossRef]
- Pietrzyński, G. Twenty-five years of using microlensing to study dark matter. Nature 2018, 562, 349–350. [Google Scholar] [CrossRef] [PubMed]
- Niikura, H.; Takada, M.; Yasuda, N.; Lupton, R.H.; Sumi, T.; More, S.; Kurita, T.; Sugiyama, S.; More, A.; Oguri, M.; et al. Microlensing constraints on primordial black holes with Subaru/HSC Andromeda observations. Nat. Astron. 2019, 3, 524–534. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.F.; Huang, Q.G.; Li, T.G.F. Constraints on the Primordial Black Hole Abundance from the First Advanced LIGO Observation Run Using the Stochastic Gravitational-Wave Background. Phys. Rev. Lett. 2018, 120, 191102. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Growth of the nonbaryonic dark matter theory. Nat. Astron. 2017, 1, 0057. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental tests of the ’invisible’ axion. Phys. Rev. Lett. 1983, 51, 1415–1417. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Kamionkowski, M. WIMP and Axion Dark Matter. High Energy Physics and Cosmology. 1997 Summer School. 1998, p. 394. Available online: https://arxiv.org/pdf/hep-ph/9710467.pdf (accessed on 23 May 2022).
- Bolte, M.; Hogan, C.J. Conflict over the age of the Universe. Nature 1995, 376, 399–402. [Google Scholar] [CrossRef]
- Jimenez, R.; Thejll, P.; Jorgensen, U.G.; MacDonald, J.; Pagel, B. Ages of globular clusters: A new approach. Mont. Notices R. Astronom. Soc. 1996, 282, 926–942. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astronom. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Phillips, M.M. The Absolute Magnitudes of Type IA Supernovae. ApJL 1993, 413, L105. [Google Scholar] [CrossRef]
- Phillips, M.M.; Lira, P.; Suntzeff, N.B.; Schommer, R.A.; Hamuy, M.; Maza, J. The Reddening-Free Decline Rate Versus Luminosity Relationship for Type IA Supernovae. Astronom. J. 1999, 118, 1766–1776. [Google Scholar] [CrossRef]
- Efstathiou, G.; Sutherland, W.J.; Maddox, S.J. The cosmological constant and cold dark matter. Nature 1990, 348, 705–707. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Steinhardt, P.J. The observational case for a low-density Universe with a non-zero cosmological constant. Nature 1995, 377, 600–602. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. ApJS 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Planck Collaboration XVI. Planck 2013 results. XVI. Cosmological parameters. Astronom. Astrophys. 2014, 571, A16. [Google Scholar] [CrossRef]
- Alpher, R.A.; Bethe, H.; Gamow, G. The Origin of Chemical Elements. Phys. Rev. 1948, 73, 803–804. [Google Scholar] [CrossRef]
- Olive, K. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Cyburt, R.H.; Fields, B.D.; Olive, K.A.; Yeh, T.H. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Howk, J.C.; Lehner, N.; Fields, B.D.; Mathews, G.J. Observation of interstellar lithium in the low-metallicity Small Magellanic Cloud. Nature 2012, 489, 121–123. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Bressan, A.; Molaro, P.; Marigo, P. Lithium evolution in metal-poor stars: From pre-main sequence to the Spite plateau. Mont. Notices R. Astronom. Soc. 2015, 452, 3256–3265. [Google Scholar] [CrossRef]
- Merritt, D. A Philosophical Approach to MOND: Assessing the Milgromian Research Program in Cosmology; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Wang, E.X.; Nordlander, T.; Asplund, M.; Lind, K.; Zhou, Y.; Reggiani, H. Non-detection of 6Li in Spite plateau stars with ESPRESSO. Mont. Notices R. Astronom. Soc. 2022, 509, 1521–1535. [Google Scholar] [CrossRef]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Der Phys. 2012, 524, 507–534. [Google Scholar] [CrossRef]
- Kroupa, P.; Famaey, B.; de Boer, K.S.; Dabringhausen, J.; Pawlowski, M.S.; Boily, C.M.; Jerjen, H.; Forbes, D.; Hensler, G.; Metz, M. Local-Group tests of dark-matter concordance cosmology. Towards a new paradigm for structure formation. Astronom. Astrophys. 2010, 523, A32. [Google Scholar] [CrossRef]
- Kroupa, P. The Dark Matter Crisis: Falsification of the Current Standard Model of Cosmology. PASA 2012, 29, 395–433. [Google Scholar] [CrossRef]
- Kroupa, P. Galaxies as simple dynamical systems: Observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 2015, 93, 169–202. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–383. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics: Implications for galaxy systems. Astrophys. J. 1983, 270, 384–389. [Google Scholar] [CrossRef]
- Baker, T.; Barreira, A.; Desmond, H.; Ferreira, P.; Jain, B.; Koyama, K.; Li, B.; Lombriser, L.; Nicola, A.; Sakstein, J.; et al. Novel Probes Project: Tests of gravity on astrophysical scales. Rev. Mod. Phys. 2021, 93, 015003. [Google Scholar] [CrossRef]
- Tully, R.B.; Fisher, J.R. A new method of determining distances to galaxies. Astronom. Astrophys. 1977, 54, 661–673. [Google Scholar]
- Sanders, R.H. A historical perspective on modified Newtonian dynamics. Can. J. Phys. 2015, 93, 126–138. [Google Scholar] [CrossRef]
- Baker, T.; Psaltis, D.; Skordis, C. Linking Tests of Gravity on All Scales: From the Strong-field Regime to Cosmology. Astrophys. J. 2015, 802, 63. [Google Scholar] [CrossRef]
- Milgrom, M. Quasi-linear formulation of MOND. Mont. Notices R. Astronom. Soc. 2010, 403, 886–895. [Google Scholar] [CrossRef]
- Milgrom, M. Can the Hidden Mass Be Negative? Astrophys. J. 1986, 306, 9. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. The External Field Dominated Solution In QUMOND & AQUAL: Application To Tidal Streams. SciFed J. Astrophys. 2018, 1, 1000008. [Google Scholar]
- Oria, P.A.; Famaey, B.; Thomas, G.F.; Ibata, R.; Freundlich, J.; Posti, L.; Korsaga, M.; Monari, G.; Müller, O.; Libeskind, N.I.; et al. The Phantom Dark Matter Halos of the Local Volume in the Context of Modified Newtonian Dynamics. Astrophys. J. 2021, 923, 68. [Google Scholar] [CrossRef]
- Kent, S.M. Dark matter in spiral galaxies. II—Galaxies with H I rotation curves. Astronom. J. 1987, 93, 816–832. [Google Scholar] [CrossRef]
- Milgrom, M. On the Use of Galaxy Rotation Curves to Test the Modified Dynamics. Astrophys. J. 1988, 333, 689. [Google Scholar] [CrossRef]
- Begeman, K.G.; Broeils, A.H.; Sanders, R.H. Extended rotation curves of spiral galaxies—Dark haloes and modified dynamics. Mont. Notices R. Astronom. Soc. 1991, 249, 523–537. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; de Blok, W.J.G. THINGS about MOND. Astronom. Astrophys. 2011, 527, A76. [Google Scholar] [CrossRef]
- McGaugh, S.; Lelli, F.; Schombert, J. The Radial Acceleration Relation in Rotationally Supported Galaxies. Phys. Rev. Lett. 2016, 117, 201101. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Sanders, R.H. The Formation of Cosmic Structure with Modified Newtonian Dynamics. Astrophys. J. 2001, 560, 1–6. [Google Scholar] [CrossRef]
- Milgrom, M. The MOND paradigm of modified dynamics. Scholarpedia 2014, 9, 31410. [Google Scholar] [CrossRef]
- Milgrom, M. The Mond Limit from Spacetime Scale Invariance. Astrophys. J. 2009, 698, 1630–1638. [Google Scholar] [CrossRef]
- Hossenfelder, S. Lost in Math: How Beauty Leads Physics Astray; Basic Civitas Books: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Peters, P.C. Where is the energy stored in a gravitational field? Am. J. Phys. 1981, 49, 564–569. [Google Scholar] [CrossRef]
- Planck Collaboration XIII. Planck 2015 results. XIII. Cosmological parameters. Astronom. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Planck Collaboration VI. Planck 2018 results. VI. Cosmological parameters. Astronom. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Milgrom, M. The modified dynamics as a vacuum effect. Phys. Lett. A 1999, 253, 273–279. [Google Scholar] [CrossRef]
- Pazy, E. Quantum statistical modified entropic gravity as a theoretical basis for MOND. Phys. Rev. D 2013, 87, 084063. [Google Scholar] [CrossRef]
- Verlinde, E. Emergent Gravity and the Dark Universe. SciPost Phys. 2017, 2, 016. [Google Scholar] [CrossRef]
- Smolin, L. MOND as a regime of quantum gravity. Phys. Rev. D 2017, 96, 083523. [Google Scholar] [CrossRef]
- Milgrom, M. High-redshift rotation curves and MOND. arXiv 2017, arXiv:1703.06110v3. [Google Scholar]
- Cadoni, M.; Tuveri, M. Galactic dynamics and long-range quantum gravity. Phys. Rev. D 2019, 100, 024029. [Google Scholar] [CrossRef]
- Giusti, A.; Buffa, S.; Heisenberg, L.; Casadio, R. A quantum state for the late Universe. Phys. Lett. B 2022, 826, 136900. [Google Scholar] [CrossRef]
- Bagchi, B.; Fring, A. Quantum, noncommutative and MOND corrections to the entropic law of gravitation. Int. J. Mod. Phys. B 2019, 33, 1950018. [Google Scholar] [CrossRef]
- Senay, M.; Mohammadi Sabet, M.; Moradpour, H. Heat capacity of holographic screen inspires MOND theory. Phys. Scr. 2021, 96, 075001. [Google Scholar] [CrossRef]
- Famaey, B.; Binney, J. Modified Newtonian dynamics in the Milky Way. Mont. Notices R. Astronom. Soc. 2005, 363, 603–608. [Google Scholar] [CrossRef]
- Bekenstein, J.; Milgrom, M. Does the missing mass problem signal the breakdown of Newtonian gravity? Astrophys. J. 1984, 286, 7–14. [Google Scholar] [CrossRef]
- Banik, I.; O’Ryan, D.; Zhao, H. Origin of the Local Group satellite planes. Mont. Notices R. Astronom. Soc. 2018, 477, 4768–4791. [Google Scholar] [CrossRef]
- Haslbauer, M.; Banik, I.; Kroupa, P. The KBC void and Hubble tension contradict ΛCDM on a Gpc scale—Milgromian dynamics as a possible solution. Mont. Notices R. Astronom. Soc. 2020, 499, 2845–2883. [Google Scholar] [CrossRef]
- Nusser, A. Modified Newtonian dynamics of large-scale structure. Mont. Notices R. Astronom. Soc. 2002, 331, 909–916. [Google Scholar] [CrossRef]
- Milgrom, M. Practically linear analogs of the Born-Infeld and other nonlinear theories. Phys. Rev. D 2012, 85, 105018. [Google Scholar] [CrossRef]
- Zhao, H. Reinterpreting MOND: Coupling of Einsteinian gravity and spin of cosmic neutrinos? arXiv 2008, arXiv:0805.4046. [Google Scholar]
- Zhao, H.; Famaey, B. Unifying all mass discrepancies with one effective gravity law? Phys. Rev. D 2012, 86, 067301. [Google Scholar] [CrossRef]
- Zhao, H. Coincidences of Dark Energy with Dark Matter: Clues for a Simple Alternative? ApJL 2007, 671, L1–L4. [Google Scholar] [CrossRef]
- Li, B.; Zhao, H. Environment-dependent dark sector. Phys. Rev. D 2009, 80, 064007. [Google Scholar] [CrossRef]
- Candlish, G.N. The velocity field in MOND cosmology. Mont. Notices R. Astronom. Soc. 2016, 460, 2571–2585. [Google Scholar] [CrossRef]
- Banik, I.; Milgrom, M.; Zhao, H. Toomre stability of disk galaxies in quasi-linear MOND. arXiv 2018, arXiv:1808.10545. [Google Scholar]
- Lüghausen, F.; Famaey, B.; Kroupa, P. Phantom of RAMSES (POR): A new Milgromian dynamics N-body code. Can. J. Phys. 2015, 93, 232–241. [Google Scholar] [CrossRef]
- Teyssier, R. Cosmological hydrodynamics with adaptive mesh refinement. A new high resolution code called RAMSES. Astronom. Astrophys. 2002, 385, 337–364. [Google Scholar] [CrossRef]
- Candlish, G.N.; Smith, R.; Fellhauer, M. RAyMOND: An N-body and hydrodynamics code for MOND. Mont. Notices R. Astronom. Soc. 2015, 446, 1060–1070. [Google Scholar] [CrossRef]
- Nagesh, S.T.; Banik, I.; Thies, I.; Kroupa, P.; Famaey, B.; Wittenburg, N.; Parziale, R.; Haslbauer, M. The Phantom of RAMSES user guide for galaxy simulations using Milgromian and Newtonian gravity. Can. J. Phys. 2021, 99, 607–613. [Google Scholar] [CrossRef]
- Banik, I.; Thies, I.; Candlish, G.; Famaey, B.; Ibata, R.; Kroupa, P. The global stability of M33 in MOND. Astrophys. J. 2020, 905, 135. [Google Scholar] [CrossRef]
- Famaey, B.; Bruneton, J.P.; Zhao, H. Escaping from modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2007, 377, L79–L82. [Google Scholar] [CrossRef]
- Jones, B.F. Internal Motions in the Pleiades. Astronom. J. 1970, 75, 563. [Google Scholar] [CrossRef]
- Jones, B.F. Internal Motions in Praesepe. Astronom. J. 1971, 76, 470. [Google Scholar] [CrossRef]
- Milgrom, M. Solutions for the modified Newtonian dynamics field equation. Astrophys. J. 1986, 302, 617–625. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. Testing gravity with wide binary stars like α Centauri. Mont. Notices R. Astronom. Soc. 2018, 480, 2660–2688. [Google Scholar] [CrossRef]
- Zonoozi, A.H.; Lieberz, P.; Banik, I.; Haghi, H.; Kroupa, P. The Kennicutt-Schmidt law and the main sequence of galaxies in Newtonian and milgromian dynamics. Mont. Notices R. Astronom. Soc. 2021, 506, 5468–5478. [Google Scholar] [CrossRef]
- Brada, R.; Milgrom, M. The Modified Dynamics is Conducive to Galactic Warp Formation. ApJL 2000, 531, L21–L24. [Google Scholar] [CrossRef]
- Zhao, H.; Li, B.; Bienaymé, O. Modified Kepler’s law, escape speed, and two-body problem in modified Newtonian dynamics-like theories. Phys. Rev. D 2010, 82, 103001. [Google Scholar] [CrossRef]
- Milgrom, M. Modified Dynamics Predictions Agree with Observations of the H i Kinematics in Faint Dwarf Galaxies Contrary to the Conclusions of Lo, Sargent, and Young. Astrophys. J. 1994, 429, 540. [Google Scholar] [CrossRef]
- Milgrom, M. General virial theorem for modified-gravity MOND. Phys. Rev. D 2014, 89, 024016. [Google Scholar] [CrossRef]
- Milgrom, M. Dynamics with a Nonstandard Inertia-Acceleration Relation: An Alternative to Dark Matter in Galactic Systems. Ann. Phys. 1994, 229, 384–415. [Google Scholar] [CrossRef]
- McGaugh, S.S. A Precise Milky Way Rotation Curve Model for an Accurate Galactocentric Distance. Res. Notes Am. Astron. Soc. 2018, 2, 156. [Google Scholar] [CrossRef]
- Hees, A.; Folkner, W.M.; Jacobson, R.A.; Park, R.S. Constraints on modified Newtonian dynamics theories from radio tracking data of the Cassini spacecraft. Phys. Rev. D 2014, 89, 102002. [Google Scholar] [CrossRef]
- Hees, A.; Famaey, B.; Angus, G.W.; Gentile, G. Combined Solar system and rotation curve constraints on MOND. Mont. Notices R. Astronom. Soc. 2016, 455, 449–461. [Google Scholar] [CrossRef]
- Milgrom, M. MOND–particularly as modified inertia. Acta Phys. Pol. B 2011, 42, 2175. [Google Scholar] [CrossRef]
- Shariati, A.; Jafari, N. Modified inertia as nonconservative Newtonian dynamics. Phys. Rev. D 2021, 104, 084070. [Google Scholar] [CrossRef]
- Petersen, J.; Lelli, F. A first attempt to differentiate between modified gravity and modified inertia with galaxy rotation curves. Astronom. Astrophys. 2020, 636, A56. [Google Scholar] [CrossRef]
- Dyson, F.W.; Eddington, A.S.; Davidson, C. A Determination of the Deflection of Light by the Sun’s Gravitational Field, from Observations Made at the Total Eclipse of May 29, 1919. R. Soc. Lond. Philos. Trans. Ser. A 1920, 220, 291–333. [Google Scholar] [CrossRef]
- Fort, B.; Mellier, Y. Arc(let)s in clusters of galaxies. A&ARv 1994, 5, 239–292. [Google Scholar] [CrossRef]
- Sanders, R.H. A Stratified Framework for Scalar-Tensor Theories of Modified Dynamics. Astrophys. J. 1997, 480, 492–502. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Zhao, H.; Bacon, D.J.; Taylor, A.N.; Horne, K. Testing Bekenstein’s relativistic Modified Newtonian Dynamics with lensing data. Mont. Notices R. Astronom. Soc. 2006, 368, 171–186. [Google Scholar] [CrossRef]
- Chiu, M.C.; Ko, C.M.; Tian, Y. Theoretical Aspects of Gravitational Lensing in TeVeS. Astrophys. J. 2006, 636, 565–574. [Google Scholar] [CrossRef]
- Tian, Y.; Ko, C.M.; Chiu, M.C. Hubble Constant, Lensing, and Time Delay in Relativistic Modified Newtonian Dynamics. Astrophys. J. 2013, 770, 154. [Google Scholar] [CrossRef][Green Version]
- Złośnik, T.G.; Ferreira, P.G.; Starkman, G.D. Modifying gravity with the aether: An alternative to dark matter. Phys. Rev. D 2007, 75, 044017. [Google Scholar] [CrossRef]
- Milgrom, M. Bimetric MOND gravity. Phys. Rev. D 2009, 80, 123536. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farèse, G.; Woodard, R.P. Nonlocal metric formulations of modified Newtonian dynamics with sufficient lensing. Phys. Rev. D 2011, 84, 124054. [Google Scholar] [CrossRef]
- Milgrom, M. Noncovariance at low accelerations as a route to MOND. Phys. Rev. D 2019, 100, 084039. [Google Scholar] [CrossRef]
- Boran, S.; Desai, S.; Kahya, E.O.; Woodard, R.P. GW170817 falsifies dark matter emulators. Phys. Rev. D 2018, 97, 041501. [Google Scholar] [CrossRef]
- Amendola, L.; Kunz, M.; Saltas, I.D.; Sawicki, I. Fate of Large-Scale Structure in Modified Gravity after GW170817 and GRB170817A. Phys. Rev. Lett. 2018, 120, 131101. [Google Scholar] [CrossRef]
- Battye, R.A.; Pace, F.; Trinh, D. Gravitational wave constraints on dark sector models. Phys. Rev. D 2018, 98, 023504. [Google Scholar] [CrossRef]
- Copeland, E.J.; Kopp, M.; Padilla, A.; Saffin, P.M.; Skordis, C. Dark Energy after GW170817 Revisited. Phys. Rev. Lett. 2019, 122, 061301. [Google Scholar] [CrossRef] [PubMed]
- Skordis, C.; Złośnik, T. Gravitational alternatives to dark matter with tensor mode speed equaling the speed of light. Phys. Rev. D 2019, 100, 104013. [Google Scholar] [CrossRef]
- Tian, Y.; Ko, C.M. Halo acceleration relation. Mont. Notices R. Astronom. Soc. 2019, 488, L41–L46. [Google Scholar] [CrossRef]
- Iocco, F.; Pato, M.; Bertone, G. Testing modified Newtonian dynamics in the Milky Way. Phys. Rev. D 2015, 92, 084046. [Google Scholar] [CrossRef]
- Van der Marel, R.P.; Kallivayalil, N. Third-epoch Magellanic Cloud Proper Motions. II. The Large Magellanic Cloud Rotation Field in Three Dimensions. Astrophys. J. 2014, 781, 121. [Google Scholar] [CrossRef]
- Van der Marel, R.P.; Sahlmann, J. First Gaia Local Group Dynamics: Magellanic Clouds Proper Motion and Rotation. ApJL 2016, 832, L23. [Google Scholar] [CrossRef]
- Vasiliev, E. Internal dynamics of the Large Magellanic Cloud from Gaia DR2. Mont. Notices R. Astronom. Soc. 2018, 481, L100–L104. [Google Scholar] [CrossRef]
- Alves, D.R.; Nelson, C.A. The Rotation Curve of the Large Magellanic Cloud and the Implications for Microlensing. Astrophys. J. 2000, 542, 789–803. [Google Scholar] [CrossRef]
- Van der Marel, R.P.; Fardal, M.A.; Sohn, S.T.; Patel, E.; Besla, G.; del Pino, A.; Sahlmann, J.; Watkins, L.L. First Gaia Dynamics of the Andromeda System: DR2 Proper Motions, Orbits, and Rotation of M31 and M33. Astrophys. J. 2019, 872, 24. [Google Scholar] [CrossRef]
- Gravity Collaboration. A geometric distance measurement to the Galactic center black hole with 0.3% uncertainty. Astronom. Astrophys. 2019, 625, L10. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mont. Notices R. Astronom. Soc. 2017, 465, 76–94. [Google Scholar] [CrossRef]
- Babcock, H.W. The rotation of the Andromeda Nebula. Lick Obs. Bull. 1939, 19, 41–51. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astrophys. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Westerhout, G. The Pioneers of H I. In Seeing through the Dust: The Detection of HI and the Exploration of the ISM in Galaxies; Taylor, A.R., Landecker, T.L., Willis, A.G., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2002; Volume 276, p. 3. [Google Scholar]
- Rogstad, D.H.; Shostak, G.S. Gross Properties of Five Scd Galaxies as Determined from 21-CENTIMETER Observations. Astrophys. J. 1972, 176, 315. [Google Scholar] [CrossRef]
- Roberts, M.S.; Whitehurst, R.N. The rotation curve and geometry of M31 at large galactocentric distances. Astrophys. J. 1975, 201, 327–346. [Google Scholar] [CrossRef]
- Bosma, A. The Distribution and Kinematics of Neutral Hydrogen in Spiral Galaxies of Various Morphological Types. Ph.D. Thesis, Groningen University, Groningen, The Netherlands, 1978. [Google Scholar]
- Bosma, A. 21-cm line studies of spiral galaxies. II. The distribution and kinematics of neutral hydrogen in spiral galaxies of various morphological types. Astronom. J. 1981, 86, 1825–1846. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; McGaugh, S.S. Testing Modified Newtonian Dynamics with Low Surface Brightness Galaxies: Rotation Curve FITS. Astrophys. J. 1998, 508, 132–140. [Google Scholar] [CrossRef]
- Sanders, R.H. Mass discrepancies in galaxies: Dark matter and alternatives. A&ARv 1990, 2, 1–28. [Google Scholar]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. 2000, 533, L99–L102. [Google Scholar] [CrossRef] [PubMed]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Desmond, H.; Katz, H. The baryonic Tully-Fisher relation for different velocity definitions and implications for galaxy angular momentum. Mont. Notices R. Astronom. Soc. 2019, 484, 3267–3278. [Google Scholar] [CrossRef]
- McGaugh, S. Predictions and Outcomes for the Dynamics of Rotating Galaxies. Galaxies 2020, 8, 35. [Google Scholar] [CrossRef]
- Milgrom, M. MOND fiducial specific angular momentum of disc galaxies. Phys. Rev. D 2021, 104, 064030. [Google Scholar] [CrossRef]
- Mancera Piña, P.E.; Posti, L.; Pezzulli, G.; Fraternali, F.; Fall, S.M.; Oosterloo, T.; Adams, E.A.K. A tight angular-momentum plane for disc galaxies. Astronom. Astrophys. 2021, 651, L15. [Google Scholar] [CrossRef]
- McGaugh, S. The Third Law of Galactic Rotation. Galaxies 2014, 2, 601–622. [Google Scholar] [CrossRef]
- Gentile, G.; Baes, M.; Famaey, B.; van Acoleyen, K. Mass models from high-resolution HI data of the dwarf galaxy NGC 1560. Mont. Notices R. Astronom. Soc. 2010, 406, 2493–2503. [Google Scholar] [CrossRef]
- Sancisi, R. The visible matter—Dark matter coupling. In Dark Matter in Galaxies; Ryder, S., Pisano, D., Walker, M., Freeman, K., Eds.; International Astronomical Union Symposium; Cambridge University Press: Cambridge, UK, 2004; Volume 220, p. 233. [Google Scholar]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. SPARC: Mass Models for 175 Disk Galaxies with Spitzer Photometry and Accurate Rotation Curves. Astronom. J. 2016, 152, 157. [Google Scholar] [CrossRef]
- Bell, E.F.; de Jong, R.S. Stellar Mass-to-Light Ratios and the Tully-Fisher Relation. Astrophys. J. 2001, 550, 212–229. [Google Scholar] [CrossRef]
- Norris, M.A.; Van de Ven, G.; Schinnerer, E.; Crain, R.A.; Meidt, S.; Groves, B.; Bower, R.G.; Furlong, M.; Schaller, M.; Schaye, J.; et al. Being WISE II: Reducing the Influence of Star formation History on the Mass-to-Light Ratio of Quiescent Galaxies. Astrophys. J. 2016, 832, 198. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. Fitting the Radial Acceleration Relation to Individual SPARC Galaxies. Astronom. Astrophys. 2018, 615, A3. [Google Scholar] [CrossRef]
- Draine, B.T. Physics of the Interstellar and Intergalactic Medium; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- McGaugh, S.S. The Baryonic Tully-Fisher Relation of Gas-rich Galaxies as a Test of ΛCDM and MOND. Astronom. J. 2012, 143, 40. [Google Scholar] [CrossRef]
- Sanders, R.H. The prediction of rotation curves in gas-dominated dwarf galaxies with modified dynamics. Mont. Notices R. Astronom. Soc. 2019, 485, 513–521. [Google Scholar] [CrossRef]
- Ghari, A.; Haghi, H.; Zonoozi, A.H. The radial acceleration relation and dark baryons in MOND. Mont. Notices R. Astronom. Soc. 2019, 487, 2148–2165. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Marra, V.; del Popolo, A.; Davari, Z. Absence of a fundamental acceleration scale in galaxies. Nat. Astron. 2018, 2, 668–672. [Google Scholar] [CrossRef]
- Chang, Z.; Zhou, Y. Is there a fundamental acceleration scale in galaxies? Mont. Notices R. Astronom. Soc. 2019, 486, 1658–1666. [Google Scholar] [CrossRef]
- Cameron, E.; Angus, G.W.; Burgess, J.M. Overconfidence in Bayesian analyses of galaxy rotation curves. Nat. Astron. 2020, 4, 132–133. [Google Scholar] [CrossRef]
- Kroupa, P.; Banik, I.; Haghi, H.; Zonoozi, A.H.; Dabringhausen, J.; Javanmardi, B.; Müller, O.; Wu, X.; Zhao, H. A common Milgromian acceleration scale in nature. Nat. Astron. 2018, 2, 925–926. [Google Scholar] [CrossRef]
- Kogut, A.; Lineweaver, C.; Smoot, G.F.; Bennett, C.L.; Banday, A.; Boggess, N.W.; Cheng, E.S.; de Amici, G.; Fixsen, D.J.; Hinshaw, G.; et al. Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps. Astrophys. J. 1993, 419, 1. [Google Scholar] [CrossRef]
- Marra, V.; Rodrigues, D.C.; de Almeida, Á.O.F. A fundamental test for MOND. Mont. Notices R. Astronom. Soc. 2020, 494, 2875–2885. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J.; Chae, K.H. A cautionary tale in fitting galaxy rotation curves with Bayesian techniques: Does Newton’s constant vary from galaxy to galaxy? Astronom. Astrophys. 2021, 646, L13. [Google Scholar] [CrossRef]
- Ogle, P.M.; Lanz, L.; Nader, C.; Helou, G. Superluminous Spiral Galaxies. Astrophys. J. 2016, 817, 109. [Google Scholar] [CrossRef]
- Ogle, P.M.; Lanz, L.; Appleton, P.N.; Helou, G.; Mazzarella, J. A Catalog of the Most Optically Luminous Galaxies at z < 0.3: Super Spirals, Super Lenticulars, Super Post-mergers, and Giant Ellipticals. ApJS 2019, 243, 14. [Google Scholar] [CrossRef]
- Ogle, P.M.; Jarrett, T.; Lanz, L.; Cluver, M.; Alatalo, K.; Appleton, P.N.; Mazzarella, J.M. A Break in Spiral Galaxy Scaling Relations at the Upper Limit of Galaxy Mass. ApJL 2019, 884, L11. [Google Scholar] [CrossRef]
- Di Teodoro, E.M.; Posti, L.; Ogle, P.M.; Fall, S.M.; Jarrett, T. Rotation curves and scaling relations of extremely massive spiral galaxies. Mont. Notices R. Astronom. Soc. 2021, 507, 5820–5831. [Google Scholar] [CrossRef]
- Posti, L.; Fraternali, F.; Di Teodoro, E.M.; Pezzulli, G. The angular momentum-mass relation: A fundamental law from dwarf irregulars to massive spirals. Astronom. Astrophys. 2018, 612, L6. [Google Scholar] [CrossRef]
- Kroupa, P.; Weidner, C. Galactic-Field Initial Mass Functions of Massive Stars. Astrophys. J. 2003, 598, 1076–1078. [Google Scholar] [CrossRef]
- Weidner, C.; Kroupa, P. The maximum stellar mass, star-cluster formation and composite stellar populations. Mont. Notices R. Astronom. Soc. 2006, 365, 1333–1347. [Google Scholar] [CrossRef]
- Jeřábková, T.; Hasani Zonoozi, A.; Kroupa, P.; Beccari, G.; Yan, Z.; Vazdekis, A.; Zhang, Z.Y. Impact of metallicity and star formation rate on the time-dependent, galaxy-wide stellar initial mass function. Astronom. Astrophys. 2018, 620, A39. [Google Scholar] [CrossRef]
- Yan, Z.; Jeřábková, T.; Kroupa, P. Downsizing revised: Star formation timescales for elliptical galaxies with an environment-dependent IMF and a number of SNIa. Astronom. Astrophys. 2021, 655, A19. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Stellar Mass-to-light Ratios: Composite Bulge+Disk Models and the Baryonic Tully-Fisher Relation. Astronom. J. 2022, 163, 154. [Google Scholar] [CrossRef]
- Mancera Piña, P.E.; Fraternali, F.; Adams, E.A.K.; Marasco, A.; Oosterloo, T.; Oman, K.A.; Leisman, L.; di Teodoro, E.M.; Posti, L.; Battipaglia, M.; et al. Off the Baryonic Tully-Fisher Relation: A Population of Baryon-dominated Ultra-diffuse Galaxies. ApJL 2019, 883, L33. [Google Scholar] [CrossRef]
- Mancera Piña, P.E.; Fraternali, F.; Oman, K.A.; Adams, E.A.K.; Bacchini, C.; Marasco, A.; Oosterloo, T.; Pezzulli, G.; Posti, L.; Leisman, L.; et al. Robust H I kinematics of gas-rich ultra-diffuse galaxies: Hints of a weak-feedback formation scenario. Mont. Notices R. Astronom. Soc. 2020, 495, 3636–3655. [Google Scholar] [CrossRef]
- O’Neil, K.; Verheijen, M.A.W.; McGaugh, S.S. Star Formation and Tidal Encounters with the Low Surface Brightness Galaxy UGC 12695 and Companions. Astronom. J. 2000, 119, 2154–2165. [Google Scholar] [CrossRef]
- Banik, I.; Togere Nagesh, S.; Haghi, H.; Kroupa, P.; Zhao, H. Overestimated inclinations of Milgromian disc galaxies: The case of the ultradiffuse galaxy AGC 114905. Mont. Notices R. Astronom. Soc. 2022, 513, 3541–3548. [Google Scholar] [CrossRef]
- Mancera Piña, P.E.; Fraternali, F.; Oosterloo, T.; Adams, E.A.K.; Oman, K.A.; Leisman, L. No need for dark matter: Resolved kinematics of the ultra-diffuse galaxy AGC 114905. Mont. Notices R. Astronom. Soc. 2022, 512, 3230–3242. [Google Scholar] [CrossRef]
- Saburova, A.; Zasov, A.; Uklein, R.; Katkov, I. Long-slit spectral observations and stellar mass-to-light ratio of spiral galaxy UGC11919. Mont. Notices R. Astronom. Soc. 2015, 453, 1344–1354. [Google Scholar] [CrossRef]
- Oh, S.H.; de Blok, W.J.G.; Brinks, E.; Walter, F.; Kennicutt, R.C., Jr. Dark and Luminous Matter in THINGS Dwarf Galaxies. Astronom. J. 2011, 141, 193. [Google Scholar] [CrossRef]
- Gentile, G.; Angus, G.W.; Famaey, B.; Oh, S.H.; de Blok, W.J.G. Isolated and non-isolated dwarfs in terms of modified Newtonian dynamics. Astronom. Astrophys. 2012, 543, A47. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S. The MOND phenomenology. arXiv 2013, arXiv:1310.4009. [Google Scholar]
- Saburova, A.S.; Chilingarian, I.V.; Kasparova, A.V.; Sil’chenko, O.K.; Grishin, K.A.; Katkov, I.Y.; Uklein, R.I. Observational insights on the origin of giant low surface brightness galaxies. Mont. Notices R. Astronom. Soc. 2021, 503, 830–849. [Google Scholar] [CrossRef]
- Wu, X.; Kroupa, P. Galactic rotation curves, the baryon-to-dark-halo-mass relation and space-time scale invariance. Mont. Notices R. Astronom. Soc. 2015, 446, 330–344. [Google Scholar] [CrossRef]
- Desmond, H. The scatter, residual correlations and curvature of the sparc baryonic Tully-Fisher relation. Mont. Notices R. Astronom. Soc. 2017, 472, L35–L39. [Google Scholar] [CrossRef]
- Desmond, H. A statistical investigation of the mass discrepancy-acceleration relation. Mont. Notices R. Astronom. Soc. 2017, 464, 4160–4175. [Google Scholar] [CrossRef]
- Oman, K.A.; Navarro, J.F.; Fattahi, A.; Frenk, C.S.; Sawala, T.; White, S.D.M.; Bower, R.; Crain, R.A.; Furlong, M.; Schaller, M.; et al. The unexpected diversity of dwarf galaxy rotation curves. Mont. Notices R. Astronom. Soc. 2015, 452, 3650–3665. [Google Scholar] [CrossRef]
- Pontzen, A.; Governato, F. How supernova feedback turns dark matter cusps into cores. Mont. Notices R. Astronom. Soc. 2012, 421, 3464–3471. [Google Scholar] [CrossRef]
- Dutton, A.A.; Macciò, A.V.; Obreja, A.; Buck, T. NIHAO—XVIII. Origin of the MOND phenomenology of galactic rotation curves in a ΛCDM universe. Mont. Notices R. Astronom. Soc. 2019, 485, 1886–1899. [Google Scholar] [CrossRef]
- Ghari, A.; Famaey, B.; Laporte, C.; Haghi, H. Dark matter-baryon scaling relations from Einasto halo fits to SPARC galaxy rotation curves. Astronom. Astrophys. 2019, 623, A123. [Google Scholar] [CrossRef]
- Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Pakmor, R.; Springel, V.; Campbell, D.J.R.; Frenk, C.S.; Jenkins, A.; White, S.D.M. The Auriga Project: The properties and formation mechanisms of disc galaxies across cosmic time. Mont. Notices R. Astronom. Soc. 2017, 467, 179–207. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M. Weighing Galaxy Disks With the Baryonic Tully-Fisher Relation. Astrophys. J. 2015, 802, 18. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M.; Pawlowski, M.S. One Law to Rule Them All: The Radial Acceleration Relation of Galaxies. Astrophys. J. 2017, 836, 152. [Google Scholar] [CrossRef]
- Salucci, P. The distribution of dark matter in galaxies. A&ARv 2019, 27, 2. [Google Scholar] [CrossRef]
- Buch, J.; Leung, J.S.C.; Fan, J. Using Gaia DR2 to constrain local dark matter density and thin dark disk. J. Cosmol. Astropart. Phys. 2019, 2019, 026. [Google Scholar] [CrossRef]
- Bienaymé, O.; Famaey, B.; Wu, X.; Zhao, H.S.; Aubert, D. Galactic kinematics with modified Newtonian dynamics. Astronom. Astrophys. 2009, 500, 801–805. [Google Scholar] [CrossRef]
- Lüghausen, F.; Famaey, B.; Kroupa, P.; Angus, G.; Combes, F.; Gentile, G.; Tiret, O.; Zhao, H. Polar ring galaxies as tests of gravity. Mont. Notices R. Astronom. Soc. 2013, 432, 2846–2853. [Google Scholar] [CrossRef]
- Lisanti, M.; Moschella, M.; Outmezguine, N.J.; Slone, O. Testing dark matter and modifications to gravity using local Milky Way observables. Phys. Rev. D 2019, 100, 083009. [Google Scholar] [CrossRef]
- Hagen, J.H.J.; Helmi, A. The vertical force in the solar neighbourhood using red clump stars in TGAS and RAVE. Constraints on the local dark matter density. Astronom. Astrophys. 2018, 615, A99. [Google Scholar] [CrossRef]
- Guo, R.; Liu, C.; Mao, S.; Xue, X.X.; Long, R.J.; Zhang, L. Measuring the local dark matter density with LAMOST DR5 and Gaia DR2. Mont. Notices R. Astronom. Soc. 2020, 495, 4828–4844. [Google Scholar] [CrossRef]
- Everall, A.; Evans, N.W.; Belokurov, V.; Schönrich, R. The tilt of the local velocity ellipsoid as seen by Gaia. Mont. Notices R. Astronom. Soc. 2019, 489, 910–918. [Google Scholar] [CrossRef]
- Hagen, J.H.J.; Helmi, A.; de Zeeuw, P.T.; Posti, L. The tilt of the velocity ellipsoid in the Milky Way with Gaia DR2. Astronom. Astrophys. 2019, 629, A70. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; Johnston, K.V.; Gómez, F.A.; Garavito-Camargo, N.; Besla, G. The influence of Sagittarius and the Large Magellanic Cloud on the stellar disc of the Milky Way Galaxy. Mont. Notices R. Astronom. Soc. 2018, 481, 286–306. [Google Scholar] [CrossRef]
- Laporte, C.F.P.; Minchev, I.; Johnston, K.V.; Gómez, F.A. Footprints of the Sagittarius dwarf galaxy in the Gaia data set. Mont. Notices R. Astronom. Soc. 2019, 485, 3134–3152. [Google Scholar] [CrossRef]
- Bennett, M.; Bovy, J.; Hunt, J.A.S. Exploring the Sgr-Milky-Way-disc interaction using high resolution N-body simulations. Astrophys. J. 2022, 927, 131. [Google Scholar] [CrossRef]
- Bershady, M.A.; Verheijen, M.A.W.; Swaters, R.A.; Andersen, D.R.; Westfall, K.B.; Martinsson, T. The DiskMass Survey. I. Overview. Astrophys. J. 2010, 716, 198–233. [Google Scholar] [CrossRef]
- Angus, G.W.; Gentile, G.; Swaters, R.; Famaey, B.; Diaferio, A.; McGaugh, S.S.; Heyden, K.J.v.d. Mass models of disc galaxies from the DiskMass Survey in modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2015, 451, 3551–3580. [Google Scholar] [CrossRef][Green Version]
- Angus, G.W. The dynamics of face-on galaxies in MOND. J. Phys. Conf. Ser. 2016, 718, 032001. [Google Scholar] [CrossRef]
- Aniyan, S.; Freeman, K.C.; Gerhard, O.E.; Arnaboldi, M.; Flynn, C. The influence of a kinematically cold young component on disc-halo decompositions in spiral galaxies: Insights from solar neighbourhood K-giants. Mont. Notices R. Astronom. Soc. 2016, 456, 1484–1494. [Google Scholar] [CrossRef][Green Version]
- Aniyan, S.; Freeman, K.C.; Arnaboldi, M.; Gerhard, O.E.; Coccato, L.; Fabricius, M.; Kuijken, K.; Merrifield, M.; Ponomareva, A.A. Resolving the disc-halo degeneracy—I: A look at NGC 628. Mont. Notices R. Astronom. Soc. 2018, 476, 1909–1930. [Google Scholar] [CrossRef]
- Aniyan, S.; Ponomareva, A.A.; Freeman, K.C.; Arnaboldi, M.; Gerhard, O.E.; Coccato, L.; Kuijken, K.; Merrifield, M. Resolving the Disc-Halo Degeneracy—II: NGC 6946. Mont. Notices R. Astronom. Soc. 2021, 500, 3579–3593. [Google Scholar] [CrossRef]
- Aumer, M.; Binney, J.; Schönrich, R. The quiescent phase of galactic disc growth. Mont. Notices R. Astronom. Soc. 2016, 459, 3326–3348. [Google Scholar] [CrossRef]
- Milgrom, M. MOND and the dynamics of NGC 628. arXiv 2018, arXiv:1802.05140. [Google Scholar]
- Sánchez-Salcedo, F.J.; Saha, K.; Narayan, C.A. The thickness of HI in galactic discs under MOdified Newtonian Dynamics: Theory and application to the Galaxy. Mont. Notices R. Astronom. Soc. 2008, 385, 1585–1596. [Google Scholar] [CrossRef]
- Das, M.; McGaugh, S.; Ianjamasimanana, R.; Schombert, J.; Dwarakanath, K.S. Tracing the Dynamical Mass in Galaxy Disks Using HI Velocity Dispersion and its Implications for the Dark Matter Distribution in Galaxies. Astrophys. J. 2020, 889, 10. [Google Scholar] [CrossRef]
- Gerhard, O.E.; Spergel, D.N. Dwarf Spheroidal Galaxies and Non-Newtonian Gravity. Astrophys. J. 1992, 397, 38. [Google Scholar] [CrossRef]
- Milgrom, M. MOND and the Seven Dwarfs. Astrophys. J. 1995, 455, 439. [Google Scholar] [CrossRef]
- Haghi, H.; Kroupa, P.; Banik, I.; Wu, X.; Zonoozi, A.H.; Javanmardi, B.; Ghari, A.; Müller, O.; Dabringhausen, J.; Zhao, H. A new formulation of the external field effect in MOND and numerical simulations of ultra-diffuse dwarf galaxies—Application to NGC 1052-DF2 and NGC 1052-DF4. Mont. Notices R. Astronom. Soc. 2019, 487, 2441–2454. [Google Scholar] [CrossRef]
- Haghi, H.; Baumgardt, H.; Kroupa, P.; Grebel, E.K.; Hilker, M.; Jordi, K. Testing fundamental physics with distant star clusters: Theoretical models for pressure-supported stellar systems. Mont. Notices R. Astronom. Soc. 2009, 395, 1549–1557. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.; Milgrom, M. MOND and the dynamics of NGC1052-DF2. Mont. Notices R. Astronom. Soc. 2018, 480, 473–476. [Google Scholar] [CrossRef]
- Plummer, H.C. On the problem of distribution in globular star clusters. Mont. Notices R. Astronom. Soc. 1911, 71, 460–470. [Google Scholar] [CrossRef]
- McGaugh, S.; Milgrom, M. Andromeda Dwarfs in Light of Modified Newtonian Dynamics. Astrophys. J. 2013, 766, 22. [Google Scholar] [CrossRef]
- McGaugh, S.; Milgrom, M. Andromeda Dwarfs in Light of MOND. II. Testing Prior Predictions. Astrophys. J. 2013, 775, 139. [Google Scholar] [CrossRef]
- Sanders, R.H. Low-surface-brightness spheroidal galaxies as Milgromian isothermal spheres. Mont. Notices R. Astronom. Soc. 2021, 507, 803–808. [Google Scholar] [CrossRef]
- Angus, G.W. Dwarf spheroidals in MOND. Mont. Notices R. Astronom. Soc. 2008, 387, 1481–1488. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Wolf, J. Local Group Dwarf Spheroidals: Correlated Deviations from the Baryonic Tully-Fisher Relation. Astrophys. J. 2010, 722, 248–261. [Google Scholar] [CrossRef]
- Angus, G.W.; Gentile, G.; Diaferio, A.; Famaey, B.; van der Heyden, K.J. N-body simulations of the Carina dSph in MOND. Mont. Notices R. Astronom. Soc. 2014, 440, 746–761. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; McGaugh, S.S. Perseus I and the NGC 3109 association in the context of the Local Group dwarf galaxy structures. Mont. Notices R. Astronom. Soc. 2014, 440, 908–919. [Google Scholar] [CrossRef]
- Martin, N.F.; Chambers, K.C.; Collins, M.L.M.; Ibata, R.A.; Rich, R.M.; Bell, E.F.; Bernard, E.J.; Ferguson, A.M.N.; Flewelling, H.; Kaiser, N.; et al. Spectroscopy of the Three Distant Andromedan Satellites Cassiopeia III, Lacerta I, and Perseus I. ApJL 2014, 793, L14. [Google Scholar] [CrossRef]
- Kirby, E.N.; Bullock, J.S.; Boylan-Kolchin, M.; Kaplinghat, M.; Cohen, J.G. The dynamics of isolated Local Group galaxies. Mont. Notices R. Astronom. Soc. 2014, 439, 1015–1027. [Google Scholar] [CrossRef]
- Taibi, S.; Battaglia, G.; Kacharov, N.; Rejkuba, M.; Irwin, M.; Leaman, R.; Zoccali, M.; Tolstoy, E.; Jablonka, P. Stellar chemo-kinematics of the Cetus dwarf spheroidal galaxy. Astronom. Astrophys. 2018, 618, A122. [Google Scholar] [CrossRef]
- Taibi, S.; Battaglia, G.; Rejkuba, M.; Leaman, R.; Kacharov, N.; Iorio, G.; Jablonka, P.; Zoccali, M. The Tucana dwarf spheroidal galaxy: Not such a massive failure after all. Astronom. Astrophys. 2020, 635, A152. [Google Scholar] [CrossRef]
- Fraternali, F.; Tolstoy, E.; Irwin, M.J.; Cole, A.A. Life at the periphery of the Local Group: The kinematics of the Tucana dwarf galaxy. Astronom. Astrophys. 2009, 499, 121–128. [Google Scholar] [CrossRef][Green Version]
- Gregory, A.L.; Collins, M.L.M.; Read, J.I.; Irwin, M.J.; Ibata, R.A.; Martin, N.F.; McConnachie, A.W.; Weisz, D.R. Kinematics of the Tucana Dwarf Galaxy: An unusually dense dwarf in the Local Group. Mont. Notices R. Astronom. Soc. 2019, 485, 2010–2025. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Lelli, F.; Schombert, J.M.; Li, P.; Visgaitis, T.; Parker, K.S.; Pawlowski, M.S. The Baryonic Tully-Fisher Relation in the Local Group and the Equivalent Circular Velocity of Pressure-supported Dwarfs. Astronom. J. 2021, 162, 202. [Google Scholar] [CrossRef]
- van Dokkum, P.; Danieli, S.; Cohen, Y.; Merritt, A.; Romanowsky, A.J.; Abraham, R.; Brodie, J.; Conroy, C.; Lokhorst, D.; Mowla, L.; et al. A galaxy lacking dark matter. Nature 2018, 555, 629–632. [Google Scholar] [CrossRef] [PubMed]
- Kroupa, P.; Haghi, H.; Javanmardi, B.; Zonoozi, A.H.; Müller, O.; Banik, I.; Wu, X.; Zhao, H.; Dabringhausen, J. Does the galaxy NGC1052-DF2 falsify Milgromian dynamics? Nature 2018, 561, E4–E5. [Google Scholar] [CrossRef]
- Shen, Z.; Danieli, S.; van Dokkum, P.; Abraham, R.; Brodie, J.P.; Conroy, C.; Dolphin, A.E.; Romanowsky, A.J.; Kruijssen, J.M.D.; Dutta Chowdhury, D. A Tip of the Red Giant Branch Distance of 22.1 ± 1.2 Mpc to the Dark Matter Deficient Galaxy NGC 1052-DF2 from 40 Orbits of Hubble Space Telescope Imaging. ApJL 2021, 914, L12. [Google Scholar] [CrossRef]
- Martin, N.F.; Collins, M.L.M.; Longeard, N.; Tollerud, E. Current Velocity Data on Dwarf Galaxy NGC 1052-DF2 do not Constrain it to Lack Dark Matter. ApJL 2018, 859, L5. [Google Scholar] [CrossRef]
- Fosbury, R.A.E.; Mebold, U.; Goss, W.M.; Dopita, M.A. The active elliptical galaxy NGC 1052. Mont. Notices R. Astronom. Soc. 1978, 183, 549–568. [Google Scholar] [CrossRef]
- Chowdhury, A. A dearth of atomic hydrogen in NGC 1052-DF2. Mont. Notices R. Astronom. Soc. 2019, 482, L99–L101. [Google Scholar] [CrossRef]
- Sardone, A.; Pisano, D.J.; Burke-Spolaor, S.; Mascoop, J.L.; Pol, N. Constraints on the HI Mass of NGC 1052-DF2. ApJL 2019, 871, L31. [Google Scholar] [CrossRef]
- Montes, M.; Infante-Sainz, R.; Madrigal-Aguado, A.; Román, J.; Monelli, M.; Borlaff, A.S.; Trujillo, I. The Galaxy “Missing Dark Matter” NGC 1052-DF4 is Undergoing Tidal Disruption. Astrophys. J. 2020, 904, 114. [Google Scholar] [CrossRef]
- Keim, M.A.; van Dokkum, P.; Danieli, S.; Lokhorst, D.; Li, J.; Shen, Z.; Abraham, R.; Chen, S.; Gilhuly, C.; Liu, Q.; et al. Tidal Distortions in NGC1052-DF2 and NGC1052-DF4: Independent Evidence for a Lack of Dark Matter. arXiv 2022, arXiv:2109.09778. [Google Scholar]
- Ciotti, L.; Londrillo, P.; Nipoti, C. Axisymmetric and Triaxial MOND Density-Potential Pairs. Astrophys. J. 2006, 640, 741–750. [Google Scholar] [CrossRef][Green Version]
- Wu, X.; Kroupa, P. The dynamical phase transitions of stellar systems and the corresponding kinematics. Mont. Notices R. Astronom. Soc. 2013, 435, 728–742. [Google Scholar] [CrossRef]
- Danieli, S.; van Dokkum, P.; Conroy, C.; Abraham, R.; Romanowsky, A.J. Still Missing Dark Matter: KCWI High-resolution Stellar Kinematics of NGC1052-DF2. ApJL 2019, 874, L12. [Google Scholar] [CrossRef]
- Hernandez, X.; Jiménez, M.A.; Allen, C. Flattened velocity dispersion profiles in globular clusters: Newtonian tides or modified gravity? Mont. Notices R. Astronom. Soc. 2013, 428, 3196–3205. [Google Scholar] [CrossRef]
- Durazo, R.; Hernandez, X.; Cervantes Sodi, B.; Sánchez, S.F. A Universal Velocity Dispersion Profile for Pressure Supported Systems: Evidence for MONDian Gravity across Seven Orders of Magnitude in Mass. Astrophys. J. 2017, 837, 179. [Google Scholar] [CrossRef]
- Claydon, I.; Gieles, M.; Zocchi, A. The properties of energetically unbound stars in stellar clusters. Mont. Notices R. Astronom. Soc. 2017, 466, 3937–3950. [Google Scholar] [CrossRef]
- Haghi, H.; Baumgardt, H.; Kroupa, P. Distant star clusters of the Milky Way in MOND. Astronom. Astrophys. 2011, 527, A33. [Google Scholar] [CrossRef][Green Version]
- Di Criscienzo, M.; Greco, C.; Ripepi, V.; Clementini, G.; Dall’Ora, M.; Marconi, M.; Musella, I.; Federici, L.; Di Fabrizio, L. A New Census of the Variable Star Population in the Globular Cluster NGC 2419. Astronom. J. 2011, 141, 81. [Google Scholar] [CrossRef]
- Ibata, R.; Sollima, A.; Nipoti, C.; Bellazzini, M.; Chapman, S.C.; Dalessandro, E. The Globular Cluster NGC 2419: A Crucible for Theories of Gravity. Astrophys. J. 2011, 738, 186. [Google Scholar] [CrossRef]
- Ibata, R.; Sollima, A.; Nipoti, C.; Bellazzini, M.; Chapman, S.C.; Dalessandro, E. Polytropic Model Fits to the Globular Cluster NGC 2419 in Modified Newtonian Dynamics. Astrophys. J. 2011, 743, 43. [Google Scholar] [CrossRef]
- Sanders, R.H. NGC 2419 does not challenge modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2012, 419, L6–L8. [Google Scholar] [CrossRef]
- Sanders, R.H. NGC 2419 does not challenge MOND, Part 2. Mont. Notices R. Astronom. Soc. 2012, 422, L21–L23. [Google Scholar] [CrossRef]
- Hodson, A.O.; Zhao, H. Are over-massive haloes of ultra-diffuse galaxies consistent with extended MOND? Astronom. Astrophys. 2017, 607, A109. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Abraham, R.; Brodie, J.; Conroy, C.; Danieli, S.; Merritt, A.; Mowla, L.; Romanowsky, A.; Zhang, J. A High Stellar Velocity Dispersion and ∼100 Globular Clusters for the Ultra-diffuse Galaxy Dragonfly 44. ApJL 2016, 828, L6. [Google Scholar] [CrossRef]
- Van Dokkum, P.; Wasserman, A.; Danieli, S.; Abraham, R.; Brodie, J.; Conroy, C.; Forbes, D.A.; Martin, C.; Matuszewski, M.; Romanowsky, A.J.; et al. Spatially Resolved Stellar Kinematics of the Ultra-diffuse Galaxy Dragonfly 44. I. Observations, Kinematics, and Cold Dark Matter Halo Fits. Astrophys. J. 2019, 880, 91. [Google Scholar] [CrossRef]
- Bílek, M.; Müller, O.; Famaey, B. Discussing the first velocity dispersion profile of an ultra-diffuse galaxy in MOND. Astronom. Astrophys. 2019, 627, L1. [Google Scholar] [CrossRef]
- Haghi, H.; Amiri, V.; Hasani Zonoozi, A.; Banik, I.; Kroupa, P.; Haslbauer, M. The Star Formation History and Dynamics of the Ultra-diffuse Galaxy Dragonfly 44 in MOND and MOG. ApJL 2019, 884, L25. [Google Scholar] [CrossRef]
- Müller, O.; Famaey, B.; Zhao, H. Predicted MOND velocity dispersions for a catalog of ultra-diffuse galaxies in group environments. Astronom. Astrophys. 2019, 623, A36. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics: Second Edition; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. Astrophys. J. 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Milgrom, M. Isothermal spheres in the modified dynamics. Astrophys. J. 1984, 287, 571–576. [Google Scholar] [CrossRef]
- Milgrom, M. Deep-MOND polytropes. Phys. Rev. D 2021, 103, 044043. [Google Scholar] [CrossRef]
- Sanders, R.H. The fundamental plane of elliptical galaxies with modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2000, 313, 767–774. [Google Scholar] [CrossRef]
- Richtler, T.; Famaey, B.; Gentile, G.; Schuberth, Y. Remarks on the properties of elliptical galaxies in modified Newtonian dynamics. Astronom. Astrophys. 2011, 531, A100. [Google Scholar] [CrossRef]
- Cappellari, M.; Scott, N.; Alatalo, K.; Blitz, L.; Bois, M.; Bournaud, F.; Bureau, M.; Crocker, A.F.; Davies, R.L.; Davis, T.A.; et al. The ATLAS3D project—XV. Benchmark for early-type galaxies scaling relations from 260 dynamical models: Mass-to-light ratio, dark matter, Fundamental Plane and Mass Plane. Mont. Notices R. Astronom. Soc. 2013, 432, 1709–1741. [Google Scholar] [CrossRef]
- Bundy, K.; Bershady, M.A.; Law, D.R.; Yan, R.; Drory, N.; MacDonald, N.; Wake, D.A.; Cherinka, B.; Sánchez-Gallego, J.R.; Weijmans, A.M.; et al. Overview of the SDSS-IV MaNGA Survey: Mapping nearby Galaxies at Apache Point Observatory. Astrophys. J. 2015, 798, 7. [Google Scholar] [CrossRef]
- SDSS Collaboration. The Sloan Digital Sky Survey: Technical Summary. Astronom. J. 2000, 120, 1579–1587. [Google Scholar] [CrossRef]
- Chae, K.H.; Bernardi, M.; Domínguez Sánchez, H.; Sheth, R.K. On the Presence of a Universal Acceleration Scale in Elliptical Galaxies. ApJL 2020, 903, L31. [Google Scholar] [CrossRef]
- Paranjape, A.; Sheth, R.K. The radial acceleration relation in a ΛCDM universe. Mont. Notices R. Astronom. Soc. 2021, 507, 632–650. [Google Scholar] [CrossRef]
- Tian, Y.; Ko, C.M. Mass discrepancy-acceleration relation in Einstein rings. Mont. Notices R. Astronom. Soc. 2017, 472, 765–771. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Conroy, C. On the Lack of Evolution in Galaxy Star Formation Efficiency. ApJL 2013, 762, L31. [Google Scholar] [CrossRef]
- Paranjape, A.; Choudhury, T.R.; Sheth, R.K. Multiwavelength mock galaxy catalogues of the low-redshift Universe. Mont. Notices R. Astronom. Soc. 2021, 503, 4147–4162. [Google Scholar] [CrossRef]
- Chae, K.H.; Bernardi, M.; Sheth, R.K.; Gong, I.T. Radial Acceleration Relation between Baryons and Dark or Phantom Matter in the Supercritical Acceleration Regime of Nearly Spherical Galaxies. Astrophys. J. 2019, 877, 18. [Google Scholar] [CrossRef]
- Li, P.; McGaugh, S.S.; Lelli, F.; Tian, Y.; Schombert, J.M.; Ko, C.M. The Effect of Adiabatic Compression on Dark Matter Halos and the Radial Acceleration Relation. Astrophys. J. 2022, 927, 198. [Google Scholar] [CrossRef]
- Forouhar Moreno, V.J.; Benítez-Llambay, A.; Cole, S.; Frenk, C. Baryon-driven decontraction in Milky Way-mass haloes. Mont. Notices R. Astronom. Soc. 2022, 511, 3910–3921. [Google Scholar] [CrossRef]
- Romanowsky, A.J.; Douglas, N.G.; Arnaboldi, M.; Kuijken, K.; Merrifield, M.R.; Napolitano, N.R.; Capaccioli, M.; Freeman, K.C. A Dearth of Dark Matter in Ordinary Elliptical Galaxies. Science 2003, 301, 1696–1698. [Google Scholar] [CrossRef]
- Milgrom, M.; Sanders, R.H. Modified Newtonian Dynamics and the “Dearth of Dark Matter in Ordinary Elliptical Galaxies”. ApJL 2003, 599, L25–L28. [Google Scholar] [CrossRef]
- Tian, Y.; Ko, C.M. Dynamics of elliptical galaxies with planetary nebulae in modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2016, 462, 1092–1100. [Google Scholar] [CrossRef]
- Klypin, A.; Prada, F. Testing Gravity with Motion of Satellites Around Galaxies: Newtonian Gravity against Modified Newtonian Dynamics. Astrophys. J. 2009, 690, 1488–1496. [Google Scholar] [CrossRef]
- Nipoti, C.; Londrillo, P.; Ciotti, L. Dissipationless Collapses in Modified Newtonian Dynamics. Astrophys. J. 2007, 660, 256–266. [Google Scholar] [CrossRef]
- Milgrom, M. Testing MOND over a Wide Acceleration Range in X-Ray Ellipticals. Phys. Rev. Lett. 2012, 109, 131101. [Google Scholar] [CrossRef] [PubMed]
- Diehl, S.; Statler, T.S. The Hot Interstellar Medium of Normal Elliptical Galaxies. I. A Chandra Gas Gallery and Comparison of X-Ray and Optical Morphology. Astrophys. J. 2007, 668, 150–167. [Google Scholar] [CrossRef]
- Buote, D.A.; Humphrey, P.J. Dark Matter in Elliptical Galaxies. In Hot Interstellar Matter in Elliptical Galaxies. Astrophysics and Space Science Library; Kim, D.W., Pellegrini, S., Eds.; Springer: New York, NY, USA, 2012; Volume 378, pp. 235–277. [Google Scholar] [CrossRef]
- Den Heijer, M.; Oosterloo, T.A.; Serra, P.; Józsa, G.I.G.; Kerp, J.; Morganti, R.; Cappellari, M.; Davis, T.A.; Duc, P.A.; Emsellem, E.; et al. The H I Tully-Fisher relation of early-type galaxies. Astronom. Astrophys. 2015, 581, A98. [Google Scholar] [CrossRef]
- Shelest, A.; Lelli, F. From spirals to lenticulars: Evidence from the rotation curves and mass models of three early-type galaxies. Astronom. Astrophys. 2020, 641, A31. [Google Scholar] [CrossRef]
- Torrealba, G.; Koposov, S.E.; Belokurov, V.; Irwin, M. The feeble giant. Discovery of a large and diffuse Milky Way dwarf galaxy in the constellation of Crater. Mont. Notices R. Astronom. Soc. 2016, 459, 2370–2378. [Google Scholar] [CrossRef]
- McGaugh, S.S. MOND Prediction for the Velocity Dispersion of the Feeble Gian Crater II. ApJL 2016, 832, L8. [Google Scholar] [CrossRef]
- Brada, R.; Milgrom, M. Dwarf Satellite Galaxies in the Modified Dynamics. Astrophys. J. 2000, 541, 556–564. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Hammer, F.; Babusiaux, C.; Pawlowski, M.S.; Yang, Y.; Arenou, F.; Du, C.; Wang, J. Gaia EDR3 Proper Motions of Milky Way Dwarfs. I. 3D Motions and Orbits. Astrophys. J. 2021, 916, 8. [Google Scholar] [CrossRef]
- Caldwell, N.; Walker, M.G.; Mateo, M.; Olszewski, E.W.; Koposov, S.; Belokurov, V.; Torrealba, G.; Geringer-Sameth, A.; Johnson, C.I. Crater 2: An Extremely Cold Dark Matter Halo. Astrophys. J. 2017, 839, 20. [Google Scholar] [CrossRef]
- Walker, M.G.; McGaugh, S.S.; Mateo, M.; Olszewski, E.W.; Kuzio de Naray, R. Comparing the Dark Matter Halos of Spiral, Low Surface Brightness, and Dwarf Spheroidal Galaxies. ApJL 2010, 717, L87–L91. [Google Scholar] [CrossRef]
- Borukhovetskaya, A.; Navarro, J.F.; Errani, R.; Fattahi, A. Galactic tides and the Crater II dwarf spheroidal: A challenge to LCDM? Mont. Notices R. Astronom. Soc. 2022, 512, 5247–5257. [Google Scholar] [CrossRef]
- Errani, R.; Navarro, J.F.; Ibata, R.; Peñarrubia, J. Structure and kinematics of tidally limited satellite galaxies in LCDM. Mont. Notices R. Astronom. Soc. 2022, 511, 6001–6018. [Google Scholar] [CrossRef]
- Fu, S.W.; Simon, J.D.; Alarcón Jara, A.G. Dynamical Histories of the Crater II and Hercules Dwarf Galaxies. Astrophys. J. 2019, 883, 11. [Google Scholar] [CrossRef]
- Thomas, G.F.; Famaey, B.; Ibata, R.; Renaud, F.; Martin, N.F.; Kroupa, P. Stellar streams as gravitational experiments. II. Asymmetric tails of globular cluster streams. Astronom. Astrophys. 2018, 609, A44. [Google Scholar] [CrossRef]
- Haghi, H.; Bazkiaei, A.E.; Zonoozi, A.H.; Kroupa, P. Declining rotation curves of galaxies as a test of gravitational theory. Mont. Notices R. Astronom. Soc. 2016, 458, 4172–4187. [Google Scholar] [CrossRef]
- Chae, K.H.; Lelli, F.; Desmond, H.; McGaugh, S.S.; Li, P.; Schombert, J.M. Testing the Strong Equivalence Principle: Detection of the External Field Effect in Rotationally Supported Galaxies. Astrophys. J. 2020, 904, 51. [Google Scholar] [CrossRef]
- Desmond, H.; Ferreira, P.G.; Lavaux, G.; Jasche, J. Reconstructing the gravitational field of the local Universe. Mont. Notices R. Astronom. Soc. 2018, 474, 3152–3161. [Google Scholar] [CrossRef]
- Chae, K.H.; Desmond, H.; Lelli, F.; McGaugh, S.S.; Schombert, J.M. Testing the Strong Equivalence Principle. II. Relating the External Field Effect in Galaxy Rotation Curves to the Large-scale Structure of the Universe. Astrophys. J. 2021, 921, 104. [Google Scholar] [CrossRef]
- Paranjape, A.; Sheth, R.K. The external field effect in cold dark matter models. arXiv 2022, arXiv:2112.00026. [Google Scholar]
- Wu, X.; Famaey, B.; Gentile, G.; Perets, H.; Zhao, H. Milky Way potentials in cold dark matter and MOdified Newtonian Dynamics. Is the Large Magellanic Cloud on a bound orbit? Mont. Notices R. Astronom. Soc. 2008, 386, 2199–2208. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. The escape velocity curve of the Milky Way in modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2018, 473, 419–430. [Google Scholar] [CrossRef]
- Monari, G.; Famaey, B.; Carrillo, I.; Piffl, T.; Steinmetz, M.; Wyse, R.F.G.; Anders, F.; Chiappini, C.; Janßen, K. The escape speed curve of the Galaxy obtained from Gaia DR2 implies a heavy Milky Way. Astronom. Astrophys. 2018, 616, L9. [Google Scholar] [CrossRef]
- Williams, A.A.; Belokurov, V.; Casey, A.R.; Evans, N.W. On the run: Mapping the escape speed across the Galaxy with SDSS. Mont. Notices R. Astronom. Soc. 2017, 468, 2359–2371. [Google Scholar] [CrossRef]
- Aguirre, A.; Schaye, J.; Quataert, E. Problems for Modified Newtonian Dynamics in Clusters and the Lyα Forest? Astrophys. J. 2001, 561, 550–558. [Google Scholar] [CrossRef]
- Hernandez, X.; Jiménez, M.A.; Allen, C. Wide binaries as a critical test of classical gravity. Eur. Phys. J. C 2012, 72, 1884. [Google Scholar] [CrossRef]
- Pittordis, C.; Sutherland, W. Testing modified gravity with wide binaries in Gaia DR2. Mont. Notices R. Astronom. Soc. 2019, 488, 4740–4752. [Google Scholar] [CrossRef]
- Gundlach, J.H.; Schlamminger, S.; Spitzer, C.D.; Choi, K.Y.; Woodahl, B.A.; Coy, J.J.; Fischbach, E. Laboratory Test of Newton’s Second Law for Small Accelerations. Phys. Rev. Lett. 2007, 98, 150801. [Google Scholar] [CrossRef]
- Sanders, R.H. A dearth of dark matter in strong gravitational lenses. Mont. Notices R. Astronom. Soc. 2014, 439, 1781–1786. [Google Scholar] [CrossRef]
- Lehár, J.; Falco, E.E.; Kochanek, C.S.; McLeod, B.A.; Muñoz, J.A.; Impey, C.D.; Rix, H.W.; Keeton, C.R.; Peng, C.Y. Hubble Space Telescope Observations of 10 Two-Image Gravitational Lenses. Astrophys. J. 2000, 536, 584–605. [Google Scholar] [CrossRef]
- Chiu, M.C.; Ko, C.M.; Tian, Y.; Zhao, H. Mass of galaxy lenses in modified gravity: Any need for dark mass? Phys. Rev. D 2011, 83, 063523. [Google Scholar] [CrossRef]
- Bolton, A.S.; Burles, S.; Koopmans, L.V.E.; Treu, T.; Moustakas, L.A. The Sloan Lens ACS Survey. I. A Large Spectroscopically Selected Sample of Massive Early-Type Lens Galaxies. Astrophys. J. 2006, 638, 703–724. [Google Scholar] [CrossRef]
- Auger, M.W.; Treu, T.; Bolton, A.S.; Gavazzi, R.; Koopmans, L.V.E.; Marshall, P.J.; Bundy, K.; Moustakas, L.A. The Sloan Lens ACS Survey. IX. Colors, Lensing, and Stellar Masses of Early-Type Galaxies. Astrophys. J. 2009, 705, 1099–1115. [Google Scholar] [CrossRef]
- Sanders, R.H.; Land, D.D. MOND and the lensing fundamental plane: No need for dark matter on galaxy scales. Mont. Notices R. Astronom. Soc. 2008, 389, 701–705. [Google Scholar] [CrossRef]
- Shapiro, I.I. Fourth Test of General Relativity. Phys. Rev. Lett. 1964, 13, 789–791. [Google Scholar] [CrossRef]
- Brimioulle, F.; Seitz, S.; Lerchster, M.; Bender, R.; Snigula, J. Dark matter halo properties from galaxy-galaxy lensing. Mont. Notices R. Astronom. Soc. 2013, 432, 1046–1102. [Google Scholar] [CrossRef]
- Milgrom, M. Testing the MOND Paradigm of Modified Dynamics with Galaxy-Galaxy Gravitational Lensing. Phys. Rev. Lett. 2013, 111, 041105. [Google Scholar] [CrossRef]
- Brouwer, M.M.; Visser, M.R.; Dvornik, A.; Hoekstra, H.; Kuijken, K.; Valentijn, E.A.; Bilicki, M.; Blake, C.; Brough, S.; Buddelmeijer, H.; et al. First test of Verlinde’s theory of emergent gravity using weak gravitational lensing measurements. Mont. Notices R. Astronom. Soc. 2017, 466, 2547–2559. [Google Scholar] [CrossRef]
- Brouwer, M.M.; Oman, K.A.; Valentijn, E.A.; Bilicki, M.; Heymans, C.; Hoekstra, H.; Napolitano, N.R.; Roy, N.; Tortora, C.; Wright, A.H.; et al. The weak lensing radial acceleration relation: Constraining modified gravity and cold dark matter theories with KiDS-1000. Astronom. Astrophys. 2021, 650, A113. [Google Scholar] [CrossRef]
- Schrabback, T.; Hoekstra, H.; Van Waerbeke, L.; van Uitert, E.; Georgiou, C.; Asgari, M.; Côté, P.; Cuillandre, J.C.; Erben, T.; Ferrarese, L.; et al. Tightening weak lensing constraints on the ellipticity of galaxy-scale dark matter haloes. Astronom. Astrophys. 2021, 646, A73. [Google Scholar] [CrossRef]
- Feix, M.; Xu, D.; Shan, H.; Famaey, B.; Limousin, M.; Zhao, H.; Taylor, A. Is Gravitational Lensing by Intercluster Filaments Always Negligible? Astrophys. J. 2008, 682, 711–720. [Google Scholar] [CrossRef][Green Version]
- Diez-Tejedor, A.; Gonzalez-Morales, A.X.; Niz, G. Verlinde’s emergent gravity versus MOND and the case of dwarf spheroidals. Mont. Notices R. Astronom. Soc. 2018, 477, 1285–1295. [Google Scholar] [CrossRef]
- Bradford, J.D.; Geha, M.C.; Blanton, M.R. A Study in Blue: The Baryon Content of Isolated Low-mass Galaxies. Astrophys. J. 2015, 809, 146. [Google Scholar] [CrossRef]
- Pardo, K. Testing emergent gravity with isolated dwarf galaxies. J. Cosmol. Astropart. Phys. 2020, 2020, 012. [Google Scholar] [CrossRef]
- Lelli, F.; McGaugh, S.S.; Schombert, J.M. Testing Verlinde’s emergent gravity with the radial acceleration relation. Mont. Notices R. Astronom. Soc. 2017, 468, L68–L71. [Google Scholar] [CrossRef]
- Hossenfelder, S. Covariant version of Verlinde’s emergent gravity. Phys. Rev. D 2017, 95, 124018. [Google Scholar] [CrossRef]
- Kobakhidze, A. Gravity is not an entropic force. Phys. Rev. D 2011, 83, 021502. [Google Scholar] [CrossRef]
- Chaichian, M.; Oksanen, M.; Tureanu, A. On gravity as an entropic force. Phys. Lett. B 2011, 702, 419–421. [Google Scholar] [CrossRef]
- Kobakhidze, A. Once more: Gravity is not an entropic force. arXiv 2011, arXiv:1108.4161. [Google Scholar]
- Wang, Z.W.; Braunstein, S.L. Surfaces away from horizons are not thermodynamic. Nat. Commun. 2018, 9, 2977. [Google Scholar] [CrossRef]
- Moffat, J.W. Scalar tensor vector gravity theory. J. Cosmol. Astropart. Phys. 2006, 2006, 004. [Google Scholar] [CrossRef]
- Negrelli, C.; Benito, M.; Landau, S.; Iocco, F.; Kraiselburd, L. Testing modified gravity theory in the Milky Way. Phys. Rev. D 2018, 98, 104061. [Google Scholar] [CrossRef]
- Bovy, J. A purely acceleration-based measurement of the fundamental Galactic parameters. arXiv 2020, arXiv:2012.02169. [Google Scholar]
- Pflamm-Altenburg, J.; Kroupa, P. The Fundamental Gas Depletion and Stellar-Mass Buildup Times of Star-Forming Galaxies. Astrophys. J. 2009, 706, 516–524. [Google Scholar] [CrossRef]
- de Martino, I.; Chakrabarty, S.S.; Cesare, V.; Gallo, A.; Ostorero, L.; Diaferio, A. Dark Matters on the Scale of Galaxies. Universe 2020, 6, 107. [Google Scholar] [CrossRef]
- Pérez-Cuéllar, G.; Sabido, M. On planetary orbits in entropic gravity. Mod. Phys. Lett. A 2021, 36, 2150050. [Google Scholar] [CrossRef]
- Berezhiani, L.; Khoury, J. Theory of dark matter superfluidity. Phys. Rev. D 2015, 92, 103510. [Google Scholar] [CrossRef]
- Berezhiani, L.; Khoury, J. Dark matter superfluidity and galactic dynamics. Phys. Lett. B 2016, 753, 639–643. [Google Scholar] [CrossRef]
- Hodson, A.O.; Zhao, H.; Khoury, J.; Famaey, B. Galaxy clusters in the context of superfluid dark matter. Astronom. Astrophys. 2017, 607, A108. [Google Scholar] [CrossRef]
- Roshan, M.; Banik, I.; Ghafourian, N.; Thies, I.; Famaey, B.; Asencio, E.; Kroupa, P. Barred spiral galaxies in modified gravity theories. Mont. Notices R. Astronom. Soc. 2021, 503, 2833–2860. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Mistele, T. The Milky Way’s rotation curve with superfluid dark matter. Mont. Notices R. Astronom. Soc. 2020, 498, 3484–3491. [Google Scholar] [CrossRef]
- Mistele, T. Cherenkov radiation from stars constrains hybrid MOND-dark-matter models. arXiv 2021, arXiv:2103.16954. [Google Scholar]
- Mistele, T.; McGaugh, S.; Hossenfelder, S. Galactic Mass-to-Light Ratios With Superfluid Dark Matter. Astronom. Astrophys. 2022; in press. [Google Scholar] [CrossRef]
- Hertzberg, M.P.; Litterer, J.A.; Shah, N. Acausality in superfluid dark matter and MOND-like theories. J. Cosmol. Astropart. Phys. 2021, 2021, 015. [Google Scholar] [CrossRef]
- Hajdukovic, D.S. On the gravitational field of a point-like body immersed in a quantum vacuum. Mont. Notices R. Astronom. Soc. 2020, 491, 4816–4828. [Google Scholar] [CrossRef]
- Maeder, A.; Gueorguiev, V.G. Scale-invariant dynamics of galaxies, MOND, dark matter, and the dwarf spheroidals. Mont. Notices R. Astronom. Soc. 2020, 492, 2698–2708. [Google Scholar] [CrossRef]
- Banik, I.; Kroupa, P. Solar System limits on gravitational dipoles. Mont. Notices R. Astronom. Soc. 2020, 495, 3974–3980. [Google Scholar] [CrossRef]
- Banik, I.; Kroupa, P. Scale-invariant dynamics in the Solar system. Mont. Notices R. Astronom. Soc. 2020, 497, L62–L66. [Google Scholar] [CrossRef]
- Privon, G.C.; Barnes, J.E.; Evans, A.S.; Hibbard, J.E.; Yun, M.S.; Mazzarella, J.M.; Armus, L.; Surace, J. Dynamical Modeling of Galaxy Mergers Using Identikit. Astrophys. J. 2013, 771, 120. [Google Scholar] [CrossRef]
- Kautsch, S.J.; Grebel, E.K.; Barazza, F.D.; Gallagher, J.S.I. A catalog of edge-on disk galaxies. From galaxies with a bulge to superthin galaxies. Astronom. Astrophys. 2006, 445, 765–778. [Google Scholar] [CrossRef]
- Graham, A.W.; Worley, C.C. Inclination- and dust-corrected galaxy parameters: Bulge-to-Disc ratios and size-luminosity relations. Mont. Notices R. Astronom. Soc. 2008, 388, 1708–1728. [Google Scholar] [CrossRef]
- Kormendy, J.; Drory, N.; Bender, R.; Cornell, M.E. Bulgeless Giant Galaxies Challenge Our Picture of Galaxy Formation by Hierarchical Clustering. Astrophys. J. 2010, 723, 54–80. [Google Scholar] [CrossRef]
- Smercina, A.; Bell, E.F.; Price, P.A.; D’Souza, R.; Slater, C.T.; Bailin, J.; Monachesi, A.; Nidever, D. A Lonely Giant: The Sparse Satellite Population of M94 Challenges Galaxy Formation. Astrophys. J. 2018, 863, 152. [Google Scholar] [CrossRef]
- van Dokkum, P.G.; Abraham, R.; Merritt, A. First Results from the Dragonfly Telephoto Array: The Apparent Lack of a Stellar Halo in the Massive Spiral Galaxy M101. ApJL 2014, 782, L24. [Google Scholar] [CrossRef]
- Merritt, A.; van Dokkum, P.; Abraham, R.; Zhang, J. The Dragonfly nearby Galaxies Survey. I. Substantial Variation in the Diffuse Stellar Halos around Spiral Galaxies. Astrophys. J. 2016, 830, 62. [Google Scholar] [CrossRef]
- Elias, L.M.; Sales, L.V.; Creasey, P.; Cooper, M.C.; Bullock, J.S.; Rich, R.M.; Hernquist, L. Stellar halos in Illustris: Probing the histories of Milky Way-mass galaxies. Mont. Notices R. Astronom. Soc. 2018, 479, 4004–4016. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Formation of the large nearby galaxies. Mont. Notices R. Astronom. Soc. 2020, 498, 4386–4395. [Google Scholar] [CrossRef]
- Kim, S.Y.; Peter, A.H.G.; Hargis, J.R. Missing Satellites Problem: Completeness Corrections to the Number of Satellite Galaxies in the Milky Way are Consistent with Cold Dark Matter Predictions. Phys. Rev. Lett. 2018, 121, 211302. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Cox, T.J.; Younger, J.D.; Hernquist, L. How do Disks Survive Mergers? Astrophys. J. 2009, 691, 1168–1201. [Google Scholar] [CrossRef]
- Haslbauer, M.; Banik, I.; Kroupa, P.; Wittenburg, N.; Javanmardi, B. The High Fraction of Thin Disk Galaxies Continues to Challenge Λ CDM Cosmology. Astrophys. J. 2022, 925, 183. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Fall, S.M.; Schaye, J.; Obreschkow, D. Spurious heating of stellar motions in simulated galactic discs by dark matter halo particles. Mont. Notices R. Astronom. Soc. 2021, 508, 5114–5137. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Bird, S.; Nelson, D.; Hernquist, L. Properties of galaxies reproduced by a hydrodynamic simulation. Nature 2014, 509, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Bottrell, C.; Torrey, P.; Simard, L.; Ellison, S.L. Galaxies in the Illustris simulation as seen by the Sloan Digital Sky Survey—I: Bulge+disc decompositions, methods, and biases. Mont. Notices R. Astronom. Soc. 2017, 467, 1033–1066. [Google Scholar] [CrossRef]
- Bottrell, C.; Torrey, P.; Simard, L.; Ellison, S.L. Galaxies in the Illustris simulation as seen by the Sloan Digital Sky Survey—II. Size-luminosity relations and the deficit of bulge-dominated galaxies in Illustris at low mass. Mont. Notices R. Astronom. Soc. 2017, 467, 2879–2895. [Google Scholar] [CrossRef]
- McGaugh, S.S.; de Blok, W.J.G. Testing the Hypothesis of Modified Dynamics with Low Surface Brightness Galaxies and Other Evidence. Astrophys. J. 1998, 499, 66–81. [Google Scholar] [CrossRef]
- Driver, S.P.; Norberg, P.; Baldry, I.K.; Bamford, S.P.; Hopkins, A.M.; Liske, J.; Loveday, J.; Peacock, J.A.; Hill, D.T.; Kelvin, L.S.; et al. GAMA: Towards a physical understanding of galaxy formation. Astron. Geophys. 2009, 50, 5.12–5.19. [Google Scholar] [CrossRef]
- Driver, S.P.; Hill, D.T.; Kelvin, L.S.; Robotham, A.S.G.; Liske, J.; Norberg, P.; Baldry, I.K.; Bamford, S.P.; Hopkins, A.M.; Loveday, J.; et al. Galaxy and Mass Assembly (GAMA): Survey diagnostics and core data release. Mont. Notices R. Astronom. Soc. 2011, 413, 971–995. [Google Scholar] [CrossRef]
- van der Kruit, P.C. The radial distribution of surface brightness in galactic disks. Astronom. Astrophys. 1987, 173, 59–80. [Google Scholar]
- Disney, M.J. Visibility of galaxies. Nature 1976, 263, 573–575. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Bothun, G.D.; Schombert, J.M. Galaxy Selection and the Surface Brightness Distribution. Astronom. J. 1995, 110, 573. [Google Scholar] [CrossRef]
- McGaugh, S.S. The number, luminosity and mass density of spiral galaxies as a function of surface brightness. Mont. Notices R. Astronom. Soc. 1996, 280, 337–354. [Google Scholar] [CrossRef]
- Zavala, J.; Avila-Reese, V.; Hernández-Toledo, H.; Firmani, C. The luminous and dark matter content of disk galaxies. Astronom. Astrophys. 2003, 412, 633–650. [Google Scholar] [CrossRef][Green Version]
- Fathi, K. Revisiting the Scale Length-μ0 Plane and the Freeman Law in the Local Universe. ApJL 2010, 722, L120–L125. [Google Scholar] [CrossRef]
- Willmer, C.N.A. The Absolute Magnitude of the Sun in Several Filters. ApJS 2018, 236, 47. [Google Scholar] [CrossRef]
- Wittenburg, N.; Kroupa, P.; Famaey, B. The Formation of Exponential Disk Galaxies in MOND. Astrophys. J. 2020, 890, 173. [Google Scholar] [CrossRef]
- Combes, F. Bulge formation in disk galaxies with MOND. Astronom. Astrophys. 2014, 571, A82. [Google Scholar] [CrossRef]
- Milgrom, M. On stability of galactic disks in the modified dynamics and the distribution of their mean surface brightness. Astrophys. J. 1989, 338, 121–127. [Google Scholar] [CrossRef]
- Saburova, A.S. Do low surface brightness galaxies have dense disks? Astron. Rep. 2011, 55, 409–415. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. On the Spiral Structure of Disk Galaxies. Astrophys. J. 1964, 140, 646. [Google Scholar] [CrossRef]
- Schombert, J.M.; Bothun, G.D.; Schneider, S.E.; McGaugh, S.S. A Catalog of Low Surface Brightness Galaxies. List II. Astronom. J. 1992, 103, 1107. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; van der Hulst, J.M.; Bothun, G.D. Surface photometry of low surface brightness galaxies. Mont. Notices R. Astronom. Soc. 1995, 274, 235–255. [Google Scholar] [CrossRef][Green Version]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D. The Morphology of Low Surface Brightness Disk Galaxies. Astronom. J. 1995, 109, 2019. [Google Scholar] [CrossRef]
- Impey, C.D.; Sprayberry, D.; Irwin, M.J.; Bothun, G.D. Low Surface Brightness Galaxies in the Local Universe. I. The Catalog. ApJS 1996, 105, 209. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Carlberg, R.G. Spiral instabilities provoked by accretion and star formation. Astrophys. J. 1984, 282, 61–74. [Google Scholar] [CrossRef]
- Athanassoula, E.; Bosma, A.; Papaioannou, S. Halo parameters of spiral galaxies. Astronom. Astrophys. 1987, 179, 23–40. [Google Scholar]
- D’Onghia, E. Disk-stability Constraints on the Number of Arms in Spiral Galaxies. ApJL 2015, 808, L8. [Google Scholar] [CrossRef]
- Fuchs, B. Massive disks in low surface brightness galaxies. Ap&SS 2003, 284, 719–722. [Google Scholar] [CrossRef]
- Saburova, A.S.; Zasov, A.V. Gravitational stability and mass estimation of stellar disks. Astron. Nachrichten 2013, 334, 785. [Google Scholar] [CrossRef]
- Hart, R.E.; Bamford, S.P.; Casteels, K.R.V.; Kruk, S.J.; Lintott, C.J.; Masters, K.L. Galaxy Zoo: Star formation versus spiral arm number. Mont. Notices R. Astronom. Soc. 2017, 468, 1850–1863. [Google Scholar] [CrossRef]
- Dobbs, C.L.; Theis, C.; Pringle, J.E.; Bate, M.R. Simulations of the grand design galaxy M51: A case study for analysing tidally induced spiral structure. Mont. Notices R. Astronom. Soc. 2010, 403, 625–645. [Google Scholar] [CrossRef]
- Miller, R.H.; Prendergast, K.H. Stellar Dynamics in a Discrete Phase Space. Astrophys. J. 1968, 151, 699. [Google Scholar] [CrossRef]
- Hockney, R.W.; Hohl, F. Effects of Velocity Dispersion on the Evolution of a Disk of Stars. Astronom. J. 1969, 74, 1102. [Google Scholar] [CrossRef]
- Athanassoula, E. Bar-Halo Interaction and Bar Growth. ApJL 2002, 569, L83–L86. [Google Scholar] [CrossRef]
- Athanassoula, E.; Misiriotis, A. Morphology, photometry and kinematics of N -body bars—I. Three models with different halo central concentrations. Mont. Notices R. Astronom. Soc. 2002, 330, 35–52. [Google Scholar] [CrossRef]
- Athanassoula, E. What determines the strength and the slowdown rate of bars? Mont. Notices R. Astronom. Soc. 2003, 341, 1179–1198. [Google Scholar] [CrossRef]
- Doroshkevich, A.G. The space structure of perturbations and the origin of rotation of galaxies in the theory of fluctuation. Astrofizika 1970, 6, 581–600. [Google Scholar]
- White, S.D.M. Angular momentum growth in protogalaxies. Astrophys. J. 1984, 286, 38–41. [Google Scholar] [CrossRef]
- Saha, K.; Naab, T. Spinning dark matter haloes promote bar formation. Mont. Notices R. Astronom. Soc. 2013, 434, 1287–1299. [Google Scholar] [CrossRef]
- Sellwood, J.A. Bar Instability in Disk-Halo Systems. Astrophys. J. 2016, 819, 92. [Google Scholar] [CrossRef]
- Berrier, J.C.; Sellwood, J.A. Mass Distribution and Bar Formation in Growing Disk Galaxy Models. Astrophys. J. 2016, 831, 65. [Google Scholar] [CrossRef]
- Bauer, J.S.; Widrow, L.M. Can stellar discs in a cosmological setting avoid forming strong bars? Mont. Notices R. Astronom. Soc. 2019, 486, 523–537. [Google Scholar] [CrossRef]
- Bauer, J.S.; Widrow, L.M.; Erkal, D. Disc-halo interactions in ΛCDM. Mont. Notices R. Astronom. Soc. 2018, 476, 198–209. [Google Scholar] [CrossRef]
- Klypin, A.; Valenzuela, O.; Colín, P.; Quinn, T. Dynamics of barred galaxies: Effects of disc height. Mont. Notices R. Astronom. Soc. 2009, 398, 1027–1040. [Google Scholar] [CrossRef]
- Masters, K.L.; Nichol, R.C.; Hoyle, B.; Lintott, C.; Bamford, S.P.; Edmondson, E.M.; Fortson, L.; Keel, W.C.; Schawinski, K.; Smith, A.M.; et al. Galaxy Zoo: Bars in disc galaxies. Mont. Notices R. Astronom. Soc. 2011, 411, 2026–2034. [Google Scholar] [CrossRef]
- Erwin, P. The dependence of bar frequency on galaxy mass, colour, and gas content-and angular resolution-in the local universe. Mont. Notices R. Astronom. Soc. 2018, 474, 5372–5392. [Google Scholar] [CrossRef]
- Eskridge, P.B.; Frogel, J.A.; Pogge, R.W.; Quillen, A.C.; Davies, R.L.; DePoy, D.L.; Houdashelt, M.L.; Kuchinski, L.E.; Ramírez, S.V.; Sellgren, K.; et al. The Frequency of Barred Spiral Galaxies in the Near-Infrared. Astronom. J. 2000, 119, 536–544. [Google Scholar] [CrossRef]
- Sheth, K.; Elmegreen, D.M.; Elmegreen, B.G.; Capak, P.; Abraham, R.G.; Athanassoula, E.; Ellis, R.S.; Mobasher, B.; Salvato, M.; Schinnerer, E.; et al. Evolution of the Bar Fraction in COSMOS: Quantifying the Assembly of the Hubble Sequence. Astrophys. J. 2008, 675, 1141–1155. [Google Scholar] [CrossRef]
- Corbelli, E.; Walterbos, R.A.M. Bar Imprints on the Inner Gas Kinematics of M33. Astrophys. J. 2007, 669, 315–326. [Google Scholar] [CrossRef]
- Kam, Z.S.; Carignan, C.; Chemin, L.; Amram, P.; Epinat, B. Kinematics and mass modelling of M33: Hα observations. Mont. Notices R. Astronom. Soc. 2015, 449, 4048–4070. [Google Scholar] [CrossRef]
- Sanders, R.H. The Published Extended Rotation Curves of Spiral Galaxies: Confrontation with Modified Dynamics. Astrophys. J. 1996, 473, 117. [Google Scholar] [CrossRef]
- Kam, S.Z.; Carignan, C.; Chemin, L.; Foster, T.; Elson, E.; Jarrett, T.H. H I Kinematics and Mass Distribution of Messier 33. Astronom. J. 2017, 154, 41. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Shen, J.; Li, Z. The global stability of M33: Still a puzzle. Mont. Notices R. Astronom. Soc. 2019, 486, 4710–4723. [Google Scholar] [CrossRef]
- Conroy, C. Modeling the Panchromatic Spectral Energy Distributions of Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 393–455. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. The mass-to-light ratios and the star formation histories of disc galaxies. Mont. Notices R. Astronom. Soc. 2019, 483, 1496–1512. [Google Scholar] [CrossRef]
- Smith, G.; Elmegreen, B.G.; Elmegreen, D.M. Comparaison of M 33 and NGC 7793: Stochastic models of spiral galaxies modulated by density waves. Mont. Notices R. Astronom. Soc. 1984, 210, 399–413. [Google Scholar] [CrossRef][Green Version]
- Elmegreen, B.G.; Elmegreen, D.M.; Montenegro, L. Optical Tracers of Spiral Wave Resonances in Galaxies. II. Hidden Three-Arm Spirals in a Sample of 18 Galaxies. ApJS 1992, 79, 37. [Google Scholar] [CrossRef]
- Regan, M.W.; Vogel, S.N. The near-infrared structure of M33. Astrophys. J. 1994, 434, 536–545. [Google Scholar] [CrossRef]
- Jarrett, T.H.; Chester, T.; Cutri, R.; Schneider, S.E.; Huchra, J.P. The 2MASS Large Galaxy Atlas. Astronom. J. 2003, 125, 525–554. [Google Scholar] [CrossRef]
- Verley, S.; Corbelli, E.; Giovanardi, C.; Hunt, L.K. Star formation in M 33: Multiwavelength signatures across the disk. Astronom. Astrophys. 2009, 493, 453–466. [Google Scholar] [CrossRef]
- Brada, R.; Milgrom, M. Stability of Disk Galaxies in the Modified Dynamics. Astrophys. J. 1999, 519, 590–598. [Google Scholar] [CrossRef]
- Tiret, O.; Combes, F. Evolution of spiral galaxies in modified gravity. Astronom. Astrophys. 2007, 464, 517–528. [Google Scholar] [CrossRef]
- Tiret, O.; Combes, F. Evolution of spiral galaxies in modified gravity. II. Gas dynamics. Astronom. Astrophys. 2008, 483, 719–726. [Google Scholar] [CrossRef]
- Nelson, D.; Springel, V.; Pillepich, A.; Rodriguez-Gomez, V.; Torrey, P.; Genel, S.; Vogelsberger, M.; Pakmor, R.; Marinacci, F.; Weinberger, R.; et al. The IllustrisTNG simulations: Public data release. Comput. Astrophys. Cosmol. 2019, 6, 2. [Google Scholar] [CrossRef]
- Crain, R.A.; Schaye, J.; Bower, R.G.; Furlong, M.; Schaller, M.; Theuns, T.; Dalla Vecchia, C.; Frenk, C.S.; McCarthy, I.G.; Helly, J.C.; et al. The EAGLE simulations of galaxy formation: Calibration of subgrid physics and model variations. Mont. Notices R. Astronom. Soc. 2015, 450, 1937–1961. [Google Scholar] [CrossRef]
- Schaye, J.; Crain, R.A.; Bower, R.G.; Furlong, M.; Schaller, M.; Theuns, T.; Dalla Vecchia, C.; Frenk, C.S.; McCarthy, I.G.; Helly, J.C.; et al. The EAGLE project: Simulating the evolution and assembly of galaxies and their environments. Mont. Notices R. Astronom. Soc. 2015, 446, 521–554. [Google Scholar] [CrossRef]
- Oh, S.; Oh, K.; Yi, S.K. Bar Effects on Central Star Formation and Active Galactic Nucleus Activity. ApJS 2012, 198, 4. [Google Scholar] [CrossRef]
- Roshan, M.; Ghafourian, N.; Kashfi, T.; Banik, I.; Haslbauer, M.; Cuomo, V.; Famaey, B.; Kroupa, P. Fast galaxy bars continue to challenge standard cosmology. Mont. Notices R. Astronom. Soc. 2021, 508, 926–939. [Google Scholar] [CrossRef]
- Zhao, D.; Du, M.; Ho, L.C.; Debattista, V.P.; Shi, J. Barred Galaxies in the IllustrisTNG Simulation. Astrophys. J. 2020, 904, 170. [Google Scholar] [CrossRef]
- Dubois, Y.; Beckmann, R.; Bournaud, F.; Choi, H.; Devriendt, J.; Jackson, R.; Kaviraj, S.; Kimm, T.; Kraljic, K.; Laigle, C.; et al. Introducing the NEWHORIZON simulation: Galaxy properties with resolved internal dynamics across cosmic time. Astronom. Astrophys. 2021, 651, A109. [Google Scholar] [CrossRef]
- Reddish, J.; Kraljic, K.; Petersen, M.S.; Tep, K.; Dubois, Y.; Pichon, C.; Peirani, S.; Bournaud, F.; Choi, H.; Devriendt, J.; et al. The NewHorizon simulation—To bar or not to bar. Mont. Notices R. Astronom. Soc. 2022, 512, 160–185. [Google Scholar] [CrossRef]
- Marasco, A.; Posti, L.; Oman, K.; Famaey, B.; Cresci, G.; Fraternali, F. Massive disc galaxies too dominated by dark matter in cosmological hydrodynamical simulations. Astronom. Astrophys. 2020, 640, A70. [Google Scholar] [CrossRef]
- Elmegreen, B. Pattern Speeds in Barred Galaxies. In Barred Galaxies; Buta, R., Crocker, D.A., Elmegreen, B.G., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 1996; Volume 91, p. 197. [Google Scholar]
- Contopoulos, G.; Papayannopoulos, T. Orbits in weak and strong bars. Astronom. Astrophys. 1980, 92, 33–46. [Google Scholar]
- Contopoulos, G. The effects of resonances near corotation in barred galaxies. Astronom. Astrophys. 1981, 102, 265–278. [Google Scholar]
- Contopoulos, G.; Grosbol, P. Orbits in barred galaxies. A&ARv 1989, 1, 261–289. [Google Scholar] [CrossRef]
- Sellwood, J.A. Galaxy models with live halos. Astronom. Astrophys. 1980, 89, 296–307. [Google Scholar]
- Weinberg, M.D. Evolution of barred galaxies by dynamical friction. Mont. Notices R. Astronom. Soc. 1985, 213, 451–471. [Google Scholar] [CrossRef]
- Debattista, V.P.; Sellwood, J.A. Dynamical Friction and the Distribution of Dark Matter in Barred Galaxies. Astrophys. J. 1998, 493, L5–L8. [Google Scholar] [CrossRef]
- Debattista, V.P.; Sellwood, J.A. Constraints from Dynamical Friction on the Dark Matter Content of Barred Galaxies. Astrophys. J. 2000, 543, 704–721. [Google Scholar] [CrossRef]
- Holley-Bockelmann, K.; Weinberg, M.; Katz, N. Bar-induced evolution of dark matter cusps. Mont. Notices R. Astronom. Soc. 2005, 363, 991–1007. [Google Scholar] [CrossRef]
- Athanassoula, E.; Machado, R.E.G.; Rodionov, S.A. Bar formation and evolution in disc galaxies with gas and a triaxial halo: Morphology, bar strength and halo properties. Mont. Notices R. Astronom. Soc. 2013, 429, 1949–1969. [Google Scholar] [CrossRef]
- Algorry, D.G.; Navarro, J.F.; Abadi, M.G.; Sales, L.V.; Bower, R.G.; Crain, R.A.; Dalla Vecchia, C.; Frenk, C.S.; Schaller, M.; Schaye, J.; et al. Barred galaxies in the EAGLE cosmological hydrodynamical simulation. Mont. Notices R. Astronom. Soc. 2017, 469, 1054–1064. [Google Scholar] [CrossRef]
- Cuomo, V.; Aguerri, J.A.L.; Corsini, E.M.; Debattista, V.P. Relations among structural parameters in barred galaxies with a direct measurement of bar pattern speed. Astronom. Astrophys. 2020, 641, A111. [Google Scholar] [CrossRef]
- Tremaine, S.; Weinberg, M.D. A kinematic method for measuring the pattern speed of barred galaxies. ApJL 1984, 282, L5–L7. [Google Scholar] [CrossRef]
- Aguerri, J.A.L.; Méndez-Abreu, J.; Corsini, E.M. The population of barred galaxies in the local universe. I. Detection and characterisation of bars. Astronom. Astrophys. 2009, 495, 491–504. [Google Scholar] [CrossRef]
- Aguerri, J.A.L.; Muñoz-Tuñón, C.; Varela, A.M.; Prieto, M. Characterizing bar structures: Application to NGC 1300, NGC 7479 and NGC 7723. Astronom. Astrophys. 2000, 361, 841–849. [Google Scholar]
- Kim, T.; Athanassoula, E.; Sheth, K.; Bosma, A.; Park, M.G.; Lee, Y.H.; Ann, H.B. Cosmic Evolution of Barred Galaxies up to z∼0.84. Astrophys. J. 2021, 922, 196. [Google Scholar] [CrossRef]
- Lee, Y.H.; Park, M.G.; Hwang, H.S.; Ann, H.B.; Chung, H.; Kim, T. Properties of Fast and Slow Bars Classified by Epicyclic Frequency Curves from Photometry of Barred Galaxies. Astrophys. J. 2022, 926, 58. [Google Scholar] [CrossRef]
- Fragkoudi, F.; Grand, R.J.J.; Pakmor, R.; Springel, V.; White, S.D.M.; Marinacci, F.; Gomez, F.A.; Navarro, J.F. Revisiting the tension between fast bars and the ΛCDM paradigm. Astronom. Astrophys. 2021, 650, L16. [Google Scholar] [CrossRef]
- Cuomo, V.; Hee Lee, Y.; Buttitta, C.; Aguerri, J.A.L.; Maria Corsini, E.; Morelli, L. Bar pattern speeds in CALIFA galaxies. III. Solving the puzzle of ultrafast bars. Astronom. Astrophys. 2021, 649, A30. [Google Scholar] [CrossRef]
- Hilmi, T.; Minchev, I.; Buck, T.; Martig, M.; Quillen, A.C.; Monari, G.; Famaey, B.; de Jong, R.S.; Laporte, C.F.P.; Read, J.; et al. Fluctuations in galactic bar parameters due to bar-spiral interaction. Mont. Notices R. Astronom. Soc. 2020, 497, 933–955. [Google Scholar] [CrossRef]
- Zana, T.; Dotti, M.; Capelo, P.R.; Bonoli, S.; Haardt, F.; Mayer, L.; Spinoso, D. External versus internal triggers of bar formation in cosmological zoom-in simulations. Mont. Notices R. Astronom. Soc. 2018, 473, 2608–2621. [Google Scholar] [CrossRef]
- Zana, T.; Capelo, P.R.; Dotti, M.; Mayer, L.; Lupi, A.; Haardt, F.; Bonoli, S.; Shen, S. Barred galaxies in cosmological zoom-in simulations: The importance of feedback. Mont. Notices R. Astronom. Soc. 2019, 488, 1864–1877. [Google Scholar] [CrossRef]
- Lee, J.W. Brief History of Ultra-light Scalar Dark Matter Models. Eur. Phys. J. Web Conf. 2018, 168, 06005. [Google Scholar] [CrossRef]
- Rogers, K.K.; Peiris, H.V. Strong Bound on Canonical Ultralight Axion Dark Matter from the Lyman-Alpha Forest. Phys. Rev. Lett. 2021, 126, 071302. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.S. Roche lobe sizes in deep-MOND gravity. Astronom. Astrophys. 2005, 444, L25–L28. [Google Scholar] [CrossRef]
- Zhao, H.; Tian, L. Roche lobe shapes for testing MOND-like modified gravities. Astronom. Astrophys. 2006, 450, 1005–1012. [Google Scholar] [CrossRef]
- Jordán, A.; Blakeslee, J.P.; Côté, P.; Ferrarese, L.; Infante, L.; Mei, S.; Merritt, D.; Peng, E.W.; Tonry, J.L.; West, M.J. The ACS Fornax Cluster Survey. I. Introduction to the Survey and Data Reduction Procedures. ApJS 2007, 169, 213–224. [Google Scholar] [CrossRef]
- Venhola, A.; Peletier, R.; Laurikainen, E.; Salo, H.; Iodice, E.; Mieske, S.; Hilker, M.; Wittmann, C.; Lisker, T.; Paolillo, M.; et al. The Fornax Deep Survey with the VST. IV. A size and magnitude limited catalog of dwarf galaxies in the area of the Fornax cluster. Astronom. Astrophys. 2018, 620, A165. [Google Scholar] [CrossRef]
- Venhola, A.; Peletier, R.F.; Salo, H.; Laurikainen, E.; Janz, J.; Haigh, C.; Wilkinson, M.H.F.; Iodice, E.; Hilker, M.; Mieske, S.; et al. The Fornax Deep Survey (FDS) with VST XII: Low surface brightness dwarf galaxies in the Fornax cluster. Astronom. Astrophys. 2022, 662, A43. [Google Scholar] [CrossRef]
- Chilingarian, I.V.; Afanasiev, A.V.; Grishin, K.A.; Fabricant, D.; Moran, S. Internal Dynamics and Stellar Content of Nine Ultra-diffuse Galaxies in the Coma Cluster Prove Their Evolutionary Link with Dwarf Early-type Galaxies. Astrophys. J. 2019, 884, 79. [Google Scholar] [CrossRef]
- Freundlich, J.; Famaey, B.; Oria, P.A.; Bílek, M.; Müller, O.; Ibata, R. Probing the radial acceleration relation and the strong equivalence principle with the Coma cluster ultra-diffuse galaxies. Astronom. Astrophys. 2022, 658, A26. [Google Scholar] [CrossRef]
- Samurović, S. Globular clusters kinematics and dynamical models of the massive early-type galaxy NGC 1399. Ap&SS 2016, 361, 199. [Google Scholar] [CrossRef]
- Fattahi, A.; Navarro, J.F.; Frenk, C.S.; Oman, K.A.; Sawala, T.; Schaller, M. Tidal stripping and the structure of dwarf galaxies in the Local Group. Mont. Notices R. Astronom. Soc. 2018, 476, 3816–3836. [Google Scholar] [CrossRef]
- Fardal, M.A.; Weinberg, M.D.; Babul, A.; Irwin, M.J.; Guhathakurta, P.; Gilbert, K.M.; Ferguson, A.M.N.; Ibata, R.A.; Lewis, G.F.; Tanvir, N.R.; et al. Inferring the Andromeda Galaxy’s mass from its giant southern stream with Bayesian simulation sampling. Mont. Notices R. Astronom. Soc. 2013, 434, 2779–2802. [Google Scholar] [CrossRef]
- Ibata, R.; Lewis, G.F.; Irwin, M.; Totten, E.; Quinn, T. Great Circle Tidal Streams: Evidence for a Nearly Spherical Massive Dark Halo around the Milky Way. Astrophys. J. 2001, 551, 294–311. [Google Scholar] [CrossRef]
- Fellhauer, M.; Belokurov, V.; Evans, N.W.; Wilkinson, M.I.; Zucker, D.B.; Gilmore, G.; Irwin, M.J.; Bramich, D.M.; Vidrih, S.; Wyse, R.F.G.; et al. The Origin of the Bifurcation in the Sagittarius Stream. Astrophys. J. 2006, 651, 167–173. [Google Scholar] [CrossRef]
- Read, J.I.; Moore, B. Tidal streams in a MOND potential: Constraints from Sagittarius. Mont. Notices R. Astronom. Soc. 2005, 361, 971–976. [Google Scholar] [CrossRef][Green Version]
- Law, D.R.; Majewski, S.R. The Sagittarius Dwarf Galaxy: A Model for Evolution in a Triaxial Milky Way Halo. Astrophys. J. 2010, 714, 229–254. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Belokurov, V.; Evans, N.W.; Martínez-Delgado, D.; Gilmore, G.; Irwin, M.; Niederste-Ostholt, M.; Zucker, D.B. Was the progenitor of the Sagittarius stream a disc galaxy? Mont. Notices R. Astronom. Soc. 2010, 408, L26–L30. [Google Scholar] [CrossRef]
- Del Pino, A.; Fardal, M.A.; van der Marel, R.P.; Łokas, E.L.; Mateu, C.; Sohn, S.T. Revealing the Structure and Internal Rotation of the Sagittarius Dwarf Spheroidal Galaxy with Gaia and Machine Learning. Astrophys. J. 2021, 908, 244. [Google Scholar] [CrossRef]
- Debattista, V.P.; Roškar, R.; Valluri, M.; Quinn, T.; Moore, B.; Wadsley, J. What’s up in the Milky Way? The orientation of the disc relative to the triaxial halo. Mont. Notices R. Astronom. Soc. 2013, 434, 2971–2981. [Google Scholar] [CrossRef]
- Pearson, S.; Küpper, A.H.W.; Johnston, K.V.; Price-Whelan, A.M. Tidal Stream Morphology as an Indicator of Dark Matter Halo Geometry: The Case of Palomar 5. Astrophys. J. 2015, 799, 28. [Google Scholar] [CrossRef]
- Vasiliev, E.; Belokurov, V.; Erkal, D. Tango for three: Sagittarius, LMC, and the Milky Way. Mont. Notices R. Astronom. Soc. 2021, 501, 2279–2304. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Ma, Y.Z.; Walker, M.G.; McConnachie, A. A dynamical model of the local cosmic expansion. Mont. Notices R. Astronom. Soc. 2014, 443, 2204–2222. [Google Scholar] [CrossRef]
- Peñarrubia, J.; Gómez, F.A.; Besla, G.; Erkal, D.; Ma, Y.Z. A timing constraint on the (total) mass of the Large Magellanic Cloud. Mont. Notices R. Astronom. Soc. 2016, 456, L54–L58. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. Dynamical History Of The Local Group In ΛCDM II—Including External Perturbers In 3D. Mont. Notices R. Astronom. Soc. 2017, 467, 2180–2198. [Google Scholar] [CrossRef][Green Version]
- Banik, I.; Zhao, H. A plane of high-velocity galaxies across the Local Group. Mont. Notices R. Astronom. Soc. 2018, 473, 4033–4054. [Google Scholar] [CrossRef]
- Banik, I.; Haslbauer, M.; Pawlowski, M.S.; Famaey, B.; Kroupa, P. On the absence of backsplash analogues to NGC 3109 in the ΛCDM framework. Mont. Notices R. Astronom. Soc. 2021, 503, 6170–6186. [Google Scholar] [CrossRef]
- Thomas, G.F.; Famaey, B.; Ibata, R.; Lüghausen, F.; Kroupa, P. Stellar streams as gravitational experiments. I. The case of Sagittarius. Astronom. Astrophys. 2017, 603, A65. [Google Scholar] [CrossRef]
- Dabringhausen, J.; Kroupa, P. Dwarf elliptical galaxies as ancient tidal dwarf galaxies. Mont. Notices R. Astronom. Soc. 2013, 429, 1858–1871. [Google Scholar] [CrossRef]
- Dierickx, M.I.P.; Loeb, A. An Upper Limit on the Milky Way Mass from the Orbit of the Sagittarius Dwarf Satellite. Astrophys. J. 2017, 847, 42. [Google Scholar] [CrossRef]
- Bonaca, A.; Pearson, S.; Price-Whelan, A.M.; Dey, A.; Geha, M.; Kallivayalil, N.; Moustakas, J.; Muñoz, R.; Myers, A.D.; Schlegel, D.J.; et al. Variations in the Width, Density, and Direction of the Palomar 5 Tidal Tails. Astrophys. J. 2020, 889, 70. [Google Scholar] [CrossRef]
- Banik, N.; Bovy, J. Effects of baryonic and dark matter substructure on the Pal 5 stream. Mont. Notices R. Astronom. Soc. 2019, 484, 2009–2020. [Google Scholar] [CrossRef]
- Bertola, F.; Galletta, G. A new type of galaxy with prolate structure. ApJL 1978, 226, L115–L118. [Google Scholar] [CrossRef]
- Combes, F. Polar Rings and the 3-Dimensional Shape of Dark Matter. In Multi-Spin Galaxies; Iodice, E., Corsini, E.M., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2014; Volume 486, p. 207. [Google Scholar]
- Lüghausen, F.; Famaey, B.; Kroupa, P. Polar Ring Galaxies Favor Milgromian Dynamics over Standard Dark-Matter-Based Models. In Multi-Spin Galaxies; Iodice, E., Corsini, E.M., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2014; Volume 486, p. 225. [Google Scholar]
- Schweizer, F. An optical study of the giant radio galaxy NGC 1316 (Fornax A). Astrophys. J. 1980, 237, 303–318. [Google Scholar] [CrossRef]
- Quinn, P.J. On the formation and dynamics of shells around elliptical galaxies. Astrophys. J. 1984, 279, 596–609. [Google Scholar] [CrossRef]
- Hernquist, L.; Quinn, P.J. Shells and Dark Matter in Elliptical Galaxies. Astrophys. J. 1987, 312, 1. [Google Scholar] [CrossRef]
- Milgrom, M. What Shells around NGC 3923 Tell Us about the Modified Dynamics. Astrophys. J. 1988, 332, 86. [Google Scholar] [CrossRef]
- Bílek, M.; Jungwiert, B.; Jílková, L.; Ebrová, I.; Bartošková, K.; Křížek, M. Testing MOND gravity in the shell galaxy NGC 3923. Astronom. Astrophys. 2013, 559, A110. [Google Scholar] [CrossRef]
- Bílek, M.; Ebrová, I.; Jungwiert, B.; Jílková, L.; Bartošková, K. Shell galaxies as laboratories for testing MOND. Can. J. Phys. 2015, 93, 203–212. [Google Scholar] [CrossRef]
- Vakili, H.; Kroupa, P.; Rahvar, S. Type I Shell Galaxies as a Test of Gravity Models. Astrophys. J. 2017, 848, 55. [Google Scholar] [CrossRef]
- Bílek, M.; Cuillandre, J.C.; Gwyn, S.; Ebrová, I.; Bartošková, K.; Jungwiert, B.; Jílková, L. Deep imaging of the shell elliptical galaxy NGC 3923 with MegaCam. Astronom. Astrophys. 2016, 588, A77. [Google Scholar] [CrossRef]
- Bílek, M.; Jungwiert, B.; Ebrová, I.; Bartošková, K. MOND implications for spectral line profiles of shell galaxies: Shell formation history and mass-velocity scaling relations. Astronom. Astrophys. 2015, 575, A29. [Google Scholar] [CrossRef]
- Bílek, M.; Fensch, J.; Ebrová, I.; Nagesh, S.T.; Famaey, B.; Duc, P.A.; Kroupa, P. Origin of the spectacular tidal shells of galaxy NGC 474. Astronom. Astrophys. 2022, 660, A28. [Google Scholar] [CrossRef]
- Toomre, A.; Toomre, J. Galactic Bridges and Tails. Astrophys. J. 1972, 178, 623–666. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Dottori, H.; Lutz, D. Genesis of a dwarf galaxy from the debris of the Antennae. Astronom. Astrophys. 1992, 256, L19–L22. [Google Scholar]
- Bournaud, F.; Duc, P.A.; Amram, P.; Combes, F.; Gach, J.L. Kinematics of tidal tails in interacting galaxies: Tidal dwarf galaxies and projection effects. Astronom. Astrophys. 2004, 425, 813–823. [Google Scholar] [CrossRef]
- Lelli, F.; Duc, P.A.; Brinks, E.; McGaugh, S. Tidal Dwarf Galaxies: Disc Formation at (z≃0). Galaxies 2015, 3, 184–191. [Google Scholar] [CrossRef]
- Okazaki, T.; Taniguchi, Y. Dwarf Galaxy Formation Induced by Galaxy Interactions. Astrophys. J. 2000, 543, 149–152. [Google Scholar] [CrossRef]
- Kaviraj, S.; Darg, D.; Lintott, C.; Schawinski, K.; Silk, J. Tidal dwarf galaxies in the nearby Universe. Mont. Notices R. Astronom. Soc. 2012, 419, 70–79. [Google Scholar] [CrossRef]
- Duc, P.A.; Paudel, S.; McDermid, R.M.; Cuillandre, J.C.; Serra, P.; Bournaud, F.; Cappellari, M.; Emsellem, E. Identification of old tidal dwarfs near early-type galaxies from deep imaging and H I observations. Mont. Notices R. Astronom. Soc. 2014, 440, 1458–1469. [Google Scholar] [CrossRef]
- López-Corredoira, M.; Kroupa, P. The Number of Tidal Dwarf Satellite Galaxies in Dependence of Bulge Index. Astrophys. J. 2016, 817, 75. [Google Scholar] [CrossRef]
- Javanmardi, B.; Raouf, M.; Khosroshahi, H.G.; Tavasoli, S.; Müller, O.; Molaeinezhad, A. The Number of Dwarf Satellites of Disk Galaxies versus their Bulge Mass in the Standard Model of Cosmology. Astrophys. J. 2019, 870, 50. [Google Scholar] [CrossRef]
- Smercina, A.; Bell, E.F.; Samuel, J.; D’Souza, R. Relating the Diverse Merger Histories and Satellite Populations of Nearby Galaxies. Astrophys. J. 2022, 930, 69. [Google Scholar] [CrossRef]
- Recchi, S.; Kroupa, P.; Ploeckinger, S. The mass-metallicity relation of tidal dwarf galaxies. Mont. Notices R. Astronom. Soc. 2015, 450, 2367–2372. [Google Scholar] [CrossRef]
- Haslbauer, M.; Dabringhausen, J.; Kroupa, P.; Javanmardi, B.; Banik, I. Galaxies lacking dark matter in the Illustris simulation. Astronom. Astrophys. 2019, 626, A47. [Google Scholar] [CrossRef]
- Barnes, J.E.; Hernquist, L. Formation of dwarf galaxies in tidal tails. Nature 1992, 360, 715–717. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Kaufman, M.; Thomasson, M. An Interaction Model for the Formation of Dwarf Galaxies and 10 8 Msun Clouds in Spiral Disks. Astrophys. J. 1993, 412, 90. [Google Scholar] [CrossRef]
- Wetzstein, M.; Naab, T.; Burkert, A. Do dwarf galaxies form in tidal tails? Mont. Notices R. Astronom. Soc. 2007, 375, 805–820. [Google Scholar] [CrossRef]
- Ploeckinger, S.; Recchi, S.; Hensler, G.; Kroupa, P. Chemodynamical evolution of tidal dwarf galaxies—II. The long-term evolution and influence of a tidal field. Mont. Notices R. Astronom. Soc. 2015, 447, 2512–2525. [Google Scholar] [CrossRef]
- Renaud, F.; Famaey, B.; Kroupa, P. Star formation triggered by galaxy interactions in modified gravity. Mont. Notices R. Astronom. Soc. 2016, 463, 3637–3652. [Google Scholar] [CrossRef]
- Kroupa, P. Dwarf spheroidal satellite galaxies without dark matter. New Astron. 1997, 2, 139–164. [Google Scholar] [CrossRef]
- Klessen, R.S.; Kroupa, P. Dwarf Spheroidal Satellite Galaxies without Dark Matter: Results from Two Different Numerical Techniques. Astrophys. J. 1998, 498, 143–155. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P.; de Boer, K.S. Making counter-orbiting tidal debris. The origin of the Milky Way disc of satellites? Astronom. Astrophys. 2011, 532, A118. [Google Scholar] [CrossRef]
- McConnachie, A.W. The Observed Properties of Dwarf Galaxies in and around the Local Group. Astronom. J. 2012, 144, 4. [Google Scholar] [CrossRef]
- Lynden-Bell, D. Dwarf galaxies and globular clusters in high velocity hydrogen streams. Mont. Notices R. Astronom. Soc. 1976, 174, 695–710. [Google Scholar] [CrossRef]
- Lynden-Bell, D. The Fornax-Leo-Sculptor system. Observatory 1982, 102, 202–208. [Google Scholar]
- Kroupa, P.; Theis, C.; Boily, C.M. The great disk of Milky-Way satellites and cosmological sub-structures. Astronom. Astrophys. 2005, 431, 517–521. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Pflamm-Altenburg, J.; Kroupa, P. The VPOS: A vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mont. Notices R. Astronom. Soc. 2012, 423, 1109–1126. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P. The rotationally stabilized VPOS and predicted proper motions of the Milky Way satellite galaxies. Mont. Notices R. Astronom. Soc. 2013, 435, 2116–2131. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P. The Milky Way’s disc of classical satellite galaxies in light of Gaia DR2. Mont. Notices R. Astronom. Soc. 2020, 491, 3042–3059. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.; Domínguez-Tenreiro, R.; Pawlowski, M.S. An updated detailed characterization of planes of satellites in the MW and M31. Mont. Notices R. Astronom. Soc. 2020, 499, 3755–3774. [Google Scholar] [CrossRef]
- Cautun, M.; Frenk, C.S. The tangential velocity excess of the Milky Way satellites. Mont. Notices R. Astronom. Soc. 2017, 468, L41–L45. [Google Scholar] [CrossRef]
- Riley, A.H.; Fattahi, A.; Pace, A.B.; Strigari, L.E.; Frenk, C.S.; Gómez, F.A.; Grand, R.J.J.; Marinacci, F.; Navarro, J.F.; Pakmor, R.; et al. The velocity anisotropy of the Milky Way satellite system. Mont. Notices R. Astronom. Soc. 2019, 486, 2679–2694. [Google Scholar] [CrossRef]
- Hammer, F.; Wang, J.; Pawlowski, M.S.; Yang, Y.; Bonifacio, P.; Li, H.; Babusiaux, C.; Arenou, F. Gaia EDR3 Proper Motions of Milky Way Dwarfs. II Velocities, Total Energy, and Angular Momentum. Astrophys. J. 2021, 922, 93. [Google Scholar] [CrossRef]
- Libeskind, N.I.; Frenk, C.S.; Cole, S.; Jenkins, A.; Helly, J.C. How common is the Milky Way-satellite system alignment? Mont. Notices R. Astronom. Soc. 2009, 399, 550–558. [Google Scholar] [CrossRef]
- Deason, A.J.; McCarthy, I.G.; Font, A.S.; Evans, N.W.; Frenk, C.S.; Belokurov, V.; Libeskind, N.I.; Crain, R.A.; Theuns, T. Mismatch and misalignment: Dark haloes and satellites of disc galaxies. Mont. Notices R. Astronom. Soc. 2011, 415, 2607–2625. [Google Scholar] [CrossRef]
- McConnachie, A.W.; Irwin, M.J.; Ibata, R.A.; Dubinski, J.; Widrow, L.M.; Martin, N.F.; Côté, P.; Dotter, A.L.; Navarro, J.F.; Ferguson, A.M.N.; et al. The remnants of galaxy formation from a panoramic survey of the region around M31. Nature 2009, 461, 66–69. [Google Scholar] [CrossRef]
- McConnachie, A.W.; Ibata, R.; Martin, N.; Ferguson, A.M.N.; Collins, M.; Gwyn, S.; Irwin, M.; Lewis, G.F.; Mackey, A.D.; Davidge, T.; et al. The Large-scale Structure of the Halo of the Andromeda Galaxy. II. Hierarchical Structure in the Pan-Andromeda Archaeological Survey. Astrophys. J. 2018, 868, 55. [Google Scholar] [CrossRef]
- Ibata, R.A.; Lewis, G.F.; Conn, A.R.; Irwin, M.J.; McConnachie, A.W.; Chapman, S.C.; Collins, M.L.; Fardal, M.; Ferguson, A.M.N.; Ibata, N.G.; et al. A vast, thin plane of corotating dwarf galaxies orbiting the Andromeda galaxy. Nature 2013, 493, 62–65. [Google Scholar] [CrossRef]
- Metz, M.; Kroupa, P.; Jerjen, H. The spatial distribution of the Milky Way and Andromeda satellite galaxies. Mont. Notices R. Astronom. Soc. 2007, 374, 1125–1145. [Google Scholar] [CrossRef]
- Sohn, S.T.; Patel, E.; Fardal, M.A.; Besla, G.; van der Marel, R.P.; Geha, M.; Guhathakurta, P. HST Proper Motions of NGC 147 and NGC 185: Orbital Histories and Test of Dynamically Coherent Andromeda Satellite Plane. Astrophys. J. 2020, 901, 43. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Tony Sohn, S. On the Co-orbitation of Satellite Galaxies along the Great Plane of Andromeda: NGC 147, NGC 185, and Expectations from Cosmological Simulations. Astrophys. J. 2021, 923, 42. [Google Scholar] [CrossRef]
- Pawlowski, M.S. The Planes of Satellite Galaxies Problem, Suggested Solutions, and Open Questions. Mod. Phys. Lett. A 2018, 33, 1830004. [Google Scholar] [CrossRef]
- Pawlowski, M.S. Phase-Space Correlations among Systems of Satellite Galaxies. Galaxies 2021, 9, 66. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Famaey, B.; Jerjen, H.; Merritt, D.; Kroupa, P.; Dabringhausen, J.; Lüghausen, F.; Forbes, D.A.; Hensler, G.; Hammer, F.; et al. Co-orbiting satellite galaxy structures are still in conflict with the distribution of primordial dwarf galaxies. Mont. Notices R. Astronom. Soc. 2014, 442, 2362–2380. [Google Scholar] [CrossRef]
- Ibata, R.A.; Ibata, N.G.; Lewis, G.F.; Martin, N.F.; Conn, A.; Elahi, P.; Arias, V.; Fernando, N. A Thousand Shadows of Andromeda: Rotating Planes of Satellites in the Millennium-II Cosmological Simulation. ApJL 2014, 784, L6. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; McGaugh, S.S. Co-orbiting Planes of Sub-halos are Similarly Unlikely around Paired and Isolated Hosts. ApJL 2014, 789, L24. [Google Scholar] [CrossRef][Green Version]
- Ahmed, S.H.; Brooks, A.M.; Christensen, C.R. The role of baryons in creating statistically significant planes of satellites around Milky Way-mass galaxies. Mont. Notices R. Astronom. Soc. 2017, 466, 3119–3132. [Google Scholar] [CrossRef]
- Shao, S.; Cautun, M.; Frenk, C.S. Evolution of galactic planes of satellites in the EAGLE simulation. Mont. Notices R. Astronom. Soc. 2019, 488, 1166–1179. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Bullock, J.S.; Kelley, T.; Famaey, B. Do Halos that Form Early, Have High Concentration, Are Part of a Pair, or Contain a Central Galaxy Potential Host More Pronounced Planes of Satellite Galaxies? Astrophys. J. 2019, 875, 105. [Google Scholar] [CrossRef]
- Metz, M.; Kroupa, P.; Jerjen, H. Discs of satellites: The new dwarf spheroidals. Mont. Notices R. Astronom. Soc. 2009, 394, 2223–2228. [Google Scholar] [CrossRef]
- Shao, S.; Cautun, M.; Frenk, C.S.; Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Simpson, C.M. The multiplicity and anisotropy of galactic satellite accretion. Mont. Notices R. Astronom. Soc. 2018, 476, 1796–1810. [Google Scholar] [CrossRef]
- Samuel, J.; Wetzel, A.; Chapman, S.; Tollerud, E.; Hopkins, P.F.; Boylan-Kolchin, M.; Bailin, J.; Faucher-Giguère, C.A. Planes of satellites around Milky Way/M31-mass galaxies in the FIRE simulations and comparisons with the Local Group. Mont. Notices R. Astronom. Soc. 2021, 504, 1379–1397. [Google Scholar] [CrossRef]
- Nichols, M.; Colless, J.; Colless, M.; Bland-Hawthorn, J. Accretion of the Magellanic System onto the Galaxy. Astrophys. J. 2011, 742, 110. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.E.; Fattahi, A.; Sales, L.V.; Navarro, J.F. Magellanic satellites in ΛCDM cosmological hydrodynamical simulations of the Local Group. Mont. Notices R. Astronom. Soc. 2021, 504, 4551–4567. [Google Scholar] [CrossRef]
- Garavito-Camargo, N.; Patel, E.; Besla, G.; Price-Whelan, A.M.; Gómez, F.A.; Laporte, C.F.P.; Johnston, K.V. The Clustering of Orbital Poles Induced by the LMC: Hints for the Origin of Planes of Satellites. Astrophys. J. 2021, 923, 140. [Google Scholar] [CrossRef]
- Correa Magnus, L.; Vasiliev, E. Measuring the Milky Way mass distribution in the presence of the LMC. Mont. Notices R. Astronom. Soc. 2022, 511, 2610–2630. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Oria, P.A.; Taibi, S.; Famaey, B.; Ibata, R. On the Effect of the Large Magellanic Cloud on the Orbital Poles of Milky Way Satellite Galaxies. Astrophys. J. 2022, 932, 70. [Google Scholar] [CrossRef]
- Pawlowski, M.S. It’s time for some plane speaking. Nat. Astron. 2021, 5, 1185–1187. [Google Scholar] [CrossRef]
- Van der Marel, R.P.; Fardal, M.; Besla, G.; Beaton, R.L.; Sohn, S.T.; Anderson, J.; Brown, T.; Guhathakurta, P. The M31 Velocity Vector. II. Radial Orbit toward the Milky Way and Implied Local Group Mass. Astrophys. J. 2012, 753, 8. [Google Scholar] [CrossRef]
- Salomon, J.B.; Ibata, R.; Reylé, C.; Famaey, B.; Libeskind, N.I.; McConnachie, A.W.; Hoffman, Y. The proper motion of Andromeda from Gaia EDR3: Confirming a nearly radial orbit. Mont. Notices R. Astronom. Soc. 2021, 507, 2592–2601. [Google Scholar] [CrossRef]
- Zhao, H.; Famaey, B.; Lüghausen, F.; Kroupa, P. Local Group timing in Milgromian dynamics. A past Milky Way-Andromeda encounter at z > 0.8. Astronom. Astrophys. 2013, 557, L3. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. The Local Group as a test system for Modified Newtonian Dynamics. Phys. Dark Universe 2020, 30, 100708. [Google Scholar] [CrossRef]
- McLeod, M.; Lahav, O. The two body problem in the presence of dark energy and modified gravity: Application to the Local Group. J. Cosmol. Astropart. Phys. 2020, 2020, 056. [Google Scholar] [CrossRef]
- Bílek, M.; Thies, I.; Kroupa, P.; Famaey, B. MOND simulation suggests the origin of some peculiarities in the Local Group. Astronom. Astrophys. 2018, 614, A59. [Google Scholar] [CrossRef]
- Banik, I.; Thies, I.; Truelove, R.; Candlish, G.; Famaey, B.; Pawlowski, M.S.; Ibata, R.; Kroupa, P. 3D hydrodynamic simulations for the formation of the local group satellite planes. Mont. Notices R. Astronom. Soc. 2022, 513, 129–158. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P.; Jerjen, H. Dwarf galaxy planes: The discovery of symmetric structures in the Local Group. Mont. Notices R. Astronom. Soc. 2013, 435, 1928–1957. [Google Scholar] [CrossRef]
- Ballero, S.K.; Matteucci, F.; Origlia, L.; Rich, R.M. Formation and evolution of the Galactic bulge: Constraints from stellar abundances. Astronom. Astrophys. 2007, 467, 123–136. [Google Scholar] [CrossRef]
- Kilic, M.; Munn, J.A.; Harris, H.C.; von Hippel, T.; Liebert, J.W.; Williams, K.A.; Jeffery, E.; DeGennaro, S. The Ages of the Thin Disk, Thick Disk, and the Halo from Nearby White Dwarfs. Astrophys. J. 2017, 837, 162. [Google Scholar] [CrossRef]
- Grady, J.; Belokurov, V.; Evans, N.W. Age demographics of the Milky Way disc and bulge. Mont. Notices R. Astronom. Soc. 2020, 492, 3128–3142. [Google Scholar] [CrossRef]
- Mackey, A.D.; Gilmore, G.F. Comparing the properties of local globular cluster systems: Implications for the formation of the Galactic halo. Mont. Notices R. Astronom. Soc. 2004, 355, 504–534. [Google Scholar] [CrossRef]
- Tully, R.B.; Libeskind, N.I.; Karachentsev, I.D.; Karachentseva, V.E.; Rizzi, L.; Shaya, E.J. Two Planes of Satellites in the Centaurus A Group. ApJL 2015, 802, L25. [Google Scholar] [CrossRef]
- Müller, O.; Jerjen, H.; Pawlowski, M.S.; Binggeli, B. Testing the two planes of satellites in the Centaurus group. Astronom. Astrophys. 2016, 595, A119. [Google Scholar] [CrossRef]
- Müller, O.; Pawlowski, M.S.; Jerjen, H.; Lelli, F. A whirling plane of satellite galaxies around Centaurus A challenges cold dark matter cosmology. Science 2018, 359, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Müller, O.; Pawlowski, M.S.; Lelli, F.; Fahrion, K.; Rejkuba, M.; Hilker, M.; Kanehisa, J.; Libeskind, N.; Jerjen, H. The coherent motion of Cen A dwarf satellite galaxies remains a challenge for ΛCDM cosmology. Astronom. Astrophys. 2021, 645, L5. [Google Scholar] [CrossRef]
- Müller, O.; Rejkuba, M.; Jerjen, H. Distances from the tip of the red giant branch to the dwarf galaxies dw1335-29 and dw1340-30 in the Centaurus group. Astronom. Astrophys. 2018, 615, A96. [Google Scholar] [CrossRef]
- Paudel, S.; Yoon, S.J.; Smith, R. A Corotating Group of Dwarf Galaxies around NGC 2750 as a Centaurus A Analog. ApJL 2021, 917, L18. [Google Scholar] [CrossRef]
- Chiboucas, K.; Jacobs, B.A.; Tully, R.B.; Karachentsev, I.D. Confirmation of Faint Dwarf Galaxies in the M81 Group. Astronom. J. 2013, 146, 126. [Google Scholar] [CrossRef]
- Martínez-Delgado, D.; Makarov, D.; Javanmardi, B.; Pawlowski, M.S.; Makarova, L.; Donatiello, G.; Lang, D.; Román, J.; Vivas, K.; Carballo-Bello, J.A. Tracing satellite planes in the Sculptor group. I. Discovery of three faint dwarf galaxies around NGC 253. Astronom. Astrophys. 2021, 652, A48. [Google Scholar] [CrossRef]
- Mutlu-Pakdil, B.; Sand, D.J.; Crnojević, D.; Jones, M.G.; Caldwell, N.; Guhathakurta, P.; Seth, A.C.; Simon, J.D.; Spekkens, K.; Strader, J.; et al. Hubble Space Telescope Observations of NGC 253 Dwarf Satellites: Three Ultra-faint Dwarf Galaxies. Astrophys. J. 2022, 926, 77. [Google Scholar] [CrossRef]
- Ibata, N.G.; Ibata, R.A.; Famaey, B.; Lewis, G.F. Velocity anti-correlation of diametrically opposed galaxy satellites in the low-redshift Universe. Nature 2014, 511, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Cautun, M.; Wang, W.; Frenk, C.S.; Sawala, T. A new spin on discs of satellite galaxies. Mont. Notices R. Astronom. Soc. 2015, 449, 2576–2587. [Google Scholar] [CrossRef]
- Ibata, R.A.; Famaey, B.; Lewis, G.F.; Ibata, N.G.; Martin, N. Eppur si Muove: Positional and Kinematic Correlations of Satellite Pairs in the Low Z Universe. Astrophys. J. 2015, 805, 67. [Google Scholar] [CrossRef]
- Li, Y.S.; White, S.D.M. Masses for the Local Group and the Milky Way. Mont. Notices R. Astronom. Soc. 2008, 384, 1459–1468. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Lahav, O. Milky Way and Andromeda past-encounters in different gravity models: The impact on the estimated Local Group mass. Astronom. Astrophys. 2021, 656, A129. [Google Scholar] [CrossRef]
- Sandage, A. The redshift-distance relation. IX—Perturbation of the very nearby velocity field by the mass of the Local Group. Astrophys. J. 1986, 307, 1–19. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. Dynamical history of the Local Group in ΛCDM. Mont. Notices R. Astronom. Soc. 2016, 459, 2237–2261. [Google Scholar] [CrossRef]
- Ma, C.; Arias, E.F.; Eubanks, T.M.; Fey, A.L.; Gontier, A.M.; Jacobs, C.S.; Sovers, O.J.; Archinal, B.A.; Charlot, P. The International Celestial Reference Frame as Realized by Very Long Baseline Interferometry. Astronom. J. 1998, 116, 516–546. [Google Scholar] [CrossRef]
- Aragon-Calvo, M.A.; Silk, J.; Szalay, A.S. Locally cold flows from large-scale structure. Mont. Notices R. Astronom. Soc. 2011, 415, L16–L20. [Google Scholar] [CrossRef]
- Shaya, E.J.; Olling, R.P. Very Wide Binaries and Other Comoving Stellar Companions: A Bayesian Analysis of the Hipparcos Catalogue. ApJS 2011, 192, 2. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Dynamics of the Local Group: The Dwarf Galaxies. arXiv 2017, arXiv:1705.10683. [Google Scholar]
- Kashibadze, O.G.; Karachentsev, I.D. Cosmic flow around local massive galaxies. Astronom. Astrophys. 2018, 609, A11. [Google Scholar] [CrossRef]
- Zhai, M.; Guo, Q.; Zhao, G.; Gu, Q.; Liu, A. Local Group Analogs in ΛCDM Cosmological Simulations. Astrophys. J. 2020, 890, 27. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mont. Notices R. Astronom. Soc. 2013, 428, 3121–3138. [Google Scholar] [CrossRef]
- Wang, J.; Hammer, F.; Yang, Y. Milky Way total Mass derived by Rotation Curve and Globular Cluster kinematics from Gaia EDR3. Mont. Notices R. Astronom. Soc. 2022, 510, 2242–2260. [Google Scholar] [CrossRef]
- McGaugh, S.S.; van Dokkum, P. Dark Matter Halo Masses from Abundance Matching and Kinematics: Tensions for the Milky Way and M31. Res. Notes Am. Astron. Soc. 2021, 5, 23. [Google Scholar] [CrossRef]
- Chemin, L.; Carignan, C.; Foster, T. H I Kinematics and Dynamics of Messier 31. Astrophys. J. 2009, 705, 1395–1415. [Google Scholar] [CrossRef]
- Kafle, P.R.; Sharma, S.; Lewis, G.F.; Robotham, A.S.G.; Driver, S.P. The need for speed: Escape velocity and dynamical mass measurements of the Andromeda galaxy. Mont. Notices R. Astronom. Soc. 2018, 475, 4043–4054. [Google Scholar] [CrossRef]
- Bellazzini, M.; Oosterloo, T.; Fraternali, F.; Beccari, G. Dwarfs walking in a row. The filamentary nature of the NGC 3109 association. Astronom. Astrophys. 2013, 559, L11. [Google Scholar] [CrossRef][Green Version]
- Sales, L.V.; Navarro, J.F.; Abadi, M.G.; Steinmetz, M. Cosmic ménage à trois: The origin of satellite galaxies on extreme orbits. Mont. Notices R. Astronom. Soc. 2007, 379, 1475–1483. [Google Scholar] [CrossRef]
- Soszyński, I.; Gieren, W.; Pietrzyński, G.; Bresolin, F.; Kudritzki, R.P.; Storm, J. The Araucaria Project: Distance to the Local Group Galaxy NGC 3109 from Near-Infrared Photometry of Cepheids. Astrophys. J. 2006, 648, 375–382. [Google Scholar] [CrossRef]
- Teyssier, M.; Johnston, K.V.; Kuhlen, M. Identifying Local Group field galaxies that have interacted with the Milky Way. Mont. Notices R. Astronom. Soc. 2012, 426, 1808–1818. [Google Scholar] [CrossRef]
- Li, P.; Lelli, F.; McGaugh, S.; Schombert, J. A Comprehensive Catalog of Dark Matter Halo Models for SPARC Galaxies. ApJS 2020, 247, 31. [Google Scholar] [CrossRef]
- Dalcanton, J.J.; Williams, B.F.; Seth, A.C.; Dolphin, A.; Holtzman, J.; Rosema, K.; Skillman, E.D.; Cole, A.; Girardi, L.; Gogarten, S.M.; et al. The ACS Nearby Galaxy Survey Treasury. ApJS 2009, 183, 67–108. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B. Galaxy Groups Within 3500 km s−1. Astrophys. J. 2017, 843, 16. [Google Scholar] [CrossRef]
- Gerke, J.R.; Kochanek, C.S.; Prieto, J.L.; Stanek, K.Z.; Macri, L.M. A Study of Cepheids in M81 with the Large Binocular Telescope (Efficiently Calibrated with Hubble Space Telescope). Astrophys. J. 2011, 743, 176. [Google Scholar] [CrossRef]
- Yun, M.S. Tidal Interactions in M81 Group. In Galaxy Interactions at Low and High Redshift; Barnes, J.E., Sanders, D.B., Eds.; International Astronomical Union Symposium; Cambridge University Press: Cambridge, UK, 1999; Volume 186, pp. 81–88. [Google Scholar]
- Rieke, G.H.; Lebofsky, M.J.; Thompson, R.I.; Low, F.J.; Tokunaga, A.T. The nature of the nuclear sources in M82 and NGC 253. Astrophys. J. 1980, 238, 24–40. [Google Scholar] [CrossRef]
- Thomson, R.C.; Laine, S.; Turnbull, A. Towards an Interaction Model of M81, M82 and NGC 3077. In Galaxy Interactions at Low and High Redshift; Barnes, J.E., Sanders, D.B., Eds.; International Astronomical Union Symposium; Cambridge University Press: Cambridge, UK, 1999; Volume 186, p. 135. [Google Scholar]
- Oehm, W.; Thies, I.; Kroupa, P. Constraints on the dynamical evolution of the galaxy group M81. Mont. Notices R. Astronom. Soc. 2017, 467, 273–289. [Google Scholar] [CrossRef]
- Hickson, P. Systematic properties of compact groups of galaxies. Astrophys. J. 1982, 255, 382–391. [Google Scholar] [CrossRef]
- Sohn, J.; Hwang, H.S.; Geller, M.J.; Diaferio, A.; Rines, K.J.; Lee, M.G.; Lee, G.H. Compact Groups of Galaxies with Complete Spectroscopic Redshifts in the Local Universe. J. Korean Astron. Soc. 2015, 48, 381–398. [Google Scholar] [CrossRef]
- Sohn, J.; Geller, M.J.; Hwang, H.S.; Zahid, H.J.; Lee, M.G. Catalogs of Compact Groups of Galaxies from the Enhanced SDSS DR12. ApJS 2016, 225, 23. [Google Scholar] [CrossRef]
- Hartsuiker, L.; Ploeckinger, S. Abundance and group coalescence time-scales of compact groups of galaxies in the EAGLE simulation. Mont. Notices R. Astronom. Soc. 2020, 491, L66–L71. [Google Scholar] [CrossRef]
- Nottale, L.; Chamaraux, P. Statistical deprojection of galaxy pairs. Astronom. Astrophys. 2018, 614, A45. [Google Scholar] [CrossRef]
- Makarov, D.; Prugniel, P.; Terekhova, N.; Courtois, H.; Vauglin, I. HyperLEDA. III. The catalogue of extragalactic distances. Astronom. Astrophys. 2014, 570, A13. [Google Scholar] [CrossRef]
- Nottale, L.; Chamaraux, P. A Catalog of Isolated Galaxy Pairs Limited to Absolute Magnitude −18.5 Drawn from HyperLEDA Database. Astrophys. Bull. 2018, 73, 310–317. [Google Scholar] [CrossRef]
- Nottale, L.; Chamaraux, P. Statistical deprojection of intervelocities, interdistances, and masses in the Isolated Galaxy Pair Catalog. Astronom. Astrophys. 2020, 641, A115. [Google Scholar] [CrossRef]
- Scarpa, R.; Falomo, R.; Treves, A. On the orbital velocity of isolated galaxy pairs: A test of gravity in the low acceleration regime. Mont. Notices R. Astronom. Soc. 2022, 510, 2167–2172. [Google Scholar] [CrossRef]
- Moreno, J.; Bluck, A.F.L.; Ellison, S.L.; Patton, D.R.; Torrey, P.; Moster, B.P. The dynamics of galaxy pairs in a cosmological setting. Mont. Notices R. Astronom. Soc. 2013, 436, 1765–1786. [Google Scholar] [CrossRef]
- Scarpa, R.; Falomo, R.; Treves, A. On the orbital velocity of isolated galaxy pairs: II accurate MOND predictions. Mont. Notices R. Astronom. Soc. 2022, 512, 544–547. [Google Scholar] [CrossRef]
- Loveday, J.; Christodoulou, L.; Norberg, P.; Peacock, J.A.; Baldry, I.K.; Bland-Hawthorn, J.; Brown, M.J.I.; Colless, M.; Driver, S.P.; Holwerda, B.W.; et al. Galaxy and Mass Assembly (GAMA): Small-scale anisotropic galaxy clustering and the pairwise velocity dispersion of galaxies. Mont. Notices R. Astronom. Soc. 2018, 474, 3435–3450. [Google Scholar] [CrossRef]
- Milgrom, M. Galaxy Groups and Modified Dynamics. ApJL 1998, 496, L89–L91. [Google Scholar] [CrossRef][Green Version]
- Milgrom, M. Modified Newtonian Dynamics Mass-to-Light Ratios for Galaxy Groups. ApJL 2002, 577, L75–L77. [Google Scholar] [CrossRef]
- Tully, R.B.; Somerville, R.S.; Trentham, N.; Verheijen, M.A.W. Squelched Galaxies and Dark Halos. Astrophys. J. 2002, 569, 573–581. [Google Scholar] [CrossRef][Green Version]
- Milgrom, M. MOND in galaxy groups. Phys. Rev. D 2018, 98, 104036. [Google Scholar] [CrossRef]
- Milgrom, M. MOND in galaxy groups: A superior sample. Phys. Rev. D 2019, 99, 044041. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M. Color-Mass-to-light-ratio Relations for Disk Galaxies. Astronom. J. 2014, 148, 77. [Google Scholar] [CrossRef]
- Müller, O.; Lelli, F.; Famaey, B.; Pawlowski, M.S.; Fahrion, K.; Rejkuba, M.; Hilker, M.; Jerjen, H. The Cen A galaxy group: Dynamical mass and missing baryons. Astronom. Astrophys. 2022, 662, A57. [Google Scholar] [CrossRef]
- Samurović, S. The Newtonian and MOND Dynamical Models of NGC 5128: Investigation of the Dark Matter Contribution. Serbian Astron. J. 2016, 192, 9–20. [Google Scholar] [CrossRef]
- Gaspari, M.; Eckert, D.; Ettori, S.; Tozzi, P.; Bassini, L.; Rasia, E.; Brighenti, F.; Sun, M.; Borgani, S.; Johnson, S.D.; et al. The X-Ray Halo Scaling Relations of Supermassive Black Holes. Astrophys. J. 2019, 884, 169. [Google Scholar] [CrossRef]
- Haynes, M.P.; Giovanelli, R. The Connection between Pisces-Perseus and the Local Supercluster. ApJL 1986, 306, L55. [Google Scholar] [CrossRef]
- Milgrom, M. Large-Scale Filaments: Newtonian versus Modified Dynamics. Astrophys. J. 1997, 478, 7–12. [Google Scholar] [CrossRef][Green Version]
- Eisenstein, D.J.; Loeb, A.; Turner, E.L. Dynamical Mass Estimates of Large-Scale Filaments in Redshift Surveys. Astrophys. J. 1997, 475, 421–428. [Google Scholar] [CrossRef]
- Sarazin, C.L. X-ray emission from clusters of galaxies. Rev. Mod. Phys. 1986, 58, 1–115. [Google Scholar] [CrossRef]
- Allen, S.W.; Evrard, A.E.; Mantz, A.B. Cosmological Parameters from Observations of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2011, 49, 409–470. [Google Scholar] [CrossRef]
- Sanders, R.H. The Virial Discrepancy in Clusters of Galaxies in the Context of Modified Newtonian Dynamics. ApJL 1999, 512, L23–L26. [Google Scholar] [CrossRef]
- Sanders, R.H. Clusters of galaxies with modified Newtonian dynamics. Mont. Notices R. Astronom. Soc. 2003, 342, 901–908. [Google Scholar] [CrossRef]
- Milgrom, M. Ultra-diffuse cluster galaxies as key to the MOND cluster conundrum. Mont. Notices R. Astronom. Soc. 2015, 454, 3810–3815. [Google Scholar] [CrossRef]
- Pointecouteau, E.; Silk, J. New constraints on modified Newtonian dynamics from galaxy clusters. Mont. Notices R. Astronom. Soc. 2005, 364, 654–658. [Google Scholar] [CrossRef]
- Gonzalez, A.H.; Zaritsky, D.; Zabludoff, A.I. A Census of Baryons in Galaxy Clusters and Groups. Astrophys. J. 2007, 666, 147–155. [Google Scholar] [CrossRef]
- Gonzalez, A.H.; Sivanandam, S.; Zabludoff, A.I.; Zaritsky, D. Galaxy Cluster Baryon Fractions Revisited. Astrophys. J. 2013, 778, 14. [Google Scholar] [CrossRef]
- COSMOS Collaboration. Stellar and Total Baryon Mass Fractions in Groups and Clusters Since Redshift 1. Astrophys. J. 2009, 703, 982–993. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M.; de Blok, W.J.G.; Zagursky, M.J. The Baryon Content of Cosmic Structures. ApJL 2010, 708, L14–L17. [Google Scholar] [CrossRef]
- Tucker, W.H.; Tananbaum, H.; Remillard, R.A. A search for ’failed clusters’ of galaxies. Astrophys. J. 1995, 444, 532–547. [Google Scholar] [CrossRef]
- Tucker, W.; Blanco, P.; Rappoport, S.; David, L.; Fabricant, D.; Falco, E.E.; Forman, W.; Dressler, A.; Ramella, M. 1E 0657-56: A Contender for the Hottest Known Cluster of Galaxies. ApJL 1998, 496, L5–L8. [Google Scholar] [CrossRef]
- Markevitch, M.; Gonzalez, A.H.; David, L.; Vikhlinin, A.; Murray, S.; Forman, W.; Jones, C.; Tucker, W. A Textbook Example of a Bow Shock in the Merging Galaxy Cluster 1E 0657-56. ApJL 2002, 567, L27–L31. [Google Scholar] [CrossRef]
- Clowe, D.; Gonzalez, A.; Markevitch, M. Weak-Lensing Mass Reconstruction of the Interacting Cluster 1E 0657-558: Direct Evidence for the Existence of Dark Matter. Astrophys. J. 2004, 604, 596–603. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. ApJL 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Lage, C.; Farrar, G. Constrained Simulation of the Bullet Cluster. Astrophys. J. 2014, 787, 144. [Google Scholar] [CrossRef]
- Deshev, B.; Finoguenov, A.; Verdugo, M.; Ziegler, B.; Park, C.; Hwang, H.S.; Haines, C.; Kamphuis, P.; Tamm, A.; Einasto, M.; et al. Galaxy evolution in merging clusters: The passive core of the “Train Wreck” cluster of galaxies, A 520. Astronom. Astrophys. 2017, 607, A131. [Google Scholar] [CrossRef]
- Shan, H.; Qin, B.; Fort, B.; Tao, C.; Wu, X.P.; Zhao, H. Offset between dark matter and ordinary matter: Evidence from a sample of 38 lensing clusters of galaxies. Mont. Notices R. Astronom. Soc. 2010, 406, 1134–1139. [Google Scholar] [CrossRef]
- Knebe, A.; Llinares, C.; Wu, X.; Zhao, H.S. On the Separation Between Baryonic and Dark Matter: Evidence for Phantom Dark Matter? Astrophys. J. 2009, 703, 2285–2290. [Google Scholar] [CrossRef]
- Angus, G.W.; Shan, H.Y.; Zhao, H.S.; Famaey, B. On the Proof of Dark Matter, the Law of Gravity, and the Mass of Neutrinos. Astrophys. J. 2007, 654, L13–L16. [Google Scholar] [CrossRef]
- Katrin Collaboration. Improved Upper Limit on the Neutrino Mass from a Direct Kinematic Method by KATRIN. Phys. Rev. Lett. 2019, 123, 221802. [Google Scholar] [CrossRef]
- Katrin Collaboration. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Natarajan, P.; Zhao, H. MOND plus classical neutrinos are not enough for cluster lensing. Mont. Notices R. Astronom. Soc. 2008, 389, 250–256. [Google Scholar] [CrossRef][Green Version]
- Angus, G.W. Is an 11eV sterile neutrino consistent with clusters, the cosmic microwave background and modified Newtonian dynamics? Mont. Notices R. Astronom. Soc. 2009, 394, 527–532. [Google Scholar] [CrossRef]
- Angus, G.W. A lower limit on the dark particle mass from dSphs. J. Cosmol. Astropart. Phys. 2010, 2010, 026. [Google Scholar] [CrossRef]
- Tremaine, S.; Gunn, J.E. Dynamical role of light neutral leptons in cosmology. Phys. Rev. Lett. 1979, 42, 407–410. [Google Scholar] [CrossRef]
- Angus, G.W.; Famaey, B.; Diaferio, A. Equilibrium configurations of 11 eV sterile neutrinos in MONDian galaxy clusters. Mont. Notices R. Astronom. Soc. 2010, 402, 395–408. [Google Scholar] [CrossRef]
- Ettori, S.; Ghirardini, V.; Eckert, D.; Pointecouteau, E.; Gastaldello, F.; Sereno, M.; Gaspari, M.; Ghizzardi, S.; Roncarelli, M.; Rossetti, M. Hydrostatic mass profiles in X-COP galaxy clusters. Astronom. Astrophys. 2019, 621, A39. [Google Scholar] [CrossRef]
- Giunti, C.; Lasserre, T. eV-Scale Sterile Neutrinos. Annu. Rev. Nucl. Part. Sci. 2019, 69, 163–190. [Google Scholar] [CrossRef]
- MicroBooNE Collaboration. Search for Neutrino-Induced Neutral Current Δ Radiative Decay in MicroBooNE and a First Test of the MiniBooNE Low Energy Excess Under a Single-Photon Hypothesis. Phys. Rev. Lett. 2022, 128, 111801. [Google Scholar] [CrossRef] [PubMed]
- Argüelles, C.A.; Esteban, I.; Hostert, M.; Kelly, K.J.; Kopp, J.; Machado, P.A.N.; Martinez-Soler, I.; Perez-Gonzalez, Y.F. MicroBooNE and the νe Interpretation of the MiniBooNE Low-Energy Excess. Phys. Rev. Lett. 2022, 128, 241802. [Google Scholar] [CrossRef]
- Argüelles, C.A.; Bertólez-Martínez, T.; Salvado, J. Impact of Wave Packet Separation in Low-Energy Sterile Neutrino Searches. arXiv 2022, arXiv:2201.05108. [Google Scholar]
- Berryman, J.M.; Coloma, P.; Huber, P.; Schwetz, T.; Zhou, A. Statistical significance of the sterile-neutrino hypothesis in the context of reactor and gallium data. JHEP 2022, 2022, 55. [Google Scholar] [CrossRef]
- Barinov, V.; Gorbunov, D. BEST impact on sterile neutrino hypothesis. Phys. Rev. D 2022, 105, L051703. [Google Scholar] [CrossRef]
- Barinov, V.V.; Cleveland, B.T.; Danshin, S.N.; Ejiri, H.; Elliott, S.R.; Frekers, D.; Gavrin, V.N.; Gorbachev, V.V.; Gorbunov, D.S.; Haxton, W.C.; et al. Search for electron-neutrino transitions to sterile states in the BEST experiment. Phys. Rev. C 2022, 105, 065502. [Google Scholar] [CrossRef]
- Barinov, V.V.; Cleveland, B.T.; Danshin, S.N.; Ejiri, H.; Elliott, S.R.; Frekers, D.; Gavrin, V.N.; Gorbachev, V.V.; Gorbunov, D.S.; Haxton, W.C.; et al. Results from the Baksan Experiment on Sterile Transitions (BEST). Phys. Rev. Lett. 2022, 128, 232501. [Google Scholar] [CrossRef]
- Feix, M.; Zhao, H.; Fedeli, C.; Pestaña, J.L.G.; Hoekstra, H. Substructure lensing in galaxy clusters as a constraint on low-mass sterile neutrinos in tensor-vector-scalar theory: The straight arc of Abell 2390. Phys. Rev. D 2010, 82, 124003. [Google Scholar] [CrossRef]
- Hodson, A.O.; Zhao, H. Generalizing MOND to explain the missing mass in galaxy clusters. Astronom. Astrophys. 2017, 598, A127. [Google Scholar] [CrossRef]
- Brownstein, J.R.; Moffat, J.W. The Bullet Cluster 1E0657-558 evidence shows modified gravity in the absence of dark matter. Mont. Notices R. Astronom. Soc. 2007, 382, 29–47. [Google Scholar] [CrossRef]
- Acedo, L. Modified Newtonian Gravity as an Alternative to the Dark Matter Hypothesis. Galaxies 2017, 5, 74. [Google Scholar] [CrossRef]
- Milgrom, M. MOND vs. dark matter in light of historical parallels. Stud. Hist. Philos. Mod. Phys. 2020, 71, 170–195. [Google Scholar] [CrossRef]
- Böhringer, H.; Chon, G.; Fukugita, M. The extended ROSAT-ESO Flux-Limited X-ray Galaxy Cluster Survey (REFLEX II). VII. The mass function of galaxy clusters. Astronom. Astrophys. 2017, 608, A65. [Google Scholar] [CrossRef]
- Böhringer, H.; Chon, G.; Collins, C.A. The extended ROSAT-ESO Flux Limited X-ray Galaxy Cluster Survey (REFLEX II). IV. X-ray luminosity function and first constraints on cosmological parameters. Astronom. Astrophys. 2014, 570, A31. [Google Scholar] [CrossRef]
- Schrabback, T.; Bocquet, S.; Sommer, M.; Zohren, H.; van den Busch, J.L.; Hernández-Martín, B.; Hoekstra, H.; Raihan, S.F.; Schirmer, M.; Applegate, D.; et al. Mass calibration of distant SPT galaxy clusters through expanded weak-lensing follow-up observations with HST, VLT, & Gemini-South. Mont. Notices R. Astronom. Soc. 2021, 505, 3923–3943. [Google Scholar] [CrossRef]
- Angus, G.W.; Diaferio, A.; Famaey, B.; van der Heyden, K.J. Cosmological simulations in MOND: The cluster scale halo mass function with light sterile neutrinos. Mont. Notices R. Astronom. Soc. 2013, 436, 202–211. [Google Scholar] [CrossRef]
- Katz, H.; McGaugh, S.; Teuben, P.; Angus, G.W. Galaxy cluster bulk flows and collision velocities in QUMOND. Astrophys. J. 2013, 772, 10. [Google Scholar] [CrossRef]
- Milosavljević, M.; Koda, J.; Nagai, D.; Nakar, E.; Shapiro, P.R. The Cluster-Merger Shock in 1E 0657-56: Faster than a Speeding Bullet? ApJL 2007, 661, L131–L134. [Google Scholar] [CrossRef]
- Springel, V.; Farrar, G.R. The speed of the ‘bullet’ in the merging galaxy cluster 1E0657-56. Mont. Notices R. Astronom. Soc. 2007, 380, 911–925. [Google Scholar] [CrossRef]
- Mastropietro, C.; Burkert, A. Simulating the Bullet Cluster. Mont. Notices R. Astronom. Soc. 2008, 389, 967–988. [Google Scholar] [CrossRef]
- Lee, J.; Komatsu, E. Bullet Cluster: A Challenge to ΛCDM Cosmology. Astrophys. J. 2010, 718, 60–65. [Google Scholar] [CrossRef]
- Thompson, R.; Nagamine, K. Pairwise velocities of dark matter haloes: A test for the Λ cold dark matter model using the bullet cluster. Mont. Notices R. Astronom. Soc. 2012, 419, 3560–3570. [Google Scholar] [CrossRef]
- Watson, W.A.; Iliev, I.T.; Diego, J.M.; Gottlöber, S.; Knebe, A.; Martínez-González, E.; Yepes, G. Statistics of extreme objects in the Juropa Hubble Volume simulation. Mont. Notices R. Astronom. Soc. 2014, 437, 3776–3786. [Google Scholar] [CrossRef]
- Thompson, R.; Davé, R.; Nagamine, K. The rise and fall of a challenger: The Bullet Cluster in Λ cold dark matter simulations. Mont. Notices R. Astronom. Soc. 2015, 452, 3030–3037. [Google Scholar] [CrossRef]
- Kraljic, D.; Sarkar, S. How rare is the Bullet Cluster (in a ΛCDM universe)? J. Cosmol. Astropart. Phys. 2015, 4, 050. [Google Scholar] [CrossRef]
- Menanteau, F.; González, J.; Juin, J.B.; Marriage, T.A.; Reese, E.D.; Acquaviva, V.; Aguirre, P.; Appel, J.W.; Baker, A.J.; Barrientos, L.F.; et al. The Atacama Cosmology Telescope: Physical Properties and Purity of a Galaxy Cluster Sample Selected via the Sunyaev-Zel’dovich Effect. Astrophys. J. 2010, 723, 1523–1541. [Google Scholar] [CrossRef]
- Menanteau, F.; Hughes, J.P.; Sifón, C.; Hilton, M.; González, J.; Infante, L.; Barrientos, L.F.; Baker, A.J.; Bond, J.R.; Das, S.; et al. The Atacama Cosmology Telescope: ACT-CL J0102-4915 “El Gordo,” a Massive Merging Cluster at Redshift 0.87. Astrophys. J. 2012, 748, 7. [Google Scholar] [CrossRef]
- Jee, M.J.; Hughes, J.P.; Menanteau, F.; Sifón, C.; Mandelbaum, R.; Barrientos, L.F.; Infante, L.; Ng, K.Y. Weighing “El Gordo” with a Precision Scale: Hubble Space Telescope Weak-lensing Analysis of the Merging Galaxy Cluster ACT-CL J0102-4915 at z = 0.87. Astrophys. J. 2014, 785, 20. [Google Scholar] [CrossRef]
- Molnar, S.M.; Broadhurst, T. A Hydrodynamical Solution for the “Twin-tailed” Colliding Galaxy Cluster “El Gordo”. Astrophys. J. 2015, 800, 37. [Google Scholar] [CrossRef]
- Ng, K.Y.; Dawson, W.A.; Wittman, D.; Jee, M.J.; Hughes, J.P.; Menanteau, F.; Sifón, C. The return of the merging galaxy subclusters of El Gordo? Mont. Notices R. Astronom. Soc. 2015, 453, 1531–1549. [Google Scholar] [CrossRef][Green Version]
- Zhang, C.; Yu, Q.; Lu, Y. Simulating the Galaxy Cluster El Gordo and Identifying the Merger Configuration. Astrophys. J. 2015, 813, 129. [Google Scholar] [CrossRef]
- Watson, W.A.; Iliev, I.T.; D’Aloisio, A.; Knebe, A.; Shapiro, P.R.; Yepes, G. The halo mass function through the cosmic ages. Mont. Notices R. Astronom. Soc. 2013, 433, 1230–1245. [Google Scholar] [CrossRef]
- Asencio, E.; Banik, I.; Kroupa, P. A massive blow for ΛCDM—The high redshift, mass, and collision velocity of the interacting galaxy cluster El Gordo contradicts concordance cosmology. Mont. Notices R. Astronom. Soc. 2021, 500, 5249–5267. [Google Scholar] [CrossRef]
- Kim, J.; Jee, M.J.; Hughes, J.P.; Yoon, M.; HyeongHan, K.; Menanteau, F.; Sifón, C.; Hovey, L.; Arunachalam, P. Head-to-Toe Measurement of El Gordo: Improved Analysis of the Galaxy Cluster ACT-CL J0102-4915 with New Wide-field Hubble Space Telescope Imaging Data. Astrophys. J. 2021, 923, 101. [Google Scholar] [CrossRef]
- Donnert, J.M.F. Initial conditions for idealized clusters mergers, simulating ‘El Gordo’. Mont. Notices R. Astronom. Soc. 2014, 438, 1971–1984. [Google Scholar] [CrossRef]
- Keenan, R.C.; Barger, A.J.; Cowie, L.L. Evidence for a ~300 Megaparsec Scale Under-density in the Local Galaxy Distribution. Astrophys. J. 2013, 775, 62. [Google Scholar] [CrossRef]
- Wong, J.H.W.; Shanks, T.; Metcalfe, N.; Whitbourn, J.R. The local hole: A galaxy underdensity covering 90 per cent of sky to 200 Mpc. Mont. Notices R. Astronom. Soc. 2022, 511, 5742–5755. [Google Scholar] [CrossRef]
- Angulo, R.E.; Springel, V.; White, S.D.M.; Jenkins, A.; Baugh, C.M.; Frenk, C.S. Scaling relations for galaxy clusters in the Millennium-XXL simulation. Mont. Notices R. Astronom. Soc. 2012, 426, 2046–2062. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Jenkins, A.; Frenk, C.S.; Yoshida, N.; Gao, L.; Navarro, J.; Thacker, R.; Croton, D.; Helly, J.; et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 2005, 435, 629–636. [Google Scholar] [CrossRef]
- Angulo, R.E.; White, S.D.M.; Springel, V.; Henriques, B. Galaxy formation on the largest scales: The impact of astrophysics on the baryonic acoustic oscillation peak. Mont. Notices R. Astronom. Soc. 2014, 442, 2131–2144. [Google Scholar] [CrossRef][Green Version]
- Rubart, M.; Schwarz, D.J. Cosmic radio dipole from NVSS and WENSS. Astronom. Astrophys. 2013, 555, A117. [Google Scholar] [CrossRef]
- Böhringer, H.; Chon, G.; Bristow, M.; Collins, C.A. The extended ROSAT-ESO Flux-Limited X-ray Galaxy Cluster Survey (REFLEX II). V. Exploring a local underdensity in the southern sky. Astronom. Astrophys. 2015, 574, A26. [Google Scholar] [CrossRef]
- Böhringer, H.; Chon, G.; Collins, C.A. Observational evidence for a local underdensity in the Universe and its effect on the measurement of the Hubble constant. Astronom. Astrophys. 2020, 633, A19. [Google Scholar] [CrossRef]
- Planck Collaboration XXVII. Planck 2013 results. XXVII. Doppler boosting of the CMB: Eppur si muove. Astronom. Astrophys. 2014, 571, A27. [Google Scholar] [CrossRef]
- Riess, A.G. The expansion of the Universe is faster than expected. Nat. Rev. Phys. 2020, 2, 10–12. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. ApJL 2021, 908, L6. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Early Data Release 3. Summary of the contents and survey properties. Astronom. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Soltis, J.; Casertano, S.; Riess, A.G. The Parallax of ω Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant. ApJL 2021, 908, L5. [Google Scholar] [CrossRef]
- Anand, G.S.; Tully, R.B.; Rizzi, L.; Riess, A.G.; Yuan, W. Comparing Tip of the Red Giant Branch Distance Scales: An Independent Reduction of the Carnegie-Chicago Hubble Program and the Value of the Hubble Constant. Astrophys. J. 2022, 932, 15. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. ApJL 2020, 891, L1. [Google Scholar] [CrossRef]
- Di Valentino, E. A combined analysis of the H0 late time direct measurements and the impact on the Dark Energy sector. Mont. Notices R. Astronom. Soc. 2021, 502, 2065–2073. [Google Scholar] [CrossRef]
- Breuval, L.; Kervella, P.; Anderson, R.I.; Riess, A.G.; Arenou, F.; Trahin, B.; Mérand, A.; Gallenne, A.; Gieren, W.; Storm, J.; et al. The Milky Way Cepheid Leavitt law based on Gaia DR2 parallaxes of companion stars and host open cluster populations. Astronom. Astrophys. 2020, 643, A115. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Burns, C.R.; Parent, E.; Phillips, M.M.; Stritzinger, M.; Krisciunas, K.; Suntzeff, N.B.; Hsiao, E.Y.; Contreras, C.; Anais, J.; Boldt, L.; et al. The Carnegie Supernova Project: Absolute Calibration and the Hubble Constant. Astrophys. J. 2018, 869, 56. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Scowcroft, V.; Burns, C.; Monson, A.; Persson, S.E.; Seibert, M.; Rigby, J. Carnegie Hubble Program: A Mid-infrared Calibration of the Hubble Constant. Astrophys. J. 2012, 758, 24. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hoyt, T.; Jang, I.S.; Beaton, R.; Lee, M.G.; Monson, A.; Neeley, J.; Rich, J. Calibration of the Tip of the Red Giant Branch. Astrophys. J. 2020, 891, 57. [Google Scholar] [CrossRef]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D.M. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Redetermination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef]
- Jang, I.S.; Lee, M.G. The Tip of the Red Giant Branch Distances to Typa Ia Supernova Host Galaxies. V. NGC 3021, NGC 3370, and NGC 1309 and the Value of the Hubble Constant. Astrophys. J. 2017, 836, 74. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and Its Implications for the Hubble Constant. ApJL 2019, 886, L27. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the SN Ia Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. Astrophys. J. 2020, 889, 5. [Google Scholar] [CrossRef]
- Kourkchi, E.; Tully, R.B.; Anand, G.S.; Courtois, H.M.; Dupuy, A.; Neill, J.D.; Rizzi, L.; Seibert, M. Cosmicflows-4: The Calibration of Optical and Infrared Tully-Fisher Relations. Astrophys. J. 2020, 896, 3. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Using the Baryonic Tully-Fisher Relation to Measure Ho. Astronom. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. Astrophys. J. 2021, 911, 65. [Google Scholar] [CrossRef]
- Khetan, N.; Izzo, L.; Branchesi, M.; Wojtak, R.; Cantiello, M.; Murugeshan, C.; Agnello, A.; Cappellaro, E.; Della Valle, M.; Gall, C.; et al. A new measurement of the Hubble constant using Type Ia supernovae calibrated with surface brightness fluctuations. Astronom. Astrophys. 2021, 647, A72. [Google Scholar] [CrossRef]
- de Jaeger, T.; Stahl, B.E.; Zheng, W.; Filippenko, A.V.; Riess, A.G.; Galbany, L. A measurement of the Hubble constant from Type II supernovae. Mont. Notices R. Astronom. Soc. 2020, 496, 3402–3411. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW—XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mont. Notices R. Astronom. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Shajib, A.J.; Birrer, S.; Treu, T.; Agnello, A.; Buckley-Geer, E.J.; Chan, J.H.H.; Christensen, L.; Lemon, C.; Lin, H.; Millon, M.; et al. STRIDES: A 3.9 per cent measurement of the Hubble constant from the strong lens system DES J0408-5354. Mont. Notices R. Astronom. Soc. 2020, 494, 6072–6102. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.F.; Christensen, L.; Collett, T.; et al. TDCOSMO. IV. Hierarchical time-delay cosmography—Joint inference of the Hubble constant and galaxy density profiles. Astronom. Astrophys. 2020, 643, A165. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 2017, 551, 85–88. [Google Scholar] [CrossRef]
- Domínguez, A.; Wojtak, R.; Finke, J.; Ajello, M.; Helgason, K.; Prada, F.; Desai, A.; Paliya, V.; Marcotulli, L.; Hartmann, D.H. A New Measurement of the Hubble Constant and Matter Content of the Universe Using Extragalactic Background Light γ-Ray Attenuation. Astrophys. J. 2019, 885, 137. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. A new method to build the (inverse) distance ladder. Mont. Notices R. Astronom. Soc. 2020, 495, 2630–2644. [Google Scholar] [CrossRef]
- Colgáin, E.Ó. A hint of matter underdensity at low z? J. Cosmol. Astropart. Phys. 2019, 2019, 006. [Google Scholar] [CrossRef]
- Luković, V.V.; Haridasu, B.S.; Vittorio, N. Exploring the evidence for a large local void with supernovae Ia data. Mont. Notices R. Astronom. Soc. 2020, 491, 2075–2087. [Google Scholar] [CrossRef]
- Kazantzidis, L.; Perivolaropoulos, L. Hints of a local matter underdensity or modified gravity in the low z Pantheon data. Phys. Rev. D 2020, 102, 023520. [Google Scholar] [CrossRef]
- Castello, S.; Högås, M.; Mörtsell, E. A Cosmological Underdensity Does Not Solve the Hubble Tension. arXiv 2021, arXiv:2110.04226. [Google Scholar]
- Kazantzidis, L.; Koo, H.; Nesseris, S.; Perivolaropoulos, L.; Shafieloo, A. Hints for possible low redshift oscillation around the best-fitting ΛCDM model in the expansion history of the Universe. Mont. Notices R. Astronom. Soc. 2021, 501, 3421–3426. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.Ó.; Ruchika, M.M.; Sen, A.A.; Sheikh-Jabbari, M.M.; Yang, T. Is there an early Universe solution to Hubble tension? Phys. Rev. D 2020, 102, 103525. [Google Scholar] [CrossRef]
- Krishnan, C.; Ó Colgáin, E.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble tension and a H0 diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble Constant Tension in the SNe Ia Pantheon Sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Migkas, K.; Reiprich, T.H. Anisotropy of the galaxy cluster X-ray luminosity-temperature relation. Astronom. Astrophys. 2018, 611, A50. [Google Scholar] [CrossRef]
- Migkas, K.; Pacaud, F.; Schellenberger, G.; Erler, J.; Nguyen-Dang, N.T.; Reiprich, T.H.; Ramos-Ceja, M.E.; Lovisari, L. Cosmological implications of the anisotropy of ten galaxy cluster scaling relations. Astronom. Astrophys. 2021, 649, A151. [Google Scholar] [CrossRef]
- Anderson, L.; Aubourg, E.; Bailey, S.; Bizyaev, D.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; Cuesta, A.J.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Release 9 spectroscopic galaxy sample. Mont. Notices R. Astronom. Soc. 2012, 427, 3435–3467. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Galaxy and Mass N-Point Correlation Functions: A Blast from the Past. In Historical Development of Modern Cosmology; Martínez, V.J., Trimble, V., Pons-Bordería, M.J., Eds.; Astronomical Society of the Pacific Conference Series; Astronomical Society of the Pacific: San Francisco, CA, USA, 2001; Volume 252, p. 201. [Google Scholar]
- DES Collaboration. More out of less: An excess integrated Sachs-Wolfe signal from supervoids mapped out by the Dark Energy Survey. Mont. Notices R. Astronom. Soc. 2019, 484, 5267–5277. [Google Scholar] [CrossRef]
- Kovács, A. The part and the whole: Voids, supervoids, and their ISW imprint. Mont. Notices R. Astronom. Soc. 2018, 475, 1777–1790. [Google Scholar] [CrossRef]
- Kovács, A.; Beck, R.; Smith, A.; Rácz, G.; Csabai, I.; Szapudi, I. Evidence for a high-z ISW signal from supervoids in the distribution of eBOSS quasars. Mont. Notices R. Astronom. Soc. 2022, 513, 15–26. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 2020, 4, 196–203. [Google Scholar] [CrossRef]
- Handley, W. Curvature tension: Evidence for a closed universe. Phys. Rev. D 2021, 103, L041301. [Google Scholar] [CrossRef]
- Nadathur, S.; Lavinto, M.; Hotchkiss, S.; Räsänen, S. Can a supervoid explain the cold spot? Phys. Rev. D 2014, 90, 103510. [Google Scholar] [CrossRef]
- Kovács, A.; Jeffrey, N.; Gatti, M.; Chang, C.; Whiteway, L.; Hamaus, N.; Lahav, O.; Pollina, G.; Bacon, D.; Kacprzak, T.; et al. The DES view of the Eridanus supervoid and the CMB cold spot. Mont. Notices R. Astronom. Soc. 2022, 510, 216–229. [Google Scholar] [CrossRef]
- Kovács, A.; Beck, R.; Szapudi, I.; Csabai, I.; Rácz, G.; Dobos, L. A common explanation of the Hubble tension and anomalous cold spots in the CMB. Mont. Notices R. Astronom. Soc. 2020, 499, 320–333. [Google Scholar] [CrossRef]
- Capak, P.L.; Riechers, D.; Scoville, N.Z.; Carilli, C.; Cox, P.; Neri, R.; Robertson, B.; Salvato, M.; Schinnerer, E.; Yan, L.; et al. A massive protocluster of galaxies at a redshift of z~5.3. Nature 2011, 470, 233–235. [Google Scholar] [CrossRef] [PubMed]
- Cucciati, O.; Lemaux, B.C.; Zamorani, G.; Le Fèvre, O.; Tasca, L.A.M.; Hathi, N.P.; Lee, K.G.; Bardelli, S.; Cassata, P.; Garilli, B.; et al. The progeny of a cosmic titan: A massive multi-component proto-supercluster in formation at z = 2.45 in VUDS. Astronom. Astrophys. 2018, 619, A49. [Google Scholar] [CrossRef]
- Champagne, J.B.; Casey, C.M.; Zavala, J.A.; Cooray, A.; Dannerbauer, H.; Fabian, A.; Hayward, C.C.; Long, A.S.; Spilker, J.S. Comprehensive Gas Characterization of a z = 2.5 Protocluster: A Cluster Core Caught in the Beginning of Virialization? Astrophys. J. 2021, 913, 110. [Google Scholar] [CrossRef]
- McConachie, I.; Wilson, G.; Forrest, B.; Marsan, Z.C.; Muzzin, A.; Cooper, M.C.; Annunziatella, M.; Marchesini, D.; Chan, J.C.C.; Gomez, P.; et al. Spectroscopic Confirmation of a Protocluster at z = 3.37 with a High Fraction of Quiescent Galaxies. Astrophys. J. 2022, 926, 37. [Google Scholar] [CrossRef]
- Steinhardt, C.L.; Capak, P.; Masters, D.; Speagle, J.S. The Impossibly Early Galaxy Problem. Astrophys. J. 2016, 824, 21. [Google Scholar] [CrossRef]
- Marrone, D.P.; Spilker, J.S.; Hayward, C.C.; Vieira, J.D.; Aravena, M.; Ashby, M.L.N.; Bayliss, M.B.; Béthermin, M.; Brodwin, M.; Bothwell, M.S.; et al. Galaxy growth in a massive halo in the first billion years of cosmic history. Nature 2018, 553, 51–54. [Google Scholar] [CrossRef]
- Wang, T.; Schreiber, C.; Elbaz, D.; Yoshimura, Y.; Kohno, K.; Shu, X.; Yamaguchi, Y.; Pannella, M.; Franco, M.; Huang, J.; et al. A dominant population of optically invisible massive galaxies in the early Universe. Nature 2019, 572, 211–214. [Google Scholar] [CrossRef]
- Rennehan, D.; Babul, A.; Hayward, C.C.; Bottrell, C.; Hani, M.H.; Chapman, S.C. Rapid early coeval star formation and assembly of the most-massive galaxies in the Universe. Mont. Notices R. Astronom. Soc. 2020, 493, 4607–4621. [Google Scholar] [CrossRef]
- Neeleman, M.; Prochaska, J.X.; Kanekar, N.; Rafelski, M. A cold, massive, rotating disk galaxy 1.5 billion years after the Big Bang. Nature 2020, 581, 269–272. [Google Scholar] [CrossRef] [PubMed]
- Tsukui, T.; Iguchi, S. Spiral morphology in an intensely star-forming disk galaxy more than 12 billion years ago. Science 2021, 372, 1201–1205. [Google Scholar] [CrossRef] [PubMed]
- Lelli, F.; Di Teodoro, E.M.; Fraternali, F.; Man, A.W.S.; Zhang, Z.Y.; De Breuck, C.; Davis, T.A.; Maiolino, R. A massive stellar bulge in a regularly rotating galaxy 1.2 billion years after the Big Bang. Science 2021, 371, 713–716. [Google Scholar] [CrossRef] [PubMed]
- Kilbinger, M. Cosmology with cosmic shear observations: A review. Rep. Prog. Phys. 2015, 78, 086901. [Google Scholar] [CrossRef]
- DES Collaboration. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Kafle, P.R.; Sharma, S.; Lewis, G.F.; Bland-Hawthorn, J. Kinematics of the Stellar Halo and the Mass Distribution of the Milky Way Using Blue Horizontal Branch Stars. Astrophys. J. 2012, 761, 98. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stölzner, B.; Tröster, T.; van den Busch, J.L.; et al. KiDS-1000 cosmology: Cosmic shear constraints and comparison between two point statistics. Astronom. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Heymans, C.; Tröster, T.; Asgari, M.; Blake, C.; Hildebrandt, H.; Joachimi, B.; Kuijken, K.; Lin, C.A.; Sánchez, A.G.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Multi-probe weak gravitational lensing and spectroscopic galaxy clustering constraints. Astronom. Astrophys. 2021, 646, A140. [Google Scholar] [CrossRef]
- DES Collaboration. Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to modeling uncertainty. Phys. Rev. D 2022, 105, 023515. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef] [PubMed]
- Pardo, K.; Spergel, D.N. What is the Price of Abandoning Dark Matter? Cosmological Constraints on Alternative Gravity Theories. Phys. Rev. Lett. 2020, 125, 211101. [Google Scholar] [CrossRef]
- Milgrom, M. Cosmological variation of the MOND constant: Secular effects on galactic systems. Phys. Rev. D 2015, 91, 044009. [Google Scholar] [CrossRef]
- Garaldi, E.; Romano-Díaz, E.; Porciani, C.; Pawlowski, M.S. Radial Acceleration Relation of ΛCDM Satellite Galaxies. Phys. Rev. Lett. 2018, 120, 261301. [Google Scholar] [CrossRef]
- Dodelson, S.; Liguori, M. Can Cosmic Structure Form without Dark Matter? Phys. Rev. Lett. 2006, 97, 231301. [Google Scholar] [CrossRef] [PubMed]
- Skordis, C. Tensor-vector-scalar cosmology: Covariant formalism for the background evolution and linear perturbation theory. Phys. Rev. D 2006, 74, 103513. [Google Scholar] [CrossRef]
- Skordis, C.; Mota, D.F.; Ferreira, P.G.; Bœhm, C. Large Scale Structure in Bekenstein’s Theory of Relativistic Modified Newtonian Dynamics. Phys. Rev. Lett. 2006, 96, 011301. [Google Scholar] [CrossRef]
- Ruchayskiy, O.; Ivashko, A. Restrictions on the lifetime of sterile neutrinos from primordial nucleosynthesis. J. Cosmol. Astropart. Phys. 2012, 2012, 014. [Google Scholar] [CrossRef]
- Adhikari, R.; Agostini, M.; Ky, N.A.; Araki, T.; Archidiacono, M.; Bahr, M.; Baur, J.; Behrens, J.; Bezrukov, F.; Bhupal Dev, P.S.; et al. A White Paper on keV sterile neutrino Dark Matter. J. Cosmol. Astropart. Phys. 2017, 2017, 025. [Google Scholar] [CrossRef]
- Sanders, R.H. Cosmology with modified Newtonian dynamics (MOND). Mont. Notices R. Astronom. Soc. 1998, 296, 1009–1018. [Google Scholar] [CrossRef]
- McGaugh, S.S. Distinguishing between Cold Dark Matter and Modified Newtonian Dynamics: Predictions for the Microwave Background. ApJL 1999, 523, L99–L102. [Google Scholar] [CrossRef]
- McGaugh, S.S. Confrontation of Modified Newtonian Dynamics Predictions with Wilkinson Microwave Anisotropy Probe First Year Data. Astrophys. J. 2004, 611, 26–39. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Doré, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; et al. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology. ApJS 2007, 170, 377–408. [Google Scholar] [CrossRef]
- Clarkson, C.; Umeh, O.; Maartens, R.; Durrer, R. What is the distance to the CMB? J. Cosmol. Astropart. Phys. 2014, 2014, 036. [Google Scholar] [CrossRef][Green Version]
- Harrison, E.R. Fluctuations at the Threshold of Classical Cosmology. Phys. Rev. D 1970, 1, 2726–2730. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. A hypothesis, unifying the structure and the entropy of the Universe. Mont. Notices R. Astronom. Soc. 1972, 160, 1P. [Google Scholar] [CrossRef]
- Meszaros, P. The behaviour of point masses in an expanding cosmological substratum. Astronom. Astrophys. 1974, 37, 225–228. [Google Scholar]
- Angus, G.W.; Diaferio, A. The abundance of galaxy clusters in modified Newtonian dynamics: Cosmological simulations with massive neutrinos. Mont. Notices R. Astronom. Soc. 2011, 417, 941–949. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. Linear stability of the new relativistic theory of modified Newtonian dynamics. arXiv 2022, arXiv:2109.13287. [Google Scholar]
- Massimi, M. Three problems about multi-scale modelling in cosmology. Stud. Hist. Philos. Mod. Phys. 2018, 64, 26–38. [Google Scholar] [CrossRef]
- Fields, B.D. The Primordial Lithium Problem. Annu. Rev. Nucl. Part. Sci. 2011, 61, 47–68. [Google Scholar] [CrossRef]
- Tytler, D.; O’Meara, J.M.; Suzuki, N.; Lubin, D. Review of Big Bang Nucleosynthesis and Primordial Abundances. Phys. Scr. Vol. T 2000, 85, 12. [Google Scholar] [CrossRef]
- Sanders, R.H. Does GW170817 falsify MOND? Int. J. Mod. Phys. D 2018, 27, 1847027. [Google Scholar] [CrossRef]
- Molnar, S.M.; Chiu, I.N.T.; Broadhurst, T.; Stadel, J.G. The Pre-merger Impact Velocity of the Binary Cluster A1750 from X-Ray, Lensing, and Hydrodynamical Simulations. Astrophys. J. 2013, 779, 63. [Google Scholar] [CrossRef]
- Birkinshaw, M.; Gull, S.F. A test for transverse motions of clusters of galaxies. Nature 1983, 302, 315–317. [Google Scholar] [CrossRef]
- Molnar, S.M.; Birkinshaw, M. Determining Tangential Peculiar Velocities of Clusters of Galaxies Using Gravitational Lensing. Astrophys. J. 2003, 586, 731–734. [Google Scholar] [CrossRef]
- Molnar, S.M.; Broadhurst, T.; Umetsu, K.; Zitrin, A.; Rephaeli, Y.; Shimon, M. Tangential Velocity of the Dark Matter in the Bullet Cluster from Precise Lensed Image Redshifts. Astrophys. J. 2013, 774, 70. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. Effects of lens motion and uneven magnification on image spectra. Mont. Notices R. Astronom. Soc. 2015, 450, 3155–3168. [Google Scholar] [CrossRef]
- Bournaud, F.; Duc, P.A.; Brinks, E.; Boquien, M.; Amram, P.; Lisenfeld, U.; Koribalski, B.S.; Walter, F.; Charmandaris, V. Missing Mass in Collisional Debris from Galaxies. Science 2007, 316, 1166. [Google Scholar] [CrossRef]
- Gentile, G.; Famaey, B.; Combes, F.; Kroupa, P.; Zhao, H.S.; Tiret, O. Tidal dwarf galaxies as a test of fundamental physics. Astronom. Astrophys. 2007, 472, L25–L28. [Google Scholar] [CrossRef]
- Milgrom, M. MOND and the Mass Discrepancies in Tidal Dwarf Galaxies. ApJL 2007, 667, L45–L48. [Google Scholar] [CrossRef][Green Version]
- Flores, H.; Hammer, F.; Fouquet, S.; Puech, M.; Kroupa, P.; Yang, Y.; Pawlowski, M. Young tidal dwarf galaxies cannot be used to probe dark matter in galaxies. Mont. Notices R. Astronom. Soc. 2016, 457, L14–L18. [Google Scholar] [CrossRef]
- Acedo, L. Modified Newtonian Gravity, Wide Binaries and the Tully-Fisher Relation. Universe 2020, 6, 209. [Google Scholar] [CrossRef]
- Banik, I.; Kroupa, P. Testing gravity with interstellar precursor missions. Mont. Notices R. Astronom. Soc. 2019, 487, 2665–2672. [Google Scholar] [CrossRef]
- Kervella, P.; Thévenin, F.; Lovis, C. Proxima’s orbit around α Centauri. Astronom. Astrophys. 2017, 598, L7. [Google Scholar] [CrossRef]
- Kervella, P.; Mignard, F.; Mérand, A.; Thévenin, F. Close stellar conjunctions of α Centauri A and B until 2050. An mK = 7.8 star may enter the Einstein ring of α Cen A in 2028. Astronom. Astrophys. 2016, 594, A107. [Google Scholar] [CrossRef]
- Beech, M. Proxima Centauri: A transitional modified Newtonian dynamics controlled orbital candidate? Mont. Notices R. Astronom. Soc. 2009, 399, L21–L23. [Google Scholar] [CrossRef]
- Beech, M. The orbit of Proxima Centauri: A MOND versus standard Newtonian distinction. Ap&SS 2011, 333, 419–426. [Google Scholar] [CrossRef]
- Bozorgnia, N.; Bertone, G. Implications of hydrodynamical simulations for the interpretation of direct dark matter searches. Int. J. Mod. Phys. A 2017, 32, 1730016. [Google Scholar] [CrossRef]
- Viswanathan, V.; Fienga, A.; Gastineau, M.; Laskar, J. INPOP17a planetary ephemerides. NSTIM 2017, 108. [Google Scholar] [CrossRef]
- Scarpa, R.; Ottolina, R.; Falomo, R.; Treves, A. Dynamics of wide binary stars: A case study for testing Newtonian dynamics in the low acceleration regime. Int. J. Mod. Phys. D 2017, 26, 1750067. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 2. Summary of the contents and survey properties. Astronom. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Andrews, J.J.; Chanamé, J.; Agüeros, M.A. Wide binaries in Tycho-Gaia: Search method and the distribution of orbital separations. Mont. Notices R. Astronom. Soc. 2017, 472, 675–699. [Google Scholar] [CrossRef]
- Hernandez, X.; Cortés, R.A.M.; Allen, C.; Scarpa, R. Challenging a Newtonian prediction through Gaia wide binaries. Int. J. Mod. Phys. D 2019, 28, 1950101. [Google Scholar] [CrossRef]
- El-Badry, K. The geometric challenge of testing gravity with wide binaries. Mont. Notices R. Astronom. Soc. 2019, 482, 5018–5022. [Google Scholar] [CrossRef]
- Banik, I. A new line on the wide binary test of gravity. Mont. Notices R. Astronom. Soc. 2019, 487, 5291–5303. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Tremaine, S. The evolution of wide binary stars. Mont. Notices R. Astronom. Soc. 2010, 401, 977–994. [Google Scholar] [CrossRef]
- Pittordis, C.; Sutherland, W. Testing Modified Gravity Theories via Wide Binaries and GAIA. Mont. Notices R. Astronom. Soc. 2018, 480, 1778–1795. [Google Scholar] [CrossRef]
- Loeb, A. Gravitational Redshift for Wide Binaries in Gaia eDR3. Res. Notes Am. Astron. Soc. 2022, 6, 55. [Google Scholar] [CrossRef]
- Clarke, C.J. The distribution of relative proper motions of wide binaries in Gaia DR2: MOND or multiplicity? Mont. Notices R. Astronom. Soc. 2020, 491, L72–L75. [Google Scholar] [CrossRef]
- Belokurov, V.; Penoyre, Z.; Oh, S.; Iorio, G.; Hodgkin, S.; Evans, N.W.; Everall, A.; Koposov, S.E.; Tout, C.A.; Izzard, R.; et al. Unresolved stellar companions with Gaia DR2 astrometry. Mont. Notices R. Astronom. Soc. 2020, 496, 1922–1940. [Google Scholar] [CrossRef]
- Hernandez, X.; Cookson, S.; Cortés, R.A.M. Internal kinematics of GAIA eDR3 wide binaries. Mont. Notices R. Astronom. Soc. 2022, 509, 2304–2317. [Google Scholar] [CrossRef]
- Banik, I.; Pittordis, C.; Sutherland, W. Detailed numerical implementation of the wide binary test. arXiv 2021, arXiv:2109.03827. [Google Scholar]
- Banik, I.; Kroupa, P. Directly testing gravity with Proxima Centauri. Mont. Notices R. Astronom. Soc. 2019, 487, 1653–1661. [Google Scholar] [CrossRef]
- Theia Collaboration. Theia: Faint objects in motion or the new astrometry frontier. arXiv 2017, arXiv:1707.01348. [Google Scholar]
- Hobbs, D.; Brown, A.; Høg, E.; Jordi, C.; Kawata, D.; Tanga, P.; Klioner, S.; Sozzetti, A.; Wyrzykowski, Ł; Walton, N.; et al. All-sky visible and near infrared space astrometry. Exp. Astron. 2021, 51, 783–843. [Google Scholar] [CrossRef]
- Malbet, F.; Boehm, C.; Krone-Martins, A.; Amorim, A.; Anglada-Escudé, G.; Brandeker, A.; Courbin, F.; Enßlin, T.; Falcão, A.; Freese, K.; et al. Faint objects in motion: The new frontier of high precision astrometry. Exp. Astron. 2021, 51, 845–886. [Google Scholar] [CrossRef]
- Milgrom, M. MOND effects in the inner Solar system. Mont. Notices R. Astronom. Soc. 2009, 399, 474–486. [Google Scholar] [CrossRef]
- Blanchet, L.; Novak, J. External field effect of modified Newtonian dynamics in the Solar system. Mont. Notices R. Astronom. Soc. 2011, 412, 2530–2542. [Google Scholar] [CrossRef]
- Matson, D.L. Cassini: A mission to Saturn and Titan. In Symposium on Titan; Kaldeich, B., Ed.; ESA Special Publication: Noordwijk, The Netherlands, 1992; Volume 338. [Google Scholar]
- Batygin, K.; Brown, M.E. Evidence for a Distant Giant Planet in the Solar System. Astronom. J. 2016, 151, 22. [Google Scholar] [CrossRef]
- Shankman, C.; Kavelaars, J.J.; Bannister, M.T.; Gladman, B.J.; Lawler, S.M.; Chen, Y.T.; Jakubik, M.; Kaib, N.; Alexandersen, M.; Gwyn, S.D.J.; et al. OSSOS. VI. Striking Biases in the Detection of Large Semimajor Axis Trans-Neptunian Objects. Astronom. J. 2017, 154, 50. [Google Scholar] [CrossRef]
- Bernardinelli, P.H.; Bernstein, G.M.; Sako, M.; Hamilton, S.; Gerdes, D.W.; Adams, F.C.; Saunders, W.R.; Aguena, M.; Allam, S.; Avila, S.; et al. Testing the Isotropy of the Dark Energy Survey’s Extreme Trans-Neptunian Objects. Planet. Sci. J. 2020, 1, 28. [Google Scholar] [CrossRef]
- Napier, K.J.; Gerdes, D.W.; Lin, H.W.; Hamilton, S.J.; Bernstein, G.M.; Bernardinelli, P.H.; Abbott, T.M.C.; Aguena, M.; Annis, J.; Avila, S.; et al. No Evidence for Orbital Clustering in the Extreme Trans-Neptunian Objects. Planet. Sci. J. 2021, 2, 59. [Google Scholar] [CrossRef]
- Bergé, J.; Baudis, L.; Brax, P.; Chiow, S.W.; Christophe, B.; Doré, O.; Fayet, P.; Hees, A.; Jetzer, P.; Lämmerzahl, C.; et al. The local dark sector. Exp. Astron. 2021, 51, 1737–1766. [Google Scholar] [CrossRef]
- Heller, R. Relativistic generalization of the incentive trap of interstellar travel with application to Breakthrough Starshot. Mont. Notices R. Astronom. Soc. 2017, 470, 3664–3671. [Google Scholar] [CrossRef]
- Merali, Z. Shooting for a star. Science 2016, 352, 1040–1041. [Google Scholar] [CrossRef]
- Bekenstein, J.; Magueijo, J. Modified Newtonian dynamics habitats within the solar system. Phys. Rev. D 2006, 73, 103513. [Google Scholar] [CrossRef]
- Penner, A.R. A proposed experiment to test gravitational anti-screening and MOND using Sun-Gas giant saddle points. Ap&SS 2020, 365, 154. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Auger, G.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Bursi, A.; Caleno, M.; et al. The LISA Pathfinder Mission. J. Phys. Conf. Ser. 2015, 610, 012005. [Google Scholar] [CrossRef]
- Bevis, N.; Magueijo, J.; Trenkel, C.; Kemble, S. MONDian three-body predictions for LISA Pathfinder. Class. Quantum Gravity 2010, 27, 215014. [Google Scholar] [CrossRef]
- Magueijo, J.; Mozaffari, A. Case for testing modified Newtonian dynamics using LISA pathfinder. Phys. Rev. D 2012, 85, 043527. [Google Scholar] [CrossRef]
- Galianni, P.; Feix, M.; Zhao, H.; Horne, K. Testing quasilinear modified Newtonian dynamics in the Solar System. Phys. Rev. D 2012, 86, 044002. [Google Scholar] [CrossRef]
- Magueijo, J.; Mozaffari, A. Time delays across saddles as a test of modified gravity. Class. Quantum Gravity 2013, 30, 092002. [Google Scholar] [CrossRef]
- Kurdubov, S.L.; Pavlov, D.A.; Mironova, S.M.; Kaplev, S.A. Earth-Moon very-long-baseline interferometry project: Modelling of the scientific outcome. Mont. Notices R. Astronom. Soc. 2019, 486, 815–822. [Google Scholar] [CrossRef]
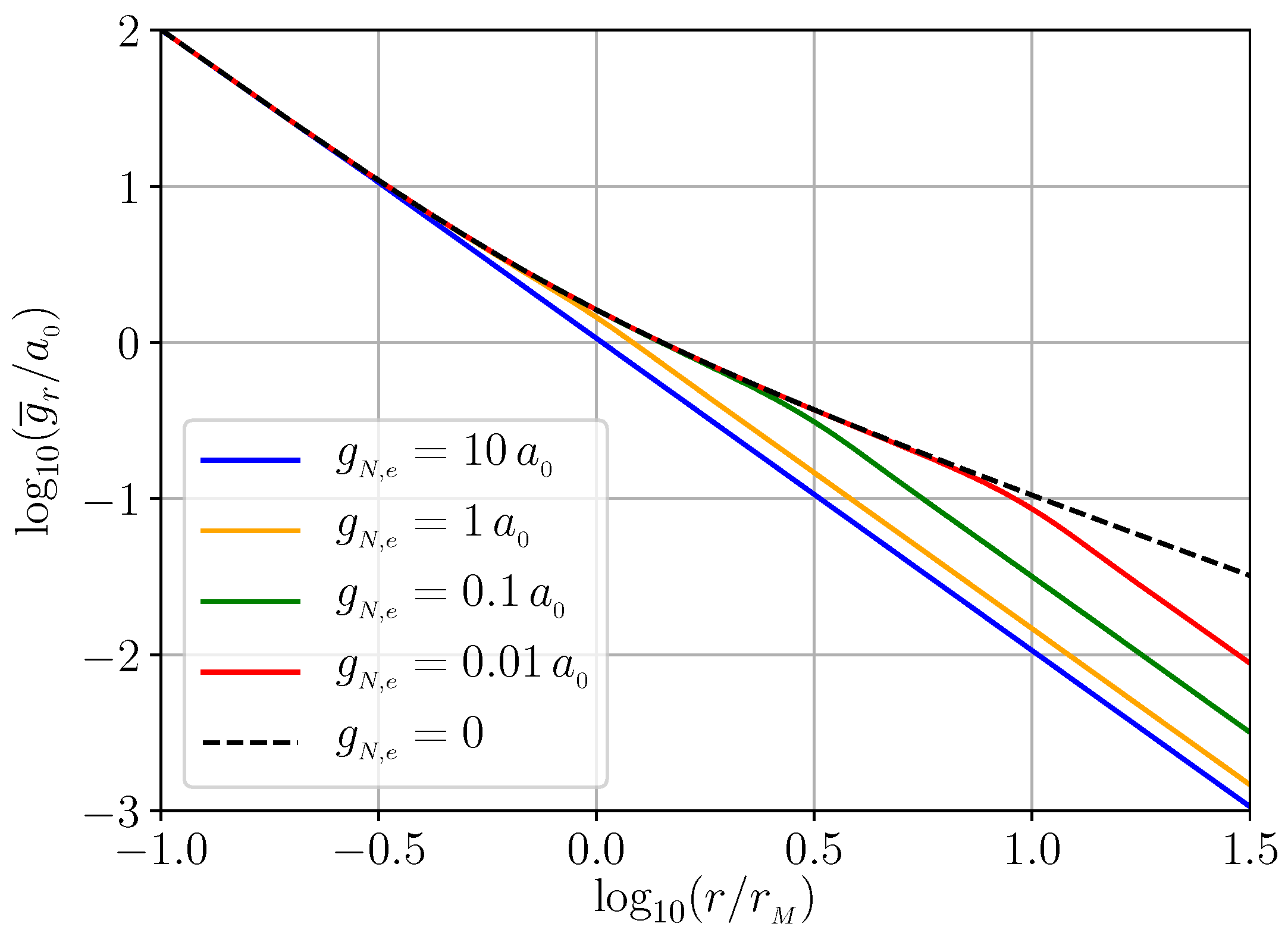
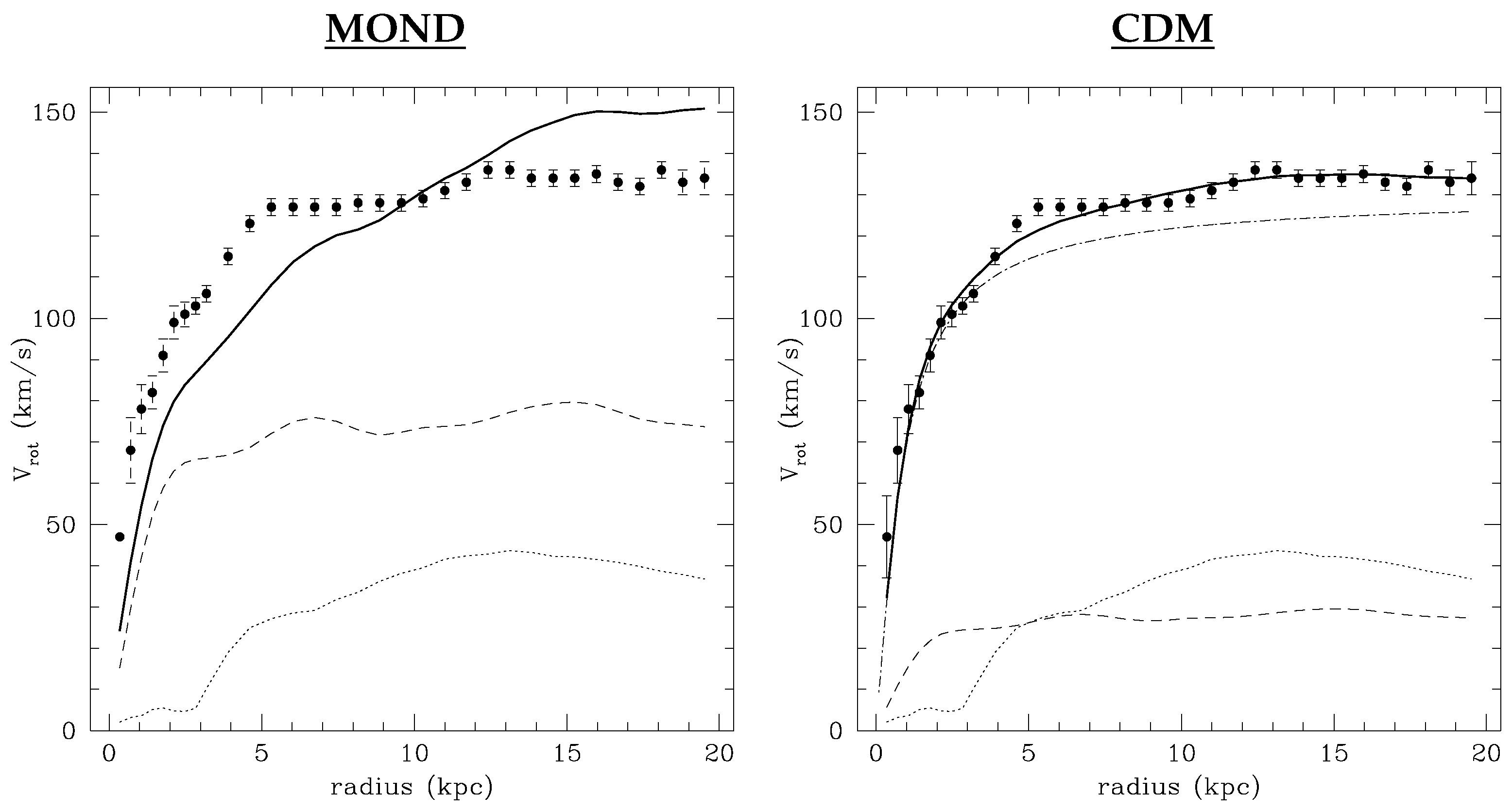
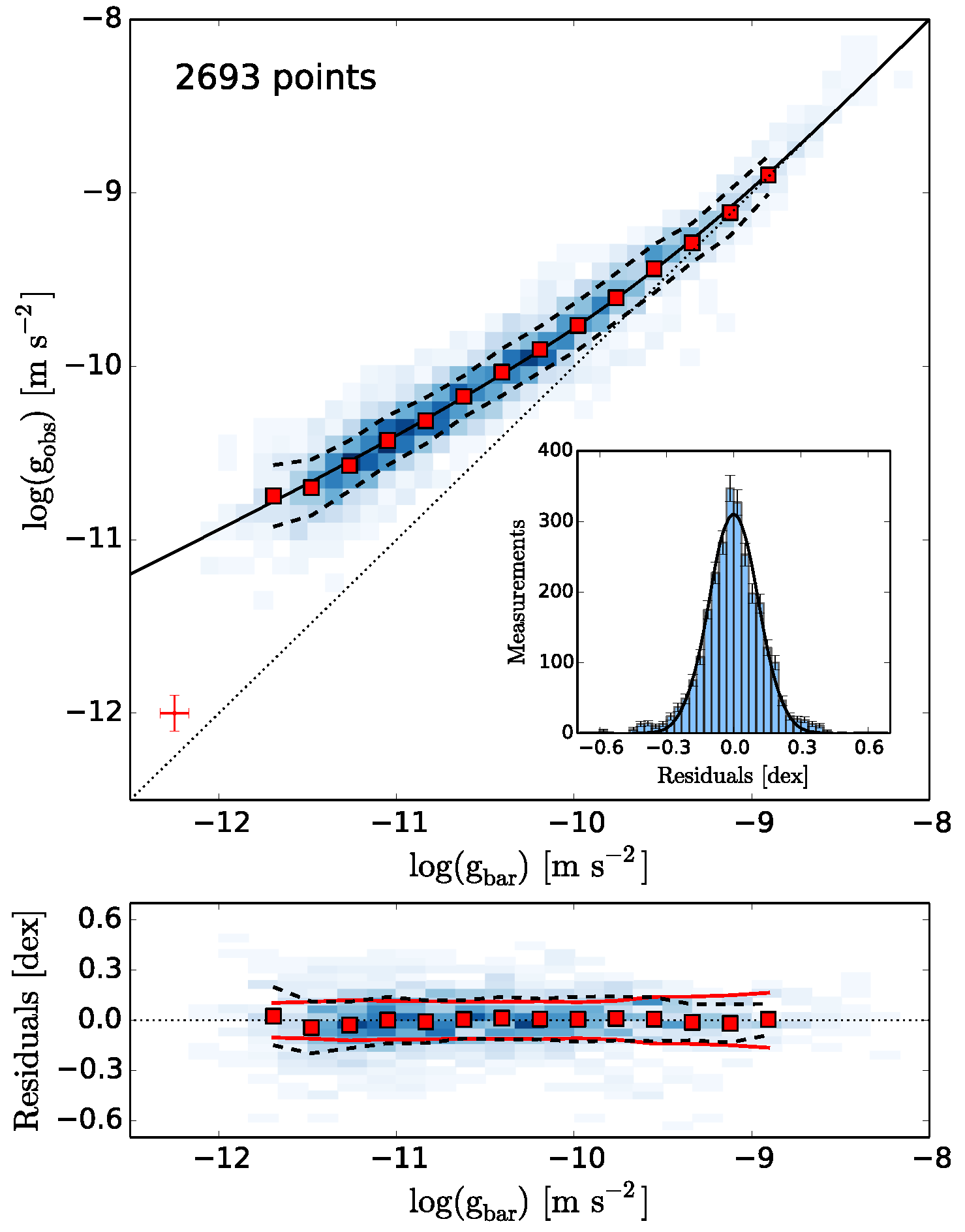
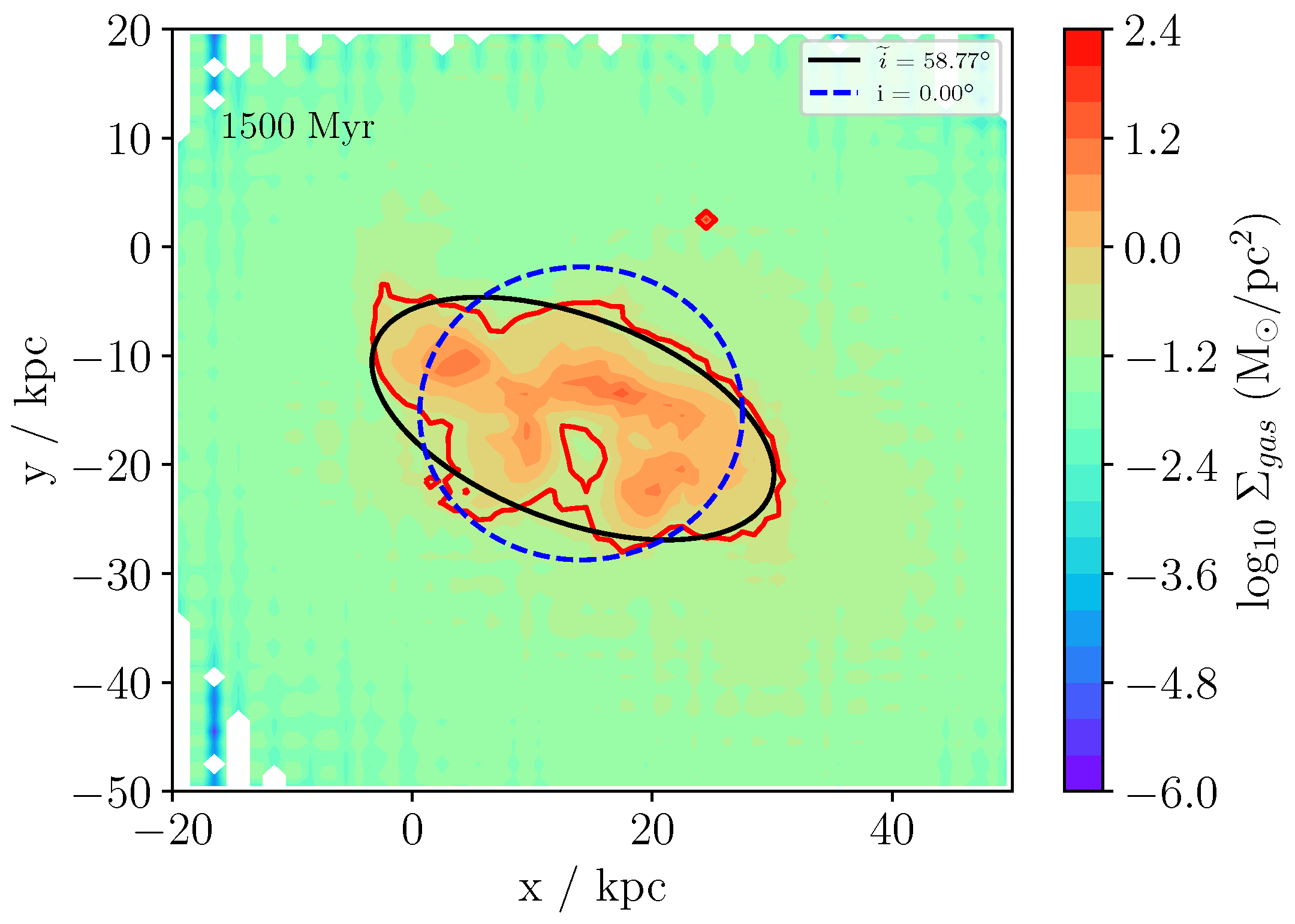
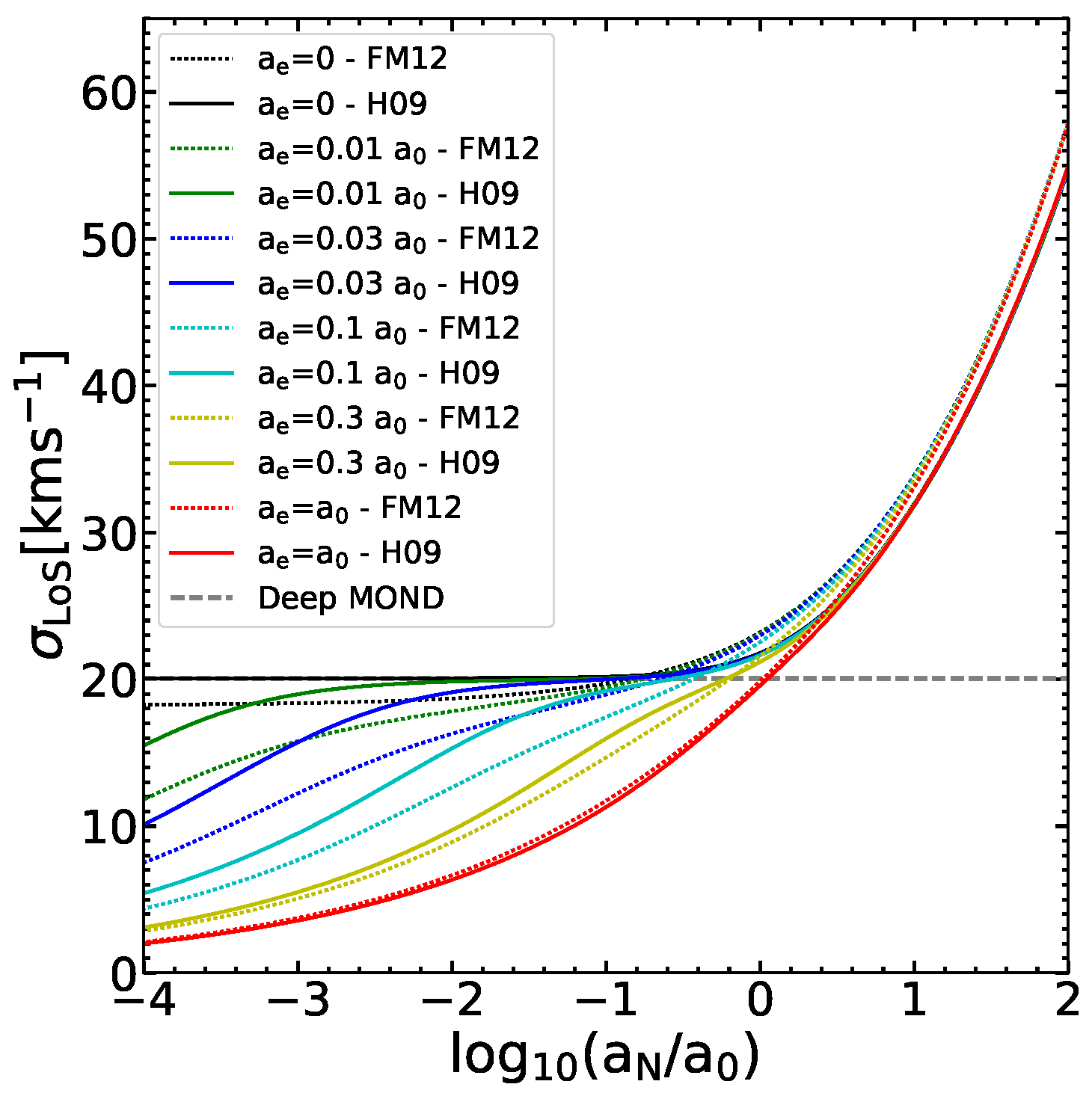
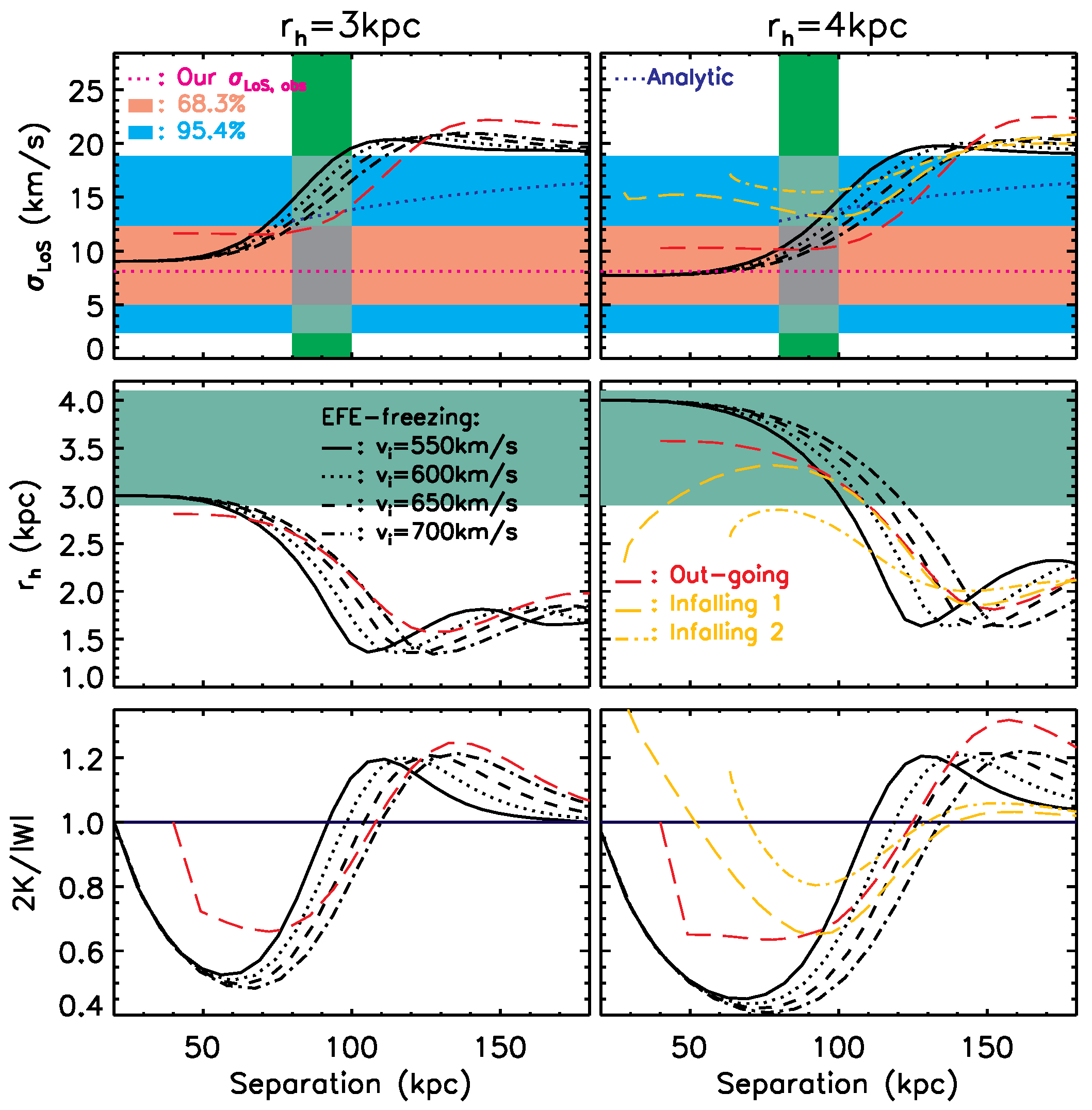
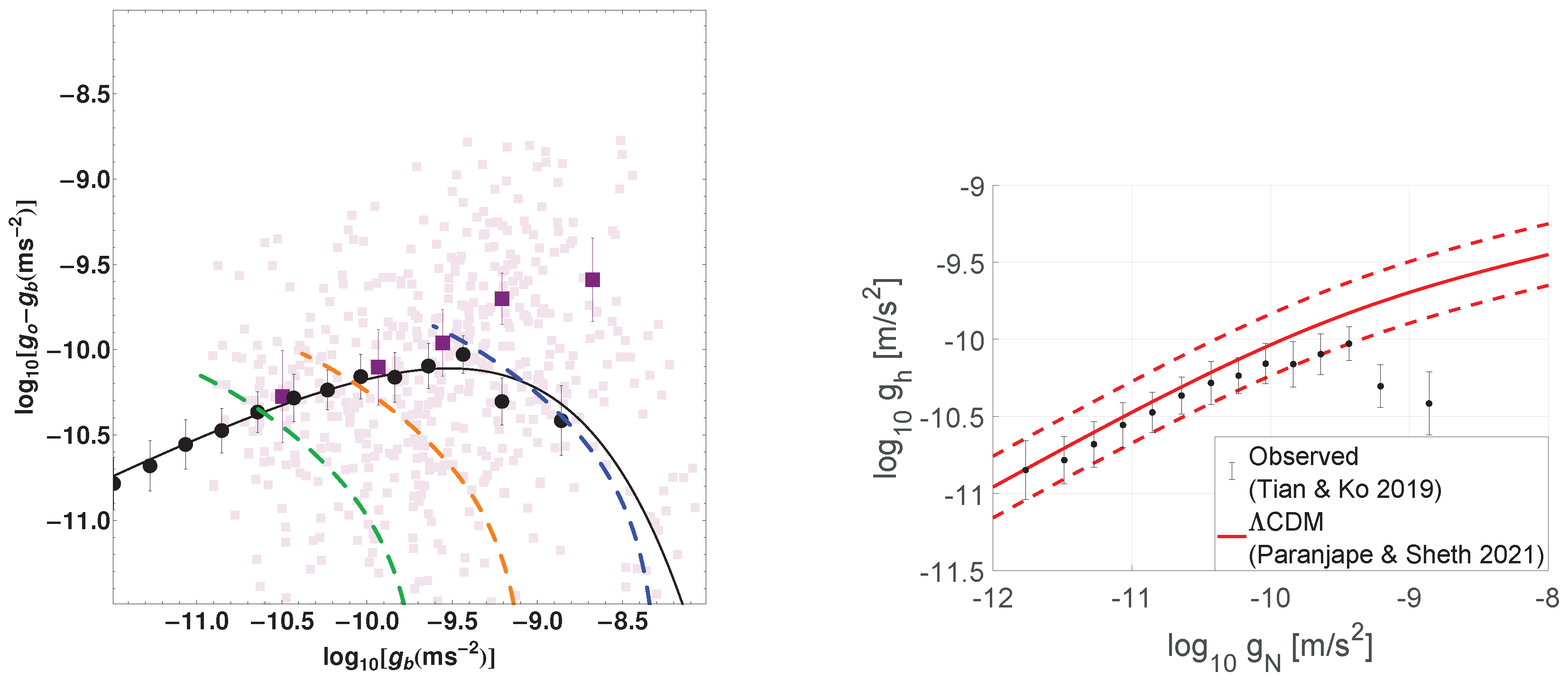
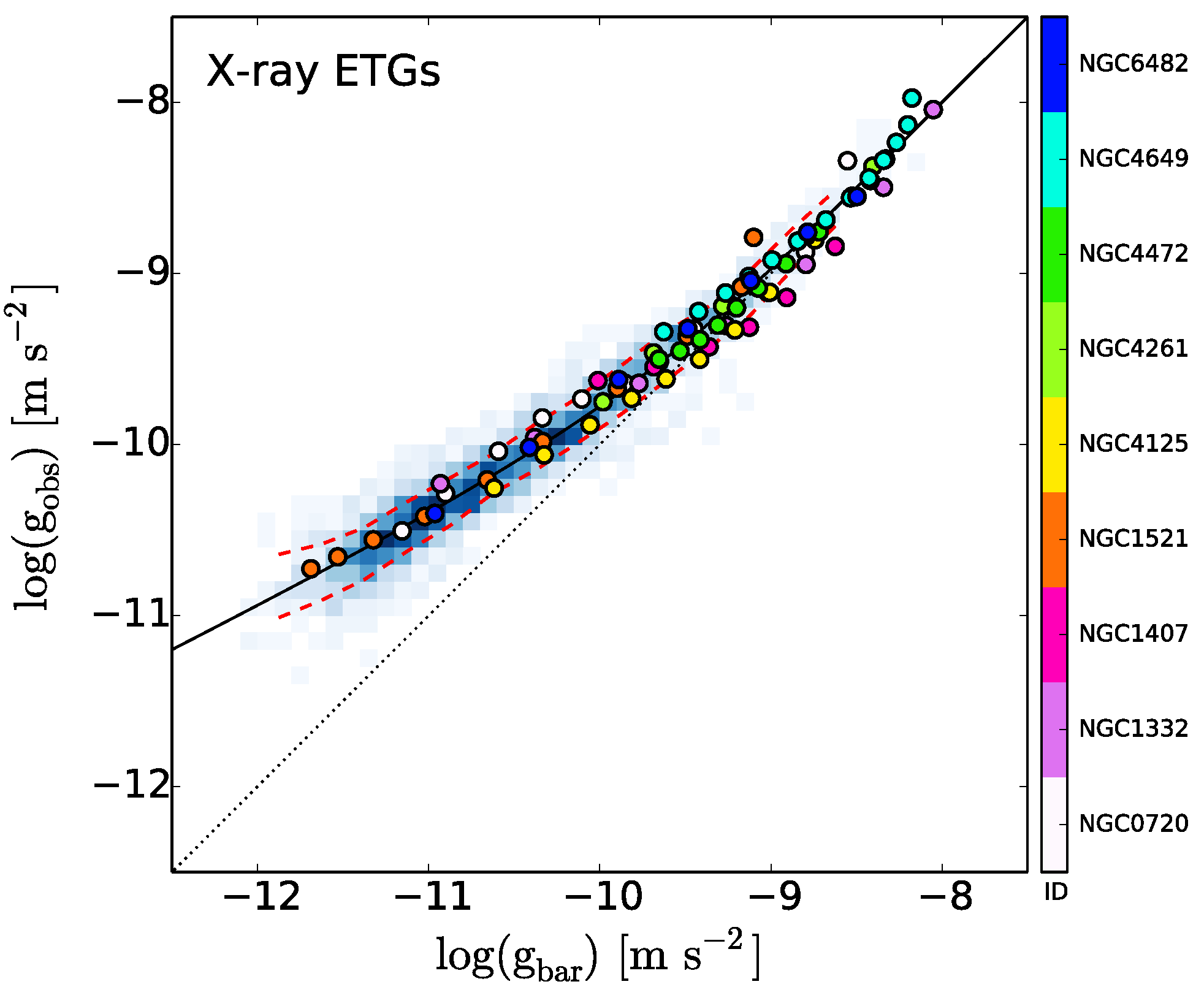
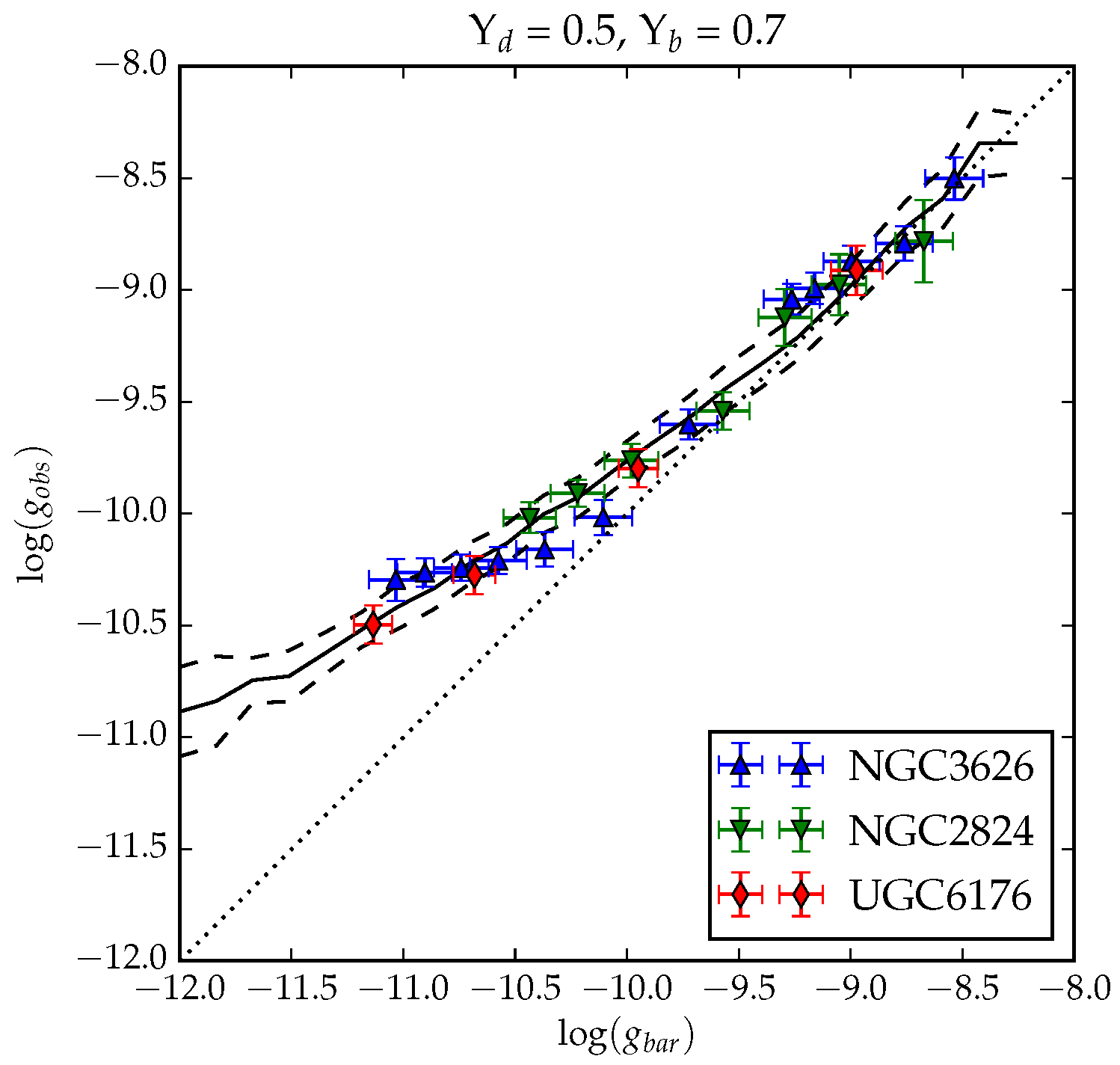
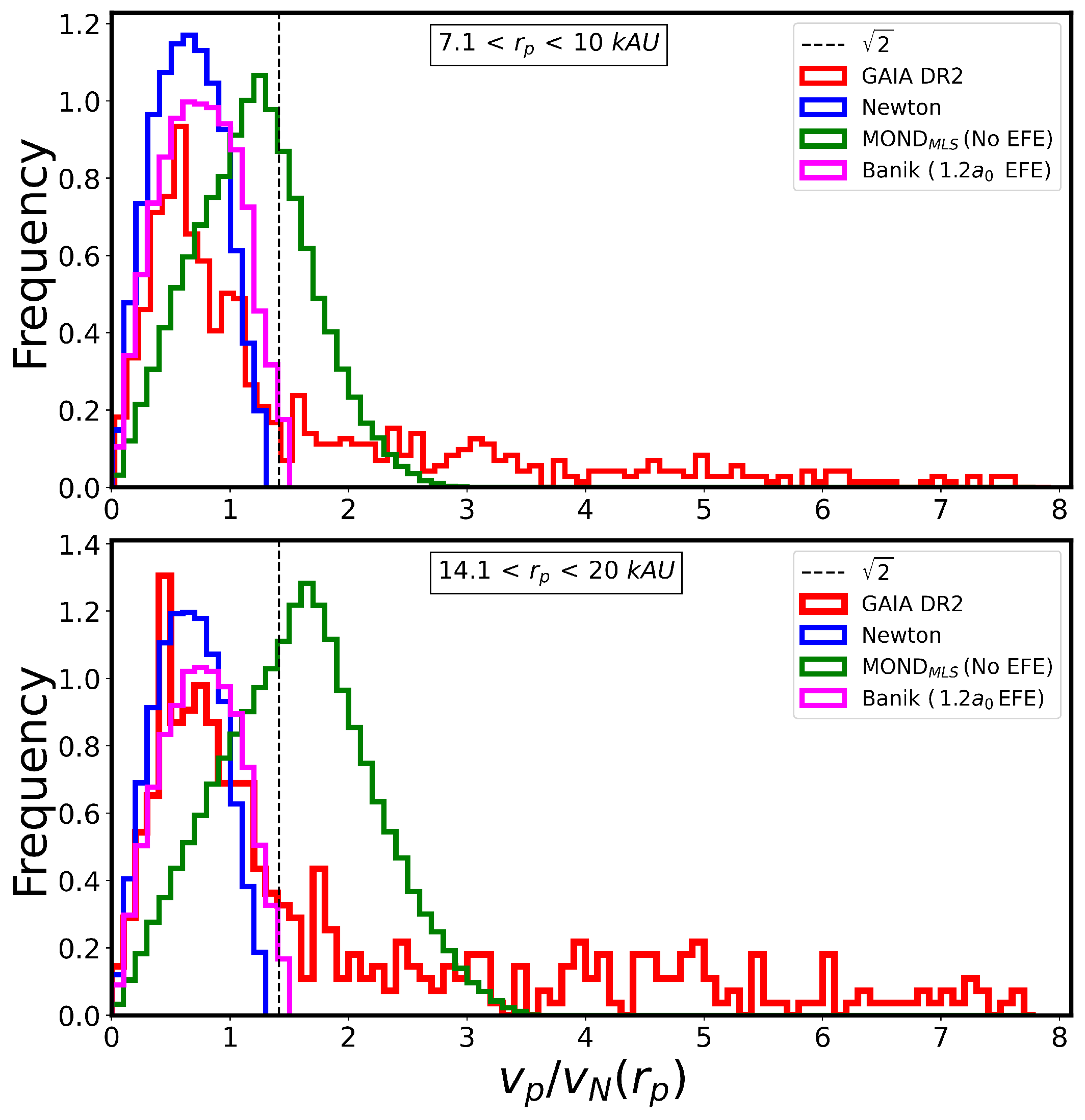
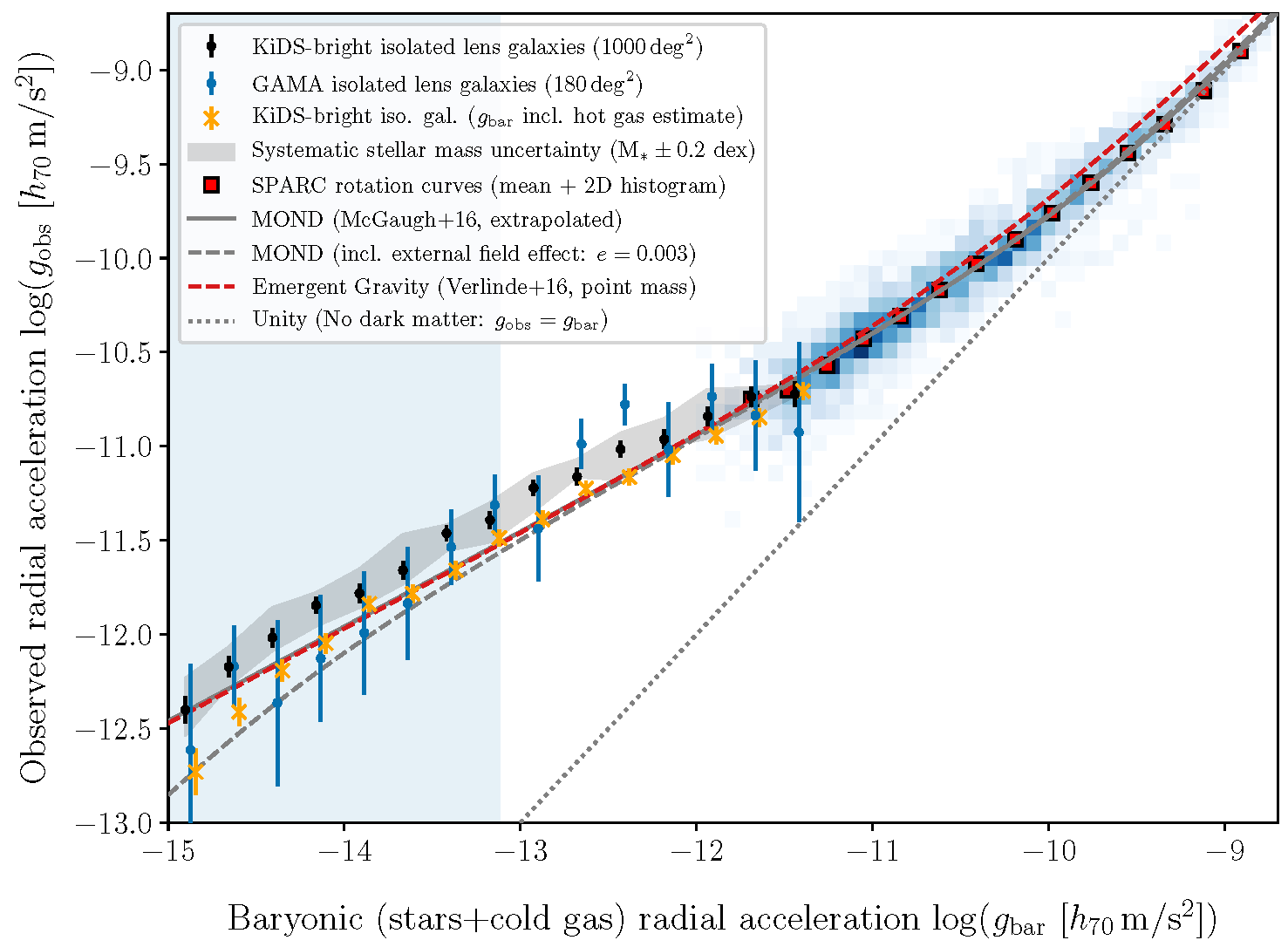

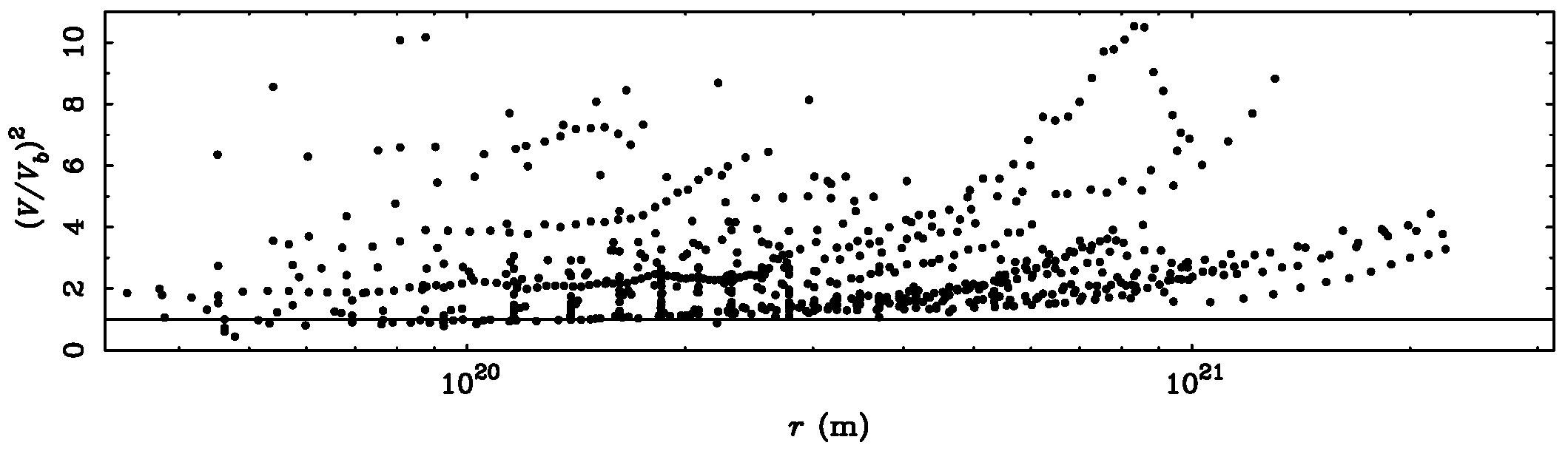
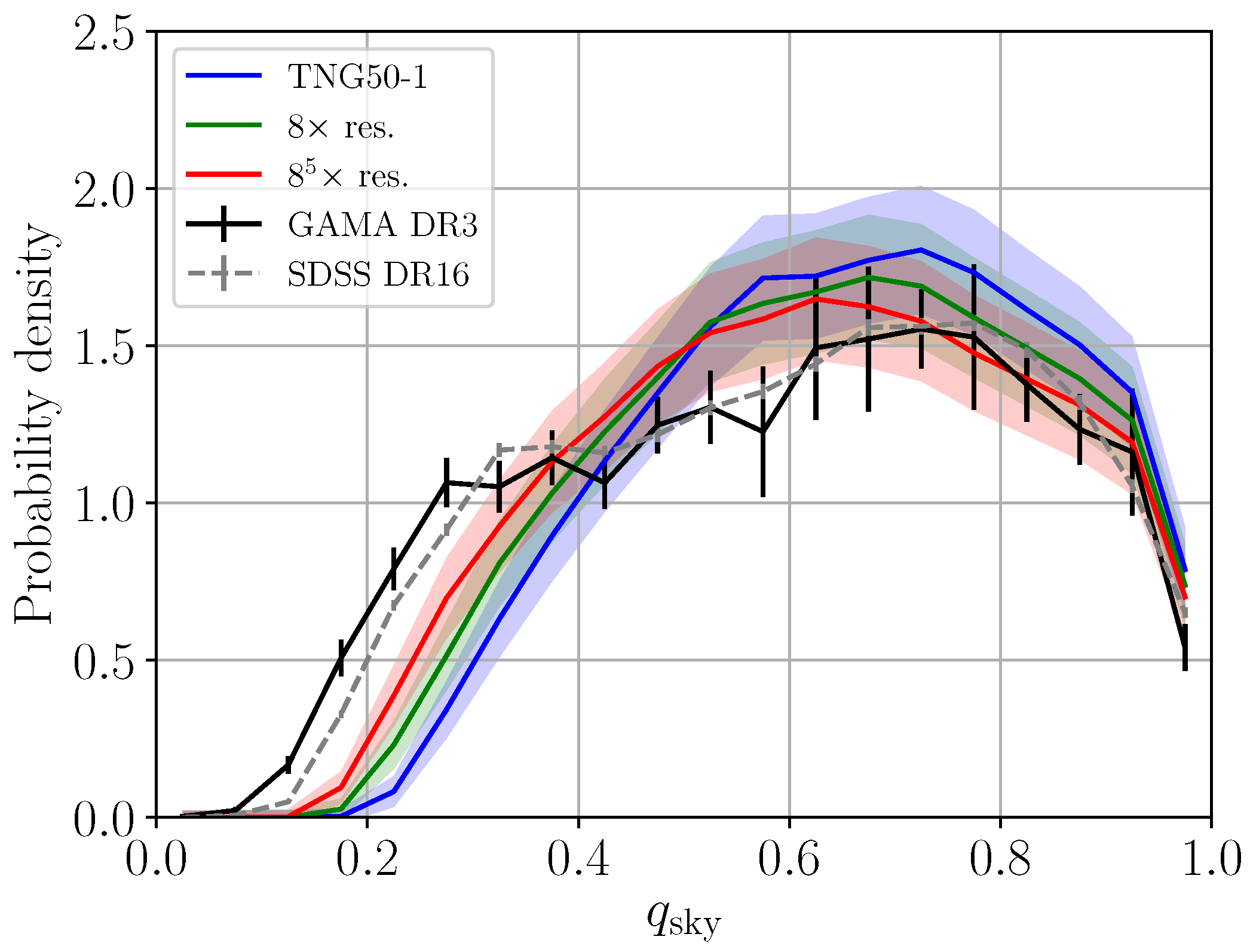
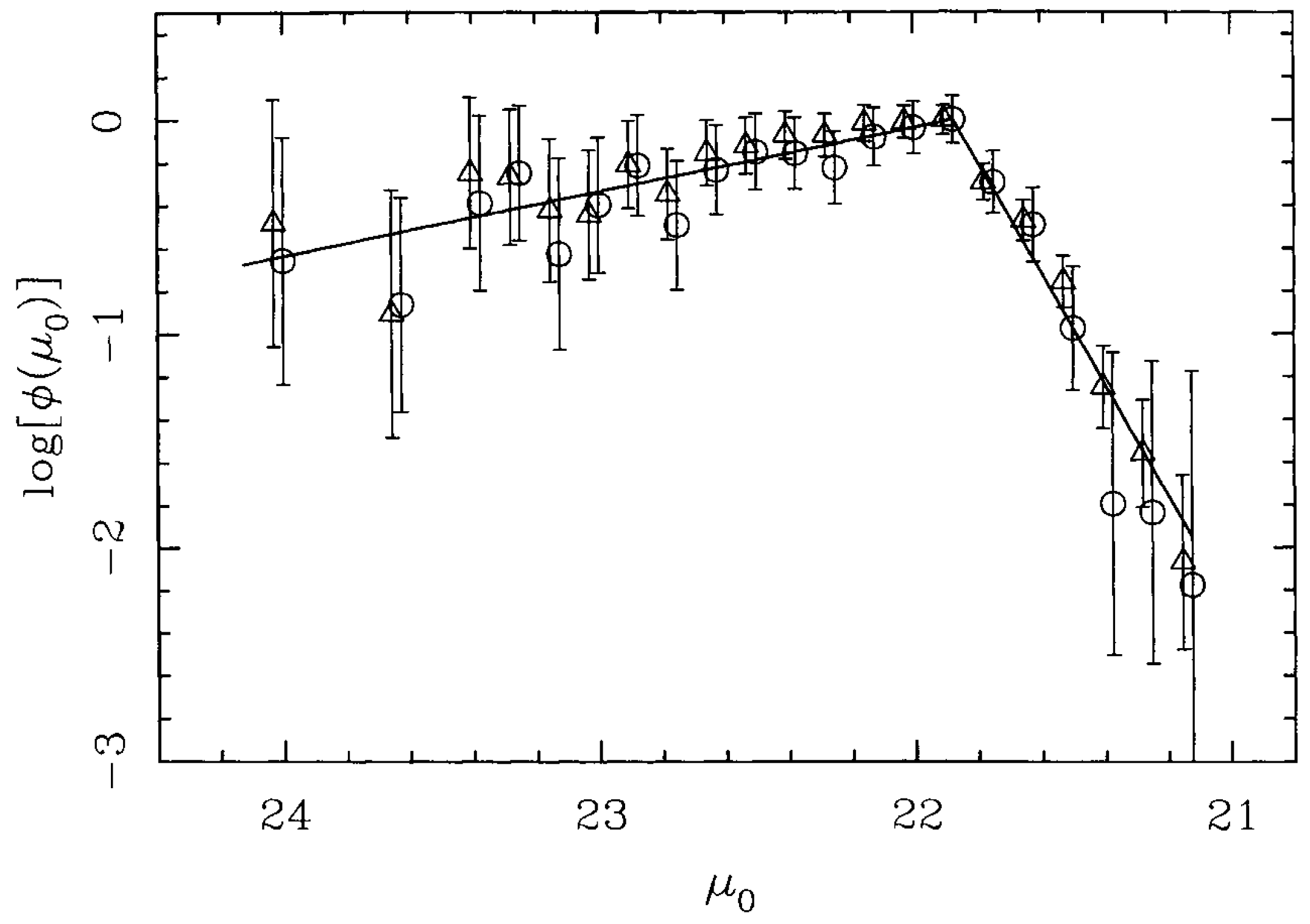
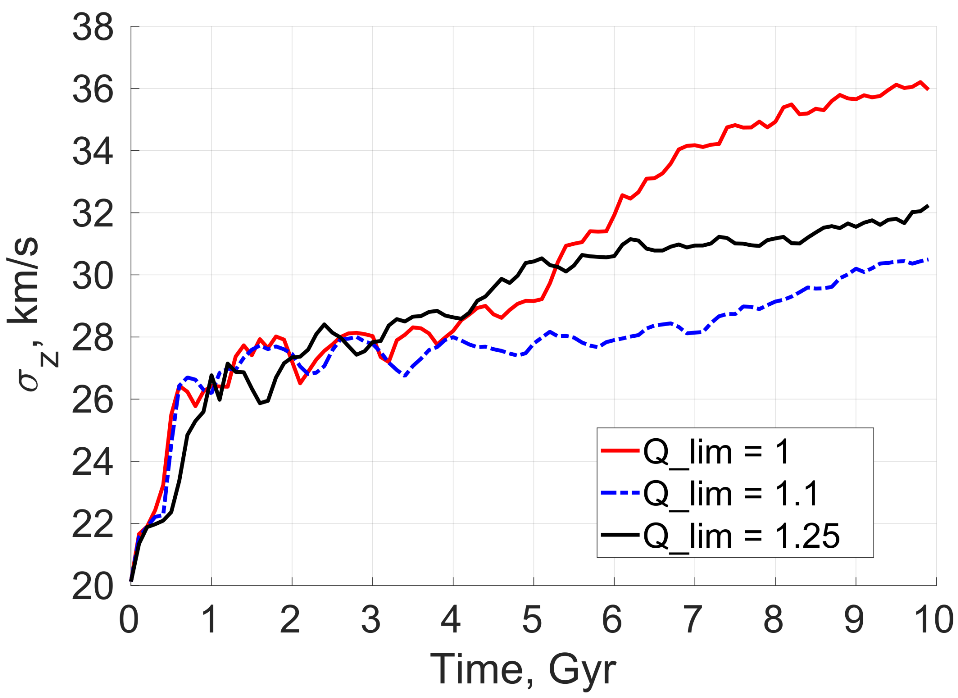
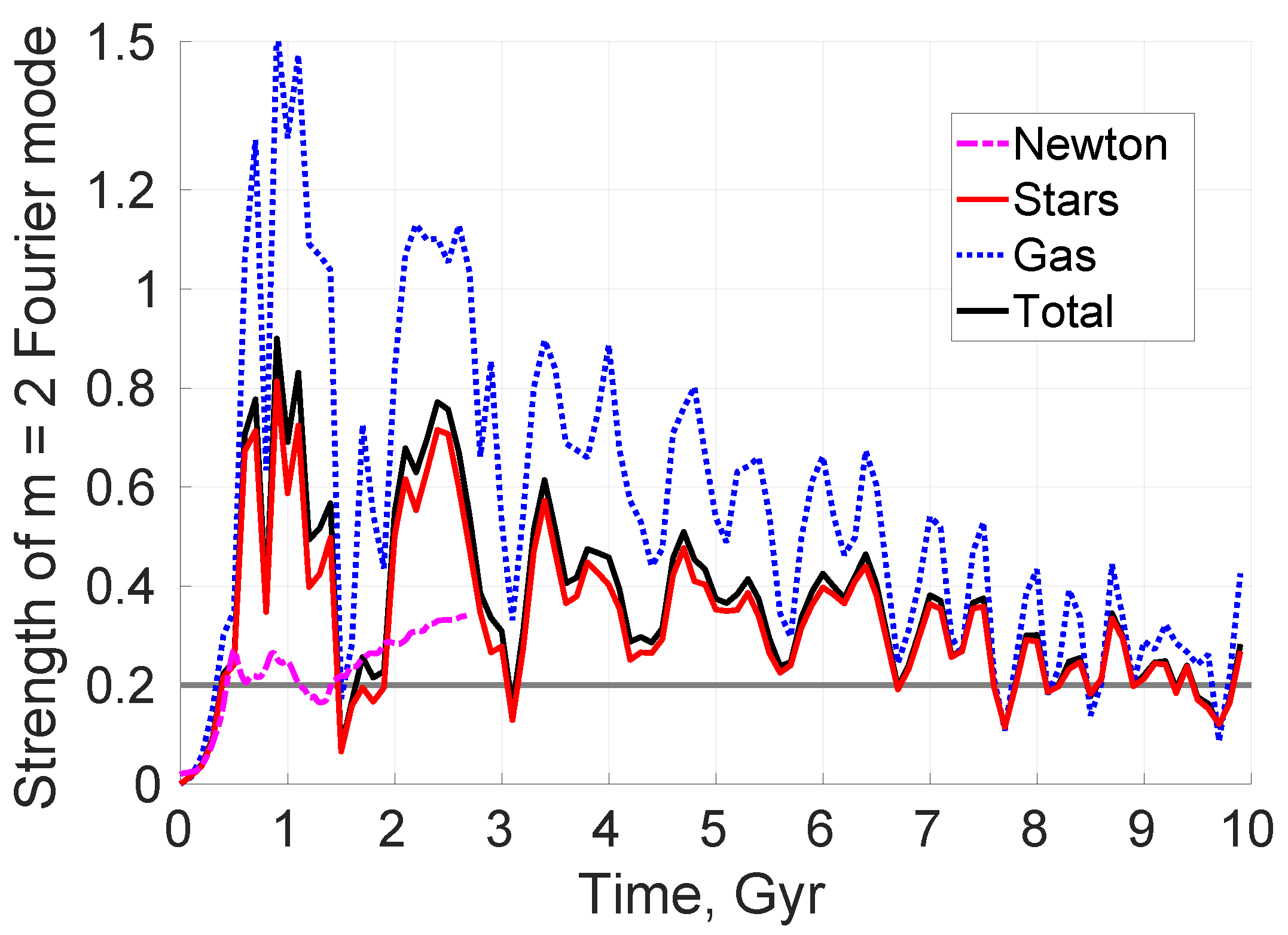
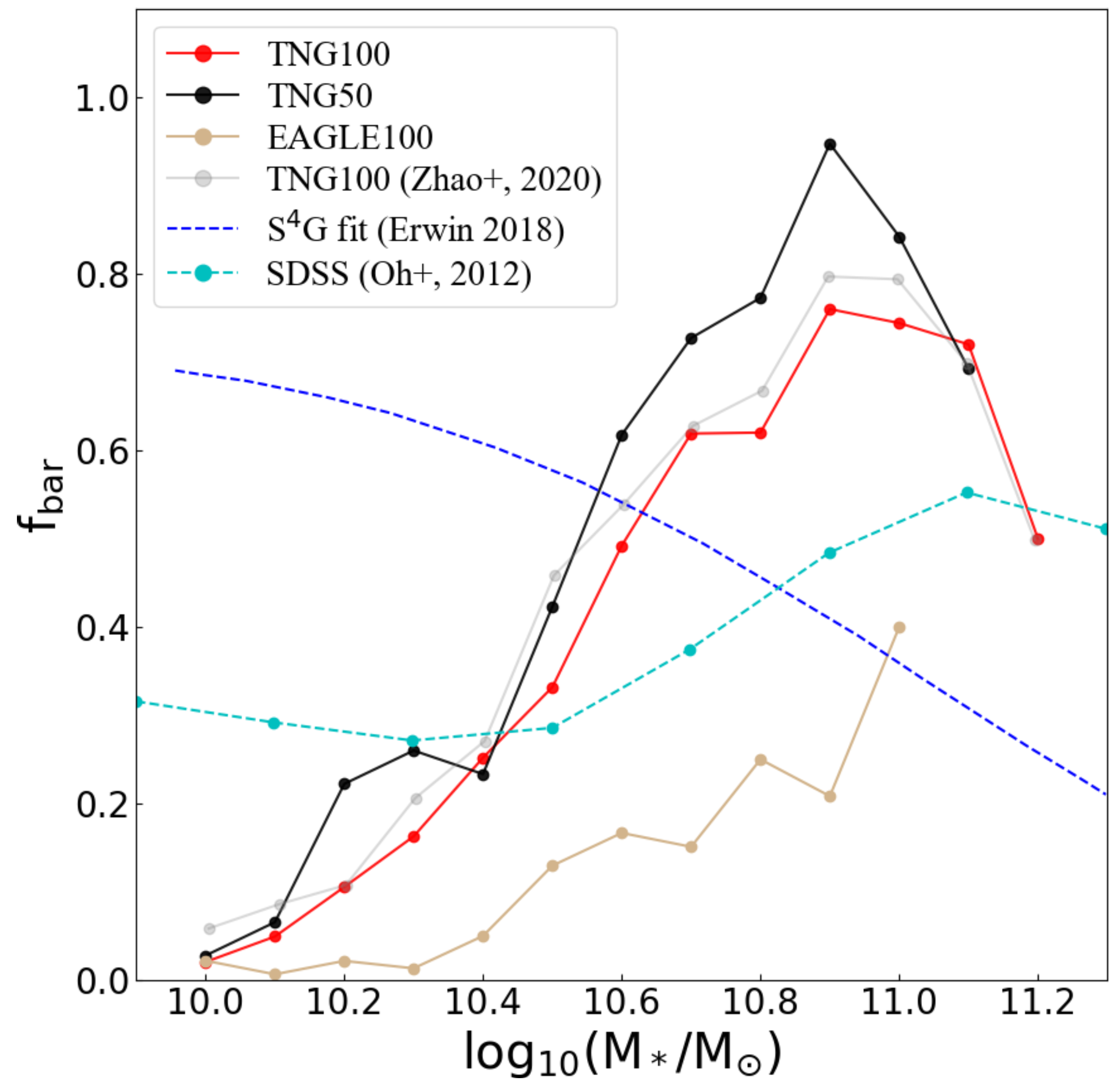
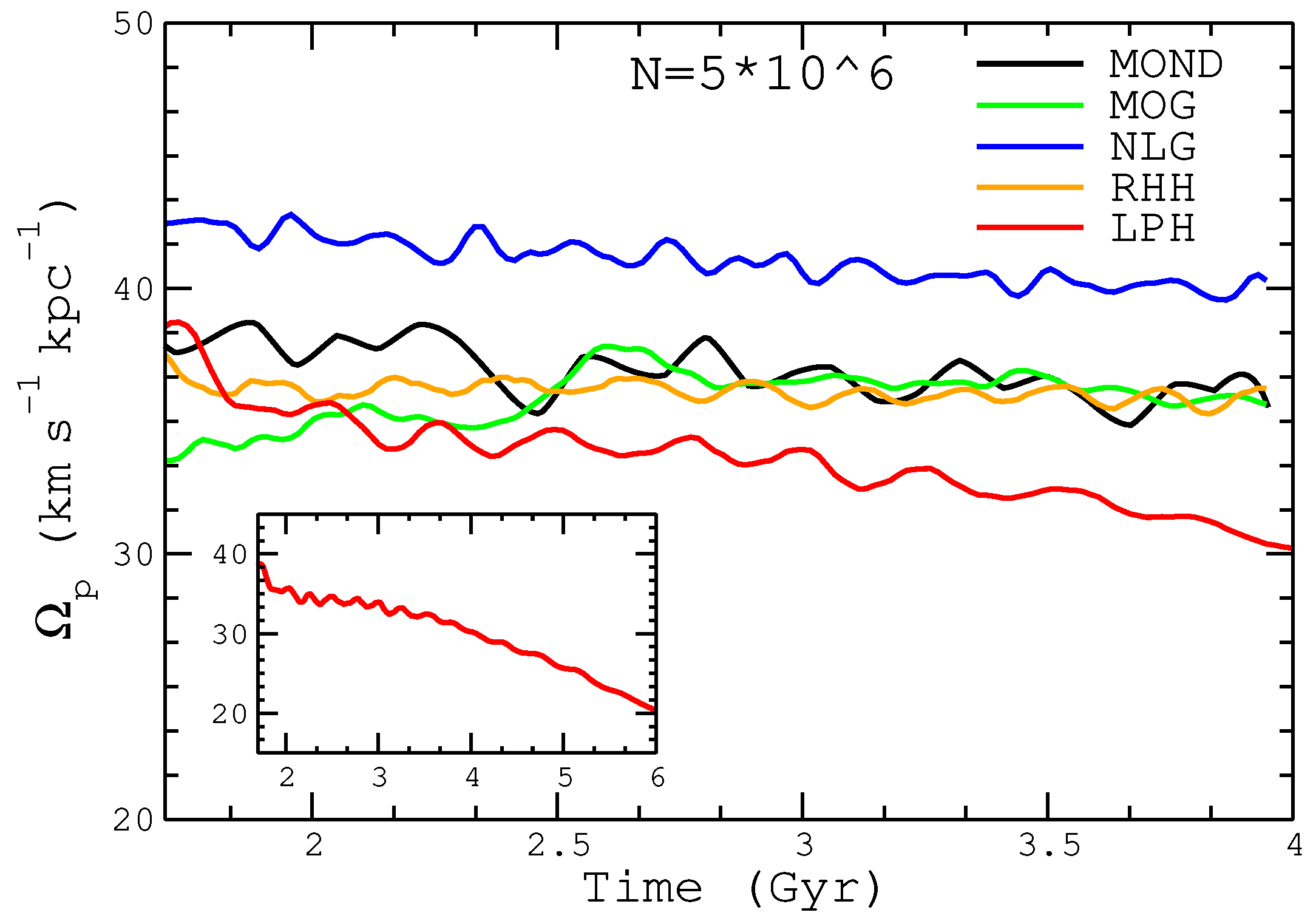


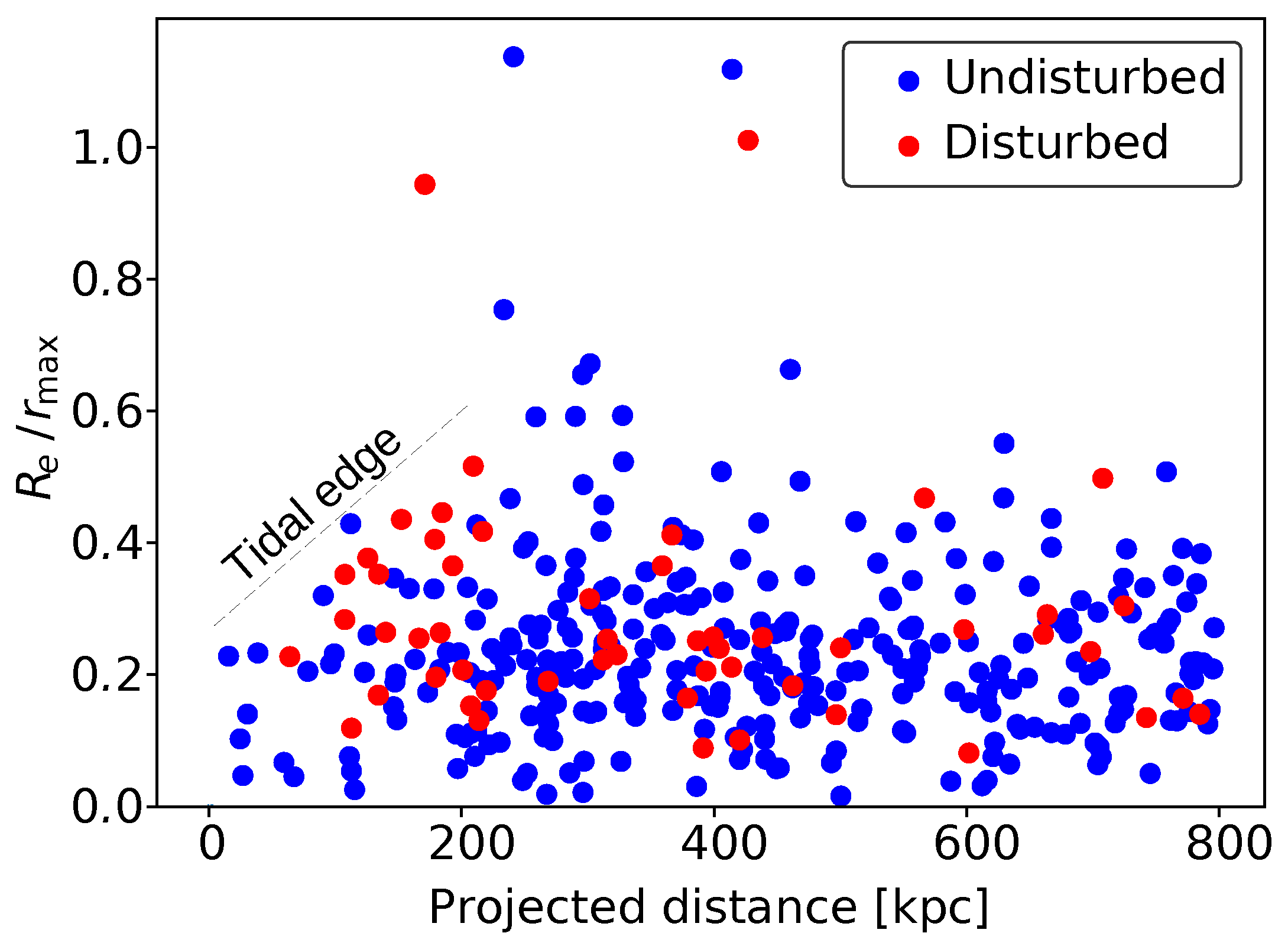

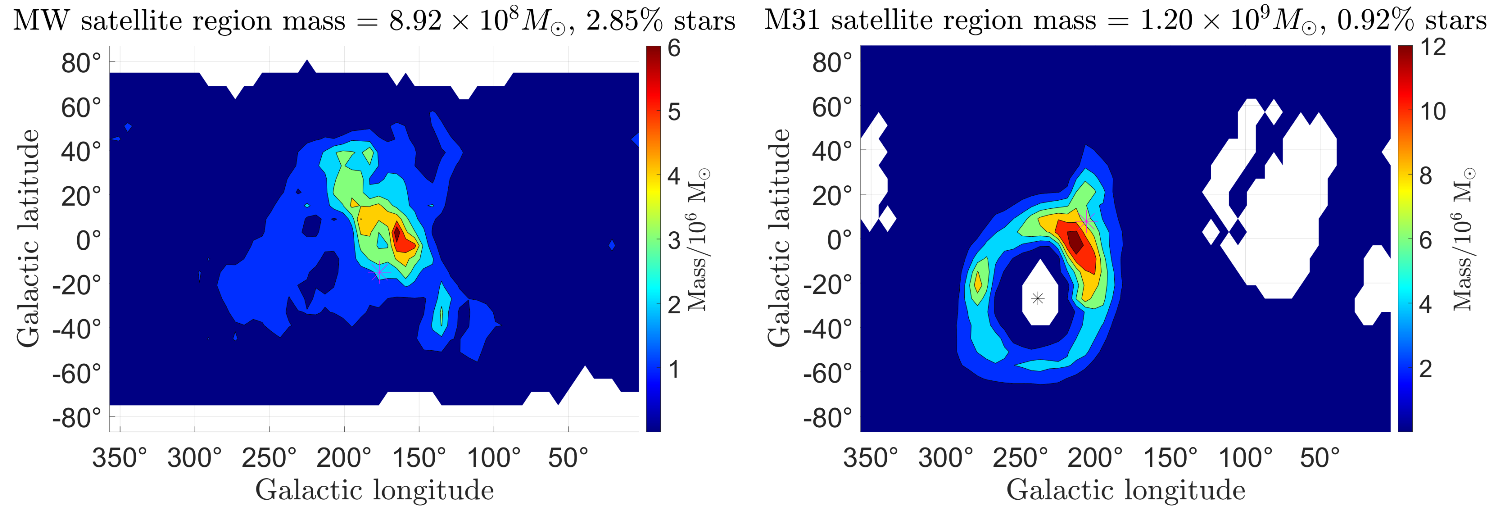
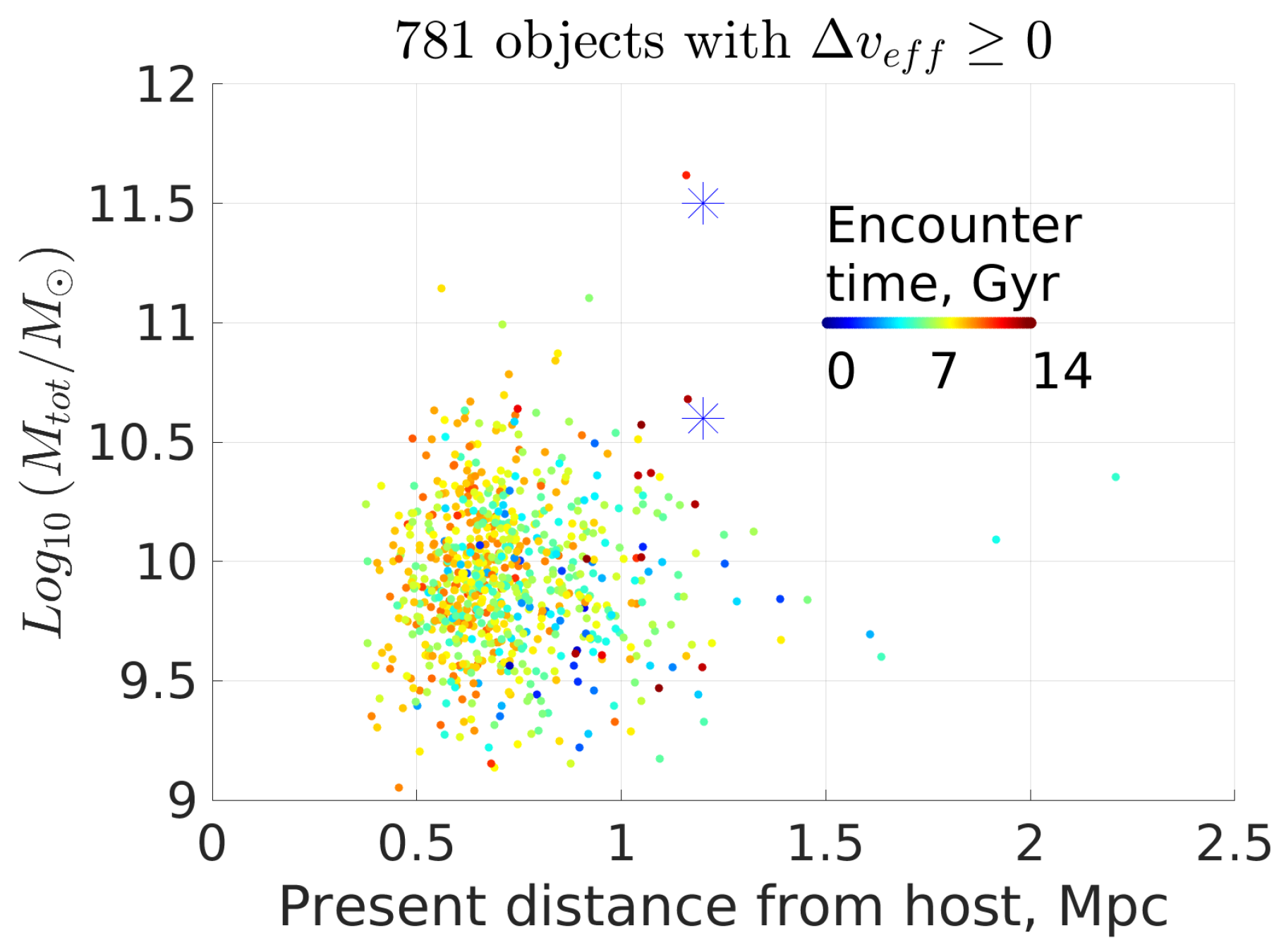
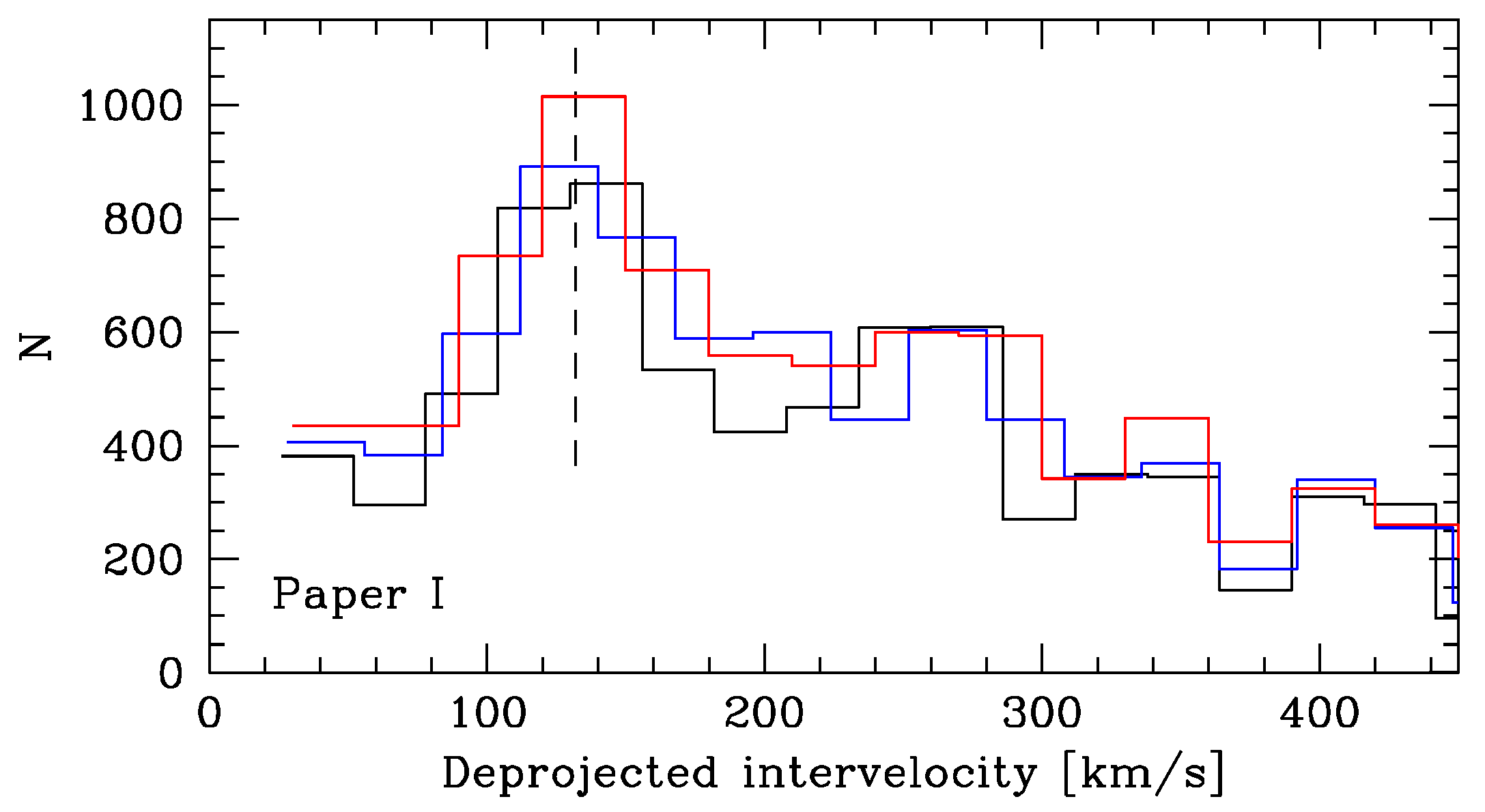
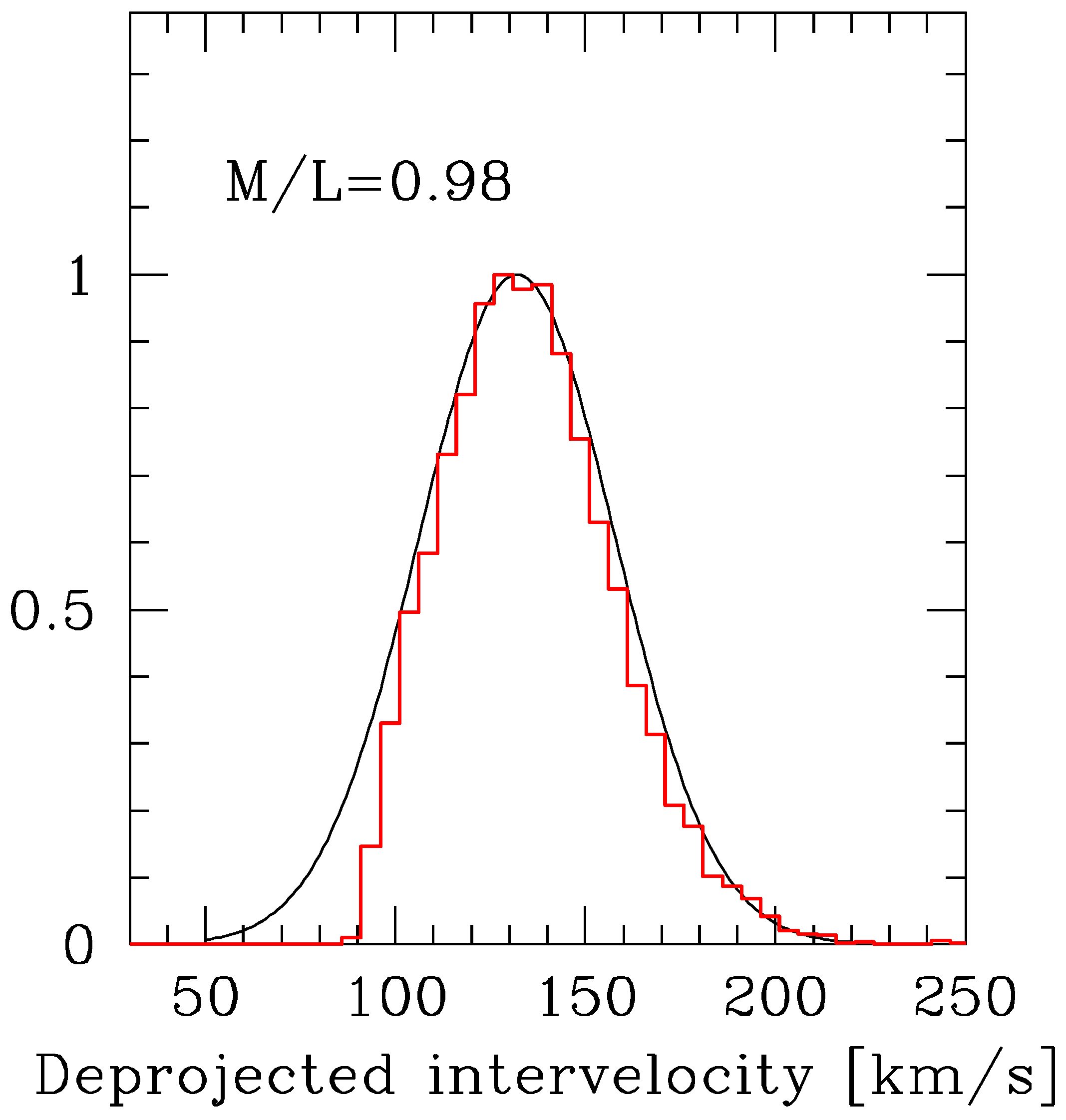
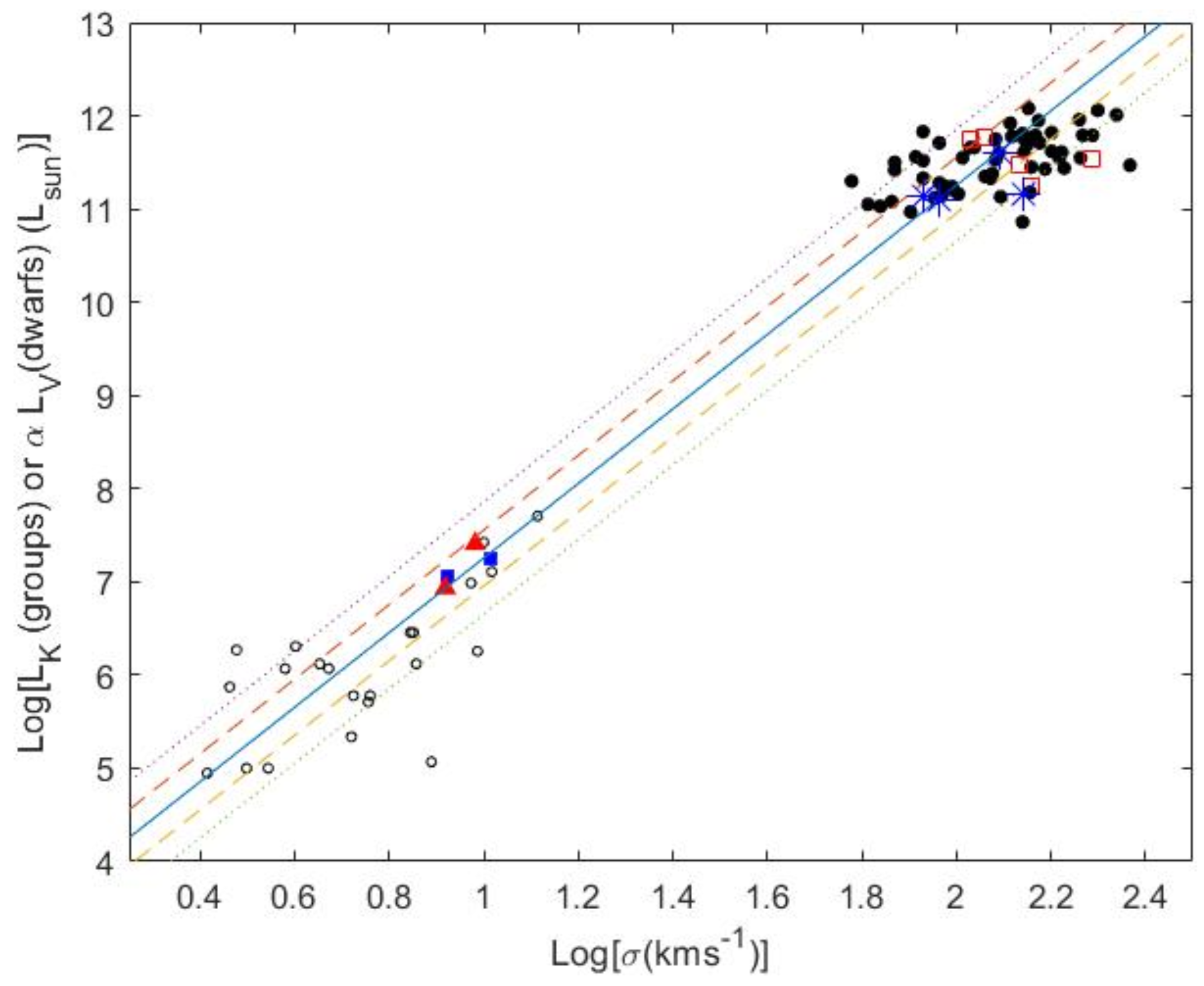
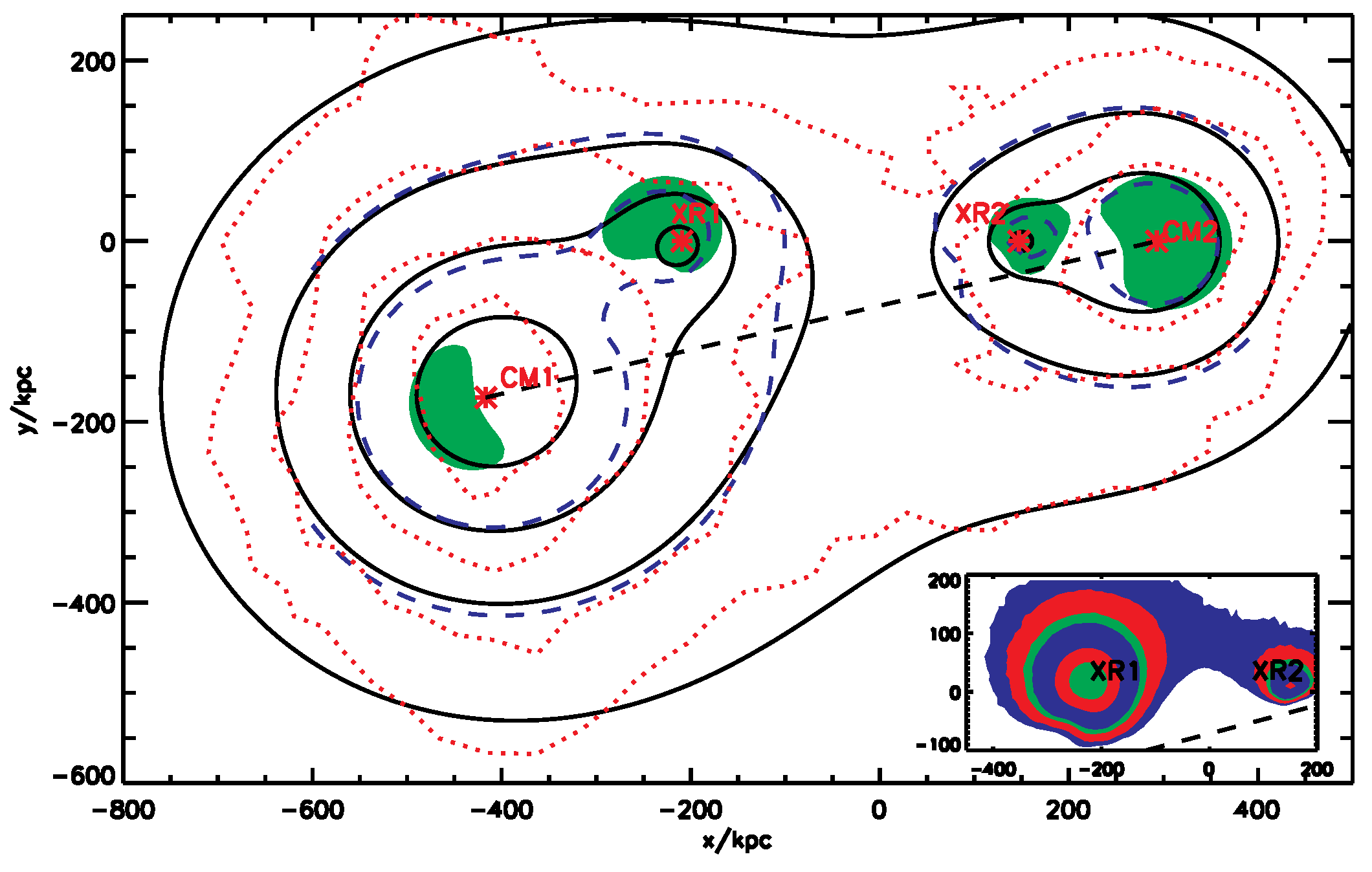
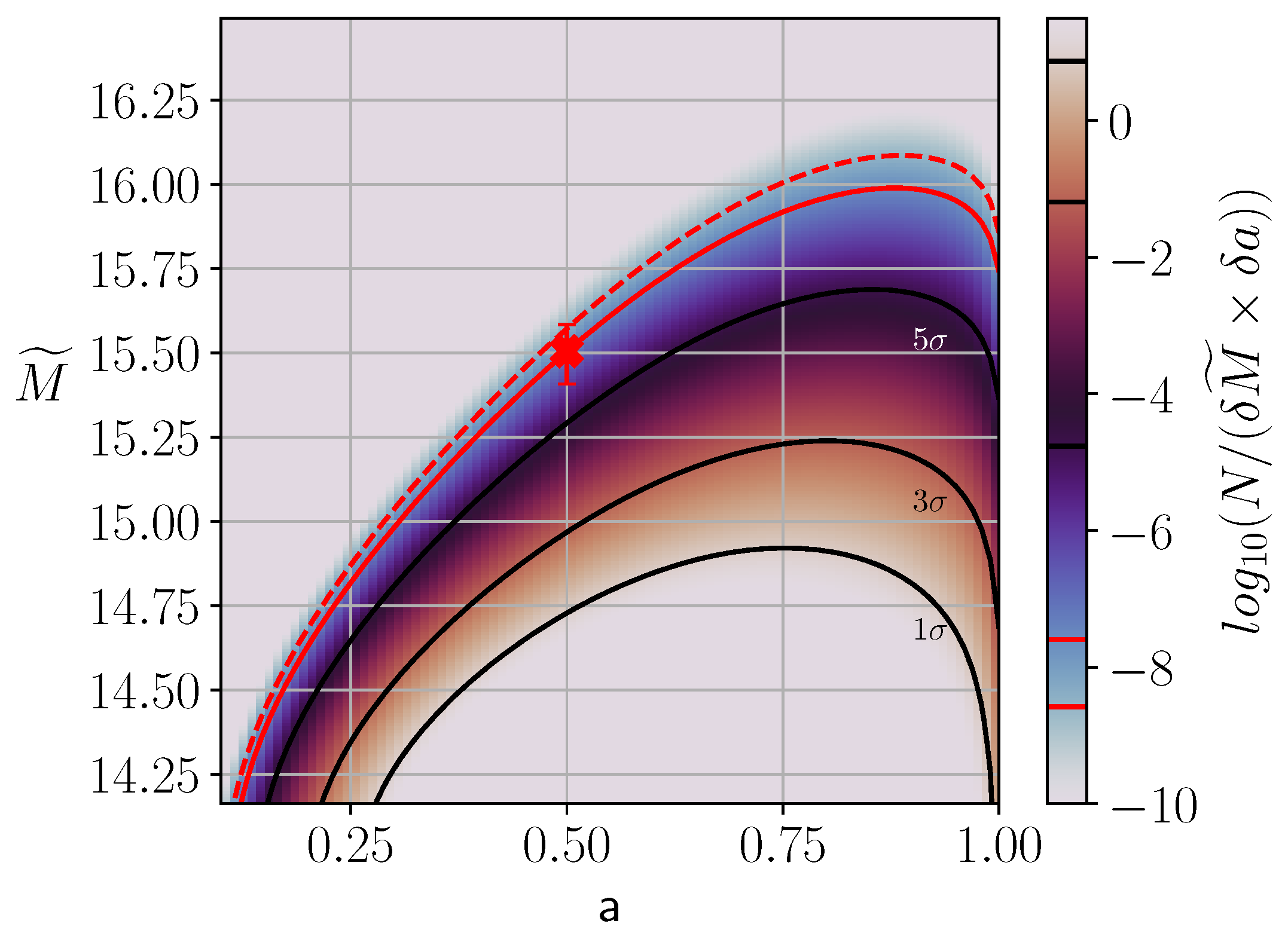
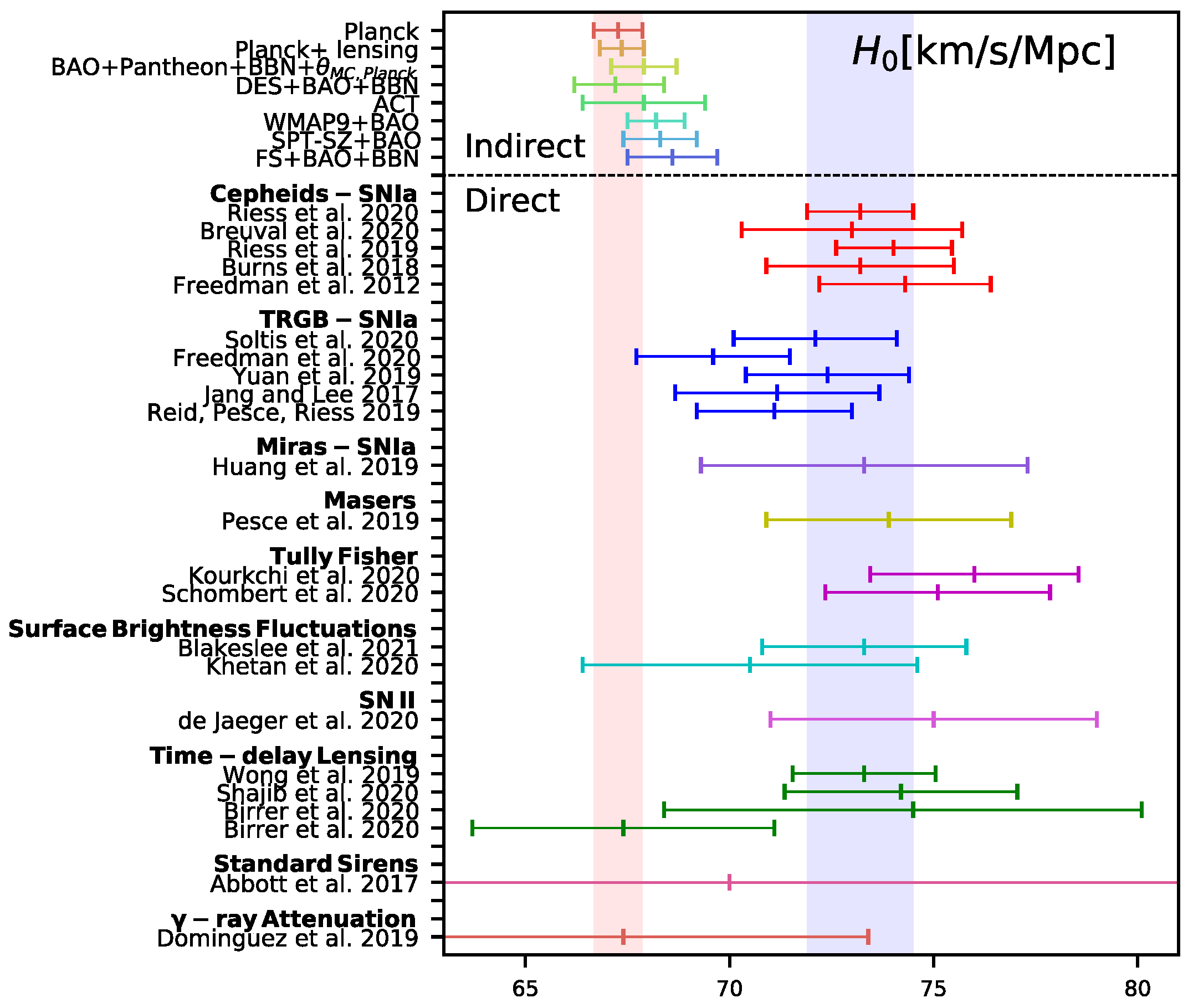
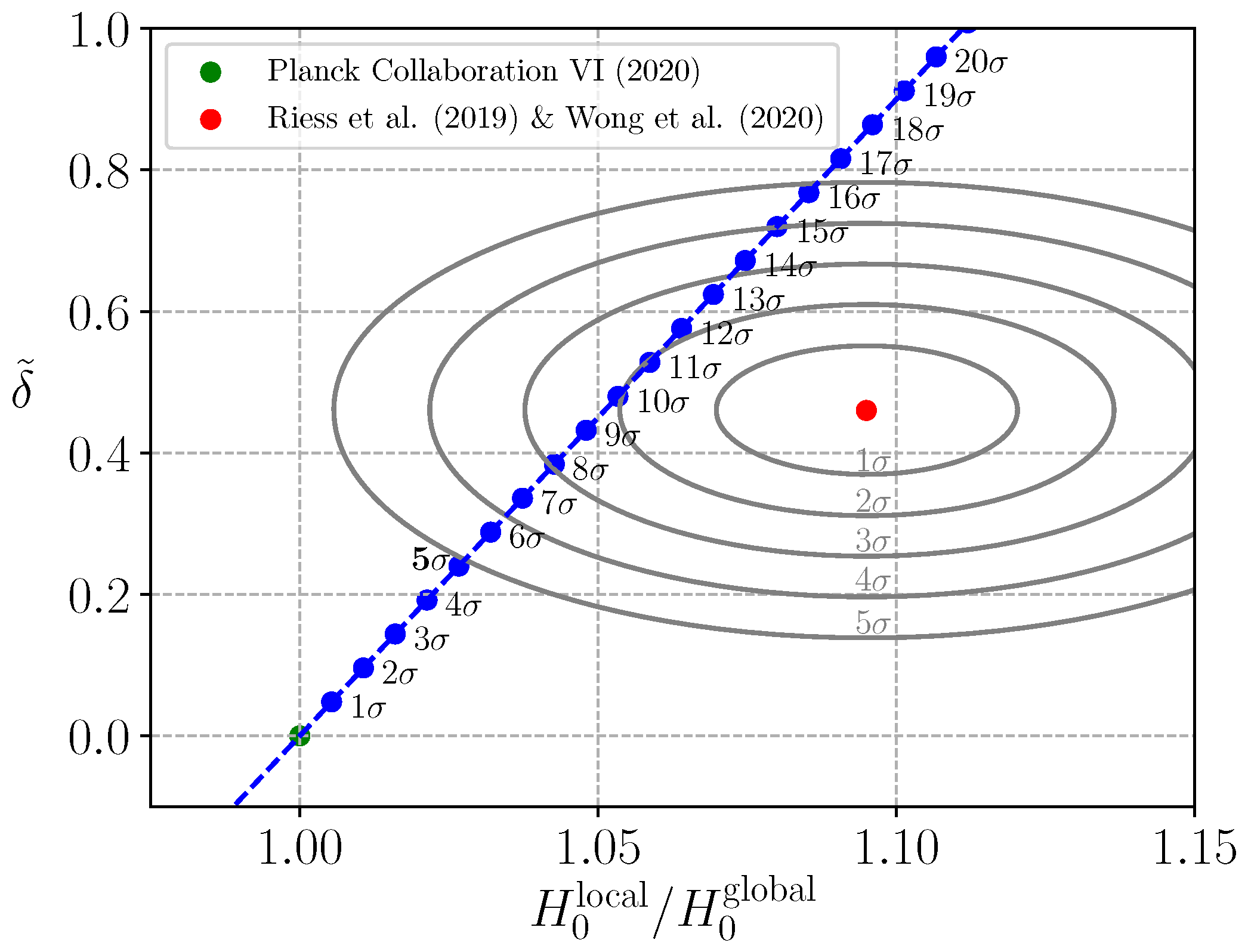
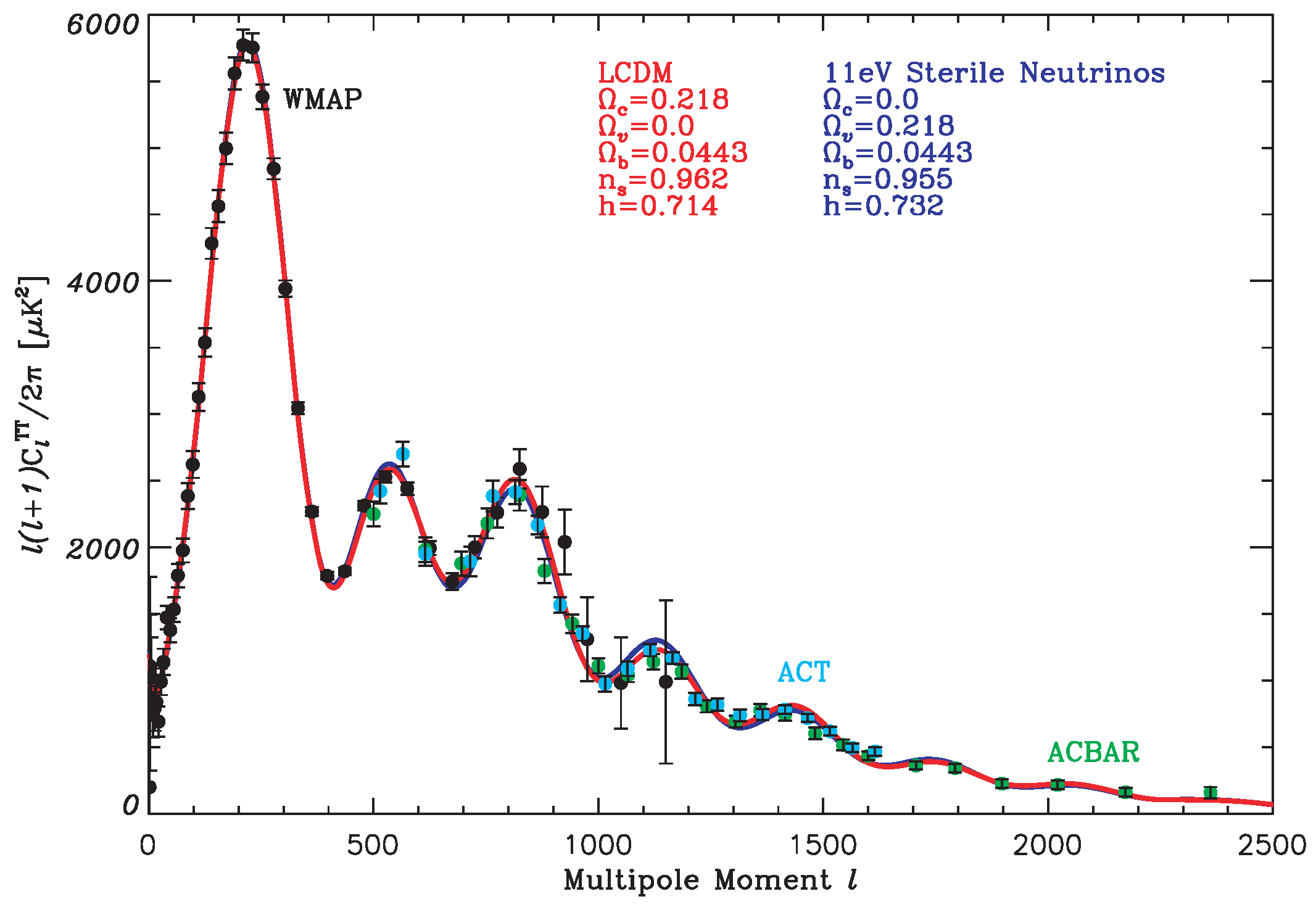

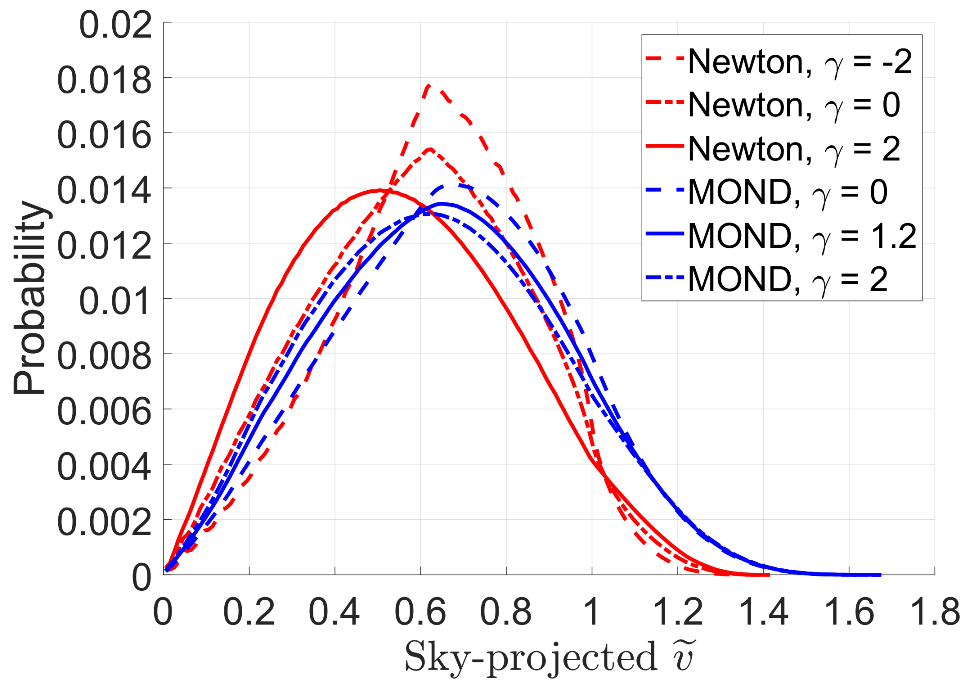
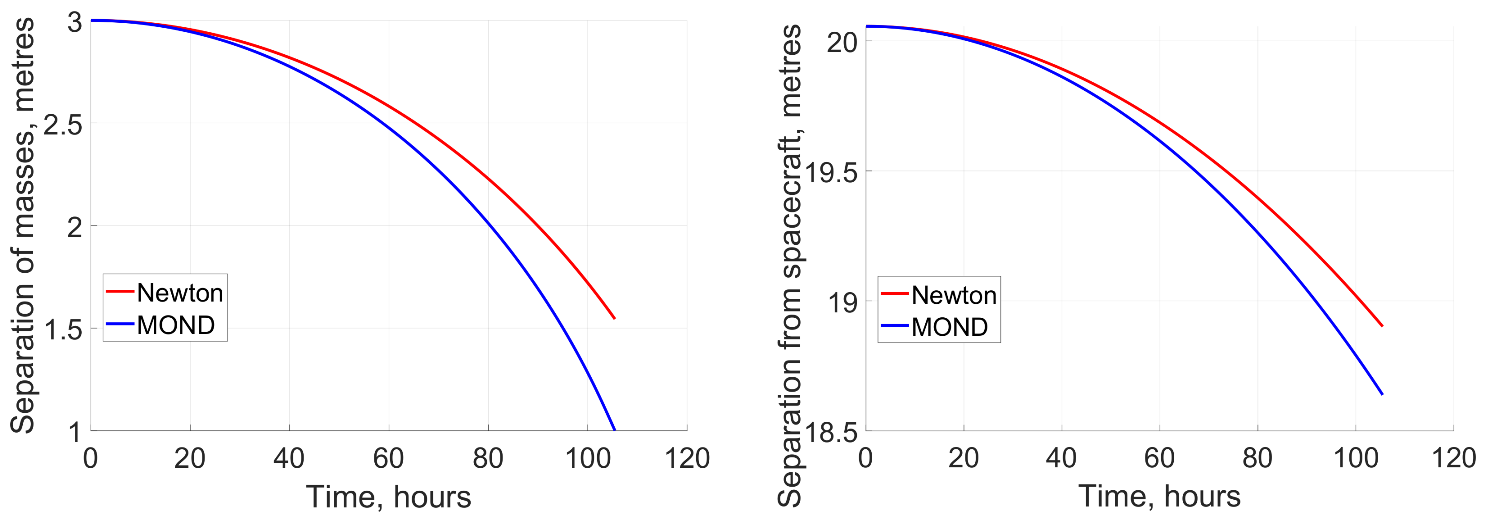
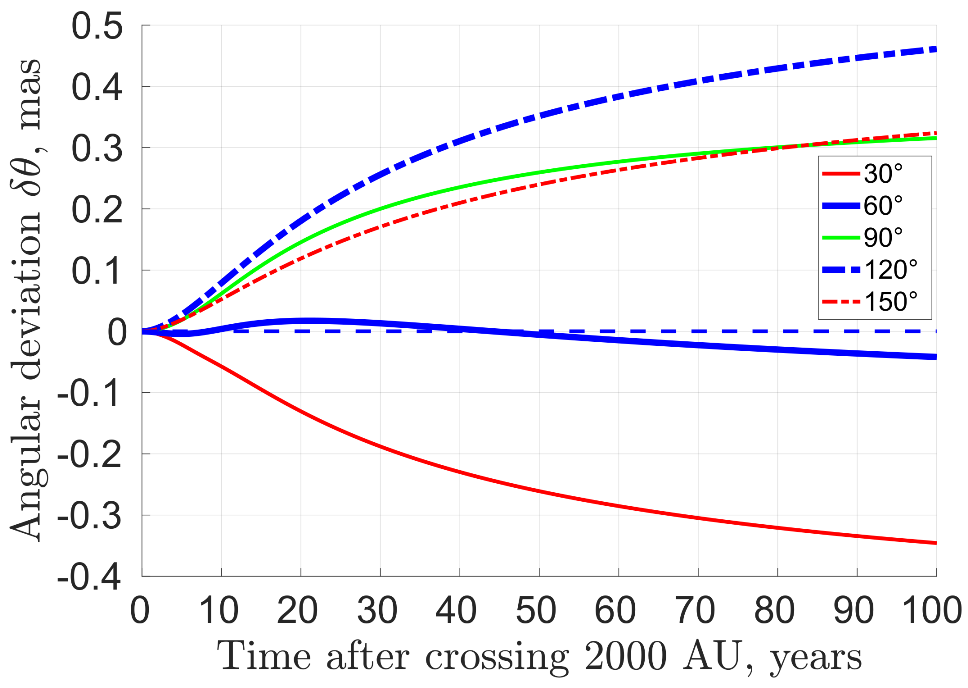
| Auxiliary | Auxiliary | Auxiliary | |||
|---|---|---|---|---|---|
| Assumptions | Assumptions | Assumptions | |||
| Not Predicted, | Needed, but | Needed, and | Allow Theory | ||
| Clear Prior | but Follows | These Have | These Have a | to Fit Any | |
| Astrophysical Scenario | Expectation | from Theory | Little Effect | Discernible Effect | Plausible Data |
| Big Bang nucleosynthesis |  |  | |||
| Gravitational wave speed |  |  | |||
| Wide binary velocities |  | ||||
| Interstellar precursor mission trajectory |  | ||||
| Cavendish experiment in saddle region |  | ||||
 | |||||
| Tidal dwarf galaxy |  | ||||
| Splitting in tidal dwarf mass–size relation |  | ||||
| Tidal limit to dwarf galaxy radii |  |  | |||
| Prevalence of thin disc galaxies |  | ||||
| Freeman limit to disc central density |  |  | |||
| Number of spiral arms |  | ||||
| Weakly barred galaxies |  |  | |||
| Bar fraction in disc galaxies |  | ||||
| Galaxy bar pattern speeds |  |  | |||
 | |||||
| Exponential profiles for disc galaxies |  |  | |||
| Disc galaxy RCs |  |  | |||
| Elliptical galaxy RCs |  |  | |||
| Spheroidal galaxy |  |  | |||
| External field effect |  | ||||
| Galactic escape velocity curve |  |  | |||
| Number of satellite galaxies |  | ||||
| Anisotropy of satellite distribution |  |  | |||
| Weak lensing by galaxies |  |  | |||
| Strong gravitational lensing |  |  | |||
| Polar ring and shell galaxies |  |  | |||
 | |||||
| Local Group timing argument |  |  | |||
| Hickson Compact Group abundance |  | ||||
| Binary galaxy relative velocity |  |  | |||
| Galaxy group |  |  | |||
| Galaxy cluster internal dynamics |  | ||||
| Baryon-lensing offsets in galaxy clusters |  |  | |||
| Galaxy cluster formation |  |  | |||
| Galaxy two-point correlation function |  | ||||
| Weak lensing correlation function |  | ||||
| CMB anisotropies |  |  | |||
| Cosmic variance on 300 Mpc scale |  | ||||
| Local Hubble diagram slope and curvature |  |  | |||
 | |||||
| Expansion history at |  |  | |||
| Expected if Gravity … | ||
|---|---|---|
| Origin of Dwarf | Newtonian | Milgromian |
| Primordial | High | High |
| Tidal | Low | High |
Clear Prior Expectation | Not Predicted, but Follows from Theory | Auxiliary Assumptions Needed, but These Have Little Effect | Auxiliary Assumptions Needed, but These Have a Discernible Effect | Auxiliary Assumptions Allow Theory to Fit Any Plausible Data | |
|---|---|---|---|---|---|
| Excellent agreement |  Gravitational Gravitationalwaves travel at c  Expansion Expansionhistory at |  Einstein Einsteinring radii |  CMB anisotropies CMB anisotropies |  MW escape MW escapevelocity curve  MW–M31 MW–M31timing argument  Galaxy cluster Galaxy clusterinternal dynamics  Galaxy two-point Galaxy two-pointcorrelation function | |
| Works well |  Big Bang Big Bangnucleosynthesis  Offset between Offset betweenX-ray and lensing in Bullet Cluster |  Hickson HicksonCompact Group abundance | |||
| Plausibly works |  Weak lensing Weak lensingcorrelation function |  Galaxy cluster Galaxy clustermass function at low redshift |  Weak lensing Weak lensingby galaxies  HSB disc HSB discgalaxy RCs | ||
| Some tension |  Number of Number ofspiral arms in disc galaxies  External Externalfield effect |  Prevalence of Prevalence ofthin disc galaxies  Weakly barred M33 Weakly barred M33 |  LSB disc LSB discgalaxy RCs  Gas-rich Gas-richgalaxy RCs  Elliptical Ellipticalgalaxy RCs  Spheroidal Spheroidalgalaxy  Galaxy Galaxygroup | ||
| Strong disagreement |  No distinct No distincttidal dwarf mass–radius relation  Local Group Local Groupsatellite planes  El Gordo El Gordoformation  KBC void KBC void Local Hubble Local Hubblediagram slope and curvature |  Galaxy bar Galaxy barpattern speeds  RV of NGC RV of NGC3109 association |  Tidal limit Tidal limitto radii of MW satellites  Bar fraction Bar fractionin disc galaxies |
Clear Prior Expectation | Not Predicted, but Follows from Theory | Auxiliary Assumptions Needed, but These Have Little Effect | Auxiliary Assumptions Needed, but These Have a Discernible Effect | Auxiliary Assumptions Allow Theory to Fit Any Plausible Data | |
|---|---|---|---|---|---|
| Excellent agreement |  LSB disc LSB discgalaxy RCs  No distinct No distincttidal dwarf mass–radius relation  External Externalfield effect |  Galaxy bar Galaxy barpattern speeds  HSB disc HSB discgalaxy RCs  Elliptical Ellipticalgalaxy RCs  El Gordo El Gordoformation |  Expansion Expansionhistory at |  Gravitational Gravitationalwaves travel at c  Einstein ring radii Einstein ring radii CMB anisotropies CMB anisotropies | |
| Works well |  Tidal limit Tidal limitto radii of MW satellites  Freeman limit Freeman limit Weak lensing Weak lensingby galaxies  Binary Binarygalaxy  Galaxy Galaxygroup |  RV of NGC RV of NGC3109 association |  Weakly barred M33 Weakly barred M33 Exponential profiles Exponential profilesof disc galaxies  Local Hubble Local Hubblediagram slope and curvature  Shell galaxies Shell galaxies |  Big Bang Big Bangnucleosynthesis  Galaxy cluster Galaxy clusterinternal dynamics  Offset between Offset betweenX-ray and lensing in Bullet Cluster | |
| Plausibly works |  Number of Number ofspiral arms in disc galaxies  Spheroidal Spheroidalgalaxy  KBC void KBC void |  MW–M31 MW–M31timing argument |  Local Group Local Groupsatellite planes |  MW escape MW escapevelocity curve | |
| Some tension | |||||
| Strong disagreement |
| Confidence Level of Agreement—Theoretical Flexibility | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Astrophysical Scenario | 0 | 1 | 2 | 3 | 4 | ||||
| Big Bang nucleosynthesis |  |  | |||||||
| Gravitational waves travel at c |  |  | |||||||
 | |||||||||
| No distinct TDG mass–radius relation |  |  | |||||||
| Tidal limit to MW satellite radii |  |  | |||||||
| Prevalence of thin disc galaxies |  | ||||||||
| Freeman limit to disc central density |  | ||||||||
| Number of spiral arms in disc galaxies |  |  | |||||||
| Weakly barred M33 |  |  | |||||||
| Bar fraction in disc galaxies |  | ||||||||
| Galaxy bar pattern speeds |  |  | |||||||
 | |||||||||
| Disc galaxies have exponential profiles |  | ||||||||
| HSB disc galaxy RCs on RAR |  |  | |||||||
| LSB disc galaxy RCs on RAR |  |  | |||||||
| Gas-rich galaxy RCs on RAR |  | ||||||||
| Elliptical galaxies on RAR |  |  | |||||||
| Spheroidal galaxy |  |  | |||||||
| External field effect |  |  | |||||||
| MW escape velocity curve |  |  | |||||||
| Shell galaxies |  | ||||||||
| Local Group satellite planes |  | ||||||||
| Weak lensing by galaxies |  |  | |||||||
| Einstein ring radii |  |  | |||||||
 | |||||||||
| MW–M31 timing argument |  |  | |||||||
| RV of NGC 3109 association |  |  | |||||||
| Hickson Compact Group abundance |  | ||||||||
| Binary galaxy |  | ||||||||
| Galaxy group |  |  | |||||||
| Galaxy cluster internal dynamics |  | ||||||||
| Offset between X-ray and lensing in Bullet Cluster |  |  | |||||||
| El Gordo formation |  |  | |||||||
| Galaxy two-point correlation function |  | ||||||||
| Galaxy cluster mass function at low redshift |  | ||||||||
| Weak lensing correlation function (cosmic shear) |  | ||||||||
| CMB anisotropies |  |  | |||||||
| KBC void |  |  | |||||||
| Local Hubble diagram slope and curvature |  |  | |||||||
 | |||||||||
| Expansion history at |  |  | |||||||
| Total | Number | Average | |
|---|---|---|---|
| Theory | Score | of Tests | Score |
| CDM | 32 | ||
| MOND | 29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banik, I.; Zhao, H. From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity. Symmetry 2022, 14, 1331. https://doi.org/10.3390/sym14071331
Banik I, Zhao H. From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity. Symmetry. 2022; 14(7):1331. https://doi.org/10.3390/sym14071331
Chicago/Turabian StyleBanik, Indranil, and Hongsheng Zhao. 2022. "From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity" Symmetry 14, no. 7: 1331. https://doi.org/10.3390/sym14071331
APA StyleBanik, I., & Zhao, H. (2022). From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity. Symmetry, 14(7), 1331. https://doi.org/10.3390/sym14071331







