Symmetric Difference Operator in Quantum Calculus

Abstract

The main focus of this paper is to develop certain types of fundamental theorems using q, $q(\alpha )$, and h difference operators. For several higher order difference equations, we get two forms of solutions: one is closed form and another is summation form. However, most authors concentrate only on the summation part. This motivates us to develop closed-form solutions, and we succeed. The key benefit of this research is finding the closed-form solutions for getting better results when compared to the summation form. The symmetric difference operator is the combination of forward and backward difference symmetric operators. Using this concept, we employ the closed and summation form for q, $q(\alpha )$, and h difference symmetric operators on polynomials, polynomial factorials, logarithmic functions, and products of two functions that act as a solution for symmetric difference equations. The higher order fundamental theorems of q and $q(\alpha )$ are difficult to find when the order becomes high. Hence, by inducing the h difference symmetric operator in q and $q(\alpha )$ symmetric operators, we find the solution easily and quickly. Suitable examples are given to validate our findings. In addition, we plot the figures to examine the value stability of q and $q(\alpha )$ difference equations.

1. Introduction

There are a variety of approaches to define a quantum derivative, such as the h-derivative $(y=x+h)$, q-derivative $(y=qx)$, and p-derivative $(y=x^p)$, but for these derivatives we do not take the limit. In the h-derivative, $h\ne 0$ has a fixed number, and in the q and p derivatives, q and p have fixed numbers that are not equal to 1. In this paper, we mainly concentrate on the q-derivative, and we utilize some concepts in the h-derivative. In [1], the authors implemented the q-derivative as ${\displaystyle \frac{\mathfrak{f}\left(\mathfrak{qt}\right)-\mathfrak{f}\left(\mathfrak{t}\right)}{\mathfrak{qt}-\mathfrak{t}}}$. The q-derivative, or Jackson derivative, is a q-analog of the usual derivative established by F. H. Jackson in the fields of combinatorics and quantum calculus, and Jackson’s q-integration is the inverse of this. Quantum calculus is also known as limitless calculus. It uses a quantum difference operator to replace the classical derivative, allowing it to handle the sets of non-differentiable functions. C. R. Adams [2], R. D. Carmichael [3], Jackson [4], T. E. Mason [5], W. J. Trjitzinsky [6], and other authors such as Picard, Poincare, and Ramanujan published extensive research on ${\Delta }_q$ equations at the turn of the twentieth century. Unfortunately, from the mid-thirties to the early eighties, there was only a smattering of interest in this area. Since the 1980s [7], there has been a resurgence of interest in this subject, especially in the fields of mathematics and applications, notably new difference calculus and orthogonal polynomials, q-arithmetic, integrable systems, variational q-calculus, and q-combinatorics. More recently, the authors in [8] developed a new concept called the q-symmetric derivative, defined by ${\displaystyle \frac{\mathfrak{f}\left(\mathfrak{qt}\right)-\mathfrak{f}\left({\mathfrak{q}}^{-\mathfrak{1}}\mathfrak{t}\right)}{(\mathfrak{q}-{\mathfrak{q}}^{-\mathfrak{1}})\mathfrak{t}}}$, where $\mathfrak{f}:\mathbb{R}\to \mathbb{R}$ and $t\in (0,\infty )$.

In 1832, Bernhard Riemann and Joseph Liouville [9] were the first to conceive the idea of fractional calculus, and it is named the Riemann–Liouville integral. In 1967, Michele Caputo [10] was the first to propose the Caputo fractional derivative, which is another method for computing fractional derivatives. When solving differential equations using Caputo’s concept, the fractional order initial conditions are not required, as they are with the Riemann–Liouville fractional derivative. Subsequently, in 1993, K. S. Miller and B. Ross Bertram introduced the concept of fractional calculus and fractional differential equations [11]. Recently, the comparison and connectedness of the Riemann–Liouville and Caputo derivatives and their applications are discussed by Y. Luchko [12,13,14,15]. In addition, the authors in [16,17,18,19] are excellent sources for more information on fractional derivatives and fractional calculus.

In [20], B. Ross and K. S. Miller developed a discrete kind of Riemann–Liouville fractional derivative and reported certain properties of the fractional difference operator in 1989. The authors in [21,22,23] provide certain applications for q-fractional calculus. Abdi in [24,25] and Hahn in [26] devised and implemented a q-Laplace transform method for q-difference equations. In addition, there is much work being done right now to re-examine and develop the q-special functions. Jackson’s [27,28,29,30] early work is notable. For contemporary and good ideas for q-special functions, we also recommend papers by De Sole and Kac [31], McAnally [32,33], Ernst [34], and Koornwinder [35,36], as well as books by Andrews, Askey, and Roy [37] and Carlson [38].

This research study focuses on the q-difference operator $d_q\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{tq}\right)-\mathfrak{f}\left(\mathfrak{t}\right)$. The study of the q-difference operator is introduced after the development of the h-difference operator. The h-difference operator is similar to the h-derivative, where the limit does not apply. For any function f defined on $\mathbb{R}=(-\infty ,\infty )$ and $h\ne 0$, the difference operator $\underset{h}{\Delta }$ on f is defined as

$$\underset{h}{\Delta }\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}(\mathfrak{t}+\mathfrak{h})-\mathfrak{f}\left(\mathfrak{t}\right).$$

(1)

The operator $\Delta$, defined as $\Delta \mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}(\mathfrak{t}+\mathfrak{1})-\mathfrak{f}\left(\mathfrak{t}\right)$ is the foundation of difference equation theory, where $\mathfrak{f}\left(\mathfrak{t}\right)$ is a sequence of numbers. The authors in [6,7,39,40] proposed the definition of generalized difference operator ${\Delta }_h$, which is defined in Equation (1), and then developed the inverse theory concept (anti-difference operator $({\Delta }_h^{-1}$) for finding the closed-form solutions. In 1984, Jerzy Popenda and Szmanda [41] suggested a specific type of ${\Delta }_{\alpha }$ operator defined as ${\Delta }_{\alpha }\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}(\mathfrak{t}+\mathfrak{1})-\alpha \mathfrak{f}\left(\mathfrak{t}\right)$, where $\alpha ,\mathfrak{t}\in (-\infty ,\infty )$. This $\alpha$-delta operator was extended by the authors in [42,43] to a generalized alpha difference operator. The $\alpha$-delta operator with shift value h is defined as ${\Delta }_{h(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}(\mathfrak{t}+\mathfrak{h})-\alpha \mathfrak{f}\left(\mathfrak{t}\right)$, where the function $\mathfrak{f}\left(\mathfrak{t}\right)$ is defined on $\mathbb{R}$. In 2014, the authors in [44,45] proposed the q-difference operator, which is defined as $d_q\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{tq}\right)-\mathfrak{f}\left(\mathfrak{t}\right)$, and applied it to polynomials and polynomial factorials. The authors in [46] focus on the $d_{q(\alpha )}$ operator by defining $d_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{tq}\right)-\alpha \mathfrak{f}\left(\mathfrak{t}\right)$. Following these q and h difference operator ideas, the authors in [8,47] extended the q and h symmetric derivatives to q and h symmetric difference operators defined by

$$D_{q}f\left(t\right)={\displaystyle \frac{f\left(qt\right)-f\left(q^{-1}t\right)}{(q-q^{-1})t}}={\displaystyle \frac{d_{q}f\left(t\right)+d^{q}f\left(t\right)}{(q-q^{-1})t}}$$

(2)

and

$$D_{h}f\left(t\right)={\displaystyle \frac{f(t+h)-f(t-h)}{2h}}={\displaystyle \frac{{\Delta }_{h}f\left(t\right)+{\nabla }_{h}f\left(t\right)}{2h}},$$

(3)

where f is a real valued function, and $\mathfrak{t}\in (\mathfrak{0},\infty )$.

From (2), the q-symmetric difference operator is defined by ${\mathfrak{D}}_{\mathfrak{q}}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{qt}\right)-\mathfrak{f}\left({\mathfrak{q}}^{-\mathfrak{1}}\mathfrak{t}\right)$, where the operator ${\mathfrak{D}}_{\mathfrak{q}}$ is the sum of q-forward and q-backward difference operators. As a result, the q-symmetric difference operator combines the forward and backward difference symmetric operators, i.e.,

$${\mathfrak{D}}_{\mathfrak{q}}\mathfrak{f}\left(\mathfrak{t}\right)=d_q\mathfrak{f}\left(\mathfrak{t}\right)+d^q\mathfrak{f}\left(\mathfrak{t}\right),$$

(4)

where the $d_q$ operator is as noted, and whereas $d_q=\mathfrak{f}\left(\mathfrak{t}\right)-\mathfrak{f}\left({\mathfrak{tq}}^{-\mathfrak{1}}\right)$. The h-symmetric difference operator, described in Equation (3), is defined as

$${\mathfrak{D}}_{\mathfrak{h}}\mathfrak{f}\left(\mathfrak{t}\right)={\Delta }_h\mathfrak{f}\left(\mathfrak{t}\right)+{\nabla }_h\mathfrak{f}\left(\mathfrak{t}\right).$$

(5)

We may easily conclude from Equations (4) and (5) that the forward and backward q and h difference operators offer the particular solutions for the q and h symmetric difference operators. These operators $d_q$ and $d^q$ are symmetric to each other (i.e., symmetry of $d_q$ is $d^q$, and vice-versa). In addition, the operators ${\Delta }_h$ and ${\nabla }_h$ are symmetric to each other. Taking these ideas together, we denote the q-difference operator $d_q$ and the anti-difference operator as $I_q$ to develop and provide the fundamental theorems for symmetric operator ${\mathfrak{D}}_{\mathfrak{q}}$. Here, the theorems are mainly based on the q-difference operator and mixed difference operators (i.e., q and h difference operators). For more information, refer to [31,40,48,49]. We construct theorems and corollaries for the operator $d_q$ that give a solution for the q-symmetric difference operator throughout this work. In the same way, the operator $d^q$ can be easily verified. In addition, we extend this work to the q-alpha difference operator, which is an extension of q-difference operator. If we take $\alpha =1$ in the q-alpha difference operator, then it becomes the ordinary q-difference operator. The theorems and corollaries developed in the q-alpha difference operator give the solution for the $q(\alpha )$-symmetric difference operator. We can do the same thing with the $d^{q(\alpha )}$ operator.

The list of symbols and descriptions used in this manuscript is shown in Table 1.

Table 1. Symbols.

∃	there exists
∋	such that
$d_q$	q-difference operator
$d_{q(\alpha )}$	q-alpha difference operator
$I_q$	Inverse q-difference operator
$I_{q(\alpha )}$	Inverse of q-alpha difference operator
$\underset{h}{\Delta }$	h-difference operator
$\underset{h}{\overset{-1}{\Delta }}$	Inverse of h-difference operator
$\underset{h/t}{\overset{-1}{\Delta }}$	Inverse of h-difference operator with respect to the variable t

The paper is arranged as follows. Section 1 is dedicated to the introduction. In Section 2 and Section 3, we present the preliminaries of the q-difference operator and the h-difference operator. In Section 4, we develop several fundamental theorems in quantum calculus. The mixed symmetric operators in quantum calculus are given in Section 5. The conclusions from our research are in Section 6.

2. Preliminaries of the q-Difference Operator

This section focuses on the basic definition of the q-difference operator and its anti- difference operator as well as concentrating on the q-polynomial factorial functions. Here, we introduce the infinite set ${\mathfrak{T}}_{\mathfrak{q}}=\{a,a{q}^{\pm 1},a{q}^{\pm 2},\dots \}$, which satisfies the condition that for any $\mathfrak{t}\in {\mathfrak{T}}_{\mathfrak{q}}$ implies ${\mathfrak{tq}}^{\pm \mathfrak{1}}\in {\mathfrak{T}}_{\mathfrak{q}}$ for any fixed number $\mathfrak{0}\ne \mathfrak{t}\in \mathbb{R}$ and $q\in \mathbb{R}-\left\{\mathfrak{1}\right\}$.

Definition 1

([44]). Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$ and $\mathfrak{1}\ne \mathfrak{q}\in [\mathfrak{0},\infty )$ be fixed. The q-difference symmetric operator or q-difference operator, denoted as $d_q$ on $f\left(t\right)$, is defined as

$$d_q\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{tq}\right)-\mathfrak{f}\left(\mathfrak{t}\right),\mathfrak{t}\in {\mathfrak{T}}_{\mathfrak{q}}.$$

(6)

If$\exists \mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$∋$d_q\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, then its inverse q-difference operator (or inverse q-difference symmetric operator) denoted as $I_q$ is defined as

$$\mathfrak{g}\left(\mathfrak{t}\right)=I_q\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{c},$$

(7)

where $\mathfrak{c}$ is a constant. We can denote $I_q=d_q^{-1}$.

Definition 2

([42]). Let $\mathfrak{n}\in \mathbb{N}\left(1\right)$ and $\mathfrak{q},\mathfrak{t}\in \mathbb{R}$. Then, the q-polynomial factorial is defined as

$${\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}=\mathfrak{t}\left(\prod _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-{\mathfrak{q}}^{\mathfrak{r}})\right).$$

(8)

The following Lemma 1 is the power rule for q-difference operator $d_q$. Here, we take ${\mathfrak{T}}_{\mathfrak{q}}=\mathbb{R}$.

Lemma 1.

For any positive integer $\mathfrak{n}>\mathfrak{1}$ and $\mathfrak{q}\ne \mathfrak{1}$, then the difference operator $d_q$ for the polynomial factorial function ${\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}$ is given by

$$d_q{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}=({\mathfrak{q}}^{\mathfrak{n}}-\mathfrak{1}){\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)},\mathfrak{t}\in \mathbb{R}.$$

(9)

Proof. 

Taking $\mathfrak{f}\left(\mathfrak{t}\right)={\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}$ in Equation (6), we get

$$d_q{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}={\left(\mathfrak{tq}\right)}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}-{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}.$$

(10)

Applying Equation (8) in (10), Equation (10) becomes

$$d_q{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}=\prod _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-{\mathfrak{rq}}^{\mathfrak{r}})\mathfrak{q}-\prod _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-{\mathfrak{q}}^{\mathfrak{r}})={\mathfrak{q}}^{\mathfrak{n}}\left\{\prod _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-{\mathfrak{q}}^{\mathfrak{r}})\right\}-\prod _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-{\mathfrak{q}}^{\mathfrak{r}})$$

which completes the proof. □

Lemma 2.

Let $\mathfrak{n}\in \mathbb{N}\left(\mathfrak{1}\right)$ and $\mathfrak{q}\ne \mathfrak{1}$. Then the anti-difference operator $I_q$ for the polynomial factorial function ${\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}$ is

$$I_q{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}={\displaystyle \frac{{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}}{{\mathfrak{q}}^{\mathfrak{n}}-\mathfrak{1}}}+\mathfrak{c},\mathfrak{t}\in \mathbb{R}.$$

(11)

Proof. 

The proof is completed by applying the $d_q^{-1}$ operator on (9) and then using (7). □

Remark 1.

Throughout this paper, we represent the anti-difference operator as $I_q$, where $I_q$ is nothing but the reciprocal of the q-difference operator.

Result 1.

Let $\mathfrak{n}\in \mathbb{N}$ and $\mathfrak{t}\in \mathbb{R}$. The q-difference operator for the polynomial function is given by

$$d_q\left({\mathfrak{t}}^{\mathfrak{n}}\right)={\mathfrak{t}}^{\mathfrak{n}}({\mathfrak{q}}^{\mathfrak{n}}-\mathfrak{1}),$$

(12)

and its anti-difference operator for the polynomial function is given by

$$I_q\left({\mathfrak{t}}^{\mathfrak{n}}\right)={\displaystyle \frac{{\mathfrak{t}}^{\mathfrak{n}}}{({\mathfrak{q}}^{\mathfrak{n}}-\mathfrak{1})}}.$$

(13)

Proof. 

The proof is complete if $f\left(t\right)=t^n$ in Definition 1. □

Lemma 3

([44]). Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$ and $\mathfrak{q}\ne \mathfrak{1}$. The product rule of the q-difference operator is defined by

$$I_q\left\{\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\right\}=\mathfrak{f}\left(\mathfrak{t}\right)I_q\mathfrak{g}\left(\mathfrak{t}\right)-I_q\left\{I_q\mathfrak{g}\left(\mathfrak{tq}\right)d_q\mathfrak{f}\left(\mathfrak{t}\right)\right\}.$$

(14)

Proof. 

By applying the operator $d_q$ on the function $\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{h}\left(\mathfrak{t}\right)$, we get

$$d_q\left\{\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{h}\left(\mathfrak{t}\right)\right\}=\mathfrak{h}\left(\mathfrak{tq}\right)d_q\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{f}\left(\mathfrak{t}\right)d_q\mathfrak{h}\left(\mathfrak{t}\right).$$

(15)

Taking $d_q\mathfrak{h}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{t}\right)$ and $\mathfrak{h}\left(\mathfrak{t}\right)=I_q\mathfrak{g}\left(\mathfrak{t}\right)$ completes the proof. □

Corollary 1

([44]). Let $t\in \mathbb{R}$ and $\mathfrak{q}\notin \{0,1\}$ be any real number. Then,

$$I_q\left(0\right)=1\mathit{and}{I}_q\left(1\right)={\displaystyle \frac{log\left(\mathfrak{t}\right)}{log\left(\mathfrak{q}\right)}}.$$

(16)

Proof. 

The proof is completed by taking $\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{1}$ and $\mathfrak{f}\left(\mathfrak{t}\right)=log\left(\mathfrak{t}\right)$ in (6) and then applying (7). □

3. Preliminaries of the h-Difference Operator

This section contains some basic concepts of the h-difference operator that are used in the upcoming sections. To get additional information about the h-difference operator, one can refer to [7,42,50]. Consider the infinite set ${\mathfrak{J}}_{\mathfrak{h}}=\{a,a\pm h,a\pm 2h,\dots \}$, which has the property that $\mathfrak{a}\in {\mathfrak{J}}_{\mathfrak{h}}$ implies $a\pm h\in {\mathfrak{J}}_{\mathfrak{h}}$, $h\ne \mathfrak{0}$.

Definition 3

([7]). Let $\mathfrak{f}:{\mathfrak{J}}_{\mathfrak{h}}\to \mathbb{R}$, $h\ne \mathfrak{0}$ and $\underset{h}{\Delta }\mathfrak{f}\left(\mathfrak{t}\right)$ be defined in Equation (1). If ∃ function $\mathfrak{g}:{\mathfrak{J}}_{\mathfrak{h}}\to \mathbb{R}$∋$\underset{h}{\Delta }\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, then the anti-difference operator (or inverse h-difference symmetric operator) $\underset{h}{\overset{-1}{\Delta }}$ is defined as

$$g\left(b\right)-g\left(a\right)=\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{a}\right)-\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{b}\right)=\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{b}}^{\mathfrak{a}}.$$

(17)

Definition 4

([6]). Let $\mathfrak{n}\in \mathbb{N}\left(\mathfrak{1}\right)$ and $\mathfrak{t},\mathfrak{h}\in \mathbb{R}$. The h-polynomial factorial function is defined as

$${\mathfrak{t}}_{\mathfrak{h}}^{\left(\mathfrak{n}\right)}=\prod _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}(\mathfrak{t}-\mathfrak{rh}).$$

(18)

Note that ${\mathfrak{t}}_{\mathfrak{h}}^{\left(\mathfrak{n}\right)}$ and ${\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}$ are not same.

Lemma 4

([7]). Let $\mathfrak{a}$,$\mathfrak{h}$ be real and $\mathfrak{b}$,$\mathfrak{m}$ be positive integers. Then,

$${(\mathfrak{a}-\mathfrak{h})}_{\mathfrak{h}}^{\left(\mathfrak{m}\right)}+{(\mathfrak{a}-\mathfrak{2}\mathfrak{h})}_{\mathfrak{h}}^{\left(\mathfrak{m}\right)}+{(\mathfrak{a}-\mathfrak{3}\mathfrak{h})}_{\mathfrak{h}}^{\left(\mathfrak{m}\right)}+\dots +{(\mathfrak{a}-\mathfrak{bh})}_{\mathfrak{h}}^{\left(\mathfrak{m}\right)}={\displaystyle \frac{\mathfrak{1}}{(\mathfrak{m}+\mathfrak{1})\mathfrak{h}}}\left[{\mathfrak{a}}_{\mathfrak{h}}^{(\mathfrak{m}+\mathfrak{1})}-{(\mathfrak{a}-\mathfrak{bh})}_{\mathfrak{h}}^{(\mathfrak{m}+\mathfrak{1})}\right].$$

(19)

Relation (19) is verified in the following example.

Example 1.

Taking $h=2.2,a=7.3,b=4$, and $m=2$, (19) becomes

$${\left(5.1\right)}_{2.2}^{\left(2\right)}+{\left(2.9\right)}_{2.2}^{\left(2\right)}+{\left(0.7\right)}_{2.2}^{\left(2\right)}+{(-1.5)}_{2.2}^{\left(2\right)}={\displaystyle \frac{{\left(7.3\right)}_{2.2}^{\left(3\right)}}{6}}-{\displaystyle \frac{{(-1.5)}_{2.2}^{\left(3\right)}}{6}}.$$

Applying (18) in the above equation, we get

$$\left(5.1\right(5.1-2.2\left)\right)+\left(2.9\right(2.9-2.2\left)\right)+\left(0.7\right(0.7-2.2\left)\right)+\left(\right(-1.5\left)\right(-1.5-2.2\left)\right)=21.32.$$

$${\displaystyle \frac{7.3(7.3-2.2)(7.3-4.4)}{6}}-{\displaystyle \frac{-1.5(-1.5-2.2)(-1.5-4.4)}{6}}=21.32.$$

Thus, Equation (19) is verified.

Corollary 2.

If $(\mathfrak{a}-\mathfrak{bh})=\mathfrak{1}$, $(\mathfrak{a}-(\mathfrak{b}-\mathfrak{1}\left)\mathfrak{h}\right)=\mathfrak{2}$, $(\mathfrak{a}-(\mathfrak{b}-\mathfrak{2}\left)\mathfrak{h}\right)=\mathfrak{3}$, …, $(\mathfrak{a}-\mathfrak{2}\mathfrak{h})=\mathfrak{n}-\mathfrak{1}$, $(\mathfrak{a}-\mathfrak{h})=\mathfrak{n}$, and taking $\mathfrak{h}=\mathfrak{1}$ in (19), then the sum of ${\mathfrak{m}}^{\mathfrak{th}}$ order polynomial factorials of the first n natural numbers is

$${\mathfrak{n}}^{\left(\mathfrak{m}\right)}+{(\mathfrak{n}-\mathfrak{1})}^{\left(\mathfrak{m}\right)}+\dots +{\mathfrak{3}}^{\left(\mathfrak{m}\right)}+{\mathfrak{2}}^{\left(\mathfrak{m}\right)}+{\mathfrak{1}}^{\left(\mathfrak{m}\right)}={\displaystyle \frac{{(\mathfrak{n}+\mathfrak{1})}^{(\mathfrak{m}+\mathfrak{1})}}{(\mathfrak{m}+\mathfrak{1})}},\mathfrak{n}\in \mathbb{N}.$$

(20)

Lemma 5

([6]). Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{J}}_{\mathfrak{h}}\to \mathbb{R}$ and $\mathfrak{h}\ne \mathfrak{0}$. Then the product of two functions is given by

$$\underset{h}{\overset{-1}{\Delta }}\left\{\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\right\}=\mathfrak{f}\left(\mathfrak{t}\right)\underset{h}{\overset{-1}{\Delta }}\mathfrak{g}\left(\mathfrak{t}\right)-\underset{h}{\overset{-1}{\Delta }}\left\{\underset{h}{\overset{-1}{\Delta }}(\mathfrak{g}\left(\mathfrak{t}\right)+\mathfrak{h})\underset{h}{\Delta }\mathfrak{f}\left(\mathfrak{t}\right)\right\}.$$

(21)

Corollary 3.

For any two real valued functions $\mathfrak{f}$ and $\mathfrak{g}$ defined on a subset of $(-\infty ,\infty )$, then

$$\underset{-1}{\overset{-1}{\Delta }}\left\{\mathfrak{x}\left(\mathfrak{t}\right)\mathfrak{y}\left(\mathfrak{t}\right)\right\}=\mathfrak{x}\left(\mathfrak{t}\right)\underset{-1}{\overset{-1}{\Delta }}\mathfrak{y}\left(\mathfrak{t}\right)-\underset{-1}{\overset{-1}{\Delta }}\left\{\underset{-1}{\overset{-1}{\Delta }}(\mathfrak{y}\left(\mathfrak{t}\right)-\mathfrak{1})\underset{-1}{\Delta }\mathfrak{x}\left(\mathfrak{t}\right)\right\}.$$

(22)

Proof.

The proof is completed by taking $\mathfrak{h}=-\mathfrak{1}$ in (21). □

Theorem 2

([7]). Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{J}}_{\mathfrak{h}}\to \mathbb{R}$, $\mathfrak{h}\ne \mathfrak{0}$ and $\underset{h}{\Delta }\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$. Then the first order anti-difference principle related to $\underset{h}{\Delta }$ is given by

$$\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{t}\right)-\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}(\mathfrak{t}-\mathfrak{nh})=\sum _{r=0}^n\mathfrak{f}(\mathfrak{t}-\mathfrak{rh}),$$

(23)

where $\mathfrak{n}\in \mathbb{N}$ and $\mathfrak{g}\left(\mathfrak{t}\right)=\underset{h}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{t}\right)$.

4. Fundamental Theorems in Quantum Calculus

4.1. Fundamental Theorems Related to the q-Difference Symmetric Operator

This section contains theorems and corollaries for the higher order anti-difference principle for the q-difference operator defined in (6). Additionally, suitable numerical examples are provided to verify and validate the results.

Theorem 3.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$ and $\mathfrak{n}\in \mathbb{N}$. If ∃$\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$∋$d_q\mathfrak{g}\left(\mathfrak{t}\right)$= $\mathfrak{f}\left(\mathfrak{t}\right)$, then $\mathfrak{g}\left(\mathfrak{t}\right)=I_{q}f\left(t\right)$, and its first order anti-difference principle related to $d_q$ is given by

$$I_q\mathfrak{f}\left(\mathfrak{t}\right)-I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(24)

Proof.

By Definition 1 and $d_q\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, we can easily find

$$\mathfrak{f}\left(\mathfrak{t}\right)=d_q\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{tq}\right)-\mathfrak{g}\left(\mathfrak{t}\right).$$

(25)

Rearranging Equation (25) gives $\mathfrak{g}\left(\mathfrak{tq}\right)=\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{g}\left(\mathfrak{t}\right)$ and then converting $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ in $\mathfrak{g}\left(\mathfrak{tq}\right)$, we get

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right).$$

(26)

Again replacing $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ in (26) and then substituting $\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ value in (26), we obtain

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right).$$

(27)

Similarly, again shifting $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)$ in (27) and then substituting $\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)$ in (27), we get

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right).$$

Proceeding like this, we get the general term as

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+\dots +\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).$$

(28)

As a result, the proof is finished by substituting $\mathfrak{g}\left(\mathfrak{t}\right)=I_q\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{c}$. □

Remark 2.

Equation (24) can be written as $I_q\mathfrak{f}\left(\mathfrak{t}\right){|}_{\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{t}}={\displaystyle \sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)$.

The following Theorem 4 is the higher order anti-difference principle for q.

Theorem 4.

For $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\notin \{\mathfrak{0},\mathfrak{1}\}$, assume that $\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$∋$d_q\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$ and $\mathfrak{n},\mathfrak{m}\in \mathbb{N}$ with $\mathfrak{n}>\mathfrak{m}$. The higher order q anti-difference principle related to $d_q$ is given by

$$I_q^m\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-\sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{m}-\mathfrak{1}}{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}{I}_q^{\mathfrak{m}-\mathfrak{r}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)=\sum _{\mathfrak{r}=\mathfrak{m}-\mathfrak{1}}^{\mathfrak{n}-\mathfrak{1}}{\displaystyle \frac{{\mathfrak{r}}_{\mathfrak{1}}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(29)

Proof.

Multiplying the operator $I_q$ on both sides of Equation (24), we get

$$I_q^2\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}=I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\dots +I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).$$

(30)

Since $I_q\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{t}\right)$, we can substitute Equation (28) in (30). Then

$$\begin{array}{c}{I}_q^2\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}=\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{2}}^{\mathfrak{n}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}+\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{3}}^{\mathfrak{n}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{4}}^{\mathfrak{n}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}+\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{2}}^{\mathfrak{n}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\dots \dots +\left\{\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).\hfill \end{array}$$

Grouping the right-hand-side terms together, we get

$$I_q^2\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{2}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\mathfrak{3}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\dots +(\mathfrak{n}-\mathfrak{1})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+\mathfrak{ng}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)$$

which is same as

$$I_q^2\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{n}-\mathfrak{1}}\mathfrak{rf}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(31)

Again, applying the $I_q$ operator on both sides of Equation (31) and then continuing with similar steps, we can easily find

$$\begin{gathered} I_q^3\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-\mathfrak{n}\left\{I_q^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+(\mathfrak{1}+\mathfrak{2})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+(\mathfrak{1}+\mathfrak{2}+\mathfrak{3})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+ \\ \dots +(\mathfrak{1}+\mathfrak{2}+\dots +\mathfrak{n}-\mathfrak{1})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+(\mathfrak{1}+\mathfrak{2}+\dots +\mathfrak{n})\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right). \end{gathered}$$

Taking $\mathfrak{m}=\mathfrak{1}$ in Equation (20) and then applying Equation (20) in the above expression, we get

$$\begin{gathered} I_q^3\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}={\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+{\displaystyle \frac{{\mathfrak{4}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right) \\ +\dots +{\displaystyle \frac{{(\mathfrak{n}-\mathfrak{1})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right) \end{gathered}$$

which is same as

$$I_q^3\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-{\displaystyle \frac{n^{\left(2\right)}}{2!}}\left\{I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{2}}^{\mathfrak{n}-\mathfrak{1}}{\displaystyle \frac{{\mathfrak{r}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

Now, again multiplying the $I_q$ operator on both sides of the above equation and proceeding with similar steps, we obtain

$$\begin{array}{c}{I}_q^4\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-{\displaystyle \frac{n^{\left(2\right)}}{2!}}\left\{I_q^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+({\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)\hfill \\ \hspace{1em}\hspace{1em}+({\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+{\displaystyle \frac{{\mathfrak{4}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{6}}}}\right)+\dots +({\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+\dots +{\displaystyle \frac{{(\mathfrak{n}-\mathfrak{1})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\hfill \\ \hspace{1em}\hspace{1em}+({\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}+\dots +{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}})\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).\hfill \end{array}$$

By Definition 4 for $\mathfrak{h}=1$ and by Equation (20) for $\mathfrak{m}=2$, we arrive at

$$\begin{gathered} I_q^4\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-{\displaystyle \frac{n^{\left(2\right)}}{2!}}\left\{I_q^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-{\displaystyle \frac{n^{\left(3\right)}}{3!}}\left\{I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}={\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{3}\right)}}{\mathfrak{3}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right) \\ +{\displaystyle \frac{{\mathfrak{4}}^{\left(\mathfrak{3}\right)}}{\mathfrak{3}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+{\displaystyle \frac{{\mathfrak{5}}^{\left(\mathfrak{3}\right)}}{\mathfrak{3}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+\dots +{\displaystyle \frac{{(\mathfrak{n}-\mathfrak{1})}^{\left(\mathfrak{3}\right)}}{\mathfrak{3}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right). \end{gathered}$$

Proceeding like this up to m times, we obtain

$$I_q^m\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-n\left\{I_q^{m-1}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-\dots -{\displaystyle \frac{{\mathfrak{n}}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\left\{I_q\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{m}-\mathfrak{1}}^{\mathfrak{n}-\mathfrak{1}}{\displaystyle \frac{{\mathfrak{r}}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right),$$

which completes the proof. □

Remark 3.

For $\mathfrak{r}\in \mathbb{N}$, the ${\mathfrak{r}}^{\mathfrak{th}}$ order anti-difference operator of $d_q$ is denoted as $I_q^r$.

Example 2.

Taking $f\left(t\right)=t_q^{\left(3\right)},m=2,n=4$ in (29), then we have

$$I_q^2{t}_q^{\left(3\right)}{|}_{\frac{t}{q^4}}^t-4\left\{I_q{\left({\displaystyle \frac{t}{q^4}}\right)}_q^{\left(3\right)}\right\}=\sum _{r=1}^3{\displaystyle \frac{r^{\left(1\right)}}{1!}}{\left({\displaystyle \frac{t}{q^{r+1}}}\right)}_q^{\left(3\right)}.$$

(32)

By Equation (11), we can quickly find $I_q{t}_q^{\left(3\right)}={\displaystyle \frac{t_q^{\left(3\right)}}{q^3-1}}$.

Multiplying the operator $I_q$ on both sides of above equation, we get $I_q^2{t}_q^{\left(3\right)}={\displaystyle \frac{t_q^{\left(3\right)}}{{(q^3-1)}^2}}$.

Taking $t=5,q=2$ in (32) and using Equation (8), the left-hand side of (32) becomes

$${\displaystyle \frac{1}{7^2}}\left\{5_2^{\left(3\right)}-{\left({\displaystyle \frac{5}{2^4}}\right)}_2^{\left(3\right)}\right\}-{\displaystyle \frac{4}{7}}{\left({\displaystyle \frac{5}{2^4}}\right)}_2^{\left(3\right)}={\displaystyle \frac{5_2^{\left(3\right)}}{7{\left(2^4\right)}^3}}\left\{{\displaystyle \frac{{\left(2^4\right)}^3}{7}}-{\displaystyle \frac{1}{7}}-4\right\}={\displaystyle \frac{5_2^{\left(3\right)}}{7·2^{12}}}\left(581\right).$$

and it is equal to the value of right-hand side of (32), which is calculated as

$$\sum _{r=1}^{3}r{\left({\displaystyle \frac{t}{q^{r+1}}}\right)}_q^{\left(3\right)}=\left({\displaystyle \frac{15}{2^6}}\right)+2\left({\displaystyle \frac{15}{2^9}}\right)+3\left({\displaystyle \frac{15}{2^{12}}}\right)={\displaystyle \frac{5_2^{\left(3\right)}}{2^{12}}}\{2^6+2^4+3\}={\displaystyle \frac{5_2^{\left(3\right)}}{7·2^{12}}}\left(581\right).$$

Corollary 4.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\ne \mathfrak{1}$ and $t\in \mathbb{R}$. Then,

$$I_q^m\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(\mathfrak{t}\right)I_q^m\mathfrak{g}\left(\mathfrak{t}\right)-mlog\left(\mathfrak{q}\right)\left\{I_q^{m+1}\mathfrak{g}\left(\mathfrak{tq}\right)\right\}.$$

(33)

Proof.

Taking $\mathfrak{f}\left(\mathfrak{t}\right)=log\left(\mathfrak{t}\right)$ in Equation (21), we get

$$I_q\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(\mathfrak{t}\right)I_q\mathfrak{g}\left(\mathfrak{t}\right)-I_q\left\{I_q\mathfrak{g}\left(\mathfrak{tq}\right)d_{q}log\left(\mathfrak{t}\right)\right\}.$$

Applying the operator $d_q$ on $log\left(\mathfrak{t}\right)$ gives $d_{q}log\left(\mathfrak{t}\right)=log\left(\mathfrak{tq}\right)-log\left(\mathfrak{t}\right)=log\left(\mathfrak{q}\right)$. Thus,

$$I_q\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(\mathfrak{t}\right)I_q\mathfrak{g}\left(\mathfrak{t}\right)-I_q\left\{I_q\mathfrak{g}\left(\mathfrak{tq}\right)log\left(\mathfrak{q}\right)\right\},$$

which is same as

$$I_q\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(\mathfrak{t}\right)I_q\mathfrak{g}\left(\mathfrak{t}\right)-log\left(\mathfrak{q}\right)\left\{I_q^2\mathfrak{g}\left(\mathfrak{tq}\right)\right\}.$$

(34)

Multiplying the $I_q$ operator on both sides of the above equation, we get

$$I_q^2\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=I_q\{log\left(\mathfrak{t}\right)I_q\mathfrak{g}\left(\mathfrak{t}\right)\}-I_q\{log\left(\mathfrak{q}\right)\left(I_q^2\mathfrak{g}\left(\mathfrak{tq}\right)\right)\}.$$

(35)

Substituting Equation (34) in (35), we get

$$I_q^3\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(t\right)I_q^{2}g\left(t\right)-I_q\{log\left(\mathfrak{q}\right)\left(I_q^2\mathfrak{g}\left(\mathfrak{tq}\right)\right)\}-I_q\{log\left(\mathfrak{q}\right)\left(I_q^2\mathfrak{g}\left(\mathfrak{tq}\right)\right)\}$$

When simplifying the above equation, we obtain

$$I_q^3\{log\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\}=log\left(\mathfrak{t}\right)I_q^2\mathfrak{g}\left(\mathfrak{t}\right)-2log\left(\mathfrak{q}\right)\left\{I_q^3\mathfrak{g}\left(\mathfrak{tq}\right)\right\}.$$

(36)

Proceeding like this, we get Equation (33). □

Corollary 5.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\ne \mathfrak{1}$, $\mathfrak{n}\in \mathbb{N}$ and $t\in \mathbb{R}$. Then,

$$I_q^m\left\{log\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=log\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)I_q^m\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)-mlog\left(\mathfrak{q}\right)\left\{I_q^{m+1}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{tq}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}.$$

(37)

Proof.

The proof is completed by replacing t by ${\displaystyle \frac{t}{q^n}}$ in Equation (33). □

Example 3.

Taking $f\left(t\right)=log\left(t\right)·t^2$ and $m=3$ in Equation (29), we get

$$I_q^3\{log\left(p\right)·p^2\}{|}_{p=\frac{t}{q^n}}^{p=t}-n{I}_q^2\left\{log\left({\displaystyle \frac{t}{q^n}}\right){\left({\displaystyle \frac{t}{q^n}}\right)}^2\right\}-{\displaystyle \frac{n^{\left(2\right)}}{2!}}{I}_q\left\{log\left({\displaystyle \frac{t}{q^n}}\right){\left({\displaystyle \frac{t}{q^n}}\right)}^2\right\}$$

$$=\sum _{m-1}^{n-1}{\displaystyle \frac{r^{(m-1)}}{(m-1)!}}\left\{log\left({\displaystyle \frac{t}{q^{r+1}}}\right){\left({\displaystyle \frac{t}{q^{r+1}}}\right)}^2\right\}.$$

(38)

Taking $m=3$ in (33) and then applying Result 1, we get

$$I_q^3\{log\left(t\right)t^2\}=log\left(t\right)\left\{{\displaystyle \frac{t^2}{{(q^2-1)}^3}}\right\}-3log\left(q\right)\left\{{\displaystyle \frac{{\left(tq\right)}^2}{{(q^2-1)}^4}}\right\}.$$

Taking $m=2$ in (33) and then applying Result 1, we get

$$I_q^3\left\{log\left({\displaystyle \frac{t}{q^n}}\right){\left({\displaystyle \frac{t}{q^n}}\right)}^2\right\}=log\left({\displaystyle \frac{t}{q^n}}\right)\left({\displaystyle \frac{t^2}{q^n{(q^2-1)}^3}}\right)-3log\left(q\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{tq}{q^n}}\right)}^2}{{(q^2-1)}^4}}\right\}.$$

Taking $m=2$ in (37) and then applying Result 1, we get

$${\displaystyle \frac{n^{\left(1\right)}}{1!}}{I}_q^2\left\{log\left({\displaystyle \frac{t}{q^n}}\right){\left({\displaystyle \frac{t}{q^n}}\right)}^2\right\}=log\left({\displaystyle \frac{t}{q^n}}\right)\left({\displaystyle \frac{t^2}{q^n{(q^2-1)}^2}}\right)-2log\left(q\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{tq}{q^n}}\right)}^2}{{(q^2-1)}^3}}\right\}.$$

Taking $m=2$ in (37) and then applying Result 1, we get

$${\displaystyle \frac{n^{\left(2\right)}}{2!}}{I}_q\left\{log\left({\displaystyle \frac{t}{q^n}}\right){\left({\displaystyle \frac{t}{q^n}}\right)}^2\right\}=log\left({\displaystyle \frac{t}{q^n}}\right)\left({\displaystyle \frac{t^2}{q^n(q^2-1)}}\right)-log\left(q\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{tq}{q^n}}\right)}^2}{{(q^2-1)}^3}}\right\}.$$

Now, inserting the values $t=12.5$, $q=9.7$, and $n=5$ in the above, we arrive at

$$log\left(12.5\right)\left\{{\displaystyle \frac{{\left(9.7\right)}^2}{{({\left(9.7\right)}^2-1)}^3}}\right\}-3log\left(9.7\right)\left\{{\displaystyle \frac{{\left(121.25\right)}^2}{{({\left(9.7\right)}^2-1)}^4}}\right\}=-0.000386,$$

(39)

$$log\left({\displaystyle \frac{12.5}{9.7^5}}\right)\left({\displaystyle \frac{12.5^2}{9.7^5{(9.7^2-1)}^3}}\right)-3log\left(9.7\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{121.25}{9.7^5}}\right)}^2}{{(9.7^2-1)}^4}}\right\}=-1.793378\times {10}^{-13},$$

(40)

$$5\left\{log\left({\displaystyle \frac{12.5}{9.7^5}}\right)\left({\displaystyle \frac{12.5^2}{9.7^5{(9.7^2-1)}^2}}\right)-2log\left(9.7\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{121.25}{9.7^5}}\right)}^2}{{(9.7^2-1)}^3}}\right\}\right\}=-7.127944\times {10}^{-11},$$

(41)

$$10\left\{log\left({\displaystyle \frac{12.5}{9.7^5}}\right)\left({\displaystyle \frac{12.5^2}{9.7^5(9.7^2-1)}}\right)-log\left(9.7\right)\left\{{\displaystyle \frac{{\left({\displaystyle \frac{121.25}{9.7^5}}\right)}^2}{{(9.7^2-1)}^3}}\right\}\right\}=-1.100064\times {10}^{-8}$$

(42)

and

$$\sum _{r=2}^4{\displaystyle \frac{r^{\left(2\right)}}{2!}}log\left({\displaystyle \frac{12.5}{9.7^{r+1}}}\right){\left({\displaystyle \frac{12.5}{9.7^{r+1}}}\right)}^2={\displaystyle \frac{2^{\left(2\right)}}{2!}}log\left({\displaystyle \frac{12.5}{9.7^3}}\right){\left({\displaystyle \frac{12.5}{9.7^3}}\right)}^2+{\displaystyle \frac{3^{\left(2\right)}}{2!}}log\left({\displaystyle \frac{12.5}{9.7^4}}\right){\left({\displaystyle \frac{12.5}{9.7^4}}\right)}^2$$

$$+{\displaystyle \frac{4^{\left(2\right)}}{2!}}log\left({\displaystyle \frac{12.5}{9.7^5}}\right){\left({\displaystyle \frac{12.5}{9.7^5}}\right)}^2=-0.000368.$$

(43)

Hence, (38) is verified by (39)–(43).

Corollary 6.

Consider the conditions given in Theorem 4. Then

(i)$I_q^m\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-{\displaystyle \sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{m}-\mathfrak{1}}}{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}\left\{I_q^{(m-r)}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}={\displaystyle \sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{m}}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$

(ii)$I_q^m\mathfrak{f}\left(\mathfrak{p}\right){|}_{\mathfrak{p}=\frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}^{\mathfrak{p}=\mathfrak{t}}-{\displaystyle \sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{m}-\mathfrak{1}}}{\displaystyle \frac{{(\mathfrak{n}+\mathfrak{m})}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}\left\{I_q^{(m-r)}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}+\mathfrak{m}}}}\right)\right\}={\displaystyle \sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$

Proof.

(i) The proof is completed by replacing ${\displaystyle \sum _{\mathfrak{r}=\mathfrak{m}-\mathfrak{1}}^{\mathfrak{n}-\mathfrak{1}}}{\displaystyle \frac{{\mathfrak{r}}_{\mathfrak{1}}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)$ into ${\displaystyle \sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{m}}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right)$ in Equation (29).

(ii) The proof is completed by replacing $\mathfrak{n}$ by $\mathfrak{n}+\mathfrak{m}$ in case (i). □

4.2. Fundamental Theorems Related to $q(\alpha )$-Difference Symmetric Operators

Definitions, lemmas, corollaries, and theorems for the higher order $q(\alpha )$ anti-difference (inverse) symmetric operator are found in this section. Suitable examples are provided for verification.

Definition 5

([46]). Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$. For $\alpha \in \mathbb{R}$ and $\mathfrak{q}\in \mathbb{R}-\left\{\mathfrak{1}\right\}$, the q-alpha difference (or q-alpha difference symmetric) operator is defined as

$$d_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{tq}\right)-\alpha \mathfrak{f}\left(\mathfrak{t}\right).$$

(44)

If ∃ a function $\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$∋$d_{q(\alpha )}\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, then the inverse q-alpha difference symmetric operator is defined as

$$\mathfrak{g}\left(\mathfrak{t}\right)=I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{c},$$

(45)

where $\mathfrak{c}$ is a constant.

Result 5

([46]).  Assume $\alpha \in \mathbb{R}-\left\{1\right\}$, $\mathfrak{t}\in (\mathfrak{0},\infty )$ and $\mathfrak{1}\ne \mathfrak{q}>\mathfrak{0}$. Then,

$$I_{q(\alpha )}\left(1\right)={\displaystyle \frac{1}{1-\alpha }}$$

(46)

and

$$I_{q(\alpha )}\mathfrak{log}\left(\mathfrak{t}\right)={\displaystyle \frac{\mathfrak{log}\left(\mathfrak{t}\right)}{1-\alpha }}-{\displaystyle \frac{\mathfrak{log}\left(\mathfrak{q}\right)}{{(1-\alpha )}^2}}.$$

(47)

Proof.

The proof is completed by taking $\mathfrak{f}\left(\mathfrak{t}\right)={\mathfrak{t}}^{\mathfrak{0}}$ and $\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{log}\left(\mathfrak{t}\right)$ in (44) and then applying (45). □

Result 6.

Assume $\alpha \in \mathbb{R}-\left\{1\right\}$, $\mathfrak{1}\ne \mathfrak{q}>\mathfrak{0}$ and $\mathfrak{t},\mathfrak{n}\in (\mathfrak{0},\infty )$. Then,

$$I_{q(\alpha )}\mathfrak{log}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)={\displaystyle \frac{\mathfrak{log}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)}{1-\alpha }}-{\displaystyle \frac{\mathfrak{log}\left(\mathfrak{q}\right)}{{(1-\alpha )}^2}}.$$

(48)

Proof.

The proof is similar to Result 5 by replacing t by ${\displaystyle \frac{t}{q^n}}$ in Equation (47). □

The following Lemma 6 is the power rule for the q-alpha difference operator.

Lemma 6.

Let $\mathfrak{n}\in \mathbb{N}$, $\alpha \in \mathbb{R}$ and ${\mathfrak{q}}^{\mathfrak{n}}\ne \alpha$. Then,

$$d_{q(\alpha )}{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}=({\mathfrak{q}}^{\mathfrak{n}}-\alpha ){\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)},\mathfrak{t}\in \mathbb{R}.$$

(49)

and

$$I_{q(\alpha )}{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}={\displaystyle \frac{{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}}{{\mathfrak{q}}^{\mathfrak{n}}-\alpha }},\mathfrak{t}\in \mathbb{R}.$$

(50)

Proof.

(i) Taking $\mathfrak{f}\left(\mathfrak{t}\right)={\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}$ in Equation (44), we get

$$d_{q(\alpha )}{\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}={\left(\mathfrak{tq}\right)}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}-\alpha {\mathfrak{t}}_{\mathfrak{q}}^{\left(\mathfrak{n}\right)}.$$

By Equation (8) and by Lemma 1, the proof of (49) is completed.

(ii) The proof of (50) is completed by multiplying the $d_{q(\alpha )}^{-1}\left(say{I}_{q(\alpha )}\right)$ on both sides of Equation (49). □

Lemma 7.

Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\ne \mathfrak{1}$ and $\alpha \in \mathbb{R}$. The product rule of the q-alpha difference operator is given by

$$I_{q(\alpha )}\left\{\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{g}\left(\mathfrak{t}\right)\right\}=\mathfrak{f}\left(\mathfrak{t}\right)I_{q(\alpha )}\mathfrak{g}\left(\mathfrak{t}\right)-I_{q(\alpha )}\left\{I_{q(\alpha )}\mathfrak{g}\left(\mathfrak{tq}\right)d_q\mathfrak{f}\left(\mathfrak{t}\right)\right\}.$$

(51)

Proof.

By applying the operator $d_{q(\alpha )}$ on the function $\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{h}\left(\mathfrak{t}\right)$, we get

$$d_{q(\alpha )}\left\{\mathfrak{f}\left(\mathfrak{t}\right)\mathfrak{h}\left(\mathfrak{t}\right)\right\}=\mathfrak{h}\left(\mathfrak{tq}\right)d_q\mathfrak{f}\left(\mathfrak{t}\right)+\mathfrak{f}\left(\mathfrak{t}\right)d_{q(\alpha )}\mathfrak{h}\left(\mathfrak{t}\right).$$

The proof is completed by taking $d_{q(\alpha )}\mathfrak{h}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{t}\right)$ and $\mathfrak{h}\left(\mathfrak{t}\right)=I_{q(\alpha )}\mathfrak{g}\left(\mathfrak{t}\right)$. □

The following theorem is the first order $q(\alpha )$ anti-difference principle.

Theorem 7.

Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $d_{q(\alpha )}\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, $\alpha >0$, $\mathfrak{n}\in \mathbb{N}\left(\mathfrak{1}\right)$ and $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$. Then $I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{t}\right)$ and

$$I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{1}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(52)

Proof.

Using Definition 5 and $d_{q(\alpha )}\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left(\mathfrak{t}\right)$, we get

$$\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{tq}\right)-\alpha \mathfrak{g}\left(\mathfrak{t}\right).$$

(53)

Shifting $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ in (53), we determine

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right).$$

(54)

Converting $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ in (54) to obtain $\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)$ value in (54), we obtain

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+{\alpha }^{\mathfrak{2}}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right).$$

(55)

Similarly, replacing $\mathfrak{t}$ by $\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)$ in (55) and again substituting $\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)$ in (55), we get

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+{\alpha }^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+{\alpha }^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+{\alpha }^4\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right).$$

Proceeding like this, we get the general form as

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\dots +{\alpha }^{n-1}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+{\alpha }^n\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).$$

(56)

Thus, Equation (52) follows by taking $I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{g}\left(\mathfrak{t}\right)$. □

Example 4.

Taking $f\left(t\right)=log\left(t\right)$ in Equation (52), we get

$$I_{q(\alpha )}log\left(t\right)-{\alpha }^n\left\{I_{q(\alpha )}log\left({\displaystyle \frac{t}{q^n}}\right)\right\}=\sum _{r=0}^{n-1}{\alpha }^{r}log\left({\displaystyle \frac{t}{q^{r+1}}}\right).$$

(57)

Taking $f\left(t\right)=logt$ in Definition 5 and then using Equations (47) and (48), it is easy to find the closed-form solution for Equation (57).

Now, inserting $t=8.2$, $q=5.3$, $\alpha =3.1$, and $n=4$ in Equation (57), we get

$$I_{5.3\left(3.1\right)}log\left(t\right){|}_{t=8.2}={\displaystyle \frac{log\left(8.2\right)}{(1-3.1)}}-{\displaystyle \frac{log\left(5.3\right)}{{(1-3.1)}^2}}=-0.599,$$

(58)

$${\left(3.1\right)}^4{I}_{5.3\left(3.1\right)}log\left({\displaystyle \frac{8.2}{5.3^4}}\right){|}_{t=8.2}={\left(3.1\right)}^4\left[{\displaystyle \frac{log\left({\displaystyle \frac{t}{5.3^4}}\right)}{(1-3.1)}}-{\displaystyle \frac{log\left(5.3\right)}{{(1-3.1)}^2}}\right]=-72.052$$

(59)

and

$$\sum _{r=0}^3{\left(3.1\right)}^{r}log\left({\displaystyle \frac{8.2}{5.3^{r+1}}}\right)=log\left({\displaystyle \frac{8.2}{5.3^1}}\right)+log\left({\displaystyle \frac{8.2}{5.3^2}}\right)+log\left({\displaystyle \frac{8.2}{5.3^3}}\right)+log\left({\displaystyle \frac{8.2}{5.3^4}}\right)=-72.651.$$

(60)

Hence, Equation (57) is verified by (58)–(60).

Corollary 7.

Let $\mathfrak{m}\in \mathbb{N}\left(\mathfrak{1}\right)$, $\mathfrak{q}\in (\mathfrak{0},\infty )$ and $\alpha >1$ be any real number. Then

$$I_{q(\alpha )}^{m}log\mathfrak{t}={\displaystyle \frac{log\mathfrak{t}}{{(1-\alpha )}^{\mathfrak{m}}}}-\mathfrak{m}{\displaystyle \frac{log\mathfrak{q}}{{(1-\alpha )}^{\mathfrak{m}+\mathfrak{1}}}}.$$

(61)

Proof.

Applying the $I_q$ operator on both sides of Equation (47), we get

$$I_{q(\alpha )}^{2}log\mathfrak{t}=\left({\displaystyle \frac{1}{1-\alpha }}\right)I_{q(\alpha )}(log\mathfrak{t})-{\displaystyle \frac{log\mathfrak{q}}{{(1-\alpha )}^2}}{I}_q\left(1\right).$$

Now, substituting Equations (46) and (47) in the above equation, it becomes

$$I_{q(\alpha )}^{2}log\mathfrak{t}=\left[{\displaystyle \frac{log\mathfrak{t}}{{(1-\alpha )}^{\mathfrak{2}}}}-{\displaystyle \frac{log\mathfrak{q}}{{(1-\alpha )}^{\mathfrak{3}}}}\right]-{\displaystyle \frac{log\mathfrak{q}}{{(1-\alpha )}^{\mathfrak{3}}}}={\displaystyle \frac{log\mathfrak{t}}{{(1-\alpha )}^{\mathfrak{2}}}}-2{\displaystyle \frac{log\mathfrak{q}}{{(1-\alpha )}^{\mathfrak{3}}}}.$$

Proceeding like this up to $\mathfrak{m}$ times, we get (61). □

Theorem 8.

Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$, $\mathfrak{n},\mathfrak{m}\in \mathbb{N}\left(\mathfrak{1}\right)$, $0\ne \alpha \in \mathbb{R}$, and $\mathfrak{n}\ge \mathfrak{m}$. Then the higher order q-alpha anti-difference principle related to $d_{q(\alpha )}$ is given by

$$I_{q(\alpha )}^m\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^m\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-\sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{m}-\mathfrak{1}}{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}{\alpha }^{n-r}\left\{I_{q(\alpha )}^{m-r}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{m}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$$

(62)

Proof.

Applying $I_{q(\alpha )}$ on both sides of Equation (52) in Theorem 7, we get

$$I_{q(\alpha )}^2\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=I_{q(\alpha )}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \left\{I_{q(\alpha )}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)\right\}+\dots +{\alpha }^{n-1}\left\{I_{q(\alpha )}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}.$$

(63)

Substituting Equation (56) in each term of the right-hand side in (63), we arrive at

$$\begin{array}{c}{I}_{q(\alpha )}^2\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{2}}^{\mathfrak{n}}}{\alpha }^{r-2}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+{\alpha }^{n-1}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}+\alpha \left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{3}}^{\mathfrak{n}}}{\alpha }^{r-3}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+{\alpha }^{n-2}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}+{\alpha }^2\left\{{\displaystyle \sum _{\mathfrak{r}=\mathfrak{4}}^{\mathfrak{n}}}{\alpha }^{r-4}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+{\alpha }^{n-3}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}+\dots \dots +{\alpha }^{n-2}\left\{\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}+{\alpha }^{n-1}{\displaystyle \underset{q}{\overset{-1}{\Delta }}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right).\hfill \end{array}$$

If we take the right-hand-side phrase together, we get

$$I_{q(\alpha )}^2\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+2\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\dots +(n-1){\alpha }^{n-2}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+n{\alpha }^{n-1}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right),$$

(64)

which is same as

$$I_{q(\alpha )}^2\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-n{\alpha }^{n-1}\left\{I_{q(\alpha )}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{2}}(\mathfrak{r}+\mathfrak{1}){\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right).$$

(65)

Again applying $I_{q(\alpha )}$ on both sides of (65) and then continuing in the same manner from Equation (63) to Equation (64), we get

$$\begin{gathered} I_{q(\alpha )}^3\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-n{\alpha }^{n-1}\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+(\mathfrak{1}+\mathfrak{2})\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right) \\ +(\mathfrak{1}+\mathfrak{2}+\mathfrak{3}){\alpha }^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+\dots +(\mathfrak{1}+\mathfrak{2}+\dots +\mathfrak{n}){\alpha }^{n-2}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right). \end{gathered}$$

Setting $\mathfrak{m}=\mathfrak{1}$ in (20) and then applying it in the above equation gives

$$\begin{gathered} I_{q(\alpha )}^3\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-n{\alpha }^{n-1}\left\{I_{q(\alpha )}^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}={\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+ \\ +{\displaystyle \frac{{\mathfrak{4}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}{\alpha }^2\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+\dots +{\displaystyle \frac{{(\mathfrak{n}-\mathfrak{1})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}{\alpha }^{n-3}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)+{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}{\alpha }^{n-2}\mathfrak{g}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right), \end{gathered}$$

which is same as

$$I_{q(\alpha )}^3\mathfrak{f}\left(\mathfrak{t}\right)-{\alpha }^n\left\{I_{q(\alpha )}^3\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}-\sum _{\mathfrak{r}=\mathfrak{1}}^{\mathfrak{2}}{\displaystyle \frac{{\mathfrak{n}}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}{\alpha }^{n-r}\left\{I_{q(\alpha )}^{3-r}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}-\mathfrak{3}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{2})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{3}}}}\right).$$

Thus the proof of (62) follows by repeating similar steps up to $\mathfrak{m}$ times, and by Equation (20). □

Corollary 8.

Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$, $0\ne \alpha \in \mathbb{R}$, and $\mathfrak{n},\mathfrak{m}\in \mathbb{N}\left(\mathfrak{1}\right)$. The higher order q-alpha anti-difference principle related to $d_q$ is given by

$$I_{q(\alpha )}^m\mathfrak{f}\left(\mathfrak{t}\right)-\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{m}-\mathfrak{1}}{\displaystyle \frac{{(\mathfrak{n}+\mathfrak{m})}^{\left(\mathfrak{r}\right)}}{\mathfrak{r}!}}{\alpha }^{n+m-r}{I}_{q(\alpha )}^{m-r}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{n}+\mathfrak{m}}}}\right)=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{n}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$$

Proof.

The proof is completed by converting $\mathfrak{n}$ by $\mathfrak{n}+\mathfrak{m}$ in Equation (62). □

The theorems developed in this section offer the solution for the q-symmetric difference operator ${\mathfrak{D}}_{\mathfrak{q}}$. We can do the same thing using the $d^q$ operator.

5. Mixed Symmetric Operators in Quantum Calculus

5.1. Symmetric Difference Operators of q and h

Here, we proposed certain theorems and corollaries using the q and h difference operators to find the fundamental theorems. This section also includes appropriate examples. The anti-difference operator on h for the function $\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)$ in relation to the variable $\mathfrak{t}$ and constant s is denoted by the operator $\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)$ throughout this section.

Theorem 9.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}\mathfrak{f}(\mathfrak{t}-\mathfrak{ih})$ is convergent and $\underset{\mathfrak{t}\to -\infty }{lim}\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{0}$, then

$$\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{t}\right)=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }\mathfrak{f}(\mathfrak{t}-\mathfrak{ih}).$$

(66)

Proof.

The proof is completed by taking $\underset{\mathfrak{n}\to \infty }{lim}$ in Equation (23). □

Corollary 9.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}-\mathfrak{ih}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to -\infty }{lim}\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)=\mathfrak{0}$, then

$$\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}-\mathfrak{ih}}}}\right).$$

(67)

Proof.

From the convergent condition $\mathfrak{f}\left(\mathfrak{0}\right)=\mathfrak{0}$ and $\mathfrak{g}\left(\mathfrak{0}\right)=\underset{h/t}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{0}\right)=\mathfrak{0}$, the proof is completed by replacing $\mathfrak{f}\left(\mathfrak{t}\right)$ by $\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)$ in Equation (66). □

Corollary 10.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{i}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to \infty }{lim}\underset{-1/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)=\mathfrak{0}$, then

$$\underset{-1/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{i}}}}\right).$$

(68)

Proof.

The proof is completed by replacing $\mathfrak{h}$ by $-\mathfrak{1}$ in (67). □

Corollary 11.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to \infty }{lim}\underset{-1/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)=\mathfrak{0}$, then

$$\underset{-1/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)=\sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right).$$

(69)

Proof.

The proof is completed by shifting $\mathfrak{t}$ by $\mathfrak{t}+\mathfrak{1}$ in (68). □

The below example is the verification of Corollary 11 for polynomial functions.

Example 5.

Taking $f\left(t\right)=t^n$ in Equation (69), we get

$$\underset{-1/t}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n=\sum _{i=t+1}^{\infty }{\left({\displaystyle \frac{s}{q^{i+1}}}\right)}^n.$$

(70)

In Definition 3, taking $h=-1$ and $t={\displaystyle \frac{s}{q^{t+1}}}$ with respect to the variable t, we obtain $\underset{-1/t}{\Delta }{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n={\left({\displaystyle \frac{s}{q^t}}\right)}^n-{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n={\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n\left({\displaystyle \frac{1}{q^{-n}}}-1\right)$.

From the above relation, it is easy to find

$$\underset{-1/t}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n={\displaystyle \frac{{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}^n}{\left({\displaystyle \frac{1}{q^{-n}}}-1\right)}}.$$

(71)

Now, set $s=7.3$, $q=2.7$, $n=1.4$, and $t=2$ in Equation (71). Then (71) becomes

$$\underset{-1/2}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{7.3}{2.7^{t+1}}}\right)}^{1.4}{|}_{t=2}={\displaystyle \frac{{\left({\displaystyle \frac{7.3}{2.7^{t+1}}}\right)}^{1.4}}{\left({\displaystyle \frac{1}{2.7^{-1.4}}}-1\right)}}{|}_{t=2}={\displaystyle \frac{{\left({\displaystyle \frac{7.3}{2.7^3}}\right)}^{1.4}}{3.017069}}=0.082668.$$

(72)

The right-hand side of Equation (70) becomes

$$\sum _{i=3}^{\infty }{\left({\displaystyle \frac{7.3}{2.7^{i+1}}}\right)}^{1.4}={\left({\displaystyle \frac{7.3}{2.7^4}}\right)}^{1.4}+{\left({\displaystyle \frac{7.3}{2.7^5}}\right)}^{1.4}+{\left({\displaystyle \frac{7.3}{2.7^6}}\right)}^{1.4}$$

$$+{\left({\displaystyle \frac{7.3}{2.7^7}}\right)}^{1.4}+{\left({\displaystyle \frac{7.3}{2.7^8}}\right)}^{1.4}+{\left({\displaystyle \frac{7.3}{2.7^9}}\right)}^{1.4}+\dots =0.082648+\dots$$

(73)

Hence, (70) is verified by (72) and (73).

The below example is a verification of Corollary 11 for the polynomial factorial function.

Example 6.

Taking $f\left(t\right)=t_q^{\left(n\right)}$ in Equation (69), we get

$$\underset{-1/t}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}=\sum _{i=t+1}^{\infty }{\left({\displaystyle \frac{s}{q^{i+1}}}\right)}_q^{\left(n\right)}.$$

(74)

Taking $h=-1$ and $t={\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}$ in Definition 3, we arrive at

$$\underset{-1/t}{\Delta }{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}={\left({\displaystyle \frac{s}{q^t}}\right)}_q^{\left(n\right)}-{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}.$$

Applying Equation (8) in the above relation, it becomes

$$\underset{-1/t}{\Delta }{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}={\displaystyle \frac{s(s-q)(s-q^2)}{q^t}}-{\displaystyle \frac{s(s-q)(s-q^2)}{q^{t+1}}}={\displaystyle \frac{s_q^{\left(n\right)}}{q^{t+1}}}\left({\displaystyle \frac{1}{q^{-1}}}-1\right).$$

Therefore, we can easily find $\underset{-1/t}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}={\displaystyle \frac{\left({\displaystyle \frac{s_q^{\left(n\right)}}{q^{t+1}}}\right)}{\left({\displaystyle \frac{1}{q^{-1}}}-1\right)}}$.

Setting $n=3$, $s=7.3$, $q=2.7$, and $t=2$ in Equation (74), it becomes

$$\underset{-1/t}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(3\right)}=\sum _{i=t+1}^{\infty }{\left({\displaystyle \frac{s}{q^{i+1}}}\right)}_q^{\left(3\right)}.$$

Now the left-hand side of (74) is

$$\underset{-1/2}{\overset{-1}{\Delta }}{\left({\displaystyle \frac{7.3}{2.7^{t+1}}}\right)}_{2.7}^{\left(3\right)}{|}_{t=2}={\displaystyle \frac{\left({\displaystyle \frac{7.3_{2.7}^{\left(3\right)}}{2.7^3}}\right)}{\left({\displaystyle \frac{1}{2.7^{-1}}}-1\right)}}={\displaystyle \frac{7.3(7.3-2.7)(7.3-2.7^2)}{1.7}}=0.010036$$

(75)

and the right-hand side of (74) is ${\left({\displaystyle \frac{7.3}{2.7^4}}\right)}_{2.7}^{\left(3\right)}+{\left({\displaystyle \frac{7.3}{2.7^5}}\right)}_{2.7}^{\left(3\right)}+{\left({\displaystyle \frac{7.3}{2.7^6}}\right)}_{2.7}^{\left(3\right)}+{\left({\displaystyle \frac{7.3}{2.7^7}}\right)}_{2.7}^{\left(3\right)}+{\left({\displaystyle \frac{7.3}{2.7^8}}\right)}_{2.7}^{\left(3\right)}$

$$+{\left({\displaystyle \frac{7.3}{2.7^9}}\right)}_{2.7}^{\left(3\right)}+{\left({\displaystyle \frac{7.3}{2.7^{10}}}\right)}_{2.7}^{\left(3\right)}+\dots =0.01001+\dots$$

(76)

Hence, (74) is verified by (75) and (76).

Remark 4.

In Example 6, $\left({\displaystyle \frac{s_q^{\left(n\right)}}{q^{t+1}}}\right)$ and ${\left({\displaystyle \frac{s}{q^{t+1}}}\right)}_q^{\left(n\right)}$ give the same meaning.

Theorem 10.

Let $\mathfrak{f},\mathfrak{g}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{s}\in \mathbb{R}$, $\mathfrak{t}\in \mathbb{N}$, $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$ and considering the conditions given in Corollary 11. Then,

$$I_q\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(77)

Proof.

Applying $\underset{\mathfrak{n}\to \infty }{lim}$ in (28) and from the convergent condition $\mathfrak{f}\left(\mathfrak{0}\right)=\mathfrak{g}\left(\mathfrak{0}\right)=\mathfrak{0}$, we get

$$\mathfrak{g}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\dots +\mathfrak{f}\left(\mathfrak{0}\right)+\mathfrak{g}\left(\mathfrak{0}\right),$$

(78)

which is written in the form of

$$I_q\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\dots +\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right)+\dots$$

(79)

Replacing $\mathfrak{t}$ by ${}^{\prime }{\mathfrak{s}}^{\prime }$ and $\mathfrak{r}$ by ${}^{\prime }{\mathfrak{t}}^{\prime }$, Equation (79) becomes

$$I_q\mathfrak{f}\left(\mathfrak{s}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{\mathfrak{q}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\dots +\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)+\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{2}}}}\right)+\dots ,$$

which is same as

$$I_q\mathfrak{f}\left(\mathfrak{s}\right)=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)+\sum _{\mathfrak{r}=\mathfrak{t}+\mathfrak{1}}^{\infty }\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(80)

The proof is completed by substituting Equation (69) in Equation (80). □

Corollary 12.

Taking $\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{t}$ in (77), then Equation (77) becomes

$$I_q\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right).$$

(81)

Applying the operator $d_q$ on the function $\mathfrak{t}$, we get $d_q\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}=\mathfrak{t}(\mathfrak{q}-\mathfrak{1}){|}_{\mathfrak{t}=\mathfrak{s}}$.

Then, its inverse operator will be

$$I_q\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}={\displaystyle \frac{\mathfrak{s}}{\mathfrak{q}-\mathfrak{1}}}.$$

(82)

Taking $\mathfrak{f}\left(\mathfrak{t}\right)={\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}$ in Equation (1), then $\underset{h/t}{\Delta }\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)={\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\left({\displaystyle \frac{\mathfrak{1}}{{\mathfrak{q}}^{\mathfrak{h}}-\mathfrak{1}}}\right)$. We can easily calculate the inverse operator for the function t with this information, i.e.,

$$\underset{h/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)={\displaystyle \frac{{\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}}{\frac{\mathfrak{1}}{{\mathfrak{q}}^{\mathfrak{h}}}-\mathfrak{1}}}.$$

(83)

Setting $\mathfrak{h}=-\mathfrak{1}$ in Equation (83), we get

$$\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)={\displaystyle \frac{{\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}}{\frac{\mathfrak{1}}{{\mathfrak{q}}^{-\mathfrak{1}}}-\mathfrak{1}}}.$$

(84)

Hence the proof is completed.

The example below is a verification of (81).

Example 7.

Taking $s=3,t=3,q=2$ in (81) and then substituting Equations (82) and (84) in (81), we obtain the left-hand side of (81) as

$$\left\{{\displaystyle \frac{3}{2-1}}\right\}-\left\{{\displaystyle \frac{{\displaystyle \frac{3}{2^4}}}{\frac{1}{2^{-1}}-1}}\right\}=3-\left({\displaystyle \frac{3}{16}}\right)={\displaystyle \frac{48-3}{16}}={\displaystyle \frac{45}{16}}.$$

and the right-hand side of (81) as

$$\sum _{r=0}^3\left({\displaystyle \frac{3}{2^{r+1}}}\right)=\left({\displaystyle \frac{3}{2^1}}\right)+\left({\displaystyle \frac{3}{2^2}}\right)+\left({\displaystyle \frac{3}{2^3}}\right)+\left({\displaystyle \frac{3}{2^4}}\right)={\displaystyle \frac{45}{16}}.$$

Theorem 11.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\mathfrak{q}\in \mathbb{R}-\{\mathfrak{0},\mathfrak{1}\}$, $\mathfrak{s}\in \mathbb{R}$, $\mathfrak{m}\in \mathbb{N}\left(\mathfrak{1}\right)$ and considerig the conditions given in Corollary 11. Then,

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }{\displaystyle \frac{{(\mathfrak{i}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{m}}}}\right).$$

(85)

Proof.

Equation (69) of Corollary 11 can expressed as

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{0})}^{\left(\mathfrak{0}\right)}}{\mathfrak{0}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }{\displaystyle \frac{{(\mathfrak{i}+\mathfrak{0})}^{\left(\mathfrak{0}\right)}}{\mathfrak{0}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right),$$

(86)

where ${(\mathfrak{t}+\mathfrak{0})}^{\left(\mathfrak{0}\right)}=\mathfrak{1}$ and $\mathfrak{0}!=\mathfrak{1}$.

The proof is completed by applying (86) to the function ${\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)$. □

Theorem 12.

Consider the conditions given in Theorem 11 and $\mathfrak{t}\in \mathbb{N}\left(\mathfrak{1}\right)$. Then,

$$I_q^m\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$$

(87)

Proof.

The proof for $\mathfrak{m}=\mathfrak{1}$ is given in Theorem 10. □

Now, multiplying the $I_q$ operator on both sides of Equation (79) and then substituting Equation (78) in each term of (79), we get

$$I_q^2\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\mathfrak{2}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+\mathfrak{3}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+\dots +\mathfrak{rf}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)+(\mathfrak{r}+\mathfrak{1})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right)+\dots .$$

(88)

Replacing $\mathfrak{t}$ by $\mathfrak{s}$ and $\mathfrak{r}$ by $\mathfrak{t}$ in (88), then the Equation (88) becomes

$$I_q^2\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}(\mathfrak{r}+\mathfrak{1})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right)+\sum _{\mathfrak{r}=\mathfrak{t}+\mathfrak{1}}^{\infty }(\mathfrak{r}+\mathfrak{1})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right).$$

(89)

If we apply Equation (85) for $\mathfrak{m}=2$ in (89), then Equation (89) becomes

$$I_q^2\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{1})}^{\left(\mathfrak{1}\right)}}{\mathfrak{1}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{2}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{1})}^{\left(\mathfrak{1}\right)}}{\mathfrak{1}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right).$$

(90)

Again, multiplying the $I_q$ operator on both sides of Equation (88), and then substituting Equation (78) in each term of (88), we get

$$I_q^3\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+(\mathfrak{1}+\mathfrak{2})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+(\mathfrak{1}+\mathfrak{2}+\mathfrak{3})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)(\mathfrak{1}+\mathfrak{2}+\mathfrak{3}+\mathfrak{4})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{6}}}}\right)+\dots$$

$$+(\mathfrak{1}+\mathfrak{2}+\dots +\mathfrak{r})\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right)+(\mathfrak{1}+\mathfrak{2}+\dots +(\mathfrak{r}+\mathfrak{1}))\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{3}}}}\right)+\dots .$$

(91)

Taking $\mathfrak{m}=\mathfrak{1}$ in (20) and then substituting Equation (20) in (91), we obtain

$$I_q^3\mathfrak{f}\left(\mathfrak{t}\right)={\displaystyle \frac{{\mathfrak{2}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{3}}}}\right)+{\displaystyle \frac{{\mathfrak{3}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{4}}}}\right)+{\displaystyle \frac{{\mathfrak{4}}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{5}}}}\right)+\dots +{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{1})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{2}}}}\right)+$$

$$+{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{2})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{3}}}}\right)+{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{3})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{4}}}}\right)+\dots .$$

(92)

Following similar steps from (89) to (90), and then using Equation (85) for $\mathfrak{m}=\mathfrak{2}$, Equation (92) becomes

$$I_q^3\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{2})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{3}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{2})}^{\left(\mathfrak{2}\right)}}{\mathfrak{2}!}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{3}}}}\right).$$

(93)

If we continue in this manner for $\mathfrak{m}$ times, we will arrive at (87).

5.2. Symmetric Difference Operators of $q(\alpha )$ and h

To find these fundamental theorems, we propose certain theorems and corollaries using the $q(\alpha )$ and h difference operators. The section also includes appropriate examples.

Theorem 13.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}{\alpha }^{t-ih}\mathfrak{f}(\mathfrak{t}-\mathfrak{ih})$ is convergent and $\underset{\mathfrak{t}\to -\infty }{lim}\underset{h/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left(\mathfrak{t}\right)\right\}=0$, then

$$\underset{h/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left(\mathfrak{t}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }{\alpha }^{t-ih}\mathfrak{f}(\mathfrak{t}-\mathfrak{ih}).$$

(94)

Proof.

Applying the $\underset{h}{\Delta }$ operator on ${\alpha }^t\mathfrak{f}\left(\mathfrak{t}\right)$ and by Theorem 9, we get (94). □

Corollary 13.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}{\alpha }^{t-ih}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}-\mathfrak{ih}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to -\infty }{lim}\underset{h/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)\right\}=0$, then

$$\underset{h/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }{\alpha }^{t-ih}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}-\mathfrak{ih}}}}\right).$$

(95)

Proof.

The proof is completed by converting $\mathfrak{f}\left(\mathfrak{t}\right)$ by $\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)$ in Equation (94). Here $\underset{h/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)\right\}$ denotes the anti-difference operator on h for the function ${\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)$ with respect to the variable $\mathfrak{t}$ and constant $\mathfrak{s}$. □

Corollary 14.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}{\alpha }^{t+i}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}+\mathfrak{i}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to \infty }{lim}\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)\right\}=0$, then

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }{\alpha }^{t+i}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}+\mathfrak{i}}}}\right).$$

(96)

Proof.

The proof is completed by replacing $\mathfrak{h}$ by $-\mathfrak{1}$ in (95). □

Corollary 15.

If ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }}{\alpha }^i\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right)$ is convergent and $\underset{\mathfrak{t}\to \infty }{lim}\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}}}}\right)\right\}=0$, then

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }{\alpha }^i\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right).$$

(97)

Proof.

The proof is completed by replacing ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{1}}^{\infty }}{\alpha }^{t+i}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}+\mathfrak{i}}}}\right)$ into ${\displaystyle \sum _{\mathfrak{i}=\mathfrak{t}+\mathfrak{1}}^{\infty }}{\alpha }^i\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{i}+\mathfrak{1}}}}\right)$ in Equation (96). □

Theorem 14.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\alpha ,\mathfrak{s}\in \mathbb{R}$, q is not a multiple of α and considering the conditions given in Corollary 15. Then

$$I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)$$

(98)

Proof.

Taking $\underset{\mathfrak{n}\to \infty }{lim}$ in Equation (52) gives

$$I_{q(\alpha )}\mathfrak{f}\left(\mathfrak{t}\right)=\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{\mathfrak{q}}}\right)+\alpha \mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{2}}}}\right)+\dots +{\alpha }^{r-1}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}}}}\right)+{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{t}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right)+\dots$$

where $\mathfrak{f}\left(\mathfrak{0}\right)=\mathfrak{0}$ and $\underset{q(\alpha )}{\overset{-1}{\Delta }}\mathfrak{f}\left(\mathfrak{0}\right)=\mathfrak{0}$. When applying the $I_{q(\alpha )}$ operator in Theorem 10, we get (98). □

Theorem 15.

Let $\mathfrak{f}:{\mathfrak{T}}_{\mathfrak{q}}\to \mathbb{R}$, $\alpha ,\mathfrak{s}\in \mathbb{R}-\left\{\mathfrak{0}\right\}$, and $\mathfrak{m}\in \mathbb{N}\left(\mathfrak{1}\right)$. If q is not a multiple of α, and the series ${\displaystyle \sum _{\mathfrak{r}=\mathfrak{t}+\mathfrak{1}}^{\infty }}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right)$ is convergent, then

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{t}+\mathfrak{1}}^{\infty }{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$$

(99)

Proof.

Equation (97) can expressed as

$$\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{0})}^{\left(\mathfrak{0}\right)}}{\mathfrak{0}!}}{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{1}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{t}+\mathfrak{1}}^{\infty }{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{0})}^{\left(\mathfrak{0}\right)}}{\mathfrak{0}!}}{\alpha }^r\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{1}}}}\right),$$

(100)

The proof is completed by applying (100) to the function ${\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)$. □

Theorem 16.

Consider the conditions given in Theorem 12 and $t\in \mathbb{N}$, then

$$I_{q(\alpha )}^m\mathfrak{f}\left(\mathfrak{t}\right){|}_{\mathfrak{t}=\mathfrak{s}}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(\mathfrak{t}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^t\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{t}+\mathfrak{m}}}}\right)\right\}=\sum _{\mathfrak{r}=\mathfrak{0}}^{\mathfrak{t}}{\displaystyle \frac{{(\mathfrak{r}+\mathfrak{m}-\mathfrak{1})}^{(\mathfrak{m}-\mathfrak{1})}}{(\mathfrak{m}-\mathfrak{1})!}}{\alpha }^{\mathfrak{r}}\mathfrak{f}\left({\displaystyle \frac{\mathfrak{s}}{{\mathfrak{q}}^{\mathfrak{r}+\mathfrak{m}}}}\right).$$

(101)

Proof.

By Theorem 15 and then applying the $I_{q(\alpha )}$ operator in Theorem 12, we get (101). □

The following example illustrates Equation (101).

Example 8.

Taking $f\left(t\right)=t$ and assuming $m=2$, then Equation (101) becomes

$$I_{q(\alpha )}^3\left(t\right){|}_{t=s}-\underset{-1/t}{\overset{-1}{\Delta }}\left\{{\displaystyle \frac{{(t+2)}^{\left(2\right)}}{2!}}{\alpha }^t{\displaystyle \frac{s}{q^{t+3}}}\right\}=\sum _{r=0}^t{\displaystyle \frac{{(r+2)}^{\left(2\right)}}{2!}}{\alpha }^r{\displaystyle \frac{s}{q^{r+3}}}.$$

(102)

By Equation (44), we get $d_{q(\alpha )}\left(t\right){|}_{t=s}=t(q-\alpha ){|}_{t=s}$, $d_{q(\alpha )}^2\left(t\right){|}_{t=s}=t{(q-\alpha )}^2{|}_{t=s}$ and

$d_{q(\alpha )}^3\left(t\right){|}_{t=s}=t{(q-\alpha )}^3{|}_{t=s}$. Therefore, the inverse operator for the function t is

$$I_{q(\alpha )}^3\left(t\right){|}_{t=s}={\displaystyle \frac{t}{{(q-\alpha )}^3}}{|}_{t=s}.$$

(103)

Using Equation (22), the second term of left-hand side $\left({\displaystyle \frac{s}{2!}}\right)\underset{-1/t}{\overset{-1}{\Delta }}\left\{{(t+2)}^{\left(2\right)}\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)\right\}$ becomes $\left({\displaystyle \frac{s}{2!}}\right)\left\{{(t+2)}^{\left(2\right)}\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)-\underset{-1/t}{\overset{-1}{\Delta }}\left\{\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{{\alpha }^{t-1}}{q^{t+2}}}\right)\underset{-1/t}{\Delta }{(t+2)}^{\left(2\right)}\right\}\right\}$.

Here, $\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)$=${\displaystyle \frac{\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)}{\left({\displaystyle \frac{{\alpha }^{-1}}{q^{-1}}}-1\right)}}$, $\underset{-1/t}{\overset{-1}{\Delta }}\left({\displaystyle \frac{{\alpha }^{t-1}}{q^{t+2}}}\right)$=${\displaystyle \frac{\left({\displaystyle \frac{{\alpha }^{t-1}}{q^{t+2}}}\right)}{\left({\displaystyle \frac{{\alpha }^{-1}}{q^{-1}}}-1\right)}}$ and $\underset{-1/t}{\Delta }{(t+2)}^{\left(2\right)}$=$(-2)(t+1)$.

Finally, we get $\left({\displaystyle \frac{s}{2!}}\right)\underset{-1/t}{\overset{-1}{\Delta }}\left\{{(t+2)}^{\left(2\right)}\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)\right\}$

$=\left({\displaystyle \frac{s}{2!}}\right)\left\{{(t+2)}^{\left(2\right)}{\displaystyle \frac{\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)}{\left({\displaystyle \frac{{\alpha }^{-1}}{q^{-1}}}-1\right)}}+{\displaystyle \frac{2}{\left({\displaystyle \frac{{\alpha }^{-1}}{q^{-1}}}-1\right)}}\underset{-1/t}{\overset{-1}{\Delta }}\left\{\left({\displaystyle \frac{{\alpha }^{t-1}}{q^{t+2}}}\right)(t+1)\right\}\right\}$.

Again applying Equation (22), the above equation becomes

$$\left({\displaystyle \frac{s}{2!}}\right)\underset{-1/t}{\overset{-1}{\Delta }}\left\{{(t+2)}^{\left(2\right)}\left({\displaystyle \frac{{\alpha }^t}{q^{t+3}}}\right)\right\}={\displaystyle \frac{\left(s\right)\left(\frac{{\alpha }^t}{q^{t+3}}\right)}{(2!)\left(\frac{{\alpha }^{-1}}{q^{-1}}-1\right)}}\left\{{(t+2)}^{\left(2\right)}+{\displaystyle \frac{2(t+1)\left(\frac{{\alpha }^{-1}}{q^{-1}}\right)}{\left(\frac{{\alpha }^{-1}}{q^{-1}}-1\right)}}+{\displaystyle \frac{2\left(\frac{{\alpha }^{-2}}{q^{-2}}\right)}{{\left(\frac{{\alpha }^{-1}}{q^{-1}}-1\right)}^2}}\right\}.$$

(104)

If we take s, q, and t values from Example 7, then (103) and (104) become

$${\displaystyle \frac{3}{{(2-3)}^3}}-{\displaystyle \frac{\left(3\right)\left(\frac{3^3}{2^6}\right)}{(2!)\left(\frac{3^{-1}}{2^{-1}}-1\right)}}\left\{5^{\left(2\right)}+{\displaystyle \frac{2\left(4\right)\left(\frac{3^{-1}}{2^{-1}}\right)}{\left(\frac{3^{-1}}{2^{-1}}-1\right)}}+{\displaystyle \frac{2\left(\frac{3^{-2}}{2^{-2}}\right)}{{\left(\frac{3^{-1}}{2^{-1}}-1\right)}^2}}\right\}=19.78$$

(105)

and

$$\left({\displaystyle \frac{1}{2!}}\right)\sum _{r=0}^3{\displaystyle \frac{3^{r+1}·{(r+2)}^{\left(2\right)}}{2^{r+3}}}={\displaystyle \frac{1}{2!}}\left\{{\displaystyle \frac{3·2^{\left(2\right)}}{2^3}}+{\displaystyle \frac{3^2·3^{\left(2\right)}}{2^4}}+{\displaystyle \frac{3^3·4^{\left(2\right)}}{2^5}}+{\displaystyle \frac{3^4·5^{\left(2\right)}}{2^6}}\right\}=19.78.$$

(106)

Hence, Equation (102) is verified by (105) and (106).

The theorems developed in this section offer the solution to the mixed symmetric difference operator. The same is true of the $d^{q(\alpha )}$ operator.

5.3. Value Stability Analysis

The $q/h$ and $q(\alpha )/h$ operators’ stability is discussed here to aid in value analysis.

Consider Example 7, where q and $\mathfrak{s}$ are fixed and $\mathfrak{t}=\mathfrak{0},\mathfrak{1},\mathfrak{2},\mathfrak{3},\mathfrak{4},\mathfrak{5}$; the solution is illustrated in Figure 1. Similarly, consider Example 8, where q, $\mathfrak{s}$, and $\alpha$ are constants and $\mathfrak{t}=\mathfrak{0},\mathfrak{1},\mathfrak{2},\mathfrak{3},\mathfrak{4},\mathfrak{5}$; the solution is shown in Figure 2. Based on Figure 1 and Figure 2, we can easily predict that the solutions for the $q/h$ and $q(\alpha )/h$ operators will diverge to infinity.

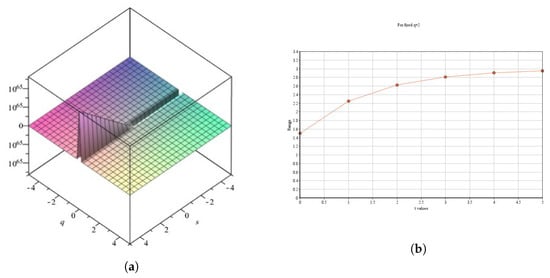
Figure 1. (a) General solution and (b) existing solution for Example 7.

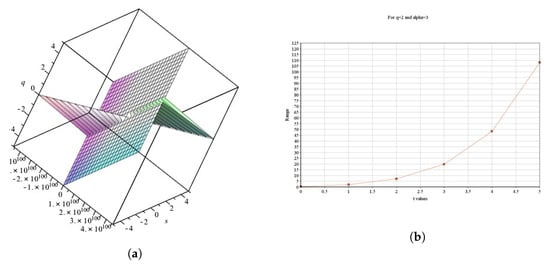
Figure 2. (a) General solution and (b) existing solution for Example 8.

Figure 1 and Figure 2 shows that if q, $q(\alpha )$, and s are fixed and t fluctuates, the solution is unbounded.

In Table 2, we list the values of Examples 7 and 8 for $\mathfrak{m}=\mathfrak{1},\mathfrak{2},\mathfrak{3},\dots ,\mathfrak{10}$. For simplicity, we denote the $\mathfrak{m}$th order of $q/h$ operator by ${\mathfrak{I}}_{\mathfrak{q}}^i\mathfrak{f}\left(\mathfrak{t}\right)$ and the $\mathfrak{m}$th order of $q(\alpha )/h$ operator by ${\mathfrak{I}}_{q(\alpha )}^i\mathfrak{f}\left(\mathfrak{t}\right)$. In addition, the stability between $q/h$ and $q(\alpha )/h$ operators is given in Figure 3.

Table 2. The table contains the value for higher orders.

${\mathfrak{I}}_{\mathit{q}}^{\mathit{m}}\mathit{f}\left(\mathit{t}\right)$	Values	${\mathfrak{I}}_{\mathfrak{q}\left(\mathit{\alpha }\right)}^{\mathfrak{m}}\mathit{f}\left(\mathit{t}\right)$	Values $(\mathit{\alpha }=2)$
${\mathfrak{I}}_{\mathfrak{q}}f\left(t\right)$	2.81 (by Example 7)	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}f\left(t\right)$	12.19
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{2}}f\left(t\right)$	2.44	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{2}}f\left(t\right)$	18.19
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{3}}f\left(t\right)$	1.97	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{3}}f\left(t\right)$	19.78 (by Example 8)
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{4}}f\left(t\right)$	1.5	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{4}}f\left(t\right)$	18.19
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{5}}f\left(t\right)$	0.93	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{5}}f\left(t\right)$	15.04
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{6}}f\left(t\right)$	0.76	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{6}}f\left(t\right)$	11.54
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{7}}f\left(t\right)$	0.52	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{7}}f\left(t\right)$	8.39
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{8}}f\left(t\right)$	0.34	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{8}}f\left(t\right)$	5.85
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{9}}f\left(t\right)$	0.22	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{9}}f\left(t\right)$	3.94
${\mathfrak{I}}_{\mathfrak{q}}^{\mathfrak{10}}f\left(t\right)$	0.14	${\mathfrak{I}}_{\mathfrak{q}(\alpha )}^{\mathfrak{10}}f\left(t\right)$	2.58

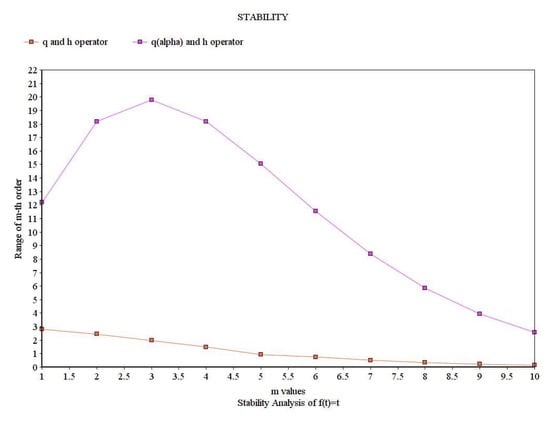
Figure 3. Value stability of the q and h operators.

Figure 3 clearly shows that if m is fixed and all other values vary, it diverges; if $\mathfrak{m}$ varies and all other values remains constant, it converges. The suitable examples are provided in Figure 1, Figure 2 and Figure 3.

6. Conclusions

In this paper, we derived a number of fundamental theorems for q and h difference operators and we also extended these theorems to $q(\alpha )$ and h difference operators that provide solutions to symmetric difference equations. Suitable examples are provided for verification. The findings of this study are applicable to integer order. As a result, future work will focus on developing the non-integer order theorems for q, $q(\alpha )$, and h difference symmetric operators. We also plotted the diagrams to confirm the value stability analysis for the q and $q(\alpha )$ operators.