Review on Higgs Hidden–Dark Sector Physics at High-Energy Colliders
Abstract
:1. Introduction
1.1. Physics of the Standard Model (SM)
1.2. BSM-New Physics (NP)
- “Neutrino masses and oscillations”: What causes neutrinos to vanish and then reappear in a new form? Why are neutrinos massless?
- “Baryon asymmetry of the Universe”: What mechanism generated the early Universe’s minor matter-antimatter imbalance?
- “Dark Matter”: what is the most common type of matter in our Universe?
- “Cosmological inflation”: What caused the Universe to expand at an accelerated rate in the early stages of its evolution?
- “Dark Energy (DE)”: What is driving the Universe’s current stage of evolution’s accelerated expansion?
1.2.1. BSM-New Physics Motivations
Neutrino Oscillations
Abundance of Matter, Absence of Anti-Matter
Cosmological Inflation and Dark Energy
Higgs Mass Fine Tuning
Strong CP Problem
Cosmological Constant and Dark Energy
New Physics at the TeV Scale and Beyond
Right-Handed Neutrinos
(WIMP) Dark Matter Models
Axion Dark Matter Models
1.2.2. Dark Matter and LHC
Dark Matter Theoretical Hypotheses
Strategies of Dark Matter Searches
Missing-Momentum Signal and Bump Hunting
Narrowing down the WIMP Territory
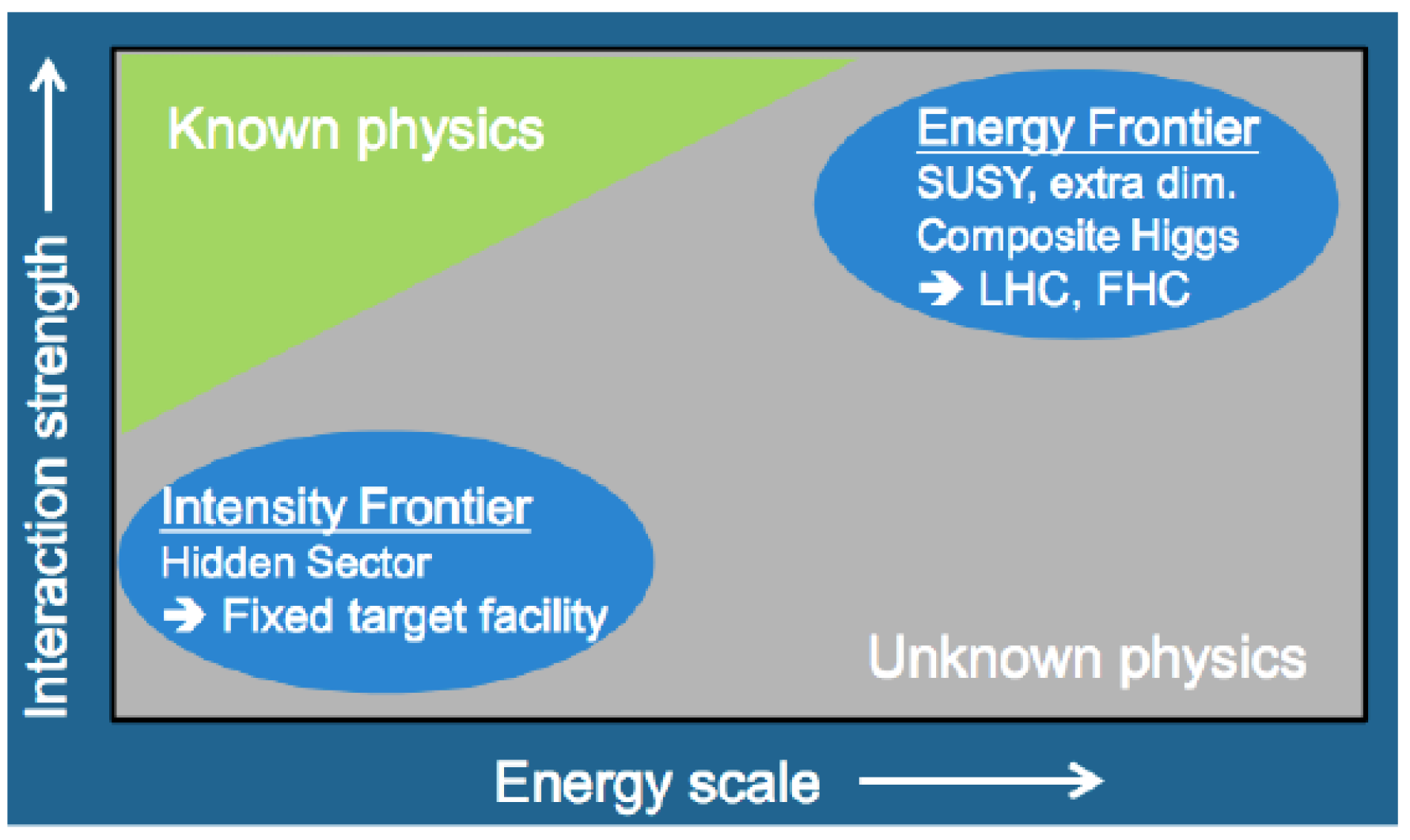
1.3. Energy and Intensity Frontiers
2. Hidden–Dark Sector
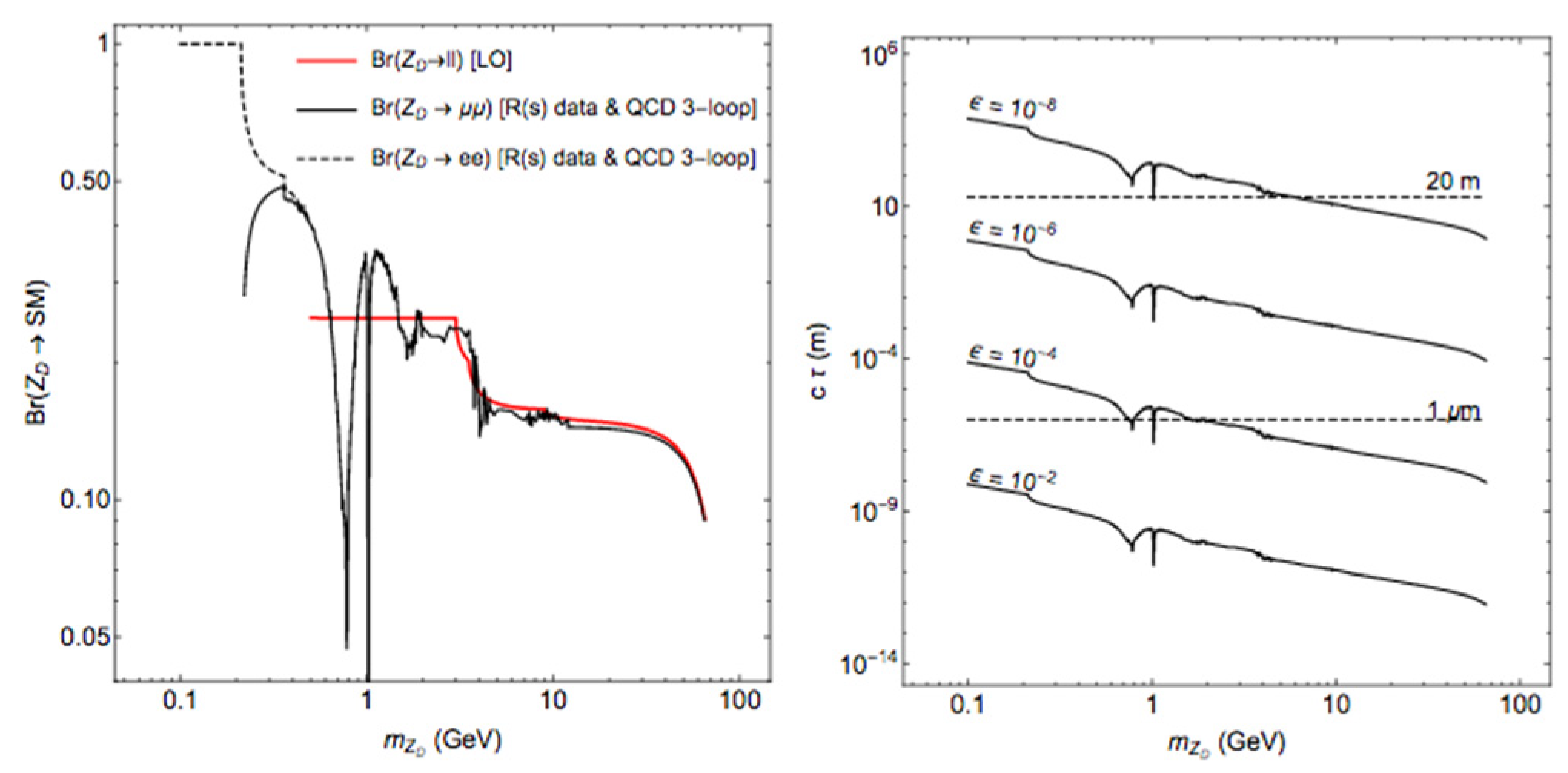
2.1. The Dark Photon Theory
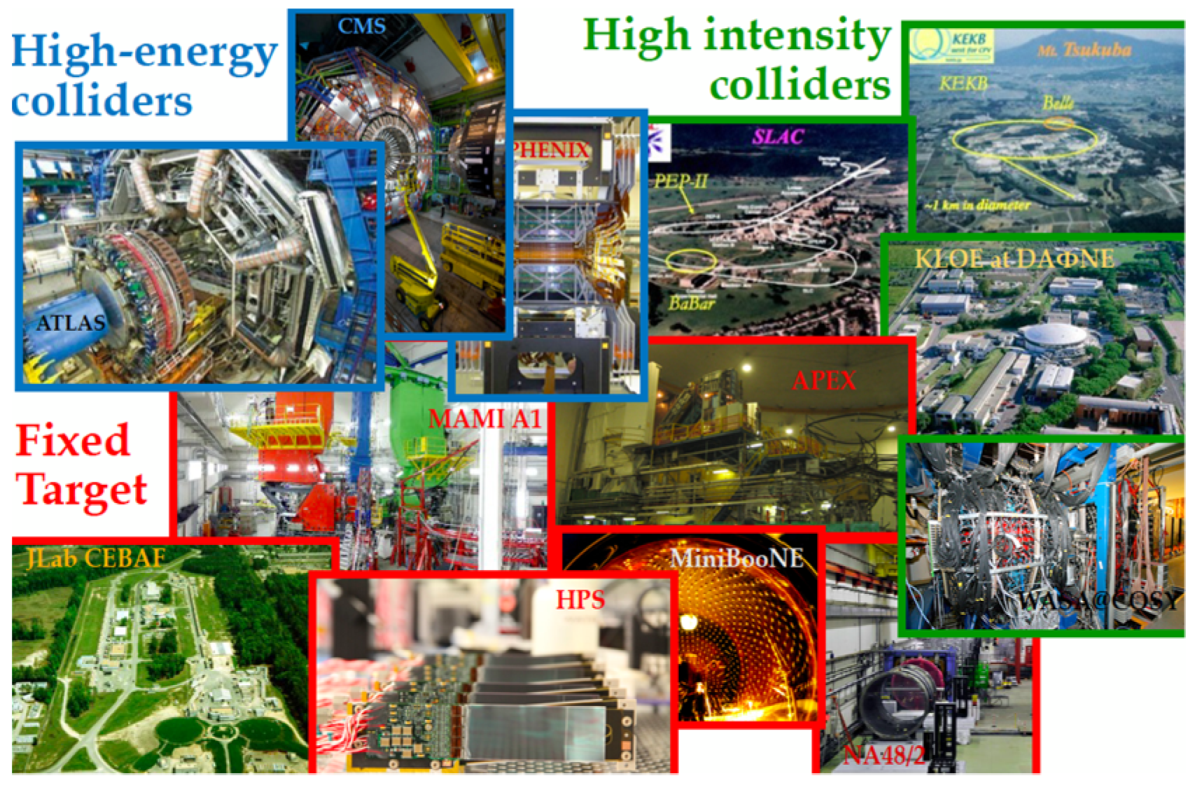
2.2. Overview of Dark Photon Experiments (above 1 GeV)
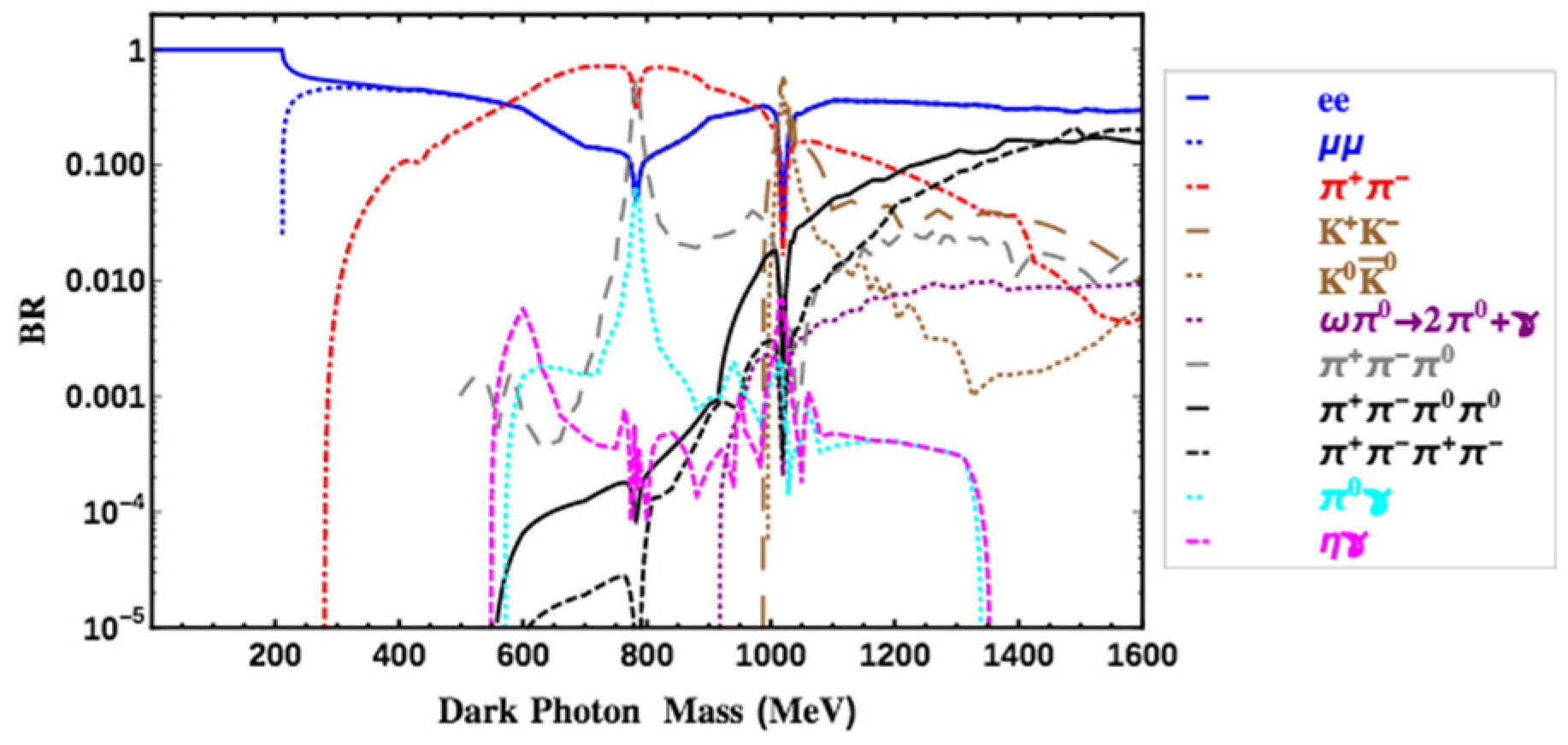
2.3. Dark Photons at Low Energy (up to 10 GeV)
2.4. Dark Photon Search Strategies
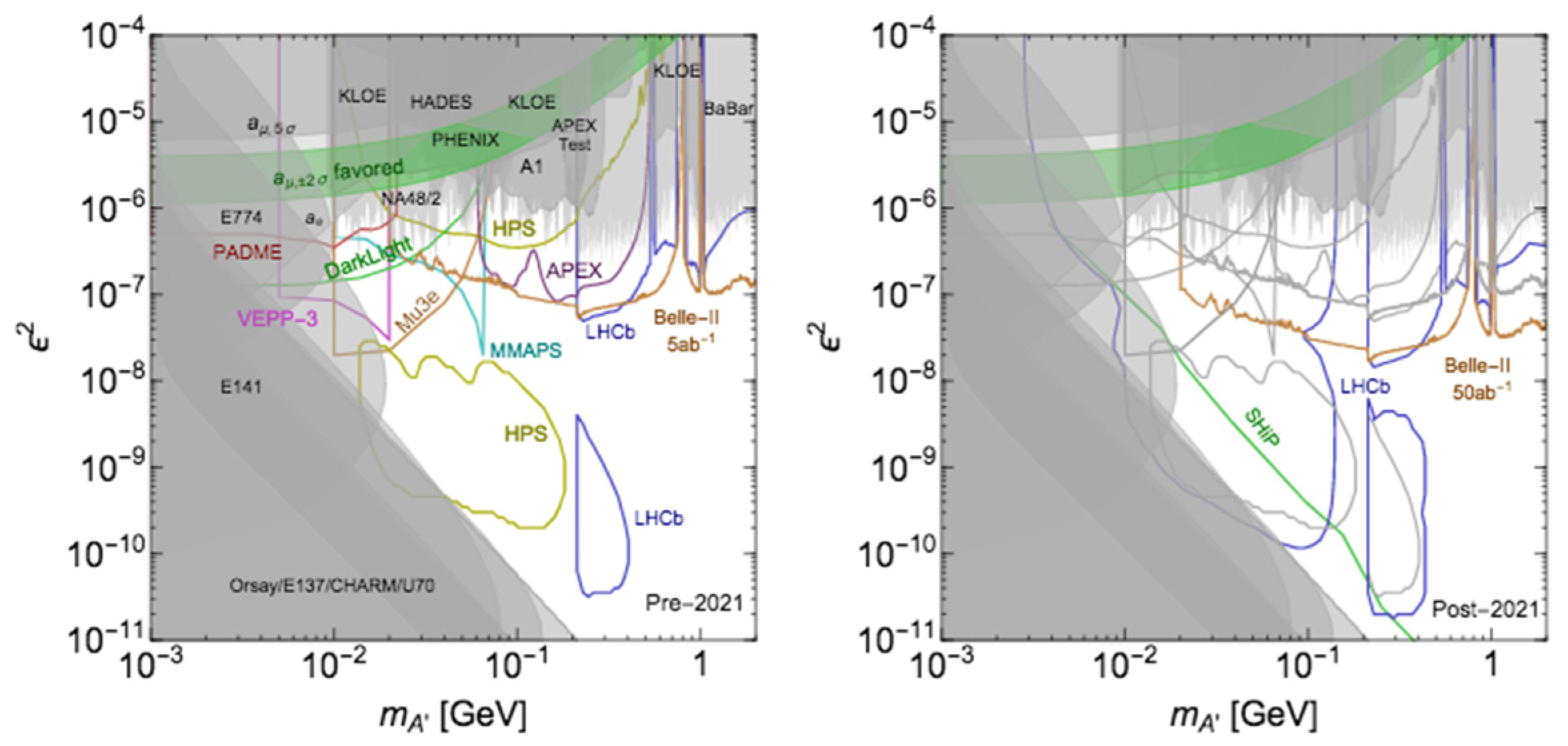
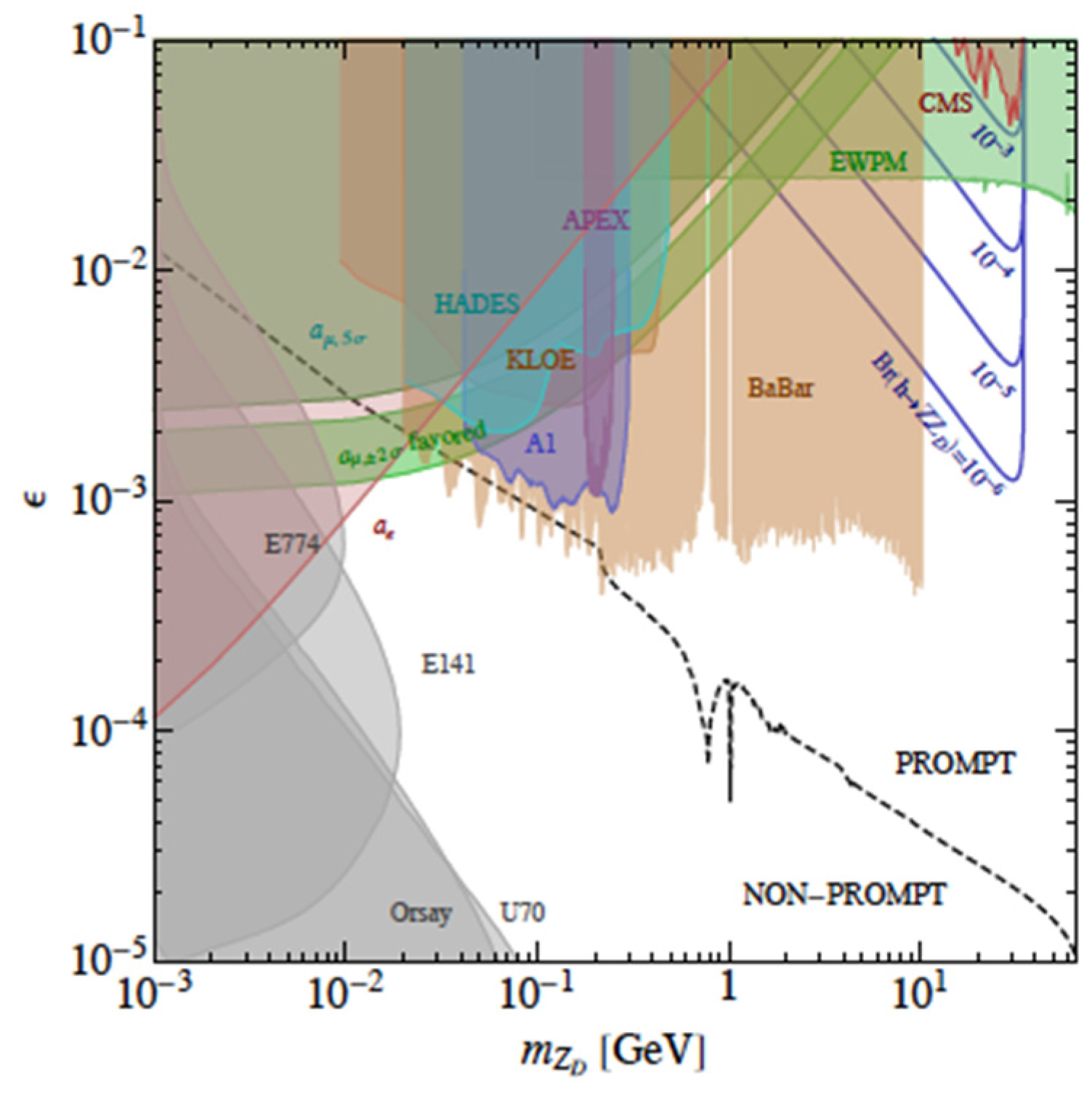
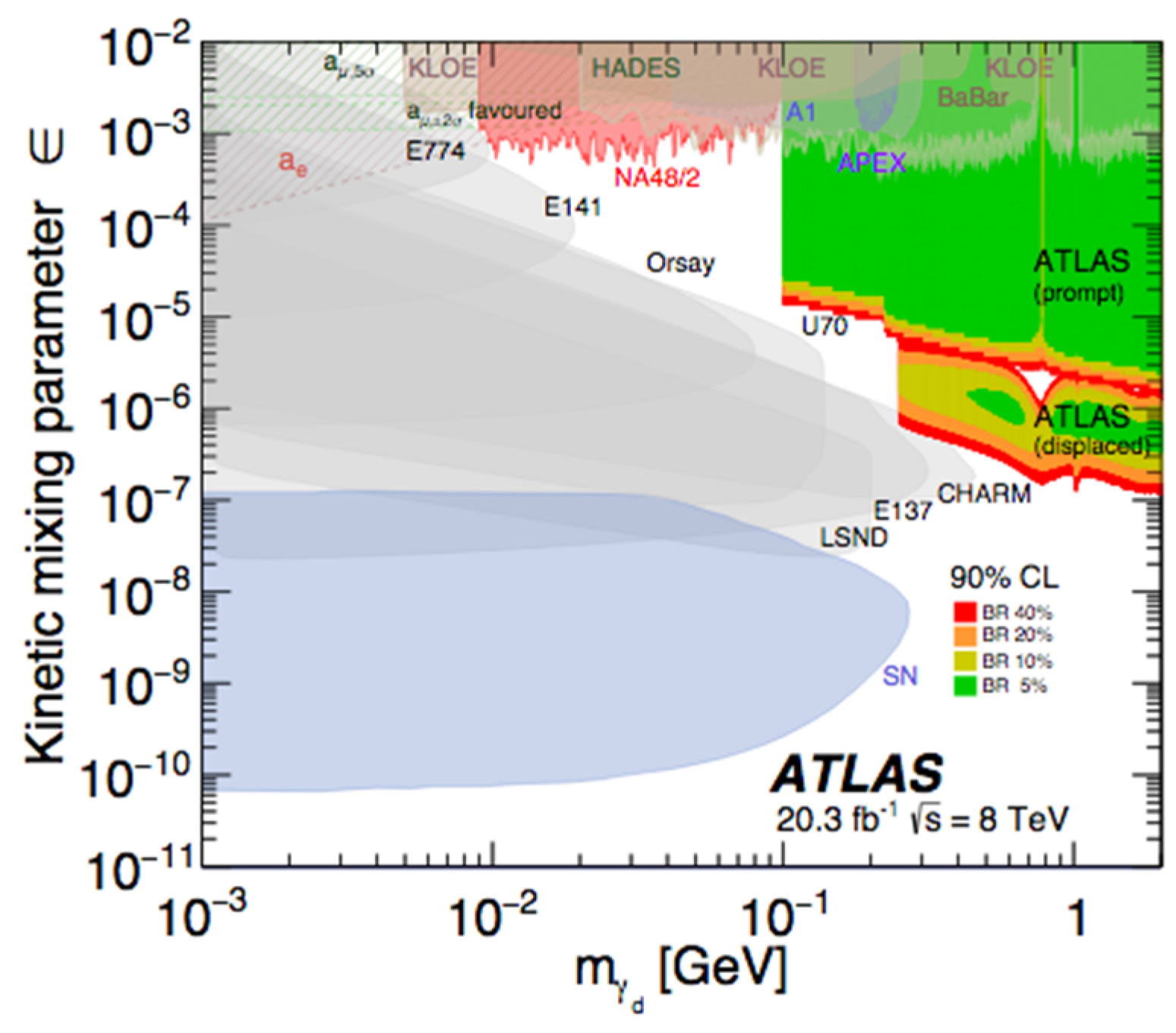
2.5. Summary of Existing Constraints and Future Experiments
3. Hidden–Dark Sector at High-Energy Colliders
3.1. Dark Sector and Exotic Higgs Decays
3.1.1. General Motivation to Search for Exotic Higgs Decays
- (1)
- “The observed Higgs at 125 GeV” is principally responsible for breaking the electroweak symmetry.
- (2)
- “The observed Higgs at 125 GeV” decays to new particles beyond the SM.
3.1.2. SM + Vector
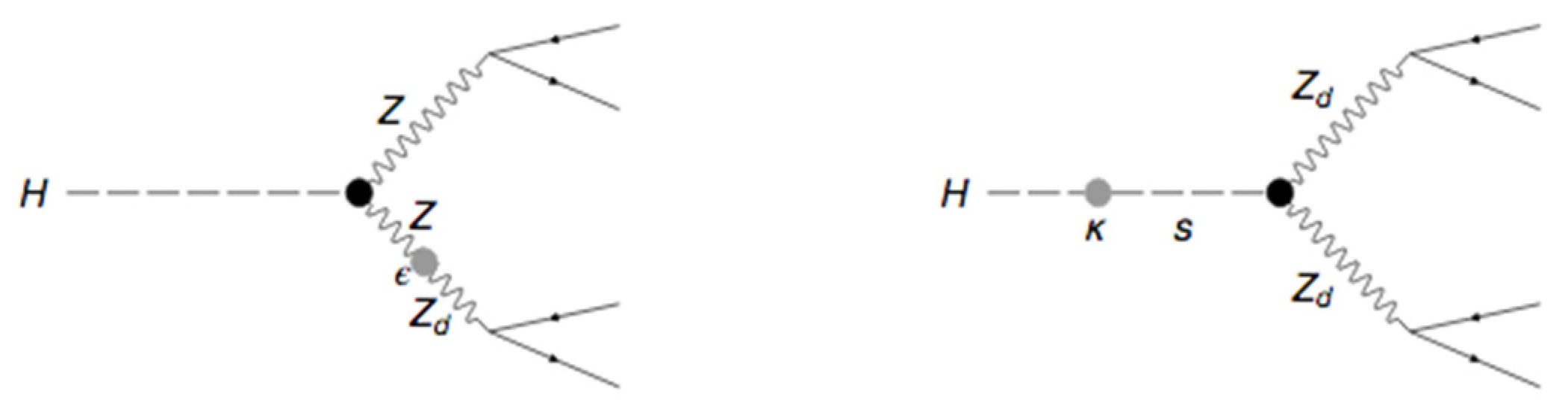
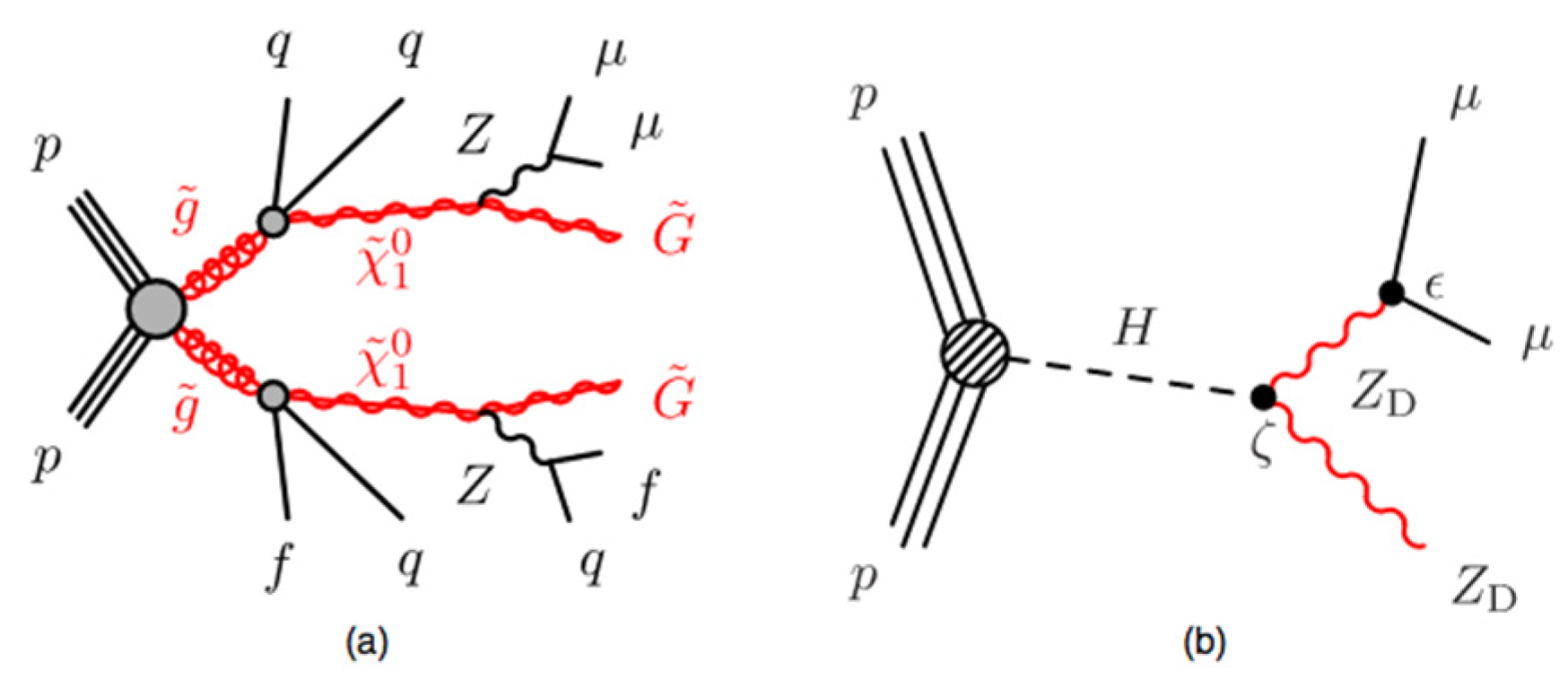
Theoretical Motivation H→ZZd→4l
Theoretical Motivation, H→ZdZd→4l
Decays H→ZdZd, ZZd
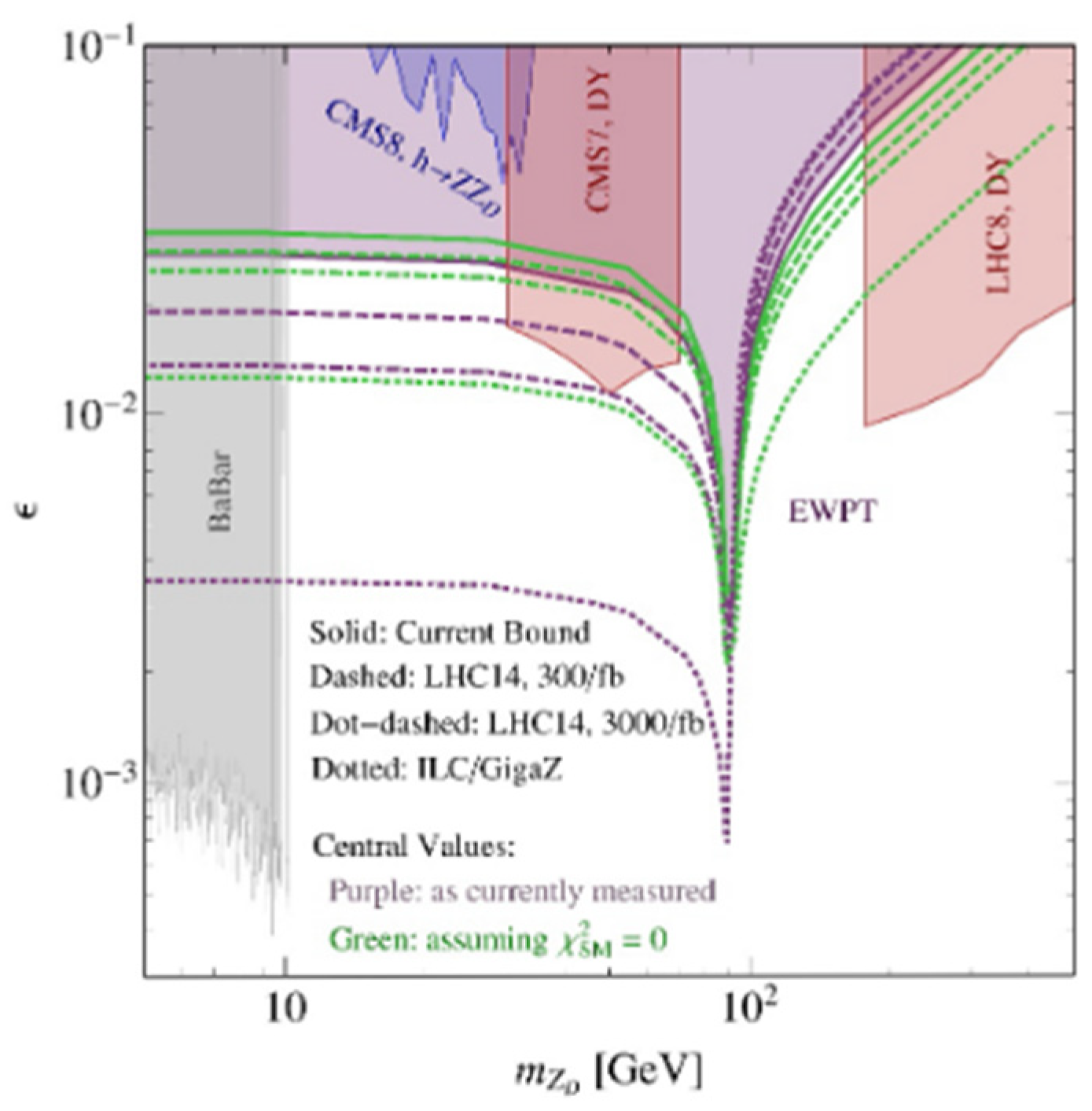
3.2. Higgs Hidden–Dark Sector and Theory Predictions for High-Energy Future Collider Searches
Summary of Dark Photon Future Collider Prospects
4. Selected Dark Photon Studies at LHC at CERN’s Large Hadron Collider (LHC)
4.1. Higgs Decays Dark Massive Photon (ATLAS, CMS)
4.1.1. Search for Higgs Decays to BSM Light Bosons in Four Leptons with ATLAS at = 13 TeV
- High-mass (HM): H→XX→4l (15 GeV < mX < 60 GeV).
- Low-mass (LM): H→XX→4µ (1 GeV< mX < 15 GeV).
- Single 𝑍 boson (ZX): H→𝑍X→4l (15 GeV< mX < 55 GeV).
Benchmark Models
- Analysis Event Selections
- ZX Analysis: H→XX→4l (15 GeV < mX < 55 GeV)
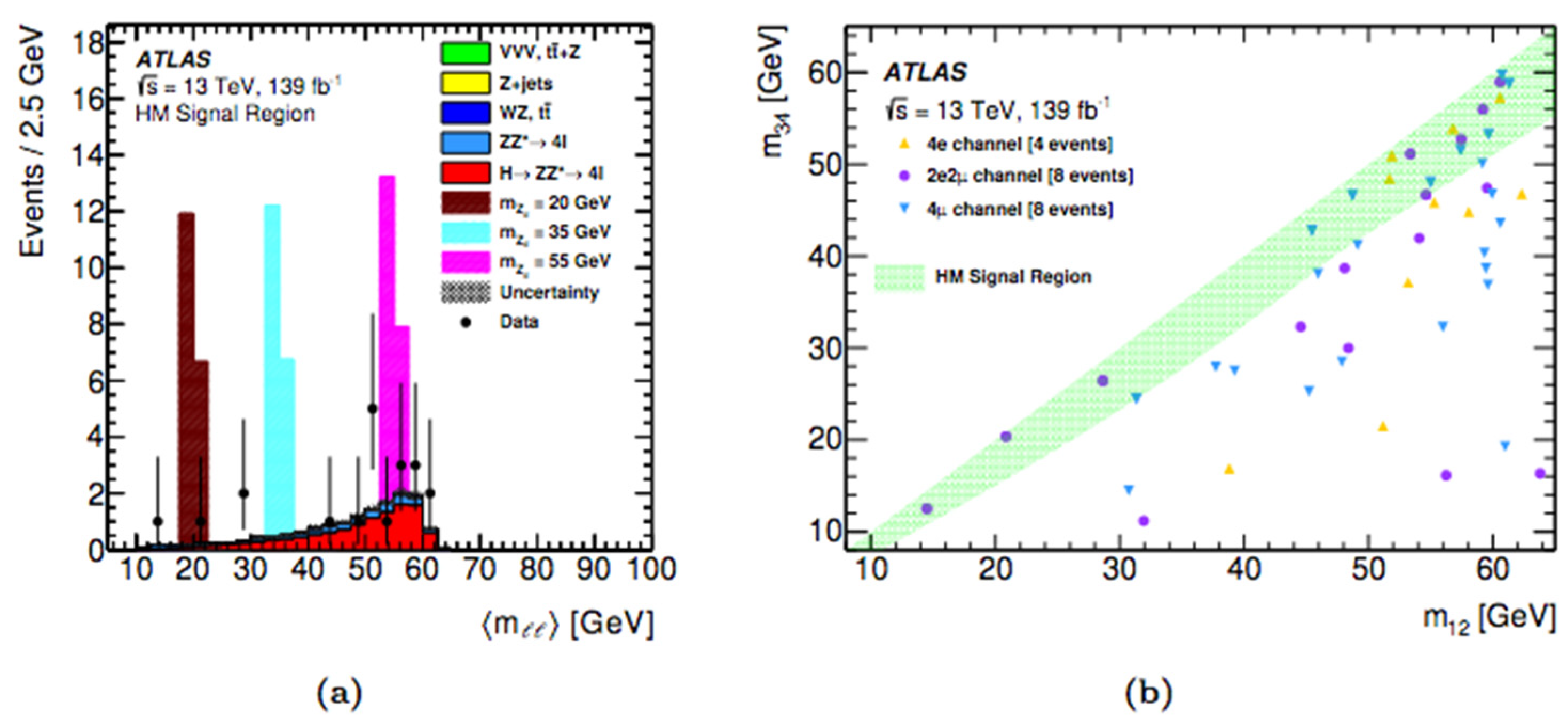
- HM Analysis: H→XX→4l (15 GeV< mX < 60 GeV)
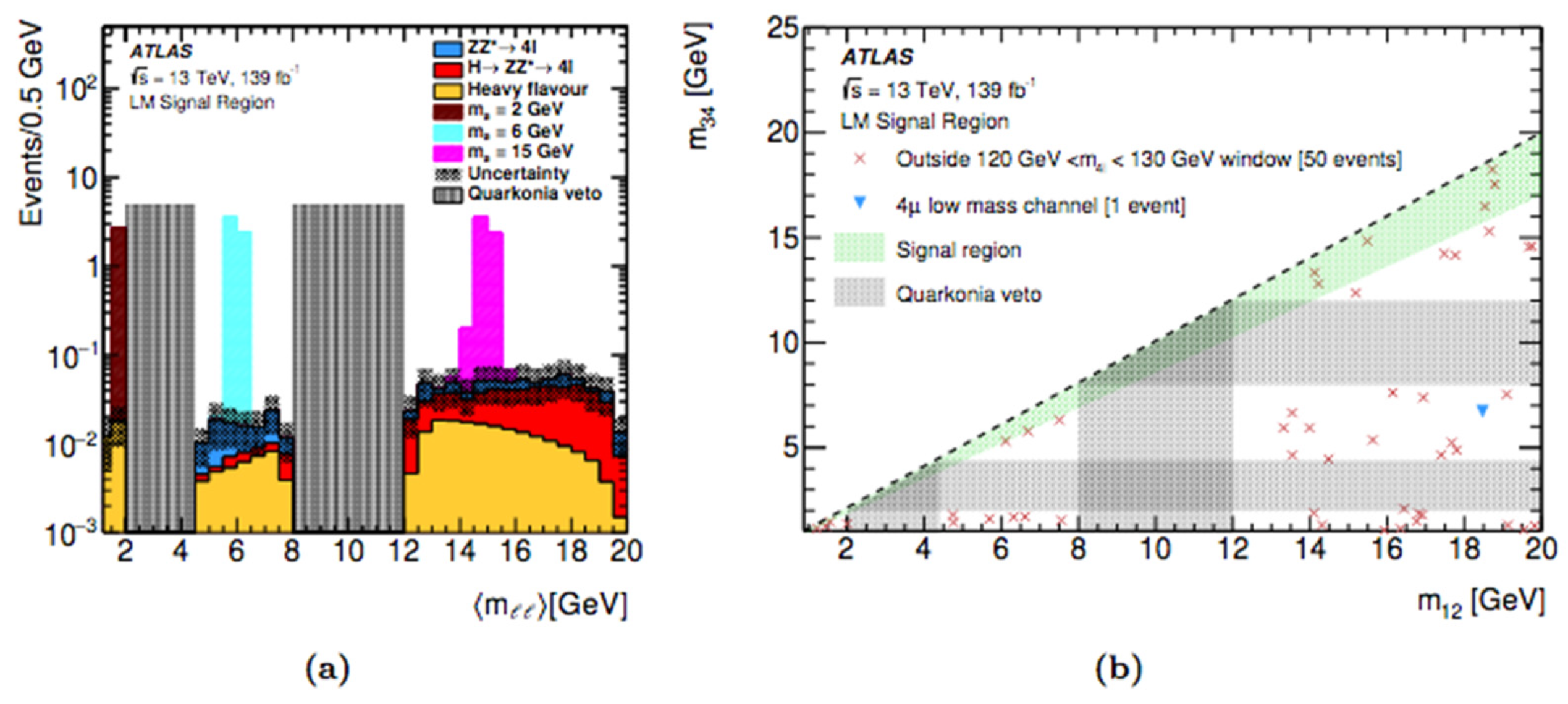
- LM Analysis: H→XX→4μ (1 GeV< mX < 15 GeV)
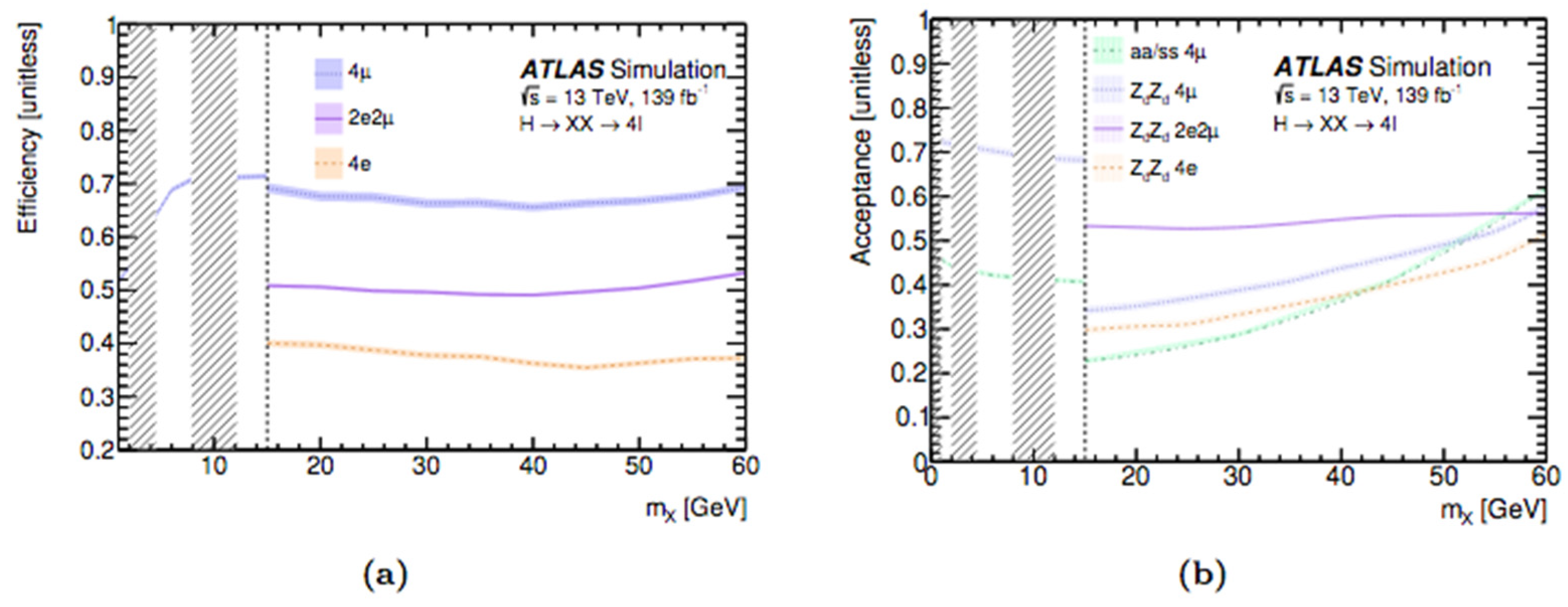
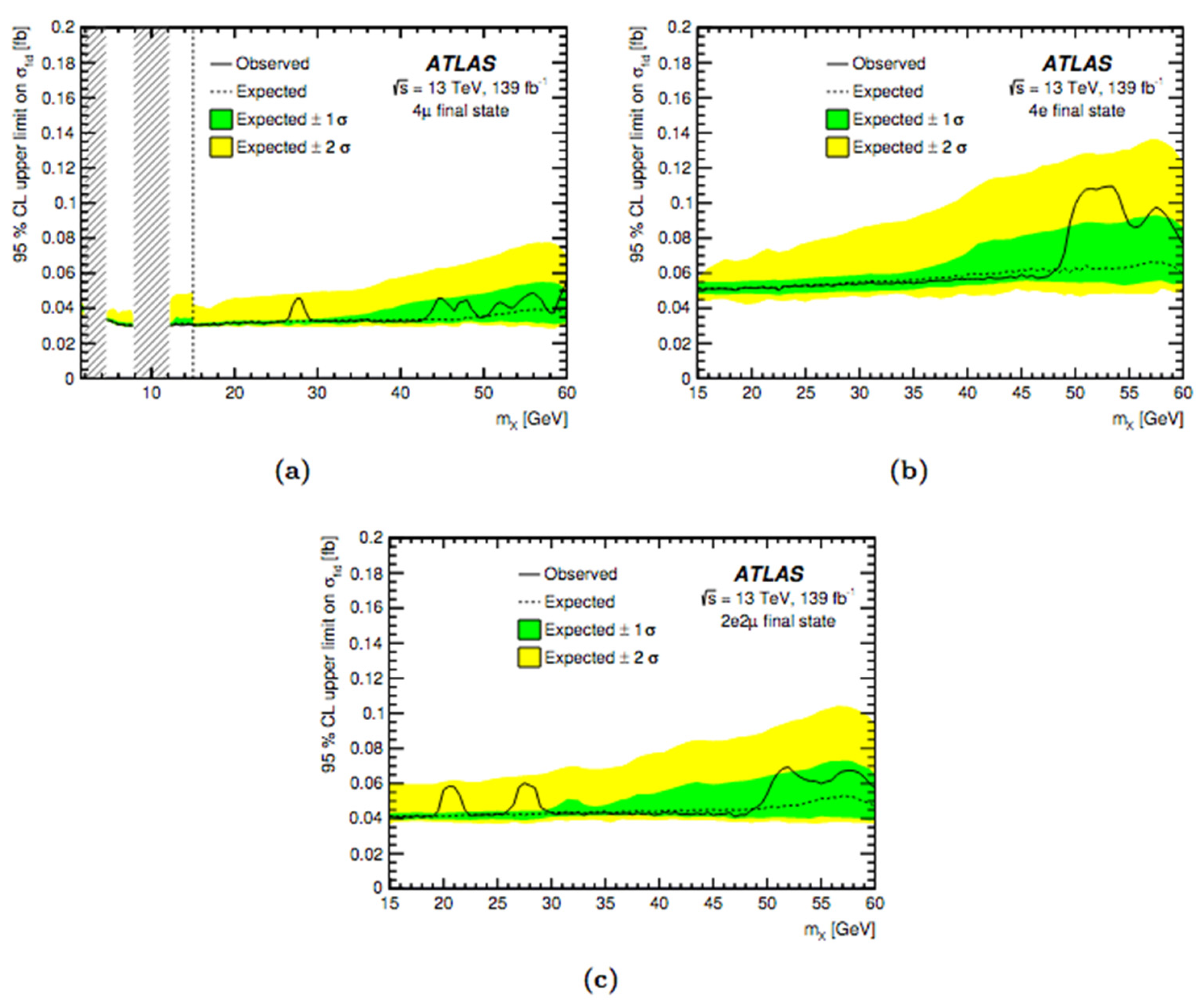
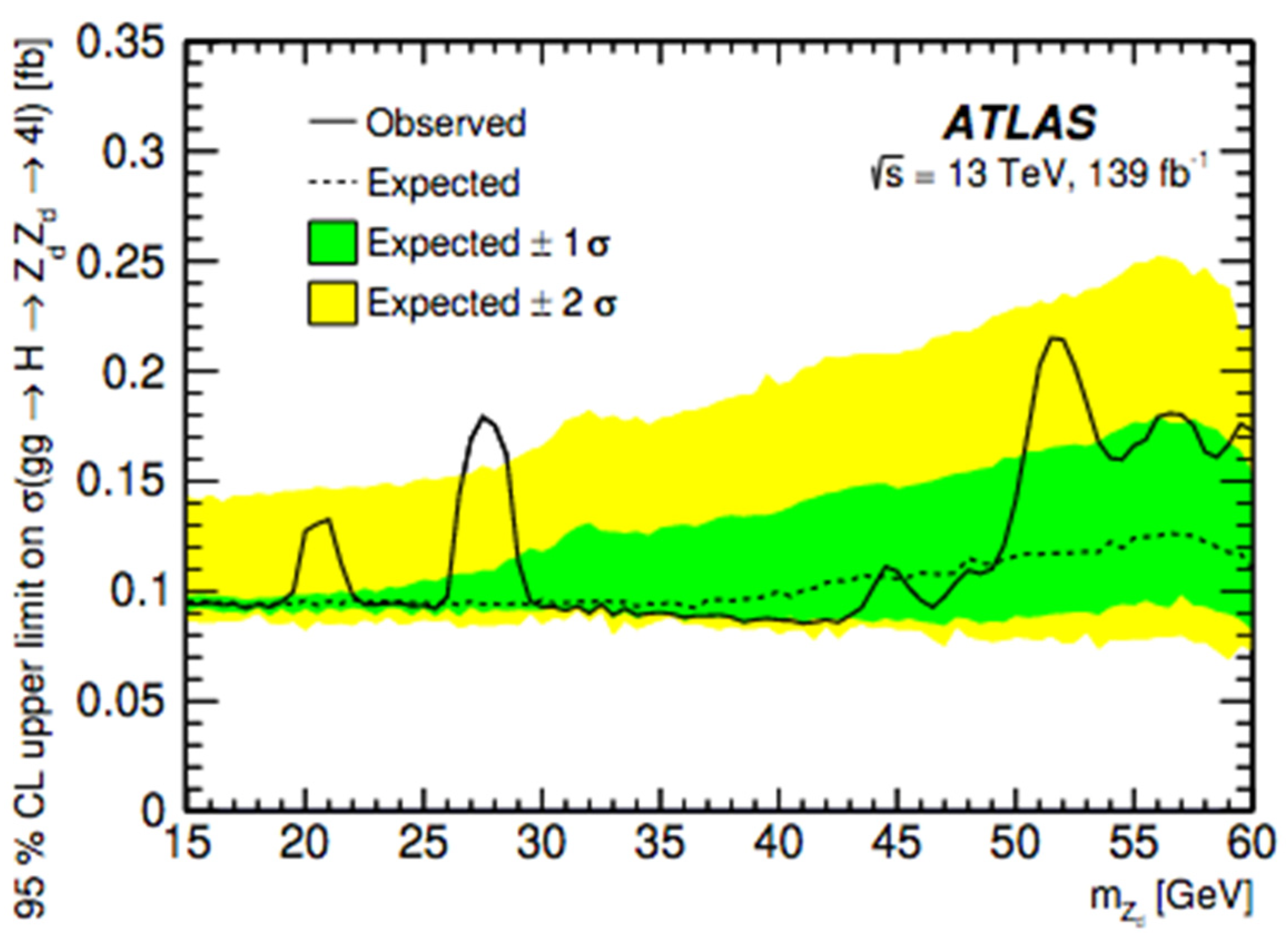
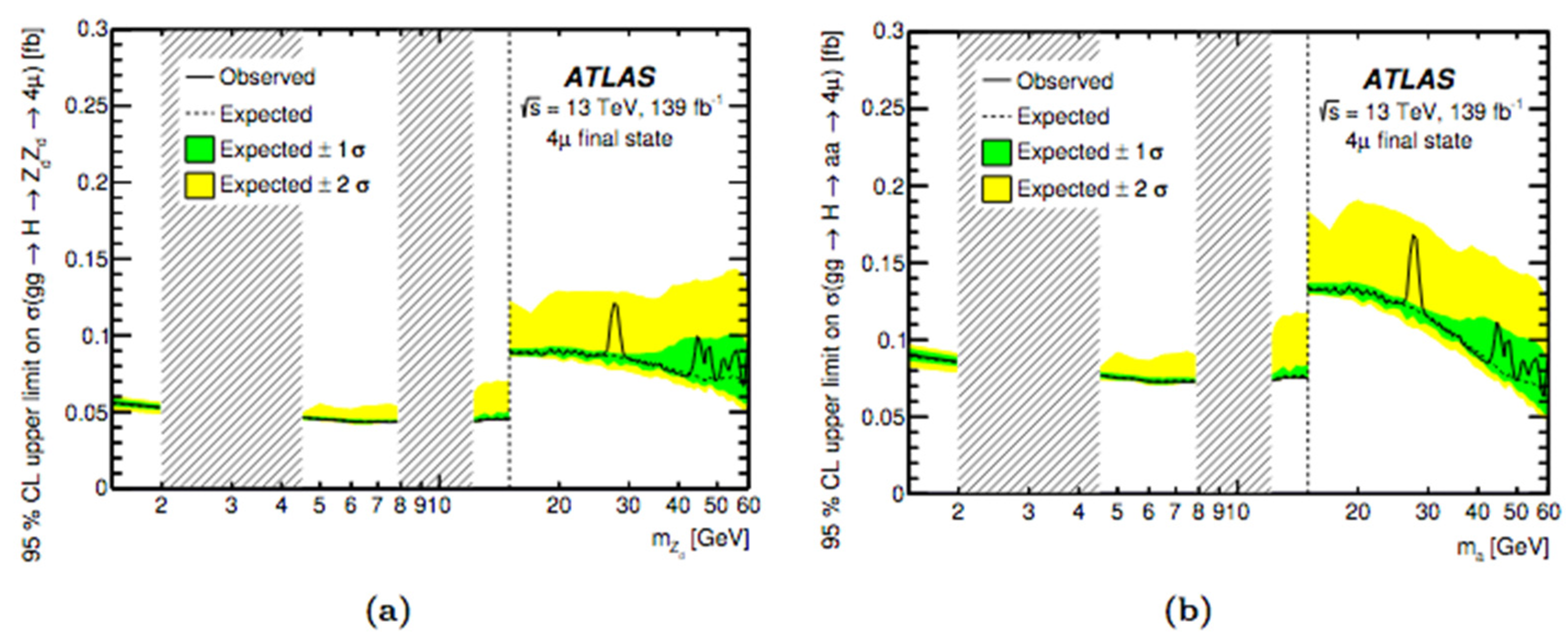
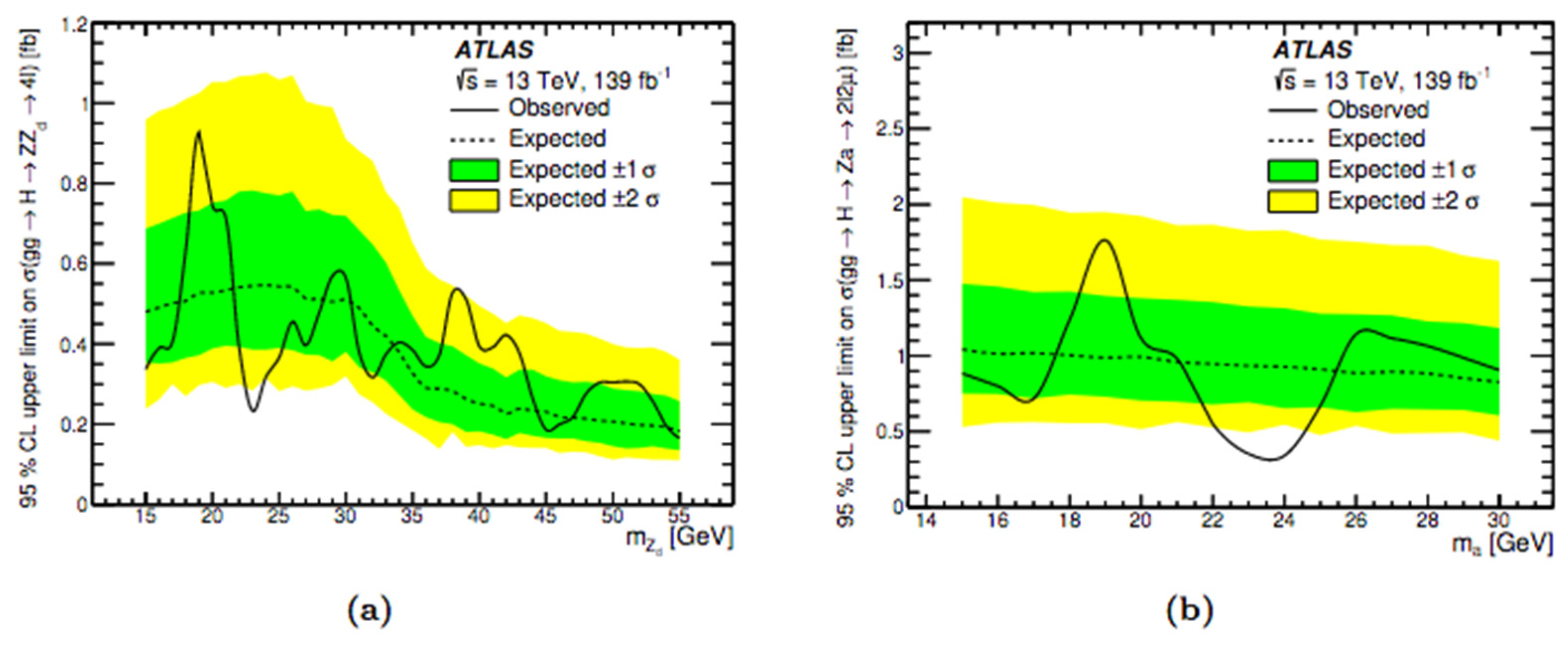
Limits and Interpretations
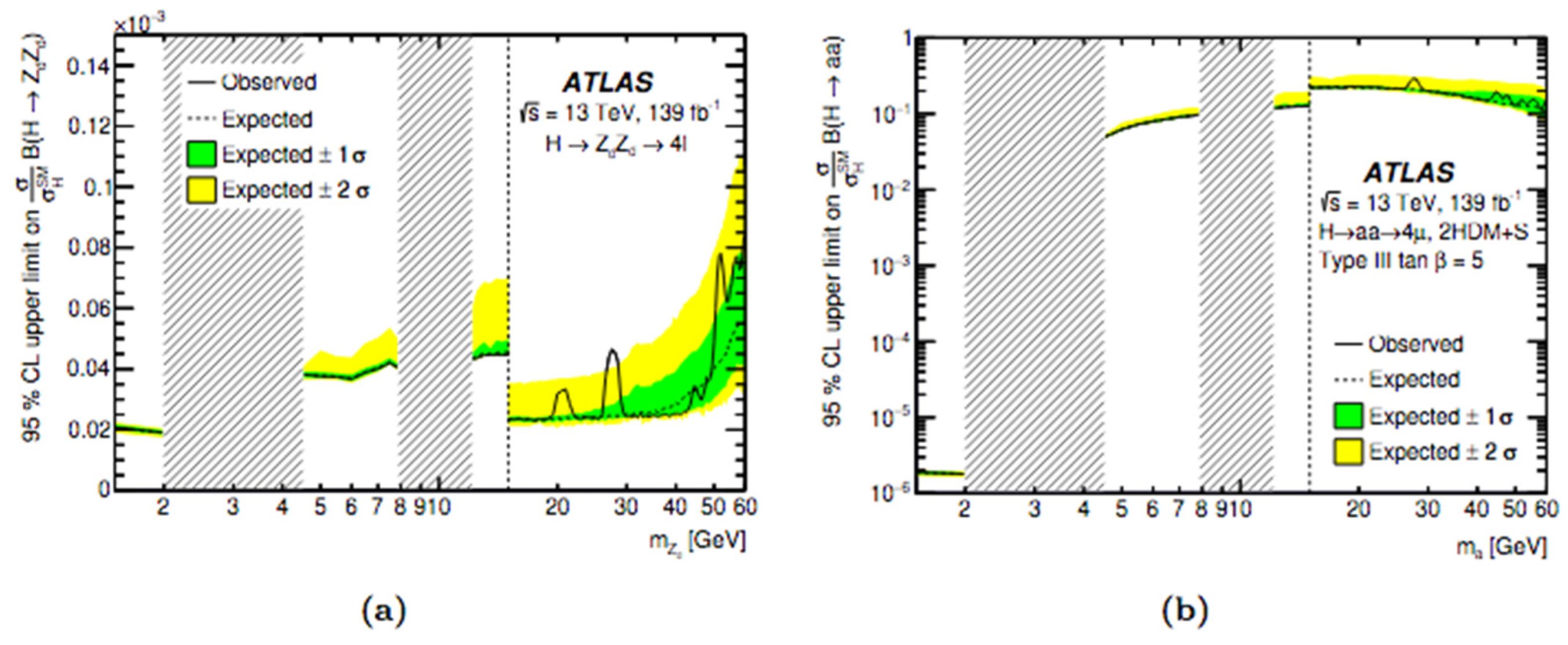
Limits on Fiducial and Total Cross-Sections
Limits on Branching Ratios
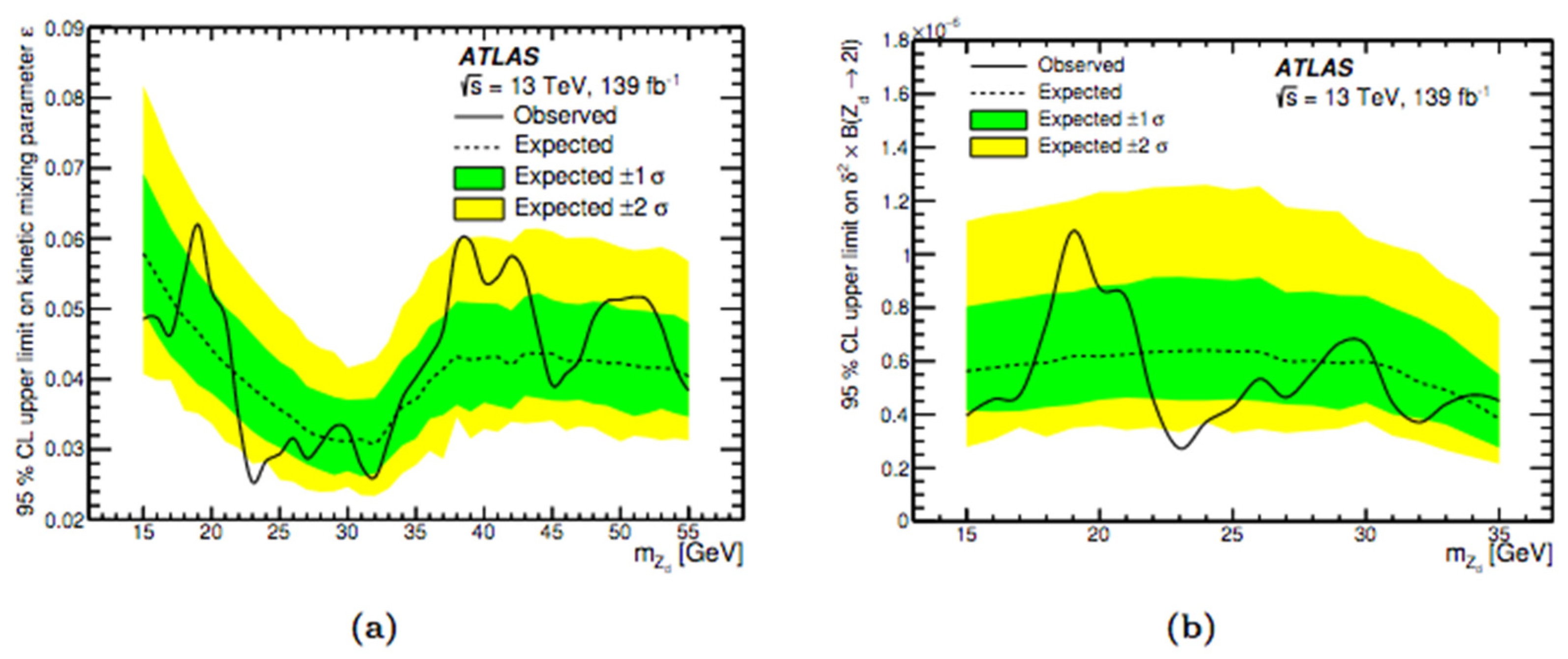
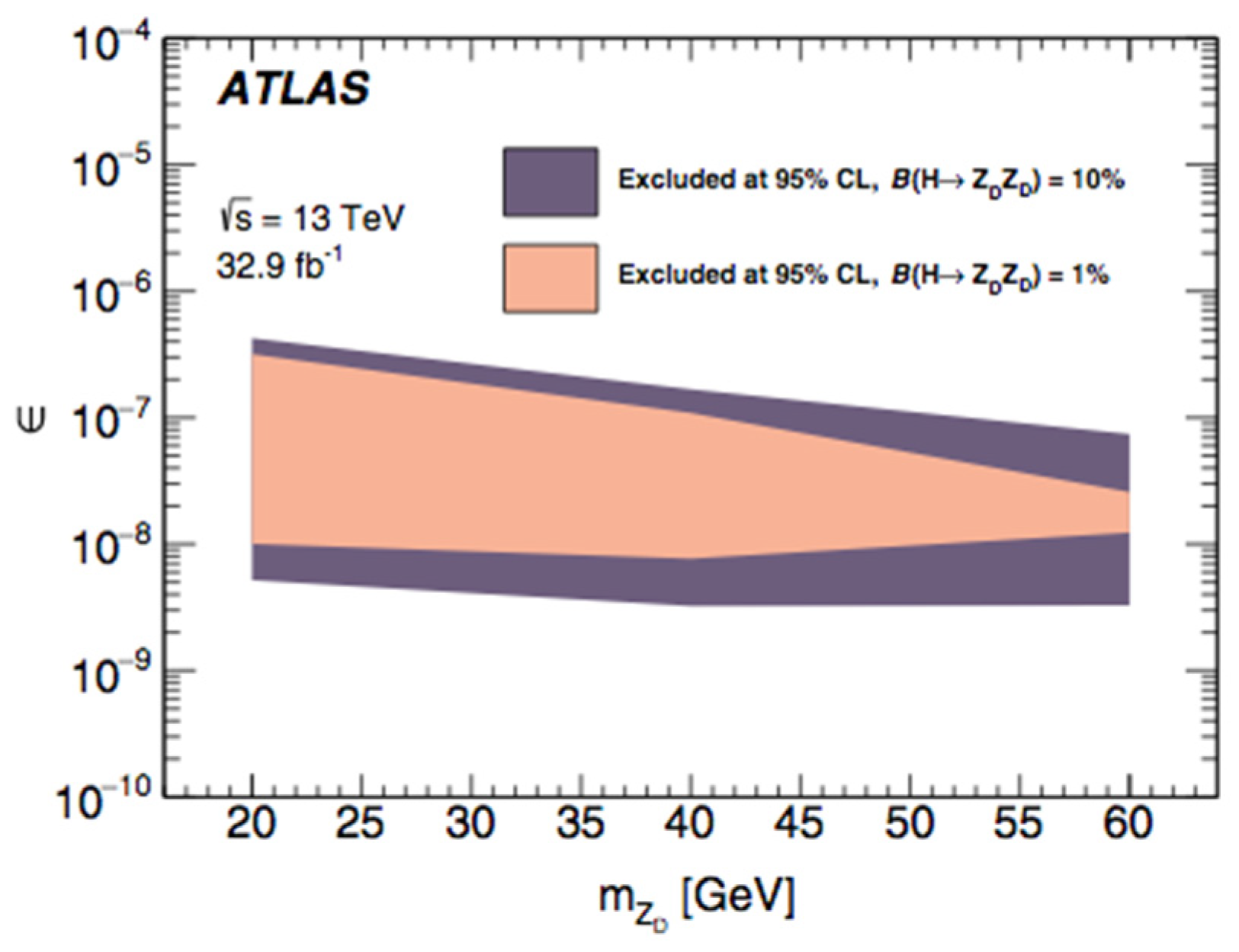
Limits on Mixing Parameters
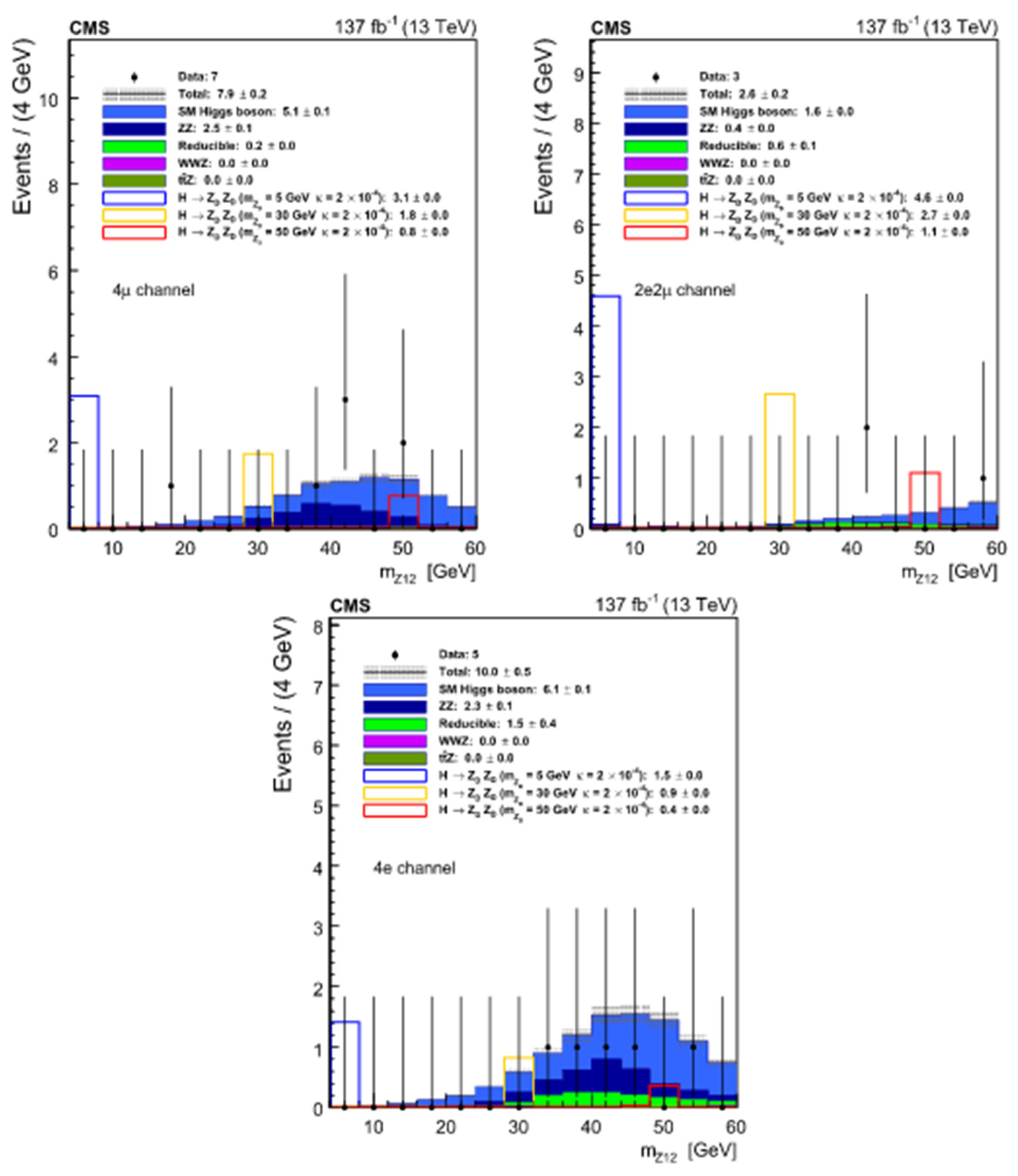
4.1.2. Search for a Low-Mass Di-Lepton Resonance in Higgs Decays to Four Leptons with CMS at = 13 TeV
Analysis Event Selection
- Background Estimation
Results
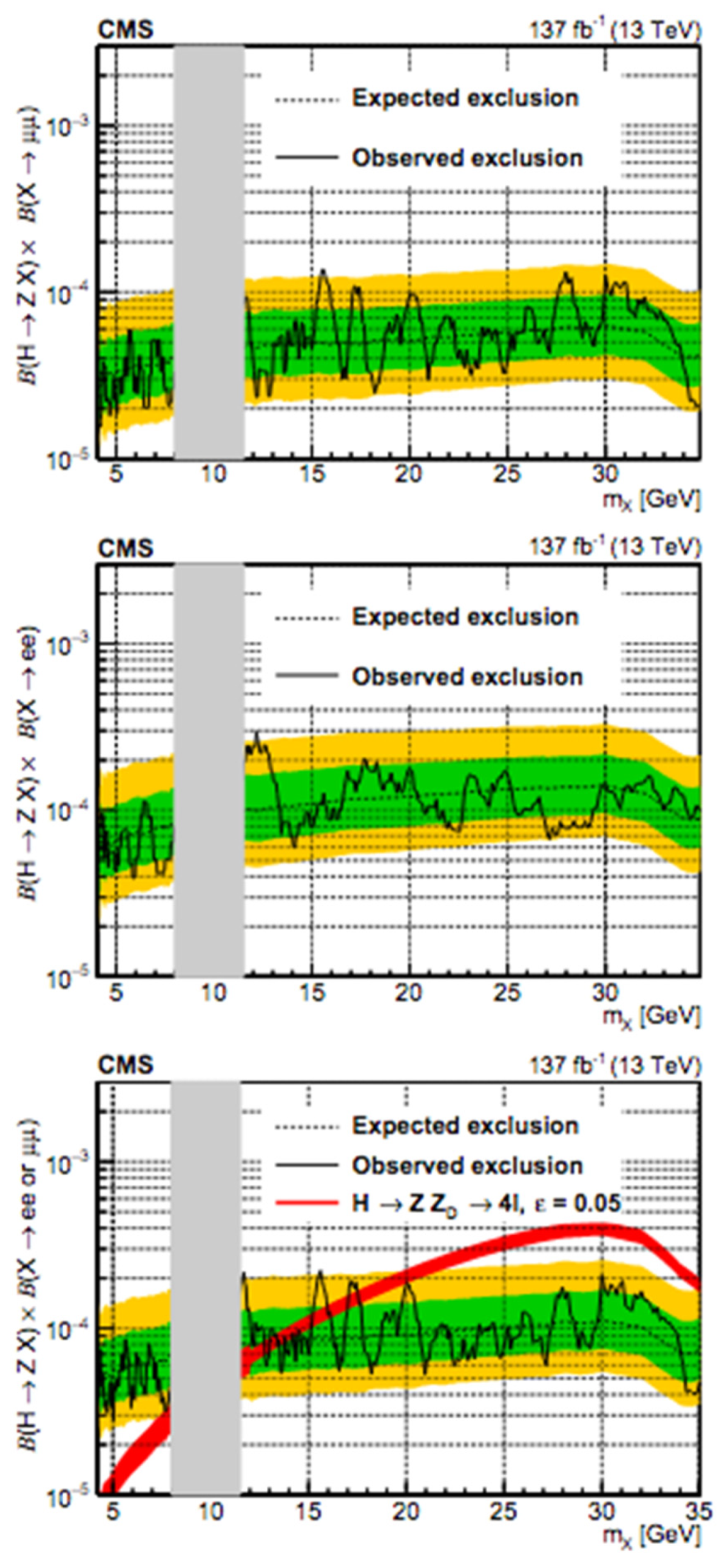
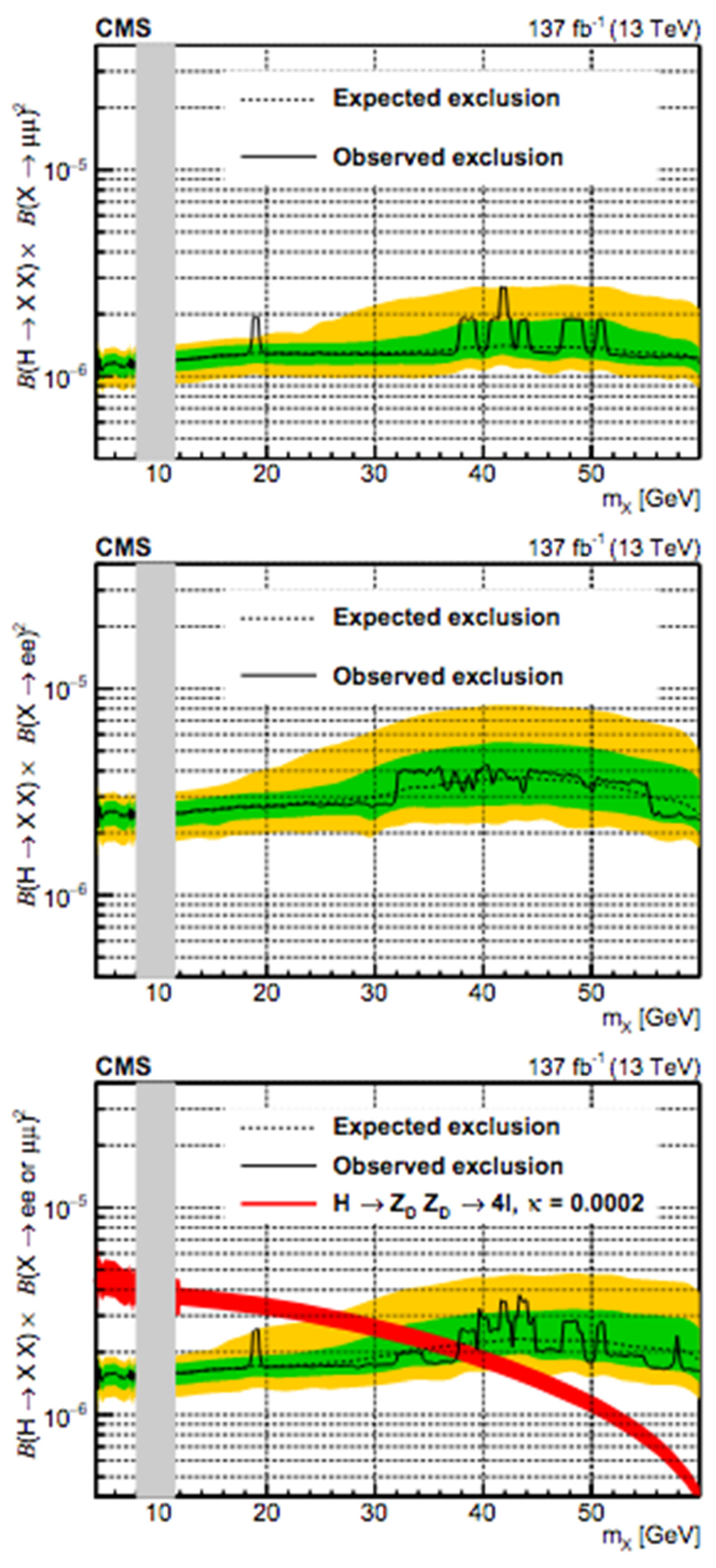
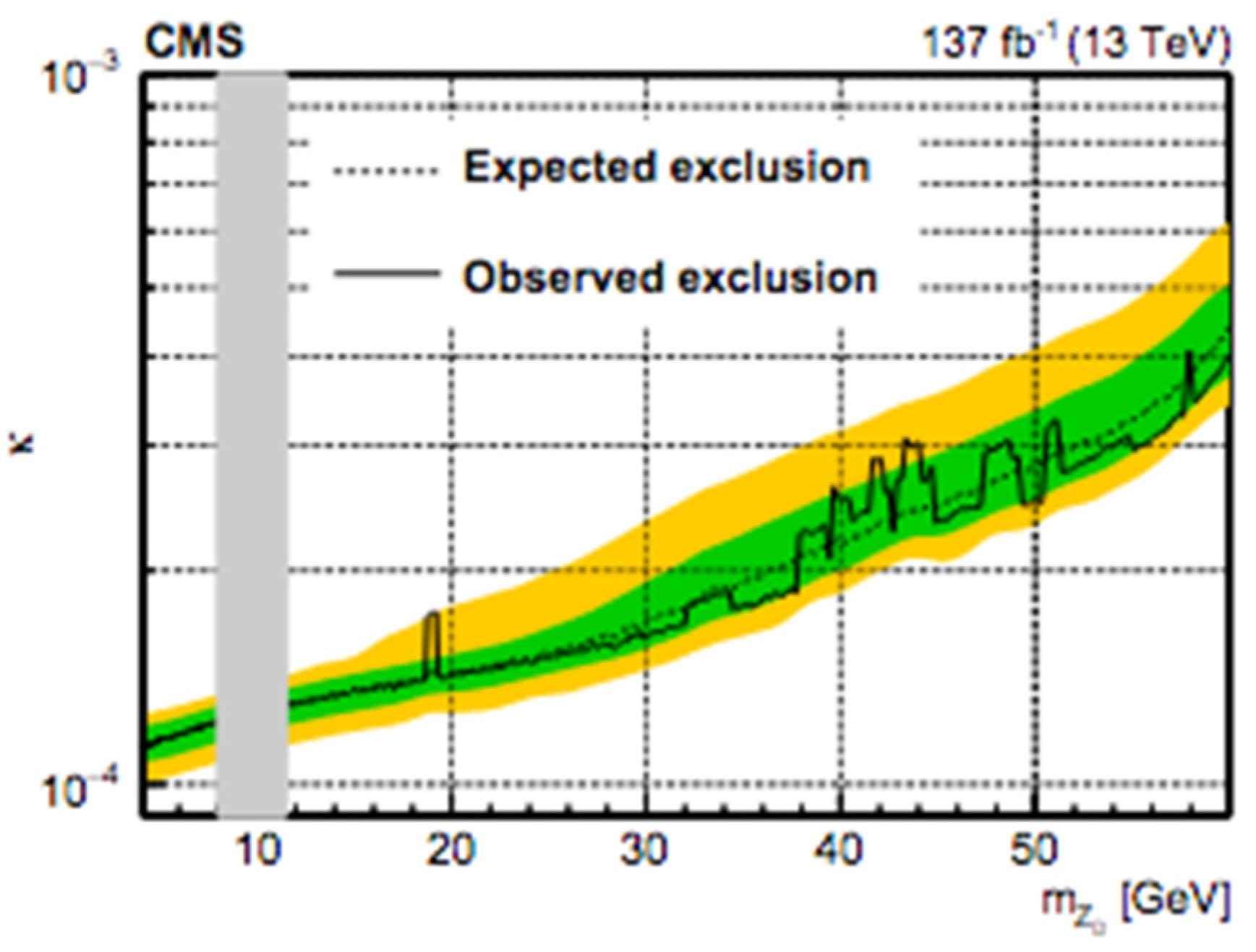
- Model-Independent Limit
- Limit on Dark Photon Model Parameters
4.2. Higgs Dacays Dark (Massless) Photon (ATLAS, CMS)
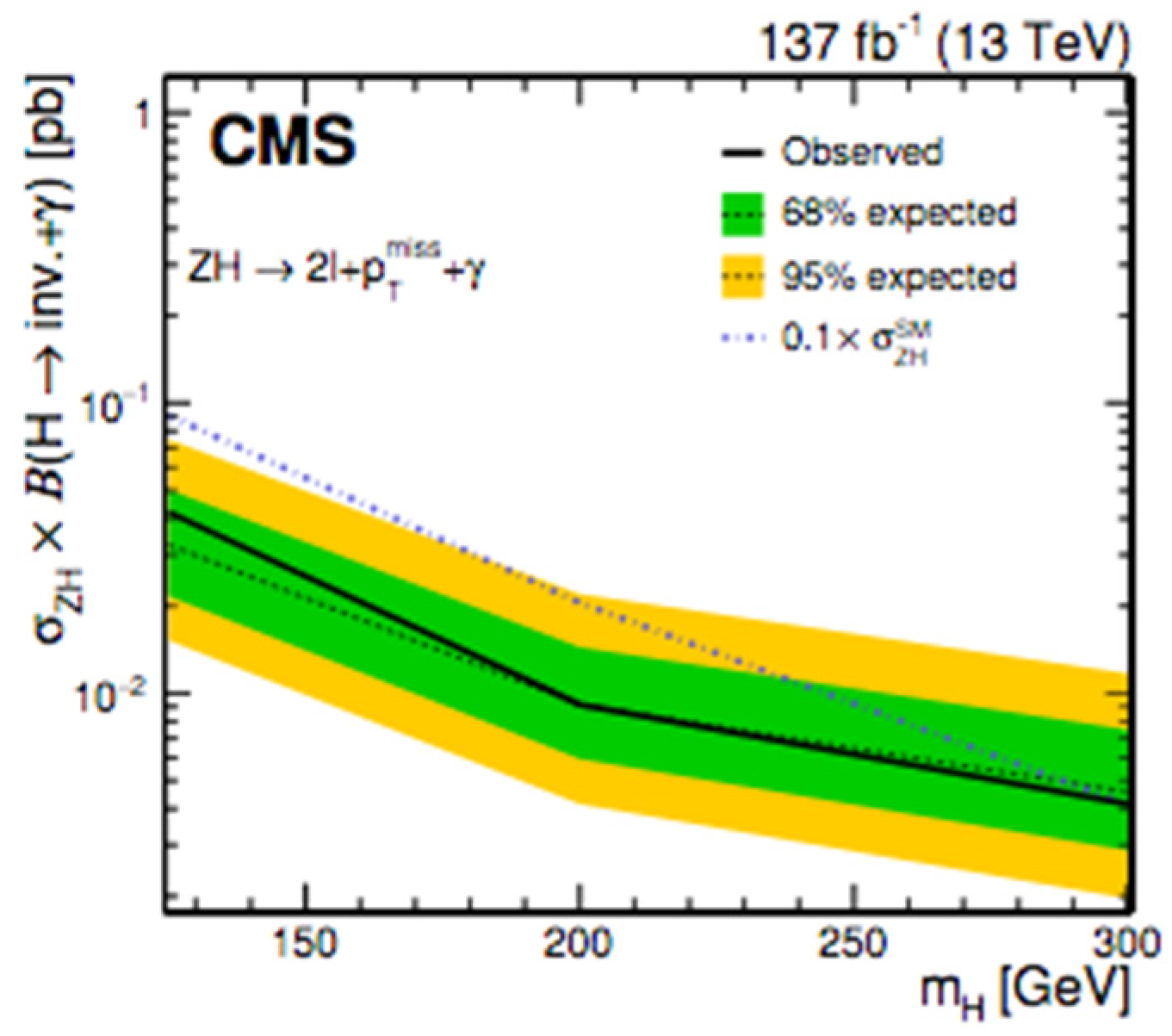
4.2.1. Dark (“Massless”) Photon in ZH Events with CMS at = 13 TeV
Analysis Event Selection
Results
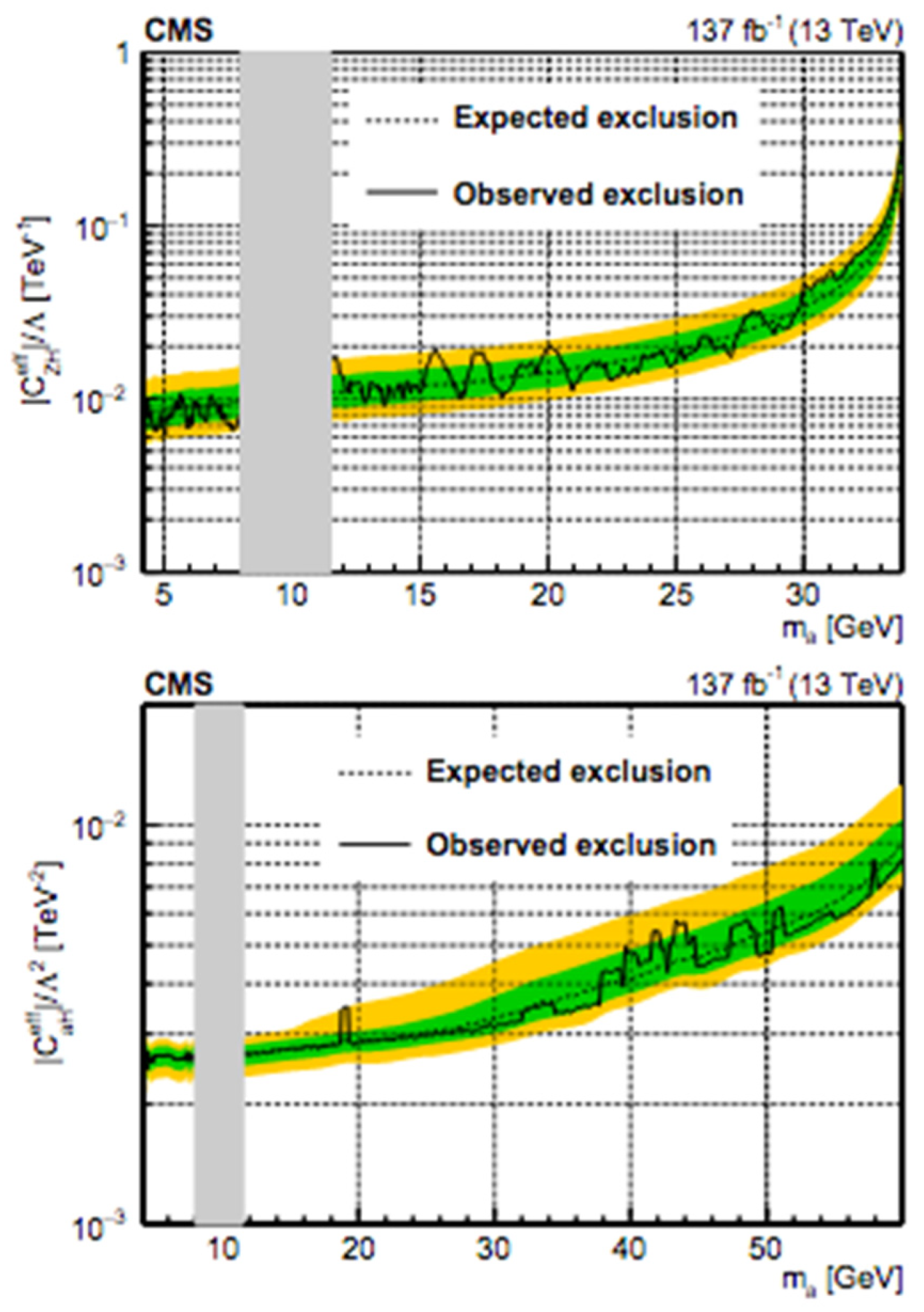
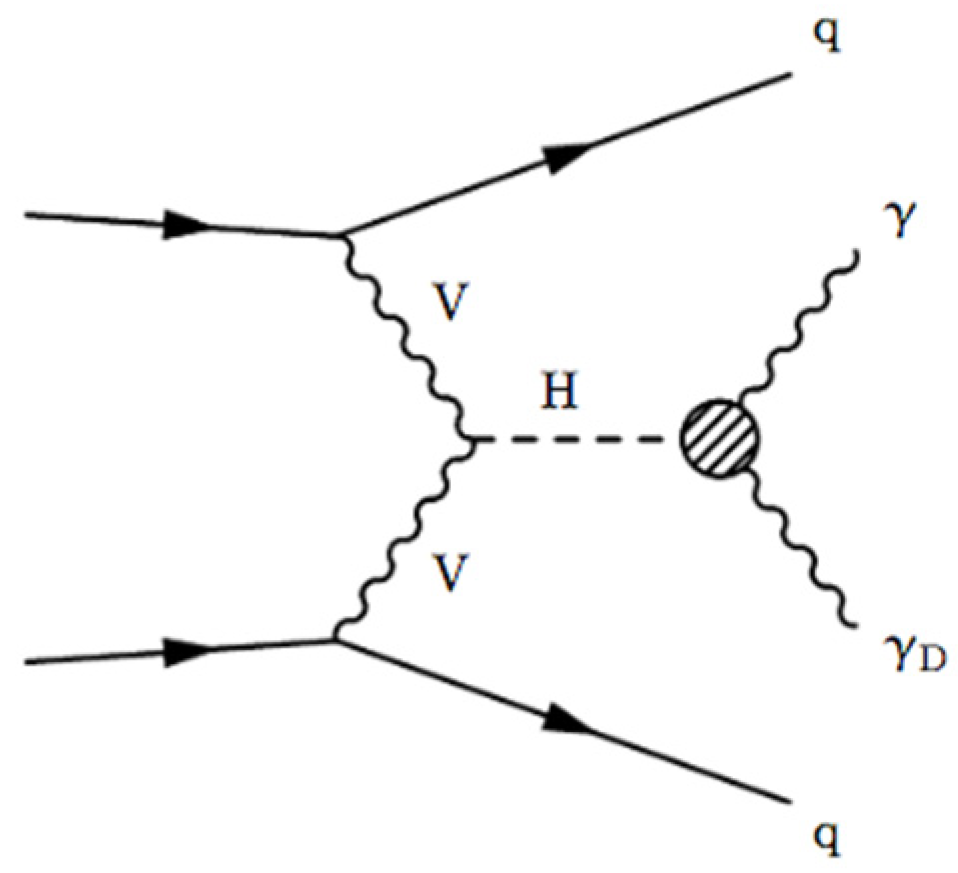
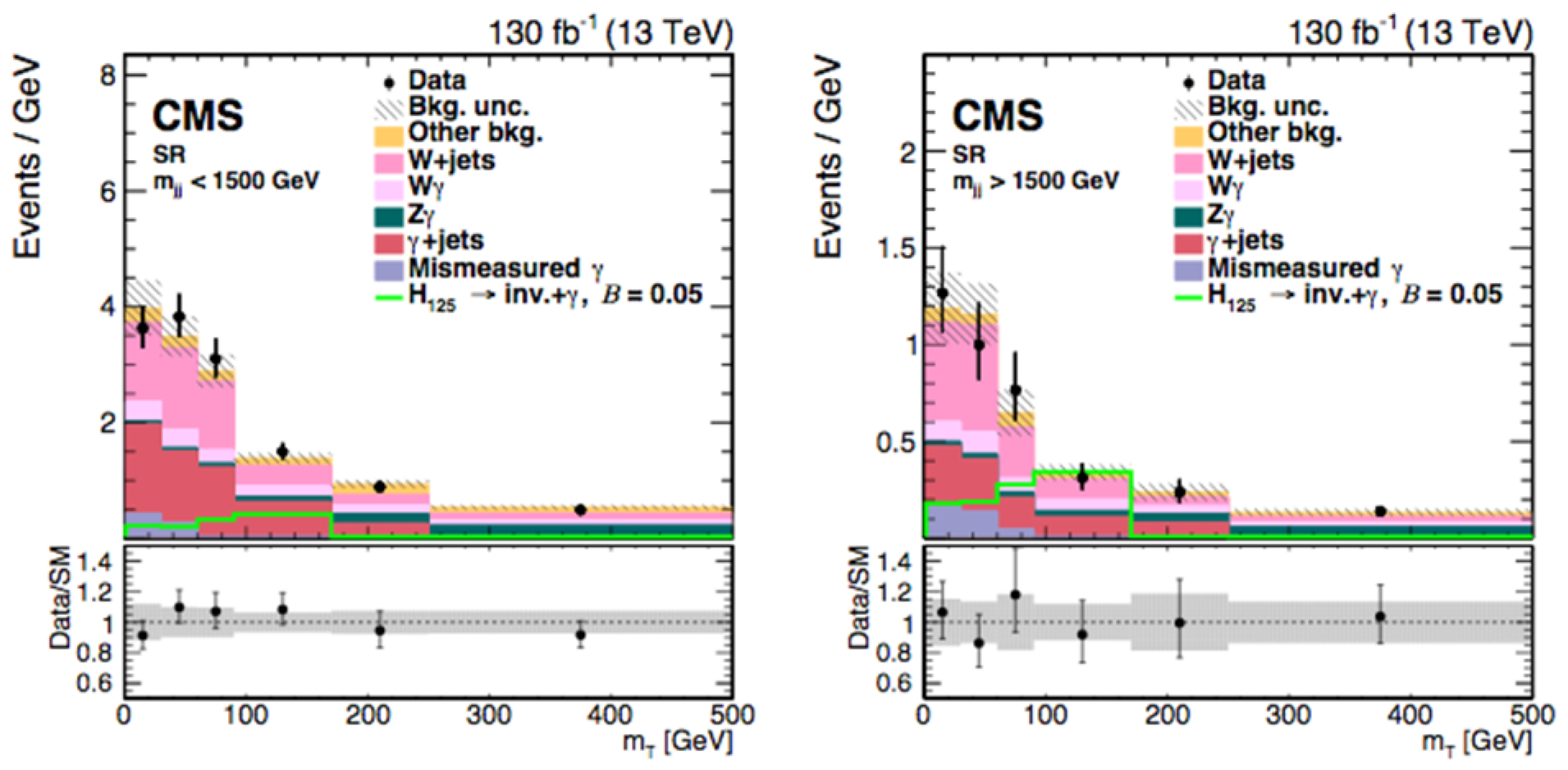
4.2.2. Dark (Massless) Photon in VBF Higgs Events with CMS at = 13 TeV
Analysis Event Selection
Results
4.2.3. Dark Photon Search with CMS at = 13 TeV: Displaced Vertex
Analysis Event Selection
Results
4.3. Long Lived Particles (LLPs) Search with Leptons-Jets (Prompt and Displaced) (ATLAS)
4.3.1. Displaced Leptons-Jets ATLAS Search at = 13 TeV
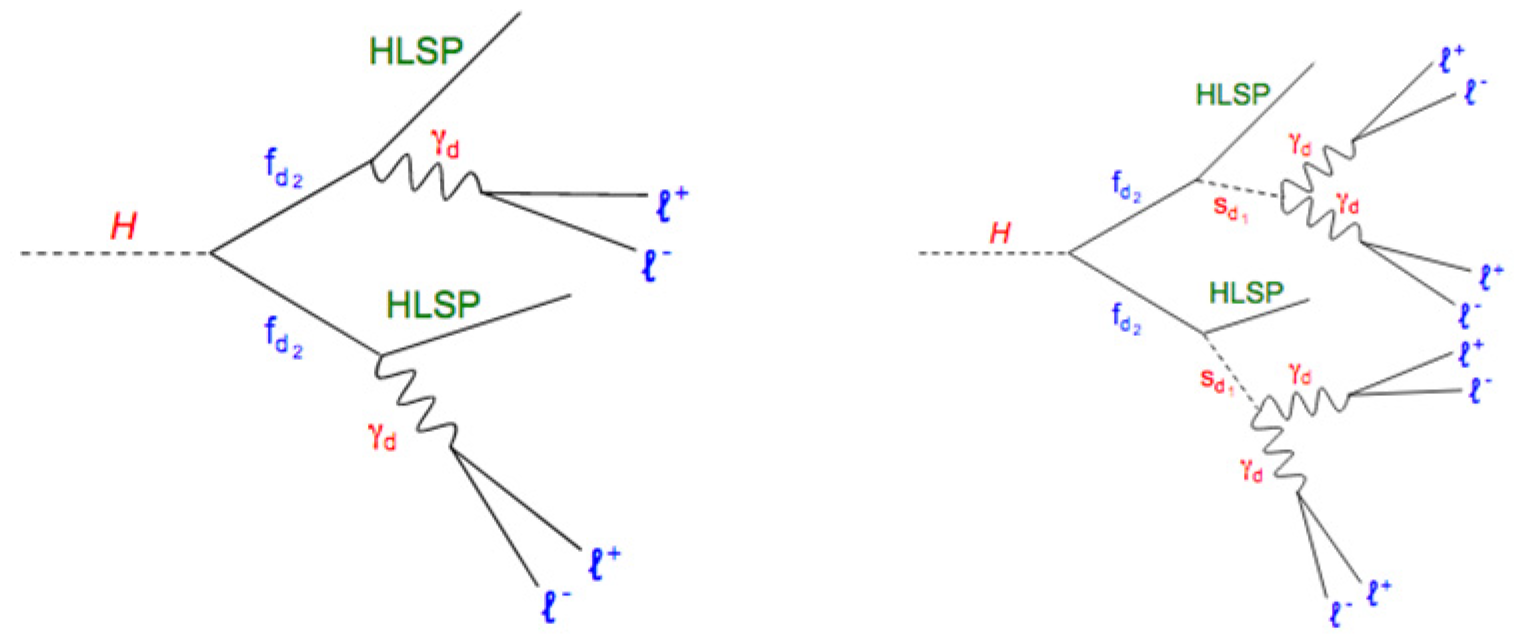
Benchmark Models
Analysis Event Selection
Results
4.3.2. Prompt Lepton Jets Search with ATLAS at = 8 TeV
Benchmark Models
Analysis Event Selection
- Electron jet (eLJ): A lepton jet candidate is called an electron jet if at least one reconstructed electron with ET > 10 GeV is discovered within ΔR = 0.5 of the lepton jet but no muons (eLJ)
- Muon jet (muLJ): A muon jet candidate is one that has at least two muons with pT > 10 GeV but no electrons within ΔR = 0.5 of the lepton jet (muLJ).
- Mixed jet (emuLJ): A lepton jet candidate is called a mixed jet if at least one reconstructed electron with ET > 10 GeV and at least one muon with pT > 10 GeV is discovered inside ΔR = 0.5 of the lepton jet cone (emuLJ).
- eLJ variables: track isolation, percentage of high-threshold TRT hits, fHT, the energy of the strip with the greatest energy deposit, Es1max, fraction of energy deposited in the EM calorimeter’s third sampling layer, fs3, electromagnetic energy fraction, fEM
- muLJ variables: calorimeter isolation, track isolation
- emuLJ variables: track isolation, the energy of the strip with the highest energy deposit, Es1max, fraction of energy deposited in the EM calorimeter’s third sampling layer, fs3, Hadronic leakage, EThad
Results
4.4. Displaced Leptons and Long-Lived Particles (LLPs) (ATLAS, CMS)
4.4.1. Higgs Decay: Displaced Muons with ATLAS at = 13 TeV
Benchmark Models
Analysis Event Selection
Results
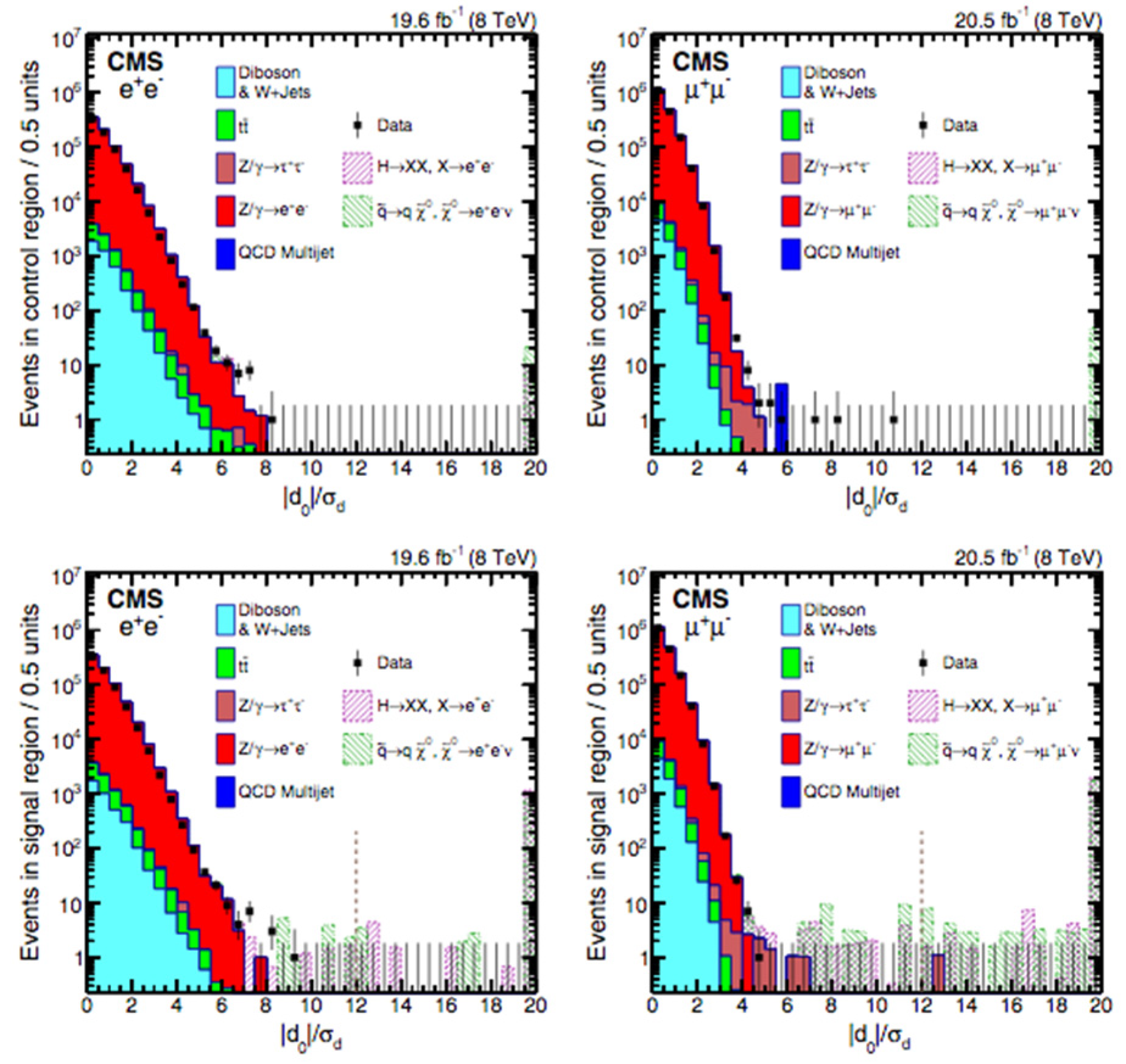
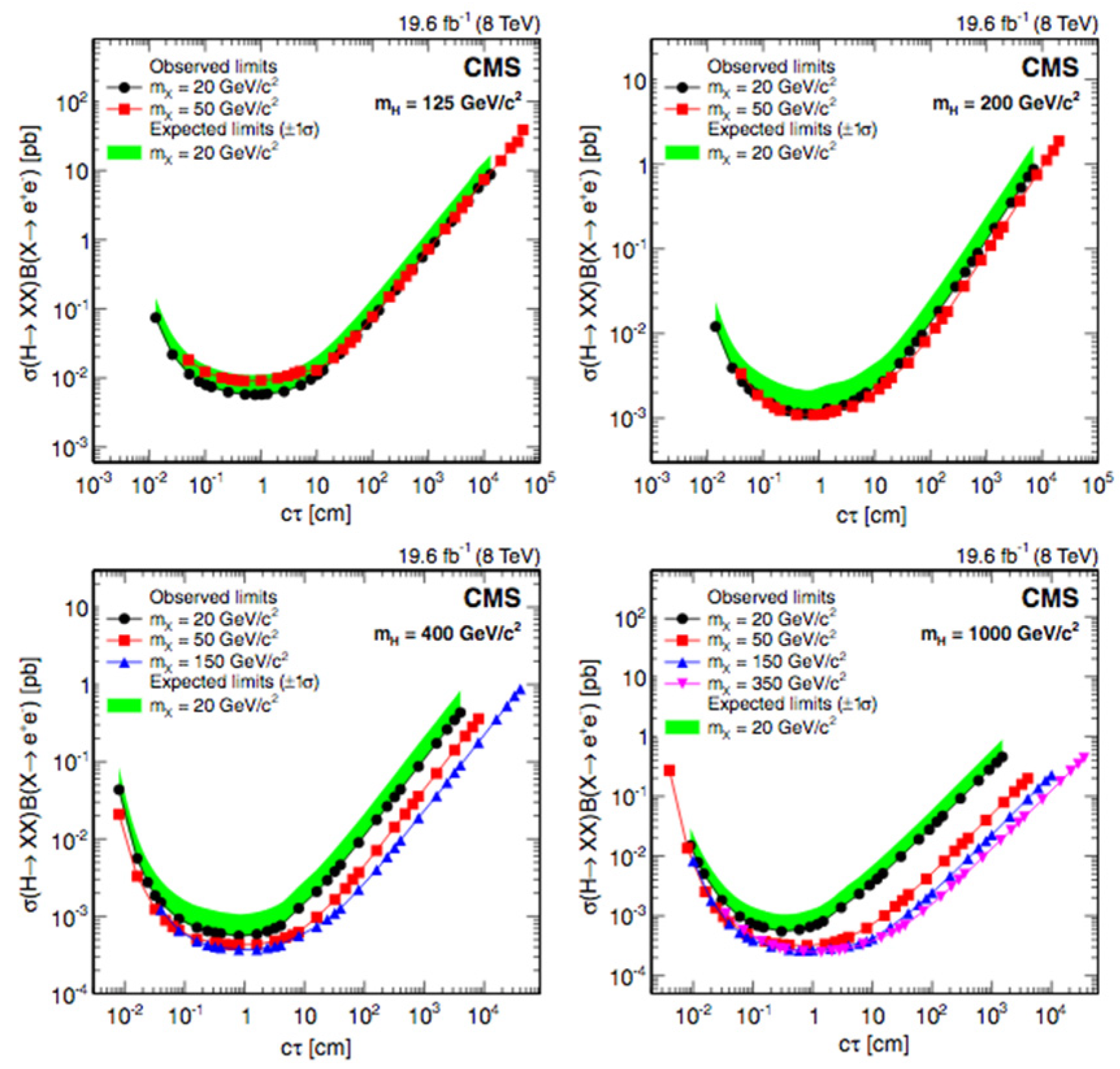
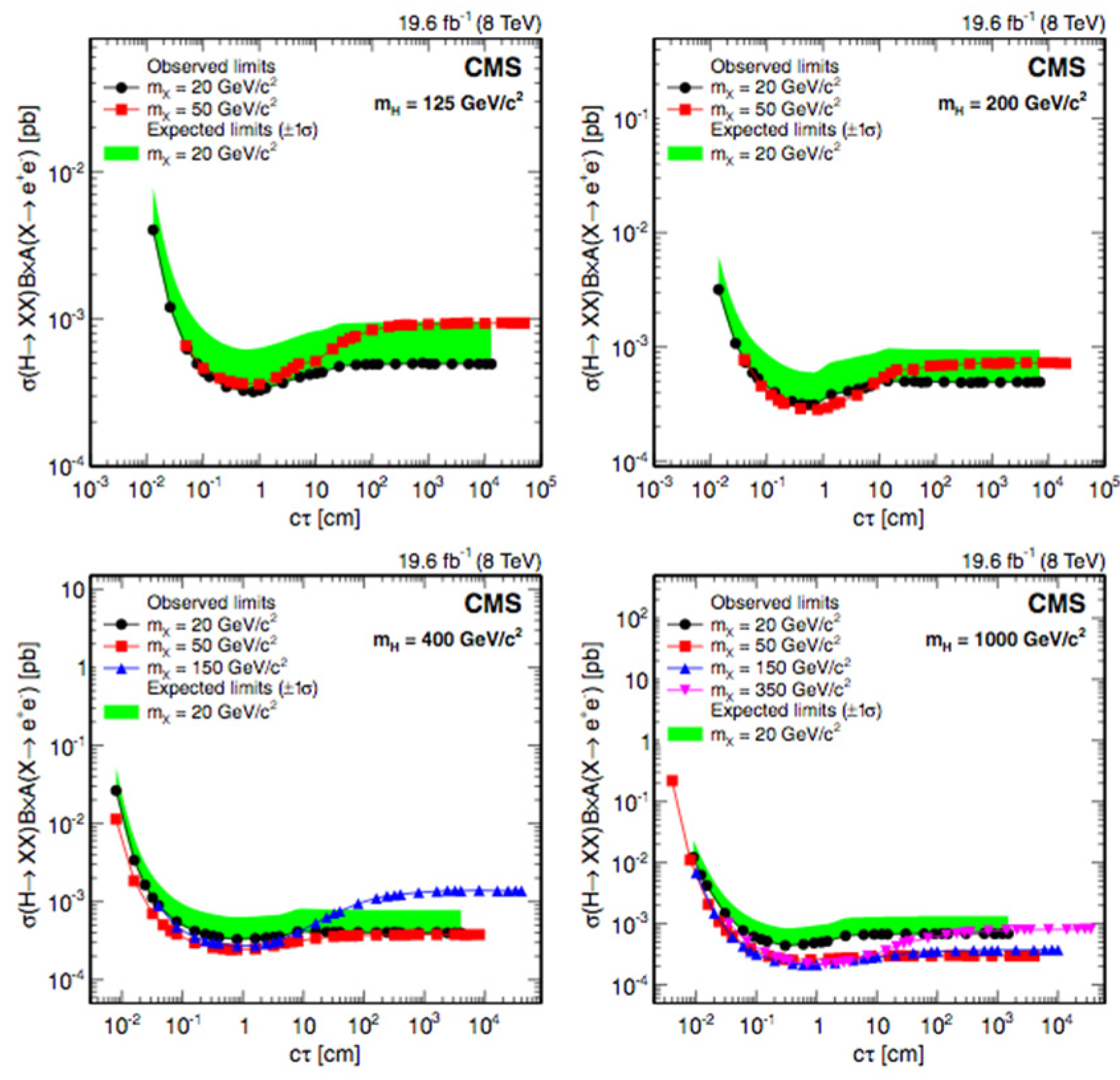
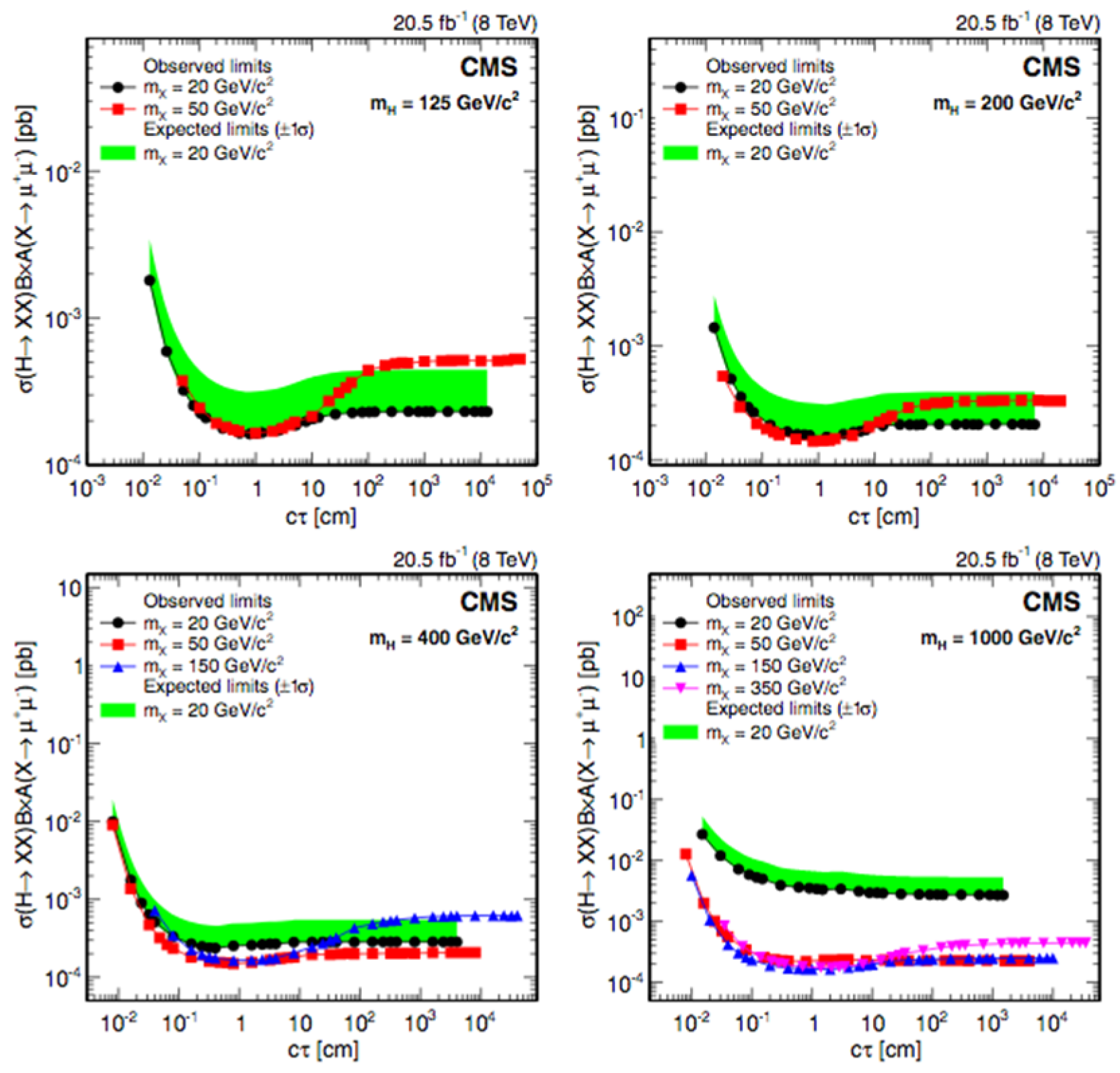
4.4.2. Higgs Decay: Displaced Leptons with CMS at = 8 TeV
Analysis Event Selection
Results
4.5. Low Mass Di-Muon Resonance Searches (CMS, LHCb)
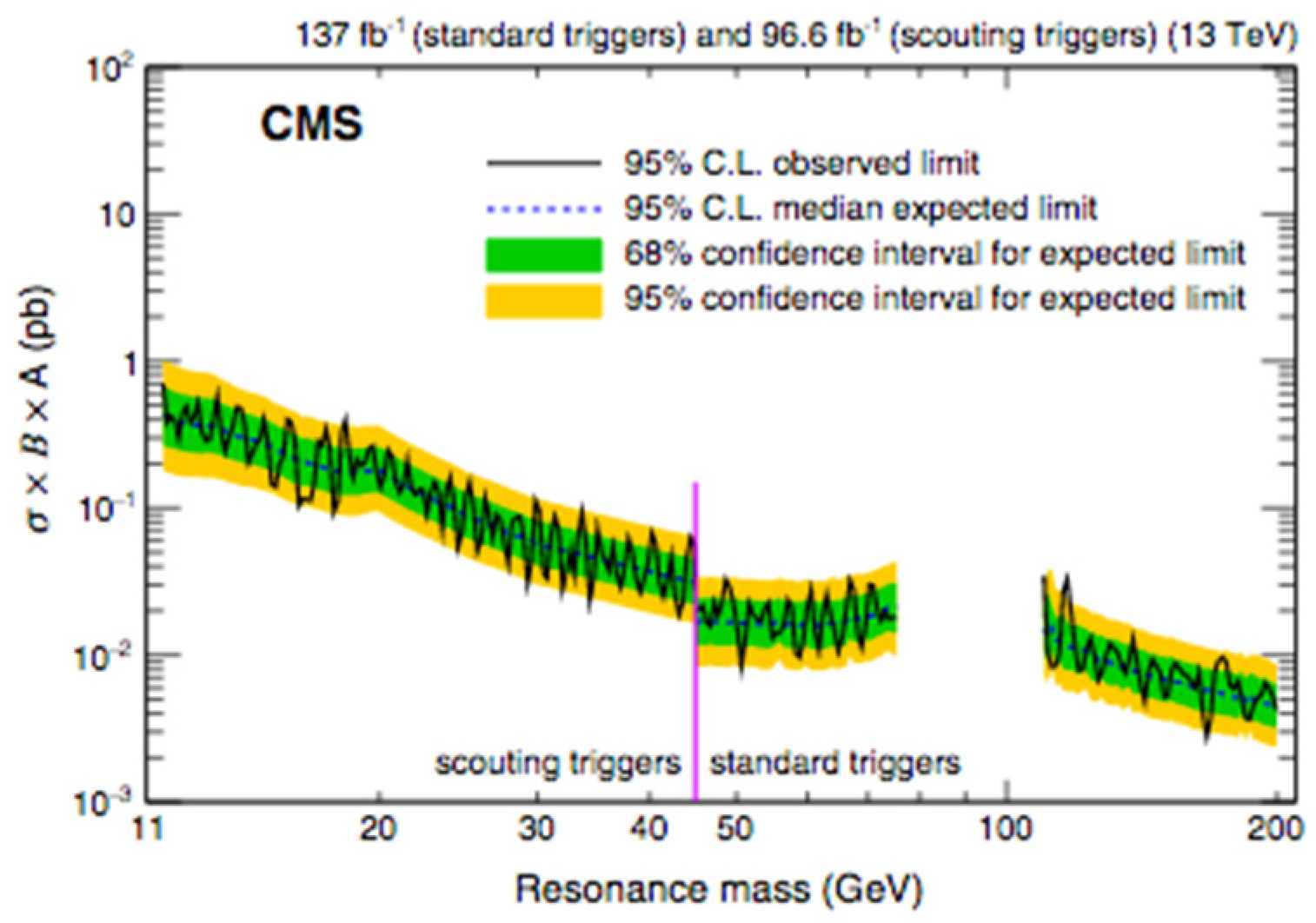
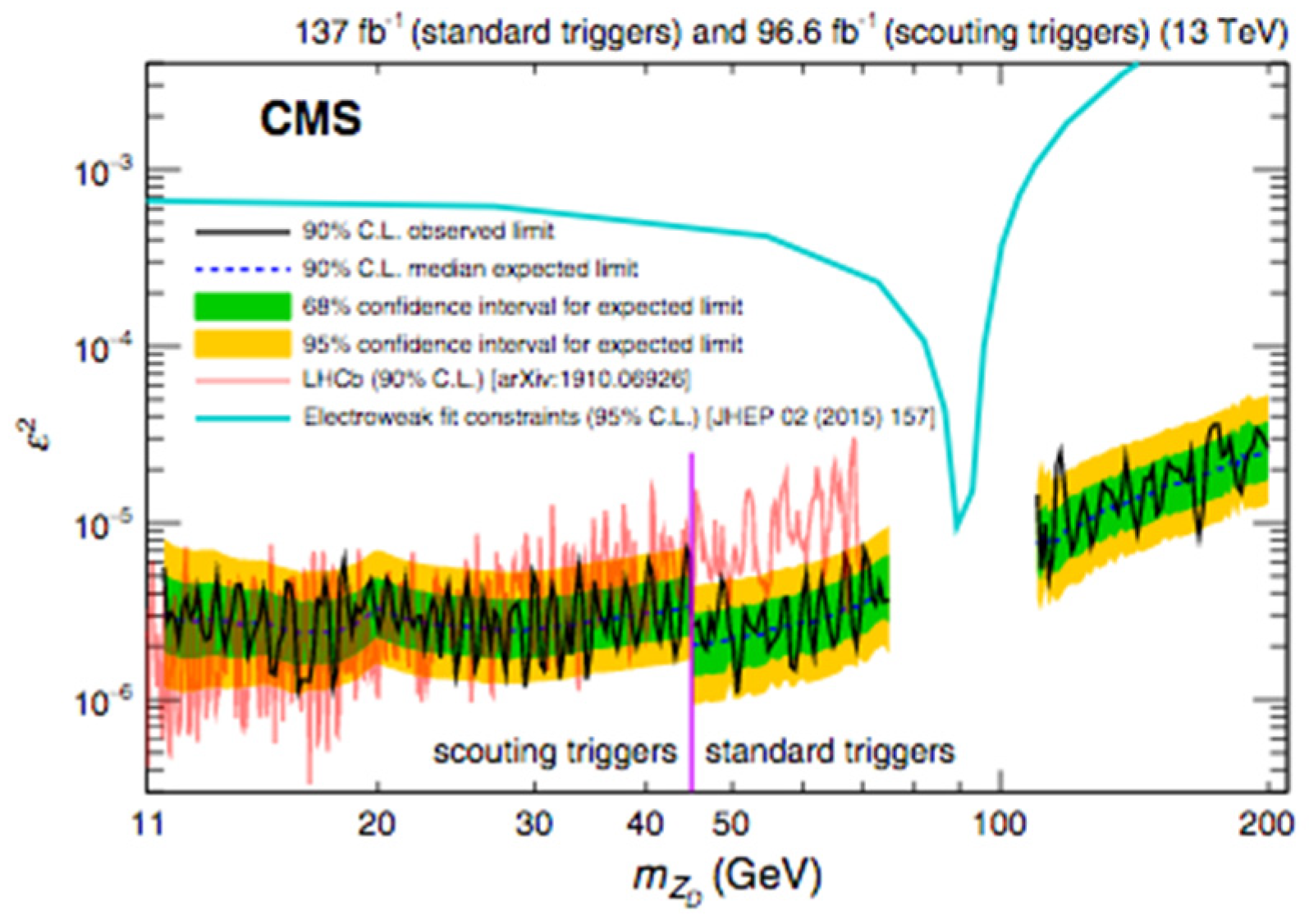
4.5.1. Dimuon Resonances Search with CMS at = 13 TeV
Analysis Event Selection
Results
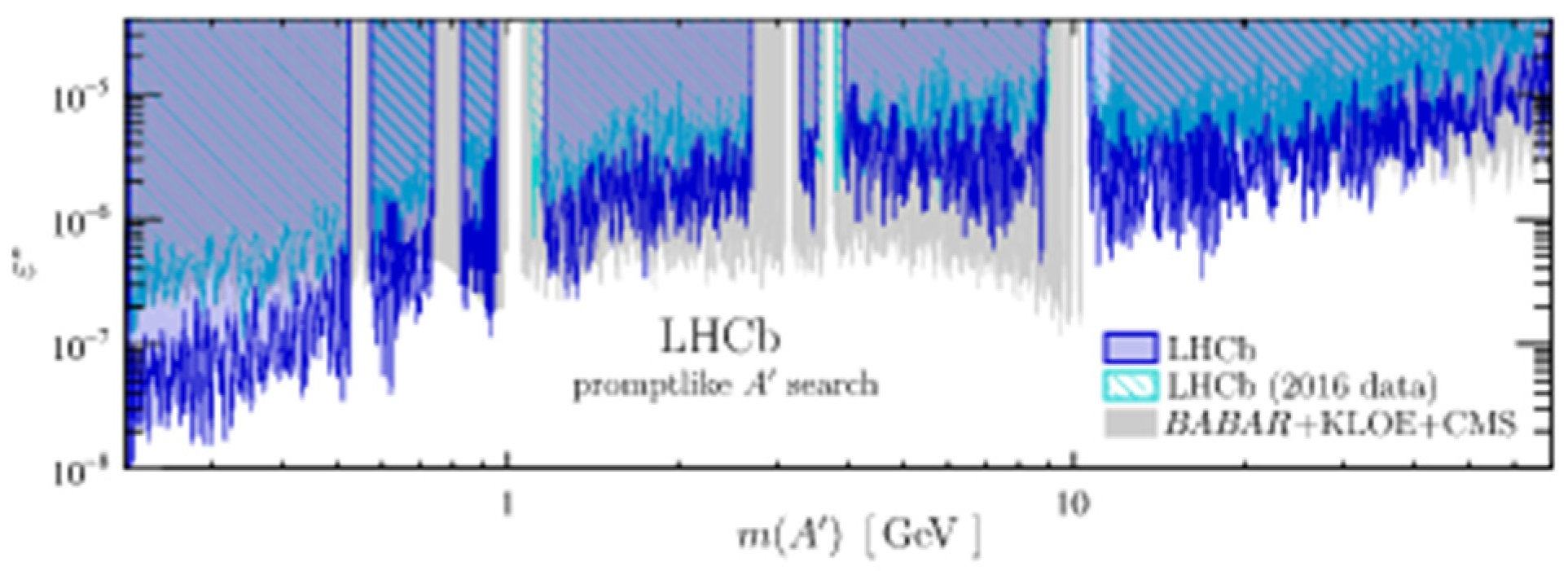
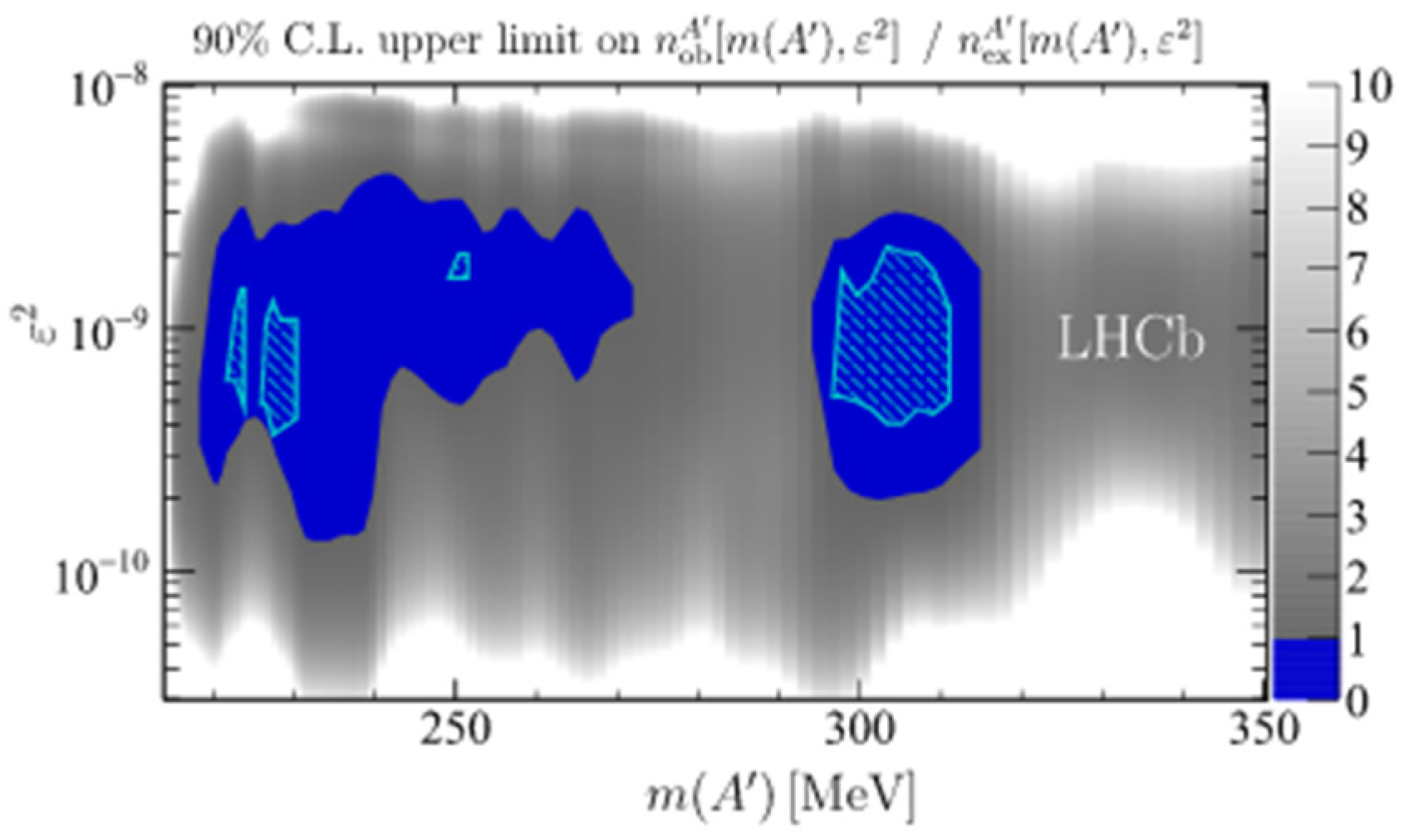
4.5.2. Dimuon Resonances Search with LHCb at = 13 TeV
Analysis Event Selection
Results
5. Summary of Dark Photon Studies at LHC
6. Conclusions and Future Prospects
Funding
Conflicts of Interest
References
- Lagouri, T. Review on Higgs Hidden-Dark Sector Physics. Phys. Scr. 2021, 97, 24001. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- CMS Collaboration. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Beacham, J.; Burrage, C.; Curtin, D.; De Roeck, A.; Evans, J.; Feng, J.L.; Gatto, C.; Gninenko, S.; Hartin, A.; Irastorza, I.; et al. Physics beyond colliders at CERN: Beyond the Standard Model working group report. J. Phys. G Nucl. Part. Phys. 2020, 47, 010501. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Aspects of Axion F(R) Gravity. Europhys. Lett. 2020, 129, 40001. [Google Scholar] [CrossRef]
- Oikonomou, V. Unifying inflation with early and late dark energy epochs in axion gravity. Phys. Rev. D 2021, 103, 44036. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of inflation with dark energy in F(R) gravity and axion dark matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef] [Green Version]
- Doglioni, C.; Tovey, D. ATLAS Communication 2019. Available online: https://atlas.cern/updates/feature/dark-matter (accessed on 5 March 2019).
- Boveia, A.; Doglioni, C. Dark Matter Searches at Colliders. Annu. Rev. Nucl. Part. Sci. 2018, 68, 429–459. [Google Scholar] [CrossRef] [Green Version]
- Available online: https://lpcc.web.cern.ch/index.php/content/lhc-dm-wg (accessed on 1 January 2022).
- Available online: http://www.xenon1t.org (accessed on 1 January 2022).
- Available online: http://luxdarkmatter.org (accessed on 1 January 2022).
- Available online: https://pandax.sjtu.edu.cn (accessed on 1 January 2022).
- Available online: https://glast.sites.stanford.edu (accessed on 1 January 2022).
- Available online: https://www.mpi-hd.mpg.de/hfm/HESS/HESS.shtml (accessed on 1 January 2022).
- Available online: https://magic.mpp.mpg.de (accessed on 1 January 2022).
- Available online: https://veritas.sao.arizona.edu (accessed on 1 January 2022).
- Available online: https://icecube.wisc.edu (accessed on 1 January 2022).
- Available online: http://www.ams02.org (accessed on 1 January 2022).
- ATLAS Collaboration. Search for new phenomena in events with an energetic jet and missing transverse momentum in pp collisions at 13 TeV with the ATLAS detector. Phys. Rev. D 2021, 103, 112006. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for new particles in events with energetic jets and large missing transverse momentum in proton-proton collisions at 13 TeV. arXiv 2021, arXiv:2107.13021. [Google Scholar]
- ATLAS Collaboration. Search for new resonances in mass distributions of jet pairs using 139 fb−1 of pp collisions at 13 TeV with the ATLAS detector. J. High Energy Phys. 2020, 145. [Google Scholar] [CrossRef] [Green Version]
- CMS collaboration. Search for high mass dijet resonances with a new background prediction method in proton-proton collisions at 13 TeV. J. High Energy Phys. 2020, 33. [Google Scholar] [CrossRef]
- Copeland, E.; Sami, M.; Tsujikawa, S. Dynamics of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef] [Green Version]
- Marsh, D.J. Axion cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef] [Green Version]
- Essig, R.; Jaros, J.A.; Wester, W.; Adrian, P.H.; Andreas, S.; Averett, T.; Baker, O.; Batell, B.; Battaglieri, M.; Beacham, J.; et al. Dark Sectors and New, Light, Weakly-Coupled Particles. arXiv 2013, arXiv:1311.0029. [Google Scholar]
- Alexander, J.; Battaglieri, M.; Echenard, B.; Essig, R.; Graham, M.; Izaguirre, E.; Jaros, J.; Krnjaic, G.; Mardon, J.; Morrissey, D.; et al. Dark Sectors 2016 Workshop: Community Report. arXiv 2016, arXiv:1608.08632. [Google Scholar] [CrossRef]
- Curtin, D.; Essig, R.; Gori, S.; Jaiswal, P.; Katz, A.; Liu, T.; Liu, Z.; McKeen, D.; Shelton, J.; Strassler, M.; et al. Exotic decays of the 125 GeV Higgs boson. Phys. Rev. D 2014, 90, 075004. [Google Scholar] [CrossRef] [Green Version]
- Curtin, D.; Essig, R.; Gori, S.; Shelton, J. Illuminating dark photons with high-energy colliders. J. High Energy Phys. 2015, 157. [Google Scholar] [CrossRef] [Green Version]
- Holdom, B. Two U(1)’s and ϵ charge shifts. Phys. Lett. B 1986, 166, 196–198. [Google Scholar] [CrossRef]
- Fabbrichesi, M.; Gabrielli, E.; Lanfranchi, G. The Physics of the Dark Photon; SpringerBriefs in Physics; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- CMS Collaboration. Measurement of the properties of a Higgs boson in the four-lepton final state. Phys. Rev. D 2014, 89, 092007. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Measurements of Higgs boson production and couplings in the four-lepton channel in pp collisions at center-of-mass energies of 7 and 8 TeV with the ATLAS detector. Phys. Rev. D 2015, 91, 012006. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Search for Higgs bosons decaying into new spin-0 or spin-1 particles in four-lepton final states with the ATLAS detector with 139 fb−1 of pp collision data at 13 TeV. J. High Energy Phys. 2022, 3, 041. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for new light gauge bosons in Higgs boson decays to four-lepton final states in pp collisions at 8 TeV with the ATLAS detector at the LHC. Phys. Rev. D 2015, 92, 092001. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration; Aaboud, M. Search for Higgs boson decays to beyond-the-Standard-Model light bosons in four-lepton events with the ATLAS detector at 13 TeV. J. High Energy Phys. 2018, 6, 166. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Search for long-lived neutral particles decaying into lepton jets in proton-proton collisions at 8 TeV with the ATLAS detector. J. High Energy Phys. 2014, 11, 88. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Measurement of the Higgs boson coupling properties in the H→ZZ∗→4ℓ decay channel at 13 TeV with the ATLAS detector. J. High Energy Phys. 2018, 3, 95. [Google Scholar]
- ATLAS Collaboration. Measurement of inclusive and differential cross sections in the H→ZZ∗→4ℓ decay channel in pp collisions at = 13 TeV with the ATLAS detector. J. High Energy Phys. 2017, 10, 132. [Google Scholar]
- Read, A.L. Presentation of search results: The CLs technique. J. Phys. G 2002, 28, 2693. [Google Scholar] [CrossRef]
- Cowan, G.; Cranmer, K.; Gross, E.; Vitells, O. Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 2011, 71, 1554. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. Search for low-mass dilepton resonances in Higgs boson decays to four-lepton final states in proton–proton collisions at 13 TeV. Eur. Phys. J. C 2022, 82, 290. [Google Scholar] [CrossRef]
- LHCb Collaboration. Search for Dark Photons Produced in 13 TeV pp Collisions. Phys. Rev. Lett. 2018, 120, 061801. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. Search for dark photons in decays of Higgs bosons produced in association with Z bosons in proton-proton collisions at 13 TeV. J. High Energy Phys. 2019, 10, 139. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. Search for dark photons in Higgs boson production via vector boson fusion in proton-proton collisions at 13 TeV. J. High Energy Phys. 2021, 3, 11. [Google Scholar] [CrossRef]
- CMS Collaboration. A search for pair production of new light bosons decaying into muons in proton-proton collisions at 13 TeV. Phys. Lett. B 2019, 796, 131. [Google Scholar] [CrossRef]
- CMS Collaboration. Search for long-lived particles that decay into final states containing two electrons or two muons in proton-proton collisions at 8 TeV. Phys. Rev. D 2015, 91, 052012. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Search for light long-lived neutral particles produced in pp collisions at 13 TeV and decaying into collimated leptons or light hadrons with the ATLAS detector. Eur. Phys. J. C 2020, 80, 450. [Google Scholar] [CrossRef]
- ATLAS Collaboration. A search for prompt lepton-jets in pp collisions at 8 TeV with the ATLAS detector. J. High Energy Phys. 2016, 2, 62. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. A search for pair production of new light bosons decaying into muons. Phys. Lett. B 2016, 752, 146. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for long-lived particles in final states with displaced dimuon vertices in pp collisions at 13 TeV with the ATLAS detector. Phys. Rev. D 2019, 99, 012001. [Google Scholar] [CrossRef] [Green Version]
- ATLAS Collaboration. Search for massive, long-lived particles using multitrack displaced vertices or displaced lepton pairs in pp collisions at 8 TeV with the ATLAS detector. Phys. Rev. D 2015, 92, 072004. [Google Scholar] [CrossRef] [Green Version]
- CMS Collaboration. Search for a Narrow Resonance Lighter than 200 GeV Decaying to a Pair of Muons in Proton-Proton Collisions at 13 TeV. Phys. Rev. Lett. 2020, 124, 131802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LHCb Collaboration. Search for A′→μ+μ− Decays. Phys. Rev. Lett. 2020, 124, 041801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
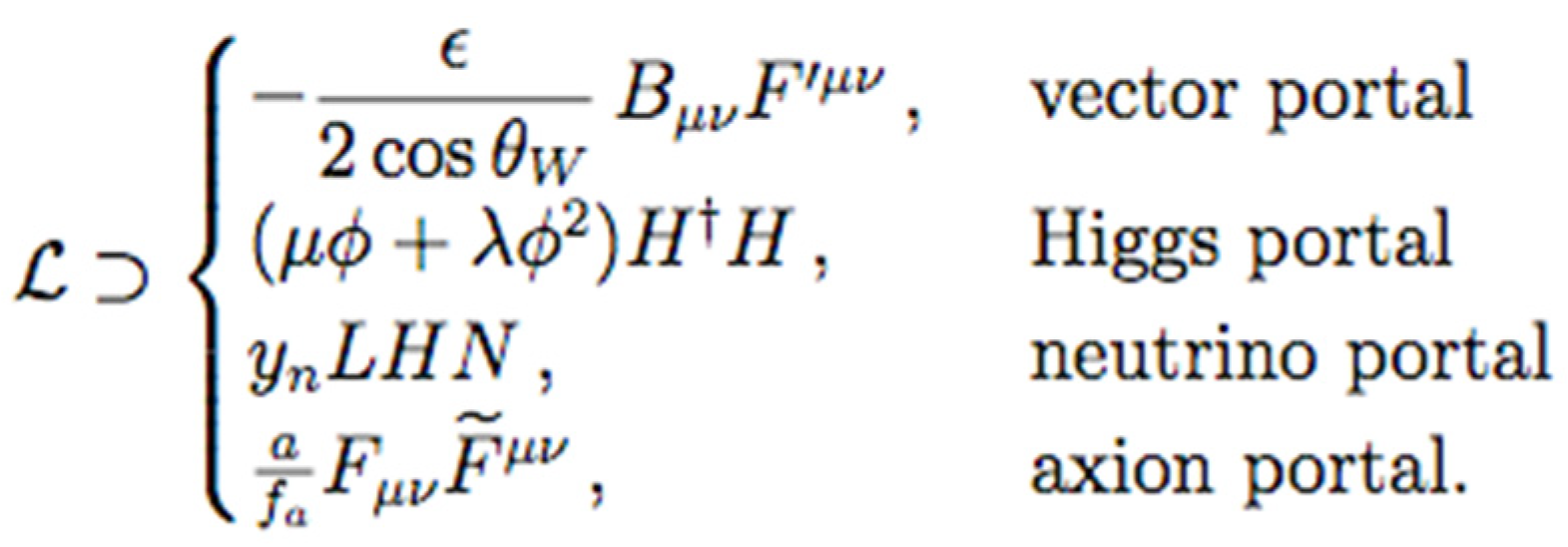





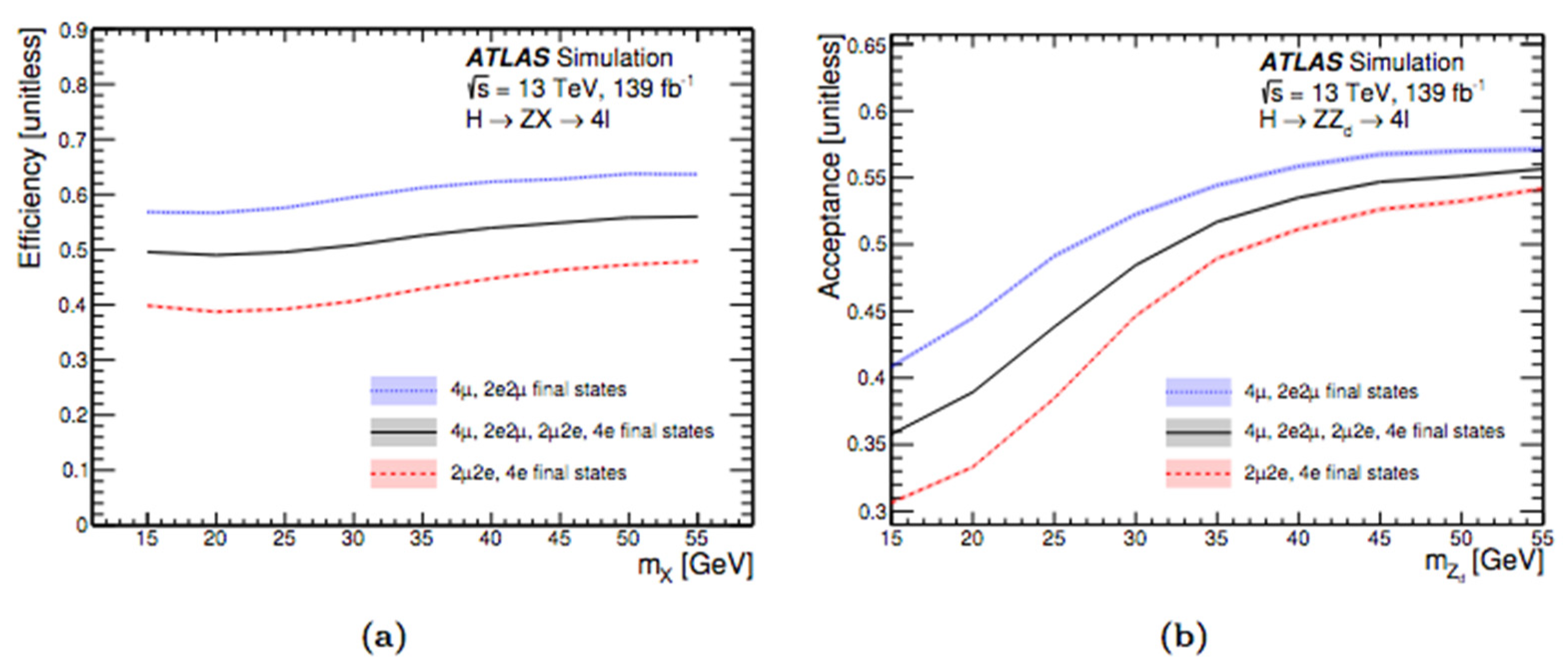






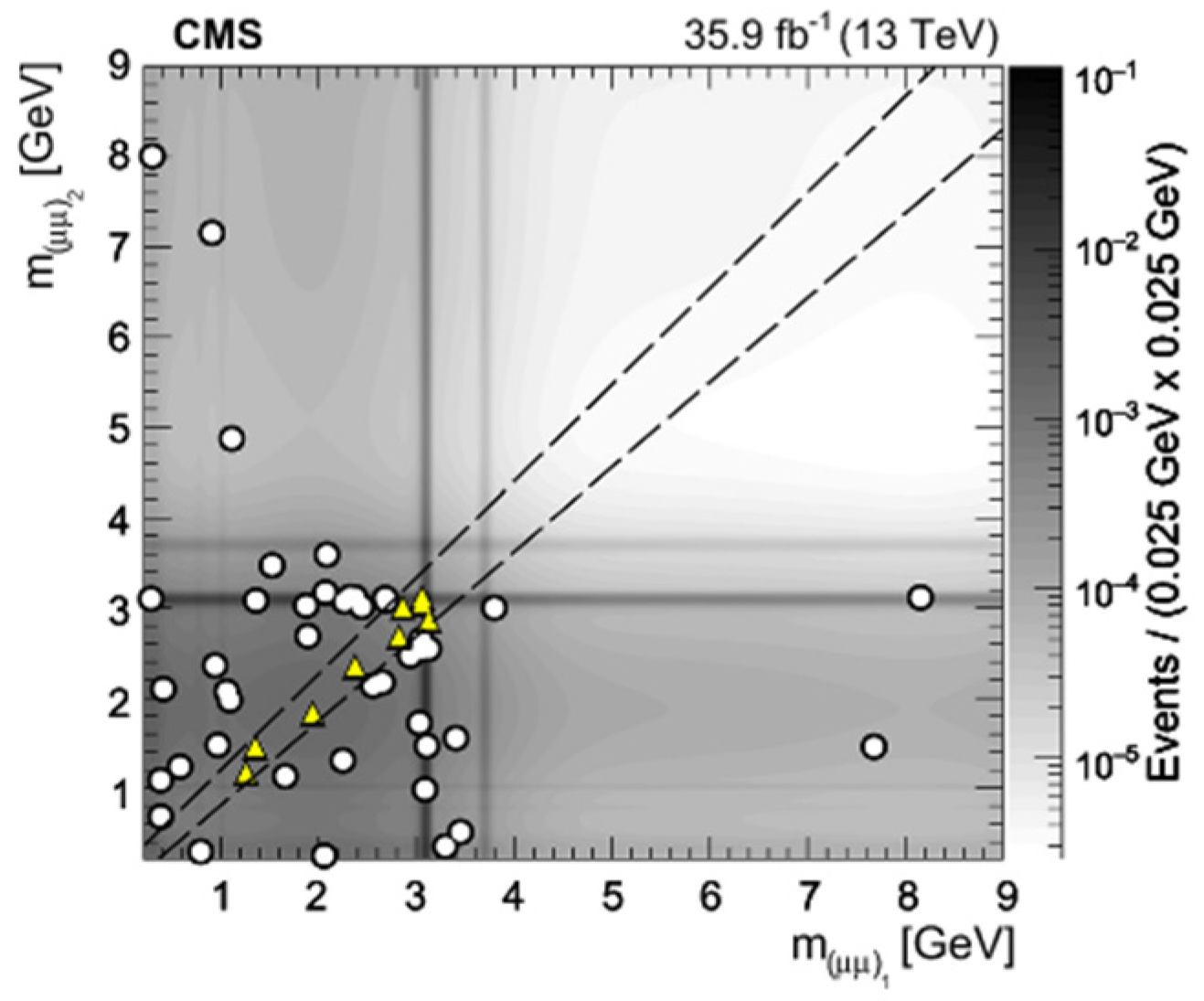
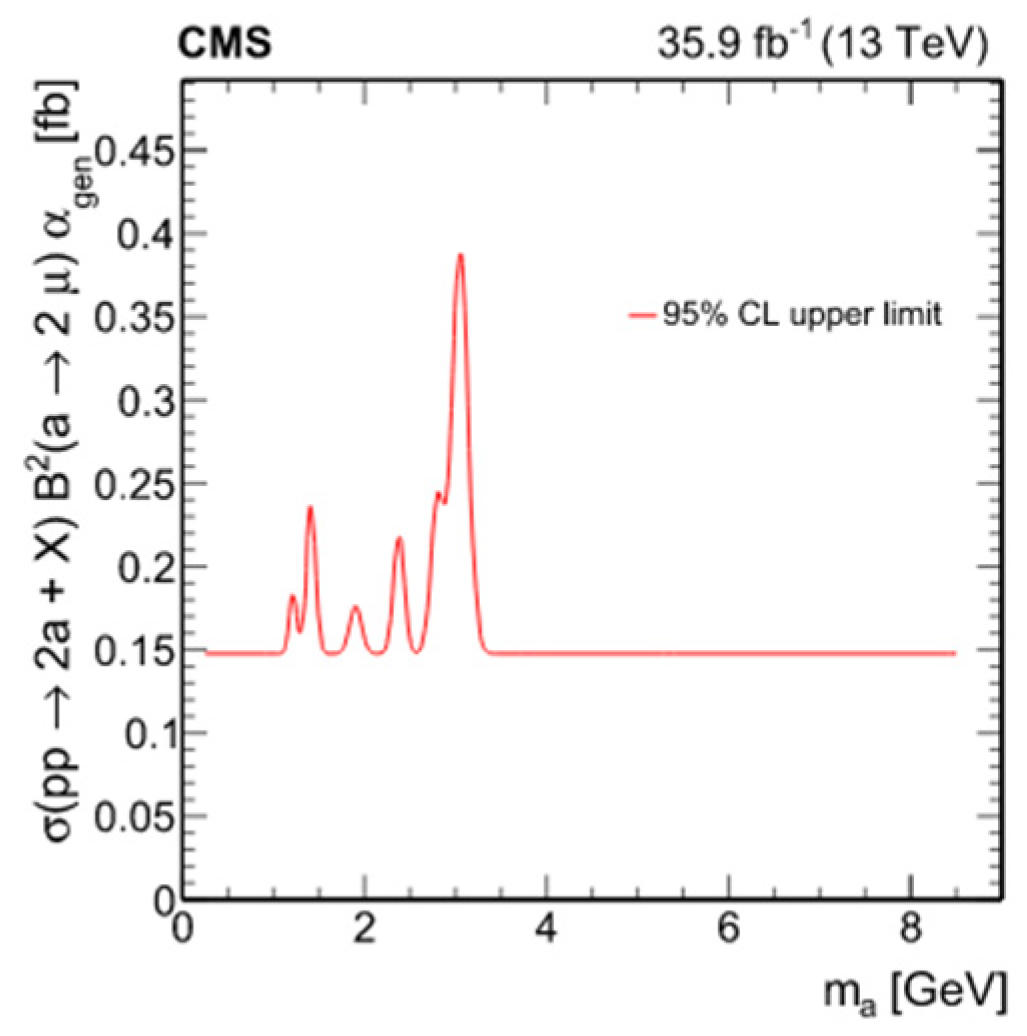
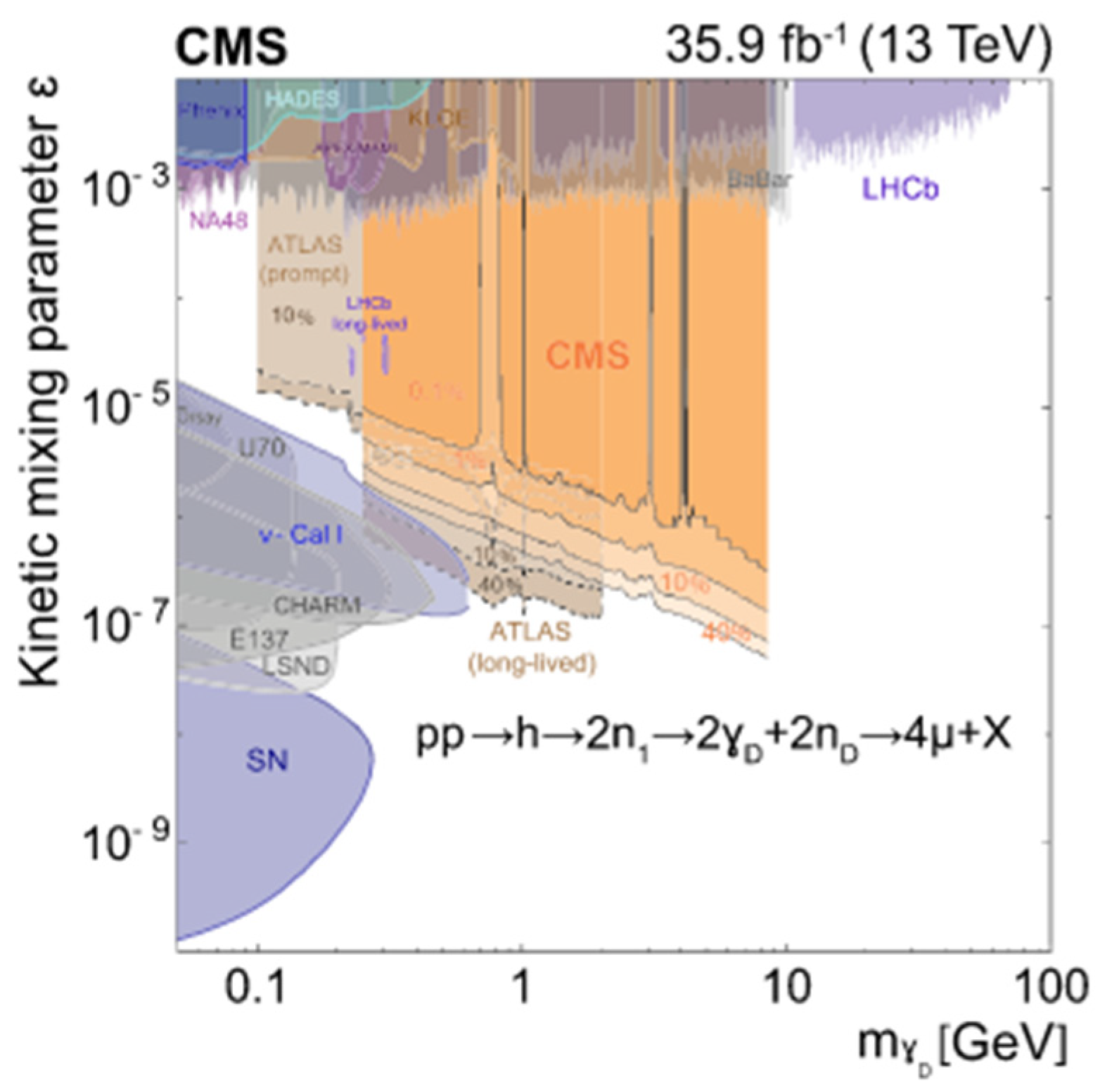

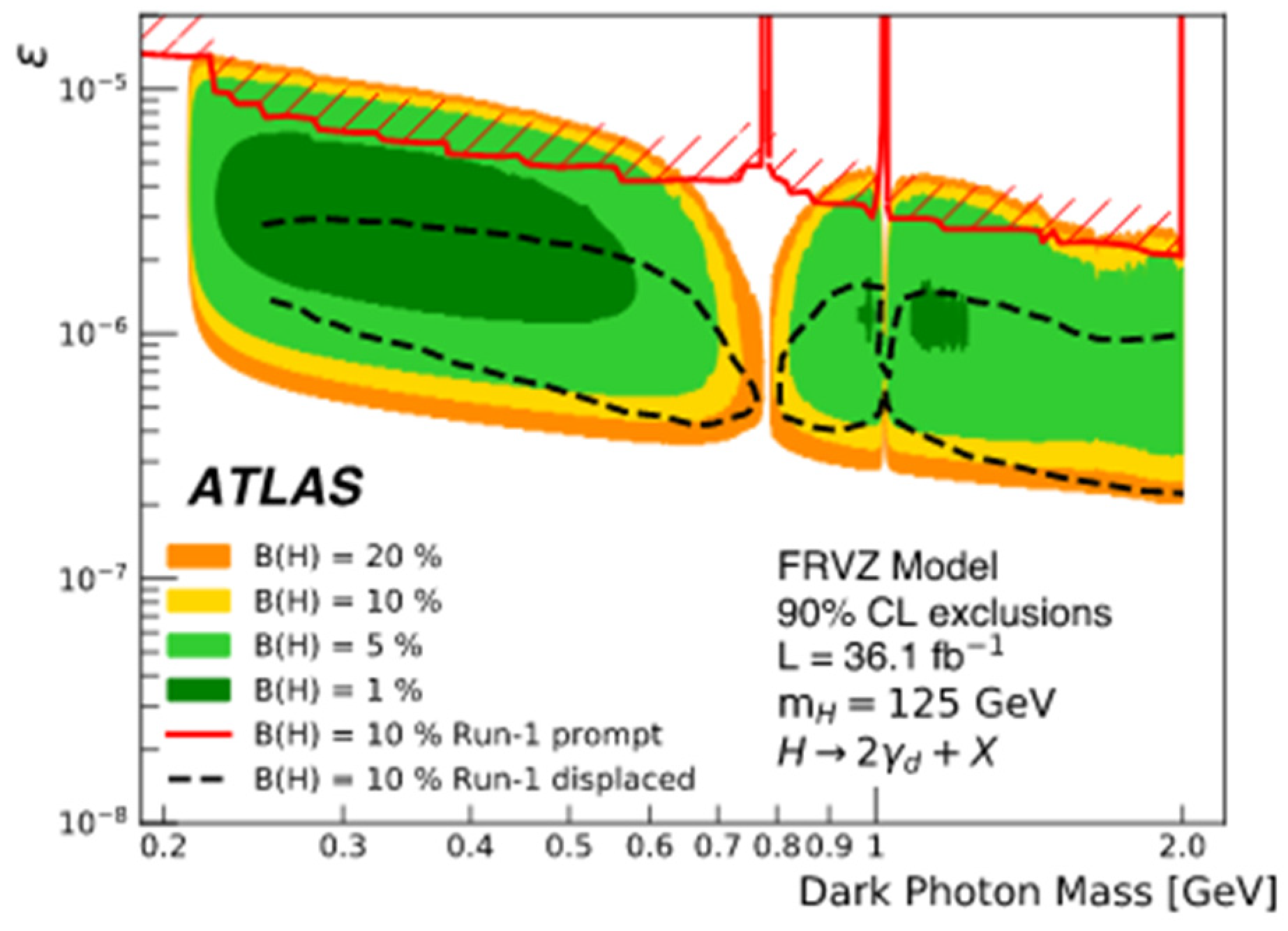


| H→ZX→4l (15 GeV < mX < 55 GeV) | H→XX→4l (15 GeV < mX < 60 GeV) | H→ZX→4µ (1 GeV < mX < 15 GeV) | |
|---|---|---|---|
| Quadruplet Selection |
| ||
| Leptons in the quadrupled tare responsible for firing at least one trigger. In the case of multi-lepton triggers, all leptons of the trigger must match to leptons in the quadruplet | ||
| ΔR(l, l′) > 0.10 (0.20) for same-flavour (different-flavour) leptons in the quadruplet | — | ||
| Quadruplet Ranking | Select first surviving quadruplet from channels, in the order: 4µ, 2e2µ, 2µ2e, 4e | Select quadruplet with smallest Δmll = │m12 − m34│ | |
| Isolation & IP | Track & Calorimeter Isolation d0/σ(d0) < 5 for e, d0/σ(d0) < 3 for μ | ||
| m4l | 115 GeV < m4l < 130 GeV | 120 GeV < m4l < 130 GeV | |
| Z-Veto | — | 10 GeV < m12,34 < 64 GeV 4e and 4µ channels: 5 GeV < m14,32 < 75 GeV | — |
| Heavy Flavor Veto | — | Reject event if: (mJ/Ψ − 0.25 GeV) < m12,34,14,32 < (mJ/Ψ − 0.30 GeV) or (mΥ(1S) − 0.70 GeV) < m12,34,14,32 < (mΥ(1S) − 0.75 GeV) | |
| Signal Region | — | m34/m12 > 0.85 − 0.1125 f(m12) | 1.2 GeV < m12,34 < 20 GeV m34/m12 > 0.85 Reject event if m12,m34 in: 2 GeV–4.4 GeV or 8–12 GeV |
| Process | Yield (±Stat. ±Syst.) | ||
|---|---|---|---|
| 2l2μ | 2l2e | Total | |
| H→ ZZ* → 4l | 127.9 ± 0.1 ± 3.6 | 76 ±0.1 ± 10 | 204 ± 0.2 ± 12 |
| ZZ* → 4l | 70.2 ± 0.2 ± 1.9 | 33.0 ± 0.2 ± 3.6 | 103 ± 0.3 ± 4.6 |
| Reducible | 4.9 ± 0.1 ± 0.3 | 5.8 ± 0.3 ±.0.6 | 10.7 ± 0.3 ± 1.0 |
| + Z | 1.1 ± 0.1 ± 0.04 | 0.7 ± 0.1 ± 0.1 | 1.8 ± 0.1 ± 0.1 |
| Total | 204.1 ± 0.3 ± 5.5 | 116 ± 0.5 ± 14 | 320 ± 0.5 ± 17 |
| Data | 237 | 119 | 356 |
| Process | Yield (±Stat. ±Syst.) |
|---|---|
| H→ZZ*→4l | 11.1 ± 0.1 ± 1.0 |
| ZZ*→4l | 3.38 ± 0.05 ± 0.25 |
| t | 0.47 ± 0.13 ± 0.09 |
| Z + jets | 0.43 |
| Z + t→4l | 0.09 ± 0.02 ± 0.02 |
| WZ | 0.05 |
| VVV/VBS | Negligible |
| Heavy Flavor | Negligible |
| Total | 15.6 ± 0.4 ± 1.2 |
| Data | 20 |
| Process | Yield (±Stat. ±Syst.) |
|---|---|
| H→ZZ*→4μ | 0.41 ± 0.01 ± 0.03 |
| ZZ*→4μ | 0.22 ± 0.04 ± 0.04 |
| VVV/VBS | Negligible |
| Heavy Flavor | 0.26 ± 0.09 ± 0.10 |
| Total | 0.89 ± 0.10 ± 0.11 |
| Data | 0 |
| Variable | Selection | Reject |
|---|---|---|
| Number of leptons | Exactly 2 leptons, pT > 25/20 GeV | WZ, ZZ, VVV |
| Number of photons | ≥1 photon, pTγ > 25 GeV | All but Zγ |
| |mll − mZ| | <15 GeV | WW, Top quark |
| pTmiss | >110 GeV | Zγ |
| pTll | >60 GeV | Zγ |
| b jet veto | Applied | Top quark, VVV |
| Jet counting | ≤2 | Top quark, VVV |
| ΔΦ(ll, pTmiss +pTγ) | >2.5 rad | Zγ |
| |pT(pTmiss +pTγ) − pTll | / pTll | <0.4 | Zγ |
| ΔΦ(jet, pTmiss) | >0.5 rad | Zγ |
| mllγ | >100 GeV | Zγ |
| mT | < 350 GeV | WW, Top quark |
| Data-taking year | 2016 | 2017/2018 | |
| Trigger | VBF + γ | Single-photon | pTmiss |
| Number of photons | ≥1 photon | ||
| pTγ | >80 GeV | >230 GeV | >80 GeV |
| Number of leptons | 0 | ||
| pTj1/pTj2 | >50 GeV | ||
| pTmiss | >100 GeV | >140 GeV | >140 GeV |
| Jet counting | 2–5 | ||
| mjj | >500 GeV | ||
| |Δηjj| | >3.0 | ||
| ηj1 ηj2 | <0 | ||
| ΔΦ(jet, pTmiss) | >1.0 radians | ||
| zγ* | <0.6 | ||
| pTtot | <150 GeV | ||
| VBF | ZH | VBF+ZH | |||
|---|---|---|---|---|---|
| Obs. (%) | Exp. (%) | Obs. (%) | Exp. (%) | Obs. (%) | Exp. (%) |
| 3.4 | 4.6 | 2.9 | |||
| Selection | Low Mass | High Mass |
|---|---|---|
| pTµ [GeV] | > 10 | >20 |
| mµµ [GeV] | 15–60 | >60 |
| Dimuon transverse boost | … | >20 |
| SRlow | SRhigh | |
| Muon candidates | Both MSonly | Both MSonly |
| Muon candidate charge | Opposite charge | Opposite charge |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagouri, T. Review on Higgs Hidden–Dark Sector Physics at High-Energy Colliders. Symmetry 2022, 14, 1299. https://doi.org/10.3390/sym14071299
Lagouri T. Review on Higgs Hidden–Dark Sector Physics at High-Energy Colliders. Symmetry. 2022; 14(7):1299. https://doi.org/10.3390/sym14071299
Chicago/Turabian StyleLagouri, Theodota. 2022. "Review on Higgs Hidden–Dark Sector Physics at High-Energy Colliders" Symmetry 14, no. 7: 1299. https://doi.org/10.3390/sym14071299
APA StyleLagouri, T. (2022). Review on Higgs Hidden–Dark Sector Physics at High-Energy Colliders. Symmetry, 14(7), 1299. https://doi.org/10.3390/sym14071299





