Abstract
The observation of gravitational waves from compact objects has now become an active part of observational astronomy. For a sound interpretation, one needs to compare such observations against detailed Numerical Relativity simulations, which are essential tools to explore the dynamics and physics of compact binary mergers. To date, essentially all simulation codes that solve the full set of Einstein’s equations are performed in the framework of Eulerian hydrodynamics. The exception is our recently developed Numerical Relativity code SPHINCS_BSSN which solves the commonly used BSSN formulation of the Einstein equations on a structured mesh and the matter equations via Lagrangian particles. We show here, for the first time, SPHINCS_BSSN neutron star merger simulations with piecewise polytropic approximations to four nuclear matter equations of state. In this set of neutron star merger simulations, we focus on perfectly symmetric binary systems that are irrotational and have 1.3 masses. We introduce some further methodological refinements (a new way of steering dissipation, an improved particle–mesh mapping), and we explore the impact of the exponent that enters in the calculation of the thermal pressure contribution. We find that it leaves a noticeable imprint on the gravitational wave amplitude (calculated via both quadrupole approximation and the formalism) and has a noticeable impact on the amount of dynamic ejecta. Consistent with earlier findings, we only find a few times as dynamic ejecta in the studied equal mass binary systems, with softer equations of state (which are more prone to shock formation) ejecting larger amounts of matter. In all of the cases, we see a credible high-velocity (∼) ejecta component of ∼ that is launched at contact from the interface between the two neutron stars. Such a high-velocity component has been suggested to produce an early, blue precursor to the main kilonova emission, and it could also potentially cause a kilonova afterglow.
1. Introduction
Detections of gravitational waves emitted during the violent collisions of compact objects are now routinely observed by ground-based gravitational wave detectors [1]. Especially if more than one messenger can be detected, such events offer unprecedented insights into the physics under the most extreme conditions: the dynamics of the last inspiral and subsequent merger stages are governed by the interplay of strong-field gravity and the equation of state at supra-nuclear densities [2]; weak interactions determine the neutrino emission and ejecta composition; see, e.g., [3,4,5,6,7,8,9,10,11]; magnetic fields that can rise to beyond magnetar field strengths [12,13,14] likely cause additional outflows and electromagnetic emission.
These violent multi-physics events can only be explored in a realistic way via full-blown numerical simulations. Thus, Numerical Relativity simulation codes have become valuable (but unfortunately, rather complicated) exploration tools. To date, there exists a “mono-culture” in the sense that practically all Numerical Relativity codes that solve the full set of Einstein equations make use of Eulerian hydrodynamics methods. We recently developed an alternative methodology [15,16] where we follow the conventional and well-tested approach to simulate the spacetime evolution via the BSSN formulation [17,18], but we evolve the fluid via freely moving Lagrangian particles. While the spacetime part is very similar to Eulerian approaches, the fluid part has additional advantages, in particular in following the material that becomes ejected in a neutron star merger. This material contains a small mass of only ∼1% of the binary system [19,20,21,22,23], but is responsible for all the electromagnetic emission and, therefore, of utmost importance for understanding the multi-messenger signals. Tracing these small amounts of matter with conventional Eulerian approaches is difficult, since (a) the accuracy of the advection of matter is resolution-dependent and the resolution away from the central collision site usually degrades substantially and (b) these methods employ artificial “atmospheres” to model the vacuum. The ejecta are expanding within these atmospheres, and this makes it hard to trace their properties with the desired accuracy. Within our particle approach, these challenges are absent since the vacuum simply corresponds to the absence of computational particles. Advection is exact in our approach: a property such as the electron fraction is attached to a particle, and it is therefore simply “carried around” as the particle moves, without any loss of information. Equally important is that, in our case, the neutron star surface remains perfectly well-behaved and does not need any special treatment, while it is a continuous source of concern in Eulerian neutron star simulations. There, the sharp transition between high-density and the vacuum, on a numerically difficult to resolve length scale, can easily lead to failures in recovering the primitive variables and to an effective reduction of the convergence order [24].
We recently presented our new SPHINCS_BSSN code [15], and we showed that it can accurately reproduce a number of challenging benchmark tests. These tests included standard hydrodynamics tests such as relativistic shock tubes, the oscillations of relativistic neutron stars, both in fixed (“Cowling approximation”) and dynamically evolving spacetimes, and the transition of an unstable neutron star either to a stable neutron star or to a black hole. In a recent paper [16], we introduced a number of new methodological elements in SPHINCS_BSSN, such as fixed mesh refinement, a new algorithm to transfer particle properties to the spacetime mesh, and we laid out in detail how we set up our fluid particles according to the “Artificial Pressure Method” (APM) [25] while making use of the library LORENE [26], using our new code SPHINCS_ID [16]. While we, for simplicity, used polytropic equations of state in the first two papers [15,16], we here adapt SPHINCS_BSSN to use piecewise polytropic approximations to nuclear equations of state [27].
The paper is structured as follows. In Section 2, we describe the methodology that we use, including the relativistic hydrodynamics, how we apply dissipation, evolve the spacetime, couple the spacetime and the matter, the equations of state that we use, and also summarize how our initial conditions are constructed. In Section 3, we present our results, starting with standard shocktube tests to demonstrate where our new steering algorithm triggers dissipation. We then show the dynamical evolution of our binary systems, their gravitational wave emission, and their dynamic mass ejection. In Section 4, we summarize the new methodological elements and discuss the main findings. Details of our recovery scheme for piecewise polytropic equations of state and some resolution experiments are shown in two appendices.
2. SPHINCS_BSSN
SPHINCS_BSSN (“Smooth Particle Hydrodynamics lN Curved Spacetime using BSSN”) [15,16] has become a rather complex code with a large number of methodological ingredients. Those parts where the current status was described already in detail in the first two papers will only be briefly summarized here, and we refer to the original publications for more information. In this paper, we include, for the first time in SPHINCS_BSSN, piecewise polytropic approximations to nuclear equations of state, and this requires a modification of our recovery algorithm; see Appendix A. We also explore the impact of the thermal component (more specifically of the thermal exponent ; see Appendix A), and we use a new way to steer dissipation in SPHINCS_BSSN that is based on [28,29].
2.1. Hydrodynamic Evolution
The hydrodynamic evolution equations are in SPHINCS_BSSN modeled via a high-accuracy version of the Smooth Particle Hydrodynamics (SPH) method. The basics of the relativistic SPH equations were derived very explicitly in Section 4.2 of [30], and we will refer to this text for many of the derivations and only present the final equations here. Many new, substantially accuracy-enhancing elements (kernels, gradient estimators, dissipation steering) were explored in [25,29,31], and most of them are also implemented in SPHINCS_BSSN.
We follow the conventions , use metric signature (−,+,+,+), and measure all energies in units of , where is the average baryon mass. This quantity depends on the actual nuclear composition, but simply using the atomic mass unit gives a precision of better than 1%. We, therefore, use the approximation in the following. Greek indices run from 0 to 3 and Latin indices from 1 to 3. Contravariant spatial indices of a vector quantity at particle a are denoted as , while covariant ones will be written as .
To discretize our fluid equations, we chose a “computing frame” in which the computations are performed. Quantities in this frame usually differ from those calculated in the local fluid rest frame. The line element in a 3 + 1 split of spacetime reads
where is the lapse function, the shift vector, and the spatial three-metric. We use a generalized Lorentz factor:
the coordinate velocities are related to the four-velocities, normalized as , by
We choose the computing frame baryon number density N as the density variable, which is related to the baryon number density as measured in the local fluid rest frame, n, by
Here, g is the determinant of the spacetime metric. Note that this density variable is very similar to what is used in Eulerian approaches [32,33,34,35]. We keep the baryon number of each SPH particle, , constant so that exact numerical baryon number conservation is guaranteed. At every time step, the computing frame baryon number density at the position of a particle a is calculated via a weighted sum (actually very similar to Newtonian SPH):
where the smoothing length characterizes the support size of the SPH smoothing kernel W. As momentum variable, we choose the canonical momentum per baryon
where is the relativistic enthalpy per baryon with u being the internal energy per baryon and P the gas pressure. This quantity evolves according to
where the hydrodynamic part is
and the gravitational part
Here, we used the abbreviations
and is a shorthand for . As the energy variable, we use, the canonical energy per baryon
which is evolved according to
with
and
Note that the hydrodynamics part of the momentum equation, Equation (8), looks very similar to the Newtonian momentum equation and possesses, in particular, the same symmetries in the particle labeling indices a and b: exchanging these indices, , leads to a sign change due to the anti-symmetry of the kernel gradient, , which, in the Newtonian and fixed-metric case, ensures in a straightforward way the exact conservation of momentum; see Section 2.4 in [30] for a detailed discussion of the anti-symmetry of kernel gradients in relation to exact numerical conservation. The hydrodynamic part of the energy equation, Equation (13), in turn, looks very similar to the Newtonian evolution equation of the “thermo-kinetic” energy, ; see Equation (34) in [30]. For the involved kernel function, we used the Wendland C6-smooth kernel [36]:
where the normalization is in 3D and the symbol denotes the cutoff function max . Our kernel choice is based on ample previous experiments [25,29], and we chose (at every Runge–Kutta substep) the smoothing length so that every particle a has exactly 300 neighbors in its own support of radius . Technically, this is achieved via a very fast tree method [37]; more details on how this is done in practice can be found in [25]. Note that this version of the relativistic SPH equations is very similar to the Newtonian case, and it has the additional advantage over older relativistic SPH formulations [38] that it does not involve numerically inconvenient terms such as time derivatives of Lorentz factors. The quantities that we evolve numerically, however, are not the physical quantities that we are interested in, and we, therefore, have to recover the physical quantities n, u, , P from N, , e at every integration (sub-)step. This “recovery step“ is performed in a very similar way as in Eulerian approaches; for the case of polytropic equations of state, our strategy is described in detail in Section 2.2.4 of [15]. One of the new elements of SPHINCS_BSSN that we introduce here is the use of piecewise polytropic equations of state that also contain a thermal pressure contribution. This requires a modified approach for the recovery that we describe in detail in Appendix A.
2.1.1. Dissipative Terms
To deal with shocks, we have to include dissipative terms. We followed the approach originally suggested by von Neumann and Richtmyer [39], which simply consists of everywhere replacing the physical pressure P with , where Q is a suitable viscous pressure. Our prescription used here does not differ substantially from the original paper [15], but since we carefully gauge the involved parameters, we will briefly summarize the basic equations for the ease of the subsequent discussion.
For the form of the viscous pressure, we followed [40] and used
The are the fluid velocities seen by an Eulerian observer, , projected onto the line connecting two particles a and b, ,
the corresponding expression with indices a and b interchanged applies for , and the parameter determines the amount of dissipation. For the signal speeds, we used
where is the relativistic sound speed, being the polytropic exponent, and
We also included a small amount of artificial conductivity by adding the following term to Equation (13):
where the are the lapse functions at the particle positions and . Apart from the limiter (see below), this expression is the same as in [40]. For the conductivity signal velocity, we use [40]
for cases when the metric is known (i.e., cases where no consistent hydrostatic equilibrium needs to be maintained) and otherwise. The prefactor was chosen after extensive experiments with shock tubes and a single neutron star, and we found good results for . The role of the limiter is to restrict the application of conductivity to regions that have large second derivatives and to suppress it elsewhere. In [15], we designed a simple dimensionless trigger aimed at quantifying the size of second-derivative effects:
where and , and the final conductivity limiter reads
The reference value 0.2 was chosen after experiments in both Sod-type shock tubes and self-gravitating neutron stars.
2.1.2. Slope-Limited Reconstruction in the Dissipative Terms
As demonstrated in a Newtonian context [25,41,42], slope-limited reconstruction can be very successfully applied within an artificial viscosity approach, and we also follow such a strategy here. In our earlier experiments [25], reconstruction massively suppressed unwanted effects of artificial dissipation. Instead of using in Equations (16) and (17), we reconstruct the velocities seen by an Eulerian observer of both particle a and b to their common mid-point, :
projected them onto the line joining particle a and b as in Equation (18), calculated the corresponding Lorentz factors, and used products based on the reconstructed values instead of . For the slope limiter , we used a modification of the minmod limiter:
where is the original minmod limiter:
The quantity in the exponential suppression factor is given by with . Our aim is to have a close-to-uniform particle distribution within the kernel support, and the purpose of the exponential factor in Equation (26) is to suppress reconstruction for particles that come closer than a (de-dimensionalized) critical separation . For this separation, we choose the typical separation of a uniform distribution of particles inside a sphere with the volume of the support, , which yields
Particles that come closer than have their reconstruction suppressed (i.e., SL going to zero) and, therefore, more dissipation, which has an ordering effect. For the fall-off scale, , we followed [42] and used their suggested value of 0.2. In practice, the exponential suppression factor has only a very small, though welcome, effect.
2.1.3. Steering the Dissipation Parameter
We applied here a dissipation steering strategy that is different from before [15,16]. Apart from enjoying the exploration of a new strategy, the main reason for this is that it liberates us from the need to define a suitable entropy variable. While this is easy for simple equations of state and delivers very good results [31], it leads to an unnecessary dependence between our dissipation scheme and the—in principle—completely unrelated equation of state/microphysics modules. A decoupling of different parts of the code is good coding practice and, in particular, desirable with regard to our future development plans that include the implementation of different, microphysical equations of state: with an independent steering mechanism, no modifications are needed when the microphysics is updated. We had previously compared an entropy-based steering mechanism with one that is based on a -steering similar to the one we use here [31]. Overall, we found very good agreement between both approaches, but slight advantages for the entropy-steering.
We want to apply dissipation only where it is needed, and to do so, we followed a variant of the strategies suggested in [28,29]. We calculated at each time step and for each particle a desired value for the dissipation parameter, and if the current value at a particle a, , is larger than , we let it decay exponentially according to
where is the particle’s dynamical time scale and is a low floor value. Otherwise, if , the value of is instantaneously raised to .
In determining the desired dissipation value , we applied two criteria, one for detecting shocks yielding and another one for detecting noise yielding , and we used . We monitored compressions that increase in time to detect shocks [28] (for the ease of notation, we omitted a particle-labeling index):
where
and is the maximally reachable dissipation parameter. Note that in Equation (30), we conservatively used a smaller prefactor (=0.1) than what is suggested in [28] (=0.25), so dissipation is increased more aggressively if an increasing compression is detected. While this works very well, it may mean that in the current set of simulations, we are applying somewhat more dissipation than is actually needed. This issue will be explored in future work, where we will try to reduce the dissipation further. Our second criterion is based on fluctuations in the sign of to detect local noise (as suggested in the special relativistic version SPHINCS_SR, [29]):
where the noise trigger is
and
and are the number of positive/negative contributions. The noise trigger is the product of two quantities, so if there are sign fluctuations, but they are small compared to , then is close to zero. If instead, we have a uniform expansion or compression, either or will be zero and, therefore, also the noise trigger. Therefore, only for sign fluctuations and significantly large compressions/expansions will the product have a substantial value and, thus, trigger a dissipation increase.
In all of the simulations shown in this paper, we use a floor value and a maximum dissipation parameter , which yields good results in shocktube tests; see below. As a side remark, we mention that [28] promoted using a vanishing floor value , and we will explore a possible reduction of this parameter in future work.
2.2. Spacetime Evolution
We evolve the spacetime according to the (“-version” of the) BSSN equations [17,18]. For this, we wrote a wrapper around the code extracted from the McLachlan thorn [43] of the Einstein Toolkit [44,45]. The variables used in this method are related to the Arnowitt–Deser–Misner (ADM) variables (three-metric), (extrinsic curvature), (lapse function), and (shift vector), and they read
where , are the Christoffel symbols related to the conformal metric and is the conformally rescaled, traceless part of the extrinsic curvature. The corresponding evolution equations read
where
and denote partial derivatives that are upwinded based on the shift vector. The superscript “TF” in the evolution equation of denotes the trace-free part of the bracketed term. Finally, , where
The derivatives on the right-hand side of the BSSN equations are evaluated via standard Finite Differencing techniques, and unless mentioned otherwise, we use sixth-order differencing as a default. We recently implemented a fixed mesh refinement for the spacetime evolution, which was described in detail in [16], to which we refer the interested reader. For the gauge choices, we use a variant of 1+log-slicing, where the lapse is evolved according to
and a variant of the -driver shift evolution with
2.3. Coupling between Fluid and Spacetime
The hydrodynamic equations need the spacetime metric and their derivatives (known on the mesh; see Equations (9) and (14)), and the BSSN equations need the energy momentum tensor (known on the particles). We therefore need an accurate and efficient mapping between the particles and mesh. In the “mesh-to-particle” step, we use a quintic Hermite interpolation, which is described in detail in Section 2.4 of [15]. For the “particle-to-mesh” step, we use a hierarchy of sophisticated kernels that have been developed in the context of “vortex methods” [46,47]. For relatively uniformly distributed particles, these kernels deliver results of excellent accuracy, but since they are (contrary to SPH kernels) not positive definite, they can deliver unphysical results, if, for example, they are applied across a sharp edge such as a neutron star surface.
For this reason, we developed a “multi-dimensional optimal order detection” (MOOD) strategy, where we calculated the results with three kernels of different accuracy, [47], and [46]. For (close to) uniform particle distributions, is most and is least accurate. Out of those kernels, only is positive definite, and it serves as a robust “parachute” for the cases for which the more accurate kernels should deliver unacceptable results (e.g., because they are applied across a sharp neutron star surface). The main idea is to choose the most accurate kernel that is still “admissible”. In our previous paper [16], we considered a mapping as “admissible” if all of the -components at a grid point g, , are bracketed by the values of the contributing particles; see Section 2.1.3 of [16]. Here, we refined the admissibility criterion further. At each grid point g, we calculated for each mapping option K (i.e., or ) how well the value agrees with the ones of the nearby SPH particles (labeled by b). More concretely, we chose the mapping option K that minimizes the expression
where b runs over all particles in the kernel support. The first term is just the squared relative energy density error, where the particle -value is used for the normalization since it is guaranteed to be non-zero. The quantity in the tensor product weight is given by . The mapping option with the smallest value of is then selected.
Clearly, this error measure is not unique, and we ran many neutron star merger experiments with alternative error measures (e.g., using different kernels for the weight, using spherical kernels rather than tensor products, etc.). While the differences were overall only moderate, the above error measure provided the smoothest results. Compared to our previous “bracketing criterion”, the new admissibility criterion based on the above error measure delivers overall similar, but somewhat smoother results.
2.4. Equations of State
In our first exploration of neutron star mergers [16], we restricted ourselves to polytropic Equations Of State (EOSs); here, we take a first step towards more realistic EOSs. We used piecewise polytropic EOSs to approximate microscopic models of cold nuclear matter [27], and we added a thermal, ideal gas-type contribution to both pressure and specific internal energy, a common practice in Numerical Relativity simulations. The explicit form of the equation of state and the recovery algorithm are explained in detail in Appendix A.
In this first SPHINCS_BSSN study with piecewise polytropic equations of state, we restrict ourselves to the following equations of state
- SLy [48]: with a maximum TOV mass , tidal deformability of a 1.4 star
- APR3 [49]: ,
- MPA1 [50]: ,
- MS1b [51]: , .
For the tidal deformabilities, we have quoted the numbers from Table 1 of [52]. For all cases, we use the piecewise polytropic fit according to Table III in [27], and we use a thermal polytropic exponent as a default; however, for one EOS (MPA1), we also used values of 1.5 and 2.0 to explore its impact on the evolution.
Given the observed mass of 2.08 for J0740+6620 [53], the SLy EOS is still above the lower bound of 1.94 , but probably too soft, and we consider it as a limiting case. Concerning the currently “best guess” of the maximum neutron star mass, a number of indirect arguments point to values of ∼2.2–2.4 [54,55,56,57,58], and a recent Bayesian study [59] suggests a maximum TOV mass of 2.52 , close to the values of APR3 and MPA1. We therefore consider these two EOSs as the most realistic ones in our selection, which is also consistent with the findings of [52]. The MS1b EOS with its very high maximum mass of 2.78 brackets our selection on the stiffer end. While its maximum TOV mass is already close to the often quoted upper limit of ∼3 [60,61], it is worth keeping in mind that the upper limit (from causality constraints alone and assuming that nuclear matter is only known close to saturation density) could be as large as 4.2 [62]. However, since its tidal deformability is disfavored by the observation GW170817 [63], we consider MS1b as a limiting case.
2.5. Constructing Initial Data for Binary Neutron Stars
To perform simulations of neutron star mergers, we need Initial Data (ID) that both satisfy the constraint equations and accurately describe the binary systems that we are interested in. Constructing ID for SPHINCS_BSSN consists of two parts: (a) solving the general relativistic constraint equations for the standard 3 + 1 variables using the library LORENE [26] and (b) placing our SPH particles so that they represent the matter distribution found by LORENE. This second step is actually non-trivial since the particle setup should—apart from representing the LORENE matter distribution—fulfil a number of additional requirements: (a) the particles should ideally have the same masses since large differences can lead to numerical noise; (b) the particles should be locally very ordered so that they provide a good interpolation accuracy; (c) however, the particles should not be on a lattice with preferred directions (as most simple lattices have), since this can lead to artifacts, e.g., for shocks traveling along those axes.
All these issues are addressed in the “Artificial Pressure Method” (APM) [25]. The main idea of this method is to place equal mass particles in an initial guess and then let the particles themselves find the position where they best approximate a given density profile (here, provided by LORENE). This is achieved in an iterative process where, at each step, the current density is measured and compared to the desired profile density. We used the relative error between both to define an “artificial pressure”, which is then applied in a position update prescription that is derived from an SPH momentum equation. In other words, at each step, each particle measures its own, current density error and then moves in a direction that reduces it. The method was initially suggested in a Newtonian context [25], then translated to a General Relativistic context to accurately construct neutron stars [15]. More recently [16], it was adapted to model binary neutron star systems where it has delivered accurate General Relativistic SPH initial conditions. The construction of APM particle distributions for binary neutron stars has been implemented in our code SPHINCS_ID, already used in [16]. By now, SPHINCS_ID has been improved so that it can also easily be extended to produce BSSN and SPH initial data for other astrophysical systems.
2.6. Summary of the New Elements
In summary, the new elements described in this study are:
- We enhance the slope limiter used in the reconstruction (minmod) by an exponential suppression term that enhances the dissipation for those rare cases where particles should get too close to each other; see Section 2.1.2. The effect of this change is only tiny, but we mention it for completeness.
- We trigger dissipation based on a shock indicator similar to [28] and a noise indicator suggested for the SPHINCS_SR code [29]; see Section 2.1.3.
- As in our previous study [16], we use a MOOD approach to decide which kernel to use in the mapping, but here, we use a more sophisticated acceptance measure; see our Section 2.3.
- We use, for the first time in SPHINCS_BSSN, piecewise polytropic approximations to nuclear equations of state. These fits to cold nuclear matter equations of state are enhanced by thermal pressure contributions; see Appendix A for a detailed description.
3. Results
After our initial code papers [15,16], we take here our next step towards more realistic simulations of neutron star mergers: we used piecewise polytropic approximations to nuclear matter equations of state. These first SPHINCS_BSSN simulations of such mergers are the main topic, but since we also implemented a new dissipation steering, we demonstrate how it works in a first “shocktube” section.
3.1. Shock Tube
This test is a relativistic version of “Sod’s shocktube” [64], which has become a standard benchmark for relativistic hydrodynamics codes [65,66,67,68,69,70]. Apart from demonstrating that our code solves the relativistic hydrodynamics equations correctly, we used this test here also to show where our steering method (see Section 2.1.3) triggers dissipation.
The test uses a polytropic exponent and as initial conditions
with velocities initially being zero everywhere. We placed particles with equal baryon numbers on close-packed lattices as described in [29], so that on the left side, the particle spacing is , and we have 12 particles in both the y- and z-direction. This test was performed with the full GR-code in a fixed Minkowski metric. The result at is shown in Figure 1 with the SPHINCS_BSSN results marked with blue squares and the exact solution [69] with the red line.
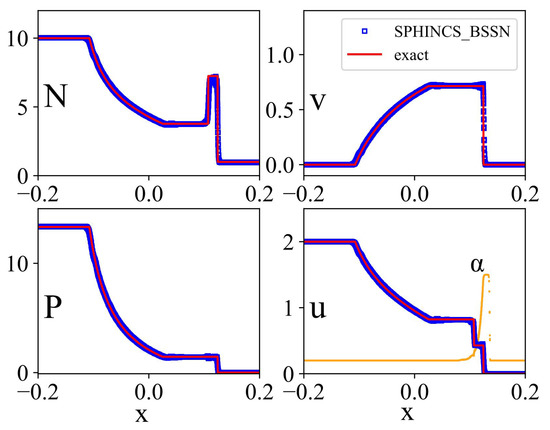
Figure 1.
Results for the 3D, relativistic shocktube test. Shown are the result (density, velocity, pressure, and internal energy; ) for our default choices; the orange dots in the “u” panel show values of the dissipation parameter . Dissipation robustly switches on ahead of the shock front, remains approximately constant around the shock front, and decays quickly in the post-shock region.
The SPHINCS_BSSN results (blue squares) are in very good agreement with the exact solution (red line). In the fourth sub-panel, we show in orange the dissipation parameter . It abruptly switches to just ahead of the shock front, stays constant around it, and decays in the post-shock region very quickly to the floor value. Overall, we have a very good agreement with the exact solution. Only directly behind the shock front (e.g., in velocity and density) is a small amount of noise visible. This is to some extent unavoidable, since the particles try to optimize their local distribution (see, e.g., Section 3.2.3 in [71]) and need to transition from their initial arrangement into a new one.
We also experimented with other slope limiters (van Leer [72], van Leer Monotonized Central [72], and superbee [73]), but all of them showed an increased velocity overshoot at the shock front and no obvious other advantage. We therefore settled on the minmod limiter; however, we do not expect to see substantial differences when other slope limiters are used, and this was also confirmed by a number of additional merger test simulations (not discussed further here).
For more special relativistic benchmark tests with SPH, the interested reader is referred to [29,74,75].
3.2. Binary Mergers
3.2.1. Performed Simulations
Our performed simulations are summarized in Table 1. We performed for each EOS several runs with at least two different resolutions (one and two million SPH particles; for the grid resolution, see below), and for a case where the cold nuclear part corresponds to the MPA1 EOS, we also varied the thermal exponent . For our presumably most realistic EOSs, MPA1 and APR3, we also performed runs with five million particles, but we note that these runs are extremely expensive for our current simulation technology and were therefore not run for as long as the other cases. For the very compact stars resulting from the SLy EOS, our current resolution may be at the lower end, especially for the one million case, and the corresponding results should be taken with a grain of salt. This case will be re-assessed in future, better resolved simulations.

Table 1.
Simulated binary systems. All binaries are irrotational and have twice 1.3 (gravitational mass of each star in the binary system), and the simulations start from an initial separation of 45 km. Unless mentioned otherwise, the thermal exponent is used. refers to the finest grid resolution length; is the minimum resolution length (=smoothing length) in the hydrodynamic evolution.
For the spacetime evolution, we employ seven levels of fixed mesh refinement with the outer boundaries in each coordinate direction at ≈2268 km and 143, 193, and 291 grid points in each direction for the 1, 2, and 5 million SPH particle runs. The corresponding resolution lengths of our finest grids, , are shown in the fourth column of Table 1. Note that due to the approach chosen in SPHINCS_BSSN, we have the freedom to choose different resolutions for the spacetime and the hydrodynamics. For example, if the spacetime is not too strongly curved, say, for a neutron star with a rather stiff equation of state, we may obtain reasonably accurate results with only a moderate grid resolution. In such cases, we can instead invest the available computational resources in a higher hydrodynamic resolution, i.e., in larger SPH particle numbers. Since all our simulation technology is very new, the relative resolutions are still to some extent a matter of experiment. This is discussed in more detail in Appendix B. The minimum smoothing lengths reached in each simulation, , are also shown in Table 1 as a measure of the hydrodynamical resolution length. Note that today’s state-of-the-art Eulerian simulations typically have a smaller finest grid length (e.g., [76] use 185 m), but our hydrodynamic resolution length can go substantially below such length scales; see Table 1.
3.2.2. Dynamical Evolution
In Figure 2, we show the density evolution in the orbital plane for each EOS, every time showing the two million particle runs (i.e., for MPA1_2mio, APR3_2mio, SLy_2mio, MS1b_2mio; see Table 1) at 1.57, 3.55 and 5.52 ms after merger (defined as the time of peak GW amplitude). As expected, the EOS has a fair impact on the last inspiral stages where tidal effects accelerate the motion and lead to an earlier merger at lower frequencies as compared to systems without tidal effects (i.e., black hole mergers); see, e.g., [77,78,79].
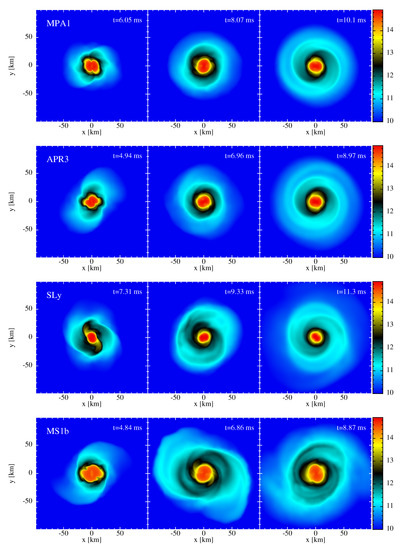
Figure 2.
Density evolution (top to bottom row) for the MPA1, APR3, SLy, and MS1b EOSs. Each time, the run with 2 million particles (see Table 1) is shown. For each EOS case, the times are chosen so that they correspond to 1.57, 3.55, and 5.52 ms after merger (defined as the time of peak GW amplitude).
Our softest EOS, SLy, produces the most compact remnant and undergoes very deep oscillations (see Figure 3), with the density in the remnant settling to more than twice the initial stellar density. Our two arguably most realistic EOSs, MPA1 and APR3, look morphologically very similar (see the first two rows in Figure 2), but also, their peak density and minimum lapse evolution look alike: they show a first, dominant compression (density increase ∼20–25%), and then, within a couple of oscillation periods, they settle onto a final central density, which is approximately the same as the first compression spike. The extremely stiff MS1b EOS shows a qualitatively similar peak density/lapse evolution, though at substantially lower densities/higher lapse values. Interestingly, none of the explored cases seem close to a collapse to a black hole; even the soft SLy EOS cases settles to a minimum lapse value of . As a rule of thumb, systems with central lapses dropping below are doomed to collapse to a black hole; see, for example, [80] or Figure 16 in our first SPHINCS_BSSN paper [15], which shows the shape of the lapse function when an apparent horizon is detected for the first time.
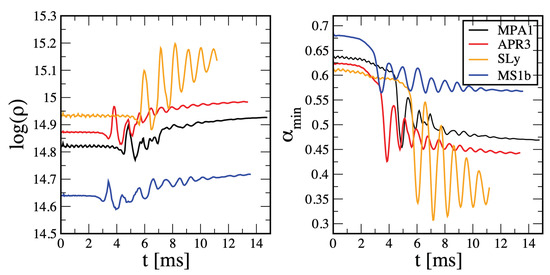
Figure 3.
Maximum density (in g cm) and minimum lapse value for the runs with 2 million particles (i.e., runs MPA1_2mio, APR3_2mio, SLy_2mio, and MS1b_2mio; see Table 1).
We also monitored the quantity , the (baryonic) mass of matter with a density smaller than g cm minus the ejected mass (see below), which we consider as a proxy for the resulting torus mass. The astrophysical relevance of the torus mass stems from its role as an energy reservoir for powering short GRBs after the collapse to a BH [81,82,83], but also since % of this mass can potentially become unbound [84,85,86,87,88,89], and therefore likely contributes the lion’s share of the ejecta budget of a neutron star merger.
We show the temporal evolution of in Figure 4. None of the simulations seem to have reached a stationary state yet; all of them keep shedding mass into the torus, but all have already reached a torus mass exceeding 0.15 . Thus, assuming an efficiency to translate this rest mass energy reservoir into radiation, bursts with a (true) energy of > could be reached. If a fraction of of the initial torus becomes unbound, one can expect neutron-rich ejecta of >, roughly consistent with the estimates for GW170817 [90,91,92,93,94,95,96].
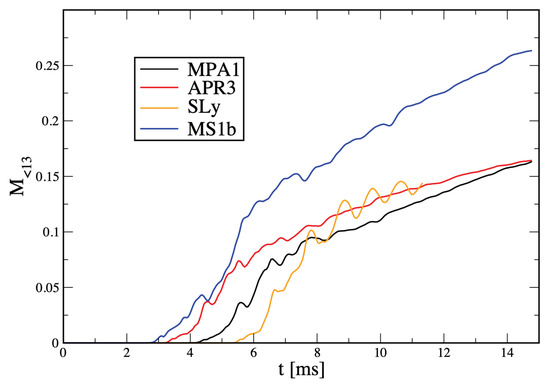
Figure 4.
Disk mass evolution for the runs with 2 million particles (i.e., runs MPA1_2mio, APR3_2mio, SLy_2mio; and MS1b_2mio; see Table 1).
3.2.3. Impact of the Thermal Index
Our treatment of thermal effects by adding an ideal gas-type pressure with a thermal index (see Appendix A) is clearly very simple, and recently, more sophisticated approaches have been developed [97,98]. In particular, if thermal effects are to be described via such an ideal gas-type index , it should vary with the local physical conditions (e.g., density). To test for the impact of , we performed two additional runs (2 with the MPA1 EOS) where we used, apart from our default choice , also the values 1.5 and 2.0. The morphology of these runs is shown in Figure 5. While the impact of on the mass distribution is overall moderate, it has some noticeable impact on the spacetime evolution, as illustrated with the minimum lapse value shown in Figure 6, left panel. To get a feeling for the effects of resolution, we plot in the right panel also the MPA1 case for three different resolutions. Smaller values of make the EOS overall more compressible, which leads to larger amplitude oscillations in the minimum lapse. Since these oscillations go along with mass shedding, there is also some impact of on the amount of ejected mass; see below.
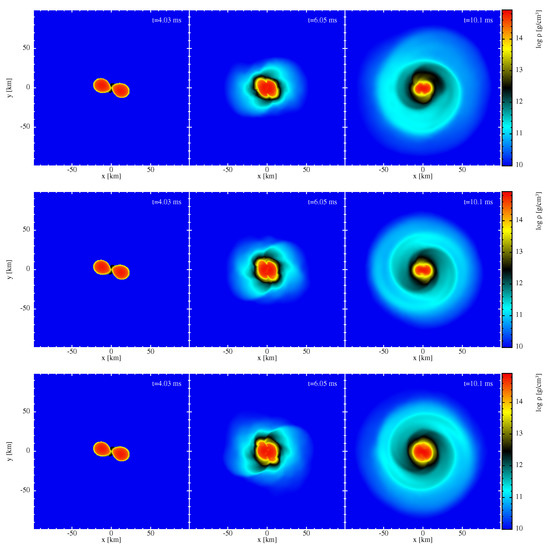
Figure 5.
Impact of the thermal exponent on the evolution. Shown is a binary merger with 2 × 13, , the MPA1 EOS, and , 1.75, and 2.0 (top to bottom row).
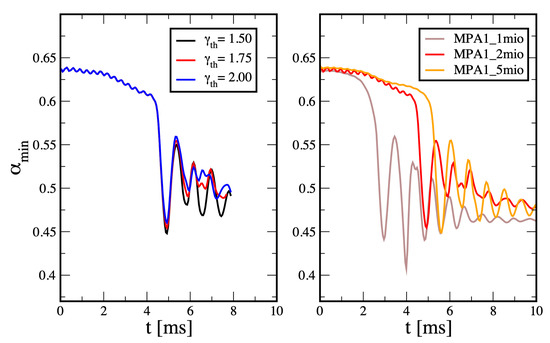
Figure 6.
Comparison of the evolution of the minimal lapse value (2 × 1.3 , MPA1 EOS) for different thermal exponents (left) and different resolutions (right).
3.2.4. The Triggering of Artificial Dissipation
To demonstrate where dissipation is triggered in a neutron star merger, we show in Figure 7 the values of the dissipation parameter for simulation MS1b_2mio. The left panel shows the dissipation parameters at the end of the inspiral, just before merger. At this stage, nearly all of the matter has dissipation parameters very close the floor value (here, ); only particles in a thin surface layer (e.g., at the cusps) have moderately larger values. As a side remark, we want to point out how well-behaved the surfaces of the neutron stars are. Contrary to Eulerian hydrodynamics, in our approach, no special treatment of the surface layers is needed; the corresponding particles are treated exactly as all the other particles. Inside the stars, the dissipation parameter values hardly increase above the floor value, not even during the merger, but the particles that are “squeezed out” of the shear layer between the stars have values . Since their sound speed drops rapidly during the decompression, their dissipation values only slowly decay towards lower values; see Equation (29). As mentioned above, we chose our dissipation triggers conservatively, so that likely more dissipation is triggered than is actually needed. A possible reduction will be explored in future work.
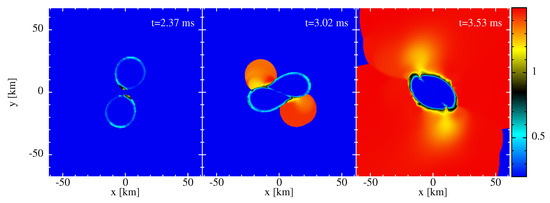
Figure 7.
Evolution of the dissipation parameter in simulation MS1b_2mio; see Table 1.
3.2.5. Gravitational Wave Emission
We extracted gravitational waves from our simulations via the quadrupole formula (using particle information only), as well as directly from the spacetime by calculating the Newman–Penrose–Weyl scalar (both methods are described in Appendix A in [16]). After (decomposed into spin weight -2 spherical harmonics) was extracted at a coordinate radius of , we used the built-in functionality in kuibit [99] to reconstruct the strain by integrating twice in time (performed in the frequency domain). In order to compare with the waveform extracted with the quadrupole formula, we evaluated the sum of multipoles at the orientation that gives the maximal signal and shifted the waveform in time in order to align the peak amplitudes to account for the difference that the waveform has to propagate from the source to the detector, whereas the quadrupole waveform is extracted at the source.
In Figure 8, we show the extracted gravitational wave signals for the four different equations of state considered here: MPA1 (top left) with thermal component , APR3 (top right), MS1b (bottom left), and SLy (bottom right) extracted from the simulations with two million particles. As can be seen, the quadrupole formula does a good job in tracking the phase of the waves, but typically underestimates (by up to 60%) the amplitude of the waveform. As mentioned earlier, the larger tidal effects with harder equations of state lead to a faster inspiral and an earlier merger. This is clearly also an effect that is visible in the waveforms, where the SLy (the softest EOS) waveform has a significantly longer inspiral part and the MS1b (the hardest EOS) waveform has the shortest inspiral part. In the post-merger part of the waveform, it is also clear that the amplitude of the wave is larger for softer equations of state.
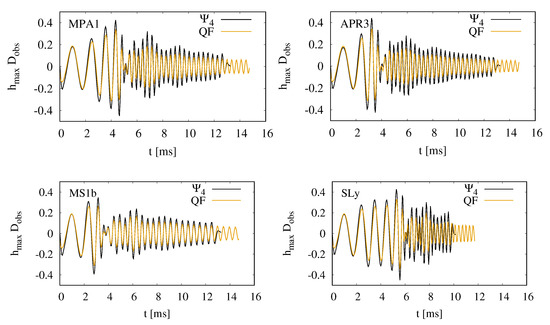
Figure 8.
The extracted gravitational wave signals for the four different equations of state considered here: MPA1 (top left, MPA1_2mio), APR3 (top right, APR3_2mio), MS1b (bottom left, MS1b_2mio), and SLy (bottom right, SLy_2mio). Both the spacetime-extracted (black) and quadrupole (QF; orange) waveforms are shown. The waveform was aligned with the quadrupole waveform by shifting it in time and, hence, appears to be shorter. The waveforms appear to go to zero at the end. This is purely an artifact of the windowing that was applied for the time integration of .
In Figure 9, we show the extracted gravitational wave signal for MPA1 (with ) at three different resolutions (1, 2, and 5 million particles). As can be seen, the effect of low resolution (and higher dissipation) is to drive the neutron stars to faster mergers. In addition, there is also a rapid decay in gravitational wave amplitude in the post-merger phase at low resolution. It is clear that we have not quite reached convergence in these simulations, even at the highest resolution, but it is encouraging to see that the differences between the two lower resolution simulations are much larger than the differences between the two higher resolutions.
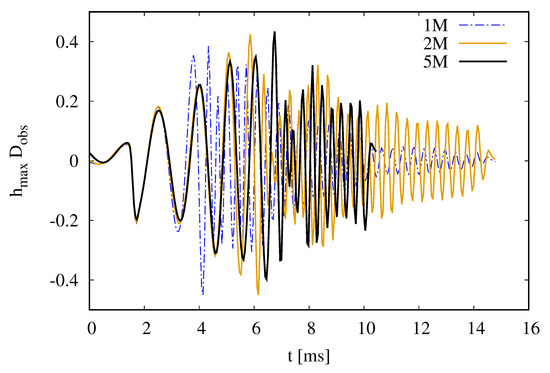
Figure 9.
The extracted gravitational wave signals for MPA1 for simulations with 1 million (dashed blue, MPA1_1mio), 2 million (solid orange, MPA1_2mio), and 5 million (solid black, MPA1_5mio) particles. Notice that the 5 million particle simulation was not run for quite as long as the lower-resolution simulations due to its higher computational cost.
We checked that the recent changes to the code did not alter the convergence properties in any significant way compared to our recent study [16]. We find that the constraint violation behavior is virtually identical to what we found there, and we therefore refer the interested reader to Figure 12 of that study. From that plot, the conclusion is that the convergence of the Hamiltonian constraint is consistent with second order.
In Figure 10, we explore the effect of the different thermal components on the extracted gravitational waveform for the two million particle simulations with the MPA1 EOS and , and . As expected, the thermal component does not make a difference during the inspiral as the waveforms are practically indistinguishable before the merger. Interestingly, after the merger, the softer simulation shows a significantly faster decay of the gravitational wave signal than the harder ones.
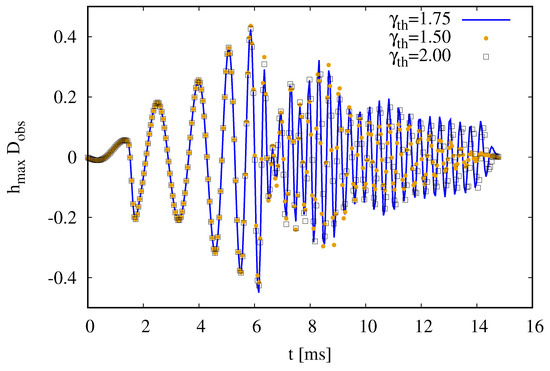
Figure 10.
The extracted gravitational wave signals for MPA1 with different thermal components . Our default, , is shown with a solid blue line; is shown with orange filled dots; is shown with black empty squares.
In Figure 11, we plot the amplitude of the Fourier transform of the dominant ℓ = 2, m = 2 mode of the strain as computed from for the four different EOS considered here in the left panel, whereas the right panel shows the spectra for the MPA1 EOS with different thermal components. In both plots, the solid lines show the Fourier transforms of the full waveforms, while the dashed lines show the Fourier transforms of the post-merger part of the waveforms only. Consistent with findings reported in the literature [100,101,102,103,104,105,106,107,108], the spectra at low (<1 kHz) frequencies are dominated by the inspiral with increasing amplitude up to a maximum at the frequency of the binary at the merger. This feature is absent in the post-merger spectra. For all the different EOS, the spectra show a dominant peak at higher frequency, and the location of that peak is strongly dependent on the EOS. The softer the EOS, the higher the frequency with values ranging from about kHZ for MS1b to kHz for SLy. For the softest EOS (SLy), there is clear evidence of sub-dominant peaks (also reported in the literature) at both lower and higher frequency separated from the dominant peak by about kHz.
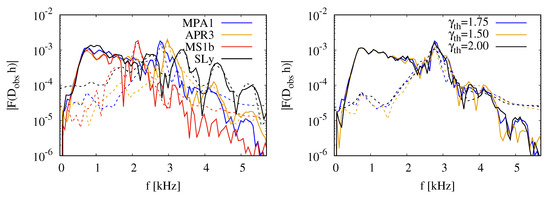
Figure 11.
Fourier spectra of the dominant mode of the strain for MPA1 (), for APR3, MS1b, and SLy (left panel), and for MPA1 (, and ) (right panel). In both cases, the solid lines shows the spectra of the full waveforms, while the dashed lines show the spectra of the post-merger waveforms only.
In Table III of [109], several peak frequencies (in the authors’ convention , the instantaneous frequency at maximal GW amplitude, , the first sub-dominant peak after merger, and , the dominant peak after merger), are reported for a number of different equations of state and masses of the binary systems. In particular, their SLy-q10-M1300 case is very similar to one of our systems (but, they used a rather our value of 1.75). Unfortunately, this is our softest equation of state that has the highest resolution requirements and, hence, is our least-trusted case. Nevertheless, we found frequencies that are in reasonable agreement. For and , we do see only small differences between the values extracted from our low- and medium-resolution runs. We found kHz and kHz for one million particles and kHZ and kHz for two million particles. These are slightly larger than the kHz and kHz values reported in [109]. On the other hand, we found substantial differences in the value for at the two different values with kHZ for one million particles and kHz for two million particles. This is to be compared with a value of kHZ in [109]. We suspect that these values are quite sensitive to the details of the inspiral, and at current resolutions, we still see significant differences for the SLy equation of state. Note that we did not use the fitting procedure described in [109] to extract the and frequency peaks, but simply found the peaks numerically from the raw power spectral density.
Turning now to a comparison of the spectra for MPA1 with different thermal components (right plot), it is clear that there is very little dependence of the location of the dominant peak with . However, consistent with the rapid decay of the post-merger waveform for , in Figure 10, we do see a smaller amplitude of the peak for that case.
3.2.6. Ejecta
The ejection of neutron-rich matter is arguably one of most important aspects of a neutron star merger [19,21,22,23,110]; it is responsible for enriching the cosmos with heavy elements and for all of the electromagnetic emission. To identify ejecta, we applied two basic criteria, the “geodesic criterion” and the “Bernoulli criterion”, both of which can be augmented by additional conditions (e.g., an outward pointing radial velocity). The geodesic criterion assumes that a fluid element is moving along a geodesic in a time-independent, asymptotically flat spacetime, e.g., [22,111]. Under these assumptions, corresponds to the Lorentz factor of the fluid element at spatial infinity, and therefore, a fluid element with
is considered as unbounded since it still has a finite velocity. In practice, however, this criterion ignores potential further acceleration due to internal energy degrees of freedom, and we therefore consider the results from the geodesic criterion as a lower limit.
The internal degrees of freedom are included in the Bernoulli criterion (see, e.g., [34]), which multiplies the left-hand side of the above criterion with the specific enthalpy:
To avoid falsely identifying hot matter near the center as unbounded, we applied the Bernoulli criterion only to matter outside of a coordinate radius of 100 (≈150 km). We find very good agreement between both criteria, with the Bernoulli criterion identifying only a slightly larger amount of unbound mass. This is illustrated in Figure 12 for run APR3_2mio. In the following, we only use the above described version of the Bernoulli criterion. The ejecta will undergo r-process nucleosynthesis and, at later times, radioactive decay. This additional energy input can unbind otherwise nearly unbound matter and may therefore further enhance the amount of unbound mass.
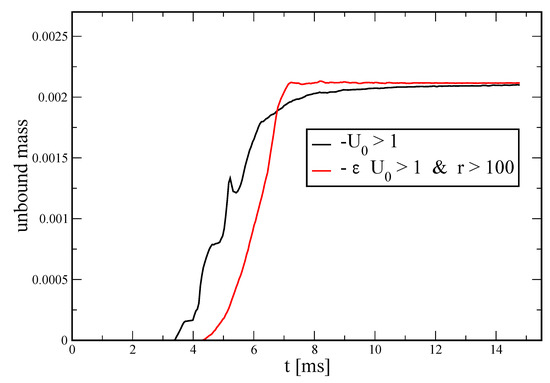
Figure 12.
Comparison of the “geodesic” and the (slightly modified) “Bernoulli” criterion to identify unbound mass.
The ejecta mass and average velocities for our runs are summarized in Table 2. Consistent with other studies (e.g., [21,22,23]), we found that the studied equal mass systems eject only a few times dynamically, i.e., the dynamical ejecta channel falls short by about an order of magnitude in reproducing the ejecta amounts that have been inferred from GW170817 [90,91,92,93,94,95,96]. While part of these large inferred masses may be explained by the fact that the interpretations of the observations largely neglect the 3D ejecta geometry and assume sphericity instead [112], it seems obvious that complementary ejecta channels are needed.

Table 2.
Dynamical ejecta masses and velocities of the simulated binary systems. refers to the amount of mass that has a velocity in excess of .
Ordering our equations of state in terms of stiffness from soft to hard (either based on or , see Section 2.4), SLy, APR3, MPA1, and MS1b, we see that they eject more mass the softer they are, consistent with shocks (that emerge more easily in soft EOSs with a lower sound speed) being the major ejection mechanism and confirming earlier results [21,22]. The thermal exponent has a noticeable impact on the ejecta masses with the case ejecting nearly twice as much as our standard case. Reference [21] actually found that ejecta from tabulated EOSs are best approximated by ; therefore, the masses in Table 2 may be considered as lower limits. Given the simplicity of how the thermal contribution is modeled and its impact on both the GW signal (see Figure 10) and the ejecta, this should also be a warning sign that a more sophisticated modeling of the thermal EOS is needed.
The ejecta velocities in GW170817 have provided additional constraints on the physical origin of the ejecta. Keeping in mind that, within the assumptions entering the Bernoulli criterion, the physical interpretation of is that of the Lorentz factor at infinity, we bin the asymptotic velocities
in Figure 13. The baryon number weighted average velocities at infinity
where the index b runs over all unbound particles and is, as before, the baryon number carried by an SPH particle, is typically around ∼0.2c, but in each of the cases, ∼ escapes with velocities above 0.5c, extending up to ∼0.7c; see Figure 13 and Table 2. Such high-velocity ejecta have been reported also by other studies [7,22,23,113]. While we cannot claim that these small amounts of mass are fully converged, Figure 14 shows that the velocity distribution in all cases smoothly extends to such large velocity values. We are therefore confident that this high-velocity ejecta component is not a numerical artifact.
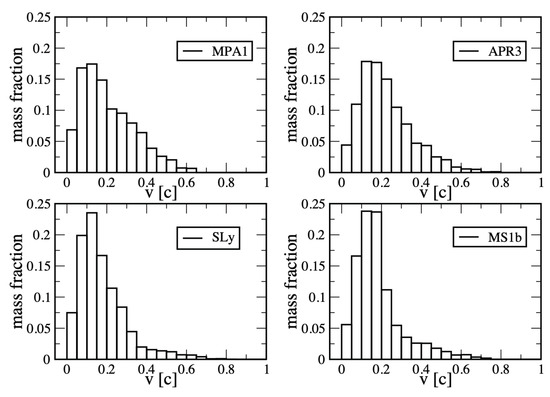
Figure 13.
Fraction of the ejected mass binned according to their velocities at infinity; for each equation of state, the simulation results with 2 million particles is shown.
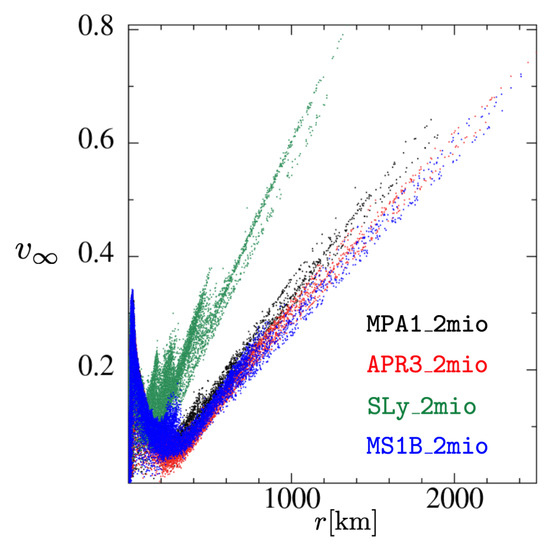
Figure 14.
Asymptotic velocities as a function of radius of the 2 million particle simulations.
To identify how the high-velocity ejecta are launched, we sort the ejecta in the last data output into four groups: : , : , : , and : . In Figure 15, Figure 16, Figure 17 and Figure 18, we plot these groups of particles at the approximate times of the merger and for the final data dumps of our two million particle runs. The highest velocity particles, (orange) and (red) emerge from the shock-heated interface between the two neutron stars. While the high-velocity ejecta are still not well-resolved, we note that our simulations here have an order of magnitude more particles than the approximate GR simulations in which these fast ejecta were originally identified [113]. This high-velocity component could have important observational consequences: it may produce an early blue/UV transient on a time scale of several minutes to an hour preceding the main kilonova event [113], and at late times, it may be responsible for synchrotron emission [114,115,116].
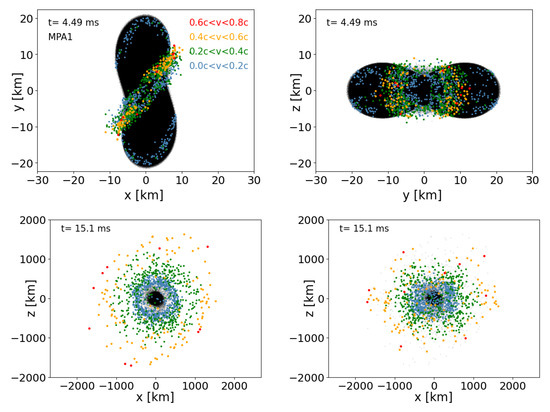
Figure 15.
Projections of the particle positions for the MPA1 EOS case (run MPA1_2mio). All particles are shown in black, ejecta with in blue, ejecta with in green, ejecta with in orange, and ejecta with in red.
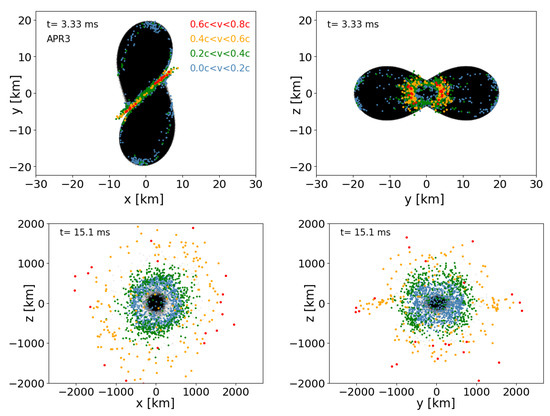
Figure 16.
Projections of the particle positions for the APR3 EOS case (run APR3_2mio). All particles are shown in black, ejecta with in blue, ejecta with in green, ejecta with in orange, and ejecta with in red.
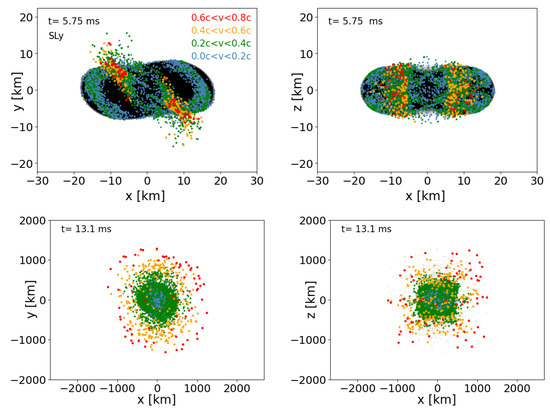
Figure 17.
Projections of the particle positions for the SLy EOS case (run SLy_2mio). All particles are shown in black, ejecta with in blue, ejecta with in green, ejecta with in orange, and ejecta with in red.
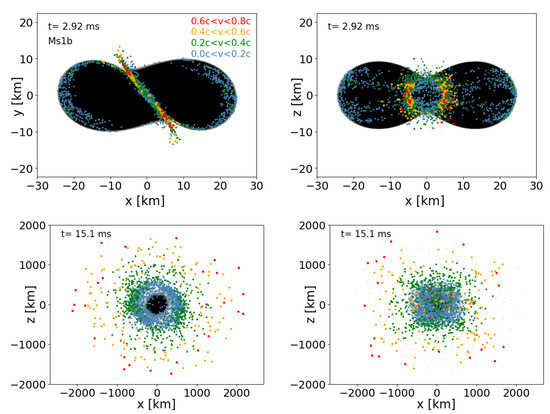
Figure 18.
Projections of the particle positions for the Ms1b EOS case (run Ms1b_2mio). All particles are shown in black, ejecta with in blue, ejecta with in green, ejecta with in orange, and ejecta with in red.
Another interesting result in a multi-messenger context is that the ejecta distribution only shows moderate deviations from spherical symmetry, so that the resulting electromagnetic emission could be reasonably modeled with simple approaches. This result, however, may be specific for our equal mass binaries and for the currently implemented physics, and it is possible that different equations of state, neutrinos, and/or magnetic fields could modify this.
4. Summary
We presented here a further methodological refinement of our Lagrangian Numerical Relativity code SPHINCS_BSSN [15,16]. The new methodological elements in SPHINCS_BSSN include a new way to steer where artificial dissipation is applied; see Section 2.1.1. We used both a compression that increases in time (as suggested in [28]) and a numerical noise indicator following [29] to determine how much dissipation is used. We also further refined our MOOD algorithm that we used in our “particle-to-mesh” step; see Section 2.3. As a step towards more realistic neutron star merger simulations, we implemented piecewise polytropic equations of state that approximate the cold nuclear matter equations of state MPA1, APR3, SLy, and MS1b, and we augmented these with a thermal contribution; see Section 2.4 and Appendix A for details.
In this first SPHINCS_BSSN study using piecewise polytropic EOSs, we restricted ourselves to neutron star binary systems with 2 × 1.3 and we explored how the results depend on both resolution and the choice of the thermal polytropic exponent . None of the explored cases seem to be prone to a BH collapse, at least not on the simulated time scale of ms. However, the SLy EOS cases undergo particularly deep pulsations, during which they shed mass into the surrounding torus, and they also eject more mass than the stiffer equations of state (MPA1,APR3, MS1b). When our simulations end, the remnant has not yet settled into a stationary state and the torus mass is still increasing. All of the torus masses are large enough to power short GRBs, and if indeed tori unbind several 10% of their mass on secular time scales [84,85,86,87,88,89], then in all cases, their ejecta amount to a few percent of a solar mass.
For all our runs, we extracted the gravitational waves, both directly from the particles via the quadrupole approximation and from the spacetime by means of the Newman–Penrose–Weyl scalar . Overall, we found rather good agreement: the waves phases are practically perfectly tracked in the quadrupole approximation, but in the post-merger phase, the amplitudes can be underestimated by several 10%. As expected, the softest EOS leads to the longest inspiral wave train and also to larger post-merger amplitudes. We further explored the impact of the thermal adiabatic exponent on the gravitational wave and spectrum.
Consistent with earlier studies, we found that these equal mass systems eject only a few dynamically, and the ejection is driven by shocks. Based on quasi-Newtonian [19,117,118,119], conformal flatness approximation [21], and full-GR simulations [22,23], however, we expect that asymmetric systems with mass ratio eject substantially more matter and, in particular, have a larger contribution from tidal ejecta. Overall, the small amount of ejecta underlines the need for additional ejection channels such as torus unbinding or neutrino-driven winds in order to reach the ejecta masses estimated for GW170817. The matter being predominantly ejected via shocks probably means that its electron fraction is increased with respect to the cold, -equilibrium values inside the original neutron stars (; see, e.g., Figure 21 in [120]). Again consistent with earlier studies, we found that the softer equation of state cases eject more mass and also reducing the exponent seems to enhance mass ejection.
Interestingly, we found in all cases that are escaping at velocities exceeding 0.5c, and this high-velocity part of the ejecta originates from the interface between the two neutron stars during merger. While we cannot claim that the properties of this matter are well converged, we see this fast component in all the simulations, and their velocity distribution (see Figure 14) extends smoothly to large velocities, so that we have confidence in the physical presence of these high-velocity ejecta. This neutron-rich matter expands sufficiently fast for most neutrons to avoid capture, and the -decay of these free neutrons has been discussed as a source of early, blue “precursor” emission before the main kilonova [113]. To “bracket” the kilonova emission, such a high-velocity ejecta component has also been suggested to be responsible for an X-ray emission excess observed three years after GW170817 [116].
While the piecewise polytropic equations of state are an important improvement over our previous merger simulations with SPHINCS_BSSN [16], they are still only a far cry from realistic microphysics. This topic is a major target for our future work.
Author Contributions
Conceptualization, S.R.; Data curation, P.D., S.R. and F.T.; Formal analysis, P.D. and S.R.; Funding acquisition, S.R.; Investigation, S.R. and P.D.; Methodology, S.R. and P.D.; Project administration, S.R.; Resources, S.R.; Software, S.R., P.D. and F.T.; Supervision, S.R. and P.D.; Validation, S.R.; Visualization, S.R. and P.D.; Writing—original draft, S.R.; Writing—review and editing, S.R., P.D. and F.T. All authors have read and agreed to the published version of the manuscript.
Funding
S.R. was supported by the Swedish Research Council (VR) under Grant Number 2020-05044, by the Swedish National Space Board under Grant Number Dnr. 107/16, by the research environment grant “Gravitational Radiation and Electromagnetic Astrophysical Transients (GREAT)” funded by the Swedish Research Council (VR) under Dnr 2016-06012, by which also F.T. was supported, and by the Knut and Alice Wallenberg Foundation under grant Dnr. KAW 2019.0112.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank E. Gourgoulhon, R. Haas, and J. Novak for useful clarifications concerning LORENE and S.V. Chaurasia for sharing his insights into the BAM code. We gratefully acknowledge inspiring interactions via the COST Action CA16104 “Gravitational waves, black holes and fundamental physics” (GWverse) and COST Action CA16214 “The multi-messenger physics and astrophysics of neutron stars” (PHAROS). P.D. would like to thank the Astronomy Department at SU and the Oscar Klein Centre for their hospitality during numerous visits in the course of the development of SPHINCS_BSSN. The simulations for this paper were performed at the facilities of the North-German Supercomputing Alliance (HLRN), on the resources provided by the Swedish National Infrastructure for Computing (SNIC) in Linköping, partially funded by the Swedish Research Council through Grant Agreement no. 2016-07213, and at the SUNRISE HPC facility supported by the Technical Division at the Department of Physics, Stockholm University. Special thanks go to Holger Motzkau and Mikica Kocic for their excellent support in upgrading and maintaining SUNRISE. Some of the plots in this paper were produced with the software SPLASH [121].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADM | Arnowitt–Deser–Misner |
| BH | Black Hole |
| BSSN | formulation according to Baumgarte, Shapiro, Shibata, and Nakamura |
| EOS | Equation Of State |
| GR | General Relativity |
| GW | Gravitational Wave |
| SPH | Smooth Particle Hydrodynamics |
| SPHINCS | Smooth Particle Hydrodynamics in Curved Spacetime |
Appendix A. Recovery Procedure for Piecewise Polytropic Equations of State
In this work we use piecewise polytropic equations of state. The part resulting from the cold, nuclear matter pressure is described by several polytropic pieces as discussed in [27], and a thermal part, , is added under the assumption that it also follows a polytropic equation of state with some thermal exponent , for which we choose a default value of 1.75. The total pressure is then given by
where the cold part is given by pieces
where the values are chosen according to the density (for ). The thermal pressure is calculated only from the “thermal” (i.e., non-degenerate) part of the internal energy and has a separate (smaller) polytropic exponent
The thermal part of u is found by subtracting the “cold/degenerate” value of the internal energy. This cold value is
and the integration constants make the internal energy continuous between different pieces, see Equation (7) of [27].
From now onwards, we will again use our conventions and measure energies in units of , being the baryon mass, so that our pressure is given as . The general strategy is similar to the purely polytropic case: we express both n and u in terms of , e, N and the pressure, substitute everything into the (here analytically known) equation of state
and solve numerically for the new pressure that is consistent with the current values of , e and N. We need
We find that the generalized Lorentz factor can be expressed as
where
This provides us with the internal energy
and, from our earlier definition, we have
The solution procedure is then the following. We first find the new pressure that fulfills Equation (A5) for the new values of . For this root finding we use Ridders’ method [122,123]. This method is a robust variant of the regula falsi method and does not require any derivates. With the consistent pressure at hand, we obtain the new from Equation (A7). It can be shown that
and this provides us with the enthalpy and the covariant spatial velocity components The time component is found from the equation for the generalized Lorentz factor, Equation (2),
The contravariant velocity is then straightforwardly calculated via , n from Equation (A10) and the internal energy as .
Appendix B. Which Resolution?
In our new simulation methodology, where we evolve the spacetime on a mesh and the matter with particles, we have two different resolution lengths and it its not a priori clear how they should be related. We therefore present here some numerical experiments to shed some light on the effects of the grid- and particle resolution. To keep the parameter space under control, we restrict ourselves here to one of our “most realistic” equations of state, MPA1. We perform the following test simulations:
- TS1: the outer boundary in each coordinate direction is located at 375 (≈554 km), five refinement levels and grid points which corresponds to the finest grid resolution length of m. We use here our default, i.e., 6th order, Finite Differencing (“FD6”).
- TS2: same as TS1, but FD4
- TS3: same as TS1, but FD8
- TS4: same as TS1, but grid points, i.e., m
- TS5: same as TS1, but grid points, i.e., m.
- TS6: same as TS1, but grid points, i.e., m.
All the variations related to the spacetime evolution accuracy indicate that the changes in the inspiral are only minor and our default of 175 grid points together with 6th order finite differencing is a good choice.
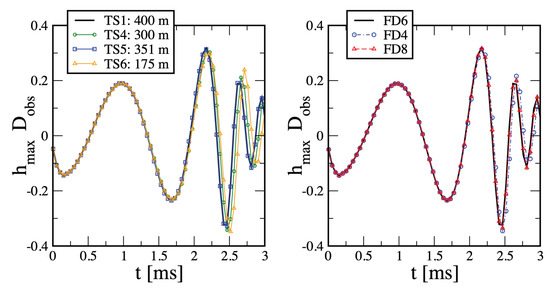
Figure A1.
Dependence of the inspiral on the grid resolution (left) and Finite Differencing order (right). The length labels in the left panel refer to the finest grid resolution .
Given that spacetime resolution has only a very minor impact on the inspiral, but we still see substantial difference between the 2 million and the 5 million particle run in Figure 9, this suggests that it is the particle number that, at the available resolutions, has the largest impact. While we currently have no accurate estimate for the number of particles that is required for a fully converged inspiral, Figure 9 seems to indicate that we need at least ∼5 million particles, but possibly more. This issue will be explored in more detail in future work.
References
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef]
- Ruffert, M.; Janka, H.; Takahashi, K.; Schaefer, G. Coalescing neutron stars-a step towards physical models. II. Neutrino emission, neutron tori, and gamma-ray bursts. Astron. Astrophys. 1997, 319, 122–153. [Google Scholar]
- Rosswog, S.; Liebendörfer, M. High-resolution calculations of merging neutron stars—II. Neutrino emission. Mon. Not. R. Astron. Soc. 2003, 342, 673–689. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Gravitational Waves and Neutrino Emission from the Merger of Binary Neutron Stars. Phys. Rev. Lett. 2011, 107, 051102. [Google Scholar] [CrossRef]
- Perego, A.; Rosswog, S.; Cabezón, R.M.; Korobkin, O.; Käppeli, R.; Arcones, A.; Liebendörfer, M. Neutrino-driven winds from neutron star merger remnants. Mon. Not. R. Astron. Soc. 2014, 443, 3134–3156. [Google Scholar] [CrossRef]
- Just, O.; Bauswein, A.; Pulpillo, R.A.; Goriely, S.; Janka, H.T. Comprehensive nucleosynthesis analysis for ejecta of compact binary mergers. Mon. Not. R. Astron. Soc. 2015, 448, 541–567. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Shibata, M.; Wanajo, S.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y. Mass ejection from disks surrounding a low-mass black hole: Viscous neutrino-radiation hydrodynamics simulation in full general relativity. Phys. Rev. D 2020, 101, 083029. [Google Scholar] [CrossRef]
- Foucart, F.; Duez, M.D.; Hébert, F.; Kidder, L.E.; Kovarik, P.; Pfeiffer, H.P.; Scheel, M.A. Implementation of Monte Carlo Transport in the General Relativistic SpEC Code. Astrophys. J. 2021, 920, 82. [Google Scholar] [CrossRef]
- Just, O.; Goriely, S.; Janka, H.T.; Nagataki, S.; Bauswein, A. Neutrino absorption and other physics dependencies in neutrino-cooled black hole accretion discs. Mon. Not. R. Astron. Soc. 2022, 509, 1377–1412. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A.; Haas, R. A New Moment-Based General-Relativistic Neutrino-Radiation Transport Code: Methods and First Applications to Neutron Star Mergers. Mon. Not. R. Astron. Soc. 2022, 512, 1499–1521. [Google Scholar] [CrossRef]
- Price, D.; Rosswog, S. Producing ultra-strong magnetic fields in neutron star mergers. Science 2006, 312, 719. [Google Scholar] [CrossRef] [PubMed]
- Kiuchi, K.; Cerdá-Durán, P.; Kyutoku, K.; Sekiguchi, Y.; Shibata, M. Efficient magnetic-field amplification due to the Kelvin-Helmholtz instability in binary neutron star mergers. Phys. Rev. D 2015, 92, 124034. [Google Scholar] [CrossRef]
- Palenzuela, C.; Liebling, S.L.; Neilsen, D.; Lehner, L.; Caballero, O.L.; O’Connor, E.; Anderson, M. Effects of the microphysical equation of state in the mergers of magnetized neutron stars with neutrino cooling. Phys. Rev. D 2015, 92, 044045. [Google Scholar] [CrossRef]
- Rosswog, S.; Diener, P. SPHINCS_BSSN: A general relativistic smooth particle hydrodynamics code for dynamical spacetimes. Class. Quantum Gravity 2021, 38, 115002. [Google Scholar] [CrossRef]
- Diener, P.; Rosswog, S.; Torsello, F. SimuLating neutron star mergers with the Lagrangian Numerical Relativity code SPHINCS_BSSN. Eur. Phys. J. A 2022, 58, 74. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical integration of Einstein’s field equations. Phys. Rev. D 1999, 59, 024007. [Google Scholar] [CrossRef]
- Rosswog, S.; Liebendörfer, M.; Thielemann, F.K.; Davies, M.; Benz, W.; Piran, T. Mass ejection in neutron star mergers. Astron. Astrophys. 1999, 341, 499–526. [Google Scholar]
- Oechslin, R.; Janka, H. Gravitational Waves from Relativistic Neutron-Star Mergers with Microphysical Equations of State. Phys. Rev. Lett. 2007, 99, 121102. [Google Scholar] [CrossRef]
- Bauswein, A.; Goriely, S.; Janka, H.T. Systematics of Dynamical Mass Ejection, Nucleosynthesis, and Radioactively Powered Electromagnetic Signals from Neutron-star Mergers. Astrophys. J. 2013, 773, 78. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.i.; Shibata, M.; Taniguchi, K. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts, and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Schoepe, A.; Hilditch, D.; Bugner, M. Revisiting hyperbolicity of relativistic fluids. Phys. Rev. D 2018, 97, 123009. [Google Scholar] [CrossRef]
- Rosswog, S. The Lagrangian hydrodynamics code MAGMA2. Mon. Not. R. Astron. Soc. 2020, 498, 4230–4255. [Google Scholar] [CrossRef]
- LORENE Library. Available online: https://lorene.obspm.fr (accessed on 1 May 2022).
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Cullen, L.; Dehnen, W. Inviscid smoothed particle hydrodynamics. Mon. Not. R. Astron. Soc. 2010, 408, 669–683. [Google Scholar] [CrossRef]
- Rosswog, S. Boosting the accuracy of SPH techniques: Newtonian and special-relativistic tests. Mon. Not. R. Astron. Soc. 2015, 448, 3628–3664. [Google Scholar] [CrossRef]
- Rosswog, S. Astrophysical Smooth Particle Hydrodynamics. New Astron. Rev. 2009, 53, 78–104. [Google Scholar] [CrossRef]
- Rosswog, S. A Simple, Entropy-based Dissipation Trigger for SPH. Astrophys. J. 2020, 898, 60. [Google Scholar] [CrossRef]
- Alcubierre, M. Introduction to 3+1 Numerical Relativity; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Baumgarte, T.W.; Shapiro, S.L. Numerical Relativity: Solving Einstein’s Equations on the Computer; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Shibata, M. Numerical Relativity; World Scientific: Singapore, 2016. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Gafton, E.; Rosswog, S. A fast recursive coordinate bisection tree for neighbour search and gravity. Mon. Not. R. Astron. Soc. 2011, 418, 770–781. [Google Scholar] [CrossRef]
- Laguna, P.; Miller, W.A.; Zurek, W.H. Smoothed particle hydrodynamics near a black hole. Astrophys. J. 1993, 404, 678–685. [Google Scholar] [CrossRef]
- von Neumann, J.; Richtmyer, R.D. A Method for the Numerical Calculation of Hydrodynamic Shocks. J. Appl. Phys. 1950, 21, 232–237. [Google Scholar] [CrossRef]
- Liptai, D.; Price, D.J. General relativistic smoothed particle hydrodynamics. Mon. Not. R. Astron. Soc. 2019, 485, 819–842. [Google Scholar] [CrossRef]
- Christensen, R.B. Godunov Methods on a Staggered Mesh—An Improved Artificial Viscosity. In Nuclear Explosives Code Developers Conference; Lawrence Livermore National Lab, Lawrence Livermore Technical Report; 1990; Volume UCRL-JC-105269. Available online: https://ntrl.ntis.gov/NTRL/dashboard/searchResults/titleDetail/DE92011973.xhtml (accessed on 1 May 2022).
- Frontiere, N.; Raskin, C.D.; Owen, J.M. CRKSPH—A Conservative Reproducing Kernel Smoothed Particle Hydrodynamics Scheme. J. Comput. Phys. 2017, 332, 160–209. [Google Scholar] [CrossRef]
- Brown, J.D.; Diener, P.; Sarbach, O.; Schnetter, E.; Tiglio, M. Turduckening black holes: An analytical and computational study. Phys. Rev. D 2009, 79, 044023. [Google Scholar] [CrossRef]
- Einstein Toolkit Web Page. 2020. Available online: https://einsteintoolkit.org/ (accessed on 9 December 2020).
- Löffler, F.; Faber, J.; Bentivegna, E.; Bode, T.; Diener, P.; Haas, R.; Hinder, I.; Mundim, B.C.; Ott, C.D.; Schnetter, E.; et al. The Einstein Toolkit: A Community Computational Infrastructure for Relativistic Astrophysics. Class. Quantum Grav. 2012, 29, 115001. [Google Scholar] [CrossRef]
- Cottet, G.H.; Koumoutsakos, P.D. Vortex Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cottet, G.; Etancelin, J.; Perignon, F.; Picard, C. High order Semi-Lagrangian particle methods for tranport equations. ESAIM Math. Model. Numer. Anal. Edp Sci. 2014, 48, 1029–1060. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151–167. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Müther, H.; Prakash, M.; Ainsworth, T.L. The nuclear symmetry energy in relativistic Brueckner-Hartree-Fock calculations. Phys. Lett. B 1987, 199, 469–474. [Google Scholar] [CrossRef]
- Müller, H.; Serot, B.D. Relativistic mean-field theory and the high-density nuclear equation of state. Nuc. Phys. A 1996, 606, 508–537. [Google Scholar] [CrossRef]
- Pacilio, C.; Maselli, A.; Fasano, M.; Pani, P. Ranking Love Numbers for the Neutron Star Equation of State: The Need for Third-Generation Detectors. Phys. Rev. Lett. 2022, 128, 101101. [Google Scholar] [CrossRef] [PubMed]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Fryer, C.L.; Belczynski, K.; Ramirez-Ruiz, E.; Rosswog, S.; Shen, G.; Steiner, A.W. The Fate of the Compact Remnant in Neutron Star Mergers. Astrophys. J. 2015, 812, 24. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817. Astrophys. J. 2017, 850, L19. [Google Scholar] [CrossRef]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star Radius Constraints from GW170817 and Future Detections. Astrophys. J. 2017, 850, L34. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. D 2017, 96, 123012. [Google Scholar] [CrossRef]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. 2018, 852, L25. [Google Scholar] [CrossRef]
- Biswas, B.; Datta, S. Constraining neutron star properties with a new equation of state insensitive approach. arXiv 2021, arXiv:2112.10824. [Google Scholar]
- Rhoades, C.E.; Ruffini, R. Maximum Mass of a Neutron Star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef]
- Kalogera, V.; Baym, G. The Maximum Mass of a Neutron Star. Astrophys. J. 1996, 470, L61. [Google Scholar] [CrossRef]
- Schaffner-Bielich, J. Compact Stars, 1st ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Sod, G. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 43, 1–31. [Google Scholar] [CrossRef]
- Marti, J.; Müller, E. Extension of the Piecewise Parabolic Method to One-Dimensional Relativistic Hydrodynamics. J. Comp. Phys. 1996, 123, 1–14. [Google Scholar] [CrossRef]
- Chow, J.E.; Monaghan, J. Ultrarelativistic SPH. J. Computat. Phys. 1997, 134, 296. [Google Scholar] [CrossRef]
- Siegler, S.; Riffert, H. Smoothed Particle Hydrodynamics Simulations of Ultrarelativistic Shocks with Artificial Viscosity. Astrophys. J. 2000, 531, 1053–1066. [Google Scholar] [CrossRef][Green Version]
- Del Zanna, L.; Bucciantini, N. An efficient shock-capturing central-type scheme for multidimensional relativistic flows. I. Hydrodynamics. Astron. Astrophys. 2002, 390, 1177–1186. [Google Scholar] [CrossRef]
- Marti, J.M.; Müller, E. Numerical Hydrodynamics in Special Relativity. Living Rev. Relativ. 2003, 6, 7. [Google Scholar] [CrossRef]
- Marti, J.M.; Müller, E. Grid-based Methods in Relativistic Hydrodynamics and Magnetohydrodynamics. Living Rev. Comput. Astrophys. 2015, 1, 3. [Google Scholar] [CrossRef]
- Rosswog, S. SPH Methods in the Modelling of Compact Objects. Living Rev. Comput. Astrophys. 2015, 1, 1. [Google Scholar] [CrossRef]
- van Leer, B. Towards the Ultimate Conservative Difference Scheme. IV. A New Approach to Numerical Convection. J. Comput. Phys. 1977, 23, 276. [Google Scholar] [CrossRef]
- Sweby, P.K. High Resolution Schemes Using Flux Limiters for Hyperbolic Conservation Laws. SIAM J. Numer. Anal. 1984, 21, 995–1011. [Google Scholar] [CrossRef]
- Rosswog, S. Conservative, special-relativistic smooth particle hydrodynamics. J. Comp. Phys. 2010, 229, 8591–8612. [Google Scholar] [CrossRef]
- Rosswog, S. Special-relativistic Smoothed Particle Hydrodynamics: A benchmark suite. In Springer Lecture Notes in Computational Science and Engineering, “Meshfree Methods for Partial Differential Equations V”; Griebel, M., Schweitzer, M.A., Eds.; Springer: Berlin, Geramny, 2011; pp. 89–103. [Google Scholar]
- Kashyap, R.; Das, A.; Radice, D.; Padamata, S.; Prakash, A.; Logoteta, D.; Perego, A.; Godzieba, D.A.; Bernuzzi, S.; Bombaci, I.; et al. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. arXiv 2021, arXiv:2111.05183. [Google Scholar] [CrossRef]
- Flanagan, E.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Effective one body description of tidal effects in inspiralling compact binaries. Phys. Rev. D 2010, 81, 084016. [Google Scholar] [CrossRef]
- Bernuzzi, S. Neutron star merger remnants. Gen. Relativ. Gravit. 2020, 52, 108. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Breschi, M.; Daszuta, B.; Endrizzi, A.; Logoteta, D.; Nedora, V.; Perego, A.; Radice, D.; Schianchi, F.; Zappa, F.; et al. Accretion-induced prompt black hole formation in asymmetric neutron star mergers, dynamical ejecta, and kilonova signals. Mon. Not. R. Astron. Soc. 2020, 497, 1488–1507. [Google Scholar] [CrossRef]
- Nakar, E. Short-hard gamma-ray bursts. Phys. Rep. 2007, 442, 166–236. [Google Scholar] [CrossRef]
- Lee, W.H.; Ramirez-Ruiz, E.; López-Cámara, D. Phase Transitions and He-Synthesis-Driven Winds in Neutrino Cooled Accretion Disks: Prospects for Late Flares in Short Gamma-Ray Bursts. Astrophys. J. 2009, 699, L93–L96. [Google Scholar] [CrossRef]
- Kumar, P.; Zhang, B. The physics of gamma-ray bursts & relativistic jets. Phys. Rep. 2015, 561, 1–109. [Google Scholar] [CrossRef]
- Metzger, B.D.; Piro, A.L.; Quataert, E. Time-dependent models of accretion discs formed from compact object mergers. Mon. Not. R. Astron. Soc. 2008, 390, 781–797. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Hyper-Accreting Black Holes; American Institute of Physics Conference Series; Axelsson, M., Ed.; American Institute of Physics: College Park, MD, USA, 2008; Volume 1054, pp. 51–70. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r -Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-dimensional GRMHD Simulations of Neutrino-cooled Accretion Disks from Neutron Star Mergers. Astrophys. J. 2018, 858, 52. [Google Scholar] [CrossRef]
- Miller, J.M.; Ryan, B.R.; Dolence, J.C.; Burrows, A.; Fontes, C.J.; Fryer, C.L.; Korobkin, O.; Lippuner, J.; Mumpower, M.R.; Wollaeger, R.T. Full transport model of GW170817-like disk produces a blue kilonova. Phys. Rev. D. 2019, 100, 023008. [Google Scholar] [CrossRef]
- Fernandez, R.; Tchekhovskoy, A.; Quataert, E.; Foucart, F.; Kasen, D. Long-term GRMHD simulations of neutron star merger accretion discs: Implications for electromagnetic counterparts. Mon. Not. R. Astron. Soc. 2019, 482, 3373–3393. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational-wave event. Nature 2017, 551, 80–84. [Google Scholar] [CrossRef]
- Cowperthwaite, P.S.; Berger, E.; Villar, V.A.; Metzger, B.D. The Electromagnetic Counterpart of the Binary Neutron Star Merger LIGO/Virgo GW170817. II. UV, Optical, and Near-infrared Light Curves and Comparison to Kilonova Models. Astrophys. J. 2017, 848, L17. [Google Scholar] [CrossRef]
- Evans, P.A.; Cenko, S.B.; Kennea, J.A.; Emery, S.W.K.; Kuin, N.P.M.; Korobkin, O.; Wollaeger, R.T.; Fryer, C.L.; Madsen, K.K.; Harrison, F.A.; et al. Swift and NuSTAR observations of GW170817: Detection of a blue kilonova. Science 2017, 358, 1565–1570. [Google Scholar] [CrossRef] [PubMed]
- Villar, V.A.; Guillochon, J.; Berger, E.; Metzger, B.D.; Cowperthwaite, P.S.; Nicholl, M.; Alexander, K.D.; Blanchard, P.K.; Chornock, R.; Eftekhari, T.; et al. The Combined Ultraviolet, Optical, and Near-infrared Light Curves of the Kilonova Associated with the Binary Neutron Star Merger GW170817: Unified Data Set, Analytic Models, and Physical Implications. Astrophys. J. 2017, 851, L21. [Google Scholar] [CrossRef]
- Kasliwal, M.M.; Nakar, E.; Singer, L.P.; Kaplan, D.L.; Cook, D.O.; Van Sistine, A.; Lau, R.M.; Fremling, C.; Gottlieb, O.; Jencson, J.E.; et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science 2017, 358, 1559–1565. [Google Scholar] [CrossRef]
- Tanvir, N.R.; Levan, A.J.; González-Fernández, C.; Korobkin, O.; Mandel, I.; Rosswog, S.; Hjorth, J.; D’Avanzo, P.; Fruchter, A.S.; Fryer, C.L.; et al. The Emergence of a Lanthanide-rich Kilonova Following the Merger of Two Neutron Stars. Astrophys. J. 2017, 848, L27. [Google Scholar] [CrossRef]
- Rosswog, S.; Sollerman, J.; Feindt, U.; Goobar, A.; Korobkin, O.; Wollaeger, R.; Fremling, C.; Kasliwal, M.M. The first direct double neutron star merger detection: Implications for cosmic nucleosynthesis. Astron. Astrophys. 2018, 615, A132. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. Finite-temperature Extension for Cold Neutron Star Equations of State. Astrophys. J. 2019, 875, 12. [Google Scholar] [CrossRef]
- Raithel, C.A.; Paschalidis, V.; Özel, F. Realistic finite-temperature effects in neutron star merger simulations. Phys. Rev. D 2021, 104, 063016. [Google Scholar] [CrossRef]
- Bozzola, G. kuibit: Analyzing Einstein Toolkit simulations with Python. J. Open Source Softw. 2021, 6, 3099. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N. Unified picture of the post-merger dynamics and gravitational wave emission in neutron star mergers. Phys. Rev. D 2015, 91, 124056. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Dietrich, T.; Nagar, A. Modeling the complete gravitational wave spectrum of neutron star mergers. Phys. Rev. Lett. 2015, 115, 091101. [Google Scholar] [CrossRef] [PubMed]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Brügmann, B. Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. Phys. Rev. D 2015, 91, 124041. [Google Scholar] [CrossRef]
- Bauswein, A.; Stergioulas, N.; Janka, H.T. Exploring properties of high-density matter through remnants of neutron-star mergers. Eur. Phys. J. A 2016, 52, 56. [Google Scholar] [CrossRef]
- Clark, J.A.; Bauswein, A.; Stergioulas, N.; Shoemaker, D. Observing Gravitational Waves From The Post-Merger Phase Of Binary Neutron Star Coalescence. Class. Quant. Grav. 2016, 33, 085003. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kastaun, W.; Giacomazzo, B.; Endrizzi, A.; Siegel, D.M.; Perna, R. General relativistic magnetohydrodynamic simulations of binary neutron star mergers forming a long-lived neutron star. Phys. Rev. D 2017, 95, 063016. [Google Scholar] [CrossRef]
- Maione, F.; De Pietri, R.; Feo, A.; Löffler, F. Spectral analysis of gravitational waves from binary neutron star merger remnants. Phys. Rev. D 2017, 96, 063011. [Google Scholar] [CrossRef]
- Sarin, N.; Lasky, P.D. The evolution of binary neutron star post-merger remnants: A review. Gen. Rel. Grav. 2021, 53, 59. [Google Scholar] [CrossRef]
- Sun, L.; Ruiz, M.; Shapiro, S.L.; Tsokaros, A. Jet Launching from Binary Neutron Star Mergers: Incorporating Neutrino Transport and Magnetic Fields. arXiv 2022, arXiv:2202.12901. [Google Scholar] [CrossRef]
- Takami, K.; Rezzolla, L.; Baiotti, L. Spectral properties of the post-merger gravitational-wave signal from binary neutron stars. arXiv 2014, arXiv:1412.3240. [Google Scholar] [CrossRef]
- Freiburghaus, C.; Rosswog, S.; Thielemann, F.K. R-Process in Neutron Star Mergers. Astrophys. J. 1999, 525, L121. [Google Scholar] [CrossRef] [PubMed]
- Foucart, F.; Mösta, P.; Ramirez, T.; Wright, A.J.; Darbha, S.; Kasen, D. Estimating outflow masses and velocities in merger simulations: Impact of r-process heating and neutrino cooling. Phys. Rev. D. 2021, 104, 123010. [Google Scholar] [CrossRef]
- Korobkin, O.; Wollaeger, R.T.; Fryer, C.L.; Hungerford, A.L.; Rosswog, S.; Fontes, C.J.; Mumpower, M.R.; Chase, E.A.; Even, W.P.; Miller, J.; et al. Axisymmetric Radiative Transfer Models of Kilonovae. Astrophys. J. 2021, 910, 116. [Google Scholar] [CrossRef]
- Metzger, B.D.; Bauswein, A.; Goriely, S.; Kasen, D. Neutron-powered precursors of kilonovae. Mon. Not. R. Astron. Soc. 2015, 446, 1115–1120. [Google Scholar] [CrossRef]
- Mooley, K.P.; Nakar, E.; Hotokezaka, K.; Hallinan, G.; Corsi, A.; Frail, D.A.; Horesh, A.; Murphy, T.; Lenc, E.; Kaplan, D.L.; et al. A mildly relativistic wide-angle outflow in the neutron-star merger event GW170817. Nature 2018, 554, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Hotokezaka, K.; Kiuchi, K.; Shibata, M.; Nakar, E.; Piran, T. Synchrotron Radiation from the Fast Tail of Dynamical Ejecta of Neutron Star Mergers. Astrophys. J. 2018, 867, 95. [Google Scholar] [CrossRef]
- Hajela, A.; Margutti, R.; Bright, J.S.; Alexander, K.D.; Metzger, B.D.; Nedora, V.; Kathirgamaraju, A.; Margalit, B.; Radice, D.; Guidorzi, C.; et al. Evidence for X-Ray Emission in Excess to the Jet-afterglow Decay 3.5 yr after the Binary Neutron Star Merger GW 170817: A New Emission Component. Astrophys. J. 2022, 927, L17. [Google Scholar] [CrossRef]
- Rosswog, S.; Davies, M.B.; Thielemann, F.K.; Piran, T. Merging neutron stars: Asymmetric systems. Astron. Astrophys. 2000, 360, 171–184. [Google Scholar]
- Korobkin, O.; Rosswog, S.; Arcones, A.; Winteler, C. On the astrophysical robustness of the neutron star merger r-process. Mon. Not. R. Astron. Soc. 2012, 426, 1940–1949. [Google Scholar] [CrossRef]
- Rosswog, S. The dynamic ejecta of compact object mergers and eccentric collisions. R. Soc. Lond. Philos. Trans. Ser. A 2013, 371, 20272. [Google Scholar] [CrossRef]
- Farouqi, K.; Thielemann, F.K.; Rosswog, S.; Kratz, K.L. Correlations of r-Process Elements in Very Metal-Poor Stars as Clues to their Nucleosynthesis Sites. arXiv 2021, arXiv:2107.03486. [Google Scholar] [CrossRef]
- Price, D.J. splash: An Interactive Visualisation Tool for Smoothed Particle Hydrodynamics Simulations. Publ. Astron. Soc. Aust. 2007, 24, 159–173. [Google Scholar] [CrossRef]
- Ridders, C. Accurate computation of F′(x) and F′(x) F″(x). Adv. Eng. Softw. 1982, 4, 75. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).