Study of Weak Solutions for a Class of Degenerate Parabolic Variational Inequalities with Variable Exponent
Abstract
1. Introduction
2. Basic Spaces and the Main Results
3. Existence and Uniqueness of Solutions
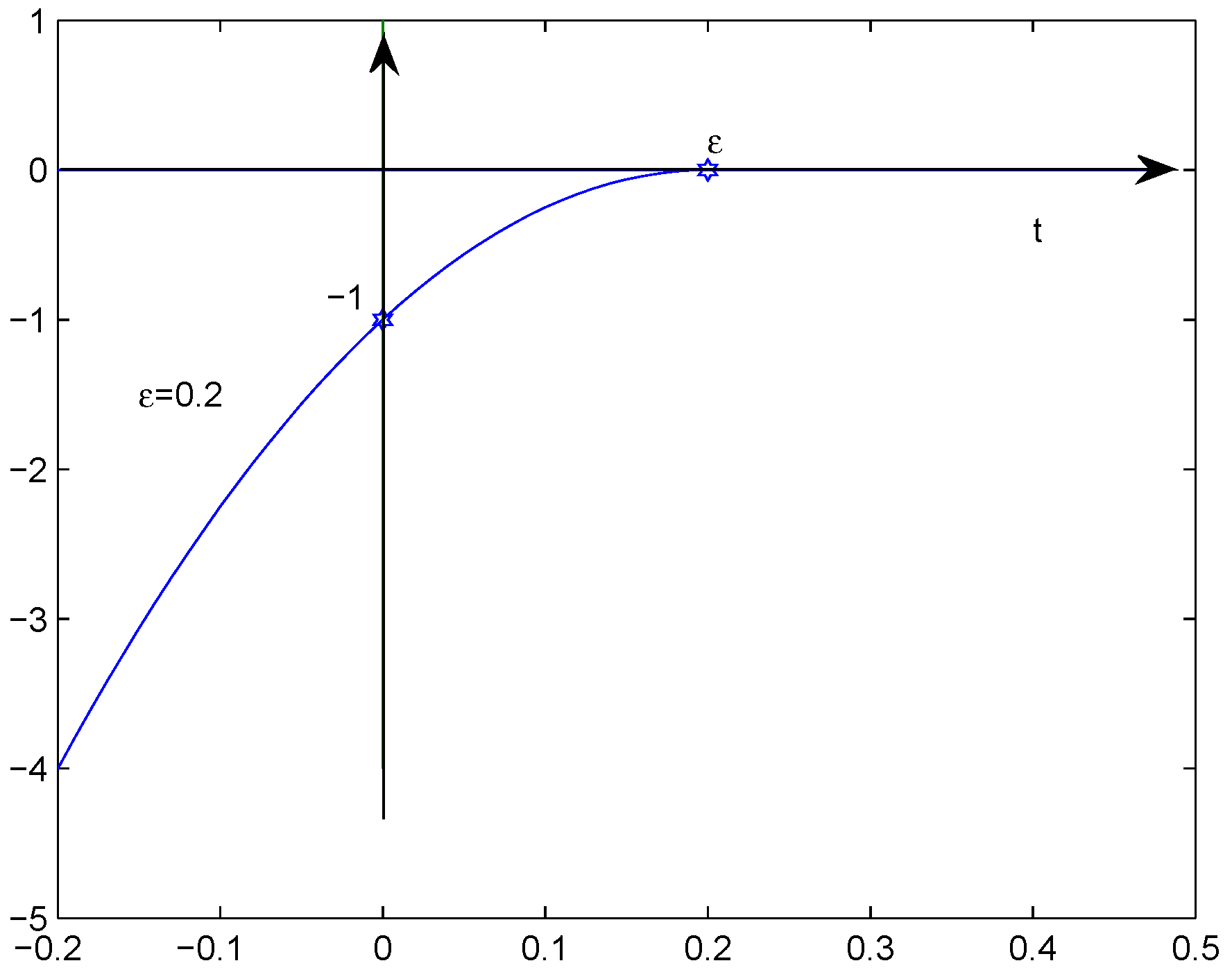
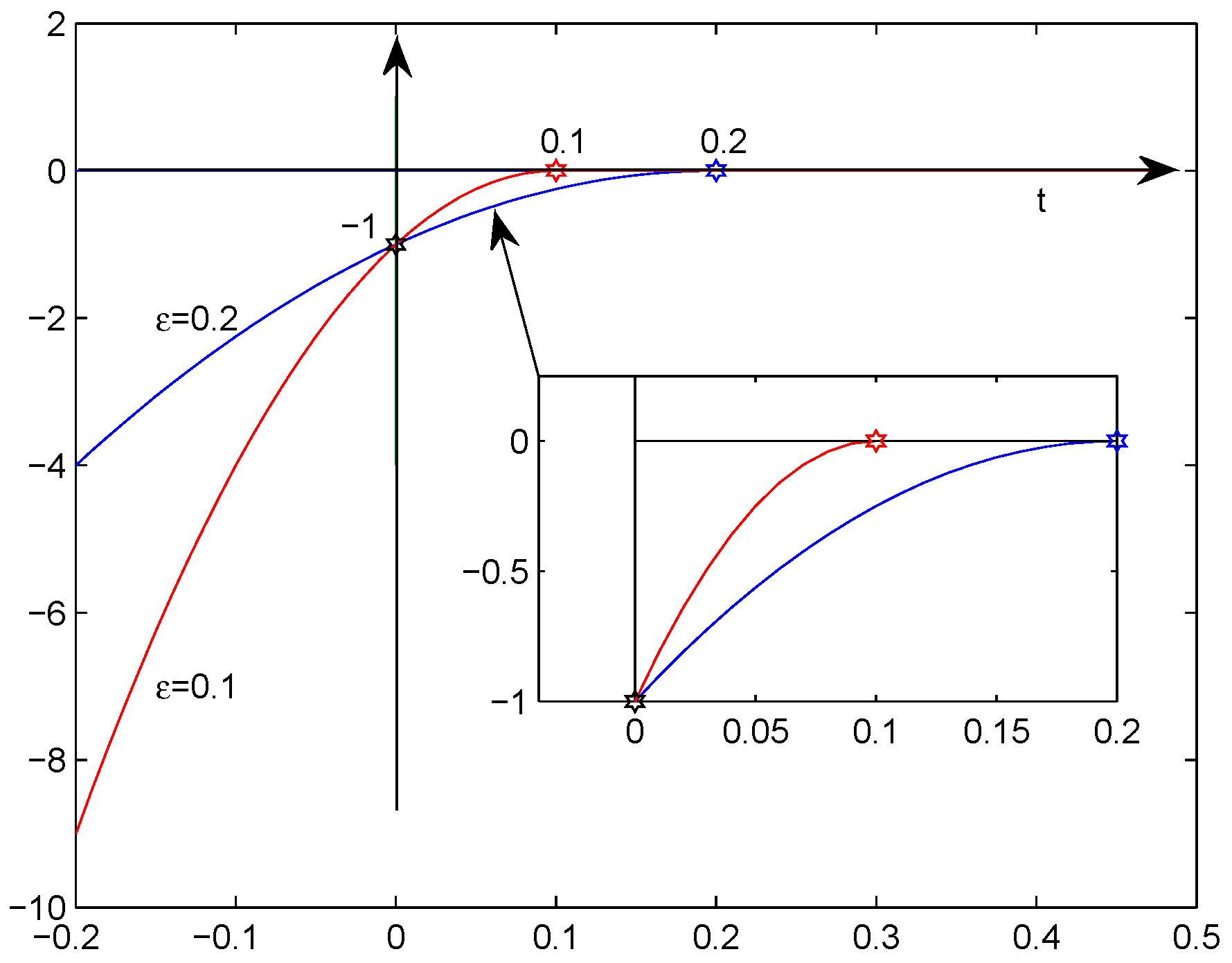
4. Nonexistence and Long-Time Behavior of Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boulaaras, S.; Haiour, M. Overlapping domain decomposition methods for elliptic quasi-variational inequalities related to impulse control problem with mixed boundary conditions. Proc. Indian Acad. Sci. Math. Sci. 2011, 121, 481–493. [Google Scholar] [CrossRef]
- Boulaaras, S.; Haiour, M. L∞-asymptotic behavior for a finite element approximation in parabolic quasi-variational inequalities related to impulse control problem. Appl. Math. Comput. 2011, 217, 6443–6450. [Google Scholar] [CrossRef]
- Boulaaras, S.; Haiour, M. The finite element approximation in parabolic quasi-variational inequalities related to impulse control problem with mixed boundary conditions. J. Taibah Univ. Sci. 2013, 7, 105–113. [Google Scholar] [CrossRef]
- Chen, X.; Yi, F.; Wang, L. American lookback option with fixed strike price 2-D parabolic variational inequality. J. Differ. Equ. 2011, 251, 3063–3089. [Google Scholar] [CrossRef][Green Version]
- Zhou, Y.; Yi, F. A free boundary problem arising from pricing convertible bond. Appl. Anal. 2010, 89, 307–323. [Google Scholar] [CrossRef]
- Chen, X.; Yi, F. Parabolic variational inequality with parameter and gradient constraints. J. Math. Anal. Appl. 2012, 385, 928–946. [Google Scholar] [CrossRef]
- Zhou, Y.; Yi, F. A variational inequality arising from American installment call options. J. Math. Anal. Appl. 2009, 357, 54–68. [Google Scholar] [CrossRef][Green Version]
- Sun, Y.; Shi, Y. The existence of solution to a class of degenerate parabolic variational. J. Inequal. Appl. 2015, 204, 1–11. [Google Scholar] [CrossRef][Green Version]
- Dibenedetto, E. Degenerate Parabolic Equations; Springer: New York, NY, USA, 2010; ISBN 0387940200. [Google Scholar]
- Lian, S.; Gao, W. Existence of solutions to an initial Dirichlet problem of evolutional p(x)-Laplace equations. Ann. I. H. Poincare 2012, 29, 863–886. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Wang, H. Study of Weak Solutions for a Class of Degenerate Parabolic Variational Inequalities with Variable Exponent. Symmetry 2022, 14, 1255. https://doi.org/10.3390/sym14061255
Sun Y, Wang H. Study of Weak Solutions for a Class of Degenerate Parabolic Variational Inequalities with Variable Exponent. Symmetry. 2022; 14(6):1255. https://doi.org/10.3390/sym14061255
Chicago/Turabian StyleSun, Yudong, and Huan Wang. 2022. "Study of Weak Solutions for a Class of Degenerate Parabolic Variational Inequalities with Variable Exponent" Symmetry 14, no. 6: 1255. https://doi.org/10.3390/sym14061255
APA StyleSun, Y., & Wang, H. (2022). Study of Weak Solutions for a Class of Degenerate Parabolic Variational Inequalities with Variable Exponent. Symmetry, 14(6), 1255. https://doi.org/10.3390/sym14061255





