A More Flexible Reliability Model Based on the Gompertz Function and the Generalized Integro-Exponential Function

Abstract

This work presents a new distribution that allows modeling data from a random variable with non-negative values. The new family is defined by a stochastic representation of a scaled mixture of a random variable with a Gompertz distribution (G) and a random variable with a uniform distribution on the interval (0,1). The result of this gives rise to a new random variable with a Slash Gompertz ($SG$) distribution that is more flexible than the Gompertz distribution, that is, it better models atypical data, presenting tails heavier than the Gompertz distribution. The density and some general properties of the resulting family are studied, including its moments and kurtosis coefficient. The inference of the parameters is carried out using the method of moments and maximum likelihood. Finally, illustrations of particular cases of this family are shown, adjusting in this case two sets of real data and estimating the parameters by maximum likelihood, where it is verified that this new family of distributions fits the reliability function better than the distributions of Gompertz (G), Slash Birnbaum Saunders ($SBS$), Slash Weibull ($SW$), and Gompertz-Verhults ($GV$).

1. Introduction

The Gompertz curve or Gompertz function is a type of mathematical model designed to describe a time series and is named after Benjamin Gompertz (1779–1865) (see [1]). The function was originally designed to describe human mortality, but has since been modified for application in biological sciences. The model is defined by

$$\begin{array}{c}\hfill {\displaystyle f\left(t\right)=a{\mathrm{e}}^{-b{\mathrm{e}}^{-ct}},}\end{array}$$

(1)

where “a” is an asymptote, since

$$\begin{array}{c}\hfill {\displaystyle \underset{t\to \infty }{lim}a{\mathrm{e}}^{-b{\mathrm{e}}^{-ct}}=a{\mathrm{e}}^0=a},\end{array}$$

“b”, “c” are positive numbers, where “b” sets the offset along the x axis y “c” sets the growth rate.

Figure 1 shows the behavior of the Gompertz function for different values of “a”.

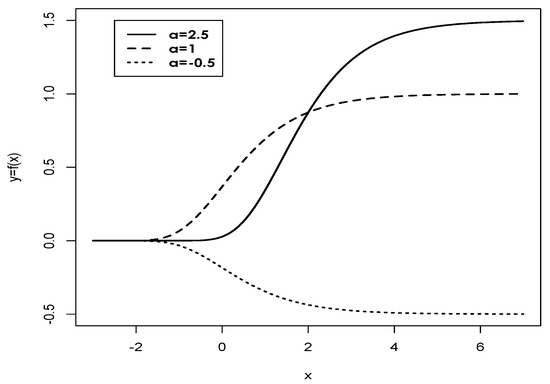
Figure 1. Plot of Gompertz function for $a=2.5$ (solid line), $a=1$ (dotted line), $a=-0.5$ (dashed line) and $b=c=1$.

1.1. The Gompertz Distribution

The Gompertz distribution is important in describing the pattern of adult deaths (Wetterstrand [2]; Gavrilov and Gavrilova [3]). For low levels of infant (and young adult) mortality, the Gompertz mortality rate extends to lifetime (Vaupel [4]) of populations with no observed mortality slowdown.

The Gompertz distribution has received considerable attention from demographers and actuaries. Pollard and Valkovics [5] were the first to study the Gompertz distribution minutely. However, their results are valid only in the case where the initial level of mortality is very close to 0. Kunimura [6] reached similar conclusions. both defined the moment-generating function of the Gompertz distribution in terms of the complete or incomplete gamma function and its results are approximated or left in the function of an integral. Willemse and Koppelaar [7] reformulated the Gompertz death rate and derived properties for this reformulation. Later, Marshall and Olkin [8] described the negative Gompertz distribution; a Gompertz distribution with a negative aging rate. Willekens [9] provided connections between Gompertz, Weibull and other distributions of extreme values of Type I.

An important function used in computing the moments of the Gompertz distribution is the generalized integro-exponential function, which is defined by the following integral representation:

$$\begin{array}{c}\hfill E_s^m\left(z\right)=\frac{1}{\Gamma \left(m+1\right)}{\int }_1^{\infty }{\left(\log w\right)}^m{e}^{-zw}{w}^{-s}dw,\end{array}$$

(2)

where $sϵ(-\infty ,\infty )$, $m>-1$ and $\Gamma \left(p\right)$ is the gamma function. For further details, the reader is referred to Milgram [10] and Chiccoli et al. [11].

The Gompertz distribution has a continuous probability density function with scale parameter $\alpha$ and shape parameter $\beta$,

$$\begin{array}{c}\hfill f\left(x\right)=\alpha e^{\beta x-\frac{\alpha }{\beta }(e^{\beta x}-1)},\end{array}$$

(3)

with support on $(-\infty ,\infty )$. In actuarial or demographic applications, X usually indicates the age which cannot be negative, leading to a bounded support at $[0,\infty )$. The Truncated Distribution produces a suitable density function by scaling the $\alpha$ parameter to correspond to $X=0$ (Mohan et al. [12]). The cumulative distribution function is

$$\begin{array}{c}\hfill F\left(x\right)=1-e^{-\frac{\alpha }{\beta }(e^{\beta x}-1)}.\end{array}$$

Moments of the Gompertz distribution can be given explicitly by the generalized integro-exponential function (Milgram [10]), which offers an exact power series representation of them. The j-th moment of a random variable X with Gompertz distribution is

$$\begin{array}{c}\hfill E\left[X^j\right]=\frac{\alpha j!}{{\beta }^{j+1}}{e}^{\frac{\alpha }{\beta }}{E}_0^j\left(\frac{\alpha }{\beta }\right),\end{array}$$

(4)

where $E_s^j\left(z\right)=\frac{1}{j!}{\int }_1^{\infty }{\left(\log x\right)}^j{x}^{-s}{e}^{-zx}dx$, is the generalized integro-exponential function (Milgram [10]).

1.2. The Slash Standard Distribution

The Slash distribution is the distribution of the ratio of two independent random variables, one with a standard normal distribution (X) and the other with a uniform distribution (U) in $(0,1)$. whose stochastic representation is,

$$Y=\frac{X}{U^{1/q}},$$

(5)

where $X\sim N(0,1)$ and $U\sim U(0,1)$ independent and q is the parameter related to the kurtosis of the distribution. It will be denoted as $Y\sim S\left(q\right)$ and its density function has the following expression

$$f_Y\left(y\right)=\frac{2^{\frac{q-2}{2}}q}{\sqrt{\pi }{\left|y\right|}^{q+1}}\left[\Gamma \left(\frac{q+1}{2}\right)-\Gamma \left(\frac{q+1}{2},\frac{y^2}{2}\right)\right],y>0,$$

(6)

where $\Gamma \left(p\right)$ is the gamma function and $\Gamma (p,x)$ is the gamma incomplete function. This distribution has heavier tails than the normal distribution. The properties of this family are discussed in Rogers and Tukey [13] and Mosteller and Tukey [14].

The maximum likelihood estimators for the location and scale parameters are discussed in Kafadar [15]. Gómez, Quintana and Torres [16], and Gómez and Venegas [16] extend the Slash distribution to the elliptical Slash family. Genc [17] presented a symmetric generalization of the Slash distribution. More recently, Gómez, Olivares-Pacheco and Bolfarine [18] use the elliptic Slash family to extend the Birnbaum Saunders distribution. Reyes, Gómez and Bolfarine [19] introduce the modified Slash distribution replacing the uniform distribution with the exponential distribution of parameter 2, transforming it into a more flexible distribution that better captures outliers.

The paper is organized as follows: In Section 2, a closed expression for the pdf of a $SG$ model is obtained along with its most relevant indicators: moments, kurtosis coefficient, etc. Section 3 presents some important properties. Section 4 is dedicated to presenting some estimation methods such as the method of moments and maximum likelihood. A simulation study has been included to evaluate the performance of the proposals. Two applications to a real data set is given in Section 5, in which the new distribution fits better than other models of similar distribution. Finally, a discussion is presented in Section 6.

2. Slash Gompertz Distribution

The Slash Gompertz distribution is introduced by replacing in (5) the standard normal distribution by a Gompertz distribution with parameters $\alpha$ and $\beta$, transforming this into a distribution with higher kurtosis. We will start by deriving its density function.

2.1. Density Function

The Slash Gompertz distribution has the following stochastic representation

$$\begin{array}{c}\hfill W\equiv \frac{X}{U^{\frac{1}{q}}},\end{array}$$

(7)

where ≡ means equivalence in distribution, and X, U are independent random variables, such that $X\sim G(\alpha ,\beta )$ and $U\sim U(0,1)$, where $\alpha >0$ is the scale parameter, $\beta >0$ is the shape parameter and $q>0$ is the kurtosis parameter, so we say $W=U^{-1/q},X$ follows a Slash Gompertz distribution and will be denoted by $W\sim SG(\alpha ,\beta ,q)$.

Proposition 1.

Let W be a random variable such that $W\sim SG(\alpha ,\beta ,q)$, then its probability density function (pdf) is given by

$$\begin{array}{c}\hfill f_W\left(w\right)=\frac{\alpha q{e}^{\frac{\alpha }{\beta }}}{{\left(\beta w\right)}^{q+1}}\Gamma (q+1)E_0^q\left(\frac{\alpha }{\beta },e^{\beta w}\right),w\ge 0,\alpha ,\beta ,q>0,\end{array}$$

(8)

where $E_s^m\left(z,x\right)=\frac{1}{\Gamma \left(m+1\right)}{\int }_1^x{\left(\log w\right)}^m{e}^{-zw}{w}^{-s}dw$ is the Incomplete Generalized Integro-Exponential function (Milgram [10]).

Proof. 

Using the stochastic representation given in (7) and the random variable transformation method, we obtain

$$\begin{array}{c}\hfill f_W(w;\alpha ,\beta ,q)=\alpha q{e}^{\frac{\alpha }{\beta }}{\int }_0^1{\upsilon }^q{e}^{\beta \upsilon w-\frac{\alpha }{\beta }{e}^{\beta \upsilon w}}d\upsilon ,w\ge 0,\alpha ,\beta >0,\end{array}$$

(9)

making the change of variable $t=e^{\beta \upsilon w}$ and developing the integral, the result is obtained. □

Corollary 1.

If $q=1$ in (8), then the probability density function (pdf) of W is given by

$$\begin{array}{c}\hfill f_W\left(w\right)=\frac{\alpha e^{\frac{\alpha }{\beta }}}{{\left(\beta w\right)}^2}{E}_0^1\left(\frac{\alpha }{\beta },e^{\beta w}\right),w\ge 0,\alpha ,\beta >0,\end{array}$$

(10)

and we will say that $W=X{U}^{-1}$ follows a canonic Gompertz Slash distribution, and is denoted by $W\sim SG(\alpha ,\beta ,1)$.

Proof. 

Making $q=1$ in (8) the result is obtained. □

Figure 2 shows the plot of the Slash Gompertz distribution with $\alpha$ = 0.0001 and $\beta$ = 0.1 and different values of q, compared to the Gompertz distribution with $\alpha$ = 0.0001 and $\beta$ = 0.1.

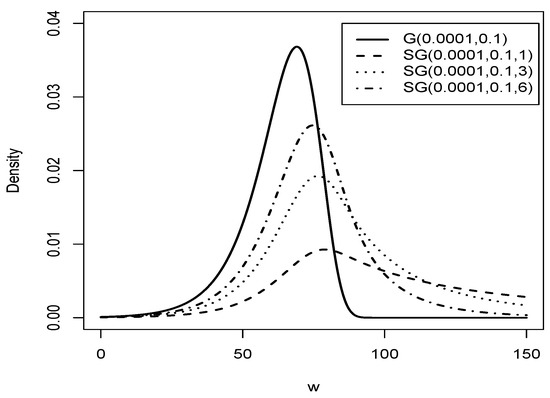
Figure 2. Graphic of comparison of the G distribution (solid line) with $SG$ distribution for $\alpha$ = 0.0001, $\beta$ = 0.01 and $q=1$ (dashed line), $q=3$ (dotted line), $q=6$ (dashed dotted line).

Figure 3 shows the graph of the Slash Gompertz distribution for different values of $\alpha$ and $\beta$ with $q=1$.

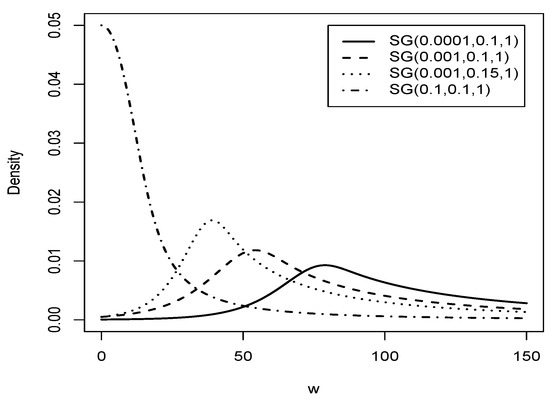
Figure 3. Graphic comparison of the $SG$ distribution for $q=1$ and different values of $\alpha$ and $\beta$.

Proposition 2.

Let $W\sim SG(\alpha ,\beta ,q)$. Then, the cdf of W is given by

$$\begin{array}{c}\hfill F_W\left(t\right)=\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\beta }^{q+1}}{\int }_0^t\frac{E_0^q\left(\frac{\alpha }{\beta },e^{\beta w}\right)}{w^{q+1}}dw.\end{array}$$

(11)

Proof. 

$$\begin{array}{ccc}\hfill F_W\left(t\right)& =& {\int }_0^t{f}_W\left(w\right)dw.\hfill \end{array}$$

Expanding the integral gives the result. □

In Figure 4, we graphically illustrate the behavior of the cumulative distribution function of the Slash Gompertz distribution and the Gompertz distribution.

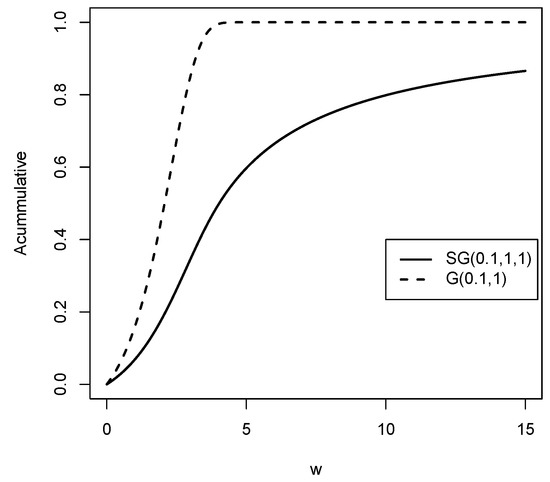
Figure 4. Cumulative distribution functions for the $SG$ distributions compared to the G distribution for values of $\alpha$, $\beta$ and q.

2.2. The Reliability and Hazard Rate Functions

Two important measures of reliability are the reliability function and the hazard (failure) rate function. The reliability function of a random variable Y is defined by $R_Y\left(t\right)=1-F_Y\left(t\right)$, where $F_Y$ denotes the cdf of Y. The hazard rate function is defined by $h_Y\left(t\right)=f_Y\left(t\right)/(1-F_Y\left(t\right))$. For the $SG$ distribution, as a direct consequence of Proposition 1 and Proposition 2, both measures of reliability can be expressed in closed form. The corresponding expressions are easily obtained.

Proposition 3.

Let $W\sim SG(\alpha ,\beta )$. Then, the Hazard function of W is given by

$$\begin{array}{ccc}\hfill h\left(t\right)& =& h_W\left(t\right)=\frac{\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\left(\beta t\right)}^{q+1}}{E}_0^q\left(\frac{\alpha }{\beta },e^{\beta t}\right)}{1-\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\beta }^{q+1}}{\int }_0^t\frac{E_0^q\left(\frac{\alpha }{\beta },e^{\beta y}\right)}{y^{q+1}}dy}.\hfill \end{array}$$

(12)

Proof. 

$$\begin{array}{c}\hfill h_W\left(t\right)=f_W\left(t\right)/(1-F_W\left(t\right)).\end{array}$$

Replacing $f_W\left(t\right)$ and $F_W\left(t\right)$ you get the result. □

Figure 5 and Figure 6 show the reliability function and the hazard rate function respectively of the Slash Gompertz law for different values of the parameters compared to the Gompertz distribution. It is clear that both functions exhibit a wide variety of forms. Therefore, the new family of distributions is flexible enough to model real data sets with high kurtosis.

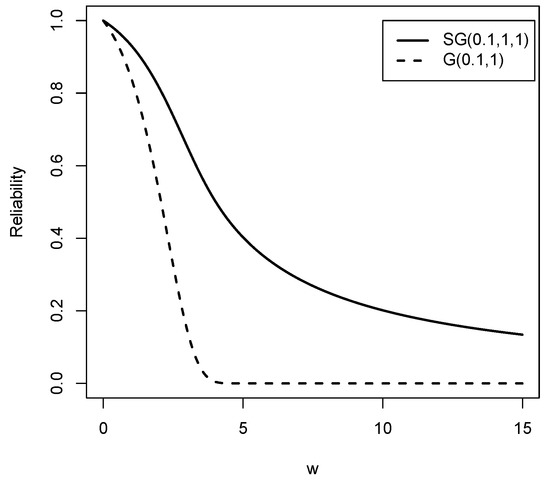
Figure 5. Reliability functions for the $SG$ distributions compared to the G distribution for values of $\alpha =0.1$, $\beta =1$ and $q=1$.

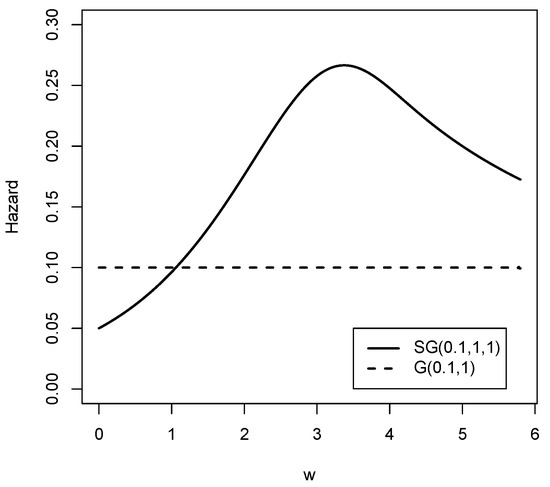
Figure 6. The hazard rate functions for the $SG$ and G distribution.

2.3. Reliability Function Comparison of Gompertz, Slash Birnbaum Saunders and Slash Gompertz Distributions

In this section, we make a brief comparison which illustrates that the tails of the Slash Gompertz distribution are heavier than the Gompertz distribution and the Slash Birnbaum Saunders distribution. For this we consider the Gompertz, Slash Birnbaum Saunders and Slash Gompertz distributions with $\alpha =0.1$, $\beta =3$ and $q=1$. Table 1 shows $P(Y>y)$ for different values of y in the mentioned distributions. It is evident that the Slash Gompertz distribution has much heavier tails than the Gompertz and Slash Birnbaum Saunders distributions.

Table 1. Reliability function comparison for distributions of G, $SBS$ and $SG$.

Distribution	$\mathit{P}(\mathit{Y}>4.1)$	$\mathit{P}(\mathit{Y}>4.2)$	$\mathit{P}(\mathit{Y}>4.3)$	$\mathit{P}(\mathit{Y}>4.4)$	$\mathit{P}(\mathit{Y}>4.5)$
G	0.0036	0.0014	0.0006	0.0003	0.0001
$SBS$	0.0260	0.0255	0.0250	0.0240	0.0241
$SG$	0.4912	0.4796	0.4685	0.4578	0.4476

Table 1 illustrates the fact that the Slash Gompertz distributions have heavier tails than the tails of the Gompertz and Slash Birnbaum Saunders distribution.

2.4. The rth Moment of a Gompertz Slash Distributed Random Variable W

The following proposition presents us with a formula that, through the use of numerical techniques, allows us to calculate the rth moment of a Slash Gompertz distribution.

Proposition 4.

Let $W\sim SG(\alpha ,\beta ,q)$ then for $r=1,2,3,...$ and $q>r$ the rth moment of random variable W is

$$\begin{array}{c}\hfill {\mu }_r=E\left[W^r\right]=\frac{\alpha qr!}{{\beta }^{r+1}(q-r)}{e}^{\frac{\alpha }{\beta }}{E}_0^r\left(\frac{\alpha }{\beta }\right),\left[0.5\mathrm{cm}\right]\end{array}$$

(13)

where

$$\begin{array}{c}\hfill E_0^r\left(\frac{\alpha }{\beta }\right)=\frac{1}{r!}{\int }_1^{\infty }{\left(\log x\right)}^r{e}^{-\frac{\alpha }{\beta }x}dx.\end{array}$$

Proof. 

Let X and U be independent random variables such that:

$$\begin{array}{c}\hfill {\mu }_r=E\left[W^r\right]=E\left[{\displaystyle {\left(\frac{X}{U^{\frac{1}{q}}}\right)}^r}\right]=E\left[X^r\right]E\left[U^{-\frac{r}{q}}\right],\end{array}$$

(14)

where $U\sim U(0,1)$, expanding we have that $E\left[U^{-\frac{r}{q}}\right]=\frac{q}{q-r}$, $q>r$.

Also as $X\sim G(\alpha ,\beta )$ we have that $E\left[X^r\right]=\frac{\alpha r!}{{\beta }^{r+1}}{e}^{\frac{\alpha }{\beta }}{E}_0^r\left(\frac{\alpha }{\beta }\right)$. Finally, substituting these results in (14) the result is obtained. □

2.5. Expected Value, Variance, Skewness and Kurtosis of a Gompertz Slash Distributed Random Variable W

Corollary 2.

The expected value of random variable $W\sim SG(\alpha ,\beta ,q)$, is

$$\begin{array}{c}\hfill E\left[W\right]=\frac{\alpha q}{{\beta }^2(q-1)}{e}^{\frac{\alpha }{\beta }}{E}_0^1\left(\frac{\alpha }{\beta }\right),\mathrm{for} \mathrm{all}q>1,where\end{array}$$

(15)

$$\begin{array}{c}\hfill E_0^1\left(\frac{\alpha }{\beta }\right)={\int }_1^{\infty }{\left(\log x\right)}^{-1}{e}^{-\frac{\alpha }{\beta }x}dx.\end{array}$$

Proof. 

From (13), the expected value of random variable W of a Gompertz Slash distribution, is given by

$$\begin{array}{ccc}\hfill E\left[W\right]& =& {\mu }_1\hfill \\ & =& \frac{\alpha q}{\beta (q-1)}{e}^{\frac{\alpha }{\beta }}{\int }_1^{\infty }{\left(\log x\right)}^{-1}{e}^{-\frac{\alpha }{\beta }x}dx\hfill \\ & =& \frac{\alpha q}{{\beta }^2(q-1)}{e}^{\frac{\alpha }{\beta }}{E}_0^1\left(\frac{\alpha }{\beta }\right),\mathrm{for} \mathrm{all}q>1.\hfill \end{array}$$

□

Corollary 3.

The variance of random variable $W\sim SG(\alpha ,\beta ,q)$, is

$$\begin{array}{c}\hfill Var\left(W\right)=\frac{\alpha q{e}^{\frac{\alpha }{\beta }}}{{\beta }^2}\left[\frac{2}{\beta (q-2)}{E}_0^2\left(\frac{\alpha }{\beta }\right)-\frac{q{e}^{\frac{\alpha }{\beta }}}{{\beta }^2{(q-1)}^2}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^2\right],\mathrm{for} \mathrm{all}q>2.\end{array}$$

(16)

Proof. 

The variance of a random variable W

$$\begin{array}{ccc}\hfill Var\left(W\right)& =& E\left[W^2\right]-{\left(E\left[W\right]\right)}^2.\hfill \end{array}$$

(17)

Concentrating on $E\left[W^2\right]$, if W is Slash Gompertz distributed, from (13):

$$\begin{array}{ccc}\hfill E\left[W^2\right]& =& \frac{2\alpha q}{{\beta }^3(q-2)}{e}^{\frac{\alpha }{\beta }}{E}_0^2\left(\frac{\alpha }{\beta }\right),\mathrm{for} \mathrm{all}q>2.\hfill \end{array}$$

(18)

Further, replacing (18) and (15) in (17), we obtain the numerical equation given in (16). □

Proposition 5.

The coefficient skewness of random variable $W\sim SG(\alpha ,\beta ,q)$, is

$$\begin{array}{c}\hfill {\gamma }_1=\frac{\frac{6\alpha q{e}^{\frac{\alpha }{\beta }}}{\beta (q-3)}{E}_0^3\left(\frac{\alpha }{\beta }\right)-\frac{6{\alpha }^{2}q{e}^{\frac{2\alpha }{\beta }}}{{\beta }^2\left(q-1\right)\left(q-2\right)}{E}_0^1\left(\frac{\alpha }{\beta }\right)E_0^2\left(\frac{\alpha }{\beta }\right)+\frac{2{\alpha }^6{q}^6{e}^{\frac{3\alpha }{\beta }}}{{\beta }^3{\left(q-1\right)}^3}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^3}{{\left(\frac{2\alpha q{e}^{\frac{\alpha }{\beta }}}{\beta (q-2)}{E}_0^2\left(\frac{\alpha }{\beta }\right)-\frac{{\alpha }^2{q}^2{e}^{\frac{2\alpha }{\beta }}}{{\beta }^2{(q-1)}^2}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^2\right)}^{\frac{3}{2},}},\end{array}$$

(19)

for all $q>3$.

Proof. 

Using the standardized symmetry coefficient given by

$$\begin{array}{c}\hfill {\gamma }_1=\frac{{\mu }_3-3{\mu }_1{\mu }_2+2{\mu }_1^3}{{({\mu }_2-{\mu }_1^2)}^{3/2}}\end{array}$$

(20)

and replacing in (20) the respective population moments ${\mu }_r$ given in (13) with $r=1,2,3$, the result given in (19). □

Proposition 6.

The coefficient kurtosis of random variable $W\sim SG(\alpha ,\beta ,q)$, is

$$\begin{array}{c}\hfill {\beta }_2=\frac{\frac{24\alpha q{e}^{\frac{\alpha }{\beta }}}{\beta (q-4)}{E}_0^4\left(\frac{\alpha }{\beta }\right)-\frac{24{\alpha }^2{q}^2{e}^{\frac{2\alpha }{\beta }}}{{\beta }^2(q-3)(q-1)}{E}_0^1\left(\frac{\alpha }{\beta }\right)E_0^3\left(\frac{\alpha }{\beta }\right)+\frac{12{\alpha }^3{q}^3{e}^{\frac{3\alpha }{\beta }}}{{\beta }^2(q-1)(q-3)}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^2{E}_0^2\left(\frac{\alpha }{\beta }\right)-\frac{3a^4{q}^4{e}^{\frac{4a}{b}}}{{\beta }^4{(q-1)}^4}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^4}{{\left(\frac{2\alpha q{e}^{\frac{\alpha }{\beta }}}{\beta (q-2)}{E}_0^2\left(\frac{\alpha }{\beta }\right)-\frac{{\alpha }^2{q}^2{e}^{\frac{2\alpha }{\beta }}}{{\beta }^2{(q-1)}^2}{E}_0^1{\left(\frac{\alpha }{\beta }\right)}^2\right)}^2},\end{array}$$

(21)

for all $q>4$.

Proof. 

Using the standardized kurtosis coefficient given by

$$\begin{array}{c}\hfill {\gamma }_2=\frac{{\mu }_4-4{\mu }_1{\mu }_3+6{\mu }_1^2{\mu }_2-3{\mu }_1^4}{{({\mu }_2-{\mu }_1^2)}^2}\end{array}$$

(22)

and replacing in (22) the respective population moments ${\mu }_r$ given in (13) with $r=1,2,3,4$, the result is obtained given in (21). □

Figure 7 graphically shows that for small values of alpha, the kurtosis coefficient is higher in the SG distribution than in the G distribution.

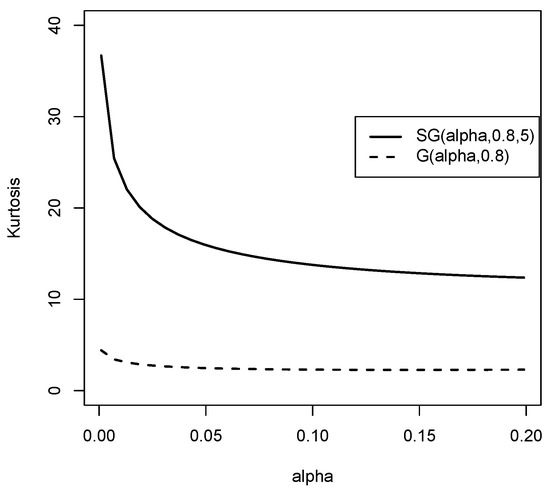
Figure 7. Kurtosis coefficient graphic for the $SG$ and the Gompertz distribution.

3. Some Statistical Properties

3.1. Failure Rate Function

The failure (or hazard) rate function of the $\mathit{SG}(\alpha ,\beta ,q)$ distribution is given by

$$h(t;\alpha ,\beta ,q)=\frac{f(t;\alpha ,\beta ,q)}{1-F(t;\alpha ,\beta ,q)}=\frac{\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\left(\beta t\right)}^{q+1}}{E}_0^q\left(\frac{\alpha }{\beta },e^{\beta t}\right)}{1-\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\beta }^{q+1}}p\left(t\right)},t>0,$$

where $p\left(t\right)={\int }_1^t\frac{E_0^q\left(\frac{\alpha }{\beta },e^{\beta y}\right)}{y^{q+1}}dy$.

Proposition 7.

For any $\alpha >0$, $\beta >0$ and $q>0$, the random variable X has increasing failure rate (IFR).

Proof. 

The first derivative of h can be written as follows

$$\begin{array}{ccc}\hfill h^{\prime }\left(t\right)& =& \frac{q\alpha \beta E_0^q{e}^{\beta t}\Gamma \left(q+1\right)e^{\frac{\alpha }{\beta }}}{{\left(1-p\left(t\right)q\alpha \Gamma \left(q+1\right)e^{\frac{\alpha }{\beta }}\right)}^2}.\hfill \end{array}$$

It is clear that $h^{\prime }(t;\alpha ,\beta ,q)>0$ since $t>0$, $\alpha >0$, $\beta >0$ and $q>0$ which implies the result. □

3.2. Mean Residual Life

An important reliability quantity for positive random variables is the mean residual life, which is defined as $\mu (t;\alpha ,\beta ,q)=\mathbb{E}\left(X-t|X>t\right)$, $t>0$. It is well-known that if a random variable has IFR, then its mean residual life is decreasing. Therefore, the mean residual life of X is a decreasing function in t. Furthermore, an analytical expression for the mean residual life is given in the following result.

Proposition 8.

The mean residual life function of X is given by

$$\mu (t;\alpha ,\beta ,q)=\mathbb{E}\left(X-t|X>t\right)=\frac{1}{S(t;\alpha ,\beta ,q)}{\int }_t^{\infty }S(x;\alpha ,\beta ,q)dx$$

$$=\frac{1}{S(t;\alpha ,\beta ,q)}{\int }_t^{\infty }\left(1-\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\beta }^{q+1}}p\left(x\right)\right)dx,$$

$t>0$, where $p\left(x\right)={\int }_0^x\frac{E_0^q\left(\frac{\alpha }{\beta },e^{\beta y}\right)}{y^{q+1}}dy,x>0.$

Proof. 

Let $S(x;\alpha ,\beta ,q)=1-F(x;\alpha ,\beta ,q)$. Then, by standard integration,

$$\mu (t;\alpha ,\beta ,q)=\mathbb{E}\left(X-t|X>t\right)=\frac{1}{S(t;\alpha ,\beta ,q)}{\int }_t^{\infty }S(x;\alpha ,\beta ,q)dx$$

which implies the result. □

3.3. Incomplete Moments

The first incomplete moment of X is defined as

$$m_1(x;\alpha ,\beta ,q)={\int }_0^{x}tf(t;\alpha ,\beta ,q)dt,x>0.$$

(23)

Proposition 9.

Let X be a random variable with $\mathit{SG}(\alpha ,\beta ,q)$ distribution. Then,

$$m_1(x;\alpha ,\beta ,q)=\frac{\alpha qr!}{{\beta }^{r+1}(q-r)}{e}^{\frac{\alpha }{\beta }}{E}_0^r\left(\frac{\alpha }{\beta },x\right),x>0.$$

(24)

$where{E}_0^r\left(\frac{\alpha }{\beta },x\right)=\frac{1}{r!}{\int }_1^x{\left(\log t\right)}^r{e}^{-\frac{\alpha }{\beta }t}dt.$

Proof. 

Substituting the density given in (8) in the first incomplete moment (23) the result is obtained. □

An interesting application of the first incomplete moment is that the mean deviation about the mean $\mu$ of X can be directly obtained, specifically by means of the relation

$$\mathbb{E}\left(|X-\mu |\right)=2\mu F(\mu ;\alpha ,\beta ,q)-2m_1(\mu ;\alpha ,\beta ,q),$$

where $\mu =E\left[X\right]$.

3.4. The Lorenz Curve and the Gini Index

The Lorenz curve, $L(x;\alpha ,\beta ,q)$, can also be obtained from the first incomplete moment and the expected value of X, specifically the following closed-form expression is obtained

$$L(x;\alpha ,\beta ,q)=\frac{m_1(x;\alpha ,\beta ,q)}{\rho }=\frac{\frac{\alpha qr!}{{\beta }^{r+1}(q-r)}{e}^{\frac{\alpha }{\beta }}{E}_0^r\left(\frac{\alpha }{\beta },x\right)}{3},x>0.$$

The Gini index is the measure of inequality associated with the Lorenz curve. For the random variable X, the Gini index is defined by

$$\begin{array}{c}\hfill G(\alpha ,\beta ,q)=1-\frac{1}{\mu }{\int }_0^{\infty }{(1-F(x;\alpha ,\beta ,q))}^{2}dx.\end{array}$$

(25)

The next result, an analytical expression is provided for $G(\alpha ,\beta ,q)$.

Proposition 10.

Let X be a random variable with $\mathit{SG}(\alpha ,\beta ,q)$ distribution. The Gini index is given by

$$\begin{array}{ccc}\hfill G(\alpha ,\beta ,q)& =& \stackrel{}{\stackrel{}{\underset{}{1-\frac{1}{\upsilon }{\int }_0^{\infty }{\left(1-\frac{\alpha q{e}^{\frac{\alpha }{\beta }}\Gamma \left(q+1\right)}{{\beta }^{q+1}}p\left(x\right)\right)}^{2}dx}}}\hfill \end{array}$$

(26)

where $p\left(x\right)={\int }_0^x\frac{E_0^q\left(\frac{\alpha }{\beta },e^{\beta y}\right)}{y^{q+1}}dy$.

Proof. 

Replacing the cumulative distribution (11) in the Gini index (25) the result is obtained. □

4. Inference

4.1. Moment Estimators

The following proposition shows us the set of equations, which through the use of numerical techniques, allow us to calculate the moment estimators of the parameters of a Slash Gompertz distribution.

Proposition 11.

Let $w_1,\cdots ,w_n$ be a random sample from the distribution of the random variable $W\sim SG(\alpha ,\beta ,q)$, so that the moment estimators from $\theta =(\alpha ,\beta ,q)$ for $q>3$ can be obtained numerically by solving the following system of nonlinear equations.

$$\begin{array}{c}\hfill {\widehat{q}}_M=\frac{{\widehat{\beta }}_M^2\overline{w}}{{\widehat{\beta }}_M^2\overline{w}-{\widehat{\alpha }}_M{e}^{\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}}{E}_0^1\left(\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}\right)},{\widehat{q}}_M>1,\end{array}$$

(27)

$$\begin{array}{c}\hfill \frac{2({\widehat{q}}_M-1)E_0^2\left(\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}\right)}{({\widehat{q}}_M-2){\widehat{\beta }}_M{E}_0^1\left(\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}\right)}=\frac{\overline{w^2}}{\overline{w}},{\widehat{q}}_M>2,\end{array}$$

(28)

$$\begin{array}{c}\hfill \frac{6({\widehat{q}}_M-2)E_0^3\left(\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}\right)}{({\widehat{q}}_M-3){\widehat{\beta }}_M{E}_0^1\left(\frac{{\widehat{\alpha }}_M}{{\widehat{\beta }}_M}\right)}=\frac{\overline{w^3}}{\overline{w}},{\widehat{q}}_M>3,\end{array}$$

(29)

where $\overline{w}=\frac{1}{n}{\sum }_{i=1}^n{w}_i$, $\overline{w^2}=\frac{1}{n}{\sum }_{i=1}^n{w}_i^2$ y $\overline{w^3}=\frac{1}{n}{\sum }_{i=1}^n{w}_i^3$ are the first three sample moments not centered respectively.

Proof. 

Replacing the population moments by the sample moments and using (13) gives that

$$E\left[W\right]=\frac{\alpha q}{{\beta }^2(q-1)}{e}^{\frac{\alpha }{\beta }}{E}_0^1\left(\frac{\alpha }{\beta }\right)=\overline{w},q>1,$$

(30)

$${\mu }_2=\frac{2\alpha q}{{\beta }^3(q-2)}{e}^{\frac{\alpha }{\beta }}{E}_0^2\left(\frac{\alpha }{\beta }\right)=\overline{w^2},q>2,$$

(31)

$${\mu }_3=\frac{6\alpha q}{{\beta }^4(q-3)}{e}^{\frac{\alpha }{\beta }}{E}_0^3\left(\frac{\alpha }{\beta }\right)=\overline{w^3},q>3,$$

(32)

and solving (30) for q gives the numerical equation for ${\widehat{q}}_M$ given in (27). Furthermore, replacing q by ${\widehat{q}}_M$ in (31) and (32), we obtain the numerical equations given in (28) and (29) for the moment estimators ${\widehat{\alpha }}_M$ and ${\widehat{\beta }}_M$, respectively. □

4.2. Maximum Likelihood Estimate

Given a random sample $Y_1,Y_2,\cdots ,Y_n$ of a distribution $SG(\alpha ,\beta ,q)$, the corresponding log-likelihood function can be written as

$$\begin{array}{c}\hfill {\displaystyle l(\alpha ,\beta ,q)=nlog\left(q\right)+nlog\left(\alpha \right)+\frac{n\alpha }{\beta }+\sum _{i=1}^{n}logG\left(y_i\right),}\end{array}$$

(33)

with $G\left(y_i\right)={\int }_0^1{v}^q{e}^{\beta y_{i}v-\left(\frac{\alpha }{\beta }\right)e^{\beta y_{i}v}}dv$ hence the likelihood equations are given by

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^n\frac{G_1\left(y_i\right)}{G\left(y_i\right)}=-\frac{n}{\alpha }-\frac{n}{\beta }}\end{array}$$

(34)

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^n\frac{G_2\left(y_i\right)}{G\left(y_i\right)}=\frac{n\alpha }{{\beta }^2}}\end{array}$$

(35)

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^n\frac{G_3\left(y_i\right)}{G\left(y_i\right)}=-\frac{n}{q},}\end{array}$$

(36)

where

$$\begin{array}{ccc}\hfill G_1\left(y_i\right)& =& \frac{\partial G\left(y_i\right)}{\partial \alpha }=-\frac{1}{\beta }{\int }_0^{1}v{e}^{2t_i-\left(\frac{\alpha }{\beta }\right)e^{t_i}}dv\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill G_2\left(y_i\right)& =& \frac{\partial G\left(y_i\right)}{\partial \beta }={\int }_0^{1}v{e}^{t_i-\left(\frac{\alpha }{\beta }\right)e^{t_i}}[t_i-\frac{\alpha (t_i-1)}{{\beta }^2}]dv\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill G_3\left(y_i\right)& =& \frac{\partial G\left(y_i\right)}{\partial q}=-{\int }_0^{1}vlnv{e}^{t_i-\left(\frac{\alpha }{\beta }\right)e^{t_i}}[t_i-\alpha t_i{e}^{t_i}+1]dv,\hfill \end{array}$$

(39)

where $t_i=\beta y_{i}v$.

The solutions of the Equations (34)–(36) can be obtained using numerical procedures such as Newton-Raphson.

An approach to obtain the MLE for the $SG$ model is through the optim function developed in the R software, the specific method is the L-BFGS-B developed by Byrd et al. [20] where each variable can be obtained by lower and/or upper bounds. This method uses a limited memory modification of the quasi-Newton method. For large samples, the estimated variance can be calculated by inverting the Hessian matrix, which can be calculated numerically using R software.

4.3. Simulation Study

Using the representation given in (7), it is possible to generate random numbers for the distribution $SG(\alpha ,\beta ,q)$, which leads to the following algorithm.

• Simulate $Y\sim U(0,1).$
• Compute $X=\left(\frac{1}{\beta }\right)ln(1-\left(\frac{\beta }{\alpha }\right)ln(1-Y)).$
• Simulate $V\sim U(0,1).$
• Compute $W=\frac{X}{V^{1/q}}.$

It then follows that $X\sim G(\alpha ,\beta )$ then $W\sim SG(\alpha ,\beta ,q)$. Table 2 shows the results of the simulation studies, illustrating the behavior of the MLEs for 2000 generated samples of sizes $n=50$, 100, 200 and 500 of the distributed population as $SG(\alpha ,\beta ,q)$. For each sample generated, the MLEs were calculated numerically using the Newton-Raphson procedure. The means, standard deviation (sd), average length of interval (ali) is the average length of the condence interval and the empirical coverage (c) of the respective EMV of the parameters, based on a 95% confidence interval.

Table 2. Simulation of 2000 iterations of the model $SG(\alpha ,\beta ,q)$.

n	$\mathit{\alpha }$	$\mathit{\beta }$	q	$\widehat{\mathit{\alpha }}$	$\mathit{sd}\left(\widehat{\mathit{\alpha }}\right)$	$\mathit{ali}\left(\widehat{\mathit{\alpha }}\right)$	$\mathit{c}\left(\widehat{\mathit{\alpha }}\right)$	$\widehat{\mathit{\beta }}$	$\mathit{sd}\left(\widehat{\mathit{\beta }}\right)$	$\mathit{ali}\left(\widehat{\mathit{\beta }}\right)$	$\mathit{c}\left(\widehat{\mathit{\beta }}\right)$	$\widehat{\mathit{q}}$	$\mathit{sd}\left(\widehat{\mathit{q}}\right)$	$\mathit{ali}\left(\widehat{\mathit{q}}\right)$	$\mathit{c}\left(\widehat{\mathit{q}}\right)$
50	0.3	0.8	2	0.2856	0.1097	0.4300	95.80	0.9213	0.5182	2.0312	94.20	2.3408	0.9507	3.7266	94.20
100	0.3	0.8	2	0.2970	0.0814	0.3191	95.25	0.8320	0.3327	1.3041	95.05	2.2171	0.6490	2.5441	94.50
200	0.3	0.8	2	0.2967	0.0574	0.2252	95.35	0.8281	0.2219	0.8700	95.10	2.0702	0.3626	1.4215	95.05
500	0.3	0.8	2	0.2987	0.0367	0.1437	95.25	0.8068	0.1330	0.5215	94.45	2.0334	0.1891	0.7413	94.65
50	0.5	0.8	2	0.4674	0.1669	0.6543	95.40	1.0022	0.6540	2.5639	93.80	2.2997	0.9467	3.7110	94.40
100	0.5	0.8	2	0.4884	0.1237	0.4849	95.25	0.8579	0.4110	1.6110	95.30	2.2498	0.7464	2.9260	94.95
200	0.5	0.8	2	0.4931	0.0886	0.3472	95.40	0.8361	0.2822	1.1064	95.00	2.1004	0.4795	1.8795	96.20
500	0.5	0.8	2	0.4973	0.0560	0.2196	95.10	0.8080	0.1658	0.6499	94.40	2.0424	0.2122	0.8318	94.60
50	1	0.8	2	0.9335	0.3183	1.2476	95.35	1.1682	1.0244	4.0156	94.05	2.2903	1.0496	4.1145	94.60
100	1	0.8	2	0.9627	0.2253	0.8833	95.35	0.9407	0.6059	2.3751	94.70	2.2923	0.9649	3.7823	95.95
200	1	0.8	2	0.9803	0.1607	0.6299	95.10	0.8621	0.4150	1.6269	95.40	2.1575	0.6500	2.5478	96.00
500	1	0.8	2	0.9918	0.1014	0.3973	94.65	0.8131	0.2407	0.9434	95.00	2.0629	0.2691	1.0547	94.55
50	0.5	0.8	1.5	0.4698	0.1779	0.6972	95.45	0.9858	0.7284	2.8553	93.25	1.7562	0.7416	2.9073	95.30
100	0.5	0.8	1.5	0.4905	0.1325	0.5196	95.05	0.8556	0.4724	1.8519	95.70	1.6659	0.5575	2.1852	96.40
200	0.5	0.8	1.5	0.4926	0.0941	0.3688	95.45	0.8431	0.3125	1.2249	95.00	1.5527	0.2592	1.0161	95.45
500	0.5	0.8	1.5	0.4979	0.0606	0.2376	95.30	0.8084	0.1863	0.7303	94.20	1.5237	0.1330	0.5215	94.55
50	0.5	0.2	1.2	0.4550	0.1628	0.6382	95.90	0.3419	0.4403	1.7260	93.60	1.4528	0.7541	2.9559	95.70
100	0.5	0.2	1.2	0.4779	0.1177	0.4614	95.10	0.2615	0.2816	1.1037	94.35	1.3398	0.4652	1.8235	96.50
200	0.5	0.2	1.2	0.4870	0.0844	0.3310	95.55	0.2398	0.1942	0.7611	94.50	1.2495	0.2177	0.8535	94.70
500	0.5	0.2	1.2	0.4957	0.0554	0.2172	95.45	0.2040	0.1177	0.4615	95.70	1.2288	0.1245	0.4880	94.35
50	1.5	1.8	2	1.4001	0.4905	1.9227	95.25	2.4105	1.7908	7.0200	93.95	2.2794	0.9683	3.7958	94.75
100	1.5	1.8	2	1.4543	0.3550	1.3918	95.40	2.0053	1.0838	4.2486	94.75	2.2610	0.8222	3.2230	95.30
200	1.5	1.8	2	1.4767	0.2547	0.9985	95.30	1.8987	0.7376	2.8913	95.10	2.1147	0.5043	1.9769	95.70
500	1.5	1.8	2	1.4899	0.1607	0.6299	95.10	1.8223	0.4313	1.6907	94.70	2.0497	0.2287	0.8966	94.40
50	0.2	0.5	1.2	0.1920	0.0814	0.3192	96.25	0.5700	0.3803	1.4909	94.35	1.3811	0.5239	2.0538	95.65
100	0.2	0.5	1.2	0.1987	0.0610	0.2392	95.35	0.5259	0.2618	1.0264	95.25	1.2864	0.2698	1.0575	94.20
200	0.2	0.5	1.2	0.1996	0.0429	0.1683	94.80	0.5078	0.1719	0.6738	94.85	1.2382	0.1577	0.6183	94.55
500	0.2	0.5	1.2	0.2006	0.0274	0.1074	95.15	0.4975	0.1032	0.4044	95.50	1.2189	0.0904	0.3544	94.65

sd corresponds to the standard deviation, ali (average length of interval) is the average length of the confidence interval and c the empirical coverage of the respective EMV of the parameters, based on a 95% confidence interval.

Table 2 shows that as the sample size increases, the parameter estimates converge. asymptotically to the true value of the parameters. Also, the standard deviations and the average length of the confidence intervals decrease as n increases, showing the consistency of the estimates. On the other hand, the empirical coverage is adequate, since it is close to 95%.

5. Applications with Real Data

The numerical illustrations below are intended to show that the $SG$ model can be an alternative to modeling unimodal data from different areas.

5.1. Application 1

We consider data from a study of warp breakage during weaving of fabrics (see Quesenberry, C.P., & Kent, J. [21]), 100 yarn samples were tested. The number of stress cycles was determined until rupture for each yarn sample, for which their statistical measurements were obtained and the maximum likelihood estimators of the parameters of the Slash Gompertz distribution are obtained and compared with those of the Gompertz distribution and the Slash Birnbaum Saunders distribution with their corresponding standard errors.

Table 3 shows a summary of statistical measures for the data set where the number of stress cycles until rupture was determined for each thread sample, it can be seen that the data has a high level of kurtosis.

Table 3. Summary statistics for the rupture data set.

n	$\overline{\mathit{Y}}$	${\mathit{S}}_{\mathit{Y}}$	$\sqrt{{\mathit{\beta }}_1}$	${\mathit{\beta }}_2$
100	221.98	144.6181	1.3396	5.7435

In Table 4 is shown the best fit of the new model compared to the Gompertz and Slash Birnbaum Saunders distribution, since the Akaike Information Criterion (AIC) and Bayesian information criterion (BIC) values are much lower than their competitors.

Table 4. Maximum likelihood estimators for rupture data with their corresponding standard errors in parentheses and AIC, BIC criteria.

Parameters	MLE (G)	MLE ($\mathit{SBS}$)	MLE ($\mathit{SG}$)
$\alpha$	0.0031 (0.0003)	0.4307 (0.0967)	0.0024 (0.0003)
$\beta$	0.0022 (0.0004)	193.4896 (16.0376)	0.0083 (0.0018)
q		2.1425 (0.7495)	3.1919 (0.8035)
AIC	1266.907	1265.789	1256.003
BIC	1272.918	1273.602	1263.818

The histogram plot of the rupture data with the Slash Gompertz distribution fitted with the maximum likelihood estimators of its parameters is shown in Figure 8 compared with the Gompertz distribution and the Slash Birnbaum Saunders distribution.

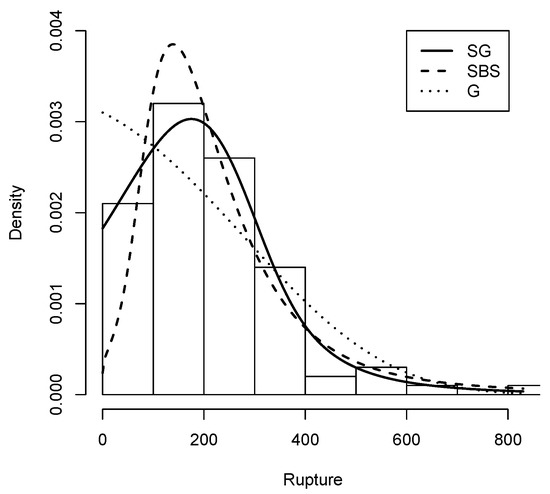
Figure 8. Rupture data histogram with Density $SG$ (solid line), G density (dashed line) and $SBS$ density (dotted line).

Figure 9 and Figure 10 visually show the best fit of the studied model compared to the Gompertz and Slash birnbaum Saunders distributions. In the first, the theoretical quantiles approximate the line $y=x$ much better than the competing distributions. While in the second, the approximation of the empirical CDF of the model of interest is closer to the empirical CDF of the data.

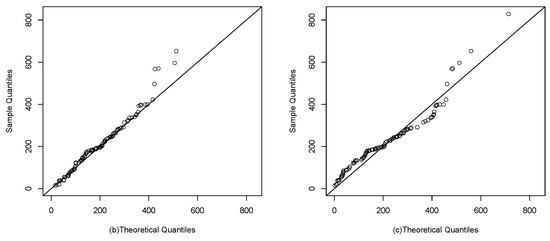
Figure 9. Q-q plots: $SG$ (a), $SBS$ (b) and G (c).

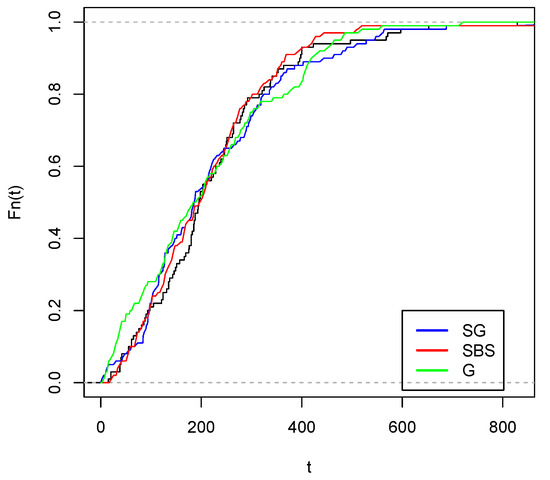
Figure 10. Empirical cdf with estimated $SBS$ c.d.f. (red color), estimated G c.d.f. (green color) and estimated $SG$ cdf (blue color).

5.2. Application 2

In this application we consider the Gompertz-Verhulst ($GV$) distribution M. Ahsanullah et al. [22], whose density function is given by

$$\begin{array}{c}{f}_X(x;\alpha ,\lambda ,\sigma )=\alpha \lambda \sigma e^{-\lambda x}{(1-\sigma e^{-\lambda x})}^{\alpha -1}\end{array}$$

(40)

and the Slash Weibull distribution, Olivares-Pacheco, J.O., Cornide-Reyes H.C., Monasterio, M. [23], whose density function is given by:

$$\begin{array}{c}{f}_X(x;\alpha ,\beta ,q)=\frac{q^{\beta }{x}^{\beta -1}}{{\alpha }^{\beta }}{T}_X\left(x\right)\end{array}$$

(41)

with $T_X\left(x\right)={\int }_0^1{w}^{\beta +q-1}{e}^{-{\left(\frac{xw}{\alpha }\right)}^{\beta }}dw$.

Following illustration is related to the nickel content in soil samples analyzed at the Mining Department (Department of Mines) of University of Atacama, Chile. The parameters of the Slash Gompertz distribution are estimated and compared with the Gompertz, Slash Weibull and Gompertz-Verhulst distributions with their corresponding standard errors.

Table 5 shows a summary of statistical measures for the data set on nickel content, it can be seen that the data has a high level of kurtosis.

Table 5. Summary statistics for the nickel content data set.

n	$\overline{\mathit{Y}}$	${\mathit{S}}_{\mathit{Y}}$	$\sqrt{{\mathit{\beta }}_1}$	${\mathit{\beta }}_2$
85	21.588	16.573	2.392	8.325

Table 6 shows the best fit of the Slash Gompertz compared to the Gompertz, Slash Weibull and Gompertz-Verhulst distribution, because the AIC and BIC values are lower than those of its competitors.

Table 6. Maximum likelihood estimators for nickel data with their corresponding standard errors in parentheses and AIC, BIC criteria.

Parámetros	MLE (G)	MLE ($\mathit{SW}$)	MLE($\mathit{GV}$)	MLE ($\mathit{SG}$)
$\alpha$	0.0378 (0.0057)	2.0890 (0.3200)	2.0631 (0.7925)	0.0118 (0.0046)
$\beta$	0.0112 (0.0049)	14.4769 (1.7959)		0.2146 (0.0433)
$\lambda$			0.0737 (0.0114)
$\sigma$			1.0498 (0.1254)
q		2.4182 (0.6042)		2.0852 (0.3395)
AIC	698.112	677.936	681.128	674.276
BIC	703.021	685.339	688.481	681.633

The histogram plot of the nickel data with the Slash Gompertz distribution fitted with the maximum likelihood estimators of its parameters is shown in Figure 11 compared with the Gompertz-Verhulst, Slash Weibull and Gompertz distributions. It also better captures outlier data.

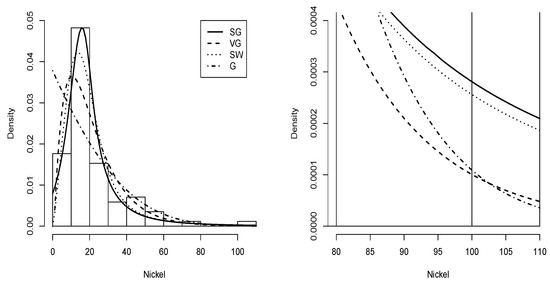
Figure 11. Data nickel histogram with density $SG$ (solid line), $GV$ density (dashed line), $SW$ density (dotted line) and G density (dashed-dotted line).

Figure 12 and Figure 13 show the best fit of the Slash Gompertz model compared to the Slash Weibull and Gompertz-Verhulst distributions. In the first, it can be seen that the theoretical quantiles are quite close to the $y=x$ line with respect to the Slash Gompertz, Gompertz-Verhulst and Slash Weibull distributions. In the second figure, the approximation of the empirical CDF of the studied model is closer to the empirical CDF than the other distributions.

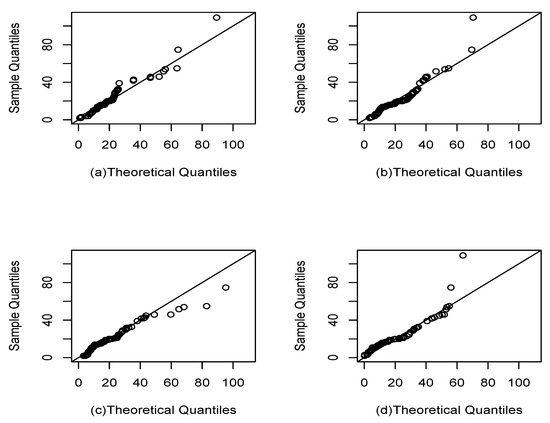
Figure 12. Q-q plots: $SG$ (a), $GV$ (b) $SW$ (c) and G (d).

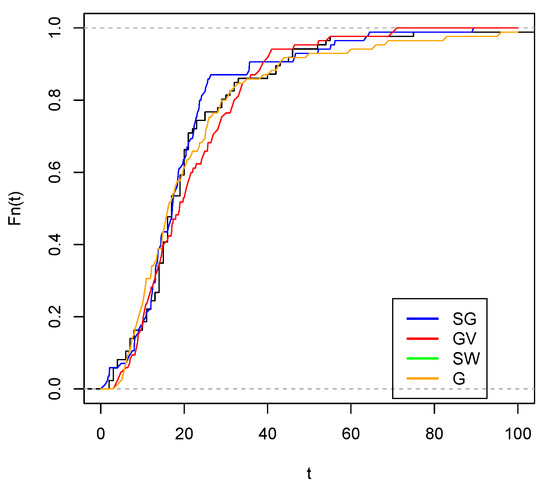
Figure 13. Empirical cdf with estimated G c.d.f. (orange color), $SW$ c.d.f. (green color), estimated $GV$ c.d.f. (red color) and estimated $SG$ cdf (blue color).

5.3. Comparison of Estimated Reliability

Figure 14 visually confirms that the Slash Gompertz distribution captures a greater amount of extreme data compared to its competitors.

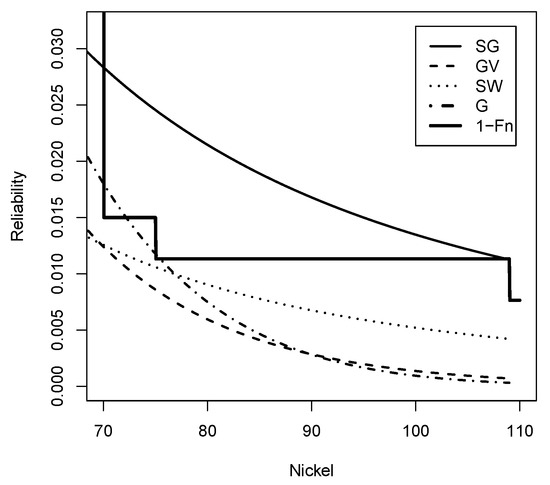
Figure 14. Reliability function $SG$ (Solid line), $GV$ (dashed line), $SW$ (dotted line), G (dashed-dotted line) and Empirical reliability (Solid Line) for nickel data set.

Table 7 theoretically demonstrates that the studied model has a higher kurtosis compared to the competing distributions.

Table 7. Estimation of reliability for $SG$, $GV$, $SW$ and G models for the rupture dataset.

	$\mathit{SG}$	$\mathit{SW}$	$\mathit{GV}$	G
Number of Cycles (t)	$\mathit{P}(\mathit{Y}>\mathit{t})$	$\mathit{P}(\mathit{Y}>\mathit{t})$	$\mathit{P}(\mathit{Y}>\mathit{t})$	$\mathit{P}(\mathit{Y}>\mathit{t})$
70	0.0283	0.0125	0.0124	0.0180
80	0.0214	0.0090	0.0059	0.0079
90	0.0167	0.0087	0.0028	0.0028
100	0.0134	0.0052	0.0013	0.0009
110	0.0211	0.0041	0.0006	0.0002

6. Discussion

We introduce a new distribution with positive support based on the Gompertz distribution. The objective is to obtain a more flexible model that models asymmetric data with high kurtosis. We consider a study of the univariate version. We perform parametric estimation using the method of moments and maximum likelihood. We carry out a simulation study to see the behavior of the estimators of the parameters of the new distribution. We present two illustrations with data sets, where we show that the Slash Gompertz distribution fits real data better than the Gompertz, Birnbaum Saunders Slash, Slash Weibull, and Gompertz-Verhulst distributions, to model the reliability function of the data distribution.