Abstract
The kernel ridge regression (KRR) and its updated version taking into account the odd-even effects (KRRoe) are employed to improve the mass predictions of the relativistic density functional theory. Both the KRR and KRRoe approaches can improve the mass predictions to a large extent. In particular, the KRRoe approach can significantly improve the predictions of the one-nucleon separation energies. The extrapolation performances of the KRR and KRRoe approaches to neutron-rich nuclei are examined, and the impacts of the KRRoe mass corrections on the r-process simulations are studied. It is found that the KRRoe mass corrections for the nuclei in the r-process path are remarkable in the light mass region, e.g., , and this could influence the corresponding r-process abundances.
1. Introduction
Nuclear mass plays an important role not only in nuclear physics [1] but also in astrophysics [2,3]. Great progress has been made in mass measurements of atomic nuclei during the past decades, and masses of about 2500 nuclei have been measured to date [4], mainly by the time-of-flight, the Penning-trap, and the storage-ring mass spectrometers. Nevertheless, the masses of a large number of neutron-rich nuclei relevant to the r-process remain unknown and cannot be measured in the foreseeable future. Therefore, reliable theoretical predictions for nuclear masses are important at the present time.
In despite of the great efforts on the theoretical descriptions for nuclear masses, the current accuracies of the obtained mass tables are still not sufficient for accurate studies of astrophysical nucleosynthesis [5,6]. The microscopic models are usually believed to have a better reliability of extrapolation for neutron-rich nuclei than the macroscopic-microscopic models. Therefore, in the past decades, both the non-relativistic and relativistic nuclear energy density functional theories (DFTs) have been developed for building nuclear mass tables [7,8,9,10,11,12,13].
The relativistic DFT has been proved to be a powerful theory in nuclear physics by its successful descriptions of many nuclear phenomena [14,15,16,17,18,19,20]. It takes Lorentz symmetry into account in a self-consistent way and provides an efficient description of nuclei with the underlying large scalar and vector fields of the order of a few hundred MeV, which are hidden in the non-relativistic DFTs. This is clearly seen in the non-relativistic reduction of CDFT via a similarity renormalization method, which provides a possible means to bridge the relativistic and non-relativistic DFTs [21,22].
In most cases, the relativistic DFT is realized with the relativistic mean-field (RMF) model, and several nuclear mass tables have been established up to date [7,8,11,12,13]. Two of them contain the masses of all even-even, even-odd, odd-even, and odd-odd nuclei [7,8]. The first one [7] was built via the RMF calculations with the TMA interaction [23]. Though the deformation effects were taken into account, the pairing correlations were treated with the Bardeen-Cooper-Schrieffer (BCS) approach, which is not proper for weakly-bound nuclei. The other one [8] is based on the relativistic continuum Hartree Bogoliubov (RCHB) theory with the PC-PK1 interaction [24], where the pairing correlations are treated with the more justified Bogoliubov approach, but the deformation effects are missing.
To further improve the mass descriptions, in recent years, the machine learning (ML) approach has attracted a lot of attentions, and has been successfully employed in many topics in nuclear physics [25]. In particular for nuclear masses, many ML approaches have been employed to improve the mass description, such as the kernel ridge regression (KRR) [26,27], the radial basis function (RBF) [28,29,30], the Bayesian neural network (BNN) [31,32,33], the Levenberg-Marquardt neural network [34], the gaussian process regression [35], the light gradient boosting machine [36], the Bayesian probability classifier [37], etc. In particular, the RBF approach has been employed to improve the mass predictions of the microscopic RMF model, and it reduces the root-mean-square (rms) deviation from to MeV [38]. Furthermore, it was found that the RBF corrections of the neutron-rich nuclei have obvious effects on the r-process abundances [38]. However, one should note that the reliability of the ML extrapolation for neutron-rich nuclei is sometimes questionable, since different approaches may provide completely different extrapolations [39].
In the recent study [26], it shows that the RBF approach would worsen the mass predictions at large extrapolation distances towards the neutron-rich side. In contrast, the KRR approach can automatically identify the limit of the extrapolation distance and avoid the risk of worsening the mass predictions for neutron-rich nuclei at large extrapolation distances. Furthermore, by taking the odd-even effects into account, the extended KRR approach could significantly improve the description of one-nucleon separation energies [27], which are especially important in the r-process simulations. Therefore, in the present work, we would like to employ the KRR approach and its updated version taking into account the odd-even effects to improve the mass predictions of the RMF model, and explore the impacts on the r-process simulations.
2. Theoretical Framework
In the KRR approach [26,27,40], the predictive function is written as
where represent the proton and neutron numbers of nuclei, m is the total number of nuclei in the training set, are weight parameters, and is the kernel function that represents the similarity between two nuclei. In the flat version of the KRR approach [26], the kernel function is taken as
while later, it is updated as remodulated kernel function in the extended KRR approach with the odd-even effects (KRRoe) [27],
where when two nuclei and have the same parity of neutron and proton numbers, otherwise . Here, , , and are hyperparameters to be determined.
The weights are obtained via minimizing the loss function written as
where . The first term represents the variance between the KRR prediction and the data , and the second one is a penalty term to avoid overfitting. Minimizing the loss function (4) yields
where is the kernel matrix with elements , and is the identity matrix.
3. Numerical Details
The predictive function (1) is trained to reconstruct the nuclear mass residuals, i.e., the mass deviations between the experimental data and the theoretical predictions . Once the weight parameters are determined, the reconstructed function can be obtained with Equation (1) for every nucleus . The predicted mass by the KRR approach for a nucleus is, thus, given by .
In the present work, the experimental masses are taken from the AME2020 [4], while only those nuclei with are considered. The entire data set includes totally 2421 nuclei. The theoretical predictions of nuclear masses are taken from the RMF mass table from Ref. [7].
The 110 nuclei newly appear in the AME2020 [4] as compared with AME2012 [41] are taken as validation data to optimize the hyperparameters. With a given set of hyperparameters, the KRR predictions of the 110 nuclear masses can be given by the network trained with the data of the other 2311 nuclei. The optimized hyperparameters are obtained when the rms deviation between the experimental data and the predictions of the 110 nuclear masses attains its minimum. The optimized hyperparameters are for the KRR approach, and for the KRRoe approach.
4. Results and Discussion
In Figure 1, the rms deviations of masses, one-neutron separation energies (), and one-proton separation energies () between the experimental data and the predictions of the RMF mass model, the RBF, the KRR, and the KRRoe approaches are shown. The ML predictions for every nucleus are determined with the corresponding networks being trained on all other nuclei with known masses, which is known as the leave-one-out cross validation. It is seen that all ML approaches significantly improve the descriptions of nuclear masses, in particular for the KRRoe approach with the odd-even effects. For the one-nucleon separation energies, however, only the KRRoe approach can obviously improve the descriptions. This is understandable because the odd-even effects play an essential role in the description of one-nucleon separation energies.
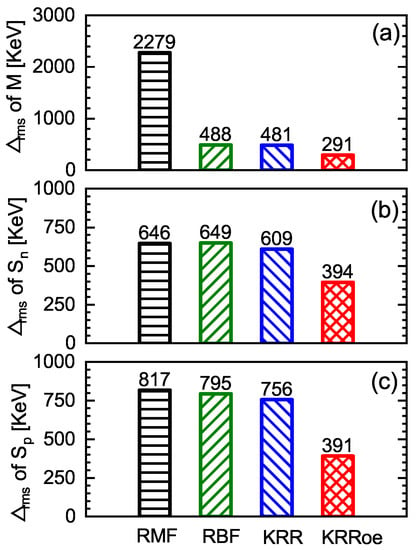
Figure 1.
The rms deviations of masses (a), one-neutron separation energies (b), and one-proton separation energies (c) between the experimental data and the predictions of the RMF mass model, the RBF, the KRR, and the KRRoe approaches.
Mass differences between the experimental data [4] and the predictions of the RMF mass model, the KRR, and the KRRoe approaches for the 2421 nuclei are shown in Figure 2. The differences between the experimental data and the RMF masses are roughly 2–3 MeV for most nuclei, and this gives rise to a rms deviation of 2.279 MeV. More specifically, there are several strongly overbound regions around , and , and several strongly underbound regions around and . This description is greatly improved by the KRR approach (see Figure 2b). The corresponding differences are mainly within 500 keV, and the corresponding rms deviation is reduced to 481 keV. Note that the strongly overbound and underbound regions are well eliminated. However, one can see obvious odd-even staggering between the masses improved by the KRR approach and the experimental data, and they are well eliminated by the KRRoe approach. As seen in Figure 2c, the differences between the experimental data and the KRRoe approach are visible only for a small fraction of nuclei, and the corresponding rms deviation is reduced to 291 keV.
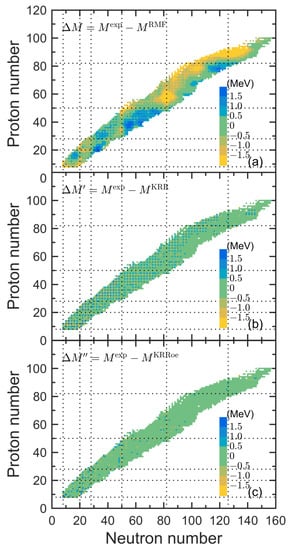
Figure 2.
Mass differences between the experimental data [4] and the predictions of the RMF mass model [7] (a), the KRR approach (b), and the KRRoe approach (c). Note that contour scale of panel (a) is different from those of panels (b,c).
To examine the predictive powers of the KRR and KRRoe approaches when extrapolating to the neutron-rich nuclei, the entire set of 2421 nuclei with known masses is redivided as shown in Figure 3. Similar to Refs. [26,27], the sixteen most neutron-rich nuclei for each isotopic chain are removed out from the training set, and then, they are reclassified into sixteen test sets respectively, according to the extrapolation distances from the training set along the neutron direction. Note that the nuclei included in the training set are now even less than the ones included in the sixteen test sets.
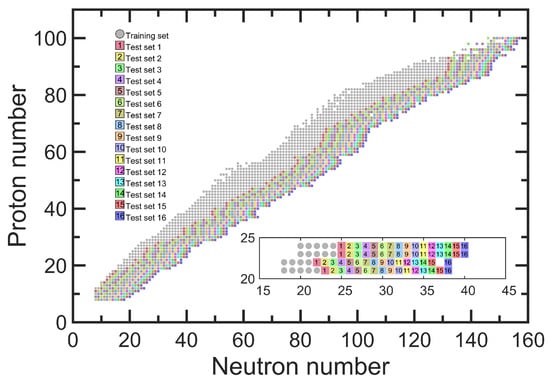
Figure 3.
Classifications of nuclei into one training set and sixteen test sets to examine the extrapolation power for the neutron-rich nuclei. The inset zooms in the region from to 24.
In Figure 4a, the rms deviations of the predicted masses by the RMF model, the KRR, and the KRRoe approaches with respect to the experimental data are shown as functions of the extrapolation distances for the sixteen test sets classified as in Figure 3. It can be seen that both the KRR and KRRoe approaches can improve the mass descriptions of nuclei to a large extent even when the extrapolation distance reaches to 10. The KRRoe approach achieves a further improvement of about 200 keV when the extrapolation distances are smaller than 8. With the increase of the extrapolation distances, the improvements achieved by both the KRR and KRRoe approaches become less significant, and the corresponding rms deviations at large extrapolation distances are similar or slightly smaller than the RMF ones. This indicates that the KRR-based approaches can nicely avoid the risk of worsening the predictions for nuclei at large extrapolation distances, as discussed in detail in Ref. [26].
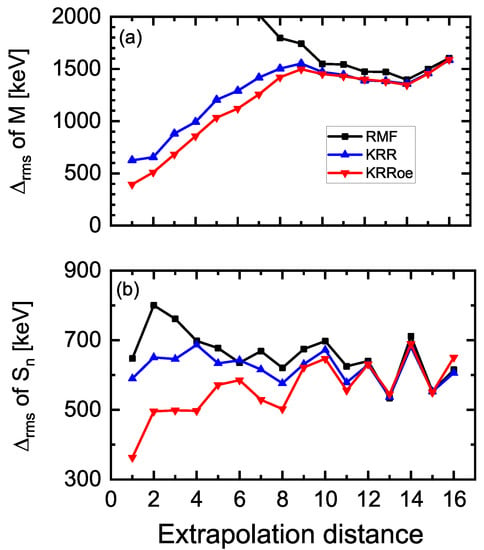
Figure 4.
The rms deviations of the predicted masses M (a) and one-neutron separation energies (b) by the RMF mass model (squares), the KRR (up triangles), and the KRRoe (down triangles) approaches with respect to the experimental data as functions of the extrapolation distances for the sixteen test sets as denoted in Figure 3.
In Figure 4b, similar extrapolation performances for the one-neutron separation energies are depicted. For the KRR approach, a significant improvement of the one-neutron separation energy can only be seen for nuclei with the extrapolation distances less than 4, while for the KRRoe approach, the description of the one-neutron separation energy can be improved for nuclei with the extrapolation distances up to 11. Even for nuclei with small extrapolation distances, the improvements given by the KRRoe approach could be larger than that of the KRR approach by more than 200 keV. When the extrapolation distance reaches 12, both the KRRoe and KRR approaches give similar results with the RMF mass model, and this again avoids the worsening of the RMF descriptions.
To investigate the impacts of the KRRoe corrections on the r-process simulations, the classical r-process model is employed to calculate the r-process abundances in a specific astrophysical condition with the temperature GK, the irradiation time s, and the neutron density . For more details on the classical r-process model, one can see Refs. [6,42,43,44,45,46]. The classical r-process simulations require the nuclear physics inputs of nuclear masses and -decay half-lives. For the nuclear masses, the RMF mass table and the KRRoe mass predictions are employed unless the experimental data are available. Accordingly, the experimentally unknown -decay half-lives are taken from the quasiparticle random-phase approximation based on the finite-range droplet model (FRDM + QRPA) [47], while their consistencies with respect to the mass inputs are achieved approximately by the relation . In Figure 5, the r-process abundances obtained from the classical r-process simulations with the mass inputs from the RMF and the KRRoe models are depicted. The abundance patterns associated with the RMF and the KRRoe models are similar at large mass numbers, e.g., , while apparent differences can be seen for relatively small mass numbers, e.g., and .
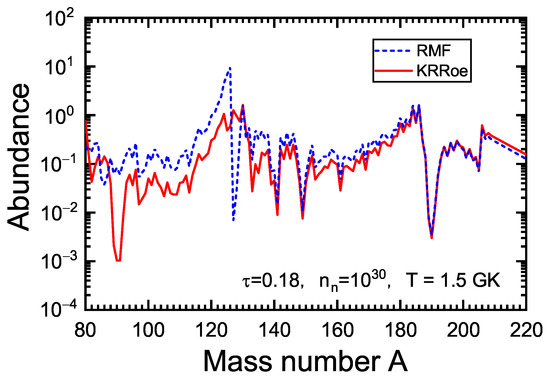
Figure 5.
The r-process abundances from the classical r-process simulations with a specific astrophysical condition (temperature , irradiation time , and neutron density ) with the mass inputs from the RMF (dashed line) and the KRRoe (solid line) models.
To understand the impacts of the KRRoe corrections on the r-process abundances, in Figure 6, the KRRoe reconstructed function for nuclei in the whole nuclear chart are depicted together with the r-process path. Here, the nuclei in the r-process path are chosen from the isotopes with the abundances larger than 10% of the total abundance among each isotopic chain in the equilibrium phase of simulations. Since the simulations with either RMF masses or KRRoe ones give similar r-process paths, in Figure 6, only the path obtained with the RMF masses is drawn. It is seen that the r-process path is close to the experimentally known nuclei in the light mass region, while it is far away from the experimental boundary in the heavy mass region. At the meantime, the KRRoe reconstructed function decays along the extrapolation away from the experimentally known region. Therefore, the KRRoe mass corrections for the nuclei in the r-process path are remarkable only in the light mass region. This explains the differences of the abundance patterns associated with the RMF and the KRRoe models as seen in Figure 5.
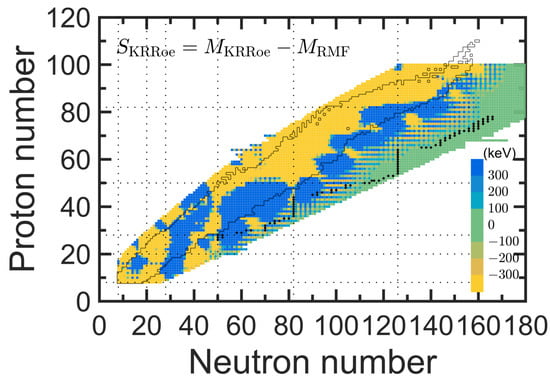
Figure 6.
The KRRoe corrections for the RMF mass model. The nuclei in the r-process path are shown by black filled circles (see text), and the boundary of nuclei inAME2020 [4] is represented by black contour lines.
Finally, it should be noted that since the aim of the present study is not to reproduce the solar r-process abundances, the weighted superposition of different astrophysical conditions is not performed in the classical r-process simulations. However, by considering such superpositions, the influence of the KRRoe mass corrections on the r-process abundance patterns could be smeared. It would be interesting to consider the superposition of different neutron flows in the classical r-process simulation or the superposition of different density and temperature evolution profiles in the dynamical r-process simulation. Such studies are important to address to what extent the KRRoe mass corrections can affect the understanding of the origin of heavy elements, and will be done in the future.
5. Summary
In summary, the KRR and KRRoe approaches have been employed to improve the mass predictions of the microscopic RMF mass table. Both the KRR and KRRoe approaches can improve the mass predictions to a large extent. The KRRoe approach achieves a higher accuracy than the KRR approach by taking into account the odd-even effects, and it also significantly improves the predictions of the one-nucleon separation energies. The extrapolation abilities of the KRR and KRRoe approaches to neutron-rich nuclei have also been examined. The performance of the KRRoe approach is better than that of the KRR approach, not only in the length of the extrapolation distance, but also in the reduction of the rms deviation at a given distance. Finally, the impacts of the KRRoe mass corrections on the r-process simulations have been studied. The KRRoe mass corrections of nuclei in the r-process path are remarkable in the light mass region, e.g., , and this could influence the corresponding r-process abundances.
Author Contributions
Conceptualization, X.W. and P.Z.; methodology, L.G. and X.W.; software, L.G.; validation, X.W.; formal analysis, L.G.; data curation, L.G.; investigation, L.G.; resources, P.Z.; writing—original draft preparation, L.G. and X.W.; writing—review and editing, P.Z.; visualization, L.G.; supervision, P.Z.; project administration, P.Z.; funding acquisition, X.W. and P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the National Key R&D Program of China (Contracts No. 2018YFA0404400 and No. 2017YFE0116700), the National Natural Science Foundation of China (Grants No. 11875075, No. 11935003, No. 11975031, No. 12141501 and No. 12070131001), the China Postdoctoral Science Foundation under Grant No. 2021M700256, and the High-performance Computing Platform of Peking University.
Data Availability Statement
The dataset can be accessed upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lunney, D.; Pearson, J.M.; Thibault, C. Recent trends in the determination of nuclear masses. Rev. Mod. Phys. 2003, 75, 1021–1082. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the Elements in Stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef] [Green Version]
- Mumpower, M.; Surman, R.; McLaughlin, G.; Aprahamian, A. The impact of individual nuclear properties on r-process nucleosynthesis. Prog. Part. Nucl. Phys. 2016, 86, 86–126. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME2020 atomic mass evaluation. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Mumpower, M.R.; Surman, R.; Fang, D.L.; Beard, M.; Möller, P.; Kawano, T.; Aprahamian, A. Impact of individual nuclear masses on r-process abundances. Phys. Rev. C 2015, 92, 035807. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.F.; Wu, X.H.; Zhao, P.W. Sensitivity Study of r-process Abundances to Nuclear Masses. Astrophys. J. 2021, 915, 29. [Google Scholar] [CrossRef]
- Geng, L.S.; Toki, H.; Meng, J. Masses, deformations and charge radii—Nuclear ground-state properties in the relativistic mean field model. Prog. Theor. Phys. 2005, 113, 785–800. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.W.; Lim, Y.; Zhao, P.W.; Liang, H.Z.; Qu, X.Y.; Chen, Y.; Liu, H.; Zhang, L.F.; Zhang, S.Q.; Kim, Y.; et al. The limits of the nuclear landscape explored by the relativistic continuum Hartree-Bogoliubov theory. Atom. Data Nucl. Data Tables 2018, 121, 1–215. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S.; Chamel, N.; Pearson, J.M. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef] [Green Version]
- Erler, J.; Birge, N.; Kortelainen, M.; Nazarewicz, W.; Olsen, E.; Perhac, A.M.; Stoitsov, M. The limits of the nuclear landscape. Nature 2012, 486, 509–512. [Google Scholar] [CrossRef]
- Afanasjev, A.; Agbemava, S.; Ray, D.; Ring, P. Nuclear landscape in covariant density functional theory. Phys. Lett. B 2013, 726, 680–684. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.L.; Wang, Y.K.; Zhao, P.W.; Li, Z.P. Nuclear landscape in a mapped collective Hamiltonian from covariant density functional theory. Phys. Rev. C 2021, 104, 054312. [Google Scholar] [CrossRef]
- Zhang, K.; Cheoun, M.K.; Choi, Y.B.; Chong, P.S.; Dong, J.; Dong, Z.; Du, X.; Geng, L.; Ha, E.; He, X.T.; et al. Nuclear mass table in deformed relativistic Hartree-Bogoliubov theory in continuum, I: Even-even nuclei. Atom. Data Nucl. Data Tables 2022, 144, 101488. [Google Scholar] [CrossRef]
- Meng, J. Relativistic Density Functional for Nuclear Structure; World Scientific: Singapore, 2016. [Google Scholar]
- Meng, J.; Peng, J.; Zhang, S.Q.; Zhao, P.W. Progress on tilted axis cranking covariant density functional theory for nuclear magnetic and antimagnetic rotation. Front. Phys. 2013, 8, 55–79. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193–263. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.; Lalazissis, G.; Ring, P. Relativistic Hartree–Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.; Zhang, S.; Long, W.; Geng, L. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef] [Green Version]
- Niksic, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Mean-field and beyond. Prog. Part. Nucl. Phys. 2011, 66, 519–548. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Zhao, P. Relativistic density functional theory in nuclear physics. AAPPS Bull. 2021, 31, 2. [Google Scholar] [CrossRef]
- Ren, Z.X.; Zhao, P.W. Hamiltonian flow equations for a Dirac particle in large scalar and vector potentials. Phys. Rev. C 2019, 100, 044322. [Google Scholar] [CrossRef] [Green Version]
- Ren, Z.X.; Zhao, P.W. Toward a bridge between relativistic and nonrelativistic density functional theories for nuclei. Phys. Rev. C 2020, 102, 021301(R). [Google Scholar] [CrossRef]
- Toki, H.; Hirata, D.; Sugahara, Y.; Sumiyoshi, K.; Tanihata, I. Relativistic Many-body Approach for Unstable Nuclei and Supernova. Nucl. Phys. A 1995, 588, C357–C363. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with a point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Boehnlein, A.; Diefenthaler, M.; Fanelli, C.; Hjorth-Jensen, M.; Horn, T.; Kuchera, M.P.; Lee, D.; Nazarewicz, W.; Orginos, K.; Ostroumov, P.; et al. Artificial Intelligence and Machine Learning in Nuclear Physics. arXiv 2021, arXiv:2112.02309. [Google Scholar]
- Wu, X.H.; Zhao, P.W. Predicting nuclear masses with the kernel ridge regression. Phys. Rev. C 2020, 101, 051301. [Google Scholar] [CrossRef]
- Wu, X.H.; Guo, L.H.; Zhao, P.W. Nuclear masses in extended kernel ridge regression with odd-even effects. Phys. Lett. B 2021, 819, 136387. [Google Scholar] [CrossRef]
- Wang, N.; Liu, M. Nuclear mass predictions with a radial basis function approach. Phys. Rev. C 2011, 84, 051303. [Google Scholar] [CrossRef]
- Ma, N.N.; Zhang, H.F.; Yin, P.; Bao, X.J.; Zhang, H.F. Weizsäcker-Skyrme-type nuclear mass formula incorporating two combinatorial radial basis function prescriptions and their application. Phys. Rev. C 2017, 96, 024302. [Google Scholar] [CrossRef]
- Niu, Z.; Liang, H.; Sun, B.; Niu, Y.; Guo, J.; Meng, J. High precision nuclear mass predictions towards a hundred kilo-electron-volt accuracy. Sci. Bull. 2018, 63, 759–764. [Google Scholar] [CrossRef] [Green Version]
- Utama, R.; Piekarewicz, J.; Prosper, H.B. Nuclear mass predictions for the crustal composition of neutron stars: A Bayesian neural network approach. Phys. Rev. C 2016, 93, 014311. [Google Scholar] [CrossRef] [Green Version]
- Niu, Z.; Liang, H. Nuclear mass predictions based on Bayesian neural network approach with pairing and shell effects. Phys. Lett. B 2018, 778, 48–53. [Google Scholar] [CrossRef]
- Neufcourt, L.; Cao, Y.; Nazarewicz, W.; Viens, F. Bayesian approach to model-based extrapolation of nuclear observables. Phys. Rev. C 2018, 98, 034318. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.F.; Wang, L.H.; Yin, J.P.; Chen, P.H.; Zhang, H.F. Performance of the Levenberg–Marquardt neural network approach in nuclear mass prediction. J. Phys. G-Nucl. Part. Phys. 2017, 44, 045110. [Google Scholar] [CrossRef]
- Shelley, M.; Pastore, A. A New Mass Model for Nuclear Astrophysics: Crossing 200 keV Accuracy. Universe 2021, 7, 131. [Google Scholar] [CrossRef]
- Gao, Z.P.; Wang, Y.J.; Lü, H.L.; Li, Q.F.; Shen, C.W.; Liu, L. Machine learning the nuclear mass. Nucl. Sci. Tech. 2021, 32, 109. [Google Scholar] [CrossRef]
- Liu, Y.; Su, C.; Liu, J.; Danielewicz, P.; Xu, C.; Ren, Z. Improved naive Bayesian probability classifier in predictions of nuclear mass. Phys. Rev. C 2021, 104, 014315. [Google Scholar] [CrossRef]
- Zheng, J.S.; Wang, N.Y.; Wang, Z.Y.; Niu, Z.M.; Niu, Y.F.; Sun, B. Mass predictions of the relativistic mean-field model with the radial basis function approach. Phys. Rev. C 2014, 90, 014303. [Google Scholar] [CrossRef]
- Niu, Z.M.; Fang, J.Y.; Niu, Y.F. Comparative study of radial basis function and Bayesian neural network approaches in nuclear mass predictions. Phys. Rev. C 2019, 100, 054311. [Google Scholar] [CrossRef]
- Wu, X.H.; Ren, Z.X.; Zhao, P.W. Nuclear energy density functionals from machine learning. Phys. Rev. C 2022, 105, L031303. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Wapstra, A.H.; Kondev, F.G.; MacCormick, M.; Xu, X.; Pfeiffer, B. The AME2012 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2012, 36, 1603–2014. [Google Scholar] [CrossRef]
- Kratz, K.L.; Bitouzet, J.P.; Thielemann, F.K.; Moeller, P.; Pfeiffer, B. Isotopic r-Process Abundances and Nuclear Structure Far from Stability: Implications for the r-Process Mechanism. Astrophys. J. 1993, 403, 216. [Google Scholar] [CrossRef]
- Sun, B.; Montes, F.; Geng, L.S.; Geissel, H.; Litvinov, Y.A.; Meng, J. Application of the relativistic mean-field mass model to the r-process and the influence of mass uncertainties. Phys. Rev. C 2008, 78, 025806. [Google Scholar] [CrossRef] [Green Version]
- Niu, Z.; Sun, B.; Meng, J. Influence of nuclear physics inputs and astrophysical conditions on the Th/U chronometer. Phys. Rev. C 2009, 80, 065806. [Google Scholar] [CrossRef]
- Xu, X.D.; Sun, B.; Niu, Z.M.; Li, Z.; Qian, Y.Z.; Meng, J. Reexamining the temperature and neutron density conditions for r-process nucleosynthesis with augmented nuclear mass models. Phys. Rev. C 2013, 87, 015805. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Zhang, S.Q. The r-process with the Newly Developed High-precision Mass Model WS4. Astrophys. J. 2019, 874, 5. [Google Scholar] [CrossRef]
- Möller, P.; Pfeiffer, B.; Kratz, K.L. New calculations of gross β-decay properties for astrophysical applications: Speeding-up the classical r process. Phys. Rev. C 2003, 67, 055802. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).