1. Introduction
Information about mechanical properties of engineering structures is essential equally at the stage of their manufacturing (e.g., for their quality control) as well as at the operation stage (e.g., for the periodic structural integrity assessment). Besides, prior accurate knowledge of material properties is a crucial point for computational models employed at various stages of the structural design, since discrepancies between assumed and actual values of such parameters may cause large errors in the prediction, resulting in miscellaneous undesired consequences. Numerous static or dynamic methods are being developed for accurate evaluation of the material elastic constants [
1,
2,
3]. The former include tensile, compression, and bending tests, whereas the latter typically rely on low-frequency vibration or high-frequency ultrasonic-related approaches.
Recent advancements in experimental facilities and devices caused the intensive development of non-destructive dynamic approaches for material characterization. Detailed reviews of the vibrational evaluation methods, where low frequencies are employed, can be found in [
3,
4]. Identification techniques based on ultrasonic guided waves (GW) rely on GW propagation characteristics, which carry information on the material properties in a wider frequency range compared with vibrational methods. Therefore, they require multi-modal high-resolution signals, where data collection and extraction of multiple propagating modes are necessary, which is still a challenging task [
5]. Typically, scanning of a certain area of the specimen surface is needed to obtain dispersion properties, and, therefore, various experimental techniques are used. Chen et al. [
5], Okumura et al. [
6,
7], Bochud et al. [
8] and many others used a linear array probe attached at the surface of a specimen for dispersion data extraction. Since the attachment of an ultrasonic probe changes the guiding properties of the waveguide in the area of contact, non-contact techniques are preferable. Among them, laser-based approaches are becoming widespread: GWs are excited by a laser source through thermoelastic conversion [
9] or by a piezoelectric transducer [
10,
11,
12], and surface displacement/velocity is detected by laser interferometry. A scanning procedure can also be performed by an air-coupled transducer, e.g., Takahashi et al. [
13] varied angle of incidence, in order to estimate the properties of a bi-layered structure. In addition, the non-contact technique based on the transient grating method was employed for the identification of elastic properties of a composite consisting of GaN nanowires embedded into a dielectric matrix [
14].
Waveguide mechanical properties are usually obtained via the minimization of the discrepancy between the measured and calculated wave characteristics. Therefore, an optimization problem is to be solved, where an objective function providing a stable numerical procedure fitting a waveguide model to the experimental data should be constructed. In vibrational-based material identification, the objective function can generally be defined in various forms involving natural frequencies and mode shapes [
4]. For instance, Pagnotta and Stigliano [
15] investigated the feasibility of a vibration-based approach using natural frequencies of thin isotropic plates of various shapes to determine Young’s modulus, Poisson’s ratio, mass density and thickness, showed the robustness of the identification process with respect to measurement noise. Within GW-based approaches, as soon as measurements are made, the corresponding GW characteristic features (e.g., wavenumbers, phase or group velocities or slownesses) are to be accurately extracted from the experimental data. For this purpose, the two-dimensional Fourier transform [
8,
10,
14,
16], the dynamic mode decomposition [
17] or the matrix pencil method (MPM) [
18,
19,
20] are employed.
The specific features of GWs obtained from the experiment are further used for the inverse problem solution, which also involves intensive computations using mathematical models [
8,
14,
20,
21]. In GW-based identification methods, various objective functions are constructed employing dispersion characteristics. A typical approach is to consider the discrepancy between experimental and theoretical dispersion properties of GWs [
11,
13]. Its minimization demands calculation of dispersion curves of a waveguide at each step. The latter is reduced to root-finding procedures, which are cumbersome for multi-layered waveguides. Besides, reliable mode separation and reconstruction methods allowing for individual mode extraction from dispersive multi-modal GW signals are needed [
22]. Fairuschin et al. [
23] used an alternative method, in which the dispersion properties are calculated by solving the underlying differential equations using the spectral collocation method. The latter provides a good trade-off between precision, implementation effort, and computation, but it is not always robust [
24]. It should be mentioned that additional features of GWs such as zero group velocities can be combined with waveguide modelling for material properties identification [
25]. Alternative approaches to avoiding root-finding procedures, which are time-consuming, rely also on dispersion characteristics. Thelen et al. [
21] proposed a thorough assessment of the effective mechanical behaviour of pSi using dispersion maps, where the maps are obtained by converting the modelled guided modes into a binary image. The objective function is defined as the mean value of the element-wise product between experimental and modelled dispersion maps. Chen et al. [
5] and Bochud et al. [
8] defined the objective function as the ratio of the number of experimental pairs wavenumber-frequency estimates satisfying the dispersion equation to the number of the total estimates for an isotropic layer. In this case, roots of the dispersion equation are not necessary, since the experimental wavenumber-frequency is substituted into the dispersion equation, and the objective function is defined using the signum function, showing sign change in the vicinity of a certain wavenumber at a given frequency, for more details see [
5,
8]. Also, Green’s matrices can be employed instead of the dispersion equation [
14], which demands more computational time (2–3 times), but provides a smoother objective function.
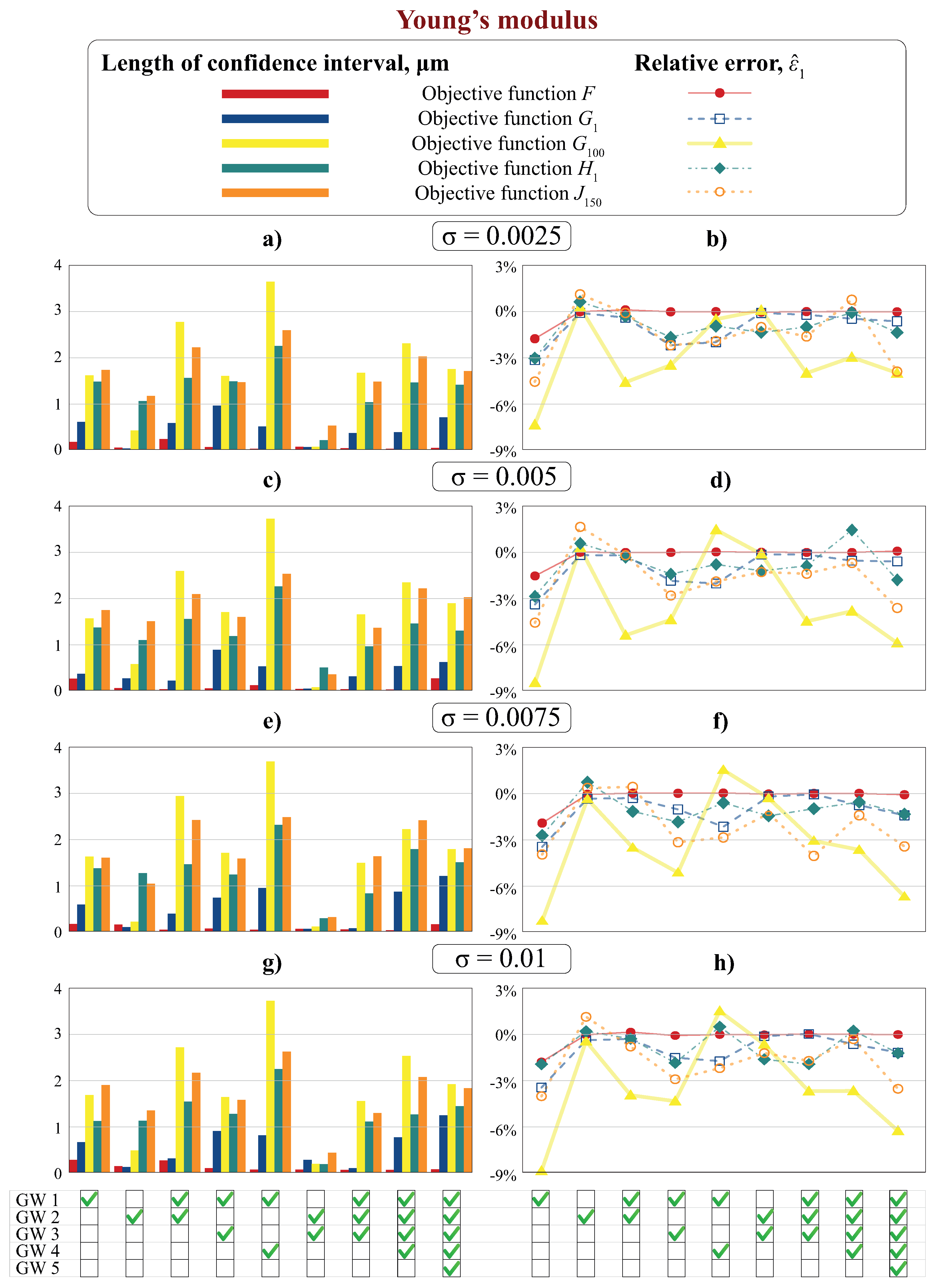
In this paper, a novel automated technique for the identification of material properties of an elastic waveguide is proposed, validated and verified using synthesized and experimental data. The approach relies on the information on the dispersion characteristics of GWs, which are extracted here by applying the MPM to the measurements obtained via laser Doppler vibrometry. Two objective functions have been composed: the first functional uses information on slownesses, while the second one employs the Fourier transform of Green’s matrix [
14]. The numerical analysis relying on the synthesized data generated via the mathematical model (the algorithm of data synthesis is described in
Section 5) shows that both approaches are stable. With the help of synthesized data, the accuracy of the two approaches is compared and the efficiency and the biasedness of the obtained estimates is tested. It is demonstrated that the approach using slownesses is more accurate, but it is more time-consuming. The influence of the presence of certain modes in the extracted data is also investigated. One can conclude that the influence of the corruptions related to the extraction of dispersion curves extraction is not critical if the majority of guided waves propagating in the considered frequency range are presented. Discussions of the possible extensions of the proposed technique for damaged and multi-layered structures are also given.
2. Theoretical Determination of Guided Waves Characteristics
Let us consider the steady-state motion of an elastic layer
of thickness
H characterized by the mass density
, Young’s modulus
E, and Poisson’s ratio
as shown in
Figure 1, so that the parameter of the model
is introduced. The mass density
is not included into the model parameter since the dispersion characteristics of the layer depend only three values, and the density can be determined without ultrasonic measurements. For the time-harmonic wave motion with the angular frequency
, the displacement vector
obeys the symmetric governing equations
Hooke’s law relates the components of the stress tensor
and the displacement vector
. The upper and lower surfaces of the layer are assumed to be stress-free
Since the solution corresponding to a guided wave propagating in a positive direction with the wavenumber
at the angular frequency
(
f is the dimensional frequency) has the form:
The latter form is substituted into governing Equation (
1), which leads to the following system of ordinary differential equations:
Differential Equation (
3) can be rewritten in the following form
The solution of (
4) can be written in terms of the matrix
composed of eigenvectors,
, where
are eigenvalues of
, and the vector of unknown coefficients
:
Replacement of (
5) into stress-free boundary conditions (
2) gives
which can be rewritten in terms of a four-by-four matrix
and differential operator
corresponding to Hooke’s law. Therefore, the solution
of the dispersion relation
gives wavenumbers of guided waves propagating in the elastic layer. In order to construct components of the Fourier transform of Green’s matrix
, the right-hand side of the system (
6) is substituted by
(
,
) assuming that the load is applied at the lower boundary
The latter leads to the following system:
The solution of (
8) is then substituted into (
5), and the Fourier transform of Green’s matrix can be represented as follows
in terms of slowness value
, which is employed further.
3. Experimental Data Extraction Using the Matrix Pencil Method
In the experimental investigations, a rectangular aluminium plate (5754 alloy) with dimensions
mm
is employed, see
Figure 2. Ultrasonic GWs are excited by a circular piezoelectric actuator of 8 mm radius and
mm thickness manufactured from PZT PIC 151 (PI Ceramic GmbH, Lederhose, Germany). It is adhesively attached on one of the plate surfaces at its central point and is driven by broadband 0.5
s rectangular pulse tone burst voltage of 100 V-pp amplitude. Out-of-plane velocities of propagating wave packages are measured at the surface of the specimen by PSV-500-V laser Doppler vibrometer (LDV) (Polytec GmbH, Waldbronn, Germany), which sensing head is placed about 1100 mm above the sample, minimizing the oblique angle laser beam measurement errors [
26]. Since the specimen surfaces remained intact with no special treatment for their reflectivity improvement applied, at least 200 times averaging are performed for each measurement point to improve the signal-to-noise ratio. Moreover, high-frequency noise is filtered out from the acquired wavesignals by 3 MHz low-pass filter applied through the vibrometer software.
For the sake of convenience, let us introduce the Cartesian coordinates so that the scan line goes along the -axis, and the transducer is situated at the origin of coordinates. The LDV allows measuring out-of-plane velocities at the surface of the specimen.
The out-of-plane velocities
measured at points (
) at moments of time
in the form of B-scans are further post-processed using the MPM to extract corresponding slowness dispersion curves of propagating GWs. According to the MPM, the Fourier transform is applied to
with respect to time-variable for a certain set of frequencies
, which gives
. In the MPM, the singular value decomposition is applied to the matrix composed of
in order to compute the discrete relation between the wavenumber
k and the frequency
f following Schöpfer et al. [
18]. The MPM returns the complex-valued wavenumbers
describing propagating GWs at the frequency
. Therefore, a set of experimental slownesses
is obtained after the application of the processing procedure, removing
, which most likely does not correspond to a propagating GW. Thus, it does not include
with large imaginary parts (
), and
corresponding to those points in the slowness-frequency plane (
), which has the lowest number of neighbouring points.
Therefore, some GWs are not included in the final set and vice versa, some do not match the actual guided wave. The LDV used in this study has an operating frequency range up to 20 MHz. However, since no special treatment to the specimen surface (i.e., spraying of the reflective paint or gluing of the retroreflective film) was applied, the spectrum of the measured signals at the frequencies higher than 2.5–3 MHz was found to be noisy. Thus, to provide better signal-to-noise ratio in the experimental signals, a 3 MHz lowpass filter was applied through the vibrometer software. Since its transition band was within 2.5 and 3 MHz, in the paper we considered frequencies up to 2.5 MHz.
4. Objective Functions for Material Properties Characterization
As soon as slownesses
at frequencies
(
) are extracted from the experimental data, an inverse problem for material properties’ identification is to be formulated and solved. With a certain model parameter vector
including Young’s modulus, Poisson’s ratio, and plate thickness, the mathematical model presented in
Section 2 can be applied for computing slownesses as roots of dispersion Equation (
7) (for instance, using the method of interval bisection) or the Fourier transform of Green’s matrix (
9). Numerical routines for calculating slownesses
s and the Fourier transform of Green’s matrix (
9) at a given frequency
f have been implemented in the FORTRAN programming language. Therefore, an inverse problem is settled, matching the experimental and theoretical results via a specially composed objective function. Two main approaches for the objective function composition are considered here, and the effectiveness of several kinds of objective functions for material properties identification are compared in the subsequent sections.
For both approaches and all the objective functions, the following optimization problem is formulated
Here
denotes the bounds of the model parameters of a certain objective function
, where the unknown parameter
incorporates information on the actual value of the parameter, and
is an estimate determined as a result of solving the optimization problem. The solution of the optimization problem has been implemented in the Python programming language using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method [
27].
4.1. Objective Function Using Residual of Slownesses
In the first approach, the multi-parameter criterion is the minimization of the residual between measured slownesses
and slownesses
calculated by employing the mathematical model described in
Section 2 with the parameter
. Therefore, an iterative correction of simulation results is to be performed with varying material properties
until the optimal match between slowness-frequency pairs is found (
), calculated using a theoretical model with parameters
and the experiment (
), which contain information about the unknown parameter vector
, as well as other factors affecting the experiment. Experimentally determined slownesses are denoted as
to show straightforwardly that information about actual material properties
is included into the data.
Formally, the optimal model parameters
are obtained from the minimization of the objective function
is composed assuming the modal decomposition of the data. Here,
k is the index of experimentally found out data for some frequency
i.e.,
,
is the number of all frequencies, and
N is the total number of pairs. Weights can also be used to take into account the sensitivity of the modes to the material properties changes, while such an investigation is out of the scope of the present study and the weights are assumed to be equal. The disadvantage of the employment of this objective function is the necessity of the numerical search of the roots of the dispersion Equation (
7) for all dissimilar frequencies
and the determination of slownesses
corresponding to the experimental ones.
4.2. Objective Function Based on the Fourier Transform of Green’s Matrix
The second approach avoids time-consuming root search procedure. Moreover, instead of direct insertion of the experimentally determined slowness-frequency pairs (
) into dispersion Equation (
7), they are substituted into the inversion of the Fourier transform of Green’s matrix
as proposed in [
14]. The latter provides a smoother surface compared with
, an example of dispersion map
is demonstrated in
Figure 3a for typical aluminium parameters
(here all values
are substituted by 100). In this case, the following objective function is employed:
Here, an additional parameter
is introduced in order to avoid large values of objective function (
11), which improves the effectiveness of the inversion procedure, since extremely large values (visible in
Figure 3b) could strongly influence the objective function, if, for instance, some points related to noise are included. Another alternative for avoiding too large values of the objective function is the employment of a logarithm procedure so that objective functions
and
which are also considered in this study. An example of dispersion map
is shown in
Figure 3b for the same parameters
as used for
Figure 3a.
5. Generation of Test Data Sets
In the case of the data obtained from a physical experiment, slownesses can be represented as a sum of the slownesses depending on the material parameters and the random component
included the actions of random factors during the experiment, which can be represented as follows for a given discrete data set
To obtain statistics proving the effectiveness of the identification procedure, the method must be validated in numerous tests, where the material properties are known, but the data have to simulate the experimental data. For this purpose, test data sets, i.e., slowness–frequency pairs, are to be prepared at first.
At the first stage of the test data preparation, theoretical slownesses are calculated for a known parameter
at the set of frequencies
Since the number of propagating guided waves varies with frequency, slowness–frequency pairs are split into sets
of various numbers of elements
in the general case, and each set corresponds to a
kth non-attenuating guided wave. Next, white noise
with the standard deviation
is added so that
is generated independently, and corrupted data sets (
) are prepared for each guided wave.
At the next stage, the noisy slownesses are damaged for getting a given percentage of gaps in the dispersion curves. To this end, the parameter describing the percentage of sole points to be removed from initial data and the parameter describing percentage of points belonging to the chains of random lengths to be deleted from are introduced so that .
For simplicity, let us introduce one-dimensional arrays of frequencies related to the
kth guided wave as follows:
and denote their lengths as
. Next, the number of slowness–frequency pairs for each guided wave, which are expected at the final stage, are defined by the relation
, where
is the number of individual points to be excluded from the initial set at random positions, while
is the number of points in
chains to also be deleted at random positions. To obtain
the auxiliary set
is composed of indices of slowness–frequency pairs to be deleted from the initially generated set
employing temporary sets
and
where
The latter allows us to simulate data gaps and white noise, which are usually observed in experimental data [
20,
28].
The sets (
) generated according to the procedure described above are employed further to analyse the behaviour of the proposed objective functions.
Figure 4 shows four corrupted data sets (
) for two values of the standard deviation (
and
) and two levels of corruption (
and
) for
.