Abstract
Recently, isogeometric analysis (IGA), which unifies the computer-aided design (CAD) model and the computer-aided engineering (CAE) model, has been adopted to develop the isogeometric topology optimization (ITO) framework. However, a critical study on the indispensability of IGA in topology optimization to take the place of the conventional finite element method (FEM) is still lacking. In the current work, two important problems are extensively discussed: (1) The lower numerical precision of the FEM resulting from the disunification between the CAD and CAE models damages the effectiveness of the topology optimization, which suggests the indispensability of IGA in the replacement of the FEM in optimization; (2) a material penalization model is required to ensure the generation of a full loading-transmission path during optimization in classic density-based methods, which causes a greater overestimation of structural stiffness and also suggests the necessity of an ersatz material model. The current paper describes a promising ITO method with point-wise design to gain smooth or binary symmetrical topologies, for which an extended density distribution function (DDF) was constructed to describe the structural topology. Two benchmarks of the stiffness-maximization problem and compliant mechanism are studied in the context of the above issues. Finally, several topologically optimized designs with symmetry are obtained using the ITO method.
1. Introduction
For the last three decades, topology optimization has been regarded as an effective and efficient numerical tool to find the optimal material distribution with the expected structural performance in fixed-design domains, subject to several prescribed constraints [1]. Since the homogenization method was proposed by Bendsøe and Kikuchi in their seminal work [2], several different topology optimization methods have been proposed in recent years, such as SIMP (solid isotropic material penalization) [3,4], ESO (evolutionary structural optimization) [5,6], LSM (level-set method) [7,8,9], and MMC/Vs (moving morphable components/voids [10,11]). According to the topology description model, these methods can be mainly classified into two branches, namely material description models (MDMs) and boundary description models (BDMs). In BDMs, a higher-dimensional function is constructed to represent the structural topology, where the iso-surface/contour of the function is applied to present structural boundaries, as in the LSM and MMC/Vs. In the case of MDMs, artificial densities are assigned to finite elements, which are not only considered in the analysis, but also present the structural topology, such as the SIMP, ESO, etc. These methods have been sufficiently discussed and then applied to several optimization problems [12,13,14,15,16,17,18,19,20].
In particular, MDMs have received a broad of discussions and applications due to their conceptual clarity and numerical ease. In earlier MDMs, the key intention was to solve a discrete optimization problem with an infinite number of design variables in {0, 1}. Subsequently, the SIMP relaxes the 0–1-integer programming and converts discrete design variables {0, 1} into the continuous [0 1] by introducing artificial densities in finite elements. The notable characteristic is that a material penalization model is defined for the elastic property with respect to the density in each finite element, while artificial densities and relevant material properties are piecewise constant in finite elements. The initial problem of the continuous material layout in topology optimization is completely converted into finding an appropriate spatial arrangement of discrete densities in finite elements. However, it is important to note that the discrete nature also introduces several numerical difficulties later in the manufacturing process, and the key problem is how to obtain smooth structural boundaries in a pure binary design with zig-zagged or jagged features or in a blurred design with a significant amount of intermediate densities. Hence, several earlier works defined nodal densities through linear interpolation in finite elements to form distinct structural boundaries; accordingly, the concept of the material density field was proposed, as a method involving the continuous approximation of material distribution [21]. Guest et al. [22] studied projection functions in topology optimization using nodal design variables to gain a minimum-length scale. In [23,24], Q4/Q4 elements with different interpolation functions were tested to maintain the continuity of the nodal design variables and eliminate the “islanding” or “layering” structural features in the optimized designs. Later, the Shepard function was adopted to interpolate nodal design variables from elements and ensure the physical meaning of the nodal densities, such as the nonnegativity and lower-upper bounds [25,26]. A similar feature to the interpolation scheme that uses the shape or Shepard functions is adopted to define nodal design variables, such that the optimized topology represented by a family of discrete elements is converted into a pixel-wise or point-wise design. The discrete nature is still present in MDMs with nodal densities.
Recently, an approach to immersed boundary description in the LSM was introduced in MDMs, in which a continuous density function is constructed to show the structural topology. Da et al. [27] studied the smooth boundary representation in BESO. Andreasen et al. [28] addressed level-set topology and shape optimization in the framework of the SIMP method using cut elements to effectively control the length scale. Huang [29,30] extensively discussed the effectiveness of the ersatz material model and the material penalization model to achieve smooth or 0/1 designs in fixed-mesh, element-based topology optimization. A critical feature is that interpolation using Lagrange polynomials is applied to construct a DDF that represents the structural topology [27,28,29,30,31]. However, it is noted that the oscillation of Lagrange polynomials in the interpolation can damage the smoothness and continuity of the DDF [32]. NURBS (non-uniform rational B-splines) with an approximate mechanism can offer a flexible approach to constructing the DDF to show its structural topology [33,34]. However, earlier works defined a series of control-design variables with the density to represent structural topology [35] or map control-design variables into IGA element densities and then describe the structural topology using discrete IGA element densities [36,37]. In order to keep the continuity and smoothness of the topology, a DDF is constructed using NURBS parametrization with a smoothing mechanism [38,39]. However, a transition area from 0 to 1 in the optimized design has a certain number of intermediate densities, which can lead to numerical errors in the evaluation of structural stiffness using the material penalization model. Overall, several of the limitations of the previous DDF still exist and affect the effectiveness of the use of MDM-based topology optimization methods to obtain optimized designs with smooth boundaries or a pure 0–1 layout.
In actual, the NURBS basis functions utilized in the construction of the CAD (computer-aided design) model can be also applied to construct the numerical response space in the CAE (computer-aided analysis) model, so that an integrated model can be developed in CAD and CAE to eliminate the numerical deficiencies in the traditional FEM (finite element method). This is the core of IGA (isogeometric analysis) [40,41]. Hence, the study of the utilization of IGA in topology optimization to eliminate the numerical issues of FEM (such as an approximant of structural geometry, the lower-order continuity of numerical responses, and poor numerical precision), has attracted many researchers [42,43,44,45]. Previous works studied the application of IGA into topology optimization methods, such as SIMP [35,36,37,38,39], LSM [46,47,48], and MMC/Vs [49,50,51], to study its effectiveness. A brief review of the combinations of IGA and topology optimization can be found in [52]. The aforementioned research works study the effectiveness of the application of IGA in topology optimization to solve several design problems. Although IGA presents several benefits compared with the conventional FEM in numerical analysis and also displays effectiveness in topology optimization, the indispensability of IGA in optimization to replace conventional FEM is still poorly understood.
Hence, the current work first aims to propose a benchmark ITO method of using MDMs, in which an extended DDF is constructed by a NURBS parameterization with a smoothing mechanism to control the smoothness degree and a threshold projection to govern the feature of binary property. The NURBS-based IGA then replaces the conventional FEM to solve structural responses with greater numerical precision; the Gauss quadrature method, considering the exact structural geometry information, is applied to evaluate the stiffness matrices. The material penalization model and the ersatz material model are both studied to show the corresponding features in the point-wise design with detailed topology information, rather than the previous element-wise design, featuring the linear interpolation of the density in finite elements. Finally, several numerical examples with stiffness-maximization and compliant mechanism designs are tested to show the effectiveness of the ITO and the indispensability of IGA in the optimization.
2. Discussion of the Problems in FEM-Based Topology Optimization Works
2.1. Smooth or 0–1 Designs in Topology Optimization
As shown in Figure 1, is the structural design domain, and in , denotes the structural design domain with the solid and indicates the structural design domain with the void. is the structural boundary, namely . It is known that the main intention behind topology optimization is to find an appropriate material distribution with the optimized structural performance, and a classic topology optimization formulation with the volume constraint is given as:
where is an optimized objective function, such as the structural compliance. denotes the maximal value of the material consumption. denotes a function that satisfies to describe the material layout. In the classical SIMP method, is transformed into a series of discrete values defined at finite elements, namely , and the initial discrete values of are also relaxed into a continuous variation, namely . It should be noted that the minimum of should be equal to a constant that is not equal to 0 to avoid numerical singularity. The corresponding mathematical model can be also written as in a discrete form:
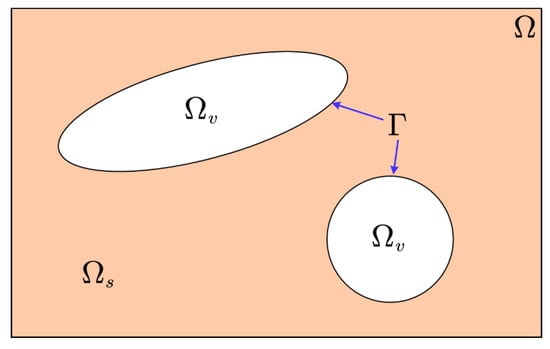
Figure 1.
Structural design domain.
2.2. FEM-Based Three-Field SIMP Method
2.2.1. A Brief Description
The classic SIMP method [3,4] has been viewed as a powerful and promising tool for topology optimization in recent years; it has been applied to many engineering optimization problems, a detailed review of which can be found in [53]. As has already been pointed out in many works, the critical feature of the SIMP method is that an isotropic material interpolation model for elastic property with respect to artificial densities can effectively convert the initial discrete design variables into a continuous version. In the latter, the three-field of design variables, topology variables, and physical variables was innovatively studied [53], and, consequently, the three-field SIMP method with the FEM, namely the FEM-based three-field SIMP, has been a benchmark method in recent years. A detailed mathematical formula can be given as:
where denotes the solid-element-stiffness matrix, and is the element-displacement vector. is the global displacement field, and denotes the imposed load. is the global stiffness matrix. and are the material volume fraction and the design domain volume, respectively. is the vector of the design variables (i.e., artificial element densities ). In the FEM-based three-field SIMP, the vector of the design variables in the detailed implementations is involved in the three fields, including the design variables, topology variables and physical variables, details of which can be found in [54] with an 88-line MATLAB code to implement the above formulation, which can be called by a MATALB line top88 (nelx, nely, volfrac, penal, rmin, ft) with six input parameters.
2.2.2. Several Critical Problems
As shown in Figure 2, three benchmarks, including cantilever beam, Michell-type structure, and MBB beam, were first optimized using the classic 88 MATLAB SIMP code [54]. The related parameters (nelx, nely, volfrac, penal, rmin, and ft) are listed below the solutions. The final parameter ft for the filtering was fixed at 2 in all the numerical examples, and it is not displayed in Figure 2. The values nelx and nely denote the total number of the finite elements in two physical directions, respectively, and are also equal to the total number of design variables in two directions. The value of volfrac is the maximum value of the material volume fraction, and penal is the penalty parameter. As we can easily see from Figure 2, when a material penalization model with a penalty parameter equal to 3 is used, the optimized topologies with the full loading-transmission path can be achieved, and a number of intermediate densities are also produced. If the ersatz material model is set with a penalty parameter equal to 1, there is no complete loading-transmission path in the final topologies, and a large number of intermediate densities is produced. This mainly results from the ersatz material model, in which the elastic property and density in each finite element have a linear relationship, and it is not possible to enable the generation of the topology with the force-transmission path.
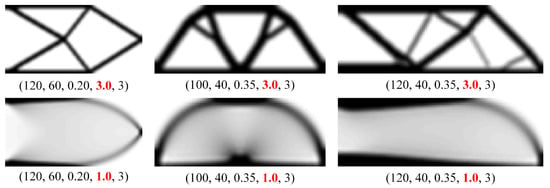
Figure 2.
Numerical results of three benchmark examples using the FEM-based SIMP method.
We then removed the intermediate densities in the optimized designs obtained by the material penalization model, which are shown in the first row of Figure 2. In [55], several morphology-based black-and-white filters were applied to develop the three-field SIMP method; the greater effectiveness of its threshold projection has received significant attention [56]. As shown in the first row of Figure 3, the threshold projection is employed in the material penalization model, and the settings of the related parameters are consistent with [56]. We found that the densities in final results were almost equal to 0 or 1, and only an extremely limited number of intermediate densities were present. Meanwhile, if the ersatz material model and threshold projection are used, the corresponding optimized solutions are provided in the second row of Figure 3. As can be observed, even if the penalization mechanism is not employed in the topology optimization, the threshold projection still has the ability to push the generation of the topology to some extent, such as the Michell-type structure and the MBB beam. However, according to the optimized results, the operation of the threshold projection as a filter is not sufficient to push the densities towards 0 or 1. The optimized solutions are different from the benchmark designs. Moreover, the optimization is not stable and cannot arrive at the convergent condition with a reasonable topology. Hence, Huang [29,30] defined a floating projection constraint in the optimization using the threshold projection that can completely force the densities towards 0 or 1.
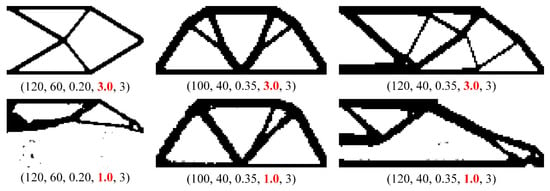
Figure 3.
Numerical results of three benchmark examples using the FEM-based three-field SIMP method.
According to the above numerical results [55,56,57] and recent studies [27,28,29,30,31], on some important problems, the following conclusions can be drawn.
- As shown in Figure 4, if the design domain uses a denser mesh, the numerical precision is improved and the optimization with the ersatz material model and threshold projection can find relatively appropriate designs. This reveals that numerical precision has a significant influence on the ability of threshold projections to generate structural topologies. However, increasing the number of finite elements results in a prohibitive computational cost, Although the optimization can find solutions to some extent, the densities dramatically change in the optimization and cannot converge in a stable process. Hence, the use of IGA to unify CAD and CAE in an integrated model with greater numerical precision at the same finite elements can offer a powerful alternative to FEM for solving unknown responses [40,41].
 Figure 4. Numerical results of three benchmarks.
Figure 4. Numerical results of three benchmarks. - Previous works [29,30] revealed that the ersatz material model is more suitable for optimization to obtain a smooth design in the density framework and the material penalization model can further benefit the optimization to obtain a pure 0–1 design. Meanwhile, the threshold projection is introduced to define the floating constraint to push the design variables towards 0 or 1. In fact, the material penalization model, with its overestimation of structural compliance, leads to numerical deviations in the structural stiffness of the final topologies, and a unified topology optimization based on the ersatz material model, using the density to produce smooth designs and pure 0–1 designs is more meaningful. Moreover, the floating constraint increases the numerical difficulties of the optimization. It is imperative to define the projection mechanism in the density distribution.
- It is imperative to construct a more effective DDF to represent the structural topology with smoothness by using NURBS approximation mechanism rather than the Lagrange interpolation. Furthermore, the DDF can combine with the threshold projection to extensively remove the intermediate densities in the transition area, and the optimizer can avoid the discrete characteristic in the topology description using the DDF. Additionally, during the optimization, the DDF with the implicit representation of structural boundaries is applied to describe the structural topology, and the DDF at the Gauss quadrature points is utilized in IGA to evaluate the material elastic properties. Hence, the current ITO can eliminate the considerable dependence on elementary densities in previous works.
3. ITO with an Extended DDF
3.1. An Extended DDF to Implicitly Represent Structural Topologies
In the optimization, the DDF is employed to represent the structural topology, and structural boundaries are immersed into the iso-surface/contour of the DDF. As already discussed in [38], the definition of the DDF should maintain three conditions: (1) Non-negativity; (2) strict binding within 0–1; and (3) non-negative derivatives. Moreover, the smoothness and continuity of the DDF have a significant effect on the optimized solutions. The development of the smoothness mechanism using the Shepard function and maintaining higher-order continuity using NURBS basis functions are imperative. However, although the optimized designs have smooth structural boundaries and distinct material interfaces, the transition area from 0 to 1 in the designs has a number of intermediate densities [38,39,52], which enhance the numerical errors due to the material penalization model in the evaluation of material elastic properties. In the current work, we first focus on developing an extended DDF by introducing threshold projection, which can reduce the number of intermediate densities in the optimization. The construction of the extended DDF involves three components: (1) Smoothness; (2) continuity; and (3) binary property. The detailed steps are given as follows, shown in Figure 5:
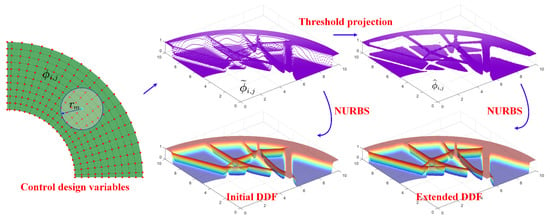
Figure 5.
The construction of an extended DDF.
- Step 1: Introducing the design variables at the control points, namely the control-design variables:
- Step 2: Using the smoothing mechanism to improve the overall smoothness of the control-design variables:
- Step 3: Introducing threshold projection [55,56,57] to reduce the intermediate densities in the transition area:
- Step 4: Using NURBS to construct a density-response surface for the design domain:
Furthermore, NURBS is a response surface for the design domain. In the construction of the extended DDF, the densities at the control points work as control coefficients, which means that the DDF can be also viewed as a density-response surface with a higher-dimension structural design domain. In the representation of the structural topology, the iso-contour/surface of the DDF is applied to represent the structural boundaries. The DDF with higher values than the iso-contour represents the solids in the design domain, and the lower values than the iso-value in the DDF describe the voids in the structural design domain, shown in Figure 6. The detailed mathematical model is expressed as follows:
where is the value of the iso-contour/surface of the DDF, which is equal to 0.5 in the latter numerical examples. However, it should be noted that although the immersed representation of the structural boundaries using the DDF inherits from the level-set implicit description model, the optimization of the DDF has an intrinsic difference compared to LSM. In the current ITO using the DDF, the main intention is to optimize the DDF by advancing the control-design variables, rather than deriving the moving and merging of the iso-contour/surface of the DDF.
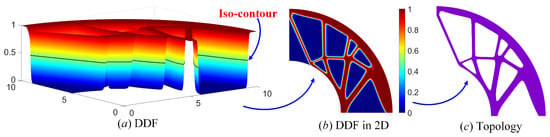
Figure 6.
The immersed representation of the structural boundaries using the DDF, (a) the density distribution function with the iso-contour; (b) the 2D viewpoint of the density distribution function; (c) the topology obtained by the iso-contour of the density distribution function.
3.2. NURBS-Based IGA
In IGA, the same NURBS basis functions used in the construction of the structural geometry are still applied to develop the numerical response space, which can ensure the integration of the CAD and CAE models. A detailed derivation of linearly elastic problems can be found in [38]. In the case of the Galerkin IGA formulation, the system stiffness matrix is achieved by assembling all the IGA element-stiffness matrices. In the physical space, the calculation of the IGA element-stiffness matrix can be stated as:
where is the IGA element stiffness matrix, is the IGA element domain, and indicates the strain-displacement matrix. In the calculation, the iso-parametric formulation is employed, in which two mappings should be defined, namely the mapping of from the parametric space to the physical space and an affine mapping of from the bi-unit parent element to the parametric element. The integration in Equation (9) needs to be pulled back first into the parametric element and then into the bi-unit parent element. It is involved the inverses of the mappings and , and the detailed form is given by:
where and are the Jacobi matrices of the two mappings, respectively. The Gauss quadrature method is adopted to calculate Equation (10), and the detailed computation is expressed by:
where and are the corresponding quadrature weights. is material constitutive elastic tensor matrix of solid. denotes the density at the Gauss quadrature point . In Figure 7, we present the comparison of the FEM and IGA in terms of the calculation of the element-stiffness matrix. As can be observed, in the FEM, a parametric element without the consideration of the structural topology information is utilized in the calculation of all the finite element-stiffness matrices. In the FEM, if the element densities are equal to 1, all the finite-element matrices are the same. However, in IGA, each element-stiffness matrix has its own parametric element considering the topology information. The stiffness matrices of all the solid elements are different. Hence, the calculation of the IGA element-stiffness matrices with structural topology information is performed point-to-point, which can offer higher numerical precision compared to the FEM. Moreover, it is noted that the current ersatz material model is considered for each point with the topological information, rather than the conventional element-wise design, which features a linear approximation, using the density.
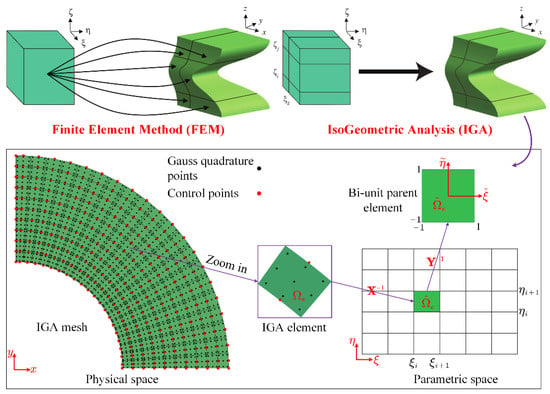
Figure 7.
Numerical integration in IGA and FEM.
3.3. Comparisons between the ITO and the FEM-Based Three-Field SIMP
As shown in Figure 8, two flowcharts of the ITO method and the FEM-based three-field SIMP are provided. The distinct differences mainly contain the following points: (1) The extended DDF in the ITO method offers a promising approach to topology representation using a smooth and continuous function, rather than a series of discrete-element densities in the three-field SIMP method; (2) the same NURBS basis functions adopted in the extended DDF and numerical analysis can effectively ensure their integration in the topology optimization. However, the linear function in the construction of the three-field element densities and the shape function in the numerical analysis using FEM are completely different, which can result in numerical deviations; (3) in the numerical analysis, the geometry information of the design domain and the topology information of the DDF can be exactly considered in the IGA, whereas only the topology information stemming from the discrete element densities is utilized in the FEM. The difference is discussed in the last paragraph of Section 3.2, as shown in Figure 7. The development of the current ITO method is based on the FEM-based three-field SIMP method. For example, the filtering scheme and a threshold projection in the FEM-based three-field SIMP method are inherited in the construction of the DDF, where the only difference is the NURBS parameterization to ensure the features of the continuity. Overall, the application of IGA in the optimization can improve the numerical precision. However, the effectiveness of the higher numerical precision under the same finite elements in IGA and the indispensability of IGA are still not applied in topology optimization.
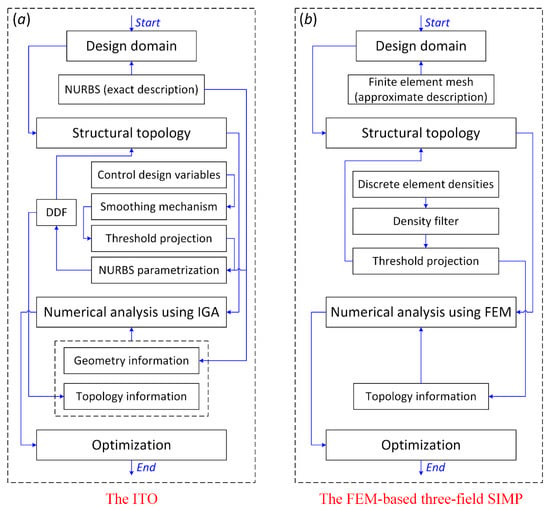
Figure 8.
Flowcharts of (a) the ITO and (b) the FEM-based three-field SIMP.
4. The Problems of Compliance-Minimization and the Compliant Mechanism
The optimization problems of structural compliance and the compliant mechanism are discussed to show the effectiveness of ITO with the extended DDF and ersatz material model.
4.1. Compliance-Minimization Formulation
As already discussed in Section 3, the control densities work as design variables, and the optimizer focuses on finding the optimized DDF with the expected structural performance. As far as the structural stiffness problem is concerned, the objective function is structural compliance, and the detailed formula is given as:
where denotes the control-design variable. is the objective function, which is defined by the mean structural compliance. corresponds to the volume constraint, where denotes the maximum material consumption. is the DDF to represent the structural topology. denotes the bilinear energy function, and is the linear load function. is the displacement field in structural design domain, and is the prescribed displacement vector at the Dirichlet boundary . is the virtual displacement field belonging to the Sobolev space . The variational weak form of the equilibrium-state equation can be established, and the detailed form is given as:
where is the body force and is the boundary traction on the Neumann boundary .
Meanwhile, the sensitivities of the objective function and constraint functions with respect to the control-design variables are required in the gradient-based optimization algorithm to derive the advancement of the structural topology. The details can be found in [38,39]. The first-order derivative of structural compliance with respect to the control-design variables can be expressed as:
Similarly, the derivative of the volume constraint with respect to the control-design variables is given by:
4.2. Compliant Mechanism Design Formulation
As far as the optimization of the compliant mechanism is concerned, the objective function should correspond to the maximum output displacement, and the material consumption works as the constraint function. The final form of the mathematical model can be stated as:
where is the output displacement. is a column vector; the value of at the output position is equal to 1, and the other values are equal to 0. The first-order derivative of the output displacement with respect to the control-design variables can be given as follows. First, a general form of the derivative of the objective function with respect to the control-design variables is given as:
According to the elastic equilibrium equation, a new form of Equation (17) is given as:
Hence, we gain a detailed form that can be expressed by:
The derivative of the volume constraint with the control-design variables remains consistent with Equation (15). A known gradient-based mathematical optimization algorithm, namely the OC (optimality criteria) method, is applied to solve the optimization problems in the current work.
5. Numerical Examples
In this section, several 2D and 3D numerical examples are performed to show the effectiveness of the ITO method. Three benchmark examples, namely cantilever beam, Michell-type structure, and MBB beam, are considered to maximize the structural stiffness. First, the importance of the threshold projection in the extended DDF is sufficiently discussed to present the indispensability of the extended DDF compared to the initial DDF in [38,39]. Second, the effectiveness and indispensability of the IGA in replacing the conventional FEM in topology optimization are extensively discussed. Third, the problem of stiffness overestimation using the material penalization model is studied, and the effectiveness of the use of the ITO method with the ersatz material model to achieve smooth or binary topologies is also addressed. Next, three 3D numerical examples are also tested using the ITO method with the ersatz material model. Finally, the example of a classic force-inventor design is also studied using the ITO method with the ersatz material model to achieve smooth or binary designs. In all the examples, the Young’s moduli of the solid and void materials are defined as 1 and 1 × 10−9 to avoid the numerical singularity, respectively. The Poisson’s ratio is set as 0.3. The imposed point load magnitude is defined as 1, except for the special definition. Gauss quadrature points with 2 × 2 (2D) or 2 × 2 × 2 (3D) are chosen in each IGA element. In the threshold projection, the parameter is set as 0.5, increases within the optimization, and the increasing criterion is listed in Algorithm 1. It is noted that only linearly elastic materials are considered. The initial values of the control-design variables in all the examples are set at 1. The radius in the Shepard function is equal to 2 in the numerical examples. The convergent condition is that the norm of the difference of control-design variables between two consecutive iterations is less than 1% within the maximum 400 steps. In the case of three benchmarks, the corresponding boundary and load conditions are shown in Figure 9, where the structural sizes are denoted by L and H.
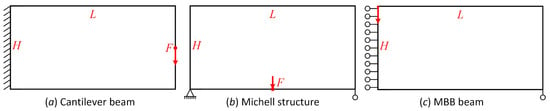
Figure 9.
Three benchmarks with boundary and load conditions: (a) Cantilever beam with boundary and loads conditions; (b) Michell structure with boundary and loads conditions; (c) MBB beam with boundary and loads conditions.
| Algorithm 1.The iterative algorithm in the code for the parameterin threshold projection. |
| if loop <= 200 if beta < 10 && (loopbeta >= 40 || change <= 0.01) beta = beta*2; loopbeta = 0; change = 1; end else if beta < 128 && (loopbeta >= 20 || change <= 0.01) beta = beta + 5; loopbeta = 0; change = 1; end end |
5.1. The Effectiveness of the Extended DDF
In this subsection, the key intention is to study the effectiveness of the extended DDF and show the necessity of the initial DDF. The material penalization model is used in this subsection, and the penalty parameter is set as 3. The detailed design parameters of the three benchmarks are defined in Table 1, including the structural sizes, the degrees of the NURBS basis functions in parametric directions, the number of control points or control-design variables, the number of IGA elements, and the maximum material consumption.

Table 1.
The related parameters of the three benchmarks.
As shown in Figure 10, the optimized cantilever beam solutions using the ITO method with the initial DDF and the extended DDF are provided, including the optimized layouts of the control-design variables, the DDF, and the corresponding topologies. The optimized designs of the Michell structure and MBB beam are presented in Figure 11 and Figure 12, respectively. As we can easily find, the optimized values of the control-design variables in Figure 10, Figure 11 and Figure 12(a1) are mostly equal to 0 or 1, demonstrating a binary density distribution. However, a certain number of intermediate values (0–1) of control-design variables emerge in the optimized distributions shown in Figure 10, Figure 11 and Figure 12(a2). As shown in Figure 13, the data layouts of the values of the control-design variables in Figure 10, Figure 11 and Figure 12(a1,a2) are all provided. We may conclude that applying threshold projection in the construction of the extended DDF can be beneficial for reducing the number of intermediate densities and lowering the gray scale in the optimized DDF.
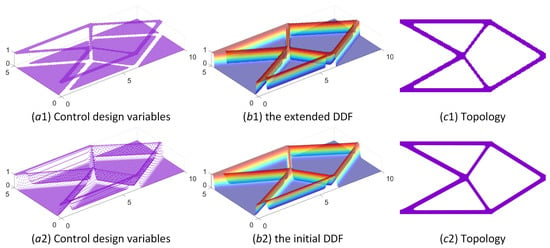
Figure 10.
The optimized designs of cantilever beam: (a1–c1) The ITO method using the extended DDF; (a2–c2) the ITO method using the initial DDF.
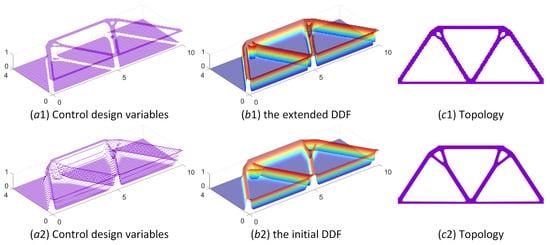
Figure 11.
The optimized designs of the Michell structure: (a1–c1) The ITO method using the extended DDF; (a2–c2) the ITO method using the initial DDF.
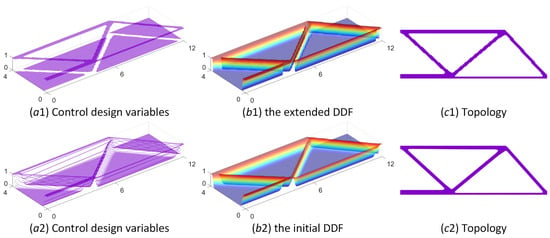
Figure 12.
The optimized designs of the MBB beam: (a1–c1) The ITO method using the extended DDF; (a2–c2) the ITO method using the initial DDF.
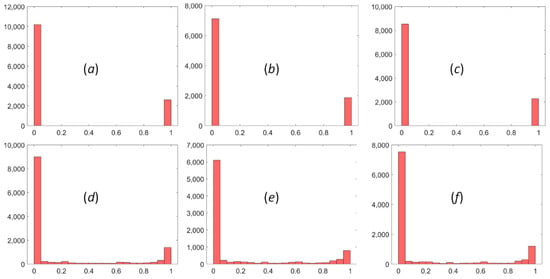
Figure 13.
The data layout of the density values of the control-design variables in the optimized designs presented: (a) the corresponding layout in Figure 10(a1); (b) the corresponding layout in Figure 11(a1); (c) the corresponding layout in Figure 12(a1); (d) the corresponding layout in Figure 10(a2); (e) the corresponding layout in Figure 11(a2); (f) the corresponding layout in Figure 12(a2).
5.2. The Indispensability of the IGA in Replacing the FEM in Topology Optimization
In this subsection, the key intention is to discuss the indispensability of the IGA in replacing the FEM in topology optimization. First, the FEM-based three-field SIMP method is applied to optimize the three examples above with the same design parameters, namely the number of finite elements, the maximum volume fraction, and the same increasing criterion of the parameters in the threshold projection. In Figure 14, the optimized topologies of the three examples are provided. The topologies in the first row are optimized by the FEM-based three-field SIMP method with the material penalization model, and the second row corresponds to the designs optimized by the FEM-based three-field SIMP method with the ersatz material model. The related parameters (nelx, nely, volfrac, penal, and rmin) are defined below the optimized topologies. We can easily infer that the FEM-based three-field SIMP method with the ersatz material model cannot achieve a reasonable topology with a full loading-transmission path, and the optimization cannot arrive at the convergent condition.
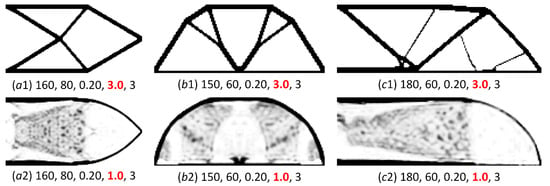
Figure 14.
Numerical results of three benchmark examples: (a1) the design of cantilever beam using material penalization model; (a2) the design of cantilever beam using ersatz material model; (b1) the design of Michell structure using material penalization model; (b2) the design of Michell structure using ersatz material model; (c1) the design of MBB beam using material penalization model; (c2) the design of MBB beam using ersatz material model.
Secondly, the proposed ITO method is employed to optimize the three benchmark examples; the related design parameters are also listed in Table 1. A critical difference is that the ersatz material model is used in the current subsection. As already discussed in Section 3, there is no penalization mechanism in the ersatz material model. As shown in Figure 15, three topologies optimized by the ITO method with the ersatz material model are presented, which are similar to the optimized designs shown in Figure 10, Figure 11 and Figure 12. Meanwhile, the convergent histories of the structural compliance of the three benchmark examples are shown in Figure 16, plotted in red. It can be easily seen that the iterative curves of the three benchmarks are all characterized by a clear and smooth variation during the optimization. Additionally, some slight fluctuations emerge in the convergent process, such as the iteration 29, 70 in the iterative curve. This results from the increase in the parameter Beta in the threshold projection during the optimization, which intends to push the control-design variables toward 0 or 1. Hence, we may conclude that the extended DDF with the threshold projection in the current ITO method tends to gradually approach the binary layout with a reasonable topology when the parameter Beta of the threshold projection increases during the optimization.

Figure 15.
The optimized designs of three benchmark examples using the ITO method with the ersatz material model: (a) the design of cantilever beam using the ITO with ersatz material model; (b) the design of Michell structure using the ITO with ersatz material model; (c) the design of MBB beam using the ITO with ersatz material model.
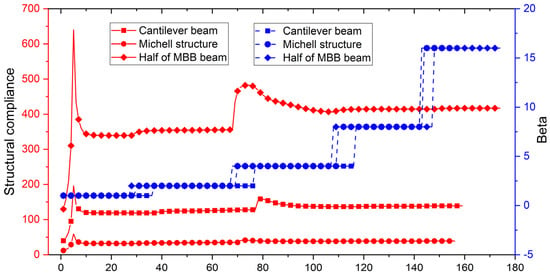
Figure 16.
Convergent histories of structural compliance and parameter Beta from Figure 15a–c.
Additionally, several intermediate cantilever-beam topologies are presented in Figure 17. We can easily see that the earlier iterations with the increase in the parameter Beta facilitate the generation of the key structural members in the design domain, until a full loading-transmission path is generated in the final topology. In the latter iterations, the increase in the parameter Beta aims to push all the control-design variables towards 0 or 1 and form a nearly pure 0–1 distribution of the extended DDF. However, the FEM-based three-filed SIMP method with the ersatz material model has no ability to seek a reasonable topology in a stable process, as presented in Figure 14(a2–c2). With the increase in the finite elements in the FEM to improve the numerical precision, it can enhance the stability of the optimization to find several ineffective designs, as shown in Figure 3. Hence, the higher numerical precision of IGA in replacing the FEM can maintain the effectiveness of the ITO method with the ersatz material model to find an appropriate design. Hence, it is indispensable to develop the framework of the ITO to seek the optimal material distribution in the design domain.
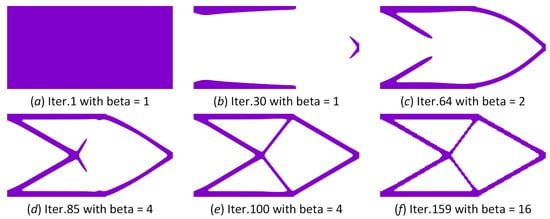
Figure 17.
Several intermediate topologies of the cantilever beam using the ITO method with the ersatz material model: (a) the design of cantilever beam in iterative step 1; (b) the design of cantilever beam in iterative step 30; (c) the design of cantilever beam in iterative step 64; (d) the design of cantilever beam in iterative step 85; (e) the design of cantilever beam in iterative step 100; (f) the design of cantilever beam in iterative step 159.
5.3. The Effectiveness of the Ersatz Material Model Compared to the Material Penalization Model in the ITO
As already described in [29,30], the use of the material penalization model to evaluate elastic properties can lead to the critical problem of the overestimation of the structural stiffness in the optimization. In Section 5.1, the ITO method with the material penalization model is employed to optimize three benchmark examples, and the ITO method with the ersatz material model is used in Section 5.1 to discuss the indispensability of IGA. Based on several numerical results in [29,30], the problem of stiffness overestimation always emerges with the intermediate densities. The development of the extended DDF aims to reduce a nearly binary topology in the ITO method. This means that there is no difference between the material penalization model and the ersatz material model when a binary design is formed in the optimization. However, while a binary design can completely reduce the intermediate values of the density, it also introduces several difficulties later in the manufacturing process. Hence, it is compulsory to retain a limited number of intermediate densities to develop a small transition area that can construct smooth boundaries from solids to voids using the iso-contour of the extended DDF. The index used to present the gray scale should be defined to rationally choose a criterion that can determine the smooth or binary designs in the optimization. In a similar manner to [55,56], the detailed mathematical equation is stated as:
where is the indicator parameter of the degree of the gray scale in the optimized design. As already described in Section 4, the developed DDF is applied to not only represent structural topology, but also calculate the related material elastic properties. However, as described in [29,30,31,38], the structural compliance of the final topology represented by the iso-value of the DDF is not equal to the optimized objective function calculated by the DDF; this difference is due to the direct step process of the density in the representation of solids and voids. Hence, we should re-analysis the optimized topology and calculate the numerical error. A symbol is applied to denote the re-calculated structural compliance according to the optimized topology, and the detailed mathematical model of the numerical error can be expressed by:
where denotes the numerical error.
In Figure 15 and Figure 18, the optimized topologies of the three benchmark examples are provided. The former presents the topologies optimized by the ITO method with the ersatz material model, and the latter gives the results obtained by the ITO method with the material penalization model. The corresponding designs have slight differences. Meanwhile, the related objective functions in the three benchmarks, namely the optimized objective function calculated by the DDF and the re-calculated structural compliance using the optimized topology, their numerical error, and the total iterative step, are provided in Table 2. As can easily be seen, the optimized objective functions of three benchmarks using the ITO with the material penalization model are all larger than the values using the ersatz material model. Meanwhile, the numerical results obtained using the material penalization model have larger objective functions of the extended DDF than the re-calculated structural compliance, with a deviation of almost 10%, which suggests the overestimation of the material penalization model in the evaluation of structural compliance.

Figure 18.
The optimized designs of the three benchmark examples using the ITO method with the material penalization model: (a) the design of cantilever beam using the ITO with material penalization model; (b) the design of Michell structure using the ITO with material penalization model; (c) the design of MBB beam using the ITO with material penalization model.

Table 2.
Numerical results of three benchmarks using the ITO method with two models.
Several of the intermediate topologies of the cantilever beam in Figure 18a are shown in Figure 19. It can be seen that the earlier iterations quickly push the control-design variables toward 0 or 1 due to the material penalization model. After the generation of a full loading-transmission path in the design domain, the initial appropriate topology is formed. In the latter iterations, the role of the threshold projection is to work as a step function to gradually reduce the degree of gray scale, as clearly shown by the convergent curves of the degree of the gray scale in Figure 20. Hence, in the ITO method with the material penalization model, the penalization mechanism plays a key role in generating the topology, whereas the threshold projection in the extended DDF affords this function in the ITO method with the ersatz material model.
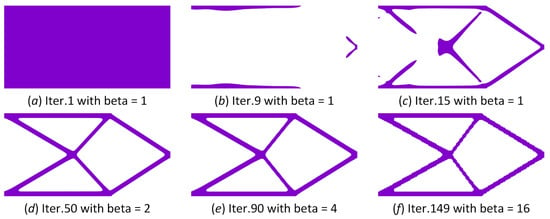
Figure 19.
Several of the intermediate topologies of the cantilever beam using the ITO method with the material penalization model: (a) the design of cantilever beam in iterative step 1; (b) the design of cantilever beam in iterative step 9; (c) the design of cantilever beam in iterative step 15; (d) the design of cantilever beam in iterative step 50; (e) the design of cantilever beam in iterative step 90; (f) the design of cantilever beam in iterative step 149.
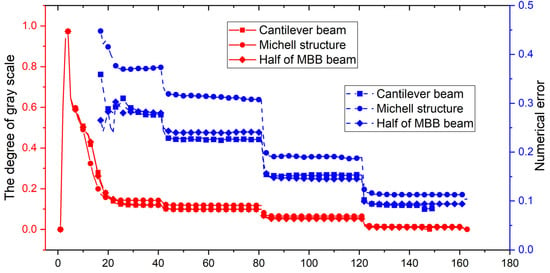
Figure 20.
Convergent histories of the degree of gray scale and numerical error in the ITO with the material penalization model for the three benchmark examples.
In Figure 20, the iterative histories of the degree of gray scale and the numerical error in the ITO with the material penalization model for the three benchmark examples are provided. With the increase in the parameter Beta in the threshold projection, the numerical error gradually becomes reduces, and finally reaches 8.46% of the cantilever beam, even if the degree of gray scale is extremely small, equal to 0.073%. This difference in numerical error mainly results from the fact that the objective function is calculated by the DDF at the Gauss quadrature points. As defined in Section 3, the values of the extended DDF at the Gauss quadrature points are calculated by the NRUBS basis functions and control-design variables. Even if the values of control-design variables approach 0 or 1, some intermediate densities are still introduced at the Gauss quadrature points because the values of the NURBS basis functions range from 0 to 1. Similarly, the degree of gray scale and numerical error in the designs of the three benchmarks optimized by the ITO method with the ersatz material model are shown in Figure 21. As can be easily observed, if the parameter Beta in the threshold projection increases, the degree of gray scale gradually decreases and reaches 0.092% (almost equal to 0). Meanwhile, the re-analysis of structural compliance is performed after the generation of the complete loading-transmission path in the optimized topology. As can be observed, the numerical error also increases until the convergent condition is reached, and the final value is equal to −1.8%. This reveals one important feature in the optimization using the ITO method with the ersatz material model: the structural compliance calculated from the optimized topology is lower than the objective function evaluated from the DDF in the optimization.
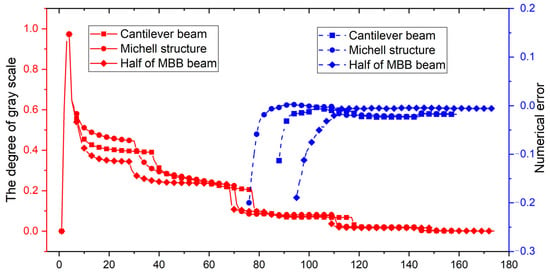
Figure 21.
Convergent histories of the degree of gray scale and numerical error in the ITO with the ersatz material model for the three benchmark examples.
Additionally, the other two cantilever-beam numerical designs are shown in Figure 22, where the 30th design in Figure 22a is consistent with the final topology in [38]. As can be seen, the numerical error is significantly larger, equal to 28.9%. This introduces a large numerical deviation. Even if the degree of gray scale decreases to 5.8%, as in Figure 22b, the corresponding numerical error, equal to 15.2%, is still much larger than the value of the error in Figure 23b, which is equal to −0.92%. In Figure 23, three of the numerical designs of the cantilever beam are given. In Figure 23b, the degree of gray scale is equal to 6.8%, the optimized design features smooth structural boundaries, and the final numerical error is extremely small, equal to −0.92%. Hence, an optimized topology with smooth boundaries but an extremely small numerical error can be obtained, which can perfectly meet the requirements of practical engineering using the current ITO method. Hence, it can be concluded that the ITO method with the ersatz material model has superior capabilities. The limited value of the degree of gray scale is 5%, based on the numerical results. When the value is larger than 5%, the optimized topologies have smooth boundaries, and vice versa.
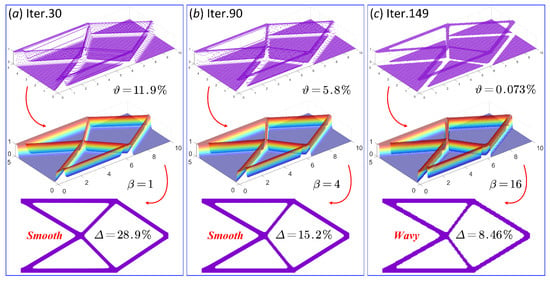
Figure 22.
Three numerical designs of the cantilever beam using the ITO with the material penalization model: (a) the design of cantilever beam in iterative step 30; (b) the design of cantilever beam in iterative step 90; (c) the design of cantilever beam in iterative step 149.
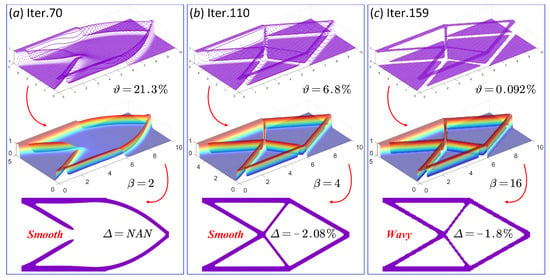
Figure 23.
Three numerical designs of the cantilever beam using the ITO with the ersatz material model: (a) the design of cantilever beam in iterative step 70; (b) the design of cantilever beam in iterative step 110; (c) the design of cantilever beam in iterative step 159.
5.4. Discussion of the Influence of the IGA Mesh
In the current subsection, the key focus is to address the influence of the IGA mesh on the effectiveness of the threshold projection in the ITO method, and also to discuss the effect of the IGA mesh on the numerical error using the immersed representation model of the extended DDF. In this subsection, the ersatz material model is used in the ITO method. The other design parameters remain consistent with the second row of Table 1 and with the change in the IGA mesh. In the current example, three different IGA meshes, namely 100 × 50, 160 × 80 and 200 × 100, are considered for the later optimization of the cantilever beam.
In Figure 24, three smooth cantilever beam designs are given based on the settings in Section 5.3, and three binary designs for the cantilever beam are presented in Figure 25. As can be easily seen in Figure 24 and Figure 25, the ITO method with the ersatz material model can effectively optimize reasonable topologies with the complete full-loading path in the design domain, even if the IGA mesh is coarse in the design, with dimensions of 100 × 50. Hence, we can state that the coarser or denser IGA mesh has no influence on the ability of the threshold projection to remove intermediate densities and force the densities to be 0 or 1. In the FEM-based three-field SIMP method, the finite element mesh also has no effect on the threshold projection, which has an effect on the ability of the SIMP method to seek the optimized topologies. Furthermore, the related numerical errors of the structural compliance are also presented in Figure 24 and Figure 25. We can easily infer that the numerical error gradually reduces with the increase in the IGA mesh, and this feature is present in the optimization of both smooth and binary designs. The main reason for this is that the denser IGA mesh can effectively enhance the numerical precision in the analysis and lower the evaluation errors in the structural compliance, which originates from the immersed representation model of the extended DDF.
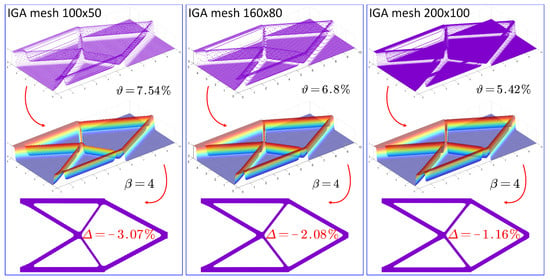
Figure 24.
Three smooth cantilever-beam designs using the ITO with three different IGA meshes.
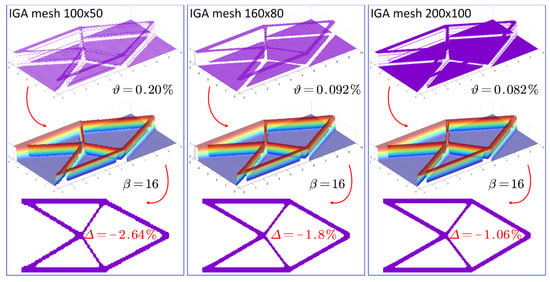
Figure 25.
Three binary designs of cantilever beam using the ITO with three different IGA meshes.
5.5. Stiffness-Maximization Designs in 3D
In this subsection, the main intention is to discuss the utility of the proposed ITO method with the extended DDF and ersatz material model in the optimization of 3D structures. In Figure 26, three different 3D structures with loads and boundary conditions are defined, including Michell structure, L-type structure, and Bridge-type structure. The related optimization parameters of the three benchmarks are provided in Table 3, namely, the orders of the NURBS basis functions in three parametric directions, the number of control points or control-design variables, the number of IGA elements, and the maximum material consumption.
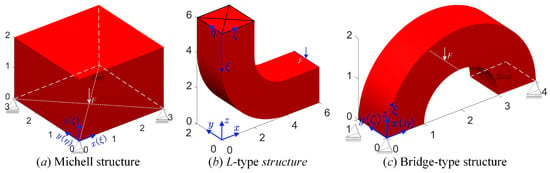
Figure 26.
Bboundary and load conditions: (a) the design domain of Michell structure; (b) the design domain of L-type structure; (c) the design domain of Bridge-type structure.

Table 3.
The related parameters of the three benchmarks.
In Figure 27, the optimized designs of the Michell structure, L-type structure, and Bridge-type structure are provided, including the smooth structural topologies that can be manufactured and the nearly pure 0–1 designs, which show the effectiveness of the current ITO method with the extended DDF. The convergent histories of the structural compliance, the parameter Beat, the degree of gray scale, and the numerical error of the Michell structure are provided in Figure 28. As can easily be observed, the iterative trajectories feature smooth variations and a stable convergence process. Some of the intermediate topologies of the Michell structure are presented in Figure 29. The role of the threshold projection in the earlier iterations focused on generating a complete loading-transmission path. In the latter iterations, the increase in the parameter Beta in the threshold projection gradually transformed the smooth design into a wavy topology with a 0–1 density layout.
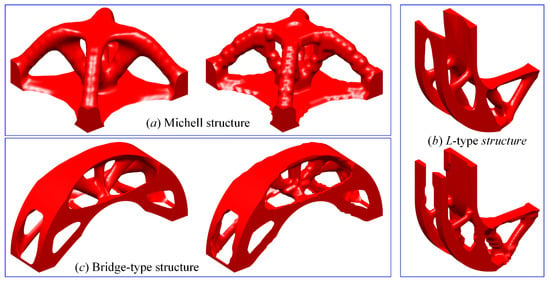
Figure 27.
The optimized designs of three structures using the ITO method: (a) the binary and smooth designs of Michell structure; (b) the binary and smooth designs of L-type structure; (c) the binary and smooth designs of Bridge type structure.
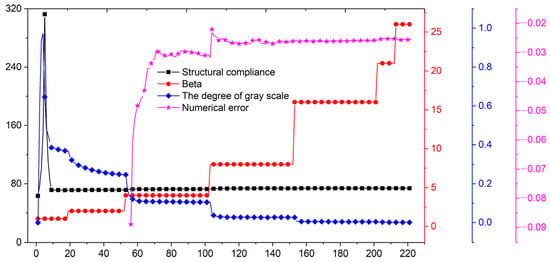
Figure 28.
Convergent histories of numerical results in the optimization of 3D Michell structure.
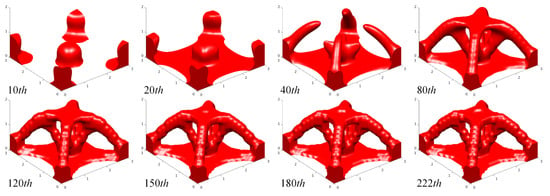
Figure 29.
Intermediate designs of 3D Michell structure.
5.6. The Design of a Force Inventor
In this subsection, the key intention is to demonstrate the effectiveness and utility of the currently developed ITO method in the optimization problem of the compliant mechanism. A classic force-inverter design problem is considered here, and the corresponding loads and boundary conditions are presented in Figure 30. In Table 4, the related optimization parameters are defined, including the orders of the NURBS basis functions, the structural sizes, the number of control points, the number of IGA elements, and the maximum material volume fraction. Meanwhile, in the calculation of the IGA stiffness matrix, the input and output should add the spring stiffness, which should be equal to 0.1.
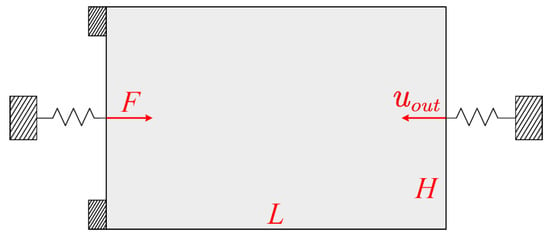
Figure 30.
Force-inverter design with boundary and loading conditions.

Table 4.
The related parameters of the force inverter.
In Figure 31, the optimized structural topologies with the smooth and 0–1 feature are both provided, including the distribution of the control-design variables, the DDF, and the corresponding topology. As can easily be observed, there is a limited number of intermediate densities in the control-design variables, which can be applied to construct a transition area from 0 to 1 in the DDF that features smooth boundaries. In the smooth design of the force inverter, the degree of gray scale is equal to 7.04%, and the value of the numerical error is equal to −4.1%. In the final 0–1 design of the force inverter, the control-design variables almost approach the 0–1 density distribution, the degree of gray scale is equal to 0.096%, and the corresponding numerical error is equal to −0.0028%. In conclusion, the developed ITO method with the extended DDF and ersatz material model considering the topology information has a superior ability to solve problems.
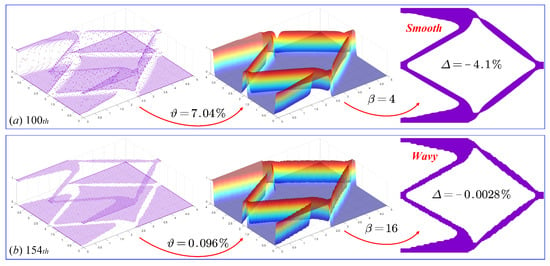
Figure 31.
Two numerical designs of the force inverter using the ITO method with the ersatz material model: (a) the smooth design of force-inverter design; (b) the binary design of force-inverter design.
6. Concluding Remarks
The main intention of the current work was to address three important problems in previous works on topology optimization: (1) The necessity of using isogeometric analysis to replace the finite element method in optimization; (2) the overestimation problem of structural stiffness in density-based methods using the material penalization model; and (3) the segmented representations of smooth and binary topologies. Hence, a promising method of isogeometric topology optimization (ITO), with powerful effectiveness and high efficiency, is proposed. The main conclusions obtained based on several 2D and 3D numerical examples are as follows:
- IGA with higher numerical precision than the conventional FEM plays a significant role in optimization by maintaining the form of a full loading-transmission path in the topology.
- The extended DDF with the ersatz material model can be more beneficial by lowering the overestimation of the structural stiffness resulting from the material penalization model.
- The development of the extended DDF to unify the representations of binary and smooth designs can offer more benefits for optimization.
- In the ITO method with the ersatz material model, the threshold projection in the extended DDF can effectively support the generation of an appropriate topology.
Author Contributions
Conceptualization, X.W. and J.G.; methodology, X.W., Y.Z. and J.G.; software, X.W. and Y.Z.; validation, X.W. and J.G.; formal analysis, X.W.; investigation, Y.Z. and J.G.; data curation, Y.Z., L.G. and J.G.; writing—original draft preparation, X.W. and J.G.; writing—review and editing, X.W., L.G. and J.G.; visualization, Y.Z.; supervision, L.G. and J.G.; project administration, L.G. and J.G.; funding acquisition, L.G. and J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the National Natural Science Foundation of China (grant number: 52105255), and partially supported by the National Key R&D Program of China (grant number: 2020YFB1708300), and partially supported by the Tencent Foundation or XPLORER PRIZE, and partially supported by the Fundamental Research Funds for the Central Universities of the Huazhong University of Science and Technology (HUST) (grant number: 5003123025).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Bendsøe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Zhou, M.; Rozvany, G.I.N. The COC Algorithm, Part II: Topological, Geometrical and Generalized Shape Optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material Interpolation Schemes in Topology Optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A Simple Evolutionary Procedure for Structural Optimization. Comput. Struct. 1993, 49, 885–969. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Bi-Directional Evolutionary Topology Optimization of Continuum Structures with One or Multiple Materials. Comput. Mech. 2009, 43, 393–401. [Google Scholar] [CrossRef]
- Sethian, J.A.; Wiegmann, A. Structural Boundary Design via Level Set and Immersed Interface Methods. J. Comput. Phys. 2000, 163, 489–528. [Google Scholar] [CrossRef]
- Wang, M.Y.; Wang, X.; Guo, D. A Level Set Method for Structural Topology Optimization. Comput. Methods Appl. Mech. Eng. 2003, 192, 227–246. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.M. Structural Optimization Using Sensitivity Analysis and a Level-Set Method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Zhang, W.; Zhong, W. Doing Topology Optimization Explicitly and Geometrically—A Mew Moving Morphable Components Based Framework. J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, W.; Zhou, J.; Li, D.; Guo, X. Structural Topology Optimization through Explicit Boundary Evolution. J. Appl. Mech. 2017, 84, 011011. [Google Scholar] [CrossRef]
- Gao, J.; Xue, H.; Gao, L.; Luo, Z. Topology Optimization for Auxetic Metamaterials Based on Isogeometric Analysis. Comput. Methods Appl. Mech. Eng. 2019, 352, 211–236. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Li, H.; Gao, L. Topology Optimization for Multiscale Design of Porous Composites with Multi-Domain Microstructures. Comput. Methods Appl. Mech. Eng. 2019, 344, 451–476. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiao, M.; Gao, L.; Gao, J.; Li, H. Multiscale Topology Optimization for Minimizing Frequency Responses of Cellular Composites with Connectable Graded Microstructures. Mech. Syst. Signal Process. 2020, 135, 106369. [Google Scholar] [CrossRef]
- Li, Q.; Sigmund, O.; Jensen, J.S.; Aage, N. Reduced-Order Methods for Dynamic Problems in Topology Optimization: A Comparative Study. Comput. Methods Appl. Mech. Eng. 2021, 387, 114149. [Google Scholar] [CrossRef]
- Chu, S.; Townsend, S.; Featherston, C.; Kim, H.A. Simultaneous Layout and Topology Optimization of Curved Stiffened Panels. AIAA J. 2021, 59, 2768–2783. [Google Scholar] [CrossRef]
- Chu, S.; Featherston, C.; Kim, H.A. Design of Stiffened Panels for Stress and Buckling via Topology Optimization. Struct. Multidiscip. Optim. 2021, 64, 3123–3146. [Google Scholar] [CrossRef]
- Xiao, M.; Liu, X.; Zhang, Y.; Gao, L.; Gao, J.; Chu, S. Design of Graded Lattice Sandwich Structures by Multiscale Topology Optimization. Comput. Methods Appl. Mech. Eng. 2021, 384, 113949. [Google Scholar] [CrossRef]
- Li, Q.; Xu, R.; Wu, Q.; Liu, S. Topology Optimization Design of Quasi-Periodic Cellular Structures Based on Erode–Dilate Operators. Comput. Methods Appl. Mech. Eng. 2021, 377, 113720. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Ding, Z.; Gao, L.; Xiao, M.; Liao, W.-H. A Multiscale Topological Design Method of Geometrically Asymmetric Porous Sandwich Structures for Minimizing Dynamic Compliance. Mater. Des. 2022, 214, 110404. [Google Scholar] [CrossRef]
- Matsui, K.; Terada, K. Continuous Approximation of Material Distribution for Topology Optimization. Int. J. Numer. Methods Eng. 2004, 59, 1925–1944. [Google Scholar] [CrossRef]
- Guest, J.K.; Prévost, J.H.; Belytschko, T. Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions. Int. J. Numer. Methods Eng. 2004, 61, 238–254. [Google Scholar] [CrossRef]
- Rahmatalla, S.F.; Swan, C.C. A Q4/Q4 Continuum Structural Topology Optimization Implementation. Struct. Multidiscip. Optim. 2004, 27, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Paulino, G.H.; Le, C.H. A Modified Q4/Q4 Element for Topology Optimization. Struct. Multidiscip. Optim. 2009, 37, 255–264. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, Y. Structural Topology Optimization Based on Non-Local Shepard Interpolation of Density Field. Comput. Methods Appl. Mech. Eng. 2011, 200, 3515–3525. [Google Scholar] [CrossRef]
- Kang, Z.; Wang, Y. A Nodal Variable Method of Structural Topology Optimization Based on Shepard Interpolant. Int. J. Numer. Methods Eng. 2012, 90, 329–342. [Google Scholar] [CrossRef]
- Da, D.; Xia, L.; Li, G.; Huang, X. Evolutionary Topology Optimization of Continuum Structures with Smooth Boundary Representation. Struct. Multidiscip. Optim. 2018, 57, 2143–2159. [Google Scholar] [CrossRef]
- Andreasen, C.S.; Elingaard, M.O.; Aage, N. Level Set Topology and Shape Optimization by Density Methods Using Cut Elements with Length Scale Control. Struct. Multidiscip. Optim. 2020, 20, 685–707. [Google Scholar] [CrossRef]
- Huang, X. Smooth Topological Design of Structures Using the Floating Projection. Eng. Struct. 2020, 208, 110330. [Google Scholar] [CrossRef]
- Huang, X. On Smooth or 0/1 Designs of the Fixed-Mesh Element-Based Topology Optimization. Adv. Eng. Softw. 2021, 151, 102942. [Google Scholar] [CrossRef]
- Fu, Y.F.; Rolfe, B.; Chiu, L.N.S.; Wang, Y.; Huang, X.; Ghabraie, K. SEMDOT: Smooth-Edged Material Distribution for Optimizing Topology Algorithm. Adv. Eng. Softw. 2020, 150, 102921. [Google Scholar] [CrossRef]
- Berrut, J.-P.; Trefethen, L.N. Barycentric Lagrange Interpolation. SIAM Rev. 2004, 46, 501–517. [Google Scholar] [CrossRef] [Green Version]
- De Boor, C. A Practical Guide to Splines. Math. Comput. 1978, 27, 325. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hassani, B.; Khanzadi, M.; Tavakkoli, S.M. An Isogeometrical Approach to Structural Topology Optimization by Optimality Criteria. Struct. Multidiscip. Optim. 2012, 45, 223–233. [Google Scholar] [CrossRef]
- Qian, X. Topology Optimization in B-Spline Space. Comput. Methods Appl. Mech. Eng. 2013, 265, 15–35. [Google Scholar] [CrossRef]
- Liu, H.; Yang, D.; Hao, P.; Zhu, X. Isogeometric Analysis Based Topology Optimization Design with Global Stress Constraint. Comput. Methods Appl. Mech. Eng. 2018, 342, 625–652. [Google Scholar] [CrossRef]
- Gao, J.; Gao, L.; Luo, Z.; Li, P. Isogeometric Topology Optimization for Continuum Structures Using Density Distribution Function. Int. J. Numer. Methods Eng. 2019, 119, 991–1017. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xiao, M.; Gao, L.; Li, P. A NURBS-Based Multi-Material Interpolation (N-MMI) for Isogeometric Topology Optimization of Structures. Appl. Math. Model. 2020, 81, 818–843. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.A.; Bazilevs, Y. Isogeometric Analysis: CAD, Finite Elements, NURBS, Exact Geometry and Mesh Refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef] [Green Version]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 9780470748732. [Google Scholar]
- Kang, P.; Youn, S.K. Isogeometric Analysis of Topologically Complex Shell Structures. Finite Elem. Anal. Des. 2015, 99, 68–81. [Google Scholar] [CrossRef]
- Gu, J.; Yu, T.; Van Lich, L.; Nguyen, T.T.; Bui, T.Q. Adaptive Multi-Patch Isogeometric Analysis Based on Locally Refined B-Splines. Comput. Methods Appl. Mech. Eng. 2018, 339, 704–738. [Google Scholar] [CrossRef]
- Gu, J.; Yu, T.; Van Lich, L.; Nguyen, T.-T.; Tanaka, S.; Bui, T.Q. Multi-Inclusions Modeling by Adaptive XIGA Based on LR B-Splines and Multiple Level Sets. Finite Elem. Anal. Des. 2018, 148, 48–66. [Google Scholar] [CrossRef]
- Huynh, G.D.; Zhuang, X.; Bui, H.G.; Meschke, G.; Nguyen-Xuan, H. Elasto-Plastic Large Deformation Analysis of Multi-Patch Thin Shells by Isogeometric Approach. Finite Elem. Anal. Des. 2020, 173. [Google Scholar] [CrossRef]
- Wang, Y.; Benson, D.J. Isogeometric Analysis for Parameterized LSM-Based Structural Topology Optimization. Comput. Mech. 2016, 57, 19–35. [Google Scholar] [CrossRef]
- Jahangiry, H.A.; Tavakkoli, S.M. An Isogeometrical Approach to Structural Level Set Topology Optimization. Comput. Methods Appl. Mech. Eng. 2017, 319, 240–257. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Zhou, M.; Gao, L. Isogeometric Topology and Shape Optimization for Composite Structures Using Level-Sets and Adaptive Gauss Quadrature. Compos. Struct. 2022, 285, 115263. [Google Scholar] [CrossRef]
- Xie, X.; Wang, S.; Xu, M.; Wang, Y. A New Isogeometric Topology Optimization Using Moving Morphable Components Based on R-Functions and Collocation Schemes. Comput. Methods Appl. Mech. Eng. 2018, 339, 61–90. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Kang, P.; Guo, X.; Youn, S.-K.K. Explicit Topology Optimization Using IGA-Based Moving Morphable Void (MMV) Approach. Comput. Methods Appl. Mech. Eng. 2020, 360, 112685. [Google Scholar] [CrossRef]
- Hou, W.; Gai, Y.; Zhu, X.; Wang, X.; Zhao, C.; Xu, L.; Jiang, K.; Hu, P. Explicit Isogeometric Topology Optimization Using Moving Morphable Components. Comput. Methods Appl. Mech. Eng. 2017, 326, 694–712. [Google Scholar] [CrossRef]
- Gao, J.; Xiao, M.; Zhang, Y.; Gao, L. A Comprehensive Review of Isogeometric Topology Optimization: Methods, Applications and Prospects. Chinese J. Mech. Eng. 2020, 33, 87. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology Optimization Approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient Topology Optimization in MATLAB Using 88 Lines of Code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sigmund, O. Morphology-Based Black and White Filters for Topology Optimization. Struct. Multidiscip. Optim. 2007, 33, 401–424. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On Projection Methods, Convergence and Robust Formulations in Topology Optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- Xu, S.; Cai, Y.; Cheng, G. Volume Preserving Nonlinear Density Filter Based on Heaviside Functions. Struct. Multidiscip. Optim. 2010, 41, 495–505. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).