A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops
Abstract
:1. Introduction
- (1)
- Concerning the problem model, a mathematical model of energy-efficient FJSP-CPT was formulated.
- (2)
- Concerning the optimization algorithm, a new multi-objective cellular memetic optimization algorithm (MOCMOA) was designed to handle this energy-efficient FJSP-CPT.
- (3)
- Concerning the experiment, experiments were performed to prove the effectiveness of the MOCMOA.
2. Problem Statement and Mathematical Model
2.1. Problem Statement
- (1)
- Interruption is not permitted and all machines are in good condition.
- (2)
- Transportation and setup times are overlooked.
- (3)
- Machines/jobs are independent of each other.
2.2. Mathematical Model
3. Proposed Multi-Objective Optimization Approach
3.1. Framework of MOCMOA
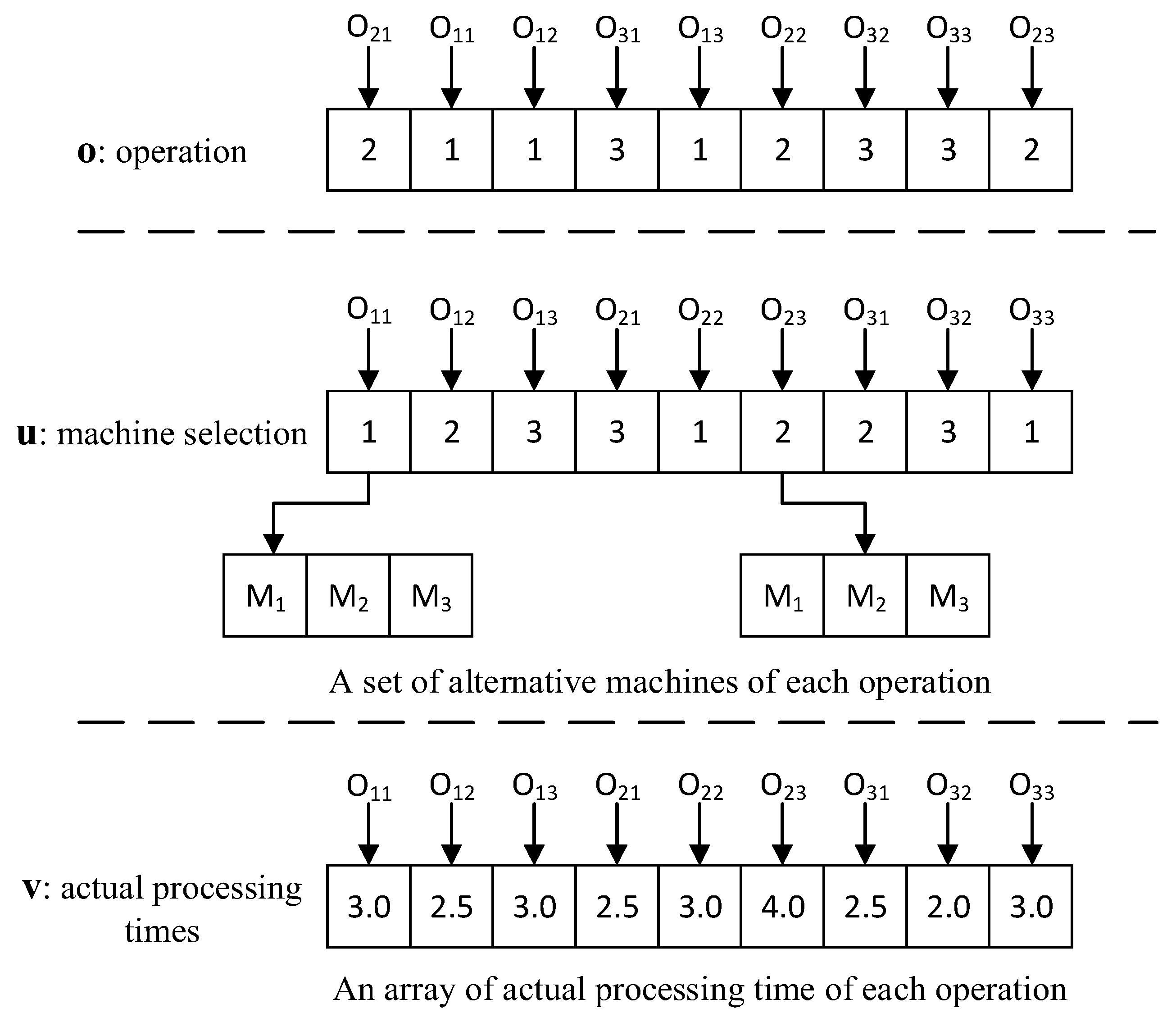
3.1.1. Encoding and Decoding
3.1.2. Initialization and Cellular Structure Assignment
3.1.3. Fitness
3.1.4. Selection
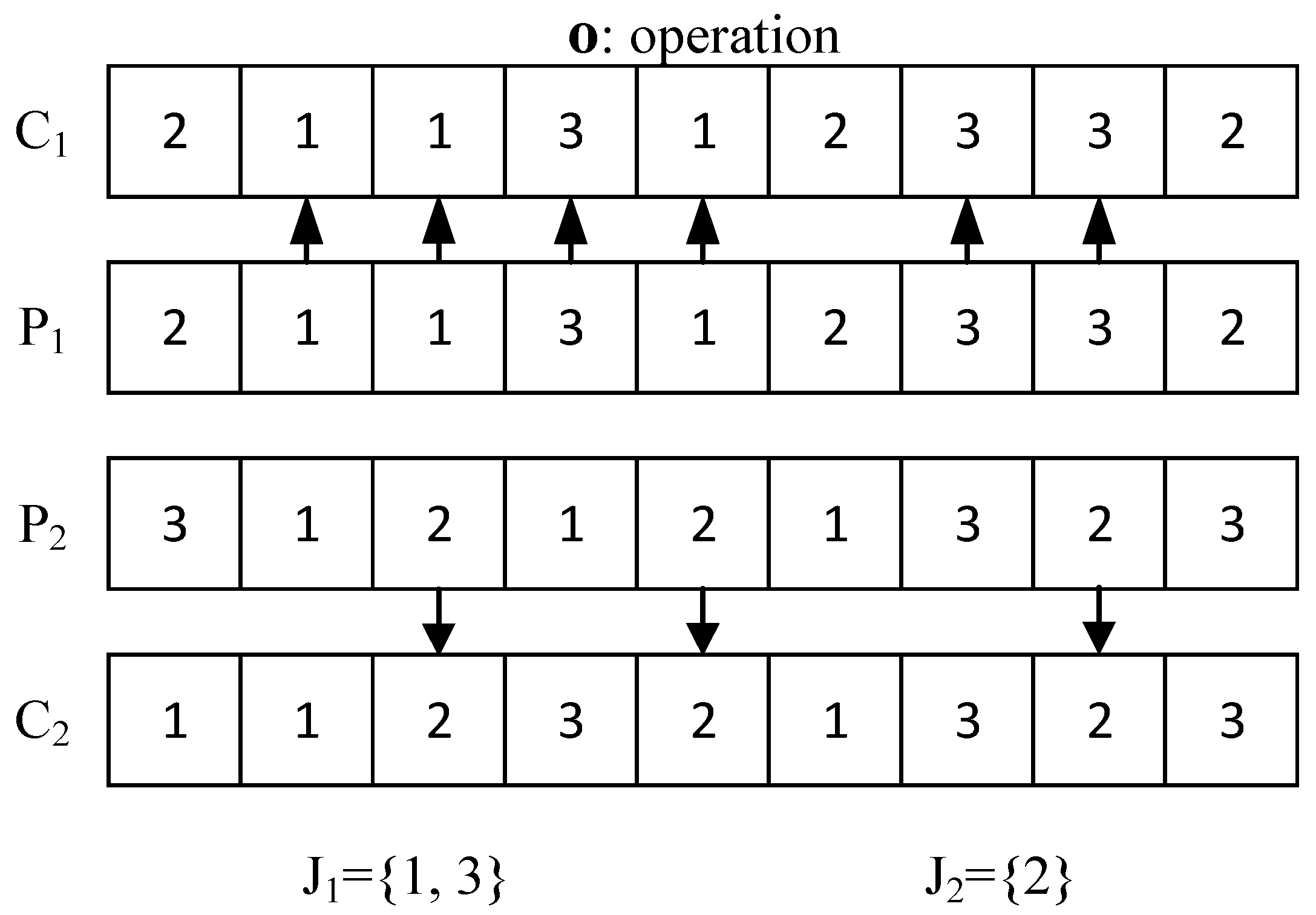
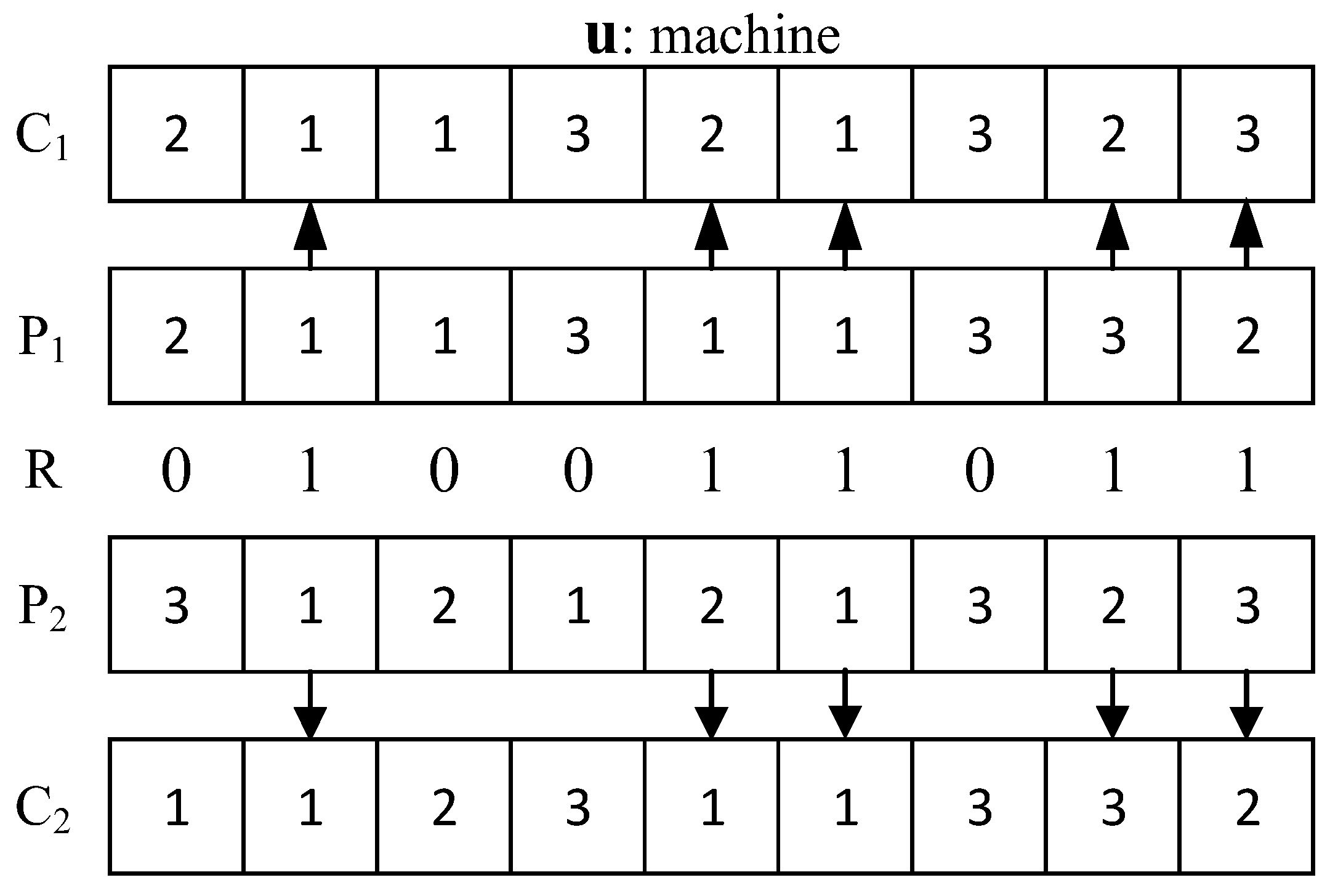
3.1.5. Search Operator
3.1.6. Local Search
- (1)
- Insert operator: Two different positions on the first part of one solution are chosen at random, and then the operation in the latter position is inserted into the former position.
- (2)
- Swap operator: Two different positions on the first part of one solution are chosen at random and the two corresponding operations are exchanged.
- (3)
- Reverse operator: Two different positions on the first part of one solution are chosen at random and a set of operations between two positions are reversed.
4. Numerical Experiments
4.1. Instances and Metrics
- (1)
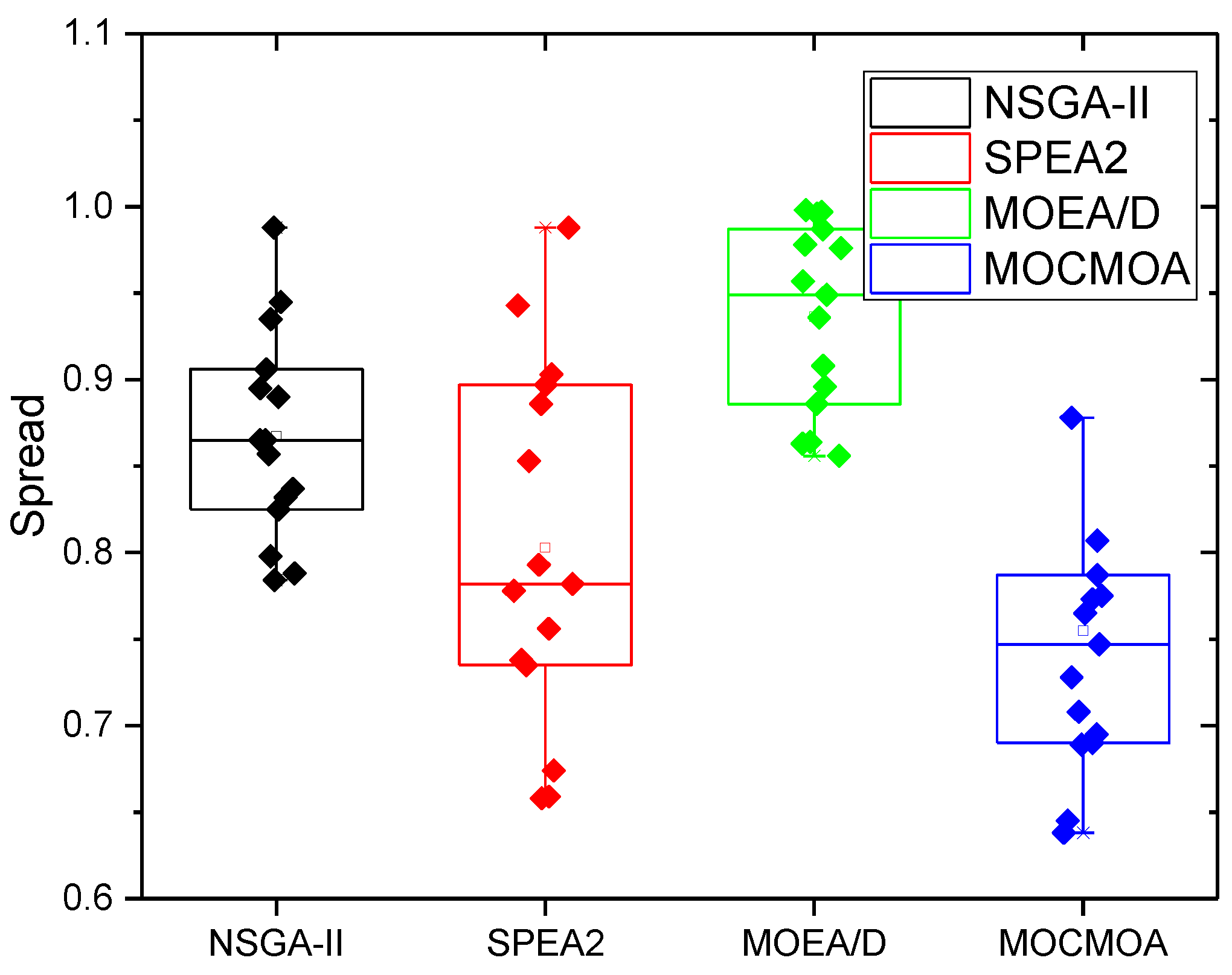
- Spread (Δ). It is a measure of solution distribution. It is capable of determining the distribution situation along the front. This metric’s definition is as follows [36]:
- (2)
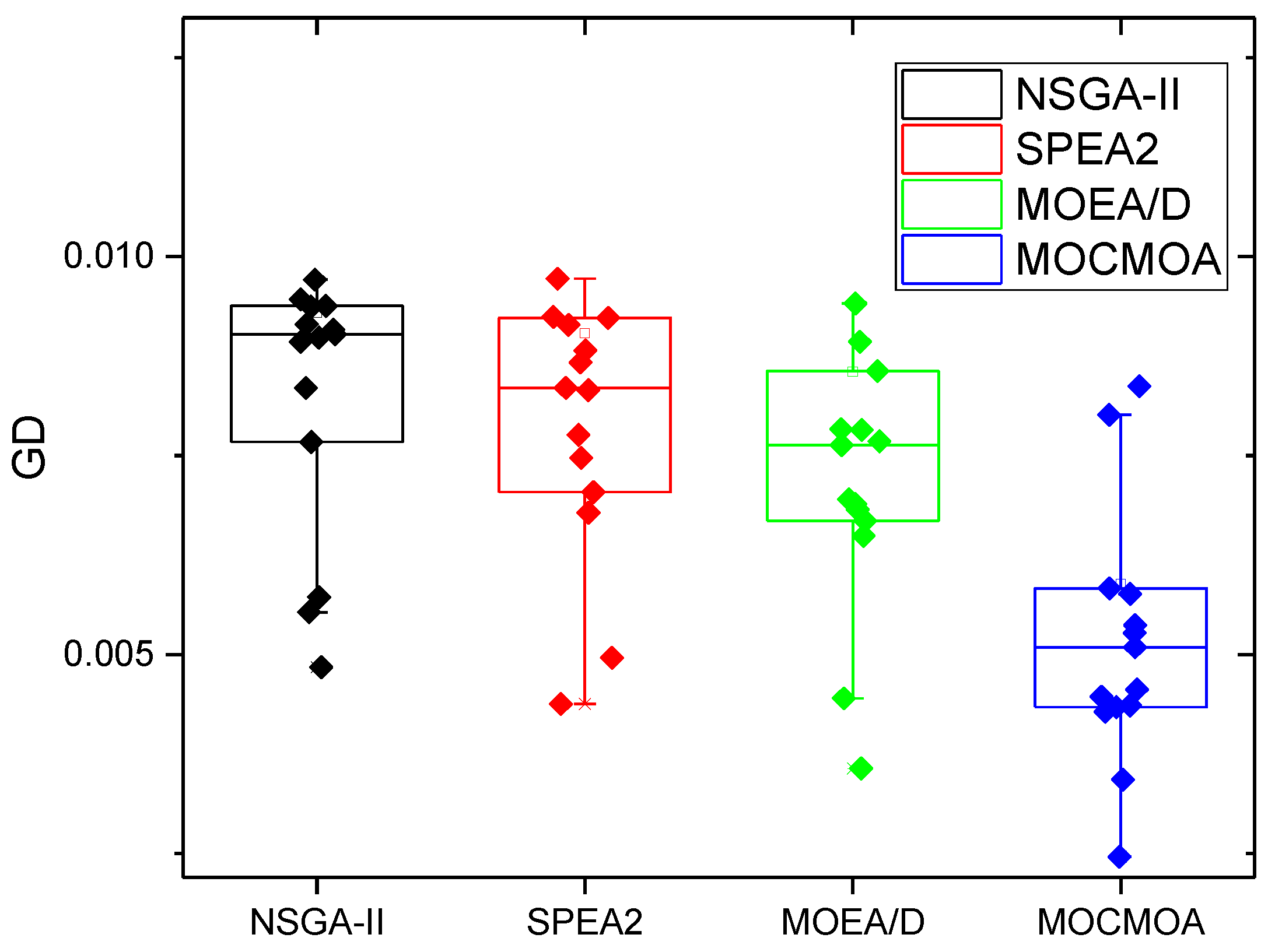
- Generational Distance (GD). The convergence performance is represented by the GD measure. Its average gap is between PF and PF*. The formula for this metric is as follows:
- (3)
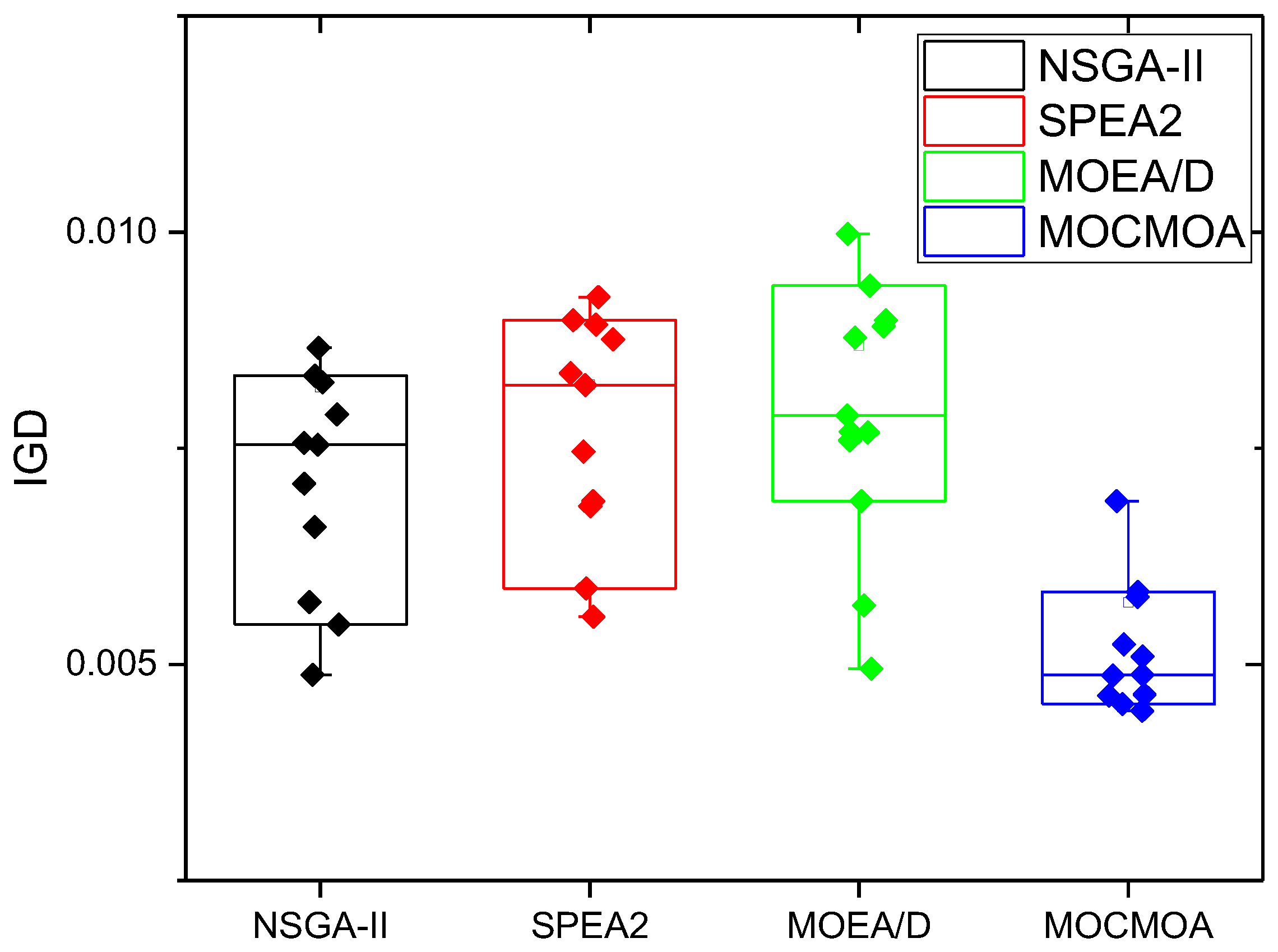
- Inverted Generational Distance (IGD). It is a different version of the GD; however, it is a more thorough indicator. It determines the average distance between PF* and PF. The following is a definition of IGD:
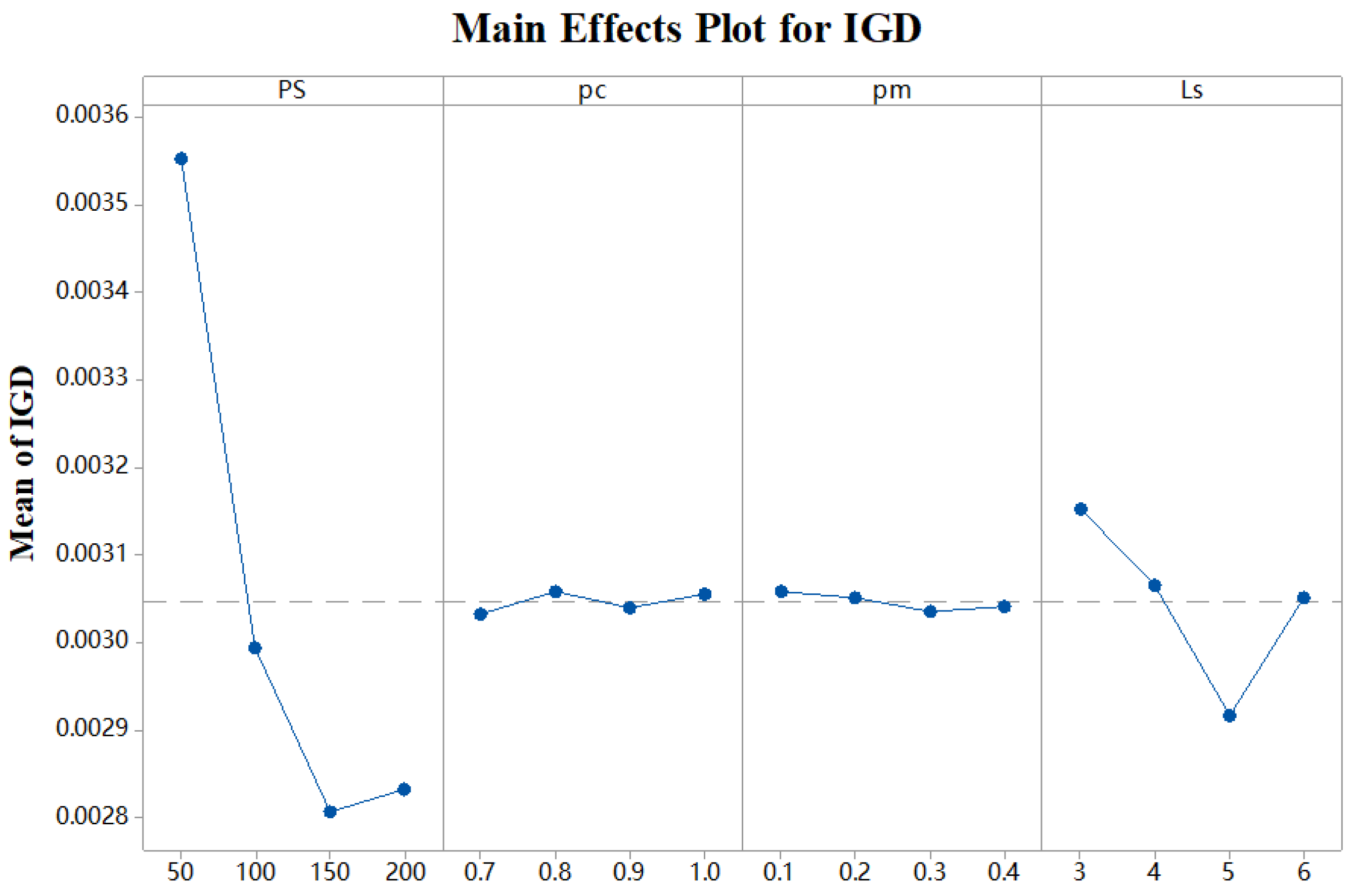
4.2. Parameter Calibration
4.3. Comparison Experiment
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| (1) Parameters | |
| total number of jobs | |
| total number of machines. | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| . | |
| the makespan of the schedule. | |
| . | |
| . | |
| the energy consumption during the work phase. | |
| the energy consumption during the idle phase. | |
| one very large number. | |
| (2) Decision variables | |
| on machine k | |
References
- Lu, C.; Huang, Y.; Meng, L.; Gao, L.; Zhang, B.; Zhou, J. A Pareto-based collaborative multi-objective optimization algorithm for energy-efficient scheduling of distributed permutation flow-shop with limited buffers. Robot. Comput. Manuf. 2022, 74, 102277. [Google Scholar] [CrossRef]
- Lu, C.; Zhang, B.; Gao, L.; Yi, J.; Mou, J. A Knowledge-Based Multiobjective Memetic Algorithm for Green Job Shop Scheduling With Variable Machining Speeds. IEEE Syst. J. 2022, 16, 844–855. [Google Scholar] [CrossRef]
- Jia, J.; Lu, C.; Yin, L. Energy Saving in Single-Machine Scheduling Management: An Improved Multi-Objective Model Based on Discrete Artificial Bee Colony Algorithm. Symmetry 2022, 14, 561. [Google Scholar] [CrossRef]
- Gahm, C.; Denz, F.; Dirr, M.; Tuma, A. Energy-efficient scheduling in manufacturing companies: A review and research framework. Eur. J. Oper. Res. 2016, 248, 744–757. [Google Scholar] [CrossRef]
- Gao, K.; Huang, Y.; Sadollah, A.; Wang, L. A review of energy-efficient scheduling in intelligent production systems. Complex Intell. Syst. 2020, 6, 237–249. [Google Scholar] [CrossRef] [Green Version]
- Mansouri, S.A.; Aktas, E.; Besikci, U. Green scheduling of a two-machine flowshop: Trade-off between makespan and energy consumption. Eur. J. Oper. Res. 2016, 248, 772–788. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Yan, J.; Cheng, Q.; Yang, C.; Sun, S.; Xue, D. The mixed production mode considering continuous and intermittent processing for an energy-efficient hybrid flow shop scheduling. J. Clean. Prod. 2020, 246, 119071. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Li, X.; Pan, Q.-K.; Wang, Q. Energy-efficient permutation flow shop scheduling problem using a hybrid multi-objective backtracking search algorithm. J. Clean. Prod. 2017, 144, 228–238. [Google Scholar] [CrossRef]
- Li, J.-Q.; Sang, H.-Y.; Han, Y.-Y.; Wang, C.-G.; Gao, K.-Z. Efficient multi-objective optimization algorithm for hybrid flow shop scheduling problems with setup energy consumptions. J. Clean. Prod. 2018, 181, 584–598. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Pan, Q.-K.; Li, X.; Zheng, J. A multi-objective cellular grey wolf optimizer for hybrid flowshop scheduling problem considering noise pollution. Appl. Soft Comput. 2019, 75, 728–749. [Google Scholar] [CrossRef]
- Li, M.; Lei, D.; Cai, J. Two-level imperialist competitive algorithm for energy-efficient hybrid flow shop scheduling problem with relative importance of objectives. Swarm Evol. Comput. 2019, 49, 34–43. [Google Scholar] [CrossRef]
- Zuo, Y.; Fan, Z.; Zou, T.; Wang, P. A Novel Multi-Population Artificial Bee Colony Algorithm for Energy-Efficient Hybrid Flow Shop Scheduling Problem. Symmetry 2021, 13, 2421. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Chu, F.; Yu, J. An energy-efficient two-stage hybrid flow shop scheduling problem in a glass production. Int. J. Prod. Res. 2020, 58, 2283–2314. [Google Scholar] [CrossRef]
- Lei, D.; Gao, L.; Zheng, Y. A novel teaching-learning-based optimization algorithm for energy-efficient scheduling in hybrid flow shop. IEEE Trans. Eng. Manag. 2018, 65, 330–340. [Google Scholar] [CrossRef]
- Gong, G.; Chiong, R.; Deng, Q.; Han, W.; Zhang, L.; Lin, W.; Li, K. Energy-efficient flexible flow shop scheduling with worker flexibility. Expert Syst. Appl. 2020, 141, 112902. [Google Scholar] [CrossRef]
- Zhang, B.; Pan, Q.-K.; Gao, L.; Meng, L.-L.; Li, X.-Y.; Peng, K.-K. A Three-Stage Multiobjective Approach Based on Decomposition for an Energy-Efficient Hybrid Flow Shop Scheduling Problem. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4984–4999. [Google Scholar] [CrossRef]
- May, G.; Stahl, B.; Taisch, M.; Prabhu, V. Multi-objective genetic algorithm for energy-efficient job shop scheduling. Int. J. Prod. Res. 2015, 53, 7071–7089. [Google Scholar] [CrossRef]
- Zhang, R.; Chiong, R. Solving the energy-efficient job shop scheduling problem: A multi-objective genetic algorithm with enhanced local search for minimizing the total weighted tardiness and total energy consumption. J. Clean. Prod. 2016, 112, 3361–3375. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. Energy-efficient job shop scheduling problem with variable spindle speed using a novel multi-objective algorithm. Adv. Mech. Eng. 2017, 9, 1687814017695959. [Google Scholar] [CrossRef] [Green Version]
- Giglio, D.; Paolucci, M.; Roshani, A. Integrated lot sizing and energy-efficient job shop scheduling problem in manufacturing/remanufacturing systems. J. Clean. Prod. 2017, 148, 624–641. [Google Scholar] [CrossRef]
- He, L.; Chiong, R.; Li, W.; Dhakal, S.; Cao, Y.; Zhang, Y. Multiobjective Optimization of Energy-Efficient JOB-Shop Scheduling with Dynamic Reference Point-Based Fuzzy Relative Entropy. IEEE Trans. Ind. Inform. 2022, 18, 600–610. [Google Scholar] [CrossRef]
- Abedi, M.; Chiong, R.; Noman, N.; Zhang, R. A multi-population, multi-objective memetic algorithm for energy-efficient job-shop scheduling with deteriorating machines. Expert Syst. Appl. 2020, 157, 113348. [Google Scholar] [CrossRef]
- Yin, L.; Li, X.; Gao, L.; Lu, C.; Zhang, Z. A novel mathematical model and multi-objective method for the low-carbon flexible job shop scheduling problem. Sustain. Comput. Inform. Syst. 2017, 13, 15–30. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, Q.; Wu, Z.; Wang, F. Mathematical modeling and evolutionary generation of rule sets for energy-efficient flexible job shops. Energy 2017, 138, 210–227. [Google Scholar] [CrossRef]
- Luo, S.; Zhang, L.; Fan, Y. Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J. Clean. Prod. 2019, 234, 1365–1384. [Google Scholar] [CrossRef]
- Duan, J.; Wang, J. Energy-efficient scheduling for a flexible job shop with machine breakdowns considering machine idle time arrangement and machine speed level selection. Comput. Ind. Eng. 2021, 161, 107677. [Google Scholar] [CrossRef]
- Li, M.; Lei, D. An imperialist competitive algorithm with feedback for energy-efficient flexible job shop scheduling with transportation and sequence-dependent setup times. Eng. Appl. Artif. Intell. 2021, 103, 104307. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Gao, L.; Liao, W.; Yi, J. An effective multi-objective discrete virus optimization algorithm for flexible job-shop scheduling problem with controllable processing times. Comput. Ind. Eng. 2017, 104, 156–174. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Gong, W.; Hu, C.; Yan, X.; Li, X. Sustainable scheduling of distributed permutation flow-shop with non-identical factory using a knowledge-based multi-objective memetic optimization algorithm. Swarm Evol. Comput. 2021, 60, 100803. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Yi, J. Grey wolf optimizer with cellular topological structure. Expert Syst. Appl. 2018, 107, 89–114. [Google Scholar] [CrossRef]
- Golchin, M.; Liew, A.W.C. Parallel biclustering detection using strength Pareto front evolutionary algorithm. Inf. Sci. 2017, 415, 283–297. [Google Scholar] [CrossRef]
- Mladenovic, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Yi, J.; Li, X. Energy-Efficient Scheduling of Distributed Flow Shop with Heterogeneous Factories: A Real-World Case From Automobile Industry in China. IEEE Trans. Ind. Inform. 2020, 17, 6687–6696. [Google Scholar] [CrossRef]
- Zitzler, E.; Deb, K.; Thiele, L. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the Strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.-N.; Yao, X. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems. Inf. Sci. 2015, 298, 198–224. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, Q. Multiobjective Optimization Problems with Complicated Pareto Sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]

| Parameter | Distribution |
|---|---|
| 30 min | |
| 50 min | |
| continuous uniform (0, 2] kW | |
| continuous uniform [2, 5] kW |
| Instances | NSGA-II (Mean/Standard Deviation) | SPEA2 (Mean/Standard Deviation) | MOEA/D (Mean/Standard Deviation) | MOCMOA (Mean/Standard Deviation) |
|---|---|---|---|---|
| MK01 | 5.72 × 10−3/3.3 × 10−3 | 4.38 × 10−3/3.6 × 10−3 | 4.45 × 10−3/4.2 ×10−3 | 2.46 × 10−3/1.3 × 10−3 |
| MK02 | 4.84 × 10−3/4.3 × 10−3 | 4.96 × 10−3/4.7 × 10−3 | 3.57 × 10−3/5.5 ×10−3 | 3.43 × 10−3/1.6 × 10−3 |
| MK03 | 5.53 × 10−3/2.8 × 10−3 | 6.78 × 10−3/3.5 × 10−3 | 6.68 × 10−3/3.2 ×10−3 | 4.47 × 10−3/2.1 × 10−3 |
| MK04 | 7.67 × 10−3/2.6 × 10−3 | 8.35 × 10−3/2.8 × 10−3 | 7.82 × 10−3/3.7 ×10−3 | 5.27 × 10−3/2.6 × 10−3 |
| MK05 | 8.35 × 10−3/2.1 × 10−3 | 7.47 × 10−3/2.6 × 10−3 | 6.95 × 10−3/2.9 ×10−3 | 4.28 × 10−3/1.7 × 10−3 |
| MK06 | 2.4 × 10−2/1.9 × 10−2 | 2.56 × 10−2/1.9 × 10−2 | 2.86 × 10−2/2.0 × 10−2 | 1.67 ×10−2/1.6 ×10−2 |
| MK07 | 9.46 × 10−3/1.9 × 10−3 | 8.67 × 10−3/1.8 × 10−3 | 7.68 × 10−3/1.8 × 10−3 | 5.83 × 10−3/1.1 × 10−3 |
| MK08 | 9.37 × 10−3/2.7 × 10−3 | 7.76 × 10−3/1.9 × 10−3 | 6.89 × 10−3/2.5 × 10−3 | 4.36 × 10−3/1.1 × 10−3 |
| MK09 | 8.93 × 10−3/2.3 × 10−3 | 8.82 × 10−3/2.1 × 10−3 | 6.49 × 10−3/2.4 × 10−3 | 5.09 × 10−3/1.8 × 10−3 |
| MK10 | 9.02 × 10−3/2.1 × 10−3 | 8.32 × 10−3/2.2 × 10−3 | 6.82 × 10−3/2.1 × 10−3 | 4.56 × 10−3/1.6 × 10−3 |
| MK11 | 9.71 × 10−3/2.7 × 10−3 | 7.04 × 10−3/1.9 × 10−3 | 7.83 × 10−3/1.9 × 10−3 | 4.34 × 10−3/1.2 × 10−3 |
| MK12 | 9.38 × 10−3/3.2 × 10−3 | 9.24 × 10−3/3.1 × 10−3 | 9.41 × 10−3/2.2 × 10−3 | 8.37 × 10−3/2.1 × 10−3 |
| MK13 | 8.98 × 10−3/2.8 × 10−3 | 9.14 × 10−3/2.7 × 10−3 | 7.63 × 10−3/2.9 × 10−3 | 5.76 × 10−3/2.2 × 10−3 |
| MK14 | 9.08 × 10−3/2.5 × 10−3 | 9.23 × 10−3/2.6 × 10−3 | 8.56 × 10−3/2.7 × 10−3 | 5.37 × 10−31.9 × 10−3 |
| MK15 | 9.15 × 10−3/4.6 × 10−3 | 9.72 × 10−3/4.2 × 10−3 | 8.93 × 10−3/3.7 × 10−3 | 8.01 × 10−3/2.8 × 10−3 |
| MOEAs | Rank | p-Value |
|---|---|---|
| NSGA-II | 4.00 | 1.35 × 10−9 |
| SPEA2 | 3.05 | |
| MOEA/D | 2.85 | |
| MOCMOA | 1.00 |
| Instances | NSGA-II (Mean/Standard Deviation) | SPEA2 (Mean/Standard Deviation) | MOEA/D (Mean/Standard Deviation) | MOCMOA (Mean/Standard Deviation) |
|---|---|---|---|---|
| MK01 | 8.90 × 10−1/4.5 × 10−2 | 7.38 × 10−1/3.7 × 10−2 | 9.78 × 10−1/4.9 × 10−2 | 6.89 × 10−1/3.5 × 10−2 |
| MK02 | 9.45 × 10−1/4.4 × 10−2 | 7.82 × 10−1/3.5 × 10−2 | 9.87 × 10−1/4.3 × 10−2 | 7.65 × 10−1/3.0 × 10−2 |
| MK03 | 8.57 × 10−1/5.2 × 10−2 | 6.59 × 10−1/4.9 × 10−2 | 9.49 × 10−1/5.3 × 10−2 | 6.38 × 10−1/3.6 × 10−2 |
| MK04 | 9.35 × 10−1/5.9 × 10−2 | 7.35 × 10−1/4.8 × 10−2 | 9.08 × 10−1/5.7 × 10−2 | 6.95 × 10−1/4.2 × 10−2 |
| MK05 | 8.65 × 10−1/4.3 × 10−2 | 6.58 × 10−1/4.6 × 10−2 | 8.64 × 10−1/6.2 × 10−2 | 6.45 × 10−1/4.1 × 10−2 |
| MK06 | 9.88 × 10−1/5.8 × 10−2 | 9.03 × 10−1/4.1 × 10−2 | 9.98 × 10−1/6.8 × 10−2 | 9.97 × 10−1/6.4 × 10−2 |
| MK07 | 8.65 × 10−1/6.3 × 10−2 | 8.86 × 10−1/5.8 × 10−2 | 9.76 × 10−1/5.8 × 10−2 | 7.28 × 10−1/3.9 × 10−2 |
| MK08 | 7.98 × 10−1/4.8 × 10−2 | 7.93 × 10−1/5.8 × 10−2 | 8.86 × 10−1/6.8 × 10−2 | 6.90 × 10−1/3.8 × 10−2 |
| MK09 | 8.95 × 10−1/6.3 × 10−2 | 8.97 × 10−1/7.2 × 10−2 | 8.96 × 10−1/5.6 × 10−2 | 7.87 × 10−1/4.9 × 10−2 |
| MK10 | 7.88 × 10−1/4.4 × 10−2 | 7.56 × 10−1/5.5 × 10−2 | 9.36 × 10−1/4.6 × 10−2 | 7.47 × 10−1/4.2 × 10−2 |
| MK11 | 7.84 × 10−1/5.6 × 10−2 | 6.74 × 10−1/5.9 × 10−2 | 8.63 × 10−1/7.1 × 10−2 | 7.08 × 10−1/4.7 × 10−2 |
| MK12 | 8.32 × 10−1/5.7 × 10−2 | 7.78 × 10−1/5.5 × 10−2 | 9.96 × 10−1/6.6 × 10−2 | 7.75 × 10−1/4.8 × 10−2 |
| MK13 | 8.25 × 10−1/6.3 × 10−2 | 8.53 × 10−1/6.5 × 10−2 | 9.57 × 10−1/7.3 × 10−2 | 7.73 × 10−1/4.8 × 10−2 |
| MK14 | 8.37 × 10−1/6.2 × 10−2 | 9.88 × 10−1/5.9 × 10−2 | 8.56 × 10−1/6.9 × 10−2 | 8.07 × 10−1/5.5 × 10−2 |
| MK15 | 9.06 × 10−1/6.5 × 10−2 | 9.43 × 10−1/6.5 × 10−2 | 9.97 × 10−1/8.3 × 10−2 | 8.78 × 10−1/6.1 × 10−2 |
| MOEAs | Rank | p-Value |
|---|---|---|
| NSGA-II | 2.86 | 4.95 × 10−5 |
| SPEA2 | 2.05 | |
| MOEA/D | 4.00 | |
| MOCMOA | 1.45 |
| Instances | NSGA-II (Mean/Standard Deviation) | SPEA2 (Mean/Standard Deviation) | MOEA/D (Mean/Standard Deviation) | MOCMOA (Mean/Standard Deviation) |
|---|---|---|---|---|
| MK01 | 5.56 × 10−4/6.6 × 10−5 | 4.98 × 10−4/6.7 × 10−5 | 7.59 × 10−3/6.8 × 10−5 | 4.42 × 10−4/5.3 × 10−5 |
| MK02 | 4.76 × 10−4/6.3 × 10−5 | 4.87 × 10−4/6.6 × 10−5 | 6.93 × 10−4/8.2 × 10−5 | 4.37 × 10−4/5.8 × 10−5 |
| MK03 | 4.88 × 10−3/2.2 × 10−3 | 5.55 × 10−3/2.4 × 10−3 | 4.95 × 10−3/4.5 × 10−3 | 4.64 × 10−3/1.6 × 10−3 |
| MK04 | 8.34 × 10−3/2.6 × 10−3 | 8.37 × 10−3/2.7 × 10−3 | 7.68 × 10−3/3.1 × 10−3 | 5.46 × 10−3/1.8 × 10−3 |
| MK05 | 5.72 × 10−3/6.7 × 10−4 | 5.88 × 10−3/7.8 × 10−4 | 8.78 × 10−3/9.2 × 10−4 | 4.87 × 10−3/4.6 × 10−4 |
| MK06 | 7.54 × 10−3/2.4 × 10−3 | 8.93 × 10−3/2.3 × 10−3 | 7.69 × 10−3/2.6 × 10−3 | 7.54 × 10−3/1.9 × 10−3 |
| MK07 | 7.56 × 10−3/2.0 × 10−3 | 8.23 × 10−3/1.8 × 10−3 | 8.98 × 10−3/1.9 × 10−3 | 4.89 × 10−3/1.4 × 10−3 |
| MK08 | 6.59 × 10−3/2.6 × 10−3 | 7.46 × 10−3/2.3 × 10−3 | 6.89 × 10−3/1.8 × 10−3 | 4.78 × 10−3/1.5 × 10−3 |
| MK09 | 7.09 × 10−3/2.4 × 10−3 | 6.83 × 10−3/1.7 × 10−3 | 9.38 × 10−3/1.5 × 10−3 | 5.09 × 10−3/1.2 × 10−3 |
| MK10 | 5.46 × 10−3/1.7 × 10−3 | 6.89 × 10−3/2.1 × 10−3 | 5.68 × 10−3/1.9 × 10−3 | 4.65 × 10−3/1.5 × 10−3 |
| MK11 | 8.66 × 10−3/1.5 × 10−3 | 9.25 × 10−3/1.8 × 10−3 | 7.88 × 10−3/1.2 × 10−3 | 4.23 × 10−3/1.1 × 10−3 |
| MK12 | 1.67 × 10−2/2.6 × 10−3 | 1.76 × 10−2/2.6 × 10−3 | 1.77 × 10−2/1.6 × 10−3 | 1.34 × 10−2/1.2 × 10−3 |
| MK13 | 8.26 × 10−3/2.7 × 10−3 | 8.98 × 10−3/2.9 × 10−3 | 9.98 × 10−3/2.8 × 10−3 | 4.84 × 10−3/2.2 × 10−3 |
| MK14 | 7.89 × 10−3/2.9 × 10−3 | 8.76 × 10−3/2.4 × 10−3 | 8.91 × 10−3/2.4 × 10−3 | 4.88 × 10−3/1.9 × 10−3 |
| MK15 | 2.73 × 10−3/2.8 × 10−3 | 1.98 × 10−2/2.4 × 10−3 | 1.75 × 10−2/2.9 × 10−3 | 1.45 × 10−2/2.2 × 10−3 |
| MOEAs | Rank | p-Value |
|---|---|---|
| NSGA-II | 2.05 | 2.82 × 10−7 |
| SPEA2 | 2.58 | |
| MOEA/D | 3.32 | |
| MOCMOA | 1.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Peng, W.; Lu, C.; Xia, H. A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops. Symmetry 2022, 14, 832. https://doi.org/10.3390/sym14040832
Wang Y, Peng W, Lu C, Xia H. A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops. Symmetry. 2022; 14(4):832. https://doi.org/10.3390/sym14040832
Chicago/Turabian StyleWang, Yong, Wange Peng, Chao Lu, and Huan Xia. 2022. "A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops" Symmetry 14, no. 4: 832. https://doi.org/10.3390/sym14040832
APA StyleWang, Y., Peng, W., Lu, C., & Xia, H. (2022). A Multi-Objective Cellular Memetic Optimization Algorithm for Green Scheduling in Flexible Job Shops. Symmetry, 14(4), 832. https://doi.org/10.3390/sym14040832







