Abstract
Mirror models lead to the possibility that neutron (n) can oscillate into its mirror partner (), inspiring several experimental searches for this phenomenon. The condition for observability of this oscillation is a high degree of degeneracy between the n and masses, which can be guaranteed if there is exact parity symmetry taking all particles to their mirror partners. However, consistency of these models with big-bang nucleosynthesis requires that this parity symmetry be broken in the early universe in a scenario called asymmetric inflation. In this paper, we study the consistency of an observable oscillations signal with asymmetric inflation and derive various theoretical constraints. In particular, we find that the reheat temperature after inflation should lie below 2.5 TeV, and we predict a singlet fermion with a mass below 100 GeV. In simple models, where the right-handed neutrino is a mediator of baryon-number-violating interactions, we find that the light neutrinos are Dirac fermions with their masses arising radiatively through one-loop diagrams.
1. Introduction
The mirror models [1,2,3,4,5] were proposed many years ago by Lee and Yang as a possible way to reconcile the observed parity violation in weak interactions with a more fundamental theory that conserves parity. They proposed that parity could be taking observed particles to their parity partners in a different world, which interacts with our world only via gravity. The second world has been called the mirror world in recent literature. The success of the standard model (SM) has provided a very specific platform for exploring more detailed phenomenological implications of this idea. In this framework, one duplicates all the SM particles and forces in the mirror sector with identical couplings. While both sides were initially assumed to be connected only by gravitational interactions as stated, they could also be connected by other fields that are SM singlets. This basic setup has the implication that there is a duplication of all observed SM baryons and leptons in the mirror sector, which are dark particles as far as the visible world is concerned. Mirror models could therefore provide candidates for dark matter of the universe with mirror baryons being the ideal candidates to play that role. This framework also has the potential to solve the problems of baryogenesis, neutrino masses and inflation by extending the particle spectrum of each sector in a symmetric fashion. Thus, in principle, mirror models could provide a unified platform for solving many of the puzzles of the standard model.
There are two distinct realizations of the mirror models in the literature: one class, called the symmetric mirror model [6,7,8,9,10] has all scales in the mirror sector the same as the corresponding scales in the visible sector, and a second class where the two weak scales are different [11,12] after spontaneous parity breaking. In the former class of models, it has been pointed out that if there are new interactions beyond the standard model connecting the two sectors, there will occur a new phenomenon known as neutron–mirror-neutron () oscillation [13]. Since our knowledge about the mirror sector of the universe is very limited, such oscillations can take place with low oscillation time (or high rate) without conflicting with any other observations. Several experiments have searched for this process over the past decade [14,15,16,17,18,19,20,21], with plans for improving the sensitivity in forthcoming experiments [22].
The evolution of a mixed system in vacuum and in the absence of magnetic fields is governed by the equation
With initial beam of neutrons, the probability for the appearance of mirror neutron at time t is given by
where and is the mixing parameter in the Lagrangian . In the presence of external magnetic fields and absorption in matter, the diagonal entries of the evolution matrix in Equation (2) should be replaced by the respective energies of n and given by , where V is the optical potential of the neutron and its magnetic moment, with an analogous expression for [23]. Our main focus here is in scenarios where mirror matter and magnetic fields are absent.
The coupling in Equation (2), which violates baryon number B, but preserves where is the mirror baryon number, should arise from some new interactions in the quark Lagrangian that connects the two sectors. Since the best limit on oscillation time defined as to date is , Section (see Serebrov et al. in Ref. [14] and Ref. [15]), derived under the assumption that there is no mirror magnetic field on Earth and there is no mass splitting between n and , GeV should be satisfied. For a discussion on the effects of mirror magnetic field and mass splitting on oscillations see Ref. [24]. If the parameter is much larger than , oscillation would be suppressed, . For unsuppressed oscillations to develop, GeV would be required. Ongoing and proposed experiments [16] are expected to improve the limit on considerably. These searches are also motivated by one interpretation of the neutron lifetime puzzle in terms of oscillations [25], which prefers a range for GeV and . Such values will be shown to arise naturally in the models we develop here. It is therefore important to estimate how large can be in different realistic theoretical frameworks for BSM physics that lead to observable oscillation while being consistent with big-bang cosmology.
If mirror symmetry were exact in the evolution of the early universe, the success of big-bang nucleosynthesis would be spoiled, as the number of light degrees of freedom during the MeV era would be double that of the standard scenario. Asymmetric inflation was proposed in the context of mirror models [26] as a way to reconcile this problem. In the standard BBN theory, during the epoch of nucleosynthesis, the light degrees of freedom present in the plasma are three light neutrinos, electron, the photon and their antiparticles, leading to an effective degree of freedom of . This is consistent with light element abundances derived from BBN. In the mirror model with exact parity symmetry, the effective number of light degrees would be doubled to during BBN, which would spoil its success. Asymmetric inflation reduces this abundance by realizing the temperature of the mirror world to be a factor of 1/3 or so below that of the SM plasma. Since energy density scales as the fourth power of T, the effective number of degrees would now be lowered by a factor of . The effective light degrees from the mirror world would be then decreased to 0.13, which is consistent with BBN. Other ways of reducing the number of light degrees, such as by late decay of particles’ dumping entropy, would appear fortuitous in the mirror framework due to the large number of extra degrees present in the theory.
Neutron–mirror-neutron oscillation is similar in many respects to neutron–anti-neutron () oscillation [27,28,29]. The main difference between the two are two-fold: (i) The degeneracy of n and required for oscillation to take place is guaranteed by CPT invariance which holds in all local and Lorentz invariant theories. On the other hand, the mass degeneracy between n and requires that there be an exact parity symmetry that transforms the visible constituents and forces in the SM to the mirror sector. When asymmetric inflation is implemented in order to preserve the success of BBN [26], an asymmetry in the spectrum of particle masses between the two sectors is introduced. In particular, this will break the mass degeneracy required for efficient oscillation [30]. (ii) The mirror neutron does not feel the normal nuclear force. As a result, a bound neutron cannot undergo oscillation except in a neutron star, where the binding force is gravity. However, a bound neutron can undergo oscillation. For constraints on oscillation arising from pulsars and neutron stars, see Refs. [31,32,33].
Our main goal in this paper is to study the consistency between asymmetric inflation and an observable oscillation in realistic mirror models which also accommodate non-vanishing neutrino masses. We find this to be quite constraining. There are several sources of these constraints. First, the two sectors should not be in equilibrium after inflationary reheating in order to be consistent with BBN. This, when combined with an observable oscillation signal, sets an upper limit on the reheat temperature of 2.5 TeV. We find that the effective B-violating interaction can be generated in renormalizable models in a unique way, which requires a singlet fermion with a mass below 100 GeV. When this fermion is identified as the right-handed neutrino which takes part in neutrino mass generation, two possible scenarios arise: one where the neutrinos are Majorana fermions, which obtain their small mass via the seesaw mechanism, with one flavor decoupled from the rest; and a second, more symmetric one, where the neutrinos are Dirac fermions. In the second scenario, we show that small Dirac masses arise as radiative corrections through one-loop diagrams, somewhat similar to the case in scotogenic models [34]. In both scenarios, it is possible to have observable as well as oscillations, which are accessible to ongoing and forthcoming experiments.
The rest of the paper is organized as follows. In Section 2, we describe a minimal mirror model framework which is compatible with asymmetric inflation. Here, we show why the mass-splitting makes oscillations highly suppressed. Various constraints arising from the two sectors not establishing thermal equilibrium are also derived here. In Section 3, we present a modified framework which has B-violating interactions. Here, we derive an upper limit on the reheat temperature. We also estimate mass-splitting and show that there exist parameters which are consistent with observable oscillations. In Section 4, we draw a connection between oscillations and neutrino mass generation. Here, we develop a Dirac neutrino mass model where the masses arise as one-loop radiative corrections. Finally, in Section 5, we conclude.
2. A Minimal Mirror Model Framework
We begin with a description of a minimal framework where the mirror parity symmetry can be realized and asymmetric inflation can be successfully implemented. As we shall see, this minimal framework will not lead to observable oscillations for two reasons: baryon number is separately conserved in the SM sector and in the mirror sector (denoted as SM); and the mass splitting between n and turns out to be too large when asymmetric inflation is implemented, which suppresses oscillations well below current experimental sensitivity. Nevertheless, this framework would serve as our starting point for a realistic scenario where oscillations can be in the observable range. This framework would also provide insight into the modifications needed in order to circumvent various theoretical constraints to bring oscillations into the observable range.
The gauge symmetry of the minimal mirror model is . The particle content of the mirror sector (indicated with a prime) is identical to that of the SM sector, but transforming under the mirror gauge symmetry. The Lagrangian of the model is the SM Lagrangian and its mirror replica, as well as new interaction terms needed to implement asymmetric inflation through a parity odd singlet scalar field . It is given by
where under the mirror parity symmetry and is mirror parity invariant (see below). This implies that the parameters of are identical to those of , which makes the scenario very predictive. We define to contain right-handed neutrino fields N, which are used for generating small neutrino masses via the seesaw mechanism. Similarly, contains the fields that generate small mirror neutrino masses. (We use the notation N and to indicate right-handed neutrinos and its mirror partner.) Mirror parity implies that the masses and couplings of the N and fields are identical. Specifically, the seesaw sector of the Lagrangian contains the terms (along with the kinetic energies of N and )
where denotes the left-handed lepton doublets and with H being the Higgs doublet with , along with similar definitions for the primed fields.
of Equation (3) contains interaction terms involving a parity odd inflaton field , which is a real scalar singlet under the SM and SM gauge symmetries. It also contains cross terms between the two sectors, and is given by
We now turn to the mechanism of realizing asymmetric inflation from this Lagrangian and derive constraints on the model parameters for achieving this consistently.
2.1. Realizing Asymmetric Inflation
The scalar field acquires a vacuum expectation value (VEV) , which breaks the mirror parity symmetry spontaneously. This is achieved by choosing in Equation (5). The field is also the inflaton, with its potential sufficiently flat so that the slow roll conditions are satisfied. With only the renormalizable quadratic and quartic terms for in the potential, as in Equation (5), chaotic inflation is realized, which is generally successful. However, it turns out that detailed predictions for the spectral index and the tensor-to-scalar ratio r lie slightly outside the range allowed by observations by the Planck satellite [35]. This conflict can be overcome by non-minimally coupling the field to gravity, see for example [36,37]. This is the scenario of inflation that we shall adopt here. For a recent analysis showing the consistency of this approach see Ref. [38].
In the standard picture of inflationary reheating, the inflaton decays while it oscillates around the minimum of its potential. The energy stored in the inflaton field is transferred into its relativistic decay products in the process. These daughter particles thermalize and constitute a radiation-dominated universe. The reheat temperature is determined by the decay width of the inflaton into daughter particles. The decay width differs from the width , since mirror parity symmetry is broken, leading to an asymmetry in the reheat temperatures. This asymmetry is essential for the mirror model to be compatible with big-bang nucleosynthesis. We now show how this can happen in the minimal mirror model framework given in Equations (3)–(5).
Once field develops a VEV, the masses of the Higgs doublet H and its mirror partner, , split, and are given by
where is the coefficient of the term in the SM Lagrangian. The widths for the decay of into and are given by
In the radiation-dominated era, the Hubble expansion rate is given by
where is the effective light degrees of freedom in equilibrium with the plasma at temperature T and GeV is the Planck mass. The reheat temperature is obtained by equating the Hubble rate to the decay rate of the inflaton into the SM fields—the Higgs field in the present case. This yields
Similarly, the reheat temperature of the mirror world is obtained by equating the decay rate of into the mirror sector. We therefore obtain, in the approximation , a relation
The maximum value of , consistent with BBN constraints. If we choose the maximum value, it can be realized by choosing . For such a choice, the mass parameter can be related to the reheat temperature as
where we have set . We have normalized the reheat temperature to be relatively low here, since that will be shown to be a requirement for observable oscillations in the next section.
One important constraint on oscillation arises from this analysis where the inflaton decays asymmetrically to the Higgs fields of the two sectors. The masses of the two Higgs fields are now split, with the splitting given by
Here, in the second step, we have shown the minimum value of the mass splitting, where we used the relation , and the fact that cannot be more than . This splitting would lead to a shift in the VEVs of H and fields, which for GeV and of order 100 GeV is of order
As a result, the neutron and mirror-neutron masses would split, with the splitting of order GeV, which takes into account the fact that the Higgs VEV contributes to these masses only at the level of 1%, with the dominant contribution arising from QCD and mirror QCD dynamics. This splitting is too large, and would suppress oscillations to a level unobservable in experiments.
A second way to realize asymmetric inflation in the same minimal framework is to utilize the coupling of with the right-handed neutrinos, as given in Equation (5). Including the parity asymmetric contribution from , the mass matrices for the N and fields are given by
where is the common mass term for N and defined in Equation (4). These mass matrices are diagonalized by unitary transformations and . The widths for decay into N pairs and pairs are given by
where and stand for the mass eigenvalues of the and fields. Unlike in the case of decays into Higgs fields, here an asymmetry would have to rely on the kinematic factors of Equation (15), since in the limit of ignoring and in relation to , the decay rates become identical, in spite of the presence of two different unitary matrices V and in the decay-rate formulas.
If asymmetric inflation is realized via kinematics in these decays, there is still difficulty with observable oscillations. To illustrate this constraint, consider decaying dominantly to one flavor of N and fields with masses and . The ratio of reheat temperatures in the mirror sector to that in the SM sector is then given by
This ratio can be set to a value such as by a suitable choice of and . However, this would require and to differ by at least one order. Between these two mass scales, the QCD coupling and the mirror QCD coupling will evolve differently, as can be seen from a three-loop diagram shown in Figure 1. Recall that the QCD scale parameter is defined through one-loop renormalization group evolution as
where is the one-loop beta function coefficient with six flavors of quarks. An analogous expression can be written for , the mirror QCD scale parameter. In the momentum regime , the two couplings run differently owing to diagrams such as Figure 1. This results in a difference in the effective values of and which we estimate to be
where is the top quark Yukawa coupling and the Dirac neutrino Yukawa coupling defined in Equation (4). Now, the coupling cannot be too small, as it is responsible for bringing the N () states into equilibrium with the rest of the SM (SM) plasma. The width of N decaying into and its CP conjugate states is given by
which can compete with the Hubble rate at temperatures in the order the N mass, provided that the condition
is satisfied. Inserting this lower limit on in Equation (18), we obtain (for GeV)
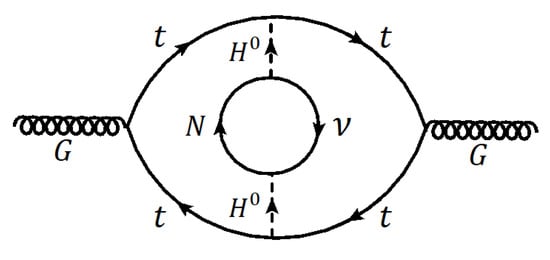
Figure 1.
Feynman diagram that generates an asymmetry in the strong coupling and its mirror counterpart in the minimal mirror framework, where asymmetric inflation is realized through inflaton decays into N and . The masses of N and are different in this case, leading to the asymmetry in the strong couplings.
The difference causes a difference in the two QCD scale parameters which follows from Equation (18):
Consequently, the masses of n and will split by about GeV, as these masses arise primarily proportional to and , making oscillations strongly suppressed. It may be possible to evade this suppression by applying an external magnetic field in the experimental setup of order 17 Tesla, which could cancel the mass splitting. However, the minimal framework still lacks a source for B violation. Including such a source, which is described in Section 3.5, our estimate of mass splitting is of order GeV in the minimal framework, which would make oscillation difficult to observe (see discussions after Equation (55) of Section 3.5).
We note that the lower bound on given in Equation (20) is only a general example and could be different in specific models. For example, if the N and did not decay away before , they could dominate the mass density of the universe and affect the success of BBN. The bound in Equation (20) would guarantee that this does not happen.
To summarize, in this minimal mirror model framework, asymmetric inflation can be realized, but the mass splitting between the neutron and mirror neutron is too large for oscillations to be observable. This framework also lacks baryon-number-violating interactions that are needed for oscillations to occur.
2.2. Constraints on Mixed Couplings from BBN
The success of asymmetric inflation relies on the condition that the SM sector and the mirror sector do not come into equilibrium once reheating is established. There are three sets of interaction terms in the minimal framework that can potentially bring the two sectors into thermal equilibrium, see Equation (5). We develop the necessary conditions to achieve these in this subsection.
1. Constraint on the mixed quartic Higgs coupling: First, the quartic coupling of Equation (5) cannot be of order unity. In its presence, scattering processes such as would occur, which can bring the two sectors into equilibrium. The cross section for this process is given by
The reaction rate can be estimated by multiplying this cross section with the equilibrium number density of , a boson, given by
where is the internal degrees of this complex field. Demanding that remains smaller than the Hubble expansion rate to temperatures down to the Higgs boson mass, we obtain (for ) the condition
Such a small cross coupling is technically natural, since other interactions do not induce this coupling through quantum corrections. In what follows, we shall assume that this condition is always satisfied.
2. Constraints on the inflaton coupling to the two sectors: The inflaton field couples to both sectors, and thus can potentially bring the two sectors into thermal equilibrium. The cross section for mediated by the field (after integrating it out) is given by:
Choosing parameters such that , we find the condition for this process to be not in equilibrium at to be
(For a more refined treatment of this process and reheating in general, see Ref. [39]). This condition is satisfied easily, since for a low reheat temperature is necessary anyway.
3. Constraint on photon–mirror-photon kinetic mixng: A third constraint arises from the kinetic mixing term in Equation (5) between the two hypercharge gauge fields parametrized by the coupling . This term will result in a kinetic mixing between the photon and the mirror photon with a Lagrangian given by
where with being the weak mixing angle. A shift in the gauge boson fields would remove this mixed kinetic term from the Lagrangian, but in the process mirror fermions would acquire milli-charges under usual electromagnetism [40]. For example, the mirror electron will acquire a coupling to the photon given by . Consequently, scattering processes such as would occur with a cross section given in the relativistic limit by
These reactions should be out of thermal equilibrium down to temperatures in the order the electron mass. The number density of fermions in a relativistic plasma is given by
where is used for the two spin degrees of the fermion. Demanding to be smaller than the Hubble rate at we obtain
This estimate is in agreement with the estimate of Ref. [41]. An improved estimate obtained in Ref. [42] by solving the Boltzmann equation is an order of magnitude stronger.
This constraint on photon–mirror-photon kinetic mixing can be satisfied in the minimal framework, as the particle content of the model is such that no kinetic mixing is induced at lower loop levels. However, in more extended models, this can provide a strong constraint. For example, in a theory where there is a complex scalar field charged under both Y and , a nonzero (and therefore ) would be induced, given via the renormalization group equation as [43,44]
where m is the mass of the scalar. This condition would preclude the presence of any particle in the theory that it is charged under both the SM and SM gauge symmetries. This result relies only on the success of asymmetric inflation and is independent of whether oscillation is in the observable range or not.
3. Modified Framework for Observable Oscillation
Here, we present a modification of the minimal framework that allows for observable oscillations which is compatible with asymmetric inflation. To the particle content of the minimal mirror model discussed in Section 2, we add a parity-even real scalar field X and its parity partner which are singlets of the gauge symmetry. The Lagrangian involving these fields includes the terms
Asymmetric inflation can now be realized in the decays of and , and as in the case of decaying into Higgs pairs, the ratio of reheat temperatures is given by
Here, we assume that asymmetries arising from decays into Higgs pairs are negligible by choosing of Equation (5) to be vanishingly small. The advantage here is that there will not be a significant splitting in , and thus the two VEVs v and can be maintained at almost exactly equal. The mass splitting that arose in the minimal model from the VEV difference given in Equation (13) is therefore absent in the present case.
The scalar field X is kept in thermal equilibrium with the SM plasma via its decay into a pair of N fields via the coupling of Equation (33), and similarly maintains its thermal equilibrium with the SM plasma through its decay into . For this to occur, there is a minimum value of the coupling that is needed. In the approximation , the width for the decay is given by
Requiring this rate to be of the order the Hubble expansion rate at , one obtains (with and assuming a single Yukawa coupling to be dominant in the decay)
The constraint of Equation (36) can be used to estimate the minimum splitting in the mass of n and . The one-loop diagram shown in Figure 2 would renormalize the wave function of N differently compared to that of , since the masses of X and scalars differ by an order of one. Once this wave-function correction is inserted in the diagram of Figure 1, the strong coupling and its mirror counterpart would evolve differently, with the effective function difference given by (see Equation (18))
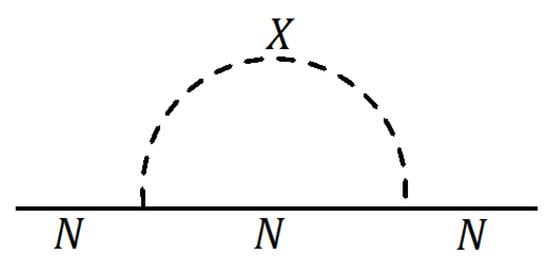
Figure 2.
Asymmetric wave function correction for N and in the modified model.
Note that this shift arises in the running of the couplings in the momentum range . The resulting shift in the QCD scale parameters is , leading to GeV, which is fully consistent with observable oscillations.
3.1. Baryon-Number-Violating Interactions
For oscillation to occur, there must be baryon-number violation in the theory with an effective quark level operator of the form , suppressed by the fifth power of an effective mass scale . This operator, which breaks both B and (baryon number of the mirror world) by one unit, preserves as a global symmetry. If this symmetry remains unbroken in the full Lagrangian, oscillation would be permitted, while oscillation, which breaks B by two units, would be forbidden. Since the energy scale probed by present limits on oscillation ( s) is significantly larger than that probed by oscillations ( Section), for the latter process to be in the observable range it would be desirable to maintain symmetry to a good approximation.
Before presenting possible UV completions, we write down effective operators with definite chiral and Lorentz structures, as follows:
along with an analogous operator (with a different strength) where the left-handed fermion fields are replaced by right-handed fields. It will turn out that these are the two operators that are induced in simple UV complete models presented in the next subsection. In Equation (38), a charge conjugation matrix which is not shown contracts each spinor pair. This effective operator has to be converted to neutron and mirror-neutron operators in order to discuss oscillations. The hadronic matrix elements relevant for this conversion are defined as
Here, and stand for the left-handed and right-handed neutron spinors respectively. Analogous matrix elements involving the mirror quarks and mirror neutron can be defined, with the coefficients and identical to those in Equation (39) due to mirror parity. These matrix elements have been computed on the lattice rather accurately in the context of nucleon decay. Ref. [45] quotes the continuum limit values of these coefficients to be GeV and GeV. (For lattice evaluation of hadronic matrix element see Ref. [46]). The effective Lagrangian of Equation (38) can then be converted to a nucleon-level Lagrangian as
Consequently, the off-diagonal entry in the Hamiltonian matrix relevant for oscillation (see Equation (1)) is , where we have used the fact that in the non-relativistic limit the term does not contribute. The oscillation lifetime follows from Equation (40) as and is given (with the lattice value of quoted above) by
It is clear that the near-future sensitivity of oscillation would be in the range TeV, which is what we shall focus on in what follows.
3.2. The Need for Low Reheat Temperature
It turns out that the reheat temperature after inflation should be relatively low in the mirror world setup with observable oscillations. Recall that the success of asymmetric inflation relies on the SM and SM sectors remaining thermally decoupled. The two sectors could be brought into thermal equilibrium through the effective interaction of Equation (38) which is needed to induce oscillation. Here, we derive an upper limit on the reheat temperature arising from demanding that such equilibration does not occur.
In presence of the Lagrangian of Equation (38), the following two-body-to-four-body scattering process can occur:
For a fixed color configuration both in the initial state and in the final state, the spin-averaged squared amplitude for this process, in the limit of massless quarks, is given by
where , and . Following the four-body phase space variables defined in Ref. [47], we obtain an analytic expression for the integrated cross section for this process:
At temperatures below the effective mass and above 1 GeV, this reaction could potentially be faster than the Hubble expansion rate . These two rates become equal at , where is given by
which is obtained by equating to . Here, we used (where E is the CM energy of the incident particles) and . Since observability of oscillations suggests a range TeV, for some temperature will be realized unless this is above the reheat temperature. We thus conclude that should obey the condition
This is an improved estimate, including the phase-space-suppression factors shown in Equation (44), compared to Refs. [13,48]. It is interesting to note that the reheat temperature, while low, can still be above the electroweak symmetry-breaking scale, which allows the framework to realize baryogenesis via leptogenesis as well as electroweak baryogenesis. We emphasize that the above estimate of is valid when all exchanged particles giving rise to the dimension-9 operator have masses above 10 TeV or so. In specific models, this has to be reevaluated properly, taking into the the detailed mass profile. Typically, this would lead to slightly stronger constraints. See for example the model discussed in the following section.
3.3. UV Completion of the Effective Operator for Oscillation
We now turn to the generation of of Equation (38) that induces oscillations from microscopic physics. When this operator is opened up at tree level, two different topologies arise. The first one is shown in Figure 3, which we shall see is essentially the only one that is compatible with asymmetric inflation. This is the diagram suggested in Ref. [13]. The renormalizable Lagrangian generating Figure 3 is
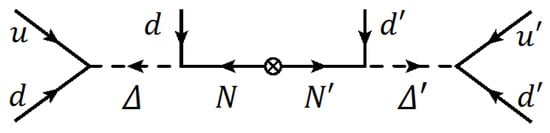
Figure 3.
Feynman diagram generating the oscillation operator in an UV complete theory.
Here, all primed fields transform under the SM gauge symmetry, while the un-primed fields transform under SM symmetry in identical fashion. is a complex scalar with quantum numbers of , and is its mirror partner. is a fermionic singlet of the SM, with being its mirror partner. Note that the Lagrangian of Equation (47) breaks baryon number B and mirror baryon number , but it conserves symmetry. This can be seen by assigning fields baryon numbers of , along with charges of for the fields. If the symmetry is maintained, oscillations would be forbidden, but oscillations would be allowed. This symmetry may be broken down to a subgroup by adding Majorana masses for the and fields of the type
In this case, the mass parameter will have to be of order or smaller for observable oscillations, since in the presence of Equation (48) , oscillations would occur, which is constrained by experiments ( Section) at a level which is about five orders of magnitude stronger than oscillations ( Section). We shall entertain including such a small term in the next section, but focus here on the exact symmetric limit where the RHS of Equation (48) is identically zero.
Integrating out the and fields in Equation (47) one would obtain an effective four-Fermi Lagrangian carrying nonzero baryon number given by
Here, we have not displayed B-conserving terms, which are irrelevant for oscillations. If we also integrate out the and fields from here, one would obtain the effective six-fermion Lagrangian of Equation (38), with the identification
along with a similar term where all quarks are right-handed and the coupling is replaced by . The mass scale should be in the range TeV for observable oscillations, which sets upper limits on the masses of and N. As an example, consider , TeV and GeV, which would lead to TeV, which is consistent with all experimental constraints. Of course, other choices of the Yukawa couplings are possible, leading to different masses of and N fields. Lower values of the Yukawa couplings would lower the mass of , in which case it may be within reach of the LHC. However, as we shall see in the next subsection, the mass of N has to lie in the range GeV, or else spin-flip transitions involving the N field would bring the SM sector and the mirror sector into equilibrium.
One point worth noting here is that in the example above, since the N and have masses below 100 GeV, we have to re-evaluate the reheat temperature, and not simply use the limit derived in Equation (46) which was derived assuming an effective operators leading to the scattering process. We sketch this re-evaluation below. The condition that the rate for at GeV does not exceed the Hubble expansion rate is given approximately by
This leads to an estimate of to be
which is slightly stronger than the result in Equation (46).
A second possible way of generating the six-fermion operator of Equation (38) is by integrating out only scalar fields, as shown in Figure 4. However, in this topology, at least one of the scalars should carry hypercharge under both SM and SM. For example, the three scalars could be having Yukawa couplings to quarks of the type . The field carries both hypercharges Y and in this case. This would lead to an induced kinetic mixing term between the photon and mirror photon at the level of , see Equation (32), which would violate the bound derived in Equation (31). The same remark applies to the general topology of the type shown in Figure 3 with fermions and scalars, unless the fermion is a singlet of both gauge symmetries. Topologies of Figure 3 and Figure 4 are the only ones that allow for inducing the six-fermion operator of Equation (38) at tree level. We thus conclude that the diagram of Figure 3 is the only way to generate oscillations at the observable level in the framework of asymmetric inflation.
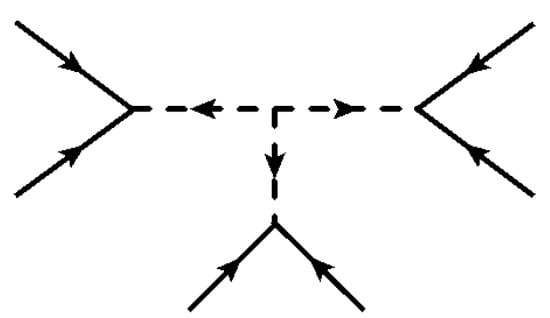
Figure 4.
A second possible topology for inducing the operator for oscillation.
3.4. Spin-Flip Transition Constraint
The SM and SM sectors could be brought into thermal equilibrium via a spin-flip transition involving the N and fields. As shown in Section 3.3, and form right-handed and left-handed components of a Dirac fermion. Since N is in equilibrium with the SM plasma and is in equilibrium with the SM plasma, any interaction that leads to spin-flip of this Dirac fermion could bring the two sectors into equilibrium. In order to derive the constraint for this not to happen, we focus on the first term of the four-Fermi Lagrangian of Equation (49). This term can be recast after a Fierz rearrangement as
We have computed the spin-flip cross section for the process (with denoting the helicity eigenvalue) following the formalism developed in Ref. [49], and find this cross section to be
Here, we have defined obeying the relation (with defined in Equation (38)). We demand that be less than the Hubble rate with . The two rates become equal if, for example, we choose TeV and GeV (corresponding to TeV) at GeV, with the spin-flip rate exceeding the Hubble rate at higher temperatures. This choice would require the reheat temperature to be less than 56 GeV so that this cross-equilibrium is not established. As the mass of N field is lowered, the reheat temperature can be raised. If we choose GeV and TeV (so that TeV), the equality of the two rates occurs at TeV, which is consistent with observable oscillation and asymmetric inflation. The scenario prefers lower mass of the N field, in the range of GeV within the framework. (The lower limit arises from nucleon stability, as the proton would decay into N and a for lower masses of N.) Since the exchange of such a singlet fermion field is essentially unique in inducing oscillation at an observable level, the existence of a light N in this mass range may be regarded as a prediction of the framework. This opens up the possibility that this singlet fermion can be potentially discovered at the LHC.
3.5. Mass Splitting in the UV Complete Theory
The new interactions of Equation (47) can potentially induce a mass splitting between the neutron and mirror neutron. We find the most important diagram in the model that induces such a splitting to be the one given in Figure 5. Here, the scalar , being colored, couples directly to the gluon, and it also has coupling to N and d. N in turn couples to the X scalar, which has a different mass compared to its mirror. Following the discussions around Equation (18), we now obtain for the difference in the effective QCD and QCD beta functions
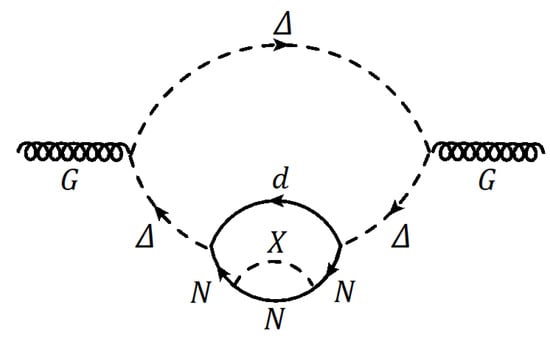
Figure 5.
Leading contribution to the mass splitting in the UV complete theory.
Now, is needed for X to be in equilibrium with N for X mass of about 1 TeV, see Equation (36). If the coupling is of order one, the two QCD scales would differ by a factor , leading to unacceptably large mass splitting. One could take small values of , but in this the scale of Equation (38) that controls oscillations will become large. A judicious choice which avoids this conflict is to take , TeV, and GeV, in which case TeV (see Equation (50)). Our estimate for this choice is GeV, which is just about sufficient for unsuppressed oscillations. Note that such a choice of parameters would make the colored scalar relatively light, which may be within reach of the LHC.
In the minimal mirror model framework discussed in Section 2, it was noted that when inflaton decays to right-handed neutrinos, consistency with BBN would require GeV. Since B violation in that framework requires the introduction of a colored field, the estimate of Equation (55) would be applicable there, but without the factor . It is this estimate that would lead to the quoted mass splitting.
It should be pointed out that when the mass splitting is of order GeV, which happens quite naturally in the model, it may be possible to cancel this energy difference by applying a magnetic filed in the search experiment of order 167 Gauss. This is an interesting way to achieve an MSW-like resonance in the oscillation even when there is small mass splitting. It would remain to be a challenge, since theoretically the mass splitting cannot be computed with accuracy needed for experiments.
There is one simple modification of the model presented here that would make the mass splitting well below GeV without sacrificing the successful features of the model. Suppose that there is an additional scalar singlet Y and its mirror partner in the model. One could now couple Y and asymmetrically to the inflaton field through the couplings
If the quartic coupling is of order or larger, that would keep X and Y in equilibrium (and similarly in the mirror sector). It is the masses of Y and that are split by an order one in this case, and not those of X and . Note that Y does not have a significant Yukawa coupling with N in this modification. The diagram of Figure 6 will not lead to an asymmetric running of and . One would need to insert a Y loop connected to the X line of Figure 6 to generate asymmetry. However, this four-loop diagram would be suppressed by an additional factor of compared to Equation (55), which could bring in a suppression of order . In this case, the Yukawa coupling that appears in Equation (55) can be of order 0.1, and the parameter space for oscillation would open up considerably.
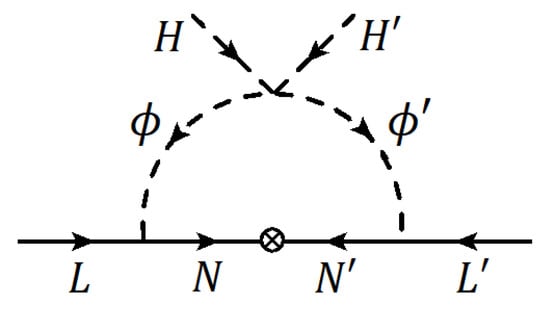
Figure 6.
One-loop diagram inducing Dirac neutrino masses. Here, is a second Higgs doublet that carries baryon number.
4. A Connection with Neutrino Mass Generation
Since an almost unique way of generating the operator of Equation (38) that induces oscillation is by the exchange of a neutral singlet fermion N, it is very tempting to explore if this field can be identified as the right-handed neutrino. If it has the canonical couplings of the seesaw mechanism, as shown in Equation (4), this identification is problematic, since after electroweak symmetry breaking N mixes with the light neutrino. The effective operator would lead to proton decay , the constraint from which would require the scale to be close to the GUT scale. One possible way out is to identify N appearing in the operator as one of the three right-handed neutrinos which decouples from the seesaw mechanism [50]. Realistic neutrino masses and mixings can be produced involving only two right-handed neutrinos. In this scenario, one could adopt resonant leptogenesis to explain the observed baryon asymmetry of the universe.
A second alternative, which we develop here further, would treat all three right-handed neutrino fields on the same footing, but their Dirac Yukawa couplings involve a second Higgs doublet (and its mirror partner that does not acquire a VEV. The new Yukawa couplings are
In this case, can be maintained as a good symmetry, as can be seen by assigning B of to (and similarly of to ) field. The Higgs potential would now contain a -conserving quartic coupling, given as
Although such a coupling could potentially bring the SM and SM into equilibrium, this can be avoided by taking the (common) masses of and above the reheat temperature of order TeV. The neutrinos will now acquire Dirac masses with the right-handed partners being the fields of the mirror sector. These arise through the one-loop diagram shown in Figure 6. We estimate the induced Dirac masses to be
As an example of a consistent parameter set, let GeV, , and GeV, which would lead to eV. Note that the quartic coupling would induce a term of the type through a one-loop diagram with a strength , which for the choice of parameters quoted above is of order . This is below the critical value derived in Equation (25) that would bring the two sectors into equilibrium.
In this version, diagrams such as the one shown in Figure 7 would lead to a splitting of the masses of n and . The shift in the QCD and QCD beta function coefficients arising from this diagram can be estimated to be
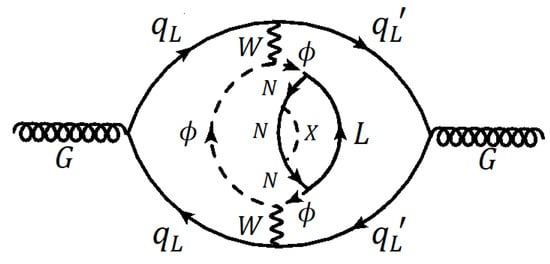
Figure 7.
A higher loop diagram inducing mass splitting in the model with a second Higgs doublet .
Owing to the presence of more loops, the induced mass splitting can be below GeV. For example, the choice would lead to GeV.
4.1. A Scenario with Observable and Oscillations
There is an interesting possibility in the model with a second Higgs doublet to realize oscillation and oscillations at the observable level simultaneously. Consider the addition of the Majorana masses to the N and fields, as shown in Equation (48). These mass terms should be of order times the leading Dirac mass terms . The symmetry is now broken down to a subgroup. For this choice of parameters, both and oscillations can be near the current experimental limits. The Higgs potential would now have an additional quartic coupling given by
This term preserves a subgroup of symmetry, which guarantees the proton stability. Note that the lightest of the fields is not a dark-matter candidate, as it can decay into N and a neutrino. The N field is unstable as it decays into three quarks. Mirror baryons are the only dark-matter candidates in this setup. In addition to the diagram of Figure 6 that induces Dirac masses for the neutrinos, now there would also be Majorana masses as in the scotogenic model [34]. The use of the scotogenic model to avoid the proton decay problem in the case of oscillation was discussed in [51]. The relevant diagram is shown in Figure 8. This Majorana mass can be estimate to be
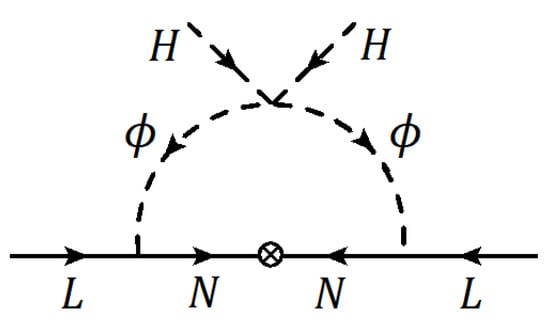
Figure 8.
One-loop diagram inducing Majorana neutrino masses as in the scotogenic model.
These induced Majorana masses are much smaller than the Dirac masses given in Equation (57), since , and since we can take quite naturally. Although the neutrino is now a pseudo-Dirac particle, the mass-splitting between the two states could be of order eV, well below experimental requirements.
4.2. A Comment on Symmetric Inflationary Scenario
Here, we wish to comment on the possibility that mirror models can be made consistent with BBN in symmetric inflationary scenarios. It has been suggested that if inflation is driven by two inflaton fields which are mirror partners, quantum fluctuations could possibly generate asymmetry in the two reheat temperatures [52]. If such a scenario can be realized, mass splitting would not be an issue with observable oscillation among them. However, it is not clear if such an asymmetry in the reheat temperatures can be dynamically induced in renormalizable models. A recent analysis has found that simple integer power potentials involving the inflaton fields do not lead to an asymmetric reheat temperature, although fractional power potentials can realize an asymmetry [53]. In contrast, the asymmetric inflation follows from simple renormalizable power law potentials, and are calculable within effective quantum field theory.
5. Summary and Conclusions
We have examined in this paper theoretical constraints arising from observable oscillation signals compatible with asymmetric inflation. One of the main constraints arises from the mass splitting induced by parity violation needed for asymmetric inflation in the masses of the neutron and mirror neutron. In realistic scenarios, we have estimated the minimum value of this splitting and found it to lie in the range – GeV. We have also proposed a mechanism to suppress this splitting to much smaller values.
We have found that the post-inflationary reheat temperature has an upper bound of about 2.5 TeV in order to not establish equilibrium between the standard model and the mirror sectors, if oscillation lies in the observable range. We have argued that the UV completion of such models is essentially unique, and found that a neutral singlet fermion should exist with a mass below 100 GeV.
We have also tried to connect the neutral fermion present in the theory to neutrino mass generation. Two scenarios are realized: one where the neutrinos are Majorana particles and the singlet fermion inducing oscillations is decoupled from the other two right-handed neutrinos, and another where the neutrinos are Dirac particles with their masses arising radiatively from one-loop diagrams. This framework suggests the possibility of observing both and oscillations in near future experiments.
Author Contributions
Conceptualization, K.S.B. and R.N.M.; methodology, K.S.B. and R.N.M.; formal analysis, K.S.B. and R.N.M.; investigation, K.S.B. and R.N.M.; resources, K.S.B. and R.N.M.; writing—original draft preparation, K.S.B. and R.N.M.; writing—review and editing, K.S.B. and R.N.M.; project administration, K.S.B. and R.N.M.; funding acquisition, K.S.B. and R.N.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work of KSB is supported by the US Department of Energy Grant No. DE-SC 0016013 and that of RNM is supported by NSF grant No. PHY-1914631.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Zurab Berezhiani and Yuri Kamyshkov for discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, T.D.; Yang, C.N. Question of Parity Conservation in Weak Interactions. Phys. Rev. 1956, 104, 254–258. [Google Scholar] [CrossRef]
- Kobzarev, Y.; Okun, L.; Pomeranchuk, Y.I. On the possibility of experimental observation of mirror particles. Yad. Fiz. 1966, 3, 1154. [Google Scholar]
- Pavsic, M. External inversion, internal inversion, and reflection invariance. Int. J. T. P. 1974, 9, 229. [Google Scholar]
- Kolb, E.W.; Seckel, D.; Turner, M. The shadow world of superstring theories. Nature 1985, 514, 415. [Google Scholar]
- Foot, R.; Lew, H.; Volkas, R. A Model with fundamental improper space-time symmetries. Phys. Lett. B 1991, 272, 67. [Google Scholar] [CrossRef]
- Foot, R.; Volkas, R.R. Neutrino physics and the mirror world: How exact parity symmetry explains the solar neutrino deficit, the atmospheric neutrino anomaly and the LSND experiment. Phys. Rev. D 1995, 52, 6595–6606. [Google Scholar]
- Berezhiani, Z.; Comelli, D.; Villante, F.L. The Early mirror universe: Inflation, baryogenesis, nucleosynthesis and dark matter. Phys. Lett. B 2001, 503, 362–375. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.; Ciarcelluti, P.; Comelli, D.; Villante, F.L. Structure formation with mirror dark matter: CMB and LSS. Int. J. Mod. Phys. D 2005, 14, 107–120. [Google Scholar]
- Ignatiev, A.Y.; Volkas, R.R. Mirror dark matter and large scale structure. Phys. Rev. D 2003, 68, 023518. [Google Scholar]
- Foot, R. Mirror dark matter: Cosmology, galaxy structure and direct detection. Int. J. Mod. Phys. A 2014, 29, 1430013. [Google Scholar]
- Berezhiani, Z.G.; Mohapatra, R.N. Reconciling present neutrino puzzles: Sterile neutrinos as mirror neutrinos. Phys. Rev. D 1995, 52, 6607–6611. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chacko, Z.; Goh, H.S.; Harnik, R. Natural electroweak breaking from a mirror symmetry. Phys. Rev. Lett. 2006, 96, 231802. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.; Bento, L. Neutron-mirror neutron oscillations: How fast might they be? Phys. Rev. Lett. 2006, 96, 081801. [Google Scholar] [CrossRef] [Green Version]
- Serebrov, A.P.; Aleksandrov, E.B.; Dovator, N.A.; Dmitriev, S.P.; Fomin, A.K.; Geltenbort, P.; Kharitonov, A.G.; Krasnoschekova, I.A.; Lasakov, M.S.; Murashkin, A.N.; et al. Experimental search for neutron: Mirror neutron oscillations using storage of ultracold neutrons. Phys. Lett. B 2008, 663, 181–185. [Google Scholar] [CrossRef] [Green Version]
- Serebrov, A.P.; Aleksandrov, E.B.; Dovator, N.A.; Dmitriev, S.P.; Fomin, A.K.; Geltenbort, P.; Kharitonov, A.G.; Krasnoschekova, I.A.; Lasakov, M.S.; Murashkin, A.N.; et al. Search for neutronmirror neutron oscillations in a laboratory experiment with ultracold neutrons. Nucl. Instrum. Meth. A 2009, 611, 137–140. [Google Scholar] [CrossRef] [Green Version]
- Ban, G.; Lefort, T.; Naviliat-Cuncic, O.; Bodek, K.; Kistryn, S.; Kuzniak, M.; Zejma, J.; Khomutov, N.; Knowles, P.; Rebetez, M.; et al. A Direct experimental limit on neutron: Mirror neutron oscillations. Phys. Rev. Lett. 2007, 99, 161603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altarev, I.; Baker, C.A.; Ban, G.; Bodek, K.; Daum, M.; Fierlinger, P.; Geltenbort, P.; Green, K.; Grinten, M.G.D.v.; Gutsmiedl, E.; et al. Neutron to Mirror-Neutron Oscillations in the Presence of Mirror Magnetic Fields. Phys. Rev. D 2009, 80, 032003. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.; Nesti, F. Magnetic anomaly in UCN trapping: Signal for neutron oscillations to parallel world? Eur. Phys. J. C 2012, 72, 1974. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.; Biondi, R.; Geltenbort, P.; Krasnoshchekova, I.A.; Varlamov, V.E.; Vassiljev, A.V.; Zherebtsov, O.M. New experimental limits on neutron—Mirror neutron oscillations in the presence of mirror magnetic field. Eur. Phys. J. C 2018, 78, 717. [Google Scholar] [CrossRef] [Green Version]
- Abel, C.; Ayres, N.J.; Ban, G.; Bison, G.; Bodek, K.; Bondar, V.; Chanel, E.; Chiu, P.J.; Crawford, C.; Daum, M. A search for neutron to mirror-neutron oscillations using the nEDM apparatus at PSI. Phys. Lett. B 2021, 812, 135993. [Google Scholar] [CrossRef]
- Broussard, L.J.; Barrow, J.L.; DeBeer-Schmitt, L.; Dennis, T.; Fitzsimmons, M.R.; Frost, M.J.; Gilbert, C.E.; Gonzalez, F.M.; Heilbronn, L.; Iverson, E.B.; et al. Experimental Search for Neutron to Mirror Neutron Oscillations as an Explanation of the Neutron Lifetime Anomaly. arXiv 2012, arXiv:2111.05543. [Google Scholar]
- Ayres, N.J.; Berezhiani, Z.; Biondi, R.; Bison, G.; Bodek, K.; Bondar, V.; Chiu, P.J.; Daum, M.; Dinani, R.T.; Doorenbos, C.B.; et al. Improved search for neutron to mirror-neutron oscillations in the presence of mirror magnetic fields with a dedicated apparatus at the PSI UCN source. Symmetry 2022, 14, 503. [Google Scholar] [CrossRef]
- Kamyshkov, Y.; Ternullo, J.; Varriano, L.; Berezhiani, Z. Neutron-Mirror Neutron oscillations in Matter. arXiv 2021, arXiv:2111.01791. [Google Scholar] [CrossRef]
- Berezhiani, Z. More about neutron–mirror neutron oscillation. Eur. Phys. J. C 2009, 64, 421–431. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z. Neutron lifetime puzzle and neutron–mirror neutron oscillation. Eur. Phys. J. C 2019, 79, 484. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.G.; Dolgov, A.D.; Mohapatra, R.N. Asymmetric inflationary reheating and the nature of mirror universe. Phys. Lett. B 1996, 375, 26–36. [Google Scholar] [CrossRef] [Green Version]
- Kuzmin, V.A. CP violation and baryon asymmetry of the universe. Pisma Zh. Eksp. Teor. Fiz. 1970, 12, 335. [Google Scholar]
- Glashow, S.L. Future of particle physics. NATO Sci. Ser. B 1980, 61, 687. [Google Scholar]
- Mohapatra, R.N.; Marshak, R.E. Local B-L symmetry of electroweak interactions, majorana neutrinos, and neutron oscillations. Phys. Rev. Lett. 1980, 44, 1316, Erratum in Phys. Rev. Lett. 1980, 44, 1643.. [Google Scholar] [CrossRef]
- Mohapatra, R.N.; Nussinov, S. Constraints on Mirror Models of Dark Matter from Observable Neutron-Mirror Neutron Oscillation. Phys. Lett. B 2018, 776, 22–25. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S. Bounds on neutron-mirror neutron mixing from pulsar timing. Phys. Rev. D 2019, 100, 123021. [Google Scholar] [CrossRef] [Green Version]
- Berezhiani, Z.; Biondi, R.; Mannarelli, M.; Tonelli, F. Neutron-mirror neutron mixing and neutron stars. Eur. Phys. J. C 2021, 81, 1036. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Raj, N. Neutron Star Internal Heating Constraints on Mirror Matter. Phys. Rev. Lett. 2021, 127, 061805. [Google Scholar] [CrossRef]
- Ma, E. Verifiable radiative seesaw mechanism of neutrino mass and dark matter. Phys. Rev. D 2006, 73, 077301. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703–706. [Google Scholar] [CrossRef] [Green Version]
- Okada, N.; Rehman, M.U.; Shafi, Q. Tensor to Scalar Ratio in Non-Minimal ϕ4 Inflation. Phys. Rev. D 2010, 82, 043502. [Google Scholar] [CrossRef] [Green Version]
- Okada, N.; Şenoğuz, V.N.; Shafi, Q. The Observational Status of Simple Inflationary Models: An Update. Turk. J. Phys. 2016, 40, 150–162. [Google Scholar] [CrossRef] [Green Version]
- Adshead, P.; Cui, Y.; Shelton, J. Chilly Dark Sectors and Asymmetric Reheating. JHEP 2016, 06, 016. [Google Scholar] [CrossRef] [Green Version]
- Holdom, B. Two U(1)’s and Epsilon Charge Shifts. Phys. Lett. B 1986, 166, 196–198. [Google Scholar] [CrossRef]
- Carlson, E.D.; Glashow, S.L. Nucleosynthesis Versus the Mirror Universe. Phys. Lett. B 1987, 193, 168–170. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Lepidi, A. Cosmological bounds on the ‘millicharges’ of mirror particles. Phys. Lett. B 2009, 681, 276–281. [Google Scholar] [CrossRef] [Green Version]
- del Aguila, F.; Coughlan, G.D.; Quiros, M. Gauge Coupling Renormalization with Several U(1) Factors. Nucl. Phys. B 1988, 307, 633. [Google Scholar] [CrossRef]
- Babu, K.S.; Kolda, C.F.; March-Russell, J. Leptophobic U(1) s and the R(b) - R(c) crisis. Phys. Rev. D 1996, 54, 4635–4647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, J.S.; Aoki, Y.; Boyle, P.; Izubuchi, T.; Soni, A.; Syritsyn, S. Proton decay matrix elements on the lattice at physical pion mass. arXiv 2021, arXiv:2111.01608. [Google Scholar]
- Rinaldi, E.; Syritsyn, S.; Wagman, M.L.; Buchoff, M.I.; Schroeder, C.; Wasem, J. Neutron-antineutron oscillations from lattice QCD. Phys. Rev. Lett. 2019, 122, 162001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pois, H.; Weiler, T.J.; Yuan, T.C. Higgs boson decay to four fermions including a single top quark below tt¯ threshold. Phys. Rev. D 1993, 47, 3886–3897. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, R.N.; Nasri, S.; Nussinov, S. Some implications of neutron mirror neutron oscillation. Phys. Lett. B 2005, 627, 124–130. [Google Scholar] [CrossRef] [Green Version]
- Gaemers, K.J.F.; Gandhi, R.; Lattimer, J.M. Neutrino Helicity Flips via Electroweak Interactions and SN1987A. Phys. Rev. 1989, D 40, 309. [Google Scholar]
- Babu, K.S.; Mohapatra, R.N.; Nasri, S. Unified TeV scale picture of baryogenesis and dark matter. Phys. Rev. Lett. 2007, 98, 161301. [Google Scholar] [CrossRef] [Green Version]
- Bhupal Dev, P.S.; Mohapatra, R.N. TeV scale model for baryon and lepton number violation and resonant baryogenesis. Phys. Rev. 2015, D 92, 016007. [Google Scholar]
- Berezinsky, V.S.; Vilenkin, A. Ultrahigh-energy neutrinos from hidden sector topological defects. Phys. Rev. D 2000, 62, 083512. [Google Scholar] [CrossRef] [Green Version]
- Cline, J.M.; Roux, J.S. Asymmetric reheating from a symmetric inflationary potential. Phys. Rev. D 2022, 105, 043506. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).