Sweeping Surfaces in theThree-Dimensional Lie Group

Abstract

This paper investigated the rotation minimizing frames that are related to the space curves and the sweeping surfaces that are traced by these frames in the three-dimensional Lie group. Then, the sufficient and necessary conditions for the sweeping surface to be a developable ruled surface were obtained. In particular, we mostly focused on the study of the resulting developable surface is a cylinder, cone, or tangent surface. Meanwhile, to support the results in the paper, some illustrative examples are presented.

1. Introduction

The common aspects of geometry and algebra, which are two significant subjects of mathematics, are collected Lie groups in two forms: one is that a Lie group is a group, and the second is that it is a differentiable manifold. Thus, the geometric and algebraic framework of Lie groups should be coherent in a specific manner. The study of Lie groups is essential to the common new path to geometry. Therefore, there are numerous study results on curves and surfaces in the three-dimensional Lie group [1,2,3,4,5,6,7].

In the Euclidean three-space ${\mathbb{E}}^3$, the sweeping surface is the surface traced by a continuously moving 2D curve (the generatrix or profile curve) on a spine curve (trajectory) in the space. The outcome of such growth, be it composed of movement in the space or substantial shape distortion, is a sweep subject. The sweep subject type is specified by the choice of the generator and the position. Sweeping surfaces are a considerable and essential types of surfaces in geometric modeling and are universally used in industrial design, which shows why these surfaces are one of the charming subjects of surface theory, as well as being applied in many areas of science such as computer-aided geometric design, computer-aided design, and so on [8,9,10,11,12]. One of the paramount facts about the sweeping surface is that the sweeping surface can be a developable ruled surface [13,14]. Developable surfaces are the distinctive ruled surfaces that are rather interesting and have many applications in many subjects. Therefore, many geometers and engineers have investigated and obtained many properties of the ruled and developable surfaces (see, for example, [8,9,10,11,12,13,14,15,16]). However, to the authors’ knowledge, there is no work devoted to discussing the notions of sweeping surfaces immersed in Lie groups.

In this study, we investigated how to design sweeping surfaces using the rotation-minimizing frames in the three-dimensional Lie group. Then, we investigated the necessary and sufficient conditions for the sweeping surface to turn into a developable ruled surface to establish the Bishop frame along a unit speed curve and develop the local differential geometry of the sweeping surface in the three-dimensional Lie group $\mathbb{G}$. Then, we summarize some results concerning the differential geometry of the sweeping surfaces that are generated by these frames. Consequently, we give the necessary and sufficient conditions for the sweeping surface to be a developable ruled surface. We also investigated the uniqueness of such developable surfaces. In particular, we mainly focused on the study of the resulting developable surface to be a cylinder, cone, or tangential surface. Finally, some examples of its applications are introduced and explained in detail.

Hopefully, these results will lead to a connection with the similarities between the theory of the sweeping surfaces in Euclidean three-space and with that in the three-dimensional Lie group.

2. Preliminaries

This section gives an introduction to Lie group theory (see [1,2,3,4,5,6,7]). Consider $\mathbb{G}$ to be a Lie group with a bi-invariant metric <, > and ∇ to be the Levi-Civita connection of $\mathbb{G}$. If $\mathfrak{g}$ indicates the Lie algebra of $\mathbb{G}$, then $\mathfrak{g}$ is isomorphic to $T_e\mathbb{G}$ where e is the identity (neutral) element of $\mathbb{G}$. For any three vector fields $\mathbf{X}$, $\mathbf{Y}$, and $\mathbf{Z}$ in $\mathfrak{g}$, we have the following:

$$<\mathbf{X},[\mathbf{Y},\mathbf{Z}]>=-<\mathbf{Y},[\mathbf{X},\mathbf{Z}]>,$$

and:

$${\nabla }_{\mathbf{X}}\mathbf{Y}=\frac{1}{2}[\mathbf{X},\mathbf{Y}].$$

(1)

Let $\mathit{\gamma }:I\subset \mathbb{R}\to \mathbb{G}$ be an arc-length smooth curve and {${\mathbf{E}}_1$, ${\mathbf{E}}_2$,...,${\mathbf{E}}_n$} be an orthonormal basis of $\mathfrak{g}$. In this case, any two vector fields $\mathbf{X}$ and $\mathbf{Y}$ can be written as $\mathbf{X}={\displaystyle \sum _{i=1}^n}{x}_i{\mathbf{E}}_i$ and $\mathbf{Y}={\displaystyle \sum _{i=1}^n}{y}_i{\mathbf{E}}_i$, where $y_i$, $x_i$: $I\to \mathbb{R}$ are smooth functions. The Lie bracket of $\mathbf{X}$ and $\mathbf{Y}$ is given by:

$$[\mathbf{X},\mathbf{Y}]=\stackrel{n}{\sum _{i,i=1}}{x}_i{y}_j[{\mathbf{E}}_i,{\mathbf{E}}_j],$$

and the directional derivative of $\mathbf{X}$ on the curve $\mathit{\gamma }$ is given as follows:

$${\nabla }_{\mathbf{T}}\mathbf{X}={\mathbf{X}}^{{}^{\prime }}+\frac{1}{2}[\mathbf{T},\mathbf{X}],$$

(2)

where $\mathbf{T}={\mathit{\gamma }}^{{}^{\prime }}=\frac{d\mathit{\gamma }}{ds}$ and ${\mathbf{X}}^{{}^{\prime }}={\displaystyle \sum _{i=1}^n}{x}_i^{{}^{\prime }}{\mathbf{E}}_i$, where $x_i^{{}^{\prime }}=\frac{d{x}_i}{ds}$. It is necessary to note that if $\mathbf{X}$ is the left-invariant vector field to the curve, then ${\mathbf{X}}^{{}^{\prime }}=\mathbf{0}$ (see for details [14,15,16,17,18]). Here, a “dash” denotes the derivative with respect to the parameter s.

Let $\mathit{\alpha }:I\subset \mathbb{R}\to \mathbb{G}$ be a regular curve in the three-dimensional Lie group $\mathbb{G}$ with the Serret–Frenet system {$\mathbf{T}$, $\mathbf{N}$, $\mathbf{B}$, $\kappa$, $\tau \}$. Then, a smooth function ${\tau }_G$, which is called Lie torsion, is defined by:

$${\tau }_G\left(s\right)=\frac{1}{2}<\mathbf{T},[\mathbf{N},\mathbf{B}]>,$$

(3)

and:

$${\tau }_G\left(s\right)=\frac{1}{2{\kappa }^2\tau }<{\mathbf{T}}^{{}^{″}},[\mathbf{T},{\mathbf{T}}^{{}^{\prime }}]>+\frac{1}{4{\kappa }^2\tau }{∥[\mathbf{T},{\mathbf{T}}^{{}^{\prime }}]∥}^2.$$

(4)

Proposition 1.

Let α be an arc-length parametrized curve in $\mathbb{G}$. Then,

$$\begin{array}{cc}& [\mathbf{T},\mathbf{N}]=<\mathbf{T},[\mathbf{N},\mathbf{B}]>\mathbf{B}=2{\tau }_G\left(s\right)\mathbf{B},\\ & [\mathbf{B},\mathbf{T}]=<[\mathbf{B},\mathbf{T}],\mathbf{N}>\mathbf{B}=2{\tau }_G\left(s\right)\mathbf{N},\\ & [\mathbf{N},\mathbf{B}]=<[\mathbf{N},\mathbf{B}],\mathbf{T}>\mathbf{B}=2{\tau }_G\left(s\right)\mathbf{T}.\end{array}$$

In view of Equation (2) and Proposition 1, the Serret–Frenet formulas of $\mathit{\alpha }$ in $\mathbb{G}$ are written as:

$${\nabla }_{\mathbf{T}}( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} )=( \begin{array}{ccc} 0\hfill & \kappa \hfill & 0\hfill \\ -\kappa \hfill & 0\hfill & \tau -{\tau }_G\hfill \\ 0\hfill & -(\tau -{\tau }_G)\hfill & 0\hfill \end{array} )( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} ),$$

where $\mathbf{T}={\mathit{\alpha }}^{{}^{\prime }}\left(s\right),$ $\kappa \left(s\right)=∥{\nabla }_{\mathbf{T}}\mathbf{T}∥=∥{\mathbf{T}}^{{}^{\prime }}∥$ and $\tau \left(s\right)=∥{\nabla }_{\mathbf{T}}\mathbf{B}∥-{\tau }_G$.

Remark 1.

Let $\mathbb{G}$ be a three-dimensional Lie group with a bi-invariant metric. Then:

(1) If $\mathbb{G}$ is the special orthogonal group $\mathbb{SO}$(3), then ${\tau }_G=1/2$;

(2) If $\mathbb{G}$ is the special unitary group $\mathbb{SU}$(2), then ${\tau }_G=1$;

(3) If $\mathbb{G}$ is a commutative (Abelian) group, then ${\tau }_G=0$.

Bishop Frame or Rotation-Minimizing Frame

From the Serret–Frenet formulas, we see that:

$$\mathit{\omega }\left(s\right)=(\tau -{\tau }_G)\mathbf{T}+\kappa \mathbf{B},$$

(5)

is the instantaneous dual Darboux vector along the curve $\mathit{\alpha }$. This vector allows writing the Serret–Frenet formulas as:

$${\nabla }_{\mathbf{T}}( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} )=\mathit{\omega }\left(s\right)\times ( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} ).$$

(6)

Definition 1.

A moving orthonormal frame $\{{\mathit{\xi }}_1,$ ${\mathit{\xi }}_2$, ${\mathit{\xi }}_3\}$, through a space curve $\mathit{\gamma }\left(s\right)$ in $\mathbb{G}$, is a rotation-minimizing frame (RMF) with respect to ${\mathit{\xi }}_1$ if its angular velocity ω satisfies $<\mathit{\omega },{\mathit{\xi }}_1>=0$, or equivalently, the derivatives of ${\mathit{\xi }}_2$ and ${\mathit{\xi }}_3$ are both parallel to ${\mathit{\xi }}_1$. A similar description holds when ${\mathit{\xi }}_2$ or ${\mathit{\xi }}_3$ is selected as the reference orientation [10,17,18].

In view of Definition 1, we see that the Serret–Frenet frame is an RMF with respect to the principal normal $\mathbf{N}$, but not with respect to the tangent $\mathbf{T}$(resp. the binormal $\mathbf{B}$). However, the Serret–Frenet frame is not an RMF with respect to $\mathbf{T}$, and one can simply obtain such an RMF from it. The new normal plane vectors (${\mathbf{N}}_1$, ${\mathbf{N}}_2$) are given through a rotation of ($\mathbf{N}$, $\mathbf{B}$) according to:

$$( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} )=( \begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\varphi \hfill & sin\varphi \hfill \\ 0\hfill & -sin\varphi \hfill & cos\varphi \hfill \end{array} )( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} ),$$

(7)

with a certain angle $\varphi \left(s\right)$. Here, we call the set $\{\mathbf{T},$ ${\mathbf{N}}_1$, ${\mathbf{N}}_2\}$ the RMF or Bishop frame. Thus, the Bishop formulae are:

$${\nabla }_{\mathbf{T}}( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} )=( \begin{array}{ccc}0\hfill & {\kappa }_1\hfill & {\kappa }_2\hfill \\ -{\kappa }_1\hfill & 0\hfill & 0\hfill \\ -{\kappa }_2\hfill & 0\hfill & 0\hfill \end{array} )( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} )=\tilde{\mathit{\omega }}\times ( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} ),$$

(8)

where $\tilde{\mathit{\omega }}\left(s\right)=-{\kappa }_2{\mathbf{N}}_1+{\kappa }_1{\mathbf{N}}_2$ is the Bishop Darboux vector. Furthermore, the Bishop curvatures are defined by ${\kappa }_1\left(s\right)=\kappa cos\varphi$, ${\kappa }_2\left(s\right)=\kappa sin\varphi$. One can show that:

$$\begin{array}{c} {\kappa }_1^2+{\kappa }_2^2={\kappa }^2, \mathrm{and} \varphi ={tan}^{-1}\left(\frac{{\kappa }_2}{{\kappa }_1}\right); {\kappa }_1\ne 0,\hfill \\ \varphi \left(s\right)=-\underset{s_0}{\stackrel{s}{\int }}(\tau -{\tau }_G)ds+{\varphi }_0, {\varphi }_0=\varphi \left(s_0\right),\hfill \end{array}\}$$

(9)

where $s_0$ is the initial value of s. In this study, we supposed that $s_0=0$. Comparing Equation (6) with Equation (8), we see that the relative velocity is:

$$\mathit{\omega }\left(s\right)-\tilde{\mathit{\omega }}\left(s\right)=(\tau -{\tau }_G)\mathbf{T}.$$

This proves that the Serret–Frenet frame has an extra revolution along the tangent, whose speed equals $(\tau -{\tau }_G)$. This shows that the integral formula of Equation (9) for evaluating the RMF results in the undesirable rotation of the Serret–Frenet frame. Therefore, we have the following:

Corollary 1.

Assume $\mathit{\alpha }:I\subset \mathbb{R}\to \mathbb{G}$ is a regular curve with the arc-length parameter s in $\mathbb{G}$ and $\{\mathbf{T}$, $\mathbf{N}$, $\mathbf{B}$, κ, $\tau \}$ comprise its Serret–Frenet apparatus. Then, the Serret–Frenet frame is obtainedalong with the RMF if and only if the binormal vector $\mathbf{B}$ is a constant vector field, that is $\tau -{\tau }_G=0$.

3. Sweeping Surfaces in the Three-Dimensional Lie Group $\mathbb{G}$

Kinematically, the concept of a sweeping surface is generated by a plane curve moving over the space such that the motion of any point on the surface is constantly orthogonal to the plane. Hence, by using the RMF frame, the sweeping surface family in $\mathbb{G}$ is given by [13]:

$$M:\mathbf{Y}(s,t)=\mathit{\alpha }\left(\mathbf{s}\right)+A\left(s\right)\mathbf{r}\left(t\right)=\mathit{\alpha }\left(s\right)+r_1\left(t\right){\mathbf{N}}_1\left(s\right)+r_2\left(t\right){\mathbf{N}}_2\left(s\right),$$

(10)

where $\mathit{\alpha }\left(s\right)$ is called the spine curve. Here, the planar profile (cross-section) curve is specified by the parametric exemplification $\mathbf{r}\left(t\right)=(0,$ $r_1\left(t\right),r_2{\left(t\right))}^t$, where the character “t” represents transposition, with different parameters $0\le t\le T$. The particular orthogonal matrix $A\left(s\right)=\left\{\mathbf{T}\right(s),$ ${\mathbf{N}}_1\left(s\right)$, ${\mathbf{N}}_2\left(s\right)\}$ is assignedto the RMF along $\mathit{\alpha }\left(s\right)$.

Without loss of generality, we can suppose the profile curve $\mathbf{r}\left(t\right)$ is a unit speed curve, that is, ${\stackrel{.}{r}}_1^2+{\stackrel{.}{r}}_2^2=1$. In the next, we use “dot” to indicate the derivative with respect to the arc-length parameter of the profile curve $\mathbf{r}\left(t\right)$. It is readily checked that the two tangent vectors of M are given by:

$$\begin{array}{c}{\mathbf{Y}}_t={\stackrel{.}{r}}_1{\mathbf{N}}_1+{\stackrel{.}{r}}_2{\mathbf{N}}_2,\hfill \\ {\mathbf{Y}}_s=(1-r_1{\kappa }_1-r_2{\kappa }_2)\mathbf{T}.\hfill \end{array}\}$$

(11)

The first fundamental form is then given by:

$$I:=g_{11}d{s}^2+2g_{12}dsdt+g_{22}d{t}^2={(1-r_1{\kappa }_1-r_2{\kappa }_2)}^{2}d{s}^2+d{t}^2,$$

(12)

where:

$$g_{11}=<{\mathbf{Y}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}>={(1-r_1{\kappa }_1-r_2{\kappa }_2)}^2,g_{12}=<{\mathbf{Y}}_s,{\mathbf{Y}}_t>=0,g_{22}=<{\mathbf{Y}}_t,{\mathbf{Y}}_t>=1.$$

(13)

The surface unit normal vector is given by:

$$\mathbf{U}(s,t):=\frac{{\mathbf{Y}}_t\times {\mathbf{Y}}_s}{\parallel {\mathbf{Y}}_t\times {\mathbf{Y}}_s\parallel }={\stackrel{.}{r}}_2{\mathbf{N}}_1-{\stackrel{.}{r}}_1{\mathbf{N}}_2.$$

(14)

By a simple derivation, we have:

$$\begin{array}{c}{\mathbf{Y}}_{ss}=-(r_1{\kappa }_1^{{}^{\prime }}+r_2{\kappa }_2^{{}^{\prime }})\mathbf{T}+(1-r_1{\kappa }_1-r_2{\kappa }_1)({\kappa }_1{\mathbf{N}}_1+{\kappa }_2{\mathbf{N}}_2),\hfill \\ {\mathbf{Y}}_{st}=-({\stackrel{.}{r}}_1{\kappa }_1+{\stackrel{.}{r}}_2{\kappa }_2)\mathbf{T},\hfill \\ {\mathbf{Y}}_{\mathrm{tt}}={\stackrel{..}{r}}_1{\mathbf{N}}_1+{\stackrel{..}{r}}_2{\mathbf{N}}_2.\hfill \end{array}\}$$

This leads to the elements of the second fundamental form $h_{11}$, $h_{12}$, and $h_{22}$, where:

$$\begin{array}{c}{h}_{11}=<{\mathbf{Y}}_{ss},\mathbf{U}>=(1-r_1{\kappa }_1-r_2{\kappa }_1)({\kappa }_1{\stackrel{.}{r}}_2-{\kappa }_2{\stackrel{.}{r}}_1),\hfill \\ h_{12}=<{\mathbf{Y}}_{st},\mathbf{U}>=0,\hfill \\ h_{22}=<{\mathbf{Y}}_{\mathrm{tt}},\mathbf{U}>={\stackrel{.}{r}}_2{\stackrel{..}{r}}_1-{\stackrel{.}{r}}_1{\stackrel{..}{r}}_2.\hfill \end{array}\}$$

(15)

Hence, the t and s curves of M are curvature lines, that is $g_{12}=h_{12 }=0$. Thereby, the isoparametric curve:

$$\pi \left(t\right):\mathit{\beta }\left(t\right):=\mathbf{Y}(t,s_0)=\mathit{\alpha }\left(s_0\right)+r_1\left(t\right){\mathbf{N}}_1\left(s_0\right)+r_2\left(t\right){\mathbf{N}}_2\left(s_0\right),$$

(16)

is a 2D unit speed curvature line. Equation (16) determines a family of planes. The unit tangent vector to $\mathit{\beta }\left(t\right)$ is:

$${\mathbf{T}}_{\beta }\left(t\right)={\stackrel{.}{r}}_1\left(t\right){\mathbf{N}}_1\left(s_0\right)+{\stackrel{.}{r}}_2\left(t\right){\mathbf{N}}_2\left(s_0\right),$$

(17)

and consequently, the unit principal normal vector of $\mathit{\beta }\left(t\right)$ is:

$${\mathbf{N}}_{\beta }\left(t\right)={\mathbf{T}}_{\beta }\left(t\right)\times \mathbf{T}\left(s_0\right)={\stackrel{.}{r}}_2{\mathbf{N}}_1-{\stackrel{.}{r}}_1{\mathbf{N}}_2=\mathbf{U}(s_0,t).$$

(18)

From Equation (18), it is interesting to note that the surface normal $\mathbf{U}(s_0,t)$ is identical to the principal normal ${\mathbf{N}}_{\beta }\left(t\right)$, that is the curve $\mathit{\beta }\left(t\right)$ is a geodesic 2D curvature line on $\mathbf{Y}(t,s_0)$. Surfaces for which parametric curves are curvature lines have numerous implementations in geometric design [9]. In the case of sweeping surfaces, one has to evaluate the offset surfaces ${\mathbf{Y}}_f(t,s)=\mathbf{Y}(t,s)+f\mathbf{U}(s,t)$ of a given surface $\mathbf{Y}(t,s)$ at a constant distance f. As a result of this equation, the offsetting procedure for the sweeping surface can be performed more easily than the offsetting of the 2D profile curve, which is much easier to deal with.

Proposition 2.

Let a sweeping surface M be defined by Equation (10). Assume ${\mathbf{r}}_f\left(t\right)$ is the planar offset of the 2D profile $\mathbf{r}\left(t\right)$ at distance f. Then, the offset surface ${\mathbf{Y}}_f(r,s)$ is still a sweeping surface, defined by the spine curve $\mathit{\alpha }\left(s\right)$ and the 2D profile curve ${\mathbf{r}}_f\left(r\right)$.

3.1. Local Singularities

Singularities are fundamental for the realization of the sweeping surfaces and are inspected next: It can be seen that the sweeping surface M has singular points if and only if:

$$\parallel {\mathbf{Y}}_t\times {\mathbf{Y}}_s\parallel =\rho -r_{1}cos\varphi -r_{2}sin\varphi =0,$$

where $\rho =\rho \left(s\right)$ is the curvature radius of $\mathit{\alpha }\left(s\right)$. Using $\rho \left(s\right)$, we have the correlations:

$$r_1=\rho \left(s\right)cos\varphi ,r_2=\rho \left(s\right)sin\varphi .$$

We can obtain the singular curve of M as follows:

$$\mathbf{C}\left(s\right)=\mathit{\alpha }\left(s\right)+\rho \left(s\right)(cos\varphi {\mathbf{N}}_1\left(s\right)+sin\varphi {\mathbf{N}}_2\left(s\right)).$$

(19)

We mention that singular points happen at the intersection amidst the 2D profile curve $\mathbf{r}=\mathbf{r}\left(t\right)$ and the instantaneous axis of rotation:

$$L\left(t\right)=\{(r_1,r_2)\mid r_{1}cos{\varphi }_0+r_{2}sin{\varphi }_0=\rho \left(s_0\right).$$

Corollary 2.

Assume that M is a sweeping surface Equation (10), with the profile and spine curves having non-vanishing curvatures anywhere. Then, M has no singular points if:

$$r_{1}cos\varphi +r_{2}sin\varphi \ne \rho \left(s\right),$$

(20)

is satisfied for all s and t.

The conditions that guarantee the convexity or curves that produce parabolic points of a surface are desired in various implementations (such as manufacturing of sculpted surfaces or layered manufacturing). Therefore, we discuss in what conditions the parametric curves are parabolic curves as follows: The Gaussian curvature of M at a regular point can be obtained as:

$$K(s,t):=\frac{h_{11}{h}_{22}-h_{12}^2}{g_{11}{g}_{22}-g_{12}^2}=\frac{({\stackrel{.}{r}}_2{\stackrel{..}{r}}_1-{\stackrel{.}{r}}_1{\stackrel{..}{r}}_2)({\stackrel{.}{r}}_{2}cos\varphi -{\stackrel{.}{r}}_{1}sin\varphi )}{(\rho -r_{2}cos\varphi -r_{2}sin\varphi )}.$$

(21)

Let $\vartheta (s,t)$ be the angle between the normal $\mathbf{N}\left(s\right)$ of the isoparametric curve t=const. and $\mathbf{U}(s,t)$ be the normalof the surface M, then we have:

$$\mathbf{U}(s,t)=cos\vartheta \mathbf{N}\left(s\right)+sin\vartheta \mathbf{B}\left(s\right),$$

(22)

where:

$$cos\vartheta ={\stackrel{.}{r}}_{1}sin\varphi +{\stackrel{.}{r}}_{2}cos\varphi , \mathrm{and} sin\vartheta =-{\stackrel{.}{r}}_{1}cos\varphi +{\stackrel{.}{r}}_{2}sin\varphi .$$

(23)

Since every generating 2D profile curve is a curvature line for the sweeping surface, the value of one principal curvature is:

$${\chi }_1(s,t):=\frac{\parallel \stackrel{.}{\mathbf{r}}\times \stackrel{..}{\mathbf{r}}\parallel }{{\parallel \stackrel{.}{\mathbf{r}}\parallel }^3}={\stackrel{.}{r}}_1{\stackrel{..}{r}}_2-{\stackrel{.}{r}}_2{\stackrel{..}{r}}_1.$$

(24)

Furthermore, the curvature of the parametric curves $t=const$. is:

$$\chi (s,t):=\frac{\parallel {\mathbf{Y}}_s\times {\mathbf{Y}}_{ss}\parallel }{{\parallel {\mathbf{Y}}_s\parallel }^3}=\frac{1}{\rho -r_{1}cos\varphi +r_{2}sin\varphi }.$$

(25)

Substituting Equations (23)–(25) into Equation (21) yields:

$$K(s,t)=-{\chi }_1(s,t)\chi (s,t)cos\vartheta .$$

(26)

In order to describe the shape of M, we attempted to obtain the curves on M that are traced by parabolic points, that is points with zero Gaussian curvature. These curves divide the elliptic ($K>0$, locally convex) and hyperbolic ($K<0$, hence non-convex) parts of the surface. As a result of Equation (26), there three cases emerge when parabolic points are considered:

Case (1) exists when ${\chi }_1=0$. If ${\chi }_1=0$, the 2D profile curve $\mathbf{r}=\mathbf{r}\left(t\right)$ is turned into a straight line, and from Equation (24), it can be seen that:

$${\chi }_1=0 \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} \stackrel{.}{\mathbf{r}}\times \stackrel{..}{\mathbf{r}}=\mathbf{0} \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} \stackrel{.}{\mathbf{r}}\Vert \stackrel{..}{\mathbf{r}}.$$

(27)

This equation shows that a flat or inflection point of $\mathbf{r}=\mathbf{r}\left(t\right)$ forms a parabolic curve $s=$ const. on parts of the sweeping surface.

Case (2) exists when $\chi (s,t)=0$. From Equation (25), it can be found that if $\kappa \left(s\right)=0$, then $\chi \left(s\right)=0$. This means that the spine curve $\mathit{\alpha }=\mathit{\alpha }\left(s\right)$ is turned into a straight line. Likewise, a flat or inflection point of the spine curve forms a parabolic curve $t=$ const. on parts of the sweeping surface.

Case (3) exists when $\vartheta =\pi /2$. From Equation (22), it can be found that if $\mathbf{U}(s,t)\Vert \mathbf{B}$, hence $cos\vartheta =0$. Then, the curve $\mathit{\alpha }\left(s\right)$ is not only a curvature line, but also an asymptotic of the sweeping surface. Thus, for the parabolic points, the condition:

$${\stackrel{.}{r}}_{1}sin\varphi +{\stackrel{.}{r}}_{2}cos\varphi =0,$$

(28)

is satisfied for all s and t. Thus, the following corollary can be given:

Corollary 3.

Consider M to be a sweeping surface Equation (10), with the profile and spine curves having non-vanishing curvatures everywhere. Then, M has parabolic points if and only if the spine curve is an asymptotic curve.

By the integration of Equation (28), the following can be acquired:

$$r_{1}cos\varphi +r_{2}sin\varphi =\zeta \left(s\right),$$

(29)

where $\zeta =\zeta \left(s\right)$ is an arbitrary function. Then, we have the relationships:

$$r_1=\zeta \left(s\right)cos\varphi ,r_2=\zeta \left(s\right)sin\varphi .$$

(30)

Therefore, from Equation (10), it follows that the parabolic curve is:

$$\mathbf{P}\left(s\right)=\mathit{\alpha }\left(s\right)+\zeta \left(s\right)\mathbf{N}\left(s\right).$$

(31)

Corollary 4.

Consider M to be a sweeping surface Equation (10), with the spine and profile curves having non-vanishing curvatures everywhere. Then, M has precisely one parabolic curve if and only if the spine curve is an asymptotic curve.

Example 1.

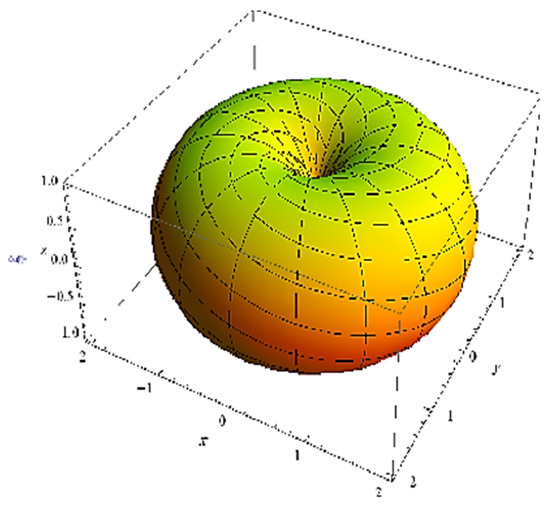
Let the spine curve $\mathit{\alpha }\left(s\right)$ be:

$$\mathit{\alpha }\left(s\right)=(coss,sins,0),0\le s\le 2\pi .$$

For this curve,

$$\begin{array}{ccc}\hfill \mathbf{T}\left(s\right)& =& (-sins,coss,0),\hfill \\ \hfill \mathbf{N}\left(s\right)& =& (-coss,-sins,0),\hfill \\ \hfill \mathbf{B}\left(s\right)& =& (0,0,1),\hfill \end{array}$$

where $\kappa \left(s\right)=1,\tau \left(s\right)=0$ and ${\tau }_G\left(s\right)=\frac{1}{2}$. Then $\varphi \left(s\right)=\frac{s}{2}$, and the Bishop curvatures are, respectively, as follows:

$${\kappa }_1\left(s\right)=cos\frac{s}{2}, \mathrm{and} {\kappa }_2\left(s\right)=sin\frac{s}{2}.$$

Using Equation (7), we obtain the Bishop frame {$\mathbf{T}$, ${\mathbf{N}}_1$, ${\mathbf{N}}_2$} as:

$$( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} )=( \begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\frac{s}{2}\hfill & sin\frac{s}{2}\hfill \\ 0\hfill & -sin\frac{s}{2}\hfill & cos\frac{s}{2}\hfill \end{array} )( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} );$$

therefore:

$$\begin{array}{ccc}\hfill {\mathbf{N}}_1& =& (-cos\frac{s}{2}coss,-cos\frac{s}{2}sins,sin\frac{s}{2}),\hfill \\ \hfill {\mathbf{N}}_2& =& (sin\frac{s}{2}coss,sin\frac{s}{2}sins,cos\frac{s}{2}).\hfill \end{array}$$

If we consider $\mathbf{r}\left(t\right)=(0,$ $cost,sint)$, then we obtain a member of the sweeping surface family in the special orthogonal group $\mathbb{SO}$(3), as shown in Figure 1:

$$M:\mathbf{Y}(s,t)=(coss,sins,0)+cost{\mathbf{N}}_1+sint{\mathbf{N}}_2.$$

Figure 1. Sweeping surface over a circle.

Example 2.

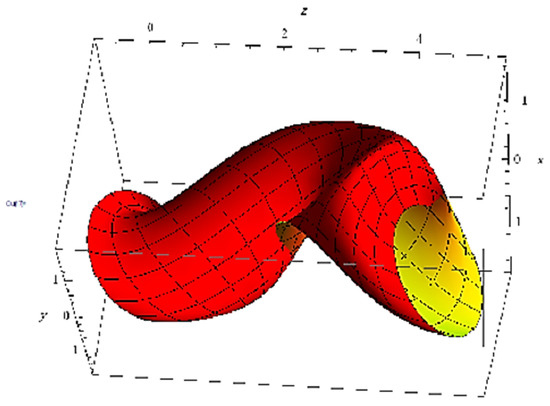
Let the spine curve $\mathit{\alpha }\left(s\right)$ be:

$$\mathit{\alpha }\left(s\right)=(\frac{1}{\sqrt{2}}coss,\frac{1}{\sqrt{2}}sins,\frac{s}{\sqrt{2}}),0\le s\le 2\pi .$$

Then,

$$\begin{array}{ccc}\hfill \mathbf{T}\left(s\right)& =& (-\frac{1}{\sqrt{2}}sins,\frac{1}{\sqrt{2}}coss,\frac{1}{\sqrt{2}}),\hfill \\ \hfill \mathbf{N}\left(s\right)& =& (-coss,-sins,0),\hfill \\ \hfill \mathbf{B}\left(s\right)& =& (\frac{1}{\sqrt{2}}sins,-\frac{1}{\sqrt{2}}coss,\frac{1}{\sqrt{2}}),\hfill \end{array}$$

where $\kappa \left(s\right)=\tau \left(s\right)=\frac{1}{\sqrt{2}}$, ${\tau }_G\left(s\right)=0$. Then, $\varphi \left(s\right)=-\frac{s}{\sqrt{2}}$, and:

$${\kappa }_1\left(s\right)=\frac{1}{\sqrt{2}}cos\frac{s}{2} \mathrm{and} {\kappa }_2\left(s\right)=\frac{1}{\sqrt{2}}sin\frac{s}{2}.$$

Similarly, we obtain:

$$( \begin{array}{c}\mathbf{T}\hfill \\ {\mathbf{N}}_1\hfill \\ {\mathbf{N}}_2\hfill \end{array} )=( \begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\frac{s}{\sqrt{2}}\hfill & -sin\frac{s}{\sqrt{2}}\hfill \\ 0\hfill & sin\frac{s}{\sqrt{2}}\hfill & cos\frac{s}{\sqrt{2}}\hfill \end{array} )( \begin{array}{c}\mathbf{T}\hfill \\ \mathbf{N}\hfill \\ \mathbf{B}\hfill \end{array} ),$$

from which we have:

$$\begin{array}{ccc}\hfill {\mathbf{N}}_1& =& ( \begin{array}{c}{N}_{11}\hfill \\ N_{12}\hfill \\ N_{13}\hfill \end{array} )=( \begin{array}{c}-cos\frac{s}{\sqrt{2}}coss-\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}sins\hfill \\ cos\frac{s}{\sqrt{2}}sins+\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}coss\hfill \\ -\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}\hfill \end{array} ),\hfill \\ \hfill {\mathbf{N}}_2& =& ( \begin{array}{c}{N}_{21}\hfill \\ N_{22}\hfill \\ N_{23}\hfill \end{array} )=( \begin{array}{c}-sin\frac{s}{\sqrt{2}}coss+\frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}sins\hfill \\ -sin\frac{s}{\sqrt{2}}sins-\frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}coss\hfill \\ \frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}\hfill \end{array} ).\hfill \end{array}$$

If we consider $\mathbf{r}\left(t\right)=(0,$ $cost,sint)$, then we obtain a member of the sweeping surface family in a commutative group $\mathbb{G}$ as shown in Figure 2:

$$M:\mathbf{Y}(s,t)=(\frac{1}{\sqrt{2}}coss,\frac{1}{\sqrt{2}}sins,\frac{s}{\sqrt{2}})+cost{\mathbf{N}}_1+sint{\mathbf{N}}_2.$$

Figure 2. Sweeping surface over a helix.

3.2. Developable Surfaces

Developable surfaces are curved surfaces developing on planes without tearing and stretching. The significance of such surfaces is illustrated in manufacturing and engineering applications such as automobile components, ship hulls, and apparel modeling (see, e.g., [13,14,15,16]). Therefore, we analyzed the case in which the profile curve $\mathbf{r}\left(t\right)$ degenerates into a line. Then, we have two developable surfaces as follows:

$$M:\mathbf{Y}(s,t)=\mathit{\alpha }\left(s\right)+t{\mathbf{N}}_2\left(s\right), t\in \mathbb{R},$$

(32)

and:

$$M^{\perp }:{\mathbf{Y}}^{\perp }(s,t)=\mathit{\alpha }\left(s\right)+t{\mathbf{N}}_1\left(s\right), t\in \mathbb{R}.$$

(33)

Moreover,

$$M:{\mathbf{Y}}_s\times {\mathbf{Y}}_t=-(1-t{\kappa }_2){\mathbf{N}}_1\left(s\right),$$

(34)

and:

$$M^{\perp }:{\mathbf{Y}}_s\times {\mathbf{Y}}_t=(1-t{\kappa }_1){\mathbf{N}}_2\left(s\right).$$

(35)

Then, M (resp. $M^{\perp }$) is the normal developable surface of $M^{\perp }$(resp. M) along $\mathit{\alpha }\left(s\right)$, and $\mathit{\alpha }\left(s\right)$ is a curvature line of M (resp. $M^{\perp }$).

Proposition 3.

Let M be a sweeping surface Equation (10); if the profile curve $\mathbf{r}\left(t\right)$ degenerates into a straight line, then M is a developable surface.

Theorem 1

(Existence and uniqueness). Under the above notations, there exists a unique developable surface Equation (32).

Proof. 

For the existence, we have the developable surface Equation (32). On the other hand, since M is a ruled surface, we assume that:

$$\left.\begin{array}{c}M:\mathbf{Y}(s,t)=\mathit{\alpha }\left(s\right)+t\mathbf{a}\left(s\right), t\in \mathbb{R},\hfill \\ \\ \mathbf{a}\left(s\right)=a\left(s\right)\mathbf{T}+a_1\left(s\right){\mathbf{N}}_1+a_2\left(s\right){\mathbf{N}}_2,\hfill \\ \\ {\parallel \mathbf{a}\left(s\right)\parallel }^2=a^2+a_1^2+a_2^2=1,{\mathbf{a}}^{{}^{\prime }}\left(s\right)\ne \mathbf{0}.\hfill \end{array}\right\}$$

(36)

It can be instantly seen that M is developable if and only if:

$$det({\mathit{\alpha }}^{{}^{\prime }},\mathbf{a},{\mathbf{a}}^{{}^{\prime }})=0\mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} a_1(a_2^{{}^{\prime }}+a{\kappa }_2)-a_2(a_1^{{}^{\prime }}+a{\kappa }_1)=0.$$

(37)

Further, we have:

$$({\mathbf{Y}}_s\times {\mathbf{Y}}_t)(s,t)=\pm \lambda (s,t){\mathbf{N}}_1,$$

(38)

where $\lambda =\lambda (s,t)$ is a differentiable function. In addition, the normal vector ${\mathbf{Y}}_s\times {\mathbf{Y}}_t$ at the point $(s,0)$ is:

$$({\mathbf{Y}}_s\times {\mathbf{Y}}_t)(s,0)=-a_2{\mathbf{N}}_1+a_1{\mathbf{N}}_2.$$

(39)

Thus, from Equations (38) and (39), one finds that:

$$a_1=0, \mathrm{and} a_2=\lambda (s,0),$$

(40)

and it follows from Equation (37) that $a_{2}a{\kappa }_1=0$, which leads to $a_{2}a=0$, with ${\kappa }_1\ne 0$. If $(s,0)$ is a regular point (i.e., $\lambda (s,0)\ne 0$), then $a_2\left(s\right)\ne 0$ and $a=0$. Therefore, the direction of $\mathbf{a}\left(s\right)$ is the direction of ${\mathbf{N}}_2\left(s\right)$. This means that the uniqueness holds. □

In analogous arguments for $M^{\perp }$, we can give the corresponding Theorem 1, and we omit the details here. Thus, the Joachimsthal theorem in $\mathbb{G}$ can be stated as follows:

Theorem 2

(Joachimsthal). Let M and $M^{\perp }$ be two developable surfaces in $\mathbb{G}$ such that $M\cap M^{\perp }=\mathit{\alpha }\left(s\right)$ is a regular curve and $<{\mathbf{N}}_1,{\mathbf{N}}_2>=0$ along $\mathit{\alpha }\left(s\right)$, where ${\mathbf{N}}_1$ and ${\mathbf{N}}_2$ are unitary normal vector fields to M and $M^{\perp }$, respectively. Then, $\mathit{\alpha }\left(s\right)$ is a curvature line of M if and only if it is a curvature line of $M^{\perp }$.

As a utility (such as cylindrical or flank milling), through the movement of the RMF, consider a cylindrical cutter that is rigidly linked to this frame. Hence, the equation of a family of cylindrical cutters, which is traced by the movement of a cylindrical cutter along $\mathit{\alpha }\left(s\right)$, can be obtained as follows:

$$\overline{M}:\overline{\mathbf{Y}}(s,t)=\mathbf{Y}(s,t)+\varrho {\mathbf{N}}_1\left(s\right),$$

(41)

where $\varrho$ indicates the cylindrical cutter’s radius. This surface is a developable surface offset of the surface $\mathbf{Y}(s,t)$. The equation of $\overline{M}$ can therefore be written as:

$$\overline{M}:\overline{\mathbf{Y}}(s,t)=\mathit{\alpha }\left(\mathbf{s}\right)+t{\mathbf{N}}_2\left(s\right)+\varrho {\mathbf{N}}_1\left(s\right).$$

(42)

The normal vector of the cylindrical cutter can be represented as:

$$\overline{\mathbf{U}}(s,t)=\frac{{\overline{\mathbf{Y}}}_s\times {\overline{\mathbf{Y}}}_t}{\parallel {\overline{\mathbf{Y}}}_s\times {\overline{\mathbf{Y}}}_t\parallel }={\mathbf{N}}_1\left(s\right).$$

(43)

On the other hand, we can rewrite Equation (42) as:

$$M:\mathbf{Y}(s,t)=\overline{\mathbf{Y}}(s,t)-\varrho {\mathbf{N}}_1\left(s\right).$$

(44)

Moreover, we have:

$${\overline{\mathbf{Y}}}_s(s,t)={\mathbf{Y}}_s(s,t)+\tilde{\mathit{\omega }}\left(s\right)\times \left(\varrho {\mathbf{N}}_1\left(s\right)\right)$$

(45)

from which ${\overline{\mathbf{Y}}}_s(s,t)$ is orthogonal to the normal vector ${\mathbf{N}}_1$. Furthermore, the vector ${\mathbf{N}}_1$ is orthogonal to the tool axis vector $\mathbf{T}\left(s\right)$. Hence, the developable surface $\mathbf{Y}(s,t)$ and the envelope surface of the cylindrical cutter have a common normal vector, and the length between the two surfaces is the cylindrical cutter’s radius $\varrho$.

Therefore, we conclude the following:

Proposition 4.

If the developable surface Equation (32) possessing $\mathit{\alpha }\left(s\right)$ as a curvature line and the envelope surface of the cylindrical cutter $\overline{\mathbf{Y}}(s,t)$ are regular, the two surfaces are offset developable surfaces.

Regarding curves with developable surfaces, we studied the conditions when the developable surface M is a cylinder, cone, or tangent surface, respectively.

Theorem 3.

The developable surface Equation (32) in $\mathbb{G}$ is a cylinder surface if and only if $\phi \left(s\right)=0$.

Proof. 

M is a cylindrical surface if and only if:

$${\mathbf{N}}_2\left(s\right)\times {\nabla }_{\mathbf{T}}{\mathbf{N}}_2\left(s\right)=\mathbf{0} \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} \kappa sin\varphi {\mathbf{N}}_1=\mathbf{0}.$$

(46)

Since ${\mathbf{N}}_1$ is a non-zero unit vector, then M is a cylinder if and only if:

$$sin\varphi =0 \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} \varphi \left(s\right)=0.$$

□

Remark 2.

In Theorem 3, by $sin\varphi =0$, we know $\varphi =0$ or π. However, in any case, we have ${\varphi }^{{}^{\prime }}=0$, then $\tau -{\tau }_G=0$. Therefore, in terms of the Serret–Frenet formulas in $\mathbb{G}$, we have that $\mathbf{B}$ is a constant vector, the curve $\mathit{\alpha }\left(s\right)$ is a planar curvature line, and M is a binormal surface.

Theorem 4.

The developable surface Equation (32) is a cone if and only if $\kappa sin\varphi ={\kappa }_{0}sin{\varphi }_0$, where ${\varphi }_0=\varphi \left(0\right)$ and ${\kappa }_0=\kappa \left(0\right)$.

Proof. 

The first derivative of the directrix is:

$${\mathit{\alpha }}^{{}^{\prime }}\left(s\right)={\mathit{\beta }}^{{}^{\prime }}\left(s\right)+\sigma \left(s\right){\mathbf{N}}_2^{{}^{\prime }}\left(s\right)+{\sigma }^{{}^{\prime }}\left(s\right){\mathbf{N}}_2\left(s\right),$$

where ${\mathit{\beta }}^{{}^{\prime }}$ is the first derivative of the striction curve and $\sigma \left(s\right)$ is a regular function. Then, M is a cone if and only if the striction curve $\mathit{\beta }\left(s\right)$ degenerates into a point, that is ${\mathit{\beta }}^{{}^{\prime }}\left(s\right)=0$. This means that:

$$\mathbf{T}\left(s\right)=-{\kappa }_2\sigma \left(s\right)\mathbf{T}\left(s\right)+{\sigma }^{{}^{\prime }}\left(s\right){\mathbf{N}}_2\left(s\right).$$

Hence, by equating the coefficients of $\mathbf{T}$ and ${\mathbf{N}}_2$, $\sigma {\kappa }_2=-1,{\sigma }^{{}^{\prime }}=0$, this implies that:

$$\sigma =const.=-\frac{1}{\kappa sin\varphi } \mathrm{if} \mathrm{and} \mathrm{only} \mathrm{if} \kappa sin\varphi ={\kappa }_{0}sin{\varphi }_0,$$

where ${\varphi }_0=\varphi \left(0\right)$ and ${\kappa }_0=\kappa \left(0\right)$. □

In Theorem 4, we have that if $\varphi$ is a constant, that is $\tau -{\tau }_G=0$, then the curve $\mathit{\alpha }\left(s\right)$ is a planar curvature line with a constant curvature. Similarly, if $\kappa$ is also a constant, we can have $\tau -{\tau }_G=0$, and $\varphi$ is also constant. Then, the curve $\mathit{\alpha }\left(s\right)$ is the arc of a circle.

Theorem 5.

The developable surface Equation (32) is tangential developable if and only if $\kappa sin\varphi \ne {\kappa }_{0}sin{\varphi }_0$, where ${\varphi }_0=\varphi \left(0\right)$ and ${\kappa }_0=\kappa \left(0\right)$.

Proof. 

According to the proof of Theorem 4, when $\kappa sin\varphi \ne {\kappa }_{0}sin{\varphi }_0$, we have ${\mathit{\beta }}^{{}^{\prime }}\ne \mathbf{0}$. Since det(${\mathit{\beta }}^{{}^{\prime }},{\mathbf{N}}_2,{\mathbf{N}}_2^{{}^{\prime }})=0,$ $<{\mathit{\beta }}^{{}^{\prime }},{\mathbf{N}}_2^{{}^{\prime }}>=0$, and $<{\mathbf{N}}_2,{\mathbf{N}}_2^{{}^{\prime }}>=0$, then ${\mathit{\beta }}^{{}^{\prime }}\parallel {\mathbf{N}}_2$. This means that M is tangential developable. □

3.3. Examples

In this subsection, we confirm the correctness of the formulae obtained above.

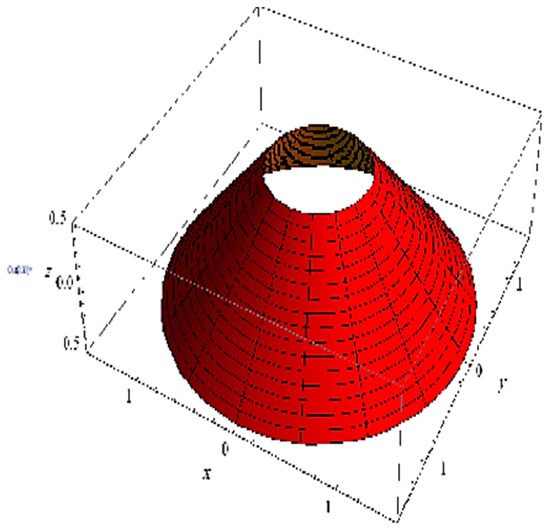
Example 3.

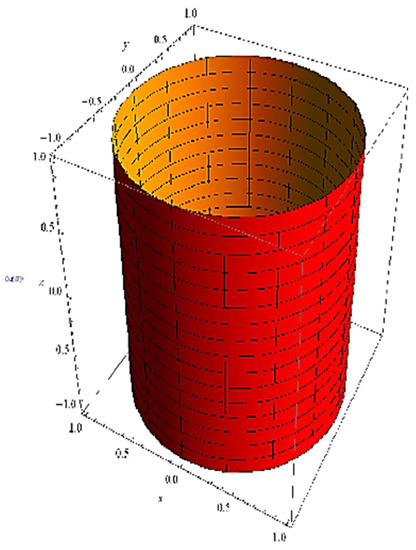
Based on Example 1, we construct a cylinder in $\mathbb{G}$ with the following equation (Figure 3):

$$M:\mathbf{Y}(s,t)=(coss,sins,0)+t(0,0,1), t\in \mathbb{R}.$$

(47)

Figure 3. A right cylinder.

Obviously, it does not satisfy Theorem 3, that is $\tau -{\tau }_G\ne 0$. This means that a cylinder in a commutative group $\mathbb{G}$ is developable, but a cylinder in a three-dimensional Lie group $\mathbb{G}$ is not developable. More explicitly, since ${\tau }_G=0$, then $\varphi \left(s\right)$ is a constant. If $\varphi \left(s\right)=0$ or π, the developable surface $M$ is a cylinder. If we take $\varphi =0$ for example, then M is shown in Figure 3. Take $\varphi \left(s\right)=\frac{\pi }{4}$ for example; the developable surface:

$$M:\mathbf{Y}(s,t)=(coss,sins,0)+\frac{t}{\sqrt{2}}(-coss,-sins,1)$$

is a cone (Figure 4). Then, we state the following: in the three-dimensional Lie group, there exists no developable cylinder (resp. cone) surface possessing a given planar curve as a curvature line.

Figure 4. A circular cone.

Example 4.

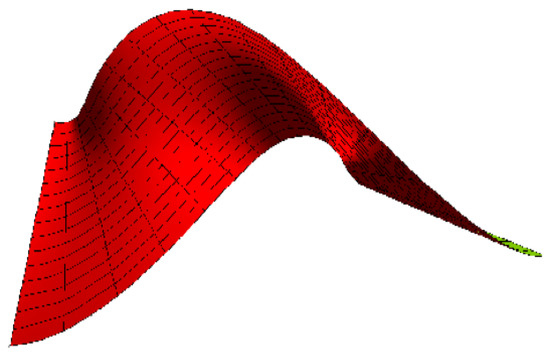
Based on Example 2 and Theorem 3, we have $\kappa sin\varphi \ne {\kappa }_{0}sin{\varphi }_0$. Then, the developable surface:

$$M:\mathbf{Y}(s,t)=(\frac{1}{\sqrt{2}}coss,\frac{1}{\sqrt{2}}sins,\frac{s}{\sqrt{2}})+t\left(\begin{array}{c}-cos\frac{s}{\sqrt{2}}coss-\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}sins\hfill \\ cos\frac{s}{\sqrt{2}}sins+\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}coss\hfill \\ -\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}\hfill \end{array}\right)$$

is a tangential developable surface in a commutative group $\mathbb{G}$ (Figure 5).

Figure 5. A tangential developable.

4. Conclusions

In the three-dimensional Lie group $\mathbb{G}$, we developed a new mathematical framework for finding a sweeping surface family. We also showed that the parameter curves are curvature lines and gave their Gaussian curvatures. This led us to study their geometric properties and local singularities. In the process of the derivation, the necessary and sufficient conditions when the resulting sweeping surface is a developable ruled surface were also analyzed.