The Behavior and Structures of Solution of Fifth-Order Rational Recursive Sequence

Abstract

In this work, we aim to study some qualitative properties of higher order nonlinear difference equations. Specifically, we investigate local as well as global stability and boundedness of solutions of this equation. In addition, we will provide solutions to a number of special cases of the studied equation. Also, we present many numerical examples that support the results obtained. The importance of the results lies in completing the results in the literature, which aims to develop the theoretical side of the qualitative theory of difference equations.

1. Introduction

Consider the difference equation

$${\mathsf{\Psi }}_{l+1}={\gamma }_0{\mathsf{\Psi }}_{l-1}+{\displaystyle \frac{{\gamma }_1{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\gamma }_2{\mathsf{\Psi }}_{l-4}+{\gamma }_3{\mathsf{\Psi }}_{l-2}}},l=0,1,\dots ,$$

(1)

where the coefficients ${\gamma }_k,$ $k=0,1,2,3$, are real numbers and the initial values ${\mathsf{\Psi }}_{-s}$, $s=0,1,\dots ,4$, are arbitrary positive real numbers. Recently, the study of qualitative properties, such as stability, oscillation, symmetry, and periodicity of solutions of difference equations has attracted the attention of many researchers. This interest is due to the fact that many varied nonlinear phenomena that occur in engineering and the natural sciences are modeled by using forms of difference equations. One such interesting model is the Riccati difference equation

$${\mathsf{\Psi }}_{l+1}=\frac{a_0+a_1{\mathsf{\Psi }}_l}{a_2+a_3{\mathsf{\Psi }}_l},$$

where $a_s$ and ${\mathsf{\Psi }}_0$ are real numbers, and $s=0,1,2,3$. The richness of Riccati equations’ dynamics is well known [1], and a special instance of these equations gives the famous Beverton–Holt model on the dynamics of exploited fish populations [2]. Kuruklis, et al. analyzed the behavior of Pielou’s discrete logistic model in [3] as another example

$${\mathsf{\Psi }}_{l+1}=\frac{a{\mathsf{\Psi }}_l}{1+{\mathsf{\Psi }}_{l-1}},$$

where $a\le 1$. Pielou developed this equation as a discrete version of the delay logistic differential equation in [4]. In Reference [5], the case $a>1$ in Pielou’s equation was considered. Stevic [6] studied the periodic character of the general equation

$${\mathsf{\Psi }}_{l+1}=\frac{g\left({\mathsf{\Psi }}_l,{\mathsf{\Psi }}_{l-1}\right)}{A+{\mathsf{\Psi }}_l},$$

where $A,$ ${\mathsf{\Psi }}_{-1}$ and ${\mathsf{\Psi }}_0$ are positive real numbers and $g:{\left(0,\infty \right)}^2\to \left(0,\infty \right)$ is continuous and satisfies

$$g\left(u,v\right)-g\left(v,w\right)=\left(u-w\right)h\left(u,v,w\right)-A\left(u-v\right)$$

for some continuous function $h:{\left(0,\infty \right)}^3\to \left(0,\infty \right),$ such that

$$\frac{1}{u}h\left(u,v,w\right)\to 0\mathrm{as}u,v,w\to \infty \mathrm{and}sup\frac{1}{A+u}h\left(u,v,w\right)<\infty .$$

The asymptotic properties of the nonnegative solutions of the equation

$${\mathsf{\Psi }}_{l+1}=a+\frac{{\mathsf{\Psi }}_{l-k}}{f\left({\mathsf{\Psi }}_l,{\mathsf{\Psi }}_{l-1},\dots ,{\mathsf{\Psi }}_{l-k+1}\right)}$$

is investigated in [7], where a is a nonnegative real number and f is a continuous function, nondecreasing in each variable and increasing in at least one. Elsayed [8] studied the qualitative behavior of the solution of

$${\mathsf{\Psi }}_{l+1}=a{\mathsf{\Psi }}_l+{\displaystyle \frac{b{\mathsf{\Psi }}_l{\mathsf{\Psi }}_{l-1}}{c{\mathsf{\Psi }}_{l-1}+d{\mathsf{\Psi }}_{l-2}.}}$$

The behavior of solutions of

$${\mathsf{\Psi }}_{l+1}={\displaystyle \frac{a{\mathsf{\Psi }}_{l-27}}{1+{\mathsf{\Psi }}_{l-3}{\mathsf{\Psi }}_{l-7}{\mathsf{\Psi }}_{l-11}{\mathsf{\Psi }}_{l-15}{\mathsf{\Psi }}_{l-19}{\mathsf{\Psi }}_{l-23}}}$$

is examined by Ogul, et al. [9]. For more interesting results about techniques and developments in the study of the qualitative behavior of solutions of difference equations, see also [10,11,12,13,14,15,16,17,18]. Also of interest in the study of difference equations is the field of symmetries, as it has many applications in different branches of science [19,20,21].

The results in this paper are divided into two main parts. The first part studies the local and global stability and boundedness of solutions to Equation (1). The second part is concerned with finding solutions to Equation (1) in four special cases. It should be noted that the study of the behavior of solutions of these equations contributes mainly to the theoretical development of the qualitative theory of solutions to difference equations, and this contributes to helping in the study of models resulting from various phenomena. Moreover, the obtainment of solutions to nonlinear difference equations is not prevalent in the works of most of the aforementioned researchers, who are only interested in studying the behavior of solutions.

Next, we provide some definitions and theorems that are essential for presenting our main results.

Let I be some interval of real numbers and let $g:I^{k+1}\to I,$ be a continuously differentiable function, where k is a positive integer. Then for every set of initial values ${\mathsf{\Psi }}_{-k},{\mathsf{\Psi }}_{-k+1},$$\dots ,{\mathsf{\Psi }}_0\in I,$ the difference equation

$${\mathsf{\Psi }}_{n+1}=g({\mathsf{\Psi }}_n,{\mathsf{\Psi }}_{n-1},\dots ,{\mathsf{\Psi }}_{n-k}),n=0,1,\dots ,$$

(2)

has a unique solution ${\left\{{\mathsf{\Psi }}_n\right\}}_{n=-k}^{\infty }$. For more, see [5]. A point $\overline{\mathsf{\Psi }}\in I$ is called an equilibrium point of Equation (2) if $\overline{\mathsf{\Psi }}=g(\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }},\dots ,\overline{\mathsf{\Psi }})$.

Definition 1.

(i) The equilibrium point $\overline{\mathsf{\Psi }}$ of Equation (2) is locally stable if for every $ϵ>0,$ there exists $\delta >0$ such that for all ${\mathsf{\Psi }}_{-k},{\mathsf{\Psi }}_{-k+1},\dots ,{\mathsf{\Psi }}_{-1},{\mathsf{\Psi }}_0\in I$ with $\left|{\mathsf{\Psi }}_{-k}-\overline{\mathsf{\Psi }}\right|+\left|{\mathsf{\Psi }}_{-k+1}-\overline{\mathsf{\Psi }}\right|+\dots +\left|{\mathsf{\Psi }}_0-\overline{\mathsf{\Psi }}\right|<\delta ,$ we have

$$\left|{\mathsf{\Psi }}_n-\overline{\mathsf{\Psi }}\right|<ϵ\mathit{for}\mathit{all}n\ge -k.$$

(ii) The equilibrium point $\overline{\mathsf{\Psi }}$ of Equation (2) is locally asymptotically stable if $\overline{\mathsf{\Psi }}$ is the locally stable solution of Equation (2) and there exists $\gamma >0,$ such that for all ${\mathsf{\Psi }}_{-k},{\mathsf{\Psi }}_{-k+1},\dots ,{\mathsf{\Psi }}_{-1},{\mathsf{\Psi }}_0\in I$ with

$$\left|{\mathsf{\Psi }}_{-k}-\overline{\mathsf{\Psi }}\right|+\left|{\mathsf{\Psi }}_{-k+1}-\overline{\mathsf{\Psi }}\right|+\dots +\left|{\mathsf{\Psi }}_0-\overline{\mathsf{\Psi }}\right|<\gamma ,$$

we have ${lim}_{n\to \infty }$${\mathsf{\Psi }}_n=\overline{\mathsf{\Psi }}.$

(iii) The equilibrium point $\overline{\mathsf{\Psi }}$ of Equation (2) is a global attractor if for all ${\mathsf{\Psi }}_{-k},{\mathsf{\Psi }}_{-k+1},\dots ,{\mathsf{\Psi }}_{-1},{\mathsf{\Psi }}_0\in I,$ we have

$$\underset{n\to \infty }{lim}{\mathsf{\Psi }}_n=\overline{\mathsf{\Psi }}.$$

(iv) The equilibrium point $\overline{\mathsf{\Psi }}$ of Equation (2) is globally asymptotically stable if $\overline{\mathsf{\Psi }}$ is locally stable, and $\overline{\mathsf{\Psi }}$ is also a global attractor of Equation (2).

Definition 2.

The linearized Equation (2) of the equilibrium $\overline{\mathsf{\Psi }}$ is the linear difference equation

$$y_{n+1}=\sum _{i=0}^k{\left.\frac{\partial g}{\partial {\mathsf{\Psi }}_{n-i}}\right|}_{(\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }},\dots ,\overline{\mathsf{\Psi }})}{y}_{n-i}.$$

(3)

Theorem 1.

See [5]. Assume that $p,$ $q\in \mathbb{R}$ and $k\in \{0,1,2,\dots \}$. Then

$$\left|p\right|+\left|q\right|<1,$$

is a sufficient condition for the asymptotic stability of the difference equation

$${\mathsf{\Psi }}_{n+1}+p{\mathsf{\Psi }}_n+q{\mathsf{\Psi }}_{n-k}=0,n=0,1,\dots .$$

Remark 1.

Theorem 1 can be easily extended to a general linear equations of the form

$${\mathsf{\Psi }}_{n+k}+p_1{\mathsf{\Psi }}_{n+k-1}+\dots +p_k{\mathsf{\Psi }}_n=0,n=0,1,\dots ,$$

(4)

where $p_1,p_2,\dots ,p_k\in R$ and $k\in \{1,2,\dots \}$. Then Equation (4) is asymptotically stable provided that

$$\sum _{i=1}^k\left|p_i\right|<1.$$

Theorem 2.

See [5]. Let $[a,b]$ be an interval of real numbers and assume that

$$h:{[a,b]}^3\to [a,b]$$

is a continuous function. Then the difference equation ${\mathsf{\Psi }}_{n+1}=h({\mathsf{\Psi }}_n,{\mathsf{\Psi }}_{n-1},{\mathsf{\Psi }}_{n-2})$ has a unique equilibrium $\overline{\mathsf{\Psi }}\in [a,b]$ and every solution of this equation converges to $\overline{\mathsf{\Psi }}$ if the following conditions are satisfied:

(a) $h(x,y,z)$ is non-decreasing in x and z in $[a,b]$ for each $y\in [a,b],$ and is non-increasing in $y\in [a,b]$ for each x and z in $[a,b]$;

(b) If $(m,M)\in [a,b]\times [a,b]$ is a solution of the system

$$M=h(M,m,M)andm=h(m,M,m),$$

then

$$m=M.$$

2. Stability and Boundedness of Solutions

We study, in this section, the behavior of solution Equation (1). Namely, we investigate the local and global stability, and boundedness of Equation (1).

The equilibrium point of Equation (1) is given by

$$\overline{\mathsf{\Psi }}={\gamma }_0\overline{\mathsf{\Psi }}+\frac{{\gamma }_1{\overline{\mathsf{\Psi }}}^2}{{\gamma }_2\overline{\mathsf{\Psi }}+{\gamma }_3\overline{\mathsf{\Psi }}}.$$

Therefore

$${\overline{\mathsf{\Psi }}}^2\left(1-{\gamma }_0\right)\left({\gamma }_2+{\gamma }_3\right)={\gamma }_1{\overline{\mathsf{\Psi }}}^2.$$

If $\left(1-{\gamma }_0\right)\left({\gamma }_2+{\gamma }_3\right)\ne {\gamma }_1,$ then $\overline{\mathsf{\Psi }}=0$ is unique equilibrium point. Now, we define the function $G:(0,\infty )\to (0,\infty )$ as

$$G(u,v,z)={\gamma }_{0}u+\frac{{\gamma }_{1}uz}{{\gamma }_{2}z+{\gamma }_{3}v}.$$

Hence, we obtain

$$\begin{array}{cc}\hfill G_u(u,v,z)& ={\gamma }_0+\frac{{\gamma }_{1}uz}{{\gamma }_{2}z+{\gamma }_{3}v},\hfill \\ \hfill G_v(u,v,z)& =-\frac{{\gamma }_3{\gamma }_{1}uz}{{\left({\gamma }_{2}z+{\gamma }_{3}v\right)}^2},\hfill \\ \hfill G_z(u,v,z)& =\frac{{\gamma }_3{\gamma }_{1}uz}{{\left({\gamma }_{2}z+{\gamma }_{3}v\right)}^2},\hfill \end{array}$$

where $G_u,$$G_v$ and $G_z$ are partial derivatives of G.

It follows that

$$\begin{array}{cc}\hfill G_u(\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }})& ={\gamma }_0+\frac{{\gamma }_1}{{\gamma }_2+{\gamma }_3},\hfill \\ \hfill G_v(\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }})& =-\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2},\hfill \\ \hfill G_z(\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }},\overline{\mathsf{\Psi }})& =\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}.\hfill \end{array}$$

Therefore, the linearized form of Equation (1) becomes

$$V_{l+1}=\left({\gamma }_0+\frac{{\gamma }_1}{{\gamma }_2+{\gamma }_3}\right)V_{l-1}-\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}{V}_{l-2}+\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}{V}_{l-4}.$$

Theorem 3.

Assume that

$${\gamma }_1{\gamma }_2+3{\gamma }_3{\gamma }_1<\left(1-{\gamma }_0\right){\left({\gamma }_2+{\gamma }_3\right)}^2.$$

Then the unique equilibrium point $\overline{\mathsf{\Psi }}=0$ of (1) is locally asymptotically stable.

Proof. 

In view of [15] (Theorem 1.1.1), we see that $\overline{\mathsf{\Psi }}$ is locally asymptotically stable if

$$\left|{\gamma }_0+\frac{{\gamma }_1}{{\gamma }_2+{\gamma }_3}\right|+\left|\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}\right|+\left|\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}\right|<1.$$

Hence

$$\begin{array}{cc}\hfill 1-{\gamma }_0& >\frac{{\gamma }_1}{{\gamma }_2+{\gamma }_3}+\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}+\frac{{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}\hfill \\ \hfill & >\frac{{\gamma }_1{\gamma }_2+3{\gamma }_3{\gamma }_1}{{\left({\gamma }_2+{\gamma }_3\right)}^2}.\hfill \end{array}$$

Then, it follows that

$${\gamma }_1{\gamma }_2+3{\gamma }_3{\gamma }_1<\left(1-{\gamma }_0\right){\left({\gamma }_2+{\gamma }_3\right)}^2.$$

This means that the proof is complete. □

Theorem 4.

If ${\gamma }_2\left(1-{\gamma }_0\right)\ne {\gamma }_1$, then the unique equilibrium point of Equation (1) is globally asymptotically stable.

Proof. 

We define the function $f:{\left[p,q\right]}^3\to \left[p,q\right]$ as $f(u,v,z)={\gamma }_{0}u+\frac{{\gamma }_{1}uz}{{\gamma }_{2}z+{\gamma }_{3}v},$ where $p,q$ are positive real numbers. It is easy to see the function f increasing in $u,$ z and decreasing in v. Next, taking $\left(m,M\right)$ as the solution to the system

$$\begin{array}{ccc}\hfill M& =& f(M,m,M),\hfill \\ \hfill m& =& f(m,M,m)\hfill \end{array}$$

We therefore get

$$\begin{array}{ccc}\hfill M& =& {\gamma }_{0}M+\frac{{\gamma }_1{M}^2}{{\gamma }_{2}M+{\gamma }_{3}m},\hfill \\ \hfill m& =& {\gamma }_{0}m+\frac{{\gamma }_1{m}^2}{{\gamma }_{2}m+{\gamma }_{3}M}.\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill M(1-{\gamma }_0)\left({\gamma }_{2}M+{\gamma }_{3}m\right)& ={\gamma }_1{M}^2,\hfill \\ \hfill m(1-{\gamma }_0)\left({\gamma }_{2}m+{\gamma }_{3}M\right)& ={\gamma }_1{m}^2.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill (1-{\gamma }_0){\gamma }_2{M}^2+M(1-{\gamma }_0){\gamma }_{3}m& ={\gamma }_1{M}^2,\hfill \\ \hfill (1-{\gamma }_0){\gamma }_2{m}^2+m(1-{\gamma }_0){\gamma }_{3}M& ={\gamma }_1{m}^2.\hfill \end{array}$$

Therefore, we have

$$(1-{\gamma }_0){\gamma }_2\left(M^2-m^2\right)={\gamma }_1\left(M^2-m^2\right).$$

This implies that $M=m$ if $(1-{\gamma }_0){\gamma }_2\ne {\gamma }_1$. Thus, the equilibrium point $\overline{\mathsf{\Psi }}$ of Equation (1) is a global attractor. This means that the proof is complete. □

Theorem 5.

All solutions of Equation (1) are bounded when

$${\gamma }_0+\frac{{\gamma }_1}{{\gamma }_2}<1.$$

(5)

Proof. 

Assume that ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=-4}^{\infty }$ is a solution of Equation (1). From Equation (5), we obtain

$${\mathsf{\Psi }}_{l+1}\le {\mathsf{\Psi }}_{l-1}\mathrm{for}l\ge 0.$$

This means that the sequence ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=-4}^{\infty }$ is decreasing and hence it is bounded from above by $m=max\left\{{\mathsf{\Psi }}_{-4},{\mathsf{\Psi }}_{-3},{\mathsf{\Psi }}_{-2},{\mathsf{\Psi }}_{-1},{\mathsf{\Psi }}_0\right\}$. This means that the proof is complete. □

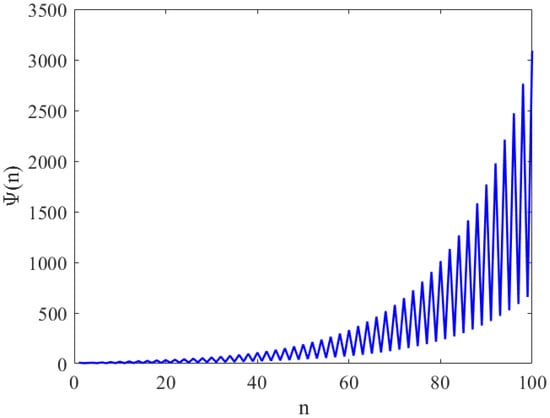
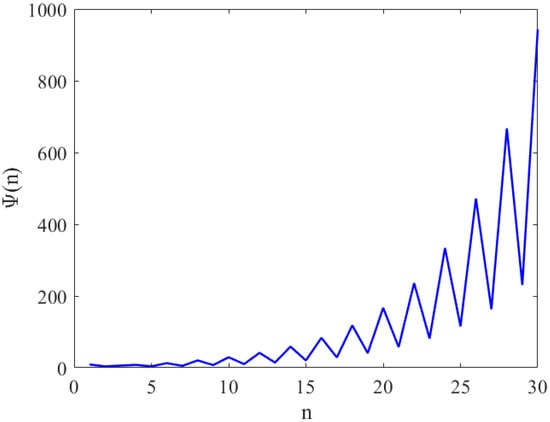
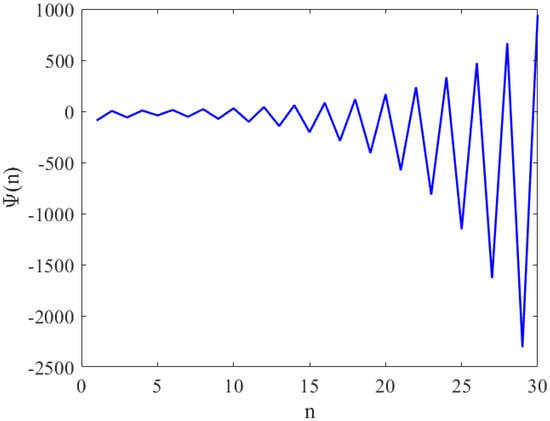
In the following, we present some numerical simulations to confirm the results of this section.

Example 1.

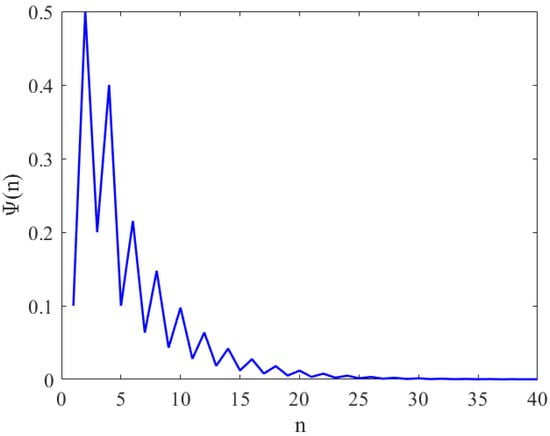
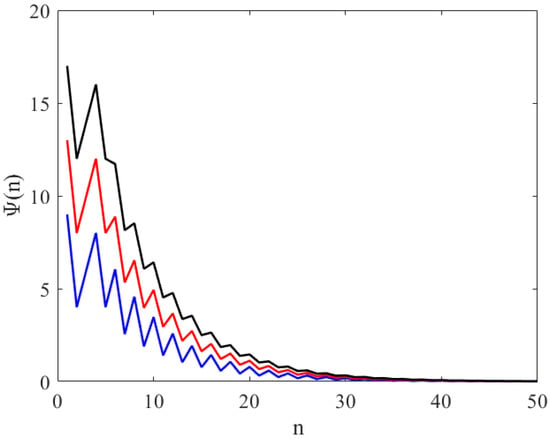
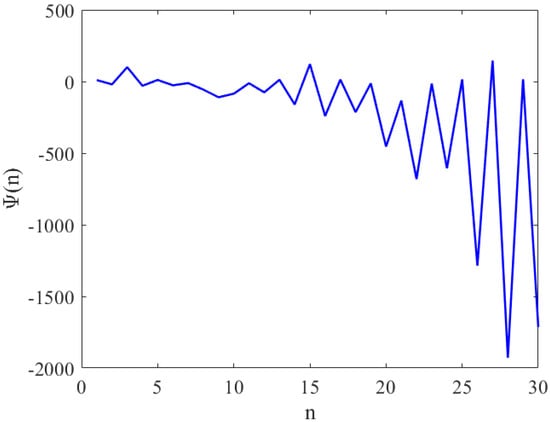
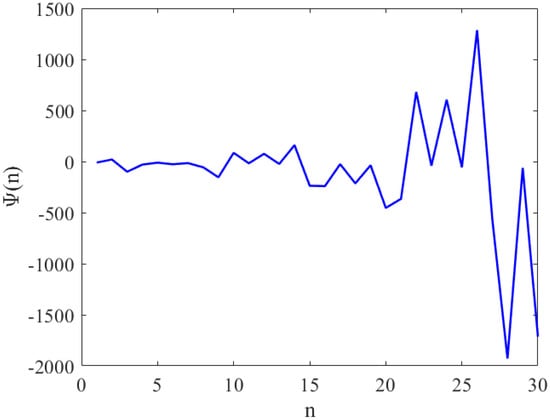
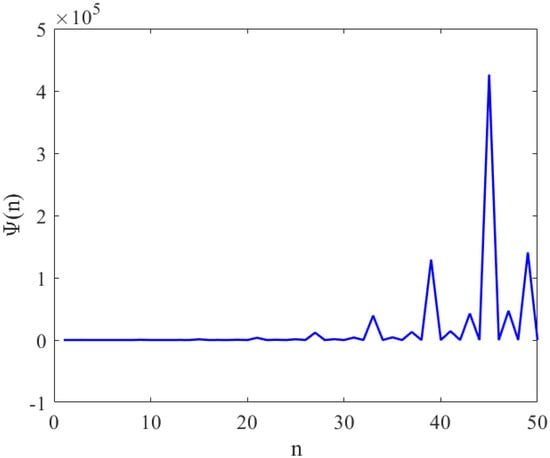
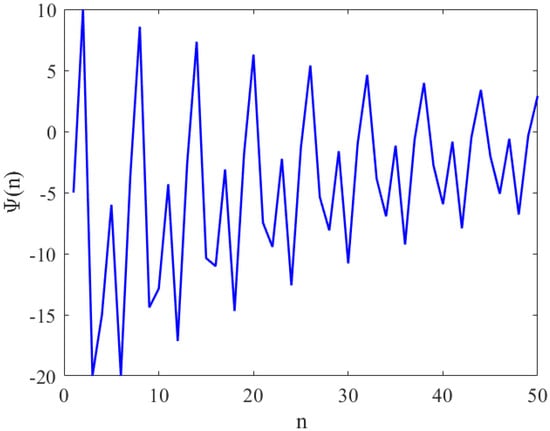
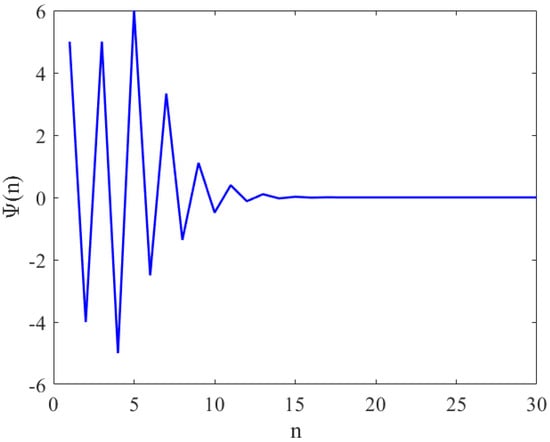
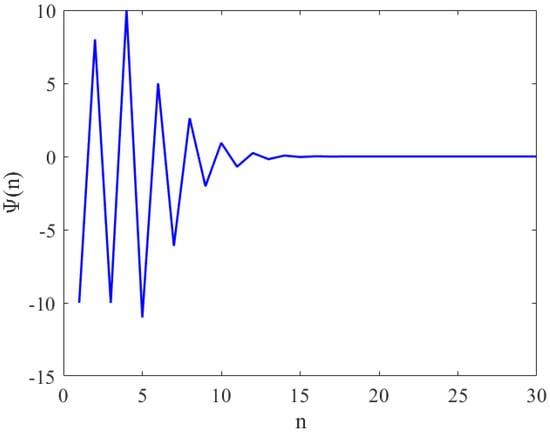
Assume that ${\gamma }_0=0.4$, ${\gamma }_1=0.4$, ${\gamma }_2=0.9$, and ${\gamma }_3=1,$ with initial condition ${\mathsf{\Psi }}_{-4}=10$, ${\mathsf{\Psi }}_{-3}=5$, ${\mathsf{\Psi }}_{-2}=2$, ${\mathsf{\Psi }}_{-1}=9$, and ${\mathsf{\Psi }}_0=9$. See Figure 1.

Figure 1. This figure shows the local stability equilibrium point of Equation (1) with ${\mathsf{\Psi }}_{-4}=0.1,{\mathsf{\Psi }}_{-3}=0.5,{\mathsf{\Psi }}_{-2}=0.2,{\mathsf{\Psi }}_{-1}=0.4,{\mathsf{\Psi }}_0=0.1$ if ${\gamma }_0,{\gamma }_1,{\gamma }_2,{\gamma }_1$ satisfies the condition of Theorem 1.

Example 2.

Assume that ${\gamma }_0=0.5$, ${\gamma }_1=0.4$, ${\gamma }_2=0.9$, and ${\gamma }_3=1$, with initial condition

• IC1: ${\mathsf{\Psi }}_{-4}=9$, ${\mathsf{\Psi }}_{-3}=4$, ${\mathsf{\Psi }}_{-2}=6$, ${\mathsf{\Psi }}_{-1}=8$, and ${\mathsf{\Psi }}_0=4$.
• IC2: ${\mathsf{\Psi }}_{-4}=13$, ${\mathsf{\Psi }}_{-3}=8$, ${\mathsf{\Psi }}_{-2}=10$, ${\mathsf{\Psi }}_{-1}=12$, and ${\mathsf{\Psi }}_0=8$.
• IC3: ${\mathsf{\Psi }}_{-4}=17$, ${\mathsf{\Psi }}_{-3}=12$, ${\mathsf{\Psi }}_{-2}=14$, ${\mathsf{\Psi }}_{-1}=16,$ and ${\mathsf{\Psi }}_0=12$.

See Figure 2.

Figure 2. This figure shows global stability of equilibrium points of Equation (1) with IC1-IC3 if ${\gamma }_0,{\gamma }_1,{\gamma }_2,{\gamma }_3$ satisfies the condition of Theorem 2.

Example 3.

Assume that ${\gamma }_0=0.5$, ${\gamma }_1=1$, ${\gamma }_2=0.5$, and ${\gamma }_3=1$, with initial condition ${\mathsf{\Psi }}_{-4}=10$, ${\mathsf{\Psi }}_{-3}=5$, ${\mathsf{\Psi }}_{-2}=7$, ${\mathsf{\Psi }}_{-1}=9,$ and ${\mathsf{\Psi }}_0=5$. See Figure 3.

Figure 3. Unbounded solution of Equation (1).

3. Solutions of Some Particular Cases

The section introduces solve four particular cases of difference Equation (1).

3.1. Case 1: ${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}+\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}+{\mathsf{\Psi }}_{l-2}}$

Next, we present the solution of difference equation

$${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}+\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}+{\mathsf{\Psi }}_{l-2}},l=0,1,\dots .$$

(6)

Theorem 6.

If ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=1}^{\infty }$ is the solution to difference Equation (6), then this solution is obtained by the given formulas

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}C+Y_{k}E\right){\displaystyle \prod _{k=1}^l}\left(X_{k}A+Y_{k}C\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+Y_k)B+Z_{k}D\right)(Y_{k}C+\frac{X_k}{2}E){\displaystyle \prod _{k=1}^l}(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-4}& =\frac{E{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left({(X_k+2Y_k)}_{k}C+(X_k+Y_k)E\right){\displaystyle \prod _{k=1}^l}\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^l}(Y_{k}B+\frac{X_k}{2}D){\displaystyle \prod _{k=1}^{l-1}}\left(\left(X_k+Y_k\right)A+Z_{k}C\right)\left(\left(X_k+Y_k\right)C+Z_{k}E\right)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-3}& =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right){\displaystyle \prod _{k=1}^l}\left(X_{k}A+Y_{k}C\right)\left(X_{k}C+Y_{k}E\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+Y_k)B+Z_{k}D\right){\displaystyle \prod _{k=1}^l}(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-2}& =\frac{E{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)C+(X_k+Y_k)E\right){\displaystyle \prod _{k=1}^l}\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^l}\left(\left(X_k+Y_k\right)A+Z_{k}C\right)(Y_{k}B+\frac{X_k}{2}D){\displaystyle \prod _{k=1}^{l-1}}\left(\left(X_k+Y_k\right)C+Z_{k}E\right)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-1}& =\frac{D{\displaystyle \prod _{k=1}^l}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}A+Y_{k}C\right)\left(X_{k}C+Y_{k}E\right)}{{\displaystyle \prod _{k=1}^l}\left((X_k+Y_k)B+Z_{k}D\right)(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l}& =\frac{E{\displaystyle \prod _{k=1}^l}\left({(X_k+2Y_k)}_{k}C+(X_k+Y_k)E\right)\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^l}(Y_{k}B+\frac{X_k}{2}D)\left(\left(X_k+Y_k\right)A+Z_{k}C\right)\left(\left(X_k+Y_k\right)C+Z_{k}E\right)},\hfill \end{array}$$

where ${\mathsf{\Psi }}_{-4}=A,{\mathsf{\Psi }}_{-3}=B,{\mathsf{\Psi }}_{-2}=C,{\mathsf{\Psi }}_{-1}=D,$ ${\mathsf{\Psi }}_0=E,$ and the sequences ${\left\{X_l\right\}}_{l=1}^{\infty },$${\left\{Y_l\right\}}_{l=1}^{\infty },$ and ${\left\{Y_l\right\}}_{l=1}^{\infty }$ are obtained by the following relations, for $k\ge 2,$

$$\begin{array}{cc}\hfill X_k& =2Z_{k-1}+2X_{k-1}+2Y_{k-1},\hfill \\ \hfill Y_k& =2X_{k-1}+3Y_{k-1},\hfill \end{array}$$

$$Z_k=\sum _{j=1}^{k}Xj,$$

$$\begin{array}{cc}\hfill \frac{X_k}{2}-Y_k+Z_{k-1}& =0,\hfill \\ \hfill Y_k+X_{k-1}+Y_{k-1}-X_k& =0,\hfill \\ \hfill Y_k+\frac{X_k}{2}-Z_k& =0,\hfill \end{array}$$

and so

$$\begin{array}{ccc}\hfill {\left\{X_l\right\}}_{l=1}^{\infty }& =& \left\{2,10,58,338,\dots \right\},\hfill \\ \hfill {\left\{Y_l\right\}}_{l=1}^{\infty }& =& \left\{1,7,41,239,\dots \right\},\hfill \\ \hfill {\left\{Z_l\right\}}_{l=1}^{\infty }& =& \left\{2,12,70,408,\dots \right\}.\hfill \end{array}$$

Proof. 

It is easy to see that the result holds if $l=1$. Next, assume that $l>0$ and the assumption holds for $l-1$, which is

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-11}& =\frac{D{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}C+Y_{k}E\right){\displaystyle \prod _{k=1}^{l-1}}\left(X_{k}A+Y_{k}C\right)}{{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+Y_k)B+Z_{k}D\right)(Y_{k}C+\frac{X_k}{2}E){\displaystyle \prod _{k=1}^{l-1}}(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-10}& =\frac{E{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left({(X_k+2Y_k)}_{k}C+(X_k+Y_k)E\right){\displaystyle \prod _{k=1}^{l-1}}\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^{l-1}}(Y_{k}B+\frac{X_k}{2}D){\displaystyle \prod _{k=1}^{l-2}}\left(\left(X_k+Y_k\right)A+Z_{k}C\right)\left(\left(X_k+Y_k\right)C+Z_{k}E\right)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-9}& =\frac{D{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right){\displaystyle \prod _{k=1}^{l-1}}\left(X_{k}A+Y_{k}C\right)\left(X_{k}C+Y_{k}E\right)}{{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+Y_k)B+Z_{k}D\right){\displaystyle \prod _{k=1}^{l-1}}(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-8}& =\frac{E{\displaystyle \prod _{k=1}^{l-2}}\left((X_k+2Y_k)C+(X_k+Y_k)E\right){\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left(\left(X_k+Y_k\right)A+Z_{k}C\right)(Y_{k}B+\frac{X_k}{2}D){\displaystyle \prod _{k=1}^{l-2}}\left(\left(X_k+Y_k\right)C+Z_{k}E\right)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-7}& =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)(X_{k}A+Y_{k}C)(X_{k}C+Y_{k}E)}{{\displaystyle \prod _{k=1}^{l-1}}((X_k+Y_k)B+Z_{k}D)(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-6}& =\frac{E{\displaystyle \prod _{k=1}^{l-1}}\left({(X_k+2Y_k)}_{k}C+(X_k+Y_k)E\right)\left((X_k+2Y_k)A+(X_k+Y_k)C\right)\left(X_{k}B+Y_{k}D\right)}{{\displaystyle \prod _{k=1}^{l-1}}(Y_{k}B+\frac{X_k}{2}D)\left(\left(X_k+Y_k\right)A+Z_{k}C\right)\left(\left(X_k+Y_k\right)C+Z_{k}E\right)}.\hfill \end{array}$$

From the formula of difference Equation (6),

$${\mathsf{\Psi }}_{6l-7}+\frac{{\mathsf{\Psi }}_{6l-7}{\mathsf{\Psi }}_{6l-10}}{{\mathsf{\Psi }}_{6l-10}+{\mathsf{\Psi }}_{6l-8}}.$$

After substitution and some simple computation, we obtain

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}A+Y_{k}C\right)\left(X_{k}C+Y_{k}E\right)(Y_{l}A+\frac{X_l}{2}C+\left(X_{l-1}+Y_{l-1}\right)A+Z_{l-1}C)}{{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+Y_k)B+Z_{k}D\right)(Y_{k}C+\frac{X_k}{2}E){\displaystyle \prod _{k=1}^l}(Y_{k}A+\frac{X_k}{2}C)}\hfill \\ \hfill & =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}C+Y_{k}E\right){\displaystyle \prod _{k=1}^l}(X_{k}A+Y_{k}C)}{{\displaystyle \prod _{k=1}^{l-1}}((X_k+Y_k)B+Z_{k}D)(Y_{k}C+\frac{X_k}{2}E){\displaystyle \prod _{k=1}^l}(Y_{k}A+\frac{X_k}{2}C)},\hfill \end{array}$$

Also, we have

$${\mathsf{\Psi }}_{6l-3}={\mathsf{\Psi }}_{6l-5}+\frac{{\mathsf{\Psi }}_{6l-5}{\mathsf{\Psi }}_{6l-8}}{{\mathsf{\Psi }}_{6l-8}+{\mathsf{\Psi }}_{6l-6}}.$$

After substitution and some simple computation, we obtain

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-3}& =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right)\left(X_{k}C+Y_{k}E\right){\displaystyle \prod _{k=1}^l}\left(X_{k}A+Y_{k}C\right)(Y_{l}C+\frac{X_l}{2}E+\left(X_{l-1}+Y_{l-1}\right)C+Z_{l-1}E)}{{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+Y_k)B+Z_{k}D\right){\displaystyle \prod _{k=1}^l}(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)}\hfill \\ \hfill & =\frac{D{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+2Y_k)B+(X_k+Y_k)D\right){\displaystyle \prod _{k=1}^l}\left(X_{k}A+Y_{k}C\right)\left(X_{k}C+Y_{k}E\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left((X_k+Y_k)B+Z_{k}D\right){\displaystyle \prod _{k=1}^l}(Y_{k}C+\frac{X_k}{2}E)(Y_{k}A+\frac{X_k}{2}C)}.\hfill \end{array}$$

Moreover, we can prove the other relations. The proof is complete. □

Example 4.

We consider numerical simulations to verify the results presented in this subsection for the difference Equation (6) with the initial conditions ${\mathsf{\Psi }}_{-4}=9,{\mathsf{\Psi }}_{-3}=4,{\mathsf{\Psi }}_{-2}=4,{\mathsf{\Psi }}_{-1}=8,$ and ${\mathsf{\Psi }}_0=4$. See Figure 4.

Figure 4. The numerical solution of Equation (6) with ${\mathsf{\Psi }}_{-4}=9,{\mathsf{\Psi }}_{-3}=4,{\mathsf{\Psi }}_{-2}=4,{\mathsf{\Psi }}_{-1}=8,$ and ${\mathsf{\Psi }}_0=4$.

Example 5.

In order to confirm the results of this subsection, we consider numerical simulations for the difference Equation (6) with the initial conditions ${\mathsf{\Psi }}_{-4}=-90,{\mathsf{\Psi }}_{-3}=4,{\mathsf{\Psi }}_{-2}=-60,{\mathsf{\Psi }}_{-1}=8,$ and ${\mathsf{\Psi }}_0=-04$. See Figure 5.

Figure 5. The numerical solution of Equation (6) with ${\mathsf{\Psi }}_{-4}=-90,{\mathsf{\Psi }}_{-3}=4,{\mathsf{\Psi }}_{-2}=-60,{\mathsf{\Psi }}_{-1}=8,$ and ${\mathsf{\Psi }}_0=-40$.

3.2. Case 2: ${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}+\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}-{\mathsf{\Psi }}_{l-2}}$

The subsection introduces solve the following difference equation

$${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}+\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}-{\mathsf{\Psi }}_{l-1}.}$$

(7)

Theorem 7.

The solution ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=1}^{\infty }$ to difference Equation (7) can be expressed by the given formulas

$$\begin{array}{ccc}{\mathsf{\Psi }}_{6l-5}=\frac{D^l{\left(2A-C\right)}^l{\left(2C-E\right)}^{l-1}}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-4}=\frac{E^l{\left(2B-D\right)}^l}{A^{l-1}{\left(B-D\right)}^l},\hfill \\ {\mathsf{\Psi }}_{6l-3}=\frac{D^l{\left(2A-C\right)}^l{\left(2C-E\right)}^l}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l},\hfill & & {\mathsf{\Psi }}_{6l-2}=\frac{C{E}^l{\left(2B-D\right)}^l}{A^l{\left(B-D\right)}^l},\hfill \\ {\mathsf{\Psi }}_{6l-1}=\frac{D^{l+1}{\left(2A-C\right)}^l{\left(2C-E\right)}^l}{B^l{\left(A-C\right)}^l{\left(C-E\right)}^l},\hfill & & {\mathsf{\Psi }}_{6l}=\frac{E^{l+1}{\left(2B-D\right)}^l}{A^l{\left(B-D\right)}^l},\hfill \end{array}$$

where ${\mathsf{\Psi }}_{-4}=A,{\mathsf{\Psi }}_{-3}=B,{\mathsf{\Psi }}_{-2}=C,{\mathsf{\Psi }}_{-1}=D$ and ${\mathsf{\Psi }}_0=E$.

Proof. 

It is easy to see that the result holds if $l=1$. Next, suppose that $l>0$ and assumption holds for $l-1$, which is

$$\begin{array}{ccc}{\mathsf{\Psi }}_{6l-11}=\frac{D^{l-1}{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-2}}{B^{l-2}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-2}},\hfill & & {\mathsf{\Psi }}_{6l-10}=\frac{E^{l-1}{\left(2B-D\right)}^{l-1}}{A^{l-2}{\left(B-D\right)}^{l-1}},\hfill \\ {\mathsf{\Psi }}_{6l-9}=\frac{D^{l-1}{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-1}}{B^{l-2}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-8}=\frac{C{E}^{l-1}{\left(2B-D\right)}^{l-1}}{A^{l-1}{\left(B-D\right)}^{l-1}},\hfill \\ {\mathsf{\Psi }}_{6l-7}=\frac{D^l{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-1}}{B^{l-1}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-6}=\frac{E^l{\left(2B-D\right)}^{l-1}}{A^{l-1}{\left(B-D\right)}^{l-1}}.\hfill \end{array}$$

From the formula of difference Equation (7), we find

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& ={\mathsf{\Psi }}_{6l-7}+\frac{{\mathsf{\Psi }}_{6l-7}{\mathsf{\Psi }}_{6l-10}}{{\mathsf{\Psi }}_{6l-10}-{\mathsf{\Psi }}_{6l-8}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-7}+\frac{D^l{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-1}A}{B^{l-1}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}\left(A-C\right)}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-7}+\frac{D^l{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-1}A}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}}\hfill \\ \hfill & =\frac{D^l{\left(2A-C\right)}^{l-1}{\left(2C-E\right)}^{l-1}\left(2A-C\right)}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}}.\hfill \end{array}$$

Similarly, we have

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-3}& ={\mathsf{\Psi }}_{6l-5}+\frac{{\mathsf{\Psi }}_{6l-5}{\mathsf{\Psi }}_{6l-8}}{{\mathsf{\Psi }}_{6l-8}-{\mathsf{\Psi }}_{6l-6}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-5}+\frac{D^l{\left(2A-C\right)}^l{\left(2C-E\right)}^{l-1}C}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}\left(C-E\right)}\hfill \\ \hfill & =\frac{D^l{\left(2A-C\right)}^l{\left(2C-E\right)}^{l-1}\left(C-E+C\right)}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l}\hfill \\ \hfill & =\frac{D^l{\left(2A-C\right)}^l{\left(2C-E\right)}^l}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l}.\hfill \end{array}$$

Also, we can prove the other relations. The proof is complete. □

Example 6.

In order to confirm the results of this subsection, we consider numerical simulations for difference Equation (7) with the initial conditions ${\mathsf{\Psi }}_{-4}=10,{\mathsf{\Psi }}_{-3}=-20,{\mathsf{\Psi }}_{-2}=100,{\mathsf{\Psi }}_{-1}=-30,$ and ${\mathsf{\Psi }}_0=-11$. See Figure 6.

Figure 6. The numerical solution of Equation (7) with ${\mathsf{\Psi }}_{-4}=10,{\mathsf{\Psi }}_{-3}=-20,{\mathsf{\Psi }}_{-2}=100,{\mathsf{\Psi }}_{-1}=-30,$ and ${\mathsf{\Psi }}_0=-11$.

Example 7.

We consider numerical simulations to verify the results presented in this subsection for difference Equation (7) with the initial conditions ${\mathsf{\Psi }}_{-4}=-10,{\mathsf{\Psi }}_{-3}=20,{\mathsf{\Psi }}_{-2}=-100,{\mathsf{\Psi }}_{-1}=30,$ and ${\mathsf{\Psi }}_0=11$. See Figure 7.

Figure 7. The numerical solution of Equation (7) with ${\mathsf{\Psi }}_{-4}=-10,{\mathsf{\Psi }}_{-3}=20,{\mathsf{\Psi }}_{-2}=-100,{\mathsf{\Psi }}_{-1}=-30,$ and ${\mathsf{\Psi }}_0=-20$.

3.3. Case 3: ${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}-\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}-{\mathsf{\Psi }}_{l-1}}$

The subsection solves the following difference equation

$${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}-\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}-{\mathsf{\Psi }}_{l-1}}.$$

(8)

Theorem 8.

If ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=1}^{\infty }$ is the solution to difference Equation (8), then this solution is obtained by the given formulas

$$\begin{array}{ccc}{\mathsf{\Psi }}_{6l-5}=\frac{-C^l{D}^l{E}^{l-1}}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-4}=\frac{{(-1)}^l{D}^l{E}^l}{A^{l-1}{\left(B-D\right)}^l},\hfill \\ {\mathsf{\Psi }}_{6l-3}=\frac{C^l{D}^l{E}^l}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l},\hfill & & {\mathsf{\Psi }}_{6l-2}=\frac{{(-1)}^{l}C{D}^l{E}^l}{A^l{\left(B-D\right)}^l},\hfill \\ {\mathsf{\Psi }}_{6l-1}=\frac{C^l{D}^{l+1}{E}^l}{B^l{\left(A-C\right)}^l{\left(C-E\right)}^l},\hfill & & {\mathsf{\Psi }}_{6l}=\frac{{(-1)}^l{D}^l{E}^{l+1}}{A^l{\left(B-D\right)}^l},\hfill \end{array}$$

where ${\mathsf{\Psi }}_{-4}=A,{\mathsf{\Psi }}_{-3}=B,{\mathsf{\Psi }}_{-2}=C,{\mathsf{\Psi }}_{-1}=D$ and ${\mathsf{\Psi }}_0=E$.

Proof. 

It is easy to see that the result holds if $l=1$. Next, assume that $l>0$ and assumption holds for $l-1$, which is

$$\begin{array}{ccc}{\mathsf{\Psi }}_{6l-11}=\frac{-C^{l-1}{D}^{l-1}{E}^{l-2}}{B^{l-2}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-2}},\hfill & & {\mathsf{\Psi }}_{6l-10}=\frac{{(-1)}^{l-1}{D}^{l-1}{E}^{l-1}}{A^{l-2}{\left(B-D\right)}^{l-1}},\hfill \\ {\mathsf{\Psi }}_{6l-9}=\frac{C^{l-1}{D}^{l-1}{E}^{l-1}}{B^{l-2}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-8}=\frac{{(-1)}^{l-1}C{D}^{l-1}{E}^{l-1}}{A^{l-1}{\left(B-D\right)}^{l-1}},\hfill \\ {\mathsf{\Psi }}_{6l-7}=\frac{C^{l-1}{D}^l{E}^{l-1}}{B^{l-1}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}},\hfill & & {\mathsf{\Psi }}_{6l-6}=\frac{{(-1)}^{l-1}{D}^{l-1}{E}^l}{A^{l-1}{\left(B-D\right)}^{l-1}},\hfill \end{array}$$

From the formula difference Equation (8), we arrive at

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& ={\mathsf{\Psi }}_{6l-7}-\frac{{\mathsf{\Psi }}_{6l-7}{\mathsf{\Psi }}_{6l-10}}{{\mathsf{\Psi }}_{6l-10}-{\mathsf{\Psi }}_{6l-8}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-7}-\frac{C^l{D}^l{E}^{l-1}A}{B^{l-1}{\left(A-C\right)}^{l-1}{\left(C-E\right)}^{l-1}\left(A-C\right)}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^{l-1}\left(A-C-A\right)}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}}\hfill \\ \hfill & =\frac{-C^l{D}^l{E}^{l-1}}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}}.\hfill \end{array}$$

Similarly, we get

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-3}& ={\mathsf{\Psi }}_{6l-5}-\frac{{\mathsf{\Psi }}_{6l-5}{\mathsf{\Psi }}_{6l-8}}{{\mathsf{\Psi }}_{6l-8}-{\mathsf{\Psi }}_{6l-6}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-5}+\frac{C^{l+1}{D}^l{E}^{l-1}}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^{l-1}\left(C-E\right)}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^{l-1}\left(C-E+C\right)}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^l}{B^{l-1}{\left(A-C\right)}^l{\left(C-E\right)}^l}.\hfill \end{array}$$

Also, we can prove the other relations. The proof is complete. □

Example 8.

We consider numerical simulations to verify the results presented in this subsection for difference Equation (8) with the initial conditions ${\mathsf{\Psi }}_{-4}=10,{\mathsf{\Psi }}_{-3}=-20,{\mathsf{\Psi }}_{-2}=100,{\mathsf{\Psi }}_{-1}=-30,$ and ${\mathsf{\Psi }}_0=11$. See Figure 8.

Figure 8. The numerical solution of Equation (8) with ${\mathsf{\Psi }}_{-4}=10,{\mathsf{\Psi }}_{-3}=-20,{\mathsf{\Psi }}_{-2}=100,{\mathsf{\Psi }}_{-1}=-30,$ and ${\mathsf{\Psi }}_0=11$.

Example 9.

In order to confirm the results of this subsection, we consider numerical simulations for difference Equation (8) with the initial conditions ${\mathsf{\Psi }}_{-4}=-5,{\mathsf{\Psi }}_{-3}=10,{\mathsf{\Psi }}_{-2}=-20,{\mathsf{\Psi }}_{-1}=-15,$ and ${\mathsf{\Psi }}_0=-6.$ See Figure 9.

Figure 9. The numerical solution of Equation (8) with ${\mathsf{\Psi }}_{-4}=-5,{\mathsf{\Psi }}_{-3}=10,{\mathsf{\Psi }}_{-2}=-20,{\mathsf{\Psi }}_{-1}=-15,$ and ${\mathsf{\Psi }}_0=-6$.

3.4. Case 4: ${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}-\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}+{\mathsf{\Psi }}_{l-1}}$

The subsection introduces solve the following difference equation

$${\mathsf{\Psi }}_{l+1}={\mathsf{\Psi }}_{l-1}-\frac{{\mathsf{\Psi }}_{l-1}{\mathsf{\Psi }}_{l-4}}{{\mathsf{\Psi }}_{l-4}+{\mathsf{\Psi }}_{l-1}}.$$

(9)

Theorem 9.

The solution ${\left\{{\mathsf{\Psi }}_l\right\}}_{l=1}^{\infty }$ to difference Equation (9) can be expressed by the given formulas

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& =\frac{C^l{D}^l{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^l}\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l-4}=\frac{C^{l-1}{D}^l{E}^l}{{\displaystyle \prod _{k=1}^{l-1}}\left(A+2kC\right)\left(C+2kE\right){\displaystyle \prod _{k=1}^l}\left(B+\left(2k-1\right)D\right)},\hfill \\ \hfill {\mathsf{\Psi }}_{6l-3}& =\frac{C^l{D}^l{E}^l}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right){\displaystyle \prod _{k=1}^l}\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l-2}=\frac{C^l{D}^l{E}^l}{{\displaystyle \prod _{k=1}^{l-1}}\left(C+2kE\right){\displaystyle \prod _{k=1}^l}\left(A+2kC\right)\left(B+\left(2k-1\right)D\right)},\hfill \\ \hfill {\mathsf{\Psi }}_{6l-1}& =\frac{C^l{D}^{l+1}{E}^l}{{\displaystyle \prod _{k=1}^l}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l}=\frac{C^l{D}^l{E}^{l+1}}{{\displaystyle \prod _{k=1}^l}\left(A+2kC\right)\left(C+2kE\right)\left(B+\left(2k-1\right)D\right)},\hfill \end{array}$$

where ${\mathsf{\Psi }}_{-4}=A,{\mathsf{\Psi }}_{-3}=B,{\mathsf{\Psi }}_{-2}=C,{\mathsf{\Psi }}_{-1}=D$ and ${\mathsf{\Psi }}_0=E.$

Proof. 

It is easy to see that the result holds if $l=1$. Next, assume that $l>0$ and assumption holds for $l-1$, which is

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-11}& =\frac{C^{l-1}{D}^{l-1}{E}^{l-2}}{{\displaystyle \prod _{k=1}^{l-2}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^{l-1}}\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l-10}=\frac{C^{l-2}{D}^{l-1}{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-2}}\left(A+2kC\right)\left(C+2kE\right){\displaystyle \prod _{k=1}^{l-1}}\left(B+\left(2k-1\right)D\right)},\hfill \\ \hfill {\mathsf{\Psi }}_{6l-9}& =\frac{C^{l-1}{D}^{l-1}{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-2}}\left(B+2kD\right){\displaystyle \prod _{k=1}^{l-1}}\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l-8}=\frac{C^{l-1}{D}^{l-1}{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-2}}\left(C+2kE\right){\displaystyle \prod _{k=1}^{l-1}}\left(A+2kC\right)\left(B+\left(2k-1\right)D\right)},\hfill \\ \hfill {\mathsf{\Psi }}_{6l-7}& =\frac{C^{l-1}{D}^l{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)},{\mathsf{\Psi }}_{6l-6}=\frac{C^{l-1}{D}^{l-1}{E}^l}{{\displaystyle \prod _{k=1}^{l-1}}\left(A+2kC\right)\left(C+2kE\right)\left(B+\left(2k-1\right)D\right)},\hfill \end{array}$$

From the formula of difference Equation (9), we obtain

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-5}& ={\mathsf{\Psi }}_{6l-7}-\frac{{\mathsf{\Psi }}_{6l-7}{\mathsf{\Psi }}_{6l-10}}{{\mathsf{\Psi }}_{6l-10}+{\mathsf{\Psi }}_{6l-8}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-7}-\frac{C^{l-1}{D}^l{E}^{l-1}\left(A+2\left(l-1\right)C\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^{l-1}}\left(A+\left(2k-1\right)C\right)\left(A+2\left(l-1\right)C+C\right)}\hfill \\ \hfill & =\frac{C^{l-1}{D}^l{E}^{l-1}\left(A+(2l-1)C-A-2\left(l-1\right)C\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^l}\left(A+\left(2k-1\right)C\right)}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^{l-1}}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^l}\left(A+\left(2k-1\right)C\right)},\hfill \end{array}$$

Similarly, we get

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{6l-3}& ={\mathsf{\Psi }}_{6l-5}-\frac{{\mathsf{\Psi }}_{6l-5}{\mathsf{\Psi }}_{6l-8}}{{\mathsf{\Psi }}_{6l-8}+{\mathsf{\Psi }}_{6l-6}}\hfill \\ \hfill & ={\mathsf{\Psi }}_{6l-5}-\frac{C^l{D}^l{E}^{l-1}\left(C+2(l-1)E\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right)\left(C+\left(2k-1\right)E\right){\displaystyle \prod _{k=1}^l}\left(A+\left(2k-1\right)C\right)\left(C+2(l-1)E+E\right)}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^{l-1}\left(C+\left(2l-1\right)E-C-2(l-1)E\right)}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right){\displaystyle \prod _{k=1}^l}\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)}\hfill \\ \hfill & =\frac{C^l{D}^l{E}^l}{{\displaystyle \prod _{k=1}^{l-1}}\left(B+2kD\right){\displaystyle \prod _{k=1}^l}\left(C+\left(2k-1\right)E\right)\left(A+\left(2k-1\right)C\right)}.\hfill \end{array}$$

Also, we can prove the other relations. The proof is complete. □

Example 10.

In order to confirm the results of this subsection, we consider numerical simulations for difference Equation (9) with the initial conditions ${\mathsf{\Psi }}_{-4}=5,{\mathsf{\Psi }}_{-3}=-4,{\mathsf{\Psi }}_{-2}=5,{\mathsf{\Psi }}_{-1}=-5,$ and ${\mathsf{\Psi }}_0=6$. see Figure 10.

Figure 10. The numerical solution of Equation (9) with ${\mathsf{\Psi }}_{-4}=5,{\mathsf{\Psi }}_{-3}=-4,{\mathsf{\Psi }}_{-2}=5,{\mathsf{\Psi }}_{-1}=-5,$ and ${\mathsf{\Psi }}_0=6$.

Example 11.

We consider numerical simulations to verify the results presented in this subsection for difference Equation (9) with the initial conditions ${\mathsf{\Psi }}_{-4}=-10,{\mathsf{\Psi }}_{-3}=8,{\mathsf{\Psi }}_{-2}=-10,{\mathsf{\Psi }}_{-1}=10,$ and ${\mathsf{\Psi }}_0=-11.$ See Figure 11.

Figure 11. The numerical solution of Equation (9) with ${\mathsf{\Psi }}_{-4}=-10,{\mathsf{\Psi }}_{-3}=8,{\mathsf{\Psi }}_{-2}=-10,{\mathsf{\Psi }}_{-1}=10,$ and ${\mathsf{\Psi }}_0=-11$.

4. Conclusions

In this paper, we discussed some properties of solutions of a class of fifth-order rational difference equations. Specifically, we studied the conditions of local and global stability of the equilibrium points, as well as the conditions of boundedness.

It has been verified that condition ${\gamma }_1{\gamma }_2+3{\gamma }_3{\gamma }_1<\left(1-{\gamma }_0\right){\left({\gamma }_2+{\gamma }_3\right)}^2$ guarantees the local stability of the equilibrium point of Equation (1). The unique equilibrium point of Equation (1) is a global attractor if ${\gamma }_2\left(1-{\gamma }_0\right)\ne {\gamma }_1$. Moreover, every solution of Equation (1) is bounded if ${\gamma }_0+\frac{{\gamma }_1}{{\gamma }_2}<1.$ Furthermore, we obtained solutions of four special cases of the studied equation which covers most of the possibilities of coefficient signs. Finally, we confirm our results by numerical simulations. It would be interesting to study the oscillatory and periodic behavior of solutions to this Equation (1).