A Generalization of Quaternions and Their Applications

Abstract

There are a total of 64 possible multiplication rules that can be defined starting with the generalized imaginary units first introduced by Hamilton. Of these sixty-four choices, only eight lead to non-commutative division algebras: two are associated to the left- and right-chirality quaternions, and the other six are generalizations of the split-quaternion concept first introduced by Cockle. We show that the $4\times 4$ matrix representations of both the left- and right-chirality versions of the generalized split-quaternions are algebraically isomorphic and can be related to each other by $4\times 4$ permutation matrices of the $C_2\times C_2$ group. As examples of applications of the generalized quaternion concept, we first show that the left- and right-chirality quaternions can be used to describe Lorentz transformations with a constant velocity in an arbitrary spatial direction. Then, it is shown how each of the generalized split-quaternion algebras can be used to solve the problem of quantum-mechanical tunneling through an arbitrary one-dimensional (1D) conduction band energy profile. This demonstrates that six different spinors ($4\times 4$ matrices) can be used to represent the amplitudes of the left and right propagating waves in a 1D device.

1. Introduction

Hamilton first introduced the concept of a quaternion in 1843 [1]. Over the years, quaternions have been applied in many areas including control theory, signal processing, robotics, number theory, computer vision and graphics, flight dynamics and navigation systems of aircraft, orbital mechanics, bioinformatics, molecular dynamics, robotics, quantum mechanics, and crystallographic structure analysis, among others [2,3,4,5,6].

Girard described the use of the quaternion group in modern physics [7]. Adler has analyzed in great detail how quaternions can be used to outline a new formulation of quantum mechanics and quantum field theory [5]. Recently, Cahay and Morris have shown how a quaternion representation of the Pauli spinor [8,9] can be used to reformulate a quaternionic approach to quantum computing [10] and the Pauli–Schrödinger equation [11,12].

A few years after the pioneering work on quaternions by Hamilton, James Cockle introduced the concept of split-quaternions, also referred to as coquaternions, which are also elements of a four-dimensional associative algebra [13]. Contrary to quaternions, split-quaternions have nontrivial zero divisors, idempotents, and nilpotent elements [14,15,16]. Split-quaternions have found important applications in many fields such as spatial geometry, physics, quantum mechanics, signal processing, and cryptography, among others [17,18,19,20,21,22,23,24,25,26]. Thakur and Tripathi proposed a new multidimensional public key cryptosystem using split-quaternion algebra [27]. Babaarslan and Yayli derived some relations between split-quaternions and space-like contact slope surfaces in Minkowski three-space [28]. Pop and Cretu used a split-quaternion formalism to formulate a transfer matrix approach to 1D longitudinal elastic wave propagation through multilayered media [29].

In Section 2, it is shown that there are a total of 64 possible multiplication rules that can be defined starting with the imaginary units first introduced by Hamilton to define the fundamental concept of quaternion. Of these sixty-four possibilities, only eight lead to non-commutative division algebras, two of which are associated to the left- and right-chirality quaternions, while the other six are generalizations of the split-quaternion concept first introduced by Cockle [13]. For the latter, as shown by Morris [2], their $4\times 4$ real matrix representations form the six four-dimensional representations of the order eight dihedral group. The $4\times 4$ of both the left- and right-chirality versions of the generalized split-quaternions are algebraically isomorphic and can be related to each other by $4\times 4$ permutation matrices of the $C_2\times C_2$ group.

In Section 3, both left- and right-chirality quaternions are used to describe Lorentz transformations or boosts in an arbitrary direction. In Section 4, the split-quaternion formalism is used to reformulate the transmission matrix technique, which is a well-known approach to tackle tunneling problems through an arbitrary conduction band energy profile in quantum mechanics. In this approach, the transmission and reflection probabilities through an arbitrary conduction band energy profile can then be easily derived by multiplying real $4\times 4$ matrices. The approach is illustrated by revisiting the tunneling problems bt using a one-dimensional (1D) delta-scatterer and by examining the resonant tunneling structure composed of two and three delta-scatterers separated by a distance L. The split-quaternion formalism is also related to the transfer matrix approach to solve the tunneling problem [30]. The split-quaternion associated to a barrier with finite width and height is then derived and used to calculate transmission probability by using realistic resonant tunneling structures. It is shown that six different spinors ($4\times 4$ matrices) can be used to represent the amplitudes of the left and right propagating waves in a device and tackle tunneling problems in quantum mechanics.

In Section 5, an interesting connection between the non-commutative split-quaternion division algebras and the uniqueness of our four-dimensional spacetime is pointed out by introducing a super split-quaternion formed of a superposition of either the left- or right-chirality versions of the generalized split-quaternions. It is shown that the norm of this super split-quaternion has a form identical to the distance function of our four-dimensional spacetime. This paves a way to an interpretation of our four-dimensional spacetime and its physical properties based on a superposition principle of fundamental structures of our physical world, which can be represented by division algebras.

Finally, Section 5 contains our conclusions.

2. Generalization of the Quaternion Concept

We first describe for the sake of completeness the well-known $4\times 4$ matrix representations of the quaternion and split-quaternion concepts first introduced by Hamilton [1] and Cockle [13], respectively. We then show that out of the sixty-four possible generalizations of the quaternion concept, only eight can be used to define algebras that satisfy the axioms of proper division algebras.

2.1. Quaternions and Their 4 × 4 Matrix Representations

In the original work of Hamilton [1], quaternions are defined as follows:

$$Q=a+ib+jc+kd,$$

(1)

where a, b, c, and d are real numbers; the quaternion units i, j, k obey the following multiplication rules.

$$i^2=j^2=k^2=-1,$$

(2)

$$ij=k,ji=-k,jk=i,kj=-i,ki=j,ik=-j.$$

(3)

These commutation rules are isomorphic to SU(2). These quaternions are usually referred to as left-chirality quaternions [2,11].

Expressing the quaternions in a row format with the four components a, b, c, and d, i.e., $Q=(a,b,c,d)$, and using the multiplication rules (Equations (2) and (3)), the following quaternion multiplication rule is obtained.

$$\begin{array}{ccc}\hfill Q_1{Q}_2& =& (a_1,b_1,c_1,d_1)(a_2,b_2,c_2,d_2)\hfill \\ & =& (a_1{a}_2-b_1{b}_2-c_1{c}_2-d_1{d}_2,a_1{b}_2+b_1{a}_2+c_1{d}_2-d_1{c}_2,\hfill \\ & & a_1{c}_2-b_1{d}_2+c_1{a}_2+d_1{b}_2,a_1{d}_2+b_1{c}_2-c_1{b}_2+d_1{a}_2).\hfill \end{array}$$

(4)

This last equation shows that quaternion multiplication is non-commutative, as can readily be seen by swapping the indices 1 and 2 on the right-hand side of Equation (4).

The quaternion $Q=(a,b,c,d)$ defined above is referred to as the left-chirality quaternion [2] and is sometimes represented by using a $4\times 4$ matrix [2,11].

$$Q_L<=>\left(\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ -c& d& a& -b\\ -d& -c& b& a\end{array}\right).$$

(5)

The determinant of the $4\times 4$ matrix in Equation (5) is equal to $det\left(Q_L\right)={(a^2+b^2+c^2+d^2)}^2$ and is related to the norm of the quaternion Q, which is equal to $\sqrt{Q_L\overline{Q_L}}=\sqrt{a^2+b^2+c^2+d^2}$, where $\overline{Q_L}=a-bi-cj-dk$ is the conjugate of $Q_L$.

If, on the other hand, we assume that the quaternion units i, j, and k satisfy the following multiplication rules:

$$i^2=j^2=k^2=-1$$

(6)

$$ij=-k,ji=k,jk=-i,kj=i,ki=-j,ik=j,$$

(7)

then the signs of the products of the complex units are opposite to the signs used in Equation (3) to define the left-chirality quaternions, and we obtain the so-called right-chirality quaternions, which were already known to Hamilton [1,2].

The right-chirality quaternion has a $4\times 4$ matrix representation given by the following.

$$Q_R<=>\left(\begin{array}{cccc}a& b& c& d\\ -b& a& \mathbf{d}& -\mathbf{c}\\ -c& -\mathbf{d}& a& \mathbf{b}\\ -d& \mathbf{c}& -\mathbf{b}& a\end{array}\right).$$

(8)

The elements marked as bold in the expression of $Q_R$ have the opposite signs to the same matrix elements in the expression of $Q_L$ in Equation (5).

2.2. Split-Quaternions and Their 4 × 4 Matrix Representation

A split-quaternion is defined as follows:

$$SQ=w+ix+jy+kz,$$

(9)

where w, x, y, and z are real numbers and the split-quaternion units i, j, and k satisfy the following multiplication rules:

$$i^2=-1,j^2=k^2=1,$$

(10)

and the Hamilton multiplication rules for left-chirality quaternions given by Equation (3).

The set (1, i, j, k, −1, −i, −j, −k) forms a group under split-quaternion multiplication, which is isomorphic to dihedral group $D_4$ and is the symmetry group of the square [2]. If we represent the split-quaternions in a row format with the four components w, x, y, and z, i.e., $SQ=(w,x,y,z)$, and take into account the multiplication rules (Equations (3) and (10)) given above; the following rule for multiplying split-quaternions can easily be derived:

$$\begin{array}{ccc}\hfill S{Q}_{1}S{Q}_2& =& (w_1,x_1,y_1,z_1)(w_2,x_2,y_2,z_2)\hfill \\ & =& (w_1{w}_2-x_1{x}_2+y_1{y}_2+z_1{z}_2,w_1{x}_2+w_2{x}_1-y_1{z}_2+y_2{z}_1,\hfill \\ & & w_1{y}_2-x_1{z}_2+y_1{w}_2+z_1{x}_2,w_1{z}_2+x_1{y}_2-y_1{x}_2+z_1{w}_2),\hfill \end{array}$$

(11)

showing that the product of two split-quaternions is non-commutative.

The split-quaternion $SQ=(w,x,y,z)$ can be represented using the following $4\times 4$ real matrix [2].

$$SQ<=>\left(\begin{array}{cccc}w& x& y& z\\ -x& w& -z& y\\ y& -z& w& -x\\ z& y& x& w\end{array}\right).$$

(12)

The determinant of this last $4\times 4$ matrix is equal to the following:

$$det\left(SQ\right)={(w^2+x^2-y^2-z^2)}^2,$$

(13)

and is related to the norm of the split-quaternion $\mathit{SQ}$, which is equal to $\sqrt{SQ\overline{SQ}}=\sqrt{w^2+x^2-y^2-z^2}$, where $\overline{SQ}=w-ix-jy-kz$ is the conjugate of $\mathit{SQ}$.

The multiplication rule of split-quaternions given in Equation (11) can then be easily generated by multiplying $4\times 4$ matrices associated to two split-quaternions $S{Q}_1$ and $S{Q}_2$ using the rule of matrix multiplication.

2.3. The Generalized Quaternion Concept

Hereafter, we address the question whether it is possible to extend the concept of quaternion, as defined by Equation (1), for which the quaternion units would satisfy the only possible multiplication rules listed in

Table 1. Multiplication rules of generalized quaternion units.

Multiplication	Possible Products
$i^2$	$\pm 1$
$j^2$	$\pm 1$
$k^2$	$\pm 1$
$ij$	$\pm k$
$jk$	$\pm i$
$ik$	$\pm j$

.

There are only 64 possible combinations for the products $i^2$, $j^2$, $k^2$, ij, jk, and ki, corresponding to the fact that $i^2$, $j^2$, and $k^2$ can only take the values $\pm 1$ and the products ij, jk, and ki can only be equal to $\pm k$, $\pm i$, and $\pm j$, respectively.

We proceed to find a $4\times 4$ matrix representation of all 64 possible quaternion generalizations using the following procedure. The most general form $\mathbb{G}$ of the product of two generalized quaternions will be of the following form:

$$\mathbb{G}={\mathbb{G}}_1{\mathbb{G}}_2,$$

$$\begin{array}{cc}\hfill \mathbb{G}& =(a_1+b_{1}i+c_{1}j+d_{1}k)(a_2+b_{2}i+c_{2}j+d_{2}k)\hfill \\ \hfill & =a_1{a}_2+a_1{b}_{2}i+a_1{c}_{2}j+a_1{d}_{2}k+b_1{a}_{2}i+b_1{b}_2{i}^2+b_1{c}_{2}ij+b_1{d}_{2}ik\hfill \\ \hfill & +c_1{a}_{2}j+c_1{b}_{2}ji+c_1{c}_2{j}^2+c_1{d}_{2}jk+d_1{a}_{2}k+d_1{b}_{2}ki+d_1{c}_{2}kj+d_1{d}_2{k}^2,\hfill \end{array}$$

(14)

where the different terms can be written explicitly according to which one of the sixty-four possible multiplication rules we select from the table above for imaginary units.

Proceeding with the procedure for the 64 potential generalized quaternions with the multiplication rules listed in Table 1 results in only eight acceptable division algebras that are closed under multiplication. Their multiplication rules and $4\times 4$ matrix representations are provided in

Table 2. List of properties of 8 non-commutative division algebras.

$\mathit{Algebra}$	${\mathit{i}}^2$	${\mathit{j}}^2$	${\mathit{k}}^2$	$\mathit{ij}$	$\mathit{jk}$	$\mathit{ki}$	$\mathit{ji}$	$\mathit{kj}$	$\mathit{ik}$	$\mathit{Equivalent}\mathit{Matrix}$	$\mathit{Determinant}$
$H_{left}$	−1	−1	−1	k	i	j	−k	−i	−j	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ -c& d& a& -b\\ -d& -c& b& a\end{array}\right]$	$\begin{array}{c}{(a^2+b^2+c^2+d^2)}^2\end{array}$
$H_{right}$	−1	−1	−1	−k	−i	−j	k	i	j	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& d& -c\\ -c& -d& a& b\\ -d& c& -b& a\end{array}\right]$
$Q_{++-}^{k,-i,-j}$	1	1	−1	k	−i	−j	−k	i	j	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& d& c\\ c& -d& a& -b\\ -d& c& -b& a\end{array}\right]$	$\begin{array}{c}{(a^2-b^2-c^2+d^2)}^2\end{array}$
$Q_{++-}^{-k,i,j}$	1	1	−1	−k	i	j	k	−i	−j	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& -d& -c\\ c& d& a& b\\ -d& -c& b& a\end{array}\right]$
$Q_{+-+}^{k,i,-j}$	1	−1	1	k	i	−j	−k	−i	j	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& d& c\\ -c& d& a& -b\\ d& -c& -b& a\end{array}\right]$	$\begin{array}{c}{(a^2-b^2+c^2-d^2)}^2\end{array}$
$Q_{+-+}^{-k,-i,j}$	1	−1	1	−k	−i	j	k	i	−j	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& -d& -c\\ -c& -d& a& b\\ d& c& b& a\end{array}\right]$
$Q_{-++}^{-k,i,-j}$	−1	1	1	−k	i	−j	k	−i	j	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& d& -c\\ c& d& a& b\\ d& -c& -b& a\end{array}\right]$	$\begin{array}{c}{(a^2+b^2-c^2-d^2)}^2\end{array}$
$Q_{-++}^{k,-i,j}$	−1	1	1	k	−i	j	−k	i	−j	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ c& -d& a& -b\\ d& c& b& a\end{array}\right]$

. The last column in the table below gives the values of the determinant of the $4\times 4$ matrix associated with each of the generalized quaternions. The latter are equal to the square of the norm associated with each generalized quaternion. These norms are defined as follows: for each of the eight generalized quaternions, its complex conjugate is defined as follows:

$$\overline{Q}=(a,-b,-c,-d),$$

(15)

and norm N of the generalized quaternion is then given by the following.

$$N^2=Q\overline{Q}.$$

(16)

Hence, for Q = a + ib + jc + kd, $\overline{Q}$ = a − ib − jc − kd, we obtain the following.

$$N^2=a^2-i^2{b}^2-j^2{c}^2-k^2{d}^2-ij\left(bc\right)-ji\left(bc\right)-ik\left(bd\right)-ki\left(bd\right)-jk\left(cd\right)-kj\left(cb\right).$$

(17)

Taking into account the fact that, for each of the eight division algebras identified in Table 2, the following anti-commutation rules apply.

$$ij=-ji;ik=-ki;jk=-kj.$$

(18)

Hence, we obtain the following.

$$N^2=a^2-i^2{b}^2-j^2{c}^2-k^2{d}^2.$$

(19)

In Table 2, the two top generalized quaternions have $4\times 4$ matrix representations given by Equation (5) and Equation (8), respectively, and are referred to as left- and right-chirality quaternions, respectively. The characterization of the other six algebras as the generalization of the split-quaternion introduced in Section 2.3 and their left- or right-chirality characters will be discussed in Section 4.5. The values of the determinants of the $4\times 4$ matrices listed in Table 2 are found to be equal to the fourth power of the norm of the generalized quaternions.

To prevent zero-divisors in the division algebras, the norms of the generalized quaternions must be greater than zero. It turns out that only two out of the eight $4\times 4$ matrices always have a norm greater than zero, with both of their determinants being described as follows.

$$det\left(G\right)={(a^2+b^2+c^2+d^2)}^2,\{a,b,c,d\ne 0\}$$

(20)

The associated matrices correspond to the left- and right-chirality quaternions, which are discussed in Section 2.1 and Section 2.2. The other six division algebras in Table 2 have the square of their norms equal to one of the following forms: $a^2-b^2+c^2-d^2$, $a^2-b^2-c^2+d^2$, and $a^2+b^2-c^2-d^2$; they constitute generalizations of the split-quaternion introduced by Cockle [13].

Since the norms associated with these six algebras contain terms with negative signs, these division algebras have zero divisors. As discussed by Morris [2], the exponential forms of their $4\times 4$ matrix representations have a positive determinant and can be, therefore, used as proper division algebras. The $4\times 4$ real matrix representations of those six division algebras consist of the six four-dimensional representations of the order eight dihedral group [2].

Next, we show on a specific example why any of the other 56 possible generalized quaternions cannot be used as elements of a proper division algebra. The proof for all other 55 cases proceed in a similar fashion. Particularly, for those 56 generalized quaternions, their multiplication rules are such that their quaternion units (i, j, k) do not obey the anti-commuting principle, i.e., they do not satisfy the following commutation rules, which are satisfied by the eight algebras listed in Table 2.

$$\begin{array}{c}ij=-ji,jk=-kj,ki=-ik.\end{array}$$

(21)

2.4. Proof That 56 Other Generalized Quaternions Are Not Proper Division Algebras

Hereafter, we consider the product of two generalized quaternions of the following form:

$$\begin{array}{c}\hfill Q_1=a_1+i{b}_1+j{c}_1+k{d}_1,\\ \hfill Q_2=a_2+i{b}_2+j{c}_2+k{d}_2,\end{array}$$

(22)

for which the following multiplication rules are used:

$$i^2=1,j^2=-1,k^2=1,ij=-k,jk=i,ki=j,$$

(23)

from which we derive that result that the following additional relations are satisfied.

$$ji=ij=-k,jk=-kj=i,ki=ik=j.$$

(24)

There is actually an inconsistency in the multiplication rules (23), as evidenced by the fact that they result in the following contradiction: $ji=\left(ki\right)\left(jk\right)=-k^{2}k=k$ and $ji=j^{2}k=k$.

Using a similar simple argument for the other 55 possible quaternion generalizations, it can be shown that the only generalized quaternions for which their algberas are closed under multiplication are listed in Table 2.

The simple argument does not explicitly show the impossibility to find a $4\times 4$ matrix expression for the generalized quaternions satisfying multiplication rules (23), which render them closed under multiplication. The procedure outlined below was actually used to derive the explicit $4\times 4$ matrix representations of the only eight divisions algebras listed in Table 2, which are closed under multiplication.

Using the multiplication rules (23), the product, P = $Q_1{Q}_2$, is found to be as follows.

$$\begin{array}{cc}\hfill P=& (a_1+i{b}_1+j{c}_1+k{d}_1)(a_2+i{b}_2+j{c}_2+k{d}_2)\hfill \\ \hfill =& (a_1{a}_2+b_1{b}_2-c_1{c}_2+d_1{d}_2)+i(c_1{d}_2-d_1{c}_2+b_1{a}_2+a_1{b}_2)\hfill \\ \hfill & j(a_2{c}_1+a_1{c}_2+d_1{b}_2+b_1{d}_2)+k(a_2{d}_1+a_1{d}_2-c_1{b}_2-b_1{c}_2).\hfill \end{array}$$

(25)

According to this last equation, the real and imaginary components of P can be obtained as the first row of the product of the following two $4\times 4$ matrices.

$$\left[\begin{array}{cccc}{a}_1& b_1& c_1& d_1\\ \times & \times & \times & \times \\ \times & \times & \times & \times \\ \times & \times & \times & \times \end{array}\right]\left[\begin{array}{cccc}{a}_2& b_2& c_2& d_2\\ b_2& a_2& d_2& -c_2\\ -c_2& d_2& a_2& -b_2\\ d_2& -c_2& b_2& a_2\end{array}\right]$$

(26)

Indeed, the elements of the top row of the $4\times 4$ matrix resulting from the product above are given by the following:

$$\begin{array}{cc}\hfill P(1,1)=& a_1{a}_2+b_1{b}_2-c_1{c}_2+d_1{d}_2,\hfill \\ \hfill P(1,2)=& a_1{b}_2+b_1{a}_2+c_1{d}_2-d_1{c}_2,\hfill \\ \hfill P(1,3)=& a_1{c}_2+b_1{d}_2+c_1{a}_2+d_1{b}_2,\hfill \\ \hfill P(1,4)=& a_1{d}_2-b_1{c}_2-c_1{b}_2+d_1{a}_2,\hfill \end{array}$$

(27)

where P(1,1) agrees with the real part of the product in Equation (25), and P(1,2), P(1,3), and P(1,4) agree with the three imaginary components found above.

For the type of generalized quaternions to form a proper division algebra, the rest of the matrix elements represented by crosses in Equation (26) should be of the following form:

$$\left[\begin{array}{cccc}{a}_1& b_1& c_1& d_1\\ b_1& a_1& d_1& -c_1\\ -c_1& d_1& a_1& -b_1\\ d_1& -c_1& b_1& a_1\end{array}\right]$$

(28)

of the same canonical form as the $4\times 4$ matrix associated to $Q_2$. Since the product must be closed under multiplication, the $4\times 4$ matrix elements associated with the product of $Q_1$ and $Q_2$ must satisfy the following relations.

$$\begin{array}{cc}\hfill P(1,1)& =P(2,2)=P(3,3)=P(4,4),\hfill \\ \hfill P(2,1)& =P(1,2),\hfill \\ \hfill P(3,1)& =-P(1,3),\hfill \\ \hfill P(4,1)& =P(1,4),\hfill \\ \hfill P(2,3)& =P(3,2)=P(1,4),\hfill \\ \hfill P(2,4)& =-P(1,3)=P(4,2),\hfill \\ \hfill P(3,4)& =-P(1,2)=-P(4,3).\hfill \end{array}$$

(29)

By performing the matrix multiplication of the $4\times 4$ matrices associated with $Q_1$ and $Q_2$:

$$\left[\begin{array}{cccc}{a}_1& b_1& c_1& d_1\\ b_1& a_1& d_1& -c_1\\ -c_1& d_1& a_1& -b_1\\ d_1& -c_1& b_1& a_1\end{array}\right]\left[\begin{array}{cccc}{a}_2& b_2& c_2& d_2\\ b_2& a_2& d_2& -c_2\\ -c_2& d_2& a_2& -b_2\\ d_2& -c_2& b_2& a_2\end{array}\right],$$

(30)

we obtain the following expressions for the diagonal elements associated with product P:

$$\begin{array}{cc}\hfill P(1,1)& =a_1{a}_2+b_1{b}_2-c_1{c}_2+d_1{d}_2,\hfill \\ \hfill P(2,2)& =a_1{a}_2+b_1{b}_2+c_1{c}_2+d_1{d}_2,\hfill \\ \hfill P(3,3)& =a_1{a}_2-b_1{b}_2-c_1{c}_2+d_1{d}_2,\hfill \\ \hfill P(4,4)& =a_1{a}_2-b_1{b}_2+c_1{c}_2+d_1{d}_2.\hfill \end{array}$$

(31)

They are not equal to the following.

$$\begin{array}{cc}\hfill P(1,1)& =a_1{a}_2+b_1{b}_2-c_1{c}_2+d_1{d}_2.\hfill \end{array}$$

(32)

Similarly, we find the following.

$$\begin{array}{cc}\hfill P(2,1)& =a_2{b}_1+a_1{b}_2-c_2{d}_1-c_1{d}_2,\hfill \\ \hfill P(1,2)& =a_1{b}_2+a_2{b}_1+c_1{d}_2-d_1{c}_2,\hfill \\ \hfill P(3,1)& =-a_2{c}_1+b_2{d}_1-a_1{c}_2-b_1{d}_2,\hfill \\ \hfill P(1,3)& =a_1{c}_2+c_1{a}_2{b}_1{d}_2+d_1{b}_2.\hfill \end{array}$$

(33)

Thus, $P(2,1)\ne P(1,2)$ and $P(3,1)\ne -P(1,3)$.

Therefore, the $4\times 4$ matrices of form (28) are not closed under multiplication.

The fact that the generalized quaternions of the form (28) with the multiplication rules (23) and (24) do not form a proper division algebra is related to the fact that the following is the case.

$$ij=ji,ki=ik,jk=-kj,$$

(34)

In other words, the (i, j) and (i, k) complex units commute but the (j, k) units anti-commute.

Using a similar proof for the other 55 possible quaternion generalizations, it can be shown that no $4\times 4$ matrix representations can be found for those generalized quaternions, which would render them closed under multiplication. The only division algebras for which its $4\times 4$ matrix representations are closed under multiplication are those listed in Table 2.

2.5. Isomorphism between the Non-Commutative Division Algebra

In this section, we establish the isomorphism between the split-quaternions listed in Table 2. Introducing the permutation matrix $p_{23}$:

$$\begin{array}{c}{p}_{23}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right],\end{array}$$

(35)

we have the following.

$$\left[\begin{array}{cccc}a& c& b& d\\ c& a& -d& -b\\ -b& -d& a& c\\ d& b& c& a\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ c& -d& a& -b\\ d& c& b& a\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$

(36)

Since $p_{23}$ is equal to its own inverse, Equation (36) is a similarity transformation connecting $Q_{-++}^{k,-i,j}(a,b,c,d)$ and $Q_{+-+}^{-k,-i,j}(a,c,b,d)$ split-quaternions. The latter has the $4\times 4$ matrix representation listed in Table 2, with elements b and c interchanged.

The $Q_{-++}^{k,-i,j}(a,b,c,d)$ split-quaternion can be transformed into all five others using the following similarity transformation:

$$\begin{array}{ccc}{Q}_{+-+}^{-k,-i,j}(a,c,b,d)& =& p_{23}\ast Q_{-++}^{k,-i,j}(a,b,c,d)\ast p_{23},\\ Q_{++-}^{-k,i,j}(a,c,d,b)& =& p_{34}\ast p_{23}\ast Q_{-++}^{k,-i,j}(a,b,c,d)\ast p_{23}\ast p_{34},\\ Q_{++-}^{k,-i,-j}(a,d,c,b)& =& p_{24}\ast Q_{-++}^{k,-i,j}(a,b,c,d)\ast p_{24},\\ Q_{-++}^{-k,i,j}(a,b,d,c)& =& p_{34}\ast Q_{-++}^{k,-i,j}(a,b,c,d)\ast p_{34},\\ Q_{+-+}^{k,i,-j}(a,d,b,c)& =& p_{24}\ast p_{23}\ast Q_{-++}^{k,-i,j}(a,b,c,d)\ast p_{23}\ast p_{24},\end{array}$$

(37)

with the permutation matrices are given by the following.

$$\begin{array}{cc}{p}_{34}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right];& p_{24}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\end{array}\right].\end{array}$$

(38)

A similar isomorphism can be established between the left-chirality and right-chirality quaternions in Table 2. In fact, using the permutation matrices defined above, we have the following.

$$\begin{array}{ccc}{H}_{right}(a,c,b,d)& =& p_{23}\ast H_{left}(a,b,c,d)\ast p_{23},\\ H_{right}(a,d,c,b)& =& p_{24}\ast H_{left}(a,b,c,d)\ast p_{24},\\ H_{right}(a,b,d,c)& =& p_{34}\ast H_{left}(a,b,c,d)\ast p_{34}.\end{array}$$

(39)

Notice that the following is the case.

$$p_{23}\ast p_{23}=p_{24}\ast p_{24}=p_{34}\ast p_{34}=\mathbb{I}.$$

(40)

Notice that all the transformations listed in Equations (37) and (39) are similar transformations since each permutation matrix listed above is equal to its own inverse.

Finally, as shown in Table 2, the determinant of each of $4\times 4$ matrix representation of the eight proper division algebras is equal to the fourth power of its norm of the corresponding generalized split-quaternion. This last property can be used to show that the left- and right-chirality quaternions cannot be mapped by using a unitary transformation to any of the six generalized quaternions listed at the end of Table 2.

Indeed, if such a transformation existed, there would be a $4\times 4$ unitary matrix U such that the following is the case:

$$U^{-1}QU=H_{left}or{H}_{right}$$

(41)

for each of the six Q’s associated with the split-quaternions listed in Table 2. Hence, this would imply the following:

$$det\left(U^{-1}QU\right)=det\left(Q\right)=det\left(H_{left}\right)=det\left(H_{right}\right)$$

(42)

but $det\left(Q\right)$ is equal to the following:

$$\begin{array}{c}\hfill {(a^2+b^2-c^2-d^2)}^2,\\ \hfill {(a^2-b^2+c^2-d^2)}^2,or\\ \hfill {(a^2-b^2-c^2+d^2)}^2,\end{array}$$

(43)

for the six generalized split-quaternions, whereas the following is the case.

$$det\left(H_{left}\right)=det\left(H_{right}\right)={(a^2+b^2+c^2+d^2)}^2.$$

(44)

The unitary transformation U only exists for the trivial case where $b=c=d=0$.

3. Examples of Generalized Quaternion Applications

Recently, Cahay et al. [11] used a quaternion formalism to solve the time dependent Pauli–Schrödinger equation. They showed that both the unitary operator describing the time evolution of the Pauli spinor and the Pauli spinor itself can be written either as left- or right-chirality quaternions [11]. They also show a method for reformulating different quantum gates and the evolution of a qubit on a Bloch sphere using quaternions. Quaternions were also used to derive the Larmor precession of an electron spin in an uniform magnetic field and revisit the issue of measurements in quantum mechanics.

In [12], it was shown that a quaternion algebraic approach can be used to solve the spatially invariant time-dependent Pauli–Schrödinger equation. It was applied to derivation of the Rabi formula and to the calculation of the transmission probabilities by using a one-dimensional delta scatterer and by using a resonant tunneling structure composed of two one-dimensional quaternionic delta-scatterers in series.

Hereafter, we illustrate how both the left- and right-chirality quaternion formalisms can be used to describe Lorentz boosts in special relativity [31]. The Lorentz transformation or boost is a linear transformation from one coordinate frame in spacetime to another moving at a constant velocity relative to the first. The connections between the four dimensional coordinates of two Lorentzian frames where the second (with prime coordinates) moves with constant velocity confined in the x-direction compared to the first are given by the following relations [31]:

$$c{t}^{\prime }=\gamma (ct-\beta x),$$

(45)

$$x^{\prime }=\gamma (x-\beta ct),$$

(46)

$$y=y^{\prime };z=z^{\prime },$$

(47)

where $\beta =v/c$, $\gamma =1/\sqrt{1-{\beta }^2}$, and c is the speed of light in vacuum.

The more general relations between the coordinates in the two frames when the second moves at constant velocity in a direction characterized by unit vector $\overrightarrow{n}$ in the first frame are given by the following [31].

$$c{t}^{\prime }=\gamma ct-\beta \gamma (\widehat{n}·\overrightarrow{r})$$

(48)

$$\overrightarrow{r}{}^{\prime }=\overrightarrow{r}-\beta \gamma ct\widehat{n}+(\gamma -1)(\widehat{n}·\overrightarrow{r})\widehat{n}.$$

(49)

Hereafter, we show that these can be obtained fairly easily by using a quaternion formalism. First, we describe the approach developed by Sweetser to derive the equations describing the Lorentz boost along the x-direction using left-chirality quaternions [32]. The derivation can be readily extended to describe boosts along y and z directions. Next, we show how the use of the multiplication rule for quaternions can be used to generate relations (48) and (49). Finally, we show how the formulation of a general Lorentz boost can also be described using right-chirality quaternions.

3.1. Lorentz Boost along the x, y, or z Directions Using Left-Chirality Quaternions

Recently, Sweetser has been able to formulate a derivation of a Lorentz boost along the x direction using left-chirality quaternions with real components [32]. The derivation is reproduced here for the sake of completeness and then generalized to a boost along the y and z directions; finally, it is generalized to a boost with constant velocity v in an arbitrary direction characterized by unit vector $\widehat{n}$.

Sweetser first performed the following transformation of the left-chirality quaternion $Q_L$, ${L_x}^l{Q}_L\overline{{L_x}^l}$, where $Q_L$ and ${L_x}^l$ are the left-chirality quaternions given by the following:

$$Q_L=(ct,x,y,z),$$

(50)

and the following is the case:

$${L_x}^l=(cosh\alpha ,sinh\alpha ,0,0),$$

(51)

respectively, and parameter $\alpha$ must be determined so that the components of ${Q_L}^{\prime }=(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime })$ in the second Lorentz frame moving with a constant velocity v along the x axis of the initial Lorentz frame agree with Equations (45)–(47).

The explicit $4\times 4$ matrix representation of the quaternion ${L_x}^l$ is given by the following.

$${L_x}^l\left(\begin{array}{cccc}cosh\alpha & sinh\alpha & 0& 0\\ -sinh\alpha & cosh\alpha & 0& 0\\ 0& 0& cosh\alpha & -sinh\alpha \\ 0& 0& sinh\alpha & cosh\alpha \end{array}\right).$$

(52)

Using the multiplication rule for left-chirality quaternions given in Equation (4), we obtain the following.

$$Q_L\overline{{L_x}^l}=(ctcosh\alpha +xsinh\alpha ,-ctsinh\alpha +xcosh\alpha ,ycosh\alpha -zsinh\alpha ,ysinh\alpha +zcosh\alpha ).$$

(53)

Using the multiplication rule (4) one more time and taking into account of the following hyperbolic trigonometric identities:

$${cosh}^2\alpha +{sinh}^2\alpha =cosh2\alpha ,$$

(54)

and the following as well:

$$sinh2\alpha =2cosh\alpha sinh\alpha ,$$

(55)

we obtain the following.

$${L_x}^l{Q}_L\overline{{L_x}^l}=(ctcosh2\alpha ,xcosh2\alpha ,y-2zcosh\alpha sinh\alpha ,z+2ysinh\alpha cosh\alpha ).$$

(56)

If we select $\alpha$, the following is the case:

$$cosh2\alpha =\gamma .$$

(57)

since the relations between $\gamma$ and $\beta$ and the relation between $cosh2\alpha$ and $sinh2\alpha$ are as follows.

$$\gamma =\frac{1}{\sqrt{1-{\beta }^2}}$$

(58)

$${cosh}^{2}2\alpha -{sinh}^{2}2\alpha =1$$

(59)

We can derive a hyperbolic expression for $\gamma \beta$.

$$2cosh\alpha sinh\alpha =sinh2\alpha =\gamma \beta .$$

(60)

Equation (56) can then be rewritten.

$${L_x}^l{Q}_L\overline{{L_x}^l}=(ct\gamma ,x\gamma ,y-\beta \gamma z,z+\gamma \beta y).$$

(61)

In order for this quantity to be equal $(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime })$, where $c{t}^{\prime }$, $x^{\prime }$, $y^{\prime }$, and $z^{\prime }$ are given by Equations (45)–(47), the following left-chirality quaternion must be added to Equation (61).

$$(-\gamma \beta x,-\gamma \beta ct,\gamma \beta z,-\gamma \beta y).$$

(62)

This last quaternion can be generated by first calculating the following quaternion ${L_x}^l{L_x}^l{Q}_L$. We find the following.

$${L_x}^l{L_x}^l=(1,sinh2\alpha ,0,0).$$

(63)

Hence, the following is the case.

$${L_x}^l{L_x}^l{Q}_L=(ct-\gamma \beta x,x+\gamma \beta ct,y-\gamma \beta z,z+\gamma \beta y).$$

(64)

The conjugate of the latter quaternion is equal to the following.

$$\overline{{L_x}^l{L_x}^l{Q}_L}=(ct-\gamma \beta x,-x-\gamma \beta ct,-y+\gamma \beta z,-z-\gamma \beta y).$$

(65)

Substracting $\overline{Q_L}=(ct,-x,-y,-z)$ from the latter, we obtain the following.

$$\overline{{L_x}^l{L_x}^l{Q}_L}-\overline{Q_L}=(-\gamma \beta x,-\gamma \beta ct,\gamma \beta z,-\gamma \beta y).$$

(66)

Adding the latter to Equation (61), we obtain the desired result.

$${Q_L}^{\prime }={\mathcal{L}}_x\left[Q_L\right]=(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime })={L_x}^l{Q}_L\overline{{L_x}^l}+\left(\overline{{L_x}^l{L_x}^l{Q}_L}-\overline{Q_L}\right).$$

(67)

This last expression can be rewritten using the property for the conjugate of the product of two quaternions.

$${Q_L}^{\prime }={\mathcal{L}}_x\left[Q_L\right]={L_x}^l{Q}_L\overline{{L_x}^l}+\overline{Q_L}\left(\overline{{L_x}^l{L_x}^l}-1\right).$$

(68)

Following a similar derivation, it can be shown that a Lorentz boost along the y-axis can be generated by using the following transformation:

$${Q_L}^{\prime }={\mathcal{L}}_y\left[Q_L\right]={L_y}^l{Q}_L\overline{{L_y}^l}+\overline{Q_L}\left(\overline{{L_y}^l{L_y}^l}-1\right).$$

(69)

where the following is the case:

$${L_y}^l=(cosh\alpha ,0,sinh\alpha ,0),$$

(70)

and a Lorentz boost along the z-direction can be generated by using the following transformation:

$${Q_L}^{\prime }={\mathcal{L}}_z\left[Q_L\right]={L_z}^l{Q}_L\overline{{L_z}^l}+\overline{Q_L}\left(\overline{{L_z}^l{L_z}^l}-1\right).$$

(71)

where

$${L_z}^l=(cosh\alpha ,0,0,sinh\alpha ).$$

(72)

3.2. Lorentz Boost along an Arbitrary Direction $\widehat{n}$ Using Left-Chirality Quaternions

In this section, we show that the results of the previous section can be extended to describe a Lorentz boost with constant velocity v along an arbitrary direction $\widehat{n}$ using the following relation link between the left-chirality quaternions $Q_L=(ct,x,y,z)$ and ${Q_L}^{\prime }=(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime })$ associated with the spatio-temporal coordinates of the two Lorentz frames:

$${Q_L}^{\prime }={\mathcal{L}}_{\widehat{n}}^l\left[Q_L\right]={L_{\widehat{n}}}^l{Q}_L\overline{L_{\widehat{n}}^l}+\overline{Q_L}\left(\overline{{L_{\widehat{n}}}^l{L_{\widehat{n}}}^l}-1\right),$$

(73)

where quaternion $L_{\widehat{n}}^l$ reduces to ${L_x}^l$, ${L_y}^l$, and ${L_z}^l$ for a Lorentz boost along the x-, y-, and z-axis, respectively, as found in the previous section.

To prove that the quaternionic transformation in Equation (73) leads to general Equations (48) and (49), we first rewrite the product of two left-chirality quaternions as follows.

A left-chirality quaternion can be represented as follows:

$$Q_{1,L}=(a_1,b_1,c_1,d_1)=(s,\overrightarrow{v}),$$

(74)

where s = $a_1$ and $\overrightarrow{v}=(b_1,c_1,d_1)$ are the real and vector parts of the quaternion $Q_{1,L}$, respectively.

Taking the product of this quaternion with another quaternion as follows:

$$Q_{2,L}=(a_2,b_2,c_2,d_2)=(t,\overrightarrow{w}),$$

(75)

and using the multiplication rule of quaternion Equation (4), product $Q_{1,L}{Q}_{2,L}$ can be written as follows:

$$(s,\overrightarrow{v})(t,\overrightarrow{w})=(st-\overrightarrow{v}·\overrightarrow{w})+(s\overrightarrow{w}+t\overrightarrow{v}+\overrightarrow{v}\times \overrightarrow{w}),$$

(76)

where $\overrightarrow{v}·\overrightarrow{w}$, and $\overrightarrow{v}\times \overrightarrow{w}$ is the dot and vector product of the two three-dimensional vectors $\overrightarrow{v}$ and $\overrightarrow{w}$, respectively.

Using this last equation, we first calculate product P = $L_{\widehat{n}}^l{Q}_L\overline{L_{\widehat{n}}^l}$:

$$\begin{array}{cc}\hfill P=& (cosh\alpha ,sinh\alpha \widehat{n})\left((ct,\overrightarrow{r})(cosh\alpha ,-sinh\alpha \widehat{n})\right)\hfill \\ \hfill =& (cosh\alpha ,sinh\alpha \widehat{n})(ctcosh\alpha +sinh\alpha \overrightarrow{r}·\widehat{n},-ctsinh\alpha \widehat{n}+cosh\alpha \overrightarrow{r}-sinh\alpha \overrightarrow{r}\times \widehat{n})\hfill \\ \hfill =& (cosh\alpha (ctcosh\alpha +sinh\alpha \overrightarrow{r}·\widehat{n})-(sinh\alpha \widehat{n})·(-ctsinh\alpha \widehat{n}+cosh\alpha \overrightarrow{r}-sinh\alpha \overrightarrow{r}\times \widehat{n}),\hfill \\ \hfill & cosh\alpha (-ctsinh\alpha \widehat{n}+cosh\alpha \overrightarrow{r}-sinh\alpha \overrightarrow{r}\times \widehat{n})+sinh\alpha \widehat{n}(ctcosh\alpha +sinh\alpha \overrightarrow{r}·\widehat{n})\hfill \\ \hfill & +(sinh\alpha \widehat{n})\times (-ctsinh\alpha \widehat{n}+cosh\alpha \overrightarrow{r}-sinh\alpha \overrightarrow{r}\times \widehat{n})),\hfill \end{array}$$

(77)

where $\overrightarrow{r}=(x,y,z)$.

This last expression can be simplified using the following identities.

$$\begin{array}{cc}\hfill \widehat{n}\times \widehat{n}& =0,\hfill \\ \hfill \widehat{n}·\overrightarrow{r}\times \widehat{n}& =0,\hfill \\ \hfill \widehat{n}·\widehat{n}& =1,\hfill \\ \hfill \widehat{n}\times \overrightarrow{r}\times \widehat{n}& =(\widehat{n}·\widehat{n})\overrightarrow{r}-(\widehat{n}·\overrightarrow{r})\widehat{n}.\hfill \end{array}$$

(78)

Then, using hyperbolic function identities, Equation (77) becomes the following.

$$\begin{array}{cc}\hfill P=& ct({cosh}^2\alpha +{sinh}^2\alpha ),{cosh}^2\alpha \overrightarrow{r}+2sinh\alpha cosh\alpha (\widehat{n}\times \overrightarrow{r})\hfill \\ \hfill & +{sinh}^2\alpha \widehat{n}(\overrightarrow{r}·\widehat{n})-{sinh}^2\alpha ((\widehat{n}·\widehat{n})\overrightarrow{r}-(\widehat{n}·\overrightarrow{r})\widehat{n})\hfill \\ \hfill =& (ctcosh2\alpha ,{cosh}^2\alpha \overrightarrow{r}+sinh2\alpha (\widehat{n}\times \overrightarrow{r})+2{sinh}^2\alpha (\widehat{n}·\overrightarrow{r})\widehat{n}-{sinh}^2\alpha \overrightarrow{r}).\hfill \end{array}$$

(79)

On the other hand, we have the following.

$$\overline{Q_L}({L_{\widehat{n}}}^l{L_{\widehat{n}}}^l-1)=(-sinh2\alpha (\widehat{n}·\overrightarrow{r}),-ctsinh2\alpha \widehat{n}+sinh2\alpha (\overrightarrow{r}\times \widehat{n}))$$

(80)

Combining Equations (79) and (80), we obtain the following.

$$\begin{array}{cc}\hfill {Q_L}^{\prime }={\mathcal{L}}_{\widehat{n}}^l\left[Q_L\right]=& (ctcosh2\alpha -sinh2\alpha (\widehat{n}·\overrightarrow{r}),{cosh}^2\alpha \overrightarrow{r}+sinh2\alpha (\widehat{n}\times \overrightarrow{r})\hfill \\ \hfill & +2{sinh}^2\alpha (\widehat{n}·\overrightarrow{r})\widehat{n}-{sinh}^2\alpha \overrightarrow{r}-ctsinh2\alpha \widehat{n}+sinh2\alpha (\overrightarrow{r}\times \widehat{n}))\hfill \\ \hfill =& (ctcosh2\alpha -sinh2\alpha (\widehat{n}·\overrightarrow{r}),\overrightarrow{r}-ctsinh2\alpha \widehat{n}+2{sinh}^2\alpha (\widehat{n}·\overrightarrow{r})\widehat{n}).\hfill \end{array}$$

(81)

Taking into account the following relations:

$$\begin{array}{cc}\hfill cosh2\alpha & =\gamma ,\hfill \\ \hfill sinh2\alpha & =\beta \gamma ,\hfill \\ \hfill 2{sinh}^2\alpha & =({sinh}^2\alpha +{cosh}^2\alpha )-({cosh}^2\alpha -{sinh}^2\alpha )\hfill \\ \hfill & =cosh2\alpha -1=\gamma -1,\hfill \end{array}$$

(82)

we arrive at the desired quaternionic expression for the Lorentz boost with velocity v in an arbitrary direction $\overrightarrow{n}$.

$$\begin{array}{c}\hfill {Q_L}^{\prime }={\mathcal{L}}_{\widehat{n}}^l\left[Q_L\right]=(\gamma ct-\beta \gamma (\widehat{n}·\overrightarrow{r}),\overrightarrow{r}-\beta \gamma ct\widehat{n}+(\gamma -1)(\widehat{n}·\overrightarrow{r})\widehat{n}).\end{array}$$

(83)

Equating the real and vectorial parts of the quaternions on both sides of this last equation results in the following:

$$\begin{array}{cc}\hfill c{t}^{\prime }=& \gamma ct-\beta \gamma (\widehat{n}·\overrightarrow{r}),\hfill \\ \hfill \overrightarrow{r}{}^{\prime }=& \overrightarrow{r}-\beta \gamma ct\widehat{n}+(\gamma -1)(\widehat{n}·\overrightarrow{r})\widehat{n},\hfill \end{array}$$

(84)

which are the well-known relations connecting two Lorentz frames where the second one moves with a constant velocity in direction $\widehat{n}$ in the first frame [31].

3.3. Three Lorentz Boosts along an Arbitrary Direction $\widehat{n}$ Using Right-Chirality Quaternions

A Lorentz boost in an arbitrary direction $\widehat{n}$ can also be described in terms of right-chirality quaternions. The multiplication rule (11) for right-chirality quaternions is first rewritten as follows:

$$Q_{1,R}{Q}_{2,R}=(s,\overrightarrow{v})(t,\overrightarrow{w})=(st-\overrightarrow{v}·\overrightarrow{w})+(s\overrightarrow{w}+t\overrightarrow{v}-\overrightarrow{v}\times \overrightarrow{w}),$$

(85)

which differs from Equation (76) by the sign in front of the vector product, $\overrightarrow{v}\times \overrightarrow{w}$.

A proof similar to the one provided in Section 3.2 can be used to show that the general formula describing the connection between two Lorentz frame for which its 4-dimensional variables are given by the right-chirality quaternions $Q_R=(ct,x,y,z)$ and ${Q_R}^{\prime }=(c{t}^{\prime },x^{\prime },y^{\prime },z^{\prime })$ is provided by the following:

$$Q_R^{\prime }={\mathcal{L}}_{\widehat{n}}^l\left[Q_L\right]=\overline{L_{\widehat{n}}^r}{Q}_R{L}_{\widehat{n}}^r+\left(\overline{L_{\widehat{n}}^r{L}_{\widehat{n}}^r}-1\right)\overline{Q_R},$$

(86)

where the $4\times 4$ expression of the right-chirality quaternion $Q_R$ is given by the following:

$$Q_R<=>\left(\begin{array}{cccc}ct& x& y& z\\ -x& ct& z& -y\\ -y& -z& ct& x\\ -z& y& -x& ct\end{array}\right),$$

(87)

and where the $4\times 4$ representation of the quaternion $L_{\widehat{n}}^r$ is given by the following.

$$L_{\widehat{n}}^r=\left(\begin{array}{cccc}cosh\alpha & sinh\alpha n_x& sinh\alpha n_y& sinh\alpha n_z\\ -sinh\alpha n_x& cosh\alpha & sinh\alpha n_z& -sinh\alpha n_y\\ -sinh\alpha n_y& -sinh\alpha n_z& cosh\alpha & sinh\alpha n_x\\ -sinh\alpha n_z& sinh\alpha n_y& -sinh\alpha n_x& cosh\alpha \end{array}\right).$$

(88)

3.4. Lorentz Invariant

In this section, starting with Equation (83), we show that the real part of ${Q_L}^2$ is a Lorentz invariant, i.e., it is identical in two frames related by a Lorentz boost.

We first rewrite ${Q_L}^{\prime }=(s^{\prime },\overrightarrow{v^{\prime }})$ where the real part is given by the following:

$$s^{\prime }=ct-\beta \gamma (\widehat{n}·\overrightarrow{r}),$$

(89)

and the vectorial part is given by the following.

$$\overrightarrow{r^{\prime }}=\overrightarrow{r}-ctsinh2\alpha \widehat{n}+2{sinh}^2\alpha (\widehat{n}·\overrightarrow{r})\widehat{n}.$$

(90)

Now, using Equation (76), the real part of ${Q_L}^{\prime }{Q_L}^{\prime }$ is given by the following.

$$real\left({Q_L}^{\prime }{Q_L}^{\prime }\right)={s^{\prime }}^2-\overrightarrow{v^{\prime }}·\overrightarrow{v^{\prime }}.$$

(91)

It can easily be shown that the following is the case.

$${s^{\prime }}^2=c^2{t}^2{cosh}^{2}2\alpha +{sinh}^{2}2\alpha +{(\widehat{n}·\overrightarrow{r})}^2-2ct{cosh}^2\alpha sinh2\alpha (\widehat{n}·\overrightarrow{r}).$$

(92)

Moreover, we have the following.

$$\overrightarrow{v^{\prime }}·\overrightarrow{v^{\prime }}=r^2-2ct(sinh2\alpha +2sinh2\alpha {sinh}^2\alpha )(\widehat{n}·\overrightarrow{r})+4({sinh}^2\alpha +{sinh}^4\alpha ){(\widehat{n}·\overrightarrow{r})}^2.$$

(93)

Using the last two equations and some hyperbolic trigonometric identities, it is then easy to show that the following is the case.

$$real\left({Q_L}^{\prime }{Q_L}^{\prime }\right)={s^{\prime }}^2-\overrightarrow{v^{\prime }}·\overrightarrow{v^{\prime }}=c^2{t}^2-r^2=real\left(Q_L{Q}_L\right),$$

(94)

In other words, it is indeed invariant.

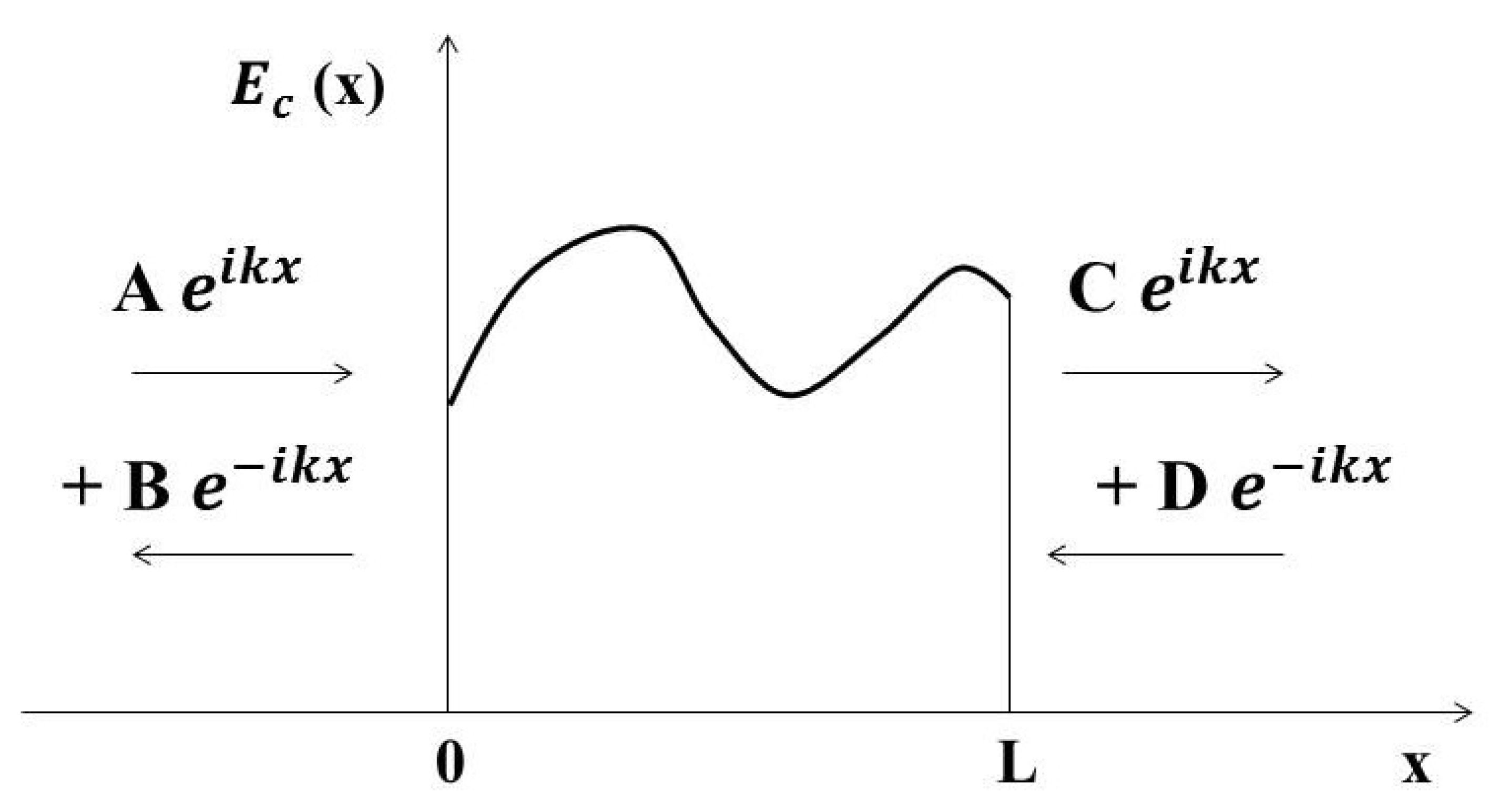
4. A Generalized Split-Quaternion Approach to Tunneling Problems

The transmission matrix technique is a well-known approach for tackling tunneling problems by using an arbitrary conduction band energy profile in quantum mechanics. Hereafter, the transmission matrix approach is reformulated using split-quaternion formalism. The transmission and reflection probabilities through an arbitrary 1D conduction band energy profile can then be easily derived by multiplying real $4\times 4$ matrices. The approach is illustrated by revisiting the tunneling problems by using a 1D delta-scatterer and by using a resonant tunneling structure composed of two and three delta-scatterers separated by distance L. We show that the tunneling problems can be treated using any of the six split-quaternions introduced in Section 2.3 and Table 2.

4.1. Split Quaternion Formulation of Transmission Matrix

Consider a device with an arbitrary 1D conduction band energy profile sandwiched between two contacts, as shown in Figure 1. Hereafter, we assume that the two contacts are identical and that there is no bias across the device (the analysis described hereafter can easily be extended to the case of a finite bias). Assuming a constant effective mass $m^{\ast }$ throughout, the general solution of the 1D Schrödinger equation in the left contact is given as the superposition of left and right propagating plane waves:

$${\varphi }_I\left(x\right)=A{e}^{ikx}+B{e}^{-ikx},$$

(95)

where $k=\frac{1}{\hslash }\sqrt{2m^{\ast }E}$, and E is the kinetic energy of the electron in the contact ($E_c$ is assumed to be zero in both contacts).

Similarly, in the right contact, we have the following.

$${\varphi }_{II}\left(x\right)=C{e}^{ikx}+D{e}^{-ikx}.$$

(96)

By definition, the transmission matrix T associated with the device between the two contacts is the $2\times 2$ complex matrix such that the following is the case.

$$\left[\begin{array}{c}C\\ D\end{array}\right]=T\left[\begin{array}{c}A\\ B\end{array}\right].$$

(97)

Starting with the fundamental properties of the 1D Schrödinger equation, i.e., current density conservation and time reversal symmetry, it can be shown that the matrix T is of the general form:

$$T=\left(\begin{array}{cc}m& n\\ n^{\ast }& m^{\ast }\end{array}\right),$$

(98)

where m and n are complex functions of energy and $det\left(T\right)={\left|m\right|}^2-{\left|n\right|}^2=1$.

The matrix elements m and n are related to the transmission and reflection amplitudes of an electron incident from the contacts. Considering an electron incident from the left with $A=1$ and $B=r$, the reflection amplitude, and $D=0$ and $C=t$, which are the transmission amplitudes, using Equations (95) and (96), we obtain the following.

$$\left[\begin{array}{c}t\\ 0\end{array}\right]=\left(\begin{array}{cc}m& n\\ n^{\ast }& m^{\ast }\end{array}\right)\left[\begin{array}{c}1\\ r\end{array}\right].$$

(99)

It can be easily shown that the following is the case:

$$t=1/m^{\ast },r=-n^{\ast }/m^{\ast },$$

(100)

and the following is the case:

$${\left|t\right|}^2+{\left|r\right|}^2=1,$$

(101)

where ${\left|t\right|}^2$ and ${\left|r\right|}^2$ are the transmission and reflection probabilities of the device, respectively. Equation (101) expresses the conservation of the current density in the scattering problem.

Starting with Equation (97), we obtain the following.

$$\Re C=\Re m\Re A-\Im m\Im A+\Re n\Re B-\Im n\Im B,$$

(102)

$$\Im C=\Re m\Im A+\Im m\Re A+\Re n\Im B+\Im n\Re B,$$

(103)

$$\Re D=\Re n\Re A+\Im n\Im A+\Re m\Re B+\Im m\Im B,$$

(104)

$$\Im D=\Re n\Im A-\Im n\Re A+\Re m\Im B-\Im m\Re B.$$

(105)

Replacing the complex elements of the transmission matrix (Equation (98)) by their $2\times 2$ matrix representations [11], we obtain the following $4\times 4$ real matrix representation of the transmission matrix.

$$T=\left(\begin{array}{cc}m& n\\ n^{\ast }& m^{\ast }\end{array}\right)<=>\left[\begin{array}{cccc}\Re m& \Im m& \Re n& \Im n\\ -\Im n& \Re m& -\Im n& \Re n\\ \Re n& -\Im n& \Re m& -\Im m\\ \Im n& \Re n& \Im m& \Re m\end{array}\right].$$

(106)

The latter is of the generic form of the $4\times 4$ matrix representation of a split-quaternion given by Equation (12) if we select w = Rem, x = Imm, y = Ren, and z = Imn.

If we replace the column vector associated with the amplitudes of the incident and reflected amplitudes in the left contact by the following split-quaternion:

$$\left[\begin{array}{c}A\\ B\end{array}\right]<=>\left[\begin{array}{cccc}\Re A& \Im A& \Re B& -\Im B\\ -\Im A& \Re A& \Im B& \Re B\\ \Re B& \Im B& \Re A& -\Im A\\ -\Im B& \Re B& \Im A& \Re A\end{array}\right],$$

(107)

and multiply it on the left by the split-quaternion (106) associated with the transmission matrix; we obtain a split-quaternion P for which its $4\times 4$ matrix has the following elements in its top row.

$$P(1,1)=\Re m\Re A-\Im m\Im A+\Re n\Re B-\Im n\Im B,$$

(108)

$$P(1,2)=\Re m\Im A+\Im m\Re A+\Re n\Im B+\Im n\Re B,$$

(109)

$$P(1,3)=\Re n\Re A+\Im n\Im A+\Re m\Re B+\Im m\Im B,$$

(110)

$$P(1,4)=-\Re n\Im A+\Im n\Re A-\Re m\Im B+\Im m\Re B.$$

(111)

Comparing these results with Equations (102)–(105), we obtain the following:

$$P(1,1)=\Re C,P(1,2)=\Im C,P(1,3)=\Re D,Im(1,4)=-\Im D,$$

(112)

which is the split-quaternion associated with the outgoing and incoming wave amplitudes in the right contact.

$$\left[\begin{array}{c}C\\ D\end{array}\right]<=>\left[\begin{array}{cccc}\Re C& \Im C& \Re D& -\Im D\\ -\Im C& \Re C& \Im D& \Re D\\ \Re D& \Im D& \Re C& -\Im C\\ -\Im D& \Re D& \Im C& \Re C\end{array}\right].$$

(113)

The rules outlined above establish a one-to-one correspondence between the $2\times 2$ complex transmission formalism and the $4\times 4$ real split-quaternion approach to the general tunneling problem in 1D.

If a general conduction band energy profile is divided into subsections, the overall split-quaternion associated with the scattering problem describing the tunneling of an electron incident from the left contact can be obtained by multiplying, from right to left, the individual split-quaternions associated with the subsections of the device moving from the left to right through the device. The overall split-quaternion associated with the device will then be of a general form in Equation (106) from which the transmission probability can be obtained as the sum of square magnitudes of the first two components in the top row of the overall split-quaternion.

Starting with Equation (106) in its quaternion form and using Equation (99) results in the following:

$${\left|t\right|}^4={\left(\right|m|}^2-{\left|n\right|}^2{)}^2{(1-|r|}^2{)}^2={(1-|r|}^2{)}^2,$$

(114)

which results in relation ${\left|t\right|}^2+{\left|r\right|}^2=1$, i.e., the conservation of the probability current density. Equation (114) also has solution ${\left|r\right|}^2-{\left|t\right|}^2=1$, which is not physical.

Next, we illustrate the split-quaternion formalism by revisiting several tunneling problems, including transmission through a one-dimensional delta-scatterer and resonant tunneling structures composed of two and three delta-scatterers separated by free propagating regions of length L.

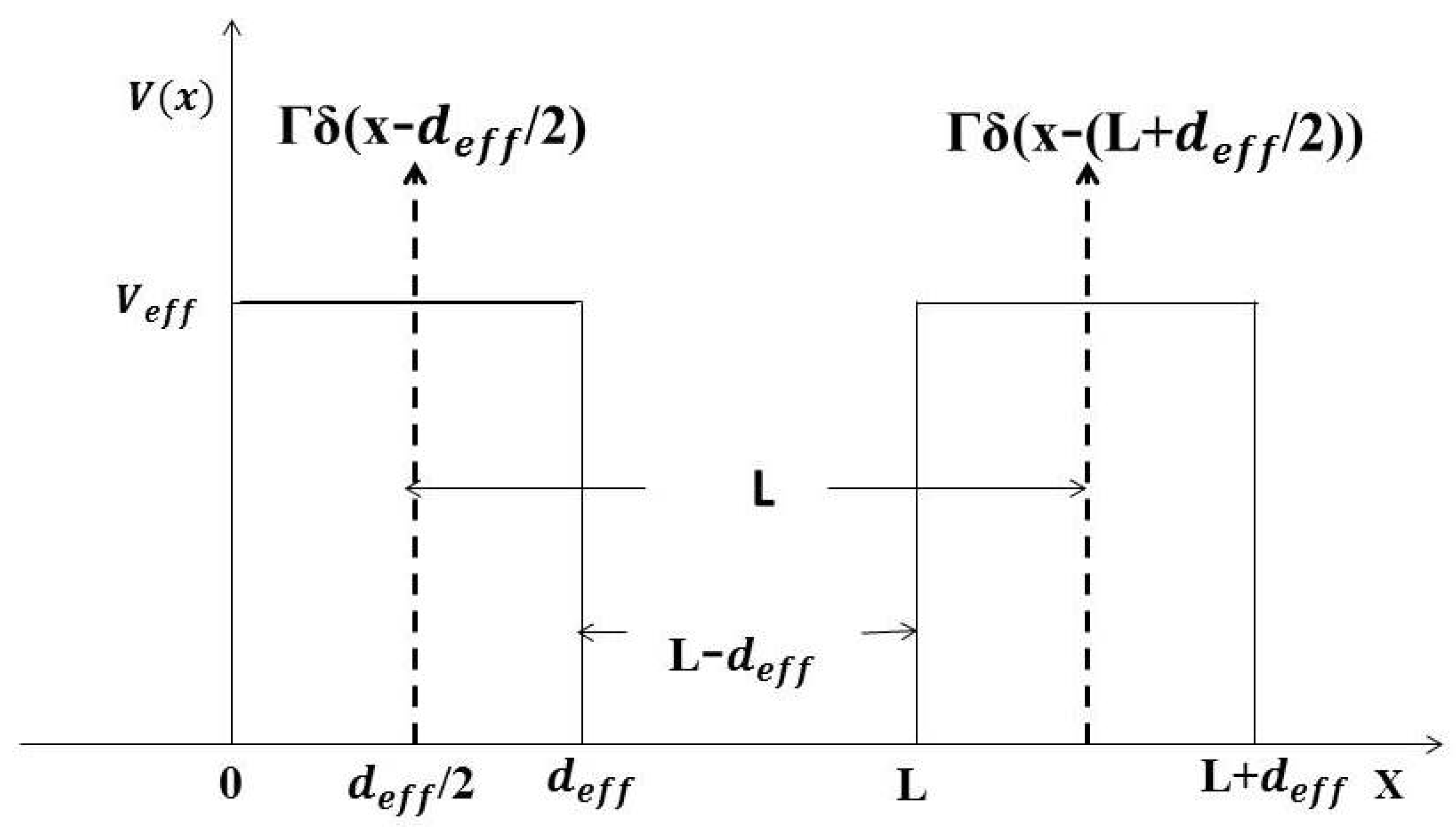
4.2. Split-Quaternion Associated to a 1D Delta Scatterer

The 1D Schrödinger equation for an electron with effective mass $m^{\ast }$ in the presence of a 1D delta-scatterer is given by the following:

$$-\frac{{\hslash }^2}{2m^{\ast }}\frac{d^2\psi }{d{x}^2}+V\left(x\right)\psi \left(x\right)=E\psi \left(x\right)$$

(115)

with potential energy profile $V\left(x\right)=\Gamma \delta \left(x\right)$ and $\Gamma$ being the strength of the delta-scatterer.

To calculate the transmission matrix associated with the delta-scatterer, we seek solutions to the 1D Schrödinger equation to the left and right of the scatterer of the following form.

$$\begin{array}{c}\hfill {\psi }_L=A{e}^{ikx}+B{e}^{-ikx}(x<0)\\ \hfill {\psi }_R=C{e}^{ikx}+D{e}^{-ikx}(x>0)\end{array}.$$

(116)

Imposing continuity of the wavefunction at x = 0 results in the following.

$$C+D=A+B.$$

(117)

Integrating Equation (115) on both sides from $-ϵ$ to $+ϵ$ and letting $ϵ$ tends to zero results in the following.

$$\frac{d\psi }{dx}(x=0_{+})-\frac{d\psi }{dx}(x=0_{-})=\frac{2m^{\ast }}{{\hslash }^2}\psi \left(0\right).$$

(118)

Making use of Equation (116), this last equation results in another relation between coefficients A, B, C, and D.

$$C-D=A-B-\frac{2i{m}^{\ast }\Gamma }{{\hslash }^2}(A+B).$$

(119)

Equations (117) and (119) can be rewritten as follows.

$$\left[\begin{array}{c}C\\ D\end{array}\right]=\left[\begin{array}{cc}1-i\frac{m^{\ast }\Gamma }{k{\hslash }^2}& -i\frac{m^{\ast }\Gamma }{k{\hslash }^2}\\ i\frac{m^{\ast }\Gamma }{k{\hslash }^2}& 1+i\frac{m^{\ast }\Gamma }{k{\hslash }^2}\end{array}\right]\left[\begin{array}{c}A\\ B\end{array}\right].$$

(120)

Hence, the transmission matrix T through a one-dimensional delta scatterer is of the generic form (98) with the following being the case:

$$m=1-i\frac{m^{\ast }\Gamma }{k{\hslash }^2},$$

(121)

and the following.

$$n=-i\frac{m^{\ast }\Gamma }{k{\hslash }^2}.$$

(122)

Using the expressions for m and n, we easily check the following.

$$det\left(T\right)={\left|m\right|}^2-{\left|n\right|}^2=(1+{\left[\frac{m^{\ast }\Gamma }{k{\hslash }^2}\right]}^2)-{\left[\frac{m^{\ast }\Gamma }{k{\hslash }^2}\right]}^2=1.$$

(123)

Using Equations (106) and (120), the $4\times 4$ matrix associated with the split-quaternion of a delta-scatterer is given by the following.

$$T_{\delta }=\left[\begin{array}{cccc}1& -\frac{m\Gamma }{k{\hslash }^2}& 0& -\frac{m\Gamma }{k{\hslash }^2}\\ \frac{m\Gamma }{k{\hslash }^2}& 1& \frac{m\Gamma }{k{\hslash }^2}& 0\\ 0& \frac{m\Gamma }{k{\hslash }^2}& 1& \frac{m\Gamma }{k{\hslash }^2}\\ -\frac{m\Gamma }{k{\hslash }^2}& 0& -\frac{m\Gamma }{k{\hslash }^2}& 1\end{array}\right].$$

(124)

In order to calculate the transmission probability through an array of identical delta-scatterers with the same separation L between them, we determine next the split-quaternion associated to a free propagation region. The overall split-quaternion associated with the array of delta-scatterers is then obtained by cascading (i.e., multiplying), from right to left, the $4\times 4$ split-quaternion matrices associated with the individual scatterers and free propagation regions between them.

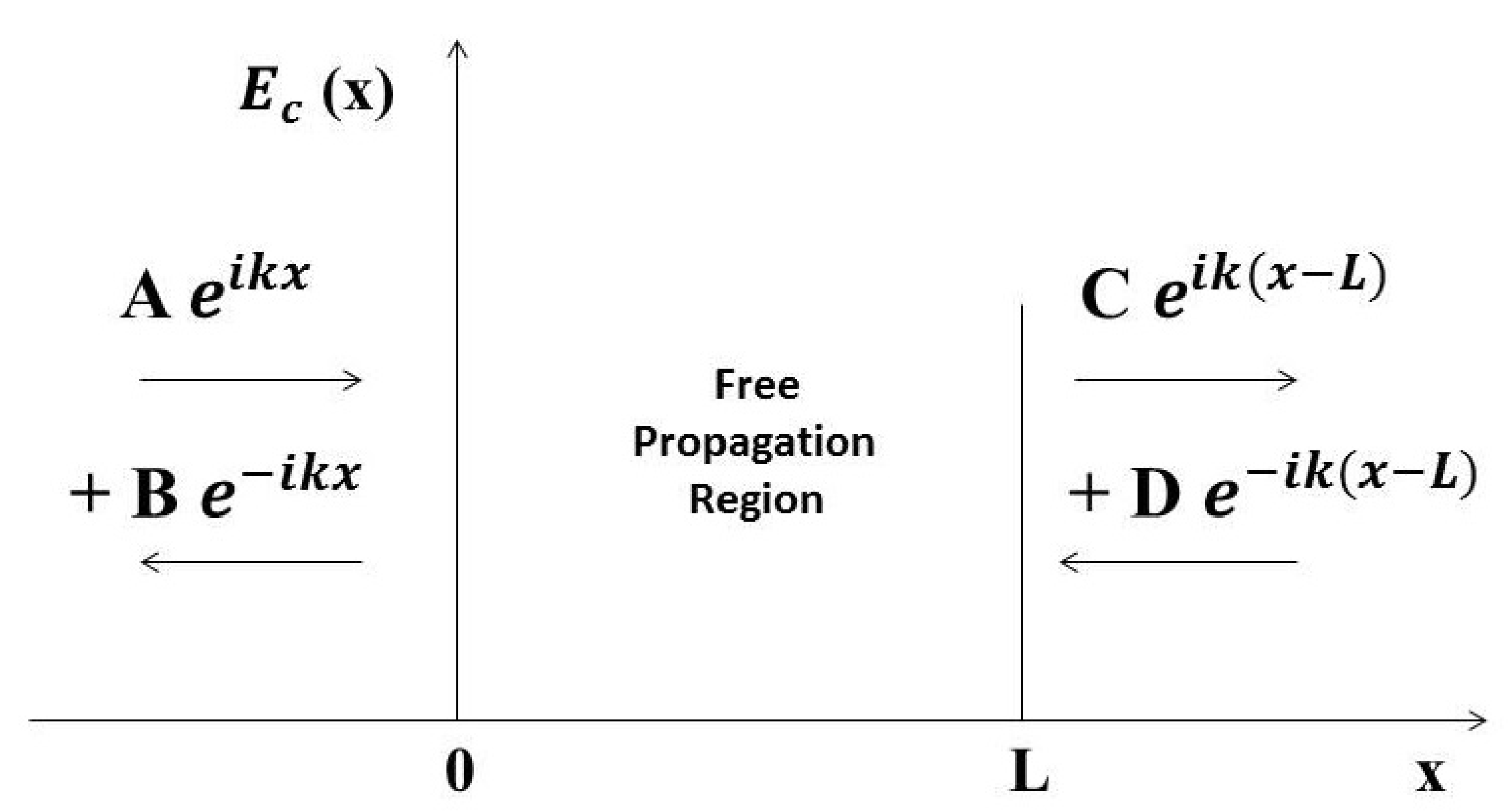
4.3. Split-Quaternion Associated to a Free Propagation Region of Length L

Consider a free propagation region of length L (see Figure 2) between two contacts and assume that the conduction band energy profile is constant and the same throughout. The following relations are found between the wave amplitudes of the left- and right-propagating waves in the two contacts.

$$C=A{e}^{ikL},$$

(125)

$$D=B{e}^{-ikL}.$$

(126)

This leads to the following expression for the transmission matrix associated with a free propagation of length L:

$$T_{prop}=\left(\begin{array}{cc}{e}^{ikL}& 0\\ 0& e^{-ikL}\end{array}\right),$$

(127)

which is of generic form (98) with $m=e^{ikL}$ and $n=0$. Using Equation (106), the split-quaternion associated with a free propagation region of length L is, therefore, given by the following.

$$T_{prop}<=>\left[\begin{array}{cccc}coskL& sinkL& 0& 0\\ -sinkL& coskL& 0& 0\\ 0& 0& coskL& -sinkL\\ 0& 0& sinkL& coskL\end{array}\right].$$

(128)

4.4. Split-Quaternion Associated to a Finite Square Barrier

To derive the split-quaternion associated with a square barrier, we need to establish the connection between the transmission matrix and the transfer matrix, which is another well-known technique for solving tunneling problems in quantum mechanics [30].

For a region of length d sandwiched between two contacts, the transfer matrix is defined as the matrix which relates solution $\varphi$ of the 1D Schrödinger equation and its derivatives on both sides of the device as follows.

$$\left[\begin{array}{c}\dot{\varphi }\left(d\right)\\ \varphi \left(d\right)\end{array}\right]=\left[\begin{array}{cc}{W}_{11}& W_{12}\\ W_{21}& W_{22}\end{array}\right]\left[\begin{array}{c}\dot{\varphi }\left(0\right)\\ \varphi \left(0\right)\end{array}\right].$$

(129)

If ${\varphi }_1\left(x\right)$ and ${\varphi }_2\left(x\right)$ are two linearly independent solutions of the Schrödinger equation satisfying the boundary conditions at the left contact, then the following is the case.

$$\left[\begin{array}{cc}{\dot{\varphi }}_1\left(0\right)& {\dot{\varphi }}_2\left(0\right)\\ {\varphi }_1\left(0\right)& {\varphi }_2\left(0\right)\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$$

(130)

The transfer matrix can be written as follows [30].

$$W=\left[\begin{array}{cc}{\dot{\varphi }}_1\left(d\right)& {\dot{\varphi }}_2\left(d\right)\\ {\varphi }_1\left(d\right)& {\varphi }_2\left(d\right)\end{array}\right].$$

(131)

For a square barrier with height $V_0$ and width d, the explicit form of the linearly independent solutions ${\varphi }_1\left(x\right)$ and ${\varphi }_2\left(x\right)$ are well-known, leading to the following transfer matrix [30]:

$$W=\left[\begin{array}{cc}cos\left(k^{\prime }d\right)& -k^{\prime }sin\left(k^{\prime }d\right)\\ \frac{1}{k^{\prime }}sin\left(k^{\prime }d\right)& cos\left(k^{\prime }d\right)\end{array}\right],$$

(132)

when $E>V_0$. In Equation (132), the following is the case.

$$k^{\prime }=\frac{1}{\hslash }\sqrt{2m^{\ast }(E-V_0)}.$$

(133)

When $V_0>E$, the transfer matrix is given by the following [30]:

$$W=\left[\begin{array}{cc}cosh\left(\kappa d\right)& \kappa sinh\left(\kappa d\right)\\ \frac{1}{\kappa }sinh\left(\kappa d\right)& cosh\left(\kappa d\right)\end{array}\right],$$

(134)

with the following being the case.

$$\kappa =\frac{1}{\hslash }\sqrt{2m^{\ast }(V_0-E)}.$$

(135)

For the 1D scattering problem, the solution to the Schrödinger equation can be written as follows.

$$\left\{\begin{array}{c}{\varphi }_L\left(x\right)=A^{+}{e}^{ikx}+A^{-}{e}^{-ikx}(x<0)\hfill \\ \varphi \left(x\right)=c_1{\varphi }_1\left(x\right)+c_2{\varphi }_2\left(x\right)(0<x<d)\hfill \\ {\varphi }_R\left(x\right)=B^{+}{e}^{ikx}+B^{-}{e}^{-ikx}(x>d).\hfill \end{array}\right.$$

(136)

At x = 0, we obtain the following:

$$c_1{\dot{\varphi }}_1\left(0\right)+c_2{\dot{\varphi }}_2\left(0\right)=ik(A^{+}-A^{-}),$$

(137)

and the following is also obtained.

$$c_1{\varphi }_1\left(0\right)+c_2{\varphi }_2\left(0\right)=A^{+}+A^{-}.$$

(138)

Similarly, at x = d, the following relations must be satisfied:

$$c_1{\dot{\varphi }}_1\left(d\right)+c_2{\dot{\varphi }}_2\left(d\right)=ik(B^{+}-B^{-}),$$

(139)

and the following must be satisfied as well.

$$c_1{\varphi }_1\left(d\right)+c_2{\varphi }_2\left(d\right)=B^{+}+B^{-}.$$

(140)

Starting with Equations (137) and (138), we obtain the following relations between cofficients $(A^{+},A^{-})$ and $(B^{+},B^{-})$.

$$\left[\begin{array}{cc}ik& -ik\\ 1& 1\end{array}\right]\left[\begin{array}{c}{A}^{+}\\ A^{-}\end{array}\right]=W^{-1}\left[\begin{array}{cc}ik& -ik\\ 1& 1\end{array}\right]\left[\begin{array}{c}{B}^{+}\\ B^{-}\end{array}\right].$$

(141)

Using Equation (97), the connection between the transmission and transfer matrix of the device between the two contacts is then given by the following:

$$T_{device}={\left[\begin{array}{cc}ik& -ik\\ 1& 1\end{array}\right]}^{-1}W\left[\begin{array}{cc}ik& -ik\\ 1& 1\end{array}\right]=\frac{1}{2ik}\left[\begin{array}{cc}1& ik\\ -1& ik\end{array}\right]W\left[\begin{array}{cc}ik& -ik\\ 1& 1\end{array}\right],$$

(142)

where k is the wavevector in the contact regions. Carrying out matrix multiplication on the right-hand side of Equation (142) leads to the following.

$$T_{device}=\left[\begin{array}{cc}\frac{1}{2}(W_{11}+W_{22})-\frac{i}{2k}(W_{12}-k^2{W}_{21})& -\frac{1}{2}(W_{11}-W_{22})-\frac{i}{2k}(W_{12}+k^2{W}_{21})\\ -\frac{1}{2}(W_{11}-W_{22})+\frac{i}{2k}(W_{12}+k^2{W}_{21})& \frac{1}{2}(W_{11}+W_{22})+\frac{i}{2k}(W_{12}-k^2{W}_{21})\end{array}\right].$$

(143)

For the particular case of a square barrier, Equations (132) and (134) show that $W_{11}$ = $W_{22}$. Therefore, the transmission matrix has the following simplified form:

$$T_{barrier}=\left[\begin{array}{cc}{W}_{11}-\frac{i}{2k}(W_{12}-k^2{W}_{21})& -\frac{i}{2k}(W_{12}+k^2{W}_{21})\\ +\frac{i}{2k}(W_{12}+k^2{W}_{21})& W_{11}+\frac{i}{2k}(W_{12}-k^2{W}_{21})\end{array}\right],$$

(144)

which, in its $4\times 4$ split-quaternion form, is given by the following.

$$T_{barrier}=\left[\begin{array}{cccc}{W}_{11}& -{\displaystyle \frac{1}{2k}}(W_{12}-k^2{W}_{21})& 0& -{\displaystyle \frac{1}{2k}}(W_{12}+k^2{W}_{21})\\ {\displaystyle \frac{1}{2k}}(W_{12}-k^2{W}_{21})& W_{11}& {\displaystyle \frac{1}{2k}}(W_{12}+k^2{W}_{21})& 0\\ 0& {\displaystyle \frac{1}{2k}}(W_{12}+k^2{W}_{21})& W_{11}& {\displaystyle \frac{1}{2k}}(W_{12}-k^2{W}_{21})\\ -{\displaystyle \frac{1}{2k}}(W_{12}+k^2{W}_{21})& 0& -{\displaystyle \frac{1}{2k}}(W_{12}-k^2{W}_{21})& W_{11}\end{array}\right].$$

(145)

The tunneling probability through an RTD composed of two identical square barriers separated by a free propagation region can then be obtained from the split-quaternion formalism by first calculating the overall split-quaternion associated with this structure:

$$T_{RTD}=T_{barrier}{T}_{prop}{T}_{barrier},$$

(146)

where $T_{prop}$ and $T_{barrier}$ are given by Equations (124) and (145), respectively.

Once the overall $4\times 4$ matrix $T_{RTD}$ is found, the tunneling probability through RTD can then be found from Equation (100).

Hereafter, we illustrate how an RTD consisting of two 1D delta scatterers separated by distance L can be replaced by a realistic resonant tunneling device composed of two square barriers of height $V_{eff}$ and width $d_{eff}$ with a free propagation of length $L-d_{eff}$ between them by increasing the effective barrier height $V_{eff}$ and reducing its width $d_{eff}$ while keeping product $V_{eff}{d}_{eff}$ constant and equal to $\Gamma$, as illustrated in Figure 3.

Figure 4 shows the energy dependence of the tunneling probability through an RTD composed of two delta scatterers of strength $\Gamma =15$ eV separated by distance L = 100. The effective mass was assumed to be $m^{\ast }=0.067m_0$. Moreover, the transmission probabilities through an RTD composed of two square barriers of height $V_{eff}$ and separated by a distance $L-d_{eff}$ for four different $V_{eff}$ are shown as red dashed lines: (a) 0.3, (b) 1, (c) 5, and (d) 10 eV. In each plot, the effective width of the barrier $d_{eff}$ was adjusted to keep the product $V_{eff}{d}_{eff}=\Gamma =15$ eV. Figure 4 clearly shows that the transmission probability through the two delta scatterers can be well approximated by tunneling through two square barriers of increasing height and decreasing width.

This analysis can be extended to the case of multiple barriers. Figure 5 shows a comparison of the transmission probability through an array of three delta scatterers of strength $\Gamma =15$ eV and with a separation of $100$ between adjacent scatterers. The frames (a), (b), (c), and (d) in Figure 5 correspond to a value of $V_{eff}$ equal to 0.3, 1, 5, and 10 eV, respectively.

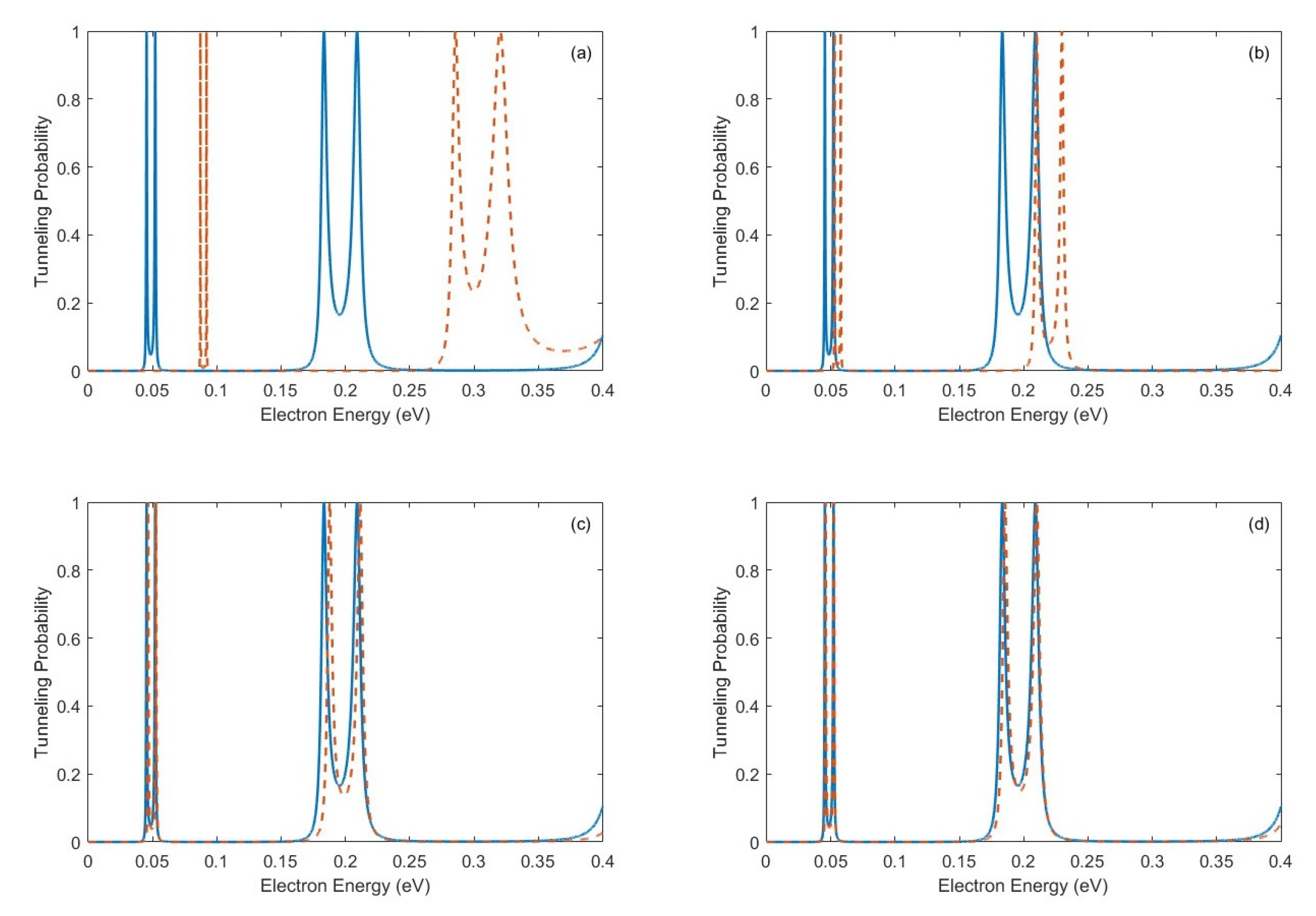
4.5. Solving Tunneling Problems with Alternative Split-Quaternions

In Section 2.3, we found that there are five division algebras that are generalizations of the split-quaternion first introduced by Cockle [13]. In fact, the formulation of tunneling problems can be performed using any of the split-quaternion algebras listed in

Table 3. Chilarity properties of the six split-quaternion algebras.

$\mathit{Algebra}$	$\mathit{Chirality}$	$\mathit{Equivalent}\mathit{Matrix}$	$\mathit{Determinant}$
$Q_{-++}^{k,-i,j}(a,b,c,d)$	Left	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& -d& c\\ c& -d& a& -b\\ d& c& b& a\end{array}\right]$	$\begin{array}{c}{(a^2+b^2-c^2-d^2)}^2\end{array}$
$Q_{-++}^{-k,i,-j}(a,b,c,d)$	Right	$\left[\begin{array}{cccc}a& b& c& d\\ -b& a& d& -c\\ c& d& a& b\\ d& -c& -b& a\end{array}\right]$
$Q_{+-+}^{-k,-i,j}(a,b,c,d)$	Left	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& -d& -c\\ -c& -d& a& b\\ d& c& b& a\end{array}\right]$	$\begin{array}{c}{(a^2-b^2+c^2-d^2)}^2\end{array}$
$Q_{+-+}^{k,i,-j}(a,b,c,d)$	Right	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& d& c\\ -c& d& a& -b\\ d& -c& -b& a\end{array}\right]$
$Q_{++-}^{k,-i,-j}(a,b,c,d)$	Left	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& d& c\\ c& -d& a& -b\\ -d& c& -b& a\end{array}\right]$	$\begin{array}{c}{(a^2-b^2-c^2+d^2)}^2\end{array}$
$Q_{++-}^{-k,i,j}(a,b,c,d)$	Right	$\left[\begin{array}{cccc}a& b& c& d\\ b& a& -d& -c\\ c& d& a& b\\ -d& -c& b& a\end{array}\right]$

since Equation (37) establishes isomorphism between the six generalized split-quaternions algebras listed in Table 2.

Next, we illustrate how to derive the left- and right-chirality nature of the six split-quaternions listed in Table 2.

In Section 4.1, we formulated tunneling problems using split-quaternion $Q_{-++}^{k,-i,j}$$(a,b,c,d)$ for which its $4\times 4$ matrix representation is given at the bottom of Table 2. In that case, the split-quaternion associated with the outgoing wave amplitudes (C,D) in Equation (113) was obtained as a product of the split-quaternion associated with the transmission matrix in Equation (106) and the split-quaternion associated with the incoming wave amplitudes (A,B) in Equation (107). Because the $4\times 4$ matrix associated with the split-quaternion of the transmission matrix is applied to the left of the split-quaternion associated with the incoming wave amplitudes, we refer to the $4\times 4$ matrix at the bottom of Table 2 as the left-chirality split-quaternion. Next, we show that tunneling problems can also be solved using any of the other five split-quaternion algebras listed in Table 2.

Starting with the split-quaternion labelled as $Q_{-++}^{-k,i,-j}(a,b,c,d)$ for which its $4\times 4$ matrix representation is given by the following:

$$Q_{-++}^{-k,i,-j}(a,b,c,d)=\left[\begin{array}{cccc}a& b& c& d\\ -b& a& d& -c\\ c& d& a& b\\ d& -c& -b& a\end{array}\right],$$

(147)

we introduce the following split-quaternion associated with the incoming wave amplitudes (A, B):

$$\left[\begin{array}{c}A\\ B\end{array}\right]<=>\left[\begin{array}{cccc}\Re A& \Im A& \Re B& -\Im B\\ -\Im A& \Re A& -\Im B& -\Re B\\ \Re B& -\Im B& \Re A& \Im A\\ -\Im B& -\Re B& -\Im A& \Re A\end{array}\right],$$

(148)

with components (a, b, c, d) = $(\Re A,\Im A,\Re B,-\Im B)$, and the split-quaternion associated with the transmission matrix.

$$T<=>\left[\begin{array}{cccc}\Re m& \Im m& \Re n& \Im n\\ -\Im m& \Re m& \Im n& -\Re n\\ \Re n& \Im n& \Re m& \Im m\\ \Im n& -\Re n& -\Im m& \Re m\end{array}\right].$$

(149)

Multiplying the split-quaternion in Equation (148) on the right by the split-quaternion in Equation (149), the resulting split-quaternion associated with outgoing amplitudes (C, D) is found to be of the following form:

$$\left[\begin{array}{c}C\\ B\end{array}\right]<=>\left[\begin{array}{cccc}\Re C& \Im C& \Re D& -\Im D\\ -\Im C& \Re C& -\Im D& -\Re D\\ \Re D& -\Im D& \Re C& \Im C\\ -\Im D& -\Re D& -\Im C& \Re C\end{array}\right],$$

(150)

where ReC, ImC, ReD, and ImD have the same expressions as in Equations (102)–(105), respectively.

Because this result was obtained by applying the split-quaternion associated with the transmission matrix T to the right of the split-quaternion matrix associated with the incoming amplitudes (A, B), we refer to the split-quaternion of the form $Q_{-++}^{-k,i,-j}(a,b,c,d)$ as a right-chirality split-quaternion.

Following similar derivations, it can be shown that the four other split-quaternions division algebras listed in Table 2 have chirality properties listed in Table 3.

Similarly to quaternions, split-quaternions are elements of a 4-dimensional associative algebra [13]. They have found important applications in many fields such as spatial geometry, physics, quantum mechanics, signal processing, and cryptography, among others [16,17,18,19,20,21,22,23,24,25].

5. Conclusions and Suggestions for Future Work

This paper outlines a formalism to study various physical phenomena using proper non-commutative division algebras based on a generalization of the concept of quaternions first introduced by Hamilton. It was shown that there are a total of 64 possible multiplication rules, which can be defined starting with the generalized imaginary units first introduced by Hamilton. Of these sixty-four choices, only eight lead to non-commutative division algebras, two of which are associated with the left- and right-chirality quaternions while the other six are generalizations of the split-quaternion concept first introduced by Cockle. For the latter, their $4\times 4$ real matrix representations consist of the six four-dimensional representations of the order eight dihedral group. Next, we showed that the $4\times 4$ of both the left- and right-chirality versions of the generalized split-quaternions are algebraically isomorphic and can be related to each other by $4\times 4$ permutation matrices of the $C_2\times C_2$ group.

It was also shown that the left- and right-chirality quaternions can be used to describe Lorentz boosts with constant velocity in an arbitrary direction. Next, the generalized split-quaternion algebras were used to solve the problem of quantum-mechanical tunneling by using an arbitrary one-dimensional conduction band energy profile. This demonstrates that six different spinors ($4\times 4$ matrices) can be used to represent the amplitudes of the left and right propagating waves in a device.

The generalized quaternion formalism introduced in this paper could be used to reformulate a derivation of the Maxwell equations [33,34,35,36,37,38] and a quaternionic form of the Dirac equations [39,40,41,42,43]. These topics will be the subject of future investigations.