Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer
Abstract
:1. Introduction
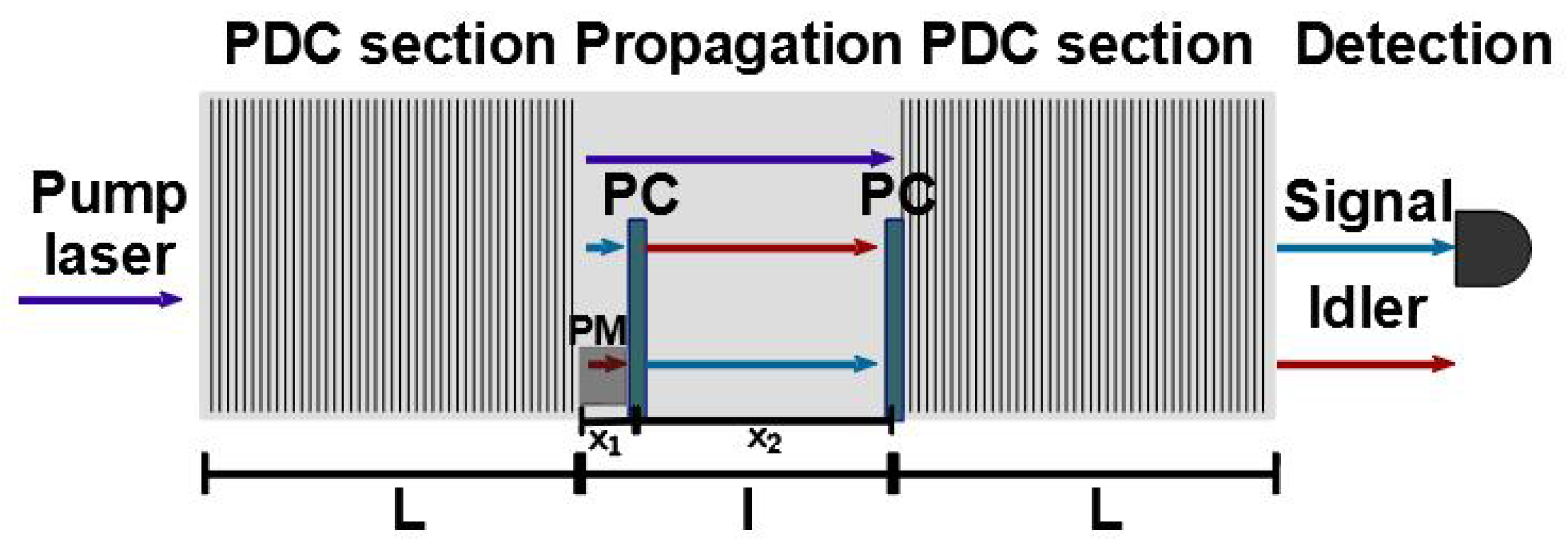
2. Theoretical Model
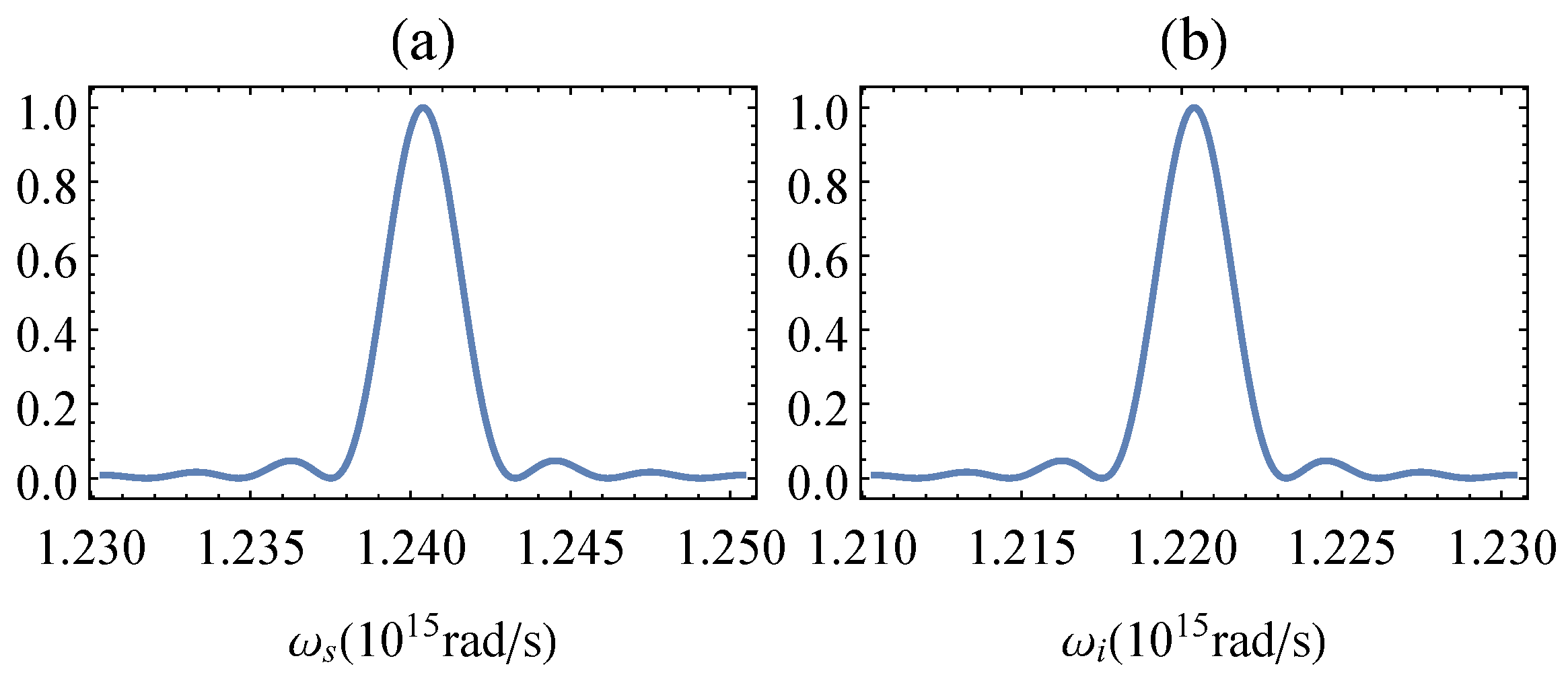
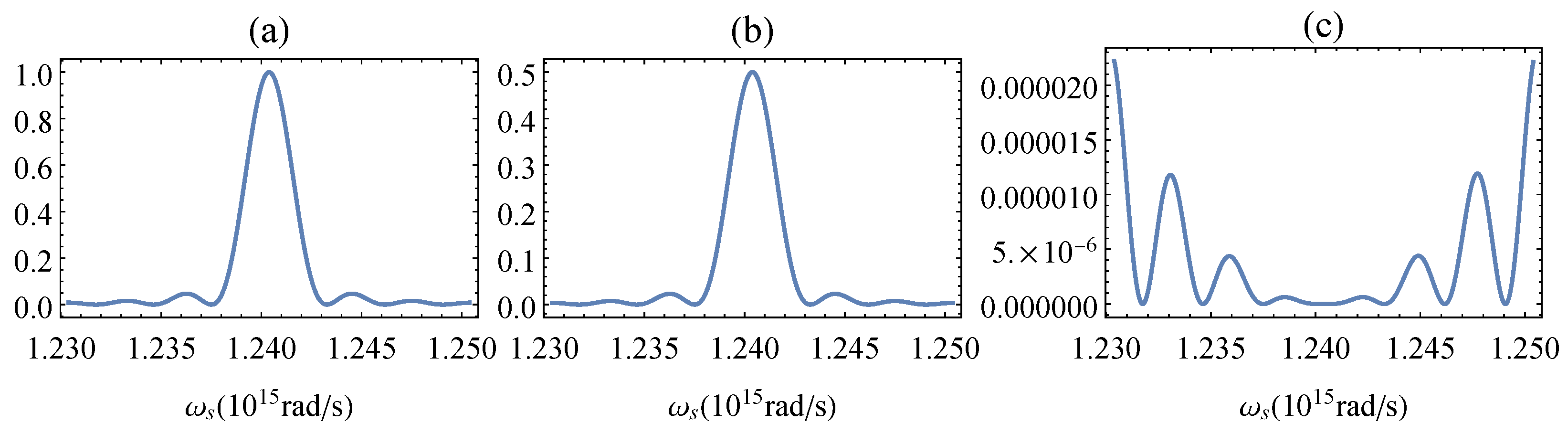
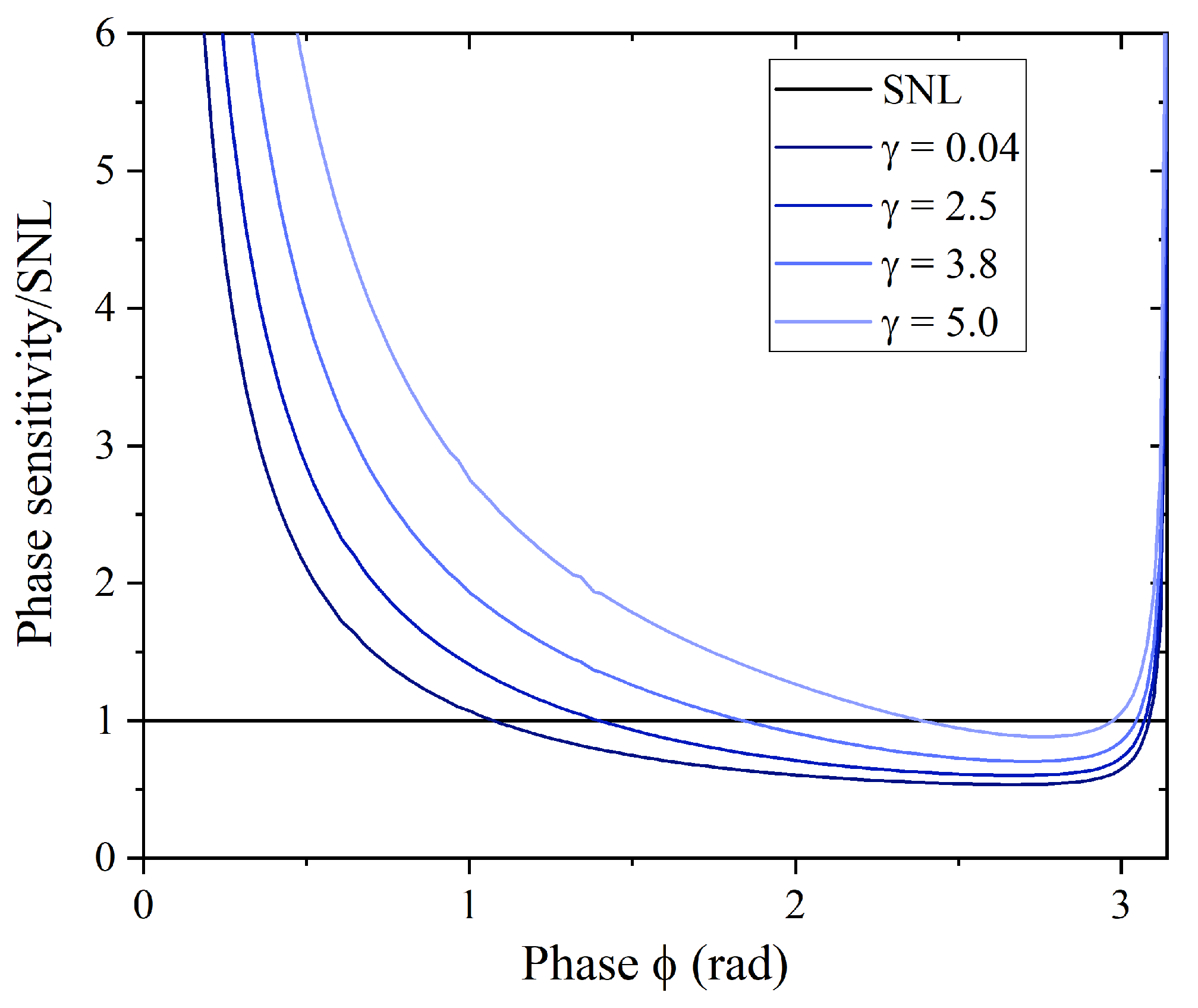
3. Dispersion Suppression and Phase Sensitivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum Metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic quantum metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
- Tóth, G.; Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 2014, 47, 424006. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Řehaček, J.; Hradil, Z.; Stoklasa, B.; Paúr, M.; Grover, J.; Krzic, A.; Sánchez-Soto, L.L. Multiparameter quantum metrology of incoherent point sources: Towards realistic superresolution. Phys. Rev. A 2017, 96, 062107. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Luo, K.H.; Santandrea, M.; Stefszky, M.; Sperling, J.; Massaro, M.; Ferreri, A.; Sharapova, P.R.; Herrmann, H.; Silberhorn, C. Quantum optical coherence: From linear to nonlinear interferometers. arXiv 2021, arXiv:2104.02641. [Google Scholar]
- Chekhova, M.V.; Ou, Z.Y. Nonlinear interferometers in quantum optics. Adv. Opt. Photonics 2016, 8, 104–155. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef] [Green Version]
- Dowling, J.P. Quantum optical metrology—the lowdown on high-N00N states. Contemp. Phys. 2008, 49, 125–143. [Google Scholar] [CrossRef]
- Slussarenko, S.; Weston, M.M.; Chrzanowski, H.M.; Shalm, L.K.; Verma, V.B.; Nam, S.W.; Pryde, G.J. Unconditional violation of the shot-noise limit in photonic quantum metrology. Nat. Photonics 2017, 11, 700. [Google Scholar] [CrossRef] [Green Version]
- Demkowicz-Dobrzański, R.; Jarzyna, M.; Kołodyński, J. Chapter Four—Quantum Limits in Optical Interferometry. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 60, pp. 345–435. [Google Scholar]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033–4054. [Google Scholar] [CrossRef] [PubMed]
- Ou, Z.Y. Fundamental quantum limit in precision phase measurement. Phys. Rev. A 1997, 55, 2598–2609. [Google Scholar] [CrossRef]
- Shih, Y.H.; Sergienko, A.V.; Rubin, M.H.; Kiess, T.E.; Alley, C.O. Two-photon entanglement in type-II parametric down-conversion. Phys. Rev. A 1994, 50, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Rubin, M.H.; Klyshko, D.N.; Shih, Y.H.; Sergienko, A.V. Theory of two-photon entanglement in type-II optical parametric down-conversion. Phys. Rev. A 1994, 50, 5122–5133. [Google Scholar] [CrossRef]
- Keller, T.E.; Rubin, M.H. Theory of two-photon entanglement for spontaneous parametric down-conversion driven by a narrow pump pulse. Phys. Rev. A 1997, 56, 1534–1541. [Google Scholar] [CrossRef]
- Marino, G.; Solntsev, A.S.; Xu, L.; Gili, V.F.; Carletti, L.; Poddubny, A.N.; Rahmani, M.; Smirnova, D.A.; Chen, H.; Lemaître, A.; et al. Spontaneous photon-pair generation from a dielectric nanoantenna. Optica 2019, 6, 1416–1422. [Google Scholar] [CrossRef] [Green Version]
- Santiago-Cruz, T.; Fedotova, A.; Sultanov, V.; Weissflog, M.A.; Arslan, D.; Younesi, M.; Pertsch, T.; Staude, I.; Setzpfandt, F.; Chekhova, M. Photon Pairs from Resonant Metasurfaces. Nano Lett. 2021, 21, 4423–4429. [Google Scholar] [CrossRef]
- Alibart, O.; Fulconis, J.; Wong, G.K.L.; Murdoch, S.G.; Wadsworth, W.J.; Rarity, J.G. Photon pair generation using four-wave mixing in a microstructured fibre: Theory versus experiment. New J. Phys. 2006, 8, 67. [Google Scholar] [CrossRef]
- Zhang, D.; Ahmed, I.; Hao, L.; Cai, Y.; Li, C.; Zhang, Y.; Zhang, Y. Temporally Correlated Narrowband Biphoton Interference Based on Mach-Zehnder Interferometer. Ann. Der Phys. 2019, 531, 1900300. [Google Scholar] [CrossRef]
- Lemieux, S.; Manceau, M.; Sharapova, P.R.; Tikhonova, O.V.; Boyd, R.W.; Leuchs, G.; Chekhova, M.V. Engineering the Frequency Spectrum of Bright Squeezed Vacuum via Group Velocity Dispersion in an SU(1,1) Interferometer. Phys. Rev. Lett. 2016, 117, 183601. [Google Scholar] [CrossRef] [Green Version]
- Triginer, G.; Vidrighin, M.D.; Quesada, N.; Eckstein, A.; Moore, M.; Kolthammer, W.S.; Sipe, J.E.; Walmsley, I.A. Understanding High-Gain Twin-Beam Sources Using Cascaded Stimulated Emission. Phys. Rev. X 2020, 10, 031063. [Google Scholar] [CrossRef]
- Roux, F.S. Stimulated parametric down-conversion for spatiotemporal metrology. Phys. Rev. A 2021, 104, 043514. [Google Scholar] [CrossRef]
- Ou, Z.Y.; Li, X. Quantum SU(1,1) interferometers: Basic principles and applications. APL Photonics 2020, 5, 080902. [Google Scholar] [CrossRef]
- Frascella, G.; Mikhailov, E.E.; Takanashi, N.; Zakharov, R.V.; Tikhonova, O.V.; Chekhova, M.V. Wide-field SU(1,1) interferometer. Optica 2019, 6, 1233–1236. [Google Scholar] [CrossRef] [Green Version]
- Ferreri, A.; Ansari, V.; Silberhorn, C.; Sharapova, P.R. Temporally multimode four-photon Hong–Ou–Mandel interference. Phys. Rev. A 2019, 100, 053829. [Google Scholar] [CrossRef] [Green Version]
- Ferreri, A.; Santandrea, M.; Stefszky, M.; Luo, K.H.; Herrmann, H.; Silberhorn, C.; Sharapova, P.R. Spectrally multimode integrated SU(1,1) interferometer. Quantum 2021, 5, 461. [Google Scholar] [CrossRef]
- Paterova, A.V.; Krivitsky, L.A. Nonlinear interference in crystal superlattices. Light. Sci. Appl. 2020, 9, 82. [Google Scholar] [CrossRef]
- Kitaeva, G.K.; Kornienko, V.V.; Leontyev, A.A.; Shepelev, A.V. Generation of optical signal and terahertz idler photons by spontaneous parametric down-conversion. Phys. Rev. A 2018, 98, 063844. [Google Scholar] [CrossRef]
- Dvernik, L.S.; Prudkovskii, P.A. Azimuthal eigenmodes at strongly non-degenerate parametric down-conversion. Appl. Phys. B 2021, 127, 1–10. [Google Scholar] [CrossRef]
- Luo, K.H.; Herrmann, H.; Krapick, S.; Brecht, B.; Ricken, R.; Quiring, V.; Suche, H.; Sohler, W.; Silberhorn, C. Direct generation of genuine single-longitudinal-mode narrowband photon pairs. New J. Phys. 2015, 17, 073039. [Google Scholar] [CrossRef]
- Kuznetsov, K.A.; Malkova, E.I.; Zakharov, R.V.; Tikhonova, O.V.; Kitaeva, G.K. Nonlinear interference in the strongly nondegenerate regime and Schmidt mode analysis. Phys. Rev. A 2020, 101, 053843. [Google Scholar] [CrossRef]
- Riedmatten, H.d.; Marcikic, I.; Tittel, W.; Zbinden, H.; Gisin, N. Quantum interference with photon pairs created in spatially separated sources. Phys. Rev. A 2003, 67, 022301. [Google Scholar] [CrossRef] [Green Version]
- Tanzilli, S.; Martin, A.; Kaiser, F.; De Micheli, M.; Alibart, O.; Ostrowsky, D. On the genesis and evolution of Integrated Quantum Optics. Laser Photonics Rev. 2012, 6, 115–143. [Google Scholar] [CrossRef] [Green Version]
- Caspani, L.; Xiong, C.; Eggleton, B.J.; Bajoni, D.; Liscidini, M.; Galli, M.; Morandotti, R.; Moss, D.J. Integrated sources of photon quantum states based on nonlinear optics. Light. Sci. Appl. 2017, 6, e17100. [Google Scholar] [CrossRef]
- O’Brien, J.; Patton, B.; Sasaki, M.; Vučković, J. Focus on integrated quantum optics. New J. Phys. 2013, 15, 035016. [Google Scholar] [CrossRef] [Green Version]
- Sharapova, P.R.; Luo, K.H.; Herrmann, H.; Reichelt, M.; Meier, T.; Silberhorn, C. Toolbox for the design of LiNbO3-based passive and active integrated quantum circuits. New J. Phys. 2017, 19, 123009. [Google Scholar] [CrossRef]
- Ono, T.; Sinclair, G.F.; Bonneau, D.; Thompson, M.G.; Matthews, J.C.F.; Rarity, J.G. Observation of nonlinear interference on a silicon photonic chip. Opt. Lett. 2019, 44, 1277–1280. [Google Scholar] [CrossRef]
- Krapick, S.; Herrmann, H.; Quiring, V.; Brecht, B.; Suche, H.; Silberhorn, C. An efficient integrated two-color source for heralded single photons. New J. Phys. 2013, 15, 033010. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, H.; Yang, X.; Thomas, A.; Poppe, A.; Sohler, W.; Silberhorn, C. Post-selection free, integrated optical source of non-degenerate, polarization entangled photon pairs. Opt. Express 2013, 21, 27981–27991. [Google Scholar] [CrossRef] [Green Version]
- Sharapova, P.R.; Tikhonova, O.V.; Lemieux, S.; Boyd, R.W.; Chekhova, M.V. Bright squeezed vacuum in a nonlinear interferometer: Frequency and temporal Schmidt-mode description. Phys. Rev. A 2018, 97, 053827. [Google Scholar] [CrossRef] [Green Version]
- Klyshko, D. Ramsey interference in two-photon parametric scattering. J. Exp. Theor. Phys. 1993, 104, 2676–2684. [Google Scholar]
- Klyshko, D. Parametric generation of two-photon light in anisotropic layered media. J. Exp. Theor. Phys. 1994, 105, 1574–1582. [Google Scholar]
- Santandrea, M.; Stefszky, M.; Ansari, V.; Silberhorn, C. Fabrication limits of waveguides in nonlinear crystals and their impact on quantum optics applications. New J. Phys. 2019, 21, 033038. [Google Scholar] [CrossRef]
- Helmfrid, S.; Arvidsson, G.; Webjörn, J. Influence of various imperfections on the conversion efficiency of second-harmonic generation in quasi-phase-matching lithium niobate waveguides. J. Opt. Soc. Am. B 1993, 10, 222–229. [Google Scholar] [CrossRef]
- Law, C.K.; Walmsley, I.A.; Eberly, J.H. Continuous Frequency Entanglement: Effective Finite Hilbert Space and Entropy Control. Phys. Rev. Lett. 2000, 84, 5304–5307. [Google Scholar] [CrossRef]
- Manceau, M.; Khalili, F.; Chekhova, M. Improving the phase super-sensitivity of squeezing-assisted interferometers by squeeze factor unbalancing. New J. Phys. 2017, 19, 013014. [Google Scholar] [CrossRef]
- Anderson, B.E.; Schmittberger, B.L.; Gupta, P.; Jones, K.M.; Lett, P.D. Optimal phase measurements with bright- and vacuum-seeded SU(1,1) interferometers. Phys. Rev. A 2017, 95, 063843. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Yuan, C.H.; Ou, Z.Y.; Zhang, W. The phase sensitivity of an SU(1,1) interferometer with coherent and squeezed-vacuum light. New J. Phys. 2014, 16, 073020. [Google Scholar] [CrossRef]
- Plick, W.N.; Dowling, J.P.; Agarwal, G.S. Coherent-light-boosted, sub-shot noise, quantum interferometry. New J. Phys. 2010, 12, 083014. [Google Scholar] [CrossRef]
- Li, D.; Yuan, C.H.; Yao, Y.; Jiang, W.; Li, M.; Zhang, W. Effects of loss on the phase sensitivity with parity detection in an SU(1,1) interferometer. J. Opt. Soc. Am. B 2018, 35, 1080–1092. [Google Scholar] [CrossRef] [Green Version]
- Marino, A.M.; Corzo Trejo, N.V.; Lett, P.D. Effect of losses on the performance of an SU(1,1) interferometer. Phys. Rev. A 2012, 86, 023844. [Google Scholar] [CrossRef]
- Xin, J.; Wang, H.; Jing, J. The effect of losses on the quantum-noise cancellation in the SU(1,1) interferometer. Appl. Phys. Lett. 2016, 109, 051107. [Google Scholar] [CrossRef]
- Hu, X.L.; Li, D.; Chen, L.Q.; Zhang, K.; Zhang, W.; Yuan, C.H. Phase estimation for an SU(1,1) interferometer in the presence of phase diffusion and photon losses. Phys. Rev. A 2018, 98, 023803. [Google Scholar] [CrossRef] [Green Version]
- Tiedau, J.; Schapeler, T.; Anant, V.; Fedder, H.; Silberhorn, C.; Bartley, T.J. Single-channel electronic readout of a multipixel superconducting nanowire single photon detector. Opt. Express 2020, 28, 5528–5537. [Google Scholar] [CrossRef]
- Ferrari, S.; Kahl, O.; Kovalyuk, V.; Goltsman, G.N.; Korneev, A.; Pernice, W.H.P. Waveguide-integrated single- and multi-photon detection at telecom wavelengths using superconducting nanowires. Appl. Phys. Lett. 2015, 106, 151101. [Google Scholar] [CrossRef]
- Luo, K.H.; Brauner, S.; Eigner, C.; Sharapova, P.R.; Ricken, R.; Meier, T.; Herrmann, H.; Silberhorn, C. Nonlinear integrated quantum electro-optic circuits. Sci. Adv. 2019, 5, eaat1451. [Google Scholar] [CrossRef] [Green Version]
- Quesada, N.; Sipe, J.E. Effects of time ordering in quantum nonlinear optics. Phys. Rev. A 2014, 90, 063840. [Google Scholar] [CrossRef] [Green Version]
- Christ, A.; Brecht, B.; Mauerer, W.; Silberhorn, C. Theory of quantum frequency conversion and type-II parametric down-conversion in the high-gain regime. New J. Phys. 2013, 15, 053038. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreri, A.; Sharapova, P.R. Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer. Symmetry 2022, 14, 552. https://doi.org/10.3390/sym14030552
Ferreri A, Sharapova PR. Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer. Symmetry. 2022; 14(3):552. https://doi.org/10.3390/sym14030552
Chicago/Turabian StyleFerreri, Alessandro, and Polina R. Sharapova. 2022. "Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer" Symmetry 14, no. 3: 552. https://doi.org/10.3390/sym14030552
APA StyleFerreri, A., & Sharapova, P. R. (2022). Two-Colour Spectrally Multimode Integrated SU(1,1) Interferometer. Symmetry, 14(3), 552. https://doi.org/10.3390/sym14030552







