Abstract
Symmetries are ubiquitous in nature. Almost all organisms have some kind of “symmetry”, meaning that their shape does not change under some geometric transformation. This geometrical concept of symmetry is intuitive and easy to recognize. On the other hand, the behavior of many biological systems over time can be described with ordinary differential equations. These dynamic models may also possess “symmetries”, meaning that the time courses of some variables remain invariant under certain transformations. Unlike the previously mentioned symmetries, the ones present in dynamic models are not geometric, but infinitesimal transformations. These mathematical symmetries can be related to certain features of the system’s dynamic behavior, such as robustness or adaptation capabilities. However, they can also arise from questionable modeling choices, which may lead to non-identifiability and non-observability. This paper provides an overview of the types of symmetries that appear in dynamic models, the mathematical tools available for their analyses, the ways in which they are related to system properties, and the implications for biological modeling.
1. Introduction
Symmetrical features are abundant in the biological world. Practically all organisms have some kind of symmetry in three-dimensional space. Due to developmental noise, these symmetries are approximate; the deviation from perfect symmetry is called fluctuating asymmetry [1]. Such geometrical symmetries can often be easily noticed.
On the other hand, symmetries may also appear in equations that do not represent a geometric shape. For example, an equation may contain two parameters that have exactly the same influence in its outcome, e.g., if they always multiply each other. More generally, these symmetries refer to an invariance of some variables under certain transformations of other variables.
The dynamic behavior of many biological processes can be accurately described by systems of differential equations, which are often ordinary differential equations (ODEs). Such systems of ODEs, along with the definition of the inputs and outputs, constitutes a dynamic model [2]. It is often the case that said dynamic models of biosystems have symmetries, whose significance may vary depending on the context. For example, for the purpose of system identification, if two parameters can be interchanged without affecting the model output, this means that they cannot be distinguished by observing (measuring) the output—and thus, they are unidentifiable. However, from a different point of view, this feature may be interpreted as biological robustness—variations in the value of one parameter, due for example to environmental fluctuations, can be compensated by variations in other parameter, leaving the output invariant. The former view is relevant for model building and the latter for the system behavior, but both of them are connected.
The symmetries in dynamic models are less obviously noticed than symmetric shapes. They can be of different types, and some of them defy intuition—but they can nevertheless play an important role. Fortunately, there exists a well established theory for its study. The symmetry analysis of differential equations was founded in the nineteenth century by the Norwegian mathematician Sophus Lie, and there are many review articles [3] and books [4,5] on the topic of Lie groups of transformations.
The purpose of the present review is threefold. First, it presents the fundamental concepts of Lie symmetries and related mathematical tools (Section 2). Second, it describes a number of features found in dynamic models of biological systems, and their connections to symmetries, as well as the biological and modeling implications (Section 3). Third, it discusses some subtleties and relationships between properties, providing some remarks and lines for future research (Section 4).
2. Mathematical Concepts and Analysis Tools
We consider ODE models of the general form:
where is the state vector, is the parameter vector, is the known input vector, is the unknown input vector, is the output vector, and f and g are vectors of (possibly nonlinear) analytical functions.
To simplify the notation, we will usually omit the dependency on time. Furthermore, despite the fact that the distinction made in (1) between states, parameters, and inputs is the usual practice in dynamic modeling, we will group them together in an augmented state vector with dimension . The reason for this is that all those variables can be involved in the symmetries that we consider. Thus, the Equation (1) may be rewritten as:
It should be noted that the simplicity of this notation conceals certain subtleties related to the inputs, both known (u) and unknown (w). Since the aim of this Section is not to describe those aspects in depth, but instead to provide an overview of the fundamental math, we will proceed with this abuse of notation. The reader interested in a more rigorous treatment is referred to, e.g., [6,7,8,9].
The remainder of this section discusses concepts related to symmetries in models such as (2). The definitions in Section 2.1 are taken from [3,4,5], and the procedure in Section 2.2 mostly follows [6].
2.1. Lie Symmetries: Definitions
Definition 1.
A transformation of variables is called a “symmetry transformation”, a “Lie symmetry”, or a “point symmetry” of a system of differential equations (2) if
A symmetry transformation maps the set of all solutions of (2) into itself. If the equations admit such a symmetry, the model variables can be transformed by it without altering the dynamics nor the output.
A closely related concept is equivariance, which can be defined as follows [10]:
Definition 2.
Given a group of operators Γ acting on , a vector field is said to be “Γ invariant” if for all and .
Note that can be a Lie group, and it does not need to be a linear operator. If f from (2) is invariant, then is a symmetry of (2).
Definition 3.
A “one-parameter Lie group of transformations” is a mapping of the form
where ε is the parameter, if it constitutes a group — i.e., it satisfies the four group axioms: (1) closure, (2) associativity, and existence of (3) an identity and (4) an inverse—and, additionally, the transformation is (5) smooth in x and (6) analytic in ε, and (7) the identity element can be chosen as.
Note that, expanding (3) in a neighborhood of , we obtain the following expression for a Lie group:
where the following term appears:
Definition 4.
The “infinitesimal” of a Lie group (3) is:
Definition 5.
The “infinitesimal transformation” of a Lie group (3) is:
Definition 6.
The “infinitesimal generator” of a Lie group (3) is:
The infinitesimal generator X is an equivalent representation of a Lie group. Using X, the infinitesimal transformation (6) can be written as
In order to calculate the transformation of , we can extend the definition of X so that (8) acts on the derivatives:
where
Types of Lie symmetries. We can classify symmetries according to their expressions. Below we list some of the most common ones, along with their infinitesimal generators.
Translation:
Scaling:
Moebius:
Higher order:
The symmetries most commonly found in dynamic models of biological systems are traslation and scaling.
2.2. Finding Lie Symmetries
Lie symmetries can be found by solving a system of differential equations, whose solutions are the expressions of the transformations admitted by the model. To formulate the problem, we use the following result:
Theorem 1.
Application of Theorem 1 to the equations of (2) yields the following set of partial differential equations (PDEs):
By solving these equations we obtain the infinitesimals, , and by replacing them in (6), we calculate the transformations that we are looking for.
Unfortunately, in the general case it is not possible to solve equations (17) analytically. A way of simplifying the problem is to assume that and are rational functions, that is:
where , , , and are polynomial expressions. Most dynamic models encountered in biology are of this form. If we replace (18) in (17), the PDEs are transformed into ODEs. Next, we introduce an assumption about the shape of the solutions (or ansatz), which amounts to restricting the search to certain classes of symmetries. To choose a suitable ansatz, we may note that the infinitesimals of the generators (11)–(14) are polynomial expressions. Thus, a possible ansatz could be:
Note, however, that in this expression every variable is allowed to depend on any other variable. In reality, parameters (which are constant) cannot have symmetries depending on states or inputs (which can be time-varying), so the corresponding coefficients must be zero. Using the ansatz above, after some modifications Equation (17) become:
When the infinitesimals are polynomials as in (19), the equations (20) are of the form:
where r is the vector of all , and the coefficients are linear in r. Equation (21) holds if the following condition holds:
where all the coefficients have been grouped in a matrix C. Thus, if a model has symmetries defined by (19), said symmetries can be found by solving a system of linear equations, which amounts to computing the kernel of C.
2.3. Structural Identifiability and Observability
Identifiability is a mathematical property that describes the ability to infer the parameters in a model from observations of its output vector over time. It is common to distinguish between structural and practical identifiability; the former is determined exclusively by the model ODEs and output equations, while the latter is also affected by the quantity and quality of the available data. Thus, structural identifiability is necessary but not sufficient for practical identifiability. A recent review of both concepts is [11].
Structural identifiability is related to another property, observability, which refers to states instead of parameters [12]. These concepts are defined in the following paragraphs.
Definition 7.
A parameter (that is, the ith element of the parameter vector) is structurally locally identifiable (SLI) if, for almost any parameter vector , there is a neighbourhood where the following condition holds [2]:
If (23) is not true in any neighborhood of , the parameter is structurally unidentifiable (SU). If (23) is true for all model parameters, the model is said to be SLI as well, and SU otherwise.
Definition 8.
A state is observable if it can be determined from the output vector and the known input vector in an interval , for a finite . Otherwise, it is unobservable.
A model is observable if all its states are observable.
We will use the acronym SIO to refer to Structural Identifiability and Observability jointly.
3. Connections: Symmetries and Other Properties
3.1. Symmetries and SIO
The presence of symmetries in the equations of a model is a possible source of structural non-identifiability and non-observability [13]. It has been shown that symmetries allow for similarity transformations, i.e., transformations of parameters and states that do not change the model output [14,15,16]. If that is the case, it is not possible to infer the values of the parameters and states involved in such symmetries by observing the output. Therefore, those parameters are unidentifiable and those states are unobservable. Since structural identifiability and observability are desirable properties for the purpose of system identification, it may be useful to break the symmetries that prevent them. Symmetries can be removed by reparameterizing the model equations, or by measuring additional outputs when possible. Several efforts have been made in this regard.
Meshkat and Sullivant addressed this problem for a class of linear compartment models, which are used in systems biology and pharmacokinetics [17]. They provided partial results for determining which models allow for scaling reparameterizations that make them identifiable, and an algorithm for finding them. A different solution was sought in [18], where an algorithm for finding the minimal output sets for obtaining structural identifiability (i.e., which subsets of state variables must be measured) was presented. The method relies on finding translation, scaling, and affine symmetries, and then breaking these symmetries by adding states to the output vector. A Mathematica implementation of the identifiability analysis method is available. Exact simplification methods based on Lie symmetries, including scaling and affine transformations, were presented in [19,20,21] and implemented in the Maple package MABSys.
An algorithm capable of detecting higher-order Lie symmetries, along with its Python implementation, was provided in [6], where the implications for predictability of the dynamic model were also discussed. A related algorithm, which finds symmetries and their symmetry-breaking transformations, was presented in [9] and included in the Matlab toolbox STRIKE-GOLDD [22]. Shi and Chatzis studied this problem in the context of monitoring the state of mechanical structures, for which it is important to consider unknown inputs. Initially, they assumed that the symmetries are translations or scalings [7]; their results were later extended so as to relax those assumptions [8]. A computational method called AutoRepar was presented in [23] as a follow-up to [9]. AutoRepar extends the preceding algorithm by calculating the reparameterizations associated to the symmetry breaking transformations, thus rendering a model structurally identifiable and observable.
There are many software packages available for finding symmetries in dynamic models. A few of them are focused on structural identifiability, some of which are listed in Table 1. The first four rows in Table 1 list algorithms that have computational implementations in several symbolic environments. Software implementations are convenient due to the complexity of these methods, which makes computations by hand infeasible for all but the simplest models. In contrast, the last entry on the table, the Scaling Invariance Method (SIM), is a simple technique that can be applied manually [24]. It detects scaling symmetries, which are arguably the most frequently found in biological models. However, it must be taken into account that, if a model contains other types of symmetries, the results of SIM do not inform about structural identifiability [25].

Table 1.
Some methods for finding symmetries in dynamic models and analysing their SIO.
3.2. Symmetries and Biological Robustness
The term robustness refers to the ability of a biological system to maintain its behavior in varying environmental conditions. It is a desirable property, since organisms must be able to tolerate uncertainty—both in external inputs and in internal components—in order to survive. From a modeling point of view, one way of achieving robustness is insensitivity. A model may be largely insensitive to changes in an external input or parameter [27]. However, biological systems also need to be sensitive to certain signals or variations, so as to sense the environment and adapt to changes in it. Thus, there must be a balance between sensitivity and robustness. Organisms must change their behavior in response to certain (types of) changes, and keep it unaltered in response to others. A number of mechanisms exist which can achieve this goal.
The concept of fold-change detection (FCD) describes the behavior of sensory systems whose response depends only on relative changes to the input, instead of on its absolute values [28] (that is, the output is the same when the input changes from 1 to 2 and when it changes from 3 to 6). FCD entails two properties: exact adaptation (i.e., the steady state is the same) and the Weber-Fechner law (i.e., the maximal initial response is the same), but it is more general than both of them: FCD concerns the whole dynamic response. Examples of biological systems that exhibit FCD include bacterial chemotaxis, vision, and cellular signaling. A few mechanisms have been shown to produce FCD, including incoherent feed-forward loops (IFFL) and nonlinear integral feedback (NLIFL), which are shown in Figure 1. FCD is a scale invariance: it corresponds to the existence of a scaling symmetry involving input and state [29]. FCD is a particular case of symmetry invariance; Shoval et al. [30] characterized systems whose transient behaviors are invariant under a set of symmetries.
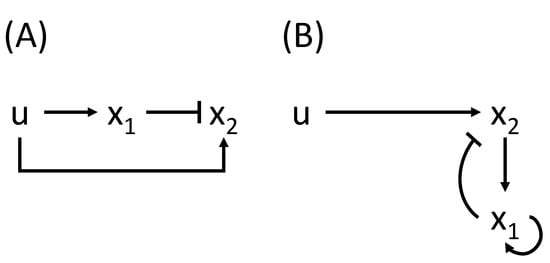
Figure 1.
(A) An incoherent feedforward loop and (B) a nonlinear integral feedback loop (NLIFL). The controlled variable is , and the input is u. The equations are: (A): , ; (B): , . Adapted from [29].
More recently, a related concept, dynamical compensation (DC), was introduced [31]. It was presented as a design principle that provides robustness to physiological circuits, in the face of uncertainties in certain parameters. It was shown by Sontag [32] that DC and FCD are manifestations of the same phenomenon.
The interplay between symmetries and stability of dynamical systems was discussed in [10]. Both concepts were linked by means of a third property, contraction; an approach that is able to explain FCD. It was also shown how the invariance under input scaling can be exploited for network synchronization, thus playing a key role in biological applications such as quorum-sensing networks in bacteria.
4. Discussion and Conclusions
In the preceding section two different viewpoints have been discussed. On the one hand, Section 3.1 has noted that the presence of symmetries in dynamic models can lead to non-identifiability and non-observability, which hampers system identification and is a possible source of wrong predictions (that is bad!). On the other hand, Section 3.2 has presented symmetries as providers of robust behavior, which allow for adaptation to changes in external and internal conditions (that is good!).
Albeit conflicting, these two viewpoints are not mutually exclusive and they can be subtly related. Here we illustrate them with a case study. Figure 2A shows a graphical representation of a plausible physiological mechanism for regulating plasma glucose levels. An external input representing ingestion (u) increases glucose concentration (G), and indirectly influences the cells’ mass (). In turn, cells secrete insulin (I), and insulin decreases glucose concentration. In this way, plasma glucose concentration tends to be pushed back to a reference level after each meal, as can be seen in Figure 2B. The model ODEs are:
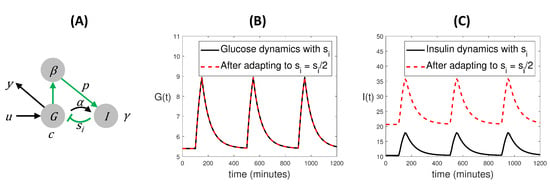
Figure 2.
Interplay between SIO and adaptation in a system with symmetries. (A) Diagram of a glucose-insulin regulation circuit that keeps plasma glucose concentration within admissible levels. The model equations are given by (24)–(28). (B) Time-courses of glucose concentration over the course of three meals, before and after the system adapts to a change in parameter . The plot illustrates the phenomenon of dynamical compensation: both curves are exactly the same. (C) Lack of identifiability is linked to lack of observability: the two different values of yield two different insulin curves.
This model was presented in [31] to illustrate the DC property, which in this case can be summarized as follows: if the rate at which insulin removes glucose from the system (which is given by parameter ) changes, the system goes through an adaptation process which eventually leads to the glucose response being identical to the pre-change one. This is shown in Figure 2B, where it can be seen that the two time courses of glucose are indistinguishable. That is, the model exhibits the DC property, which, as explained in Section 3.2, is related to the existence of a scaling symmetry. Indeed, it can be seen [23] that the model admits the following transformations:
which leave the model output, , invariant. The resulting equations are:
The mechanism that gives rise to these symmetries is a feedforward loop, shown in green in Figure 2A, that resembles the IFFL depicted in Figure 1A.
Let us now adopt the other viewpoint. It was noted in [32,33,34] that, at least according to its initial definition, DC amounts to non-identifiability. Indeed, the two parameters involved in the symmetries, and p, are structurally unidentifiable. This means that their values cannot be determined by measuring the system output (glucose). In system identification terms, this model is over-parameterized, since it contains more unknowns that can be inferred from data. In contrast, in the reparameterized equations given by (31)–(33) and p have been removed, and the model is identifiable.
Importantly, the non-identifiability of the model given by (24)–(28) also entails non-observability: insulin is an non-observable state variable, and hence it cannot be estimated from output measurements. This is shown in Figure 2C, where it can be seen that the two values of yield two different time courses of I; since it is not possible to know from data, it is also impossible to determine I. This limitation may be problematic, e.g., if we want to implement an artificial pancreas controller that requires knowledge of I. In this regard, it should be noted that the reparameterization given by (29)–(33) transforms I, so even though the transformed variable becomes observable, it no longer corresponds to insulin concentration. Fortunately, the transformation given by (24)–(28) is not the only admissible one. As was discussed in [23], if the input u is considered unknown it is possible to lump other terms in it, obtaining a model reformulation that leaves not only G, but also I invariant. To this end, we perform the following transformations:
obtaining the following reparameterized model:
The model above would be suitable for implementing the previously mentioned type of controller.
It should be stressed that structural non-identifiability and/or non-observability should not be invariably interpreted as signs of biological robustness. While these features may sometimes be related to adaptation mechanisms, they always reveal deficiencies in the model formulation for the purpose of system identification and monitoring. As the example in the present Section has shown, the absence of SIO hampers the information that a model can provide, and, if unnoticed, it can lead to wrong predictions and conclusions. Hence, it is essential to perform a proper SIO analysis and to address any issues found by it. In this regard, we remark that a biosystem’s adaptation capabilities (such as, e.g., the DC property) do not necessarily entail lack of SIO; indeed, it is possible to use alternative definitions of DC that preserve its intended mechanistic meaning while avoiding the implication of non-identifiability, as was proposed in [34].
The example discussed above contains scaling symmetries. While they are arguably the most commonly found type of symmetry, dynamic models of biological systems may admit symmetry transformations of other types, instead or in addition to scaling. Since the absence of scaling symmetries does not exclude the existence of other types, caution must be exercised when interpreting the results of analyses based exclusively on scalings [25].
The study of symmetries in dynamic models of biosystems presents multiple opportunities for future research. The extent to which symmetry invariances such as FCD are present in different biological contexts is still an open question. So is the determination of all the mechanisms capable of producing said behavior, as well as the comparison of their relative advantages. The implementation of these mechanisms in synthetic biology circuits is a challenging problem, which is likely to inspire many developments. Other avenues for future research are discussed in [28].
From the mathematical point of view, the study of Lie symmetries has a long and rich history. However, there is still a need for computationally efficient algorithms for finding symmetries, especially of higher order and non-conventional types. Likewise, their systematic exploitation for the analysis of identifiability, observability, and other control-theoretic properties such as stability and controllability still poses many challenges.
In order to succeed, these research efforts will necessitate a truly interdisciplinary collaboration between biologists, mathematicians, and engineers.
Funding
The author acknowledges funding from MCIN/AEI/10.13039/501100011033 through grant PID2020-113992RA-I00 (PREDYCTBIO), from the Xunta de Galicia, Consellería de Cultura, Educación e Universidade through grant ED431F 2021/003, and from grant RYC-2019-027537-I funded by MCIN/AEI/10.13039/501100011033 and by “ESF Investing in your future”.
Acknowledgments
The present paper is partially based on past work that the author carried out in collaboration with Gemma Massonis and Julio R. Banga (CSIC). The author thanks both of them for helpful discussions on these topics.
Conflicts of Interest
The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DC | Dynamical compensation |
| FCD | Fold-Change Detection |
| IFFL | Incoherent Feed-Forward Loop |
| IVP | Initial value problem |
| ODE | Ordinary differential equation |
| PDE | Partial differential equation |
| SIM | Scaling Invariance Method |
| SIO | Structural Identifiability and Observability |
| SLI | Structurally locally identifiable |
| SU | Structurally unidentifiable |
References
- Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory, and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef] [Green Version]
- DiStefano, J., III. Dynamic Systems Biology Modeling and Simulation; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Oliveri, F. Lie symmetries of differential equations: Classical results and recent contributions. Symmetry 2010, 2, 658–706. [Google Scholar] [CrossRef] [Green Version]
- Bluman, G.; Anco, S. Symmetry and integration methods for differential equations. In Applied Mathematical Sciences; Springer: New York, NY, USA, 2008; Volume 154. [Google Scholar]
- Arrigo, D.J. Symmetry Analysis of Differential Equations: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Merkt, B.; Timmer, J.; Kaschek, D. Higher-order Lie symmetries in identifiability and predictability analysis of dynamic models. Phys. Rev. E 2015, 92, 012920. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, X.; Chatzis, M. Lie Symmetries, Observability and Model Transformation of Nonlinear Systems with Unknown Inputs. In Proceedings of the XI International Conference on Structural Dynamics, EURODYN 2020, Athens, Greece, 23–26 November 2020. [Google Scholar]
- Shi, X.; Chatzis, M. Computational Framework of Lie Symmetries of Nonlinear Systems with Unmeasured Inputs. In Proceedings of the 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure, SHMII 10, International Society for Structural Health Monitoring of Intelligent Infrastructure, Porto, Portugal, 30 June–2 July 2021. [Google Scholar]
- Massonis, G.; Villaverde, A.F. Finding and breaking Lie symmetries: Implications for structural identifiability and observability in biological modelling. Symmetry 2020, 12, 469. [Google Scholar] [CrossRef] [Green Version]
- Russo, G.; Slotine, J.J.E. Symmetries, stability, and control in nonlinear systems and networks. Phys. Rev. E 2011, 84, 041929. [Google Scholar] [CrossRef] [Green Version]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tonsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Villaverde, A.F. Observability and Structural Identifiability of Nonlinear Biological Systems. Complexity 2019, 2019, 8497093. [Google Scholar] [CrossRef] [Green Version]
- Sedoglavic, A. A probabilistic algorithm to test local algebraic observability in polynomial time. J. Symb. Comput. 2002, 33, 735–755. [Google Scholar] [CrossRef] [Green Version]
- Vajda, S.; Godfrey, K.R.; Rabitz, H. Similarity transformation approach to identifiability analysis of nonlinear compartmental models. Math. Biosci. 1989, 93, 217–248. [Google Scholar] [CrossRef]
- Evans, N.D.; Chapman, M.J.; Chappell, M.J.; Godfrey, K.R. Identifiability of uncontrolled nonlinear rational systems. Automatica 2002, 38, 1799–1805. [Google Scholar] [CrossRef]
- Yates, J.W.; Evans, N.D.; Chappell, M.J. Structural identifiability analysis via symmetries of differential equations. Automatica 2009, 45, 2585–2591. [Google Scholar] [CrossRef] [Green Version]
- Meshkat, N.; Sullivant, S. Identifiable reparametrizations of linear compartment models. J. Symb. Comput. 2014, 63, 46–67. [Google Scholar] [CrossRef] [Green Version]
- Anguelova, M.; Karlsson, J.; Jirstrand, M. Minimal output sets for identifiability. Math. Biosci. 2012, 239, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Sedoglavic, A. Reduction of algebraic parametric systems by rectification of their affine expanded lie symmetries. In Proceedings of the International Conference on Algebraic Biology, Castle of Hagenberg, Hagenberg, Austria, 2–4 July 2007; pp. 277–291. [Google Scholar]
- Lemaire, F.; Ürgüplü, A. A method for semi-rectifying algebraic and differential systems using scaling type Lie point symmetries with linear algebra. In Proceedings of the 2010 International Symposium on Symbolic and Algebraic Computation, Munich, Germany, 25–28 July 2010; pp. 85–92. [Google Scholar]
- Ürgüplü, A. Contributions to Symbolic Effective Qualitative Analysis of Dynamical Systems; Application to Biochemical Reaction Networks. Ph.D. Thesis, Université de Lille 1, Lille, France, February 2010. [Google Scholar]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states, and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Massonis, G.; Banga, J.R.; Villaverde, A.F. AutoRepar: A method to obtain identifiable and observable reparameterizations of dynamic models with mechanistic insights. Internat. J. Robust Nonlinear Control, 2021; in press. [Google Scholar] [CrossRef]
- Castro, M.; de Boer, R.J. Testing structural identifiability by a simple scaling method. PLoS Comput. Biol. 2020, 16, e1008248. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Massonis, G. On testing structural identifiability by a simple scaling method: Relying on scaling symmetries can be misleading. PLoS Comput. Biol. 2021, 17, e1009032. [Google Scholar] [CrossRef]
- Lemaire, F.; Ürgüplü, A. Mabsys: Modeling and analysis of biological systems. In Algebraic and Numeric Biology; Springer: Hagenberg, Austria, 2012; pp. 57–75. [Google Scholar]
- Ingalls, B. Sensitivity analysis: From model parameters to system behaviour. Essays Biochem. 2008, 45, 177–194. [Google Scholar]
- Adler, M.; Alon, U. Fold-change detection in biological systems. Curr. Opin. Syst. Biol. 2018, 8, 81–89. [Google Scholar] [CrossRef]
- Shoval, O.; Goentoro, L.; Hart, Y.; Mayo, A.; Sontag, E.; Alon, U. Fold-change detection and scalar symmetry of sensory input fields. Proc. Natl. Acad. Sci. USA 2010, 107, 15995–16000. [Google Scholar] [CrossRef] [Green Version]
- Shoval, O.; Alon, U.; Sontag, E. Symmetry invariance for adapting biological systems. SIAM J. Appl. Dyn. Syst. 2011, 10, 857–886. [Google Scholar] [CrossRef] [Green Version]
- Karin, O.; Swisa, A.; Glaser, B.; Dor, Y.; Alon, U. Dynamical compensation in physiological circuits. Mol. Syst. Biol. 2016, 12, 886. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sontag, E.D. Dynamic compensation, parameter identifiability, and equivariances. PLoS Comput. Biol. 2017, 13, e1005447. [Google Scholar] [CrossRef]
- Karin, O.; Alon, U.; Sontag, E. A note on dynamical compensation and its relation to parameter identifiability. bioRxiv 2017, 123489. [Google Scholar] [CrossRef] [Green Version]
- Villaverde, A.F.; Banga, J.R. Dynamical compensation and structural identifiability of biological models: Analysis, implications, and reconciliation. PLoS Comput. Biol. 2017, 13, e1005878. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).