Variational Quantum Circuits to Prepare Low Energy Symmetry States
Abstract
:1. Introduction
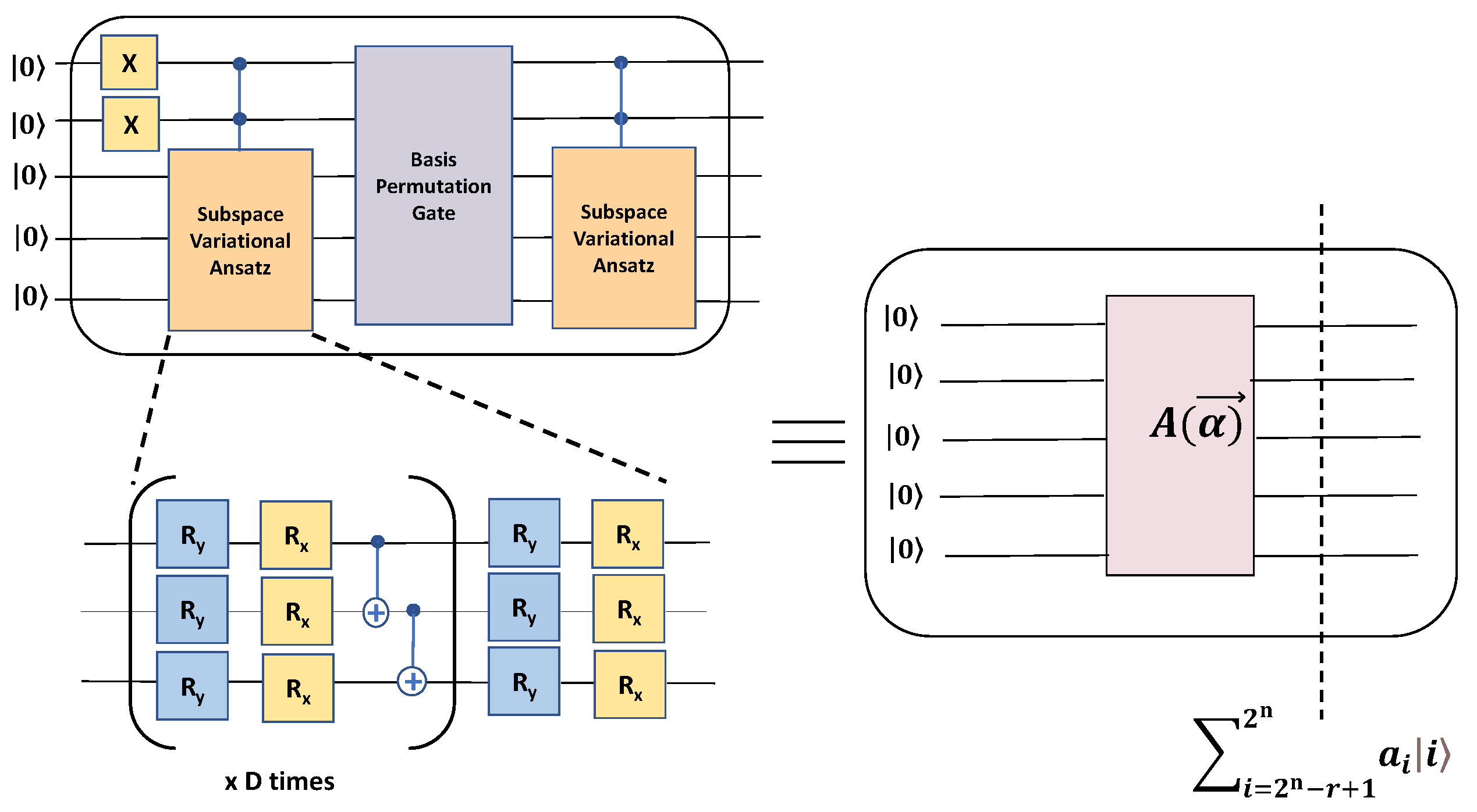
2. Method
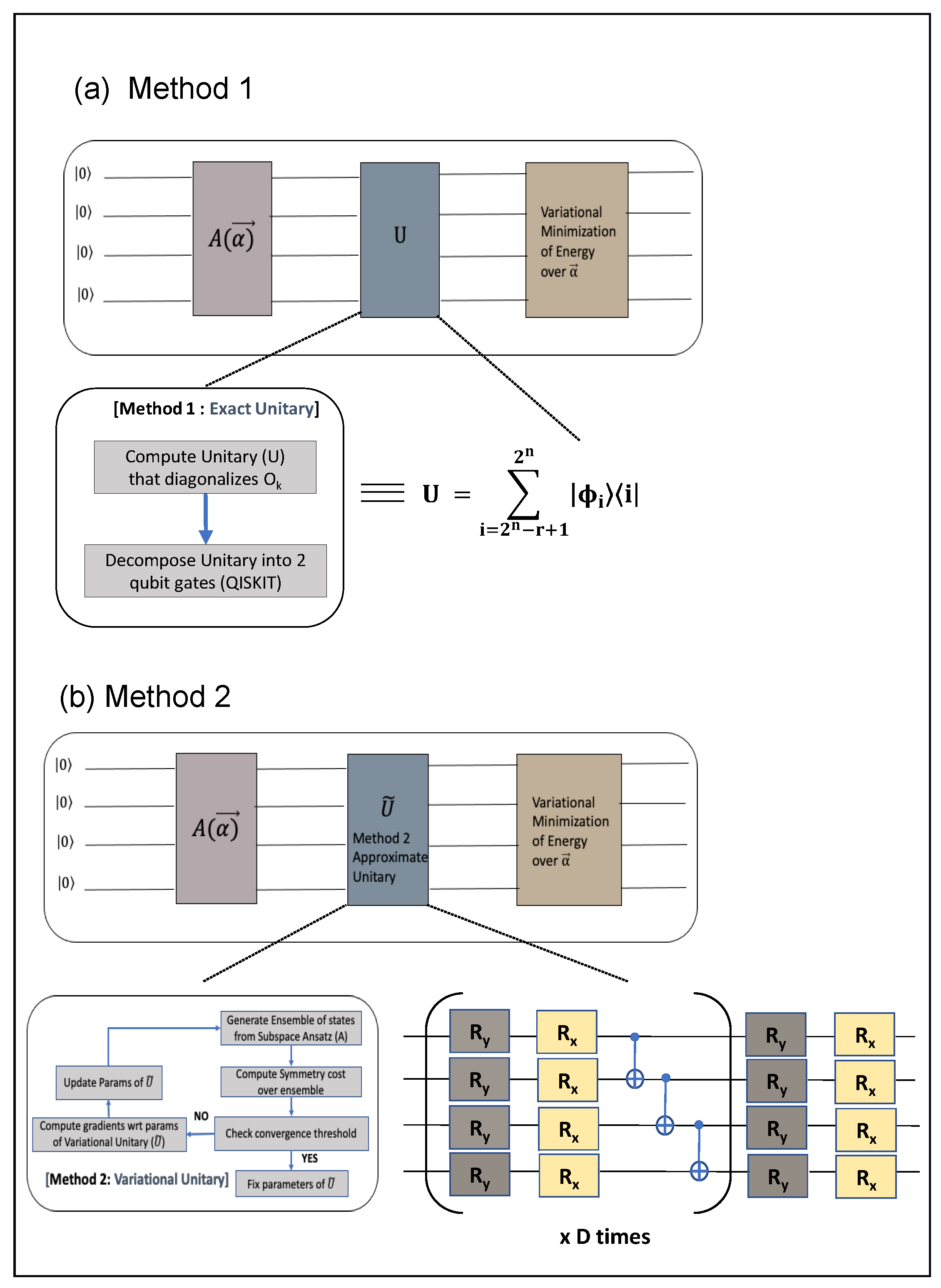
2.1. Method 1—Exact Unitary
2.2. Method 2—Approximate Unitary Construction
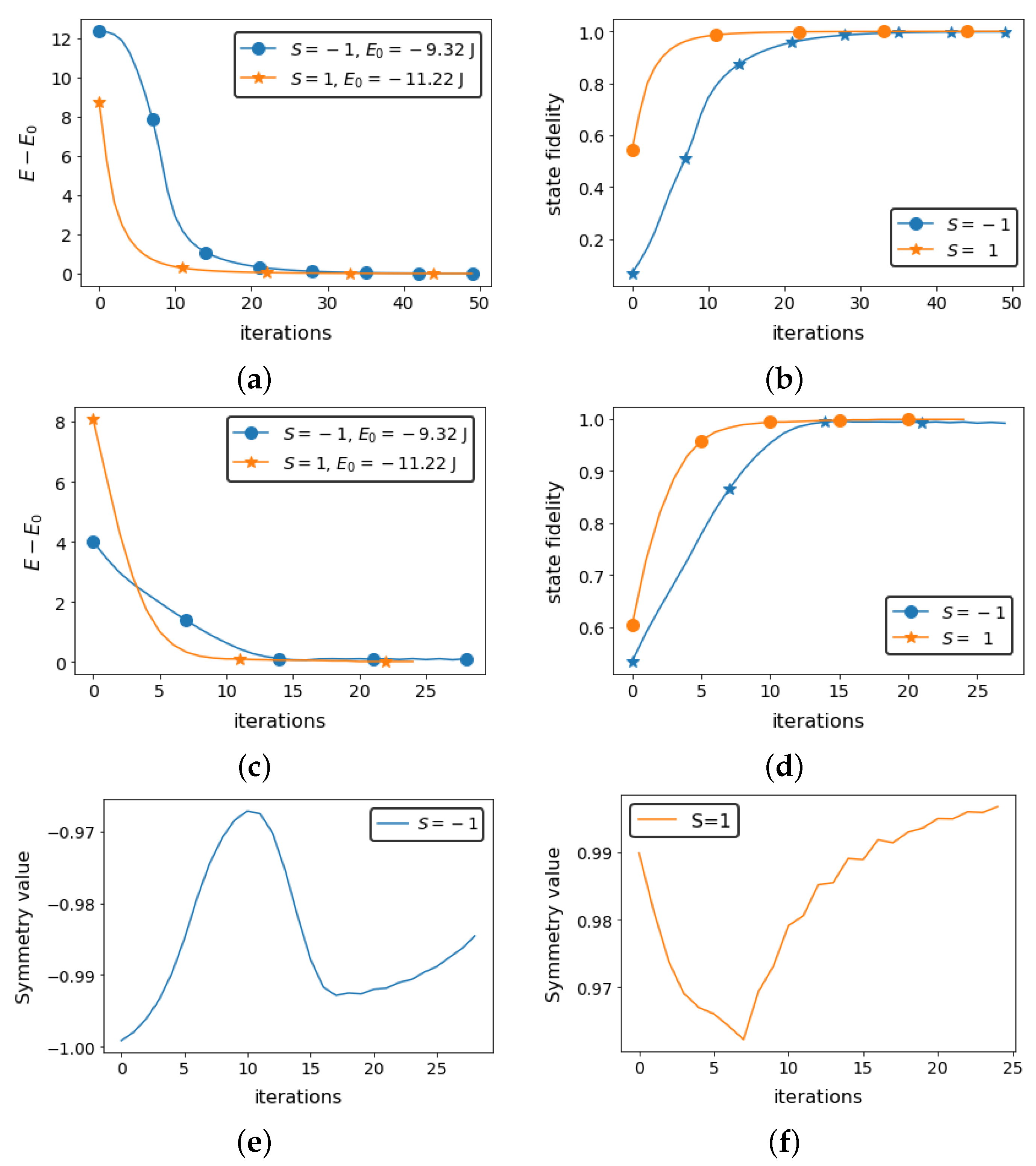
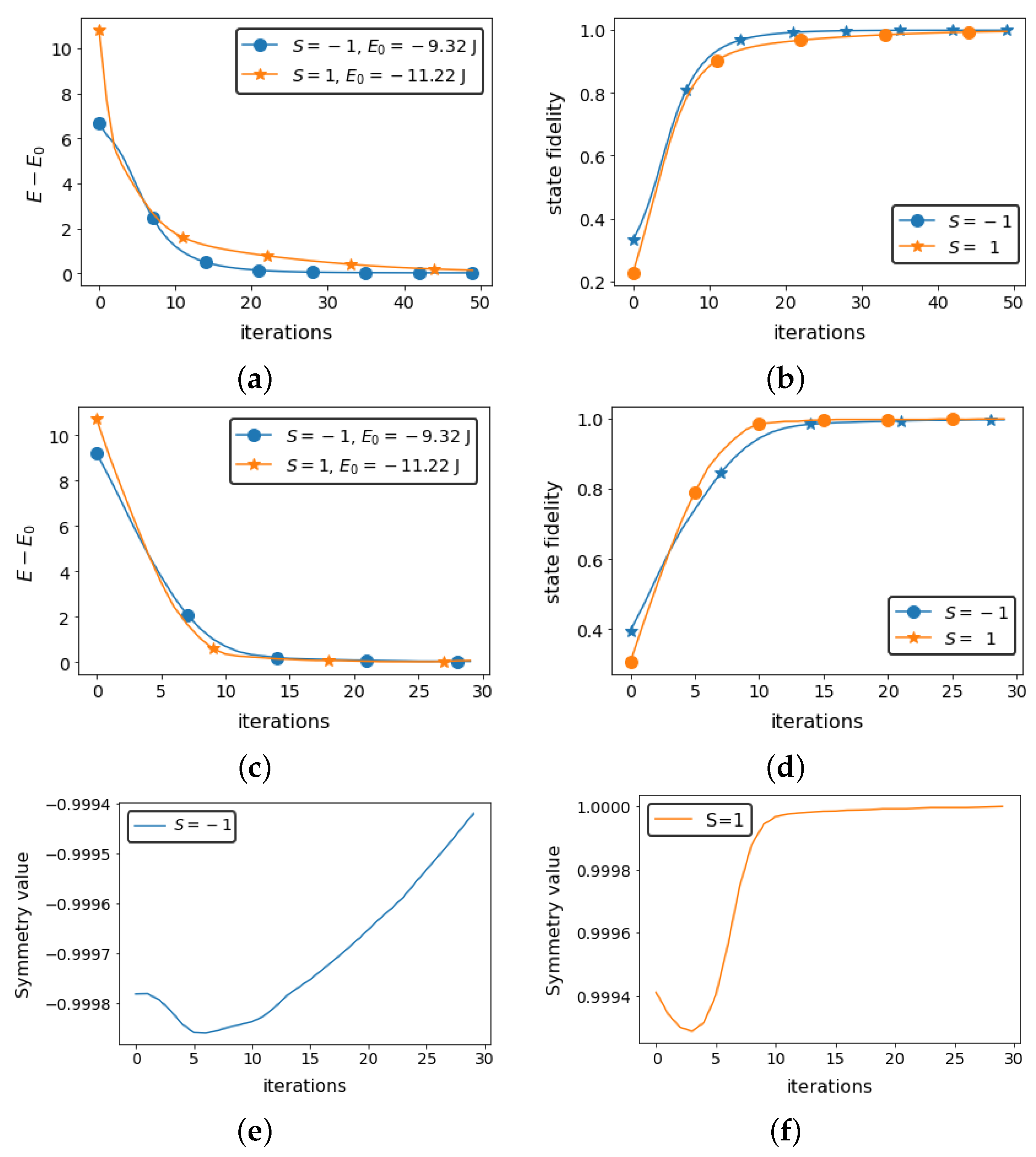
3. Results
3.1. Spin Hamiltonian
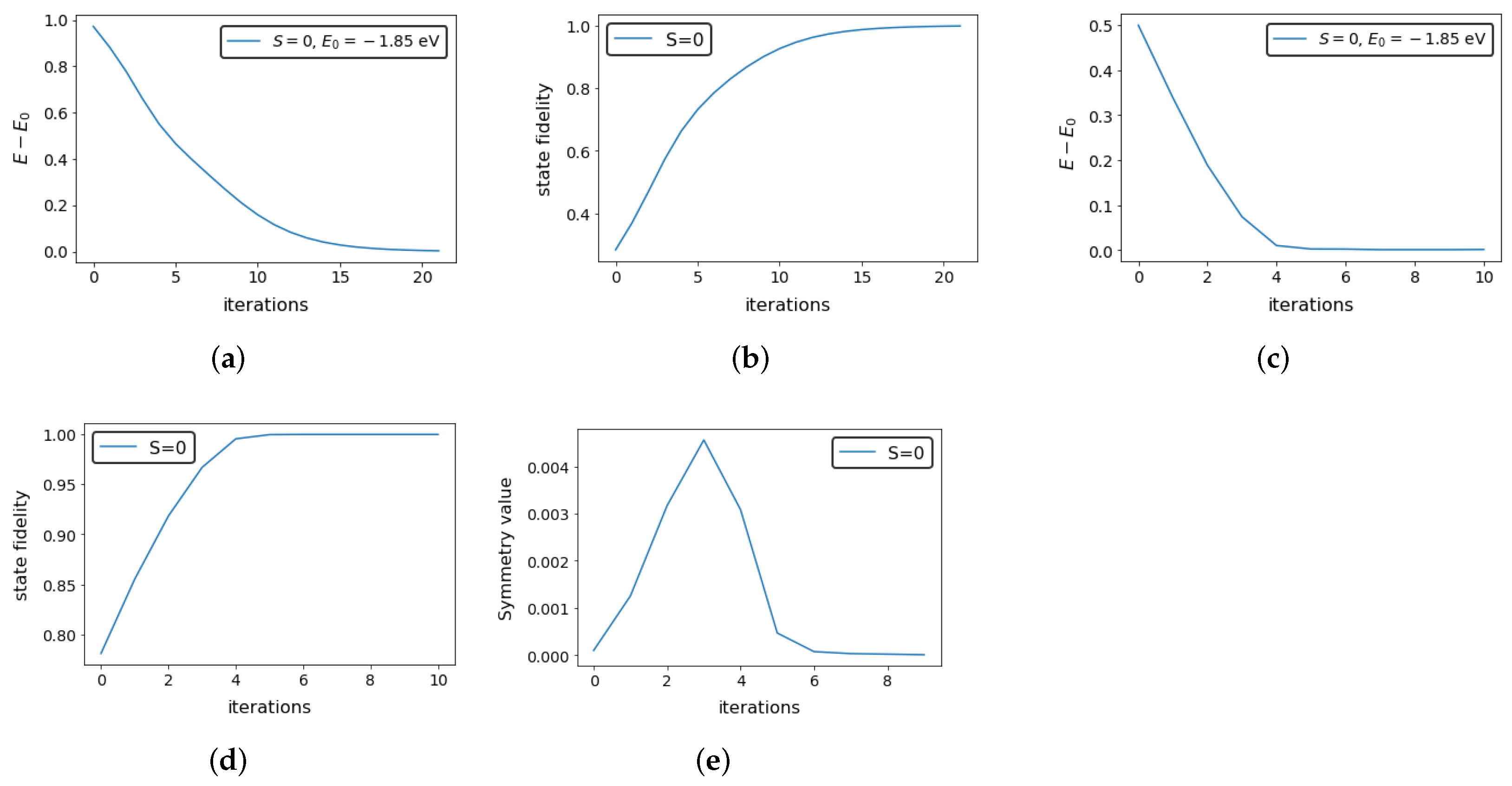
3.1.1. Reflection Symmetry
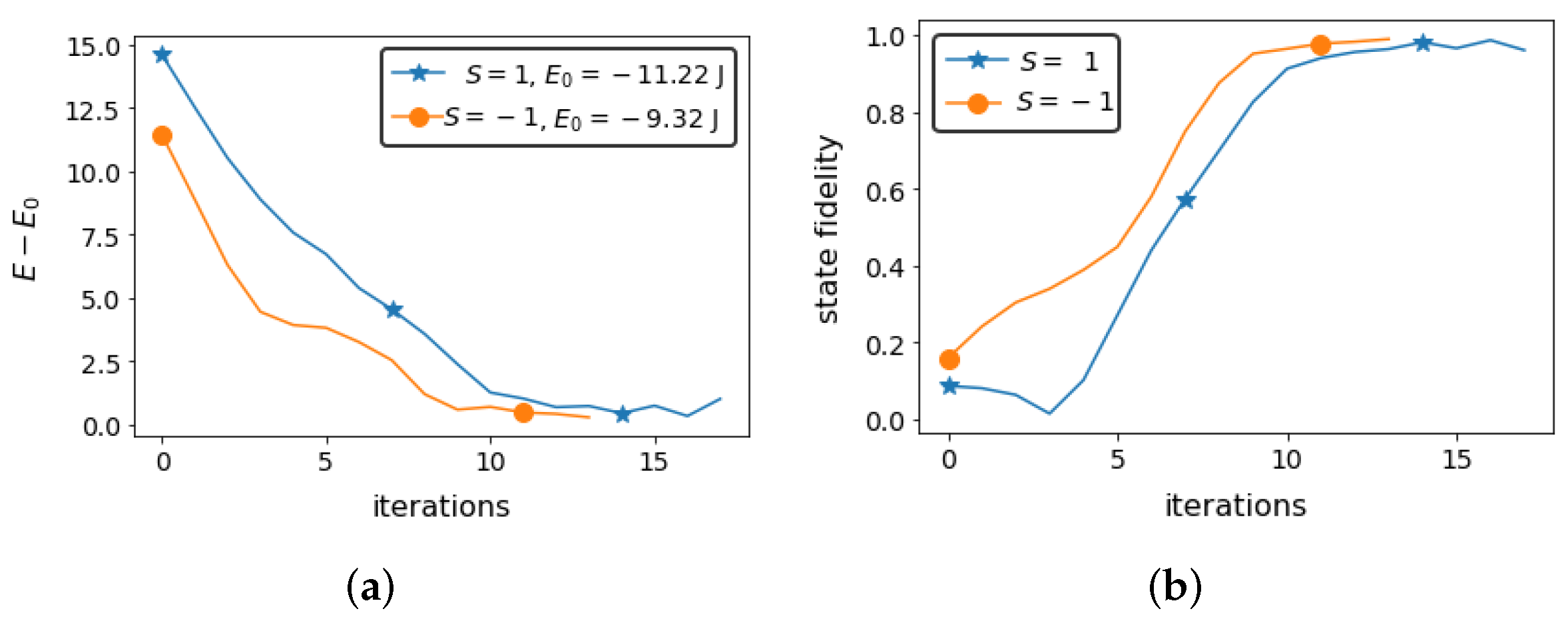
3.1.2. Rotation Symmetry
3.2. Hamiltonian
3.3. Simulation against Noise Models
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Abrams, D.S.; Lloyd, S. Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors. Phys. Rev. Lett. 1999, 83, 5162–5165. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, M.; Chuang, I.; Chuang, I. Quantum Computation and Quantum Information; Cambridge Series on Information and the Natural Sciences; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’Brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Selvarajan, R.; Dixit, V.; Cui, X.; Humble, T.; Kais, S. Prime factorization using quantum variational imaginary time evolution. Sci. Rep. 2021, 11, 20835. [Google Scholar] [CrossRef] [PubMed]
- O’Malley, P.J.J.; Babbush, R.; Kivlichan, I.D.; Romero, J.; McClean, J.R.; Barends, R.; Kelly, J.; Roushan, P.; Tranter, A.; Ding, N.; et al. Scalable Quantum Simulation of Molecular Energies. Phys. Rev. X 2016, 6, 031007. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Huggins, W.J.; Head-Gordon, M.; Whaley, K.B. Generalized Unitary Coupled Cluster Wave functions for Quantum Computation. J. Chem. Theory Comput. 2018, 15, 311–324. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Huang, H.Y.; Campbell, E.T. Nearly tight Trotterization of interacting electrons. Quantum 2021, 5, 495. [Google Scholar] [CrossRef]
- Xia, R.; Kais, S. Quantum Machine Learning for Electronic Structure Calculations. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [Green Version]
- Kandala, A.; Mezzacapo, A.; Temme, K.; Takita, M.; Brink, M.; Chow, J.M.; Gambetta, J.M. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 2017, 549, 242–246. [Google Scholar] [CrossRef]
- Ryabinkin, I.G.; Genin, S.N.; Izmaylov, A.F. Constrained Variational Quantum Eigensolver: Quantum Computer Search Engine in the Fock Space. 2018. Available online: http://xxx.lanl.gov/abs/1806.00461 (accessed on 22 December 2021).
- Barkoutsos, P.; Gonthier, J.; Sokolov, I.; Moll, N.; Salis, G.; Fuhrer, A.; Ganzhorn, M.; Egger, D.; Troyer, M.; Mezzacapo, A.; et al. Quantum algorithms for electronic structure calculations: Particle/hole Hamiltonian and optimized wavefunction expansions. Phys. Rev. A 2018, 98, 022322. [Google Scholar] [CrossRef] [Green Version]
- Gard, B.T.; Zhu, L.; Barron, G.S.; Mayhall, N.J.; Economou, S.E.; Barnes, E. Efficient symmetry-preserving state preparation circuits for the variational quantum eigensolver algorithm. npj Quantum Inf. 2020, 6. [Google Scholar] [CrossRef]
- Nam, Y.; Chen, J.S.; Pisenti, N.C.; Wright, K.; Delaney, C.; Maslov, D.; Brown, K.R.; Allen, S.; Amini, J.M.; Apisdorf, J.; et al. Ground-State Energy Estimation of the Water Molecule on a Trapped Ion Quantum Computer. 2019. Available online: http://xxx.lanl.gov/abs/1902.10171 (accessed on 22 December 2021).
- Colless, J.I.; Ramasesh, V.V.; Dahlen, D.; Blok, M.S.; Kimchi-Schwartz, M.E.; McClean, J.R.; Carter, J.; de Jong, W.A.; Siddiqi, I. Computation of Molecular Spectra on a Quantum Processor with an Error-Resilient Algorithm. Phys. Rev. X 2018, 8, 011021. [Google Scholar] [CrossRef] [Green Version]
- McCaskey, A.J.; Parks, Z.P.; Jakowski, J.; Moore, S.V.; Morris, T.; Humble, T.S.; Pooser, R.C. Quantum Chemistry as a Benchmark for Near-Term Quantum Computers. 2019. Available online: http://xxx.lanl.gov/abs/1905.01534 (accessed on 22 December 2021).
- Shen, Y.; Zhang, X.; Zhang, S.; Zhang, J.N.; Yung, M.H.; Kim, K. Quantum implementation of the unitary coupled cluster for simulating molecular electronic structure. Phys. Rev. A 2017, 95. [Google Scholar] [CrossRef] [Green Version]
- Kuroiwa, K.; Nakagawa, Y.O. Penalty methods for a variational quantum eigensolver. Phys. Rev. Res. 2021, 3, 013197. [Google Scholar] [CrossRef]
- Sajjan, M.; Sureshbabu, S.H.; Kais, S. Quantum Machine-Learning for Eigenstate Filtration in Two-Dimensional Materials. J. Am. Chem. Soc. 2021, 143. [Google Scholar] [CrossRef]
- Schuld, M.; Bergholm, V.; Gogolin, C.; Izaac, J.; Killoran, N. Evaluating analytic gradients on quantum hardware. Phys. Rev. A 2019, 99. [Google Scholar] [CrossRef] [Green Version]
- Mitarai, K.; Negoro, M.; Kitagawa, M.; Fujii, K. Quantum circuit learning. Phys. Rev. A 2018, 98. [Google Scholar] [CrossRef] [Green Version]
- Mitarai, K.; Fujii, K. Methodology for replacing indirect measurements with direct measurements. Phys. Rev. Res. 2019, 1, 013006. [Google Scholar] [CrossRef] [Green Version]
- Aleksandrowicz, G.; Alexander, T.; Barkoutsos, P.; Bello, L.; Ben-Haim, Y.; Bucher, D.; Cabrera-Hernández, F.J.; Carballo-Franquis, J.; Chen, A.; Chen, C.-F.; et al. Qiskit: An Open-Source Framework for Quantum Computing. Zenodo 2019. [Google Scholar] [CrossRef]
- Joel, K.; Kollmar, D.; Santos, L.F. An introduction to the spectrum, symmetries, and dynamics of spin-1/2 Heisenberg chains. Am. J. Phys. 2013, 81, 450–457. [Google Scholar] [CrossRef] [Green Version]
- Iten, R.; Colbeck, R.; Kukuljan, I.; Home, J.; Christandl, M. Quantum circuits for isometries. Phys. Rev. A 2016, 93. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Gomes, N.; Berthusen, N.F.; Orth, P.P.; Wang, C.Z.; Ho, K.M.; Yao, Y.X. Shallow-circuit variational quantum eigensolver based on symmetry-inspired Hilbert space partitioning for quantum chemical calculations. Phys. Rev. Res. 2021, 3. [Google Scholar] [CrossRef]
- Nakajima, Y.; Kawano, Y.; Sekigawa, H. A New Algorithm for Producing Quantum Circuits Using KAK Decompositions. 2005. Available online: http://xxx.lanl.gov/abs/quant-ph/0509196 (accessed on 22 December 2021).
- Larocca, M.; Czarnik, P.; Sharma, K.; Muraleedharan, G.; Coles, P.J.; Cerezo, M. Diagnosing Barren Plateaus with Tools from Quantum Optimal Control. 2021. Available online: http://xxx.lanl.gov/abs/2105.14377 (accessed on 22 December 2021).
- Cerezo, M.; Sone, A.; Volkoff, T.; Cincio, L.; Coles, P.J. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nat. Commun. 2021, 12, 1791. [Google Scholar] [CrossRef] [PubMed]

| Qubit No. | T1 (us) | T2 (us) | Readout-Error (%) | Frequency (GHz) | Anharomonicity (GHz) |
|---|---|---|---|---|---|
| 1 | 121.70 | 17.04 | 7.50 | 4.79 | −0.31 |
| 2 | 111.68 | 132.02 | 2.24 | 4.94 | −0.30 |
| 3 | 101.82 | 68.98 | 1.45 | 4.83 | −0.31 |
| 4 | 116.71 | 85.88 | 2.15 | 4.80 | −0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvarajan, R.; Sajjan, M.; Kais, S. Variational Quantum Circuits to Prepare Low Energy Symmetry States. Symmetry 2022, 14, 457. https://doi.org/10.3390/sym14030457
Selvarajan R, Sajjan M, Kais S. Variational Quantum Circuits to Prepare Low Energy Symmetry States. Symmetry. 2022; 14(3):457. https://doi.org/10.3390/sym14030457
Chicago/Turabian StyleSelvarajan, Raja, Manas Sajjan, and Sabre Kais. 2022. "Variational Quantum Circuits to Prepare Low Energy Symmetry States" Symmetry 14, no. 3: 457. https://doi.org/10.3390/sym14030457
APA StyleSelvarajan, R., Sajjan, M., & Kais, S. (2022). Variational Quantum Circuits to Prepare Low Energy Symmetry States. Symmetry, 14(3), 457. https://doi.org/10.3390/sym14030457







