Lower Triangular Factor-Based Fault Estimation and Fault-Tolerant Control for Descriptor Markovian Jump Systems with Multiple Faults
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
- regular—if there is a constant scalar s such thator equivalently, the polynomial is not identically zero for .
- impulse free—if , .
3. Main Results
3.1. Lower Triangular Factor-Based Estimation Observer Design
3.2. Fault-Tolerant Control
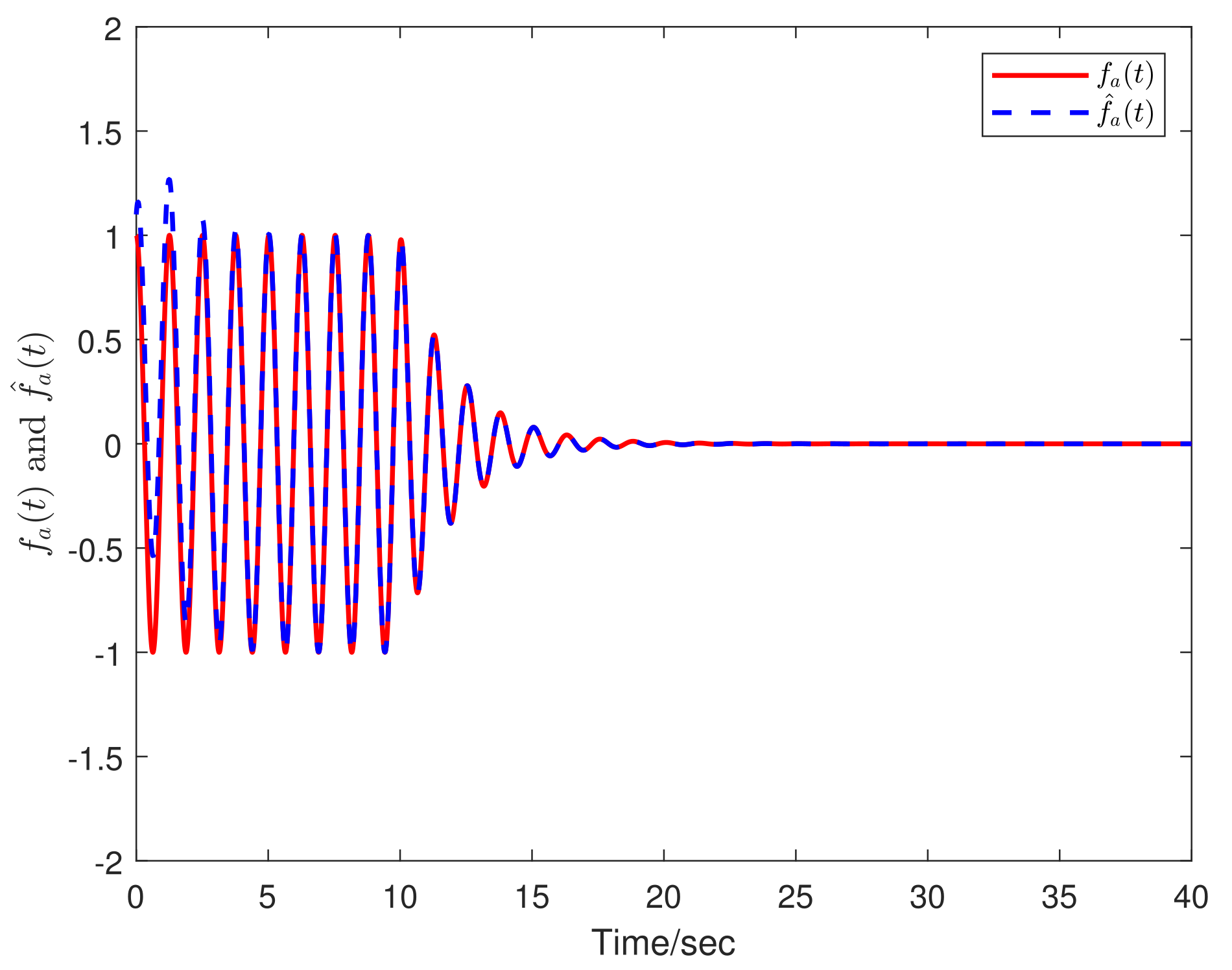
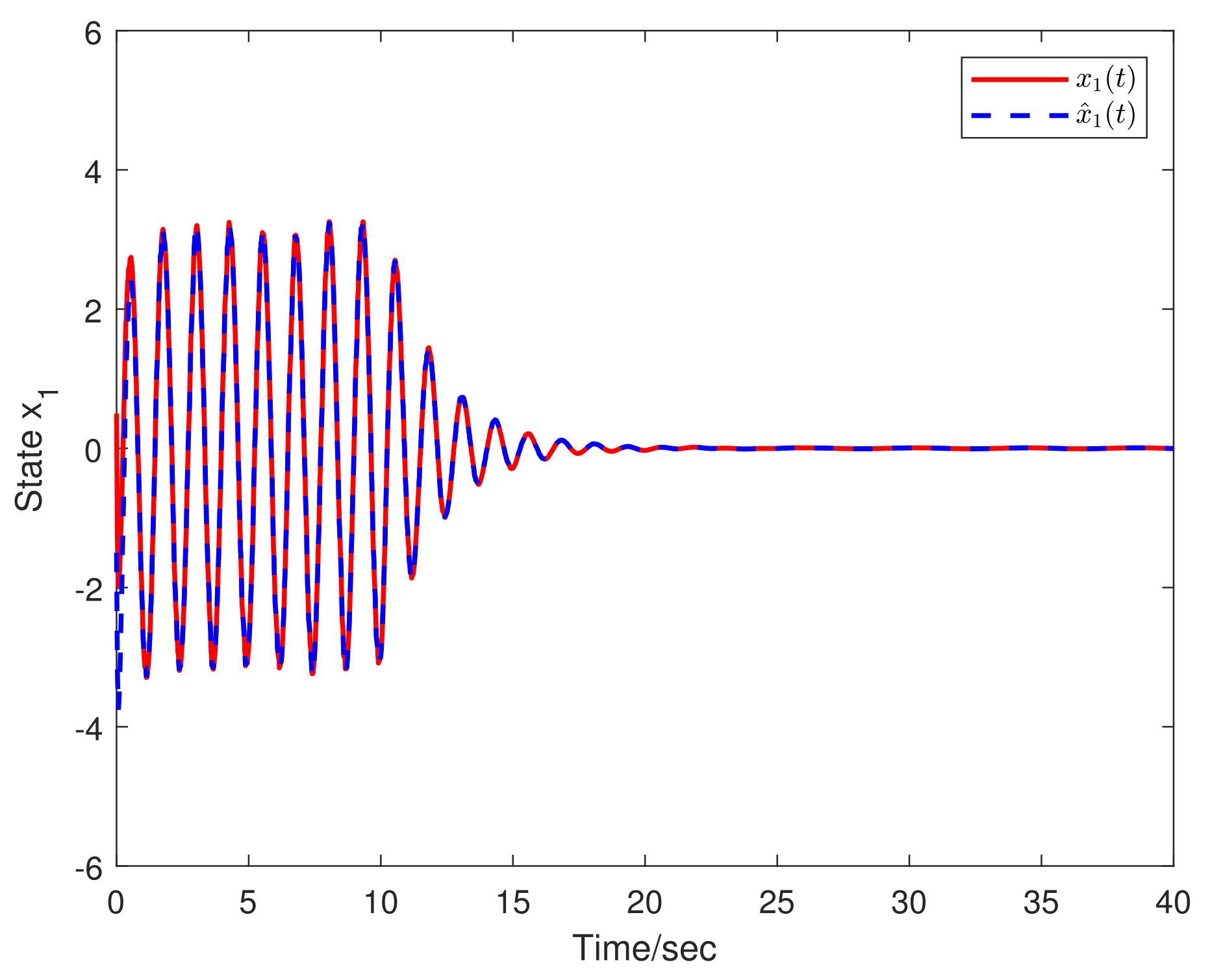
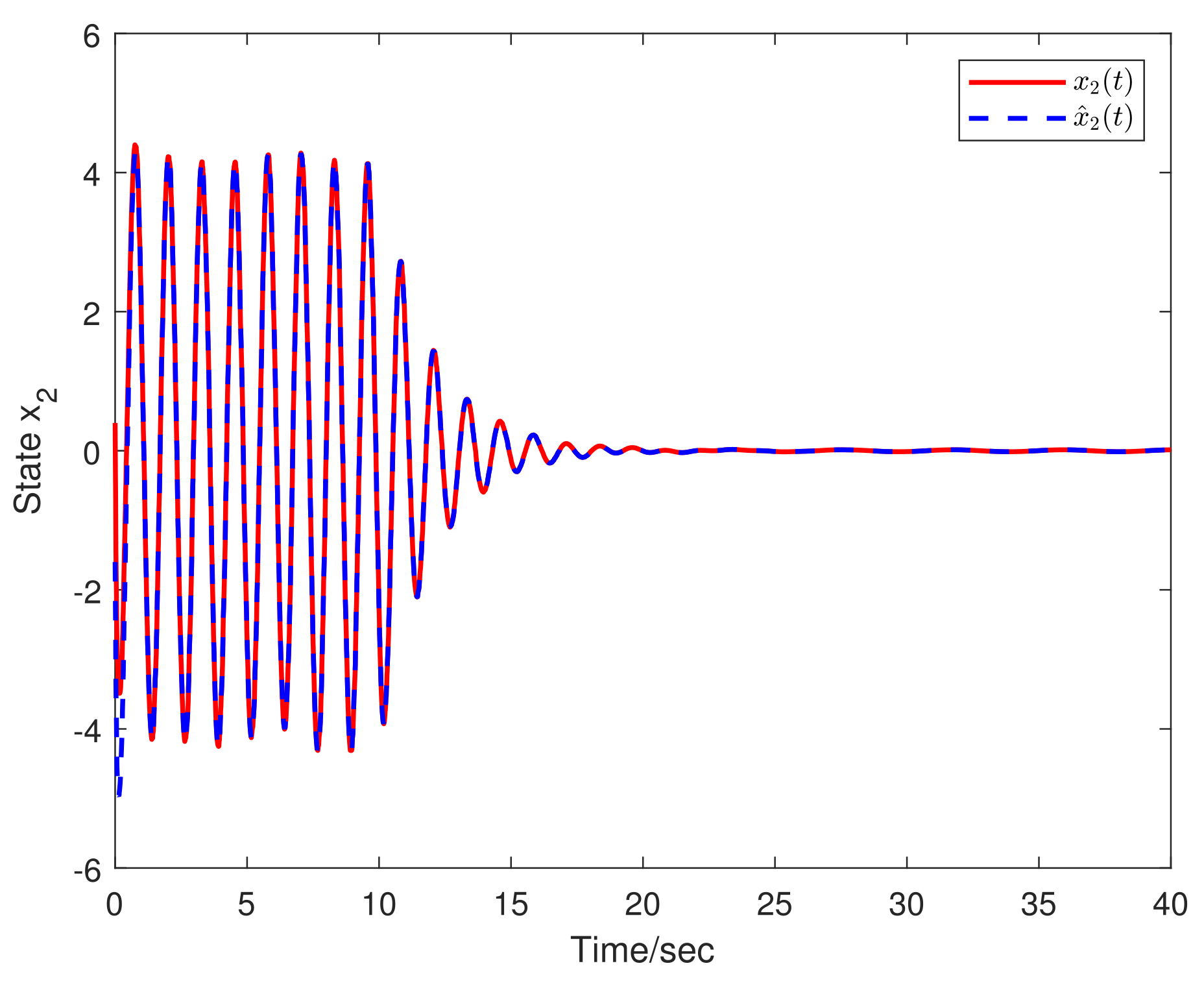
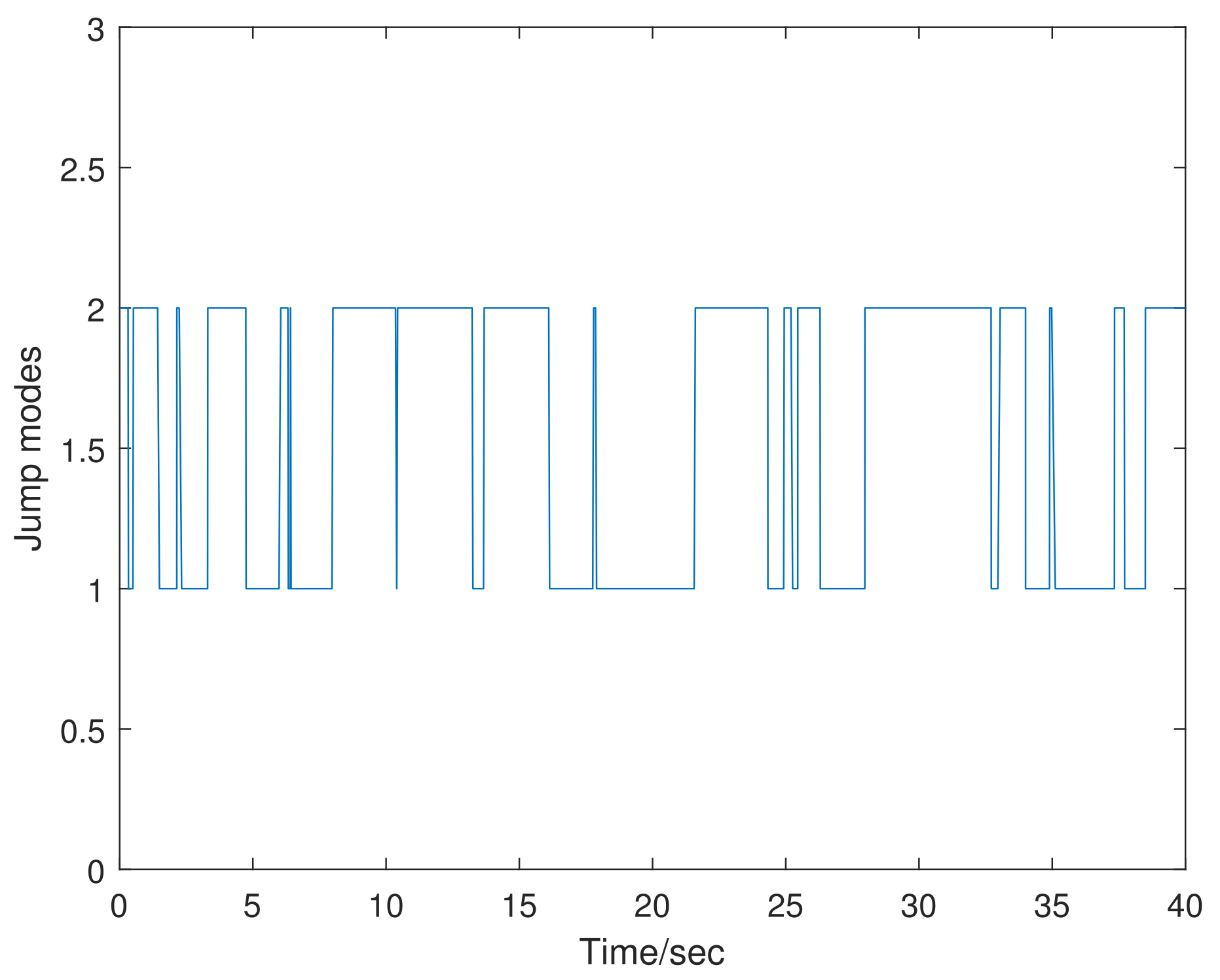
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, S.; Lam, J. Robust Control and Filtering of Singular Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Li, J.; Yang, G.H. Fuzzy descriptor sliding mode observer design: A canonical form-based method. IEEE Trans. Fuzzy Syst. 2019, 28, 2048–2062. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Zhang, X. Complexity, Analysis and Control of Singular Biological Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 421. [Google Scholar]
- Duan, G.R. Analysis and Design of Descriptor Linear Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 23. [Google Scholar]
- Li, J.; Zhai, D. A descriptor regular form-based approach to observer-based integral sliding mode controller design. Int. J. Robust Nonlinear Control 2021, 31, 5134–5148. [Google Scholar] [CrossRef]
- Dai, L. Singular Control Systems; Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 1989; Volume 118. [Google Scholar]
- Li, Y.; Yu, Z.; Liu, Y.; Ren, J. Stochastic Stabilization for Discrete-Time Markovian Jump Systems With Time-Varying Delay and Two Markov Chains Under Partly Known Transition Probabilities. IEEE Access 2021, 9, 26937–26947. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Q.; Ren, J.; Liu, Y. Sliding mode control of one-sided Lipschitz nonlinear Markovian jump systems with partially unknown transition rates. IEEE Access 2020, 8, 158306–158316. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Yan, X.G.; Spurgeon, S.K. Integral sliding mode control for Markovian jump T–S fuzzy descriptor systems based on the super-twisting algorithm. IET Control Theory Appl. 2017, 11, 1134–1143. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.G.; Park, J.H.; Su, H.; Chu, J. Delay-dependent passivity for singular Markov jump systems with time-delays. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 669–681. [Google Scholar] [CrossRef]
- Wang, G.L. Robust stabilization of singular Markovian jump systems with uncertain switching. Int. J. Control Autom. Syst. 2013, 11, 188–193. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q. Finite-time H∞ control for singular Markovian jump systems with partly unknown transition rates. Appl. Math. Model. 2016, 40, 302–314. [Google Scholar] [CrossRef]
- Lam, J.; Shu, Z.; Xu, S.; Boukas, E.K. Robust control of descriptor discrete-time Markovian jump systems. Int. J. Control 2007, 80, 374–385. [Google Scholar] [CrossRef]
- Hamayun, M.T.; Edwards, C.; Alwi, H. Fault Tolerant Control Schemes Using Integral Sliding Modes; Springer: Berlin, Germany, 2016. [Google Scholar]
- Chakravarty, A.; Mahanta, C. Actuator fault-tolerant control (FTC) design with post-fault transient improvement for application to aircraft control. Int. J. Robust Nonlinear Control 2016, 26, 2049–2074. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin, Germany, 2006; Volume 2. [Google Scholar]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Li, X.; Karimi, H.R.; Wang, Y.; Lu, D.; Guo, S. Robust fault estimation and fault-tolerant control for Markovian jump systems with general uncertain transition rates. J. Frankl. Inst. 2018, 355, 3508–3540. [Google Scholar] [CrossRef]
- Rodrigues, M.; Hamdi, H.; Theilliol, D.; Mechmeche, C.; BenHadj Braiek, N. Actuator fault estimation based adaptive polytopic observer for a class of LPV descriptor systems. Int. J. Robust Nonlinear Control 2015, 25, 673–688. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.J.; Yang, G.H. Fault estimation for fuzzy delay systems: A minimum norm least squares solution approach. IEEE Trans. Cybern. 2016, 47, 2389–2399. [Google Scholar] [CrossRef]
- Liu, M.; Shi, P.; Zhang, L.; Zhao, X. Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique. IEEE Trans. Circuits Syst. Regul. Pap. 2011, 58, 2755–2764. [Google Scholar] [CrossRef]
- Zhu, J.W.; Yang, G.H.; Wang, H.; Wang, F. Fault estimation for a class of nonlinear systems based on intermediate estimator. IEEE Trans. Autom. Control 2015, 61, 2518–2524. [Google Scholar] [CrossRef]
- Huang, S.J.; Zhang, D.Q.; Guo, L.D.; Wu, L.B. Lower Triangle Factor-Based Fault Estimation and Fault Tolerant Control for Fuzzy Systems. IEEE Trans. Fuzzy Syst. 2019, 28, 2533–2542. [Google Scholar] [CrossRef]
- Shi, P.; Liu, M.; Zhang, L. Fault-tolerant sliding-mode-observer synthesis of Markovian jump systems using quantized measurements. IEEE Trans. Ind. Electron. 2015, 62, 5910–5918. [Google Scholar] [CrossRef] [Green Version]
- Jin, X. Adaptive fault-tolerant control for a class of output-constrained nonlinear systems. Int. J. Robust Nonlinear Control 2015, 25, 3732–3745. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, D. Distributed adaptive fault-tolerant control of pure-feedback nonlinear multi-agent systems with actuator failures. Neurocomputing 2017, 221, 72–84. [Google Scholar] [CrossRef]
- Liu, M.; Ho, D.W.; Shi, P. Adaptive fault-tolerant compensation control for Markovian jump systems with mismatched external disturbance. Automatica 2015, 58, 5–14. [Google Scholar] [CrossRef]
- Liu, M.; Cao, X.; Shi, P. Fault estimation and tolerant control for fuzzy stochastic systems. IEEE Trans. Fuzzy Syst. 2012, 21, 221–229. [Google Scholar] [CrossRef]
- Angeli, D.; Sontag, E.D.; Wang, Y. Input-to-state stability with respect to inputs and their derivatives. Int. J. Robust Nonlinear Control.-Ifac-Affil. J. 2003, 13, 1035–1056. [Google Scholar] [CrossRef]
- Khargonekar, P.P.; Petersen, I.R.; Zhou, K. Robust stabilization of uncertain linear systems: Quadratic stabilizability and H/sup infinity/control theory. IEEE Trans. Autom. Control 1990, 35, 356–361. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Staroswiecki, M. Dynamic output feedback-fault tolerant controller design for Takagi–Sugeno fuzzy systems with actuator faults. IEEE Trans. Fuzzy Syst. 2009, 18, 194–201. [Google Scholar] [CrossRef]
- Huang, S.J.; Yang, G.H. Fault tolerant controller design for T–S fuzzy systems with time-varying delay and actuator faults: A K-step fault-estimation approach. IEEE Trans. Fuzzy Syst. 2014, 22, 1526–1540. [Google Scholar] [CrossRef]
- Wang, G.; Yi, C. Fault estimation for nonlinear systems by an intermediate estimator with stochastic failure. Nonlinear Dyn. 2017, 89, 1195–1204. [Google Scholar] [CrossRef]
- Dynkin, E.B. Functionals of Markov Processes: Markov Processes; Springer: Berlin/Heidelberg, Germany, 1965. [Google Scholar]
- Li, X.; Zhu, F. Fault-tolerant control for Markovian jump systems with general uncertain transition rates against simultaneous actuator and sensor faults. Int. J. Robust Nonlinear Control 2017, 27, 4245–4274. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Hoboken, NJ, USA, 2001. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, X.; Shi, H.; Bao, A. Lower Triangular Factor-Based Fault Estimation and Fault-Tolerant Control for Descriptor Markovian Jump Systems with Multiple Faults. Symmetry 2022, 14, 382. https://doi.org/10.3390/sym14020382
Su X, Shi H, Bao A. Lower Triangular Factor-Based Fault Estimation and Fault-Tolerant Control for Descriptor Markovian Jump Systems with Multiple Faults. Symmetry. 2022; 14(2):382. https://doi.org/10.3390/sym14020382
Chicago/Turabian StyleSu, Xiaoming, Haoda Shi, and Adiya Bao. 2022. "Lower Triangular Factor-Based Fault Estimation and Fault-Tolerant Control for Descriptor Markovian Jump Systems with Multiple Faults" Symmetry 14, no. 2: 382. https://doi.org/10.3390/sym14020382
APA StyleSu, X., Shi, H., & Bao, A. (2022). Lower Triangular Factor-Based Fault Estimation and Fault-Tolerant Control for Descriptor Markovian Jump Systems with Multiple Faults. Symmetry, 14(2), 382. https://doi.org/10.3390/sym14020382





