A Lévy Distribution Based Searching Scheme for the Discrete Targets in Vast Region

Abstract

This paper investigates the Discrete Targets Search Problem, (DTSP), which aims to quickly search for discrete objects scattered in a vast symmetry region. Different from continuous function extremal value search, the discrete points search cannot make use of the properties of regular functions, such as function analytic, single/multiple extreme, and monotonicity. Thus, in this paper a new search scheme based on Lévy random distribution is investigated. In comparison with the $Traditional$ $Carpet$ search or $Random$ search based on other distributions, DTSP can provide much faster search speed which is demonstrated by simulation with different scales problems for the selected scenarios. The simulations experiment proves that DTSP is faster for searching for a discrete single target or multiple targets in a wide area. It provides a new method for solving the discrete target search problem.

1. Introduction

This paper is motivated by a world-wide focused case, the lost connection of the Malaysia Airlines Flight 370 (MH370). It has been missing up to now since then. Dozens of countries around the world have attempted the search using different kinds of most advanced technology such as radio “pings” between the aircraft and an Inmarsat satellite based on military radar data. Unfortunately, there has been neither confirmation of flight debris nor indication of crash sites. This paper defines the sea target search, grassland target search, desert target search, etc., in a large area as Discrete Targets Search Problem which is $DTSP$ for short. $DTSP$ has a wide range of applications, such as in the case of war, how to quickly search the enemy warships group. In addition, the rescue of airplane crashes, shipwrecks, and the desert search, etc. can be conversed with $DTSP$ to be solved. Because search goal area is very large, the search target is a decentralized point, and characteristics of targets are not clear, $DTSP$ is very difficult, and the research report on it is more visible. In a large area, see in Figure 1 for how to quickly search target. Research $DTSP$ has great practical meaning.

There are some reports on the study of target recognition search, mainly through radar, infrared, robot, and other tracking. Some pioneer researchers reported about target recognition, target acquisition, and target tracking. For example, references [1,2] considered the case of heuristic search where the location of the goal may change during the course of the search. They introduced ideas from the area of resource-bounded planning into a Moving Target Search ($MTS$) algorithm, including commitment to god and deliberation for selecting plans. J. R. R. Uijlings et al. [3] addresses the problem of generating possible object locations for the use in object recognition. They introduce selective search by combining the strength of both an exhaustive search and segmentation. Grimaldo Silva et al. [4] proposed the use of saliency information to organize regions based on their probability of containing objects. Xin, ZH et al. introduced a new ground moving-target-focused method for airborne synthetic aperture radar in [5]. Compared to conventional $SAR$ imaging methods, it can eliminate the effects of Doppler ambiguity and azimuth spectrum split. Mohamed Abd Allah El-Hadidy in [6] presented a search model that finds n-dimensional randomly moving target in which no information of the target position is available to the searchers. Zhen Shi et al. in [7] proposed a parallel search strategy based on kernel sparse representation to perform the tracking task in the FLIR sequences. The kernel method is used to deal with complex appearance variations. A variety of different target search problems were reported with different technical strategies, such as $UAVs$ [8] and robots [9,10,11]. However, there are a few references about the discrete point object search problem. This paper discusses different strategies to study how to search discrete point object efficiently. In addition, there are more researches on the problem of discrete target search from the aspects of infrared and radar technology but fewer research reports from the perspective of image processing and algorithms.

The discrete point search problem is very different from the extreme value of function search problem (see Figure 2). In this case, the objects are isolated, and they are not related to each other. However, in the extreme value of function search problem, extreme points and other points are related, such that intelligent iterative calculation can be used to find their extreme point. Aiming at the particularity of discrete target search problem, this article proposes an efficient and reliable search method to achieve rapid searching target in a wide range of areas. We study the effectiveness of Traditional Carpet search, random search, and Lévy distribution random search for discrete point object, with the following differences from existing ones: Firstly, based on the practical problems of searching for discrete targets in people’s production and life, $DTSP$ is proposed. From an actual target search problem analysis, it summarized and extracted a common technical problem. From the actual target search problem analysis, it summed up the common technical solutions to the problem; secondly, it formulates a new search with different evolution mode, for discrete point object problem; thirdly, it strictly analyzes and compares different search method performance. We show that the proposed search method is more efficient than tradition search and discuss the implication of the results and suggestion for further research.

The remainder of this paper is organized as follows: In Section 2, we sum up the search method for discrete targets in the current reality. In Section 3, we develop the general framework of the search solution. In Section 4, we formulate some dominance properties and model mathematical of $DTSP$. In Section 5, we discuss the Traditional Carpet search, random search, and Lévy distribution random search for discrete point object. The Lévy distribution random search was developed to enhance the search efficiency for the $DTSP$. The results of a computational experiment are provided in Section 6. Some conclusions are given in the last section.

2. The Current Search Method

The traditional search methods are usually used for search in plane crash, ship sank, and desert missing, as well as the search of landslide spot, forest fire spot and rescue, grassland, and enemy warships group, etc. For example, sending aircraft flights to the target area to search for suspicious targets or sending ground and rescue personnel for on-site search. Most of the current searches are Traditional Carpet search, which divide the target area into many lattices to be searched one by one in turn, as shown by Figure 3:

In the past, most actual discrete point object search problems use the Traditional Carpet search to look for target. Rescuers use any possible means; aircraft and ships deploy equipment to listen for signals from the underwater locator beacons attached to the aircraft’s “black box” flight recorders. However the batteries of the beacons become exhausted in a short time. For example in MH370 search, the search operation continued in the area of the signals using a robotic submarine for a long time but without obtaining any evidence of debris.

The efficiency of Traditional Carpet search method is low due to its enumeration nature. It is almost invalid when the target is in a big area. The paper [12] presented a FogLight approach for searching metabolic networks utilizing Boolean (AND-OR) operations represented in matrix notation to efficiently reduce the search space. This paper presents a new idea and method for discrete point object search.

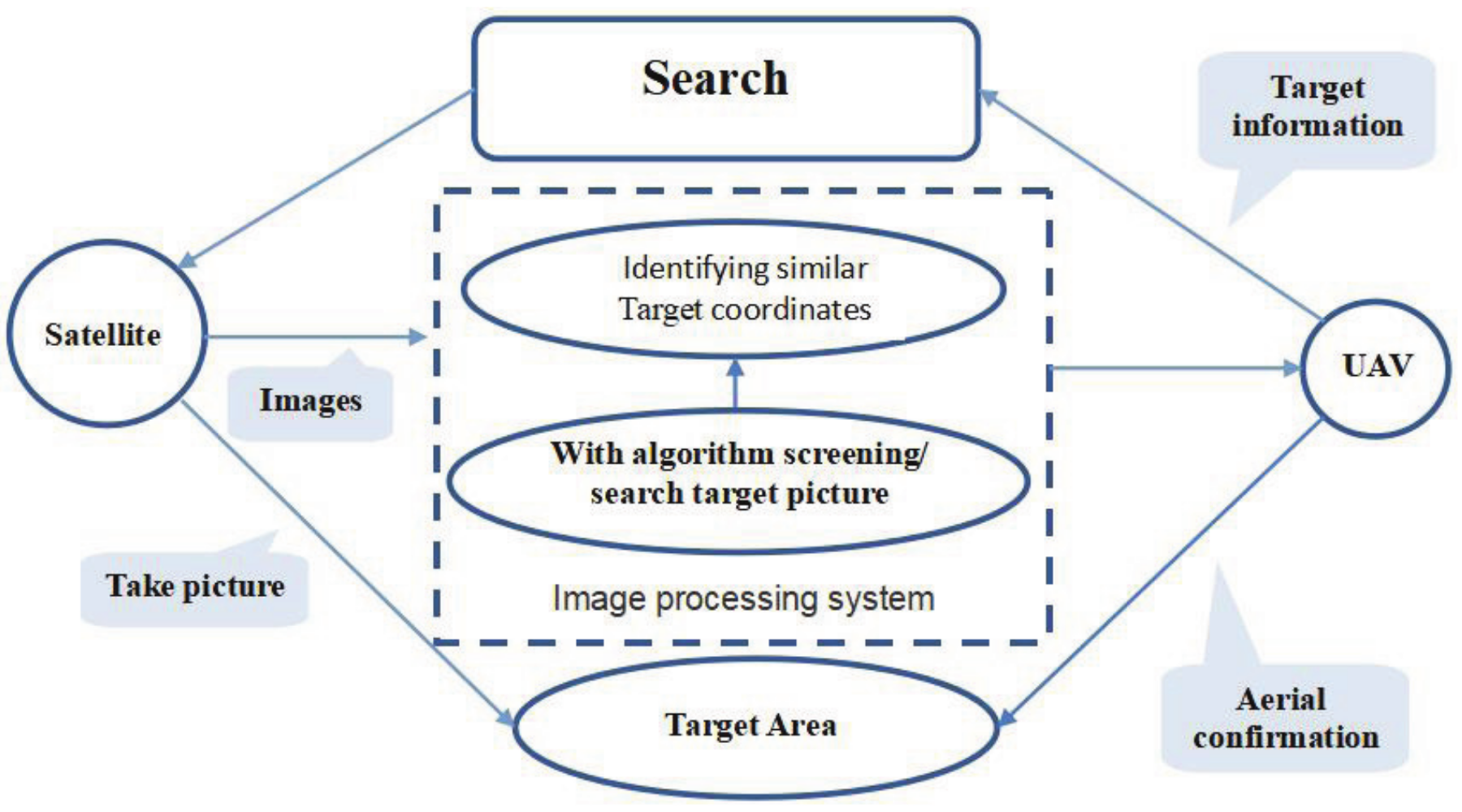
3. New Search Solution Based on Satellite Image

Currently the image processing technology is very mature, and satellite images can be used to look for targets. Methods for image processing include the so-called “M-estimators” (from robust statistics) [13], among others machine learning techniques. This reinforces the credibility of satellite images than can be used in discrete search problems. Robust M-estimators, which are generalizations of maximum-likelihood estimators, tend to look at the bulk of the data/image information and ignore atypical values (outliers or multiple outliers) during estimation procedure (pattern recognition), due to their mathematical structure.

The new algorithm based on satellite images processing operations is as follows:

(1) The search command center informs the satellite control station to adjust satellite attitude and direction to target search area;

(2) The satellite takes a picture of search target area and then promptly sends the image to the processing center;

(3) The image processing center first amplifies satellite photographs and cuts them into the lattice images. Secondly, the algorithm chooses the lattice images to identify which image is the target. Thirdly, it determines the actual position of the target image and then quickly identifies the suspected target coordinates;

(4) It sends the coordinates of the suspected target to the $UAV$, search aircraft, ship, or ground rescuers to affirm the target and obtain more detailed information;

(5) All information of targets is sent to the search center.

The Discrete Targets search diagram based on the new algorithm with satellite image processing is illustrated in Figure 4:

4. Discrete Target Search Problem

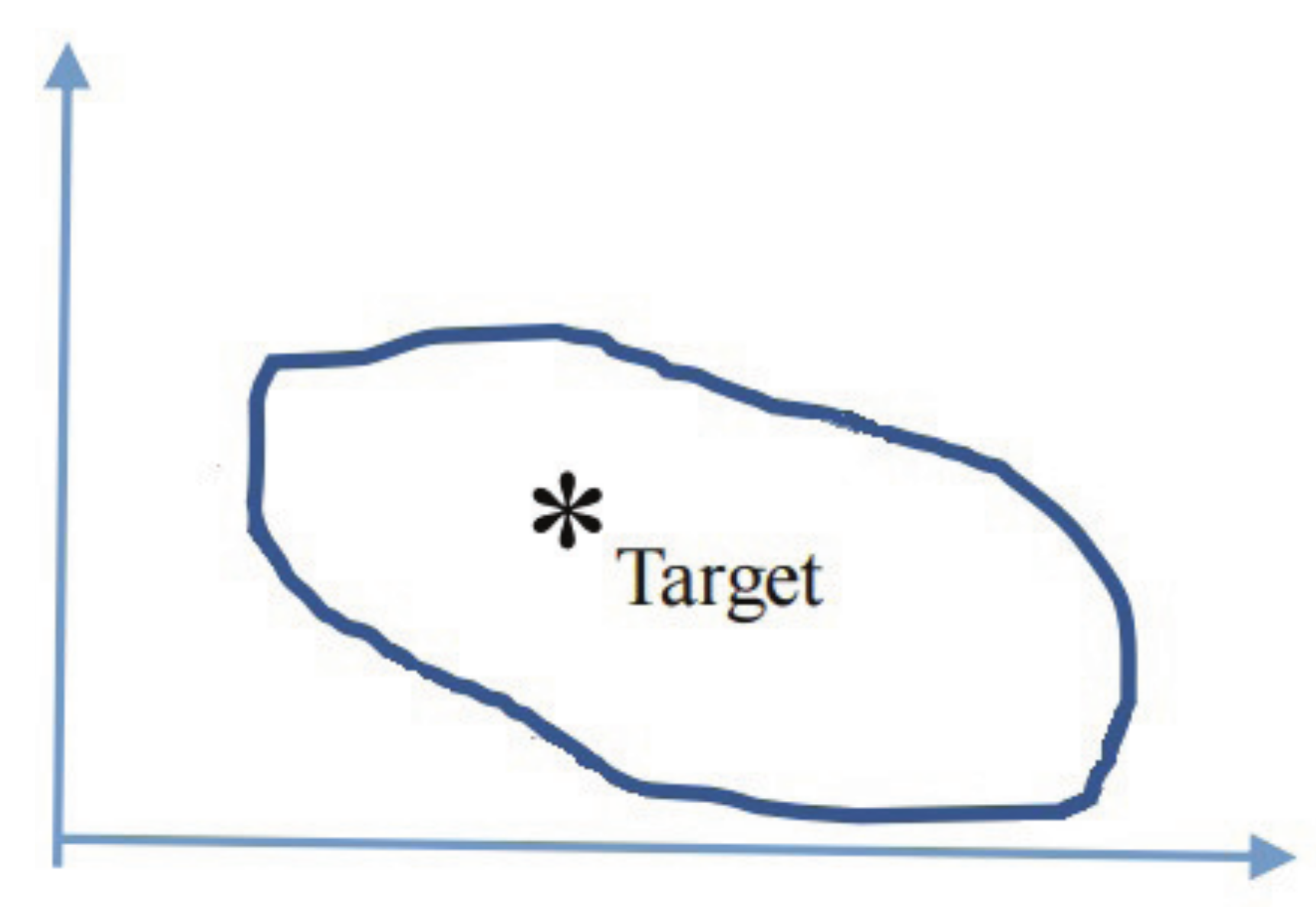
4.1. Target (Black Box) Search Problem

In extreme value of function search problem, the extreme point and other points are related and can share useful information for looking for object. However, with the discrete point target search problem, its target is isolated, and all points are not relative each other. With $DTSP$, other points are not able to provide the useful information to help find the target point. For the special case of $DTSP$, it is impossible to use a traditional method such as intelligent iterative calculation to solve it. Here, we present a new method to solve $DTSP$.

Put the target into the coordinate system. If the coordinate value of target is focused, it is a successful search. The problem of discrete point search is translated into a search problem of a target element in the matrix to look for the coordinate of 1 in one target search matrix (1).

$$\left(\begin{array}{ccccc}0\hfill & 0& \cdots & 0& 0\\ 0\hfill & 0& \cdots & 0& 0\\ \cdots \hfill & \cdots & \cdots & \cdots & \cdots \\ 0\hfill & 0& \cdots & 1& 0\\ 0\hfill & 0& \cdots & 0& 0\end{array}\right)$$

(1)

Code rule/0-1: The target area image is divided into lattice images. If a grid image is an object, the element of the grid image is set to 1 in the matrix. Put all lattice images into matrix with the target image denoted by truth/1 and others by false/0. In the search process, if the coordinate of the 1 point is found the search is successful.

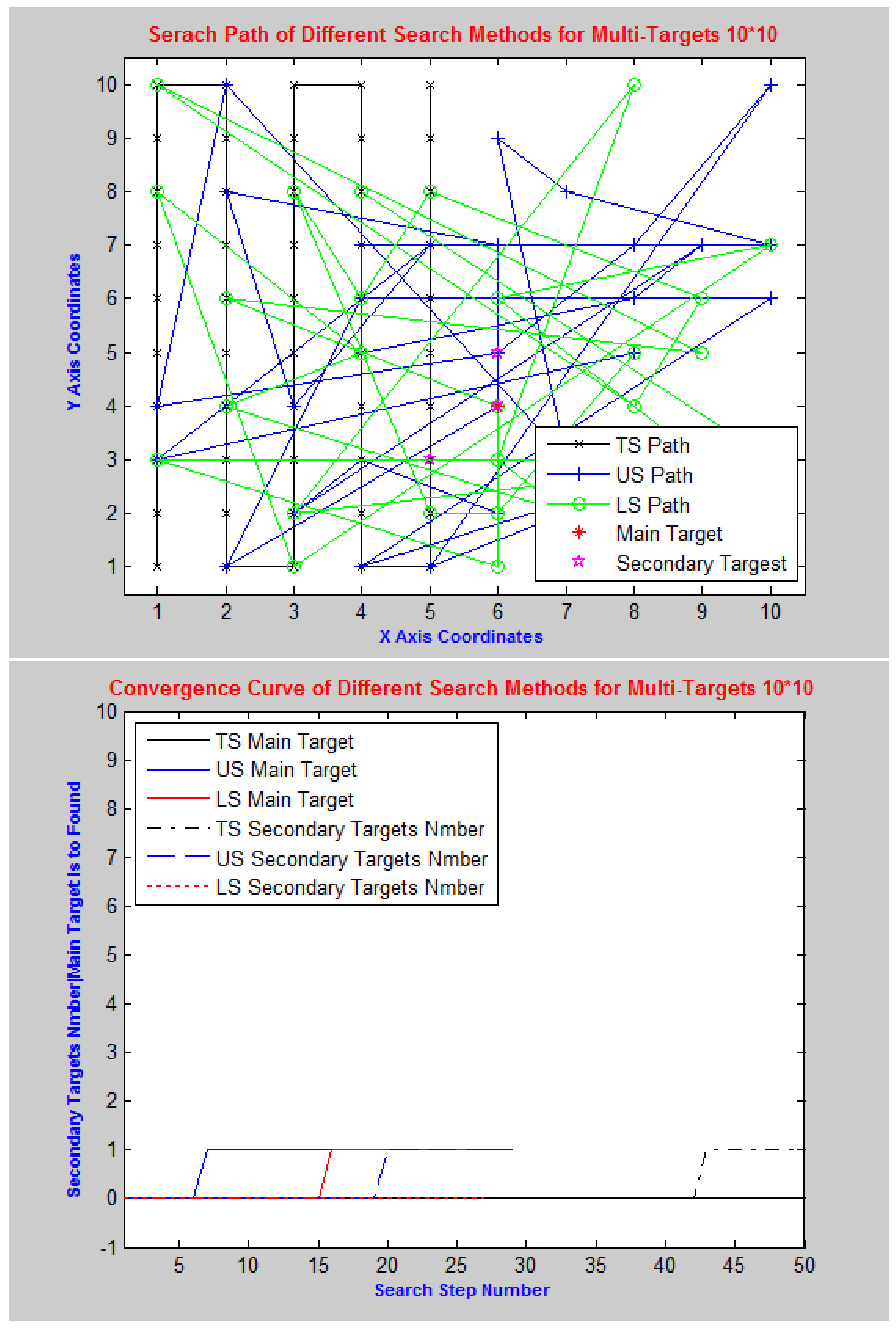
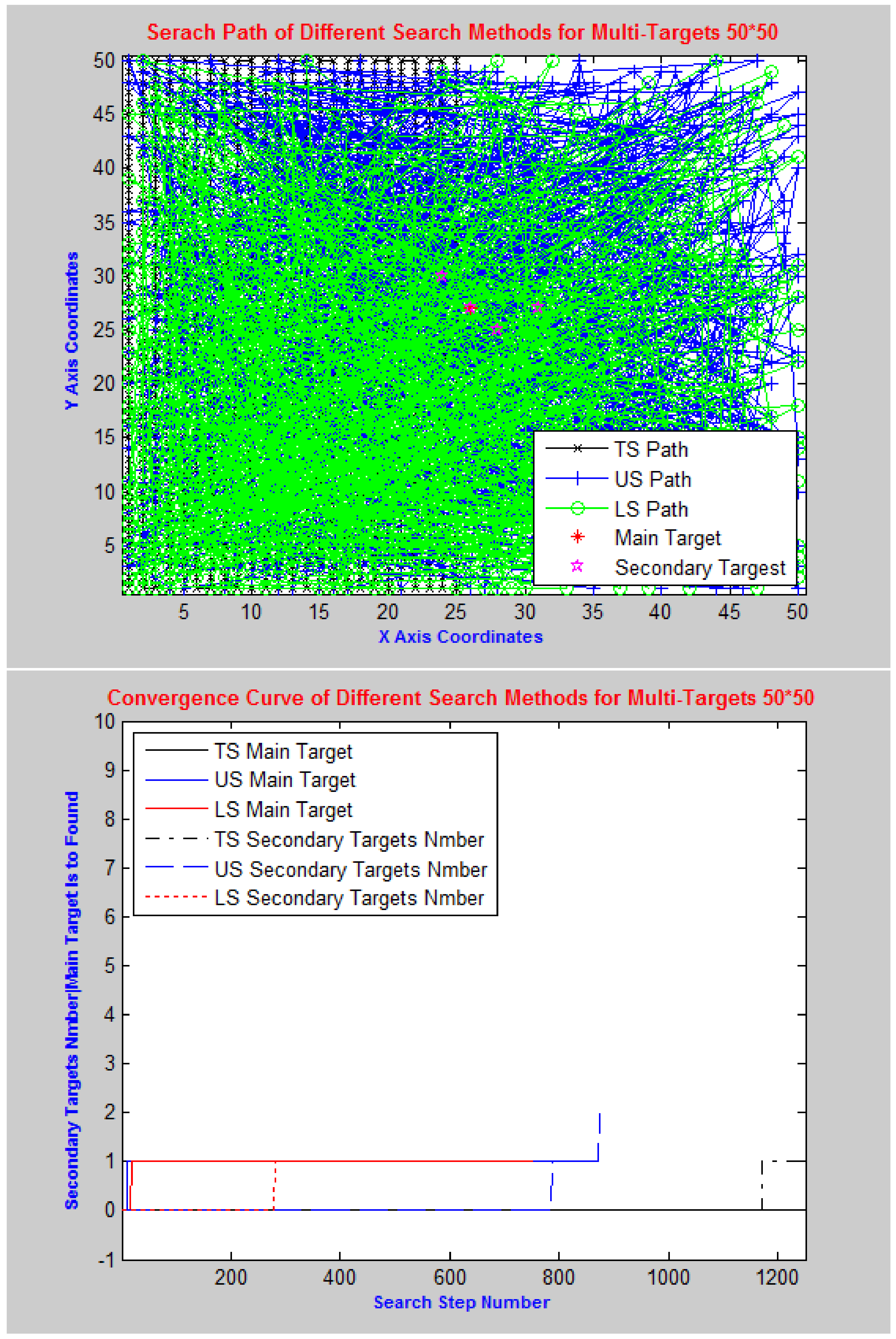
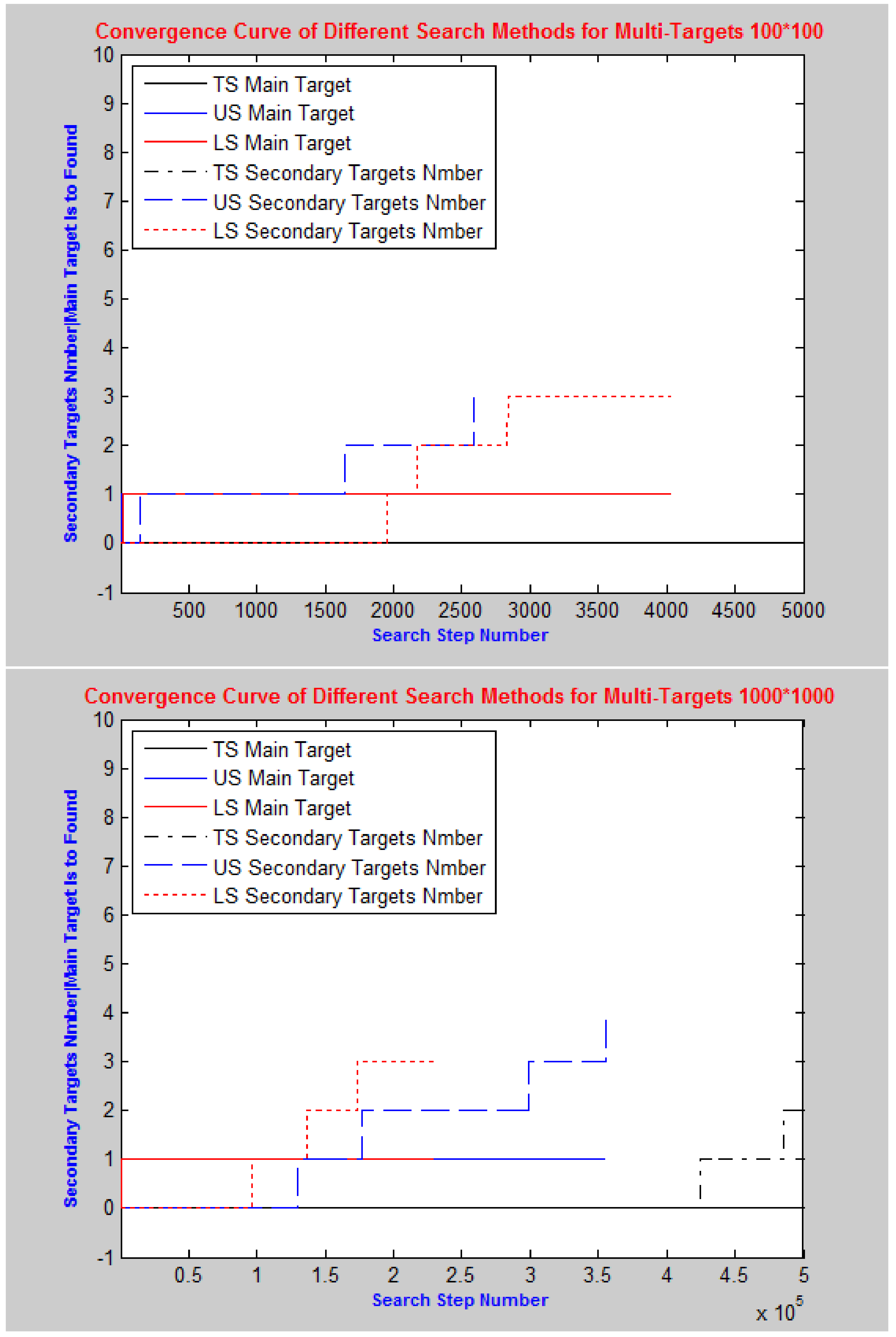
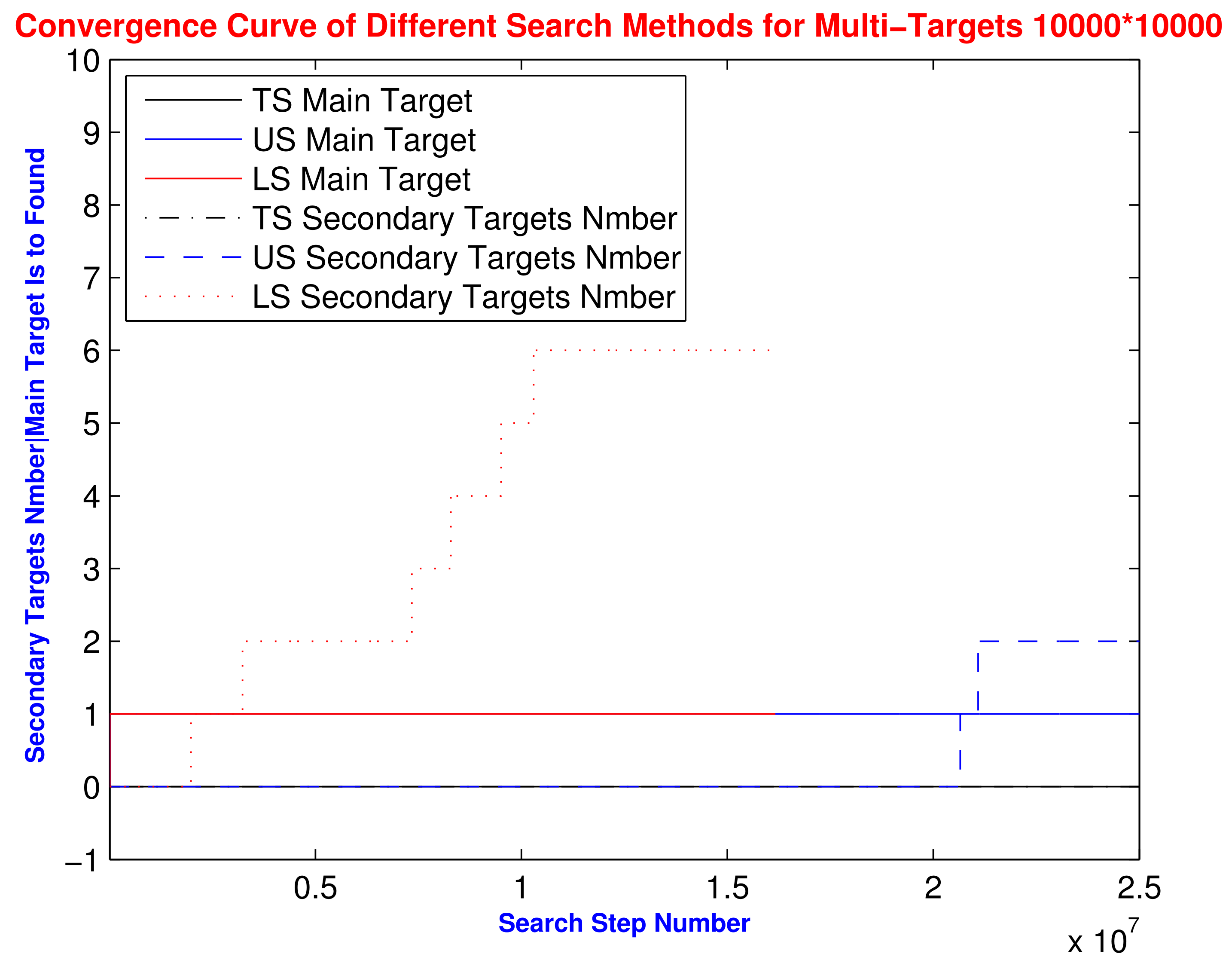
4.2. Multi-Targets (Black Box and Wreckage) Search

Put the main target(black box) and wreckage into the coordinate system. If the main target and some wreckage coordinate value are found, it is a successful search. The problem of some discrete target search, is translated into a search problem of target elements, i.e., the coordinates of targets B(black box) and $w_i$ ($0<w_i<A$ wreckage), in multi-targets matrix (2), in which the B and $w_i$ denote the black box and wreckage, respectively.

$$\left(\begin{array}{cccccccccc}0\hfill & 0& \cdots & 0& 0& 0& 0& 0& 0& 0\\ 0\hfill & 0& \cdots & 0& 0& w_1& 0& w_2& 0& 0\\ \cdots \hfill & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0\hfill & 0& \cdots & 0& 0& 0& B& 0& w_i& 0\\ 0\hfill & 0& \cdots & 0& 0& 0& 0& 0& 0& 0\end{array}\right)$$

(2)

Code rule/0-$\mathit{B}$-${\mathit{w}}_{\mathit{i}}$: Put all lattice images into a matrix. Main target/black box image are denoted by B, wreckage is $w_i$, and others are false/0. In matrix (2), B is the goal/black box, $w_i$ is the wreckage, and 0 is blank. A successful search aims to find the black box image or most of wreckage coordinates or the black box and a small part of the wreckage coordinates. If the coordinates of black box B point or wreckage $w_i$ point with the total number more than X are found, the search is successful.

In the following section, we further discuss how to use minimum step to look for the coordinate of targets, how image processing center uses the least number processing picture, and how to judge and look for a target and determine its coordinates.

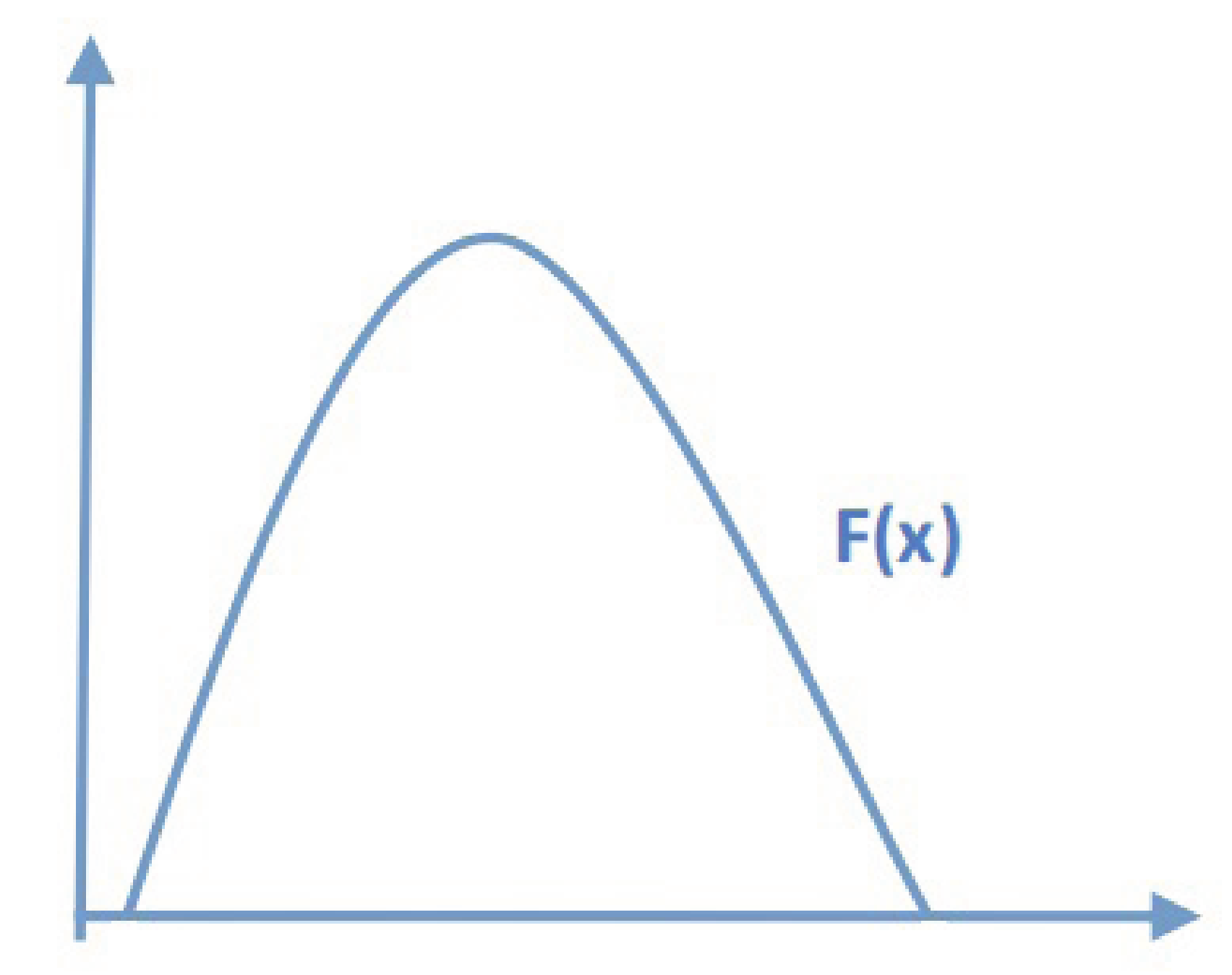
5. Screening/Search Target Picture

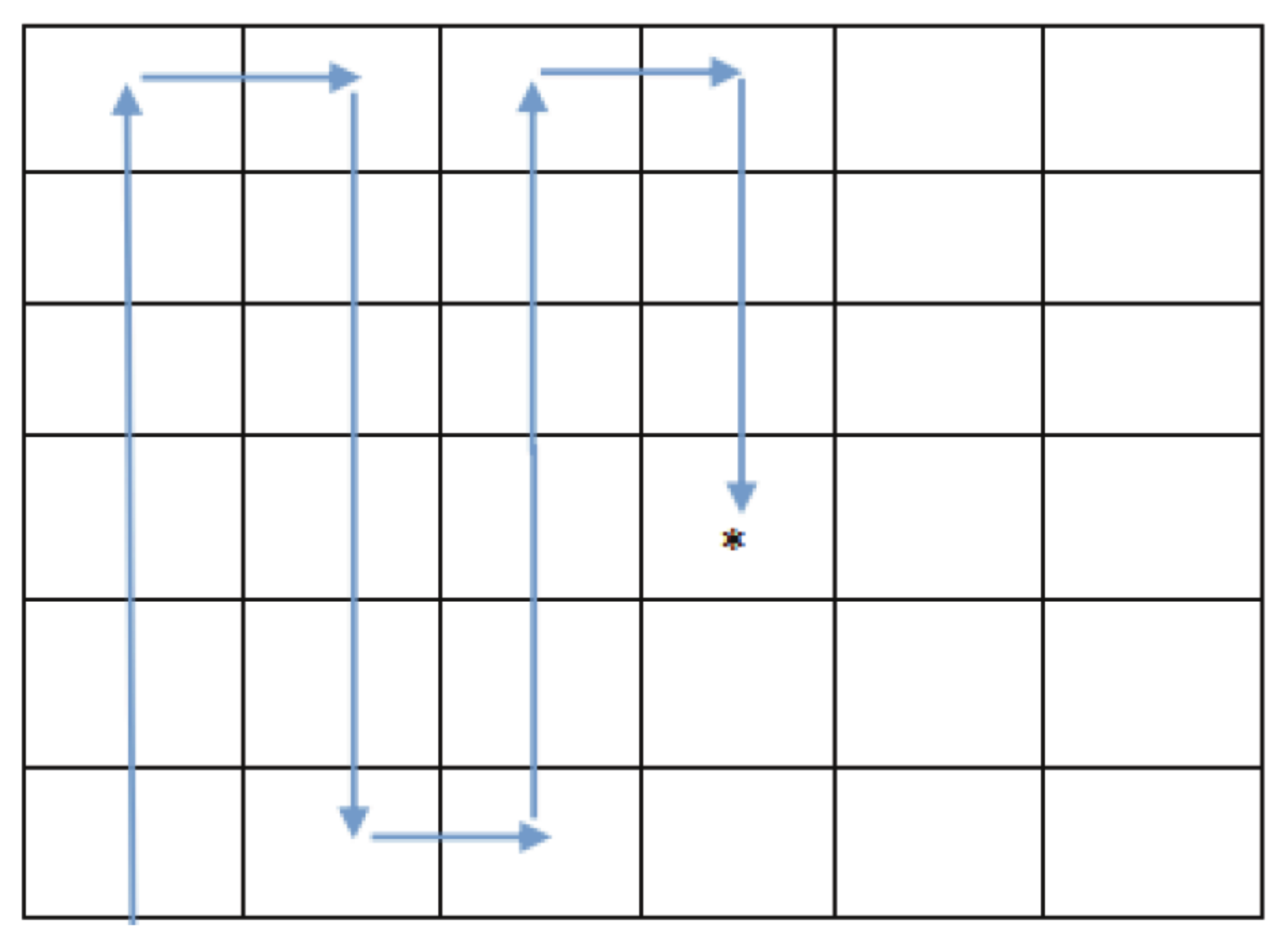
5.1. A Uniform Distribution Search Method

A uniform random search target image method is as follows:

Step 1: Based on $Uniform$ distribution, randomly generate two integers $(x,y)$ as the ordinate and abscissa of the candidate target;

Step 2: It is judged whether or not the generated random number $(x,y)$ is within the search area, and if it is not, using $Uniform$ distribution, reproduce the number of random integers $(a,b)$ as coordinates;

Step 3: Take the satellite grid image in the $(x,y)$ coordinates, judge whether is it real target. If it is not a target, go to step 1.

Step 4: If the target is searched, the coordinates of the target and its image are output;

Above using uniform distribution, the search random extracts the satellite picture judgment target, which is the $Uniform$ distribution search method. Of course, one can also use other random distribution methods to generate coordinates to extract the satellite picture judgment search target.

5.2. A Lévy Distribution Search Method

Lévy stable distributions are a rich class of probability distributions that have many intriguing mathematical properties. Lévy flights are a class of random walks in which the step lengths are drawn from a probability distribution with a power law tail. The application of Lévy fight pattern in the Cuckoo search algorithm [14] greatly improves the algorithm search speed to solve the design optimization [15], selected engineering applications of gradient free optimization [16], traveling salesman problem [17,18], and the selection of optimal machine parameters in milling operations [19]. Tarik Ljouad et al. [20] presented a new tracking approach. Gurjit S. W and Rajiv K [21] proposed an evolutionary particle filter based on improved cuckoo search which overcomes the sample impoverishment problem of generic particle filter. Lévy flights are commonly used in physics to model a variety of processes including diffusion. Broadly speaking, Lévy flights are a random walk by step size following Lévy distribution, and the walking direction is Uniform distribution.

In the Mantegna rule, steps size s design is as follows:

$$s=\frac{\mu }{{\left|\upsilon \right|}^{\frac{1}{\beta }}}$$

(3)

The $\mu$, $\upsilon$ follows Uniform distribution, i.e.,

$$\mu \sim N(0,{\sigma }_{\mu }^2),\upsilon \sim N(0,{\sigma }_{\upsilon }^2)$$

(4)

Here,

$${\sigma }_{\upsilon }={\left\{\frac{\mathsf{\Gamma }(1+\beta )sin\left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }[(1+\beta )/2]\beta \ast 2^{(\beta -1)/2}}\right\}}^{\frac{1}{\beta }}$$

(5)

$${\sigma }_{\mu }=1$$

(6)

This paper presents the Lévy distribution search method for $DTSP$. Based on Lévy distribution with the Mantegna rule, it generates the ordinate and abscissa $(x,y)$ of the candidate target, in turn grabbing the picture of coordinate’s points $(x,y)$ and then determining whether it is real target. The Lévy distribution generation coordinates $(x,y)$ of candidate target must be in the search area. This random extracts satellite picture judgment method, that is the Lévy distribution search method.

5.3. Pseudo Code of One Target Search

• Step 1: Let parameters; including maximum generation Endgen;
• Step 2: Iteration process;
  • Generate stochastically (use Uniform distribution or Lévy distribution) search start point coordinate $(x_0,y_0)$;
  • Judge the picture of the start point coordinate $(x_0,y_0)$ to see whether it is the target;
  • t := 0.
  While ($t<Endgen$) or (Other stop criterion)
  • t := t + 1;
  • Generate next step search point coordinate $(x_t,y_t)$ (use Uniform distribution or Lévy distribution); If the picture of point coordinate $(x_t,y_t)$ has been searched, skip it and re-search;
  • Judge the picture of search point coordinate $(x_t,y_t)$ to see whether it is the black box target; If the picture of point coordinate $(x_t,y_t)$ is the black box target, break.
• Step 3: Output last step search point coordinates and its image.

5.4. Pseudo Code of Multi-Targets Search

• Step 1: Let parameters; including maximum generation Endgen; the total num of wreckages searched.
• Step 2: Iteration process
  • Generate stochastically (use Uniform distribution or Lèvy distribution) search start point coordinate $(x_0,y_0)$;
  • Judge the picture of search start point coordinate $(x_0,y_0)$ to see whether it is the black box target or secondary target;
  • Count wreckages found;
  • t := 0.
  While ($t<Endgen$ and secondary target $\ge num$) or (black box target==1) or (Other stop criterion)
  • t := t + 1;
  • Generate next step search point coordinate $(x_t,y_t)$ (use Uniform distribution or Lèvy distribution); If the image of point coordinate $(x_t,y_t)$ has been searched, skip it, and re-research;
  • Judge the picture of search point coordinate $(x_t,y_t)$ see whether it is the black box target or secondary target;
  • Count wreckage found.
• Step 3: Output secondary target number and their coordinates, last step search point coordinate, and their images.

6. Experiment for Target Search Problem

6.1. Test Example

To proof-test the effectiveness and performance of $Traditional$ $carpet$ search, $Uniform$ distribution and Lèvy distribution search for $DTSP$, a set of 10 test examples with different dimensions was employed to evaluate it. The experimental test examples are as follows:

One target search examples:

E1: [0,10]; [0,10]; Target = [6,5].

E2: [0,50]; [0,50]; Target = [31,29].

E3: [0,100]; [0,100]; Target = [51,55].

E4: [0,1000]; [0,1000]; Target = [509,469].

E5: [0,10,000]; [0,10,000]; Target = [5049,5198].

Multi-targets example:

E6: [0,10]; [0,10]; Main Target = [6,4]. Secondary targets = [5,3;6,5]; WN = 1;

E7: [0,50]; [0,50]; Main Target = [26,27]. Secondary targets = [24,30;31,27;28,25];

WN = 2;

E8: [0,100]; [0,100]; Main Target = [65,44]. Secondary targets = [60,39; 71,46; 74,45; 62,40]; WN = 3;

E9: [0,1000]; [0,1000]; Main Target = [654,598]. Secondary Targets = [514,597;735,

525;486,562;753,556;579,499; 425,786]; WN = 4;

E10: [0,10,000]; [0,10,000]; Main Target = [5149,4809]. Secondary targets = [6514,

5897;7035,5035;4986,5562;6013,5026;5179,5099;4125,4986;6056,5165;7022,5983;

7022,5983]; WN = 5.

6.2. Comparison Test with Different Search Methods

This paper compares the minimum search step number, mean search step number, and standard deviation searched by $Traditional$ $Carpet$ search, Uniform distribution, and Lévy distribution search run 32 times. The experimental parameters and results comparison on each target search are listed in

Table 1. The comparison results of T, U, and L search for one target search.

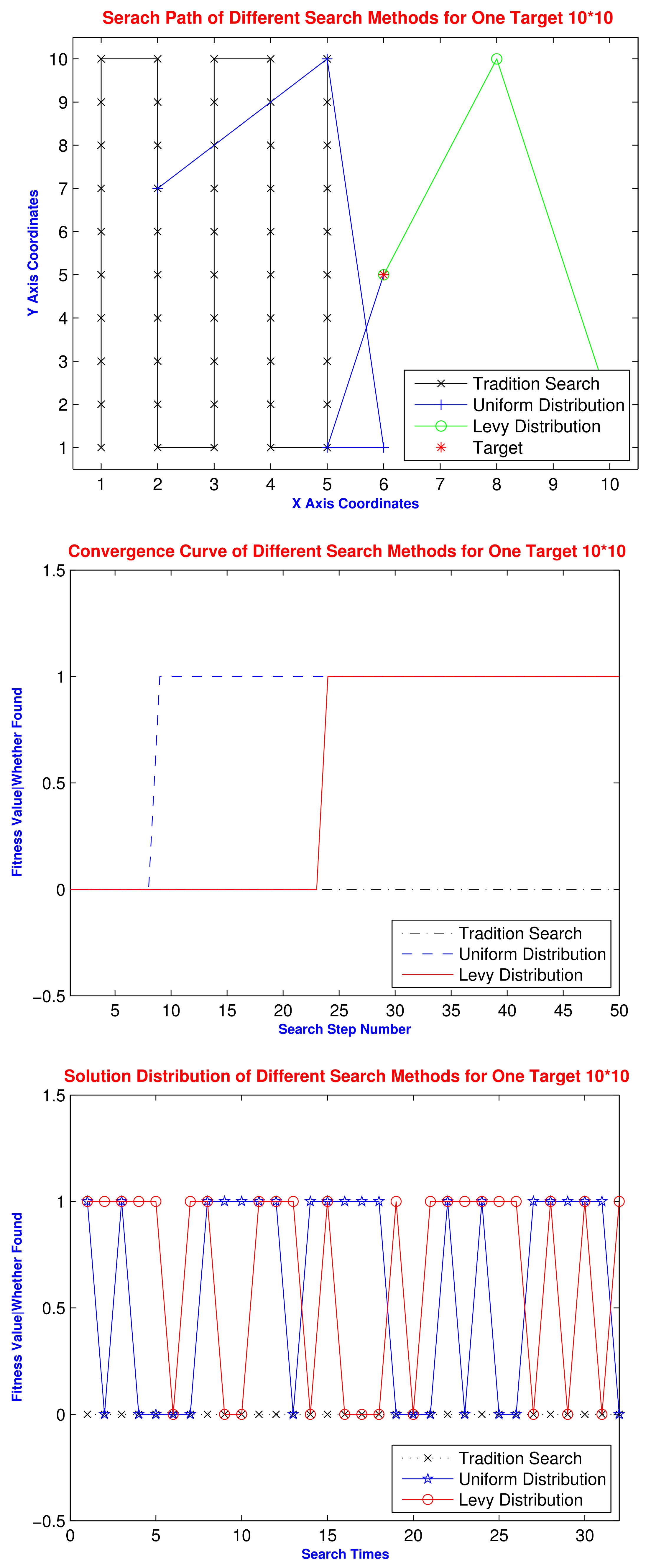
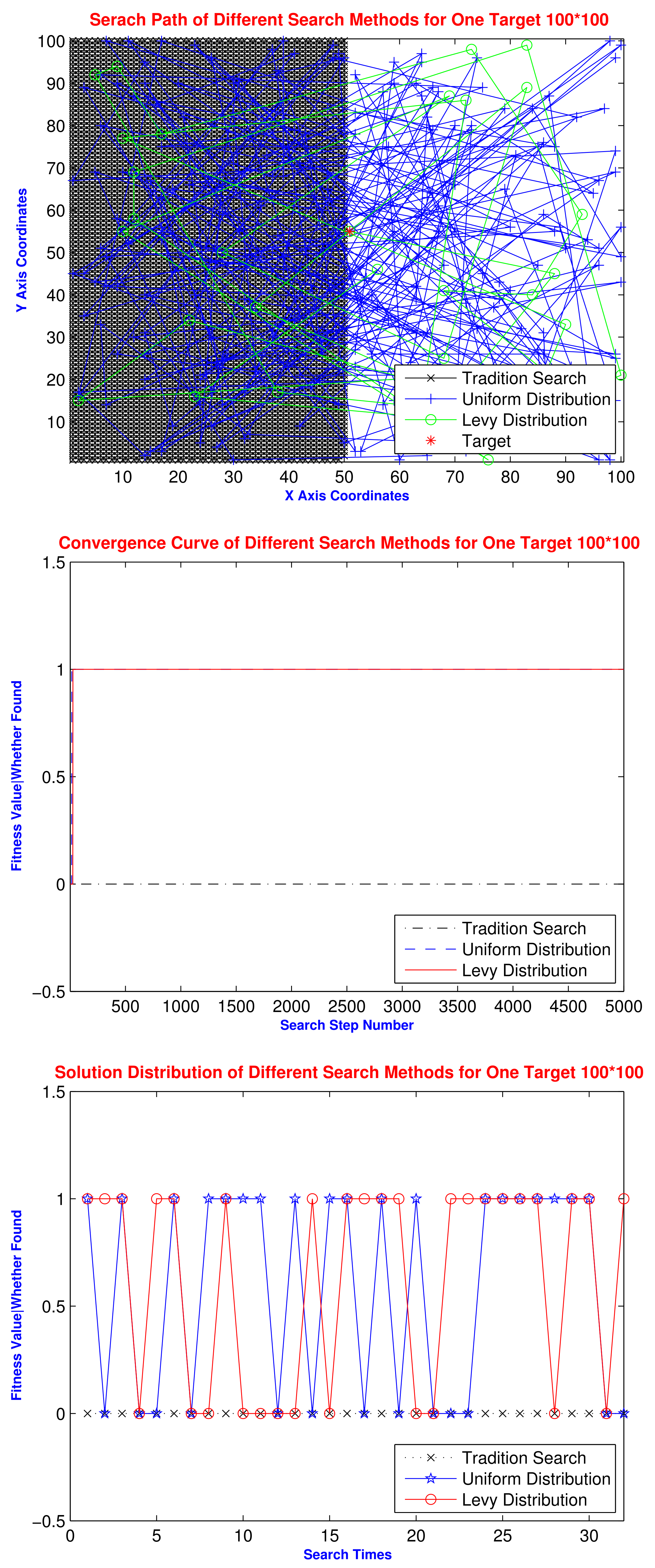
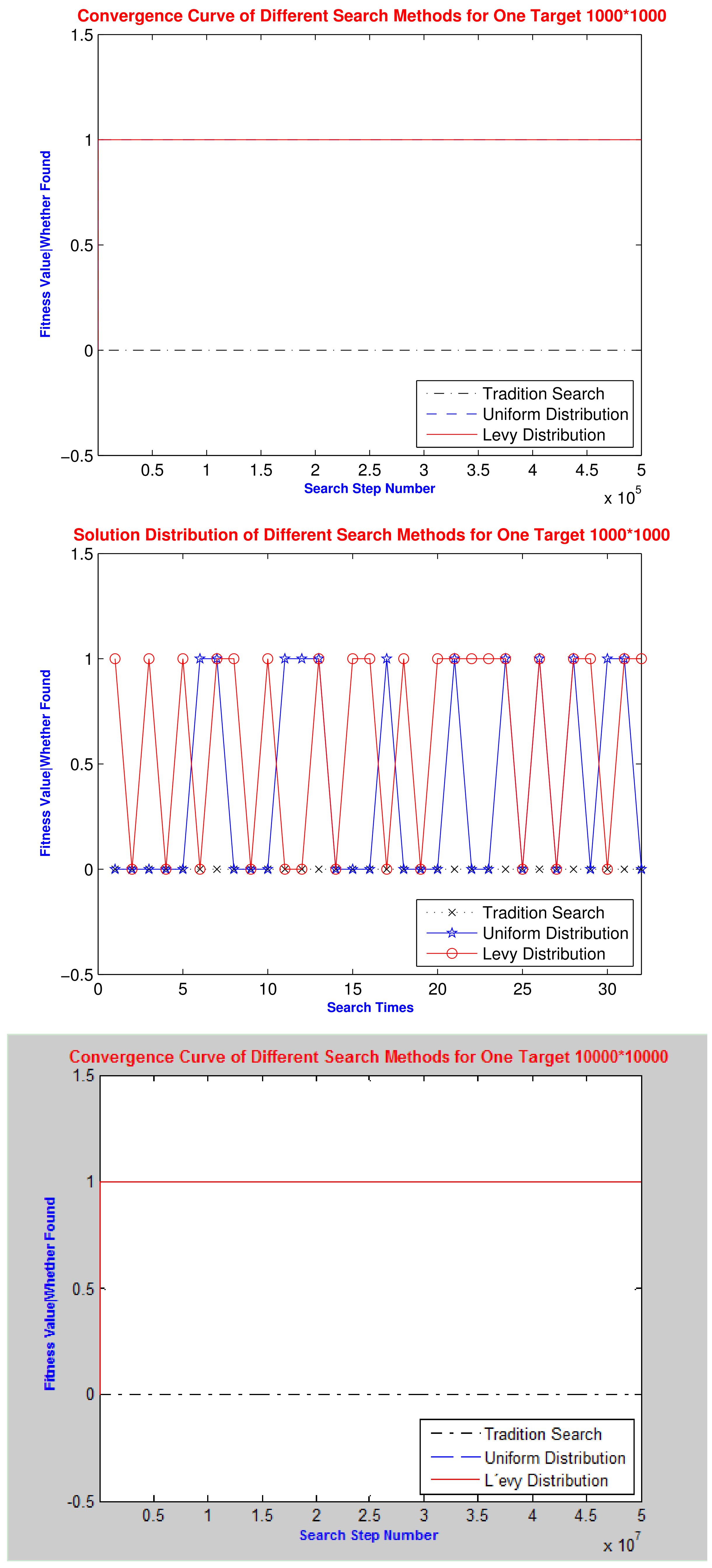
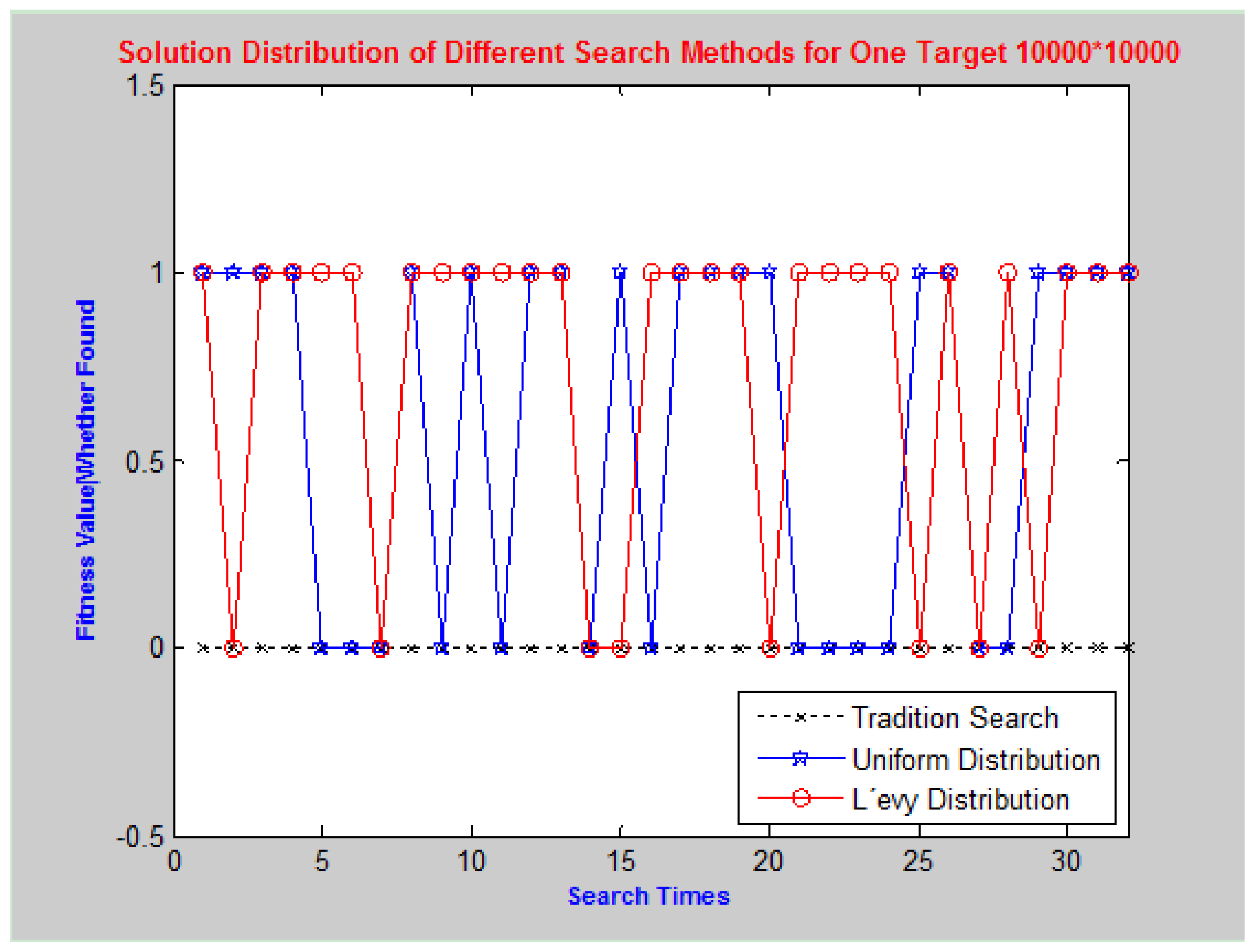
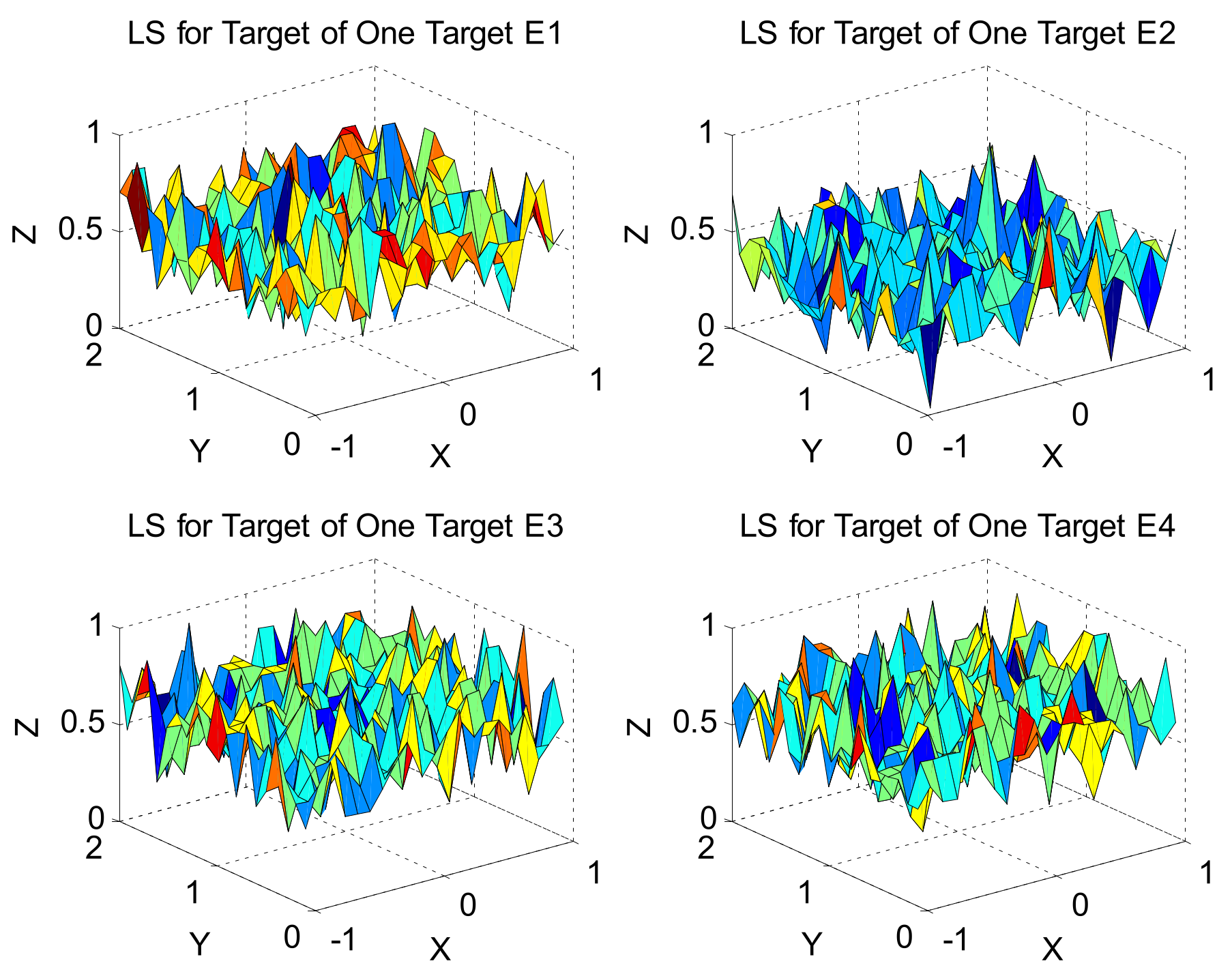
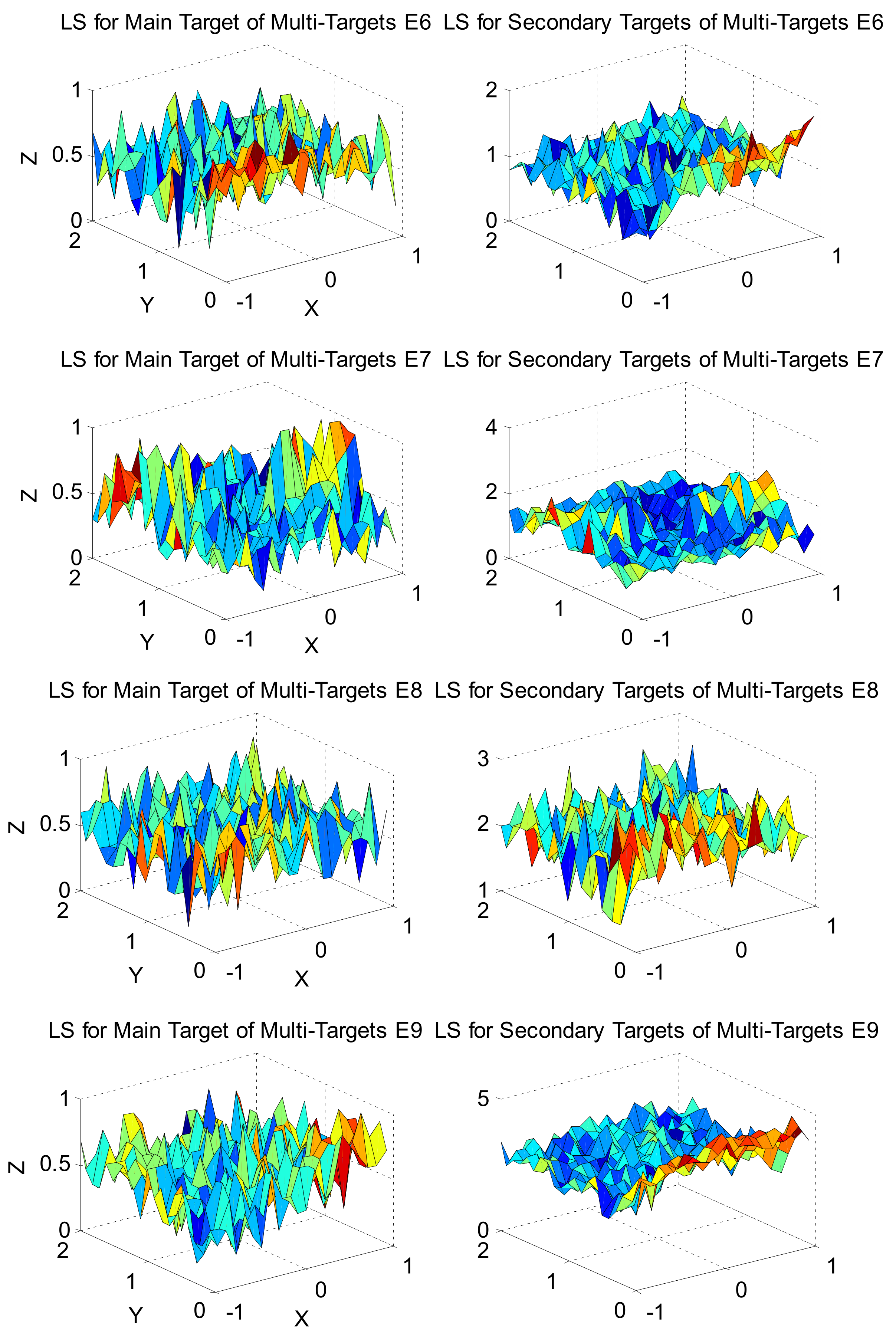
	Search Methods	Abbreviation	Min/Average/Std	Search Solution	Succeed Times	Successful Rate
E1	Traditional	T	50/50/0	0	0	0
EG = 50 X = [0,10]	Uniform distribution	U	5/37.1563/15.7544	1	19	0.5938
Y = [0,10]	Lévy distribution	L	3/33.5938/16.3408	1	21	0.6563
E2	Traditional	T	1250/1250/0	0	0	0
EG = 1250 X = [0,50]	Uniform distribution	U	89/994.4688/391.3227	1	14	0.4375
Y = [0,50]	Lévy distribution	L	56/1.0228 × 10${}^3$/359.3115	1	14	0.4375
E3	Traditional	T	5000/5000/0	0	0	0
EG = 5000 X = [0,100]	Uniform distribution	U	1070/4179.5/1162.7	1	15	0.4688
Y = [0,100]	Lévy distribution	L	292/3390.3/1724.1	1	20	0.625
E4	Traditional	T	500,000/500,000/0	0	0	0
EG = 500,000 X = [0,1000]	Uniform distribution	U	1564/399,200/169,030	1	12	0.375
Y = [0,1000]	Lévy distribution	L	55,876/126,110/384,780	1	20	0.625
E5	Traditional	T	50,000,000/50,000,000/0	0	0	0
EG = 50,000,000 X = [0,10,000]	Uniform distribution	U	1,344,005/3.9177 × 10${}^7$/1.237 × 10${}^7$	1	19	0.4688
Y = [0,10,000]	Lévy distribution	L	223,230/3.0076 × 10${}^7$/1.8725 × 10${}^7$	1	24	0.8438

. In the following table, the Tradition Carpet search, Uniform distribution, and Lévy distribution search are called T, U, and L, respectively.

Remark 1.

In Table 1, $Ex$ is the search example; $Abbreviation$ is the search methods shortened form; $Min/Average/Std$ denote that search target used minimum run step, average step, and step standard deviation in run 32 times; $e+n$ mean $\times {10}^n$. Solution denotes whether to find the target, 1 denotes found, and 0 is not found. $Succeed$ $times$ is the successful search times in run 32 times. Successful rate is a successful search rate in 32 run times. The better solutions found in different search methods are illustrated with bold letters, and the best minimum average is shown with an underline, respectively.

Remark 2.

In Lévy distribution search $\alpha \in [0,2];\beta \in [-1,1];\mathsf{\Gamma }=X;\delta =\mathsf{\Gamma }/2$. If the Lévy distribution generation number is negative, we use its absolute value or re-generate with $Uniform$ distribution.

From Table 1, the Lévy distribution search has the highest performance since using it has smaller minimum and arithmetic mean search steps found target compared to solutions obtained by others, and especially for bigger size target search problems, it has better search efficiency. In above test examples, the Lévy distribution search can obtain a higher search successful rate. If the target is in the search area center, the $Traditional$ $Carpet$ search method using less half steps of search area grid cannot find the target, but using U or L search method with the probability of more 40% and 60% can find the target. From the above experiments, we can find that scale is larger, the performance of L is more outstanding compared with T and U search. For a huge size search problem experiment, because of the experimental conditions limited, the data storage runs out of memory. In the real environment, because the search range is very large, the $Traditional$ $Carpet$ search is difficult for finding the target. From simulation results, we can obtain that the Lévy distribution search as being clearly better than $Traditional$ $Carpet$ search and $Uniform$ distribution search for one target search problem. Especially for large size problem, the L search has strong ability.

Search paths, the convergence and succeed search times distribution figures of most effective of $Traditional$ $Carpet$ search, $Uniform$ distribution, and Lévy distribution search run 32 rounds for five one-target search instances are as in Figure 5. For E4 and E5, the search paths are very complex, drawing a figure that almost cannot be seen clearly; therefore, we do not show their search paths.

From Figure 5, in search target path picture we can see U and T can quickly find target. The $Traditional$ $Carpet$ search method is the enumeration method, gradually slow search, efficiency is very low. From surface view $Traditional$ $Carpet$ search method, it can find target with a finite step, but the actual search area is too big, and it cannot use large search steps greatly to search. Within finite steps to search the target, using the random search method is more effective than the $Traditional$ $Carpet$ search. In addition, when the search area is huge, the $Uniform$ distribution search compared to the Lévy distribution search efficiency is obviously much lower. In the following section, we test the multi-targets search using different search methods.

In order for more scientific evaluation search methods for a multi-targets search problem, this paper compares the minimum search step number, mean search step number, and standard deviation searched by $Traditional$ $carpet$ search, $Uniform$ distribution, and Lévy distribution search run 20 times. The solutions of multi-targets test examples are listed in

Table 2. The comparison results of T, U, and L search for multi-targets.

	Search	Min/Average/Std	Main Target			Secondary Targets
	Methods		Search Solution	Succeed Times	Successful Rate	Found Average	Succeed Times	Successful Rate
E6	Traditional	50/50/0	0	0	0	1	20	1
WN = 1 EG = 50	Uniform distribution	29/45.6/7.074	1	9	0.45	0.8	14	0.7
X = [0,10] Y = [0,10]	Lévy distribution	27/45.05/7.2655	1	11	0.55	1.05	18	0.9
E7	Traditional	1250/1250/0	0	0	0	1	0	0
WN = 2 EG = 1250	Uniform distribution	873/1.1872 × 10${}^3$ 129.1191	1	7	0.35	1.6	11	0.55
X = [0,50] Y = [0,50]	Lévy distribution	753/1.215 × 10${}^3$ /117.8882	1	9	0.45	1.25	7	0.35
E8	Traditional	5000/5000/0	0		0	0	0	0
WN = 3 EG = 5000	Uniform distribution	2585/4795 /585.0487	1	8	0.4	1.85	6	0.3
X = [0,100] Y = [0,100]	Lévy distribution	4036/4.8501 × 10${}^3$ /3339.8648	1	14	0.7	2.1	7	0.35
E9	Traditional	5× 10${}^5$/5 × 10${}^5$	0	0	0	2	0	0
WN = 4 EG = 5× 10${}^5$	Uniform distribution	355,541/4.8573 × 10${}^5$ /3.8108× 10${}^4$	1	10	0.5	2.9	5	0.25
X = [0,1000] Y = [0,1000]	Lévy distribution	230,160/4.4476 × 10${}^5$ /7.9752× 10${}^4$	1	15	0.75	3.4	12	0.6
E10	Traditional	2.5 × 10${}^6$/2.5× 10${}^6$ /2.5× 10${}^6$	0	0	0	0	0	0
WN = 5 EG = 2.5 × 10${}^6$	Uniform distribution	2.5× 10${}^6$/2.5× 10 /2.5 × 10${}^6$${}^6$	1	5	0.25	2	0	0
X = [0,10,000] Y = [0,10,000]	Lévy distribution	16,166,752/2.3883 × 10${}^7$ /2.7461× 10${}^6$	1	9	0.45	3.85	7	0.35

, and the about parameters are the same in Table 1.

From Table 2, the Lévy distribution search clearly has the highest performance, and especially for bigger size targets search problem, it has better search efficiency. In above test examples, the Lévy distribution search can obtain higher main and secondary search successful rate; at the same time, it can find more secondary targets, as well as use less search steps. Especially for large size problems, L optimal has strong search ability.

The search paths, the convergence, and succeed search times distribution figures of most effective of $Traditional$ $Carpet$ search, $Uniform$ distribution, and Lévy distribution search run 20 rounds for five multi-targets search instances are in Figure 6. At the same time, for E8∼E10, the search paths are very complex and cannot be seen clearly; therefore, we do not show their search paths.

From Figure 6 we can see that the convergence rate of Lévy distribution search is clearly faster than Traditional Carpet search and $Uniform$ distribution search. Lévy distribution search can not only fast find the main target but also find more secondary targets than T and U search method. Due to the particularity of this kind of target search problem, in general secondary targets stochastically scattered on the main target around, it is more suitable for Lévy distribution search which can quickly find the targets.

Targets can be found by only processing a few images (search steps) using Lévy distribution search. In the scenario under discussion, the advantages lie in that the convergence speed of Lévy distribution search being clearly faster than Traditional Carpet search and random search based on some other distributions. In limited search steps, Lévy distribution search can not only quickly find the main target but also find more secondary targets than the aforementioned search methods.

Accordingly, we can state that the Lévy distribution search is more effective than Traditional Carpet search and $Uniform$ distribution search method for discrete targets search. In limited search steps, the Lévy distribution search can, with higher probability, quickly and accurately find the main target and more secondary targets. Lévy distribution search is one better search tool.

6.3. Experiment of Lévy Distribution Search

From the above experiment, we find that the Lévy distribution search is efficient for discrete targets search. Lévy distribution search has many parameters, in order to find their different search performance, we simulate and obtain optimal parameters. Lévy distributions solve the test problems, in which $\alpha$ from 0 to 2 with 0.1 step changes and $\beta$ from −1 to 1 with 0.1 step changes for the X axis and for Y axis, respectively. The L uses a group of parameters $\alpha$ and $\beta$ combination run 10 times, using the average to search results. The best parameters configuration of L for search one target and multi-targets are in the following

Table 3. The optimum parameters of L for target search.

Main Target of One Target Search			Main Target of Multi-Target Search
Test Problem	Opimum Average	$\mathbf{\alpha },\mathbf{\beta }$	Test Problem	Main Target	Secondary Targets	$\mathbf{\alpha },\mathbf{\beta }$
E1 EG = 50	0.9	1.8, −0.9 0.4, −0.6 0.2, −0.4 0.8, −0.3 1.0, −0.3 1.2, −0.2 1.3, −0.1 1.5, 0.1 1.4, 0.7 1.4, 0.8 0.2, 0.9	E6 WN = 1 EG = 50	1	1.8	0.1, −0.5; 0.1, −0.1; 0.8, 0.
E2 EG = 1250	0.9	1.2, 0.5	E7 WN = 2 EG = 1250	1	2.5	1.3, −0.9; 1.3, −0.7; 1.2, −0.5 0.9, 0.4; 0.9, 0.5; 0.8, 0.9; 0.8, 1
E3 EG = 5000	1	1.8, −0.5 0.5, 1.0	E8 WN = 3 EG = 5000	1	2.9	0.3, −0.7
E4 EG = 500,000	1	0.4, −0.1 0.9, 0.3 0.5, 0.9	E9 WN = 4 EG = 500,000	1	4.8	0.4, 0.8; 0.2, 0.9

.

From above Table 3, we can see when $\beta$ approximately equal to 0.9 have a good search performance. Especially for large-scale one target and multi-targets search problems, $\beta$ equal to 0.9 is effective and stable. About $\alpha$ for L is not obvious influence and is not stable, relatively speaking in most cases, $\alpha$ is equal to 1.5 has a better search efficiency. As a result of the experiment and paper length limit, this paper do not analyze testing results for large problems E4 and E5.

With the Lévy distributions search run 10 times with X and Y each parameters combination, and use the mean main target and the mean secondary targets number of round 10 times, respectively, as Z axis, the three-dimensional graphics are as following (Figure 7 and Figure 8):

From the above figures we can discover that the parameters have greater influence on performance of L algorithm for target search problem. Clearly, we can see when $\beta \approx 0.9$L has better performance for bigger size target search problem and $\alpha$ influence the performance of L is not stable. Experiments show that L search performance is strong, with fewer steps to find the target.

7. Conclusions and Perspectives

The plane crashed, the ship sank, and desert missing, landslide spot search, forest fire spot search and rescue, grassland search, enemy warships group search, etc., are all called discrete target search problem. According to production and living needs and shortcoming of the tradition search method, this paper offers comprehensive and systematic research on the discrete targets search problem.

This paper analyzes the particularity and complexity of the discrete target search problem, and the paper simulates and analyzes the different and performance characteristics of $Tradition$ $Carpet$ search, $Uniform$ distribution search, and Lévy distribution search for one target and multi-targets. We give that the computer quickly selects, grabs the satellite images and image analysis method to determine the target coordinate position by software system, and greatly improves the target recognition speed. Preliminary experiments show that the efficiency of Lévy distribution search is better than $Tradition$ $Carpet$ search and $Uniform$ distribution search. Using Lévy distribution search only process, a few images (search steps) can find targets. We find the Lévy distribution search is one better search tool, which can, with higher probability, quickly and accurately find targets for discrete targets search problem. The simulations experiment prove that DTSP is faster to search for discrete single target or multiple targets in a wide area. It provides a new method for solving the discrete target search problem.

There are a number of research directions that can be considered as useful extensions of this research. Although the proposed search method is tested with 10 instances, a more comprehensive computational research should be made to test the efficiency of proposed new method. This paper is the only research on the target of rectangular areas search and study a new method to search target in circular area and irregular graphics area. Recently, 48 robust M-estimators were presented for regression analysis [22]. In addition to image processing, M-estimators have been used in several areas of knowledge such as astronomy, pharmaceutics, medical, econometric, finance, geodesy, and engineering (electrical, telecommunications, civil, mechanical, chemical, and nuclear). In future we will research on other more effective search methods, different distribution search such Mittag-Leffler [23] or multi-population pattern searching algorithm [24] for one target and multi-targets search problem. For future work, as well as in data regression analysis, it is possible to use a function that measures the distance from each location estimated point to the correct locations as performance criteria, principally for multi-targets.