Abstract
We studied the --T phase diagram of the -dimensional Gross-Neveu model, where denotes the ordinary chemical potential, the chiral chemical potential and T the temperature. We use the mean-field approximation and two different lattice regularizations with naive chiral fermions. An inhomogeneous phase at finite lattice spacing was found for one of the two regularizations. Our results suggest that there is no inhomogeneous phase in the continuum limit. We showed that a chiral chemical potential is equivalent to an isospin chemical potential. Thus, all results presented in this work can also be interpreted in the context of isospin imbalance.
1. Introduction
The Gross-Neveu (GN) model describes a theory of fermion flavors with a quartic interaction. It is a rather simple model commonly used to explore and describe the spontaneous breaking of chiral symmetry [1] in the -T plane, where denotes the chemical potential and T the temperature. In the limit (corresponding to the mean-field approximation or, equivalently, the neglect of bosonic quantum fluctuations) the -dimensional GN model exhibits three phases: a symmetric phase (with a vanishing chiral condensate), a homogeneous symmetry-broken phase (with a non-zero, but spatially constant condensate) and an inhomogeneous phase, where the chiral condensate is an oscillating function of space [2,3,4]. The phase diagrams of the GN model and related theories were also investigated at finite , i.e., with bosonic quantum fluctuations included, using lattice Monte-Carlo simulations [5,6,7,8,9,10,11] and the functional renormalization group (FRG) [12].
Inhomogeneous phases are not limited to the GN model, but were found in several models in the mean-field approximation in dimensions [13,14,15,16] and in dimensions [17,18,19,20,21,22,23]. For a review, we refer to ref. [24]. In recent works [25,26,27,28] it has been discussed that inhomogeneous phases might be related to so-called moat regimes, where the bosonic wave function renormalization Z is negative. Such a regime has been found in an FRG study of the phase diagram of quantum chromodynamics (QCD) [29]. A similar regime has been observed in the -dimensional GN model (see Figure 9 of ref. [30], where the wave function renormalization Z is plotted in the -T plane). One finds that a negative Z accompanies the instability of a homogeneous condensate with respect to inhomogeneous perturbations as a necessary, but not a sufficient condition. The possible existence of a moat regime in the QCD phase diagram encourages us to improve our understanding of inhomogeneous condensation and related phenomena in QCD-inspired models.
Recently, the existence of inhomogeneous phases was also explored in the -dimensional GN model in the mean-field approximation [31,32,33]. Such -dimensional four-fermion theories are of interest both in high energy physics [34,35,36,37,38] and in condensed matter physics [39,40,41,42,43,44,45,46], but also to study conceptual questions, e.g., renormalizability in the expansion or in a perturbative approach [47,48,49,50]. Hence, confirming the existence of an inhomogeneous phase in such a model could have a significant impact. Early seminal studies of the -T phase diagram of the -dimensional GN model [51,52] reported a second-order phase transition between the symmetric and the homogeneous symmetry-broken phase at finite T and and a first-order phase transition at . However, in these studies only a homogeneous order parameter was considered. In our recent publication ref. [33] we studied the existence of an inhomogeneous phase in the -dimensional GN model within the mean-field approximation. Our main findings were that an inhomogeneous phase is present at finite regulator and for certain regularization schemes (a Pauli-Villars cutoff and a specific lattice discretization), but it disappears when the regulator is removed, as previously observed in ref. [38].
In this work we continue our investigations from ref. [33] by extending the -dimensional GN model with a chiral chemical potential. We studied its phase diagram, where our main focus was on possibly existing inhomogeneous phases. While the GN model might be too simple to realistically describe the effect of chiral imbalance on QCD, it might still improve our conceptual understanding of inhomogeneous condensation in the presence of chiral imbalance, which is an important problem. A difference in the densities of left- and right-handed quarks is relevant in physical systems such as heavy-ion collisions [53,54] or compact stars [55,56]. The impact of chiral imbalance on chiral symmetry breaking has been studied (e.g., in -dimensional models) [14], where it had no influence on the existence of the inhomogeneous chiral spiral, and in -dimensional models [57,58,59], where only homogeneous order parameters were considered. A chirally imbalanced -dimensional GN model, extended by a quartic difermion interaction, was explored in refs. [60,61] with the aim to clarify the competition of homogeneous fermion–fermion condensation and homogeneous chiral condensation. In recent two-color and three-color QCD studies [62,63] a chiral chemical potential was investigated and found to increase the chiral transition temperature. This result is supported by a Nambu-Jona-Lasinio (NJL) model study [64].
This paper is structured as follows. We start in Section 2 by discussing the theoretical basics of the GN model in dimensions including details on the underlying chiral symmetry. We also add a chiral chemical potential to the model and show the equivalence of chiral imbalance and isospin imbalance. In Section 3 we discretize the effective action of the model using lattice field theory. Section 4 is the main part of our paper, where numerical results are presented and discussed. Finally, we conclude in Section 5. Preliminary results from this project were presented at a recent conference [65].
2. Theoretical Basics
2.1. Action and Partition Function
The action of the GN model in dimensions with fermion flavors is
where represents massless fermion fields; is the chemical potential; and is the coupling of the four-fermion interaction. with and T denoting the temperature given by the inverse extent of the periodic temporal direction of Euclidean space-time.
The action (1) is equivalent to
where is a scalar boson field; is the rescaled coupling; and
is the Dirac operator. Integration over the fermion fields leads to the so-called effective action and the corresponding partition function
One can show that is related to the condensate according to
As in previous studies of chiral inhomogeneous phases, we restricted the dependence of to the spatial coordinates, i.e., . With this restriction is real, which is shown in the Appendix of Ref. [33]. For even , the effective action is then real. (Our numerical calculations of the determinant showed that is exclusively positive, i.e., the effective action is real for all values of ).
Since , the limit reduces the relevant configurations in the partition function (4) to the global minima of . Thus, the computation of a path integral is reduced to an optimization problem. In the case of degenerate global minima, spontaneous symmetry breaking selects one of these minima. Consequently, an expectation value is identical to the value of O evaluated at the corresponding global minimum, i.e., . In particular, . For the remainder of this paper we exclusively consider the limit .
2.2. Representation of the Dirac Matrices and Chiral Symmetry
Typically one uses either an irreducible representation or a reducible representation of the Dirac algebra for the matrices appearing in the Dirac operator (3) (for details see, e.g., refs. [33,36,37,66]). In the case of an irreducible representation, there is no symmetry, which can be interpreted as chiral symmetry, because it is impossible to define a matrix , which anticommutes with , and . Therefore, a reducible representation is more appropriate in our context, e.g.:
where denote the Pauli matrices. The three matrices , and as well as the three matrices , and form irreducible representations, which are inequivalent. The corresponding upper two and lower two entries of the fermion fields can be interpreted as left-handed and right-handed components, respectively.
The Dirac operator (3) is then block-diagonal,
where
represent Dirac operators for left-handed and right-handed fermion fields (see also Equations (14) and (15) in ref. [33]). One can show that and are invariant under both and . Using the latter one can show
The action with is invariant under the discrete chiral transformations. (For free fermions one can define continuous axial chiral symmetry transformations with both and . The four-fermion interaction in Equation (1) breaks the corresponding symmetries explicitly, see, e.g., ref. [33]).
with
Both and anticommute with , and , thus fulfilling the necessary properties for generating an axial chiral transformation. The symmetries (11) and (12) are also present for the action (2), where the corresponding transformation of is in both cases . Thus, is an order parameter for chiral symmetry breaking. (When using an irreducible fermion representation, there is no chiral symmetry; however, can still be interpreted as an order parameter for parity breaking).
In addition to the transformations (11) and (12) the action is also invariant under the continuous vector chiral transformations
where denotes the generators of flavor rotations and
(see also refs. [36,66]).
The transformations (11), (12) and (15) are not independent. For example, (11) can be written as combination of (12) and (15) with ,
Thus, there is only one independent symmetry, i.e., the structure of chiral symmetry is .
A chiral chemical potential can be introduced in a straightforward way by extending and replacing the Dirac operator in (3) or equivalently (7) according to
contributes to the chemical potentials of the left-handed (upper two) components and the right-handed (lower two) components with opposite sign, thus causing chiral imbalance. We note that there are other possibilities to define chirality and chiral imbalance (see, e.g., refs. [60,61] and Section 5) differing from our definition, where left- and right-handed fermion fields are projected from the fermion fields as
with denoting the corresponding projectors.
As done for in Appendix A of ref. [33], one can show that is invariant under both and . Since
is also invariant under the exchange of the ordinary and the chiral chemical potential, . Clearly, as well as the phase diagram share this invariance. In Section 4 we use this property to cross-check our numerical results.
We note that the effective action can be written as the sum of a left-handed and a right-handed part,
with and . Of course, the two parts are not independent but coupled via . Moreover, both parts are equivalent to the chirally balanced effective action (see Section II C. of ref. [33]), i.e.,
This property will be useful when we discuss our numerical results in Section 4.
2.3. Equivalence of Isospin and Chiral Imbalance
In this subsection we consider an even number of fermion flavors , again in the 4-component reducible representation, and assign half of them (the “u flavors”) a chemical potential , the other half (the “d flavors”) a chemical potential . Clearly, generates an imbalance between the u and the d flavors and, thus, can be interpreted as isospin chemical potential.
The corresponding effective action is
where the Dirac operator is an matrix in spin and isospin space,
Using Equation (20) one can show
Consequently, the effective action for the GN model with isospin imbalance, Equation (23), is identical to the the effective action for the GN model with chiral imbalance, Equation (21), when identifying . Thus, all numerical results presented in Equation (4) can either be interpreted in the context of chiral imbalance or of isospin imbalance. We note that this equivalence of isospin and chiral imbalance is specific to the GN model in dimensions.
3. Lattice Discretization
We used a lattice discretization of the effective action (21), which was similar to the discretization discussed in Section IV of our previous work [33]. The key difference is that we use the naive fermion discretization also in temporal and not only in the spatial directions.
We considered a 3-dimensional space-time volume , where was the inverse temperature and the quadratic spatial volume. The boundary conditions were periodic in the 2 spatial directions and periodic and antiperiodic in temporal direction for the fields and , respectively. We used a cubic lattice with lattice sites and lattice spacing a, i.e., and . In the following, all dimensionful quantities are expressed in units of the lattice spacing, e.g., , . Because of the finite space-time volume, the 3-dimensional momenta were quantized,
with
and , corresponding to periodic and antiperiodic boundary conditions in the temporal direction.
In our numerical implementation, the effective action and fields were treated in momentum space,
where
are the Fourier coefficients of the field .
is the Dirac operator in momentum space. On the lattice, this operator is a matrix with columns and rows labeled by the momenta p and q, respectively. The sin for contains the matrix but can be simplified according to
The Dirac operator has eight regions of soft modes, where the dispersion relation is approximately linear, in the first Brioullin zone and where each region describes a fermion flavor. In the continuum limit, these fermion flavors do not interact with each other but with the scalar field in the same manner (for details see ref. [5] and the Appendix of ref. [7]). Thus, in order to study fermion fields on the lattice, where is restricted to a multiple of 8, one has to use naive fermions in the discretization of the fermion bilinear in Equation (2) resulting in the factor in Equation (27) (compare Section IV A. in ref. [33]). An appropriately chosen weight function was necessary to ensure the correct continuum limit (see refs. [5,7,33] for details). We investigated and compared two possible choices,
with denoting the Heaviside function.
Because of the restriction of to the spatial coordinates, i.e., , the Dirac operator (29) was block-diagonal with respect to and . This simplified the computation of to the computation of determinants of smaller matrices of size .
4. Numerical Results
Using lattice field theory the phase diagram of the -dimensional GN model with was extensively explored in refs. [31,32,33]. There is a symmetric phase with at large or large T and a homogeneous symmetry-broken phase with a constant at small and small T. Moreover, at finite lattice spacing and for certain discretizations (e.g., ) there is additionally an inhomogeneous phase, where is a varying function of the spatial coordinates. However, this inhomogeneous phase shrinks, when decreasing the lattice spacing, and seems to vanish in the continuum limit.
The main focus of this paper is to investigate in particular the phase structure for to clarify whether inhomogeneous phases exist. At first, we recalled that the effective action can be written as the sum of a left-handed part and a right-handed part with chemical potentials and , respectively (see Equation (21)). Moreover, each of the two parts was equivalent to the action of the chirally balanced GN model, which was investigated in detail in our previous work [33]. Thus, for and both and had their respective minima at (, denoting the location of the phase boundary of the symmetric phase at and temperature T). (We ignored the existence of an “inhomogeneous island” or “inhomogeneous continent” at large chemical potentials where cutoff effects were particularly strong [33].). Consequently, the minimum of also corresponded to . In other words, from numerical results obtained in ref. [33] at we could conclude that chiral symmetry was restored in the chirally imbalanced GN model for and . In the remaining regions of the space, and compete and the behavior of the condensate needed to be investigated numerically. We started doing that in Section 4.1 by restricting our computations to a homogeneous condensate. After that, in Section 4.2, we carried out a stability analysis of the favored value of the homogeneous condensate with respect to inhomogeneous perturbations. Finally, in Section 4.3, we performed numerical minimizations of the effective action, allowing arbitrary inhomogeneous modulations.
The lattice spacing a was a function of the coupling . As explained in our previous work [33] we tuned such that the temporal extent corresponded to the inverse critical temperature , which separated at , the symmetric and homogeneous symmetry-broken phase. Then, at fixed , the temperature could be changed in discrete steps by increasing or decreasing . A summary of the lattice parameters used to generate all following numerical results is given in Table 1. We note that throughout this section dimensionful quantities are expressed in units of the vacuum expectation value of ,

Table 1.
Lattice parameters (: number of lattice sites in temporal direction corresponding to the critical temperature ; : coupling; a: lattice spacing; : number of lattice sites in each of the two spatial directions).
4.1. Restriction to a Homogeneous Condensate
In the case of a homogeneous condensate, i.e., or equivalently , the two lattice discretizations with and (Equations (31) and (32)) were identical. The Dirac operator corresponded to a block-diagonal matrix with blocks of size . Thus, the term in the effective action (27) could be computed quite efficiently by summing over determinants of matrices. Moreover, the effective action at given , and T is a function of just a single variable ; hence, it could be minimized numerically in a straightforward and rather cheap way to obtain the physically preferred value of the homogeneous condensate.
Figure 1 shows the phase diagram in space for and . For the phase boundary is quite similar to the analytically obtained continuum result [51] with slight deviations due to discretization and finite volume effects. At high temperature the phase boundary exhibited an approximate rotational symmetry in the - plane, i.e., it was crudely described by . In contrast to that, at low temperature, the phase boundary approached a square-like shape in the - plane.
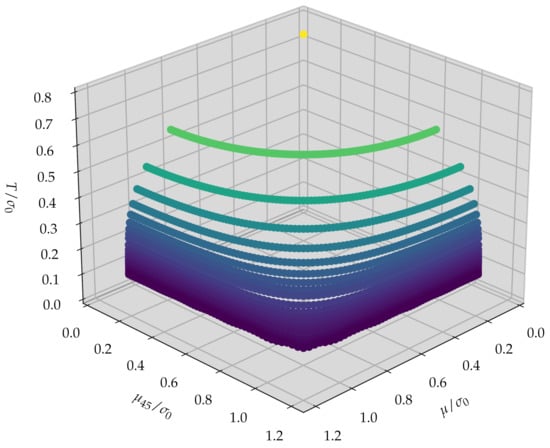
Figure 1.
Phase diagram of the chirally imbalanced -dimensional GN model with the restriction to a homogeneous condensate in space for and .
The left plot of Figure 2 shows sectional views of the phase diagram at fixed lattice spacing for two different spatial extents, and . At low temperature the phase boundary exhibits an oscillatory behavior, which was more pronounced for the smaller lattice volume. We expected that the oscillations would disappear in the infinite volume limit. The right plot of Figure 2 shows sectional views of the phase diagram for two different lattice spacings, and , at fixed ratio implying similar spatial extents and . There were visible discrepancies due to discretization effects, in particular when both T is small and . Continuum results at from Ref. [51] as well as our lattice results at various small temperatures, lattice spacings and spatial volumes point towards phase boundaries at for and at for in the continuum limit.
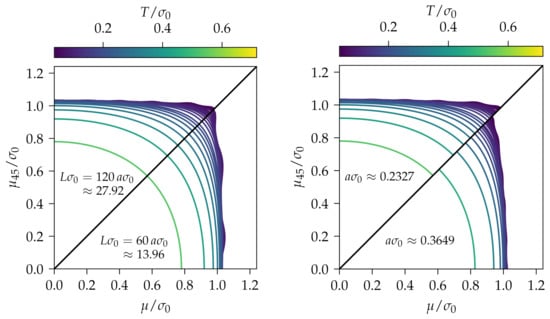
Figure 2.
Phase diagram of the chirally imbalanced -dimensional GN model with the restriction to a homogeneous condensate in the - plane for several temperatures. Since the phase diagram is invariant with respect to , each octant in the - plane contains full information and one can compare the two lattice extents (left plot) or two lattice spacings (right plot) in a convenient way within the same plot. (left) . (right) , i.e., similar spatial lattice extents and .
We also studied the behavior of at small temperature , and . is shown as function of and in the left plot of Figure 3 and as function of and in the right plot of Figure 3. To explain these results, we noted that the effective action (21) was the sum of a left-handed part and a right-handed part with chemical potentials and , respectively. At the beginning of Section 4, we had already concluded that , if and . Similarly, we argue now that both parts favor , if and . The numerical results from Figure 3 are consistent with that expectation. In particular, the yellow regions, where , corresponds to and . In the remaining regions of the - plane, or equivalently the - plane, and compete, leading to a continuous transition of the condensate from to . This continuous behavior was consistent with the fact that the lattice GN model with the effective action or equivalently , restricted to a homogeneous condensate, had a second-order phase transition at , and .
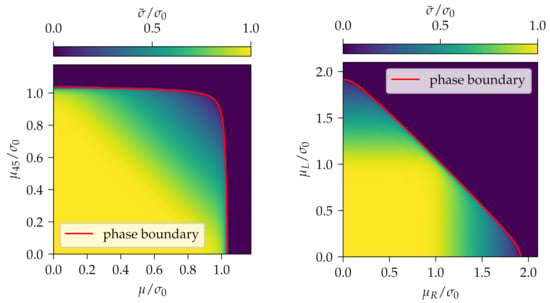
Figure 3.
for the chirally imbalanced -dimensional GN model with the restriction to a homogeneous condensate for , and . (left) as function of and . (right) as function of and .
We note that the lattice data shown in this subsection also represents a non-trivial cross-check of our implementation: all numerical results were consistent with the symmetry within machine precision.
4.2. Stability of a Homogeneous Condensate
Now, we relaxed the constraint that was a homogeneous condensate. To determine the preferred modulation of the condensate in a possibly existing inhomogeneous phase, we had to allow arbitrary spatial modulations of , i.e., consider , and minimize the effective action with respect to these modulations. In lattice field theory this is possible but numerically very challenging. As a first step, therefore, we explored whether the homogeneous minima , which were determined in Section 4.1 for many different , were stable or unstable with respect to spatially inhomogeneous perturbations . Boundaries between stable and unstable regions in space were identical to phase boundaries if the amplitude of the inhomogeneity became infinitesimal when approaching the boundary. However, a stability analysis failed to detect inhomogeneous condensates in regions of the phase diagram where the homogeneous minimum (found, e.g., as described in Section 4.1) corresponded to a local, but not global, minimum of . This was, e.g., the case in the -dimensional GN model [30,67].
A detailed derivation of the formalism to probe the stability of a homogeneous condensate with respect to arbitrary spatial perturbations can be found in ref. [33] for a continuum approach. This formalism can be transferred to lattice discretizations in a straightforward way, which is discussed in the same reference. A quantity of central importance is
where runs over all 3-dimensional lattice momenta (26), , the trace refers to spinor space and is defined via and Equation (29), i.e.,
Negative values of with indicate instability of the condensate with respect to harmonic perturbations with momentum . Such perturbations decrease ; consequently, an inhomogeneous condensate was preferred. By evaluating for suitably chosen parameters we could identify regions that were part of an inhomogeneous phase.
We searched extensively for regions, where was unstable, using both discretizations (31) and (32). For such regions did not seem to exist. For and finite lattice spacing there was a region of instability at small T consistent with the findings at reported in ref. [33]. Figure 4 shows the lattice with the finer lattice spacing, , and spatial extent . The region of instability was located within the tetrahedral shape. At smaller temperature it had a larger extent in the - plane. A somewhat unexpected result was the large extent of the region of instability in direction (e.g., for and up to ). Its boundary is plotted in Figure 5 in the - plane. The plot shows that the instability region extended up to and at the same time down to . A symmetric phase was preferred by with chemical potential , while with chemical potential prefered a homogeneous symmetry-broken phase. Thus, neither of the two parts of the effective action (21) favored an inhomogeneous phase, but in combination they did. This highlighted the non-trivial interplay of and gave rise to a rather large inhomogeneous phase at finite lattice spacing for certain discretizations. Note that Figure 5 also reveals that the homogeneous phase boundary was engulfed by the region of instability, which was not the case in our previous study at [33], where a different lattice regularization was used.
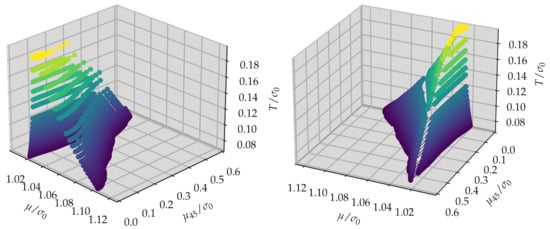
Figure 4.
Boundaries of the region of instability in the chirally imbalanced -dimensional GN model for the discretization in space for and . Both plots show the same data and differ only in angle of view.
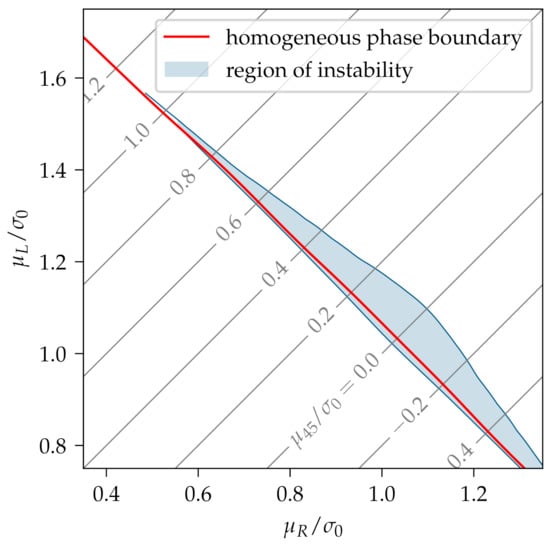
Figure 5.
Region of instability and homogeneous phase boundary in the chirally imbalanced -dimensional GN model for the discretization in the - plane for , and . The chiral chemical potential was constant along the diagonal straight lines.
In Figure 6 we show sectional views of the region of instability for the discretization and various temperatures. The upper row corresponds to the larger lattice spacing and the lower row to the smaller lattice spacing, , while the left column corresponds to smaller and the right column to larger spatial extent . From comparing the upper and the lower row, it is obvious that the instability region shrank when the lattice spacing decreased, most prominently in the direction. This is particularly evident in the right column, where the boundaries are significantly less distorted by finite volume effects. In the plots in the left column, however, there are pronounced oscillations that seem to be caused by small spatial volume. These oscillations are reminiscent of those observed in the -T plane in lattice studies of the chirally balanced GN model in and dimensions [31,33,67].
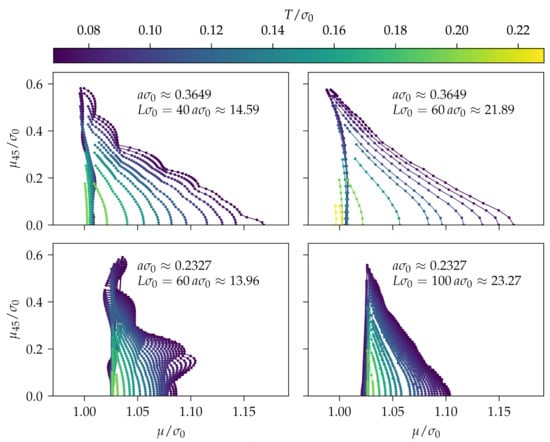
Figure 6.
Boundaries of the region of instability in the chirally imbalanced -dimensional GN model for the discretization in the - plane for several temperatures, two different (upper versus lower row) and two different (left versus right column).
In summary, we found no region of instability for but a shrinking region of instability for decreasing lattice spacing for . This strongly suggests that there is no region of instability in the chirally imbalanced -dimensional GN model in the continuum limit.
4.3. Arbitrary Spatial Modulations of the Condensate
Now, we discuss the minimization of the effective action (27) with respect to the condensate allowing arbitrary spatial modulations, i.e., arbitrary Fourier coefficients . We did this for selected parameters by carrying out several conjugate gradient minimizations, which differed in starting values for . For each we found only a small number of local minima although a significantly larger number of different starting values for were provided to the minimization algorithm. This might have indicated that for all considered the corresponding global minimum was among the found local minima. We note that in our previous work [33] only 1-dimensional modulations were studied, i.e., . In this work we relaxed that constraint to allow arbitrary 2-dimensional modulations, i.e., . Since this was a numerically difficult and computer time-intensive task, we used a rather small lattice with coarse lattice spacing , temperature , and discretization corresponding to .
First, we studied the chirally balanced model, i.e., . As an example, the upper left plot in Figure 7 shows a configuration corresponding to one of the global minima of the effective action at . An inhomogeneous condensate was favored, as we learned from the stability analysis discussed in Section 4.2. Even though the minimization algorithm allows arbitrary 2-dimensional modulations, the resulting global minimum was just a plane wave with wave vector . Similarly, the upper-right plot in Figure 7 shows a minimizing condensate at a larger chemical potential . Again, we found a plane wave, but this time with wave vector , i.e., with a smaller wavelength. Even though the found plane waves were 1-dimensional structures, by allowing arbitrary 2-dimensional modulations it reduced finite volume corrections. This was so because, in contrast to our previous work [33], the direction of the wave vector was no longer restricted to being parallel to one of the coordinate axes; thus, its magnitude could be changed in finer steps.
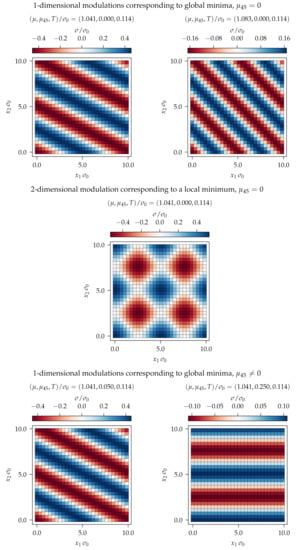
Figure 7.
Modulations of the condensate corresponding to minima of the effective action (27) for the discretization , , and .
The minimization algorithm also found 2-dimensional modulations. These, however, corresponded exclusively to local minima of the effective action (27). An example is shown in the center of Figure 7.
We also investigated, how chiral imbalance, i.e., , affected the preferred modulation of the condensate. The plots in the lower row of Figure 7 show the global minima of the effective action for and . At fixed the frequency was almost independent of (cf. the upper left plot, the lower left plot and the lower right plot of Figure 7). The amplitude, however, decreased when increasing , suppored a second-order phase transition, also at . We searched extensively for inhomogeneous condensates outside the instability region explored and discussed in Section 4.2, but did not find any. Thus, we concluded that the boundaries of the instability region were identical to phase boundaries and that the corresponding phase transitions were of the second order.
5. Conclusions
In this work we studied the phase diagram of the -dimensional GN model with chiral imbalance introduced via a chiral chemical potential using the mean-field approximation. Our lattice field theory results indicated that an inhomogeneous phase exists at finite lattice spacing a, when using a specific lattice discretization (). Non-vanishing , however, seems to disfavor inhomogeneous modulations. Moreover, the inhomogeneous phase shrank for decreasing a and was expected to disappear in the continuum limit. These findings are consistent with our previous work [33], which was restricted to . (For completeness we note that inhomogeneous condensates at and , which are energetically degenerate to the homogenous condensate in the homogeneous symmetry-broken phase, were found in ref. [68]. Our numerical lattice studies were, however, limited to ). Investigations of -dimensional GN-type models [5,6,7,8,9,10,11,12] at finite showed that bosonic quantum fluctuations can influence the extent and existence of (in-)homogeneous phases significantly. Such fluctuations are likely to affect the extent of the homogeneous symmetry-broken phase in the present -dimensional GN model. The inhomogeneous phase was expected to remain absent since bosonic quantum fluctuations tend to disfavor ordered phases even more.
Moreover, for our chirally imbalanced -dimensional GN model, we showed that an isospin chemical potential is equivalent to the chiral chemical potential . Thus, all results presented can either be interpreted in the context of chiral imbalance or of isospin imbalance. In particular the --T phase diagram was identical to the --T phase diagram. Interestingly, a recent study of the -dimensional NJL model in the large- limit [57] conjectured a similar approximate duality of the phase diagram.
Color-superconductivity might play an important role in such studies [69,70], especially at finite isospin chemical potential [71,72]. In the considered -dimensional GN model this could, however, not be investigated, because the necessary difermion interaction was not present. Thus, we are not yet in a position to compare our results to up-to-date lattice QCD simulations at finite (see, e.g., refs. [73,74,75,76,77]), where a phase with Bose–Einstein condensation of charged pions was observed. As a next step, it might therefore be interesting to establish contact with refs. [60,61], where a color-superconducting channel was added to the chirally imbalanced -dimensional GN model. It should be noted, however, that these references introduced the chiral chemical potential in a conceptually different way using spin matrices as well as , instead of , as in Equation (18).
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
L.P., M.W. (Marc Wagner) and M.W. (Marc Winstel) acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the CRC-TR 211 “Strong-interaction matter under extreme conditions”—project number 315477589—TRR 211. L.P. and M.W. (Marc Winstel) acknowledge the support of the Helmholtz Graduate School for Hadron and Ion Research. M.W. (Marc Wagner) acknowledges support by the Heisenberg Programme of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project number 399217702. M.W. (Marc Winstel) acknowledges support by the GSI Forschungs- und Entwicklungsvereinbarungen (GSI F&E). M.W. (Marc Winstel) acknowledges the support of the Giersch Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data set is included in the source files of the pre-print uploaded on https://arxiv.org/abs/2112.11183 (accessed on 20 December 2021).
Acknowledgments
We would like to thank M. Buballa, A. Königstein, L. Kurth, A. Sciarra and M. Thies for valuable discussions regarding this work. We further thank J. Lenz, M. Mandl, R.D. Pisarksi and A. Wipf for general valuable discussions regarding inhomogeneous phases and four-fermion theories. Numerical results in this work were produced with C++ code using the nlopt library [78] for numerical minimization and the eigen3 library for matrix operations [79]. The data used in the figures were processed with the pandas [80] and numpy [81] packages. All figures in this work were produced with the matplotlib package [82]. Calculations on the GOETHE-HLR and on the FUCHS-CSC high-performance computer of the Frankfurt University were conducted for this research. We would like to thank HPC-Hessen, funded by the State Ministry of Higher Education, Research and the Arts, for programming advice.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gross, D.J.; Neveu, A. Dynamical Symmetry Breaking in Asymptotically Free Field Theories. Phys. Rev. 1974, D10, 3235. [Google Scholar] [CrossRef]
- Thies, M.; Urlichs, K. Revised Phase Diagram of the Gross-Neveu Model. Phys. Rev. 2003, D67, 125015. [Google Scholar] [CrossRef]
- Schnetz, O.; Thies, M.; Urlichs, K. Phase Diagram of the Gross-Neveu Model: Exact Results and Condensed Matter Precursors. Ann. Phys. 2004, 314, 425–447. [Google Scholar] [CrossRef]
- Thies, M. From Relativistic Quantum Fields to Condensed Matter and Back Again: Updating the Gross-Neveu Phase Diagram. J. Phys. A Math. Gen. 2006, 39, 12707–12734. [Google Scholar] [CrossRef]
- Cohen, Y.; Elitzur, S.; Rabinovici, E. A Monte Carlo Study of the Gross-Neveu Model. Nucl. Phys. 1983, B220, 102–118. [Google Scholar] [CrossRef]
- Karsch, F.; Kogut, J.B.; Wyld, H.W. The Gross-Neveu Model at Finite Temperature and Density. Nucl. Phys. 1987, B280, 289–303. [Google Scholar] [CrossRef]
- Lenz, J.; Pannullo, L.; Wagner, M.; Wellegehausen, B.; Wipf, A. Inhomogeneous Phases in the Gross-Neveu Model in 1+1 Dimensions at Finite Number of Flavors. Phys. Rev. D 2020, 101, 94512. [Google Scholar] [CrossRef]
- Lenz, J.J.; Pannullo, L.; Wagner, M.; Wellegehausen, B.; Wipf, A. Baryons in the Gross-Neveu Model in 1+1 Dimensions at Finite Number of Flavors. Phys. Rev. D 2020, 102, 114501. [Google Scholar] [CrossRef]
- Lenz, J.J.; Mandl, M.; Wipf, A. Inhomogeneities in the 2-Flavor Chiral Gross-Neveu Model. arXiv 2021, arXiv:2109.05525. [Google Scholar]
- Lenz, J.J.; Mandl, M. Remnants of Large-Nf Inhomogeneities in the 2-Flavor Chiral Gross-Neveu Model. arXiv 2021, arXiv:2110.12757. [Google Scholar]
- Horie, K.; Nonaka, C. Inhomogeneous Phases in the Chiral Gross-Neveu Model on the Lattice. In Proceedings of the 38th International Symposium on Lattice Field Theory, Virtual Conference, 26 July–4 August 2021. [Google Scholar]
- Stoll, J.; Zorbach, N.; Koenigstein, A.; Steil, M.J.; Rechenberger, S. Bosonic Fluctuations in the (1+1)-Dimensional Gross-Neveu(-Yukawa) Model at Varying mu and T and Finite N. arXiv 2021, arXiv:2108.10616. [Google Scholar]
- Basar, G.; Dunne, G.V.; Thies, M. Inhomogeneous Condensates in the Thermodynamics of the Chiral NJL(2) Model. Phys. Rev. 2009, D79, 105012. [Google Scholar] [CrossRef]
- Thies, M. Chiral Spiral in the Presence of Chiral Imbalance. Phys. Rev. D 2018, 98, 96019. [Google Scholar] [CrossRef]
- Thies, M. Phase Structure of the 1+1 Dimensional Nambu–Jona-Lasinio Model with Isospin. Phys. Rev. D 2020, 101, 14010. [Google Scholar] [CrossRef]
- Thies, M. Twisted kink dynamics in multiflavor chiral Gross–Neveu model. J. Phys. A 2022, 55, 15401. [Google Scholar] [CrossRef]
- Kutschera, M.; Broniowski, W.; Kotlorz, A. Quark Matter With Neutral Pion Condensate. Phys. Lett. B 1990, 237, 159–163. [Google Scholar] [CrossRef]
- Kutschera, M.; Broniowski, W.; Kotlorz, A. Quark Matter With Pion Condensate in an Effective Chiral Model. Nucl. Phys. A 1990, 516, 566–588. [Google Scholar] [CrossRef]
- Nakano, E.; Tatsumi, T. Chiral Symmetry and Density Wave in Quark Matter. Phys. Rev. D 2005, 71, 114006. [Google Scholar] [CrossRef]
- Nickel, D. Inhomogeneous Phases in the Nambu-Jona-Lasino and Quark-Meson Model. Phys. Rev. 2009, D80, 74025. [Google Scholar] [CrossRef]
- Broniowski, W. Chiral waves in quark matter. Acta Phys. Polon. Supp. 2012, 5, 631. [Google Scholar] [CrossRef]
- Carignano, S.; Buballa, M.; Schaefer, B.J. Inhomogeneous Phases in the Quark-Meson Model with Vacuum Fluctuations. Phys. Rev. D 2014, 90, 14033. [Google Scholar] [CrossRef]
- Heinz, A.; Giacosa, F.; Wagner, M.; Rischke, D.H. Inhomogeneous Condensation in Effective Models for QCD Using the Finite-Mode Approach. Phys. Rev. 2016, D93, 14007. [Google Scholar] [CrossRef]
- Buballa, M.; Carignano, S. Inhomogeneous Chiral Condensates. Prog. Part. Nucl. Phys. 2015, 81, 39–96. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Tsvelik, A.M.; Valgushev, S. How Transverse Thermal Fluctuations Disorder a Condensate of Chiral Spirals into a Quantum Spin Liquid. Phys. Rev. D 2020, 102, 16015. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Rennecke, F.; Tsvelik, A.; Valgushev, S. The Lifshitz Regime and Its Experimental Signals. Nucl. Phys. A 2021, 1005, 121910. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Rennecke, F. Signatures of Moat Regimes in Heavy-Ion Collisions. Phys. Rev. Lett. 2021, 127, 152302. [Google Scholar] [CrossRef]
- Rennecke, F.; Pisarski, R.D. Moat Regimes in QCD and their Signatures in Heavy-Ion Collisions. In Proceedings of the International Conference on Critical Point and Onset of Deconfinement, Online Conference, 15–19 March 2021. [Google Scholar]
- Fu, W.j.; Pawlowski, J.M.; Rennecke, F. The QCD Phase Structure at Finite Temperature and Density. Phys. Rev. D 2020, 101, 54032. [Google Scholar] [CrossRef]
- Koenigstein, A.; Pannullo, L.; Rechenberger, S.; Winstel, M.; Steil, M.J. Detecting Inhomogeneous Chiral Condensation from the Bosonic Two-Point Function in the (1+1)-Dimensional Gross-Neveu Model in the Mean-Field Approximation. arXiv 2021, arXiv:2112.07024. [Google Scholar]
- Winstel, M.; Stoll, J.; Wagner, M. Lattice investigation of an inhomogeneous phase of the 2 + 1-dimensional Gross-Neveu model in the limit of infinitely many flavors. J. Phys. Conf. Ser. 2020, 1667, 12044. [Google Scholar] [CrossRef]
- Narayanan, R. Phase diagram of the large N Gross-Neveu model in a finite periodic box. Phys. Rev. D 2020, 101, 96001. [Google Scholar] [CrossRef]
- Buballa, M.; Kurth, L.; Wagner, M.; Winstel, M. Regulator Dependence of Inhomogeneous Phases in the 2+1-Dimensional Gross-Neveu Model. Phys. Rev. D 2021, 103, 34503. [Google Scholar] [CrossRef]
- Hands, S.; Kocic, A.; Kogut, J. The Four-Fermi Model in Three Dimensions at Non-Zero Density and Temperature. Nucl. Phys. B 1993, 390, 355–378. [Google Scholar] [CrossRef][Green Version]
- Hands, S.J.; Kogut, J.B.; Strouthos, C.G. The (2+1)-Dimensional Gross-Neveu Model with a U(1) Chiral Symmetry at Non-Zero Temperature. Phys. Lett. B 2001, 515, 407–413. [Google Scholar] [CrossRef][Green Version]
- Gies, H.; Janssen, L. UV Fixed-Point Structure of the Three-Dimensional Thirring Model. Phys. Rev. D 2010, 82, 85018. [Google Scholar] [CrossRef]
- Scherer, D.D.; Gies, H. Renormalization Group Study of Magnetic Catalysis in the 3d Gross-Neveu Model. Phys. Rev. B 2012, 85, 195417. [Google Scholar] [CrossRef]
- Narayanan, R. The Relevance of the Three Dimensional Thirring Coupling at Finite Temperature and Density. Phys. Rev. D 2020, 102, 16014. [Google Scholar] [CrossRef]
- MacKenzie, R.; Panigrahi, P.K.; Sakhi, S. Superconductivity in a Planar Field Theory through the Kosterlitz-Thouless Mechanism. Phys. Rev. B 1993, 48, 3892–3895. [Google Scholar] [CrossRef]
- Tesanovic, Z.; Vafek, O.; Franz, M. Chiral Symmetry Breaking and Phase Fluctuations in Cuprate Superconductors: A QED3 Unified Theory of the Pseudogap State. Phys. Rev. B 2002, 65, 180511. [Google Scholar] [CrossRef]
- Wen, X.G. Quantum Orders and Symmetric Spin Liquids. Phys. Rev. B 2002, 65, 165113. [Google Scholar] [CrossRef]
- Rantner, W.; Wen, X.G. Spin Correlations in the Algebraic Spin Liquid - Implications for High Tc Superconductors. Phys. Rev. B 2002, 66, 144501. [Google Scholar] [CrossRef]
- Ohsaku, T. Relativistic Model for Two-Band Superconductivity. arXiv 2003, arXiv:cond-mat/0306472. [Google Scholar]
- Kalinkin, A.; Skorikov, V.M. Phase Transitions in Four Fermion Models. Inorg. Mater. 2003, 39, 765–779. [Google Scholar] [CrossRef]
- Hands, S.; Strouthos, C. Quantum Critical Behaviour in a Graphene-like Model. Phys. Rev. B 2008, 78, 165423. [Google Scholar] [CrossRef]
- Ziegler, L.; Tirrito, E.; Lewenstein, M.; Hands, S.; Bermudez, A. Correlated Chern Insulators in Two-Dimensional Raman Lattices: A Cold-Atom Regularization of Strongly-Coupled Four-Fermi Field Theories. arXiv 2020, arXiv:2011.08744. [Google Scholar]
- Hands, S.; Kocic, A.; Kogut, J.B. Compositeness, Anomalous Dimensions and Renormalizability in Four Fermi Theories. Phys. Lett. B 1991, 273, 111–117. [Google Scholar] [CrossRef]
- Wellegehausen, B.H.; Schmidt, D.; Wipf, A. Critical Flavor Number of the Thirring Model in Three Dimensions. Phys. Rev. 2017, D96, 94504. [Google Scholar] [CrossRef]
- Hands, S.; Mesiti, M.; Worthy, J. Critical Behaviour in the Single Flavor Thirring Model in 2+1d. Phys. Rev. D 2020, 102, 94502. [Google Scholar] [CrossRef]
- Hands, S. The Planar Thirring Model with K"ahler-Dirac Fermions. Symmetry 2021, 13, 1523. [Google Scholar] [CrossRef]
- Klimenko, K.G. Phase Structure of Generalized Gross-Neveu Models. Z. Phys. C 1988, 37, 457. [Google Scholar] [CrossRef]
- Rosenstein, B.; Warr, B.J.; Park, S.H. Thermodynamics of (2+1)-Dimensional Four Fermi Models. Phys. Rev. D 1989, 39, 3088. [Google Scholar] [CrossRef]
- Kharzeev, D.; Krasnitz, A.; Venugopalan, R. Anomalous Chirality Fluctuations in the Initial Stage of Heavy Ion Collisions and Parity Odd Bubbles. Phys. Lett. B 2002, 545, 298–306. [Google Scholar] [CrossRef]
- Kharzeev, D. Parity Violation in Hot QCD: Why It Can Happen, and How to Look for It. Phys. Lett. B 2006, 633, 260–264. [Google Scholar] [CrossRef]
- Charbonneau, J.; Zhitnitsky, A. Topological Currents in Neutron Stars: Kicks, Precession, Toroidal Fields, and Magnetic Helicity. J. Cosmol. Astropart. Phys. 2010, 2010, 10. [Google Scholar] [CrossRef]
- Ohnishi, A.; Yamamoto, N. Magnetars and the Chiral Plasma Instabilities. arXiv 2014, arXiv:1402.4760. [Google Scholar]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. QCD Phase Diagram with Chiral Imbalance in NJL Model: Duality and Lattice QCD Results. J. Phys. Conf. Ser. 2019, 1390, 12015. [Google Scholar] [CrossRef]
- Chernodub, M.N.; Ambrus, V.E. Phase Diagram of Helically Imbalanced QCD Matter. Phys. Rev. D 2021, 103, 94015. [Google Scholar] [CrossRef]
- Khunjua, T.G.; Klimenko, K.G.; Zhokhov, R.N. Influence of chiral asymmetry on phase structure of the two-color quark matter. arXiv 2021, arXiv:2105.04952. [Google Scholar]
- Ebert, D.; Khunjua, T.G.; Klimenko, K.G.; Zhukovsky, V.C. Competition and Duality Correspondence between Chiral and Superconducting Channels in (2+1)-Dimensional Four-Fermion Models with Fermion Number and Chiral Chemical Potentials. Phys. Rev. D 2016, 93, 105022. [Google Scholar] [CrossRef]
- Zhukovsky, V.C.; Klimenko, K.G.; Khunjua, T.G. Superconductivity in Chiral-Asymmetric Matter within the (2 + 1)-Dimensional Four-Fermion Model. Moscow Univ. Phys. 2017, 72, 250–256. [Google Scholar] [CrossRef]
- Braguta, V.V.; Goy, V.A.; Ilgenfritz, E.M.; Kotov, A.Y.; Molochkov, A.V.; Muller-Preussker, M.; Petersson, B. Two-Color QCD with Non-zero Chiral Chemical Potential. JHEP 2015, 6, 94. [Google Scholar] [CrossRef]
- Braguta, V.V.; Ilgenfritz, E.M.; Kotov, A.Y.; Petersson, B.; Skinderev, S.A. Study of QCD Phase Diagram with Non-Zero Chiral Chemical Potential. Phys. Rev. D 2016, 93, 34509. [Google Scholar] [CrossRef]
- Braguta, V.V.; Kotov, A.Y. Catalysis of Dynamical Chiral Symmetry Breaking by Chiral Chemical Potential. Phys. Rev. D 2016, 93, 105025. [Google Scholar] [CrossRef]
- Winstel, M.; Pannullo, L.; Wagner, M. Phase diagram of the 2+1-dimensional Gross-Neveu model with chiral imbalance. In Proceedings of the 38th International Symposium on Lattice Field Theory, Virtual Conference, 26 July–4 August 2021. [Google Scholar]
- Pisarski, R.D. Chiral Symmetry Breaking in Three-Dimensional Electrodynamics. Phys. Rev. D 1984, 29, 2423. [Google Scholar] [CrossRef]
- De Forcrand, P.; Wenger, U. New Baryon Matter in the Lattice Gross-Neveu Model. In Proceedings of the 24th International Symposium on Lattice Field Theory (Lattice 2006), Tucson, AZ, USA, 23–28 July 2006; Volume LAT2006, p. 152. [Google Scholar] [CrossRef][Green Version]
- Urlichs, K. Baryons and Baryonic Matter in Four-Fermion Interaction Models. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2007. [Google Scholar]
- Sadzikowski, M. Comparison of the non-uniform chiral and 2SC phases at finite temperatures and densities. Phys. Lett. B 2006, 642, 238–243. [Google Scholar] [CrossRef][Green Version]
- Lakaschus, P.; Buballa, M.; Rischke, D.H. Competition of inhomogeneous chiral phases and two-flavor color superconductivity in the NJL model. Phys. Rev. D 2021, 103, 34030. [Google Scholar] [CrossRef]
- Fukushima, K.; Iida, K. Larkin-Ovchinnikov-Fulde-Ferrell state in two-color quark matter. Phys. Rev. D 2007, 76, 54004. [Google Scholar] [CrossRef]
- Nowakowski, D.; Carignano, S. Color-superconductivity and inhomogeneous chiral symmetry breaking in isospin-asymmetric quark matter. PoS 2016, 262, 10. [Google Scholar] [CrossRef]
- Brandt, B.B.; Endrodi, G. QCD phase diagram with isospin chemical potential. PoS 2016, 256, 39. [Google Scholar] [CrossRef]
- Brandt, B.B.; Cuteri, F.; Endrodi, G.; Schmalzbauer, S. The Dirac spectrum and the BEC-BCS crossover in QCD at nonzero isospin asymmetry. Particles 2020, 3, 80–86. [Google Scholar] [CrossRef]
- Brandt, B.B.; Cuteri, F.; Endrodi, G.; Schmalzbauer, S. Exploring the QCD phase diagram via reweighting from isospin chemical potential. PoS 2019, 363, 189. [Google Scholar] [CrossRef]
- Cao, X.; Liu, H.; Li, D.; Ou, G. QCD Phase Diagram at Finite Isospin Chemical Potential and Temperature in an IR-improved Soft-Wall AdS/QCD Model. Chin. Phys. C 2020, 44, 83106. [Google Scholar] [CrossRef]
- Brandt, B.B.; Cuteri, F.; Endrodi, G. QCD thermodynamics at non-zero isospin asymmetry. In Proceedings of the 38th International Symposium on Lattice Field Theory, Virtual Conference, 26 July–4 August 2021. [Google Scholar]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. 2011. Available online: http://github.com/stevengj/nlopt (accessed on 20 July 2021).
- Guennebaud, G.; Jacob, B. Eigen v3. 2010. Available online: http://eigen.tuxfamily.org (accessed on 20 July 2021).
- The Pandas Development Team. Pandas-Dev/Pandas: Pandas. 2020. Available online: https://zenodo.org/record/5893288 (accessed on 14 December 2021).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).