Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators
Abstract
1. Introduction
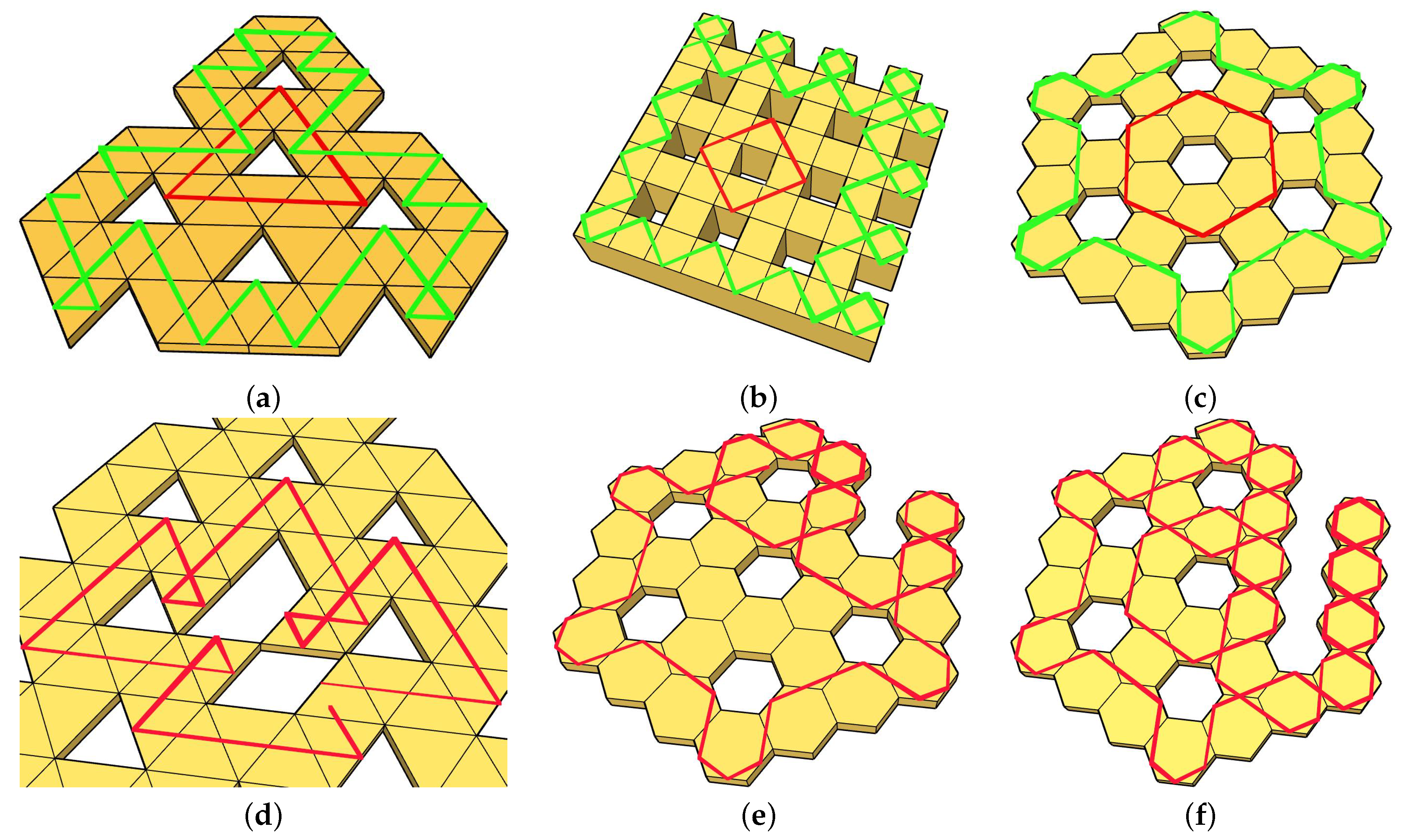
2. Formulation of the Problem
- Introducing a defect into an infinite FTIR array (creating a hole), Figure 2d.
- Creating a finite FTIR array by discarding the neighborhood of an infinitely distant point from the structure.
3. Methodology and Limitations
4. Results and Discussion
5. Conclusions
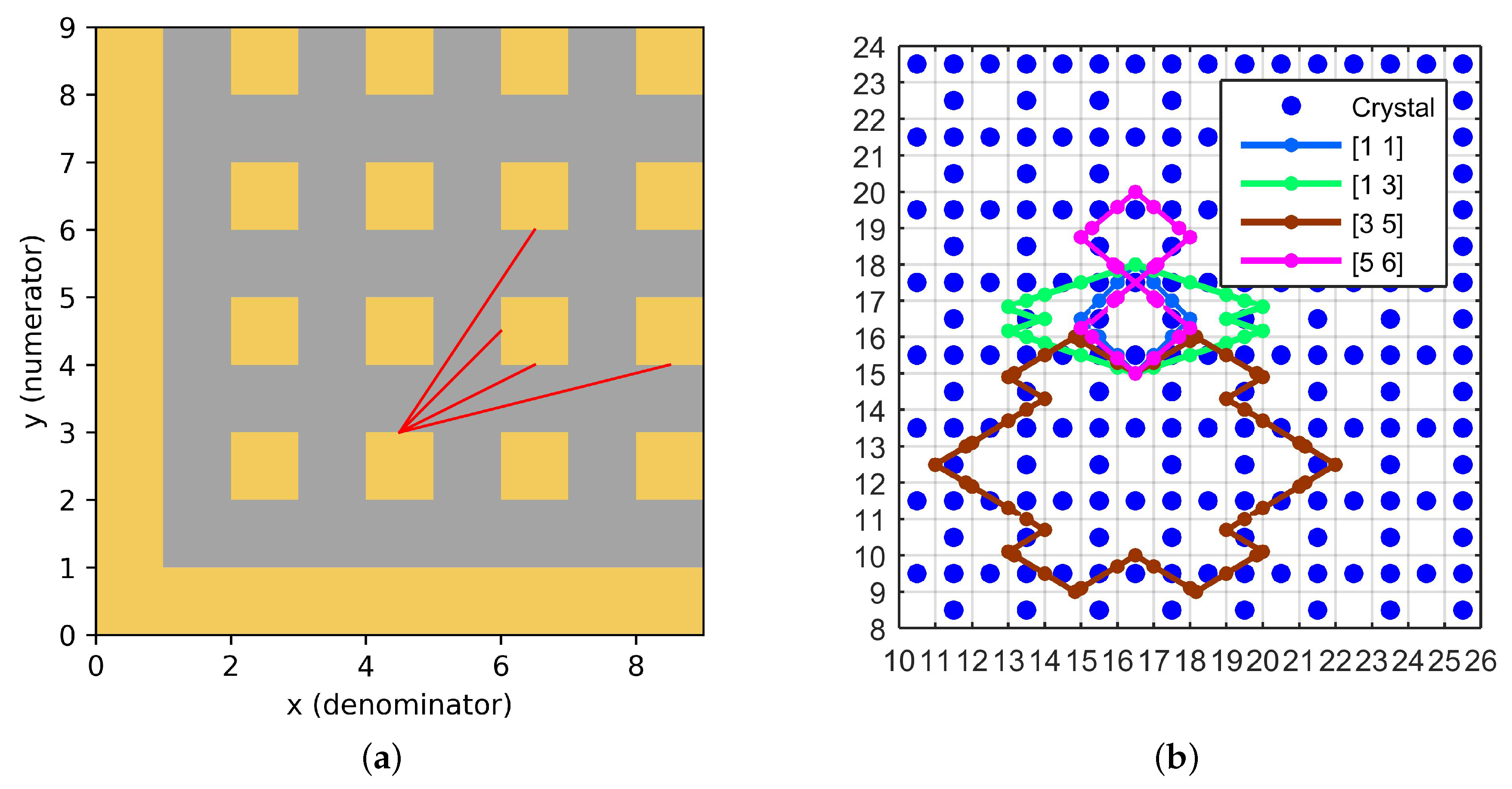
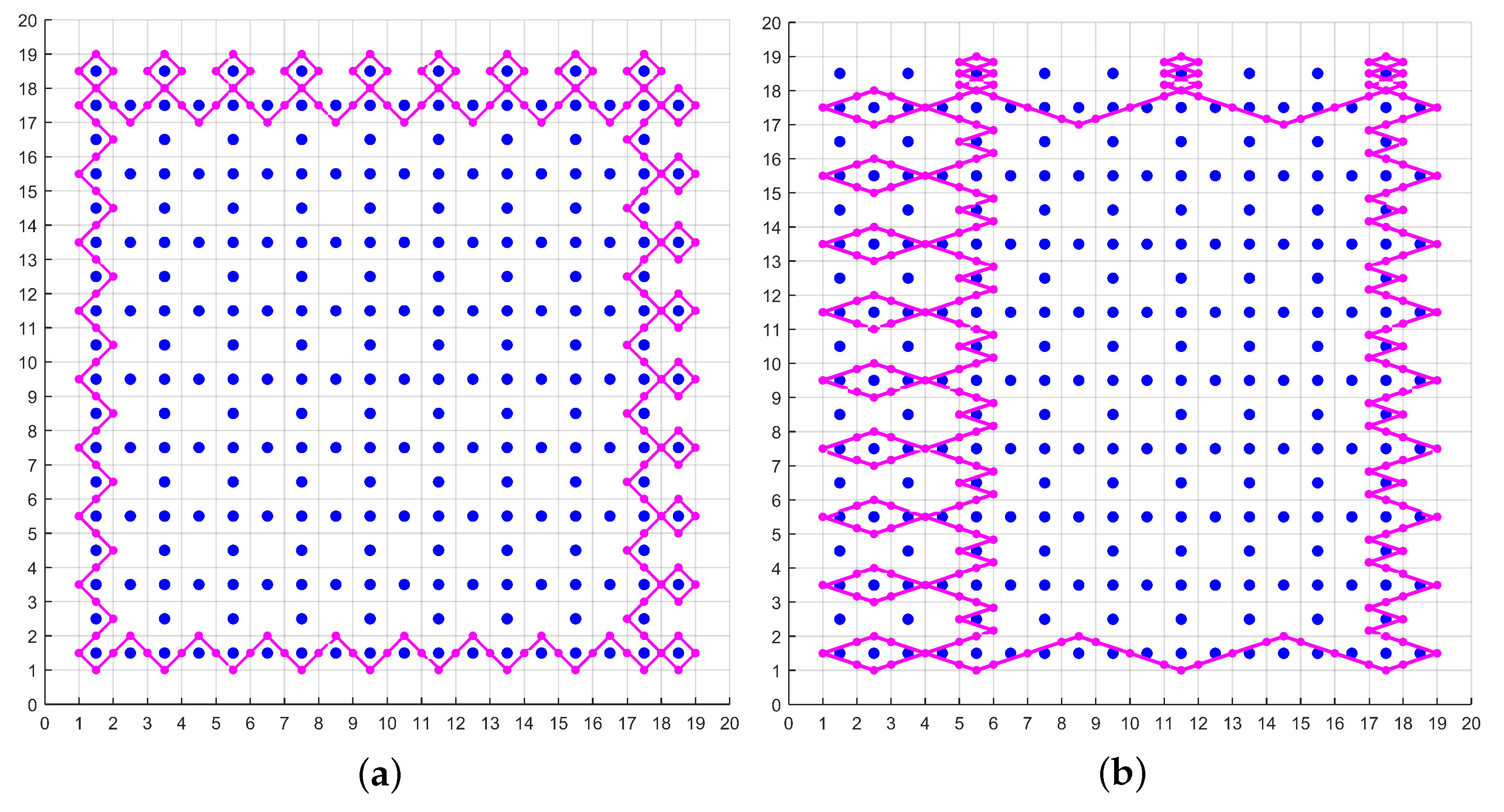
- Beyond Rudner’s solutions, fundamentally new edge solutions were found. This new class of solutions is infinite and can be classified by rational numbers, where Rudner’s solution is a particular case corresponding to the number 1. Most solutions correspond to ratios with an odd numerator and denominator.
- The ray penetrates into the array crossing several resonator layers. This behavior differs from Rudner’s solutions which are completely localized inside the surface layer of resonators. At the same time, the ray cannot penetrate deeper, since only closed trajectories with zero group velocity can occur in an infinite array (the gapless insulator case).
- The new class of trajectories breaks the array symmetry. This behavior is also different to Rudner’s solutions that bear the same symmetry as the resonator array.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FTIR | Frustrated Total Internal Reflection |
| TI | Topological Insulator |
| RI | Reversible Topological Insulator |
| LC | Loop Conductor |
References
- Haldane, F.D.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [PubMed]
- Khanikaev, A.B.; Shvets, G. Two-dimensional topological photonics. Nat. Photonics 2017, 11, 763–773. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum Spin hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed]
- Grushevskaya, H.; Krylov, G. Vortex dynamics of charge carriers in the quasi-relativistic graphene model: High-energy k→·p→ approximation. Symmetry 2020, 12, 261. [Google Scholar] [CrossRef]
- Grushevskaya, H.V.; Krylov, G.G.; Kruchinin, S.P.; Vlahovic, B.; Bellucci, S. Electronic properties and quasi-zero-energy states of graphene quantum dots. Phys. Rev. B 2021, 103, 235102. [Google Scholar] [CrossRef]
- Sergeev, A.G. On mathematical problems in the theory of topological insulators. Theor. Math. Phys. 2021, 208, 1144–1155. [Google Scholar] [CrossRef]
- Kitagawa, T.; Berg, E.; Rudner, M.; Demler, E. Topological characterization of periodically driven quantum systems. Phys. Rev. B 2010, 82, 235114. [Google Scholar] [CrossRef]
- Farrelly, T. A review of quantum cellular automata. Quantum 2020, 4, 368. [Google Scholar] [CrossRef]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601. [Google Scholar] [CrossRef]
- McMullen, C.T. Billiards, heights, and the arithmetic of non-arithmetic groups. Invent. Math. 2022, 228, 1309–1351. [Google Scholar] [CrossRef]
- Maczewsky, L.J.; Zeuner, J.M.; Nolte, S.; Szameit, A. Observation of photonic anomalous Floquet topological insulators. Nat. Commun. 2017, 8, 13756. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Gao, Z.; Shi, X.; Yang, Z.; Lin, X.; Xu, H.; Joannopoulos, J.D.; Soljaaia, M.; Chen, H.; Lu, L.; et al. Probing topological protection using a designer surface plasmon structure. Nat. Commun. 2016, 7, 11619. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Chong, Y.D. Edge Solitons in Nonlinear-Photonic Topological Insulators. Phys. Rev. Lett. 2016, 117, 143901. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Smirnova, D.A. Probing bulk topological invariants using leaky photonic lattices. Nat. Phys. 2021, 17, 632–638. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, A.W.; Hawley, D.; Roy, R. Frustrated total internal reflection: A demonstration and review. Am. J. Phys. 1986, 54, 601–607. [Google Scholar] [CrossRef]
- Shvartsburg, A.B. Tunneling of electromagnetic waves: Paradoxes and prospects. Physics-Uspekhi 2007, 50, 37. [Google Scholar] [CrossRef]
- Galperin, G.; Zemlyakov, A. Mathematical Billiards; Library “Kvant”: Moscow, Russia, 1990; Volume 77. [Google Scholar]
- Wright, A. From rational billiards to dynamics on moduli spaces. Bull. Am. Math. Soc. 2016, 53, 41–56. [Google Scholar] [CrossRef]
- Li, M.; Zhirihin, D.; Gorlach, M.; Ni, X.; Filonov, D.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Higher-order topological states in photonic kagome crystals with long-range interactions. Nat. Photonics 2020, 14, 89–94. [Google Scholar] [CrossRef]

| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | TI | C | TI | C | TI | C | TI | C | TI | C | TI | C | TI |
| 2 | # | C | # | C | # | C | # | C | # | C | # | C | |
| 3 | # | C | TI | # | TI | C | # | C | TI | # | TI | ||
| 4 | # | C | # | C | # | C | # | C | # | C | |||
| 5 | # | LC | TI | C | TI | # | TI | C | TI | ||||
| 6 | # | LC | # | # | # | C | # | C | |||||
| 7 | # | C | TI | C | TI | C | TI | ||||||
| 8 | # | C | # | C | # | C | |||||||
| 9 | # | C | RI | # | TI | ||||||||
| 10 | # | C | # | C | |||||||||
| 11 | # | LC | RI | ||||||||||
| 12 | # | LC | |||||||||||
| 13 | # |
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | |
|---|---|---|---|---|---|---|---|
| 1 | TI | TI | TI | TI | TI | TI | TI |
| 3 | # | TI | TI | # | TI | TI | |
| 5 | # | TI | TI | TI | TI | ||
| 7 | # | TI | TI | TI | |||
| 9 | # | RI | TI | ||||
| 11 | # | RI | |||||
| 13 | # |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedchenko, D.P.; Kim, P.N.; Timofeev, I.V. Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators. Symmetry 2022, 14, 2673. https://doi.org/10.3390/sym14122673
Fedchenko DP, Kim PN, Timofeev IV. Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators. Symmetry. 2022; 14(12):2673. https://doi.org/10.3390/sym14122673
Chicago/Turabian StyleFedchenko, Dmitry P., Petr N. Kim, and Ivan V. Timofeev. 2022. "Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators" Symmetry 14, no. 12: 2673. https://doi.org/10.3390/sym14122673
APA StyleFedchenko, D. P., Kim, P. N., & Timofeev, I. V. (2022). Photonic Topological Insulator Based on Frustrated Total Internal Reflection in Array of Coupled Prism Resonators. Symmetry, 14(12), 2673. https://doi.org/10.3390/sym14122673







