Abstract
The purpose of this article is to solve a nonlinear fractional Klein–Fock–Gordon equation that involves a recently created non-singular kernel fractional derivative by Caputo–Fabrizio. Motivated by some physical applications related to the fractional Klein–Fock–Gordon equation, we focus our study on this equation and some phenomena rated to it. The findings are crucial and essential for explaining a variety of physical processes. In order to find satisfactory approximations to the offered problems, this work takes into account a modern methodology and fractional operator in this context. We first take the Yang transform of the Caputo–Fabrizio fractional derivative and then implement it to solve fractional Klein–Fock–Gordon equations. We will consider three cases of the nonlinear fractional Klein–Fock–Gordon equation to ensure the applicability and effectiveness of the suggested technique. In order to determine an approximate solution to the fractional Klein–Fock–Gordon equation in the fast convergent series form, we can use the fractional homotopy perturbation transform approach. The numerical simulation is provided to demonstrate the effectiveness and dependability of the suggested method. Furthermore, several fractional orders will be used to describe the behavior of the given solutions. The results achieved demonstrate the high efficiency, ease of use, and applicability of this strategy for resolving other nonlinear issues.
1. Introduction
Fractional calculus (FC) was first introduced more than 324 years ago, but it has only recently drawn the interest of numerous academics working in many different fields of science and engineering. This interest is due to its advantageous qualities, including analyticality, heredity, nonlocality, and memory effect. FC has developed over the last several decades into the most potent instrument for analyzing and describing nonlinear complex processes. Due to the complexity associated with the occurrence of heterogeneities, the idea of derivatives with an arbitrary order has been established [1,2,3]. Non-integer order-differential operators can capture complicated media with diffusion mechanisms. Numerous scholars began working on the fundamentals and applications of fractional calculus as a result of the quick development of computer and mathematical techniques and software [4,5,6]. Numerous pioneering approaches that prescribed the basis for fractional calculus have been made available for diverse definitions of the subject. The FC has been used in practical projects and has been applied to biomathematics [7], chaos theory [8], financial models [9], optics [10], and other fields [11,12,13,14,15,16,17].
Due to the soliton-like solutions found in many mathematical physics models, the idea of solitons is crucial, especially in plasma physics [18,19,20,21,22,23,24,25]. One type of common physical system that represents weakly nonlinear dispersive partial differential equations (PDEs) is called a soliton. The term “generalization” refers to the fractional PDEs that are composed of a non-integer order as opposed to the classical integer-order PDEs. Due to its numerous theoretical and practical applications in applied sciences, engineering problems, and in the modeling of many nonlinear problems in different plasma physics, fractional nonlinear differential equations (FNDEs) have gained a lot of interest in past years [26,27,28]. In a scientific study, the approximate solution of fractional nonlinear differential equations (FNDEs) is a topic that has both theoretical and practical applications. It draws a large number of scholars to create unique methods to find precise and approximative solutions of FNDEs. Numerous scientists and mathematicians have created effective direct strategies for the approximative and closed-form solutions of FNDEs over the last few of years. Several effective methods include the Yang transform decomposition method [29,30], the Sine–Gordon expansion method [31], the fractional variational iteration method [32], the q-homotopy analysis Sumudu transform method [33], the natural transform decomposition method via the Caputo–Fabrizio fractional-order derivative [34,35], the reduced differential transform method [36], the homotopy perturbation Sumudu transform method [37], the Elzaki transform decomposition method [38], the Laplace transform decomposition method via the Atangana–Baleanu fractional derivative [39], the variational iteration method via the Atangana–Baleanu fractional derivative [40], the F-expansion method [41], and many other techniques [42,43,44,45,46,47] have been applied for analyzing the FNDEs.
On the other hand, the Klein–Fock–Gordon (KFG) equation, which was developed by physicists Klein, Fock, and Gordon, explains relativistic electrons. This equation, also referred to as the relativistic wave equation, is a quantized representation of the relativistic energy-momentum relation and is connected to the Schrodinger equation. The KFG equation and the Dirac equation both have theoretical applications. The following fractional-order KFG equation is taken into consideration in our investigation:
along with the initial conditions (ICs): and where represents the Caputo–Fabrizio fractional derivative, n is a positive integer, and are real constants. The Klein–Fock–Gordon equation appeared in a variety of physical processes, including condensed-matter physics, nonlinear optics, quantum field theory, and the interaction of solitons in a collisionless plasma. Different numerical techniques have been devoted to the study of the KFG equation, such as the homotopy analysis method (HAM) [48], the variational iteration method [49], the modified differential transform method [50], the differential transform method (DTM) [51], the q-homotopy analysis transform method [52], the homotopy analysis transform method [53], and many others [54,55].
The homotopy perturbation method (HPM) [56], which is the combination of the homotopy method and the conventional perturbation methodology, was proposed by He in 1999. This technique has been successfully used for solving both linear and nonlinear problems [57,58]. As HPM does not require a small parameter in the equation, it has fewer limitations than conventional perturbation techniques. The major goal of this study is to solve nonlinear fractional order PDEs by using Yang’s newly introduced integral transform, commonly known as the “Yang Transform”, which was discovered with HPM via the Caputo–Fabrizio fractional derivative. The analysis of fractional differential equations has taken on a new dimension as a result of the Caputo–Fabrizio fractional derivative. The nonsingular kernel of the new derivative is one of its most attractive features. The Caputo–Fabrizio derivative has the same additional motivating characteristics of heterogeneity and configuration [59,60], with different scales to the Caputo and Riemann–Liouville fractional derivatives despite being created through the convolution of an ordinary derivative and an exponential function. Using the suggested approach, we can resolve three well-known nonlinear PDEs. In the context of a swiftly converging series, we acquire a power-series solution, and just a few iterations are designed to accomplish outstanding results. A solution that can be easily determined using these strategies can be reached after only a few iterations, without the need for a method such as discretizing the problem or linearizing the nonlinear problem.
The following is information about the paper’s classification: Section 2 illustrates the fundamental concept pertaining to Caputo–Fabrizio definitions. The Yang–Laplace duality property and the Caputo–Fabrizio fractional derivative are presented in Section 3. We demonstrate the general application of the suggested approach in Section 4, together with convergence and error analysis. In Section 5, the numerical solution of the fractional model is briefly explained, and then it is concluded in Section 6.
2. Preliminaries
We presented some definitions related to our present work. Simply put, we present the exponential decay kernel as .
Definition 1.
If , the derivative in terms of Caputo–Fabrizio (CF) is stated as:
where represents the normalization function having . Additionally, if , then the proposed derivative is stated as:
Definition 2.
The CF integral that has fractional order is stated as:
Definition 3.
For , the Laplace transform of the CF derivative leads to the result:
Definition 4.
The Yang transform (YT) of is given as:
here, μ is the transform variable.
Remark 1.
Some important functions YT is stated as.
3. Main Work
First, using the Yang–Laplace duality property, we construct the formula for the YT of the CF fractional derivative. To verify the accuracy and effectiveness of the unique method, we provide a few examples with complete solutions at the end of this section.
Lemma 1 (Laplace-Yang duality).
If is the Laplace transform of then .
Proof.
By inserting as in Equation (6), we obtain another form of YT.
Since ,
Put in (9), we obtain
Now, from Equation (8), we have
Lemma 2.
The YT of the CF derivative of is given if is a continuous function.
Proof.
The CF fractional’s Laplace transform is represented by
Additionally, there is a connection between the Laplace and Yang properties, i.e., . The Equation (14) variable is changed to to achieve the desired result, and we obtain
which completes the proof. □
4. Algorithm of the Suggested Technique
In this part, we go over the method for differential equations of fractional order with an exponential-decay kernel. We show a few cases with comprehensive solutions and a comparison to the precise solutions.
4.1. Implementation to Caputo–Fabrizio Fractional Differential Equations
First, using YTHPM, we create a technique to solve general nonlinear Caputo–Fabrizio (CF) fractional partial differential equations. Take a look at a general nonlinear CF PDE with a nonlinear term of and a linear term of , as shown below
where the term denotes the source term. On employing YT to Equation (17), we have
By employing Yang inverse transform, we obtain
here, shows the source term and initial condition. Now, by utilizing HPM:
The decomposition of the nonlinear term reads
where shows the He’s polynomial and is determined as:
On comparing the coefficients in (22), we obtain:
Hence, we obtain the solution as given below:
4.2. Convergence and Error Analysis
The convergence and error analysis of the original problem (16) are dealt with in the following theorems, which are based on the mechanism of the approach [61].
Theorem 1.
Suppose the exact solution of (16) is and let , , and , where H represents the Hilbert space. The solution obtained will converge if , i.e., for any , such that
Proof.
We take a sequence of
We must demonstrate that forms a “Cauchy sequence” in order to achieve the desired outcome. Additionally, let us take
For , we have
As , and are bound, so take , and we obtain
Hence, makes a “Cauchy sequence” in H. This proves that the sequence is a convergent sequence with the limit for , which completes the proof. □
Theorem 2.
Let us assume that is finite and reflects the series solution that was found. Assuming such that , the maximum absolute error is given by the following relation:
Proof.
Suppose is finite, which implies that .
Let us consider
which completes the proof of the theorem. □
5. Applications
The YT-HPM is implemented to nonlinear FKFG equations in this study.
Example 1.
Let us assume the nonlinear FKFG equation in the case when , and as
having initial conditions
On taking YT of Equation (46), we have
By employing inverse YT, we obtain
Utilizing the HPT approach, we obtain
where the nonlinear terms are determined by He’s polynomial and are calculated as
Thus, by comparing the same powers of in (50), we obtain
Now,
The solution in series form is stated as below:
Example 2.
Let us assume the nonlinear FKFG equation in the case when , and as
having the ICs
On taking the YT of Equation (46), we have
By employing inverse YT, we have
Utilizing the HPT, we obtain
where the nonlinear terms are determined by He’s polynomial and are calculated as
Thus, by comparing the same powers of in (50), we obtain
The solution in series form is stated as given below:
Example 3.
Let us assume the cubic nonlinear FKFG equation as
having the ICs
On taking the YT of Equation (46), we have
By employing inverse YT, we have
Utilizing the HPT approach, we obtain
where the nonlinear terms are determined by He’s polynomial and are calculated as
Thus, by comparing the same powers of in (50), we obtain
The solution in series form is stated as below:
Results and Discussion
The numerical results for the FKFG equation are shown with FHPTM via the CF derivative in this section. With the help of Maple, the above problems are displayed in tabular and graphical form. Table 1 compares the approximations for the solutions to Example 1 for various values of and . The numerical results for the FKFG equation via the FHPTM via the CF derivative are similarly shown in Table 2 and Table 3, with distinct and for various values of fractional-order . The approximate solutions for various fractional-order values are shown in Figure 1, Figure 2 and Figure 3, respectively. This illustrates how the graphical behavior varies on the order of the fractional derivative. For Examples 1–3, all of the figures depict the approximate surface of solution for various values of fractional order. It is clear from the figures that the solution is dependent on the order of the fractional derivative.

Table 1.
Solution by means of proposed method with distinct and for various values of fractional orders of Example 1.

Table 2.
Solution by means of proposed method with distinct and for various values of fractional orders of Example 2.

Table 3.
Solution by means of proposed method with distinct and for various values of fractional orders of Example 3.
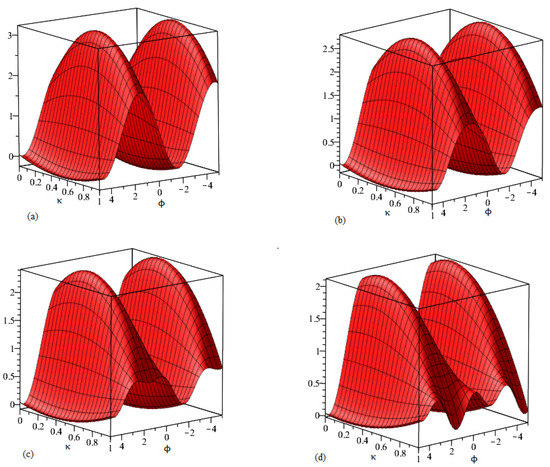
Figure 1.
Behavior of the of suggested method solutions for at different values of and . (a) Graphical layout of the function at . (b) Graphical layout of the function at . (c) Graphical layout of the function at . (d) Graphical layout of the function at of Example 1.
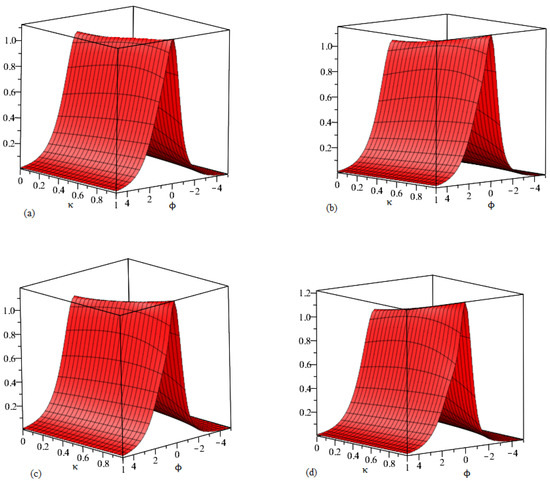
Figure 2.
Behavior of the of suggested method solutions for at different values of and . (a) Graphical layout of the function at . (b) Graphical layout of the function at . (c) Graphical layout of the function at . (d) Graphical layout of the function at of Example 2.
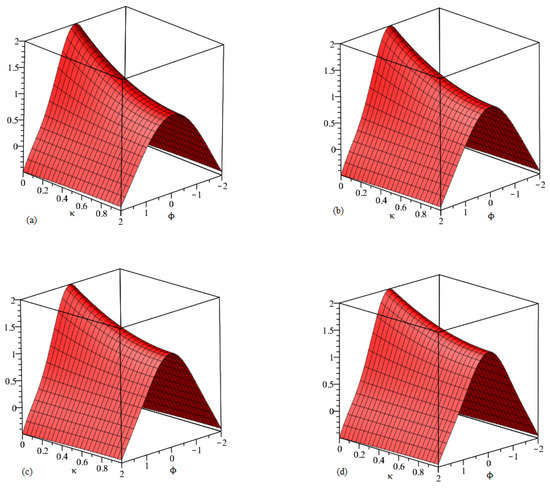
Figure 3.
Behavior of the of suggested method solutions for at different values of and . (a) Graphical layout of the function at . (b) Graphical layout of the function at . (c) Graphical layout of the function at . (d) Graphical layout of the function at of Example 3.
6. Conclusions
In this article, we have made an effort to understand and analyze the Caputo–Fabrizio fractional derivative-based fractional homotopy perturbation transform method, which is used to provide a rough solution to the nonlinear Klein–Fock–Gordon problem. We have taken into account three instances of the FKFG equation together with various initial conditions. The suggested approach provides more precise and speedily decipherable solutions in the form of a series. Tables and graphs have been used to present the calculated results. The vast results demonstrate the effectiveness and simplicity of this strategy, which may also be used to address other nonlinear issues. The obtained results can help numerous authors to study and interpret their experimental and observation data, especially the authors that specialize in nonlinear sciences such as plasma physics and nonlinear optics.
Author Contributions
Conceptualization, H.A.A. and R.S.; methodology, R.S. and S.A.E.-T.; software, R.S. and S.A.E.-T.; validation, H.A.A., K.N. and L.S.E.-S.; formal analysis, H.A.A., K.N. and L.S.E.-S.; investigation, S.A.E.-T.; resources, R.S. and S.A.E.-T.; data curation, H.A.A., K.N. and L.S.E.-S.; writing—original draft preparation, R.S.; writing—review and editing, H.A.A. and S.A.E.-T.; visualization, R.S. and K.N.; supervision, H.A.A.; project administration, S.A.E.-T. All authors have read and agreed to the published version of the manuscript.
Funding
The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2023R17), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to Princess Nourah bint Abdulrahman University Researchers Supporting Project (Grant No. PNURSP2023R17), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liouville, J. Memoire surquelques questions de geometrieet de mecanique, etsurun nouveau genre de calcul pour resoudreces questions. J. Ec. Polytech. 1832, 13, 1–69. [Google Scholar]
- Riemann, G.F.B. Versucheinerallgemeinen Auffassung der Integration und Differentiation. In Gesammelte Mathematische Werke; Springer: Leipzig, Germany, 1896. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Liu, K.; Yang, Z.; Wei, W.; Gao, B.; Xin, D.; Sun, C.; Wu, G. Novel detection approach for thermal defects: Study on its feasibility and application to vehicle cables. High Voltage 2022, 1–10. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, K.; Li, J.; Guo, Y.; Zhang, A.; Chen, Q. Millimeter-Wave E-Plane Waveguide Bandpass Filters Based on Spoof Surface Plasmon Polaritons. IEEE Trans. Microw. Theory Tech. 2022, 70, 4399–4409. [Google Scholar] [CrossRef]
- Xi, Y.; Jiang, W.; Wei, K.; Hong, T.; Cheng, T.; Gong, S. Wideband RCS Reduction of Microstrip Antenna Array Using Coding Metasurface with Low Q Resonators and Fast Optimization Method. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 656–660. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.A.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. Solution for fractional Zakharov-Kuznetsov equations by using two reliable techniques. Chin. J. Phys. 2019, 60, 313–330. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Baskonus, H.M. Analysis of the dynamics of hepatitis E virus using the Atangana-Baleanu fractional derivative. Eur. Phys. J. Plus 2019, 134, 241. [Google Scholar] [CrossRef]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A new efficient technique for solving fractional coupled Navier-Stokes equations using q-homotopy analysis transform method. Pramana-J. Phys. 2019, 93, 6. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Ullah, R.; Khan, A.; Shah, R.; Kafle, J.; Mahariq, I.; Jarad, F. Numerical analysis of the fractional-order nonlinear system of Volterra integro-differential equations. J. Funct. Spaces 2021, 2021, 1537958. [Google Scholar] [CrossRef]
- Al-Habahbeh, A. Exact solution for commensurate and incommensurate linear systems of fractional differential equations. J. Math. Comput. Sci. 2023, 28, 123–136. [Google Scholar] [CrossRef]
- Wang, Y.; Han, X.; Jin, S. MAP based modeling method and performance study of a task offloading scheme with time-correlated traffic and VM repair in MEC systems. Wirel. Netw. 2022, 1–22. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, L.; Pan, G.; Zhang, S. Robust yaw control of autonomous underwater vehicle based on fractional-order PID controller. Ocean Eng. 2022, 257, 111493. [Google Scholar] [CrossRef]
- Alharthi, M.R.; Alharbey, R.A.; El-Tantawy, S.A. Novel analytical approximations to the nonplanar Kawahara equation and its plasma applications. Eur. Phys. J. Plus 2022, 137, 1172. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Alyousef, H.A.; Alharthi, M.R. Novel approximations to a nonplanar nonlinear Schrodinger equation and modeling nonplanar rogue waves/breathers in a complex plasma. Chaos Solitons Fractals 2022, 163, 112612. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; El-Tantawy, S.A. Novel anlytical solution to the damped Kawahara equation and its application for modeling the dissipative nonlinear structures in a fluid medium. J. Ocean Eng. Sci. 2022, 7, 492. [Google Scholar] [CrossRef]
- Shohaib, M.; Masood, W.; Alyousef, H.A.; Siddiq, M.; El-Tantawy, S.A. Formation and interaction of multi-dimensional electrostatic ion-acoustic solitons in two-electron temperature plasmas. Phys. Fluids 2022, 34, 093107. [Google Scholar] [CrossRef]
- Alyousef, H.A.; Salas, A.H.; Matoog, R.T.; El-Tantawy, S.A. On the analytical and numerical approximations to the forced damped Gardner Kawahara equation and modeling the nonlinear structures in a collisional plasma. Phys. Fluids 2022, 34, 103105. [Google Scholar] [CrossRef]
- Douanla, D.V.; Tiofack, C.G.L.; Alim; Aboubakar, M.; Mohamadou, A.; Albalawi, W.; El-Tantawy, S.A.; El-Sherif, L.S. Three-dimensional rogue waves and dust-acoustic dark soliton collisions in degenerate ultradense magnetoplasma in the presence of dust pressure anisotropy. Phys. Fluids 2022, 34, 087105. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Wakif, A.; Shah, N.A.; Singh, J. A study on cylindrical moving boundary problem with variable thermal conductivity and convection under the most realistic boundary conditions. Int. Commun. Heat Mass Transf. 2022, 138, 106312. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Upadhyay, S.; Rai, K.N.; Singh, J. A new look in heat balance integral method to a two-dimensional Stefan problem with convection. Numer. Heat Transf. Part A Appl. 2022, 82, 529–542. [Google Scholar] [CrossRef]
- Zheng, H.; Jin, S. A Multi-Source Fluid Queue Based Stochastic Model of the Probabilistic Offloading Strategy in a MEC System with Multiple Mobile Devices and a Single MEC Server. Int. J. Appl. Math. Comput. Sci. 2022, 32, 125–138. [Google Scholar] [CrossRef]
- Lu, S.; Ban, Y.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Adaptive control of time delay teleoperation system with uncertain dynamics. Front. Neurorobot. 2022, 16, 928863. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Tian, J.; Zhang, X.; Yang, B.; Liu, S.; Yin, L.; Zheng, W. Control of Time Delay Force Feedback Teleoperation System with Finite Time Convergence. Front. Neurorobot. 2022, 16, 877069. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Fayyaz, R.; Khan, A.; Shah, R.; Abdo, M.S. Analytical investigation of Noyes-Field model for time-fractional Belousov-Zhabotinsky reaction. Complexity 2021, 2021, 3248376. [Google Scholar] [CrossRef]
- Zidan, A.M.; Khan, A.; Shah, R.; Alaoui, M.K.; Weera, W. Evaluation of time-fractional Fisher’s equations with the help of analytical methods. AIMS Math. 2022, 7, 18746–18766. [Google Scholar] [CrossRef]
- Yel, G.; Baskonus, H.M.; Bulut, H. Novel archetypes of new coupled Konno-Oono equation by using sine-Gordon expansion method. Opt. Quantum Electron. 2017, 49, 285. [Google Scholar] [CrossRef]
- Wu, G.C. A fractional variational iteration method for solving fractional nonlinear differential equations. Comput. Math. Appl. 2011, 61, 2186–2190. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Al Qurashi, M.; Baleanu, D. A novel numerical approach for a nonlinear fractional dynamical model of interpersonal and romantic relationships. Entropy 2017, 19, 375. [Google Scholar] [CrossRef]
- Alaoui, M.K.; Nonlaopon, K.; Zidan, A.M.; Khan, A.; Shah, R. Analytical investigation of fractional-order cahn-hilliard and gardner equations using two novel techniques. Mathematics 2022, 10, 1643. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A comparative analysis of fractional-order kaup-kupershmidt equation within different operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Gepreel, K.A.; Mahdy, A.M.S.; Mohamed, M.S.; Al-Amiri, A. Reduced differential transform method for solving nonlinear biomathematics models. Comput. Mater. Contin. 2019, 61, 979–994. [Google Scholar]
- Singh, J.; Kumar, D.; Sushila, D. Homotopy perturbation Sumudu transform method for nonlinear equations. Adv. Theor. Appl. Mech. 2011, 4, 165–175. [Google Scholar]
- Shah, N.A.; El-Zahar, E.R.; Akgül, A.; Khan, A.; Kafle, J. Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform. J. Funct. Spaces 2022, 2022, 2754507. [Google Scholar] [CrossRef]
- Areshi, M.; Khan, A.; Shah, R.; Nonlaopon, K. Analytical investigation of fractional-order Newell-Whitehead-Segel equations via a novel transform. AIMS Math. 2022, 7, 6936–6958. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Aly, S.; Fayyaz, R.; Khan, A.; Shah, R.; Wyal, N. The analysis of fractional-order nonlinear systems of third order KdV and Burgers equations via a novel transform. Complexity 2022, 2022, 4935809. [Google Scholar] [CrossRef]
- Kaur, B.; Gupta, R.K. Dispersion analysis and improved F-expansion method for space-time fractional differential equations. Nonlinear Dyn. 2019, 96, 837–852. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Khan, A.; Ababneh, O.Y.; Botmart, T. Fractional view analysis of Kersten-Krasil’shchik coupled KdV-mKdV systems with non-singular kernel derivatives. AIMS Math. 2022, 7, 18334–18359. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Alsharif, A.M.; Zidan, A.M.; Khan, A.; Hamed, Y.S.; Shah, R. Numerical investigation of fractional-order Swift-Hohenberg equations via a Novel transform. Symmetry 2021, 13, 1263. [Google Scholar] [CrossRef]
- Sunthrayuth, P.; Alyousef, H.A.; El-Tantawy, S.A.; Khan, A.; Wyal, N. Solving Fractional-Order Diffusion Equations in a Plasma and Fluids via a Novel Transform. J. Funct. Spaces 2022, 2022, 1899130. [Google Scholar] [CrossRef]
- Alshehry, A.S.; Imran, M.; Khan, A.; Shah, R.; Weera, W. Fractional View Analysis of Kuramoto-Sivashinsky Equations with Non-Singular Kernel Operators. Symmetry 2022, 14, 1463. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Machado, J.T. An efficient local meshless approach for solving nonlinear time-fractional fourth-order diffusion model. J. King Saud Univ.-Sci. 2021, 33, 101243. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shareef, M.A. On approximate solutions for fractional system of differential equations with Caputo–Fabrizio fractional operator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Khan, N.A.; Rasheed, S. Analytical solutions of linear and nonlinear Klein–Fock–Gordon equation. Nonlinear Eng.-Model. Appl. 2015, 4, 43–48. [Google Scholar] [CrossRef]
- Yusufoglu, E. The variational iteration method for studying the Klein-Gordon equation. Appl. Math. Lett. 2008, 21, 669–674. [Google Scholar] [CrossRef]
- Aruna, K.; Ravi Kanth, A.S.V. Two-dimensional differential transform method and modifed differential transform method for solving nonlinear fractional Klein-Gordon equation. Nat. Acad. Sci. Lett. 2014, 37, 163–171. [Google Scholar] [CrossRef]
- Ravi Kanth, A.S.V.; Aruna, K. Differential transform method for solving the linear and nonlinear Klein-Gordon equation. Comput. Phys. Commun. 2009, 180, 708–711. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Kumar, D. An effcient technique for nonlinear time-fractional Klein–Fock–Gordon equation. Appl. Math. Comput. 2020, 364, 124637. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. Numerical computation of Klein-Gordon equations arising in quantum feld theory by using homotopy analysis transform method. Alex. Eng. J. 2014, 53, 469–474. [Google Scholar] [CrossRef]
- Rehman, H.U.; Iqbal, I.; Subhi Aiadi, S.; Mlaiki, N.; Saleem, M.S. Soliton Solutions of Klein–Fock–Gordon Equation Using Sardar Subequation Method. Mathematics 2022, 10, 3377. [Google Scholar] [CrossRef]
- Alquran, M.; Yousef, F.; Alquran, F.; Sulaiman, T.A.; Yusuf, A. Dual-wave solutions for the quadratic-cubic conformable-Caputo time-fractional Klein–Fock–Gordon equation. Math. Comput. Simul. 2021, 185, 62–76. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P.K. An approximate analytical solution ofthe fractional diffusion equation with absorbent term and external force by homotopy perturbation method. Z. Naturforsch. A 2010, 65, 182–190. [Google Scholar] [CrossRef]
- Atangana, A.; Alkahtani, B.S.T. Extension of the resistance, inductance, capacitance electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1687814015591937. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; López-López, M.G.; Alvarado-Martínez, V.M.; Reyes-Reyes, J.; Adam-Medina, M. Modeling diffusive transport with a fractional derivative without singular kernel. Phys. A Stat. Mech. Appl. 2016, 447, 467–481. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Akgül, A.; De la Sen, M. A novel homotopy perturbation method with applications to nonlinear fractional order KdV and Burger equation with exponential-decay kernel. J. Funct. Spaces 2021, 2021, 8770488. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).