Identification of the Initial Value for a Time-Fractional Diffusion Equation
Abstract
1. Introduction
2. Auxiliary Results
3. The Exact Solution and Regularization Strategies
4. Estimate for the a Priori Rule
5. Estimate for a Posteriori Rule
- (a)
- is a continuous function;
- (b)
- (c)
- (d)
- is a strictly decreasing function.
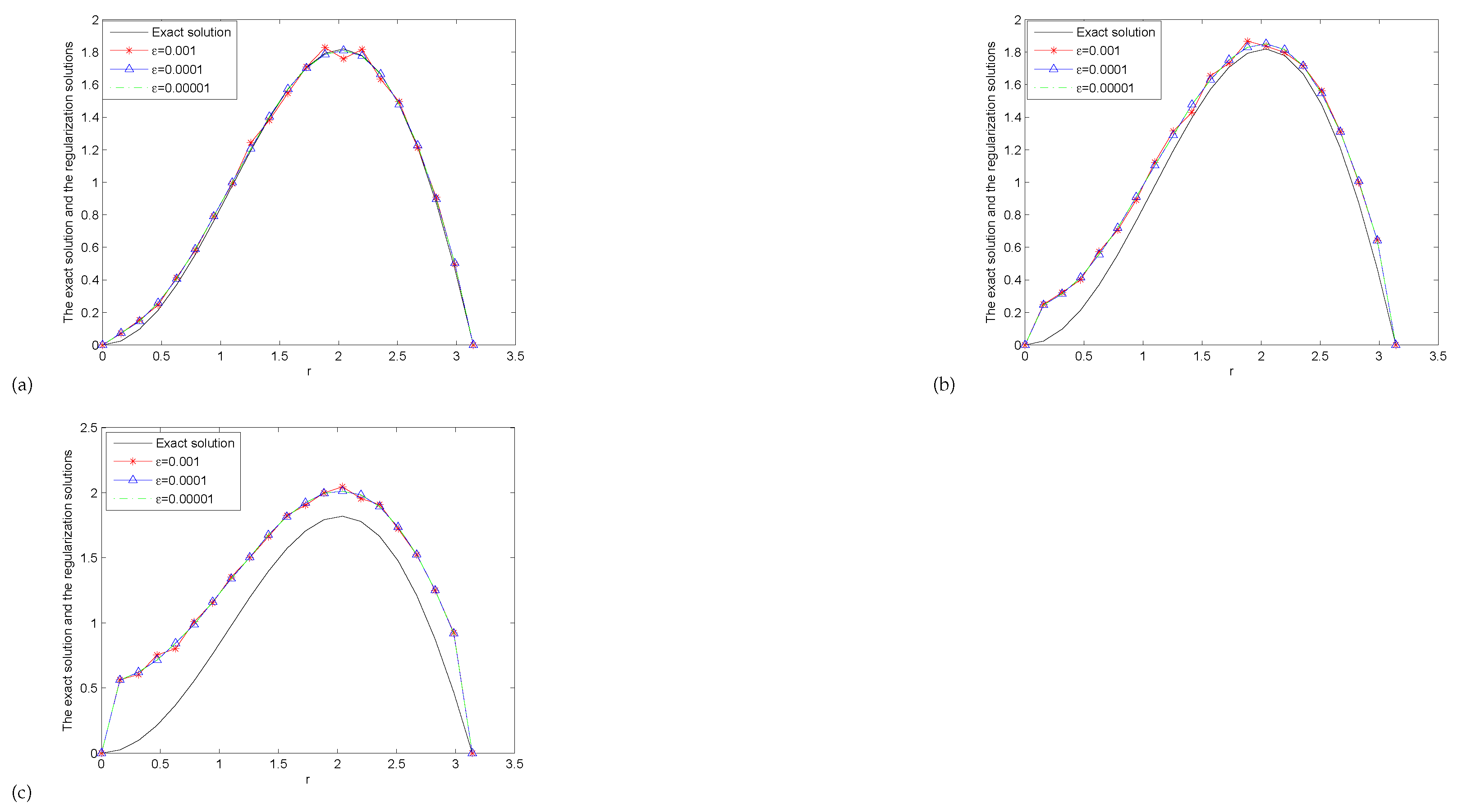
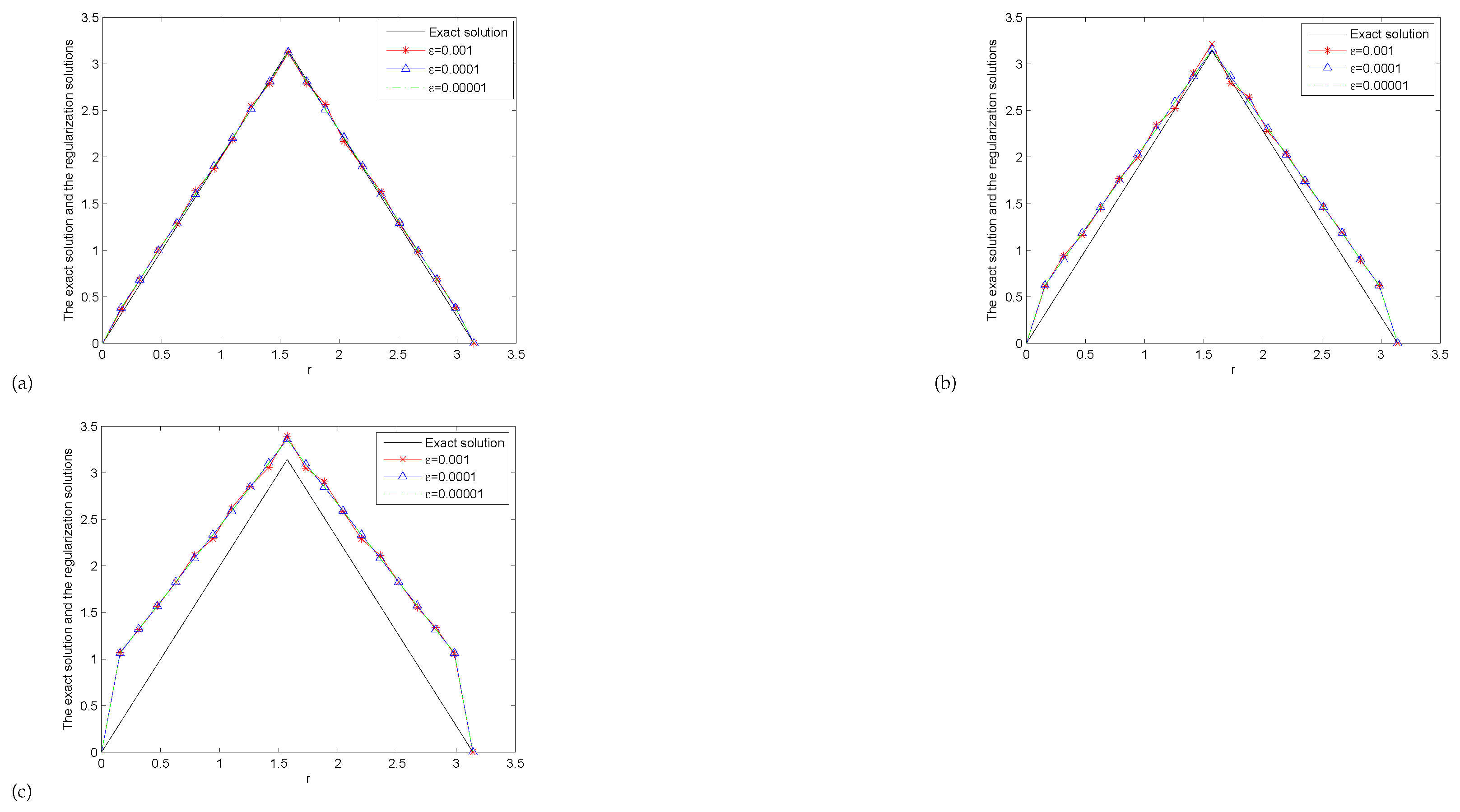
6. Numerical Examples
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Young, D.L.; Tsai, C.C.; Murugesan, K.; Fan, C.M.; Chen, C.W. Time-dependent fundamental solutions for homogeneous diffusion problems. Eng. Anal. Bound. Elem. 2004, 28, 1463–1473. [Google Scholar] [CrossRef]
- Alcouffe, R.E.; Brandt, A.; Dendy, J.E.; Painter, J.W. The multi-grid method for the diffusion equation with strongly discontinuous coefficients. SIAM J. Sci. Comput. 1981, 2, 430–454. [Google Scholar] [CrossRef]
- Luchko, Y. Initial-boundary-value problems for the one-dimensional time-fractional diffusion equation. Fract. Calc. Appl. Anal. 2012, 15, 141–160. [Google Scholar] [CrossRef]
- Kemppainen, J. Existence and uniqueness of the solution for a time-fractional diffusion equation. Fract. Calc. Appl. Anal. 2011, 14, 411–417. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, Y. The backward problem for a time-fractional diffusion-wave equation in a bounded domain. Comput. Math. Appl. 2018, 75, 3632–3648. [Google Scholar] [CrossRef]
- Tuan, N.H.; Long, L.D.; Tatar, S. Tikhonov regularization method for a backward problem for the inhomogeneous time-fractional diffusion equation. Appl. Anal. 2018, 97, 842–863. [Google Scholar] [CrossRef]
- Liu, J.J.; Yamamoto, M. A backward problem for the time-fractional diffusion equation. Appl. Anal. 2010, 89, 1769–1788. [Google Scholar] [CrossRef]
- Yang, F.; Wu, H.H.; Li, X.X. Three regularization methods for identifying the initial value of time fractional advection-dispersion equation. Comput. Appl. Math. 2022, 41, 60. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl. Numer. Math. 2014, 78, 95–111. [Google Scholar] [CrossRef]
- Wei, T.; Zhang, Z.Q. Reconstruction of a time-dependent source term ina time-fractional diffusion equation. Eng. Anal. Bound. Elem. 2013, 37, 23–31. [Google Scholar] [CrossRef]
- Luc, N.H.; Baleanu, D.; Agarwal, R.P. Identifying the source function for time fractional diffusion with non-local in time conditions. Comput. Appl. Math. 2021, 40, 1–21. [Google Scholar] [CrossRef]
- Ozbilge, E.; Demir, A. Inverse problem for a time-fractional parabolic equation. J. Inequal. Appl. 2015, 2015, 81. [Google Scholar] [CrossRef]
- Li, G.; Zhang, D.; Jia, X.; Yamamoto, M. Simultaneous inversion for the space-dependent diffusion coefficient and the fractional order in the time-fractional diffusion equation. Inverse Probl. 2013, 29, 065014. [Google Scholar] [CrossRef]
- Cheng, W.; Fu, C.L.; Qian, Z. A modified Tikhonov regularization method for a spherically symmetric three-dimensional inverse heat conduction problem. Math. Comput. Simulat. 2007, 75, 97–112. [Google Scholar] [CrossRef]
- Cheng, W.; Fu, C.L.; Qian, Z. Two regularization methods for a spherically symmetric inverse heat conduction problem. Appl. Math. Model. 2008, 32, 432–442. [Google Scholar] [CrossRef]
- Cheng, W.; Ma, Y.J. A modified quasi-boundary value method for solving the radially symmetric inverse heat conduction problem. Appl. Anal. 2016, 96, 1–11. [Google Scholar] [CrossRef]
- Cheng, W. Stability estimate and regularization for a radially symmetric inverse heat conduction problem. Bound. Value Probl. 2017, 2017, 53. [Google Scholar] [CrossRef]
- Yu, J.N.; Luo, G.W.; Deng, Z.C. Numerical identification of source terms for a two dimensional heat conduction problem in polar coordinate system. Appl. Math. Model. 2013, 37, 939–957. [Google Scholar]
- Xiong, X.T.; Ma, X.J. A Backward Identifying Problem for an Axis-Symmetric Fractional Diffusion Equation. Math. Model. Anal. 2017, 22, 311–320. [Google Scholar] [CrossRef]
- Djerrar, I.; Alem, L.; Chorfi, L. Regularization method for the radially symmetric inverse heat conduction problem. Bound. Value Probl. 2017, 2017, 159. [Google Scholar] [CrossRef]
- Yang, F.; Ren, Y.P.; Li, X.X. Landweber iteration regularization method for identifying unknown source on a columnar symmetric domain. Inverse Probl. Sci. Eng. 2018, 26, 1109–1129. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, P.; Li, X.X.; Ma, X.Y. Tikhonov regularization method for identifying the space-dependent source for time-fractional diffusion equation on a columnar symmetric domain. Adv. Differ. Equ. 2020, 2020, 128. [Google Scholar] [CrossRef]
- Yang, F.; Wang, N.; Li, X.X. Landweber iterative method for an inverse source problem of time-fractional diffusion-wave equation on spherically symmetric domain. J. Appl. Anal. Comput. 2020, 10, 514–529. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equation; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Bakushinsky, A.B.; Kokurin, M.Y. Iterative Methods for Approximate Solution of Inverse Problems; Springer: New York, NY, USA, 2004. [Google Scholar]
- Beilina, L.; Klibanov, M. Approximate Global Convergence and Adaptivity for Coefficient Inverse Problems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ito, K.; Jin, B. Inverse Problems: Tikhonov Theory and Algorithms; Series on Applied Mathematics; World Scientific: Danvers, MA, USA, 2015. [Google Scholar]
- Tikhonov, A.N.; Goncharsky, A.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Kluwer Academic Publishes: Boston, MA, USA, 1996. [Google Scholar]
| K | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Relative error | 0.1968 | 0.0993 | 0.1326 | 0.1433 | 0.1665 | 0.1602 | 0.1772 |
| M | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| Relative error | 0.1602 | 0.0993 | 0.2822 | 0.4498 | 0.5678 | 0.6043 | 0.7543 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Gao, Y.-X.; Li, D.-G.; Li, X.-X. Identification of the Initial Value for a Time-Fractional Diffusion Equation. Symmetry 2022, 14, 2569. https://doi.org/10.3390/sym14122569
Yang F, Gao Y-X, Li D-G, Li X-X. Identification of the Initial Value for a Time-Fractional Diffusion Equation. Symmetry. 2022; 14(12):2569. https://doi.org/10.3390/sym14122569
Chicago/Turabian StyleYang, Fan, Yin-Xia Gao, Dun-Gang Li, and Xiao-Xiao Li. 2022. "Identification of the Initial Value for a Time-Fractional Diffusion Equation" Symmetry 14, no. 12: 2569. https://doi.org/10.3390/sym14122569
APA StyleYang, F., Gao, Y.-X., Li, D.-G., & Li, X.-X. (2022). Identification of the Initial Value for a Time-Fractional Diffusion Equation. Symmetry, 14(12), 2569. https://doi.org/10.3390/sym14122569





