Extending the Applicability of Cordero Type Iterative Method
Abstract
1. Introduction
2. Convergence Analysis of (4) and (5)
3. Estimation of Radius of Convergence and Computational Order
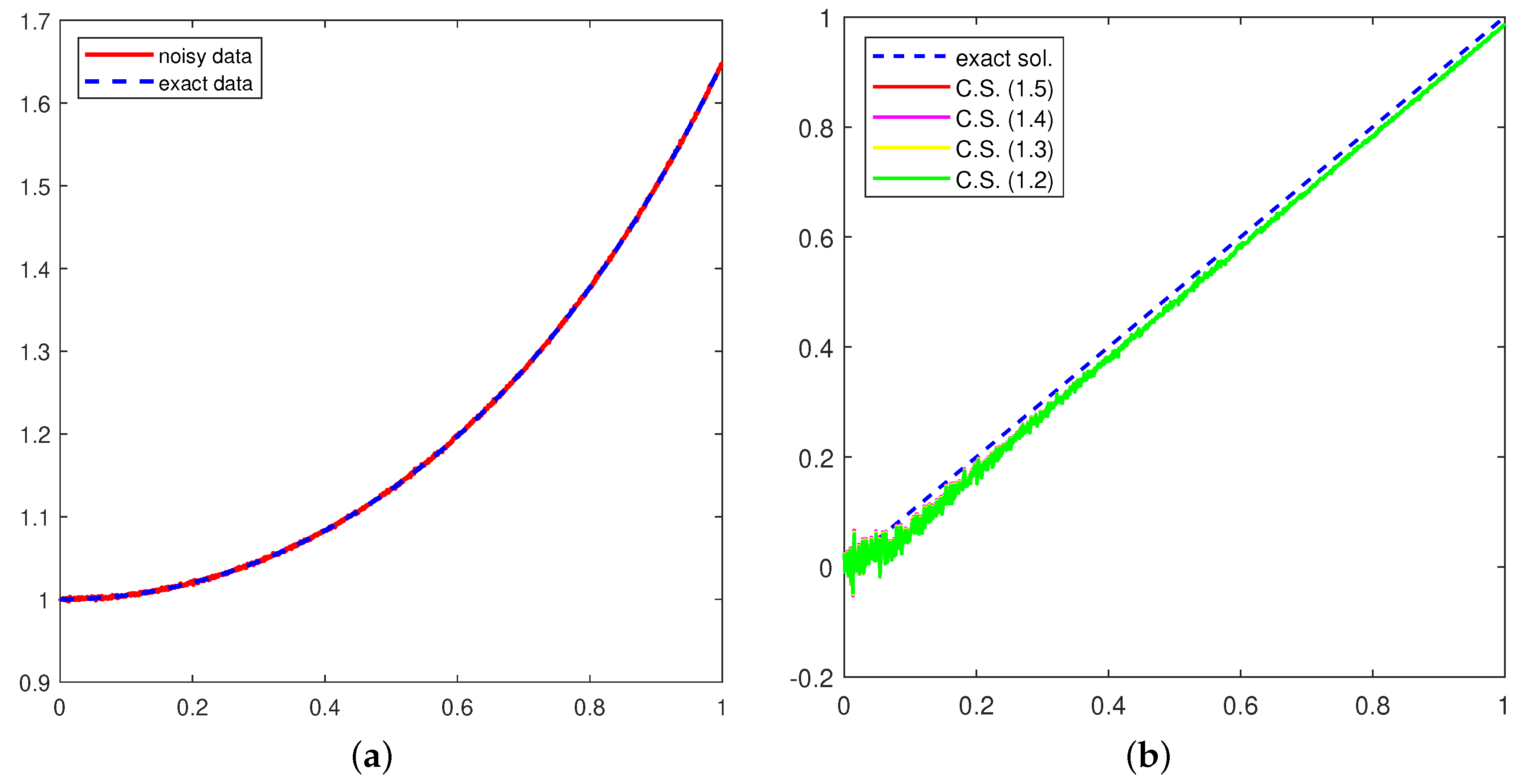
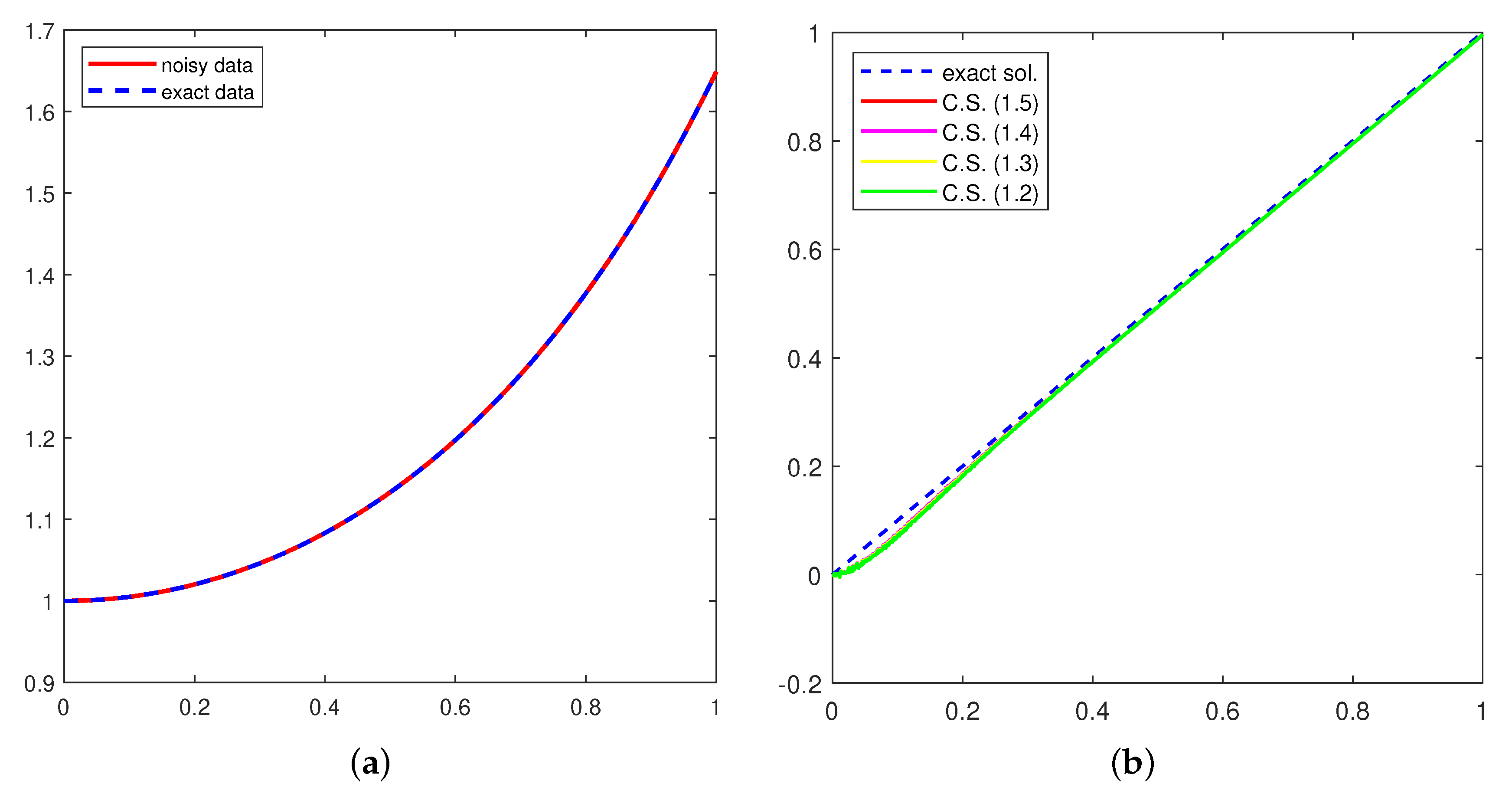
4. Application to Ill-Posed Problem
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. Increasing the convergence order of an iterative method for nonlinear systems. Appl. Math. Lett. 2012, 25, 2369–2374. [Google Scholar]
- Cordero, A.; Martínez, E.; Toregrossa, J.R. Iterative methods of order four and five for systems of nonlinear equations. J. Comput. Appl. Math. 2012, 231, 541–551. [Google Scholar] [CrossRef]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton Jarratt’s composition. Numer. Algor. 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Cordero, A.; Ezquerro, J.A.; Hernández-Verón, M.A.; Torregrosa, J.R. On the local convergence of a fifth-order iterative method in Banach spaces. Appl. Math. Comput. 2012, 251, 396–403. [Google Scholar] [CrossRef]
- Fang, L.; Sun, L.; He, G. An efficient newton-type method with fifthorder convergence for solving nonlinear equations. Comput. Appl. Math. 2008, 227, 269–274. [Google Scholar]
- Grau-Sánchez, M.; Grau, A.; Noguera, M. On the computational efficiency index and some iterative methods for solving systems of nonlinear equations. J. Comput. Appl. Math. 2021, 236, 1259–1266. [Google Scholar] [CrossRef]
- Sharma, J.R.; Gupta, P. An efficient fifth order method for solving systems of nonlinear equations. Comput. Math. Appl. 2014, 67, 591–601. [Google Scholar] [CrossRef]
- Sharma, J.R.; Sharma, R.; Kalra, N. A novel family of composite Newton–Traub methods for solving systems of nonlinear equations. Appl. Math. Comput. 2015, 269, 520–535. [Google Scholar] [CrossRef]
- Parhi, S.K.; Sharma, D. On the Local Convergence of a Sixth-Order Iterative Scheme in Banach Spaces. In New Trends in Applied Analysis and Computational Mathematics; Springer: Singapore, 2021; pp. 79–88. [Google Scholar]
- Argyros, I.K. The Theory and Applications of Iteration Methods, 2nd ed.; Engineering Series; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2022. [Google Scholar]
- Ostrowski, A.M. Solution of Equations in Euclidean and Banach Spaces; Elsevier: Amsterdam, The Netherlands, 1973. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for Solution of Equations; Prentice-Hal: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- George, S.; Saeed, M.; Argyros, I.K.; Jidesh, P. An apriori parameter choice strategy and a fifth order iterative scheme for Lavrentiev regularization method. J. Appl. Math. Comput. 2022, 1–21. [Google Scholar] [CrossRef]
- George, S.; Jidesh, P.; Krishnendu, R.; Argyros, I.K. A new parameter choice strategy for Lavrentiev regularization method for nonlinear ill-posed equations. Mathematics 2022, 10, 3365. [Google Scholar] [CrossRef]
- Nair, M.T.; Ravishankar, P. Regularized versions of continuous Newton’s method and continuous modified Newton’s method under general source conditions. Numer. Funct. Anal. Optim. 2008, 29, 1140–1165. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Remesh, K.; Argyros, I.K.; Saeed K, M.; George, S.; Padikkal, J. Extending the Applicability of Cordero Type Iterative Method. Symmetry 2022, 14, 2495. https://doi.org/10.3390/sym14122495
Remesh K, Argyros IK, Saeed K M, George S, Padikkal J. Extending the Applicability of Cordero Type Iterative Method. Symmetry. 2022; 14(12):2495. https://doi.org/10.3390/sym14122495
Chicago/Turabian StyleRemesh, Krishnendu, Ioannis K. Argyros, Muhammed Saeed K, Santhosh George, and Jidesh Padikkal. 2022. "Extending the Applicability of Cordero Type Iterative Method" Symmetry 14, no. 12: 2495. https://doi.org/10.3390/sym14122495
APA StyleRemesh, K., Argyros, I. K., Saeed K, M., George, S., & Padikkal, J. (2022). Extending the Applicability of Cordero Type Iterative Method. Symmetry, 14(12), 2495. https://doi.org/10.3390/sym14122495









