Extending the Applicability of Cordero Type Iterative Method

Abstract

Symmetries play a vital role in the study of physical systems. For example, microworld and quantum physics problems are modeled on the principles of symmetry. These problems are then formulated as equations defined on suitable abstract spaces. Most of these studies reduce to solving nonlinear equations in suitable abstract spaces iteratively. In particular, the convergence of a sixth-order Cordero type iterative method for solving nonlinear equations was studied using Taylor expansion and assumptions on the derivatives of order up to six. In this study, we obtained order of convergence six for Cordero type method using assumptions only on the first derivative. Moreover, we modified Cordero’s method and obtained an eighth-order iterative scheme. Further, we considered analogous iterative methods to solve an ill-posed problem in a Hilbert space setting.

1. Introduction

As already mentioned in the abstract, the main goal is to obtain convergence order of the method studied in [1] without using assumptions on the higher-order derivatives. Throughout this paper $\mathcal{U},\mathcal{V}$ denote Banach spaces and $\Omega \subset \mathcal{U}$ is a convex set. We are interested in approximating the solution $u^{*}$ of the equation

$$\mathcal{J}\left(u\right)=0,$$

(1)

where $\mathcal{J}:\Omega \subset \mathcal{U}\to \mathcal{V}$ is a nonlinear operator that is Frèchet differentiable. A considerable number of nonlinear problems of the form (1) that arise in physics, chemistry, biology, finance, and mathematics are modeled on principles of symmetry. In general, the classical Newton method of second-order defines $\forall k=0,1,2,\cdots ,$ by

$$u_{k+1}=u_k-{\mathcal{J}}_{u_k}^{-1}\mathcal{J}\left(u_k\right),$$

(2)

where ${\mathcal{J}}_{u_k}={\mathcal{J}}^{\prime }\left(u_k\right),$ is considered to be the most efficient iterative method to solve Equation (1). Cordero et al. [2] modified the classical Newton method by employing Adomian polynomial decomposition and obtained a fourth-order iterative scheme. The iterative scheme in [2] is defined $\forall k=0,1,2,\cdots ,$ by

$$\begin{array}{ccc}\hfill v_k& =& u_k-{\mathcal{J}}_{u_k}^{-1}\mathcal{J}\left(u_k\right)\hfill \\ \hfill u_{k+1}& =& v_k-(2{\mathcal{J}}_{u_k}^{-1}-{\mathcal{J}}_{u_k}^{-1}{\mathcal{J}}_{v_k}{\mathcal{J}}_{u_k}^{-1})\mathcal{J}\left(v_k\right),\hfill \end{array}$$

(3)

where ${\mathcal{J}}_{v_k}={\mathcal{J}}^{\prime }\left(v_k\right).$ This new fourth-order Cordero method has better stability than the classical Newton method with higher-order convergence.

A new technique was introduced by Cordero et al. in [1] to improve the convergence order of an iterative method from q to $q+2$ by combining it with the classical Newton method. By using this technique, the authors modified the fourth-order iterative method (3) to a sixth-order iterative scheme that is defined $\forall k=0,1,2,\cdots ,$ by

$$\begin{array}{ccc}\hfill v_k& =& u_k-{\mathcal{J}}_{u_k}^{-1}\mathcal{J}\left(u_k\right)\hfill \\ \hfill w_k& =& v_k-{\mathcal{J}}_{u_k}^{-1}(2I-{\mathcal{J}}_{v_k}{\mathcal{J}}_{u_k}^{-1})\mathcal{J}\left(v_k\right)\hfill \\ \hfill u_{k+1}& =& w_k-{\mathcal{J}}_{v_k}^{-1}\mathcal{J}\left(w_k\right).\hfill \end{array}$$

(4)

However, the disadvantage of the convergence analysis conducted by Cordero et al. [1] is that they use Taylor expansion which involves the Fréchet derivative of the function up to order six. The convergence analysis of iterative methods in Banach space is conducted by using Taylor expansion which requires assumptions on the higher-order derivatives of the operator involved [1,3,4,5,6,7,8]. If the higher-order derivatives are unbounded, these schemes bear limited applicability. For example, consider the equation $\mathcal{G}\left(t\right)=0,$ where $\mathcal{G}:[-\frac{1}{2},\frac{5}{2}]\to \mathbb{R}$ is defined by

$$\mathcal{G}\left(t\right)=\left\{\begin{array}{cc}{t}^{3}log\left(t^2\right)+t^5-t^4\hfill & t\ne 0\hfill \\ 0\hfill & t=0.\hfill \end{array}\right.$$

Since the third-order derivative of $\mathcal{G}$ is unbounded, the convergence analysis depends on Taylor expansion which is not applicable in this example.

In this study, we could obtain the sixth-order convergence for the method (4) without using Taylor expansion. We employed only the assumptions on the Fréchet derivative of order one. The novelty of our approach is that it does not require higher-order Fréchet derivatives of the operator and Taylor expansion in the convergence analysis. Thus, we enhance the method’s utility. We also modify the last step of the method (4) and obtain a new eighth-order iterative scheme that is defined $\forall k=0,1,2,\cdots ,$ by

$$\begin{array}{ccc}\hfill v_k& =& u_k-{\mathcal{J}}_{u_k}^{-1}\mathcal{J}\left(u_k\right)\hfill \\ \hfill w_k& =& v_k-{\mathcal{J}}_{u_k}^{-1}(2I-{\mathcal{J}}_{v_k}{\mathcal{J}}_{u_k}^{-1})\mathcal{J}\left(v_k\right)\hfill \\ \hfill u_{k+1}& =& w_k-{\mathcal{J}}_{w_k}^{-1}\mathcal{J}\left(w_k\right).\hfill \end{array}$$

(5)

where ${\mathcal{J}}_{w_k}={\mathcal{J}}^{\prime }\left(w_k\right).$

In [9], Parhi and Sharma proved the convergence of the method (4) without using Taylor expansion. However, the authors could not obtain the sixth-order convergence theoretically for method (4).

In this study, we also estimate the radius of convergence of the methods (4) and (5) under assumptions on first-order Fréchet derivative and compute the efficiency indices. We numerically demonstrate that the radius of convergence in our study is superior to the estimates of Parhi and Sharma. We also considered the analogous iterative methods of these two iterative schemes to solve an ill-posed problem in a Hilbert space.

The convergence analysis of methods (4) and (5) is provided in Section 2. The radius of convergence and Approximate Computational Order of Convergence (ACOC) is computed numerically in Section 3. A numerical example of an ill-posed problem is given in Section 4 and the paper concludes in Section 5.

2. Convergence Analysis of (4) and (5)

We use notations $B(t_0,\rho )=\{t\in \mathcal{U}:\parallel t-t_0\parallel <\rho \}$ and $\overline{B(t_0,\rho )}=\{t\in \mathcal{U}:$$\parallel t-t_0\parallel \le \rho \}$ for some $\rho >0.$ The following definition and assumptions are used to prove our results.

Definition 1. 

A sequence $\left\{u_n\right\}$ is said to converge to solution $u^{*}$ with order q if there exists $K>0$ such that

$$\parallel u_{n+1}-u^{*}\parallel \le K\parallel u_n-u^{*}{\parallel }^q.$$

Assumption A1. 

$\exists {\zeta }_1>0$ such that $\forall u,v\in D\left(\mathcal{J}\right),$

$$\parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}({\mathcal{J}}^{\prime }\left(v\right)-{\mathcal{J}}^{\prime }\left(u\right))\parallel \le {\zeta }_1\parallel v-u\parallel .$$

Assumption A2. 

$\exists {\zeta }_2>0,\rho >0$ such that $\forall u,v\in B(u^{*},\rho ),$

$$\parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}{\mathcal{J}}^{\prime }\left(v\right)\parallel \le {\zeta }_2.$$

The local convergence is based on functions ${\varphi }_i,{\psi }_i,i=1,2,$ which are defined as follows. Let ${\varphi }_1:[0,\infty )\to [0,\infty )$ be defined by

$${\varphi }_1\left(t\right)=\frac{{\zeta }_1^3}{32}[16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^{2}t+{\zeta }_1^3{t}^2]t^3$$

and

$${\psi }_1\left(t\right)={\varphi }_1\left(t\right)-1.$$

We observe that ${\psi }_1\left(0\right)=-1$ and ${\psi }_1\left(t\right)\to \infty$ as $t\to \infty$. So, by intermediate value theorem ${\psi }_1\left(t\right)=0$ has a minimal zero ${\rho }_1>0.$ Similarly, define ${\varphi }_2:[0,\infty )\to [0,\infty )$ by

$${\varphi }_2=\frac{{\zeta }_1^2}{2}\left(1+\frac{{\varphi }_1\left(t\right)}{{\zeta }_{1}t}\right){\varphi }_1\left(t\right)t^2$$

and

$${\psi }_2\left(t\right)={\varphi }_2\left(t\right)-1.$$

Furthermore, let ${\rho }_2>0$ be the minimal zero of ${\psi }_2\left(t\right)=0.$ Let

$$\rho =min\{\frac{2}{{\zeta }_1},{\rho }_1,{\rho }_2\}.$$

(6)

Then, $0<{\varphi }_1\left(t\right),{\varphi }_2\left(t\right)<1,\forall t\in (0,\rho ).$ Let $e_n^u=\parallel u_n-u^{*}\parallel ,e_n^v=\parallel v_n-u^{*}\parallel ,$ and $e_n^w=\parallel w_n-u^{*}\parallel ,\forall n=0,1,2,\cdots$

Theorem 1. 

(Existence and Uniqueness)Let ρ be as in (6). Then $\left\{u_k\right\}$ defined by (4) with $u_0\in B(u^{*},\rho )-\left\{u^{*}\right\},$ converges to $u^{*}$ with order of convergence six, i.e.,

$$e_{k+1}^u\le C{\left(e_k^u\right)}^6,$$

where $C=\frac{{\zeta }_1^5}{64}\left(1+\frac{{\varphi }_1\left(\rho \right)}{{\zeta }_1\rho }\right)\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2\rho +{\zeta }_1^3{\rho }^2\right).$ Suppose that (1) has a simple solution in the set $S=\Omega \cap \overline{B(u^{*},\rho )}$. Then $u^{*}$ is the unique solution of equation $\mathcal{J}\left(u\right)=0$ in the set $S,$ provided that ${\zeta }_1\rho <2.$

Proof. 

(Existence Part) By induction, we shall prove the following inequalities:

$$\begin{array}{ccc}\hfill v_n\in B(u^{*},\rho ),e_n^v& \le & \frac{{\zeta }_1}{2}{\left(e_n^u\right)}^2,\hfill \\ \hfill w_n\in B(u^{*},\rho ),e_n^w& \le & {\varphi }_1\left(e_n^u\right)e_n^u,\hfill \\ \hfill u_{n+1}\in B(u^{*},\rho ),e_{n+1}^u& \le & C{\left(e_n^u\right)}^6.\hfill \end{array}$$

For $u_0\in B(u^{*},r),$ by (4) we have,

$$\begin{array}{ccc}\hfill v_0-u^{*}& =& u_0-u^{*}-{\mathcal{J}}_{u_0}^{-1}(\mathcal{J}\left(u_0\right)-\mathcal{J}\left(u^{*}\right))\hfill \\ & =& \left(-{\mathcal{J}}_{u_0}^{-1}{\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(u_0-u^{*}))-{\mathcal{J}}_{u_0}dt\right)(u_0-u^{*}),\hfill \end{array}$$

So by Assumption A1, we obtain,

$$e_0^v\le \frac{{\zeta }_1}{2}{\left(e_0^u\right)}^2.$$

(7)

By (6), $\frac{{\zeta }_1}{2}{\left(e_0^u\right)}^2\le \frac{{\zeta }_1}{2}{\rho }^2\le \rho ,$ so we have $v_0\in B(u^{*},\rho ).$ Again, from the second step of (4),

$$\begin{array}{ccc}\hfill w_0-u^{*}& =& v_0-u^{*}-\left({\mathcal{J}}_{u_0}^{-1}(2I-{\mathcal{J}}_{v_0}{\mathcal{J}}_{u_0}^{-1})\right)(\mathcal{J}\left(v_0\right)-\mathcal{J}\left(u^{*}\right))\hfill \\ & =& {\mathcal{J}}_{u_0}^{-1}({\mathcal{J}}_{u_0}(v_0-u^{*})-(2I-{\mathcal{J}}_{v_0}{\mathcal{J}}_{u_0}^{-1})\hfill \\ & & \times {\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))(v_0-u^{*})dt)\hfill \\ & =& -{\mathcal{J}}_{u_0}^{-1}{\int }_0^1({\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))-{\mathcal{J}}_{u_0})(v_0-u^{*})dt\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}(I-{\mathcal{J}}_{v_0}{\mathcal{J}}_{u_0}^{-1}){\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))(v_0-u^{*})dt\hfill \\ & =& -{\mathcal{J}}_{u_0}^{-1}{\int }_0^1({\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))-{\mathcal{J}}_{u_0})(v_0-u^{*})dt\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}({\mathcal{J}}_{u_0}-{\mathcal{J}}_{v_0}){\mathcal{J}}_{u_0}^{-1}\left({\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))(v_0-u^{*})dt\right).\hfill \end{array}$$

By adding and subtracting the term $\mathrm{\Gamma }={\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))dt$ we get,

$$\begin{array}{ccc}\hfill w_0-u^{*}& =& -{\mathcal{J}}_{u_0}^{-1}{\int }_0^1({\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))-{\mathcal{J}}_{u_0})(v_0-u^{*})dt)\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}({\mathcal{J}}_{u_0}+\mathrm{\Gamma }-\mathrm{\Gamma }-{\mathcal{J}}_{v_0})\hfill \\ & & \times \left({\mathcal{J}}_{u_0}^{-1}\left({\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(v_0-u^{*}))(v_0-u^{*})dt\right)\right)\hfill \\ & =& -{\mathcal{J}}_{u_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{u_0}dt\right)(v_0-u^{*})\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}\left({\mathcal{J}}_{u_0}-\mathrm{\Gamma }\right){\mathcal{J}}_{u_0}^{-1}\mathrm{\Gamma }(v_0-u^{*})\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{v_0}dt\right){\mathcal{J}}_{u_0}^{-1}\mathrm{\Gamma }(v_0-u^{*})\hfill \\ & =& -{\mathcal{J}}_{u_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{u_0}dt\right)\left(I-{\mathcal{J}}_{u_0}^{-1}\mathrm{\Gamma }\right)(v_0-u^{*})\hfill \\ & & -{\mathcal{J}}_{u_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{v_0}dt\right){\mathcal{J}}_{u_0}^{-1}\mathrm{\Gamma }(v_0-u^{*})\hfill \\ & =& -{\mathcal{J}}_{u_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{u_0}dt\right){\mathcal{J}}_{u_0}^{-1}({\mathcal{J}}_{u_0}-\mathrm{\Gamma })(v_0-u^{*})\hfill \\ & & -\left({\mathcal{J}}_{u_0}^{-1}{\mathcal{J}}_{v_0}{\mathcal{J}}_{v_0}^{-1}\left(\mathrm{\Gamma }-{\int }_0^1{\mathcal{J}}_{v_0}dt\right)\right){\mathcal{J}}_{u_0}^{-1}\mathrm{\Gamma }(v_0-u^{*}).\hfill \end{array}$$

Therefore, by (7), Assumptions A1 and A2, we obtain

$$\begin{array}{ccc}\hfill e_0^w& \le & {\zeta }_1^2{\left(e_0^u+\frac{e_0^v}{2}\right)}^2{e}_0^v+\frac{{\zeta }_1{\zeta }_2^2}{2}{\left(e_0^v\right)}^2\hfill \\ & =& {\zeta }_1^2\left({\left(e_0^u\right)}^2+e_0^u{e}_0^v+\frac{{\left(e_0^v\right)}^2}{4}\right)e_0^v+\frac{{\zeta }_1{\zeta }_2^2}{2}{\left(e_0^v\right)}^2\hfill \\ & \le & {\zeta }_1^2\left({\left(e_0^u\right)}^2+\frac{{\zeta }_1}{2}{\left(e_0^u\right)}^3+\frac{{\zeta }_1^2}{16}{\left(e_0^u\right)}^4\right)\frac{{\zeta }_1^2}{2}{\left(e_0^u\right)}^2+\frac{{\zeta }_1{\zeta }_2^2}{2}{\left(\frac{{\zeta }_1}{2}{\left(e_0^u\right)}^2\right)}^2\hfill \\ & =& \frac{{\zeta }_1^4}{32}\left(16+8{\zeta }_1{e}_0^u+{\zeta }_1^2{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^4+\frac{{\zeta }_1^3{\zeta }_2^2}{8}{\left(e_0^u\right)}^4\hfill \\ & =& \frac{{\zeta }_1^3}{32}\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^4\hfill \\ & =& {\varphi }_1\left(e_0^u\right)e_0^u<e_0^u.\hfill \end{array}$$

(8)

Thus, $w_0\in B(u^{*},\rho ).$ By the third step of (4) we have,

$$\begin{array}{ccc}\hfill u_1-u^{*}& =& w_0-u^{*}-{\mathcal{J}}_{v_0}^{-1}(\mathcal{J}\left(w_0\right)-\mathcal{J}\left(u^{*}\right))\hfill \\ & =& -{\mathcal{J}}_{v_0}^{-1}{\int }_0^1({\mathcal{J}}^{\prime }(u^{*}+t(w_0-u^{*}))-{\mathcal{J}}_{v_0})(w_0-u^{*})dt.\hfill \end{array}$$

Again, by using Assumption A1, (7) and (8) we get,

$$\begin{array}{ccc}\hfill e_1^u& \le & {\zeta }_1(e_0^v+\frac{e_0^w}{2})e_0^w\hfill \\ & \le & {\zeta }_1(\frac{{\zeta }_1}{2}{\left(e_0^u\right)}^2+\frac{{\zeta }_1^3}{64}\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^4)\hfill \\ & & \frac{{\zeta }_1^3}{32}\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^4\hfill \\ & =& \frac{{\zeta }_1^5}{64}\left(1+\frac{{\zeta }_1^2}{32}\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^2\right)\hfill \\ & & \left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^6\hfill \\ & =& \frac{{\zeta }_1^5}{64}\left(1+\frac{{\varphi }_1\left(e_0^u\right)}{{\zeta }_1{e}_0^u}\right)\frac{32}{{\zeta }_1^3}{\varphi }_1\left(e_0^u\right){\left(e_0^u\right)}^3\hfill \\ & =& {\varphi }_2\left(e_0^u\right)e_0^u.\hfill \end{array}$$

(9)

Note that,

$$\begin{array}{ccc}\hfill {\varphi }_2\left(e_0^u\right)& =& \frac{{\zeta }_1^2}{2}\left(1+\frac{{\varphi }_1\left(e_0^u\right)}{{\zeta }_1{e}_0^u}\right)\left({\varphi }_1\left(e_0^u\right)\right){\left(e_0^u\right)}^2\hfill \\ & =& \frac{{\zeta }_1^5}{64}\left(1+\frac{{\varphi }_1\left(e_0^u\right)}{{\zeta }_1{e}_0^u}\right)\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^5,\hfill \end{array}$$

So by (9), we get,

$$\begin{array}{ccc}\hfill e_1^u& =& \frac{{\zeta }_1^5}{64}\left(1+\frac{{\varphi }_1\left(e_0^u\right)}{{\zeta }_1{e}_0^u}\right)\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^6\hfill \\ & \le & C{\left(e_0^u\right)}^6.\hfill \end{array}$$

Further, since ${\varphi }_2\left(e_0^u\right)<1,$ we have $u_1\in B(u^{*},\rho ).$ The induction is complete, by replacing $u_0,v_0,w_0,u_1$ by $u_n,v_n,w_n,u_n+1,$, respectively, in the preceding arguments.

(Uniqueness Part) Let $\overline{u}$ be another solution of the Equation (1) in the set $S.$

Let $T={\int }_0^1{\mathcal{J}}^{\prime }(u^{*}+t(\overline{u}-u^{*}))dt.$ By using Assumption A1, we have

$$\begin{array}{ccc}\hfill \parallel {\mathcal{J}}^{\prime }{\left(u^{*}\right)}^{-1}(T-{\mathcal{J}}^{\prime }\left(u^{*}\right))\parallel & \le & {\zeta }_1{\int }_0^1\parallel u^{*}+t(\overline{u}-u^{*})-u^{*}\parallel dt\hfill \\ & =& {\zeta }_1{\int }_0^{1}t\parallel \overline{u}-u^{*}\parallel dt\hfill \\ & \le & \frac{{\zeta }_1}{2}\rho <1.\hfill \end{array}$$

Therefore, by using Banach lemma [10], one can conclude that T is invertible.

Hence $\overline{u}=u^{*}$ follows from $0=\mathcal{J}\left(\overline{u}\right)-\mathcal{J}\left(u^{*}\right)=T(\overline{u}-u^{*}).$ □

Next, we prove the convergence of method (5). Let $\widetilde{{\varphi }_2}:[0,\infty )\to [0,\infty )$ be defined by

$$\widetilde{{\varphi }_2}\left(t\right)=\frac{{\zeta }_1}{2}{\varphi }_1\left(t\right)t^4.$$

Again, by intermediate value theorem $\widetilde{{\psi }_2}\left(t\right)=\widetilde{{\varphi }_2}\left(t\right)-1=0$ has a minimal zero $\widetilde{{\rho }_2}>0.$ Let us define

$$\tilde{\rho }=min\{\frac{2}{{\zeta }_1},{\rho }_1,\widetilde{{\rho }_2}\}.$$

(10)

Theorem 2. 

Let $\tilde{\rho }$ be as in (10). Then $\left\{u_k\right\}$ defined by (5) with $u_0\in B(u^{*},\tilde{\rho })-\left\{u^{*}\right\},$ converges to $u^{*}$ with the order of convergence eight. i.e.,

$$e_{k+1}^u\le \tilde{C}{\left(e_k^u\right)}^8,$$

where $\tilde{C}=\frac{{\zeta }_1{\varphi }_1\left(\tilde{\rho }\right)}{2{\tilde{\rho }}^3}.$ Furthermore, $u^{*}$ is the unique solution of Equation (1) in the set $S=\Omega \cap \overline{B(u^{*},\tilde{\rho })}$ provided that ${\zeta }_1\tilde{\rho }<2.$

Proof. 

By the third sub-step of (5), we have

$$u_1-u^{*}=w_0-u^{*}-{\mathcal{J}}_{w_0}^{-1}(\mathcal{J}\left(w_0\right)-\mathcal{J}\left(u^{*}\right))$$

so, by (8), we get

$$\begin{array}{ccc}\hfill e_1^u& \le & \frac{{\zeta }_1}{2}{\left(e_0^w\right)}^2\hfill \\ & \le & \frac{{\zeta }_1}{2}{\left(\frac{{\zeta }_1^3}{32}\left(16{\zeta }_1+4{\zeta }_2^2+8{\zeta }_1^2{e}_0^u+{\zeta }_1^3{\left(e_0^u\right)}^2\right){\left(e_0^u\right)}^4\right)}^2\hfill \\ & =& \frac{{\zeta }_1}{2}\left(\frac{{\varphi }_1\left(e_0^u\right)}{{\left(e_0^u\right)}^3}\right){\left(e_0^u\right)}^8\hfill \\ & =& \widetilde{{\varphi }_2}\left(e_0^u\right)e_0^u<e_0^u.\hfill \end{array}$$

(11)

From (11), we get

$$\begin{array}{ccc}\hfill e_1^u& \le & \frac{{\zeta }_1{\varphi }_1\left(\tilde{\rho }\right)}{2{\tilde{\rho }}^3}{\left(e_0^u\right)}^8\hfill \\ & =& \tilde{C}{\left(e_0^u\right)}^8.\hfill \end{array}$$

The rest of the proof proceeds in the same manner as in Theorem 1. □

Remark 1. 

Note that by (8), we obtain the convergence order four for the Cordero method (3).

3. Estimation of Radius of Convergence and Computational Order

We estimate the radius of convergence $\rho$ and $\tilde{\rho }$ to validate the theoretical results.

Example 1. 

Let $\mathcal{U}=\mathcal{V}=\mathbb{R},u_0=1,\Omega =[u_0-(1-k),u_0+(1-k)],k\in (2-\sqrt{2},1)$ and $F:\Omega \to \mathcal{K}$ be defined by

$$\mathcal{J}\left(u\right)=u^3-k.$$

We have, $\parallel {\mathcal{J}}_{u_0}^{-1}\parallel =\frac{1}{3}$.

$$\begin{array}{ccc}\hfill \parallel {\mathcal{J}}_{u_0}^{-1}({\mathcal{J}}^{\prime }\left(u\right)-{\mathcal{J}}_{u_0})\parallel & =& \frac{1}{3}\parallel (3u^2-3)\parallel \hfill \\ & \le & \parallel u+1\parallel \parallel u-1\parallel \hfill \\ & =& (3-k)(1-k).\hfill \end{array}$$

By using Banach Lemma,

$$\begin{array}{ccc}\hfill \parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}\parallel & \le & \frac{\parallel {\mathcal{J}}_{u_0}^{-1}\parallel }{1-\parallel {\mathcal{J}}_{u_0}^{-1}{\mathcal{J}}^{\prime }\left(u\right)-I\parallel }\hfill \\ & =& \frac{1}{3(1-(3-k\left)\right(1-k\left)\right)},\hfill \end{array}$$

So,

$$\begin{array}{ccc}\hfill \parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}({\mathcal{J}}^{\prime }\left(v\right)-{\mathcal{J}}^{\prime }\left(u\right))\parallel & \le & \parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}\parallel \parallel 3v^2-3u^2\parallel \hfill \\ & \le & \frac{3(v+u)(v-u)}{3(1-(3-k\left)\right(1-k\left)\right)}\hfill \\ & =& \frac{2(2-k)}{(1-(3-k\left)\right(1-k\left)\right)}\parallel v-u\parallel .\hfill \end{array}$$

Therefore, ${\zeta }_1=\frac{2(2-k)}{(1-(3-k\left)\right(1-k\left)\right)}$.

$$\begin{array}{ccc}\hfill \parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}{\mathcal{J}}^{\prime \prime }\left(v\right)\parallel & \le & \parallel {\mathcal{J}}^{\prime }{\left(u\right)}^{-1}\parallel \parallel {\mathcal{J}}^{\prime \prime }\left(v\right)\parallel \hfill \\ & \le & \frac{6v}{3(1-(3-k\left)\right(1-k\left)\right)}\hfill \\ & =& \frac{2(2-k)}{(1-(3-k\left)\right(1-k\left)\right)}={\zeta }_2.\hfill \end{array}$$

Set $k=0.85,$ we then get, ${\zeta }_1={\zeta }_2\approx 3.3948,{\rho }_1\approx 0.1899,{\rho }_2\approx 0.2092,\frac{2}{{\zeta }_1}=0.35,$

$\rho =min\{\frac{2}{{\zeta }_1},{\rho }_1,{\rho }_2\}\approx 0.1899.$ Furthermore, we have $\widetilde{{\rho }_2}\approx 0.4409$ and $\tilde{\rho }=min\{\frac{2}{{\zeta }_1},{\rho }_1,\widetilde{{\rho }_2}\}=0.1899.$ Using the convergence analysis in [9], we obtain the radius $R=0.1123.$

Example 2. 

Let $\mathcal{U}=\mathcal{V}={\mathbb{R}}^3,\Omega =B[0,1],u_0={(0,0,0)}^T.$ Define function $\mathcal{J}$ on $\mathrm{\Omega }$ for $x={(u,v,w)}^T$ by

$$\mathcal{J}\left(x\right)={\left(e^u-1,\frac{e-1}{2}{v}^2+v,w\right)}^T.$$

Then,

$${\mathcal{J}}^{\prime }\left(x\right)=\left(\begin{array}{ccc}{e}^u& 0& 0\\ 0& (e-1)v+1& 0\\ 0& 0& 1\end{array}\right).$$

Thus, ${\zeta }_1=e-1$ and ${\zeta }_2=e.$ Furthermore, we get, $\frac{2}{{\zeta }_1}\approx 1.1639,{\rho }_1\approx 0.4510,{\rho }_2\approx 0.4779$ and the radius of convergence $\rho =min\{\frac{2}{{\zeta }_1},{\rho }_1,{\rho }_2\}\approx 0.4510.$ Furthermore, we have $\widetilde{{\rho }_2}\approx 0.7154$ and $\tilde{\rho }=min\{\frac{2}{{\zeta }_1},{\rho }_1,\widetilde{{\rho }_2}\}\approx 0.4510.$ Parhi and Sharma [9] considered this example 2 and obtained the radius $R=0.133649$.

Remark 2. 

We observe that, $\tilde{\rho }=\rho$ in the above examples. Furthermore, note that we can obtain a better radius of convergence than that of Parhi and Sharma’s convergence analysis in [9].

To ensure the methods (4) and (5) attain the order of convergence computationally, we calculated the Approximate Computational Order of Convergence (ACOC) (Table 1), that is defined as [1]

$$\Sigma =ln\left(\frac{\parallel u_{k+1}-u_k\parallel }{\parallel u_k-u_{k-1}\parallel }\right)/ln\left(\frac{\parallel u_k-u_{k-1}\parallel }{\parallel u_{k-1}-u_{k-2}\parallel }\right).$$

Table 1. ACOC for methods (2), (3), (4) and (5).

Eq. No.	${\mathit{u}}^{*}$	${\mathit{u}}_0$	N	N	N	N	ACOC	ACOC	ACOC	ACOC
			NM	CM	CM1	CM2	NM	CM	CM1	CM2
			(2)	(3)	(4)	(5)	(2)	(3)	(4)	(5)
(12)	$(0,0,0)$	$(\frac{1}{2},0,0)$	6	4	4	4	2	$4.3$	$6.2$	$7.6$
		$(1.1,1.1,1.1)$	8	5	5	4	$1.98$	$3.7$	$5.9$	$6.4$
(13)	$0.9472$	$1.6$	7	5	4	4	2	$3.9$	5	$6.8$
		$0.5$	8	10	41	7	2	$3.9$	$5.6$	$6.5$
(14)	$(0.3542,1.1364)$	$(0.6,0.7)$	7	5	4	4	2	$3.5$	$5.8$	8
(15)	$(\frac{1}{2},\frac{\sqrt{3}}{2})$	$(0.35,0.5)$	7	5	4	4	$1.5$	$3.9$	$6.3$	$8.4$
		$(0.9,1)$	6	4	4	3	2	$3.4$	$5.4$	Not defined
(16)	$(1,1)$	$(1.1.,0.75)$	7	5	4	4	2	$3.7$	$5.8$	$9.5$
(17)	$(-\frac{1}{2},-\frac{\sqrt{3}}{2})$	$(-0.4,-\frac{1}{2})$	8	7	8	5	$1.2$	$4.2$	$5.2$	$7.9$

We considered the following functions and used the stopping criterion $\parallel u_{k+1}-u_k\parallel +\parallel \mathcal{J}\left(u_{k+1}\right)\parallel \le {10}^{-10}.$

$$\begin{array}{ccc}\hfill \mathcal{J}(t_1,t_2,t_3)& =& (e^{t_1}-1,\frac{e-1}{2}{t}_2^2+t_2,t_3),\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill \mathcal{J}\left(t\right)& =& t^3-0.85,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \mathcal{J}(t_1,t_2)& =& (t_1^2-4t_2+t_2^2,2t_1-t_2^2-2),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill \mathcal{J}(t_1,t_2)& =& (t_1^2+t_2^2-1,t_1^2-t_2^2+0.5),\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \mathcal{J}(t_1,t_2)& =& (t_1^3-t_2,t_2^3-t_2),\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill \mathcal{J}(t_1,t_2)& =& (3t_1^2{t}_2-t_2^3,t_1^3-3t_1{t}_2^2-1).\hfill \end{array}$$

(17)

Note that the oscillatory nature of the approximations and slow convergence in the initial stage present the main disadvantages in the computation of ACOC in higher-order iterative methods. In Table 1, we observe that the choice of a suitable initial approximation plays a vital role to achieve the maximum order of convergence (see Equations (12), (13) and (14)). Furthermore, it requires at least four iterations to compute ACOC (see Equation (15)). Specifically in Table 1, we provide ACOC for nonlinear equations using Newton method (NM) (2), Cordero’s fourth-order method (CM) (3), first extension (CM1) (4) and second extension (CM2) (5). Here, $N,u^{*}$, and $u_0$ denote the number of iterations, root, and initial value, respectively.

Remark 3. 

The efficiency index $c_f$ is defined as $c_f=q^{\frac{1}{m}},$ where q is the order of convergence and m is the number of functions (and derivatives) [11]. The informational efficiency I is defined as $I=\frac{q}{m}$ [12]. The efficiency index and informational efficiency of the fourth-order Cordero method (3) are $c_f=4^{1/4}=1.41$ and $I=4/4=1,$, respectively, which coincide with that of the Newton method. Whereas $c_f=6^{1/5}=1.43,I=6/5=1.2$ for the sixth-order method (4) and $c_f=8^{1/6}=1.41,I=8/6=1.33$ for the eighth-order method (5).

4. Application to Ill-Posed Problem

We implemented the analogous iterative methods (2), (3), (4) and (5) to solve the nonlinear ill-posed problem (see [13,14] for details).

Example 3. 

Let $c>0$ be a constant. Consider the inverse problem of identifying the distributed-growth law $u\left(t\right),t\in (0,1)$, in the initial value problem

$$\frac{dy}{dt}=u\left(t\right)y\left(t\right),y\left(0\right)=c,$$

from the noisy data $y^{\delta }\left(t\right)\in L^2(0,1)$. One can reformulate the above problem as an ill-posed operator equation

$$\mathcal{J}\left(u\right)=y,$$

(18)

with

$$\left[\mathcal{J}\left(u\right)\right]\left(t\right)=c{e}^{{\int }_0^{t}u\left(\theta \right)d\theta },u\in L^2(0,1),t\in (0,1).$$

The Fréchet derivative of $\mathcal{J}$ is given by

$$\left[{\mathcal{J}}^{\prime }\left(u\right)h\right]\left(t\right)=\left[\mathcal{J}\left(u\right)\right]\left(t\right){\int }_0^{t}h\left(\theta \right)d\theta .$$

It is proved in [15], that ${\mathcal{J}}^{\prime }$ is positive type and spectrum of ${\mathcal{J}}_u$ is the singleton set $\left\{0\right\}$. We use the Lavrentiev regularization method with $\alpha >0$ (see [14] for details), i.e.,

$$\mathcal{J}\left(u\right)+\alpha (u-u_0)=y,$$

(19)

to approximate the exact solution $\widehat{u}$ of (18). To solve (19), we consider the analogous iterative methods (2), (3), (4) and (5) defined $\forall k=0,1,\cdots ,$ by

$$u_{k+1}=u_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(\mathcal{J}\left(u_k\right)+\alpha (u_k-u_0)-y^{\delta }),$$

$$\begin{array}{ccc}\hfill v_k& =& u_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(\mathcal{J}\left(u_k\right)+\alpha (u_k-u_0)-y^{\delta })\hfill \\ \hfill u_{k+1}& =& v_k-(2{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}-({({\mathcal{J}}_{u_k}+\alpha I)}^{-1}\hfill \\ & & ({\mathcal{J}}_{v_k}+\alpha I){({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(\mathcal{J}\left(v_k\right)+\alpha (v_k-u_0)-y^{\delta })\left)\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill v_k& =& u_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(\mathcal{J}\left(u_k\right)+\alpha (u_k-u_0)-y^{\delta })\hfill \\ \hfill w_k& =& v_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(2I-({\mathcal{J}}_{v_k}+\alpha I)\hfill \\ & & {({\mathcal{J}}_{u_k}+\alpha I)}^{-1})(\mathcal{J}\left(v_k\right)+\alpha (v_k-u_0)-y^{\delta })\hfill \\ \hfill u_{k+1}& =& w_k-{({\mathcal{J}}_{v_k}+\alpha I)}^{-1}(\mathcal{J}\left(w_k\right)+\alpha (w_k-u_0)-y^{\delta }),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill v_k& =& u_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(\mathcal{J}\left(u_k\right)+\alpha (u_k-u_0)-y^{\delta })\hfill \\ \hfill w_k& =& v_k-{({\mathcal{J}}_{u_k}+\alpha I)}^{-1}(2I-({\mathcal{J}}_{v_k}+\alpha I)\hfill \\ & & {({\mathcal{J}}_{u_k}+\alpha I)}^{-1})(\mathcal{J}\left(v_k\right)+\alpha (v_k-u_0)-y^{\delta })\hfill \\ \hfill u_{k+1}& =& w_k-{({\mathcal{J}}_{w_k}+\alpha I)}^{-1}(\mathcal{J}\left(w_k\right)+\alpha (w_k-u_0)-y^{\delta }),\hfill \end{array}$$

respectively.

Remark 4. 

We choose a priori α which satisfies the following condition;

$$\Psi (\alpha ,y^{\delta }):=\parallel {\alpha }^2{\left({\mathcal{J}}_{u_0}+\alpha I\right)}^{-2}\left(\mathcal{J}\left(u_0\right)-y^{\delta }\right)\parallel =d\delta$$

(20)

for some $d>1$ with $d\delta \le \parallel \mathcal{J}\left(u_0\right)-y^{\delta }\parallel$ (see [13,14] for details).

For computation, we have taken $\widehat{u}\left(t\right)=t,u_0\left(t\right)=0$ and $y\left(t\right)=e^{\frac{t^2}{2}}.$ Table 2 provides the relative error $E_{\alpha }=\frac{\parallel CS-\widehat{u}\parallel }{\parallel \widehat{u}\parallel }$ of each iterative method, where CS is the computed solution. We choose α according to (20). The accuracy of reconstruction increases as the relative error decreases.

Table 2. Relative errors for Example 3.

Method	$\mathit{\alpha }$ and ${\mathit{E}}_{\mathit{\alpha }}$	$\mathit{\delta }=0.01$	$\mathit{\delta }=0.001$	$\mathit{\delta }=0.0001$	$\mathit{\delta }=0.00001$
	$\alpha$	$3.719646\times {10}^{-2}$	$1.147848\times {10}^{-2}$	$3.601858\times {10}^{-3}$	$1.136730\times {10}^{-3}$
(5)	$E_{\alpha }$	$1.323726\times {10}^{-1}$	$3.780750\times {10}^{-2}$	$1.912899\times {10}^{-2}$	$1.532976\times {10}^{-2}$
stopping index		11	11	11	11
(4)	$E_{\alpha }$	$1.323724\times {10}^{-1}$	$3.780538\times {10}^{-2}$	$1.912626\times {10}^{-2}$	$1.532735\times {10}^{-2}$
stopping index		15	15	15	15
(3)	$E_{\alpha }$	$1.314847\times {10}^{-1}$	$3.852680\times {10}^{-2}$	$2.047544\times {10}^{-2}$	$1.680669\times {10}^{-2}$
stopping index		11	11	11	11
(2)	$E_{\alpha }$	$1.305499\times {10}^{-1}$	$3.947806\times {10}^{-2}$	$2.210599\times {10}^{-2}$	$1.856438\times {10}^{-2}$
stopping index		27	27	27	27

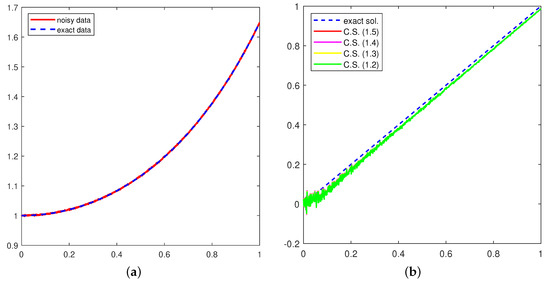
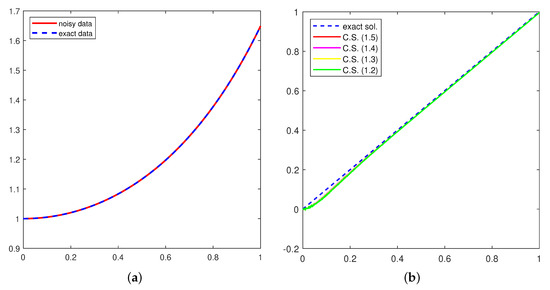
For $\delta =0.001,0.0001$, the exact and noisy data are shown in subfigure (a) and the computed solution is in subfigure (b), respectively, in both Figure 1 and Figure 2.

Figure 1. Data (a) and Solution (b) with δ = 0.001.

Figure 2. Data (a) and Solution (b) with δ = 0.0001.

5. Conclusions

We studied the convergence analysis of a three-step Cordero type method of order six and modified it to a new eighth-order iterative method. The convergence analysis of these methods was studied without using Taylor’s expansion. We use assumptions based only on the first-order Fréchet derivative. We computed the radius of convergence and computational efficiencies of these methods. Furthermore, we considered analogous iterative methods to solve an ill-posed problem in a Hilbert space. The developed process can also be applied to any other method using inverses of linear operators with the same benefits. This represents the topic of our future study.