Heat and Mass Transfer Analysis of MHD Jeffrey Fluid over a Vertical Plate with CPC Fractional Derivative

Abstract

Free convection flow of non-Newtonian fluids over flat, heated surfaces is an important natural phenomenon that also occurs in human-made engineering processes under various physical and mechanical situations. In the current study, the free convection magnetohydrodynamic flow of Jeffrey fluid with heat and mass transfer over an infinite vertical plate is examined. Mathematical modeling is performed using Fourier’s and Fick’s laws, and heat and momentum equations have been obtained. The non-dimensional partial differential equations for energy, mass, and velocity fields are determined using the Laplace transform method in a symmetric manner. Later on, the Laplace transform method is employed to evaluate the results for the temperature, concentration, and velocity fields with the support of Mathcad software. The governing equations, as well as the initial and boundary conditions, satisfy these results. The impacts of fractional and physical characteristics have been shown by graphical illustrations. The obtained fractionalized results are generalized by a more decaying nature. By taking the fractional parameter $\beta ,\gamma \to 1$, the classical results with the ordinary derivatives are also recovered, making this a good direction for symmetry analysis. The present work also has applications with engineering relevance, such as heating and cooling processes in nuclear reactors, the petrochemical sector, and hydraulic apparatus where the heat transfers through a flat surface. Moreover, the magnetized fluid is also applicable for controlling flow velocity fluctuations.

1. Introduction

In some complex situations, the impact of heat and mass transfer is an essential component of the non-Newtonian fluid flow. There are numerous industrial applications for modeling non-Newtonian fluid flow with heat and mass transport systems, including the food perseveration process, formation of heat, designing of the carburetor automobile, etc. A non-Newtonian fluid has an important role in industrial engineering, it gains significant attention from the theorist of fluid mechanics, and several theoretical models are constructed and then solved to address the engineering relevance. Yang and Du [1] provide a creative study of non-Newtonian fluid with heat transfer analysis and boundary layer flow. Aleem et al. [2] investigated a viscoelastic fluid with the pulsatile flow in heat transfer. A viscous fluid of unsteady motion across a vertical plate is discussed by Waqas et al. [3]. Ahmad et al. [4] used mathematical modeling to examine water-based Maxwell hybrid nanofluids, utilizing the CF fractional derivative. Ayub et al. [5] analyzed viscous flow with heat transfer analysis inside a rotating regime by Newtonian heating and the influence of magnetic force.

Jeffrey’s fluid is a non-Newtonian fluid with viscosity and elasticity. Because creep resistance is present and it has high shear viscosity, it is classified as a shear-thinning fluid. After the shear stress exceeds the elastic limit, it behaves in a similar manner as a Newtonian fluid, as shown by Reddy et al. [6]. Retardation and relaxation times in the Jeffrey fluid model are important for denoting the viscoelastic properties of polymeric materials, as shown by Bajwa et al. [7]. Shafique et al. [8] reported that Jeffrey’s fluid is utilized in order to develop a mathematical model of blood flow in small arteries. Peristalsis, a classification of biological fluid movement, also uses it [9,10]. There are some additional Jeffrey fluid efforts in [11,12,13,14,15].

The study of differential operators of any order is known as fractional calculus, and the viscoelastic behavior of fluids is also described. The Caputo, Caputo–Fabrizio, and Caputo constant proportionality techniques are the most common fractional differentiation approaches [16,17,18]. For steady-state heat conduction, Hristov [19] employed the CF fractional derivative. The results of Hristov [20] for transient flow with a space-time derivative are studied. Hristov [21] investigated the Cattaneo constitutive equation, derived from the CF (Caputo–Fabrizio) fractional derivative, to research non-singular leak memory used for transient heat diffusion. Cruz et al. [22] addressed fractional variational calculus for non-differentiable functions.

Shafique et al. [23] explored fluid mechanics for fractional calculus. They investigated how fractional calculus and random differentiation may be employed to solve problems involving time-dependent viscous diffusion. El-Nabulsi [24] discussed the construction of integral Lagrangian oscillators, which are fractionally difficult on a path. The exact results of the nonlinear, unsteady, and natural, free convection flow of a radiating fluid with the heat were described by Ahmad et al. [25]. The examination of its collective transmission was related to an inclined plane. Shah et al. [26] investigated analytical solutions using the Caputo and Caputo-Fabrizio (CF) derivatives over a vertical surface, where a viscous fluid is flowing in the time-fractional boundary layer. Jassim et al. [27] described the analytical solutions of the Daftardar-Jafari and Sumudu decomposition methods to the fractional differential equations system with the Caputo–Fabrizio (CF) fractional derivative. Prasada et al. [28] discussed and compared the traditional model; the ZIKV transmission dynamics fractional-order model provides significantly improved disease parameter estimation, analysis, and prediction. The modified Jeffrey fluid’s free convection flow was accurately calculated using the Caputo–Fabrizio (CF) fractional model by Saqib et al. [29]. Ahmad et al. [30] described an unsteady Newtonian natural convection flow of a second-grade fluid across a vertical plate with a CPC non-integer order derivative. Pavlovskii [31] first proposed the Jeffrey fluid’s constitutive equation to better understand the behavior of an aqueous polymer solution. Goud et al. [32] investigated the magnetohydrodynamic flow of a micropolar fluid across a movable, vertical porous plate to assess the presence of heat radiation. Biswas et al. [33] studied the unsteady magnetohydrodynamic free convection flow of viscous Maxwell nanofluids over a stretched sheet. The Maxwell embodiment has been used to singularize the non-Newtonian nanofluid. Casson fluid flow with free convection and mass flow over a parallel plate with a constant magnetic field was studied by Afikuzzaman et al. [34]. Oskolkov [35] investigated the initial and boundary problems for penalized equations with a free surface condition in aqueous polymer solutions. Baranovskii [36] analyzed the problems of initial and boundary values for Kelvin–Voigt fluid flow models with mixed boundary conditions.

The literature review indicates that all flow models are made with either ordinary or fractional derivatives. The focus of this research work is to discuss the application of the newly proposed hybrid fractional derivatives by Baleanu et al. [37] to the flow of Jeffrey’s fluid. The constitutive equations for heat and mass fluxes use the generalized fractional derivative previously mentioned, which is also known as the constant proportional Caputo fractional derivative. This is a useful direction for symmetry analysis since by utilizing the fractional parameter approaches to one, the ordinary derivative is obtained. The obtained results are also graphically explained by sketching several graphs of velocity, temperature, and concentration fields for various parameter modifications of interest.

2. Problem Formulation

Consider a Jeffrey flow over a flat surface by considering the non-homogenous thermal and concentration fields. The influence of the magnetic field of a constant magnitude is also included for the momentum balance. For the Jeffrey fluid, the constitutive equations are [31]

$$T=-pI+S,$$

$$S=\frac{\mu }{1+{\lambda }_1}\left(A+{\lambda }_2\frac{dA}{dt}\right),$$

$$\frac{d}{dt}=\frac{\partial }{\partial t}+\nabla ·V,$$

where $\lambda$ and ${\lambda }_1$ are Jeffrey fluid material properties, S is the extra stress tensor, and -pI is the indeterminate portion of the stress. The definition of the Rivlin–Ericksen tensor is

$$A=L_1+L_1^T,L_1=\nabla V.$$

The velocity, temperature, and stress fields for unidirectional and one-dimensional flow is given as

$$T=\overline{T}(\overline{y},\overline{t}),V=\overline{u}(\overline{y},\overline{t})i,S=S(\overline{y},\overline{t}),$$

where the condition $S(\overline{y},0)$ = 0 is satisfied by the stress field and i represents the unit vector along the x-axis. Hence, we get S${}_{xz}$ = S${}_{zx}$ = S${}_{yz}$ = S${}_{zy}$ = S${}_{xx}$ = S${}_{yy}$ = S${}_{zz}$ = 0 and

$$S_{xy}=\frac{\mu }{1+{\lambda }_1}\left(1+{\lambda }_2\frac{\partial }{\partial t}\right)·\frac{\partial \overline{u}}{\partial \overline{y}},$$

where the non-trivial tangential stress is $S_{xy}$. Transversely to the flow, $Bo$ is subjected to a constant magnetic field. Here, the current density is j, the magnetic field strength overall is $\overline{B}=({\overline{B}}_1+{\overline{B}}_o)$, the magnetic field that is generated $({\overline{B}}_1\ll {\overline{B}}_o)$ is ${\overline{B}}_1$, and Lorentz’s force is $\overline{j}\times \overline{B}$. Ohm’s law and the Maxwell equations are presented as

$$\nabla \times \overline{B}={\mu }_m\overline{j},\nabla ·\overline{B}=0,\overline{j}=\sigma (\overline{E}+\overline{q}\times \overline{E}),\nabla \times \overline{E}=-\frac{\partial \overline{B}}{\partial t},$$

where the electrical conductivity = $\sigma$, the magnetic permeability = ${\mu }_m$, and the electric field is $\overline{E}$. The induced magnetic field is ignored because it is supposed that the magnetic Reynolds number is small. Consequently, the $\overline{j}\times \overline{B}$ force is reduced to $\overline{j}\times \overline{B}=-\sigma B_o^{2}u$. The y-axis is generally pointed out toward the plane of the surfaces, and the orientation of the flat surface is chosen such that the plane of the flat surface is concise on the $xy$-plane. The physical condition of the temperature and concentration are described by $T_o$ and $C_o$, respectively. Subsequently, for time $t>0$, the plate starts to move, and hence the does fluid too. In this new situation, the physical conditions are described by temperature $T_s$ and concentration $C_s$, and moreover, the slip effect at the boundary of the flow domain is also considered. The flow diagram is shown in Figure 1. According to our supposition of the governing equation of the flow model, we assume the following forms [29]

$$\rho {\partial }_{t}U(\xi ,t)=\mu \frac{(1+{\lambda }_2{\partial }_t)}{1+{\lambda }_1}{\partial }_{\xi }^{2}U(\xi ,t)+\rho g{B}_T(T-T_o)+\rho g{B}_c(C-C_o)-\sigma B_o^{2}u(\xi ,t),$$

(1)

$$\rho C_p{\partial }_{t}T(\xi ,t)=K{\partial }_{\xi }^{2}T(\xi ,t)-Q(T-T_o),$$

(2)

$${\partial }_{t}C(\xi ,t)=D{\partial }_{\xi }^{2}C(\xi ,t)-Kr(C-C_o),$$

(3)

subject to IBCs

$$U(\xi ,0)=0,T(\xi ,0)=T_o,C(\xi ,0)=C_o,\mathrm{for}\mathrm{all}0\le \xi ,$$

(4)

$$U(0,t)-S\frac{\partial u}{\partial \xi }(\xi ,t){|}_{\xi =0}=U_{0}n\left(t\right),T(0,t)=T_s,C(0,t)=C_s,t\in [0,\infty ),$$

(5)

$$U(\xi ,t)⟶0,T(\xi ,t)⟶T_o,C(\xi ,t)⟶C_o,\mathrm{as}\xi ⟶\infty .$$

(6)

Dimensionalization is applied to get a better understanding of the intrinsic behavior of the mathematical flow model. Moreover, this process also recovered the characteristic properties of the mathematical model; hence, the governing equations of the proposed model are transformed into the dimensionless form. Inserting the following non-dimensional variables

$$\eta =\frac{U_0\xi }{\nu },\tau =\frac{U_o^{2}t}{\nu },U=\frac{u}{U_o},\theta =\frac{T-T_o}{T_s-T_o},\varphi =\frac{C-C_o}{C_s-C_o}.$$

(7)

into Equations (1)–(6), we get the dimensionless model as follows

$${\partial }_{\tau }u=\frac{1}{1+{\lambda }_1}\left(1+\lambda {\partial }_{\tau }\right){\partial }_{\eta }^{2}u+\mathrm{Gr}\theta +\mathrm{Gm}\varphi -F_{M}u,$$

(8)

$${\partial }_{\tau }\theta =\frac{1}{\mathrm{Pr}}{\partial }_{\eta }^2\theta -E\theta ,$$

(9)

$${\partial }_{\tau }\varphi =\frac{1}{\mathrm{Sc}}{\partial }_{\eta }^2\varphi -H\varphi ,$$

(10)

with IBCs

$$u(\eta ,0)=0,\theta (\eta ,0)=0,\varphi (\eta ,0)=0,\mathrm{for}\mathrm{all}0\le \eta ,$$

(11)

$$u(0,\tau )-S_p{\partial }_{\eta }u(\eta ,\tau ){|}_{\eta =0}=N\left(\tau \right),\theta (0,\tau )=1,\varphi (0,\tau )=1,\tau \in [0,\infty ),$$

(12)

$$u(\eta ,\tau )⟶0,\theta (\eta ,\tau )⟶0,\varphi (\eta ,\tau )⟶0,\mathrm{as}\eta ⟶\infty ,$$

(13)

where the heat generation is E = $\frac{Q{\nu }^2}{K{u}_o^2}$, chemical reaction is H = $\frac{Kr{\nu }^2}{D{u}_o^2}$, unit step function is $N\left(t\right)$, Grashof number is $\mathrm{Gr}=\frac{\nu g{\beta }_T(T_s-T_{\infty })}{u_o^3}$, mass Grashof number is $\mathrm{Gm}=\frac{\nu g{\beta }_c(C_s-C_{\infty })}{u_o^3}$, magnetic force is ${\mathrm{F}}_{\mathrm{M}}=\frac{\nu \sigma B_o^2}{\rho u_o^2}$, Prandtl number is $\mathrm{Pr}=\frac{\mu C_p}{k}$, and Schmidt number is $\mathrm{Sc}=\frac{\nu }{D}.$

3. Ordinary Solution

This section discusses the Laplace transform technique and the solutions for concentration, temperature, and velocity fields without a fractional derivative.

3.1. Calculation of Temperature

Using both sides of Equation (9), the Laplace transform, and we obtain

$$\frac{d^2\overline{\theta }(\eta ,s)}{d{\eta }^2}-\mathrm{Pr}(s+E)\overline{\theta }(\eta ,s)=0.$$

(14)

Equation (14) satisfies

$$\overline{\theta }(0,s)=\frac{1}{s},\mathrm{and}\overline{\theta }(\infty ,s)=0.$$

(15)

Equation (15) is used to solve Equation (14)

$$\overline{\theta }(\eta ,s)=\frac{1}{s}{e}^{-\sqrt{\mathrm{Pr}(s+E)}\eta }.$$

(16)

Inverting the Laplace transform; see Appendix A, we obtain

$$\theta (\eta ,\tau )=\frac{1}{2}\left[\mathrm{erfc}\left(\frac{\eta }{2}\sqrt{\frac{\mathrm{Pr}}{\tau }}+\sqrt{E\tau }\right)e^{\eta \sqrt{E\mathrm{Pr}}}+\mathrm{erfc}\left(\frac{\eta }{2}\sqrt{\frac{\mathrm{Pr}}{\tau }}-\sqrt{E\tau }\right)e^{-\eta \sqrt{E\mathrm{Pr}}}\right].$$

(17)

3.2. Calculation of Concentration

Taking both sides of the Laplace transform from Equation (10), we get

$$\frac{d^2\overline{\varphi }(\eta ,s)}{d{\eta }^2}-\mathrm{Sc}(s+H)\overline{\varphi }(\eta ,s)=0.$$

(18)

Equation (18) satisfies

$$\overline{\varphi }(0,s)=\frac{1}{s},\mathrm{and}\overline{\varphi }(\infty ,s)=0.$$

(19)

Equation (18) is solved using Equation (19)

$$\overline{\varphi }(\eta ,s)=\frac{1}{s}{e}^{-\sqrt{\mathrm{Sc}(s+H)}\eta }.$$

(20)

Taking the inverse Laplace transform from Equation (20); see Appendix A,

$$\varphi (\eta ,\tau )=\frac{1}{2}\left[\mathrm{erfc}\left(\frac{\eta }{2}\sqrt{\frac{\mathrm{Sc}}{\tau }}+\sqrt{H\tau }\right)·e^{\eta \sqrt{H\mathrm{Sc}}}+\mathrm{erfc}\left(\frac{\eta }{2}\sqrt{\frac{\mathrm{Sc}}{\tau }}-\sqrt{H\tau }\right)·e^{-\eta \sqrt{H\mathrm{Sc}}}\right].$$

(21)

3.3. Calculation of Velocity

Laplace transform is applied to Equation (8), we obtain

$$\frac{d^2\overline{u}}{d{y}^2}-\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}\overline{u}=-Gr\frac{1+{\lambda }_1}{1+\lambda s}\overline{\theta }-Gm\frac{1+{\lambda }_1}{1+\lambda s}\overline{\varphi }.$$

(22)

Equation (22) satisfies

$$\overline{u}(0,s)-S_p\frac{\partial \overline{u}}{\partial \eta }{|}_{\eta =0}=N\left(s\right)\mathrm{and}\overline{u}(\infty ,s)=0.$$

(23)

The solution of Equation (22), using Equations (16), (20) and (23), we get

$$\begin{array}{ccc}& & \overline{u}(\eta ,s)=N\left(s\right)\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}}+Gr\frac{1+{\lambda }_1}{[\mathrm{Pr}(s+E)(1+\lambda s)-(s+F_M)(1+{\lambda }_1)]}\hfill \\ & & \times \left[\left(\frac{1+S_p\sqrt{\mathrm{Pr}(s+E)}}{1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}}\right)\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{s}-\frac{e^{-\sqrt{\mathrm{Pr}(s+E)}\eta }}{s}\right]\hfill \\ & & +Gm\frac{1+{\lambda }_1}{[\mathrm{Sc}(s+H)(1+\lambda s)-(s+F_M)(1+{\lambda }_1)]}\hfill \\ & & \times \left[\left(\frac{1+S_p\sqrt{\mathrm{Sc}(s+H)}}{1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}}\right)\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{s}-\frac{e^{-\sqrt{\mathrm{Sc}(s+H)}\eta }}{s}\right].\hfill \end{array}$$

(24)

Definition 1.

The fractional derivative of order with a constant proportional Caputo δ in (0,1) is [31]

$$\begin{array}{c}\hfill {}^{CPC}{D}_t^{\delta }f\left(t\right)=\frac{1}{\delta (1-\delta )}{\int }_0^t\left(k_1\left(\delta \right)f\left(\tau \right)+k_0\left(\delta \right)f^{{}^{\prime }}\left(\delta \right)\right){(t-\tau )}^{-\delta }d\tau .\end{array}$$

(25)

We see Equation (25) as $k_1\left(\delta \right)\to 0$ and $k_0\left(\delta \right)\to 1$.

Definition 2.

Laplace transform of CPC fractional derivative [31]

$$\begin{array}{c}\hfill \pounds {\{}^{CPC}{D}_t^{\delta }f\left(t\right)\}=\left[\frac{k_1\left(\delta \right)}{s}+k_0\right]s^{\delta }\overline{f}\left(s\right)-k_0\left(\delta \right)s^{\delta -1}f\left(0\right).\end{array}$$

(26)

4. Fractional Solution

This section identifies the concentration, temperature, and velocity field solutions to the Laplace transform method and fractional derivative.

4.1. Fractional Thermal Diffusion

The thermal balance equation

$$\rho C_p{\partial }_{t}T=-{\partial }_{y}q-Q(T-T_o).$$

(27)

where q is the dimensionless thermal flux of heat conduction by applying Fourier’s law

$$q=-K_{\beta }{}^{CPC}{D}_t^{\beta }\left[\frac{\partial T}{\partial y}\right],0<\beta \le 1,$$

(28)

substituting Equation (28) into Equation (27) and using the dimensionless relation from Equation (7), we get

$$\mathrm{Pr}\frac{\partial \theta }{\partial \tau }={}^{CPC}{D}_t^{\beta }\left[\frac{{\partial }^2\theta }{\partial {\eta }^2}\right]-\mathrm{Pr}H\theta ,0<\beta \le 1,$$

(29)

the solution of Equation (29) by using the Laplace transform method is

$$\frac{d^2\overline{\theta }}{d{\eta }^2}-\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}\overline{\theta }=0.$$

(30)

The solution to Equation (30) using Equation (15) is

$$\overline{\theta }(\eta ,s)=\frac{1}{s}{e}^{-\sqrt{\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}}\eta }.$$

(31)

4.2. Fractional Concentration

The concentration equation is

$${\partial }_{t}C=-{\partial }_{y}J-Kr(C-C_o),$$

(32)

where J is the dimensionless molecular flux of concentration by applying Fick’s law

$$J=-D_{\gamma }{}^{CPC}{D}_t^{\gamma }\left[\frac{\partial C}{\partial y}\right],0<\gamma \le 1,$$

(33)

substituting Equation (33) into Equation (32) and using the relation from Equation (7), we get

$$\mathrm{Sc}\frac{\partial \varphi }{\partial \tau }={}^{CPC}{D}_t^{\gamma }\left[\frac{{\partial }^2\varphi }{\partial {\eta }^2}\right]-\mathrm{Sc}H\varphi ,0<\gamma \le 1,$$

(34)

The solution to Equation (34) by using the Laplace transform method is

$$\frac{d^2\overline{\varphi }(\eta ,s)}{d{\eta }^2}-\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}\overline{\varphi }=0.$$

(35)

Equation (35) is solved using Equation (19)

$$\overline{\varphi }(\eta ,s)=\frac{1}{s}{e}^{-\sqrt{\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}}\eta }.$$

(36)

Inversion of transformed temperature and concentration fields are made by Tzou’s and Stehfest’s algorithms, and the inverted results are presented in Figure 2 and Figure 3. The ordinary inverse of Equations (31) and (36) is more complex.

4.3. Fractional Velocity

The constitutive fractional model is first created for the concentration and temperature equations, then solved by using the Laplace transform method. The velocity field is then determined

$$\rho {\partial }_{t}U=\frac{1+{\lambda }_2{\partial }_t}{1+{\lambda }_1}{\partial }_{y}M+\rho g{B}_T(T-T_o)+\rho g{B}_c(C-C_o)-\sigma B_o^{2}u,$$

(37)

where

$$M(y,t)=\mu {\partial }_{y}u.$$

(38)

For analytical solutions to momentum equations, we use Equations (31) and (36) in Equation (37), and we use the dimensionless relation Equation (7); using Laplace transform method, we get

$$\begin{array}{ccc}\frac{d^2\overline{u}(\eta ,s)}{d{y}^2}-\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}\overline{u}(\eta ,s)& =& -\mathrm{Gr}\frac{1+{\lambda }_1}{1+\lambda s}\left[\frac{1}{s}{e}^{-\sqrt{\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}}\eta }\right]\hfill \\ & & -\mathrm{Gm}\frac{1+{\lambda }_1}{1+\lambda s}\left[\frac{1}{s}{e}^{-\sqrt{\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}}\eta }\right].\hfill \end{array}$$

(39)

The solution of Equation (39) using Equation (23) is

$$\begin{array}{ccc}& & \overline{u}(\eta ,s)=G\left(s\right)\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{\left[1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\right]}+\mathrm{Gr}\frac{1+{\lambda }_1}{(1+\lambda s)}\frac{1}{\left[\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}-\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}\right]}\hfill \\ & & \times \frac{1+S_p\sqrt{\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}}}{s}·\left[\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{\left(1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\right)}-\frac{e^{-\sqrt{\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}}\eta }}{\left(1+S_p\sqrt{\frac{\mathrm{Pr}(s+E)}{[K_1\left(\beta \right)s^{\beta -1}+K_o\left(\beta \right)s^{\beta }]}}\right)}\right]\hfill \\ & & +\mathrm{Gm}\frac{1+{\lambda }_1}{(1+\lambda s)}\frac{1}{\left[\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}-\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}\right]}\hfill \\ & & \times \frac{1+S_p\sqrt{\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)S^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}}}{s}·\left[\frac{e^{-\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\eta }}{\left(1+S_p\sqrt{\frac{(s+F_M)(1+{\lambda }_1)}{1+\lambda s}}\right)}-\frac{e^{-\sqrt{\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}}\eta }}{\left(1+S_p\sqrt{\frac{\mathrm{Sc}(s+H)}{[K_1\left(\gamma \right)s^{\gamma -1}+K_o\left(\gamma \right)s^{\gamma }]}}\right)}\right].\hfill \end{array}$$

(40)

The inversion of the transformed ordinary and fractional velocity fields are made by Tzou’s and Stehfest’s algorithms, and the inverted results are presented in Figure 4 and Figure 5. The ordinary inverse of Equation (24) and Equation (40) is more complex.

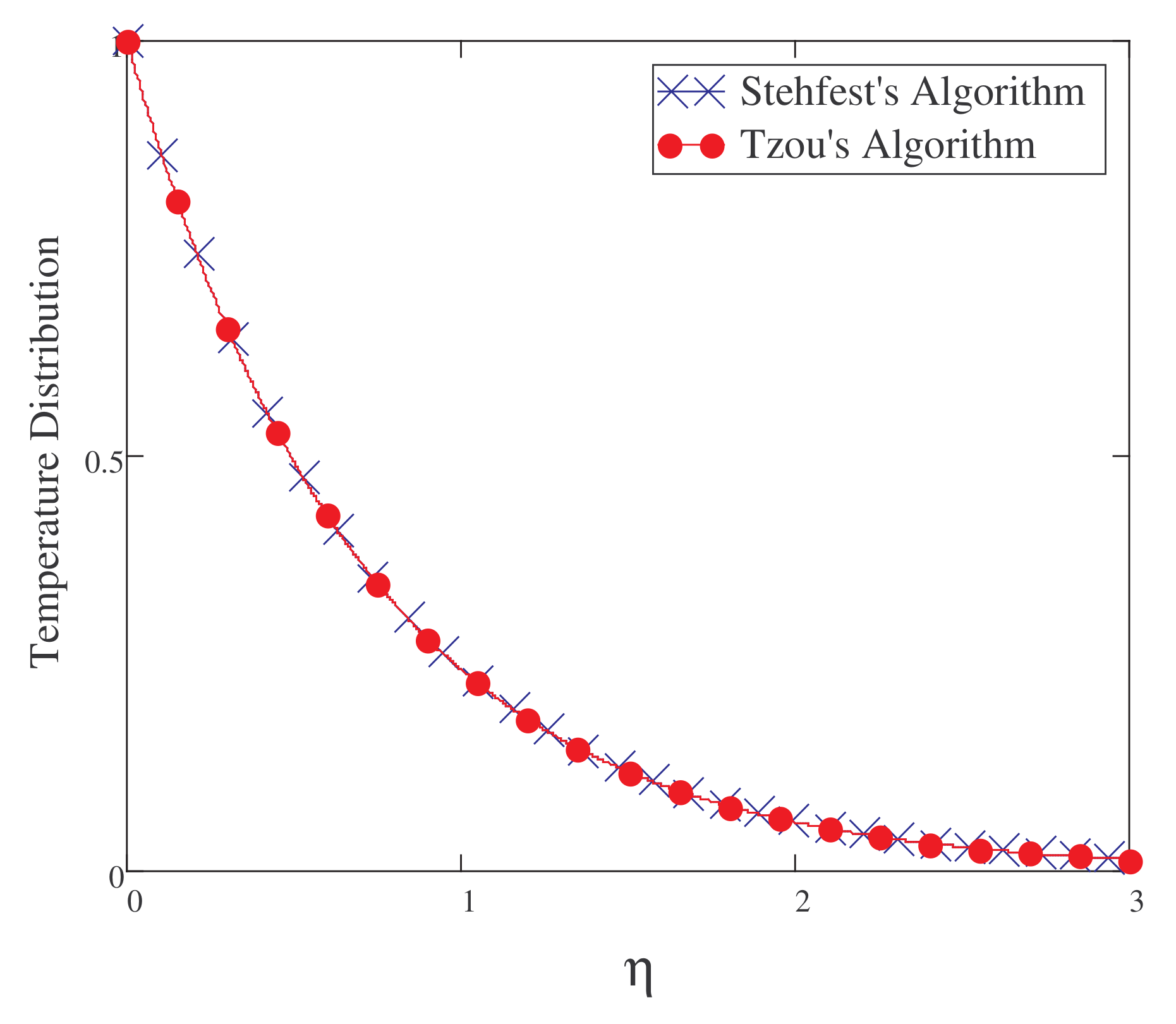
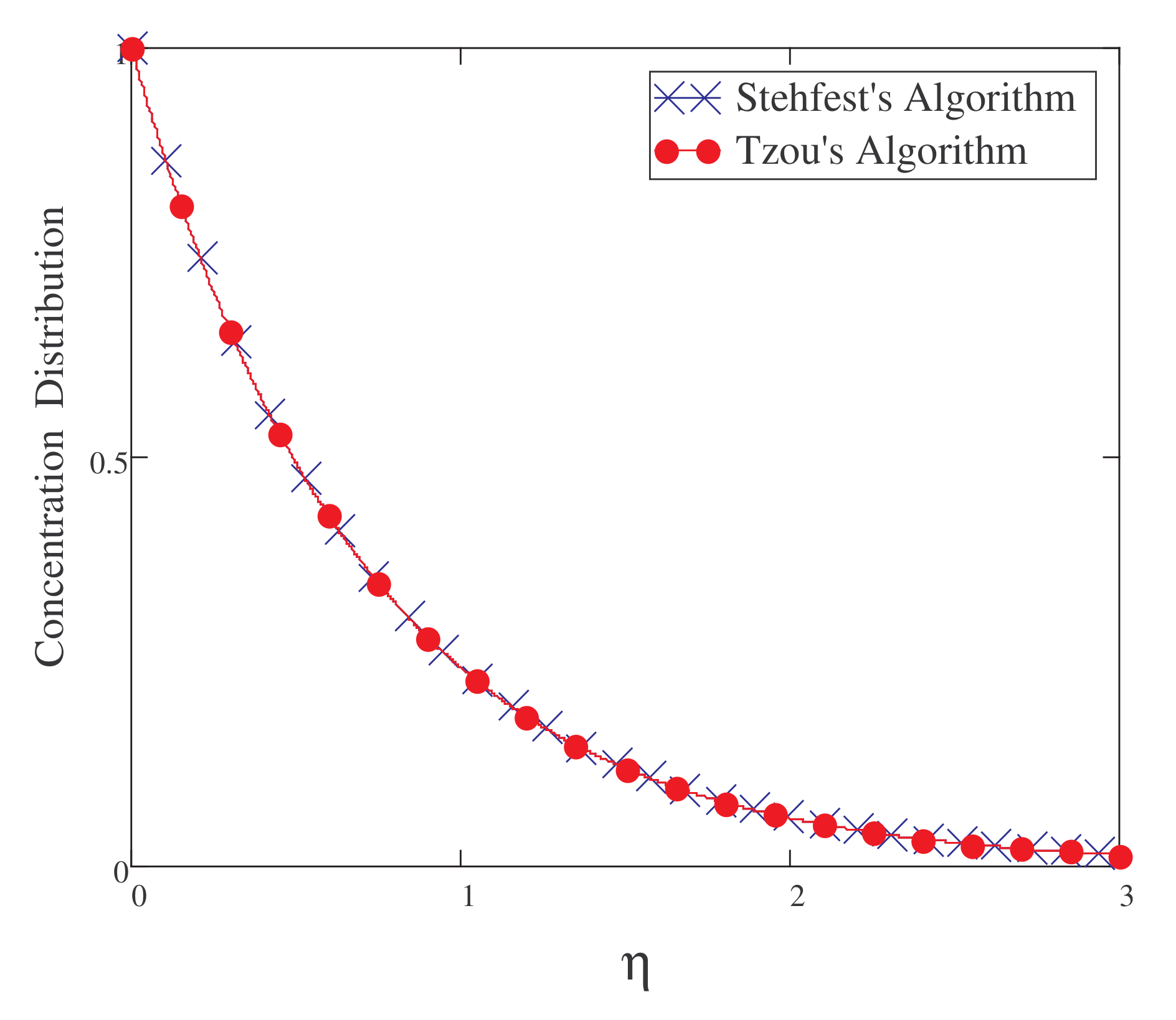
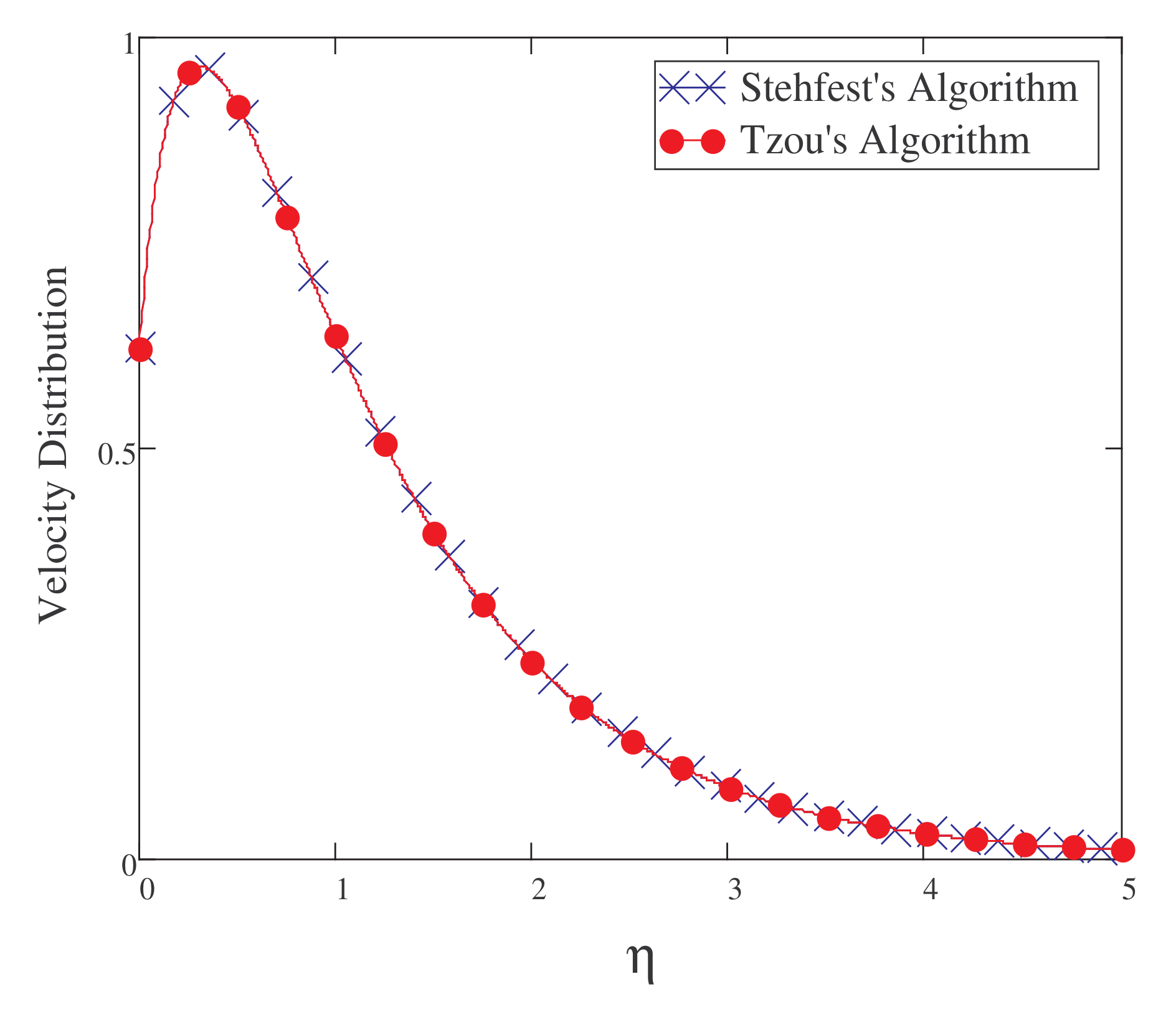
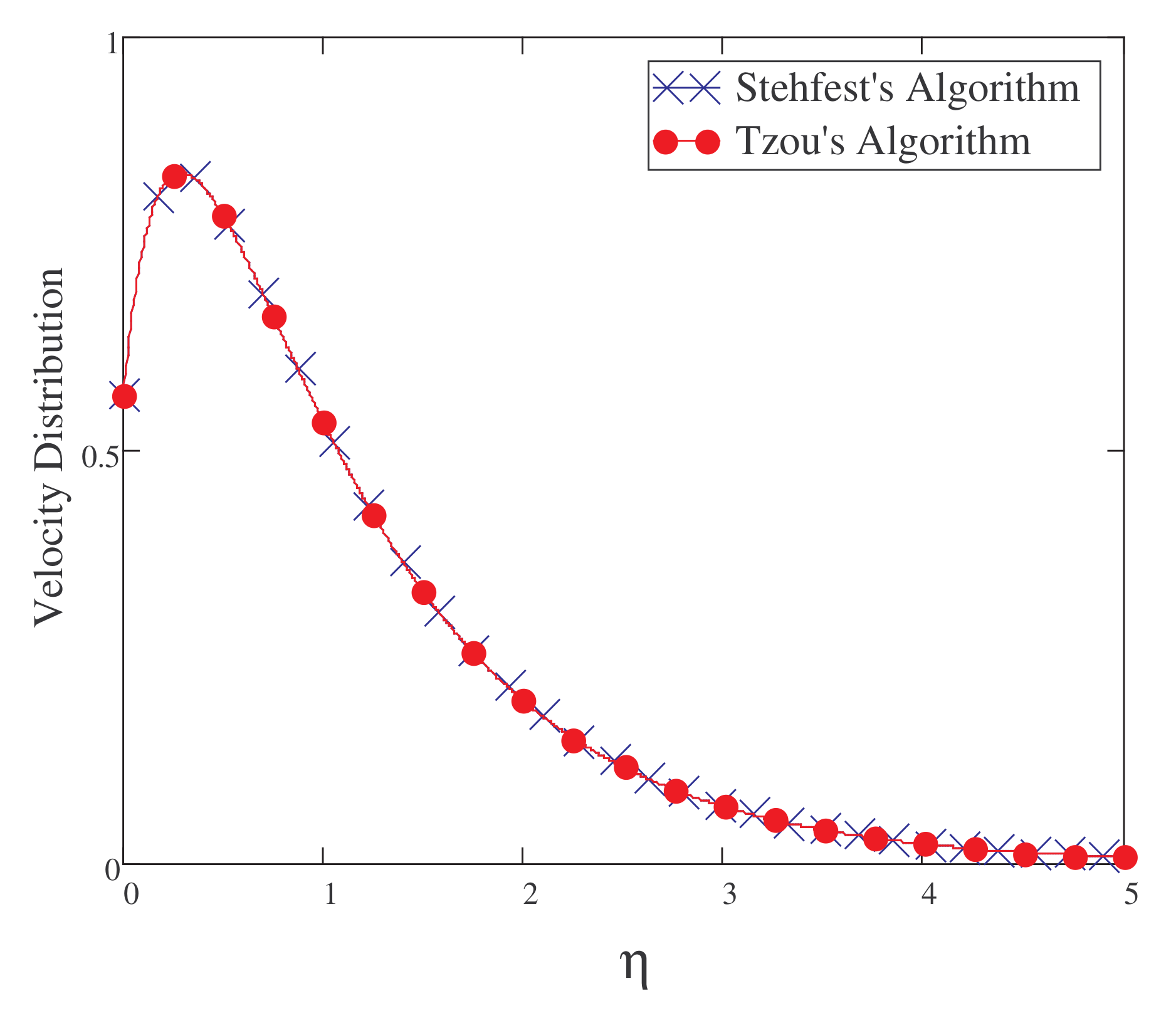
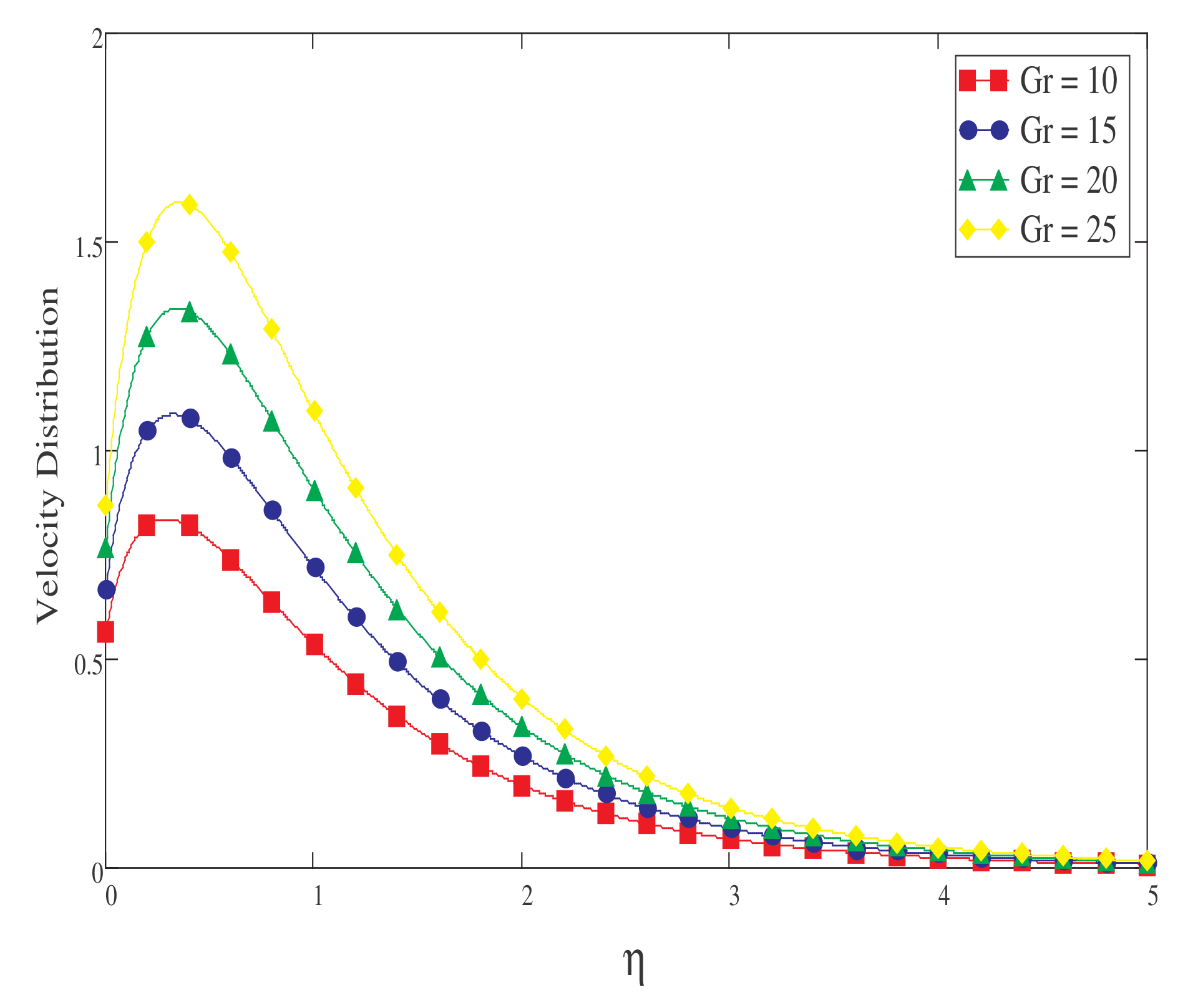
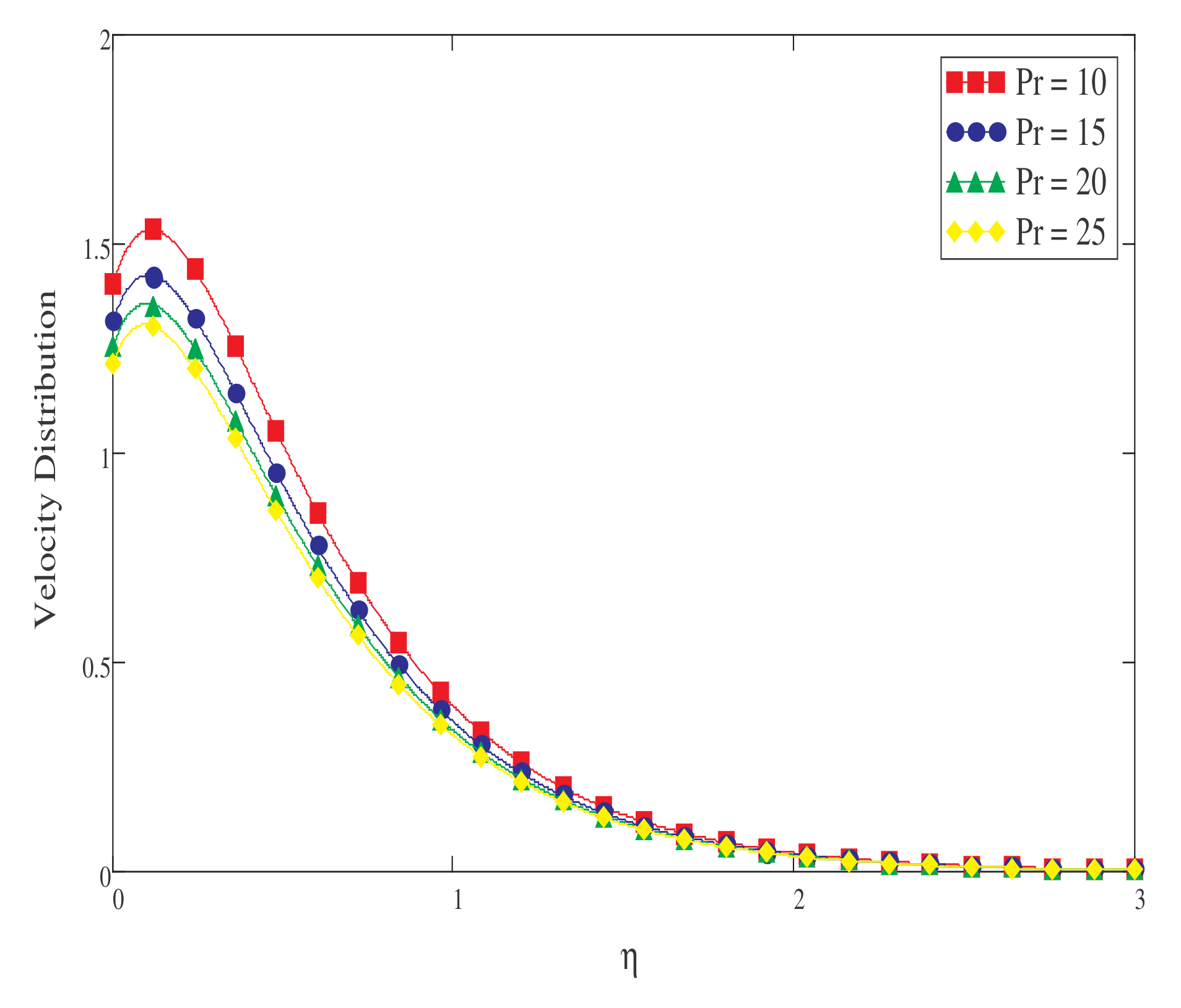
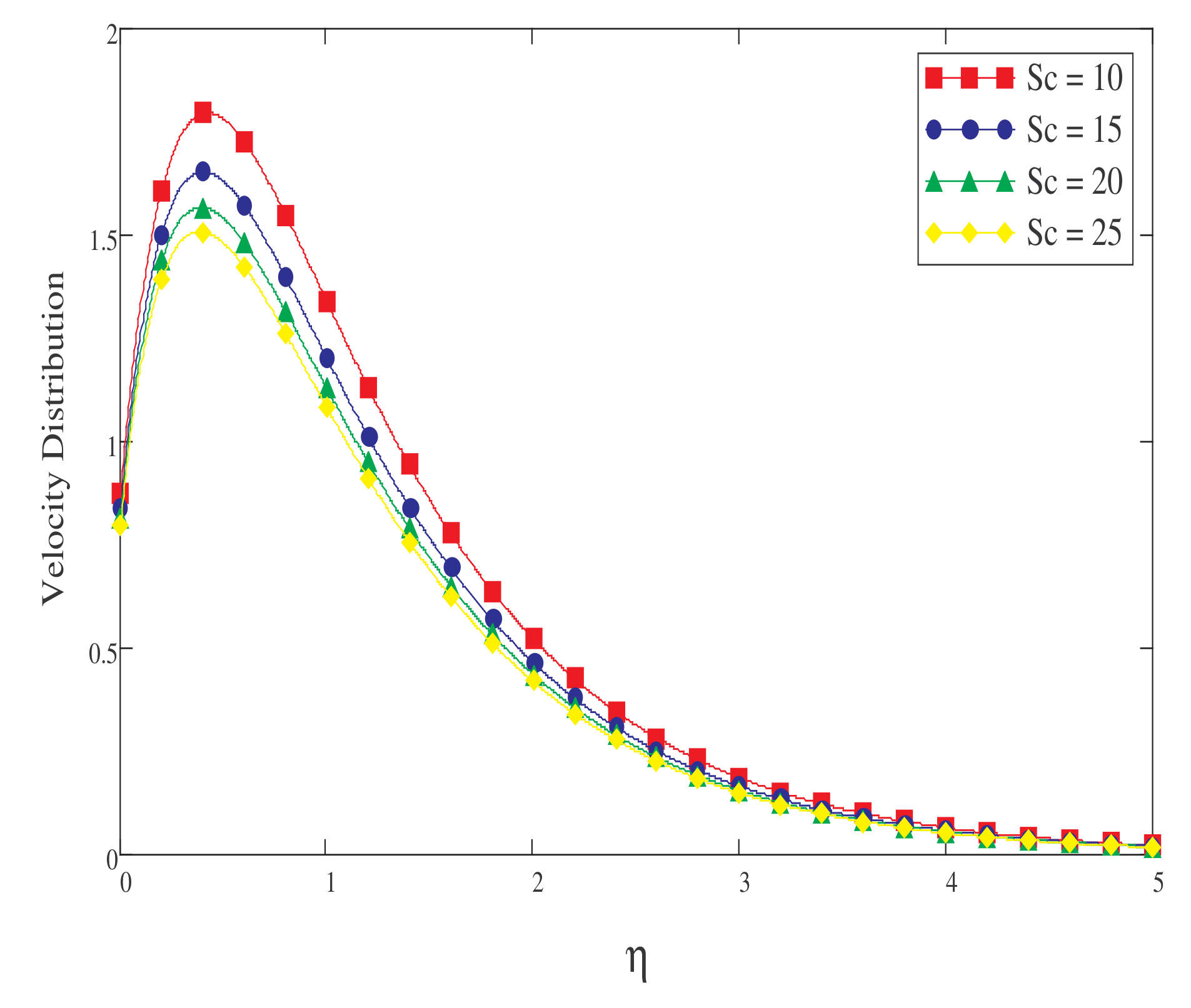
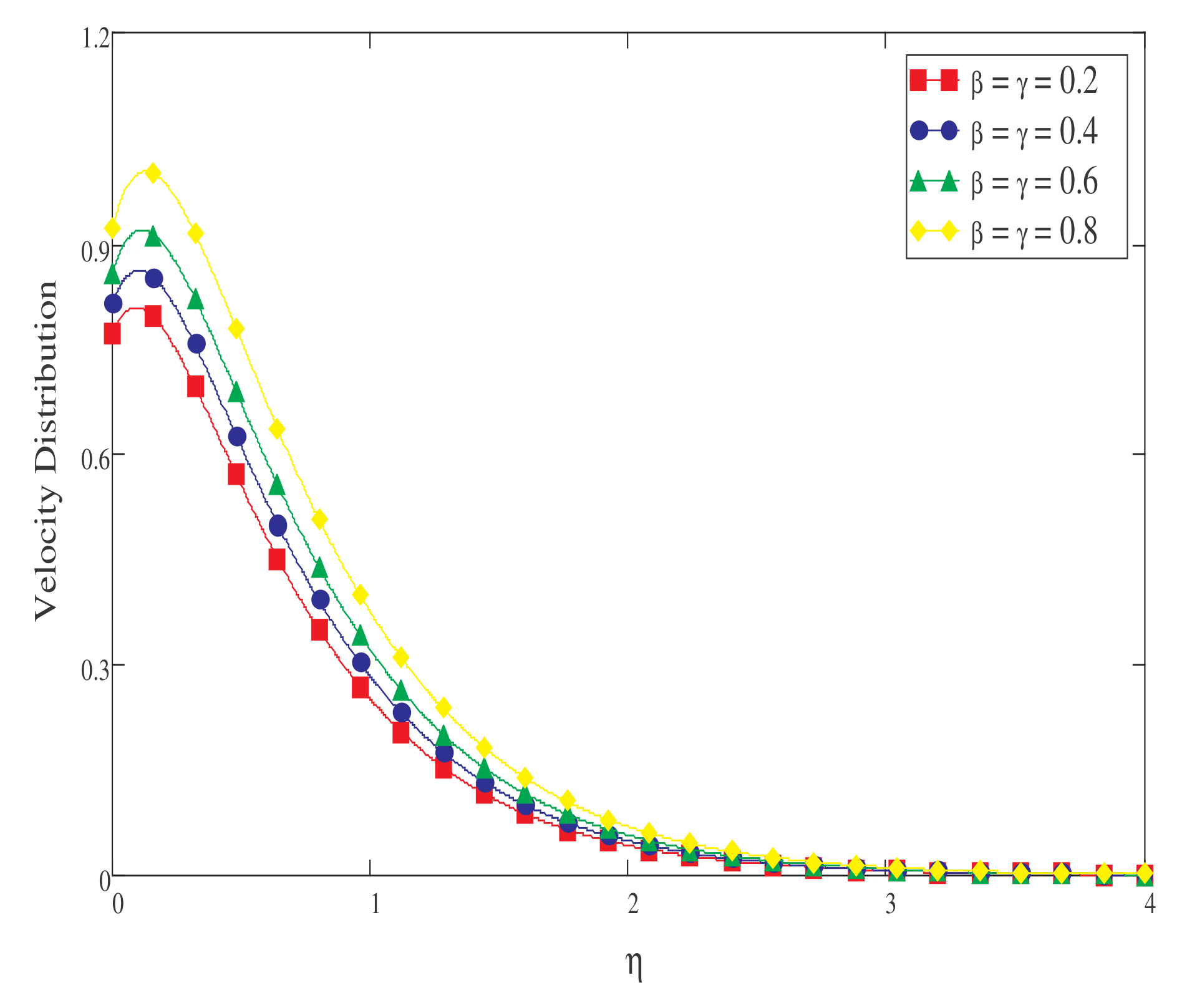
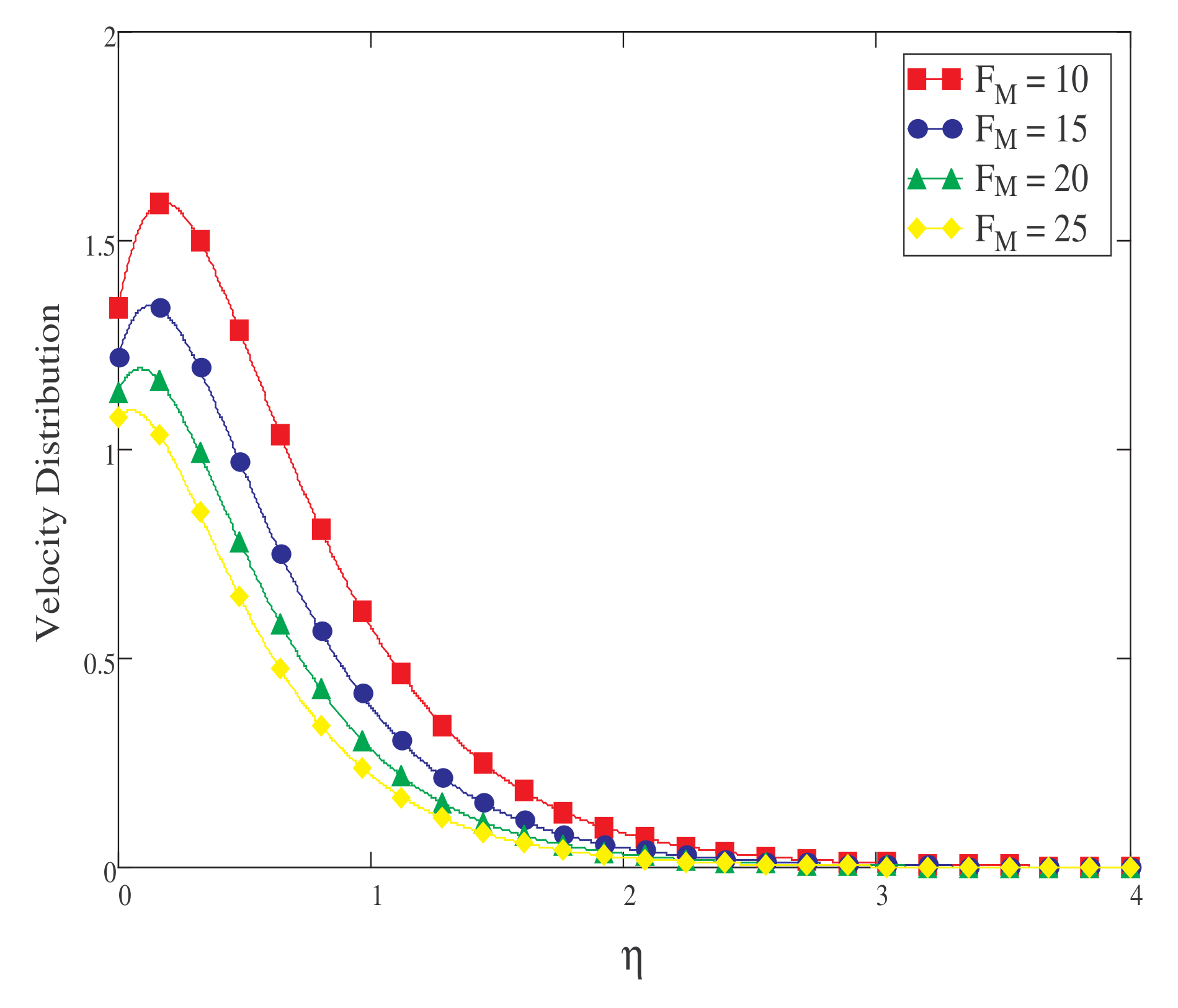
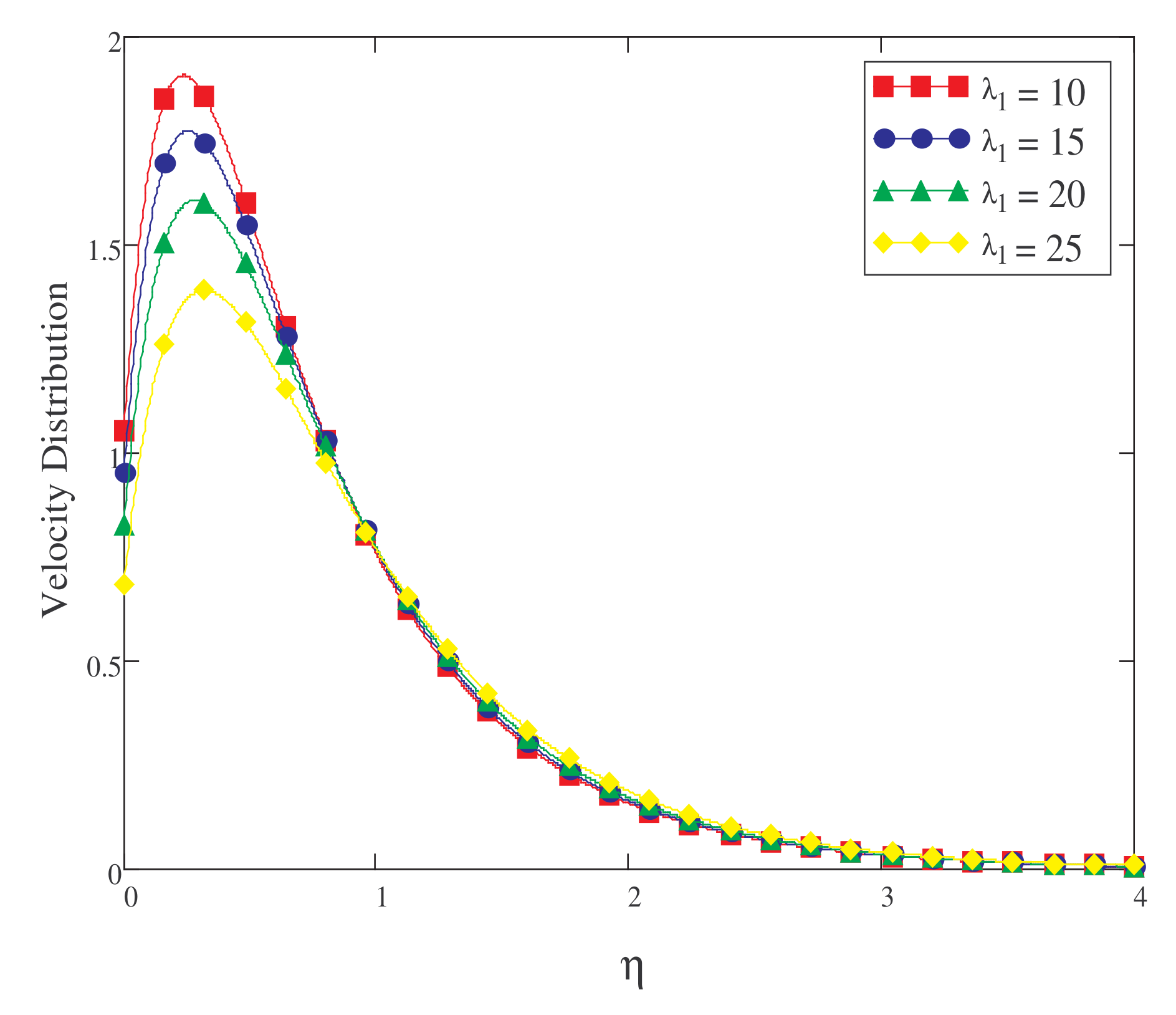
5. Result and Discussion

In Figure 6, by analyzing the fractional parameter $\beta$ while maintaining all other factors constant, greater values of $\beta$ can cause a decrease in the fractional parameter field. Because thermal diffusivity is reciprocal to Pr, its higher values decrease the fractional parameter profile. In Figure 7, by analyzing the temperature while maintaining all other factors constant, greater values of Pr can cause a decrease in the temperature field. It is clear that raising Pr values lowers thermal diffusivity, and as a result, thermal boundary layer thickness decreases as Pr rises. In Figure 8, by analyzing the fractional parameter $\gamma$ while maintaining all other factors constant, greater values of $\gamma$ can cause a decrease in the fractional parameter field. In Figure 9, by analyzing the concentration while maintaining all other factors constant, higher values of Sc cause decay in the concentration field. Because mass diffusivity is reciprocal to Sc, its greater values decrease the concentration.

The graphical results for various values of the parameters, such as Gr, Gm, Pr, Sc, $\beta$, $\gamma$$F_M$, $\lambda$, and ${\lambda }_1$, are sketched in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Figure 10 depicts the Grashof number’s influence on velocity distribution. Increasing the values of Gr, the fluid rate can be accelerated. The ratio of buoyancy to viscous forces is the physical definition of the Grashof number. Buoyancy forces rise with larger values of Gr, which results in causing the resultant flow to rise. Hence, the fluid velocity can rise. Figure 11 shows the influence of the mass of the Grashof number on velocity. These depicted numbers show that the velocity is these numbers’ increasing function. It is physically true since Gm raises the upthrust forces, which causes the fluid’s viscosity to decrease and its velocity to increase. The impact of the Prandtl number on the velocity profile is illustrated in Figure 12. The ratio of viscous to thermal forces is known as the Prandtl number. As the Prandtl number increases, it indicates that the viscous forces have begun to dominate thermal forces, resulting in a decrease in velocity. Figure 13 depicts the velocity profile effect by Schmidt number. Since the relationship between the viscous forces and mass diffusion is called the Schmidt number, increasing this number leads to an increase in viscous forces and a decay in mass diffusion, which decreases the fluid velocity.

Figure 14 examines the fractional parameters of velocity. The fractional parameters $\beta$ and $\gamma$ increase, and then the fluid velocity also rises. In the plate region, the boundary layer’s thickness grows, and its velocity reaches its maximum. The characteristics of $F_M$ on velocity are shown in Figure 15. The increase in $F_M$ causes the velocity profile to decrease. Lorentz’s force is the cause of this behavior because the larger value of $F_M$ refers to a larger retarding force due to the magnetic field’s presence. Due to this trend, velocity slows down. Figure 16 shows how changing the values of the Jeffrey fluid parameter $\lambda$ causes the velocity distribution to change. As the Jeffrey fluid parameter values rise, the velocity profile will decay because the boundary layer momentum thickness will increase as the Jeffrey fluid parameter values rise, and the velocity profile will decay. As a result, as the value of $\lambda$ increases, so does the velocity distribution. Figure 17 depicts the parameters affecting the flow of the velocity field, the ratio of retardation, and relaxation time, ${\lambda }_1$. It turns out that the velocity profile decreases as the parameter value ${\lambda }_1$ increases because higher values of ${\lambda }_1$ cause the relaxation time (or retardation time) to increase, which implies that the fluid particles need more time to return to equilibrium after a perturbation. As a result, the fluid velocity decreases.

6. Conclusions

This manuscript deals with the classical model, which is converted into a time-fractional model utilizing the definition of the CPC fractional derivative using the modern method of Fick’s and Fourier’s laws. The Laplace transform is used to receive precise solutions for temperature, concentration, and velocity. The impacts of the associated parameters of fluid flow are examined. The following are the key findings:

• Increasing the values of $\beta$, $\gamma$, Gr, and Gm increases the fluid’s velocity.
• Rises in the values of Pr, Sc, F${}_M$, $\lambda$, and ${\lambda }_1$ slow the fluid’s velocity down.
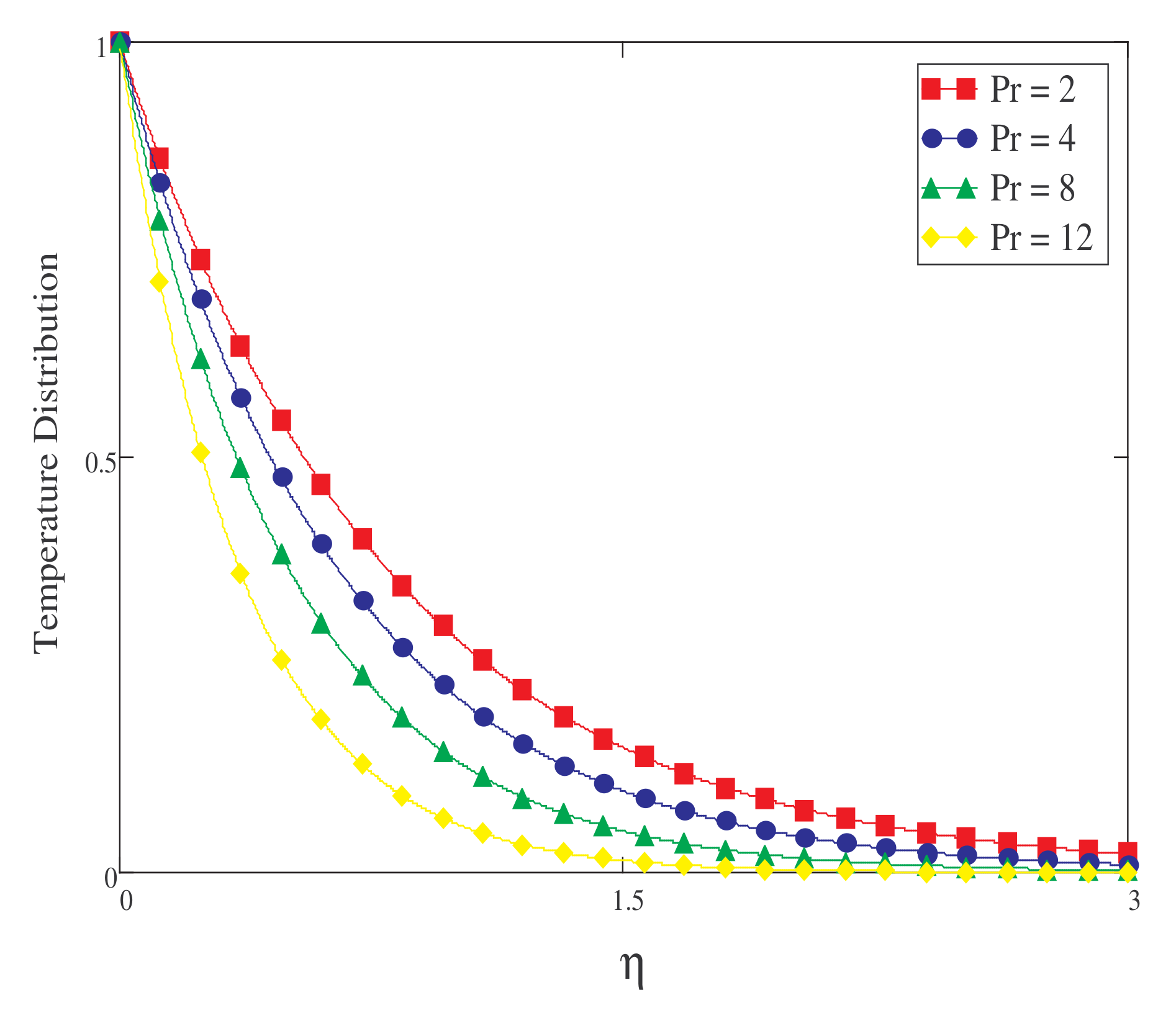
• Rises in the value of Pr decrease the fluid temperature.
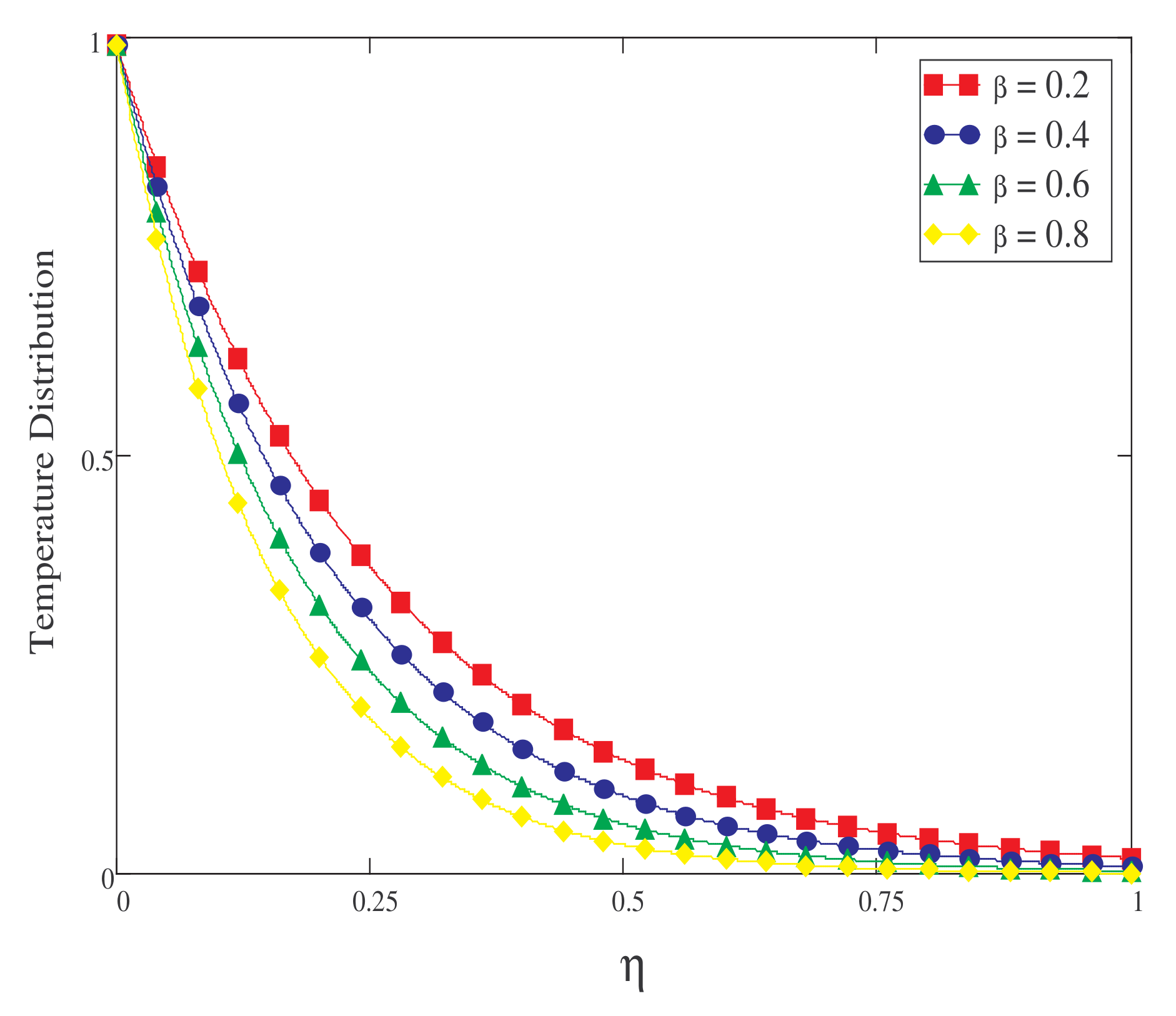
• For a short time, the temperature field is a decreasing function of $\beta$.
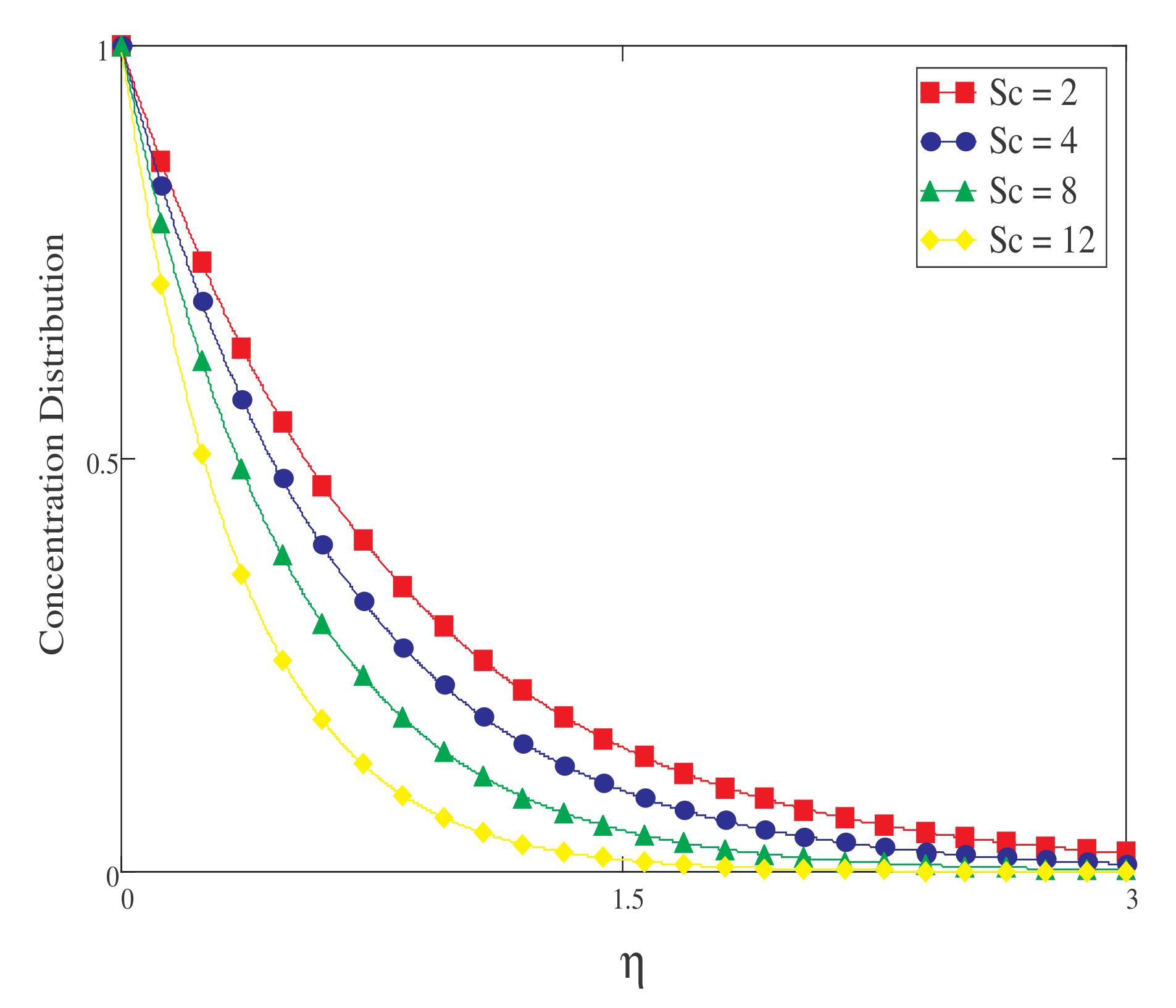
• Increasing the value of Sc decreases the concentration of the fluid.
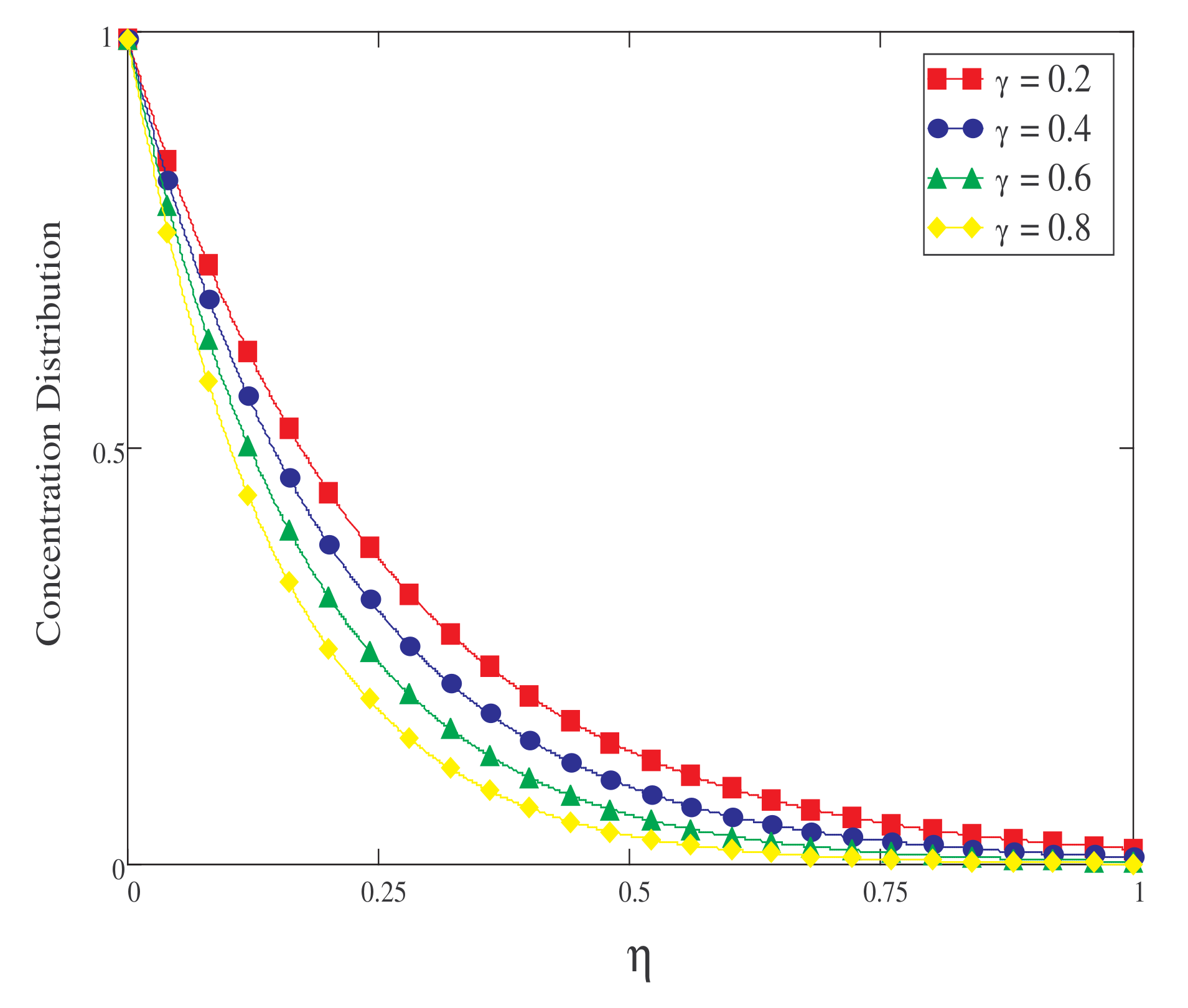
• For a short time, the concentration field is a decreasing function of $\gamma$.
• The fractionalized outcomes for velocity, temperature, and concentration are generalized and are of a more decaying nature.