Design of the Algorithm for Packaging of Water Molecules in a Fixed Volume
Abstract
1. Introduction
2. Algorithm
- 1.
- Firstly, it is necessary to specify a volume that is available for completion.
- 2.
- Then, we form a matrix that will contain information about the coordinates of the vertices of all added molecules.
- 3.
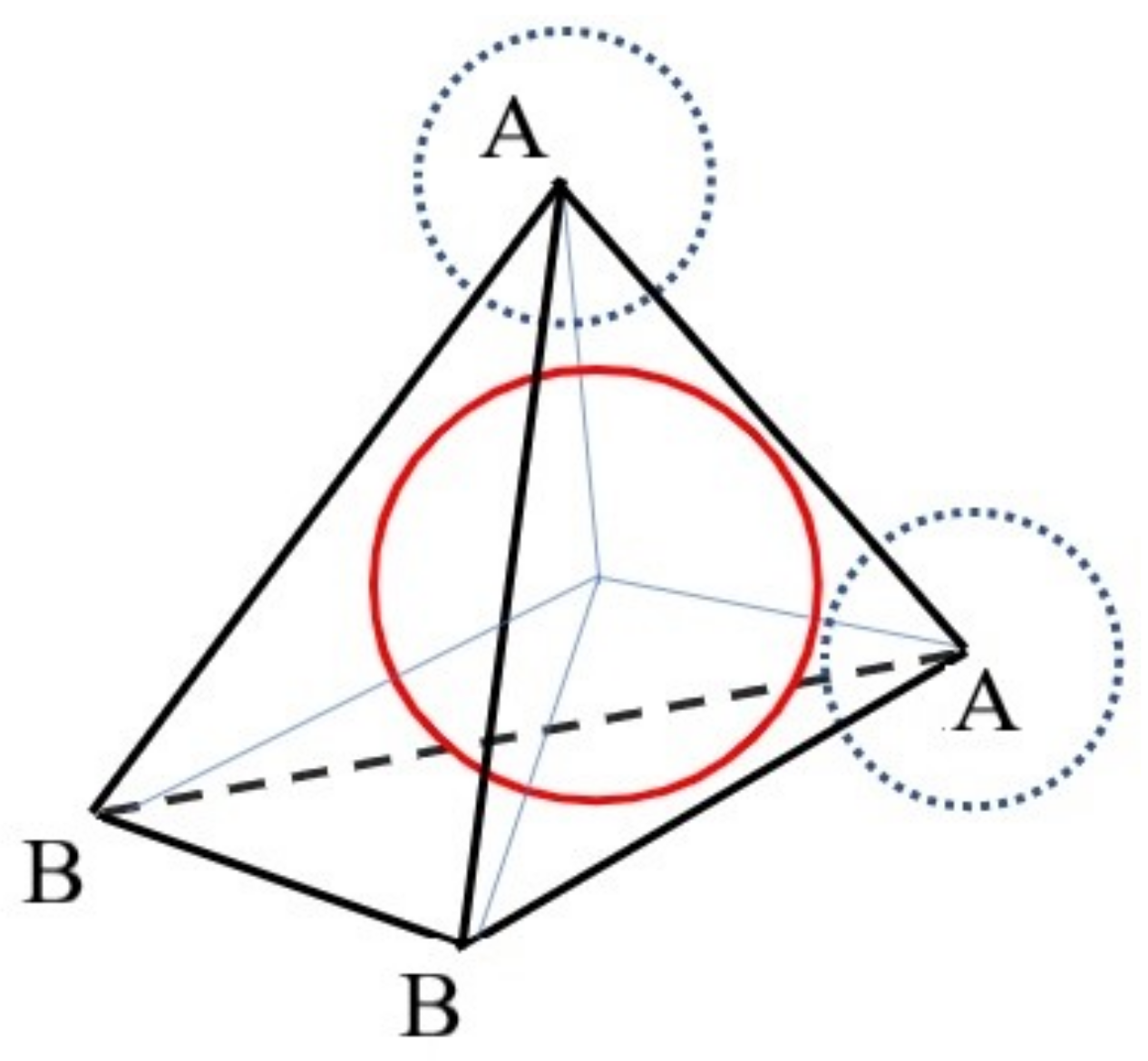
- In accordance with the representation of the water molecule, we need to determine the coordinates of the vertices of the tetrahedron for the first molecule.
- 4.
- The coordinates of the nodes of the molecule are recorded in the matrix formed in step 2.
- 5.
- Afterwards, it is reasonable to apply the image of the tetrahedron corresponding to the added molecule to the graph.
- 6.
- Two variables are defined that store the position of the last added tetrahedron. One of them represents the coordinates of the tetrahedron vertex with the largest abscissa and another one is the number of vertices with the largest abscissa (1 or 2). It is essential to update these variables after each new molecule is added.
- 7.
- Similarly, we define two variables that store the position of the first tetrahedron in a row. It is important to update them after moving to the new line.
- 8.
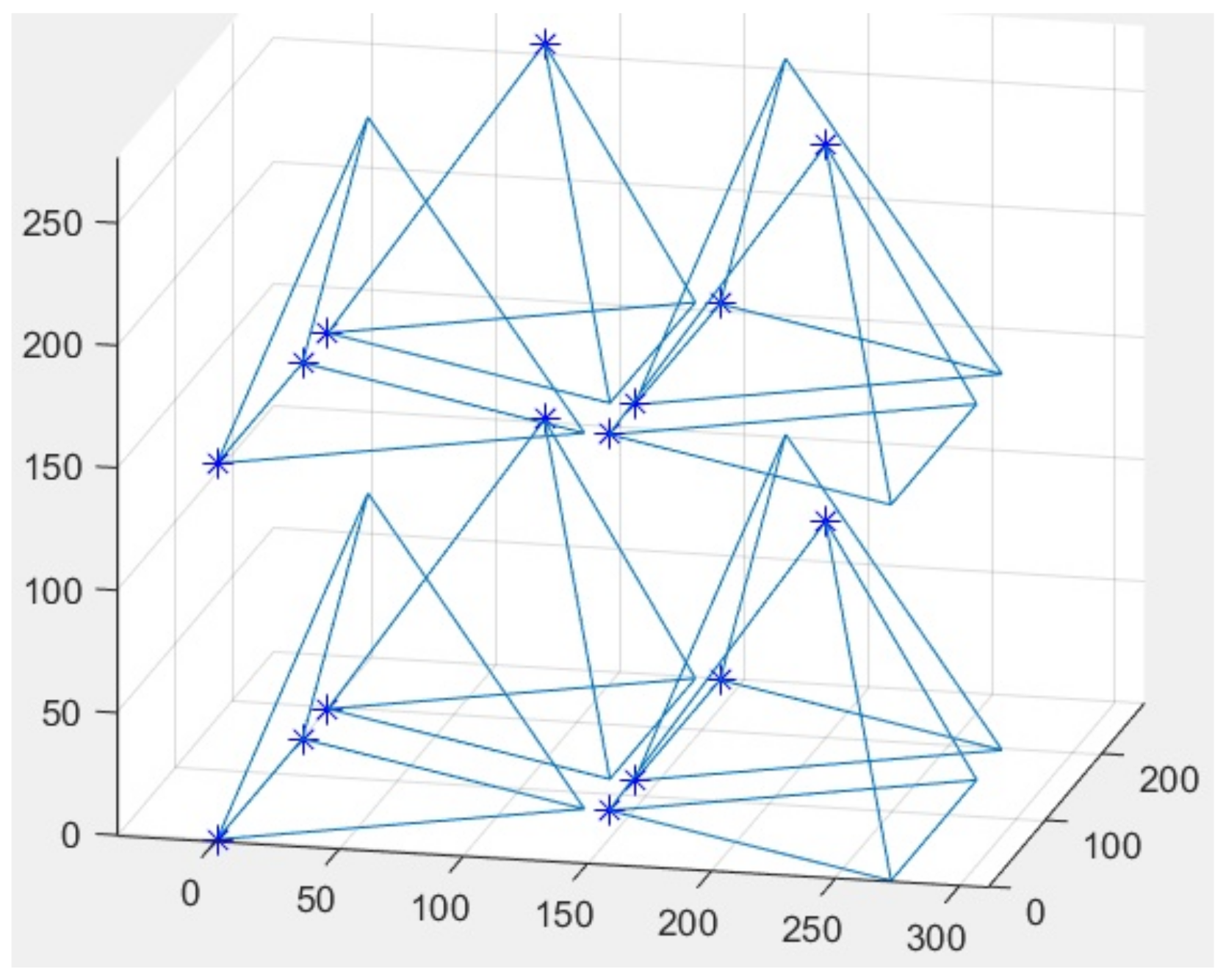
- The cycle of molecular attachment is carried out. Firstly, it is necessary to check the ability to include a new molecule in one row with the previous one. If it is possible, we add the molecule using the function that defines vertex coordinates. Steps 4–6 are repeated. Otherwise, the molecule enters the next row. Steps 4–7 are repeated. If in this instance it exceeds the allowable volume as well, the algorithm has to attach the molecule in the first row of a new layer. In this case, steps 4–7 are repeated.
3. Procedure in MATLAB Language
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novikov, A.C. Symmetry in quantum and computational chemistry. Symmetry 2020, 12, 2028. [Google Scholar] [CrossRef]
- Fischer, C.C. A Machine Learning Approach to Crystal Structure Prediction. Ph.D. Thesis, MIT, Cambridge, MA, USA, 16 August 2007. [Google Scholar]
- Braun, N.; Huttner, G. Packing and molecular shape: Layers of centred hexagons as a guiding principle. Acta Cryst. 2005, B61, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Thomasr, N.W. A novel characterization of organic molecular crystal structures for the purpose of crystal engineering. Acta Cryst. 2015, B71, 463–477. [Google Scholar]
- Falls, Z.; Avery, P.; Wang, X.; Hilleke, K.P.; Zurek, E. The XtalOpt evolutionary algorithm for crystal structure prediction. J. Phys. Chem. 2021, 125, 1601–1620. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using evolutionary algorithms: Principles and applications. J. Chem. Phys. 2006, 124, 24470. [Google Scholar]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Peresypkina, E.V.; Blatov, V.A. Topology of molecular packings in organic crystals. Acta Cryst. 2000, B56, 1035–1045. [Google Scholar] [CrossRef] [PubMed]
- Gavezzotti, A.; Lo Presti, L. Molecular dynamics simulation of organic crystals: Introducing the CLP-dyncry environment. J. Appl. Cryst. 2019, 52, 1253–1263. [Google Scholar] [CrossRef]
- Nekrasov, B.V. The Basics of General Chemistry. T.1, 3rd ed.; Chemistry: Moscow, Russia, 1973; pp. 131–134. [Google Scholar]

| X, pm | Y, pm | Z, pm | Volume, pm | Number of Molecules | Time, s |
|---|---|---|---|---|---|
| 130 | 150 | 130 | 2.535 × 106 | 1 | 0.075858 |
| 290 | 330 | 290 | 2.7753 × 107 | 8 | 0.11618 |
| 290 | 330 | 550 | 5.2635 × 107 | 16 | 0.17162 |
| 290 | 690 | 550 | 1.1006 × 108 | 48 | 0.30239 |
| 570 | 690 | 550 | 2.1632 × 108 | 96 | 0.47833 |
| 980 | 980 | 980 | 9.4119 × 108 | 441 | 2.1261 |
| 1270 | 980 | 980 | 1.2197 × 109 | 567 | 2.8386 |
| 1270 | 980 | 1250 | 1.5558 × 109 | 729 | 3.6441 |
| 1550 | 1150 | 1250 | 2.2281 × 109 | 1089 | 5.6193 |
| 2550 | 1150 | 1250 | 3.6656 × 109 | 1782 | 10.339 |
| 2550 | 1750 | 1250 | 5.5781 × 109 | 2754 | 21.02 |
| 2550 | 1750 | 1850 | 8.2556 × 109 | 3978 | 45.271 |
| 2550 | 2550 | 2550 | 1.6581 × 1010 | 8424 | 201.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lorits, E.M.; Gubar, E.A.; Novikov, A.S. Design of the Algorithm for Packaging of Water Molecules in a Fixed Volume. Symmetry 2022, 14, 2453. https://doi.org/10.3390/sym14112453
Lorits EM, Gubar EA, Novikov AS. Design of the Algorithm for Packaging of Water Molecules in a Fixed Volume. Symmetry. 2022; 14(11):2453. https://doi.org/10.3390/sym14112453
Chicago/Turabian StyleLorits, Ekaterina M., Elena A. Gubar, and Alexander S. Novikov. 2022. "Design of the Algorithm for Packaging of Water Molecules in a Fixed Volume" Symmetry 14, no. 11: 2453. https://doi.org/10.3390/sym14112453
APA StyleLorits, E. M., Gubar, E. A., & Novikov, A. S. (2022). Design of the Algorithm for Packaging of Water Molecules in a Fixed Volume. Symmetry, 14(11), 2453. https://doi.org/10.3390/sym14112453







