Particle Production in Strong Electromagnetic Fields and Local Approximations
Abstract
1. Introduction
2. External Field Configuration. Turning Points
3. Locally Constant Field Approximation
3.1. Momentum Distributions
3.2. Total Number of Pairs
4. Quantum Kinetic Equations
5. Results
5.1. Momentum Distributions for Positive
5.2. Negative . Interference Effects
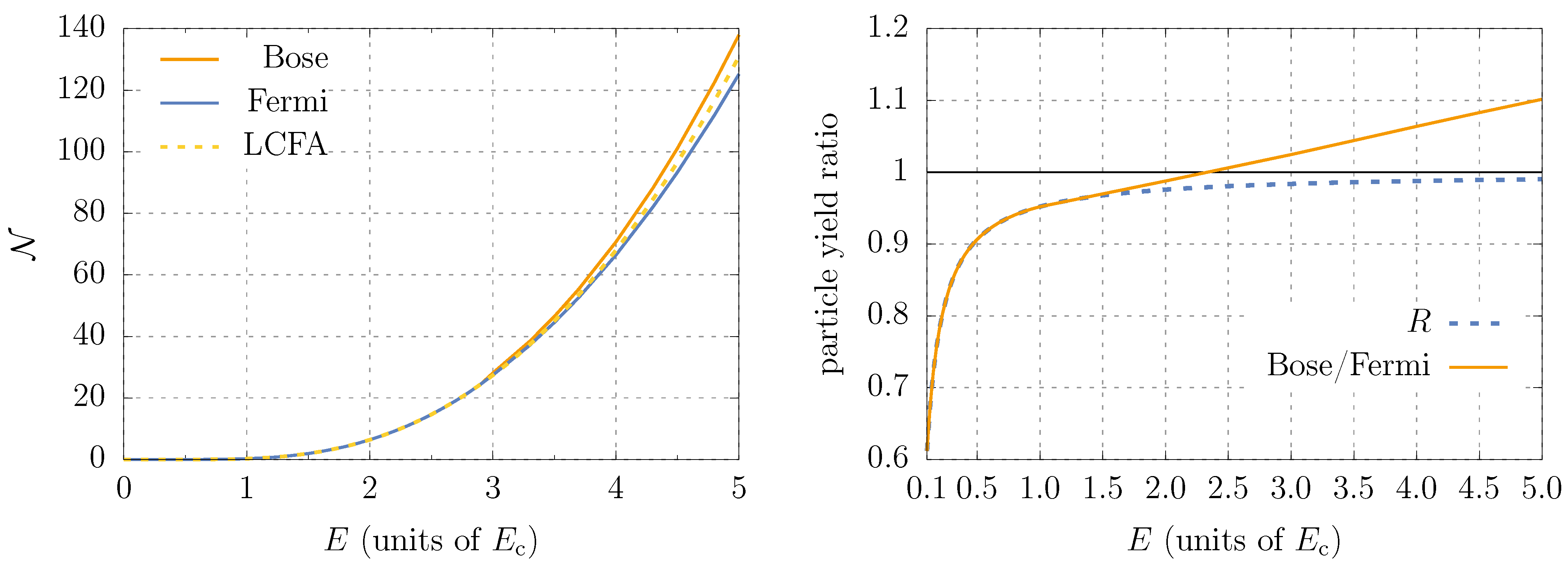
5.3. Total Number of Particles
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| QED | Quantum electrodynamics |
| LCFA | Locally constant field approximation |
| QKE | Quantum kinetic equations |
| TP | Turning point |
References
- Euler, H.; Kockel, B. Über die Streuung von Licht an Licht nach der Diracschen Theorie. Naturwissenschaften 1935, 23, 246–247. [Google Scholar] [CrossRef]
- Weisskopf, V. Über die Elektrodynamik des Vakuums auf Grund der Quantentheorie des Elektrons. Kong. Dan. Vid. Sel. Mat. Fys. Med. 1936, XIV, 1–39. [Google Scholar]
- Karplus, R.; Neuman, M. Non-linear interactions between electromagnetic fields. Phys. Rev. 1950, 80, 380–385. [Google Scholar] [CrossRef]
- Karplus, R.; Neuman, M. The scattering of light by light. Phys. Rev. 1951, 83, 776–784. [Google Scholar] [CrossRef]
- Baier, R.; Breitenlohner, P. Photon propagation in external fields. Act. Phys. Austriaca 1967, 25, 212. [Google Scholar]
- Baier, R.; Breitenlohner, P. The vacuum refraction index in the presence of external fields. Nuovo Cimento B 1967, 47, 117–120. [Google Scholar] [CrossRef]
- Aleksandrov, E.B.; Ansel’m, A.A.; Moskalev, A.N. Vacuum birefringence in an intense laser radiation field. Zh. Eksp. Teor. Fiz. 1985, 62, 1181, Translated: Sov. Phys. JETP 1985, 62, 680. [Google Scholar]
- Sauter, F. Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Z. Phys. 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664–679. [Google Scholar] [CrossRef]
- Dunne, G.V. New strong-field QED effects at extreme light infrastructure. Eur. Phys. J. D 2009, 55, 327. [Google Scholar] [CrossRef]
- Heinzl, T.; Ilderton, A. Exploring high-intensity QED at ELI. Eur. Phys. J. D 2009, 55, 359. [Google Scholar] [CrossRef]
- Marklund, M.; Lundin, J. Quantum vacuum experiments using high intensity lasers. Eur. Phys. J. D 2009, 55, 319. [Google Scholar] [CrossRef]
- Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177–1228. [Google Scholar] [CrossRef]
- Blaschke, D.; Gevorgyan, N.T.; Panferov, A.D.; Smolyansky, S.A. Schwinger effect at modern laser facilities. J. Phys. Conf. Ser. 2016, 672, 012020. [Google Scholar] [CrossRef]
- Xie, B.S.; Li, Z.L.; Tang, S. Electron-positron pair production in ultrastrong laser fields. Matter Radiat. Extremes. 2017, 2, 225–242. [Google Scholar] [CrossRef]
- Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, H.; Torgrimsson, G. Advances in QED with intense background fields. arXiv 2022, arXiv:2203.00019. [Google Scholar]
- Bunkin, F.V.; Tugov, I.I. The possibility of electron-positron pair production in vacuum when laser radiation is focussed. Dokl. Akad. Nauk SSSR 1969, 187, 541–544, Translated: Sov. Phys. Dokl. 1970, 14, 678. [Google Scholar]
- Narozhny, N.B.; Bulanov, S.S.; Mur, V.D.; Popov, V.S. e+e−-pair production by a focused laser pulse in vacuum. Phys. Lett. A 2004, 330, 1–6. [Google Scholar] [CrossRef]
- Dunne, G.V.; Wang, Q.; Gies, H.; Schubert, C. Worldline instantons and the fluctuation prefactor. Phys. Rev. D 2006, 73, 065028. [Google Scholar] [CrossRef]
- Hebenstreit, F.; Alkofer, R.; Gies, H. Pair production beyond the Schwinger formula in time-dependent electric fields. Phys. Rev. D 2008, 78, 061701(R). [Google Scholar] [CrossRef]
- Bulanov, S.S.; Mur, V.D.; Narozhny, N.B.; Nees, J.; Popov, V.S. Multiple colliding electromagnetic pulses: A way to lower the threshold of e+e− pair production from vacuum. Phys. Rev. Lett. 2010, 104, 220404. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M. Vacuum instability in slowly varying electric fields. Phys. Rev. D 2017, 95, 076013. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Plunien, G.; Shabaev, V.M. Locally-constant field approximation in studies of electron-positron pair production in strong external fields. Phys. Rev. D 2019, 99, 016020. [Google Scholar] [CrossRef]
- Sevostyanov, D.G.; Aleksandrov, I.A.; Plunien, G.; Shabaev, V.M. Total yield of electron-positron pairs produced from vacuum in strong electromagnetic fields: Validity of the locally constant field approximation. Phys. Rev. D 2021, 104, 076014. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Sevostyanov, D.G.; Shabaev, V.M. Schwinger particle production: Rapid switch off of the external field versus dynamical assistance. arXiv 2022, arXiv:2210:15626. [Google Scholar]
- Grib, A.A.; Mamaev, V.M.; Mostepanenko, V.M. Vacuum Quantum Effects in Strong External Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1994. [Google Scholar]
- Schmidt, S.M.; Blaschke, D.; Röpke, G.; Smolyansky, S.A.; Prozorkevich, A.V.; Toneev, V.D. A quantum kinetic equation for particle production in the Schwinger mechanism. Int. J. Mod. Phys. E 1998, 7, 709–722. [Google Scholar] [CrossRef]
- Kluger, Y.; Mottola, E.; Eisenberg, J.M. Quantum Vlasov equation and its Markov limit. Phys. Rev. D 1998, 58, 125015. [Google Scholar] [CrossRef]
- Schmidt, S.; Blaschke, D.; Röpke, G.; Prozorkevich, A.V.; Smolyansky, S.A.; Toneev, V.D. Non-Markovian effects in strong-field pair creation. Phys. Rev. D 1999, 59, 094005. [Google Scholar] [CrossRef]
- Hebenstreit, F.; Alkofer, R.; Dunne, G.V.; Gies, H. Momentum signatures for Schwinger pair production in short laser pulses. Phys. Rev. Lett. 2009, 102, 150404. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Gelfer, E.G.; Korolev, K.Y.; Smolyansky, S.A. Kinetic equation approach to pair production by a time-dependent electric field. Phys. Rev. D 2011, 83, 025011. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Dmitriev, V.V.; Sevostyanov, D.G.; Smolyansky, S.A. Kinetic description of vacuum e+e− production in strong electric fields of arbitrary polarization. Eur. Phys. J. Spec. Top. 2020, 229, 3469–3485. [Google Scholar] [CrossRef]
- Kluger, Y.; Eisenberg, J.M.; Svetitsky, B.; Cooper, F.; Mottola, E. Pair production in a strong electric field. Phys. Rev. Lett. 1991, 67, 2427–2430. [Google Scholar] [CrossRef]
- Kluger, Y.; Eisenberg, J.M.; Svetitsky, B.; Cooper, F.; Mottola, E. Fermion pair production in a strong electric field. Phys. Rev. D 1992, 45, 4659–4671. [Google Scholar] [CrossRef]
- Nikishov, A.I. Pair production by a constant external field. Zh. Eksp. Teor. Fiz. 1969, 57, 1210, Translated: Sov. Phys. JETP 1970, 30, 660. [Google Scholar]
- Fradkin, E.S.; Gitman, D.M.; Shvartsman, S.M. Quantum Electrodynamics with Unstable Vacuum; Springer: Berlin, Germany, 1991. [Google Scholar]
- Ilderton, A. Physics of adiabatic particle number in the Schwinger effect. Phys. Rev. D 2022, 105, 016021. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Panferov, A.D.; Smolyansky, S.A. Radiation signal accompanying the Schwinger effect. Phys. Rev. A 2021, 103, 053107. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M. Vacuum instability in external fields. Phys. Rev. D 1996, 53, 7162–7175. [Google Scholar] [CrossRef]
- Dumlu, C.K.; Dunne, G.V. Stokes phenomenon and Schwinger vacuum pair production in time-dependent laser pulses. Phys. Rev. Lett. 2010, 104, 250402. [Google Scholar] [CrossRef]
- Dumlu, C.K.; Dunne, G.V. Interference effects in Schwinger vacuum pair production for time-dependent laser pulses. Phys. Rev. D 2011, 83, 065028. [Google Scholar] [CrossRef]
- Dumlu, C.K.; Dunne, G.V. Complex worldline instantons and quantum interference in vacuum pair production. Phys. Rev. D 2011, 84, 125023. [Google Scholar] [CrossRef]
- Akkermans, E.; Dunne, G.V. Ramsey fringes and time-domain multiple-slit interference from vacuum. Phys. Rev. Lett. 2012, 108, 030401. [Google Scholar] [CrossRef] [PubMed]
- Aleksandrov, I.A.; Plunien, G.; Shabaev, V.M. Pulse shape effects on the electron-positron pair production in strong laser fields. Phys. Rev. D 2017, 95, 056013. [Google Scholar] [CrossRef]
- Aleksandrov, I.A.; Kohlfürst, C. Pair production in temporally and spatially oscillating fields. Phys. Rev. D 2020, 101, 096009. [Google Scholar] [CrossRef]
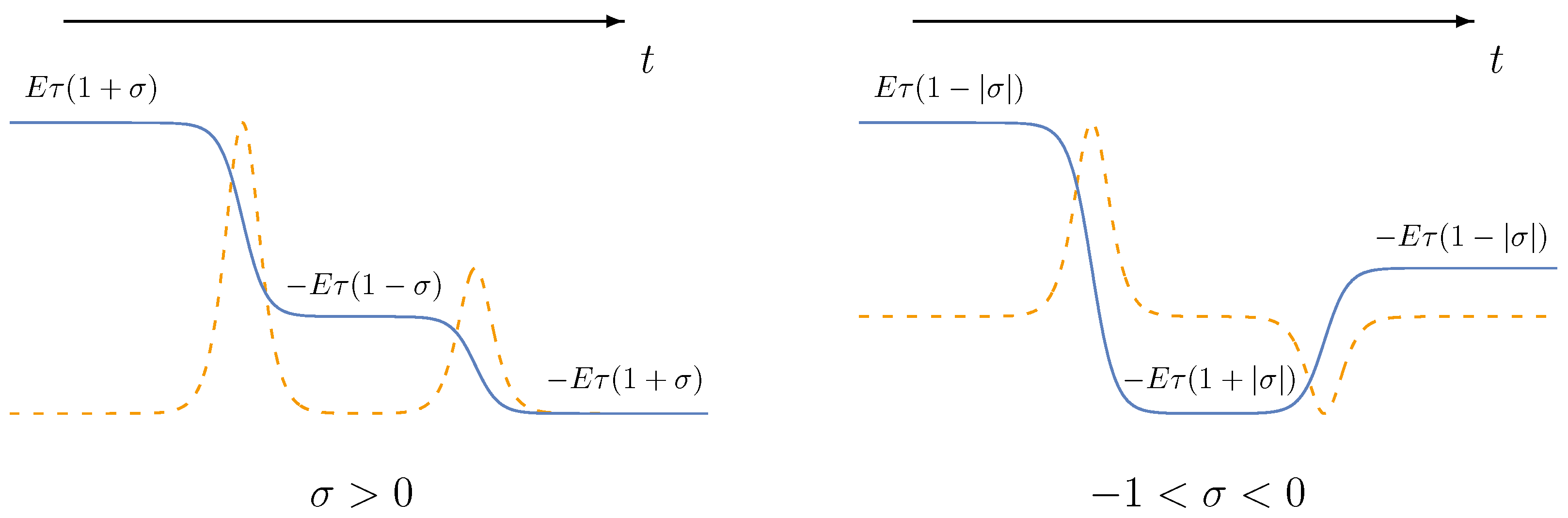
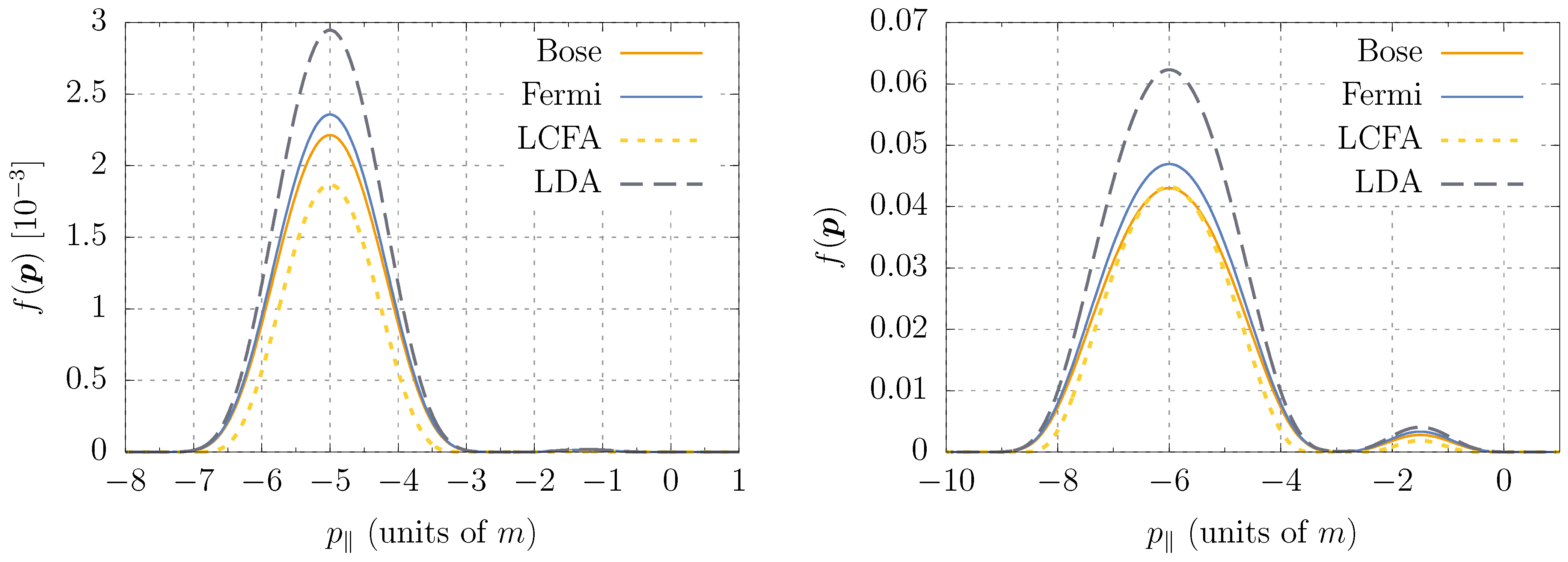

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleksandrov, I.A.; Sevostyanov, D.G.; Shabaev, V.M. Particle Production in Strong Electromagnetic Fields and Local Approximations. Symmetry 2022, 14, 2444. https://doi.org/10.3390/sym14112444
Aleksandrov IA, Sevostyanov DG, Shabaev VM. Particle Production in Strong Electromagnetic Fields and Local Approximations. Symmetry. 2022; 14(11):2444. https://doi.org/10.3390/sym14112444
Chicago/Turabian StyleAleksandrov, Ivan A., Denis G. Sevostyanov, and Vladimir M. Shabaev. 2022. "Particle Production in Strong Electromagnetic Fields and Local Approximations" Symmetry 14, no. 11: 2444. https://doi.org/10.3390/sym14112444
APA StyleAleksandrov, I. A., Sevostyanov, D. G., & Shabaev, V. M. (2022). Particle Production in Strong Electromagnetic Fields and Local Approximations. Symmetry, 14(11), 2444. https://doi.org/10.3390/sym14112444




