Some New Results for (α, β)-Admissible Mappings in $\mathbb{F}$-Metric Spaces with Applications to Integral Equations

Abstract

In this paper, we consider and extend some fixed point results in $\mathbb{F}$-complete $\mathbb{F}$-metric spaces by relaxing the symmetry of complete metric spaces. We generalize $\left(\alpha ,\beta \right)$-admissible mappings in the setting of $\mathbb{F}$-metric spaces. The derived results are supplemented with suitable examples, and the obtained results are applied to find the existence of the solution to the integral equation. The analytical results are compared through numerical simulation. We pose certain open problems for extending and applying our results in the future.

1. Introduction and Preliminaries

In functional and nonlinear analysis, the standard metric space is an extremely useful tool. Several generalizations of conventional metric spaces have surfaced in recent years. The famous Banach contraction principle [1] of 1922 laid the foundation of modern metric fixed point theory. Many mathematicians generalized the contraction mapping theorem (CMT) in various types of metric spaces using different contractive conditions. In the sequel, in 1989, Bakhtin [2] developed the notion of b-metric spaces and proposed the contraction mapping in b-metric spaces as an extension of the CMT. Matthews [3] proposed the concept of a partial metric space, which is a generalization of the standard metric space. Subsequently, in 2007, Huang and Zhang [4] defined the cone metric space and substituted real numbers by the ordered Banach space. Many fixed point theorems of contractive mapping on cone metric spaces have been proven in the setting of cone metric spaces. We recommend readers see [5,6,7,8,9] and several references therein for quantitative information. Recently, in 2018, Jleli and Samet proposed the notion of the $\mathbb{F}$-metric space in [10]. Since then, several fixed point results have been established in the setting of the $\mathbb{F}$-metric space. In 2019, Mitrović et al. [11] established fixed point results of Banach, Jungck, Reich, and Berinde, on the $\mathbf{F}$-metric space; see also [12,13,14,15,16,17,18]. In the sequel, we recall some of the basic concepts and outcomes that are required in our main results.

Throughout this paper, we indicate $[0,+\infty )$ as the set of non-negative real numbers ${\Re }_0^{+}$, and $(-\infty ,+\infty )$ indicate the real numbers ℜ, respectively.

Definition 1. 

Let $\mathbb{F}$ be the set of functions $\mathfrak{g}:{\Re }_0^{+}\to \Re$ satisfying the following conditions:

$\left({\mathbb{F}}_1\right)$$\mathfrak{g}$ is non-decreasing,

$\left({\mathbb{F}}_2\right)$ For every sequence $\left\{{\mathfrak{p}}_{\sigma }\right\}\subset {\Re }_0^{+}$, we have

${lim}_{\sigma \to +\infty }{\mathfrak{p}}_{\sigma }=0ifandonlyif{lim}_{\sigma \to +\infty }\mathfrak{g}\left({\mathfrak{p}}_{\sigma }\right)=-\infty .$

Definition 2 

([10]). Let $\Gamma$ be a non-void set. A function $\mathcal{V}:\Gamma \times \Gamma \to {\Re }_0^{+}$ is said to be an $\mathbb{F}$-metric (${\mathbb{F}}_{-M}$) on Γ if there exists $\left(\mathfrak{g},\alpha \right)\in \mathbb{F}\times {\Re }_0^{+}$ such that $\forall \phi ,\mu \in \Gamma$, the following hypotheses are satisfied:

• $\left({\mathcal{V}}_1\right) \mathcal{V}(\phi ,\mu )=0$ if and only if $\phi =\mu$;
• $\left({\mathcal{V}}_2\right) \mathcal{V}(\phi ,\mu )=\mathcal{V}(\mu ,\phi )$;
• $\left({\mathcal{V}}_3\right)$ For every $N\in \mathbb{N},N\ge 2$, and for every ${\left\{{\mathfrak{u}}_i\right\}}_{i=1}^N\subset \Gamma$ with $\left({\mathfrak{u}}_1,{\mathfrak{u}}_N\right)=\left(\phi ,\mu \right)$, we have

  $$\begin{array}{c}\hfill \mathcal{V}\left(\phi ,\mu \right)>0\Rightarrow \mathfrak{g}\left(\mathcal{V}\left(\phi ,\mu \right)\right)\le \mathfrak{g}\left({\displaystyle \sum _{i=1}^{N-1}}\mathcal{V}\left({\mathfrak{u}}_i,{\mathfrak{u}}_{i+1}\right)\right)+\alpha .\end{array}$$

Then, the pair $\left(\Gamma ,\mathcal{V}\right)$ is said to be the $\mathbb{F}$-metric space (${\mathbb{F}}_{-MS}$).

Example 1 

([10]). Let $\Gamma =\Re$. Define a mapping $\mathcal{V}:\Gamma \times \Gamma \to {\Re }_0^{+}$ by

$$\begin{array}{c}\hfill \mathcal{V}\left(\phi ,\mu \right)=\left\{\begin{array}{c}{\left(\phi -\mu \right)}^2,\left(\phi ,\mu \right)\in [0,4)\times [0,4)\hfill \\ \left|\phi -\mu \right|,otherwise,\hfill \end{array}\right.\end{array}$$

and let $f\left(\mathfrak{p}\right)=ln\mathfrak{p}$ for all $\mathfrak{p}>0$ and $\alpha =ln3.$ Then, $\mathcal{V}$ is an ${\mathbb{F}}_{-M}$ on $\Gamma .$ Since $4=\mathcal{V}\left(1,3\right)\ge \mathcal{V}\left(1,2\right)+\mathcal{V}\left(2,3\right)=2$, then $\mathcal{V}$ is not a metric on $\Gamma .$

Example 2 

([10]). Let $\Gamma =\Re$ and $\mathcal{V}:\Gamma \times \Gamma \to {\Re }_0^{+}$ be defined as follows:

$$\begin{array}{c}\hfill \mathcal{V}\left(\phi ,\mu \right)=\left\{\begin{array}{c}{e}^{\left|\phi -\mu \right|},\phi \ne \mu ,\hfill \\ 0,\phi =\mu .\hfill \end{array}\right.\end{array}$$

Then, $\mathcal{V}$ is an ${\mathbb{F}}_{-M}$ on $\Gamma .$ Since $e^2=\mathcal{V}\left(1,3\right)\ge \mathcal{V}\left(1,2\right)+\mathcal{V}\left(2,3\right)=2e,$ then $\mathcal{V}$ is not a metric on $\Gamma .$

Definition 3 

([10]). Let $\left(\Gamma ,\mathcal{V}\right)$ be an ${\mathbb{F}}_{-MS}$ space and $\left\{{\phi }_{\sigma }\right\}$ be a sequence on $\Gamma$:

(1)

A sequence $\left\{{\phi }_{\sigma }\right\}$ is called $\mathbb{F}$-convergent to $\phi \in \Gamma$ if ${lim}_{\sigma \to +\infty }\mathcal{V}\left({\phi }_{\sigma },\phi \right)=0.$

(2)

A sequence $\left\{{\phi }_{\sigma }\right\}$ is called $\mathbb{F}$-Cauchy if ${lim}_{\sigma ,m\to +\infty }\mathcal{V}\left({\phi }_{\sigma },{\phi }_m\right)=0.$

(3)

The ${\mathbb{F}}_{-M}$ space $\left(\Gamma ,\mathcal{V}\right)$ is said to be $\mathbb{F}$-complete if every $\mathbb{F}$-Cauchy sequence in Γ is $\mathbb{F}$-convergent to some element in $\Gamma .$

Lemma 1 

([11]). Let $\left\{{\phi }_{\sigma }\right\}$ be a sequence in the ${\mathbb{F}}_{-MS}$ space $\left(\Gamma ,\mathcal{V}\right)$ such that

$$\begin{array}{c}\hfill \mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)\le \lambda \mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right),forall\sigma \in \mathbb{N},\end{array}$$

where $0\le \lambda <1.$ Then, $\left\{{\phi }_{\sigma }\right\}$ is an $\mathbb{F}$-Cauchy sequence in $\left(\Gamma ,\mathcal{V}\right)$.

Theorem 1 

([10]). Let $\left(\Gamma ,\mathcal{V}\right)$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$, and let $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a self-mapping satisfying

$$\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \alpha \mathcal{V}\left(\phi ,\mu \right),forall\phi ,\mu \in \Gamma ,\left(1\right)$$

(1)

where $0\le \alpha <1.$ Then, Υ has a unique fixed point.

We denote by $\mathsf{\Psi }$ the set of all non-decreasing functions $\psi :{\Re }_0^{+}\to [0,+\infty )$ such that, for all $\mathfrak{p}>0$, we have ${\displaystyle \sum _{\sigma =1}^{+\infty }}{\psi }^{\sigma }\left(\mathfrak{p}\right)<+\infty ,$ where ${\psi }^{\sigma }$ is the ${\sigma }^{th}$ iterate of $\psi .$ These functions are known as comparison functions. Furthermore, $\psi \left(\mathfrak{p}\right)<\mathfrak{p}$ for all $\mathfrak{p}>0.$

Samet et al. [19] first proposed the concept of an $\alpha$-$\psi$-contraction map. They established the existence and uniqueness of fixed points in the metric space for such mappings. Alizadeh et al. [20] proposed the idea of $\left(\alpha ,\beta \right)$- $\left(\psi ,\phi \right)$-contraction and weak $\alpha$- $\beta$-$\psi$-rational contractive maps through cyclic the $\left(\alpha ,\beta \right)$-admissible map and established fixed point theorems for this class of maps in the setting of the metric space.

Definition 4 

([20]). Let ${\rm Y}$ be a self-mapping on $\Gamma$ and $\alpha ,\beta :\Gamma \to {\Re }_0^{+}.$ We say that the mapping ${\rm Y}$ is a cyclic $\left(\alpha ,\beta \right)$-admissible mapping if:

(i) 

$\alpha \left(\phi \right)\ge 1$ for some $\phi \in \Gamma$ implies $\beta \left(\mathsf{{\rm Y}}\phi \right)\ge 1;$

(ii) 

$\beta \left(\phi \right)\ge 1$ for some $\phi \in \Gamma$ implies $\alpha \left(\mathsf{{\rm Y}}\phi \right)\ge 1.$

For a deep insight into the fixed point results on various generalized metric spaces, the reader can see, for example, [3,4,5,6,7,8,9,11,19,20,21,22,23], while more new results on ${\mathbb{F}}_{-MS}$ can be found in [24,25,26,27,28,29].

More recently, Hussain and Kanwal [30] introduced the concept of the $\alpha$-$\psi$-contraction in $\mathbb{F}$-metric spaces and demonstrated fixed point and linked fixed point results. Inspired by this, in our work, we introduce a new type of contraction map and establish a fixed point result in the setting of ${\mathbb{F}}_{-MS}$ generalizing some proven results of the past. The rest of the paper is organized as follows: In Section 2, we present our main results by introducing the $\left(\alpha ,\beta \right)$-admissible map in the setting of ${\mathbb{F}}_{-MS}$ and prove the fixed point results. Our results generalize and corollorizesome proven results in the past. In Section 3, the derived results are applied to find the analytical solution to the integral equation. We validate the analytical solution through numerical simulation. Finally, in Section 4, we propose some open problems for future research in this arena.

2. Main Results

We begin the section by giving the following definition.

Definition 5. 

Let $\left(\Gamma ,\mathcal{V}\right)$ be an ${\mathbb{F}}_{-MS},\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a cyclic $\left(\alpha ,\beta \right)$-admissible map, and $\psi \in \mathsf{\Psi }.$ We call Υ an $\left(\alpha ,\beta \right)$-${\psi }_M$-admissible map if

$$\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1implies\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \psi \left(M\left(\phi ,\mu \right)\right),forall\phi ,\mu \in \Gamma ,$$

(2)

where

$$\begin{array}{c}\hfill M\left(\phi ,\mu \right)=max\left\{\mathcal{V}\left(\phi ,\mu \right),\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\phi \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\mu \right)}{1+\mathcal{V}\left(\phi ,\mu \right)},\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\mu \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\phi \right)}{1+\mathcal{V}\left(\phi ,\mu \right)}\right\}.\end{array}$$

Theorem 2. 

Let $\left(\Gamma ,\mathcal{V}\right)$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$ and $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be an $\left(\alpha ,\beta \right)$-${\psi }_M$-admissible map. Assume that the following conditions hold:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1;$

(ii) 

Υ is continuous or;

(iii) 

If $\left\{{\phi }_{\sigma }\right\}$ is a sequence in Γ such that ${\phi }_{\sigma }\to \phi$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, Υ has a unique fixed point.

Proof. 

Let ${\phi }_0\in \Gamma$, and consider the sequence $\left\{{\phi }_{\sigma }\right\}$ in which ${\phi }_{\sigma }=\mathsf{{\rm Y}}{\phi }_{\sigma -1}$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ Since $\alpha \left({\phi }_0\right)\ge 1$ and $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ is a cyclic $\left(\alpha ,\beta \right)$-admissible mapping, then $\beta \left({\phi }_1\right)=\beta \left(\mathsf{{\rm Y}}{\phi }_0\right)\ge 1$, which implies $\alpha \left({\phi }_2\right)$ = $\alpha \left(\mathsf{{\rm Y}}{\phi }_1\right)\ge 1.$ By continuing this process, we have $\alpha \left({\phi }_{2\sigma }\right)\ge 1$ and $\beta \left({\phi }_{2\sigma -1}\right)\ge 1.$ Since $\mathsf{{\rm Y}}$ is a cyclic $\left(\alpha ,\beta \right)$-admissible mapping and $\beta \left({\phi }_0\right)\ge 1$, we conclude that $\beta \left({\phi }_{2\sigma }\right)\ge 1$ and $\alpha \left({\phi }_{2\sigma -1}\right)\ge 1$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ Hence, we obtain $\alpha \left({\phi }_{\sigma }\right)\ge 1$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ Since $\alpha \left({\phi }_{\sigma -1}\right)\beta \left({\phi }_{\sigma }\right)\ge 1,$ from the inequality (2), we have

$$\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)=\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }_{\sigma -1},\mathsf{{\rm Y}}{\phi }_{\sigma }\right)\le \psi \left(M\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\right),$$

where

$$\begin{array}{cc}\hfill M\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)& =max\left\{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right),\frac{\mathcal{V}\left({\phi }_{\sigma -1},\mathsf{{\rm Y}}{\phi }_{\sigma -1}\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }_{\sigma }\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)},\right.\hfill \\ & \left.\frac{\mathcal{V}\left({\phi }_{\sigma -1},\mathsf{{\rm Y}}{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }_{\sigma -1}\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)}\right\}\hfill \\ & =max\left\{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right),\frac{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)}\right\},\hfill \end{array}$$

for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ If $M\left({\phi }_{\sigma -1},{\phi }_n\right)=\frac{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)},$ we have

$$M\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\le \psi \left(\frac{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)}\right)<\frac{\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)}{1+\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)}$$

which is a contradiction. Hence, $\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)\le \psi \left(\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\right)$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ Inductively, we obtain $\mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)\le {\psi }^{\sigma }\left(\mathcal{V}\left({\phi }_0,{\phi }_1\right)\right)\forall \sigma \in \mathbb{N}\cup \left\{0\right\}.$ Now, let $\left(\mathfrak{g},\alpha \right)\in \mathbb{F}\times [0,+\infty )$ such that $\left({\mathcal{V}}_3\right)$ holds, and let $\epsilon >0$ be fixed. From $\left({\mathbb{F}}_2\right)$, we conclude that there exists $\delta >0$ such that

$$0<\mathfrak{p}<\delta \Rightarrow \mathfrak{g}\left(\mathfrak{p}\right)<\mathfrak{g}\left(\epsilon \right)-\alpha .\left(3\right)$$

(3)

Since $\psi \in \mathsf{\Psi },$ there exists some $N_0\in \mathbb{N}$ such that $0<{\displaystyle \sum _{\sigma =N_0}^{+\infty }}{\psi }^{\sigma }\left(\mathcal{V}\left({\phi }_0,{\phi }_1\right)\right)<\delta .$ Hence, from (3) and $\left({\mathbb{F}}_1\right),$ we obtain

$$f\left({\displaystyle \sum _{i=\sigma }^{m-1}}{\psi }^i\left(\mathcal{V}\left({\phi }_0,{\phi }_1\right)\right)\right)\le f\left({\displaystyle \sum _{i=N_0}^{+\infty }}{\psi }^{\sigma }\left(\mathcal{V}\left({\phi }_0,{\phi }_1\right)\right)\right)<f\left(\epsilon \right)-\alpha ,$$

(4)

where $m>\sigma \ge N_0$. From $\left({\mathcal{V}}_3\right)$ and (4) for $\mathcal{V}\left({\phi }_m,{\phi }_{\sigma }\right)>0,m>\sigma \ge N_0,$ we obtain

$$\begin{array}{cc}\hfill f\left(\mathcal{V}\left({\phi }_m,{\phi }_{\sigma }\right)\right)& \le f\left({\displaystyle \sum _{i=\sigma }^{m-1}}\mathcal{V}\left({\phi }_i,{\phi }_{i+1}\right)\right)+\alpha \hfill \\ & \le f\left({\displaystyle \sum _{i=\sigma }^{m-1}}{\psi }^i\left(\mathcal{V}\left({\phi }_i,{\phi }_{i+1}\right)\right)\right)+\alpha \hfill \\ & <f\left(\epsilon \right),\hfill \end{array}$$

and using $\left({\mathbb{F}}_1\right),$ we have $\mathcal{V}\left({\phi }_m,{\phi }_{\sigma }\right)<\epsilon .$ Hence, $\left\{{\phi }_{\sigma }\right\}$ is an $\mathbb{F}$-Cauchy sequence in the $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$$\Gamma ,$ so there exists ${\phi }^{*}\in \Gamma$ such that ${lim}_{\sigma \to +\infty }\mathcal{V}\left({\phi }_{\sigma },{\phi }^{*}\right)=0.$ Since $\mathsf{{\rm Y}}$ is continuous, then we have

$$\mathsf{{\rm Y}}{\phi }^{*}=\mathsf{{\rm Y}}\left(\underset{\sigma \to +\infty }{lim}{\phi }_{\sigma }\right)=\underset{\sigma \to +\infty }{lim}\mathsf{{\rm Y}}{\phi }_{\sigma }=\underset{\sigma \to +\infty }{lim}{\phi }_{\sigma +1}={\phi }^{*},$$

that is ${\phi }^{*}$ is a fixed point of $\mathsf{{\rm Y}}.$ Next, we suppose that (iii) holds,

that is

$$\begin{array}{c}\hfill \alpha \left({\phi }_{\sigma }\right)\beta \left({\phi }^{*}\right)\ge 1.\end{array}$$

From (2), we have

$$\begin{array}{cc}\hfill & \mathfrak{g}\left(\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }^{*},{\phi }^{*}\right)\right)\hfill \\ & \le \mathfrak{g}\left(\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }^{*},\mathsf{{\rm Y}}{\phi }_{\sigma }\right)+\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }_{\sigma },{\phi }^{*}\right)\right)+\alpha \hfill \\ & \le f\left(\psi \left(max\left\{\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right),\frac{\mathcal{V}\left({\phi }^{*},\mathsf{{\rm Y}}{\phi }^{*}\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }_{\sigma }\right)}{1+\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right)},\frac{\mathcal{V}\left({\phi }^{*},\mathsf{{\rm Y}}{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }^{*}\right)}{1+\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right)}\right\}+\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }_n,{\phi }^{*}\right)\right)\right)+\alpha .\hfill \end{array}$$

Since ${\phi }_{\sigma }\to {\phi }^{*}$ as $\sigma \to +\infty ,$ from ${\mathbb{F}}_2,$ we have

$$\underset{\sigma \to +\infty }{lim}f\left(\psi \left(max\left\{\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right),\frac{\mathcal{V}\left({\phi }^{*},\mathsf{{\rm Y}}{\phi }^{*}\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }_{\sigma }\right)}{1+\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right)},\frac{\mathcal{V}\left({\phi }^{*},\mathsf{{\rm Y}}{\phi }_{\sigma }\right)\mathcal{V}\left({\phi }_{\sigma },\mathsf{{\rm Y}}{\phi }^{*}\right)}{1+\mathcal{V}\left({\phi }^{*},{\phi }_{\sigma }\right)}\right\}\right)\right)+\alpha =-\infty ,$$

which is a contradiction. Hence, $\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }^{*},{\phi }^{*}\right)=0,$ that is $\mathsf{{\rm Y}}{\phi }^{*}={\phi }^{*}.$ To prove the unique fixed point, suppose that $\phi$ and $\mu$ are two fixed points of $\mathsf{{\rm Y}}.$ Since $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$, it follows from (2) that

$$\begin{array}{cc}\hfill \mathcal{V}\left(\phi ,\mu \right)& =\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\hfill \\ & \le \psi \left(M\left(\phi ,\mu \right)\right)\hfill \\ & =\psi \left(max\left\{\mathcal{V}\left(\phi ,\mu \right),\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\phi \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\mu \right)}{1+\mathcal{V}\left(\phi ,\mu \right)},\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\mu \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\phi \right)}{1+\mathcal{V}\left(\phi ,\mu \right)}\right\}\right)\hfill \\ & =\psi \left(\mathcal{V}\left(\phi ,\mu \right)\right)\hfill \\ & <\mathcal{V}\left(\phi ,\mu \right),\hfill \end{array}$$

which is a contradiction, that is $\mathcal{V}\left(\phi ,\mu \right)=0$ and $\phi =\mu$. □

The following are the consequences of Theorem 2.

Corollary 1. 

Let $(\Gamma ,\mathcal{V})$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$, and let $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a cyclic $(\alpha ;\beta )$-admissible mapping be such that

$${\left(\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)+l\right)}^{\alpha \left(\phi \right)\beta \left(\mu \right)}\le \psi \left(M\left(\phi ,\mu \right)\right)+l,fororall\phi ,\mu \in \Gamma ,$$

(5)

where

$$\begin{array}{c}\hfill M\left(\phi ,\mu \right)=max\left\{\mathcal{V}\left(\phi ,\mu \right),\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\phi \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\mu \right)}{1+\mathcal{V}\left(\phi ,\mu \right)},\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\mu \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\phi \right)}{1+\mathcal{V}\left(\phi ,\mu \right)}\right\},\end{array}$$

and $\psi \in \mathsf{\Psi }$ and $l>1.$ Suppose that the following conditions are satisfied:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1;$

(ii) 

$\mathsf{{\rm Y}}$ is continuous or;

(iii) 

If $\left\{{\phi }_{\sigma }\right\}$ is a sequence in $\Gamma$ such that ${\phi }_n\to \phi$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, $\mathsf{{\rm Y}}$ has a fixed point. Moreover, if $\alpha \left(\phi \right)\ge 1$ and $\beta \left(\mu \right)\ge 1,$ for all $\phi ,\mu \in Fix\left(T\right)$, then $\mathsf{{\rm Y}}$ has a unique fixed point.

Proof. 

Let $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$ for $\phi ,\mu \in \Gamma .$ Then, from (5), we have

$$\begin{array}{cc}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)+l& \le {\left(\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)+l\right)}^{\alpha \left(\phi \right)\beta \left(\mu \right)}\hfill \\ & \le \psi \left(M\left(\phi ,\mu \right)\right)+l.\hfill \end{array}$$

Then, we obtain

$$\begin{array}{c}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \psi \left(M\left(\phi ,\mu \right)\right).\end{array}$$

This implies that Equation (2) is satisfied. Therefore, the proof follows from Theorem 2. □

Corollary 2. 

Let $(\Gamma ;\mathcal{V})$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$, and let $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a cyclic $(\alpha ;\beta )$-admissible map be such that

$${\left(\alpha \left(\phi \right)\beta \left(\mu \right)+l\right)}^{\mathcal{V}\left(\mathsf{{\rm Y}}\left(\phi \right),\mathsf{{\rm Y}}\left(\mu \right)\right)}\le 2^{\psi \left(M\left(\phi ,\mu \right)\right)},\phi ,\mu \in \Gamma ,$$

(6)

where

$$\begin{array}{c}\hfill M\left(\phi ,\mu \right)=max\left\{\mathcal{V}\left(\phi ,\mu \right),\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\phi \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\mu \right)}{1+\mathcal{V}\left(\phi ,\mu \right)},\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\mu \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\phi \right)}{1+\mathcal{V}\left(\phi ,\mu \right)}\right\},\end{array}$$

and $\psi \in \mathsf{\Psi }.$ Suppose that the following conditions are satisfied:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1;$

(ii) 

$\mathsf{{\rm Y}}$ is continuous or;

(iii) 

If ${\phi }_{\sigma }$ is a sequence in $\Gamma$ such that ${\phi }_{\sigma }\to \phi$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, $\mathsf{{\rm Y}}$ has a fixed point. Moreover, if $\alpha \left(\phi \right)\ge 1$ and $\beta \left(\mu \right)\ge 1$ for all $\phi ,\mu \in Fix\left(T\right)$, then $\mathsf{{\rm Y}}$ has a unique fixed point.

Proof. 

Let $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$ for $\phi ,\mu \in \Gamma .$ Then, from (6), we have

$$\begin{array}{cc}\hfill 2^{\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)}& \le {\left(\alpha \left(\phi \right)\beta \left(\mu \right)+l\right)}^{\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)}\hfill \\ & \le 2^{\psi \left(M\left(\phi ,\mu \right)\right)}.\hfill \end{array}$$

Then, we obtain

$$\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \psi \left(M\left(\phi ,\mu \right)\right).$$

This implies that Equation (2) is satisfied, and so, the proof follows from Theorem 2. □

Corollary 3. 

Let $(\Gamma ,\mathcal{V})$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$, and let $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a cyclic $(\alpha ;\beta )$-admissible map be such that

$$\alpha \left(\phi \right)\beta \left(\mu \right)\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \psi \left(M\left(\phi ,\mu \right)\right),forall\phi ,\mu \in \Gamma ,$$

(7)

where

$$\begin{array}{c}\hfill M\left(\phi ,\mu \right)=max\left\{\mathcal{V}\left(\phi ,\mu \right),\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\phi \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\mu \right)}{1+\mathcal{V}\left(\phi ,\mu \right)},\frac{\mathcal{V}\left(\phi ,\mathsf{{\rm Y}}\mu \right)\mathcal{V}\left(\mu ,\mathsf{{\rm Y}}\phi \right)}{1+\mathcal{V}\left(\phi ,\mu \right)}\right\},\end{array}$$

and $\psi \in \mathsf{\Psi }.$ Suppose that the following conditions are satisfied:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1;$

(ii) 

$\mathsf{{\rm Y}}$ is continuous or;

(iii) 

If ${\phi }_{\sigma }$ is a sequence in $\Gamma$ such that ${\phi }_{\sigma }\to \phi$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, $\mathsf{{\rm Y}}$ has a unique fixed point.

Proof. 

Let $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$ for $\phi ,\mu \in \Gamma .$ Then, from (7), we have

$$\begin{array}{cc}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)& \le \alpha \left(\phi \right)\beta \left(\mu \right)\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\hfill \\ & \le \psi \left(M\left(\phi ,\mu \right)\right).\hfill \end{array}$$

Then, we obtain

$$\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le \psi \left(M\left(\phi ,\mu \right)\right).$$

This implies that Equation (2) is satisfied, and the proof follows Theorem 2. □

We present two examples that support the derived results.

Example 3. 

Consider the ${\mathbb{F}}_{-MS}$ given in Example 1. Let

$$\mathsf{{\rm Y}}\phi =\left\{\begin{array}{c}-\frac{\phi }{3},\phi \in [-3,3]\hfill \\ {\phi }^2,otherwise,\hfill \end{array}\right.$$

and $\alpha ,\beta :\Gamma \to {\Re }_0^{+}$ be given by

$$\alpha \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [-3,0]\hfill \\ 0,otherwise,\hfill \end{array}\right.,\beta \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [0,3]\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

Furthermore, define the function $\psi :{\Re }_0^{+}\to {\Re }_0^{+}$ by $\psi \left(t\right)=\frac{t}{3}.$

First, we show that $\mathsf{{\rm Y}}$ is an ($\alpha$,$\beta$)-admissible map. Let $\phi \in \Gamma$; if $\alpha \left(\phi \right)\ge 1$, then $\phi \in [-3,0]$, and so, $\mathsf{{\rm Y}}\phi \in [0,3]$, that is $\beta \left(\mathsf{{\rm Y}}\phi \right)\ge 1.$ Furthermore, if $\beta \left(\phi \right)\ge 1$, then $\alpha \left(\mathsf{{\rm Y}}\phi \right)\ge 1$. Thus, $\mathsf{{\rm Y}}$ is a cyclic $(\alpha ,\beta )$- admissible map. Let $\left\{{\phi }_{\sigma }\right\}\in \Gamma$ such that $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}$ and ${\phi }_{\sigma }\to \phi$ as $\alpha \to +\infty .$ Then, $\left\{{\phi }_{\sigma }\right\}\subset [0,3]$, and hence, $\phi \in [0,3]$, that is $\beta \left(\phi \right)\ge 1.$ Let $\phi ,\mu \in \Gamma$ and $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$. Then, $\phi \in [-3,0]$ and $\mu \in [0,3].$ Then, we obtain

$$\begin{array}{cc}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)& =\mathcal{V}\left(-\frac{\phi }{3},-\frac{\mu }{3}\right)\hfill \\ & =\left|\frac{\phi }{3}-\frac{\mu }{3}\right|\hfill \\ & =\frac{1}{3}\mathcal{V}\left(\phi ,\mu \right)\hfill \\ & \le \psi \left(M\left(\phi ,\mu \right)\right).\hfill \end{array}$$

Thus, all assumptions of Theorem 2 are satisfied. Hence, $\mathsf{{\rm Y}}$ has a unique fixed point 0.

Example 4. 

Consider the ${\mathbb{F}}_{-MS}$ given in Example 2, and let $\alpha ,\beta :\Gamma \to {\Re }_0^{+}$ be given by

$$\alpha \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [-1,0]\hfill \\ 0,otherwise,\hfill \end{array}\right.,\beta \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [0,1]\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

Put $\psi :{\Re }_0^{+}\to {\Re }_0^{+}$ by $\psi \left(t\right)=\sqrt{t}$ and $\mathsf{{\rm Y}}\phi =-\frac{\phi }{2}.$

We first show that $\mathsf{{\rm Y}}$ is an $(\alpha ,\beta )$-admissible map. Let $\phi \in \Gamma$; if $\alpha \left(\phi \right)\ge 1$, then $\phi \in [-1,0]$ and $\mathsf{{\rm Y}}\phi =-\frac{\phi }{2}\in [0,1]$, so $\beta \left(\mathsf{{\rm Y}}\phi \right)\ge 1.$ Furthermore, if $\beta \left(\phi \right)\ge 1$, then $\alpha \left(\mathsf{{\rm Y}}\phi \right)\ge 1.$ Therefore, $\mathsf{{\rm Y}}$ is a cyclic $(\alpha ;\beta )$-admissible map. Let $\left\{{\phi }_{\sigma }\right\}\in \Gamma$ such that $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}$ and ${\phi }_{\sigma }\to \phi$ as $\sigma \to +\infty .$ Then, $\left\{{\phi }_n\right\}\subseteq [0,1]$, and hence, $\phi \in [0,1]$, that is $\beta \left(\phi \right)\ge 1.$ Let $\phi ,\mu \in \Gamma$ and $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1.$ Then, $\phi \in [-1,0]$ and $\mu \in [0,1].$ Then, we have

$$\begin{array}{cc}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)& =e^{\left|\frac{\phi }{2}-\frac{\mu }{2}\right|}\hfill \\ & =\sqrt{\mathcal{V}\left(\phi ,\mu \right)}\hfill \\ & \le \sqrt{M\left(\phi ,\mu \right)}\hfill \\ & =\psi \left(M\left(\phi ,\mu \right)\right).\hfill \end{array}$$

Then, all assumptions of Theorem 2 are satisfied. Hence, $\mathsf{{\rm Y}}$ has a unique fixed point 0.

Now follows our second new result supplemented with an example.

Theorem 3. 

Let $(\Gamma ;\mathcal{V})$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$ and $\mathsf{{\rm Y}};S:\Gamma \to \Gamma$ be self-mappings on Γ that satisfy

$$\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1or\alpha \left(\mu \right)\beta \left(\phi \right)\ge 1\Rightarrow \mathcal{V}(\mathsf{{\rm Y}}\phi ;S\mu )\le k\mathcal{V}(\phi ;\mu ),forall\phi ,\mu \in \Gamma ,$$

(8)

where $0<k<1$. Suppose that the following conditions hold:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1$;

(ii) 

Υ and S are two ($\alpha ,\beta )$-admissible mappings;

(iii) 

If ${\phi }_{\sigma }$ is a sequence in Γ such that ${\phi }_{\sigma }\to \phi$ as $\sigma \to +\infty$ and $\beta \left({\phi }_{\sigma }\right)\ge 1,$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, Υ and S have a unique common fixed point.

Proof. 

Let ${\phi }_0\in \Gamma$, and define the sequence $\left\{{\phi }_{\sigma }\right\}$ by ${\phi }_{2\sigma +1}=\mathsf{{\rm Y}}{\phi }_{2\sigma }$ and ${\phi }_{2\sigma +2}=S{\phi }_{2\sigma +1},$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}.$ Since T and S are cyclic $(\alpha ,\beta )$-admissible mappings and $\alpha \left({\phi }_0\right)\ge 1$, then $\beta \left({\phi }_1\right)=\beta \left(\mathsf{{\rm Y}}{\phi }_0\right)\ge 1$ and $\alpha \left({\phi }_2\right)=\alpha \left(S{\phi }_1\right)\ge 1.$ By continuing this process, we have $\alpha \left({\phi }_{2\sigma }\right)\ge 1$ and $\beta \left({\phi }_{2\sigma +1}\right)\ge 1,\forall \sigma \in \mathbb{N}\cup \left\{0\right\}$. Similarly, since T and S are cyclic $(\alpha ;\beta )$-admissible mappings and $\beta \left({\phi }_0\right)\ge 1,$ it can be shown that, $\beta \left({\phi }_{2\sigma }\right)\ge 1$ and $\alpha \left({\phi }_{2\sigma +1}\right)\ge 1,$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}$. Then, we obtain $\alpha \left({\phi }_{\sigma }\right)\ge 1$ and $\beta \left({\phi }_{\sigma }\right)\ge 1,$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}$. Since $\alpha \left({\phi }_{\sigma }\right)\beta \left({\phi }_m\right)\ge 1,$ for all $\sigma ,m\in \mathbb{N}\cup \left\{0\right\}$ from (8), we have

$$\mathcal{V}\left({\phi }_1,{\phi }_2\right)=\mathcal{V}\left(\mathsf{{\rm Y}}{\phi }_0,S{\phi }_1\right)\le k\mathcal{V}\left({\phi }_0,{\phi }_1\right)$$

and

$$\mathcal{V}\left({\phi }_2,{\phi }_3\right)=\mathcal{V}\left(S{\phi }_1,\mathsf{{\rm Y}}{\phi }_2\right)\le k\mathcal{V}\left({\phi }_1,{\phi }_2\right)\le k^2\mathcal{V}\left({\phi }_0,{\phi }_1\right).$$

By repeating this procedure, we obtain

$$\begin{array}{cc}\hfill \mathcal{V}\left({\phi }_{\sigma },{\phi }_{\sigma +1}\right)& \le k\mathcal{V}\left({\phi }_{\sigma -1},{\phi }_{\sigma }\right)\hfill \\ & ⋮\hfill \\ & \le k^{\sigma }\mathcal{V}\left({\phi }_0,{\phi }_1\right),\forall \sigma =0,1,2,\dots \hfill \end{array}$$

Then, by Lemma 1, $\left\{{\phi }_{\sigma }\right\}$ is an $\mathbb{F}$-Cauchy sequence. Since $(\Gamma ;\mathcal{V})$ is $\mathbb{F}$-complete, there exists ${\phi }^{*}\in \Gamma$ such that ${lim}_{\sigma \to +\infty }\mathcal{V}\left({\phi }_{\sigma },{\phi }^{*}\right)=0$. Now, we show that ${\phi }^{*}$ is the common fixed point of $\mathsf{{\rm Y}}$ and S. Suppose that $\mathcal{V}({\phi }^{*};\mathsf{{\rm Y}}{\phi }^{*})>0$. From (iii), we have $\alpha \left({\phi }_{\sigma }\right)\beta \left({\phi }^{*}\right)\ge 1$ for all $\sigma \in \mathbb{N}$. Using ${\mathcal{V}}_3$ and (8), we have

$$\begin{array}{cc}\hfill \mathfrak{g}\left(\mathcal{V}\left({\phi }^{*},\mathsf{{\rm Y}}{\phi }^{*}\right)\right)& \le \mathfrak{g}\left(\mathcal{V}\left({\phi }^{*},{\phi }_{2\sigma }\right)+\mathcal{V}\left({\phi }_{2\sigma },\mathsf{{\rm Y}}{\phi }^{*}\right)\right)+\alpha \hfill \\ & \le \mathfrak{g}\left(\mathcal{V}\left({\phi }^{*},{\phi }_{2\sigma }\right)+\mathcal{V}\left(S{\phi }_{2\sigma -1},\mathsf{{\rm Y}}{\phi }^{*}\right)\right)+\alpha \hfill \\ & \le \mathfrak{g}\left(\mathcal{V}\left({\phi }^{*},{\phi }_{2\sigma }\right)+k\mathcal{V}\left({\phi }_{2\sigma -1},{\phi }^{*}\right)\right)+\alpha .\hfill \end{array}$$

Since ${\phi }_{\sigma }\to {\phi }^{*}$ as $\sigma \to +\infty$ and using ${\mathbb{F}}_2,$ we have

$$\underset{\sigma \to +\infty }{lim}\left(\mathfrak{g}\left(\mathcal{V}\left({\phi }^{*},{\phi }_{2\sigma }\right)+k\mathcal{V}\left({\phi }_{2\sigma -1},{\phi }^{*}\right)\right)\right)=-\infty ,$$

which is a contradiction. This implies that $\mathsf{{\rm Y}}{\phi }^{*}={\phi }^{*}$. Similarly, we can show that $S{\phi }^{*}={\phi }^{*}.$ For the uniqueness of the common fixed point $\mathsf{{\rm Y}}$ and S, assume the contrary, that $\phi ,\mu \in Fix\left(T\right)\cap Fix\left(S\right)$ and $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1$.

From (8), we have

$$\mathcal{V}\left(\phi ,\mu \right)=\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,S\mu \right)\le k\mathcal{V}\left(\phi ,\mu \right)<\mathcal{V}\left(\phi ,\mu \right),$$

which is a contradiction, that is $\mathsf{{\rm Y}}$ and S have a unique common fixed point. □

Corollary 4. 

Let $(\Gamma ;\mathcal{V})$ be an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$ and $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a self-mapping on Γ that satisfy

$$\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1\mathrm{implies}\mathcal{V}\left(\mathsf{{\rm Y}}\phi ,\mathsf{{\rm Y}}\mu \right)\le k\mathcal{V}\left(\phi ,\mu \right),forall\phi ,\mu \in \Gamma ,$$

(9)

where $0<k<1.$ Suppose that the following conditions hold:

(i) 

There exists ${\phi }_0\in \Gamma$ such that $\alpha \left({\phi }_0\right)\ge 1$ and $\beta \left({\phi }_0\right)\ge 1$;

(ii) 

Υ is an $(\alpha ,\beta )$-admissible mapping;

(iii) 

If ${\phi }_{\sigma }$ is a sequence in Γ such that ${\phi }_{\sigma }\to \phi$ as $\sigma \to +\infty$ and $\beta \left({\phi }_{\sigma }\right)\ge 1$ for all $\sigma \in \mathbb{N}$, then $\beta \left(\phi \right)\ge 1$.

Then, Υ has a unique fixed point.

Example 5. 

Consider the ${\mathbb{F}}_{-MS}$ given in Example 1. Let

$$\mathsf{{\rm Y}}\phi =-\frac{\phi }{3}forall\phi \in \Gamma ,S\phi =\left\{\begin{array}{c}-\frac{\phi }{6},\phi \in [-1,1],\hfill \\ 3\phi ,otherwise,\hfill \end{array}\right.$$

and $\alpha ,\beta :\Gamma \to {\Re }_0^{+}$ be given by

$$\alpha \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [-1,0]\hfill \\ 0,otherwise,\hfill \end{array}\right.,\beta \left(\phi \right)=\left\{\begin{array}{c}1,\phi \in [0,1]\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

We first show that Υ and S are $(\alpha ;\beta )$-admissible mapping. Let $\phi \in \Gamma$, if $\alpha \left(\phi \right)\ge 1$, then $\phi \in [-1,0]$, and so, $\mathsf{{\rm Y}}\phi =-\frac{\phi }{3},$ that is $\beta \left(\mathsf{{\rm Y}}\phi \right)\ge 1$. Furthermore, if $\beta \left(\phi \right)\ge 1$, then $\alpha \left(\mathsf{{\rm Y}}\phi \right)\ge 1$. Thus, Υ is a cyclic $(\alpha ;\beta )$-assertion mapping. Furthermore, similarly, S is an $(\alpha ;\beta )$-admissible mapping. Let $\left\{{\phi }_{\sigma }\right\}$ be a sequence in Γ such that $\beta \left({\phi }_n\right)\ge 1$ for all $\sigma \in \mathbb{N}\cup \left\{0\right\}$ and ${\phi }_n\to \phi$ as $n\to +\infty .$ Then, $\left\{{\phi }_n\right\}\subset [0,1]$, and hence, $\phi \in [0,1],$ that is $\beta \left(\phi \right)\ge 1.$ Let $\phi ,\mu \in \Gamma$ and $\alpha \left(\phi \right)\beta \left(\mu \right)\ge 1.$ Then, $\phi \in [-1,0]$ and $\mu \in [0,1],$ we have

$$\begin{array}{cc}\hfill \mathcal{V}\left(\mathsf{{\rm Y}}\phi ,S\mu \right)& =\mathcal{V}\left(-\frac{\phi }{3},-\frac{\mu }{6}\right)\hfill \\ & \le \left|\frac{\phi }{3}-\frac{\mu }{6}\right|\hfill \\ & \le \frac{\left|\phi -\mu \right|}{3}\hfill \\ & =\frac{1}{3}\mathcal{V}\left(\phi ,\mu \right).\hfill \end{array}$$

Then, all conditions of Theorem 3 are fulfilled. Hence, Υ and S have a unique common fixed point 0.

3. Application to Integral Equation

Let $\Gamma =C[0,l]$ be the set of all real continuous functions on $[0,l]$ equipped with the ${\mathbb{F}}_{-M}$:

$$\begin{array}{c}\hfill \mathcal{V}\left(\mathfrak{r},\mathfrak{q}\right)=\left\{\begin{array}{c}{e}^{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }},\mathfrak{r}\ne \mathfrak{q}\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\end{array}$$

where $l>0$. Obviously, $(\Gamma ;\mathcal{V}$) is an $\mathbb{F}$-complete ${\mathbb{F}}_{-MS}$. First, consider the following integral equation:

$$\mathfrak{r}\left(\mathfrak{p}\right)=h\left(\mathfrak{p}\right)+{\displaystyle \underset{0}{\overset{l}{\int }}}G\left(\mathfrak{p},s\right)k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)ds,$$

(10)

where

$$\begin{array}{c}\hfill h:[0,l]\to \Re ,G:[0,l]\times [0,l]\to \Re ,k:[0,l]\times [0,l]\times \Re \to \Re \mathrm{are}\mathrm{continuous}\mathrm{functions}.\end{array}$$

Let $\mathsf{{\rm Y}}:\Gamma \to \Gamma$ be a mapping defined by:

$$\mathsf{{\rm Y}}\mathfrak{r}\left(\mathfrak{p}\right)=h\left(\mathfrak{p}\right)+{\displaystyle \underset{0}{\overset{l}{\int }}}G\left(\mathfrak{p},s\right)k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)ds,\mathrm{for} \mathrm{all}\mathfrak{r}\in \Gamma ,\mathfrak{p},s\in [0,l].$$

Theorem 4. 

Assume that the following conditions are satisfied:

(1)

For all $\mathfrak{p},s\in [0,l],$ we have ${\displaystyle \underset{0}{\overset{l}{\int }}}{G}^2\left(\mathfrak{p},s\right)ds\le \frac{1}{l}$;

(2)

There exist $\phi ,\nu :\Gamma \to \Re$ such that if $\phi \left(\mathfrak{r}\right)\ge 0$ and $\nu \left(\mathfrak{q}\right)\ge 0$ for some $\phi ,v\in \Gamma ,$ then for every $s,\mathfrak{p}\in [0,l],$ we obtain

$$\begin{array}{c}\hfill \left|k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)-k\left(\mathfrak{p},s,\mathfrak{q}\left(s\right)\right)\right|\le ln\frac{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }}{2},forall\mathfrak{r}\ne \mathfrak{q};\end{array}$$

(3)

There exists ${\mathfrak{r}}_0\in \Gamma$ such that $\phi \left({\mathfrak{r}}_0\right)\ge 0$ and $\nu \left({\mathfrak{r}}_0\right)\ge 0$;

(4)

$\phi \left(\mathfrak{r}\right)\ge 0$ for some $\mathfrak{r}\in \Gamma$ implies $\nu \left(\mathsf{{\rm Y}}\mathfrak{r}\right)\ge 0,$ and $\nu \left(\mathfrak{r}\right)\ge 0$ for some $\mathfrak{u}\in \Gamma$ implies $\phi \left(\mathsf{{\rm Y}}\mathfrak{r}\right)\ge 0$;

(5)

If $\left\{{\mathfrak{r}}_{\sigma }\right\}$ is a sequence in Γ such that ${\mathfrak{r}}_{\sigma }\to \mathfrak{r}$ as $\sigma \to +\infty$ and $\phi \left({\mathfrak{r}}_{\sigma }\right)\ge 0$ for all $\sigma \in \mathbb{N},$ then $\phi \left(\mathfrak{r}\right)\ge 0.$

Then, Equation (10) has a solution in $\Gamma .$

Proof. 

Let $\mathfrak{r},\mathfrak{q}\in \Gamma$ be such that $\phi \left(\mathfrak{r}\right)\ge 0$ and $\nu \left(\mathfrak{q}\right)\ge 0.$ Using Condition (2) and the Cauchy–Schwarz inequality, we have

$$\begin{array}{cc}\hfill \left|\mathsf{{\rm Y}}\mathfrak{r}\left(\mathfrak{p}\right)-\mathsf{{\rm Y}}\mathfrak{q}\left(\mathfrak{p}\right)\right|& =\left|{\displaystyle \underset{0}{\overset{l}{\int }}}G\left(\mathfrak{p},s\right)\left(k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)-k\left(\mathfrak{p},s,\mathfrak{q}\left(s\right)\right)\right)ds\right|\hfill \\ & \le {\displaystyle \underset{0}{\overset{l}{\int }}}\left|G\left(\mathfrak{p},s\right)\right|\left|k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)-k\left(\mathfrak{p},s,\mathfrak{q}\left(s\right)\right)\right|ds\hfill \\ & \le {\left({\displaystyle \underset{0}{\overset{l}{\int }}}{\left|G\left(\mathfrak{p},s\right)\right|}^2\right)}^{\frac{1}{2}}{\left({\displaystyle \underset{0}{\overset{l}{\int }}}{\left|k\left(\mathfrak{p},s,\mathfrak{r}\left(s\right)\right)-k\left(\mathfrak{p},s,\mathfrak{q}\left(s\right)\right)\right|}^{2}ds\right)}^{\frac{1}{2}}\hfill \\ & \le ln\frac{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }}{2}.\hfill \end{array}$$

Therefore, we obtain

$${∥\mathsf{{\rm Y}}\mathfrak{r}-\mathsf{{\rm Y}}\mathfrak{q}∥}_{\infty }\le ln\frac{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }}{2},$$

then we have

$$e^{{∥\mathsf{{\rm Y}}\mathfrak{r}-\mathsf{{\rm Y}}\mathfrak{q}∥}_{\infty }}\le e^{ln\frac{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }}{2}}=e^{ln{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }-ln2}\le \frac{e^{{∥\mathfrak{r}-\mathfrak{q}∥}_{\infty }}}{2}.$$

Then, we obtain

$$\mathcal{V}\left(\mathsf{{\rm Y}}\mathfrak{r},\mathsf{{\rm Y}}\mathfrak{q}\right)leq\frac{\mathcal{V}\left(\mathfrak{r},\mathfrak{q}\right)}{2}\le \frac{M\left(\mathfrak{r},\mathfrak{q}\right)}{2}.$$

Define $\alpha ,\beta :\Gamma \to {\Re }_0^{+}$ by

$$\alpha \left(\phi \right)=\left\{\begin{array}{c}1,\phi \left(\phi \right)\ge 0,\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.\beta \left(\mu \right)=\left\{\begin{array}{c}1,\phi \left(\mu \right)\ge 0,\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.$$

Furthermore, put $\psi :{\Re }_0^{+}\to {\Re }_0^{+}$ by $\psi \left(\mathfrak{p}\right)=\frac{\mathfrak{p}}{2}.$ Therefore, $\forall \mathfrak{r},\mathfrak{q}\in \Gamma ,$ we obtain

$$\alpha \left(\mathfrak{r}\right)\beta \left(\mathfrak{q}\right)\mathcal{V}\left(\mathsf{{\rm Y}}\mathfrak{r},\mathsf{{\rm Y}}\mathfrak{q}\right)\le \psi \left(M\left(\mathfrak{r},\mathfrak{q}\right)\right).$$

Therefore, all the assumptions of Corollary 3 hold, and then, $\mathsf{{\rm Y}}$ has a fixed point. □

Example 6. 

Consider the following integral equation:

$${\int }_0^{l}cos(l-s)x\left(s\right)ds=lsinl,\left(11\right)$$

(11)

with exact solution $x\left(l\right)=2sin\left(l\right)$, for $0\le l<1$.

The numerical results are shown in Table 1. These results have good accuracy in comparison with the numerical results obtained.

Table 1. Comparison of exact solution and approximation solutions.

i	Exact Solution	Approximation Solution	Approximation Solution
		(m = 64)	(m = 128)
0.0	0	0.010417	0.005208
0.1	0.199667	0.197570	0.192399
0.2	0.397339	0.382942	0.398412
0.3	0.591040	0.605205	0.589930
0.4	0.778837	0.781174	0.785758
0.5	0.958851	0.967335	0.963098
0.6	1.129285	1.126666	1.122812
0.7	1.288435	1.276056	1.289847
0.8	1.434712	1.446451	1.433200
0.9	1.566654	1.569934	1.572171

Below is the comparison of the numerical results with the analytic results. Figure 1 and Figure 2 show that the error of the approximation solution compared to the exact solution is also relatively very small.

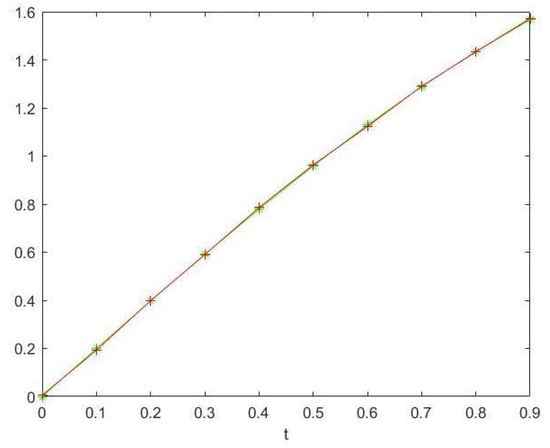
Figure 1. Graph of approximation (m = 64) compared to exact solution with h = 0.1.

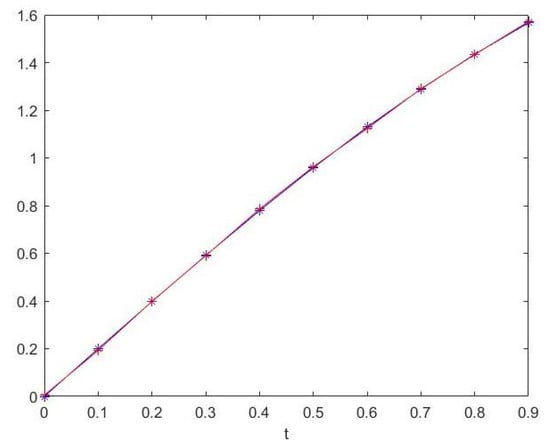
Figure 2. Graph of approximation (m = 128) compared to exact solution with h = 0.1.

4. Conclusions

We established fixed point results generalizing $\left(\alpha ,\beta \right)$-admissible mappings in the setting of $\mathbb{F}$-metric spaces. Our results extend and generalize some results proven in the past. The results were supported with non-trivial examples, and the result was applied to find the solution to the integral equations. There is an open problem of applying the derived results and their extension to find the solution to the fractional differential equations, circuit theory, etc. Furthermore, as a future research, the fixed circle problem can be studied using these new contractions on different generalized metric spaces; see [16,17,18].