The Shadows of Regular Black Holes with Asymptotic Minkowski Cores
Abstract
1. Introduction
2. Rotating Kerr-like Regular Black Hole with a Minkowski Core
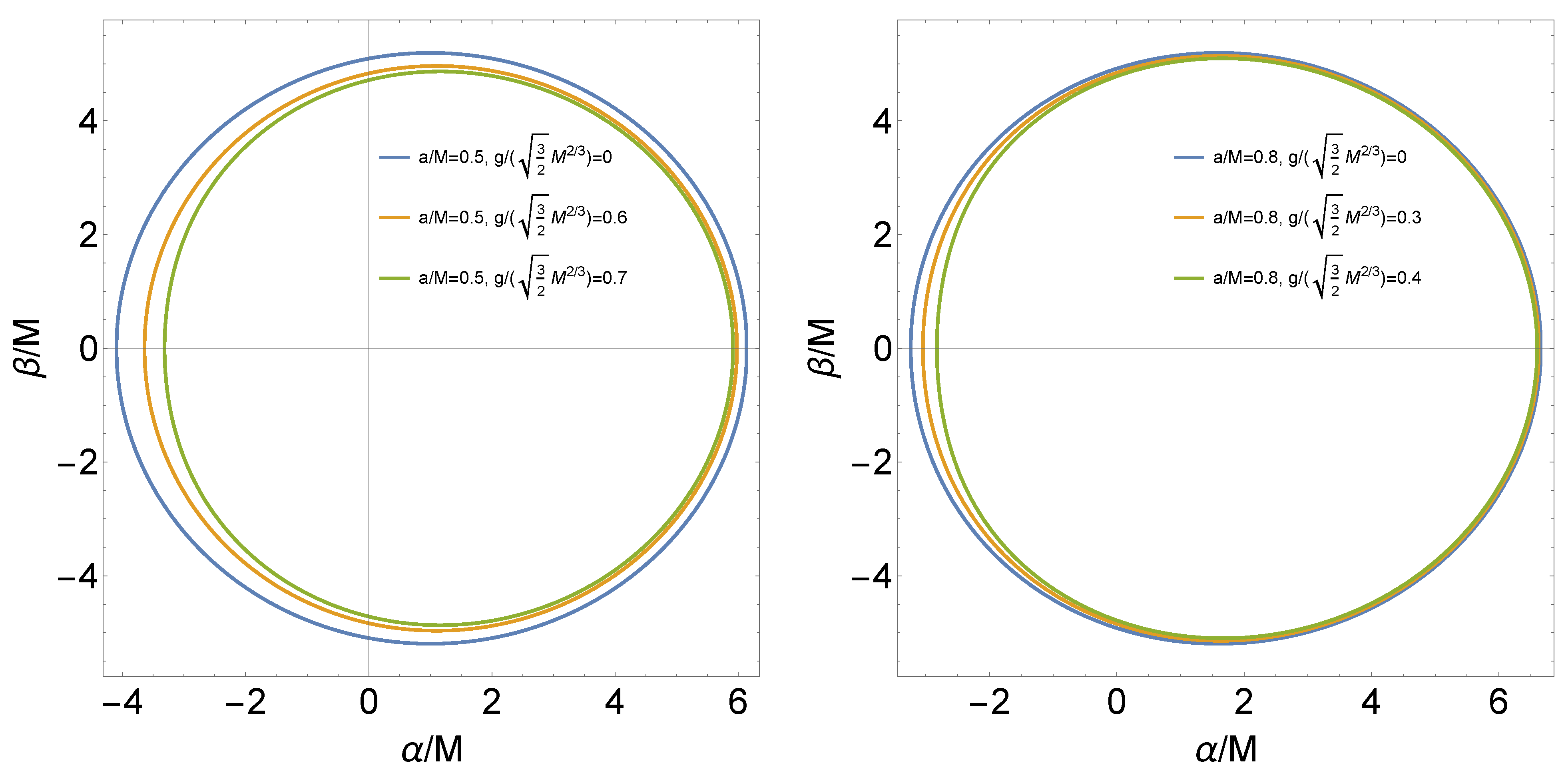
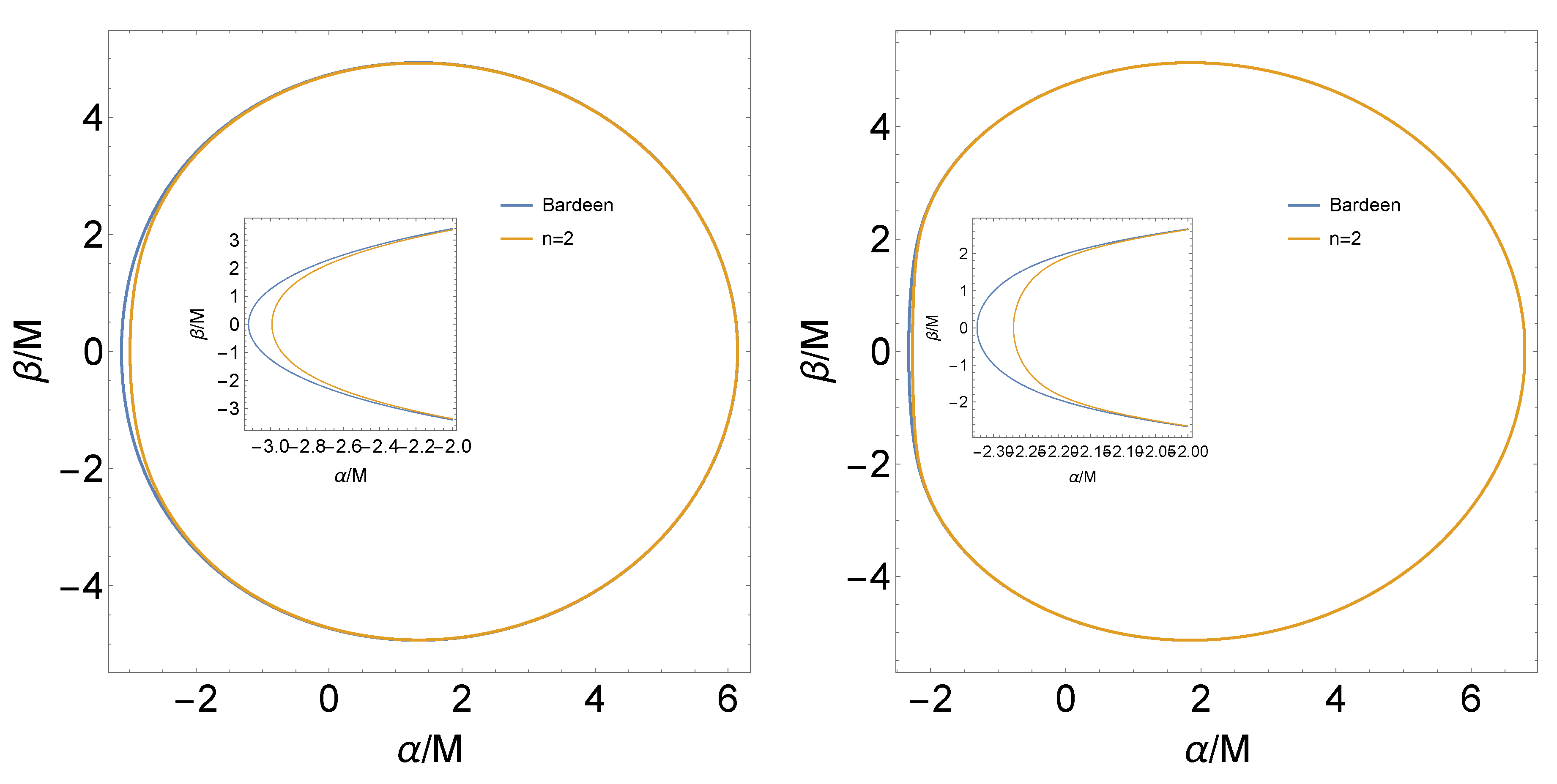
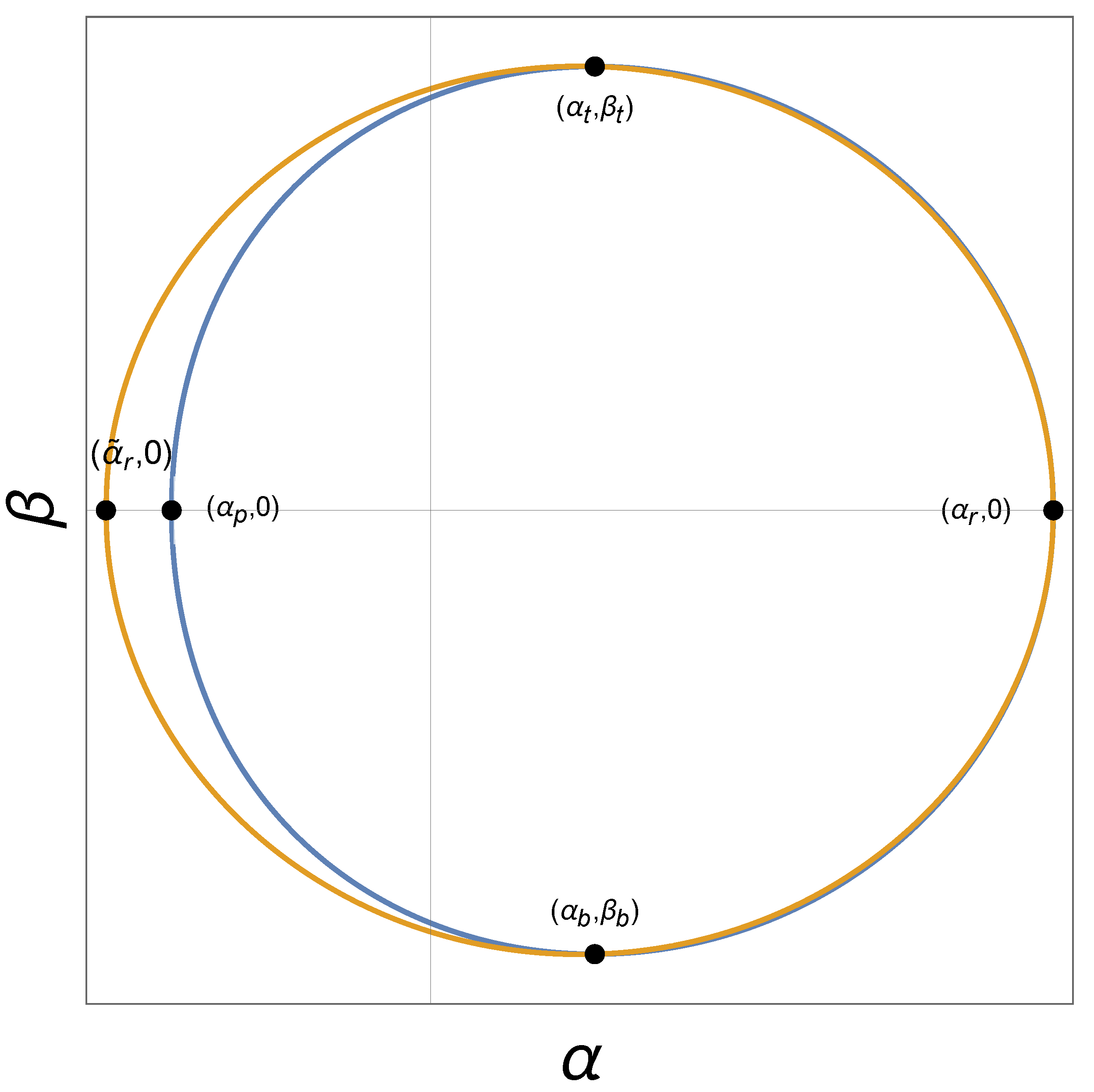
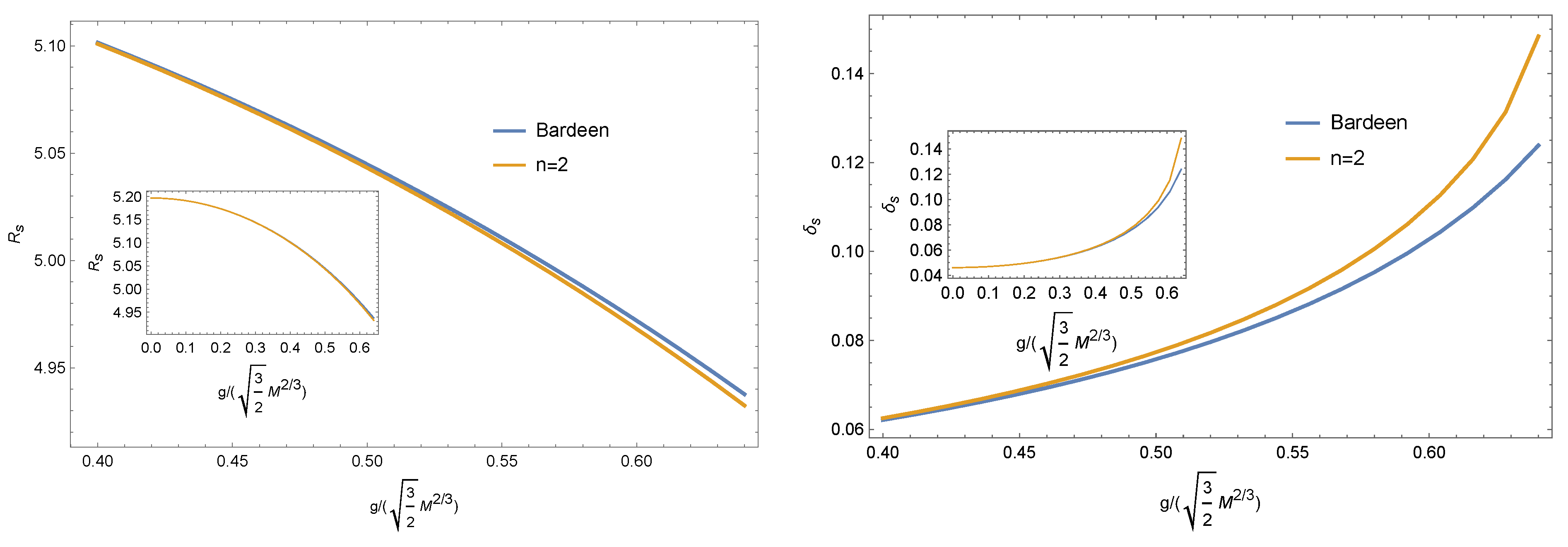
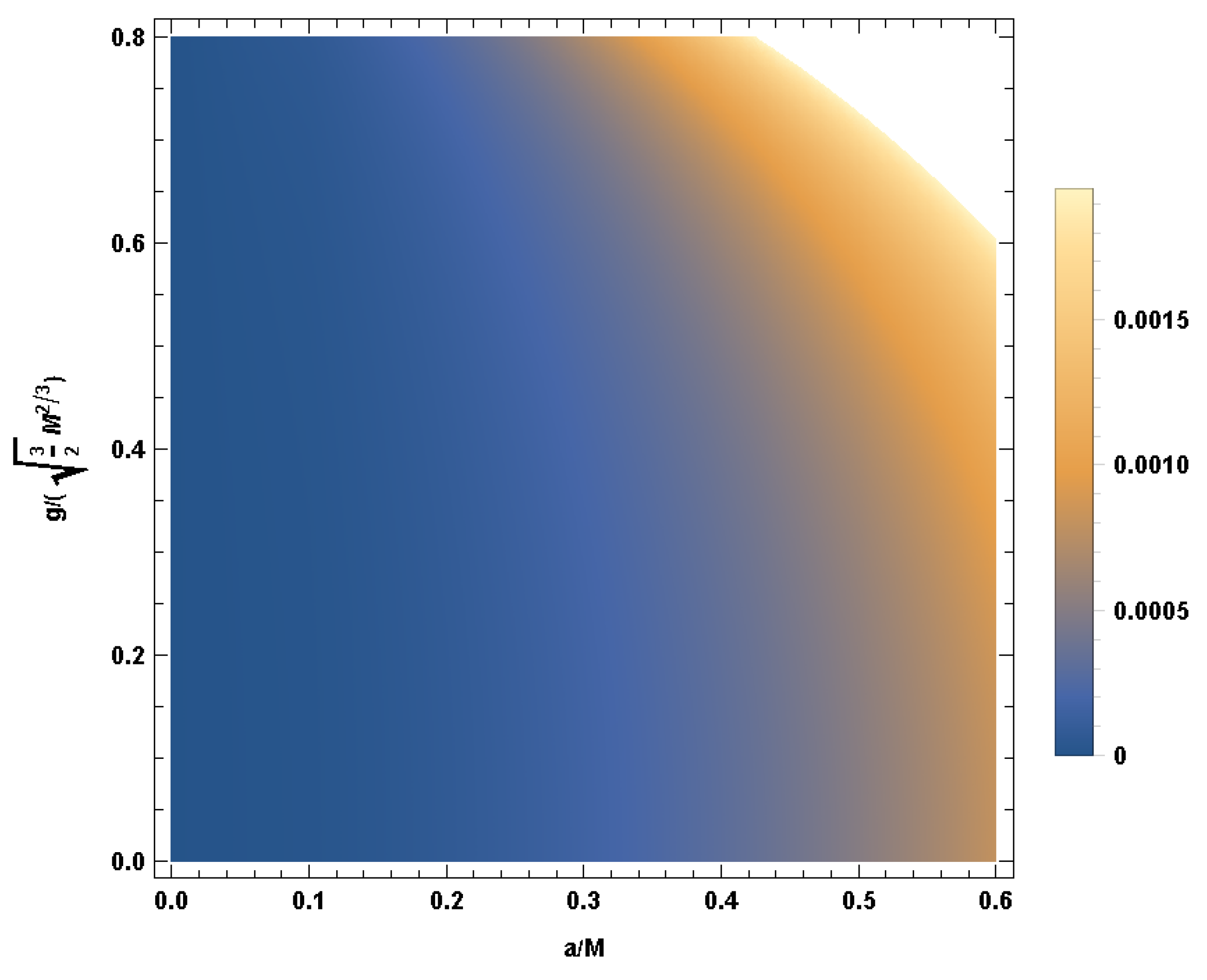
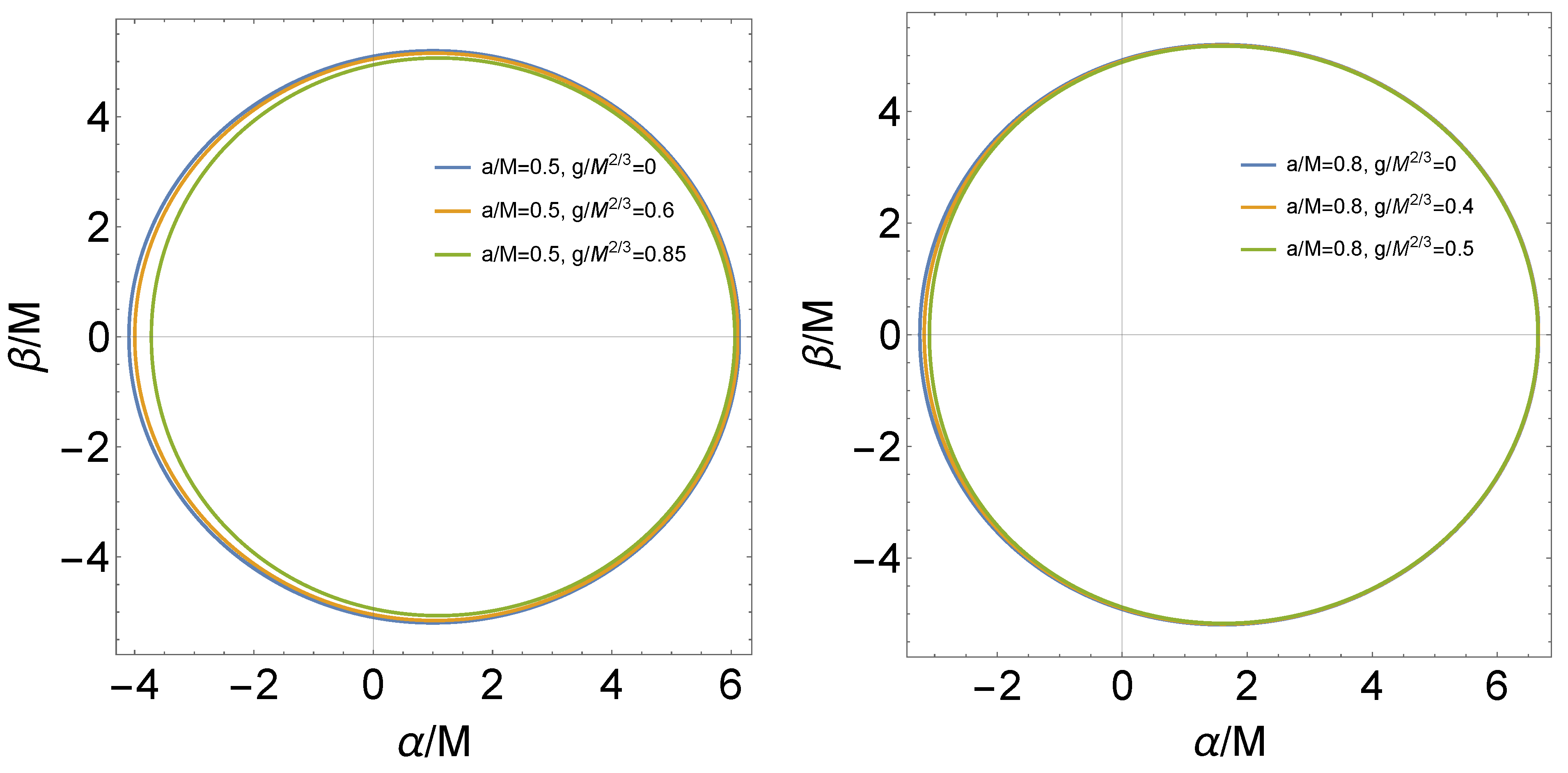
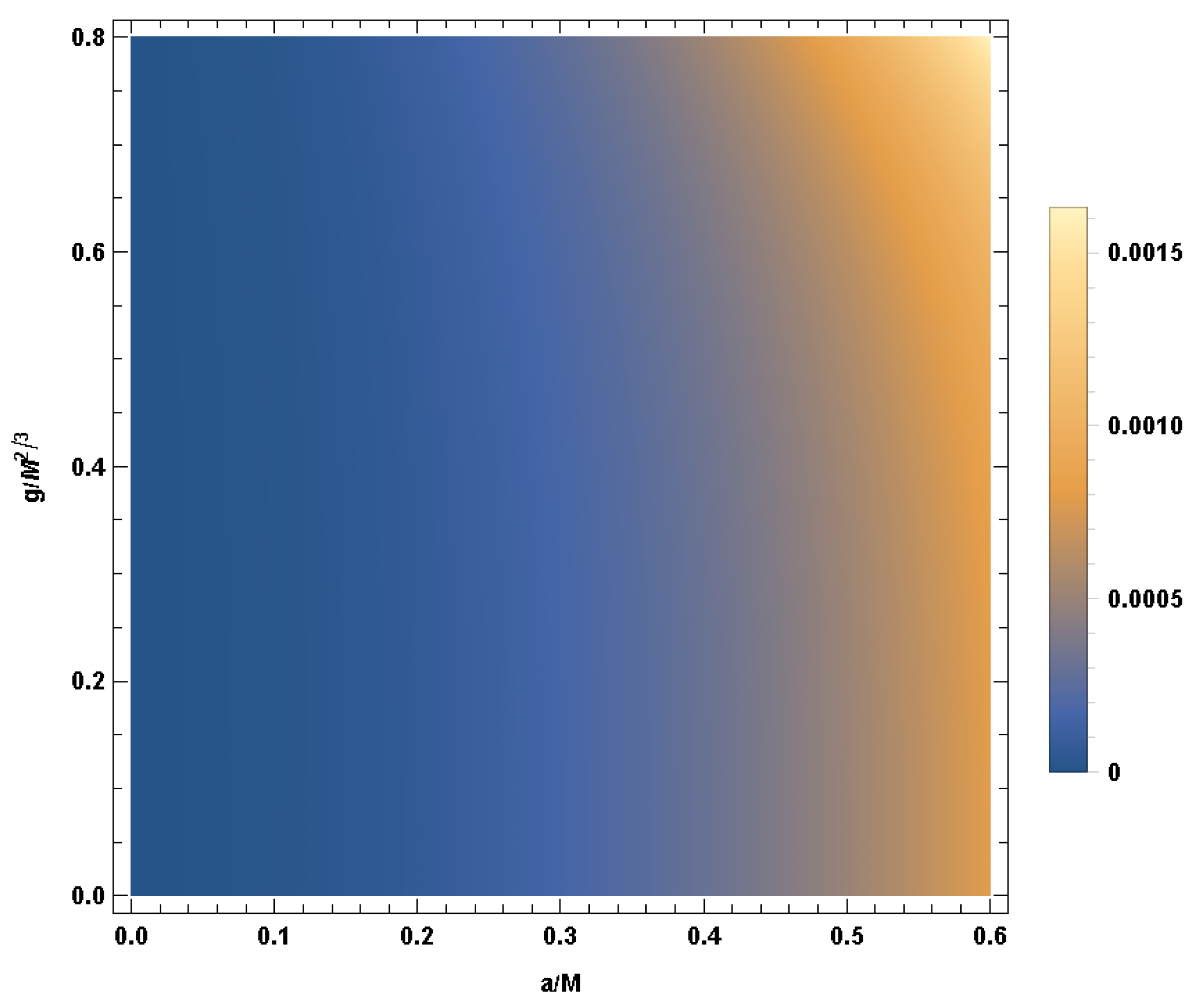
3. Shadow of a Regular Black Hole with and
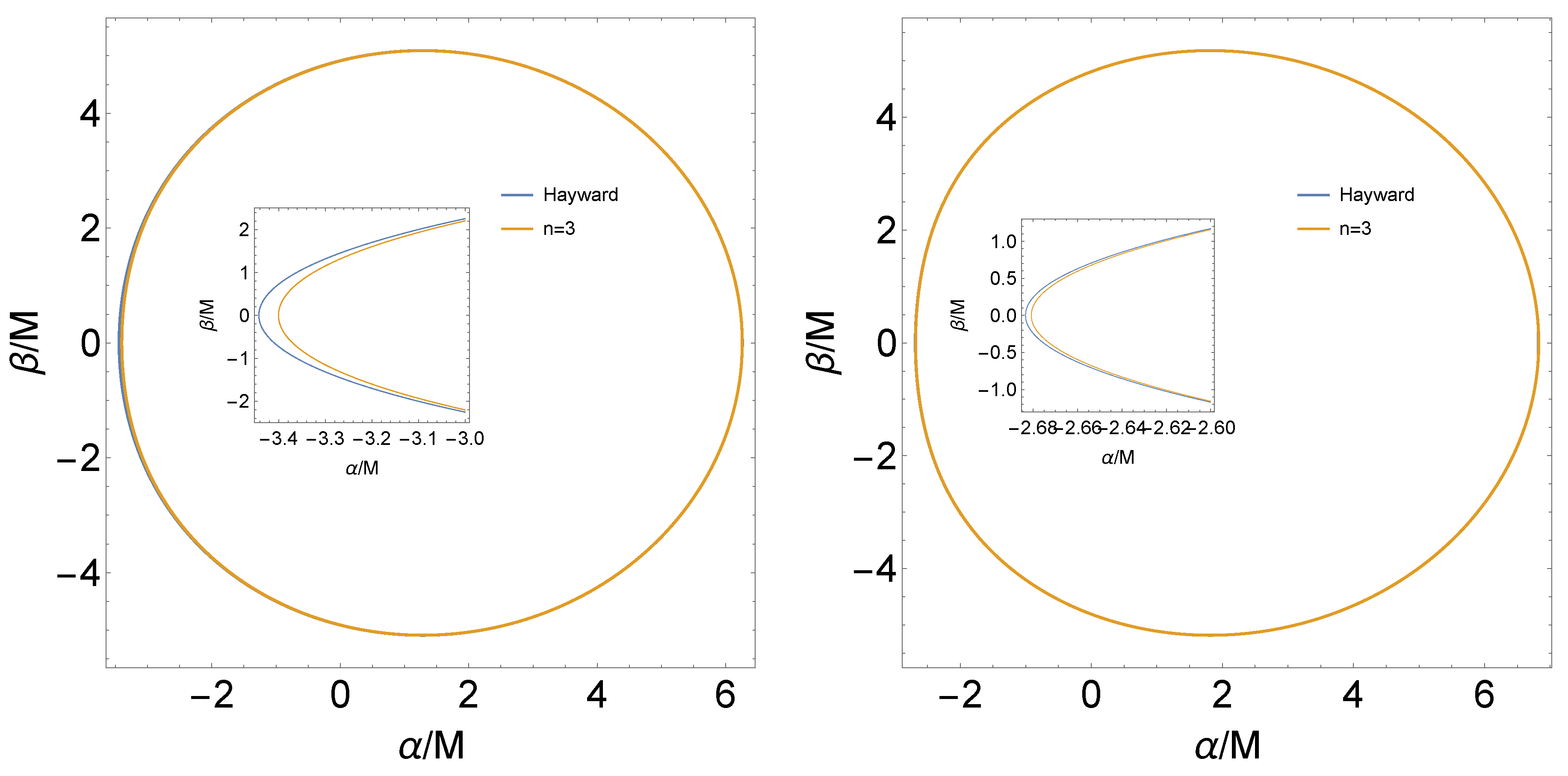
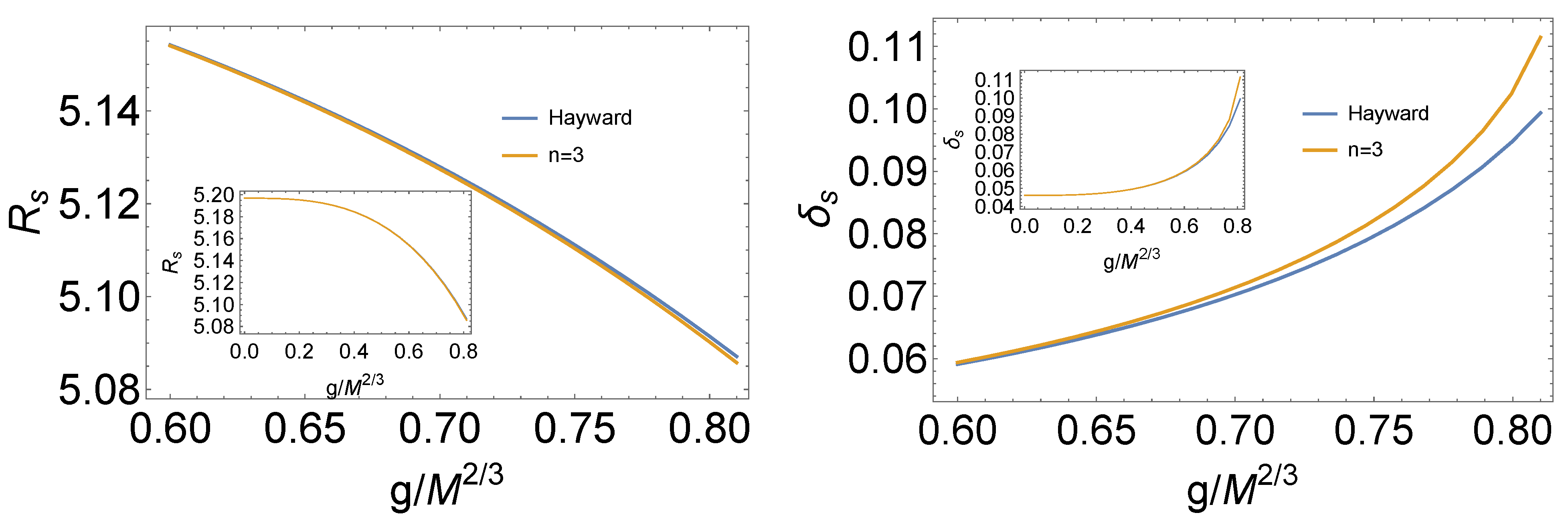
4. Shadow of the Regular Black Hole with and
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- The Event Horizon Telescope Collaboration; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L4. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. Lett. 2022, 930, L14. [Google Scholar]
- Synge, J.L. The Escape of Photons from Gravitationally Intense Stars. Mon. Not. R. Astron. Soc. 1966, 131, 463–466. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Bardeen, J.M. Black Holes (Les Astres Occlus); DeWitt, C., DeWitt, B.S., Eds.; Gordon and Breach: New York, NY, USA, 1973; pp. 215–239. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Relativ. Gravit. 2018, 50, 1–27. [Google Scholar] [CrossRef]
- Hu, Z.; Zhong, Z.; Li, P.-C.; Guo, M.; Chen, B. QED effect on a black hole shadow. Phys. Rev. D 2021, 103, 044057. [Google Scholar] [CrossRef]
- Ling, R.; Guo, H.; Liu, H.; Kuang, X.-M.; Wang, B. Shadow and near-horizon characteristics of the acoustic charged black hole in curved spacetime. Phys. Rev. D 2021, 104, 104003. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y. Calculating black hole shadows: Review of analytical studies. Phys. Rep. 2021, 947, 1–39. [Google Scholar] [CrossRef]
- Takahashi, R. Black Hole Shadows of Charged Spinning Black Holes: Fig. 1. Publ. Astron. Soc. Jpn. 2005, 57, 273–277. [Google Scholar] [CrossRef]
- Hioki, K.; Maeda, K.-I. Measurement of the Kerr spin parameter by observation of a compact object’s shadow. Phys. Rev. D 2009, 80, 024042. [Google Scholar] [CrossRef]
- Tsupko, O.Y. Analytical calculation of black hole spin using deformation of the shadow. Phys. Rev. D 2017, 95, 104058. [Google Scholar] [CrossRef]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef]
- Badía, J.; Eiroa, E.F. Shadow of axisymmetric, stationary, and asymptotically flat black holes in the presence of plasma. Phys. Rev. D 2021, 104, 084055. [Google Scholar] [CrossRef]
- Johannsen, T.; Psaltis, D. Testing the no-hair theorem with observations in the electromagnetic spectrum. II. Black hole images. Astrophys. J. Lett. 2010, 718, 446–454. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X. Observing the shadow of Einstein-Maxwell-Dilaton-Axion black hole. J. Cosmol. Astropart. Phys. 2013, 2013, 063. [Google Scholar] [CrossRef]
- Amir, M.; Ghosh, S.G. Shapes of rotating nonsingular black hole shadows. Phys. Rev. D 2016, 94, 024054. [Google Scholar] [CrossRef]
- Xu, Z.; Hou, X.; Wang, J. Possibility of identifying matter around rotating black hole with black hole shadow. J. Cosmol. Astropart. Phys. 2018, 2018, 046. [Google Scholar] [CrossRef]
- Yan, S.-F.; Li, C.; Xue, L.; Ren, X.; Cai, Y.-F.; Easson, D.A.; Yuan, Y.-F.; Zhao, H. Testing the equivalence principle via the shadow of black holes. Phys. Rev. Res. 2020, 2, 023164. [Google Scholar] [CrossRef]
- Guo, M.; Li, P.-C. Innermost stable circular orbit and shadow of the 4D Einstein–Gauss–Bonnet black hole. Eur. Phys. J. C 2020, 80, 1–8. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, T.; Wu, Q.; Jusufi, K.; Jamil, M.; Azreg-Aïnou, M.; Wang, A. Shadow and quasinormal modes of a rotating loop quantum black hole. Phys. Rev. D 2020, 101, 084001. [Google Scholar] [CrossRef]
- Badía, J.; Eiroa, E.F. Influence of an anisotropic matter field on the shadow of a rotating black hole. Phys. Rev. D 2020, 102, 024066. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef]
- Khodadi, M.; Allahyari, A.; Vagnozzi, S.; Mota, D.F. Black holes with scalar hair in light of the Event Horizon Telescope. J. Cosmol. Astropart. Phys. 2020, 2020, 026. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Lee, B.-H.; Lee, W.; Myung, Y.S. Shadow cast by a rotating black hole with anisotropic matter. Phys. Rev. D 2021, 103, 064026. [Google Scholar] [CrossRef]
- Abdujabbarov, A.; Amir, M.; Ahmedov, B.; Ghosh, S.G. Shadow of rotating regular black holes. Phys. Rev. D 2016, 93, 104004. [Google Scholar] [CrossRef]
- Tsukamoto, N. Black hole shadow in an asymptotically flat, stationary, and axisymmetric spacetime: The Kerr-Newman and rotating regular black holes. Phys. Rev. D 2018, 97, 064021. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G.; Wang, A. Shadow cast and deflection of light by charged rotating regular black holes. Phys. Rev. D 2019, 100, 124024. [Google Scholar] [CrossRef]
- Kumar, A.; Baboolal, D.; Ghosh, S.G. Nonsingular Black Holes in 4D Einstein–Gauss–Bonnet Gravity. Universe 2022, 8, 244. [Google Scholar] [CrossRef]
- Bardeen, J.M. Proceedings of the International Conference GR5; Tbilisi University Press: Tbilisi, Georgia, 1968; pp. 174–180. [Google Scholar]
- Hayward, S.A. Formation and Evaporation of Nonsingular Black Holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef]
- Frolov, V.P. Information loss problem and a ‘black hole’ model with a closed apparent horizon. J. High Energy Phys. 2014, 2014, 49. [Google Scholar] [CrossRef]
- Ansoldi, S. Spherical black holes with regular center: A Review of existing models including a recent realization with Gaussian sources. arXiv 2008, arXiv:0802.0330. [Google Scholar]
- Xiang, L.; Ling, Y.; Shen, Y.G. Singularities and the Finale of Black Hole Evaporation. Int. J. Mod. Phys. D 2013, 22, 1342016. [Google Scholar] [CrossRef]
- Ling, Y.; Wu, M.H. Regular black holes with sub-Planckian curvature. arXiv 2021, arXiv:2109.05974. [Google Scholar]
- Ling, Y.; Wu, M.-H. Modified regular black holes with time delay and 1-loop quantum correction *. Chin. Phys. C 2022, 46, 025102. [Google Scholar] [CrossRef]
- Bargueño, P. Some global, analytical, and topological properties of regular black holes. Phys. Rev. D 2020, 102, 104028. [Google Scholar] [CrossRef]
- Melgarejo, G.; Contreras, E.; Bargueño, P. Regular black holes with exotic topologies. Phys. Dark Universe 2020, 30, 100709. [Google Scholar] [CrossRef]
- Berry, T.; Lobo, F.S.N.; Simpson, A.; Visser, M. Thin-shell traversable wormhole crafted from a regular black hole with asymptotically Minkowski core. Phys. Rev. D 2020, 102, 064054. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. The eye of the storm: A regular Kerr black hole. J. Cosmol. Astropart. Phys. 2022, 2022, 011. [Google Scholar] [CrossRef]
- Banerjee, I.; Sau, S.; SenGupta, S. Signatures of regular black holes from the shadow of Sgr A* and M87*. J. Cosmol. Astropart. Phys. 2022, 2022, 066. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; García, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.I. Note on the Kerr spinning-particle metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. Generating rotating regular black hole solutions without complexification. Phys. Rev. D 2014, 90, 064041. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. From static to rotating to conformal static solutions: Rotating imperfect fluid wormholes with(out) electric or magnetic field. Eur. Phys. J. C 2014, 74, 1–11. [Google Scholar] [CrossRef]
- Wu, M.H.; Guo, H.; Kuang, X.M. Shadow Cast of Rotating Charged Black Hole with Scalar Q-Hair. Symmetry 2022, 14, 2237. [Google Scholar] [CrossRef]
- Azreg-Aïnou, M. Regular and conformal regular cores for static and rotating solutions. Phys. Lett. B 2014, 730, 95–98. [Google Scholar] [CrossRef]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlík, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef]
- Ghosh, S.G. A nonsingular rotating black hole. Eur. Phys. J. C 2015, 75, 1–7. [Google Scholar] [CrossRef]
- Walker, R.C.; Hardee, P.E.; Davies, F.B.; Ly, C.; Junor, W. The Structure and Dynamics of the Subparsec Jet in M87 Based on 50 VLBA Observations over 17 Years at 43 GHz. Astrophys. J. Lett. 2018, 855, 128. [Google Scholar] [CrossRef]
- Kuang, X.-M.; Tang, Z.-Y.; Wang, B.; Wang, A. Constraining a modified gravity theory in strong gravitational lensing and black hole shadow observations. Phys. Rev. D 2022, 106, 064012. [Google Scholar] [CrossRef]
- Afrin, M.; Kumar, R.; Ghosh, S.G. Parameter estimation of hairy Kerr black holes from its shadow and constraints from M87*. Mon. Not. R. Astron. Soc. 2021, 504, 5927–5940. [Google Scholar] [CrossRef]
- Ayón-Beato, E.; Garcia, A. Non-Singular Charged Black Hole Solution for Non-Linear Source. Gen. Relativ. Gravit. 1999, 31, 629–633. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25–29. [Google Scholar] [CrossRef]
- Ma, M.-S. Magnetically charged regular black hole in a model of nonlinear electrodynamics. Ann. Phys. 2015, 362, 529–537. [Google Scholar] [CrossRef]
- Jafarzade, K.; Zangeneh, M.K.; Lobo, F.S. Shadow, deflection angle and quasinormal modes of Born-Infeld charged black holes. J. Cosmol. Astropart. Phys. 2021, 2021, 008. [Google Scholar] [CrossRef]
- Xiang, L.; Ling, Y.; Shen, Y.-G.; Liu, C.-Z.; He, H.-S.; Xu, L.-F. Generalized uncertainty principles, effective Newton constant and the regular black hole. Ann. Phys. 2018, 396, 334–350. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, F.; Wu, X. Construction of Explicit Symplectic Integrators in General Relativity. I. Schwarzschild Black Holes. Astrophys. J. Lett. 2021, 907, 66. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, Y.; Wu, M.-H. The Shadows of Regular Black Holes with Asymptotic Minkowski Cores. Symmetry 2022, 14, 2415. https://doi.org/10.3390/sym14112415
Ling Y, Wu M-H. The Shadows of Regular Black Holes with Asymptotic Minkowski Cores. Symmetry. 2022; 14(11):2415. https://doi.org/10.3390/sym14112415
Chicago/Turabian StyleLing, Yi, and Meng-He Wu. 2022. "The Shadows of Regular Black Holes with Asymptotic Minkowski Cores" Symmetry 14, no. 11: 2415. https://doi.org/10.3390/sym14112415
APA StyleLing, Y., & Wu, M.-H. (2022). The Shadows of Regular Black Holes with Asymptotic Minkowski Cores. Symmetry, 14(11), 2415. https://doi.org/10.3390/sym14112415






