A Numerical Computation for an Impulsive Fractional Differential Equation with a Deviated Argument

Abstract

Symmetry analysis is an effective tool for understanding differential equations, particularly when analyzing equations derived from mathematical concepts. This paper is concerned with an impulsive fractional differential equation (IFDE) with a deviated argument. We implement two techniques, the Adomian decomposition method (ADM) and the fractional differential transform method (FDTM), for solving IFDEs. In these schemes, we obtain the solutions in the form of a convergent power series with easily computed components. This paper also discusses the existence and uniqueness of solutions using the Banach contraction principle. This paper presents a numerical comparison between the two methods for solving IFDEs. We illustrate the proposed methods with a few examples and find their numerical solutions. Moreover, we show the graph of numerical solutions via MATLAB. The numerical results demonstrate that the ADM approach is quite accurate and readily implemented.

1. Introduction

The concept of fractional derivatives was originally established in Leibniz’s letter to L’Hospital on 30 September 1695, when he raised the meaning of the derivative of order $\frac{1}{2}$. The issue raised by Leibniz attracted many well-known mathematicians, including Liouville, Grünwald, Riemann, Euler, Lagrange, Heaviside, Fourier, Abel, Letnikov, and many others. Since the 19th century, the theory of fractional calculus originated rapidly and was the foundation for several disciplines, such as fractional differential equations, non-integer order geometry, and fractional dynamics. Today, numerous applications exist in various branches, including optimal control, porous media, fractional filters, signal and image processing, fractals, rheology, electrochemistry, chemical engineering, fluid mechanics, polymer physics, etc. [1,2,3]. For the basics of fractional calculus and applications, see [4,5].

Fractional differential equations with deviated arguments are frequently used to study and predict many results in numerous fields of science, such as the time taken by a chemical reaction and its reactants in chemical kinetics, the production of new viruses in a biological system, etc. The applications of fractional differential equations with deviated arguments are used in laser dynamics, neural networks, population dynamics, economics, etc.

It is well known that many real-life phenomena are affected by sudden changes in their state at certain moments, such as heartbeats and blood flow in the human body. These phenomena are explained in terms of impulses, whose duration is negligible compared to entire processes that occur. The study of IFDEs has received much attention recently. Benchohra et al. [6], Lakshmikantham et al. [7], Samoilenko and Peresyuk [8], as well as the references therein, may be used in the study of the impulsive theory. It has many applications, including drug diffusion in the human body, frequency-modulated systems, metallurgy, theoretical physics, industrial robotics, engineering, etc. For more details, refer to the papers [9,10].

People realize that several real-world problems connect with the present time and their history, which can be recognized as time delay problems. The delays have been observed to be either time-dependent or constant [11,12,13]. Many practical examples illustrate time delay. The theory of delay differential equations is receiving attention and also increasing rapidly.

Since most nonlinear fractional differential equations lack analytical solutions, approximation and numerical approaches must be used to find their solution. There are several techniques used to find numerical solutions to fractional differential equations. The most commonly used techniques are ADM [14,15,16,17], variational iteration method [18,19], power series method [20,21], FDTM [22,23,24,25,26], splines [27,28], and finite element method [29,30,31]. As a result, symmetry analysis is a fabulous tool for understanding differential equations, particularly when analyzing equations derived from mathematical concepts. The foundation of nature is symmetry. However, symmetry is absent from the majority of natural observations. There are two types of symmetry: finite and infinitesimal. Finite symmetries can be discrete or continuous. Parity and temporal inversion are discrete natural symmetries, whereas space is a continuous transformation.

In this study, we used the ADM approach to find the numerical solution. ADM is a very effective approach that is used to obtain the approximate solutions of various nonlinear, partial, and ordinary differential equations [32,33]. In this method, we found the solution in the form of a series with easily computed components that converges rapidly to the exact solution. ADM is also used to obtain the numerical solutions of IFDEs [14,16,17].

In 1995, Abbaoui and Cherruault [34] presented new ideas for calculating the Adomian’s polynomials used in ADM and presented the proof of convergence of the ADM solution. Evans and Raslan [32] established the numerical solution of the delay differential equation using ADM in 2004. In 2007, Momani and Odibat [18] demonstrated the numerical comparison of methods, the variational iteration method, and the ADM for solving linear differential equations of fractional order. In 2013, Duan et al. [16] presented the ADM and its modifications combined with convergence acceleration techniques. In 2014, Mohammed and Khlaif [14] established the numerical solution for solving fractional delay differential equations via ADM. Foukrach [33] studied the approximate solution to a Bürgers system with time and space fractional derivatives using ADM in 2018. In 2019, Changyou [17] discussed a computational technique for IFDEs via ADM. Guo [35] discussed the ADM method for fractional differential Equations (2019). Afreen and Raheem [15] studied a nonlinear fractional system with deviated arguments using ADM in 2022.

Arikoglu and Ozkol [25] discussed the numerical solution of fractional differential equations using DTM in 2007. In 2008, Ertürk and Momani [26] demonstrated the numerical solution for solving systems of fractional differential equations using FDTM. In 2009, Karakoç and Bereketoğlu [22] studied the numerical solutions of delay differential equations by using FDTM. Al-rabtah et al. [24] demonstrated the numerical solutions of a fractional oscillator by using FDTM in 2010. Odibat et al. [23] discussed the implementation of the generalized differential transform scheme for simulating IFDEs.

The literature review reveals that various researchers have considered the ADM and FDTM to find the numerical solutions of fractional differential equations. Motivated by the works of [17,32,35], we discussed the existence and uniqueness of the IFDE (1) and also studied its numerical solution. We compared the numerical solution with another method: the FDTM.

This paper is organized as follows. The first two sections contain the introduction, proposed problem, assumptions, definitions, and some lemma. Section 3 is about the existence and uniqueness of the solution. In Section 4, we have given the algorithm of ADM and FDTM for IFDE. In Section 5, some examples of IFDE are provided, and their numerical solutions are obtained by ADM and FDTM. At the end, a conclusion is added.

2. Formulation of the Problem

Consider the IFDE with a deviated argument in a Banach space $(X,\parallel ·\parallel )$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\alpha }\vartheta \left(t\right)=\mathcal{K}(t,\vartheta \left(t\right),\vartheta \left(\zeta \left(t\right)\right)),t\in [0,T],t\ne t_q,\hfill & \\ \Delta \vartheta \left(t_q\right)={\mathcal{I}}_q\left(\vartheta \left(t_q\right)\right),q=1,2,\cdots ,m,\hfill & \\ \vartheta \left(0\right)=\beta ,\hfill \end{array}\right.\end{array}$$

(1)

where $\beta$ is a positive constant and ${}^C{D}_t^{\alpha }$ is the Caputo fractional derivative of order $0<\alpha \le 1$. Let $0=t_0<t_1<\cdots <t_m<t_{m+1}=T$. $\mathcal{K}$ is a nonlinear function and $\zeta :[0,T]\to \mathbb{R}$ is such that $\zeta \left(t\right)\le t$. The jumps at $t_q\in (0,T)$ are given by $\Delta \vartheta \left(t_q\right)=\vartheta \left(t_q^{+}\right)-\vartheta \left(t_q^{-}\right)$, where $\vartheta \left(t_q^{+}\right)$ and $\vartheta \left(t_q^{-}\right)$ denote the right and left hand limit values of $\vartheta \left(t\right)$ at $t=t_q$, respectively, and are determined by the nonlinear function ${\mathcal{I}}_q$, where $q=1,2,3,\cdots ,m$.

Let $PC([0,T],X)=\{\vartheta :[0,T]\to X:{\vartheta }_{\left|\right(t_q,t_{q+1}]}\in C((t_q,t_{q+1}],X),and\vartheta \left(t_q^{+}\right),\vartheta \left(t_q^{-}\right)$ exist for $q=1,2,3,\cdots ,m\}$. The space $PC:=PC\left(\right[0,T],X)$ is a Banach space with a supremum norm defined by ${\parallel \vartheta \parallel }_{PC}=\underset{t\in [0,T]}{sup}\parallel \vartheta \left(t\right)\parallel$. We assume the following assumptions:

Hypothesis 1. 

The map $\mathcal{K}:[0,T]\times PC\times PC\to PC$ satisfies

$$\parallel \mathcal{K}(t,\vartheta \left(t\right),\tilde{\vartheta }\left(t\right))-\mathcal{K}(t,\varrho \left(t\right),\tilde{\varrho }\left(t\right))\parallel \le {\mu }_1\parallel \vartheta -\varrho {\parallel }_{PC}+{\mu }_2\parallel \tilde{\vartheta }-\tilde{\varrho }{\parallel }_{PC},$$

for all $t\in [0,T]$, $\vartheta ,\tilde{\vartheta },\varrho ,\tilde{\varrho }\in PC$, and ${\mu }_1,{\mu }_2>0$ are constants.

Hypothesis 2. 

The functions ${\mathcal{I}}_q:PC\to X$ are continuous for $q=1,2,\cdots ,m$ and there exists $L_q>0$ such that

$$\sum _{j=1}^q\parallel {\mathcal{I}}_j\left(\vartheta \right)-{\mathcal{I}}_j\left(\varrho \right)\parallel \le L_q{\parallel \vartheta -\varrho \parallel }_{PC}$$

for every $\vartheta ,\varrho \in PC$.

Definition 1 

([14,29]). The (left) Riemann–Liouville integral of h of order $\alpha >0$ is defined as:

$$\begin{array}{c}\hfill J_t^{\alpha }h\left(t\right)\equiv {}_a{J}_t^{\alpha }h\left(t\right)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_a^t{(t-x)}^{\alpha -1}h\left(x\right)dx,\alpha >0,t>0,}\hfill & \\ h\left(t\right),\alpha =0.\hfill \end{array}\right.\end{array}$$

where $\mathsf{\Gamma }(·)$ denotes the Euler gamma function.

The (right) Riemann–Liouville integral of h of order $\alpha >0$ on the interval $[t,b]$ instead of $[a,t]$ is given by:

$$\begin{array}{c}\hfill J_t^{\alpha }h\left(t\right)\equiv {}_t{J}_b^{\alpha }h\left(t\right)=\left\{\begin{array}{cc}{\displaystyle {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_t^b{(x-t)}^{\alpha -1}h\left(x\right)dx,\alpha >0,t>0,}\hfill & \\ h\left(t\right),\alpha =0.\hfill \end{array}\right.\end{array}$$

Definition 2 

([14]). The Caputo fractional derivative of h of order $0<\alpha \le 1$ is defined as:

$${}^C{D}_t^{\alpha }h\left(t\right)=\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t{(t-x)}^{-\alpha }{h}^{\prime }\left(x\right)dx.$$

Definition 3 

([20]). Let $\alpha ,\beta >0$. The two-parameter Mittag–Leffler function is defined as:

$$E_{\alpha ,\beta }\left(t^{\alpha }\right)=\sum _{k=0}^{\infty }\frac{{\left(t^{\alpha }\right)}^k}{\mathsf{\Gamma }(\alpha k+\beta )}.$$

Lemma 1 

([9]). The IFDE with a deviated argument (1) is equivalent to the following integral equation:

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}\vartheta \left(0\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (0,t_1],\hfill & \\ \vartheta \left(0\right)+{\mathcal{I}}_1\left(\vartheta \left(t_1\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^m}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_m,T].\hfill \end{array}\right.\end{array}$$

(2)

3. Existence and Uniqueness of the Solution

Theorem 1. 

If the Hypotheses 1 and 2 are satisfied and

$$\underset{1\le q\le m}{max}\left\{L_q+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right\}<1,$$

then IFDE (1) has a unique solution.

Proof. 

Define the operator $F:PC\to PC$ given by:

$$\begin{array}{c}\hfill F\left(\vartheta \left(t\right)\right)=\left\{\begin{array}{cc}\vartheta \left(0\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (0,t_1],\hfill & \\ \vartheta \left(0\right)+{\mathcal{I}}_1\left(\vartheta \left(t_1\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^m}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_m,T].\hfill \end{array}\right.\end{array}$$

(3)

We show that the operator F has a unique fixed point. Let $\vartheta ,\varrho \in PC$, and $t\in (0,t_1]$; then, we have

$$\begin{array}{ccc}\hfill \parallel F\left(\vartheta \right(t\left)\right)-F\left(\varrho \right(t\left)\right)\parallel & =& \parallel J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)-\mathcal{K}(t,\varrho (t),\varrho (\zeta \left(t\right)\left)\right)\right)\parallel \hfill \\ & \le & \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-x)}^{\alpha -1}\parallel \mathcal{K}\left(x,\vartheta \left(x\right),\vartheta \left(x\right)\right)-\mathcal{K}\left(x,\varrho \left(x\right),\varrho \left(x\right)\right)\parallel dx\hfill \\ & \le & \frac{({\mu }_1+{\mu }_2)}{\mathsf{\Gamma }\left(\alpha \right)}{\parallel \vartheta -\varrho \parallel }_{PC}{\int }_0^t{(t-x)}^{\alpha -1}dx\hfill \\ & \le & \frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{\parallel \vartheta -\varrho \parallel }_{PC}.\hfill \end{array}$$

For $t\in (t_1,t_2]$, we have

$$\begin{array}{ccc}\hfill \parallel F\left(\vartheta \right(t\left)\right)-F\left(\varrho \right(t\left)\right)\parallel & \le & \parallel {\mathcal{I}}_1(\vartheta \left(t_1\right)-{\mathcal{I}}_1\left(\varrho \left(t_1\right)\right)\parallel \hfill \\ & & +\parallel J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)-\mathcal{K}(t,\varrho (t),\varrho (\zeta \left(t\right)\left)\right)\right)\parallel \hfill \\ & \le & L_1{\parallel \vartheta -\varrho \parallel }_{PC}+\frac{({\mu }_2+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{\parallel \vartheta -\varrho \parallel }_{PC}\hfill \\ & \le & \left(L_1+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right){\parallel \vartheta -\varrho \parallel }_{PC}.\hfill \end{array}$$

Similarly, for $t\in (t_q,t_{q+1}],q=1,2,3,\cdots ,m$, we have

$$\begin{array}{ccc}\hfill \parallel F\left(\vartheta \right(t\left)\right)-F\left(\varrho \right(t\left)\right)\parallel & \le & \parallel \sum _{j=1}^q\left({\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)-{\mathcal{I}}_j\left(\varrho \left(t_j\right)\right)\right)\parallel \hfill \\ & & +\parallel J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)-\mathcal{K}(t,\varrho (t),\varrho (\zeta \left(t\right)\left)\right)\right)\parallel \hfill \\ & \le & L_q{\parallel \vartheta -\varrho \parallel }_{PC}+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}{\parallel \vartheta -\varrho \parallel }_{PC}\hfill \\ & \le & \left(L_q+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right){\parallel \vartheta -\varrho \parallel }_{PC}.\hfill \end{array}$$

Thus, for all $t\in [0,T]$, we obtain

$$\begin{array}{c}\hfill \parallel F\left(\vartheta \left(t\right)\right)-F\left(\varrho \left(t\right)\right)\parallel \le \underset{1\le q\le m}{max}\left\{L_q+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right\}{\parallel \vartheta -\varrho \parallel }_{PC}.\end{array}$$

Since $\underset{1\le q\le m}{max}\left\{L_q+\frac{({\mu }_1+{\mu }_2)T^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}\right\}<1$, we conclude that F is a contraction mapping. Therefore, by the Banach contraction theorem, the map F has a unique fixed point, which is the solution of IFDE (1). □

4. Analysis of the Method

4.1. Adomian Decomposition Method (ADM)

In order to solve IFDE with a deviated argument (1) with ADM, integrating in the sense of Caputo, we have

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}\vartheta \left(0\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (0,t_1],\hfill & \\ \vartheta \left(0\right)+{\mathcal{I}}_1\left(\vartheta \left(t_1\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^m}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left(\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)\right),t\in (t_m,T].\hfill \end{array}\right.\end{array}$$

(4)

In ADM, we assume the solution in the form of the following series:

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\sum _{n=0}^{\infty }{\vartheta }_n\left(t\right),\end{array}$$

(5)

so that the components ${\vartheta }_n\left(t\right)$ will be determined recursively. Moreover, the method defines the nonlinear term $\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)$ by the Adomian polynomials

$$\begin{array}{c}\hfill \mathcal{K}(t,\vartheta \left(t\right),\vartheta \left(\zeta \left(t\right)\right))=\sum _{n=0}^{\infty }{A}_n,\end{array}$$

(6)

where $A_n$ are Adomian polynomials that can be generated for all forms of non-linearity as

$$\begin{array}{c}\hfill A_n=\frac{1}{n!}{\displaystyle \frac{d^n}{d{\lambda }^n}}{\left[\mathcal{K}\left(t,\sum _{k=0}^{\infty }{\lambda }^k{\vartheta }_k\left(t\right),\sum _{k=0}^{\infty }{\lambda }^k{\vartheta }_k\left(\zeta \left(t\right)\right)\right)\right]}_{\lambda =0},\end{array}$$

where $\lambda$ is a parameter.

Substituting the values of $\vartheta \left(t\right)$ from (5) and $\mathcal{K}$ from (6) in (4), we obtain

$$\begin{array}{c}\hfill {\displaystyle \sum _{n=0}^{\infty }}{\vartheta }_n\left(t\right)=\left\{\begin{array}{cc}\vartheta \left(0\right)+J_t^{\alpha }\left({\displaystyle \sum _{n=0}^{\infty }}{A}_n\right),t\in (0,t_1],\hfill & \\ \vartheta \left(0\right)+{\mathcal{I}}_1\left(\vartheta \left(t_1\right)\right)+J_t^{\alpha }\left({\displaystyle \sum _{n=0}^{\infty }}{A}_n\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left({\displaystyle \sum _{n=0}^{\infty }}{A}_n\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ \vartheta \left(0\right)+{\displaystyle \sum _{j=1}^m}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right)+J_t^{\alpha }\left({\displaystyle \sum _{n=0}^{\infty }}{A}_n\right),t\in (t_m,T].\hfill \end{array}\right.\end{array}$$

(7)

We obtain the following scheme if $t\in (0,t_1]$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\vartheta \left(0\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

(8)

and, if $t\in (t_q,t_{q+1}]$ for $q=1,2,3,\cdots ,m$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\vartheta \left(0\right)+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

(9)

4.2. Fractional Differential Transform Method (FDTM)

In this section, we introduce the FDTM to calculate the numerical solutions for IFDE. This method has been developed in [25] as follows:

The Riemann–Liouville fractional derivative of the function h of order $\alpha$ is defined as

$$\begin{array}{c}\hfill D_t^{\alpha }h\left(t\right)=\frac{1}{\mathsf{\Gamma }(m-\alpha )}{\displaystyle \frac{d^m}{d{t}^m}}{\int }_0^t{(t-x)}^{m-\alpha -1}h\left(x\right)dx,\end{array}$$

(10)

where $m-1<\alpha \le m,m\in \mathbb{N},t>0$. We consider that the analytical and continuous function $h\left(t\right)$ can be expressed in terms of the following fractional power series:

$$\begin{array}{c}\hfill h\left(t\right)=\sum _{k=0}^{\infty }H\left(k\right)t^{\frac{k}{\beta }},\end{array}$$

(11)

where $\beta$ is the order of the fraction and $H\left(k\right)$ denotes the fractional differential transform (FDT) of function $h\left(t\right)$. We define the Caputo fractional derivative to avoid fractional initial and boundary conditions. The Riemann–Liouville operator and the Caputo operator are related by

$$\begin{array}{ccc}\hfill {}^C{D}_t^{\alpha }h\left(t\right)& =& D_t^{\alpha }\left[h\left(t\right)-\sum _{k=0}^{m-1}{h}^{\left(k\right)}\left(0^{+}\right)\frac{t^k}{k!}\right]\hfill \\ & =& \frac{1}{\mathsf{\Gamma }(m-\alpha )}{\displaystyle \frac{d^m}{d{t}^m}}{\int }_0^t{(t-x)}^{m-\alpha -1}\left[h\left(x\right)-\sum _{k=0}^{m-1}{h}^{\left(k\right)}\left(0^{+}\right)\frac{x^k}{k!}\right]dx.\hfill \end{array}$$

(12)

Since the initial conditions are used for the integer order derivatives, the transformed initial conditions are defined as follows:

$$\begin{array}{c}\hfill H\left(k\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{(k/\beta )!}}{\left[{\displaystyle \frac{d^{k/\beta }h\left(t\right)}{d{t}^{k/\beta }}}\right]}_{t=0},fork=0,1,2,\cdots ,\alpha \beta -1,if{\displaystyle \frac{k}{\beta }}\in \mathbb{N},\hfill & \\ 0,{\displaystyle \frac{k}{\beta }}\notin \mathbb{N},\hfill \end{array}\right.\end{array}$$

(13)

where $\alpha$ is the order of the fractional differential equation. For more details on FDTM, we refer to the papers [23,25,26].

From Definition 2 and Lemma 1, the solution of IFDE (1) can be written as

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}{\vartheta }_1\left(t\right),t\in (0,t_1],\hfill & \\ {\vartheta }_2\left(t\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ {\vartheta }_{q+1}\left(t\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ {\vartheta }_{m+1}\left(t\right),t\in (t_m,T],\hfill \end{array}\right.\end{array}$$

(14)

where the solution components ${\vartheta }_k\left(t\right),k=1,2,\cdots ,m+1$ satisfies IFDE (1) with the initial conditions

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_1\left(0\right)={\vartheta }_0,t\in (0,t_1],\hfill & \\ {\vartheta }_2\left(0\right)={\vartheta }_0+{\mathcal{I}}_1\left(\vartheta \left(t_1\right)\right),t\in (t_1,t_2],\hfill & \\ ⋮\hfill & \\ {\vartheta }_{q+1}\left(0\right)={\vartheta }_0+{\displaystyle \sum _{j=1}^q}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right),t\in (t_q,t_{q+1}],\hfill & \\ ⋮\hfill & \\ {\vartheta }_{m+1}\left(0\right)={\vartheta }_0+{\displaystyle \sum _{j=1}^m}{\mathcal{I}}_j\left(\vartheta \left(t_j\right)\right),t\in (t_m,T].\hfill \end{array}\right.\end{array}$$

(15)

The basic steps to achieve the numerical solution of IFDE via FDTM are as follows. In the first step, we employ the FDT to IFDE (1); then, we obtain a recurrence relation. In the second step, simulating this relation by applying the inverse FDT, we obtain the solution component ${\vartheta }_j\left(t\right)$ of IFDE (1) as

$$\begin{array}{c}\hfill {\vartheta }_j\left(t\right)=\sum _{k=0}^{\infty }{X}_j\left(k\right)t^{\frac{k}{\beta }},\end{array}$$

(16)

where $X_j\left(k\right)$ is the FDT of solution component ${\vartheta }_j\left(t\right)$ and satisfies the recurrence relation

$$\begin{array}{c}\hfill \frac{\mathsf{\Gamma }(\alpha +1+\frac{k}{\beta })}{\mathsf{\Gamma }(1+\frac{k}{\beta })}{X}_j(k+\alpha \beta )=K\left(k\right),\end{array}$$

(17)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_1\left(0\right)={\vartheta }_0,\hfill & \\ X_{j+1}\left(0\right)={\vartheta }_0+{\displaystyle \sum _{q=1}^j}{\mathcal{I}}_q\left(\vartheta \left(t_q\right)\right),j=1,2,\cdots ,m,\hfill \end{array}\right.\end{array}$$

$K\left(k\right)$ denotes the FDT of the function $\mathcal{K}(t,\vartheta (t),\vartheta (\zeta \left(t\right)\left)\right)$. Now, by implementing the above analysis, piecewise continuous solutions of IFDE are derived.

5. Numerical Examples

Example 1. 

Consider the IFDE with a deviated argument:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\alpha }\vartheta \left(t\right)=t^2\vartheta \left(t\right)+{\vartheta }^3\left(\frac{t}{3}\right),t\in [0,10],t\ne t_q,\hfill & \\ \Delta \vartheta \left(t_q\right)=1,q=1,2,3,4,\hfill & \\ \vartheta \left(0\right)=0,\hfill \end{array}\right.\end{array}$$

(18)

where $\alpha \in (0,1],0=t_0<t_1<t_2<t_3<t_4<t_5=10$.

For $t\in (t_0,t_1]=(0,2]$, we obtain the following scheme by applying ADM:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=0,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^2{\vartheta }_n\left(t\right)\right)+J_t^{\alpha }\left(A_n\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

where $A_n\left(t\right)$ denote the Adomian polynomials of the nonlinear term ${\vartheta }^3\left(\frac{t}{3}\right)$. The first few terms are

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=0,\hfill & \\ {\vartheta }_1\left(t\right)=0,\hfill & \\ {\vartheta }_2\left(t\right)=0,\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Similarly, for $q=1$, $t\in (t_1,t_2]=(2,4]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=1,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^2{\vartheta }_n\left(t\right)\right)+J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=1,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{1}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}+\frac{3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=2,t\in (t_2,t_3]=(4,6]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^2{\vartheta }_n\left(t\right)\right)+J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{2\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{2^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{2\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{2^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}+\frac{2^5·3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=3,t\in (t_3,t_4]=(6,8]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=3,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^2{\vartheta }_n\left(t\right)\right)+J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=3,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{3\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{3^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{3\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{3^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}+\frac{3^{6-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=4,t\in (t_4,t_5]=(8,10]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^2{\vartheta }_n\left(t\right)\right)+J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{4\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{4^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{4\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{4^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}+\frac{4^5·3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (18) in [0,10] is

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}0,t\in (0,2],\hfill & \\ 1+\frac{\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{1}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}\hfill & \\ +\frac{3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },t\in (2,4],\hfill & \\ 2+\frac{2\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{2^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{2\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{2^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}\hfill & \\ +\frac{2^5·3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },t\in (4,6],\hfill & \\ 3+\frac{3\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{3^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{3\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{3^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}\hfill & \\ +\frac{3^{6-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },t\in (6,8],\hfill & \\ 4+\frac{4\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}{t}^{\alpha +2}+\frac{4^3}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{4\mathsf{\Gamma }\left(3\right)}{\mathsf{\Gamma }(\alpha +3)}·\frac{\mathsf{\Gamma }(\alpha +5)}{\mathsf{\Gamma }(2\alpha +5)}{t}^{2\alpha +4}+\frac{4^3}{\mathsf{\Gamma }(2\alpha +3)}·\left(\frac{\mathsf{\Gamma }(\alpha +3)}{\mathsf{\Gamma }(\alpha +2)}+\frac{\mathsf{\Gamma }\left(3\right)}{3^{\alpha +1}}\right)t^{2\alpha +2}\hfill & \\ +\frac{4^5·3^{1-\alpha }}{\mathsf{\Gamma }\left(2\alpha +1\right)}{t}^{2\alpha },t\in (8,10].\hfill \end{array}\right.\end{array}$$

In Figure 1, the graph shows the piecewise solution of IFDE (18) with order $\alpha =0.10$, and impulses occur at the points $t=2,4,6,8$, whereas, in Figure 2, the graph shows the piecewise solution of IFDE (18) with order $\alpha =0.20$, with the same impulses. Moreover, we can see that the range of the solution increases as the order increases.

Example 2. 

Consider the IFDE with a deviated argument:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\alpha }\vartheta \left(t\right)=\mathsf{\Gamma }(\alpha +2)t+{\vartheta }^2\left(\frac{t}{2}\right),t\in [0,10],t\ne t_q,\hfill & \\ \Delta \vartheta \left(t_q\right)=2,q=1,2,3,4,\hfill & \\ \vartheta \left(0\right)=0,\hfill \end{array}\right.\end{array}$$

(19)

where $0<\alpha \le 1$, and $0=t_0<t_1<t_2<t_3<t_4<t_5=10$.

Using the ADM, we obtain the following scheme for $t\in (t_0,t_1]=(0,2]$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=t^{\alpha +1},\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

where $A_n\left(t\right)$ denote the Adomian polynomials of the nonlinear term ${\vartheta }^2\left(\frac{t}{2}\right)$. The first few terms are

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=t^{\alpha +1},\hfill & \\ {\vartheta }_1\left(t\right)=\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2},\hfill & \\ {\vartheta }_2\left(t\right)=\frac{1}{2^{6\alpha +4}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}·\frac{\mathsf{\Gamma }(4\alpha +4)}{\mathsf{\Gamma }(5\alpha +4)}{t}^{5\alpha +3},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Similarly, for $q=1,t\in (t_1,t_2]=(2,4]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2+t^{\alpha +1},\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2+t^{\alpha +1},\hfill & \\ {\vartheta }_1\left(t\right)=2^2·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·2}{2^{\alpha +1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=2,t\in (t_2,t_3]=(4,6]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4+t^{\alpha +1},\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4+t^{\alpha +1},\hfill & \\ {\vartheta }_1\left(t\right)=4^2·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·4}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=3,t\in (t_3,t_4]=(6,8]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=6+t^{\alpha +1},\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=6+t^{\alpha +1},\hfill & \\ {\vartheta }_1\left(t\right)=6^2·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·6}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=5,t\in (t_4,t_5]=(8,10]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=8+t^{\alpha +1},\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=8+t^{\alpha +1},\hfill & \\ {\vartheta }_1\left(t\right)=8^2·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·8}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (19) in $[0,10]$ is

$$\begin{array}{cc}\vartheta \left(t\right)=& \left\{\begin{array}{c}{t}^{\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2}+\frac{1}{2^{6\alpha +4}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}·\frac{\mathsf{\Gamma }(4\alpha +4)}{\mathsf{\Gamma }(5\alpha +4)}{t}^{5\alpha +3}+\cdots ,t\in (0,2],\hfill \\ \\ 2+t^{\alpha +1}+\frac{2^2\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·2}{2^{\alpha +1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2}+\cdots ,t\in (2,4],\hfill & \\ \\ 4+t^{\alpha +1}+\frac{4^2\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·4}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2}+\cdots ,t\in (4,6],\hfill & \\ \\ 6+t^{\alpha +1}+\frac{6^2\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·6}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2}+\cdots ,t\in (6,8],\hfill & \\ \\ 8+t^{\alpha +1}+\frac{8^2\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(\alpha +2)}{t}^{\alpha }+\frac{2·8}{2^{\alpha -1}}·\frac{\mathsf{\Gamma }(\alpha +2)}{\mathsf{\Gamma }(2\alpha +2)}{t}^{2\alpha +1}+\frac{1}{2^{2\alpha +2}}·\frac{\mathsf{\Gamma }(2\alpha +3)}{\mathsf{\Gamma }(3\alpha +3)}{t}^{3\alpha +2}+\cdots ,t\in (8,10].\hfill \end{array}\right.\end{array}$$

There are four impulse points in Figure 3 and Figure 4. The fractional orders in Figure 3 and Figure 4 are $\alpha =0.35$ and $\alpha =0.55$, respectively.

Example 3. 

Consider the IFDE with a deviated argument:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\alpha }\vartheta \left(t\right)=t^3\vartheta \left(\frac{t}{5}\right)+3{\vartheta }^2\left(t\right),t\in [0,5],t\ne t_q,\hfill & \\ \Delta \vartheta \left(t_q\right)=4,q=1,2,3,4,\hfill & \\ \vartheta \left(0\right)=\mathsf{\Gamma }\left(4\right),\hfill \end{array}\right.\end{array}$$

(20)

where $0<\alpha \le 1$, and $0=t_0<t_1<t_2<t_3<t_4<t_5=5$.

Using the ADM, we obtain the following scheme if $t\in (t_0,t_1]=(0,1]$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^3{\vartheta }_n\left(\frac{t}{5}\right)\right)+3J_t^{\alpha }\left(A_n\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

where $A_n\left(t\right)$ denote the Adomian polynomials of the nonlinear term ${\vartheta }^2\left(t\right)$. The first few terms are

$$\begin{array}{c}\left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_1\left(t\right)=\mathsf{\Gamma }\left(4\right)·\frac{\mathsf{\Gamma }\left(4\right)}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{\left[\mathsf{\Gamma }\left(4\right)\right]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{\mathsf{\Gamma }\left(4\right)}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}+\frac{{\left[\mathsf{\Gamma }\left(4\right)\right]}^2}{\mathsf{\Gamma }(2\alpha +4)}·\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{\left[\mathsf{\Gamma }\left(4\right)\right]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\hfill \end{array}$$

Similarly, for $q=1,t\in (t_1,t_2]=(1,2]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^3{\vartheta }_n\left(\frac{t}{5}\right)\right)+3J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=4+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_1\left(t\right)=\mathsf{\Gamma }\left(4\right)·\frac{[4+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[4+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[4+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}+\frac{{[4+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[4+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=2,t\in (t_2,t_3]=(2,3]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=8+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^3{\vartheta }_n\left(\frac{t}{5}\right)\right)+3J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=8+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_1\left(t\right)=\mathsf{\Gamma }\left(4\right)·\frac{[8+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[8+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[8+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}+\frac{{[8+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3\mathsf{\Gamma }(\alpha +4)}{5^{\alpha }\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[8+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=3,t\in (t_3,t_4]=(3,4]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=12+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^3{\vartheta }_n\left(\frac{t}{5}\right)\right)+3J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=12+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_1\left(t\right)=\mathsf{\Gamma }\left(4\right)·\frac{[12+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[12+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[12+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}+\frac{{[12+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3\mathsf{\Gamma }(\alpha +4)}{5^{\alpha }\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[12+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

For $q=4,t\in (t_4,t_5]=(4,5]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=16+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left(t^3{\vartheta }_n\left(\frac{t}{5}\right)\right)+3J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=16+\mathsf{\Gamma }\left(4\right),\hfill & \\ {\vartheta }_1\left(t\right)=\mathsf{\Gamma }\left(4\right)·\frac{[16+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[16+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[16+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}+\frac{{[16+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3\mathsf{\Gamma }(\alpha +4)}{5^{\alpha }\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[16+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (20) in $[0,5]$ is

$$\begin{array}{cc}\hfill \vartheta \left(t\right)=& \left\{\begin{array}{cc}\mathsf{\Gamma }\left(4\right)+\mathsf{\Gamma }\left(4\right)·\frac{\mathsf{\Gamma }\left(4\right)}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{\left[\mathsf{\Gamma }\left(4\right)\right]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{\mathsf{\Gamma }\left(4\right)}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}\hfill & \\ +\frac{{\left[\mathsf{\Gamma }\left(4\right)\right]}^2}{\mathsf{\Gamma }(2\alpha +4)}·\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{\left[\mathsf{\Gamma }\left(4\right)\right]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }+\cdots ,t\in (0,1],\hfill & \\ 4+\mathsf{\Gamma }\left(4\right)+\mathsf{\Gamma }\left(4\right)·\frac{[4+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[4+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[4+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}\hfill & \\ +\frac{{[4+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[4+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }+\cdots ,t\in (1,2],\hfill & \\ \\ 8+\mathsf{\Gamma }\left(4\right)+\mathsf{\Gamma }\left(4\right)·\frac{[8+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[8+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[8+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}\hfill & \\ +\frac{{[8+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[8+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }+\cdots ,t\in (2,3],\hfill & \\ \\ 12+\mathsf{\Gamma }\left(4\right)+\mathsf{\Gamma }\left(4\right)·\frac{[12+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[12+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[12+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}\hfill & \\ +\frac{{[12+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[12+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }+\cdots ,t\in (3,4],\hfill & \\ \\ 16+\mathsf{\Gamma }\left(4\right)+\mathsf{\Gamma }\left(4\right)·\frac{[16+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}{t}^{\alpha +3}+\frac{3{[16+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{\mathsf{\Gamma }\left(4\right)}{5^{\alpha +3}}·\frac{[8+\mathsf{\Gamma }(4\left)\right]}{\mathsf{\Gamma }(\alpha +4)}·\frac{\mathsf{\Gamma }(\alpha +7)}{\mathsf{\Gamma }(2\alpha +7)}{t}^{2\alpha +6}\hfill & \\ +\frac{{[16+\mathsf{\Gamma }\left(4\right)]}^2}{\mathsf{\Gamma }(2\alpha +4)}\left[6\mathsf{\Gamma }\left(4\right)+\frac{3}{5^{\alpha }}·\frac{\mathsf{\Gamma }(\alpha +4)}{\mathsf{\Gamma }(\alpha +1)}\right]t^{2\alpha +3}+\frac{18{[16+\mathsf{\Gamma }\left(4\right)]}^3}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }+\cdots ,t\in (4,5].\hfill \end{array}\right.\end{array}$$

In Figure 5 and Figure 6, the impulses occur at the points $t=1,2,3,4$. The graphs of the piecewise solution obtained for the order $\alpha =0.50$ and $\alpha =0.60$ are shown in Figure 5 and Figure 6, respectively.

In this example, we compared the numerical solution obtained by ADM and FDTM with the exact solution.

Example 4. 

Consider the IFDE with a deviated argument:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\alpha }\vartheta \left(t\right)=1-{\vartheta }^2\left(\frac{t}{2}\right),t\in [0,\pi ],t\ne \frac{\pi }{2},\hfill & \\ \Delta \vartheta \left(\frac{\pi }{2}\right)=-1,\hfill & \\ \vartheta \left(0\right)=0,\hfill \end{array}\right.\end{array}$$

(21)

where $0<\alpha \le 1$, and $0=t_0<t_1=\frac{\pi }{2}<t_2=\pi$.

For $\alpha =1$, the exact solution of IFDE (21) is $\vartheta \left(t\right)=sin(t-\frac{k\pi }{2}),t\in \left(\frac{k\pi }{2}-\frac{(k+1)\pi }{2}\right]$, where $k=1,2$.

Solution when using ADM: Using the ADM, we obtained the following scheme for $t\in (t_0,t_1]=\left(0,\frac{\pi }{2}\right]$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_{n+1}\left(t\right)=-2J_t^{\alpha }\left(A_n\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

where $A_n\left(t\right)$ denote the Adomian polynomials of the nonlinear term ${\vartheta }^2\left(\frac{t}{2}\right)$. The first few terms are

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_1\left(t\right)=\frac{-2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha },\hfill & \\ {\vartheta }_2\left(t\right)=\frac{8}{{\left[2^{2\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^3}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}·\frac{\mathsf{\Gamma }(4\alpha +1)}{\mathsf{\Gamma }(5\alpha +1)}{t}^{5\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Similarly, for $t\in (t_1,t_2]=\left(\frac{\pi }{2},\pi \right]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=-1+\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_{n+1}\left(t\right)=-2J_t^{\alpha }\left(A_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=-1+\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha },\hfill & \\ {\vartheta }_1\left(t\right)=\frac{-2}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }-\frac{2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }+\frac{2^2}{2^{\alpha }\mathsf{\Gamma }(\alpha +1)}·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha },\hfill \\ {\vartheta }_2\left(t\right)=\frac{-2^2}{2^{\alpha }\mathsf{\Gamma }(\alpha +1)}·\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(2\alpha +1)}{t}^{2\alpha }-\frac{2^2}{2^{3\alpha }{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}·\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(4\alpha +1)}{t}^{4\alpha }+\frac{2^3}{2^{3\alpha }\mathsf{\Gamma }(2\alpha +1)}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }\hfill & \\ +\frac{2^2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }+\frac{2^2}{2^{3\alpha }{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^3}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}·\frac{\mathsf{\Gamma }(4\alpha +1)}{\mathsf{\Gamma }(5\alpha +1)}{t}^{5\alpha }\hfill & \\ +\frac{2^2}{2^{4\alpha }\mathsf{\Gamma }(\alpha +1)}·\frac{1}{\mathsf{\Gamma }(2\alpha +1)}·\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(4\alpha +1)}{t}^{4\alpha },\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (21) in $[0,\pi ]$ is

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }+\frac{-2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }+\frac{8}{{\left[2^{2\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^3}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}·\frac{\mathsf{\Gamma }(4\alpha +1)}{\mathsf{\Gamma }(5\alpha +1)}{t}^{5\alpha }+\cdots ,t\in (0,\frac{\pi }{2}],\hfill & \\ & \\ -1-\frac{1}{\mathsf{\Gamma }(\alpha +1)}{t}^{\alpha }-\frac{2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }-\frac{2^2}{2^{3\alpha }{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(4\alpha +1)}{t}^{4\alpha }+\frac{2^3}{2^{3\alpha }\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }\hfill & \\ +\frac{2^2}{{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^2}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}{t}^{3\alpha }+\frac{2^2}{2^{3\alpha }{\left[2^{\alpha }\mathsf{\Gamma }(\alpha +1)\right]}^3}·\frac{\mathsf{\Gamma }(2\alpha +1)}{\mathsf{\Gamma }(3\alpha +1)}·\frac{\mathsf{\Gamma }(4\alpha +1)}{\mathsf{\Gamma }(5\alpha +1)}{t}^{5\alpha }\hfill & \\ +\frac{2^2}{2^{4\alpha }\mathsf{\Gamma }(\alpha +1)}·\frac{1}{\mathsf{\Gamma }(2\alpha +1)}·\frac{\mathsf{\Gamma }(3\alpha +1)}{\mathsf{\Gamma }(4\alpha +1)}{t}^{4\alpha }+\cdots ,t\in (\frac{\pi }{2},\pi ].\hfill \end{array}\right.\end{array}$$

Solution when using FDTM: Let the approximate solution of IFDE (21) be written as

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}{\vartheta }_1\left(t\right),t\in \left(0,\frac{\pi }{2}\right],\hfill & \\ {\vartheta }_2\left(t\right),t\in \left(\frac{\pi }{2},\pi \right],\hfill \end{array}\right.\end{array}$$

where ${\vartheta }_1\left(t\right)$ and ${\vartheta }_2\left(t\right)$ are solutions in the interval $\left(0,\frac{\pi }{2}\right]$ and $\left(\frac{\pi }{2},\pi \right]$, respectively. Let $X_j\left(k\right)$ denote the FDT of ${\vartheta }_j\left(t\right),j=1,2.$ Using the FDT to both the sides of IFDE (21) with its properties (see the papers [22,25]); then, we have

$$\begin{array}{c}\hfill X_j(k+\alpha \beta )=\frac{\mathsf{\Gamma }(1+\frac{k}{\beta })}{\mathsf{\Gamma }(\alpha +1+\frac{k}{\beta })}\left[\delta \left(k\right)-\frac{2}{2^k}\sum _{k_1=0}^k{X}_j\left(k_1\right)X_j(k-k_1)\right],j=1,2,\end{array}$$

(22)

with the boundary conditions are

$$\begin{array}{c}\hfill X_1\left(k\right)={\vartheta }_0=0,X_2\left(k\right)={\vartheta }_0+\Delta \vartheta (\pi /2)=-1fork=0,1,2,\cdots ,\alpha \beta -1.\end{array}$$

(23)

For the solution of order $\alpha =1$, we choose the order of fraction as $\beta =1$; then, Equations (22) and (23) are transformed as

$$\begin{array}{c}\hfill X_j(k+1)=\frac{1}{(1+k)}\left[\delta \left(k\right)-\frac{2}{2^k}\sum _{k_1=0}^k{X}_j\left(k_1\right)X_j(k-k_1)\right],j=1,2,\end{array}$$

(24)

$$\begin{array}{c}\hfill X_1\left(0\right)=0,X_2\left(0\right)=-1.\end{array}$$

(25)

Using the recurrence relation (24) with transformed initial conditions (25), some initial components of the FDT solution for IFDE (21) can be written as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_1\left(0\right)=0,\hfill & \\ X_1\left(1\right)=1,\hfill & \\ X_1\left(2\right)=0,\hfill & \\ X_1\left(3\right)=\frac{-1}{6},\hfill & \\ X_1\left(4\right)=0,\hfill & \\ X_1\left(5\right)=\frac{1}{120},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_2\left(0\right)=-1,\hfill & \\ X_2\left(1\right)=-1,\hfill & \\ X_2\left(2\right)=-1,\hfill & \\ X_2\left(3\right)=\frac{-1}{2},\hfill & \\ X_2\left(4\right)=\frac{-3}{16},\hfill & \\ X_2\left(5\right)=-1,\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the approximate solution of IFDE (21) for order $\alpha =1$ is given as

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}t-\frac{t^3}{6}+\frac{t^5}{120}+\cdots ,t\in \left(0,\frac{\pi }{2}\right],\hfill & \\ & \\ -1-t-t^2-\frac{t^3}{2}-\frac{3t^4}{16}-t^5+\cdots ,t\in \left(\frac{\pi }{2},\pi \right].\hfill \end{array}\right.\end{array}$$

Figure 7, shows the graph of the exact solution, ADM solution, and the FDT solution when $t\in (0,\pi /2],(\frac{\pi }{2},\pi ]$. In Figure 7, there is one impulse point at $t=\pi /2$ and the fractional order $\alpha$ of IFDE (21) is 1.

Table 1. The absolute errors between the exact solution and ADM’s solution, as well as the exact solution and FDTM’s solution of IFDE (21) when $\alpha =1$ and $t\in (0,\pi /2]$.

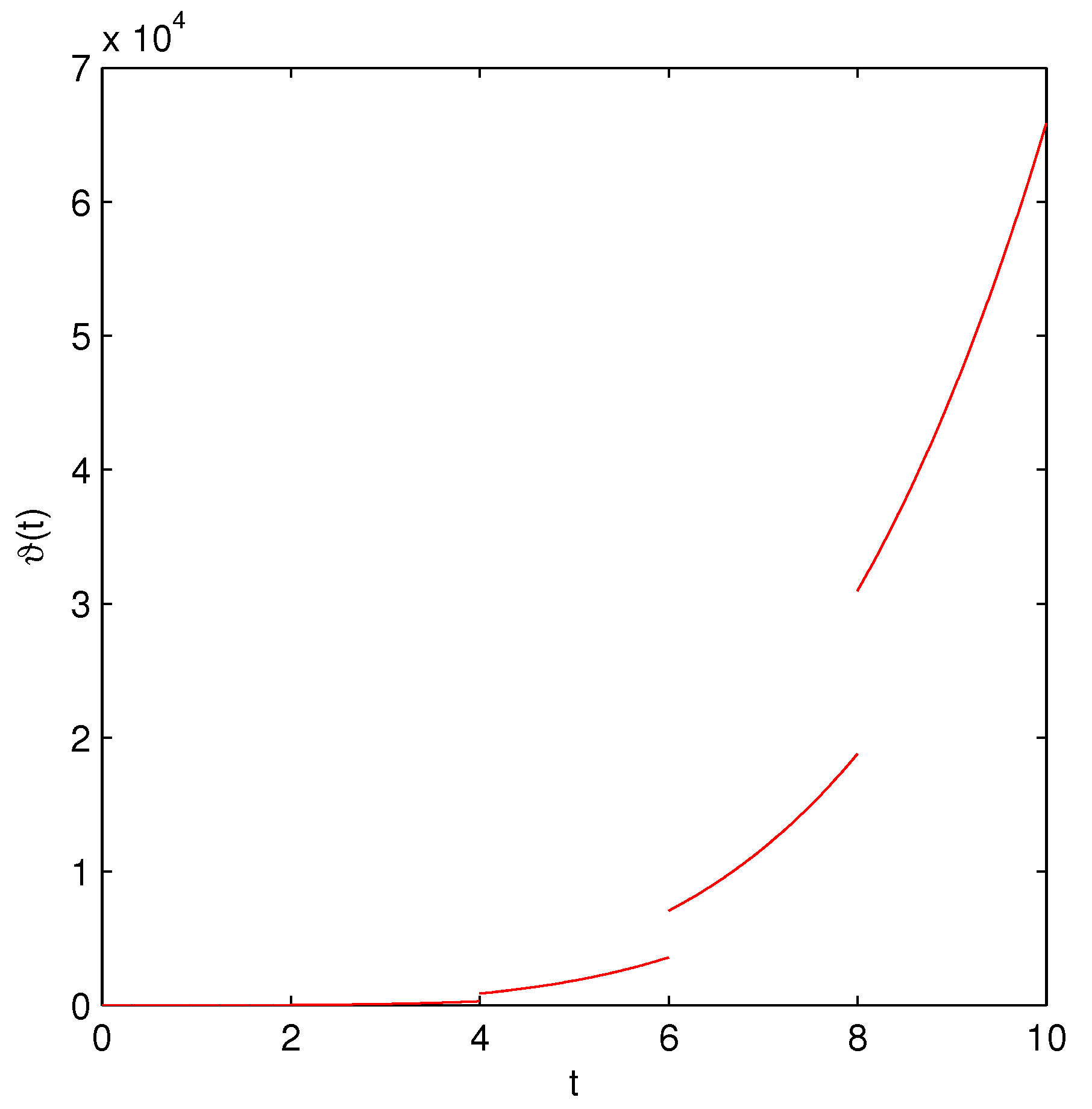
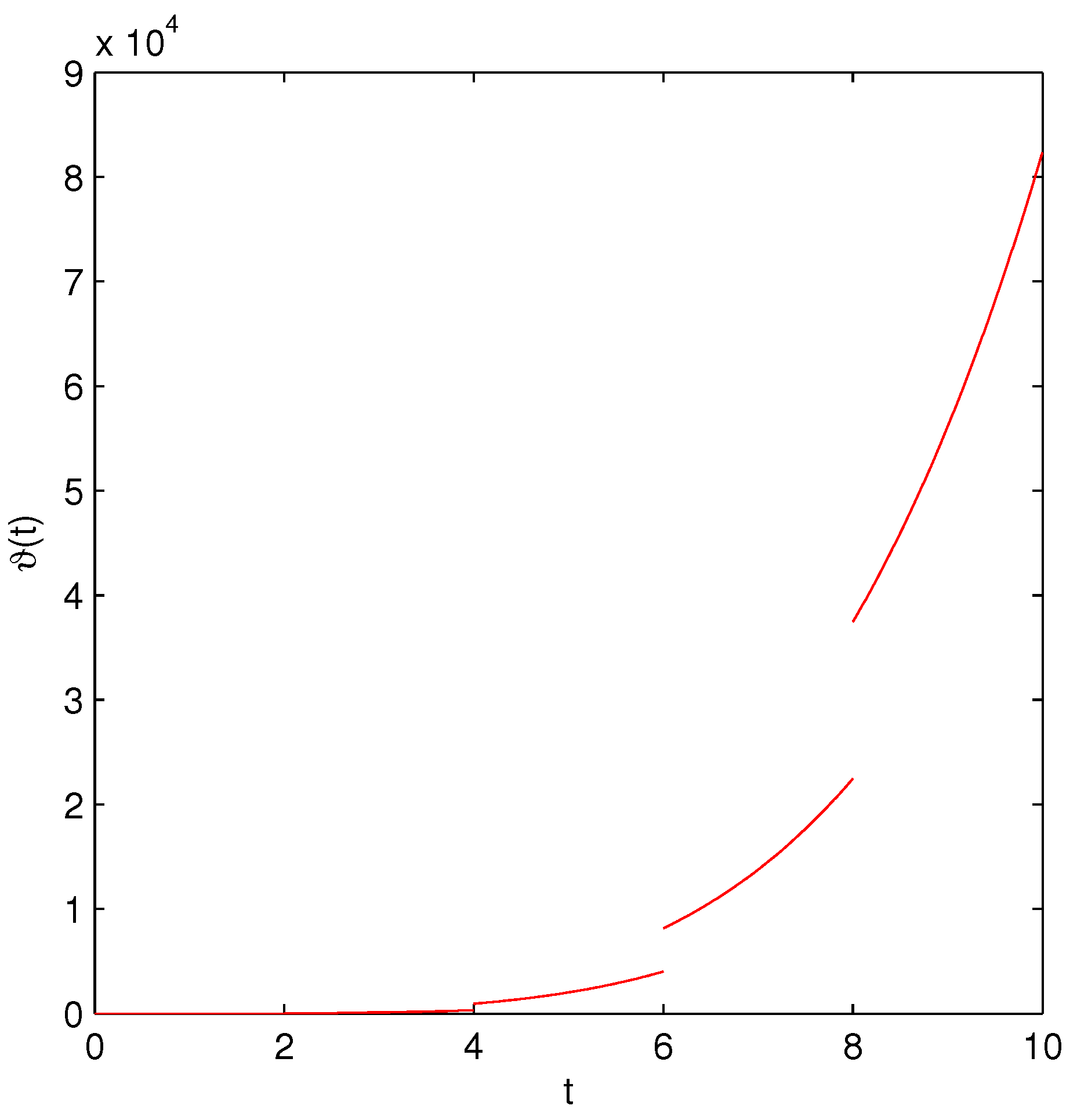
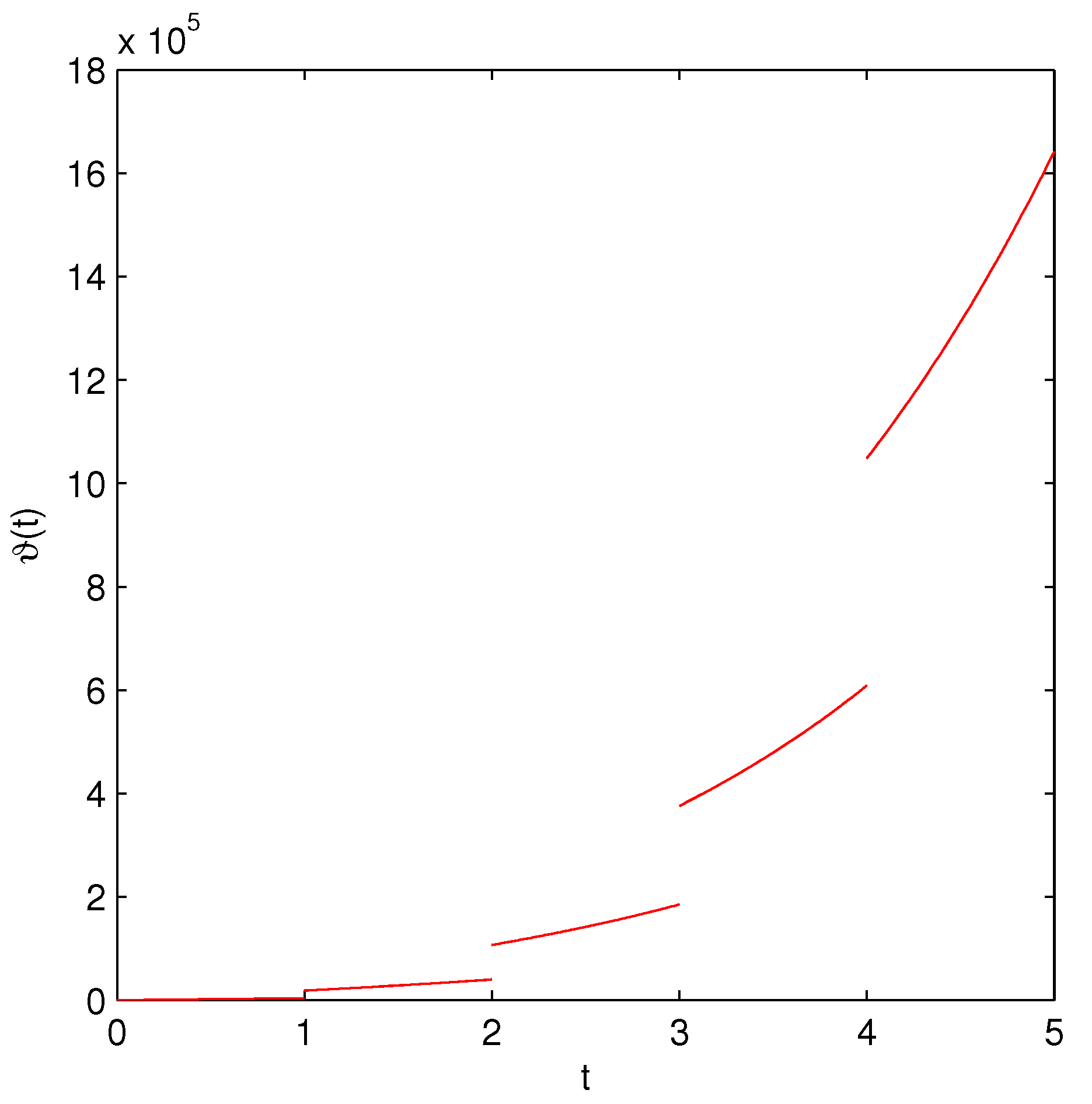
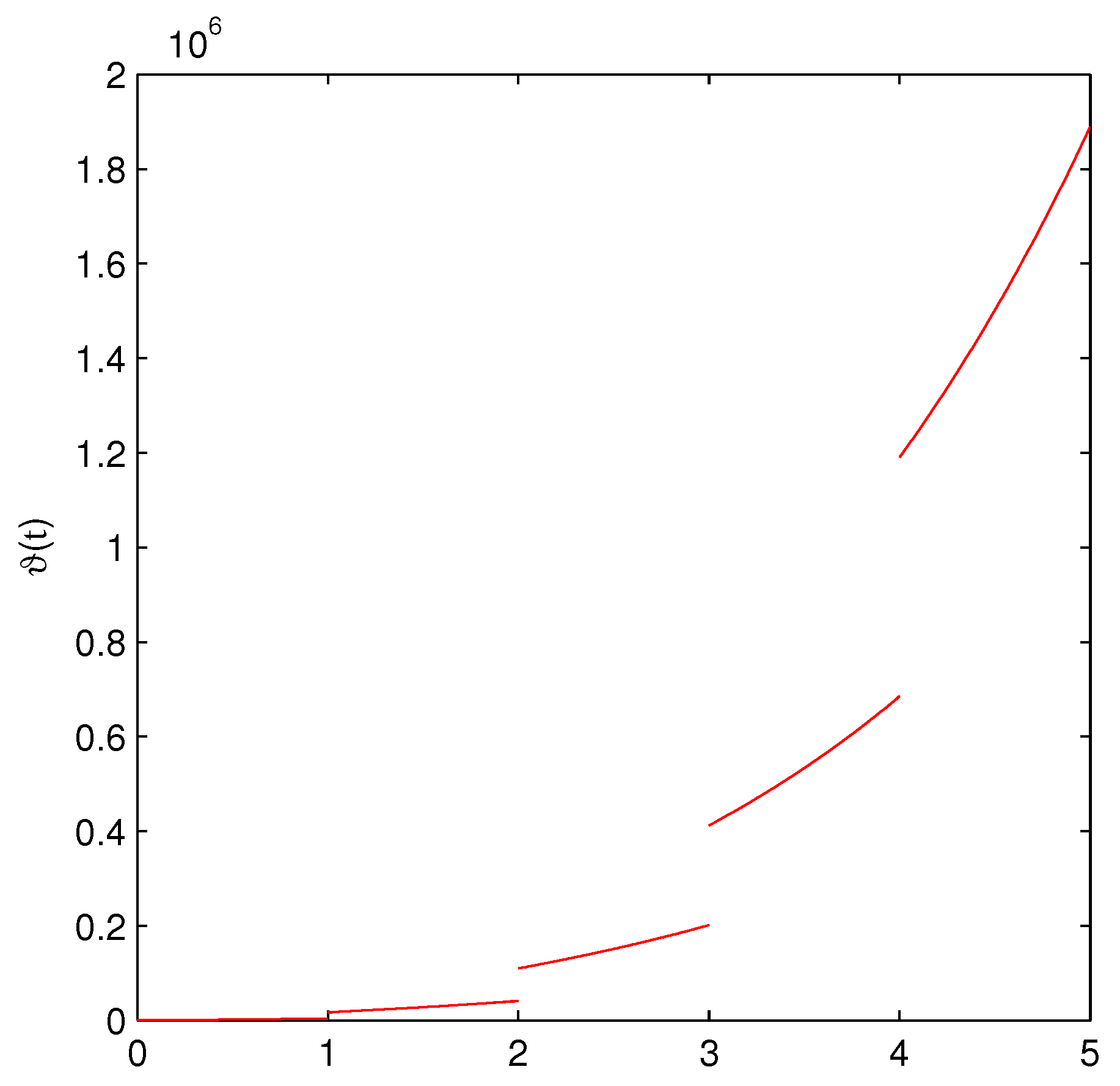
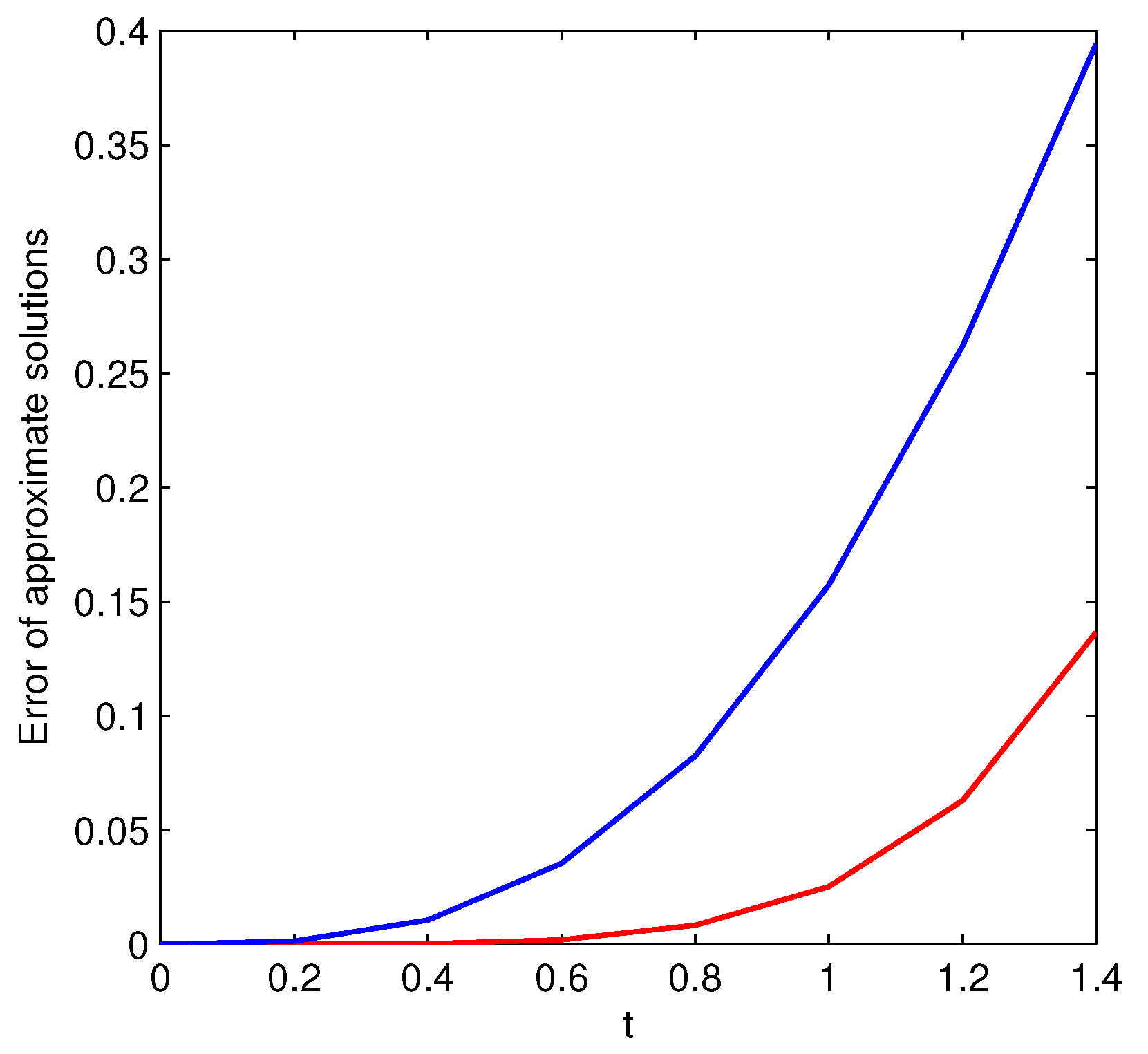
t	Exact Solution	ADM	FDTM	Error (ADM)	Error (FDTM)
0.000	0.0000	0.0000	0.0000	0.0000	0.0000
0.200	0.1987	0.1987	0.2000	0.0000	0.0013
0.400	0.3894	0.3897	0.4000	0.0003	0.0106
0.600	0.5646	0.5666	0.6000	0.0019	0.0353
0.800	0.7174	0.7256	0.7998	0.0082	0.0824
1.000	0.8415	0.8667	0.9986	0.0252	0.1571
1.200	0.9320	0.9949	1.1940	0.0629	0.2620
1.400	0.9854	1.1219	1.3795	0.1365	0.3941

shows the exact solution and the approximate solution obtained by ADM and FDTM for $t\in (0,\pi /2]$. In this example, we only use the first three terms to obtain the ADM solution and five terms to obtain the FDT solution. From the error column, we can see that the error in ADM is less compared to the solution obtained by FDTM.

Table 2. The absolute errors between the exact solution and ADM’s solution, as well as the exact solution and FDTM’s solution of IFDE (21) when $\alpha =1$ and $t\in (\pi /2,\pi ]$.

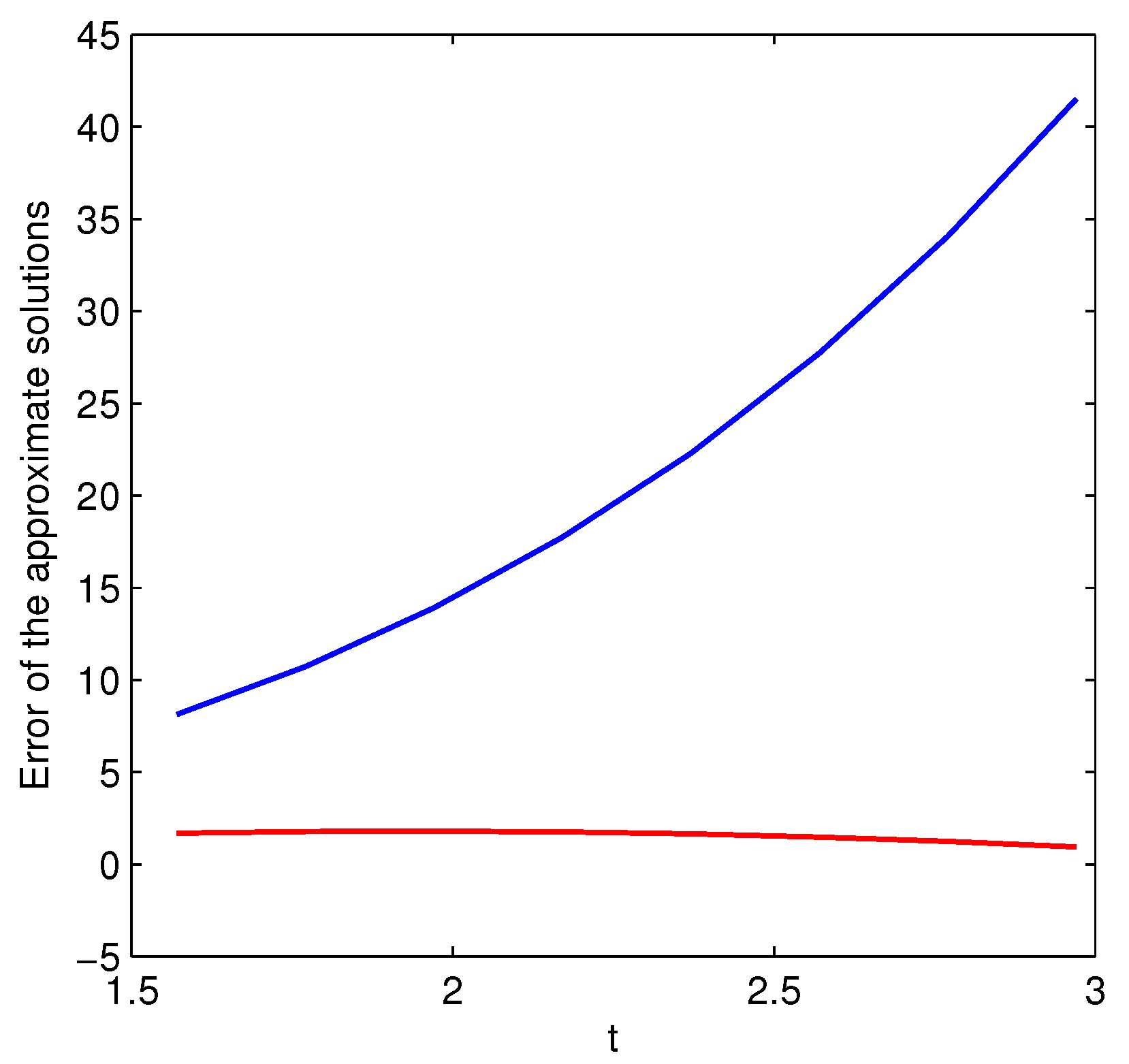
t	Exact Solution	ADM	FDTM	Error (ADM)	Error (FDTM)
1.5708	0.0000	−1.6829	−8.1176	1.6829	8.1176
1.7708	0.1987	−1.5643	−10.5265	1.7630	10.7252
1.9708	0.3894	−1.3954	−13.5107	1.7848	13.9002
2.1708	0.5646	−1.1793	−17.1616	1.7439	17.7263
2.3708	0.7174	−0.9205	−21.5777	1.6378	22.2951
2.5708	0.8415	−0.6244	−26.8648	1.4658	27.7062
2.7708	0.9320	−0.2974	−33.1357	1.2294	34.0677
2.9708	0.9854	0.0535	−40.5107	0.9320	41.4962

shows the exact solution and the approximate solution obtained by ADM and FDTM for $t\in (\pi /2,\pi ]$. In this example, we only use the first three terms to obtain the ADM solution and five terms to obtain the FDT solution. From the error column, we can find that the error in ADM is less compared to the solution obtained by FDTM. The more terms we use, the higher the accuracy we obtain.

Figure 8 and Figure 9 show the graph of the ADM error and FDTM error. We can see that the ADM error is less compared to the FDTM error.

For the solution of order $\alpha =\frac{1}{2}$, we choose the order of fraction as $\beta =2$; then, the Equations (22) and (23) are transformed as follows

$$\begin{array}{c}\hfill X_j(k+1)=\frac{\mathsf{\Gamma }(1+\frac{k}{2})}{\mathsf{\Gamma }(1+\frac{1}{2}+\frac{k}{2})}\left[\delta \left(k\right)-\frac{2}{2^k}\sum _{k_1=0}^k{X}_j\left(k_1\right)X_j(k-k_1)\right],j=1,2,\end{array}$$

(26)

$$\begin{array}{c}\hfill X_1\left(0\right)=0,X_2\left(0\right)=-1.\end{array}$$

(27)

Using the recurrence relation (26) and the transformed initial conditions (27), some initial components of the FDT solution for IFDE (21) can be written as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_1\left(0\right)=0,\hfill & \\ X_1\left(1\right)=\frac{2}{\sqrt{\pi }},\hfill & \\ X_1\left(2\right)=0,\hfill & \\ X_1\left(3\right)=\frac{-8}{3\pi \sqrt{\pi }},\hfill & \\ X_1\left(4\right)=0,\hfill & \\ X_1\left(5\right)=\frac{2^6}{45{\pi }^2\sqrt{\pi }},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_2\left(0\right)=-1,\hfill & \\ X_2\left(1\right)=\frac{-2}{\sqrt{\pi }},\hfill & \\ X_2\left(2\right)=2,\hfill & \\ X_2\left(3\right)=\frac{2}{3\sqrt{\pi }}\left(4-\frac{4}{\sqrt{\pi }}\right),\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the approximate solution of IFDE (21) for order $\alpha =\frac{1}{2}$ is given as

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}\frac{2t}{\sqrt{\pi }}-\frac{8t^3}{3\pi \sqrt{\pi }}+\frac{2^6{t}^5}{45{\pi }^2\sqrt{\pi }}\cdots t\in (0,\frac{\pi }{2}],\hfill & \\ & \\ -1-\frac{2t}{\sqrt{\pi }}+2t^2+\frac{2t^3}{3\sqrt{\pi }}\left(4-\frac{4}{\sqrt{\pi }}\right)\cdots ,t\in (\frac{\pi }{2},\pi ].\hfill \end{array}\right.\end{array}$$

Figure 10, shows the graph of ADM solution and the FDT solution when $t\in (0,\pi /2],(\frac{\pi }{2},\pi ]$. In Figure 10, there is one impulse point at $t=\pi /2$ and the fractional order $\alpha$ of IFDE (21) is $0.5$.

Example 5. 

Consider the IFDE, which is left continuous at $t=1$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{}^C{D}_t^{\frac{1}{2}}\vartheta \left(t\right)=\vartheta \left(t\right),t\in [0,2],t\ne 1,\hfill & \\ \vartheta \left(1^{+}\right)=1,\hfill & \\ \vartheta \left(0\right)=1,\hfill \end{array}\right.\end{array}$$

(28)

where $0=t_0<t_1=1<t_2=2.$

Its exact solution is given by the following equation:

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}{E}_{\frac{1}{2},1}\left(\sqrt{t}\right),t\in [0,1],\hfill & \\ E_{\frac{1}{2},1}\left(\sqrt{t}\right)+\sqrt{t-1}{E}_{\frac{1}{2},\frac{3}{2}}\left(\sqrt{t-1}\right),t\in (1,2].\hfill \end{array}\right.\end{array}$$

(29)

Solution when using ADM: Using the ADM, we obtained the following scheme for $t\in (t_0,t_1]=\left(0,1\right]$:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=1,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left({\vartheta }_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=1,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{1}{\mathsf{\Gamma }(3/2)}{t}^{1/2},\hfill & \\ {\vartheta }_2\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(2\right)}t,\hfill & \\ {\vartheta }_3\left(t\right)=\frac{1}{\mathsf{\Gamma }(5/2)}{t}^{3/2},\hfill & \\ {\vartheta }_4\left(t\right)=\frac{1}{\mathsf{\Gamma }\left(3\right)}{t}^2,\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Similarly, for $t\in (t_1,t_2]=\left(1,2\right]$,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2,\hfill & \\ {\vartheta }_{n+1}\left(t\right)=J_t^{\alpha }\left({\vartheta }_n\left(t\right)\right).\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\vartheta }_0\left(t\right)=2,\hfill & \\ {\vartheta }_1\left(t\right)=\frac{2}{\mathsf{\Gamma }(3/2)}{t}^{1/2},\hfill & \\ {\vartheta }_2\left(t\right)=\frac{2}{\mathsf{\Gamma }\left(2\right)}t,\hfill & \\ {\vartheta }_3\left(t\right)=\frac{2}{\mathsf{\Gamma }(5/2)}{t}^{3/2},\hfill & \\ {\vartheta }_4\left(t\right)=\frac{2}{\mathsf{\Gamma }\left(3\right)}{t}^2,\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (28) in $[0,2]$ is

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}1+\frac{1}{\mathsf{\Gamma }(3/2)}{t}^{1/2}+\frac{1}{\mathsf{\Gamma }\left(2\right)}t+\frac{1}{\mathsf{\Gamma }(5/2)}{t}^{3/2}+\frac{1}{\mathsf{\Gamma }\left(3\right)}{t}^2+\cdots ,t\in (0,1],\hfill & \\ & \\ 2+\frac{2}{\mathsf{\Gamma }(3/2)}{t}^{1/2}+\frac{2}{\mathsf{\Gamma }\left(2\right)}t+\frac{2}{\mathsf{\Gamma }(5/2)}{t}^{3/2}+\frac{2}{\mathsf{\Gamma }\left(3\right)}{t}^2+\cdots ,t\in (1,2].\hfill \end{array}\right.\end{array}$$

Solution by using FDTM: Let the approximate solution of IFDE (28) be written as

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}{\vartheta }_1\left(t\right),t\in \left(0,1\right],\hfill & \\ {\vartheta }_2\left(t\right),t\in \left(1,2\right],\hfill \end{array}\right.\end{array}$$

where ${\vartheta }_1\left(t\right)$ and ${\vartheta }_2\left(t\right)$ are solutions in the interval $\left(0,1\right]$ and $\left(1,2\right]$, respectively. Let $X_j\left(k\right)$ denote the FDT of ${\vartheta }_j\left(t\right),j=1,2$. Applying the FDT to both the sides of IFDE (28) and choosing the order of fraction as $\beta =4$, we have

$$\begin{array}{c}\hfill X_j(k+2)=\frac{\mathsf{\Gamma }(1+\frac{k}{4})}{\mathsf{\Gamma }(\frac{1}{2}+1+\frac{k}{4})}{X}_j\left(k\right),j=1,2,\end{array}$$

(30)

with the boundary conditions

$$\begin{array}{c}\hfill X_1\left(k\right)=1,X_2\left(k\right)=2fork=0,1.\end{array}$$

(31)

Using the recurrence relation (30) with transformed initial conditions (31), some initial components of the FDT solution for IFDE (28) can be written as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_1\left(0\right)=1,\hfill & \\ X_1\left(1\right)=1,\hfill & \\ X_1\left(2\right)=\frac{1}{\mathsf{\Gamma }(3/2)},\hfill & \\ X_1\left(3\right)=\frac{\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(7/4)},\hfill & \\ X_1\left(4\right)=\frac{1}{\mathsf{\Gamma }\left(2\right)},\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{X}_2\left(0\right)=2,\hfill & \\ X_2\left(1\right)=2,\hfill & \\ X_2\left(2\right)=\frac{2}{\mathsf{\Gamma }(3/2)},\hfill & \\ X_2\left(3\right)=\frac{2\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(7/4)},\hfill & \\ X_2\left(4\right)=\frac{2}{\mathsf{\Gamma }\left(2\right)}\hfill & \\ ⋮\hfill \end{array}\right.\end{array}$$

Hence, the numerical solution of IFDE (28) in $[0,2]$ is

$$\begin{array}{c}\hfill \vartheta \left(t\right)=\left\{\begin{array}{cc}1+t^{1/4}+\frac{1}{\mathsf{\Gamma }(3/2)}{t}^{1/2}+\frac{\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(7/4)}{t}^{3/4}+\frac{1}{\mathsf{\Gamma }\left(2\right)}t+\frac{\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(9/4)}{t}^{5/4}+\cdots ,t\in (0,1],\hfill & \\ & \\ 2+2t^{1/4}+\frac{2}{\mathsf{\Gamma }(3/2)}{t}^{1/2}+\frac{2\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(7/4)}{t}^{3/4}+\frac{2}{\mathsf{\Gamma }\left(2\right)}t+\frac{2\mathsf{\Gamma }(5/4)}{\mathsf{\Gamma }(9/4)}{t}^{5/4}+\cdots ,t\in (1,2].\hfill \end{array}\right.\end{array}$$

Figure 11, shows the graph of the exact solution, ADM solution, and the FDT solution when $t\in (0,1],(1,2]$. In Figure 11, there is one impulse point at $t=1$ and the fractional order of IFDE (28) is $1/2$.

Table 3. The absolute errors between the exact solution and ADM’s solution, as well as the exact solution and FDTM’s solution of IFDE (28) of order $1/2$ for some values of $t\in (0,1]$.

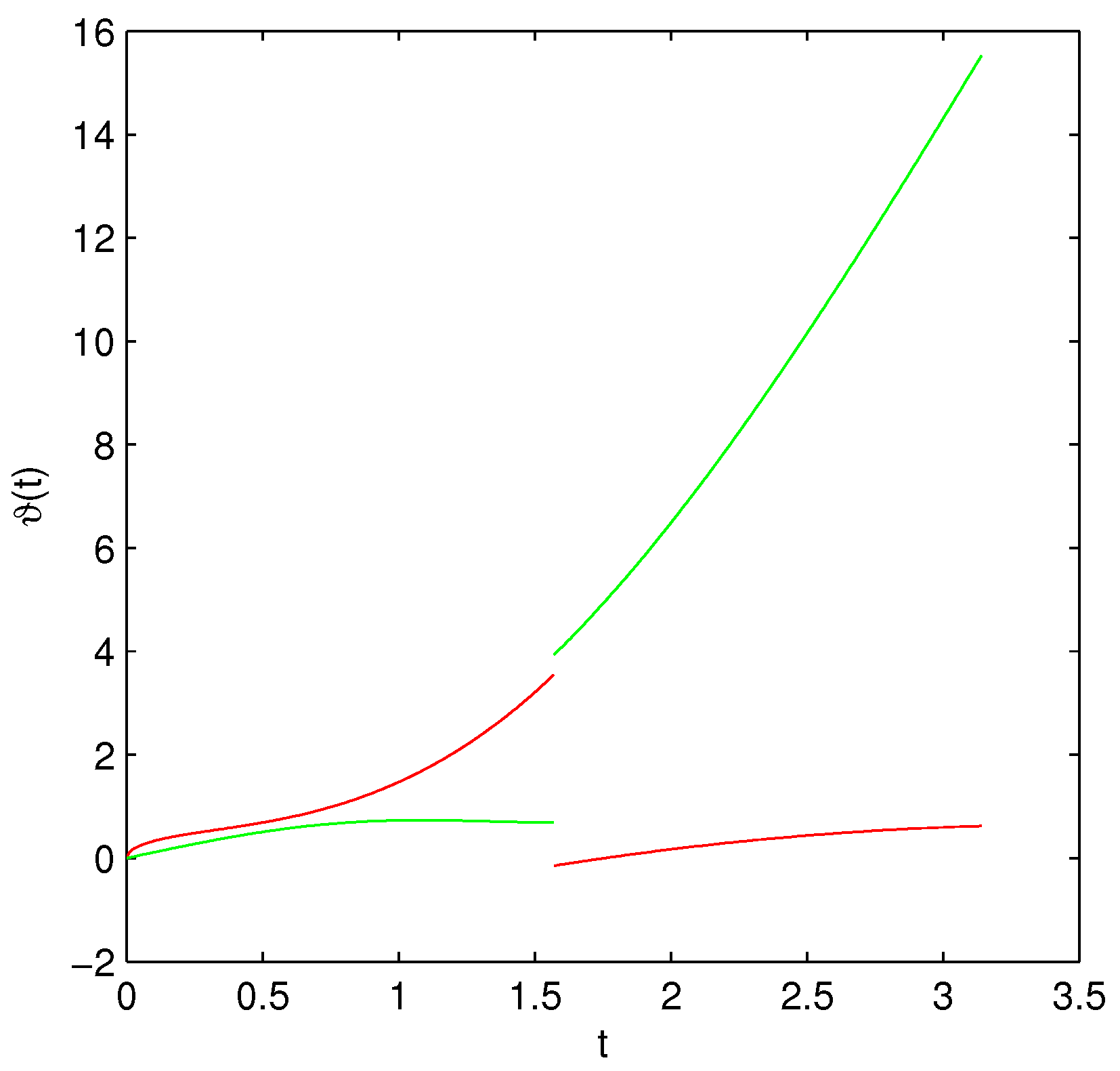
t	Exact Solution	ADM	FDTM	Error (ADM)	Error (FDTM)
0.0000	1.0000	1.0000	1.0000	0.0000	0.0000
0.2000	1.8816	1.7990	2.6683	0.0826	0.7867
0.4000	2.7719	2.4300	3.4050	0.3419	0.6331
0.6000	4.0684	3.1462	4.0265	0.9222	0.0419
0.8000	6.1153	3.9928	4.5892	2.1225	1.5261

and

Table 4. The absolute errors between the exact solution and ADM’s solution, as well as the exact solution and FDTM’s solution of IFDE (28) of order $1/2$ for some values of $t\in (1,2]$.

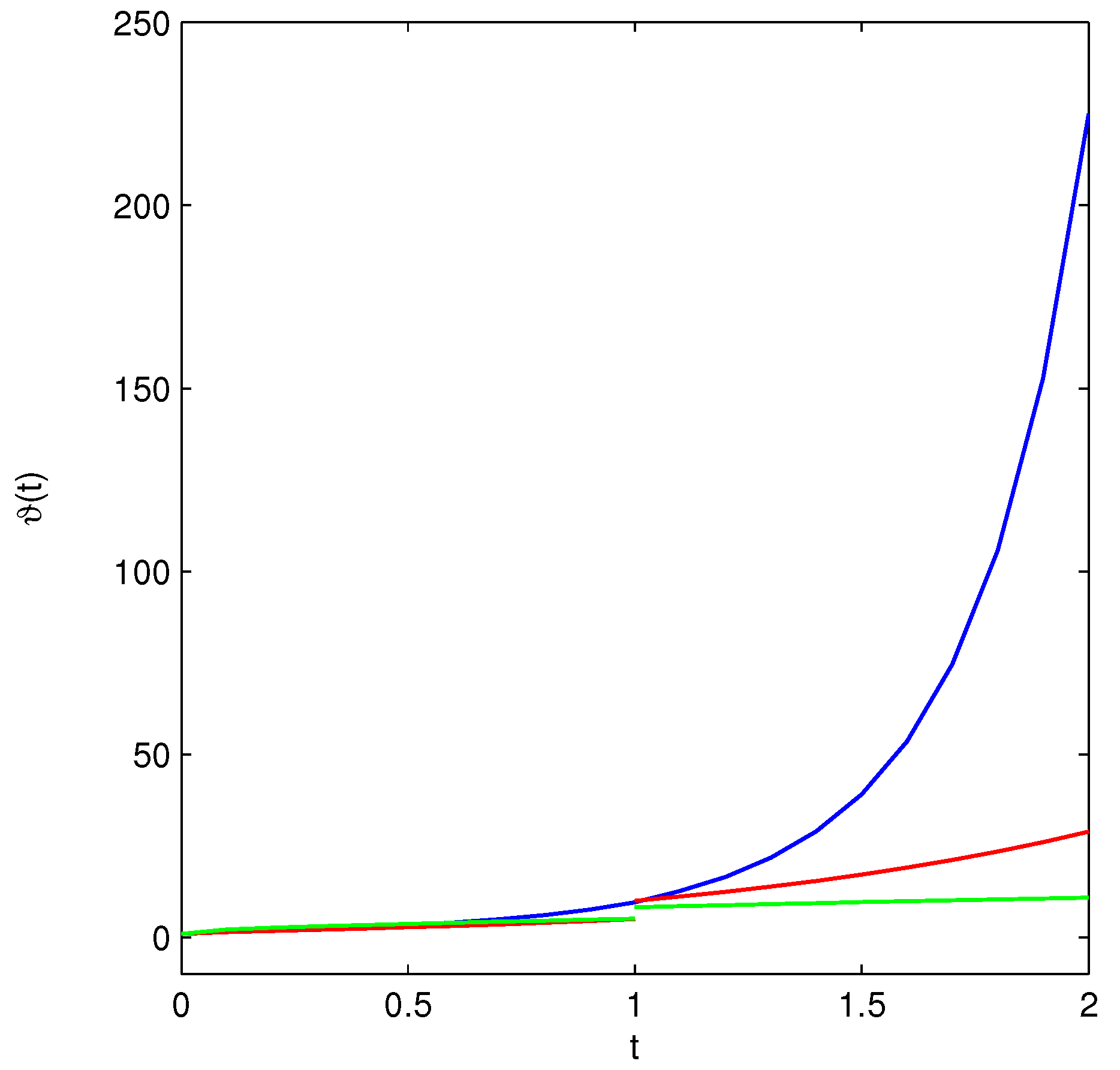
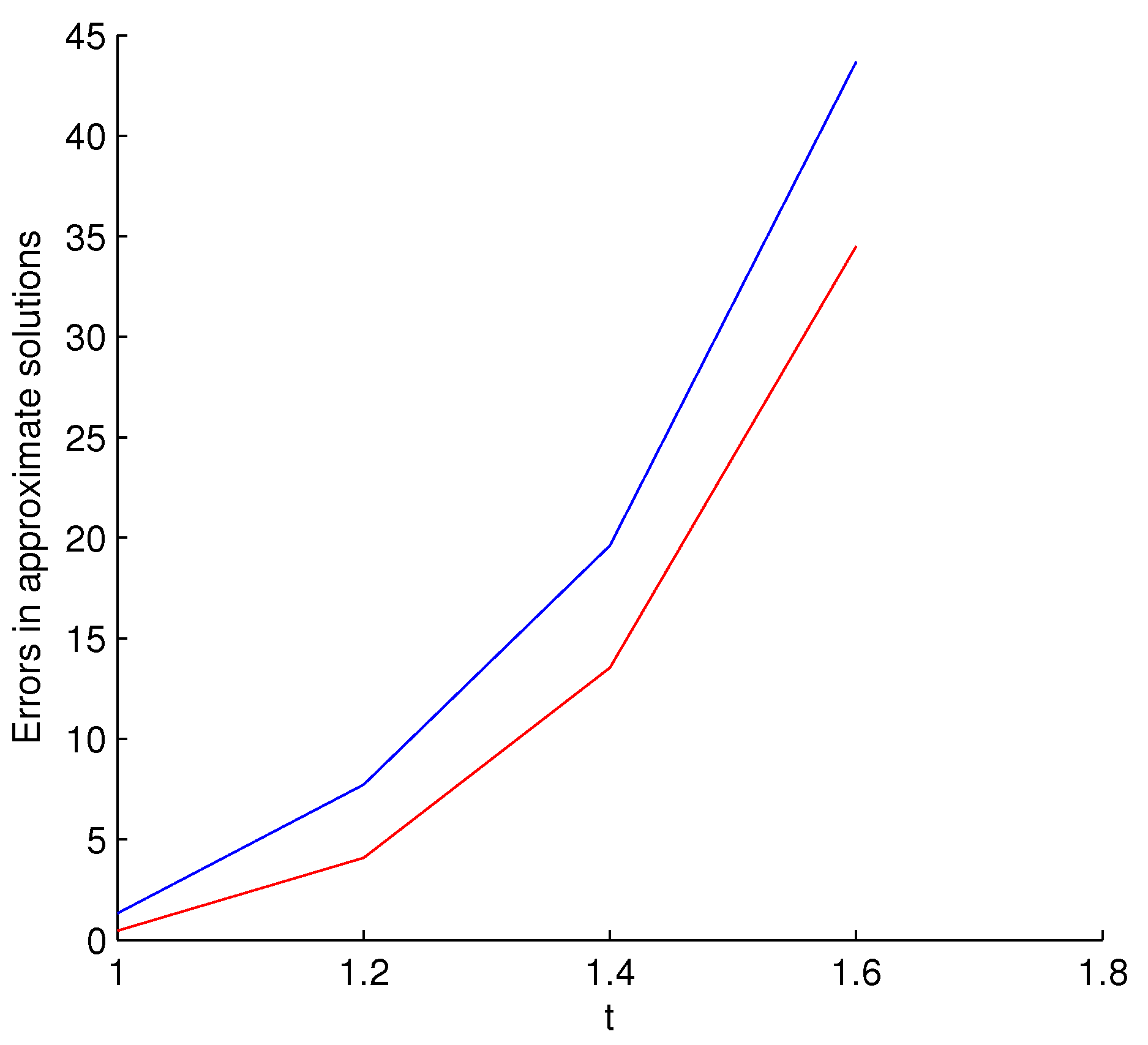
t	Exact Solution	ADM	FDTM	Error (ADM)	Error (FDTM)
1.0000	9.5541	10.0180	8.2292	0.4639	1.3249
1.2000	16.5532	12.4748	8.8269	4.0784	7.7263
1.4000	28.9970	15.4563	9.3844	13.5407	19.6126
1.6000	53.5848	19.0827	9.9100	34.5021	43.6748

show the values of the exact solution and the approximate solution obtained by ADM and FDTM for $t\in (0,1]$ and $t\in (1,2]$, respectively. Figure 12 and Figure 13 show the graph of the ADM error and DFTM error. We can see that the absolute errors in ADM are less compared to the solution obtained by FDTM, when $t\in (1,2]$.

Remark 1. 

Theoretically, we can obtain an exact solution if we add all terms in approximate solutions. Cherruault et al. [23,34] and Odibat et al. [36] have demonstrated the convergence of ADM and FDTM, respectively. Arikoglu and Ozkol [37] also discussed the error analysis of FDTM. From the numerical results, we can find that the ADM and FDTM are efficient algorithms. We used only the first several terms to approximate the exact solution, and the numerical results performed better [33,35]. The more terms that we calculate, the higher the accuracy that we achieved.

6. Conclusions

In this paper, we studied the existence and uniqueness of the solution of IFDE with a deviated argument. We obtained the numerical solution of several IFDEs using ADM and FDTM. These methods provide the solution as an infinite series of functions with easily computable components. The numerical solutions were obtained for both fractional and integer-order IFDEs. A comparison between exact and numerical solutions was made with the help of plots and tables. From the numerical tests, we can conclude that the ADM is an effective approach for solving IFDEs. However, there are still some difficulties that we need to overcome in the future. The following topics are also disadvantages that we will try to address:

• Error analysis is still a difficult task to perform. Numerous nonlinear problems lack an exact solution, making it impossible to determine numerical errors. In the near future, we will focus on this topic.
• In this method, we generally used a fractional series expansion, which is a fractional version of the Taylor series. What about other expansions that meet the requirements of the new polynomials? For example, how can boundary value problems be solved using a series solution? Therefore, it is crucial to provide fresh concepts for this subject.