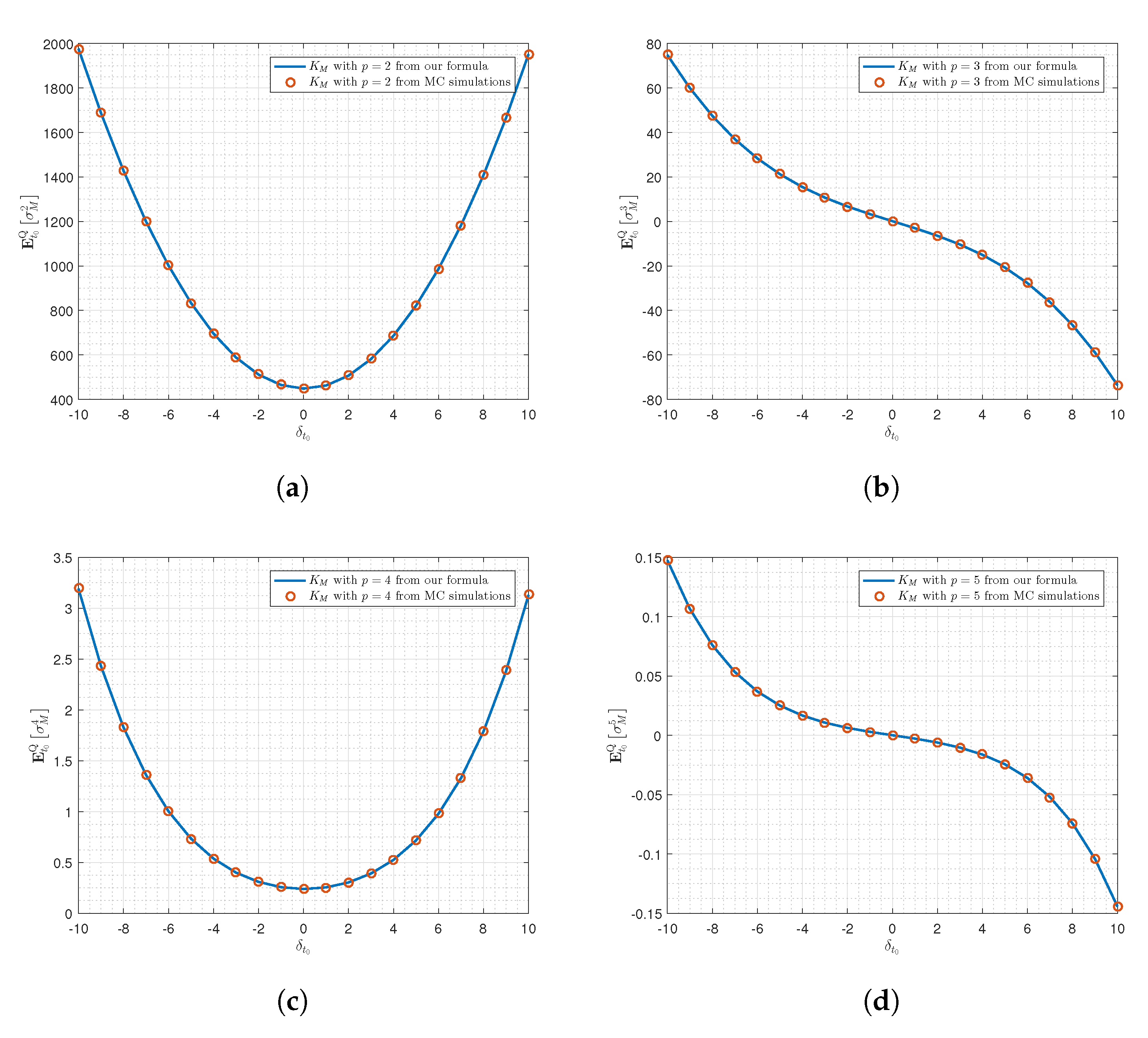1. Introduction
Pricing variance swaps in commodity derivative markets, under stochastic convenience yields with discretely sampled realized variance, have been studied via stochastic differential equations (SDEs) by a number of researchers over the past decades, see [
1,
2,
3,
4,
5]. The SDE describing the evolution of an underlying of each swap we study here is the Schwartz’s two-factor model [
6]. This model consists of a Schwartz’s one-factor model and an Ornstein–Uhlenbeck (OU) process [
7]. The model can be applied to describe the behavior of commodity prices and allows the convenience yields to bear the OU process as its mean reversion. Although, the Schwartz’model is commented upon favorably in some aspects of commodity pricing, the model is not constructed to capture some key characteristics of commodity price evolution such as seasonal effects and occasional price spikes which may produce jumps in empirical behavior of the commodities paths, see more details in [
8,
9,
10]. However, pricing swaps under the two-factor model are still a challenge. Although various analytical approaches for pricing the swaps under the two-factor model have been proposed and applied to quantify variance risk premia in commodities such as gold, see [
3], the existing results are not general and practical in use as they usually consist of more than a page-long of cluttered mathematical expressions. This makes its calculation as computationally expensive as using Monte Carlo (MC) simulations. The main focus of this paper is to provide a generalized and simplified explicit formula to price the discretely sampled generalized variance swaps, and thus significantly reducing the computational burden.
Unlike the case of the stock which has been widely studied by many researchers, see [
11,
12,
13,
14], the pricing problem in commodity is rarely investigated or used in applications. In the variance swap context reviewed by Zhu and Lian [
5], there exist two main types of swap valuation approaches: numerical methods and analytical methods. In 2021, Swishchuk [
4] applied the Brockhaus–Long approximation to obtain the variance swaps formula and also the volatility swap formula by assuming that the energy prices follow the continuous-time model, namely, GARCH(1,1) model. In 2016, under the Schwartz’s one-factor model, Chunhawiksit and Rujivan [
15] proposed an analytical formula for pricing the discretely sampled variance swaps when the underlying asset follows a commodity under the realized variance defined in terms of squared percentage return of the commodity prices. With the same model, in 2017, Weraprasertsakun and Rujivan [
16] presented an analytical formula for pricing discretely sampled variance swaps with a commodity asset under the realized variance defined in terms of squared log-returns of the commodity prices. In 2020, Chumpong [
17] provided closed-form formulas for pricing skewness and kurtosis swaps under the one-factor model which were derived by using the results of the conditional moments proposed by Chumpong et al. [
18]. However, these approaches are based on the one-factor model which do not involve the main hidden stochastic factor that affects the commodity prices, namely, convenience yields. Moreover, the existing formulas in the mentioned literature are extremely complicated, see ([
3], Proposition 3.1) for example.
Very recently, based on the two-factor model with stochastic convenience yields, an analytical formula for pricing discretely sampled variance swaps under the realized variance defined in terms of squared log-return of the commodity asset was presented by Rujivan [
3]. His main result was achieved by solving a partial differential equation (PDE) generated from the infinitesimal generator for the two-dimensional diffusion process. He provided a special case of the variance swaps in closed form which is the moment of the second order. However, the moments of higher orders are still unavailable in closed forms.
This paper establishes an affine transformation of the two-factor model [
19] based on a PDE according to the infinitesimal generator of the two-dimensional diffusion process [
20]. Under the motivation of the moment-generating function and its derivatives combined with Bell polynomials, some novel but simple closed-form formulas for the conditional moments and mixed moments are derived as consequences of the affine transformation. Several mathematical properties of the PDE corresponding to the two-factor model, such as conditional variance, conditional mixed moment, conditional covariance and conditional correlation, are given. To the best of our knowledge, these formulas are presented in closed forms for the first time.
As the major contribution points, the formulas for pricing the generalized swaps, such as the actual return-based realized
pth-moment swap, log-return realized
pth-moment swap, gamma swap, entropy swap and self-quantoed variance swap, are proposed explicitly. Such formulas significantly simplify the other approaches in the mentioned literature. The only difference between our method and Rujivan’s method in [
3] is that our results are based on the affine transformation and knowledge involving Bell polynomials, while their method assumes that any solutions of the infinitesimal generator are in the form of some polynomial expansions.
This paper also successfully derives the closed-form formulas for the moment swaps of all integer orders. More interestingly, in general, our results show that the strike price does not depend on the given spot prices but depends only on the initial convenience yield. This information will be beneficial for investors in the commodity markets who need to trade the volatility on payoff or to hedge on the volatility risk.
The rest of the paper is organized as follows.
Section 2 gives a brief overview of the two-factor model with stochastic convenience yields, its equivalent forms and also the structure of variance swaps. The key methodology is presented in
Section 3 to address the relevant ideas and to establish our main results, which are closed-form formulas for conditional moments of the two-factor model with stochastic convenience yields. Some essential properties of the formulas are explored and provided in
Section 4.
Section 5 presents five types of swaps mentioned above as consequences of our results. This section provides closed-form formulas for pricing the five types of variance swaps.
Section 6 presents experimental validations of the closed-form formulas via MC simulations.
Section 7 concludes the paper.
2. Variance Swaps under Model with Stochastic Convenience Yields
Unlike stocks and bonds, commodity assets may produce some features, such as seasonal effects and occasional price spikes which may give jumps in the empirical behavior of the commodities paths. Furthermore, there is a substantial variance in commodity prices because of the large value of their prices and seem to fluctuate by a long-term equilibrium [
21]. Since commodity derivative markets have been become increasingly significant over the past decades and commodity prices, such as gold [
3,
22], continue to reach new record highs [
3], the study of commodity price behaviors has received much more attention in risk management. This differentiates the commodity assets from stocks and bonds which have been widely studied. In contrast, commodity assets remain poorly explored. This section provides a brief overview of the Schwartz’s two-factor model with stochastic convenience yields introduced by Schwartz [
6] in 1997, and the structure of various exotic variance swaps in the risk-neutral world.
2.1. Schwartz’s Two-Factor Model
The Schwartz’s two-factor model with stochastic convenience yields is a stochastic two-factor model often used to describe the dynamics of commodity prices, see more details in [
6]. Roughly speaking, the first factor is known as the standard process for commodity prices, while the second factor is the stochastic convenience yields following the OU process. Let
be a filtered probability space generated by an adapted stochastic process
, where
is a sample space,
is a risk-neutral measure and the family
of
-field on
is a filtration. The joint dynamics of commodity spot price
and its instantaneous convenience yield
satisfy the following SDEs
where
r is a fixed risk-free interest rate,
is the speed of adjustment for the mean reversion to the long run term
of the convenience yields,
and
are the volatility of the commodity prices and convenience yields, respectively, and
is the price of the convenience yield risk. Moreover, the increments to the standard Brownian motions
and
are correlated with
, where
. Using Itô’s lemma ([
20], Section 3.3) with
for all
to the first SDE of system (
1) yields
Next, we employ the Cholesky decomposition method from ([
23], Section 6.3) to system (
2) in order to obtain a dynamical system with mutually independent Brownian motions
and
. Then, (
2) can be expressed by
where the matrices
and
C are
and the Brownian motions
and
are independent. Thus, the dynamical system (
2) becomes
2.2. Structure of Pricing Swaps
Variance swaps are essentially contracted on the future-realized variance of returns on the specified underlying assets at the fixed maturity time
. The payoff of the swap contracts over the contract life
is the difference between the annualized realized variance of the returns
and the annualized strike price
K, which can be expressed by
, where
L is the notional amount of the swap. In the risk-neutral world, the value of a variance swap at time
t, for
, whose payoff structured with a fixed interest rate
r can be defined mathematically by
Thus, should be zero at since there is no cost for the swap at the beginning of the contract. Thus, the fair value for the annualized strike price K can be determined by . Therefore, the value of this conditional expectation can consequently resolve the variance swap valuation problem.
Indeed, there are essentially two categories of variance swaps pricing. One is for pricing with continuously sampled realized variance, the other is for pricing with discretely sampled realized variance.
This paper mainly focuses on explicitly solving the conditional expectation of the annualized realized variance of returns
under stochastic convenience yields with discretely sampled realized variance. In general, there are many types of variance swaps. However, this paper studies only five types, namely, actual return-based realized
pth-moment swap, log-return realized
pth-moment swap, gamma swap, entropy swap and self-quantoed variance swap. Each of these is defined, respectively, as follows
where
is the asset price at times
for
,
N is the sampling frequency of the discrete asset prices,
is the annualized factor. A significant relation between them is
. For more details, we refer the readers to [
24].
3. Main Results
Risk-neutral pricing of derivatives such as bond derivatives, quantos, foreign bond options, chooser options, and Asian options under the affine and affine jump-diffusion processes such as Vašíček process, Cox–Ingersoll–Ross (CIR) process and Heston models through the transform and extended transform analysis methods was studied by Duffie et al. [
19], see [
25,
26] for more details. The existence and uniqueness of the processes were also studied via their stochastic invariance of the canonical state space. The admissibility conditions and a full proof were worked out by Filipović [
27] and Filipović and Mayerhofer [
28].
The same techniques are applied here in order to achieve the explicit formula for (
4) which is our main goal in this paper. We first derive an explicit formula for the affine transformation
u corresponding to model (
3) in Theorem 1 under the solution of the PDE according to the infinitesimal generator for the two-dimensional diffusion process ([
20], Section 5.1). In addition, we derive some explicit formulas for the conditional moments and mixed moments of
,
,
and their products for the model (
3) as consequences of Theorem 1.
Theorem 1. Suppose that and follow the Schwartz’s two-factor model (3) on with the initial values and . There exists an affine transformation which can be expressed aswhere and the coefficient functions are Proof. By applying the infinitesimal generator of the two-dimensional diffusion process, the Schwartz’s two-factor model (
3) corresponds to the following PDE,
where
. To solve (
6), we assume that
, where
A,
B and
C are unknown functions depending on variables
a,
b and
which will be determined later. Thus, we have
After substituting all partial derivatives into (
6) and dividing it by
, we have the following PDE
Moreover, we can see that at
or
, the initial condition satisfies
By comparing coefficients of the exponent, we have
,
and
. Since
x and
are independent, we can compare the coefficients of
x and
from both sides of (
7) to obtain three linear PDEs depending on the first-order partial derivative with respect to
only and their initial conditions, that are
By solving the above linear PDEs, respectively, it is easy to obtain the solutions , and as expressed in the statement of Theorem 1. □
Corollary 1. According to Theorem 1 with and , the closed-form formula for the conditional γ-moment of , where γ is a complex number and for all , can be expressed bywhere the functions A, B and C are defined as in Theorem 1. To obtain the conditional and mixed moments, the idea of calculating conditional moments by using the moment-generating function is applied here. Since the derivative of moment-generating function always involves the complete Bell polynomials ([
29], Section 2), we need to manipulate (
5) by finding its higher-order partial derivatives and to use the result of the complete Bell polynomials, as stated in Lemma 1, to give concise forms for each one of them.
Lemma 1 ([
29]).
Let be the nth complete Bell polynomial recurrently defined bywith the initial value . Then, its explicit form can be expressed as the following determinant: For convenience, thereafter, we use or instead of for ; instead of ; and for and , respectively, where .
Theorem 2. Suppose that and follow the Schwartz’s two-factor model (3) on with the initial values and . The closed-form formula for the conditional mixed moment of and , for all , can be expressed bywhere u is defined in (5) with γ is a complex number and n is a positive integer. Additionally, Proof. From Theorem 1 and
, it is easy to see that the
nth-order partial derivative of
u with respect to the variable
a is
Subsequently, if we let
and
. Then, (
12) becomes
. From (
5), the first three successive differentiations of
u with respect to
a are
and so on. It is a simple matter to construct by mathematical induction that
where
is defined to be an unknown combination of
. Thus, (
13) can be written into another form as
Next, to obtain the formula of
, we consider (
14) by substituting
into
n and use the Leibniz formula for differentiation of a product ([
30], page 318). Then, we have
Clearly, this recurrence relation with the initial value
satisfies the complete Bell polynomials (
9). Indeed, we see from Theorem 1 that the coefficients
A,
B and
C are polynomials of the variable
a with degrees 1, 1 and 2, respectively. The function
f, which is a linear combination of
A,
B and
C, is also a polynomial of the variable
a with at least second degree. Thus, the third- and higher-order partial derivatives of
f with respect to
a are always zero. Hence, the complete Bell polynomial
can be expressed as (
10) that is
where
and
. Note that (
15) is a determinant of a tridiagonal matrix. By using the cofactor expansion, (
15) can be expressed as a recurrence relation
Amazingly, this second-order difference Equation (
16) corresponds to the Faà di Bruno formula. Its proof and detail can be found in ([
29], Section 4). Thus, we can solve (
16) with
for all
by using this formula and
can be displayed in the following form
where
is the set of
of non-negative integers
and
such that
. Thus, if we let
, then
so that
, see also in [
31]. Finally, (
17) becomes
where the floor function
denotes the greatest integer which is less than or equal to a real number
and the double factorial of an integer
is a generalization of the usual factorial function defined by
Consequently, we substitute (
18) into (
13) to obtain
Now, let
and
. Then, we obtain the Formula (
11) in the statement of Theorem 2. □
Theorem 3. Suppose that and follow the Schwartz’s two-factor model (3) on with the initial values and . The closed-form formula for the conditional mixed moment of and , where for all , can be expressed bywhere u is defined in (5) with γ is a complex number and m is a positive integer. Additionally, Proof. By employing Theorem 1 and the fact that
, we obtain the
mth-order partial derivative of
u with respect to the variable
b as follows
After that, if
and
, then (
21) becomes
. Next, from (
5), we apply the same idea from the proof of Theorem 2 in which the partial derivatives of
u with respect to the variable
a are changed to be the one with respect to the variable
b instead for deriving
. Therefore, we have
where
and
. Finally, if
and
are substituted into (
22), we yield (
20) in the statement of Theorem 3. □
Theorem 4. Suppose that and follow the Schwartz’s two-factor model (3) on with the initial values and . The closed-form formula for the conditional mixed moment of , and , where for all , can be expressed bywhere u is defined in (5) with γ is a complex number, n and m are positive integers, the variables , , , and are defined in Theorems 1–3. While, Proof. First, we consider a partial derivative of
u in (
5) of order
n with respect to
a and order
m with respect to
b. Since
, we have
Then, if
and
are replaced into (
25), then we have
. From the proof of Theorem 2, we can rewrite (
19) in terms of the function
f and its partial derivatives, that is
Note that
and
are functions without both variables
a and
b. Thus, if we find the
mth-order partial derivative of (
26) with respect to the variable
b and also use the Leibniz rule for
m-time differentiation of a product ([
30], page 318), we have
Furthermore, by employing (
22), we obtain that
Finally, we substitute (
28) into (
27) to obtain
where
is defined in (
24). Consequently, if we substitute
,
,
,
and
into (
29) together with
and
, then (
29) becomes the required formula in (
23). □
As resulted in Theorems 2–4 which are the conditional mixed moments between
,
and
, it should be noted that those theorems are based on the closed-form formulas for the conditional expectations of the product of the price and its logarithm and the product of the price and the convenience yield provided in Theorem 1 by solving via an affine transformation involving the complete Bell polynomials. These results are simpler and more compact compared with those existing in the literature, see [
3] for more details. Consequently, by substituting
in (
11), (
20) and (
23), the following corollaries can readily be deduced from Theorems 2–4, respectively. Their proofs are omitted here.
Corollary 2. According to Theorem 2 with , the closed-form formula for the conditional n-moment of , where n is a positive integer, can be expressed bywhere u is defined in (5), Corollary 3. According to Theorem 3 with , the closed-form formula for the conditional m-moment of , where m is a positive integer, can be expressed bywhere u is defined in (5), Because our approach in Corollary 3 does not require solving any recurrence relation, the presented Formula (
31) for the
mth conditional moment of the OU process significantly simplifies the approaches provided by Chumpong et al. [
18], Forman and Sørensen [
32], Rujivan [
3] and Sutthimat et al. [
33].
Corollary 4. According to Theorem 4 with , the closed-form formula for the conditional mixed moment of and can be expressed bywhere is defined in (24), u is defined in (5) with n and m are positive integers, the variables , , , and are defined in Corollaries 2 and 3, and It should be noted that our proposed results in this section are simpler and more general than other results in the existing literature, such as those published in a recent paper [
3]. In the aforementioned paper, the authors claimed that their method would enhance computational efficiency compared to approaches using Fourier transform and direct numerical solutions, such as the methods proposed in [
5,
11,
12,
13,
34,
35,
36].
Unlike the methods based on Fourier transform presented in [
5,
11,
12,
13,
34,
35,
36], our method and the method proposed by Rujivan [
3] are based on the PDE generated from the infinitesimal generator for the two-dimensional diffusion process. The only difference between our method and Rujivan’s is that our results are based on the affine transformation
u in (
5) and constructed from the complete Bell polynomials, whereas Rujivan”s method assumed that any solutions of the infinitesimal generator are in the form of some polynomial expansions. Furthermore, their results need to solve a recurrence of ODEs. This means that the higher moment
n, the more solving steps there are that require completion.
Remark 1. Our proposed method in this section can be also applied to find a closed-form formula for conditional moments of under the Schwartz’s one-factor model [17,37] which are now unavailable in general and closed forms. For a one-dimensional model, the infinitesimal generator is known as the Feynman–Kac formula, see [38,39,40,41,42] for examples of its practical uses. Furthermore, our proposed method can be applied for pricing of commodity and energy derivative of polynomial processes such as the CIR and Jacobi processes [43,44]. 5. Pricing Generalized Swaps
According to
Section 2.2, this paper focuses solely on the discretely sampled realized type which has been considered based on two subcategories: the actual return-based realized prices and the log-return realized prices. The actual return-based realized prices are provided in
Section 5.1. The others based on the log-return realized prices,
with
and
, are in
Section 5.2,
Section 5.3,
Section 5.4,
Section 5.5 which are constructed from
where
is the asset price at times
for
,
N is the sampling frequency of the discrete asset prices,
is the annualized factor and a significant relation between them is
. Indeed, the name of each swap depends on the weight
and the positive integer
p. A special case of these swaps, for
, is the second-moment swap, better known as the variance swap; the third-moment swap
, broadly known as the skewness swap; the fourth-moment swap
, widely known as the kurtosis swap.
In this section, we derive the fair strike price formulas explicitly for pricing the five types of variance swaps as mentioned in
Section 2.2 under the Schwartz’s two-factor model (
3). As seen in
Section 3, the associated PDE is analytically solved and some essential closed-form formulas are obtained. We apply our approaches to seek analytical formulas for the fair strike price
K of generalized swaps. Remark that while we focus on solving the conditional expected value of
, our approaches can be easily employed to handle the definitions of realized variances.
5.1. Actual Return-Based Realized pth-Moment Swap
As mentioned in
Section 2.2, the conditional expectation of the realized variance in the risk-neutral world is defined by
where the variance swap valuation problem is reduced to solve the
Nth conditional expectations as follows
where
,
,
and
for all
.
5.2. Log-Return Realized pth-Moment Swap
Unlike
Section 5.1, this section constructs moment swaps based on the log returns [
53]. To the best of our knowledge, the closed-form formula for pricing the log-return realized moment swaps is now generally unavailable. This section presents a simple but novel closed-form formula for pricing the log-return realized moment swaps. As the weight
for all
, the realized variance in the risk-neutral world is defined by
where the swap valuation problem is reduced to solve the
Nth conditional expectations as follows
where
,
and
. Note that this formula is obtained by using the binomial expansion and the fact that
.
5.3. Gamma Swap
In the gamma swap [
36], the weight
is chosen to be
for all
, the realized variance in the risk-neutral world is defined by
where the variance swap valuation problem is reduced to solve the
Nth conditional expectations as follows
where
for all
,
5.4. Entropy Swap
Referring to Crosby [
54] with the weight
for all
, the realized variance in the risk-neutral world is defined by
where the variance-swap valuation problem is reduced to solve the
Nth conditional expectations as follows
where
for all
,
5.5. Self-Quantoed Variance Swap
Referring to Crosby [
54] with the weight
for all
, the realized variance in the risk-neutral world is defined by
where the variance swap valuation problem is reduced to solve the
N conditional expectations as follows
where
for all
,
As resulted in
Section 5.1,
Section 5.2,
Section 5.3,
Section 5.4,
Section 5.5, we found that the strike price
K does not depend on the given spot prices
or
but depends only on the convenience yield
. Furthermore, this technique can be applied to the other weight
. This technique can be also applied to other two-factor models such as the Heston model, in which our approach solution for the self-quantoed variance swap is simpler in use than other approaches presented in the literature [
54] for the Heston model. Moreover, the other exotic swaps, such as covariance swap and correlation swap, can be derived directly by using Corollary 4 with the idea presented in Example 4.
Note also that we only discuss the discrete sampling variance swap. However, the continuous sampling variance swap can be directly obtained by taking the limit into our formulas for , , , and . Moreover, we can easily prove that the global critical point with respect to for each K is unique by using the first and the second derivative test. For example, in the variance swap, since the strike price K is a quadratic function in , there exists only one global minimizer.
6. Numerical Validation
This experimental validation discusses the Schwartz’s two-factor model (
3), where we apply the Euler–Maruyama (EM) discretization method to the Schwartz’s two-factor model. Let
and
, respectively, be a time-discretized approximation of
and
that are generated on the time interval
into
steps, i.e.,
. Then, the EM approximate for (
3) is defined by
where the initial values
,
,
are constant sizes of the time step and the standard normal random variables
and
are independent.
We illustrate only the validations of log-return realized
pth-moment swaps given in
Section 5.2 when
and 5 via the parameters of the gold spot prices and the prices of gold futures estimated are given in [
3]. The parameters are
,
,
,
,
,
,
,
and
. To test the efficiency of the
pth-moment swaps given in
Section 5.2, we compare our obtained results with the MC simulations at various
. These simulations are constructed with the time step
and varied with 10,000 sample paths as depicted in
Figure 1. Moreover,
Figure 1a,c are formed in the symmetric graphs, while
Figure 1b,d present the skew-symmetric graphs. In these subfigures, we can clearly see that the solid blue line agrees with the red circle points obtained by the MC simulations.
In this validation, the obtained results of our formula and the MC simulations based on the EM method (
34) are run on MATLAB R2021a software, and calculated using a laptop computer configured with: Intel(R) Core(TM) i7-5700HQ, CPU @2.70 GHz, 16.0 GB RAM, Windows 10 and 64-bit Operating System. This work was implemented in MATLAB libraries available in GitHub repositories:
https://github.com/TyMathAD/Pricing-Generalized-Swaps accessed on 1 November 2022. In order to measure errors between our formula and the MC simulations, we use the average relative error. This is because it is a good statistical measurement which can be seen in ([
55] Table 3) for the model to performance metrics. As a result, the average relative errors of
with different
and 5 are shown in
Table 1. We can see that when path numbers increase, the errors decrease for all
p. This means that the results obtained from MC simulations trend toward our closed-form formula. In addition, the consuming times for our closed-form formula depending on
p and MC simulations with various numbers of sample paths are also provided in
Table 1, which are far more expansive than our formula. Thus, the MC simulations may not represent a good choice in terms of computational time, especially for a large number of sample paths. Therefore, our proposed formula is suggested as highly suitable for practical use.
The main finding of the proposed results appears similar to the results of [
3,
24] which rely on the closed-form formula for the conditional moments of the log prices
. In this respect, our results displayed in
Figure 1a are seen to be equal to the results of variance swaps in [
3] in the seam parameters. In addition, our closed-form formula for conditional moments has further beneficial aspects for pricing financial assets whose payoffs can be generated by the conditional moments.
In the case of
, we refer the readers to Schoutens [
53] whose introduces the moment swaps. The
is a type of derivatives which is depend on realized higher moments of a underlying asset. A well-known case when
is named the variance swaps which are widely studied in financial mathematics. This contrasts to the cases of
. Schoutens also shows that the classical hedging by using the variance swaps in the terms of position in log-contracts can be enhanced by using the higher moments, such as, the third moment swaps. In this work, we fulfill the study of Schoutens by showing that the strike price,
, does not depend on the initial spot price but depends only on the initial convenience yield,
. In addition, it is in polynomial in
. This means that we can easily prove that the global critical point with respect to
for each
K is unique by using the first and the second derivative test. In this respect, for the variance swap
, since the strike price
K is a quadratic function in
, there exists only one global minimizer.
7. Conclusions
This work proposes highly efficient closed-form formulas for pricing generalized swaps, such as actual return-based realized
pth-moment swap, log-return realized
pth-moment swap, gamma swap, entropy swap and self-quantoed variance swap, based on the affine transformation
u in Theorem 1 of the model (
3). To calculate
u, we rely on the solution of PDE according to the infinitesimal generator for the two-dimensional diffusion process. Under the motivation of the moment-generating function and its derivatives combined with the complete Bell polynomials, the closed-form formulas for the conditional moments and mixed moments of
,
,
and their products for the model (
3) are derived as consequences of Theorem 1, see Theorems 2–4 and Corollaries 2–4.
In addition, some essential properties of closed-form formulas, such as the first and the second conditional moments, conditional variance, conditional central moments, conditional mixed moments and conditional covariance are provided and discussed.
Future Works
Indeed, our general and explicit formulas given in
Section 3 and
Section 4 can be readily applied to other exotic variance swaps. Since our proposed closed-form formulas are in the form of
nth-conditional moments for all
, our formulas bear further beneficial aspects for pricing financial derivatives whose payoffs can be generated by the moments. Moreover, our proposed method in
Section 3 can be applied to find a closed-form formula for conditional moments of each stochastic parameter under the Heston model in addition to three-factor models such as the CIR–Heston hybrid model, which now remain still generally unavailable, as well as in closed forms. Moreover, unlike the model studied by Hilliard and Jorge [
56] and Crosby [
57], the two-factor model studied herein does not allow for the price to jump by any small magnitudes as addressed in the introduction.