A New Correlation Coefficient Based on T-Spherical Fuzzy Information with Its Applications in Medical Diagnosis and Pattern Recognition

Abstract

The T-Spherical fuzzy set (TSFS) is the most generalized form among the introduced fuzzy frameworks. It obtains maximum information from real-life phenomena due to its maximum range. Consequently, TSFS is a very useful structure for dealing with information uncertainties, especially when human opinion is involved. The correlation coefficient (CC) is a valuable tool, possessing symmetry, to determine the similarity degree between objects under uncertainties. This research aims to develop a new CC for TSFS to overcome the drawbacks of existing methods. The proposed CCs are generalized, flexible, and can handle uncertain situations where information has more than one aspect. In addition, the proposed CCs provide decision-makers independence in establishing their opinion. Based on some remarks, the usefulness of the new CC is reviewed, and its generalizability is evaluated. Moreover, the developed new CC is applied to pattern recognition for investment decisions and medical diagnosis of real-life problems to observe their effectiveness and applicability. Finally, the validity of the presented CC is tested by comparing it with the results of the previously developed CC.

1. Introduction

The fuzzy set (FS) theory was firstly introduced by Zadeh [1] in 1965. All uncertain phenomena or all types of human opinion are specified by a membership degree (MD), which is denoted by $\mathsf{\mu }$ lying between $0$ and $1,$ and the non-membership degree (NMD) denoted by $\mathsf{\eta }$ could be obtained by subtracting the MD from $1$ in the FS. After the introduction of FS, some questions were raised by Atanassov [2] about the applicability of FS for expressing uncertainty in human opinion, and then Atanassov proposed the theory of intuitionistic fuzzy set(IFS) using $\mathsf{\eta }$ along with $\mathsf{\mu }$. Atanassov allowed the sum of $\mathsf{\mu }$ and $\mathsf{\eta }$ between $0$ and $1$. However, $\mathsf{\mu }$ and $\mathsf{\eta }$ cannot be assigned in IFS independently due to the restriction that their sum must lie in $\left[0, 1\right],$ as sometimes the sum $\left(\mathsf{\mu }, \mathsf{\eta }\right)$ exceeds the interval $\left[0, 1\right]$. To create room for decision-makers to assign $\mathsf{\mu }$ and $\mathsf{\eta }$, the concept of IFS was abstracted to Pythagorean FS (PyFS) by Yager [3] by widening the domain for assigning $\mathsf{\mu }$ and $\mathsf{\eta }$. Yager [4] also suggested that even the PyFS constraints somehow restrict decision-makers in a certain domain and become problematic. This led him to introduce the notion of q-rung orthopair FS (q-ROFS), wherein a limitless range is provided for making human opinions under uncertainty.

The theory of q-ROFS correctly progressed Zadeh’s model of FS and Atanassov’s IFS. However, in a situation with the opinion of more than one kind, such as voting (vote in favor, abstinence, vote in opposition to, and refusal), q-ROFS cannot describe such a situation. Cuong [5] introduced an advanced shape and structure called a Picture FS (PFS), having the capability of describing four features of uncertain information denoted by $\mathsf{\mu }, \mathsf{\vartheta }, \mathsf{\eta },$ and $\mathsf{\delta }$ with the condition that the sum of three should belong to $\left[0, 1\right],$ i.e., sum$\left(\mathsf{\mu }, \mathsf{\vartheta }, \mathsf{\eta }\right)\in \left[0, 1\right]$, where $\mathsf{\vartheta }$ and $\mathsf{\delta }$ denote the abstinence degree (AD) and refusal degree (RD) of an element of PFS. The PFS has expanded the frames of the FS and q-ROFS by associating them with additional information, but there is still a limitation of these structures, i.e., the domain of the PFS is limited, and $\mathsf{\mu }, \mathsf{\vartheta },$ and $\mathsf{\eta }$ cannot be assigned independently. Keeping in view the restriction of all the previously defined concepts, Mahmood et al. [6] proposed a novel concept of the spherical fuzzy set (SFS) as an advanced form of the PFS by enlarging the domain of PFS. In the SFS, the restriction becomes that the sum$\left(\mathsf{\mu }, \mathsf{\vartheta }, \mathsf{\eta }\right)$ may exceed the unit interval, but the summation of their squares belongs to the unit interval, i.e., $\mathrm{sum}({\mathsf{\mu }}^2, {\mathsf{\vartheta }}^2,{ \mathsf{\eta }}^2)\in \left[0,1\right]$. This new constraint made the area of the SFS larger than the PFS for assigning uncertain parameters. The application of the PFSs and SFSs can be noticed in [7].

Sometimes, squaring all the uncertain parameters is insufficient and some trio of information exists where the square sum exceeds the unit intervals, creating many difficulties in describing uncertainties. So, to deal with these situations, Mahmood et al. [6] proposed a variation of SFS known as the T-Spherical fuzzy set (TSFS), which has no limits whatsoever; the values are assigned to $\mathsf{\mu }, \mathsf{\vartheta },$ and $\mathsf{\eta }$. The condition for TSFS becomes that $\mathrm{sum} \left({\mathsf{\mu }}^{\mathrm{n}}, {\mathsf{\vartheta }}^{\mathrm{n}},{ \mathsf{\eta }}^{\mathrm{n}}\right)\in \left[ 0, 1\right]$ where $\mathrm{n}\in {\mathbb{Z}}^{+}$. Regarding this new restriction, we can claim that TSFS is the most flexible fuzzy layout with no limitations. Hence, the TSFS is considered the most suitable and reliable framework among the fuzzy frameworks whenever we want to deal with uncertainty and ambiguity during the decision process. Due to these characteristics, the TSFS has vast applications in the various sciences fields where human opinion is involved, such as in business [8,9] and the field of energy [10]. Some useful applications of TSFS are discussed in [10,11,12].

Similarity measure (SM) and correlation coefficient (CC) are real-valued functions that quantify the similarity among items on a scale of $\left[0, 1\right]$. The SMs and CCs are symmetric in nature and analyze how similar the two objects are, using a distance with dimensions representing object attributes. Hwang et al. [13] presented a singular technique to measure the similarity among IFSs based on Hausdorff distance and discussed their applications. Zeng et al. [14] presented a multi-criteria model based on a social network for evaluating a digital reform, using an intuitionistic fuzzy trust SM to determine decision-makers’ weights. Boran and Akay [15] introduced some parametric SMs for IFSs and applied them in pattern recognition. Firzoja et al. [16] presented the technique of evaluating sets to measure the similarity of PyFSs and discussed their applications. Zeng et al. [17] presented Pythagorean fuzzy SMs and aggregation operators for unmanned ground delivery vehicle evaluation. Zhang et al. [18] presented SM for PyFSs and discussed their applications. Farhadinia et al. [19] proposed a family of SMs for q-ROFSs and their applications to MCDM. Garg et al. [20] presented generalized dice SMs for complex q-ROFSs and discussed their applications. Lu and Zhang [21] proposed a new SM between PFS and their applications. Zhao and Luo [22] introduced the distance measure for the framework of PFS and studied its application to the MCDM. Verma and Rohtagi [23] also contributed to developing the SM for the format of PFS and reviewed its application to the pattern recognition and medical diagnosis. Singh and Ganie [24] proposed the CC for the framework of PFS and studied its application to pattern recognition. As for the application of CC, Mitchell [25] presented a CC for IFSs and discussed its applications. Thao [26] proposed a new CC of IFSs and studied their applications. Thao [27] proposed a new CC of PyFSs and explored their applications in pattern recognition problems. Garg and Rani [28] presented a robust CC measure of complex IFSs and developed their applications in decision-making. Garg [29] introduced a novel CC between PyFSs and their applications to decision-making processes. Riaz et al. [30] proposed CC for cubic bipolar FSs and discussed its applications. Mahmood and Ali [31] presented entropy measures and TOPSIS method-based CC using complex q-ROF information and explored its application to MCDM. Joshi and Kumar [32] presented a novel VIKOR approach based on PF-weighted CC for MCDM.

Some shortcomings of the existing literature on the CC are described below:

• CCs proposed by Hwang et al. [12], Zeng et al. [13], and Akay [14] can only deal with the framework of the IFS. Consequently, it cannot deal with the information provided in the format of TSFS.
• CCs proposed by Firzoja et al. [15], Zeng et al. [16], and Zhang et al. [17] can only deal with the information provided in the form of the PyFS. Consequently, they cannot deal with the information in the form of the TSFNs.
• Similarly, the CCs defined in [21,22,27] cannot deal with the information provided in the form of the TSFNs.
• The CCs defined in [26,28] also cannot deal with the information in the format of TSFS because the TSFS is the most generalized framework that deals with uncertainty.

From the above key points, we can conclude that the existing CCs need to be generalized so that the generalized CCs can deal with the information provided in the TSFS format. Moreover, from the above analysis, we can observe that CC is a powerful tool in decision-making and pattern recognition areas. The TSFS has been justified as the most appropriate framework for dealing with information uncertainty. Hence, this study proposes a new CC for TSFSs and explores its application in medical diagnosis and pattern recognition problems. As a result, the character of the presented CC is further demonstrated. Moreover, some similar studies are carried out to prove the effectiveness of our proposed T-Spherical fuzzy CC (TSFCC).

The remains of this composition are separated into different sections. Some basic concepts of the CC in the TSF environment are covered in Section 2. Section 3 introduces a new TSFCC, and some of its properties are verified. In Section 4, we’ll go over some of the sequences of our purpose of obtaining information. The use and efficiency of our presented TSFCC in pattern recognition of investment decisions and medical diagnosis are also discussed in Section 4. Finally, Section 5 brings the article to something like a conclusion.

2. Preliminaries

In this section, we discuss the basic definition of PFS, CC, and the notion of TSFS for a better understanding of this manuscript.

The notion of PFS is introduced in [5] by Coung and is defined as follows.

Definition 1.

A PFS$P$on a finite set$U=\left\{u_1,u_2, u_3,\dots , u_t\right\}$is defined as:

$$P=\left\{\left(u_{\iota , }{\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_p\left(u_{\iota }\right),{\eta }_p\left(u_{\iota }\right)\right)\in U, \iota =1,2,3,\dots ,t\right\}$$

where ${\mathsf{\mu }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right),{\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)$and${\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)$denote MD, AD, and NMD of the element${\mathsf{\mu }}_{\mathrm{i}}\in \mathrm{U}$to the set$\mathrm{P}$, respectively, with the condition: $0\le {\mathsf{\mu }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)+{\mathsf{\vartheta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)+{\mathsf{\eta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)\le 1$. Additionally, RD ${\mathsf{\delta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)$can be written as${\mathsf{\delta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)=1-\left({\mathsf{\mu }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)+{\mathsf{\vartheta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)+{\mathsf{\eta }}_{\mathrm{p}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)\right)$.

The concept of TSFS is defined in [6] as below.

Definition 2

([6]). A TSFS $P^t$ on a finite set $U=\left\{u_1,u_2, u_3,\dots , u_t\right\}$ is defined as:

$$P^t=\left\{\left(u_{\iota , }{\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_p\left(u_{\iota }\right),{\eta }_p\left(u_{\iota }\right)\right)\in U, \iota =1,2,3,\dots ,t\right\}$$

where ${\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_P\left(u_{\iota }\right)$ and ${\eta }_P\left(u_{\iota }\right)$ denote MD, AD, and NMD of the element ${\mu }_i\in U$ to the set $P^t$, respectively, with the condition: $0\le {\displaystyle {\mu }_p^t}\left(u_{\iota }\right)+{\displaystyle {\mathsf{\vartheta }}_p^t}\left(u_{\iota }\right)+{\displaystyle {\eta }_p^t}\left(u_{\iota }\right)\le 1(t>1)$. Additionally, RD ${\delta }_p\left(u_{\iota }\right)$ can be written as ${\delta }_p\left(u_{\iota }\right)=1-\left({\displaystyle {\mu }_p^t}\left(u_{\iota }\right)+{\displaystyle {\mathsf{\vartheta }}_p^t}\left(u_{\iota }\right)+{\displaystyle {\eta }_p^t}\left(u_{\iota }\right)\right)$.

As discussed in the introduction, many researchers have worked on the CCs between two numbers belonging to different frameworks. However, we state some necessary CCs that were recently defined.

The definitions of new CCs introduced by Singh [33] for the framework of PFS are given below.

Definition 3

([33]). Let $P$ and $Q$ be two PFS. The CC of $P$ and $Q$ is defined as:

$$\mathsf{\rho }\left(\mathrm{P}, \mathrm{Q}\right)=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}\left\{{\mathsf{\mu }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\mu }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right\}}{\left\{\begin{array}{c}{\{{\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}{\left({\mathsf{\mu }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2\}}^{\frac{1}{2}}\times \\ {\{{\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}{\left({\mathsf{\mu }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\vartheta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\eta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\delta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2\}}^{\frac{1}{2}}\end{array}\right\}}$$

(1)

where ${\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_P\left(u_{\iota }\right)$ and ${\eta }_P\left(u_{\iota }\right)$ denote MD, AD, and NMD, ${\delta }_Q\left(u_{\iota }\right)=1-\left({\mu }_P\left(u_i\right)+{\eta }_P\left(u_i\right)+{\mathsf{\vartheta }}_P\left(u_i\right)\right)$ for all $i=1,2,3,\dots ,t$.

Definition 4

([33]). Let $P$ and $Q$ be two PFS. Another CC of $P$ and $Q$ is defined as:

$${\mathsf{\rho }}^{\prime }\left(\mathrm{P}, \mathrm{Q}\right)=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}\left\{{\mathsf{\mu }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\mu }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)+{\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right){\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right\}}{\max \left\{\begin{array}{c}{\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}{\left({\mathsf{\mu }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\delta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2\\ {\displaystyle {{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}}{\left({\mathsf{\mu }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\vartheta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\eta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2+{\left({\mathsf{\delta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right)}^2\end{array}\right\}}$$

(2)

where ${\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_P\left(u_{\iota }\right)$ and ${\eta }_P\left(u_{\iota }\right)$ denote MD, AD, and NMD, ${\delta }_Q\left(u_{\iota }\right)=1-\left({\mu }_P\left(u_i\right)+{\eta }_P\left(u_i\right)+{\mathsf{\vartheta }}_P\left(u_i\right)\right)$ for all $i=1,2,3,\dots ,t$.

Ullah et al. [34] defined CC for the framework of the TSFS which is defined as follows.

Definition 5

([34]). Let $P$ and $Q$ be two TSFS. Another CC of $P$ and $Q$ is defined as:

$${\displaystyle {\rho }_{\mathit{TSFS}}^3}\left(P, Q\right)=\frac{{\displaystyle {{\displaystyle \sum }}_{i=1}^t}\left\{{\displaystyle {\mu }_P^n}\left(u_i\right){\displaystyle {\mu }_Q^n}\left(u_i\right)+{\displaystyle {\vartheta }_P^n}\left(u_i\right){\displaystyle {\vartheta }_P^n}\left(u_i\right)+{\displaystyle {\eta }_P^n}\left(u_i\right){\displaystyle {\eta }_P^n}\left(u_i\right)+{\displaystyle {\delta }_P^n}\left(u_i\right){\displaystyle {\delta }_P^n}\left(u_i\right)\right\}}{\left\{\begin{array}{c}{\{{\displaystyle {{\displaystyle \sum }}_{i=1}^t}{\left({\displaystyle {\mu }_P^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\vartheta }_P^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\eta }_P^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\delta }_P^2}\left(u_i\right)\right)}^n\}}^{\frac{1}{2}}\times \\ {\{{\displaystyle {{\displaystyle \sum }}_{i=1}^t}{\left({\displaystyle {\mu }_Q^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\vartheta }_Q^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\eta }_Q^2}\left(u_i\right)\right)}^n+{\left({\displaystyle {\delta }_Q^2}\left(u_i\right)\right)}^n\}}^{\frac{1}{2}}\end{array}\right\}}$$

where ${\mu }_p\left(u_{\iota }\right),{\mathsf{\vartheta }}_P\left(u_{\iota }\right)$ and ${\eta }_P\left(u_{\iota }\right)$ denote MD, AD, and NMD, ${\displaystyle {\delta }_Q^n}\left(u_{\iota }\right)=1-\left({\displaystyle {\mu }_P^n}\left(u_i\right)+{\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_i\right)+{\displaystyle {\eta }_P^n}\left(u_i\right)\right)$ for all $i=1,2,3,\dots ,t$.

3. A New Correlation Coefficient for TSFSs

As discussed above, the CC introduced in the frameworks of PFS set has limitations due to the restricted information in PFS. It has also been described that the TSFS is the most appropriate framework that deals with uncertainty in real-life phenomena with minimum loss of information. Hence, we formalize this section to introduce CC based on TSFS.

The CCs defined in [33] are based on some statistical backgrounds such as variance and covariance. We are generalizing these CC for the framework of the TSFS in this section. Hence, we need to define the variance and covariance for the framework of TSFS. In the following, the definitions of variance and covariance are provided.

The variance for TSFS is defined as follows:

Definition 6.

Let$P,Q$be two on$U=\left\{u_1,u_2,u_3,\dots ,u_{t }\right\}$, then the expression for the variance is given below:

$$\theta \left(P\right)=\frac{1}{t-1}{\displaystyle {\displaystyle \sum }_{\iota =1}^t}\left\{\begin{array}{c}{\left({\displaystyle {\mu }_P^n}\left(u_{\iota }\right)-\overline{{\mu }_P}\right)}^2+{\left({\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)-\overline{{\mathsf{\vartheta }}_P}\right)}^2\\ +{\left({\displaystyle {\eta }_P^n}\left(u_{\iota }\right)-\overline{{\eta }_P}\right)}^2+{\displaystyle {\sigma }_{\iota }^2}\left(P\right)\end{array}\right\}$$

where$\overline{{\mu }_P }=\frac{1}{t}{\displaystyle {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}}{\displaystyle {\mu }_P^n}\left(u_{\iota }\right), \overline{ {\mathsf{\vartheta }}_P }=\frac{1}{t}{\displaystyle {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}}{\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)$, $\overline{{\eta }_P }=\frac{1}{t}{\displaystyle {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}}{\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)$, and

$${\mathsf{\sigma }}_{\mathrm{i}}\left(\mathrm{P}\right)=\left(({\displaystyle {\mathsf{\mu }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{P}}})-({\displaystyle {\mathsf{\vartheta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{P}}})-({\displaystyle {\mathsf{\eta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{P}}})\right), {\forall }_{\mathsf{\iota }}=\left\{1,2,\dots ,\mathrm{t}\right\}$$

The covariance of two TSFNs can be defined as follows:

Definition 7.

Let$P,Q$be two on$U=\left\{u_1,u_2,u_3,\dots ,u_{t }\right\}$, then the expression for the covariance is given below:

$$\theta \left(P,Q\right)=\frac{1}{t-1}{\displaystyle {\displaystyle \sum }_{\iota =1}^t}\left\{\begin{array}{c}\left({\displaystyle {\mu }_P^n}\left(u_{\iota }\right)-\overline{{\mu }_P}\right)\left(\left({\displaystyle {\mu }_Q^n}\left(u_{\iota }\right)-\overline{{\mu }_Q}\right)\right)+\left({\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)-\overline{{\mathsf{\vartheta }}_P}\right)\left({\displaystyle {\mathsf{\vartheta }}_Q^n}\left(u_{\iota }\right)-\overline{{\mathsf{\vartheta }}_Q}\right)\\ +\left({\displaystyle {\eta }_P^n}\left(u_{\iota }\right)-\overline{{\eta }_P}\right)\left({\displaystyle {\eta }_Q^n}\left(u_{\iota }\right)-\overline{{\eta }_Q}\right)+{\sigma }_{\iota }\left(P\right){\sigma }_{\iota }\left(Q\right)\end{array}\right\}$$

where$\overline{{\mu }_P }=\frac{1}{t}{\displaystyle {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}}{\displaystyle {\mu }_P^n}\left(u_{\iota }\right), \overline{ {\mathsf{\vartheta }}_P }=\frac{1}{t}{\displaystyle {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}}{\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)$,$\overline{{\eta }_P }=\frac{1}{t}{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)$, and

$${\sigma }_i\left(P\right)=\left(\left({\displaystyle {\mu }_P^n}\left(u_{\iota }\right)-\overline{{\mu }_P}\right)-\left({\displaystyle {\mathsf{\vartheta }}_P^n}\left(u_{\iota }\right)-\overline{{\mathsf{\vartheta }}_P}\right)-\left({\displaystyle {\eta }_P^n}\left(u_{\iota }\right)-\overline{{\eta }_P}\right)\right), {\forall }_{\iota }=\left\{1,2,\dots ,t\right\}$$

Singh [33] applied the definitions of variance and covariance and generalized the CC in the framework of the PFS. Hence, the short range of PFS described in the introduction CC defined in [33] is limited. The CC defined for TSNs with the help of the above notions aggregates the information from a more extensive range than the PFS. The CC for TSFNs can be defined as follows:

Definition 8.

Let$P$and$Q$be two TSFNs in$U=\left\{u_1,u_2,\dots ,u_t\right\}$. Then, the CC is defined as

$${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{1}{3}\left({\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2+{\mathsf{\gamma }}_3\right)$$

(3)

where

$$\begin{gathered} {\mathsf{\gamma }}_1{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}\left({\displaystyle {\mathsf{\mu }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\mu }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\mu }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\mu }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{Q}}}\right)}^2}}, \\ {\mathsf{\gamma }}_2{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{Q}}}\right)}^2}}, \\ {\mathsf{\gamma }}_3{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}\left({\displaystyle {\mathsf{\eta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\eta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\eta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\eta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{Q}}}\right)}^2}} \end{gathered}$$

A few of the properties of CC are introduced following.

Theorem 1.

Let$P=\left({\mu }_P, {\mathsf{\vartheta }}_P, {\eta }_P\right)$,$Q=\left({\mu }_Q, {\mathsf{\vartheta }}_Q, {\eta }_Q\right)$, and$R=\left({\mu }_R, {\mathsf{\vartheta }}_R, {\eta }_R\right)$be the three TSFNs. Then

(1)

$0\le {\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}\le 1$.

(2)

${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}={\mathsf{\gamma }}_{\left(\mathrm{Q}, \mathrm{P}\right)}$

(3)

${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}=1$if$P=Q$and$i=1, 2, 3, \dots m$.

(4)

If$\mathrm{P}⊑\mathrm{Q}⊑\mathrm{R}$Then${\gamma }_{\left(P, R\right)}\le {\gamma }_{\left(P, Q\right)}$,${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{R}\right)}\le {\mathsf{\gamma }}_{\left(\mathrm{Q}, \mathrm{R}\right)}$.

Proof. 

(1)

The first is true self.

(2)

Second proofs is true self.

(3)

Take $\mathrm{P}=\mathrm{Q}$ to prove the third part, i.e., ${\mathsf{\mu }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)={\mathsf{\mu }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)$, ${\mathsf{\vartheta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)={\mathsf{\vartheta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)$, ${\mathsf{\eta }}_{\mathrm{P}}\left({\mathrm{u}}_{\mathrm{i}}\right)={\mathsf{\eta }}_{\mathrm{Q}}\left({\mathrm{u}}_{\mathrm{i}}\right)$, hence Equation $\left(3\right)$ implies

$${\gamma }_{\left(P, Q\right)}=\frac{1}{3}\left({\gamma }_1+{\gamma }_2+{\gamma }_3\right)=1$$

The fourth part is obvious as geometrically, the angle of $\mathrm{P}, \mathrm{R}$ is greater than that of $\mathrm{P}, \mathrm{Q},$ and $\mathrm{Q}, \mathrm{R}$. Hence the proof is completed. □

Next, we shall discuss some consequences of our purposed CC, and we can see it generalizes most of the existing CCs, i.e., the CC presented in this article is the generalization form of the previously CCs.

Let us consider the CC presented in this article, as in Equation (3):

$$\begin{gathered} {\gamma }_{(P,Q)}=\frac{1}{3}(\frac{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}\left({\displaystyle {\mu }_P^n}\left(u_{\iota }\right)-\overline{{\mu }_P}\right)\left({\displaystyle {\mu }_Q^n}\left(u_{\iota }\right)-\overline{{\mu }_Q}\right)}{\sqrt[n]{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\mu }_P^n}\left(u_{\iota }\right)-\overline{{\mu }_P}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\mu }_Q^n}\left(u_{\iota }\right)-\overline{{\mu }_Q}\right)}^2}} \\ +\frac{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}\left({\displaystyle {\vartheta }_P^n}\left(u_{\iota }\right)-\overline{{\vartheta }_P}\right)\left({\displaystyle {\vartheta }_Q^n}\left(u_{\iota }\right)-\overline{{\vartheta }_Q}\right)}{\sqrt[n]{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\vartheta }_P^n}\left(u_{\iota }\right)-\overline{{\vartheta }_P}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\vartheta }_Q^n}\left(u_{\iota }\right)-\overline{{\vartheta }_Q}\right)}^2}} \\ +\frac{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}\left({\displaystyle {\eta }_P^n}\left(u_{\iota }\right)-\overline{{\eta }_P}\right)\left({\displaystyle {\eta }_Q^n}\left(u_{\iota }\right)-\overline{{\eta }_Q}\right)}{\sqrt[n]{{\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\eta }_P^n}\left(u_{\iota }\right)-\overline{{\eta }_P}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\iota =1}^t}{\left({\displaystyle {\eta }_Q^n}\left(u_{\iota }\right)-\overline{{\eta }_Q}\right)}^2}}) \end{gathered}$$

(1)

If we replace $\mathrm{n}=2$ then we obtain CC for SFSs.

(2)

If we replace $\mathrm{n}=1$ then we obtain CC for PFS.

(3)

If we neglect AD, then we obtain CC for q-ROFSs.

(4)

If we replace $\mathrm{n}=2$ and neglect AD, then we obtain CC for PyFSs.

(5)

If we replace $\mathrm{n}=1$ and neglect AD, then we obtain CC for IFSs.

Definition 9.

Let$\omega ={\left({\omega }_1, {\omega }_2, \dots ,{\omega }_t\right)}^T$be the weight vector of$x_i(i=1,2,\dots ,n)$with${\omega }_i\ge 0$and${\displaystyle {{\displaystyle \sum }}_{i=1}^n}{\omega }_i$, then the CC$P$and$Q$be two TSFNs in$U=\left\{u_1,u_2,\dots ,u_t\right\}$. Then the weighted CC is defined as

$${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{1}{3}\left({\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2+{\mathsf{\gamma }}_3\right)$$

(4)

where

$$\begin{gathered} {\mathsf{\gamma }}_1{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\omega }_i\left({\displaystyle {\mathsf{\mu }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\mu }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\mu }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\mu }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\mu }}_{\mathrm{Q}}}\right)}^2}}, \\ {\mathsf{\gamma }}_2{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\omega }_i\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\vartheta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\vartheta }}_{\mathrm{Q}}}\right)}^2}}, \\ {\mathsf{\gamma }}_3{}_{\left(\mathrm{P}, \mathrm{Q}\right)}=\frac{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\omega }_i\left({\displaystyle {\mathsf{\eta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{P}}}\right)\left({\displaystyle {\mathsf{\eta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{Q}}}\right)}{\sqrt[\mathrm{n}]{{\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\eta }}_{\mathrm{P}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{P}}}\right)}^2\times {\displaystyle {{\displaystyle \sum }}_{\mathsf{\iota }=1}^{\mathrm{t}}}{\left({\displaystyle {\mathsf{\eta }}_{\mathrm{Q}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)-\overline{{\mathsf{\eta }}_{\mathrm{Q}}}\right)}^2}} \end{gathered}$$

A few of the properties of weighted CC are introduced following.

Theorem 2.

Let$P=\left({\mu }_P, {\mathsf{\vartheta }}_P, {\eta }_P\right)$and$Q=\left({\mu }_Q, {\mathsf{\vartheta }}_Q, {\eta }_Q\right)$be two TSFNs. Then

(1)

$0\le {\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}\le 1$.

(2)

${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}={\mathsf{\gamma }}_{\left(\mathrm{Q}, \mathrm{P}\right)}$

(3)

${\mathsf{\gamma }}_{\left(\mathrm{P}, \mathrm{Q}\right)}=1$if$P=Q$and$i=1, 2, 3, \dots m.$

Proof. 

The proof of weighted CC is similar to the above Theorem 1. □

4. Application of the Presented T-Spherical Fuzzy Correlation Coefficient (TSFCC)

In this section, we utilize our proposed TSFCC in pattern recognition and medical diagnosis with the help of examples. The results obtained by TSFCC are tabulated and drawn geometrically as well.

4.1. Application of the Presented Correlation Coefficient of TSFSs in Pattern Recognition for Investment Decision

Pattern recognition is an interesting problem due to vagueness, which is removed with the assistance of different fuzzy data calculations, SM, divergence measure, etc. Now we utilize the present CC for pattern recognition. In this problem, suppose $\left\{{\mathrm{Q}}_1,{ \mathrm{Q}}_2,\dots ,{ \mathrm{Q}}_{\mathrm{n}}\right\}$ is some known design identified by TSFSs in the universal set $\mathrm{U}=\left\{{\mathrm{u}}_1,{\mathrm{u}}_2,\dots ,{\mathrm{u}}_{\mathrm{t}}\right\}$, and ${\mathrm{Q}}_{\mathrm{j}}=\left\{\begin{array}{c}\left({\displaystyle {\mathrm{u}}_{\mathsf{\iota }}^{\mathrm{n}}},{\displaystyle {\mathsf{\mu }}_{{\mathrm{Q}}_{\mathrm{j}}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right), {\displaystyle {\mathsf{\vartheta }}_{{\mathrm{Q}}_{\mathrm{j}}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right),{\displaystyle { \mathsf{\eta }}_{{\mathrm{Q}}_{\mathrm{j}}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)\right):{\mathrm{u}}_{\mathsf{\iota }}ϵ\mathrm{U},\\ \mathsf{\iota }=1,2,3,\dots ,\mathrm{t} \end{array}\right\},\mathrm{j}=1,2,3,\dots ,\mathrm{n}$. Let $\mathrm{R}=\left\{\begin{array}{c}\left({\displaystyle {\mathrm{u}}_{\mathsf{\iota }}^{\mathrm{n}}},{\displaystyle {\mathsf{\mu }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right), {\displaystyle {\mathsf{\vartheta }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right),{\displaystyle { \mathsf{\eta }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathsf{\iota }}\right)\right)|{\mathrm{u}}_{\mathsf{\iota }}\in \mathrm{U}, \\ \mathsf{\iota }=1,2,\dots ,\mathrm{t}\end{array}\right\}$ be previously unknown patterns. The issue is to determine the unknown pattern $\mathrm{R}$ to one of the well-known patterns ${\mathrm{Q}}_{\mathrm{j}}\left(\mathrm{j}=1,2,\dots ,\mathrm{n}\right)$.

To determine the unknown pattern, we shall calculate the CC of R from the known pattern ${\mathrm{Q}}_{\mathrm{j}}$ by the proposed TSFCC, and ordering the obtained CC is done based on values of CC of R. The maxim value of R shows that the unknown pattern is closer to the known pattern. Now, we solve an example for the application of the TSFCC in pattern recognition as follows.

Example 1.

When a risk investment project reaches a certain stage, if venture capitalists have enough reasons to determine the program is a failure or unable to continue, or have already predicted the project lacks market and economic value seriously even if barely completed in the future, then the venture capitalists should decide to terminate the venture investment project. However, when a venture capital project reaches a certain stage that its development status and prospects differ from the original plan to a certain extent, but there is still hope for success and profit, at this point, venture capitalists have difficulties making termination decisions on projects. In the actual venture capital decision, many investment projects still have little hope because the decision makers’ hesitation about terminating the investment project finally leads to more heavy losses. Therefore, it is necessary to carefully consider the termination decision of venture capital projects and make a decisive decision. In this section, we will apply the proposed TSFCC method to the project terminating the identification of venture capital.

Let us consider that a venture capital project $\mathrm{R}$ is planned to evaluate from five aspects (index attribute): management quality (${\mathrm{u}}_1$), staff quality (${\mathrm{u}}_2$), technical product characteristics (${\mathrm{u}}_3$), marketing ability (${\mathrm{u}}_4$) and policy factors (${\mathrm{u}}_5$). Three established venture capital projects, namely successful projects (${\mathrm{Q}}_1$), suspended projects (${\mathrm{Q}}_2$) and failed projects (${\mathrm{Q}}_3$), are known models. The evaluation of the three known patterns ${\mathrm{Q}}_1,{ \mathrm{Q}}_2$ and ${\mathrm{Q}}_3$, are given in the form of TSFNs, described as follows:

$$\begin{gathered} {\mathrm{Q}}_1=\left\{\begin{array}{c}\left({\displaystyle {\mathsf{\mu }}_{\mathrm{i}}^{\mathrm{n}}},{ \mathsf{\mu }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right), {\mathsf{\vartheta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right),{ \mathsf{\eta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right):{\mathrm{u}}_{\mathrm{i}}\in \mathrm{U}, \\ \mathrm{i}=1,2,3,4,5.\end{array}\right\} \\ =\left\{\begin{array}{c}\left({\mathrm{u}}_{\mathrm{i}}, 0.35,0.56,0.77\right), \left({\mathrm{u}}_2, 0.66,0.78,0.34\right),\\ \left({\mathrm{u}}_3, 0.57,0.69,0.78\right),\left({\mathrm{u}}_4, 0.35,0.43,0.58\right),\\ \left({\mathrm{u}}_5, 0.73,0.44,0.66\right)\end{array}\right\} \\ {\mathrm{Q}}_2=\left\{\begin{array}{c}\left({\displaystyle {\mathsf{\mu }}_{\mathrm{i}}^{\mathrm{n}}},{ \mathsf{\mu }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right), {\mathsf{\vartheta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right),{ \mathsf{\eta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right):{\mathrm{u}}_{\mathrm{i}}\in \mathrm{U}, \\ \mathrm{i}=1,2,3,4,5.\end{array}\right\} \\ =\left\{\begin{array}{c}\left({\mathrm{u}}_{\mathrm{i}}, 0.33,0.52,0.68\right), \left({\mathrm{u}}_2, 0.50,0.78,0.55\right),\\ \left({\mathrm{u}}_3, 0.75,0.56,0.44\right),\left({\mathrm{u}}_4, 0.22,0.65,0.55\right),\\ \left({\mathrm{u}}_5, 0.44,0.55,0.66\right)\end{array}\right\} \\ {\mathrm{Q}}_3=\left\{\begin{array}{c}\left({\displaystyle {\mathsf{\mu }}_{\mathrm{i}}^{\mathrm{n}}},{ \mathsf{\mu }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right), {\mathsf{\vartheta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right),{ \mathsf{\eta }}_{\mathrm{Q}}{\displaystyle {}_1^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right):{\mathrm{u}}_{\mathrm{i}}\in \mathrm{U}, \\ \mathrm{i}=1,2,3,4,5.\end{array}\right\} \\ =\left\{\begin{array}{c}\left({\mathrm{u}}_{\mathrm{i}}, 0.44,0.32,0.58\right), \left({\mathrm{u}}_2,0.56,0.33,0.58 \right),\\ \left({\mathrm{u}}_3, 0.53,0.56,0.45\right),\left({\mathrm{u}}_4,0.39,0.55,0.66 \right),\\ \left({\mathrm{u}}_5, 0.11,0.64,0.54\right)\end{array}\right\} \end{gathered}$$

The information of unknown $\mathrm{R}$ is given in terms of a TSFS as:

$$\begin{gathered} \mathrm{R}=\left\{\begin{array}{c}\left({\displaystyle {\mathsf{\mu }}_{\mathrm{i}}^{\mathrm{n}}},{\displaystyle {\mathsf{\mu }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right), {\displaystyle {\mathsf{\vartheta }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right),{\displaystyle { \mathsf{\eta }}_{\mathrm{R}}^{\mathrm{n}}}\left({\mathrm{u}}_{\mathrm{i}}\right)\right):{\mathrm{u}}_{\mathrm{i}}\in \mathrm{U}, \\ \mathrm{i}=1,2,3,4,5.\end{array}\right\} \\ =\left\{\begin{array}{c}\left({\mathrm{u}}_{\mathrm{i}}, 0.75,0.58,0.66\right), \left({\mathrm{u}}_2, 0.29,0.36,0.45\right),\\ \left({\mathrm{u}}_3, 0.57,0.35,0.66\right),\left({\mathrm{u}}_4, 0.22,0.48,0.68\right),\\ \left({\mathrm{u}}_5, 0.44,0.85,0.33\right)\end{array}\right\} \end{gathered}$$

We use the TSFCC to determine the best pattern among described patterns. The results obtained by the TSFCC are presented in

Table 1. CC of unknown patterns obtained from proposed CC.

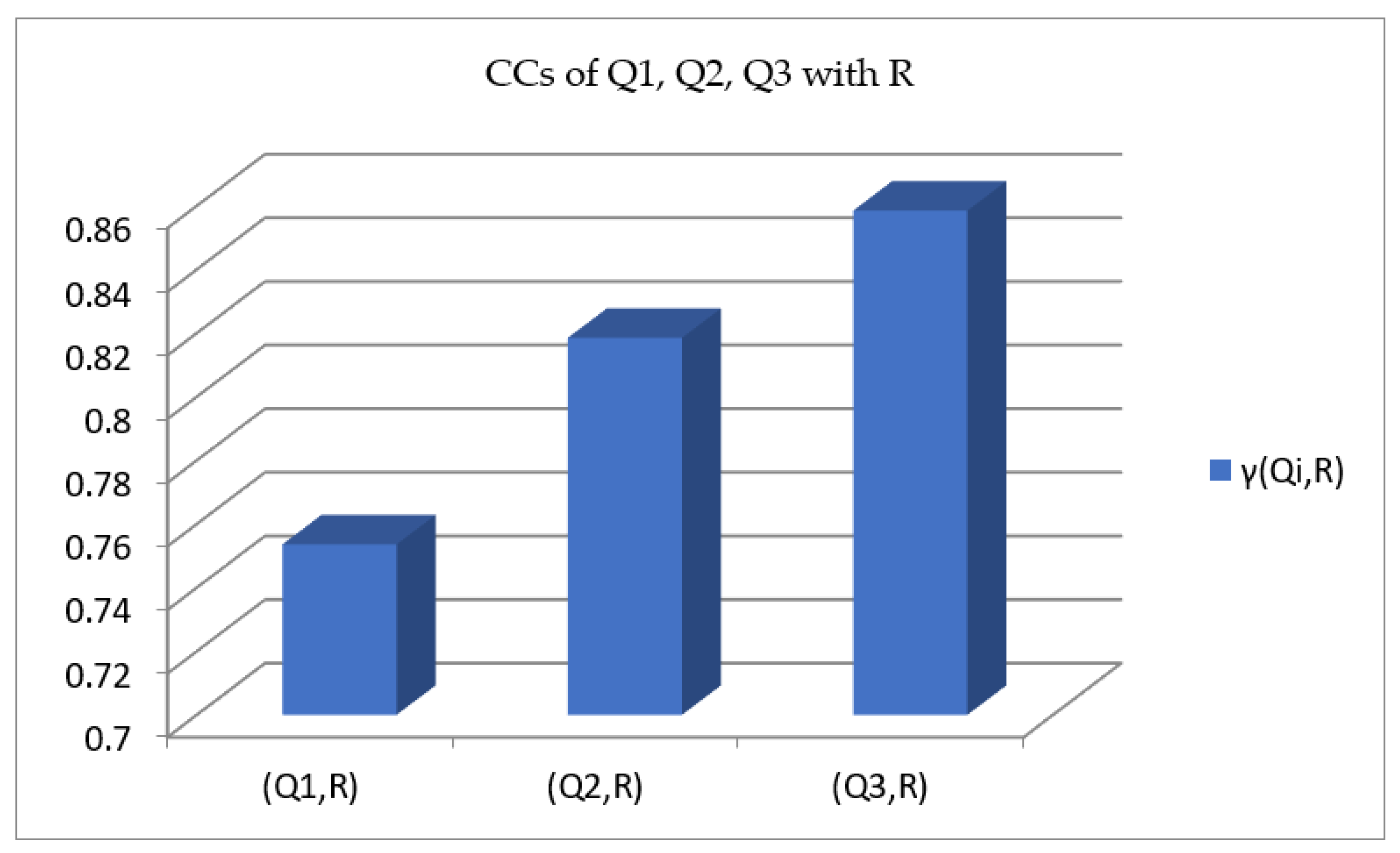
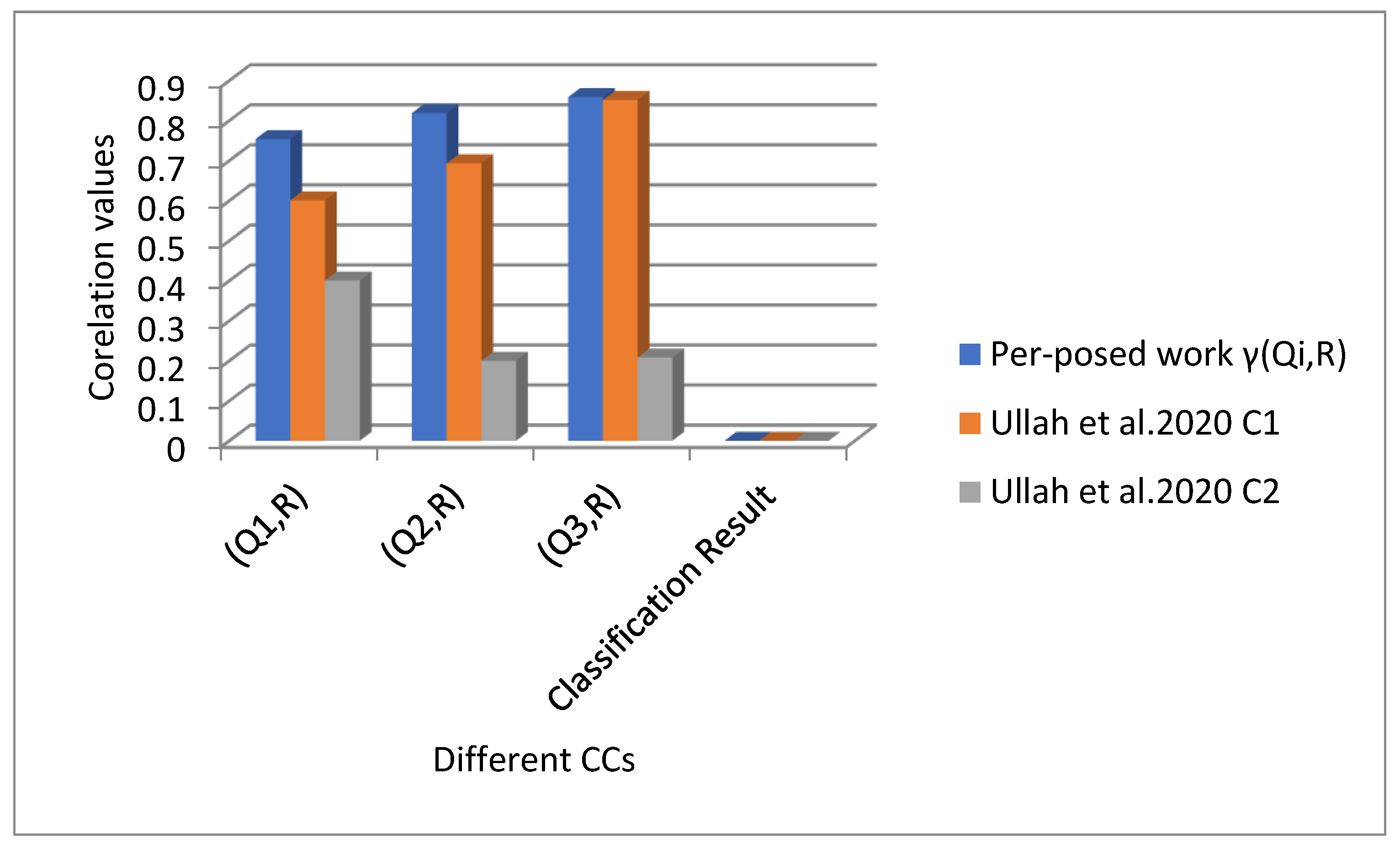
	$Q_1, R$	$Q_2, R$	$Q_3, R$	Classification Result
${\mathsf{\gamma }}_{\left(Q_i, R\right)}$	0.7536	0.8185	0.8585	${\mathrm{Q}}_3$

in the following.

With the help of the suggested CC in Equation (3), we can categorize that the known pattern $Q_3$ is near to the unknown pattern $R$.

The results described in Table 1 are drawn in Figure 1.

Figure 1 represents the results obtained in Table 1. The height of the bar graph shows the strength of the unknown pattern to the known. The higher the bar, the nearer the unknown pattern. Hence, Figure 1 shows that ${\mathrm{Q}}_3$ is the nearest pattern to the known.

Next, we compare the results obtained in Example 1 with the pre-existing CC for TSFS defined by Ullah et al. [34]. In [34], Ullah et al. defined a CC for the framework of TSFS and applied it to pattern recognition. In the following, we compared our suggested TSFCC with CC defined in [34].

Table 2. Comparison of proposed CC with CC defined in [34].

CRC	$Q_1,R$	$Q_2,R$	$Q_3,R$	Classification Result
Present work	$0.7536$	$0.8185$	$0.8585$	${\mathrm{Q}}_3$
Ullah et al. [34]	$0.600539$	$0.693059$	$0.85125$	${\mathrm{Q}}_3$
Ullah et al. [34]	$0.399962$	$0.199858$	$0.20807$	${\mathrm{Q}}_2$

represents the results of two different CC on the TSFS framework. From Table 2, we obtained ${\mathrm{Q}}_3$ as the best-known pattern for these two CCs, and thus it is clear that the results obtained are identical. The results obtained are drawn in Figure 2.

Figure 2 compares our suggested CC and CC defined in [34] on the TSFS. It is clear from Figure 2 that the results obtained from all of the CCs are compatible and acceptable. This shows the justification of the CC defined in this article.

4.2. Application in Medical Diagnosis

Medical diagnosis is the procedure of deciding an applicable affection of a person situated on his/her indication and action presented in the medical diagnosis. There is basic distrust in the utmost of the medical diagnosis that cooperates such as fuzziness and inaccurate data. In medical knowledge, there are compositions of an illness. This one owns multiple indications in routine. As a given result, determining the applicable illness from specialists presents a complex task in diagnosing a patient’s distress. A person, for example, is unlikely to be affected by the symptoms of headache and fever. A person who is facing stomach pain and chest pain will not affect the illnesses Typhoid, Malaria, and Viral Fever, but there is a major effect of symptom temperature on Malaria infection. In this scenario, the degree of equity can be defined as zero. As a result, the neutral class is an integral part of medical diagnosis, passing over other arguments that deal with contradiction.

Next, we consider using the suggested TSFCC method to deal with medical diagnosis issues. One professional doctor or the collective opinion of multiple specialists determines the symptom worth of a disease. The value of a patient’s symptoms is assessed by the doctor managing them, based on his or her knowledge. As a result, a symptom’s association with the normalized symptoms of credible illnesses is determined. The patient must be diagnosed with the illness that results in the highest CC value.

Here, we used TSFCC in medical diagnosis with the support of explaining examples.

Example 2.

We assume four patients in the structure $P=\left\{P_{1, }{P}_2,P_3,P_4\right\}$and five diseases$D=\left\{D_1, D_2,D_3, D_4, D_5\right\}=\left\{Chest problems, Stomach problem, Typhoid, Malaria, Viral fever\right\}$along with their symptoms presented in the form of a set$S=\left\{S_1, S_2, S_3, S_4, S_5\right\}=\left\{Chest pain, Cough, Stomach pain, Headache, Temperature\right\}$.

We aim for the best view by differentiating disease symptoms from patient symptoms using TSFCC. As a result, the showing symptoms of the patients ${\mathrm{P}}_{\mathrm{j}}\left(\mathrm{j}=1,2,3,4\right)$ are derived and shown in

Table 3. Symptoms of various diseases in the form of TSFNs.

	Chest Pain	Cough	Stomach Pain	Headache	Temperature
Chest problem	(0.55, 0.66, 0.55)	(0.22, 0.55, 0.65)	(0.33, 0.65, 0.78)	(0.48, 0.56, 0.72)	(0.36, 0.26, 0.77)
Stomach problem	(0.65, 0.58, 0.77)	(0.38, 0.49, 0.56)	(0.71, 0.69, 0.50)	(0.44, 0.56, 0.35)	(0.65, 0.71, 0.56)
Typhoid	(0.75, 0.58, 0.66)	(0.29, 0.36, 0.45)	(0.57, 0.35, 0.66)	(0.22, 0.48, 0.68)	(0.44, 0.85, 0.33)
Malaria	(0.58, 0.52, 0.66)	(0.71, 0.55, 0.44)	(0.44, 0.56, 0.35)	(0.36, 0.56, 0.80)	(0.39, 0.68, 0.33)
Viral fever	(0.59, 0.66, 0.72)	(0.78, 0.45, 0.36)	(0.22, 0.68, 0.55)	(0.56, 0.42, 0.38)	0.36, 0.48, 0.62)

. For improved personal views, we also utilize a variety of TSFCC measures. To initiate, we will present some T-Spherical correlation range initiatives proposed by various researchers.

Table 3 and

Table 4. Patient’s symptoms in terms of TSFNs.

	Chest Pain	Cough	Stomach Pain	Headache	Temperature
${\mathit{P}}_{\mathbf{1}}$	(0.35, 0.56, 0.77)	(0.66, 0.78, 0.34)	(0.57, 0.69, 0.78)	(0.35, 0.67, 0.43)	(0.73, 0.44, 0.66)
${\mathit{P}}_{\mathbf{2}}$	(0.33, 0.52, 0.68)	(0.50, 0.78, 0.55)	(0.75, 0.56, 0.44)	(0.22, 0.65, 0.55)	(0.44, 0.55, 0.66)
${\mathit{P}}_{\mathbf{3}}$	(0.44, 0.32, 0.58)	(0.56, 0.33, 0.58)	(0.53, 0.56, 0.45)	(0.39, 0.55, 0.66)	(0.11, 0.64, 0.54)
${\mathit{P}}_{\mathbf{4}}$	(0.53, 0.64, 0.22)	(0.66, 0.43, 0.45)	(0.33, 0.65, 0.75)	(0.36, 0.55, 0.68)	(0.80, 0.55, 0.33)

show the data of the diseases, symptoms, and patients in the form of TSFS, while

Table 5. Values obtained by CC (given in Equation (3)).

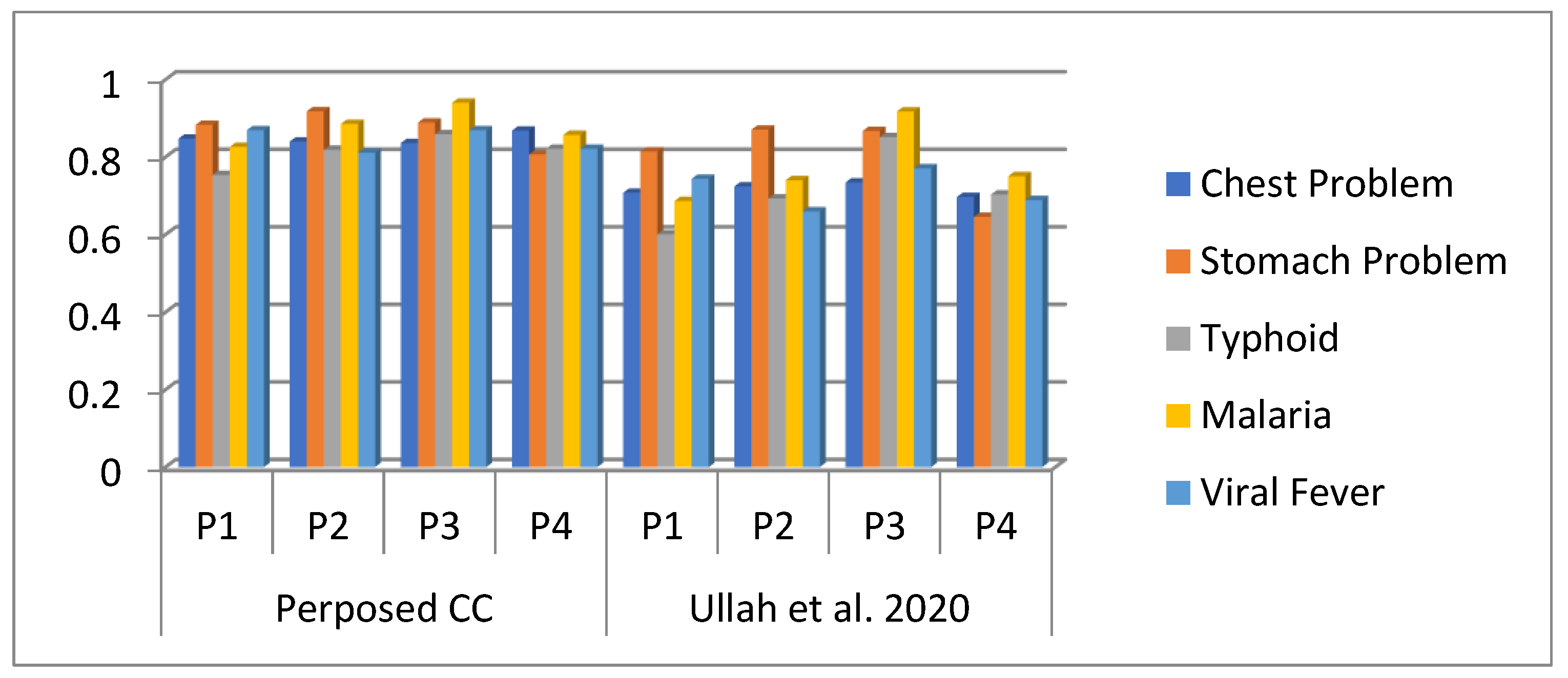
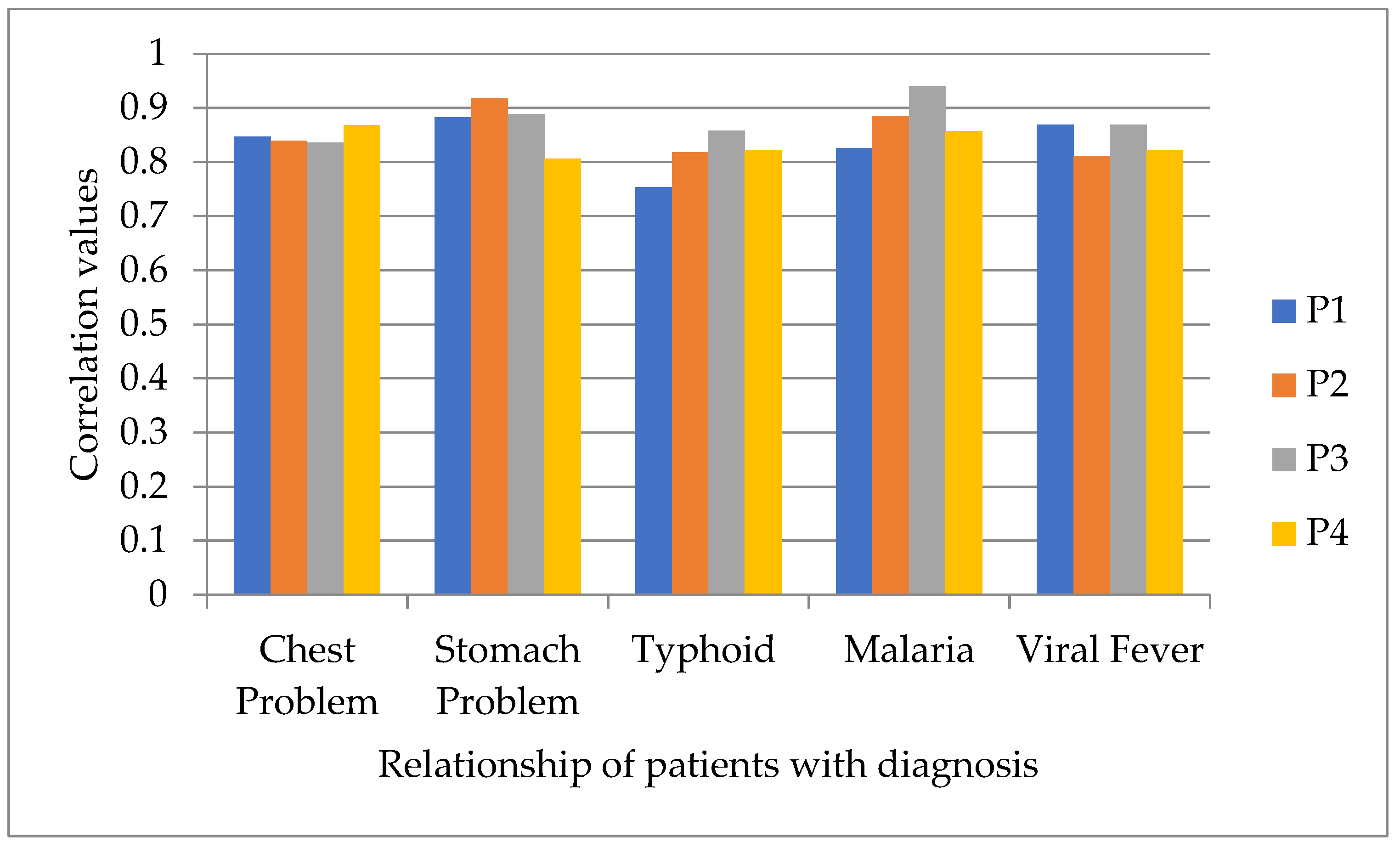
	Chest Problem	Stomach Problem	Typhoid	Malaria	Viral Fever
${\mathit{P}}_{\mathbf{1}}$	0.8473	0.8828	0.7536	0.8260	0.8690
${\mathit{P}}_{\mathbf{2}}$	0.8398	0.9178	0.8185	0.8855	0.8111
${\mathit{P}}_{\mathbf{3}}$	0.8358	0.8890	0.8585	0.9401	0.8689
${\mathit{P}}_{\mathbf{4}}$	0.8681	0.8064	0.8213	0.8570	0.8212

represents the ranking values obtained from the CC defined in Equation (3). The ranking values show the chances of diagnosing the disease ${\mathrm{D}}_{\mathrm{i}}$ to patient ${\mathrm{P}}_{\mathrm{i}}$. The highest-ranking value of disease shows that the patient is suffering from that disease. From Table 5, we observe that patients $P_1,P_2,P_3$ and $P_4$ are suffering from stomach, malaria, and chest problems. The results obtained in Table 5 are portrayed in Figure 3.

Next, we aim to compare the results obtained by Ullah et al. [34] with our presented work.

Table 6. Comparison of results of medical diagnosis.

CC	Ranking Order	Diagnosed Disease
Current work	$\mathrm{D}2>\mathrm{D}5>\mathrm{D}1>\mathrm{D}4>\mathrm{D}3$	$P_1$ has Stomach problem
	$\mathrm{D}2>\mathrm{D}4>\mathrm{D}1>\mathrm{D}4>\mathrm{D}5$	$P_2$ has Stomach problem
	$\mathrm{D}4>\mathrm{D}2>\mathrm{D}5>\mathrm{D}3>\mathrm{D}1$	$P_3$ has Malaria
	$\mathrm{D}1>\mathrm{D}4>\mathrm{D}5>\mathrm{D}3>\mathrm{D}2$	$P_4$ has Chest problem
Ullah et al. [34]	$\mathrm{D}2>\mathrm{D}5>\mathrm{D}1>\mathrm{D}4>\mathrm{D}3$	$P_1$ has Stomach problem
	$\mathrm{D}2>\mathrm{D}4>\mathrm{D}1>\mathrm{D}5>\mathrm{D}4$	$P_2$ has Stomach problem
	$\mathrm{D}4>\mathrm{D}2>\mathrm{D}3>\mathrm{D}1>\mathrm{D}5$	$P_3$ has Malaria
	$\mathrm{D}1>\mathrm{D}4>\mathrm{D}5>\mathrm{D}3>\mathrm{D}2$	$P_4$ has Chest problem
Mitchell [25]	Not applicable	Not applicable
Thao [27]	Not applicable	Not applicable
Garg and Rani [28]	Not applicable	Not applicable
Garg [29]	Not applicable	Not applicable

shows the ranking orders of the diseases obtained from the CC define in Equation (3) and CC defined in [34]. We further show that the CCs defined in [25,27,28] are unable to handle the data provided in the frame of TSFNs due to their limited nature.

According to the above result, it is concluded that by our proposed work the patient ${\mathrm{P}}_1$ is suffering from ${\mathrm{D}}_2$, the patient ${\mathrm{P}}_2$ is suffering from ${\mathrm{D}}_2$, the patient ${\mathrm{P}}_3$ is suffering from ${\mathrm{D}}_4$ and the patient ${\mathrm{P}}_4$ is suffering from ${\mathrm{D}}_1$. The results obtained from proposed approach and [34] are similar. However, there are slight differences in the ranking orders of the diseases.

The results of Table 6 are shown in Figure 4.

5. Conclusions

In this article, a new CC for the notion TSFSs has been developed, and their basic properties are studied. Then the applications of the proposed CC have been studied in pattern recognition and medical diagnosis. We have explored the application of the proposed TSFCC in practical applications relating to medical diagnosis and pattern recognition. The obtained results by the proposed CC have also been compared with the existing CC for TSFS. Our suggested TSFCC can handle some natural situations and present a patient with a clear diagnosis with the help of diagrams and numerical examples. Some key points of the study are summarized as follows.

• Our suggested TSFCC is based on the TSFS. Hence, the proposed CC accommodates the information in the more generalized form than the CC defined for IFS, PyFS, qROPFS, and PFS. It is more useful CC due to the characteristic of TSFS of obtaining maximum information from the real-life scenario.
• The proposed CC aggregates a larger range of information than the PFS. Consequently, the proposed CC can be applied more effectively to real-life problems of pattern recognition, medical diagnosis and feature selection.

The suggested work will be enhanced in the TSF soft set environment in the future and for the frameworks defined in [35,36,37]. We also aim to apply the developed approach in some methods developed in [38,39]. Moreover, we aim to study the application of our proposed CC in feature selection and fuzzy clustering [40,41]. The proposed research can also be extended to the problem discussed in [42].