On Solvable Lie Algebras of White Noise Operators

Abstract

We characterize the dimension of Lie algebras of white noise operators containing the quantum white noise derivatives of the conservation operator. We establish isomorphisms to filiform Lie algebras, Engel-type algebras, and solvable Lie algebras with Heisenberg nilradical and Abelian nilradical. A new class of solvable Lie algebras is proposed, those having an Engel-type algebra as nilradical. This arises in white noise analysis as a $2n+3$-dimensional Lie algebra containing the identity operator, annihilation operators, creation operators (Heisenberg algebra), number operator, and Gross Laplacian.

1. Introduction

Lie algebras typically arise as vector spaces of linear transformations endowed with a binary operation, which is in general, neither commutative nor associative. A Lie algebra over a field $\mathbb{K}$ is a vector space L over $\mathbb{K}$, with an operation $L\times L\to L$, denoted $(x,y)\mapsto [x,y]$, which is called the bracket or commutator of x and y, that satisfies the following conditions: (L1) The bracket operation is bilinear. (L2) $[x,x]=0$ for all $x\in L$. (L3) $[x,[y,z\left]\right]+[y,[z,x\left]\right]+[z,[x,y\left]\right]=0$ $\forall x,y,z\in L$ (Jacobi identity). A Lie algebra L is abelian if $[x,y]=0$ for all $x,y\in L$. We say that two Lie algebras L and $L^{\prime }$ over $\mathbb{K}$ are isomorphic if there exists a vector space isomorphism $\varphi :L\to L^{\prime }$ satisfying $\varphi \left(\right[x,y\left]\right)=\left[\varphi \right(x),\varphi (y\left)\right]$ for all $x,y\in L$. A subspace I of a Lie algebra L is called an ideal of L if $x\in L,y\in I$ together imply $[x,y]\in I$. The derived series is defined to be a sequence of ideals of L given by

$$L^{\left(0\right)}=L,L^{\left(1\right)}=[L,L],L^{\left(2\right)}=[L^{\left(1\right)},L^{\left(1\right)}],\dots ,L^{\left(i\right)}=[L^{(i-1)},L^{(i-1)}].$$

A Lie algebra L is solvable if $L^{\left(n\right)}=0$ for some n. Moreover, the lower central series is defined as a sequence of ideals of L given by

$$L^0=L,L^1=[L,L],L^2=[L,L^1],\dots ,L^i=[L,L^{i-1}].$$

A Lie algebra L is nilpotent if $L^n=0$ for some n. The maximal nilpotent ideal of a Lie algebra is called its nilradical. For more details on Lie algebras see [1]. Sophus Lie introduced Lie groups to study symmetries of solutions of differential equations. Their corresponding Lie algebras are vector fields generating one-parameter subgroups. Since Lie algebras are linear spaces they are easier to study than the Lie groups themselves. They have several applications in mathematics and related fields such as mathematical physics [2], stochastic calculus [3], and robotics [4], to name a few. For instance, they arise as vector spaces of linear operators which commute with a given operator, say, the Hamiltonian of a physical system [5].

One particular area of mathematics where Lie algebras are used is in white noise analysis, which was initiated by Hida [6] in 1975 to realize the time derivative of Brownian motion. It has been applied to other areas of mathematics such as mathematical physics and finance, see e.g., [7,8,9]. White noise analysis is an infinite dimensional analog of Schwartz’ distribution theory, where the roles of the Lebesgue measure on ${\mathbb{R}}^d$ and the Gelfand triple

$$E=\mathcal{S}\left({\mathbb{R}}^d\right)\subset H=L^2\left({\mathbb{R}}^d\right)\subset E^{\ast }={\mathcal{S}}^{\prime }\left({\mathbb{R}}^d\right)$$

(1)

are played by the Gaussian measure $\mu$ on $E^{\ast }$ and

$$\left(E\right)\subset \left(L^2\right)=L^2(E^{\ast },\mu )\subset {\left(E\right)}^{\ast },$$

(2)

respectively. We have the following expressions of the finite dimensional Laplacian $\Delta$ on ${\mathbb{R}}^d$:

$$\Delta =\sum _{i=1}^d{\left(\frac{\partial }{\partial x_i}\right)}^2=-\sum _{i=1}^d{\left(\frac{\partial }{\partial x_i}\right)}^{\ast }\frac{\partial }{\partial x_i},$$

(3)

when $\Delta$ acts on $\mathcal{S}\left({\mathbb{R}}^d\right)$. The Gross Laplacian and number operator are infinite dimensional analogs of the Laplacian $\Delta$ expressed as follows:

$${\Delta }_{\mathrm{G}}={\int }_T{a}_t^{2}dt,N={\int }_T{a}_t^{\ast }{a}_{t}dt.$$

However, unlike the finite dimensional case, ${\Delta }_{\mathrm{G}}$ and N are completely different from each other [10]. Moreover, ${\Delta }_{\mathrm{G}}$ and N are characterized by their rotation-invariance [11]. One-parameter transformation groups acting on the space of test white noise functionals $\left(E\right)$ and the Lie algebra spanned by their infinitesimal generators are discussed in [12]. They obtained a five-dimensional complex Lie algebra generated by the identity operator, number operator, Gross Laplacian, and the infinitesimal generators of differentiation and multiplication operators. A two-parameter transformation group has been constructed in [13] with corresponding Lie algebra $\mathbb{C}{\Delta }_{\mathrm{G}}+\mathbb{C}N$. Later on, multi-parameter transformation groups [14] and Laplacians of diagonal type [10] were also studied. The generalized Gross Laplacian was introduced in [15]. Ji and Sinha [16] studied a six-dimensional non-solvable Lie ∗-algebra containing the conservation operator and generalized Gross Laplacian as well as the quantum stochastic processes they induce.

The classification of solvable Lie algebras of finite dimension still remains unsolved. A realistic partial classification problem is to classify all solvable Lie algebras with a given nilradical [5]. The goal of this paper is to investigate Lie algebras of white noise operators and show that they are isomorphic to some known abstract Lie algebra. In the course of this investigation, we describe a Lie algebra of white noise operators that belongs to the class of solvable Lie algebras with Engel-type nilradical. This paper is organized as follows: In Section 2, we assemble standard notations used in white noise analysis. Section 3 is devoted to a review of classification of solvable Lie algebras. In Section 4, we prove isomorphisms to Lie algebras with Heisenberg nilradical and Engel-type nilradical. A solvable Lie algebra with Engel-type nilradical arises from the extension of the Heisenberg Lie algebra by the Gross Laplacian and number operator. In Section 5, we characterize the dimension of Lie algebras of white noise operators containing the quantum white noise derivatives of the conservation operator. In Section 6, we establish isomorphisms to filiform Lie algebras. Section 7 is devoted to the study of white noise Lie algebras with Abelian nilradicals. In particular, we show that the Lie algebra generated by the creation operator and the conservation operator corresponding to the Fourier–Mehler transform (fractional Fourier transform) is parametrized by the nth roots of unity. In Section 8, we show the linear independence of generalized Gross Laplacians (quadratic annihilation operators) corresponding to the nth powers of the unilateral shift.

2. Preliminaries

In this section, we introduce standard definitions and notations used in white noise analysis, for more details see [7,8,11]. To outline this section, we start with a real Gelfand triple

$$E=\mathcal{S}\left(\mathbb{R}\right)\subset H=L^2\left(\mathbb{R}\right)\subset E^{\ast }={\mathcal{S}}^{\prime }\left(\mathbb{R}\right),$$

(4)

where $S\left(\mathbb{R}\right)$ is the Schwartz space of rapidly decreasing functions, $S^{\prime }\left(\mathbb{R}\right)$ is the space of tempered distributions, and we identify H with its dual space $H^{\ast }$ by Riesz Representation Theorem. We denote the canonical bilinear form on $E^{\ast }\times E$ and the inner product of H by the same symbol $\langle ·,·\rangle$ since they are compatible. Then, we introduce a measure on $E^{\ast }$ via Bochner–Minlos theorem. Finally, spaces of test white noise functionals and generalized white functionals are constructed in Section 2.1.2. Moreover, some properties of the exponential vectors are enumerated.

2.1. Standard Countably Hilbert Space Construction

We recall the following definitions; for more details see [8]. We say that a topological vector space V together with a family $\left\{\right|·{|}_n\}$ of inner product norms is a countably Hilbert space or CH-space if V is complete with respect to its topology. Suppose that V is a CH-space together with an increasing sequence $\left\{\right|·{|}_n\}$ of norms. Denote by $V_n$ the completion V with respect to the norm ${|·|}_n$. A CH-space V is said to be a nuclear space if for any n, there exists $m\ge n$ such that the inclusion map from $V_m$ into $V_n$ is a Hilbert–Schmidt operator. There are several methods of constructing CH-spaces (see, e.g., [7,11]) but we will focus on the construction given a Hilbert space and an operator satisfying certain conditions. Since our results deal with the Schwartz space $S\left(\mathbb{R}\right)$ and the space of test white noise functionals $\left(E\right)$, the constructions in Section 2.1.1 and Section 2.1.2 are sufficient for our purposes.

2.1.1. Reconstruction of Schwartz Space

As an example of a standard countably Hilbert space, we will reconstruct the Schwartz space $S\left(\mathbb{R}\right)$ from the real Hilbert space $H=L^2\left(\mathbb{R}\right)$ and the operator

$$A=-d^2/d{x}^2+x^2+1.$$

Recall that a function $\xi$ on $\mathbb{R}$ is a rapidly decreasing function if it is smooth and for all nonnegative integers n and k, $|x^n{\xi }^{\left(k\right)}\left(x\right)|\to 0\mathrm{as}|x|\to \infty .$ Then $S\left(\mathbb{R}\right)$ is defined as the space of rapidly decreasing functions on $\mathbb{R}$. For any $n,k\ge 0$, define a norm ${|·|}_{n,k}$ on $S\left(\mathbb{R}\right)$ by

$${\left|\xi \right|}_{n,k}={\left({\int }_{\mathbb{R}}{\left|x^n{\xi }^{\left(k\right)}\right|}^{2}dx\right)}^{1/2}.$$

This family $\left\{\right|·{|}_{n,k};n,k\ge 0\}$ of norms generates a topology on $S\left(\mathbb{R}\right)$. Hence, Schwartz space $S\left(\mathbb{R}\right)$ is a topological vector space. The Hermite polynomial of degree n is defined as $H_n\left(x\right)={(-1)}^n{e}^{x^2}{(d/dx)}^n{e}^{-x^2}$ and

$$e_n\left(x\right)=\frac{1}{\sqrt{\sqrt{\pi }{2}^{n}n!}}{H}_n\left(x\right)e^{-x^2/2}$$

is the corresponding Hermite function. Then the Hermite functions form an orthonormal basis for $L^2\left(\mathbb{R}\right)$. In fact, they are eigenfunctions of A since $\forall n\ge 0$, $A{e}_n=(2n+2)e_n.$ Since A is injective, its inverse $A^{-1}:\mathcal{R}\left(A\right)\to L^2\left(\mathbb{R}\right)$ exists with the following eigenvalues $A^{-1}={(2n+2)}^{-1}{e}_n.$ Since $S\left(\mathbb{R}\right)$ is contained in the range of A and is dense in $L^2\left(\mathbb{R}\right)$, we can extend A to $L^2\left(\mathbb{R}\right)$. We have that $A^{-1}$ is a bounded operator on $L^2\left(\mathbb{R}\right)$ with $\parallel A^{-1}\parallel =1/2$. For any $p>1/2$, $A^{-p}$ is a Hilbert–Schmidt operator of $L^2\left(\mathbb{R}\right)$. In fact, its Hilbert–Schmidt norm is given by

$$\parallel A^{-p}{\parallel }_{HS}^2=\sum _{n=0}^{\infty }{(2n+2)}^{-2p}.$$

For each $p\ge 0$, define

$${\left|f\right|}_p={\left|A^{p}f\right|}_0,$$

where ${|·|}_0$ is the $L^2\left(\mathbb{R}\right)$-norm. Let $S_p\left(\mathbb{R}\right)=\{f\in L^2{\left(\mathbb{R}\right)\left|\right|f|}_p<\infty \}$. Then $S_p\left(\mathbb{R}\right)$ is a Hilbert space with norm ${|·|}_p$. Moreover, it is known that [8]:

• $S\left(\mathbb{R}\right)={\cap }_{p\ge 0}{S}_p\left(\mathbb{R}\right)$.
• The families $\left\{\right|·{|}_{n,k};n,k\ge 0\}$ and $\left\{\right|·{|}_p;p\ge 0\}$ are equivalent, i.e, they generate the same topology on $S\left(\mathbb{R}\right)$.
• $S\left(\mathbb{R}\right)$ is a nuclear space.

• We have reconstructed $S\left(\mathbb{R}\right)$ as the projective limit of $\{S_p\left(\mathbb{R}\right);p\ge 0\}$, i.e.,

$$S\left(\mathbb{R}\right)=\bigcap _{p\ge 0}{S}_p\left(\mathbb{R}\right)=\mathrm{proj}{\lim }_{p\to \infty }{S}_p\left(\mathbb{R}\right).$$

We also have the following continuous inclusions:

$$S\left(\mathbb{R}\right)\subset \cdots \subset S_{p+1}\left(\mathbb{R}\right)\subset S_p\left(\mathbb{R}\right)\subset L^2\left(\mathbb{R}\right)\subset S_p^{\prime }\left(\mathbb{R}\right)\subset S_{p+1}^{\prime }\left(\mathbb{R}\right)\subset \cdots \subset S^{\prime }\left(\mathbb{R}\right).$$

It is known that the norm of the dual space $S_p^{\prime }\left(\mathbb{R}\right)$ of $S_p\left(\mathbb{R}\right)$ is given by

$${\left|f\right|}_{-p}={\left|A^{-p}f\right|}_0,p>0.$$

and that $S_p^{\prime }\left(\mathbb{R}\right)$ is the completion of $L^2\left(\mathbb{R}\right)$ with respect to the norm ${|·|}_{-p}$. Moreover, $S^{\prime }\left(\mathbb{R}\right)$ is the dual space of $S\left(\mathbb{R}\right)$ and

$$S^{\prime }\left(\mathbb{R}\right)=\bigcup _{p\ge 0}{S}_p^{\prime }\left(\mathbb{R}\right)=\mathrm{ind}{\lim }_{p\to \infty }{S}_p^{\prime }\left(\mathbb{R}\right).$$

2.1.2. Spaces of Test and Generalized White Noise Functionals

Given a locally convex space $\mathfrak{X}$ over $\mathbb{R}$, denote by ${\mathfrak{X}}_{\mathbb{C}}$ its complexification. Then, we extend the canonical bilinear form ${\mathfrak{X}}^{\ast }\times \mathfrak{X}$, which is an $\mathbb{R}$-bilinear form, to a $\mathbb{C}$-bilinear form on ${\mathfrak{X}}_{\mathbb{C}}^{\ast }\times {\mathfrak{X}}_{\mathbb{C}}$, denoted by the same symbol [11]. As before, we start with a real Gelfand triple

$$E=\mathcal{S}\left(\mathbb{R}\right)\subset H=L^2\left(\mathbb{R}\right)\subset E^{\ast }={\mathcal{S}}^{\prime }\left(\mathbb{R}\right).$$

Applying Bochner–Minlos theorem [8], a probability measure $\mu$ on $E^{\ast }$ exists such that

$${\int }_{E^{\ast }}{e}^{i\langle x,\xi \rangle }\mu \left(dx\right)=e^{-\frac{1}{2}{\left|\xi \right|}_0^2},\xi \in E.$$

The measure $\mu$ is called the standard Gaussian measure on $E^{\ast }$ and the probability space $(E^{\ast },\mu )$ is called the white noise space. The following construction of test and generalized white noise functionals follows from [8], pp. 18–20. Let us denote by $\left(L^2\right)$ the complex Hilbert space $L^2(E^{\ast },\mu ;\mathbb{C})$. As before, we let $A=-d^2/d{x}^2+x^2+1.$ Any $\varphi \in \left(L^2\right)$ has a Wiener–Ito decomposition

$$\varphi \left(x\right)=\sum _{n=0}^{\infty }\langle :x^{\otimes n}:,f_n\rangle .$$

The $\left(L^2\right)$-norm ${\parallel \varphi \parallel }_0$ of $\varphi$ is given by

$${\parallel \varphi \parallel }_0={\left(\sum _{n=0}^{\infty }n!{\left|f_n\right|}_0^2\right)}^{1/2},$$

where ${|·|}_0$ denotes the $L_{\mathbb{C}}^2\left({\mathbb{R}}^n\right)$-norm for any n. We now use the second quantization operator of A, denoted by $\mathsf{\Gamma }\left(A\right)$, as follows. For $\varphi \in \left(L^2\right)$ satisfying the condition that ${\sum }_{n=0}^{\infty }n!{\left|A^{\otimes n}{f}_n\right|}_0^2<\infty ,$ we define $\mathsf{\Gamma }\left(A\right)\varphi \in \left(L^2\right)$ by

$$\mathsf{\Gamma }\left(A\right)\varphi \left(x\right)=\sum _{n=0}^{\infty }\langle :x^{\otimes n}:,A^{\otimes n}{f}_n\rangle .$$

This operator is densely defined on $\left(L^2\right)$ and has the following properties similar to A in Section 2.1.1:

• $\left(L^2\right)$ has an orthonormal basis consisting of eigenfunctions of $\mathsf{\Gamma }\left(A\right)$.
• $\mathsf{\Gamma }{\left(A\right)}^{-1}$ is a bounded operator of $\left(L^2\right)$ with ${\parallel \mathsf{\Gamma }\left(A\right)}^{-1}\parallel =1$.
• For $p>1$, $\mathsf{\Gamma }{\left(A\right)}^{-p}$ is a Hilbert–Schmidt operator of $\left(L^2\right)$.

• Following the same procedure in Section 2.1.1 we construct a space of test white noise functionals. For $p\ge 0$, define

$${\parallel \varphi \parallel }_p={\parallel \mathsf{\Gamma }\left(A\right)}^p\varphi {\parallel }_0,$$

where $\parallel ·{\parallel }_0$ is the $\left(L^2\right)$-norm. Let

$$\left(E_p\right)=\{\varphi \in \left(L^2\right){:\parallel \varphi \parallel }_p<\infty \}.$$

Then $\left(E_p\right)$ is a Hilbert space with norm $\parallel ·{\parallel }_p$. Moreover, we define

$$\left(E\right)=\bigcap _{p\ge 0}\left(E_p\right)=\mathrm{proj}{\lim }_{p\to \infty }\left(E_p\right),$$

which we call the space of test white noise functionals. Its dual space ${\left(E\right)}^{\ast }$ is the space of generalized white noise functionals. The bilinear pairing of ${\left(E\right)}^{\ast }$ and $\left(E\right)$ is denoted by $\langle \langle ·,·\rangle \rangle$. It is related to the inner product of $\left(L^2\right)$ by

$$\langle \langle \varphi ,\psi \rangle \rangle ={(\varphi ,\overline{\psi })}_{\left(L^2\right)},\varphi \in \left(L^2\right),\psi \in \left(E\right).$$

2.2. Exponential Vectors

We often have to deal with operators which are determined uniquely by their action on the exponential vectors. Here, we will enumerate some properties of the exponential vectors. Let $\mathfrak{h}$ be a real or complex Hilbert space with the norm $|·|$. Let $\mathsf{\Gamma }\left(\mathfrak{h}\right)$ be the space of all sequences

$$\mathbf{f}={\left(f_n\right)}_{n=0}^{\infty },f_n\in {\mathfrak{h}}^{\widehat{\otimes }n},$$

such that ${\sum }_{n=0}^{\infty }n!{\left|f_n\right|}^2<\infty$. Equipped with the norm

$${\parallel \mathbf{f}\parallel }_{\mathsf{\Gamma }\left(\mathfrak{h}\right)}^2=\sum _{n=0}^{\infty }n!{\left|f_n\right|}^2,$$

the Hilbert space $\mathsf{\Gamma }\left(\mathfrak{h}\right)$ is called the (Boson) Fock space or the symmetric Hilbert space over $\mathfrak{h}$ [11]. For $\xi \in \mathfrak{h}$ we put

$${\varphi }_{\xi }=\left(1,\xi ,\frac{{\xi }^{\otimes 2}}{2!},\dots ,\frac{{\xi }^{\otimes n}}{n!},\dots \right).$$

(5)

Then

$$\parallel {\varphi }_{\xi }{\parallel }_{\mathsf{\Gamma }\left(\mathfrak{h}\right)}^2=\sum _{n=0}^{\infty }n!{\left|\frac{{\xi }^{\otimes n}}{n!}\right|}^2=\sum _{n=0}^{\infty }\frac{{\left|\xi \right|}^{2n}}{n!}=e^{{\left|\xi \right|}^2}<\infty ,$$

and, in particular, ${\varphi }_{\xi }\in \mathsf{\Gamma }\left(\mathfrak{h}\right)$. We call ${\varphi }_{\xi }$ in (5) an exponential vector.

Proposition 1 ([11]).

The exponential vectors $\{{\varphi }_{\xi }:\xi \in \mathfrak{h}\}$ are linearly independent.

Theorem 1 (Wiener–Ito–Segal isomorphism [11]).

For each $\varphi \in L^2(E^{\ast },\mu ;\mathbb{C})$ there exists a unique $\mathbf{f}={\left(f_n\right)}_{n=0}^{\infty }\in \mathsf{\Gamma }\left(H_{\mathbb{C}}\right)$ such that

$$\varphi \left(x\right)=\sum _{n=0}^{\infty }\langle :x^{\otimes n}:,f_n\rangle ,$$

(6)

in the $L^2$-sense. Conversely, for any $\mathbf{f}={\left(f_n\right)}_{n=0}^{\infty }\in \mathsf{\Gamma }\left(H_{\mathbb{C}}\right)$, (6) defines a function in $L^2(E^{\ast },\mu ;\mathbb{C})$. In that case,

$${\parallel \varphi \parallel }^2=\sum _{n=0}^{\infty }n!|f_n{|}^2={\parallel \mathbf{f}\parallel }_{\mathsf{\Gamma }\left(H_{\mathbb{C}}\right)}^2.$$

A similar result holds for the real case. Thus, we have canonical isomorphisms:

$$L^2(E^{\ast },\mu ;\mathbb{R})\cong \mathsf{\Gamma }\left(H\right)\mathit{and}{L}^2(E^{\ast },\mu ;\mathbb{C})\cong \mathsf{\Gamma }\left(H_{\mathbb{C}}\right).$$

Taking the Wiener–Ito–Segal isomorphism into account, we define an exponential vector in $\left(L^2\right)=L^2(E^{\ast },\mu ;\mathbb{C})$ by

$${\varphi }_{\xi }\left(x\right)=\sum _{n=0}^{\infty }〈:x^{\otimes n}:,\frac{{\xi }^{\otimes n}}{n!}〉,$$

$x\in E^{\ast }$, $\xi \in E_{\mathbb{C}}$.

Lemma 1 ([11]).

Let $\xi \in H_{\mathbb{C}}$. Then, ${\varphi }_{\xi }\in \left(E\right)$ if and only if $\xi \in E_{\mathbb{C}}$.

Theorem 2 ([11]).

If $\alpha \in \mathbb{C}$, $\alpha \ne 0$, then $\{{\varphi }_{\alpha \xi }:\xi \in E\}$ spans a dense subspace of $\left(E\right)$.

2.3. White Noise Operators

The pair of annihilation and creation operators $\{a_t,a_t^{\ast }:t\in T\}$ on a time parameter space T is called a quantum white noise (field) on T [17]. For $y\in E^{\ast }$, we define

$$a\left(y\right)={\mathsf{\Xi }}_{0,1}\left(y\right)={\int }_{T}y\left(t\right)a_{t}dt,a^{\ast }\left(y\right)={\mathsf{\Xi }}_{1,0}\left(y\right)={\int }_{T}y\left(t\right)a_t^{\ast }dt.$$

(7)

These are called the annihilation and creation operators associated with y, respectively. For $\xi \in E$, it is known (see e.g., [10,11]) that the action of the annihilation operator $a\left(y\right)$ on the exponential vectors is given by

$$a\left(y\right){\varphi }_{\xi }=\langle y,\xi \rangle {\varphi }_{\xi }.$$

(8)

If $\zeta \in E$, then $a\left(\zeta \right)$ can be extended to ${\left(E\right)}^{\ast }$ so that it belongs to $\mathcal{L}({\left(E\right)}^{\ast },{\left(E\right)}^{\ast })$, denoted by the same symbol. On the other hand, the restriction of $a^{\ast }\left(\zeta \right)$ to $\left(E\right)$ belongs to $\mathcal{L}\left(\right(E),(E\left)\right)$ [18]. Thus, given any white noise operator $\mathsf{\Xi }\in \mathcal{L}(\left(E\right),{\left(E\right)}^{\ast })$ and $\zeta \in E$, the commutators

$$[a\left(\zeta \right),\mathsf{\Xi }]=a\left(\zeta \right)\mathsf{\Xi }-\mathsf{\Xi }a\left(\zeta \right),-[a^{\ast }\left(\zeta \right),\mathsf{\Xi }]=\mathsf{\Xi }{a}^{\ast }\left(\zeta \right)-a^{\ast }\left(\zeta \right)\mathsf{\Xi },$$

are well-defined and belongs to $\mathcal{L}(\left(E\right),{\left(E\right)}^{\ast })$. We define

$$D_{\zeta }^{+}\mathsf{\Xi }=[a\left(\zeta \right),\mathsf{\Xi }],D_{\zeta }^{-}\mathsf{\Xi }=-[a^{\ast }\left(\zeta \right),\mathsf{\Xi }].$$

Definition 1 ([18]).

$D_{\zeta }^{+}\mathsf{\Xi }$ and $D_{\zeta }^{-}\mathsf{\Xi }$ are called the creation derivative and annihilation derivative of Ξ, respectively. They are collectively called the quantum white noise derivatives (qwn-derivatives) of Ξ.

Theorem 3 ([17]).

$(\zeta ,\mathsf{\Xi })\mapsto D_{\zeta }^{\pm }\mathsf{\Xi }$ is a continuous bilinear map from $E\times \mathcal{L}(\left(E\right),{\left(E\right)}^{\ast })$ into $\mathcal{L}(\left(E\right),{\left(E\right)}^{\ast })$. In particular, $a\left(\zeta \right)$ and $a^{\ast }\left(\zeta \right)$ are linear in ζ.

The quantum white noise derivatives of the generalized Gross Laplacian and conservation operator are given in [17,19]. By the kernel theorem, an operator $S\in \mathcal{L}(E,E^{\ast })$, determines a unique distribution ${\tau }_S\in {(E\otimes E)}^{\ast }$ such that

$$\langle {\tau }_S,\eta \otimes \xi \rangle =\langle S\xi ,\eta \rangle ,\xi ,\eta \in E.$$

The generalized Gross Laplacian associated with S is the integral kernel operator given by

$${\Delta }_{\mathrm{G}}\left(S\right)={\mathsf{\Xi }}_{0,2}\left({\tau }_S\right)={\int }_{T\times T}{\tau }_S(s,t)a_s{a}_{t}dsdt$$

It is known that ${\Delta }_{\mathrm{G}}\left(S\right)\in \mathcal{L}(\left(E\right),\left(E\right))$. We recover the usual Gross Laplacian by taking $S=Id$, i.e., ${\Delta }_{\mathrm{G}}={\Delta }_{\mathrm{G}}\left(Id\right)$. The conservation operator associated with S is the integral kernel operator

$$\mathsf{\Lambda }\left(S\right)={\mathsf{\Xi }}_{1,1}\left({\tau }_S\right)={\int }_{T\times T}{\tau }_S(s,t)a_s^{\ast }{a}_{t}dsdt$$

Generally, $\mathsf{\Lambda }\left(S\right)\in \mathcal{L}(\left(E\right),{\left(E\right)}^{\ast })$. It is known that $\mathsf{\Lambda }\left(S\right)\in \mathcal{L}\left(\right(E),(E\left)\right)$ if and only if S is a continuous linear operator on $E_{\mathbb{C}}$ [11]. We recover the number operator by taking $S=Id$, i.e., $N=\mathsf{\Lambda }\left(Id\right)$.

Lemma 2 ([17]).

For $S\in \mathcal{L}(E,E^{\ast })$ and $\zeta \in E$, we have

$$D_{\zeta }^{+}{\Delta }_{\mathrm{G}}\left(S\right)=0,D_{\zeta }^{-}{\Delta }_{\mathrm{G}}\left(S\right)=a\left(S\zeta \right)+a\left(S^{\ast }\zeta \right),$$

(9)

$$D_{\zeta }^{+}\mathsf{\Lambda }\left(S\right)=a\left(S^{\ast }\zeta \right),D_{\zeta }^{-}\mathsf{\Lambda }\left(S\right)=a^{\ast }\left(S\zeta \right).$$

(10)

The following results will be useful in classifying Lie algebras of white noise operators.

Theorem 4 ([8,14]).

For $\zeta ,{\zeta }_1,{\zeta }_2\in E_{\mathbb{C}}$, we have the following commutation relations:

• $[a\left({\zeta }_1\right),a\left({\zeta }_2\right)]=[a^{\ast }\left({\zeta }_1\right),a^{\ast }\left({\zeta }_2\right)]=0$,
• $[a\left({\zeta }_1\right),a^{\ast }\left({\zeta }_2\right)]=\langle {\zeta }_1,{\zeta }_2\rangle Id$,
• $\left[a\right(\zeta ),N]=a\left(\zeta \right)$,
• $[a\left(\zeta \right),{\Delta }_{\mathrm{G}}]=0$,
• $[a^{\ast }\left(\zeta \right),N]=-a^{\ast }\left(\zeta \right)$,
• $[a^{\ast }\left(\zeta \right),{\Delta }_{\mathrm{G}}]=-2a\left(\zeta \right)$,
• $[{\Delta }_G,N]=2{\Delta }_{\mathrm{G}}$.

Theorem 5 ([14]).

For each nonzero $\zeta \in E_{\mathbb{C}}$, let $\mathfrak{h}=span(Id,a\left(\zeta \right),a^{\ast }\left(\zeta \right),N,{\Delta }_{\mathrm{G}}).$ Then $\mathfrak{h}$ is a five-dimensional non-nilpotent solvable complex Lie algebra.

3. Classification of Lie Algebras

We recall the classification of Lie algebras relevant to our study. This helps us classify white noise Lie algebras and propose a new class of solvable Lie algebras, those having an Engel-type algebra as nilradical.

3.1. Heisenberg Lie Algebras and Their extensions

The Heisenberg algebra $H\left(n\right)$ is defined by its standard basis

$$\{p_1,\dots ,p_n,q_1,\dots ,q_n,h\}$$

with commutation relations

$$[p_i,q_j]={\delta }_{ij}h,[p_i,p_j]=[q_i,q_j]=[p_i,h]=[q_i,h]=0,1\le i,j\le m.$$

It is of primordial importance in quantum mechanics. Extensions of $H\left(n\right)$ by further operators $s_1,\dots ,s_f$ is a question of the algebra of quantum mechanical observables. These extensions are denoted by $L(n,f)$. The construction of all finite dimensional indecomposable solvable Lie algebras $L(n,f)$ containing $H\left(n\right)$ as nilradical was performed in [20]. They also obtained the Casimir invariants of the algebras $L(n,f)$. Solvable extensions of the Heisenberg algebra $H\left(n\right)$ by the number operator are denoted as $M^{\left(3\right)}$ (2.21a) and $F_2(0,1,1)$ of Table A1 in [20], and as ${\mathfrak{s}}_{4,6}$ and ${\mathfrak{s}}_{6,162}$ with $a=1$ in [5]. The connected Lie groups with Lie algebra ${\mathfrak{s}}_{4,6}$ can be found in [21] Cor. 4.10.

An element of the Lie algebra of the symplectic group $Sp(1,\mathbb{R})$ induces a derivation of the Heisenberg Lie algebra [22]. The extension of the Heisenberg Lie algebra by this derivation has been used to classify Ricci solitons [23]. Hogan and Lakey [24] studied extensions of the Heisenberg group in two ways. The first is the affine Weyl–Heisenberg (AWH) group, which is the semi-direct product of the Heisenberg group by dilations. Another way of extending the Heisenberg group is via the group of third-order upper triangular matrices, the so-called upper triangular (UT) groups. The UT and AWH groups are very closely related. In fact, they have isomorphic Lie algebras [24]. The matrix realizations of these Lie algebras can be found in [23,24,25].

3.2. Filiform Lie Algebras

In 1983, Fialowski [26] has given a classification of infinite dimensional $\mathbb{N}$-graded Lie algebras over a field of characteristic zero with two generators and one-dimensional homogeneous components. A Lie algebra of this type, satisfying $[{\mathfrak{g}}_1,{\mathfrak{g}}_i]={\mathfrak{g}}_{i+1}$ for every i, must be isomorphic to one of the following: ${\mathfrak{m}}_0,{\mathfrak{m}}_2$ or $L_1$. They were called infinite-dimensional filiform Lie algebras as an infinite analogue of the finite-dimensional filiform Lie algebras coined by Vergne in [27]. In this paper, we focus on ${\mathfrak{m}}_0$, which has generators $e_i,i\ge 1$, and whose nontrivial relations are $[e_1,e_i]=e_{i+1}$ for all $i\ge 2$. This Lie algebra has been studied by several authors, for instance, the cohomology of ${\mathfrak{m}}_0$ were computed in [28,29,30]. We will also be dealing with a finite-dimensional filiform Lie algebra, called model filiform Lie algebra, whose nontrivial relations are given by $[e_1,e_h]=e_{h-1}$ for $3\le h\le n$ [31] (see also [5]).

3.3. Carnot Algebras

Spaces with metric structure that is viewed as a constrained geometry, wherein motion is only allowed along a set of directions, changing from point to point, are called Sub-Riemmanian spaces, or Carnot–Caratheodory spaces [32]. A Carnot algebra is a finite-dimensional graded nilpotent Lie algebra, which is generated by the first homogeneous component and is equipped with a Euclidean structure. We call Carnot group the simply connected Lie group associated with a Carnot algebra. The Heisenberg group is the unique three-dimensional Carnot group, up to metric-preserving isomorphism [33]. The graded automorphisms of Carnot algebras were studied in [34].

Engel-Type Algebras

Recently, Le Donne and Moisala [35] introduced the Engel-type algebra as a generalization of the four-dimensional Engel algebra [36]. They are the only obstruction to semigeneration in Carnot algebras [35]. The Betti numbers of Engel-type algebras were computed in [37], although Pouseele did not use the term Engel-type.

Definition 2 ([35]).

For each $n\in \mathbb{N}$, the nth Engel-type algebra, denoted by $\mathbb{E}{⋉}^n$, is the $2(n+1)$-dimensional Lie algebra with basis ${\{X,Y_i,T_i,Z\}}_{i=1}^n$, with nontrivial brackets given by

$$[Y_i,X]=T_i,\mathit{and}[Y_i,T_i]=Z\forall i\in \{1,\dots ,n\}.$$

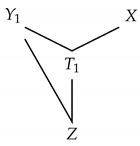
The first Engel-type algebra $\mathbb{E}{⋉}^1$, more popularly known as the Engel algebra, is the four-dimensional nilpotent Lie algebra denoted as ${\mathfrak{n}}_{4,1}$ in [5], and as $N_{4,2}$ in [38]. Following the convention in [35,38], their commutators are illustrated by the diagram below where it is read from left to right of the V and the resulting bracket is at the bottom of the V. Here, for instance, $[Y_1,X]=T_1$ and $[Y_1,T_1]=Z$.

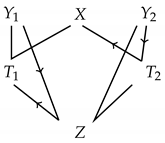
The second one, which is six-dimensional, is denoted as $\mathbb{E}{⋉}^2$. This can be found as $N_{6,3,1a}$ in [38], as $L_{6,19\left(1\right)}$ in [39], and as ${\mathfrak{n}}_{6,13}$ in [5] with $ϵ=1$. The diagram below should be read similarly except that we follow the direction of the indicated arrows, for instance, $[Y_2,X]=T_2$.

4. Solvable Lie Algebras with Engel-Type Nilradical

Rubin, Winternitz, and Ndogmo studied solvable extensions of a given nilpotent Lie algebra, such as the Heisenberg algebras [20], Abelian algebras [40], and so on (see [5]). Recently, Le Donne and Moisala [35] introduced the Engel-type algebras as a generalization of the Engel algebra. Here, we study solvable Lie algebras with Engel-type nilradical. This is a class of solvable Lie algebras that arises naturally in white noise analysis. As a starting point, a Lie algebra of white noise operators generated by annihilation and creation operators corresponding to elements of an orthonormal basis is isomorphic to the Heisenberg algebra. From here on, we assume that

$$E=\mathcal{S}\left(\mathbb{R}\right)\subset H=L^2\left(\mathbb{R}\right)\subset E^{\ast }={\mathcal{S}}^{\prime }\left(\mathbb{R}\right),$$

as defined in (4).

Remark 1.

By Theorem 3, $a(c_1{\zeta }_1+c_2{\zeta }_2)=c_{1}a\left({\zeta }_1\right)+c_{2}a\left({\zeta }_2\right)$ for all $\zeta \in E,c_1,c_2\in \mathbb{K}$. The analogous result holds for the creation operator.

Proposition 2.

If ${\left\{e_n\right\}}_0^{\infty }\subset E$ is an orthonormal basis for H, then $\{a\left(e_n\right):n\ge 0\}$ and $\{a^{\ast }\left(e_n\right):n\ge 0\}$ are linearly independent sets.

Proof. 

Let ${\left\{e_{n_k}\right\}}_1^m\subset {\left\{e_n\right\}}_0^{\infty }$. Suppose ${\sum }_1^m{\alpha }_{k}a\left(e_{n_k}\right)=0,$ where ${\alpha }_k\in \mathbb{K}$. Then

$$a(\sum _1^m{\alpha }_k{e}_{n_k})=0.$$

Let $y={\sum }_1^m{\alpha }_k{e}_{n_k}$ and $k\in \{1,\dots ,m\}$. By the action of the annihilation operator on the exponential vectors (see (8)) and orthogonality, we have

$$0=a\left(y\right){\varphi }_{e_{n_k}}=\langle y,e_{n_k}\rangle {\varphi }_{e_{n_k}}={\alpha }_k\langle e_{n_k},e_{n_k}\rangle {\varphi }_{e_{n_k}}={\alpha }_k{\varphi }_{e_{n_k}}.$$

Applying Proposition 1, ${\alpha }_k=0$ for all k. Now suppose

$$\sum _1^m{\alpha }_k{a}^{\ast }\left(e_{n_k}\right)=a^{\ast }(\sum _1^m{\alpha }_k{e}_{n_k})=0,$$

where ${\alpha }_k\in \mathbb{K}$. Let $y={\sum }_1^m{\alpha }_k{e}_{n_k}$ and $k\in \{1,\dots ,m\}$. Then

$$\begin{array}{cc}\hfill 0& =\langle \langle a^{\ast }\left(y\right){\varphi }_{e_{n_k}},{\varphi }_{e_{n_k}}\rangle \rangle \hfill \\ \hfill & =\langle \langle {\varphi }_{e_{n_k}},a\left(y\right){\varphi }_{e_{n_k}}\rangle \rangle \hfill \\ \hfill & ={({\varphi }_{e_{n_k}},\overline{a\left(y\right){\varphi }_{e_{n_k}}})}_{\left(L^2\right)}={\alpha }_k{({\varphi }_{e_{n_k}},\overline{{\varphi }_{e_{n_k}}})}_{\left(L^2\right)}.\hfill \end{array}$$

Since ${\varphi }_{e_{n_k}}\ne 0$, we must have ${\alpha }_k=0$. Therefore, ${\alpha }_k=0$ for all k. □

Theorem 6.

Suppose ${\left\{e_n\right\}}_{n=0}^{\infty }\subset E$ is an orthonormal basis for H. If $\mathfrak{h}=\langle Id,a\left(e_k\right),a^{\ast }\left(e_k\right):k=0,1,\dots ,n-1\rangle$, then $\mathfrak{h}$ is isomorphic to the Heisenberg Lie algebra $H\left(n\right)$.

Proof. 

We have the following correspondence $a\left(e_i\right)\mapsto p_i$, $a^{\ast }\left(e_i\right)\mapsto q_i$, and $Id\mapsto h$. Moreover, $[a\left(e_i\right),a^{\ast }\left(e_i\right)]=\langle e_i,e_j\rangle Id={\delta }_{ij}Id$. The result follows from Theorem 4. □

Then we extend the Heisenberg algebra $H\left(n\right)$ by the Gross Laplacian ${\Delta }_{\mathrm{G}}$. However, this extension does not have the Heisenberg algebra as nilradical since it is nilpotent. We show that this is isomorphic to the Engel-type algebra.

Theorem 7.

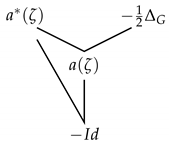
Suppose ${\left\{e_n\right\}}_{n=0}^{\infty }\subset E$ is an orthonormal basis for H. If $\mathfrak{h}=\langle Id,a\left(e_k\right),a^{\ast }\left(e_k\right),{\Delta }_{\mathrm{G}}:k=0,1,\dots ,n-1\rangle$, then $\mathfrak{h}$ is isomorphic to the Engel-type algebra $\mathbb{E}{⋉}^n$.

Proof. 

We have the following correspondence $-\frac{1}{2}{\Delta }_{\mathrm{G}}\mapsto X,a^{\ast }\left(e_i\right)\mapsto Y_i,a\left(e_i\right)\mapsto T_i,$ and $-Id\mapsto Z$ (see Section 2). The result follows from Theorem 4. □

Finally, we extend the Engel-type algebra $E{⋉}^n$ by the number operator. This we call a solvable Lie algebra with Engel-type nilradical. Few studies have been performed on this class of Lie algebras. A possible reason is that the number operator and Gross Laplacian differ only in infinite dimensions. In finite dimensions, they coincide (see (3)). An example can be found in [5] denoted as ${\mathfrak{s}}_{5,33}$ with nilradical ${\mathfrak{n}}_{4,1}$. This has also been studied in [12,14] in terms of white noise operators. The following result can be easily shown, see [14] or [41] for proof of solvability and non-nilpotency.

Theorem 8.

Suppose ${\left\{e_n\right\}}_{n=0}^{\infty }\subset E$ is an orthonormal basis for H. If $\mathfrak{h}=\langle Id,a\left(e_k\right),a^{\ast }\left(e_k\right),N,{\Delta }_{\mathrm{G}}:k=0,1,\dots ,n-1\rangle$, then $\mathfrak{h}$ is a solvable Lie algebra with nilradical $\mathbb{E}{⋉}^n$.

Remark 2.

As can be easily seen from Theorem 4, the number operator prevents nilpotency of $\mathfrak{h}$. Moreover, as a consequence of the canonical commutation relation of annihilation and creation operators, every nonzero ideal of $\mathfrak{h}$ contains the identity (see [41]). Thus $\mathfrak{h}$ cannot be semisimple; it cannot be written as direct sum of (simple) ideals.

Matrix Representation

A matrix representation of the extension of the Heisenberg Lie algebra by the number operator can be found in [25]. However, this representation is limited since it cannot be generalized to include the Gross Laplacian. Fortunately, from Calvaruso’s work in [23], we have a matrix representation of the five-dimensional Lie algebra in Theorem 8, which we reproduce here for convenience.

$$X=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],Y=\left[\begin{array}{cccc}0& -1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right],U=\left[\begin{array}{cccc}0& 0& 0& 2\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right],$$

$$S=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right],T=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right].$$

We now generalize this matrix representation to dimension $2n+3$.

Theorem 9.

Let $E_{ij}\in M_{2n+2}\left(\mathbb{K}\right)$ be the matrix having 1 in the $(i,j)$ position and 0 elsewhere. Define for $i=1,\dots ,n$,

$$\begin{array}{cc}\hfill X_i& =E_{1(2n+2-i)}+E_{(1+i)(2n+2)}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill Y_i& =-E_{1(1+i)}+E_{(2n+2-i)(2n+2)}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill U& =2E_{1(2n+2)}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill S& =-\sum _{j=2}^{n+1}{E}_{jj}+\sum _{j=n+2}^{2n+1}{E}_{jj}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill T& =2\sum _{j=2}^{n+1}{E}_{j(2n+3-j)}.\hfill \end{array}$$

(15)

Then $\langle X_i,Y_i,U,S,T:i=1,\dots ,n\rangle \cong \langle a\left(e_i\right),a^{\ast }\left(e_i\right),Id,N,{\Delta }_{\mathrm{G}}:i=0,\dots ,n-1\rangle .$

Proof. 

Let us compute their commutators. We have

$$\begin{array}{cc}\hfill [X_i,Y_i]& =X_i{Y}_i-Y_i{X}_i\hfill \\ \hfill & =E_{1(2n+2)}-(-E_{1(2n+2)})\hfill \\ \hfill & =U.\hfill \end{array}$$

It is easy to see that

$$2\le 1+i\le n+1\iff 1\le i\le n\mathrm{and}$$

(16)

$$n+2\le 2n+2-i\le 2n+1\iff -2n-1\le -2n-2+i\le -n-2\iff 1\le i\le n.$$

(17)

Then for $i=1,\dots ,n$, we have $X_{i}S=E_{1(2n+2-i)}$ and $S{X}_i=-E_{(1+i)(2n+2)}.$ Hence

$$[X_i,S]=X_{i}S-S{X}_i=X_i.$$

Moreover, $Y_{i}S=E_{1(1+i)}$ and $S{Y}_i=E_{(2n+2-i)(2n+2)}$ which implies that

$$[Y_i,S]=Y_{i}S-S{Y}_i=-Y_i.$$

From (17), and the fact that $2\le j\le n+1$ in (15), we immediately have that $X_{i}T=0.$ Moreover, using similar arguments used in (17), we have

$$2\le j\le n+1\iff n+2\le 2n+3-j\le 2n+1.$$

(18)

It then follows from (16) that $T{X}_i=0$. Hence $[X_i,T]=0.$ Furthermore from (16), we obtain $j=i+1$ in (15) so that $Y_{i}T=-2E_{1(2n+2-i)}$ and $T{Y}_i=2E_{(i+1)(2n+2)}$. We therefore have

$$[Y_i,T]=Y_{i}T-T{Y}_i=-2X_i.$$

In addition, we have $ST=-2{\sum }_{j=2}^{n+1}{E}_{j(2n+3-j)}$ and from (18) it follows that

$$TS=2\sum _{j=2}^{n+1}{E}_{j(2n+3-j)}.$$

Then

$$[T,S]=TS-ST=4\sum _{j=2}^{n+1}{E}_{j(2n+3-j)}=2T.$$

All other commutators are zero. The conclusion follows from Theorem 4 and the following correspondence $X_i\mapsto a\left(e_{i-1}\right)$, $Y_i\mapsto a^{\ast }\left(e_{i-1}\right)$, $U\mapsto N$, and $T\mapsto {\Delta }_{\mathrm{G}}$. □

5. Characterization of Dimension

Given a topological vector space X over $\mathbb{K}=\mathbb{R}$ or $\mathbb{C}$, the set of all continuous linear operators on X is denoted by $\mathcal{L}\left(X\right)$. We define the iterates $T^n:X\to X,n\ge 0$, by the following n-fold iteration of T,

$$T^n=T\circ \cdots \circ T\left(n\mathrm{times}\right)$$

with $T^0=Id$, where $Id$ is the identity operator on X. If $T\in \mathcal{L}\left(X\right)$, we define the T-orbit of a vector $x\in X$ to be the set

$$Orb(x,T)=\{x,Tx,T^{2}x,\dots \}.$$

See [42,43,44] for more details on orbits of operators. We are motivated by the quantum white noise derivatives of the conservation operator $\mathsf{\Lambda }\left(S\right)$. In particular, for $S\in \mathcal{L}\left(E\right)$ and $\zeta \in E$, it is known that

$$D_{\zeta }^{-}\mathsf{\Lambda }\left(S\right)=-[a^{\ast }\left(\zeta \right),\mathsf{\Lambda }\left(S\right)]=a^{\ast }\left(S\zeta \right),$$

$$D_{\zeta }^{+}\mathsf{\Lambda }\left(S\right)=[a\left(\zeta \right),\mathsf{\Lambda }\left(S\right)]=a\left(S^{\ast }\zeta \right).$$

Let ${\zeta }_1=S\zeta$. Then ${\zeta }_1\in E$ and $D_{{\zeta }_1}^{-}\mathsf{\Lambda }\left(S\right)=a^{\ast }\left(S{\zeta }_1\right)=a^{\ast }\left(S^2\zeta \right).$ More generally, letting ${\zeta }_n=S^n\zeta$, we have ${\zeta }_n\in E$ and

$$D_{{\zeta }_n}^{-}\mathsf{\Lambda }\left(S\right)=a^{\ast }\left(S{\zeta }_n\right)=a^{\ast }\left(S^{n+1}\zeta \right)$$

(19)

Our goal is to characterize the dimension of the Lie algebra

$$\mathfrak{h}=span\{\mathsf{\Lambda }\left(T\right),a^{\ast }\left(T^n\zeta \right):n=0,1,2,\dots \},$$

(20)

It is obvious that if $Orb(\zeta ,T)$ is finite, then $\mathfrak{h}$ is finite dimensional. We will now deal with the case that $Orb(\zeta ,T)$ is infinite.

5.1. Finite-Dimensional Case

Let us consider the case that $T\in \mathcal{L}\left(E\right)$ has eigenfunctions. For example, the Hermite functions are eigenfunctions of $A=-\frac{d^2}{d{x}^2}+x^2+1$ [8] p. 17. We are interested in answering the question: given that T has eigenfunctions, which elements $\zeta \in E$ will make $\mathfrak{h}$ in (20) finite dimensional?

Lemma 3.

Let $T\in \mathcal{L}\left(E\right)$ and $x\in E$. If $Orb(x,T)$ is linearly dependent, then there exists n such that $T^{m}x\in span\{T^{k}x:k=0,1,\dots ,n-1\}$ for all $m\ge n$.

Proof. 

Suppose $Orb(x,T)$ is linearly dependent. Then, there exists a number n such that

$$T^n\in spa{n}_{\mathbb{K}}\{x,Tx,\dots ,T^{n-1}x\}=V_n.$$

(21)

By (21), we find that $T{V}_n\subseteq V_n$, since $T^{i}x\in V_n$, if $i<n-1$ by definition. The lemma is proved. □

Lemma 4.

Let $T\in \mathcal{L}\left(E\right)$ and $x\in E$. If $Orb(x,T)$ is linearly dependent, then $\mathfrak{h}=span\left\{\mathsf{\Lambda }\right(T),$$a^{\ast }\left(T^{n}x\right):n=0,1,2,\dots \}$ is finite dimensional.

Proof. 

By previous lemma, there exists n such that $T^{m}x\in span(T^{k}x:k=0,1,\dots ,n-1)$ for all $m\ge n$. Suppose $m\ge n$. Then there are $a_k\in \mathbb{K}$ such that

$$T^{m}x=\sum _0^{n-1}{a}_k{T}^{k}x.$$

Hence

$$T^{m+1}x=\sum _0^{n-2}{a}_k{T}^{k+1}x+a_{n-1}{T}^{n}x.$$

Therefore,

$$a^{\ast }\left(T^{m+1}x\right)\in span\{a^{\ast }\left(x\right),a^{\ast }\left(Tx\right),\cdots ,a^{\ast }\left(T^{n}x\right)\}$$

for all $m\ge n$. □

Remark 3.

If x is an eigenfunction of T, then $T^{n}x={\lambda }^{n}x$ for all n. Thus, $Orb(x,T)$ is linearly dependent.

In [41], we noted that $\mathfrak{h}$ is finite dimensional if S is a finite rank operator. Here we provide a proof.

Proposition 3.

Suppose $T\in \mathcal{L}\left(E\right)$ is a finite rank operator. If $x\in E$, then $\mathfrak{h}=span\left\{\mathsf{\Lambda }\right(T),$$a^{\ast }\left(T^{n}x\right):n=0,1,2,\dots \}$ is finite dimensional.

Proof. 

We have that $di{m}_{\mathbb{K}}T\left(E\right)=n<\infty$. Hence for every $x\in E$ we find that $Orb(x,T)\subseteq Kx+T\left(E\right)$ and $di{m}_{\mathbb{K}}(Kx+T\left(E\right))\le n+1.$ Then $Orb(x,T)$ is linearly dependent and we can apply Lemma 4. □

Proposition 4.

Let $T\in \mathcal{L}\left(E\right)$. Suppose ${\left\{{\lambda }_k\right\}}_1^n$ are distinct eigenvalues corresponding to eigenfunctions ${\left\{v_k\right\}}_1^n$ of T. If $x\in span(v_1,v_2,\dots ,v_n)$, then $\mathfrak{h}=span\{\mathsf{\Lambda }\left(T\right),a^{\ast }\left(T^{n}x\right):n=0,1,2,\dots \}$ is finite dimensional.

Proof. 

Let $V=spa{n}_{\mathbb{K}}\{v_1,\dots ,v_n\}$. By definition, $T\left(V\right)\subseteq V$. Hence for every $x\in V$, we obtain $Orb(x,T)\subseteq Kx+V$. By similar arguments with the previous proof, the set $\{x,Tx,\dots ,T^{n}x\}$ is linearly dependent. Therefore, $\mathfrak{h}$ is finite dimensional. □

Example 1.

Let $x=v_1+\cdots +v_n$. Then

$$\begin{array}{cc}\hfill Tx& ={\lambda }_1{v}_1+\cdots +{\lambda }_n{v}_n\hfill \\ \hfill T^{2}x& ={\lambda }_1^2{v}_1+\cdots +{\lambda }_n^2{v}_n\hfill \\ \hfill & ⋮\hfill \\ \hfill T^{k}x& ={\lambda }_1^k{v}_1+\cdots +{\lambda }_n^k{v}_n\hfill \\ \hfill & ⋮\hfill \\ \hfill T^{n-1}x& ={\lambda }_1^{n-1}{v}_1+\cdots +{\lambda }_n^{n-1}{v}_n.\hfill \end{array}$$

Suppose ${\sum }_0^{n-1}{b}_k{T}^{k}x=0.$ Note that

$$\begin{array}{cc}\hfill \sum _0^{n-1}{b}_k{T}^{k}x& =(b_0+b_1{\lambda }_1+b_2{\lambda }_1^2+\cdots +b_{n-1}{\lambda }_1^{n-1})v_1+\dots \hfill \\ \hfill & +(b_0+b_1{\lambda }_n+b_2{\lambda }_n^2+\cdots +b_{n-1}{\lambda }_n^{n-1})v_n.\hfill \end{array}$$

Since ${\left\{v_k\right\}}_1^n$ is linearly independent,

$$b_0+b_1{\lambda }_k+b_2{\lambda }_k^2+\cdots +b_{n-1}{\lambda }_k^{n-1}=0$$

for all k. Then

$$\left[\begin{array}{cccc}1& {\lambda }_1& \dots & {\lambda }_1^{n-1}\\ 1& {\lambda }_2& \dots & {\lambda }_2^{n-1}\\ ⋮& ⋮& & ⋮\\ 1& {\lambda }_n& \dots & {\lambda }_n^{n-1}\end{array}\right]\left[\begin{array}{c}{b}_0\\ b_1\\ ⋮\\ b_{n-1}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\end{array}\right].$$

(22)

The leftmost matrix is a Vandermonde matrix whose determinant is nonzero since the ${\lambda }_i$’s are distinct. Thus it is invertible and $b_i=0$ for all i. This shows that $\{x,Tx,\dots ,T^{n-1}x\}$ is linearly independent but by previous proposition $\{x,Tx,\dots ,T^{n}x\}$ is not.

5.2. Infinite-Dimensional Case

Recall that the Hermite functions, which are elements of the Schwartz space $S\left(\mathbb{R}\right)$, form an orthonormal basis ${\left\{e_n\right\}}_0^{\infty }$ for $H=L^2\left(\mathbb{R}\right)$ [8,45]. The unique operator defined by $S{e}_n=e_{n+1},n\ge 0$ is called the unilateral shift [46].

Remark 4.

If $S\in \mathcal{L}\left(E\right)$ is the unilateral shift, then $Orb(e_0,S)=\{e_n:n\ge 0\}$ is linearly independent. Thus $\mathfrak{h}=span\{\mathsf{\Lambda }\left(S\right),a^{\ast }\left(S^n{e}_0\right):n=0,1,2,\dots \}$ is infinite dimensional.

6. Filiform Lie Algebras

By introducing a grading to Lie algebras of white noise operators, we establish isomorphism to filiform Lie algebras. The following result is due to Vergne [27] which was translated in [28].

Theorem 10 ([27]).

Let $\mathfrak{g}={⨁}_{i\ge 1}{\mathfrak{g}}_i$ be a $\mathbb{N}$-graded Lie algebra with the following properties

$$\mathit{dim}{\mathfrak{g}}_1=2,\mathit{dim}{\mathfrak{g}}_i=1,i\ge 2,[{\mathfrak{g}}_1,{\mathfrak{g}}_i]={\mathfrak{g}}_{i+1},i\ge 1.$$

Then $\mathfrak{g}$ is isomorphic to ${\mathfrak{m}}_0$.

Suppose $\mathfrak{h}$ in (20) is infinite dimensional. We introduce a grading on $\mathfrak{h}$ as follows:

$$\mathfrak{h}=\underset{i\in \mathbb{N}}{⨁}{\mathfrak{h}}_{\mathfrak{i}},$$

where ${\mathfrak{h}}_i=\mathbb{K}{f}_i$ for $i\ge 1$. The basis elements $f_i$ are given by

$$\begin{array}{cccccc}i& 1& 2& 3& & k\\ f_i& \{\mathsf{\Lambda }\left(S\right),a^{\ast }\left(\zeta \right)\}& a^{\ast }\left(S\zeta \right)& a^{\ast }\left(S^2\zeta \right)& \dots & a^{\ast }\left(S^{k-1}\zeta \right).\end{array}$$

Applying the previous Theorem, Lemma 2, and Proposition 2, we obtain the following result.

Theorem 11.

Suppose ${\left\{e_n\right\}}_{n=0}^{\infty }\subset E$ is an orthonormal basis for H. If S is the unilateral shift, then the Lie algebra $\langle \mathsf{\Lambda }\left(S\right),a^{\ast }\left(e_k\right):k\ge 0\rangle$ is isomorphic to the infinite dimensional filiform Lie algebra ${\mathfrak{m}}_0$.

It is known that the adjoint of the unilateral shift S is the backward shift $S^{\ast }$ which is characterized by $S^{\ast }{e}_0=0$ and $S^{\ast }{e}_n=e_{n-1}$ for $n\ge 1$ [46]. Let $f_1=-\mathsf{\Lambda }\left(S\right)$ and $f_i=a\left(e_{i-2}\right)$ for $i\ge 2$. From Lemma 2, we have $[f_1,f_i]=-[f_i,f_1]=-[a\left(e_{i-2}\right),\mathsf{\Lambda }\left(S\right)]=a\left(S^{\ast }{e}_{i-2}\right)=a\left(e_{i-3}\right)$ for $i\ge 3$ and $[f_1,f_2]=-[f_2,f_1]=-[a\left(e_0\right),\mathsf{\Lambda }\left(S\right)]=a\left(S^{\ast }{e}_0\right)=0$. Hence we obtain the following result.

Theorem 12.

Suppose ${\left\{e_n\right\}}_{n=0}^{\infty }\subset E$ is an orthonormal basis for H. If S is the unilateral shift, then the Lie algebra $\langle \mathsf{\Lambda }\left(S\right),a\left(e_0\right),\dots ,a\left(e_{n-1}\right)\rangle$ is isomorphic to the $(n+1)$-dimensional model filiform Lie algebra.

7. Solvable Lie Algebras with Abelian Nilradical

Solvable Lie algebras with Abelian nilradical are important in applications involving partial differential equations. A Lie algebra containing an Abelian subalgebra often arises because of equations with constant coefficients [40]. They also arise as Lie algebras of vector groups and gauge groups [2]. Examples of Abelian Lie algebras in white noise analysis include Lie algebras spanned by annihilation operators or those spanned by creation operators [8,11]. Furthermore, any two generalized Gross Laplacians or any two conservation operators of diagonal type commute with each other [10].

In finite dimensional case, it is difficult to classify $\mathfrak{h}$ in (20) without knowing the properties of the operator T. Here we deal with a solvable Lie algebra with one non-nilpotent element and an Abelian nilradical (see 10.4 [5]). Consider the following Lie algebra denoted as ${\mathfrak{s}}_{5,9}$ in [5] with nontrivial brackets given below.

$[·,·]$	$e_1$	$e_2$	$e_3$	$e_4$
$e_5$	$e_1$	$a{e}_2$	$b{e}_3$	$c{e}_4$

• The values of the parameters $a,b,c$ are

$$0<\left|c\right|\le \left|b\right|\le \left|a\right|\le 1.$$

Remark 5 ([47]).

Suppose T is an orthogonal transformation on E. If a is an eigenvalue for T, then necessarily $\left|a\right|=1$. For if $Tf=af$ and $f\ne 0$, then $\parallel f\parallel =\parallel Tf\parallel =\parallel af\parallel =\left|a\right|\parallel f\parallel ,$ so that $\left|a\right|=1$.

7.1. A solvable Lie Algebra with Abelian Nilradical ${\mathfrak{sa}}_{n+1}$

We remark that ${\mathfrak{s}}_{5,9}$ is part of a family of solvable Lie algebras with Abelian nilradical such as ${\mathfrak{s}}_{3,1}$, ${\mathfrak{s}}_{4,3}$, and ${\mathfrak{s}}_{6,17}$ (see [5]). We define its generalization as follows. Denote by ${\mathfrak{sa}}_{n+1}$ the Lie algebra with nontrivial brackets given below.

$[·,·]$	$e_1$	$e_2$	$e_3$	...	$e_n$
$e_{n+1}$	$e_1$	$a_2{e}_2$	$a_3{e}_3$	...	$a_n{e}_n$

• The values of the parameters $a_i$ are

$$0<|a_n|\le \cdots \le |a_3|\le |a_2|\le 1.$$

(23)

If one or more equalities hold, further restrictions on the parameters are necessary in order to avoid redundancies, as discussed in [5] 10.4. For our next result, we need the following commutation relation from [14]. For $\kappa \in {\left(E_{\mathbb{C}}^{\otimes m}\right)}^{\ast }$, $[N,{\mathsf{\Xi }}_{0,m}\left(\kappa \right)]=-m{\mathsf{\Xi }}_{0,m}\left(\kappa \right).$

Theorem 13 ([14]).

Let $\mathfrak{g}=span\{N,{\mathsf{\Xi }}_{0,m_1}\left({\kappa }_1\right),\dots ,{\mathsf{\Xi }}_{0,m_n}\left({\kappa }_n\right)\}$ be the complex vector space spanned by N and ${\mathsf{\Xi }}_{0,m_i}\left({\kappa }_i\right),i=1,\dots n$, where for each $i=1,\dots ,n,\kappa \in {\left(E_{\mathbb{C}}^{\otimes m_i}\right)}^{\ast }$. Then, $\mathfrak{g}$ is a $(n+1)$-dimensional non-nilpotent solvable complex Lie algebra.

Proposition 5.

The Lie algebra $\mathfrak{g}$ in Theorem 13 is isomorphic to ${\mathfrak{sa}}_{n+1}$ with parameters $m_i/m_n$, $i=1,2,\dots ,n-1$.

Proof. 

Assume without loss of generality that $0<m_1<\cdots <m_n$. Setting $e_{n+1}=-\frac{1}{m_n}N$ and $e_{n+1-i}={\mathsf{\Xi }}_{0,m_i}\left({\kappa }_i\right)$, for $i=1,\dots ,n$, we have

$$[e_{n+1},e_n]=\frac{m_1}{m_n}{e}_n,[e_{n+1},e_i]=\frac{m_{n+1-i}}{m_n}{e}_i,\mathit{and}[e_{n+1},e_1]=\frac{m_n}{m_n}{e}_1=e_1.$$

This satisfies the parameters in (23). □

7.2. The Infinite Dimensional Unitary Group

Before we define the unitary group, let us first discuss its importance and applications. Let E denote a nuclear space which is dense in $L^2\left({\mathbb{R}}^d\right)$. The rotation group of E, denoted by $O\left(E\right)$, keeps the white noise measure invariant via its adjoint action. It is known that a subgroup of $O\left(E\right)$, called the conformal group $C\left(d\right)$ generated by shifts, dilations, rotations and special conformal transformations, is isomorphic to the Lie group $SO(d+1,1)$ [48]. The diffeomorphisms of the parameter space $\mathbb{R}$ is a subclass of $O\left(E\right)$, called Class II [49]. There exists a three-dimensional subgroup of class II which describes the projective invariance of Brownian motion. Their generators span a three-dimensional Lie algebra isomorphic to the special linear Lie algebra $sl(2,\mathbb{R})$. Perhaps most important is the generator of the shift which corresponds to the flow of Brownian motion. The rotation group $O\left(E\right)$ may be regarded as a subgroup of the unitary group $U\left(E_{\mathbb{C}}\right)$ [50], which we now define below.

Let us denote by $U\left(E_{\mathbb{C}}\right)$ the set of all linear transformations g on $E_{\mathbb{C}}$ that satisfy the following properties:

• g is a homeomorphism of $E_{\mathbb{C}}$ onto itself, and
• g preserves the $L^2\left(\mathbb{R}\right)$-norm, that is, $\parallel g\zeta \parallel =\parallel \zeta \parallel ,\zeta \in E_{\mathbb{C}}.$

It can be easily seen that $U\left(E_{\mathbb{C}}\right)$ is a group under the following product:

$$\left(g_1{g}_2\right)\zeta =g_1\left(g_2\zeta \right),g_1,g_2\in U\left(E_{\mathbb{C}}\right)$$

We then call $U\left(E_{\mathbb{C}}\right)$ the infinite dimensional unitary group, or just the unitary group.

The Unitary Group $U\left(S_{\mathbb{C}}\right)$

In what follows, we take $E_{\mathbb{C}}$ to be the complex Schwartz space $S_{\mathbb{C}}$. The structure of $S_{\mathbb{C}}$ allows us to study the properties of $U\left(S_{\mathbb{C}}\right)$ in more detail. The case $E_{\mathbb{C}}=S_{\mathbb{C}}$ is emphasized because the Fourier transform plays a significant role. Recall from Section 2.1.1 that the differential operator

$$D=\frac{d^2}{d{u}^2}-(u^2+1)$$

has the Hermite functions as its eigenfunctions with eigenvalues $-2(n+1)$:

$$D{e}_n=-2(n+1)e_{n}n\ge 0.$$

In fact, $\{e_n:n\ge 0\}$ form an orthonormal basis for $L^2\left(\mathbb{R}\right)$.

Proposition 6 ([50]).

When considered as linear operators on $S_{\mathbb{C}}$, the Fourier transform $\mathcal{F}$ and the inverse Fourier transform ${\mathcal{F}}^{-1}(={\mathcal{F}}^{\ast }$) belong to $U\left(S_{\mathbb{C}}\right)$.

7.3. The Group of Fourier–Mehler Transforms

In [50], Hida investigated a one-parameter subgroup of $U\left(S_{\mathbb{C}}\right)$, which consists of powers of the Fourier transform, not necessarily integral. Start with an integral kernel

$$K_{\theta }(u,v)={\left[\pi (1-exp\left(2i\theta \right))\right]}^{1/2}exp\left[-\frac{i(u^2+v^2)}{2tan\theta }+\frac{iuv}{sin\theta }\right]$$

which defines an operator ${\mathcal{F}}_{\theta }$ given by

$$\left({\mathcal{F}}_{\theta }\right)\left(u\right)={\int }_{-\infty }^{\infty }{K}_{\theta }(u,v)\zeta \left(v\right)dv,\theta \ne \frac{1}{2}k\pi .$$

Let $\{e_n\left(u\right):n\ge 0\}$ be the Hermite functions. Then we have

$${\mathcal{F}}_{\theta }{e}_n\left(u\right)=e^{in\theta }{e}_n\left(u\right),n\ge 0.$$

We deal with exceptional points $\theta =\frac{1}{2}\pi k,k=0,\pm 1,\pm 2,\dots$, as follows: first define

$${\mathcal{F}}_{\theta }{e}_n\left(u\right)=e^{in\theta }{e}_n\left(u\right).$$

Since $\left\{e_n\left(u\right)\right\}$ forms an orthonormal basis for $L^2\left(\mathbb{R}\right)$, we may extend ${\mathcal{F}}_{\theta }$ to the entire space $S_{\mathbb{C}}$. The operators ${\mathcal{F}}_{\theta }$ on $S_{\mathbb{C}}$ defined as above, $-\infty <\theta <\infty$, all belong to $U\left(S_{\mathbb{C}}\right)$ and satisfy:

$${\mathcal{F}}_{\theta }{\mathcal{F}}_{{\theta }^{\prime }}={\mathcal{F}}_{\theta +{\theta }^{\prime }}={\mathcal{F}}_{{\theta }^{″}},\theta +{\theta }^{\prime }={\theta }^{″}\left(mod2\pi \right);$$

$${\mathcal{F}}_{\theta }\to Id\theta \to 0.$$

This gives us a one-parameter group $\{{\mathcal{F}}_{\theta }:-\infty <\theta <\infty \}$ with period $2\pi$. We recover the usual Fourier transform and its inverse by setting

$${\mathcal{F}}_{\pi /2}=\mathcal{F},{\mathcal{F}}_{3\pi /2}={\mathcal{F}}^{-1},$$

and we hence have obtained a one-parameter unitary group including them. For $r\in \mathbb{R}$, the formal identity holds

$${\mathcal{F}}_{\pi r/2}={\left(\mathcal{F}\right)}^r.$$

In this way, we may regard $\left\{{\mathcal{F}}_{\theta }\right\}$ as the subgroup of $U\left(S_{\mathbb{C}}\right)$ consisting of arbitrary powers of the Fourier transform.

Theorem 14.

Let $T={\mathcal{F}}_{\theta }$ and $n=\frac{2\pi }{\theta }$. Suppose $\zeta \in S_{\mathbb{C}}$ such that

$$\zeta ={\zeta }_0+{\zeta }_1+\cdots +{\zeta }_{n-1},$$

where each ${\zeta }_k$ is nonzero and belongs to the eigenspace of $e^{ik\theta }$. If $\mathfrak{h}$ is an $(n+1)$-dimensional complex Lie algebra spanned by

$$\mathsf{\Lambda }\left(T\right),a^{\ast }\left(\zeta \right),a^{\ast }\left(T\zeta \right),a^{\ast }\left(T^2\zeta \right),\dots ,a^{\ast }\left(T^{n-1}\zeta \right),$$

then $\mathfrak{h}\cong {\mathfrak{sa}}_{n+1}$ with parameters $e^{ik\theta }$, $k=1,\dots ,n\dots 1$.

Proof. 

Let ${\lambda }_k=e^{ik\theta }$, $k=0,1,\dots ,n\dots 1$. Observe that

$$\begin{array}{cc}\hfill \zeta & ={\zeta }_0+\cdots +{\zeta }_{n-1},\hfill \\ \hfill T\zeta & ={\lambda }_0{\zeta }_0+\cdots +{\lambda }_{n-1}{\zeta }_{n-1},\hfill \\ \hfill T^2\zeta & ={\lambda }_0^2{\zeta }_0+\cdots +{\lambda }_{n-1}^2{\zeta }_{n-1},\hfill \\ \hfill & ⋮\hfill \\ \hfill T^{n-1}\zeta & ={\lambda }_0^{n-1}{\zeta }_0+\cdots +{\lambda }_{n-1}^{n-1}{\zeta }_{n-1}.\hfill \end{array}$$

Suppose $0={\sum }_{i=0}^{n-1}{b}_i{a}^{\ast }\left({\zeta }_i\right)={\sum }_{i=0}^{n-1}{b}_i{\lambda }_i{a}^{\ast }\left(e_i\right).$ Then Lemma 2 implies that $b_i=0$ for all $i=0,1,\dots ,n-1$. Thus $\{a^{\ast }\left({\zeta }_i\right):i=0,1,\dots ,n-1\}$ is linearly independent. Since the creation operator is linear in $\zeta$, $\{\mathsf{\Lambda }\left(T\right),a^{\ast }\left({\zeta }_i\right):i=0,1,\dots ,n-1\}$ is a basis for $\mathfrak{h}$. Set $e_{n+1}=\mathsf{\Lambda }\left(S\right)$ and $e_i=a^{\ast }\left({\zeta }_{i-1}\right)$ for $i=1,2,\dots ,n$. Applying (10), we we obtain the following nontrivial brackets.

$[·,·]$	$e_1$	$e_2$	$e_3$	...	$e_n$
$e_{n+1}$	$e_1$	$e^{i\theta }{e}_2$	$e^{i2\theta }{e}_3$	...	$e^{i(n-1)\theta }{e}_n$

This completes the proof. □

Example 2.

Let T be the Fourier transform $\mathcal{F}$. Then the 5-dimensional complex Lie algebra spanned by $\mathsf{\Lambda }\left(T\right),a^{\ast }\left(\zeta \right),a^{\ast }\left(T\zeta \right),a^{\ast }\left(T^2\zeta \right),a^{\ast }\left(T^3\zeta \right)$ is isomorphic to ${\mathfrak{sa}}_5$ with parameters $i,-1$ and $-i$.

8. Quadratic Annihilation Operators

The linear independence of the generalized Gross Laplacian (quadratic annihilation operators) ${\Delta }_{\mathrm{G}}\left(S\right)$ depends on the operator S. Note that ${\Delta }_{\mathrm{G}}\left(S\right)$ is specified uniquely by the action on the exponential vectors as ${\Delta }_{\mathrm{G}}\left(S\right){\varphi }_{\xi }=\langle S\xi ,\xi \rangle {\varphi }_{\xi }$ for all $\xi \in E$ [11,51].

Lemma 5.

If S is the unilateral shift, then $\{{\Delta }_{\mathrm{G}},{\Delta }_{\mathrm{G}}\left(S\right),{\Delta }_{\mathrm{G}}\left(S^2\right),\dots ,{\Delta }_{\mathrm{G}}\left(S^k\right)\}$ is linearly independent for all $k\ge 0$.

Proof. 

Suppose $a{\Delta }_{\mathrm{G}}=0$. Let $\xi \in E$, $\xi \ne 0$. Then $0=a{\Delta }_{\mathrm{G}}{\varphi }_{\xi }=a\langle \xi ,\xi \rangle {\varphi }_{\xi }$ implying that $a=0$. We proceed by induction. Let $k\ge 0$ and suppose

$$\{{\Delta }_{\mathrm{G}},{\Delta }_{\mathrm{G}}\left(S\right),{\Delta }_{\mathrm{G}}\left(S^2\right),\dots ,{\Delta }_{\mathrm{G}}\left(S^k\right)\}$$

is linearly independent. Assume that ${\sum }_{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right)=0.$ Since ${\sum }_{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right)$ is the zero operator on $\left(E\right)$, it maps every ${\varphi }_{\xi }$ to the zero vector of $\left(E\right)$. Thus for $\xi \in E$, we have

$$\sum _{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{\xi }=0.$$

(24)

In particular, we have

$$\sum _{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{{\sum }_{i=0}^k{e}_i}=\sum _{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{e_0+e_{k+1}}=0.$$

(25)

The fact that

$$a_{k+1}{\Delta }_{\mathrm{G}}\left(S^{k+1}\right){\varphi }_{{\sum }_{i=0}^k{e}_i}=a_{k+1}\langle \sum _{i=0}^k{e}_{i+k+1},\sum _{i=0}^k{e}_i,\rangle {\varphi }_{{\sum }_{i=0}^k{e}_i}=0$$

(26)

implies

$$0=\sum _{j=0}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{{\sum }_{i=0}^k{e}_i}=\sum _{j=0}^k{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{{\sum }_{i=0}^k{e}_i}.$$

(27)

By the induction hypothesis, $a_j=0$ for $j=0,1,\dots ,k$. On the other hand,

$${\Delta }_{\mathrm{G}}\left(S^{k+1}\right){\varphi }_{e_0+e_{k+1}}=\langle e_{k+1}+e_{2(k+1)},e_0+e_{k+1}\rangle {\varphi }_{e_0+e_{k+1}}={\varphi }_{e_0+e_{k+1}}.$$

It follows from (25) that

$$0=\sum _{j=1}^{k+1}{a}_j{\Delta }_{\mathrm{G}}\left(S^j\right){\varphi }_{e_0+e_{k+1}}=a_{k+1}{\Delta }_{\mathrm{G}}\left(S^{k+1}\right){\varphi }_{e_0+e_{k+1}}=a_{k+1}{\varphi }_{e_0+e_{k+1}}.$$

Thus $a_{k+1}=0$. Therefore, $\{{\Delta }_{\mathrm{G}},{\Delta }_{\mathrm{G}}\left(S\right),{\Delta }_{\mathrm{G}}\left(S\right),{\Delta }_{\mathrm{G}}\left(S^2\right),\dots ,{\Delta }_{\mathrm{G}}\left(S^{k+1}\right)\}$ is linearly independent. □

Theorem 15.

If S is the unilateral shift, then $\{{\Delta }_{\mathrm{G}}\left(S^k\right):k\ge 0\}$ is linearly independent.

Proof. 

Suppose ${\left\{{\Delta }_{\mathrm{G}}\left(S^{k_j}\right)\right\}}_{j=1}^n\subset \{{\Delta }_{\mathrm{G}}\left(S^k\right):k\ge 0\}$. Assume, without loss of generality, that $k_1<k_2<\dots <k_n$. By Lemma 5, $\{{\Delta }_{\mathrm{G}}\left(S^k\right):0\le k\le k_n\}$ is linearly independent. Since ${\left\{{\Delta }_{\mathrm{G}}\left(S^{k_j}\right)\right\}}_{j=1}^n\subset \{{\Delta }_{\mathrm{G}}\left(S^k\right):0\le k\le k_n\}$, the conclusion follows. □

As with annihilation operators, quadratic annihilation operators commute with each other [10,11]. We have the following corollary.

Corollary 1.

If S is the unilateral shift, then Lie algebra $\langle {\Delta }_{\mathrm{G}},{\Delta }_{\mathrm{G}}\left(S\right),\dots ,{\Delta }_{\mathrm{G}}\left(S^k\right)\rangle$ is a $(k+1)$-dimensional Abelian Lie algebra.

9. Conclusions

We studied Lie algebras of white noise operators containing the quantum white noise derivatives of the conservation operator corresponding to a continuous linear operator S on Schwartz space. The dimension is characterized by the S-orbit of the initial vector $\zeta$. In [35], Le Donne and Moisala introduced Engel-type algebras, which characterize semigeneration in Carnot algebras. We have shown that Engel-type algebras also arise in white analysis. In particular, the $(2n+3)$-dimensional Lie algebra spanned by pairs of annihilation and creation operators, number operator and Gross Laplacian is a solvable Lie algebra with Engel-type nilradical. We have provided a matrix representation of this Lie algebra.

Furthermore, we have established isomorphisms between white noise Lie algebras containing a conversation operator and filiform Lie algebras. The Lie algebra spanned by the conservation operator corresponding to the unilateral shift and creation operators is isomorphic to the infinite dimensional filiform Lie algebra ${\mathfrak{m}}_0$, while the Lie algebra spanned by the conservation operator and annihilation operators is isomorphic to the finite dimensional model filiform Lie algebra.

We have introduced a solvable Lie algebra with Abelian nilradical ${\mathfrak{sa}}_{n+1}$ whose parameters have modulus less than or equal to one. For instance, Lie algebras of white noise operators spanned by the number operator and annihilation operators of any order belongs in this class. Moreover, the $(n+1)$-dimensional complex Lie algebra spanned by the conservation operator corresponding to the Fourier–Mehler transform on the complex Schwartz space is isomorphic to ${\mathfrak{sa}}_{n+1}$ with parameters nth roots of unity. We have shown the linear independence of quadratic annihilation operators corresponding to the nth powers of the unilateral shift—they form an Abelian Lie algebra.

Identifying which abstract Lie algebra a certain white noise Lie algebra is isomorphic to is valuable. For instance, a researcher who studies differential equations of white noise operators will benefit from knowing their invariants. The number operator and Gross Laplacian are infinite dimensional analogs of the finite dimensional Laplacian. An extension of the Heisenberg Lie algebra by the number operator has a different structure than its extension with the Gross Laplacian. The latter is a nilpotent Lie algebra while the former is not. The extension of Heisenberg Lie algebra with both Laplacians belongs to the class of solvable Lie algebras with Engel-type nilradical whose complete classification could be the subject of future research.