Some Aspects of Hyperatom Elements in Ordered Semihyperrings

Abstract

In this paper, first, we state an operator $L_R$ on an ordered semihyperring R. We show that if $\phi :R⟶T$ is a monomorphism and $K\subseteq R$, then $L_T\left(\phi \left(K\right)\right)=\phi \left(L_R\left(K\right)\right)$. Afterward, hyperatom elements in ordered semihyperrings are defined and some results in this respect are investigated. Denote by $A\left(R\right)$ the set of all hyperatoms of R. We prove that if R is a finite ordered semihyperring and $\left|R\right|\ge 2$, then for any $q\in R\backslash \left\{0\right\}$, there exists $h_q\in A^{*}\left(R\right)=A\left(R\right)\backslash \left\{0\right\}$ such that $h_q\le q$. Finally, we study the $L_R$-graph of an ordered semihyperring and give some examples. Furthermore, we show that if $\phi :R⟶T$ is an isomorphism, G is the $L_R$-graph of R and $G^{\prime }$ is the $L_T$-graph of T, then $G\cong G^{\prime }$.

1. Introduction and Preliminaries

The concept of the hypergroup was introduced by Marty [1] in 1934. The notion of semihyperring was introduced by Vougiouklis [2] as a generalization of semiring in 1990. The study of ordered semihypergroups is one interesting topic in hyperstructure theory. The notion of ordered semihypergroup was proposed by Heidari and Davvaz [3] in 2011. Recently, Shi et al. [4] also pioneered the notion of factorizable ordered hypergroupoids with applications. After the paper [3] was published, many authors obtained some results on ordered semihypergroups. Davvaz et al. in [5] initiated the study of pseudoorders in ordered semihypergroups. Gu and Tang in [6] and Tang et al. in [7] constructed the ordered semihypergroup from an ordered semihypergroup by using ordered regular equivalence relation.

A study on k-bi-quasi hyperideals in an ordered semihyperring is done in [8]. In [9], uni-soft interior $\Gamma$-hyperideals in ordered $\Gamma$-semihypergroups are studied. In [10], Hila et al. investigated $(k,n)$-absorbing hyperideals in Krasner $(m,n)$-hyperrings. The derivations of hyperrings [11]; the w-pseudo-orders [12]; the ordered regular equivalence relations [13]; the relative bi-(int-)$\Gamma$-hyperideals [14] and the A-$\mathbf{I}$-$\Gamma$-hyperideals [15], have been introduced and studied. Some recent studies on ordered semihyperring theory are on derivations done by Rao et al. in [16] and Kou et al. in [17].

In 2019, Panganduyon and Canoy [18] defined zero divisor graph of a hyper BCI-algebra and discussed some of its properties. In 2021, Panganduyon et al. [19] investigated some properties of the induced topology on certain hyper BCI-algebras. Many properties of hyperatom elements were extended to hyper BCK-algebras in [20,21]. We invite the readers to [22,23] to see more about the graph theory.

A physical example of hyperstructures associated with the leptons is provided in [24]. Leptons and gauge bosons along with the interactions between their members construct an $H_{\nu }$-structure [25]. Farshi et al. [26] explored some connections between graph theory and hyperstructure theory in 2014. Now, we analyze an operator $L_R$ on an ordered semihyperring R and investigae some aspects of $L_R$-graph.

A mapping $·:R\times R\to {\mathcal{P}}^{*}\left(R\right)$ is called a hyperoperation on R. If $\varnothing \ne P,Q\subseteq R$ and $r\in R$, then

$$P·Q={\displaystyle \bigcup _{\begin{array}{c}\genfrac{}{}{0pt}{}{p\in P}{q\in Q}\end{array}}}p·q,r·P=\{r\}·P \mathrm{and} Q·r=Q·\{r\}.$$

$(R,·)$ is called a semihypergroup if for every $p,q,r$ in R,

$$p·(q·r)=(p·q)·r.$$

A triple $(R,\oplus ,\odot )$ is a semihyperring [2] if ⊕ and ⊙ are both hyperoperations such that

(1)

$(R,\oplus )$ is a commutative semihypergroup;

(2)

$(R,\odot )$ is a semihypergroup;

(3)

for all $u,v,w$ in R, $u\odot (v\oplus w)=u\odot v\oplus u\odot w$ and $(u\oplus v)\odot w=u\odot w\oplus v\odot w$.

If there exists 0 in R such that $u\oplus 0=0\oplus u=\left\{u\right\}$ and $u\odot 0=0\odot u=\left\{0\right\}$ for all u in R; then 0 is called the zero element of R.

Definition 1.

[13,16] Take a semihyperring $(R,\oplus ,\odot )$ and a partial order relation ≤. Then $(R,\oplus ,\odot ,\le )$ is called an ordered semihyperring if for any $p,p^{\prime },r\in R$,

$$p\le p^{\prime }\Rightarrow \left\{\begin{array}{c}p\oplus r⪯p^{\prime }\oplus r,\hfill \\ \\ p\odot r⪯p^{\prime }\odot r,\hfill \\ \\ r\odot p⪯r\odot p^{\prime }.\hfill \end{array}\right.$$

For every $\varnothing \ne P,Q\subseteq R$, $P⪯Q$ is defined by $\forall p\in P,\exists q\in Q$ such that $p\le q$. Clearly, $P\subseteq Q$ implies $P⪯Q$, but the converse is not valid in general. Also, R is said to be positive if $0\le x$ for all $x\in R$.

Let $(R,+,·,{\le }_R)$ and $(T,\oplus ,\odot ,{\le }_T)$ be two ordered semihyperrings. We will say that a function $\phi :R\to T$ is a homomorphism of ordered semihyperrings if for all $q,q^{\prime }\in R$,

(1)

$\phi (q+q^{\prime })\subseteq \phi \left(q\right)\oplus \phi \left(q^{\prime }\right)$,

(2)

$\phi (q·q^{\prime })\subseteq \phi \left(q\right)\odot \phi \left(q^{\prime }\right)$,

(3)

$q{\le }_R{q}^{\prime }$ implies $\phi \left(q\right){\le }_T\phi \left(q^{\prime }\right)$.

We will say that $\varnothing \ne W\subseteq R$ is a left (resp. right) hyperideal of R if

(1)

for all $a,b\in W$, $a\oplus b\subseteq W$;

(2)

$R\odot W\subseteq W$ (resp. $W\odot R\subseteq W$);

(3)

$\left(W\right]\subseteq W$.

The set $\left(W\right]$ is given by

$$\left(W\right]:=\{r\in R|r\le w\mathrm{for}\mathrm{some}w\in W\}.$$

2. Main Results

In this section, for the first time, we study the operator $L_R$ in ordered semihyperrings and present some results in this respect. Moreover, we introduce hyperatom elements in ordered semihyperrings and investigate some of their properties.

Let $(R,\oplus ,\odot ,\le )$ be an ordered semihyperring and $K\subseteq R$. The set $L_R\left(K\right)$ is given by

$$L_R\left(K\right):=\{r\in R|r\le k\mathrm{for}\mathrm{all}k\in K\}.$$

For $K=\left\{x\right\}$, we write $L_R\left(x\right)$ instead of $L_R\left(\left\{x\right\}\right)$. For $\varnothing \ne H,K\subseteq R$, we have that

(1)

$L_R(\varnothing )=R$;

(2)

$q\in L_R\left(q\right)$ for all $q\in R$;

(3)

$L_R\left(K\right)=\bigcap _{\begin{array}{c}x\in K\end{array}}{L}_R\left(x\right)$;

(4)

If $H\subseteq K$, then $L_R\left(K\right)\subseteq L_R\left(H\right)$.

Furthermore, in a positive ordered semihyperring R, $L_R\left(0\right)=0$.

Remark 1.

Let $(R,\oplus ,\odot ,\le )$ be an ordered semihyperring and $(u,v)\in \le$. Then $L_R\left(u\right)\subseteq L_R\left(v\right).$ Indeed: Let $w\in L_R\left(u\right)$. Then $(w,u)\in \le$. So, $(w,v)\in \le$ and hence $w\in L_R\left(v\right)$. Thus, $L_R\left(u\right)\subseteq L_R\left(v\right).$

Proposition 1.

Let $(R,\oplus ,\odot ,\le )$ be an ordered semihyperring and $K\subseteq R$. Then

$$L_R\left(L_R\left(K\right)\right)\subseteq L_R\left(K\right).$$

Proof. 

Let $u\in L_R\left(L_R\left(K\right)\right)$. Then $u\le v$ for all $v\in L_R\left(K\right)$. By Definition of $L_R\left(K\right)$, we have $v\le x$ for all $x\in K$. Since ≤ is transitive, we get $u\le x$ for all $x\in K$. So, $u\in L_R\left(K\right)$. □

Theorem 1.

Consider $\phi :R⟶T$ as the monomorphism. If $K\subseteq R$, then $L_T\left(\phi \left(K\right)\right)=\phi \left(L_R\left(K\right)\right)$.

Proof. 

Let $K\subseteq R$. We get

$$\begin{array}{cc}u\in \phi \left(L_R\left(K\right)\right)\hfill & \iff {\phi }^{-1}\left(u\right)\in L_R\left(K\right)\hfill \\ & \iff {\phi }^{-1}\left(u\right)\leqq {}_{R}k,\forall k\in K\hfill \\ & \iff u\leqq {}_T\phi \left(k\right),\forall k\in K\hfill \\ & u\in L_T\left(\phi \left(K\right)\right)\hfill \end{array}$$

Hence, $L_T\left(\phi \left(K\right)\right)=\phi \left(L_R\left(K\right)\right)$. □

Definition 2.

We say that an element x of an ordered semihyperring $(R,\oplus ,\odot ,\le )$ is a hyperatom element if

(1)

for any $z\in R$, $z\le x$ implies $z=0$ or $z=x$;

(2)

$x\odot z\ne 0$ implies $(x\odot z)\odot m=z$ for some $m\in R$.

Remark 2.

Consider the ordered semihyperring $(R,\oplus ,\odot ,\le )$. Then R is hyperatomic if and only if $L_R\left(q\right)=\left\{q\right\}$ or $L_R\left(q\right)=\{0,q\}$ for any $q\in R$.

Theorem 2.

Let $(R,\oplus ,\odot ,\le )$ be an ordered semihyperring such that $\left|R\right|>2$. We denote by $A\left(R\right)$ the set if all hyperatom elements of R. If $m,m^{\prime }\in A\left(R\right)$, then $L_R\left(\{m,m^{\prime }\}\right)=\left\{0\right\}$ or ∅.

Proof. 

Let $m,m^{\prime }\in A\left(R\right)$. Consider the following situations.

Case 1.$0\notin L_R\left(m\right)$ for all $m\in R$.

Since $m\in A\left(R\right)$, we get $L_R\left(m\right)=\left\{m\right\}$ for all $m\in R$. Thus, $L_R\left(\{m,m^{\prime }\}\right)=\varnothing$.

Case 2.$0\in L_R\left(m\right)$ for all $m\in R$.

Then, $L_R\left(m\right)=\{0,m\}$. By Remark 2, we have $L_R\left(m^{\prime }\right)=\left\{m^{\prime }\right\}$ or $L_R\left(m^{\prime }\right)=\{0,m^{\prime }\}$. Hence, $L_R\left(\{m,m^{\prime }\}\right)=\left\{0\right\}$ or ∅. □

Theorem 3.

Let $(R,\oplus ,\odot ,\le )$ be a finite ordered semihyperring. Then, for any $q\in R\backslash \left\{0\right\}$, there exists $h_q\in A^{*}\left(R\right)=A\left(R\right)\backslash \left\{0\right\}$ such that $h_q\le q$, where $\left|R\right|\ge 2$.

Proof. 

Let $q\in R\backslash \left\{0\right\}$. Consider the following situations.

Case 1.q is a hyperatom.

Then take $h_q=q$.

Case 2.q is not a hyperatom.

Then, there exists $q_1\in R\backslash \{0,q\}$ such that $q_1\le q$.

Subcase 1.$q_1$ is a hyperatom.

Then take $h_q=q_1$.

Subcase 2.$q_1$ is not a hyperatom.

Then, there exists $q_2\in R\backslash \{0,q,q_1\}$ such that $q_2\le q_1\le q$. Since R is finite, we have

$$q_r\le q_{r-1}\le \cdots \le q_2\le q_1\le q,$$

where $q_r\in R\backslash \{0,q,q_1,\cdots ,q_{r-1}\}$. So, $q_r=0$ if $0\in L_R\left(q\right)$ or $h_q=q_r\in A^{*}\left(R\right)$ and $h_q\le q$. □

Corollary 1.

Let $(R,\oplus ,\odot ,\le )$ be a finite ordered semihyperring. Then there exists $h\in R\backslash \left\{0\right\}$ such that $h\le q$ for any $q\in R\backslash \left\{0\right\}$, where $\left|R\right|\ge 2$ if and only if $A^{*}\left(R\right)=\left\{h\right\}$.

Proof. 

Necessity. Take any $m\in A^{*}\left(R\right)$. By hypothesis, there exists $h\in R\backslash \left\{0\right\}$ such that $h\le m$. Since m is a hyperatom element and $h\ne 0$, we get $h=m$. So, $A^{*}\left(R\right)=\left\{h\right\}$.

Sufficiency. Let $A^{*}\left(R\right)=\left\{h\right\}$ and $q\in R\backslash \left\{0\right\}$. By Theorem 3, we have $h\le q$. □

Definition 3.

The $L_R$-graph G of a finite ordered semihyperring R is the graph whose vertex set $V\left(G\right)=R$ and edge set $E\left(G\right)$ satisfying the following condition:

$$\forall q,q^{\prime }\in Randq\ne q^{\prime },q{q}^{\prime }\in E\left(G\right)⟺L_R\left(\{q,q^{\prime }\}\right)=\left\{0\right\}.$$

Example 1.

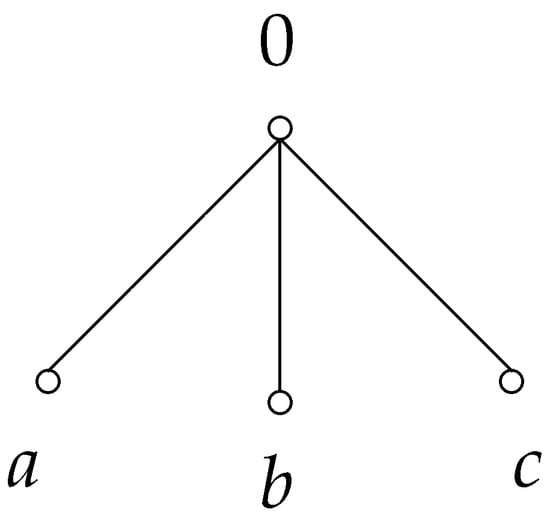
Consider the ordered semihyperring $(R,\oplus ,\odot ,\le )$, where ⊕ is a symmetrical hyperoperation (as shown in Table 1 and Table 2):

Table 1. Table of ⊕ for Example 1.

⊕	0	a	b	c
0	0	a	b	c
a	a	{a, b}	b	c
b	b	b	{ 0, b }	c
c	c	c	c	{ 0, c }

Table 1. Table of ⊕ for Example 1.

⊕	0	a	b	c
0	0	a	b	c
a	a	{a, b}	b	c
b	b	b	{ 0, b }	c
c	c	c	c	{ 0, c }

Table 2. Table of ⊙ for Example 1.

⊙	0	a	b	c
0	0	0	0	0
a	0	a	a	a
b	0	b	b	b
c	0	c	c	c

Table 2. Table of ⊙ for Example 1.

⊙	0	a	b	c
0	0	0	0	0
a	0	a	a	a
b	0	b	b	b
c	0	c	c	c

$$\begin{array}{c}0\le a\le b\le c.\hfill \end{array}$$

Then

$$L_R\left(\{0,a\}\right)=\left\{0\right\},$$

$$L_R\left(\{0,b\}\right)=\left\{0\right\},$$

$$L_R\left(\{0,c\}\right)=\left\{0\right\},$$

$$L_R\left(\{a,b\}\right)=\{0,a\},$$

$$L_R\left(\{a,c\}\right)=\{0,a\},$$

and

$$L_R\left(\{b,c\}\right)=\{0,a,b\}.$$

The $L_R$-graph G of R is shown in Figure 1:

Figure 1. $L_R$-graph for Example 1.

Clearly, G is a connected graph.

The $L_R$-graph of an ordered semihyperring is not connected in general. The following example validates it.

Example 2.

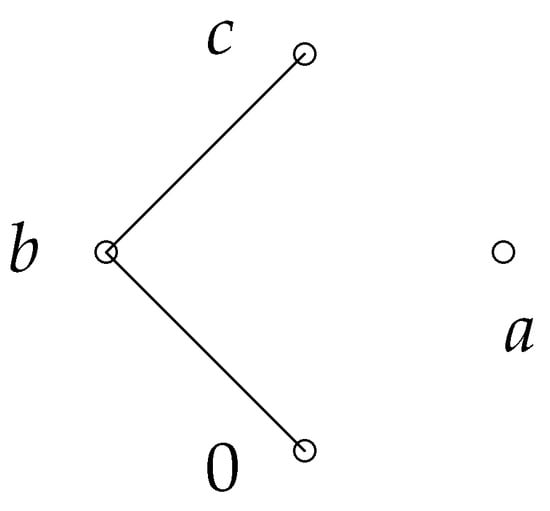
Consider the ordered semihyperring $(R,\oplus ,\odot ,\le )$, where ⊕ is a symmetrical hyperoperation (see Table 3 and Table 4):

Table 3. Table of ⊕ for Example 2.

⊕	0	a	b	c
0	0	a	b	c
a	a	a	a	a
b	b	a	{ 0, b }	{ 0, b, c }
c	c	a	{ 0, b, c }	{ 0, c }

Table 3. Table of ⊕ for Example 2.

⊕	0	a	b	c
0	0	a	b	c
a	a	a	a	a
b	b	a	{ 0, b }	{ 0, b, c }
c	c	a	{ 0, b, c }	{ 0, c }

Table 4. Table of ⊙ for Example 2.

⊙	0	a	b	c
0	0	0	0	0
a	0	a	{ 0, b }	0
b	0	0	0	0
c	0	{ 0, c }	0	0

Table 4. Table of ⊙ for Example 2.

⊙	0	a	b	c
0	0	0	0	0
a	0	a	{ 0, b }	0
b	0	0	0	0
c	0	{ 0, c }	0	0

$$\begin{array}{c}\le :=\left\{\right(0,0),(a,a),(b,b),(c,c),(0,b),(0,c\left)\right\}.\hfill \end{array}$$

Then

$$L_R\left(\{0,a\}\right)=\varnothing ,$$

$$L_R\left(\{0,b\}\right)=\left\{0\right\},$$

$$L_R\left(\{0,c\}\right)=\left\{0\right\},$$

$$L_R\left(\{a,b\}\right)=\varnothing ,$$

$$L_R\left(\{a,c\}\right)=\varnothing ,$$

and

$$L_R\left(\{b,c\}\right)=\left\{0\right\}.$$

The $L_R$-graph G of R is shown in Figure 2:

Figure 2. $L_R$-graph for Example 2.

Clearly, G is a disconnected graph.

Theorem 4.

Let $(R,\oplus ,\odot ,\le )$ be a positive ordered semihyperring. If $L_R\left(\{0,q\}\right)\ne \varnothing$ for all $q\in R$, then $L_R\left(\{0,q\}\right)=\left\{0\right\}$.

Proof. 

Let $L_R\left(\{0,q\}\right)\ne \varnothing$ for all $q\in R$ and $q^{\prime }\in L_R\left(\{0,q\}\right)$. Since R is positive, we get

$$L_R\left(0\right)=\{r\in R|r\le 0\}=\left\{0\right\}.$$

So,

$$q^{\prime }\in L_R\left(\{0,q\}\right)=L_R\left(0\right)\cap L_R\left(q\right)=\left\{0\right\}\cap L_R\left(q\right).$$

It means that $q^{\prime }=0$. Hence, $L_R\left(\{0,q\}\right)=\left\{0\right\}$ for all $q\in R$. □

Corollary 2.

Let G be the $L_R$-graph of a positive ordered semihyperring R. If $L_R\left(\{0,q\}\right)\ne \varnothing$ for all $q\in R$, then $0q\in E\left(G\right)$ for all $q\in R\backslash \left\{0\right\}$.

Theorem 5.

Let φ be an isomorphism from an ordered semihyperring R into an ordered semihyperring T. If G is the $L_R$-graph of R and $G^{\prime }$ is the $L_T$-graph of T, then $G\cong G^{\prime }$.

Proof. 

Consider $\phi :R⟶T$ as the isomorphism. We have $V\left(G\right)=R$ and $V\left(G^{\prime }\right)=T$. So, By hypothesis, there exists a one-to-one correspondence between $V\left(G\right)$ and $V\left(G^{\prime }\right)$. On the other hand,

$$\forall q,q^{\prime }\in R\mathrm{and}q\ne q^{\prime },q{q}^{\prime }\in E\left(G\right)⟺L_R\left(\{q,q^{\prime }\}\right)=\left\{0\right\}.$$

By Theorem 1, we get

$$\begin{array}{cc}{L}_T\left(\phi \left(\{q,q^{\prime }\}\right)\right)\hfill & =L_T\left(\{\phi \left(q\right),\phi \left(q^{\prime }\right)\}\right)\hfill \\ & =\phi \left(L_R\right(\{q,q^{\prime }\})\hfill \\ & =\phi \left(0\right)\hfill \\ & =0\hfill \end{array}$$

Thus,

$$q{q}^{\prime }\in E\left(G\right)⟺L_T\left(\{\phi \left(q\right),\phi \left(q^{\prime }\right)\}\right)=\left\{0\right\}.$$

Hence,

$$q{q}^{\prime }\in E\left(G\right)⟺\phi \left(q\right)\phi \left(q^{\prime }\right)\in E\left(G^{\prime }\right).$$

So, G ≅ G′. □

3. Conclusions

In this study, we have looked into the idea of hyperatom elements on an ordered semihyperring. Moreover, we introduced an operator $L_R$ on an ordered semihyperring R and investigated some aspects of $L_R$-graph. Furthermore, we have proved that if $\phi$ is an isomorphism from an ordered semihyperring R into an ordered semihyperring T, G is the $L_R$-graph of R and $G^{\prime }$ is the $L_T$-graph of T, then $G\cong G^{\prime }$. In the future, we will intend to study hyperatom elements of ordered semihypergroups.