Abstract
Currently, spatially localized electron densities and currents are considered to be candidates for use in the encoding of quantum information. For this reason, the control of their temporal dynamics is an important task. In this work, the spatiotemporal evolution of an electron wave packet in planar nanostructure in the presence of transverse magnetic and lateral electric fields is investigated by direct analytical solution of the non-stationary Schrödinger equation. Methods to control and manage the dynamics of the spatially localized electron density distribution are developed. The production of photon-like quantum states of electrons opens up opportunities for applications similar to quantum optical and quantum information technologies but implemented with charge carriers. Quantum control of the trajectory of the electron wave packet, accompanied by dramatic suppression of its spreading, is demonstrated. This study discovered methods to manage spatially localized electron behavior in a nanostructure that allows a controllable charge quantum transfer and gives rise to new prospects for quantum nanoelectronics technology.
1. Introduction
The investigation of solid state nanosystems is an interesting, and relevant, direction of modern physics research. For such systems, new physical effects arise due to nanoscale properties and spatial quantization [1]. Nanostructures, especially with reduced dimensionality, have many prospective practical applications in nanoelectronics, quantum measurements, quantum optics, and quantum information science [1,2,3,4]. To develop quantum information algorithms, different quantum systems are used as qubits. Among them, superconducting artificial atoms based on Josephson junction circuits appear to be very promising and are already implemented in various logic protocols and quantum networks schemes [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. For quantum information purposes, not only the regime of two-level coupling is important, but also Josephson multilevel systems with near-equidistant energy spectrums are also in high demand [20,21,22,23].
In our work, we consider another multilevel system, based on planar solid nanostructures, in which an oscillator-like equidistant energy spectrum appears in the presence of a transverse magnetic field. The arising discrete quantum states are known as the Landau levels [24] and can be also used for quantum logic and processing similar to photon quantum states [25]. At the same time, quantum information can be encoded, not only in multilevel excitation but also in spatially localized electron density distributions or currents. Controlling the dynamics of such localized quantum objects is an important, difficult task.
In this paper, the non-stationary Schrödinger equation for an electron wave packet in planar nanostructures in the presence of a transverse magnetic field is solved analytically, and the spatial–temporal evolution of electron density distributions is studied for various electron initial states. Methods to control and manage the dynamics of considered electron wave packets, based on the applying of additional electric field, are developed. In addition, the solution of the Heisenberg equation for electron coordinate and momentum operators is found, which allows one to obtain the trajectory of the center of mass of the electron wave packet, as well as its time-dependent width, for an arbitrary initial electron state. Different regimes of electron dynamics are found. An important effect of mutual influence and entanglement between spatial electron degrees of freedom is revealed and is shown to determine the electron motion, prevention of wave packet spreading, as well as the important interference effects arising from electron standing waves along the y-direction. As a result, the effect of dramatic suppression of wave packet spreading is established. Optimal conditions for observing cyclotron motion in a quantum case are found, and the role of symmetry in electron momentum distributions is analyzed. The ability to control the dynamics of electron wave packets in a nanostructure appears to be important for many practical applications in optoelectronics, quantum information and nanoelectronics circuit technology, memory devices, and photovoltaic systems.
2. Theoretical Methods
To analyze the spatial–temporal dynamics of an electron wave packet in a planar 2D nanostructure in the presence of a transverse magnetic and lateral constant electric field, the non-stationary Schrödinger equation is solved analytically:
with the Hamiltonian characterizing the electron energy in external constant magnetic and electric fields.
We suppose that an electron is highly excited in the conductive band of a nanostructure, as it appears to be weakly bound and is considered almost free. This state can be easily achieved in a high frequency electromagnetic field with the photon energy significantly exceeding the band gap [26,27,28,29,30]. In the case of graphene-like nanostructures, the Γ-point transitions lead to the excitation of electrons into weakly bound -orbitals (–bond), which provides confinement in the z-direction but allows free electron motion along the x–y plane if an electric or magnetic field is applied [31].
For an electron in the presence of a transverse magnetic field with the z-component equal to , the vector-potential and the Hamiltonian in (1) is given by:
Here, the term of the interaction of electron spin magnetic momentum with the magnetic field is omitted since it is independent from the electron coordinates and simply provides an additional constant energy.
By introducing the cyclotron frequency, the Hamiltonian (2) can be written as follows:
The obtained Hamiltonian conserves the y-component of electron momentum and describes the shifted oscillator of cyclotron frequency arising in the x-direction and centered at the point depending on the value :
The eigenstates of this Hamiltonian are known as the Landau level, with the wave functions represented as a plane-wave in the y-direction and the Hermite–Gauss functions describing the arising shifted magnetic oscillator [24]:
While the conserved electron momentum component is responsible for the shift of the oscillator in (3), the magnetic field determines the oscillator frequency as well as the characteristic width of the ground oscillator state , given by:
The eigenenergies of such an electron exactly coincide with the equidistant spectrum of the oscillator and do not depend on the y-momentum component:
The important feature of such an electron is the absence of the energy of its free motion in the y-direction, which is usually responsible for spreading of the free electron wave packet.
In the presence of additional constant electric field , the Hamiltonian (2) takes the form:
The shapes of the eigenfunctions (5) remain the same but they are found to have another shift since the magnetic oscillator is now centered on new point:
The correspondent eigenenergies are found to depend on both the conserved y-component of electron momentum and the value of external electric field:
The obtained eigenfunctions and corresponding eigenenergies are used to find and study the field-induced dynamics of an electron wave packet that is initially formed in the considered nanostructure or can be prepared in a certain quantum state. Different types of initial electron states are considered.
3. Results and Discussions
3.1. Oscillatory Behavior of 2D Electron in a Transverse Magnetic Field
Let us consider first the cases without an external electric field in which electron dynamics is studied in planar nanostructures in the presence of a transverse magnetic field only. We supposed that initially the electron is characterized by a certain y-component of momentum and by the Gaussian profile of the probability distribution in OX-direction, centered at the origin:
Generally, to prepare a localized electron wave packet in a nanosructure is a separate and rather difficult problem. However, recent theoretical investigations [32,33] show that the creation of an electron in the conductive band induced by few-photon quantum field is possible in the vicinity of a certain energy and corresponds to a superposition or wave packet of momentum states with a distribution close to the Gaussian distribution. For this reason, starting from the initial state (11) seems to be reasonable.
In the presence of a transverse magnetic field, the wave packet (11) was seen to be a superposition of different eigenstates of the system (5). If the width of the Gaussian wave packet exactly coincided with the characteristic width of the magnetic oscillator (6), the initial state (11) appeared to be the coherent state of this oscillator, with the time evolution given by:
Here, the expansion coefficients provided the Poisson distribution of electrons over eigenstates of magnetic oscillators and were obtained in the form:
where the dimensionless parameter determined the mean number of oscillator excited states as . In our case, we considered a magnetic field strength of the order of several Tesla for which the cyclotron frequency lies in the THz range, and the characteristic width of magnetic oscillator (6) appeared to be about 10 nm. As mentioned above, the shift of magnetic oscillator was determined by the y-momentum of an electron (see Equation (4)) and in dimensionless units is equal to .
The dynamics of such a wave packet is characterized by uniform distribution along the OY axis and oscillations of the probability density in time in dependence on the x-coordinate, with the Gaussian shape of the probability density being completely conserved (see Figure 1a). The found time-dependent density distribution along the OX-axis is given by:
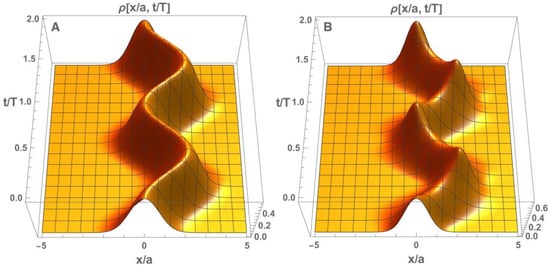
Figure 1.
The dynamics of electron probability density in dependence on x-coordinate (cut at a certain y) found in a transverse magnetic field for the initial state (11) in the case of equal (A) and different (B) widths of initial electron wave packet and the ground state in magnetic oscillator, .
Such state is referred to as the oscillating wave packet and is known as the coherent state of the oscillator [25]. It can be easily seen from (14) that the oscillations of electron density appeared symmetrically around the center of the magnetic oscillator shifted by .
If the size of the initial electron wave packet (11) does not fit to the characteristic width of magnetic oscillator (6), in addition to the oscillations of the center mass of the electron wave packet, the periodical change of the width of electron distribution along the OX-axes is observed. This means the formation of a coherent-squeezed state [25] of an electron, whose evolution is presented in Figure 1b. The squeezing effect was revealed as periodical oscillations of the variance of the x-coordinate taking place with double frequency:
It should be emphasized that the obtained results demonstrated the production of photon-like quantum states of electrons that open possibilities for applications similar to quantum-optical and quantum information technology but realized with charge carriers.
In addition, the observed quantum behavior of electrons differs dramatically from the motion of classical charge particles in the transverse magnetic field. Indeed, classical dynamics is known to result in cyclotron circular motion, while in the considered quantum case the electron is characterized by oscillatory behavior. The birth and appearance of the cyclotron motion of quantum electrons is investigated below.
3.2. Interplay of Spatial Degrees of Freedom
Let us now consider a standing wave along the y-coordinate as the initial condition for the electron:
In this case, the electron wave packet corresponds to the superposition of two initial states considered above but with opposite values of the y-component of momentum providing two equal but oppositely shifted magnetic oscillators. Using the same technique as described above, we found the time-dependent electron density distribution in the form:
where and stands for the hyperbolic cosine function.
The dynamics of this wave-packet is presented in Figure 2 and manifested itself in harmonic oscillations of two wave packets that periodically became separated or overlapped. In the latter case, the interference of these wave packets took place, which was important mainly around point and is described by the last term in Equation (17).
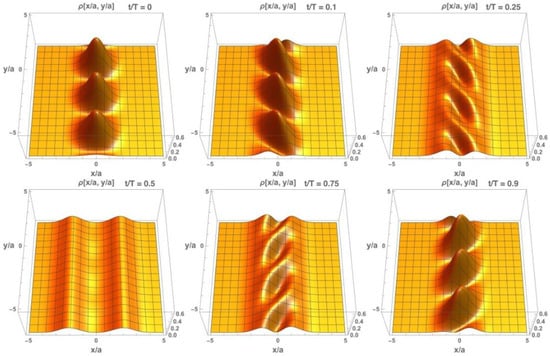
Figure 2.
The snapshots of electron probability density found in a transverse magnetic field for the initial state (16) at different instants of time during the cyclotron period, ka = 1.
The most important feature of this interference consists of the entanglement and interplay of spatial degrees of freedom. Indeed, both x- and y-coordinates are included in the argument of cosine functions responsible for the interference and cannot be separated. Moreover, the value of the y-component of electron momentum is responsible for the interference structure arising along the OX-axis. In dependence on the sign of the sine function in Equation (17), the interference was found to be most pronounced along the main diagonal (y = x) or perpendicular direction (y = −x). Such behavior, being analyzed dynamically in time, represents a partial rotation of the electron density and can be interpreted as the initiation of the cyclotron motion in quantum case. Thus, the interplay and mutual influence of spatial x and y degrees of freedom was shown to be a physical mechanism responsible for the initiation of the cyclotron motion.
At the same time, the found mechanism was responsible for the demonstrated formation and possible control of the arrays of localized electron density wave packets, which appear to be the first step to the quantum data transfer that is realized with charge carriers.
3.3. The Heisenberg Picture
As shown above, different electron initial states can be characterized by significantly different further evolution. To analyze several possible dynamics scenarios, it is appropriate to consider the system in the Heisenberg representation, to solve the Heisenberg equation for electron momentum and coordinate operators and to calculate the motion of the electron wave packet as well as the time-dependent change of its width.
In cases where only the transverse magnetic field is turned on, the Heisenberg equations for the electron operators are given by:
The found solutions for the time-dependent operators are presented as follows:
where the operators on the right-hand side of the equations are taken in Schrödinger representation, i.e., being independent on time.
It is immediately seen from (19) that instead of expected free motion in the y-direction, only oscillating behavior of the averaged y-coordinate took place. This fact results from the dramatic coupling of spatial degrees of freedom, which also results in the following relation, found directly from the solution (19):
Thus, the operator of the electron y-coordinate was found to be directly proportional to the time-derivative of the x operator.
The found evolution of operators (19) allowed one to obtain the time-dependence of various averaged observables under different initial conditions. Specifically, for the localized Gaussian electron wave packet, centered initially at the origin
the position of the center mass was determined by the averaged dimensionless y-component of momentum and was characterized by the following time-dependent averaged coordinates:
The found time-dependencies corresponded to the circular trajectory induced by the magnetic field:
Thus, for the initial wave packet (21) the cyclotron motion was predicted using the Heisenberg picture.
Another important result obtained from the Heisenberg solution (19) concerned the evolution of the wave packet width. Instead of the monotonous spreading expected for free motion in the y-direction, the oscillation behavior of the variances of both spatial coordinates was found:
The dramatic mutual influence of the wave packet widths in x- and y-directions can be seen from (24). Indeed, the growth of the x variance arose due to the final initial width of the electron wave packet (21) in the y-direction (to be more precise, the final width of the momentum distribution in y-direction). At the same time, the influence of the x degree of freedom prevented the infinite spreading of the wave packet in the perpendicular y-direction. Thus, the obtained solutions of the Heisenberg equation predicted dramatic suppression of the wave packet spreading in the y-direction in comparison to the case of free particle motion. The obtained solutions provided the theoretical basis for experimental managing and quantum control of the dynamics of both the center of mass and the width of the electron wave packet.
3.4. Symmetry of the Electron Momentum Distribution as a Key for Cyclotron Quantum Motion
The theoretical predictions of the evolution of different averaged observables, discussed above and obtained using the solution of the Heisenberg equations, can be proved by direct calculation of time-dependent electron density distributions. Moreover, the dynamics of electron density can give information which cannot be obtained directly from the Heisenberg picture and appears to be much richer than the simple center of mass-trajectory. For the well-localized initial wave packet (21), the predicted center of mass trajectory and the change in time of the coordinate variances are fully confirmed. Figure 3 demonstrates the well-pronounced cyclotron motion of an electron wave packet with its width being more or less conserved. Actually, partial spreading and squeezing of the electron wave packet, periodically changing each other in both directions, was found. However, as predicted by Equation (24), squeezing to a width smaller than the initial values did not occur. In fact, the oscillator potential formed due to the presence of the transverse magnetic field prevented the spreading along the OX-axes and was found to dramatically suppress spreading in the perpendicular y-direction.
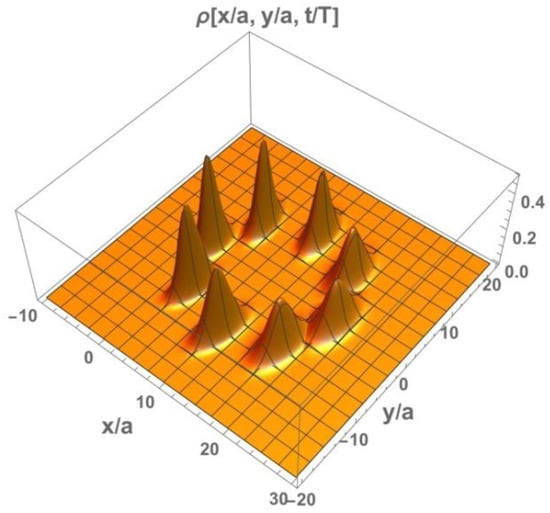
Figure 3.
Dynamics of initially localized symmetric electron wave packet (21) in a transverse magnetic field. Each position of the wave-packet corresponds to a certain instant of time during the cyclotron period, ka = 10.
An interesting question related to the studied motion is the influence of the shape of the momentum distribution on the electron wave packet behavior. Here, we consider an initial electron wave packet with significantly asymmetric momentum distribution in the y-direction:
In contrast to the state (21) with Gaussian shape of both coordinate and momentum distribution in y-direction, the momentum distribution of the wave packet (25) was strongly asymmetric and was characterized by mean momentum and position of maximum that were significantly different from each other. At the same time, the mean values of the y-momentum of the states (21) and (25) were chosen to be the same in order to compare the dynamics of these wave packets correctly. The mean y-momentum of electron in the state (25) was linearly proportional to the parameter .
The dynamics of the wave packet (25) was calculated as a superposition of the time-dependent wave functions obtained for each plane wave in y-direction, included in (25) by using the procedure described in Section 3.1. The snapshots of the electron density distribution obtained at different time moments during the cyclotron period are presented in Figure 4.
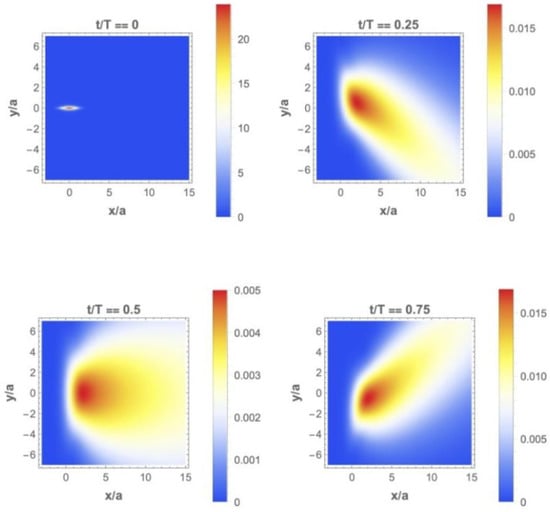
Figure 4.
The snapshots of the electron density distribution calculated for initial wave packet (25) at different time moments during the cyclotron period, .
The presented results demonstrate that in the case of asymmetric electron momentum distribution the dynamics of the wave packet appears to be far from the well pronounced cyclotron motion. Though initially the wave packet was symmetric in the spatial frame its further dynamics were characterized by fast and asymmetric spreading arising due to asymmetry of the y-momentum distribution. As a result, only mean values of x- and y-coordinates obeyed the circular trajectory (23), while the maximum and other points of the wave packet did not seem to provide a circular motion. Thus, the symmetry of the electron momentum distribution appeared to be the key for observing the cyclotron motion of a quantum wave packet.
3.5. Managing the Wave Packet Dynamics by Simultaneous Impact of Both the Transverse Magnetic and Constant Electric Fields
According to Equations (8) and (9) the simultaneous presence of both the transverse magnetic field and constant electric field led to the additional shift of the formed magnetic oscillator. For this reason, the results obtained for one plane or standing wave described by initial conditions (11) and (16), respectively, appear to be rather similar to the data discussed in Section 3.1 and Section 3.2. However, for the localized electron wave packet with symmetrical momentum distribution (21), some new effects were found, resulting in the possible control of the electron evolution and managing of the electron wave packet dynamics. Actually, the trajectory of the center of mass of electron wave packet can be significantly changed by varying the electric field strength. Such a possibility is shown from the solution of the Heisenberg equations for operators and time-dependent mean values of electron coordinates obtained in this case:
The last equation showed that the oscillations of mean y-coordinate were accompanied by linear drift, such as different trajectories of the center of mass of the electron wave packet were observed.
Figure 5 represents two possible scenarios of electron dynamics in the presence of magnetic and electric fields. In general, the trajectory of the wave packet was found to be similar to a cycloid shape (see Figure 5a). However, by changing the value and direction of the applied electric field it was possible to kill out the oscillation and to provide linear motion in the y-direction. Such dynamics arose due to the compensation of the shift of the magnetic oscillator by an opposite shift induced by a constant electric field and is illustrated by Figure 5b.
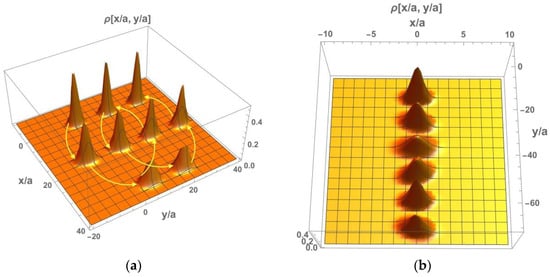
Figure 5.
Dynamics of initially symmetric electron wave packet in both magnetic and electric fields for different values of electric field strength: (a) corresponds to and ; in case (b) the shift of magnetic oscillator is compensated by the shift induced by electric field in opposite direction . Each position of the wave-packet corresponds to a certain instant of time during the cyclotron period.
It should be emphasized that the found linear motion of the electron wave packet is not accompanied by its spreading in time, since the variances are not sensitive to the electric field strength and are determined by widths of electron wave packet in coordinate and momentum domains according to Equation (24). Though the spreading was suppressed, the wave packet widths in the x- and y-directions changed over time in such a way that rotation around the symmetry axis of the wave packet took place, even in the case of linear trajectory that arose from the mutual influence of different electron degrees of freedom and echoed the cyclotron motion.
The presented results demonstrated the quantum control of the trajectory of the electron wave packet, accompanied by prevention of its spreading. Such management of spatially localized electron density allows for a controllable charge quantum transfer and opens new possibilities for quantum electronics with charge particles.
4. Conclusions
In conclusion, the dynamics of spatially localized electron wave packets in planar 2D nanostructures, which appear to be good candidates for quantum information encoding, was investigated analytically. Methods to control and manage the behavior of considered electrons, based on applying magnetic and electric fields, were developed. Different regimes of electron dynamics were found. Since, in the considered case, the characteristic frequency of the electron cyclotron motion appeared in the THz range, the observed dynamics of electron density distribution can provide the current oscillations and therefore possible generation of the THz frequency fields that are required for various practical applications.
The solution of the Heisenberg equations for electron coordinate and momentum operators was found, which was the theoretical basis of the experimental manipulation and transfer of charge quantum.
The obtained results demonstrate that the production of the photon-like quantum states of electrons, which are very useful for various applications like quantum optical and photon quantum information technologies, can be realized with charge carriers.
An important effect of mutual influence and entanglement between spatial electron degrees of freedom was revealed and is shown to allow for managing the trajectory and the width of the electron wave packet. As a result, quantum control of electron motion accompanied by dramatic suppression of electron wave packet spreading was demonstrated. The possibility of managing spatially localized electron dynamics in a nanostructure allowed a controllable charge quantum transfer and introduces new prospects in quantum nanoelectronics technology.
Author Contributions
Conceptualization, D.S. and O.T.; methodology, O.T.; software, D.S.; validation, D.S. and O.T.; formal analysis, D.S. and O.T.; investigation, D.S. and O.T.; data curation, D.S. and O.T.; writing—original draft preparation, O.T.; visualization, D.S. and O.T.; supervision, O.T.; project administration, O.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation project No. 19-42-04105.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research is performed according to the Development program of the Interdisciplinary Scientific and Educational School of Lomonosov Moscow State University «Photonic and Quantum technologies. Digital medicine».
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sattler, K.D. Handbook of Nanophysics: Nanoelectronics and Nanophotonics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Dakin, J.P.; Brown, R. Handbook of Optoelectronics Concepts, Devices, and Techniques; CRC Press: Boca Raton, FL, USA, 2020; p. 858. [Google Scholar]
- Homola, J. Surface Plasmon Resonance Based Sensors; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Belotelov, V.I.; Zvezdin, A.K. Magneto-optical properties of photonic crystals. JOSA B 2005, 22, 286–292. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef]
- Xiang, Z.-L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623. [Google Scholar] [CrossRef]
- Van der Wal, C.H.; ter Haar, A.C.J.; Wilhelm, F.K.; Schouten, R.N.; Harmans, C.J.P.M.; Orlando, T.P.; Lloyd, S.; Mooij, J.E. Quantum superposition of macroscopic persistent-current states. Science 2000, 290, 773–777. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.R.; Patel, V.; Chen, W.; Tolpygo, S.K.; Lukens, J.E. Unipolar magnetic field pulses as an advantageous tool for ultrafast spin-flip in superconducting Josephson “atoms”. Nature 2000, 406, 43–45. [Google Scholar] [CrossRef]
- Chiorescu, I.; Nakamura, Y.; Harmans, C.J.; Mooij, J.E. Coherent quantum dynamics of a superconducting flux qubit. Science 2003, 299, 1869–1871. [Google Scholar] [CrossRef] [PubMed]
- Manucharyan, V.E.; Koch, J.; Glazman, L.I.; Devoret, M.H. Fluxonium: Single cooper-pair circuit free of charge offsets. Science 2009, 326, 113–116. [Google Scholar] [CrossRef]
- Steffen, M.; Kumar, S.; DiVincenzo, D.P.; Rozen, J.R.; Keefe, G.A.; Rothwell, M.B.; Ketchen, M.B. High-coherence hybrid superconducting qubit. Phys. Rev. Lett. 2010, 105, 100502. [Google Scholar] [CrossRef]
- Bylander, J.; Gustavsson, S.; Yan, F.; Yoshihara, F.; Harrabi, K.; Fitch, G.; Cory, D.C.; Nakamura, Y.; Tsai, J.; Oliver, W.D. Suppressing relaxation in superconducting qubits by quasiparticle pumping. Nat. Phys. 2011, 7, 565–570. [Google Scholar] [CrossRef]
- Grajcar, M.; van der Ploeg, S.H.W.; Izmalkov, A.; Il’ichev, E.; Meyer, H.-G.; Fedorov, A.; Shnirman, A.; Schön, G. Sisyphus cooling and amplification by a superconducting qubit. Nat. Phys. 2008, 4, 612–616. [Google Scholar] [CrossRef]
- Schoelkopf, R.J.; Girvin, S.M. Wiring up quantum systems. Nature 2008, 451, 664–669. [Google Scholar] [CrossRef] [PubMed]
- Izmalkov, A.; van der Ploeg, S.H.W.; Shevchenko, S.N.; Grajcar, M.; Il’ichev, E.; Hübner, U.; Omelyanchouk, A.N.; Meyer, H.-G. Consistency of ground state and spectroscopic measurements on flux qubits. Phys. Rev. Lett. 2008, 101, 017003. [Google Scholar] [CrossRef] [PubMed]
- Kou, A.; Smith, W.C.; Vool, U.; Brierley, R.T.; Meier, H.; Frunzio, L.; Girvin, S.M.; Glazman, L.I.; Devoret, M.H. A fluxonium-based artificial molecule with a tunable magnetic moment. Phys. Rev. X 2017, 7, 031037. [Google Scholar] [CrossRef]
- Tacchino, F.; Macchiavello, C.; Gerace, D.; Bajoni, D. An Artificial Neuron Implemented on an Actual Quantum Processor. Npj Quantum Inf. 2019, 5, 26. [Google Scholar] [CrossRef]
- Shulga, K.V.; Il’ichev, E.; Fistul, M.V.; Besedin, I.S.; Butz, S.; Astafiev, O.V.; Hubner, U.; Ustinov, A.V. Magnetically induced transparency of a quantum metamaterial composed of twin flux qubits. Nat. Commun. 2018, 9, 150. [Google Scholar] [CrossRef]
- Hönigl-Decrinis, T.; Antonov, I.V.; Shaikhaidarov, R.; Antonov, V.N.; Dmitriev, A.Y.; Astafiev, O.V. Mixing of coherent waves in a single three-level artificial atom. Phys. Rev. A 2018, 98, 041801. [Google Scholar] [CrossRef]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef]
- Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C.; et al. Coherent josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 2013, 111, 080502. [Google Scholar] [CrossRef]
- Rigetti, C.; Gambetta, J.M.; Poletto, S.; Plourde, B.L.T.; Chow, J.M.; Córcoles, A.D.; Smolin, J.A.; Merkel, S.T.; Rozen, J.R.; Keefe, G.A.; et al. Superconducting qubit in a waveguide cavity with a coherence time approaching 0.1 ms. Phys. Rev. B 2012, 86, 100506. [Google Scholar] [CrossRef]
- Vozhakov, V.A.; Bastrakova, M.V.; Klenov, N.V.; Soloviev, I.I.; Pogosov, W.V.; Babukhin, D.V.; Zhukov, A.A.; Satanin, A.M. State control in superconducting quantum processors. Phys. Uspekhi 2022, 65, 421–439. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, L.M. Quantum Mechanics: Non-Relativistic Theory, 3rd ed.; Pergamon Press: Elmsford, NY, USA, 1976. [Google Scholar]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kira, M.; Koch, S.W. Many-body correlations and excitonic effects in semiconductor spectroscopy. Prog. Quantum Electron. 2006, 30, 155–296. [Google Scholar] [CrossRef]
- Koch, S.W.; Kira, M.; Khitrova, G.; Gibbs, H.M. Semiconductor excitons in new light. Nat. Mater. 2006, 5, 523–531. [Google Scholar] [CrossRef] [PubMed]
- Kira, M.; Koch, S.W. Quantum-optical spectroscopy of semiconductors. Phys. Rev. A 2006, 73, 013813. [Google Scholar] [CrossRef]
- Kira, M.; Koch, S.W. Semiconductor Quantum Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hargart, F.; Roy-Choudhury, K.; John, T.; Portalupi, S.L.; Schneider, C.; Höfling, S.; Michler, P.; Kamp, M.; Hughes, S. Probing different regimes of strong field light–matter interaction with semiconductor quantum dots and few cavity photons. New J. Phys. 2016, 18, 123031. [Google Scholar] [CrossRef]
- Ermin Malic, E.; Knorr, A. Graphene and Carbon Nanotubes; WILEY-VCHVerlag GmbH& Co. KGaA: Weinheim, Germany, 2013. [Google Scholar]
- Tikhonova, O.V.; Voronina, E.N. Transfer of correlations from photons to electron excitations and currents induced in semiconductor quantum wells by non-classical twisted light. J. Phys. Condens. Matter 2022, 34, 065302. [Google Scholar] [CrossRef]
- Rose, H.; Vasil’ev, A.N.; Tikhonova, O.V.; Meier, T.; Sharapova, P.R. Excitation of an electronic band structure by a single-photon Fock state. Zenodo 2021. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).