Abstract
Additional information and borrowing strength from the related sites and other sources will improve estimation in small areas. Generalized linear mixed-effects models (GLMMs) have been frequently used in small area estimation; however, the relationship between the response variable and some covariates may not be linear in many cases. In such cases, using semiparametric modeling, incorporating some nonlinear symmetric/asymmetric functions to the predictor seems more appropriate due to their flexibility. In addition, spatial dependence is observed between areas in many cases. Thus, using the semiparametric spatial models for small areas is of interest. This paper presents semiparametric spatial GLMMs and approximates the nonlinear component using splines to estimate the linear part. We apply our proposal for analyzing insurance data obtained from an Iranian insurance company. Our numerical illustrations will support the use of our proposal in situations where the spatial GLMMs may not be appropriate.
1. Introduction
Comprehensive information and appropriate statistical data are essential for planning, decision-making, and policymaking. Knowing the population requires having enough statistical information. Such information is generally obtained through surveys or censuses, typically designed for scientific purposes or population parameters (big areas). Nevertheless, for some reason, the available sample might not be enough to obtain a valid estimation in a small area or subdomain. These reasons include the lack of sufficient information in the target areas, the absence of pre-arranged planning while obtaining information, the lack of funding resources, statistical capacities, long periods between recording information, and some privacy laws. In such cases, the need for small area estimation is felt. The small area is a subdomain such as provinces, counties, and sub-populations such as specific age–sex race groups and health regions for which the sample size is not enough to obtain a valid estimation.
Statistically, the small amount of data in the small area (sometimes the sample size is zero) increases the prediction error. In such cases, the direct estimators are not accurate enough. To obtain a reliable estimation in the small area, the auxiliary information of the corresponding regions or the information of the same small area in previous study periods or extra information in the recorded statistics, administrative surveys, or a combination of these methods are used. The effect of areas on each other, which can be emerged by spatial correlation, can also be considered a valuable measure to increase estimation capabilities. In practice, the small area boundaries are contractual, and there is no reason why the effects in adjacent areas are not correlated. Therefore, it seems meaningful to test the assumption of spatial correlation of the closed regions.
In modeling the small area, valuable efforts have been made. Some of them are summarized as follows. Morales et al. [1] used the linear mixed model (LMM) to obtain the poverty ratio and the mean square prediction error (MSPE) of the small area estimator. Boubeta [2] used the Poisson regression model to estimate the small area parameter. Malee and Muller [3] present a semiparametric model to describe the geographic variability component. Chandra et al. [4] used a nonparametric generalized linear mixed model (GLMM) for non-Gaussian response variables when the data are spatially non-stationary in the small area and obtained MSE estimation for the nonlinear spline spatial model. Zhu et al. [5] considered the small area effect as an unknown function, estimated the small area using the semiparametric model, and represented the small area effect by the penalized spline. Torabi and Jiang [6] obtained an estimation of small area parameters using a spatial LMM. They used the conditional autoregressive (CAR) model to consider the spatial random effect. Torabi [7] studied the area-level spatial models in the small area. He used the proper CAR model to consider the spatial random effect of the areas and obtained the small area parameters using the spatial generalized linear model.
In this paper, our primary focus is on modeling insurance data. The insurance industry is one of the sectors for which the data analysis is placed in the category of the small area because data collecting is frequently encountered with many limitations. Life insurance has a special place among the various branches of the insurance industry due to its range of services. We intend to analyze life insurance data obtained from the database of Iran insurance companies in IRAN. These data were measured province-specifically from April to June 2018 for 32 provinces of Iran. The data include 466,759 observations. The response variable of interest for modeling is the provinces’ provincial per capita number of life insurance contracts. The explanatory variables in our analysis include the work experience of the insurance sales branch.
There are a few points to note in this data. (i) The small area estimation is generally divided into two categories: unit-level and area-level. For this data, the area level is considered due to the availability of the collected data. (ii) Due to the structure of the response variable in the study, which does not follow the normal distribution, using a kind of generalized linear models (GLMs) is unavoidable. (iii) Since the acceptance of life insurance in the basket of goods is related to income status and economic culture, and the borders between regions and provinces are contractual, there is no reason for the effects not to be interrelated in economic culture and income condition. Therefore, it seems logical to consider the correlation of regions in this study under the spatial dependence concept. (iv) As shown in Figure 1, the scatter plot of response versus explanatory variable depicts drastic fluctuations, which means that a linear trend cannot explain the relationship well. Moreover, since the relationship between response and covariate is unknown, it does not make sense to consider the parametric model. Thus, regression modeling must consider a nonlinear relationship between the response and the explanatory variable under the non-parametric component.
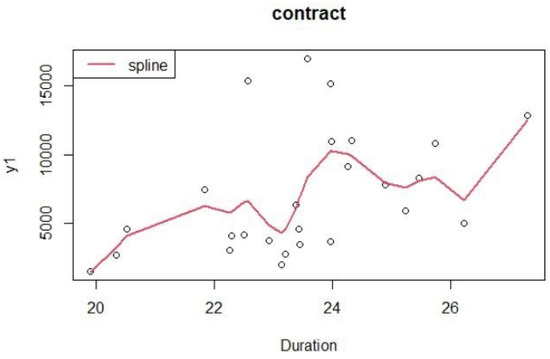
Figure 1.
Scatterplot of the provincial per capita number of life insurance contracts (response) versus the work experience of insurance sales branches in Iran.
The points (i)–(iii) provide conditions to follow the work in [7]. However, the last point leads us to add a nonparametric part as a symmetric/asymmetric function to the model in [7]. Therefore, our main contribution is to propose a semiparametric spatial generalized linear mixed model in a small area, thereby increasing flexibility in the prediction. We derive the empirical best prediction (EBP) for the small area predictor and the mean squared prediction error (MSPE) for the EBP. We also consider the small area’s spatial random effects (SRE).
This paper is organized as follows: In Section 2, we present EBP to the small area predictor and obtain the MSPE of the EB estimator. In Section 3, the proposed methodology is applied to the real data on the provincial per capita number of life insurance contracts. After that, in Section 4, we present two simulation experiments and evaluate the performance of the proposed method. Section 5 offers some results and provides concluding remarks.
2. Semiparametric Mixed-Effects Model
Semiparametric mixed-effects modeling, combining a nonlinear function with the linear predictor, has a long history and dates back to Zeger and Diggle [8]. They used a semiparametric random intercept model to analyze the CD4 cell numbers in HIV seroconverts and estimated the nonparametric component by the backfitting method. Discussions about semiparametric models can be founded in Roozbeh [9,10], Akdeniz and Roozbeh [11], Taavoni and Arashi [12], and Taavoni et al. [13].
Suppose that the number of small areas and the number of explanatory variables are denoted by m and p, respectively. Under an area-level small area model, and in the framework of GLMs, it is assumed that the response variables are conditionally independent given the latent variable , and follow the exponential families with the probability density:
where is the interested response variable in the ith small area, is the ith latent variable, and is the scale parameter. Furthermore, and are known functions. Implementing statistical inferences on the latent variable is the objective of the small-area estimation. The model of the latent variable is defined as follows:
where is a function of , is the ith row of the design matrix , is the vector of unknown regression coefficients, and is the ith row of the identity matrix . The is the vector of spatial random effect accompanied by distribution and . In this model, we assume that the relation of the with the response variable is nonlinear. Thus, it is considered a nonparametric component. The function is generally unknown, but it is assumed that it is a smooth nonlinear function and has the second derivative. The estimation of nonparametric function f is presented as below:
which is called a d-order spline estimator function with knots . In this function, are spline regression coefficients (refer to [14] for more details). Further, denotes the truncated polynomial basis function of order d defined as:
The approximation function in (3) can be summarized by , which ; is a vector of spline regression coefficients and . Thus, Equation (2) can be rewritten as:
By combining the fixed and spline effects in (4), the following equation is resulted:
wherein is the mixed design matrix of the fixed effects and spline effects, and is the vector of the regression coefficients corresponding to fixed and spline effects.
In order to predict the latent variable , the conditional density is calculated using the equation below:
where and is the vector of parameter of random effects. The Laplace approximation centered around the point is used to approximate the conditional density of [15]:
Proposition 1.
Under the conditions that the first and second derivatives of in Equation (7) are available in the closed-form, the conditional density of becomes a normal approximation with conditional mean and conditional variance , given by:
where , is a diagonal matrix with entries , , and for and . For the proof, refer to Appendix A.
If is known, the best predictor of the is the conditional expectation () and the second-order unbiased mean squared prediction errors is , which was defined in Equation (8a,b). However, when is the vector of unknown parameters, we obtained the best empirical prediction of by replacing by . Frequentist and Bayesian methods are generally used to process spatial generalized linear mixed models (SGLMMs). Due to the computational complexity in calculating maximum likelihood estimation (MLE), frequency methods require numerical solutions of high-dimensional and intractable integrals. In this paper, the MLE method is impossible due to the need to solve high-dimensional integrals. In addition, using Bayesian methods always faces the problem of selecting the appropriate prior. According to the problems mentioned in the two Frequency and Bayesian methods, the data cloning (DC) approach (see [16]) has been used to estimate the unknown parameters. DC is a computational method for calculating MLE, using MCMC (Markov chain Monte Carlo) algorithm and Bayesian methods. This method does not require numerical maximization and derivation of a complex function, which is robust to the prior choice. To see more Bayesian studies, refer to [17,18,19].
To understand the logic of the DC method, consider that the observations of and the explanatory variables are independently repeated exactly k times. The vector of random effects, by using their probabilistic explanations, generated k times, so that represents the data at k times of repetition. The maximum likelihood function is where the likelihood function is the likelihood of original data. Since the DC method is based on the asymptotic behavior of posterior density, the theoretical conditions of asymptotic posterior density can be established by increasing the sample size. In this approach, the posterior distribution of the clone answer is shown as:
where and are the normalized constant and prior distribution, respectively. Lele et al. [16] show that under some regular conditions, the posterior distribution of converges to a multivariate normal distribution with mean and identity covariance matrix . Thus, the estimation of is the mean of posterior density under the squared error loss function. The mean squared empirical prediction error is approximately calculated as below:
In the above relation, is the “little-o” notation for the asymptotic behaviour so that means . Further, denotes the mathematical expectation with respect to . Then,
where,
where denotes the trace of matrix A. It can be seen that of is a function of unknown parameters . By replacing by , Torabi [7] noticed that in this estimation, the rough value for is approximately equal to , where
It is noticeable that sometimes the calculated value of can be negative. In this case, Prasad and Rao [20] replaced negative values with positive values.
3. Life Insurance Data Analysis
Here, we model the above-mentioned number of life insurance contract data using the proposed semiparametric spatial generalized linear mixed-effects model. We consider the following spatial Poisson regression model:
where is the reported mean number of life insurance contracts of the ith province in Iran, is defined as an intercept, is the ith row of the identity matrix, and is taken from an ICAR(intrinsic conditional autoregressive) model [21]. Further, is the mean of work experience of the insurance sales branch of the ith province. It seems that the and the response variable have a nonlinear relationship, and it is not meaningful to insert it as a parametric component. Therefore, we consider it as a nonparametric function into the model where f is a smooth and unknown function of duration. We use the spline approximation method to approximate the nonparametric component.
Here, the function is a cubic spline with evenly spaced knots in the range of , at the points of , , and . This can be summarized by , in which ; are spline regression coefficients and
Hence, the semiparametric spatial mixed model is derived as:
By combining the fixed and spline effects, the above model can be rewritten as:
where the design matrix is the mixed of the fixed effect and Spline effects matrices, and is an eight-dimensional vector of parameters of the regression coefficients and spline coefficients.
The estimation of the model parameters, which were found by data cloning, are presented in Table 1. Here, the estimate of regression coefficient, spline coefficients , and spatial parameter along with the respective standard errors are given.

Table 1.
Model parameter estimates for the semiparametric spatial GLMM.
To evaluate the flexibility and the effect of the duration contract in a nonlinear manner, which leads to an increase in the flexibility of the model, we compare the above-suggested model with the following alternative model:
Figure 2 depicts the boxplot of of the for the number of life insurance contracts in IRAN. As can be seen, the MSPE of EBP in the proposed model is smaller than the spatial generalized linear mixed model, thus, the suggested model transparently provides a smoother prediction attaining better results.
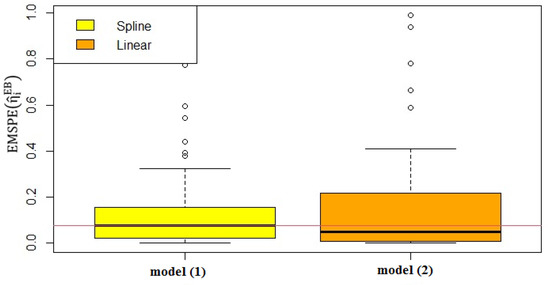
Figure 2.
Boxplot of the EMSPE of of the number of life insurance contracts in IRAN under semiparametric model (1) and parametric model (2) under the semiparametric spatial GLMM.
4. Simulation Study
This section uses the semiparametric mixed-effect model to evaluate the proposed method. Since this article expands Torabi’s proposed model [7], we have utilized the same Minnesota country map to compare our proposed model accuracy with the parametric model. The simulated data are obtained from the following model:
where is generated from the ICAR model. The other components of this pattern have the following specifications: is the offset and is the intercept. is the nonlinear function and is the fixed duration of the study generated from the uniform distribution on . First, we generate from the ICAR distribution with parameters for . We do this job independently for steps and denote , as the rth spatial random variable generated by . Inserting in the formula and getting for each step, is generated from the Poisson distribution with mean for and .
For each simulation run, based on (2), we find:
By using the data cloning approach, is given by:
where is a vector of regression and spline coefficients, is the ith row of the identity matrix, is the ICAR covariance matrix and is the ith row of the matrix . The is obtained for each of the 1000 steps. and are calculated as follows:
also the empirical MSPE (EMSPE) of is calculated by using the following formula:
To evaluate the performance of the proposed model, we compare it with the model . The estimation of model parameters by the DC method is reported in Table 2 and Table 3 for the proposed and parametric models.

Table 2.
Model parameter estimates and corresponding standard errors using the MLE approach for the semiparametric spatial Poisson model.

Table 3.
Model parameter estimates and corresponding standard errors using the MLE approach for the parametric spatial Poisson model.
Table 2 contain the estimates of regression coefficients, spline regression coefficients, and spatial parameter for the semiparametric spatial Poisson model. Moreover, the results of the parametric model are shown in Table 3.
To evaluate the performance of the semiparametric spatial Poisson model, the box plots of EMSPE of values are depicted in Figure 3, which shows the distribution of the mean square prediction error. As can be seen, the EMSPE of in the proposed model is smaller than the parametric counterpart. The third quantile and maximum point of EMSPE of in the proposed model are less than the parametric model. The maximum outlier points of EMSPE of in the proposed model is less than the parametric model, which shows that the proposed model has better performance even in the outlier. Furthermore, the MSPE and ISQR values for these two models are listed in Table 4. This table shows the superiority of our proposed model. As a result, the semiparametric model improves the model in terms of prediction.
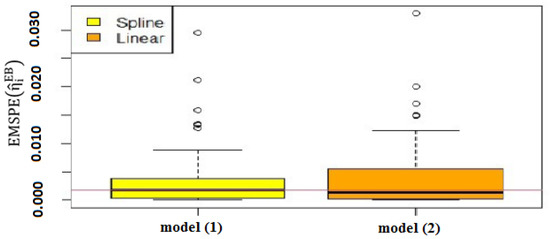
Figure 3.
Boxplots of the EMSPE of for the semiparametric and parametric spatial Poisson models.

Table 4.
Value of the EMSPE of and ISQR for the semiparametric and parametric spatial Poisson models.
In Figure 3, the box plot of MSPE of is shown in total areas. In a small area, MSPE of is important not only in all areas but also in each area. In some cases, in the small area approach, some regions are more important, and those regions should be investigated more carefully. Hence, in order to compare the performance of the proposed model against the parametric model, the heat map of EMSPE of is drawn separately by the province in Minnesota in Figure 4.
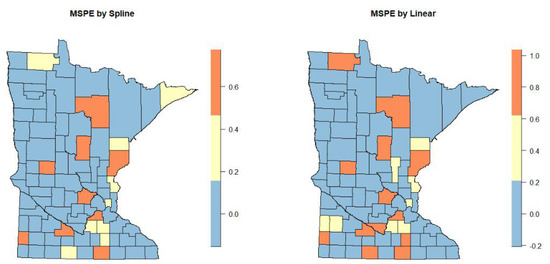
Figure 4.
Heat map of the MSPE of per provinces in the proposed model (left) and parametric model (right).
As shown in Figure 4, in some provinces, the MSPE of in the proposed model are less than the MSPE of in the parametric model and they are equal in some provinces. There is no area in which the MSPE of in the proposed model is more than the parametric model.
In addition to comparing the MSPE of , plotting the predicted values of two models versus simulated data can provide a better understanding of the performance of two models. As shown in Figure 5, the semiparametric model is more efficient than the parametric model in estimating the nonparametric component.
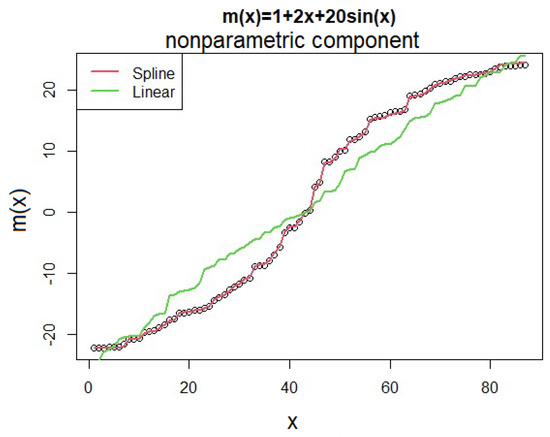
Figure 5.
Predicted values of the nonparametric component for the two semiparametric (Spline) and parametric (Linear) models in the simulated data.
5. Conclusions
The GLMMs and linear mixed-effects models are the models that are frequently used in small areas. As we demonstrated in the analysis of life insurance data obtained from an Iran Insurance Company in IRAN, a nonlinear relation may exist between the response variable and some of the covariates. In such cases, the GLM models do not have the necessary capability, and new models are needed to analyze such a data set in a small area. A semiparametric spatial generalized linear mixed-effects model (GLMM) is proposed in the small area for normal and non-normal responses. The empirical best predictor for the small area parameters and the MSPE of the EBP of small area predictors were obtained. Life insurance data analysis demonstrated the superiority of the proposed model compared to the parametric spatial Poisson model. There is still room to explore more for the future. Other estimation methods, such as backfitting and kernel approaches, can be considered for future directions. In this paper, only one nonlinear element was added to the linear predictor of the spatial model. It is worth considering an additive structure for the nonlinear component and developing an additive semiparametric spatial GLMM.
Author Contributions
Conceptualization, S.E.H., D.S., M.R.R., M.A. and H.B.; data curation, S.E.H. and M.R.R.; funding acquisition, M.A.; investigation, S.E.H., D.S., M.R.R. and M.A.; methodology, S.E.H., D.S., M.R.R., M.A. and H.B.; resources, S.E.H. and M.R.R.; software, S.E.H. and H.B.; supervision, D.S., M.R.R. and M.A.; validation, S.E.H., D.S., M.R.R., M.A. and H.B.; visualization, S.E.H., D.S., M.R.R., M.A. and H.B.; formal analysis, S.E.H., D.S., M.R.R. and M.A.; writing—original draft preparation, S.E.H.; writing—review and editing, S.E.H., D.S., M.R.R. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was based upon research supported in part by the National Research Foundation (NRF) of South Africa, SARChI Research Chair UID: 71199, the South African DST-NRF-MRC SARChI Research Chair in Biostatistics (Grant No. 114613), STATOMET at the Department of Statistics at the University of Pretoria and DSI-NRF Centre of Excellence in Mathematical and Statistical Sciences (CoE-MaSS), South Africa. The opinions expressed and conclusions arrived at are those of the authors and are not necessarily attributed to the CoE-MaSS or the NRF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are private, but are available upon request from the corresponding author under valid reasoning.
Acknowledgments
The authors would like to thank two anonymous reviewers for taking the time and efforts to review the manuscript. We sincerely appreciate all your valuable comments and suggestions, which helped us in improving the quality of the manuscript. The authors also would like to sincerely thank Mohammad Hazrati for providing the life insurance data and M. Torabi (University of Manitoba) for providing a Minnesota country map and fruitful discussion.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
We can write:
and,
by combining the fixed effects and spline effects we can write:
Since , , the posterior density is calculated as follows:
where . By using Laplace approximation centered around the point the posterior density is modeled as:
the conditional density of has a normal approximation with conditional mean and conditional variance , given by:
where , is a diagonal matrix with entries and,
where for
□
References
- Morales, D.; Pagliarella, M.C.; Salvatore, R. Small area estimation of poverty indicators under partitioned area-level time models. SORT 2015, 39, 19–34. [Google Scholar]
- Boubeta, M.; Lombardía, M.J.; Morales, D. Empirical best prediction under area-level Poisson mixed models. Test 2016, 25, 548–569. [Google Scholar] [CrossRef]
- Malec, D.; Müller, P. A Bayesian semi-parametric model for small area estimation. IMS Collect. 2008, 3, 223–236. [Google Scholar]
- Chandra, H.; Salvati, N. Small area estimation of proportions under a spatial dependent aggregated level random effects model. Commun. Stat. Theory Methods 2018, 47, 1234–1255. [Google Scholar] [CrossRef]
- Zhu, R.; Buchwald, S.L. Copper-catalyzed oxytrifluoromethylation of unactivated alkenes. J. Am. Chem. Soc. 2012, 134, 12462–12465. [Google Scholar] [CrossRef] [PubMed]
- Torabi, M.; Jiang, J. Estimation of mean squared prediction error of empirically spatial predictor of small area means under a linear mixed model. J. Stat. Plan. Inference 2020, 208, 82–93. [Google Scholar] [CrossRef]
- Torabi, M. Spatial generalized linear mixed models in small area estimation. Can. J. Stat. 2019, 47, 426–437. [Google Scholar] [CrossRef]
- Zeger, S.L.; Diggle, P.J. Semiparametric models for longitudinal data with application to CD4 cell numbers in HIV seroconverters. Biometrics 1994, 50, 689–699. [Google Scholar] [CrossRef] [PubMed]
- Roozbeh, M. Shrinkage ridge estimators in semiparametric regression models. J. Multivar. Anal. 2015, 136, 56–74. [Google Scholar] [CrossRef]
- Roozbeh, M. Robust ridge estimator in restricted semiparametric regression models. J. Multivar. Anal. 2016, 147, 127–144. [Google Scholar] [CrossRef]
- Akdeniz, F.; Roozbeh, M. Generalized difference-based weighted mixed almost unbiased ridge estimator in partially linear models. Stat. Pap. 2019, 60, 1717–1739. [Google Scholar] [CrossRef]
- Taavoni, M.; Arashi, M. Kernel estimation in semiparametric mixed effect longitudinal modeling. Stat. Pap. 2021, 62, 1095–1116. [Google Scholar] [CrossRef]
- Taavoni, M.; Arashi, M.; Wang, W.L.; Lin, T.I. Multivariate t semiparametric mixed-effects model for longitudinal data with multiple characteristics. J. Stat. Comput. Simul. 2021, 91, 260–281. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Lele, S.R.; Dennis, B.; Lutscher, F. Data cloning: Easy maximum likelihood estimation for complex ecological models using Bayesian Markov chain Monte Carlo methods. Ecol. Lett. 2007, 10, 551–563. [Google Scholar] [CrossRef] [PubMed]
- Marchand, É.; Sadeghkhani, A. On predictive density estimation with additional information. Electron. J. Stat. 2018, 12, 4209–4238. [Google Scholar] [CrossRef]
- Sadeghkhani, A.; Peng, Y.; Lin, C.D. A Parametric Bayesian Approach in Density Ratio Estimation. Stats 2019, 2, 189–201. [Google Scholar] [CrossRef]
- Sadeghkhani, A. On Improving the Posterior Predictive Distribution of the Difference Between two Independent Poisson Distribution. Sankhya B 2022, 1–13. [Google Scholar] [CrossRef]
- Prasad, N.N.; Rao, J.N. The estimation of the mean squared error of small-area estimators. J. Am. Stat. Assoc. 1990, 85, 163–171. [Google Scholar] [CrossRef]
- Besag, J.; Kooperberg, C. On conditional and intrinsic autoregressions. Biometrika 1995, 82, 733–746. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).