Solving the Adaptive Cubic Regularization Sub-Problem Using the Lanczos Method

Abstract

The adaptive cubic regularization method solves an unconstrained optimization model by using a three-order regularization term to approximate the objective function at each iteration. Similar to the trust-region method, the calculation of the sub-problem highly affects the computing efficiency. The Lanczos method is an useful tool for simplifying the objective function in the sub-problem. In this paper, we implement the adaptive cubic regularization method with the aid of the Lanczos method, and analyze the error of Lanczos approximation. We show that both the error between the Lanczos objective function and the original cubic term, and the error between the solution of the Lanczos approximation and the solution of the original cubic sub-problem are bounded up by the condition number of the optimal Hessian matrix. Furthermore, we compare the numerical performances of the adaptive cubic regularization algorithm when using the Lanczos approximation method and the adaptive cubic regularization algorithm without using the Lanczos approximation for unconstrained optimization problems. Numerical experiments show that the Lanczos method improves the computation efficiency of the adaptive cubic method remarkably.

1. Introduction

For the unconstrained optimization problem

$$\underset{\mathbf{x}\in {\mathbb{R}}^n}{min}f\left(\mathbf{x}\right),$$

Cartis et al. [1] proposed an adaptive cubic regularization (ACR) algorithm. It is an alternative to classical globalization techniques, which uses a cubic over-estimator of the objective function as a regularization technique, and uses an adaptive parameter $\sigma$ to replace the Lipschitz constant in the cubic Taylor-series model. At each iteration, the objective function is approximated by a cubic function. Numerical experiments in [1] show that the ACR is comparable with trust-region method for small-scale problems. Despite the fact that the method has been shown to have powerful local and global convergence properties, the practicality and efficiency of the adaptive cubic regularization method depend critically on the efficiency of solving its sub-problem at each iteration.

For solving the trust-region sub-problem, many efficient algorithms have been proposed. These algorithms can be grouped into three broad categories: the accurate methods for dense problems, the accurate methods for large-sparse problems, and the approximation methods for large-scale problems. The first category are the accurate methods for dense problems, such as the classical algorithm proposed by Moré and Sorensen [2], which used Newton’s method to iteratively solve symmetric positive definite linear systems via the Cholesky factorization. The second category are the accurate methods for large-sparse problems. For instance, the Lanczos method was employed to solve the large-scale trust-region sub-problem through a parameterized eigenvalue problem [3,4]. Another accurate approach [5], is based on a parametric eigenvalue problem within a semi-definite framework, which employed the Lanczos method for the smallest eigenvalue as a black box. Hager [6] and Erway et al. [7] utilized the subspace projection algorithms for accurate methods. The third category are the approximation methods for large-scale problems. The generalized Lanczos trust-region method (GLTR) [8,9] was proposed as an improved Steihaug [10]-Toint [11] conjugate-gradient method. For the GLTR method, Zhang et al. established prior upper bounds [12] and posterior error bounds [13] for the optimal objective value and the optimal solution between the original trust-region sub-problem and their projected counterparts.

For solving cubic models sub-problems, many algorithms are extensions of trust-region algorithms. Cartis et al. [1] provided the Newton’s method to solve the sub-problem of ACR, which employs Cholesky factorization at each iteration. This method usually applies to small-scale problems. Moreover, Cartis et al. briefly described the process of using the Lanczos method for the ACR sub-problem in [1]. Carmon and Duchi [14] provided the gradient descent method to approximate the cubic-regularized Newton step, and gave the convergence rate. However, the convergence rate of the gradient descent method is worse than that of the Krylov subspace method. Birgin et al. [15] proposed a Newton-like method for unconstrained optimization, whose sub-problem is similar to but different from that of ACR. They introduced a mixed factorization, which is a cheaper factorization than the Cholesky factorization. Brás et al. [16] used the Lanczos method efficiently to solve the sub-problems associated with a special type of cubic models, and also embedded the Lanczos method in a large-scale trust-region strategy. Furthermore, an accelerated first-order method for the ACR sub-problem was developed by Jiang et al. [17].

In this paper, we employ the Lanczos method to solve the sub-problem of the adaptive cubic regularization method (ACRL) for large-scale problems. The ACRL algorithm mainly includes the following three steps. Firstly, the ACRL generates the jth Krylov subspace using the Lanczos method. Next, we project the original sub-problem onto the jth Krylov subspace to obtain a smaller-sized sub-problem. Finally, we solve the resulting smaller-sized sub-problem to get an approximate solution. Such procedures are based on the minimization of the local model of the objective function over a sequence of small-sized sub-spaces. As a result, the ACRL is applicable for large-scale problems. Moreover, we analyze the error of the Lanczos approximation. For unconstrained optimization problems, we perform numerical experiments and compare our method with the method of not using the Lanczos approximation (ACRN).

The outline of this paper is as follows. In Section 2, we introduce the adaptive cubic regularization method and its optimality condition. The method using the Lanczos algorithm to solve the ACR sub-problem is introduced in Section 3. In Section 4, we show the error bounds of the approximate solution and approximate objective value obtained using the ACRL method. Numerical experiments demonstrating the efficiency of the algorithm are given in Section 5. Finally, we give some concluding remarks in Section 6.

2. Preliminaries

Throughout the paper, a matrix is represented by a capital letter, while a lower case bold letter is used for a vector and a lower case letter for a scalar.

The adaptive cubic regularization method [1,18] is proposed by Cartis et al. for unconstrained optimization problems. It mainly uses a cubic over-estimator of the objective function as a regularization technique to calculate the step at each iteration. Assuming that ${\mathbf{x}}_k$ is the current iteration point, the objective function $f\left(\mathbf{x}\right)$ is second-order continuously differentiable, and its Hessian matrix $H\left(\mathbf{x}\right)={\nabla }_{\mathbf{xx}}f\left(\mathbf{x}\right)$ is globally Lipschitz continuous. For any $\mathbf{p}\in {\mathbb{R}}^n$, by expressing the Taylor expansion of $f({\mathbf{x}}_k+\mathbf{p})$ at the point ${\mathbf{x}}_k$, we obtain

$$\begin{array}{cc}\hfill f({\mathbf{x}}_k+\mathbf{p})& =f\left({\mathbf{x}}_k\right)+{\mathbf{p}}^T\mathbf{g}\left({\mathbf{x}}_k\right)+\frac{1}{2}{\mathbf{p}}^{T}H\left({\mathbf{x}}_k\right)\mathbf{p}+{\int }_0^1(1-t){\mathbf{p}}^T[H({\mathbf{x}}_k+t\mathbf{p})-H\left({\mathbf{x}}_k\right)]\mathbf{p}\mathrm{d}t\hfill \\ \hfill & \le f\left({\mathbf{x}}_k\right)+{\mathbf{p}}^T\mathbf{g}\left({\mathbf{x}}_k\right)+\frac{1}{2}{\mathbf{p}}^T{H}_k\mathbf{p}+\frac{1}{6}L{\parallel \mathbf{p}\parallel }^3,\hfill \end{array}$$

(1)

where $\mathbf{g}\left(\mathbf{x}\right)={\nabla }_{\mathbf{x}}f\left(\mathbf{x}\right)$, $H\left(\mathbf{x}\right)={\nabla }_{\mathbf{xx}}f\left(\mathbf{x}\right)$, and L is the Lipschitz constant. Here, and for the remainder of this paper, $\parallel ·\parallel$ denotes an $l_2$ norm. The inequality is obtained by using the Lipschitz property of ${\nabla }_{\mathbf{xx}}f\left(\mathbf{x}\right)$. In [1], Cartis et al. proposed to replace the constant $\frac{1}{2}L$ in Equation (1) with a dynamic positive parameter ${\sigma }_k$. In the cubic regularization model, the matrix $H\left(\mathbf{x}\right)$ needs not to be globally or locally continuous in general. Furthermore, the approximation of $H\left(\mathbf{x}\right)$ by a symmetric matrix $B_k$ is employed at each iteration. Therefore, the model

$$min{m}_k\left(\mathbf{p}\right):=f\left({\mathbf{x}}_k\right)+{\mathbf{p}}^T\mathbf{g}\left({\mathbf{x}}_k\right)+\frac{1}{2}{\mathbf{p}}^T{B}_k\mathbf{p}+\frac{1}{3}{\sigma }_k{\parallel \mathbf{p}\parallel }^3$$

(2)

is used to estimate $f\left({\mathbf{x}}_k\right)$ at each iteration. Then, the adaptive cubic regularization method sub-problem aims to compute a descent direction vector $\mathbf{p}$. Finally, the sub-problem is given with the form of

$$min{q}_k\left(\mathbf{p}\right):={\mathbf{p}}^T{\mathbf{g}}_{\mathbf{k}}+\frac{1}{2}{\mathbf{p}}^T{B}_k\mathbf{p}+\frac{1}{3}{\sigma }_k{\parallel \mathbf{p}\parallel }^3,$$

(3)

in which ${\mathbf{g}}_{\mathbf{k}}$ is short for $\mathbf{g}\left({\mathbf{x}}_k\right).$

Cartis et al. introduced the following global optimality result of ACR, which is similar to the optimality conditions of the trust-region method.

Theorem 1

([1], Theorem 3.1). The vector ${\mathbf{p}}_{opt}$ is a global minimizer of the sub-problem (3) if and only if there is a scalar ${\lambda }_{opt}\ge 0$ satisfying the following system of equations:

$$(B_k+{\lambda }_{opt}I){\mathbf{p}}_{opt}=-{\mathbf{g}}_k,$$

(4)

where ${\lambda }_{opt}={\sigma }_k\parallel {\mathbf{p}}_{opt}\parallel$, and $B_k+{\lambda }_{opt}I$ is a positive semi-definite matrix. If $B_k+{\lambda }_{opt}I$ is positive definite, then ${\mathbf{p}}_{opt}$ is unique.

The optimality condition of the trust-region sub-problem [19] aims to minimize ${\mathbf{g}}_k^T\mathbf{p}+\frac{1}{2}{\mathbf{p}}^T{B}_k\mathbf{p}$ within an $l_2$-norm trust region $\parallel \mathbf{p}\parallel \le {△}_k$, where ${△}_k>0$ is the trust-region radius. For a trust-region sub-problem, the vector ${\mathbf{p}}_{opt}$ satisfies ${\lambda }_{opt}({△}_k-\parallel {\mathbf{p}}_{opt}\parallel )=0$, which means either ${\lambda }_{opt}=0\mathrm{or}\parallel {\mathbf{p}}_{opt}\parallel ={△}_k$. When both the trust-region sub-problem and the cubic regularization sub-problem approximate the original objective function precisely enough, we get ${△}_k={\lambda }_{opt}/{\sigma }_k$ from Theorem 1. Therefore, the parameter ${\sigma }_k$ in the ACR algorithm is inversely proportional to the trust-region radius, and it plays the same role as the trust region-radius, while we adjust the estimation accuracy of the sub-problem.

3. Computation of the ACR Sub-Problem with the Lanczos Method

The Lanczos algorithm [20] was proposed to solve sparse linear systems and to find the eigenvalues of sparse matrices. It builds up an orthogonal basis $Q{}_j=\{{\mathbf{q}}_{\mathbf{0}},{\mathbf{q}}_{\mathbf{1}},\dots ,{\mathbf{q}}_{\mathbf{j}}\}$ for the Krylov space ${\mathcal{K}}_j(B,\mathbf{g}):=\{\mathbf{g},B\mathbf{g},B^2\mathbf{g},\dots ,B^j\mathbf{g}\}.$ By utilizing the orthogonal basis $Q{}_j,$ the original symmetric matrix B is transformed into a tridiagonal matrix.

Normally, the dimension of the ${\mathcal{K}}_j(B,\mathbf{g})$ increases by 1 as j increases by 1. However, the Lanczos process may break down and the dimension of ${\mathcal{K}}_j(B,\mathbf{g})$ stops increasing at a certain j. We define $j_{max}$ as the smallest nonnegative integer, such that the Lanczos process breaks down. If the dimension of the Krylov space is much less than the size of the matrix, it greatly saves the storage space and highly improves the calculation speed by projecting B onto a $j+1$ subspace. Specially, we find a proper $Q_j$ using the Lanczos method, such that $Q_j^{T}B{Q}_j=T_j$ is tridiagonal. We state the procedure in the following algorithm.

Algorithm 1 computes an orthogonal matrix $Q_j=[{\mathbf{q}}_0,{\mathbf{q}}_1,...,{\mathbf{q}}_j]\in {\mathbb{R}}^{n\times (j+1)}$, where

$$T_j=\left(\begin{array}{cccccc}{\alpha }_0& {\beta }_1& & & & \\ {\beta }_1& {\alpha }_1& \ddots & & & \\ & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & {\beta }_{j-1}& \\ & & & {\beta }_{j-1}& {\alpha }_j& \end{array}\right)$$

is tridiagonal. Moreover, it follows directly from Algorithm 1 that

$$Q_j^T{Q}_j=I,T_j=Q_j^{T}B{Q}_j,Q_j^T\mathbf{g}={\beta }_0{\mathbf{e}}_1,$$

(5)

where ${\mathbf{e}}_1$ is the first unit vector of $j+1$ in length.

Algorithm 1 Lanczos algorithm

1: $j=0,{\beta }_0=\parallel \mathbf{g}\parallel ,{\mathbf{r}}_0=\mathbf{g},{\mathbf{q}}_0={\mathbf{r}}_0/\parallel {\mathbf{r}}_0\parallel$ 2: while  $j=0$ or ${\beta }_j\ne 0$  do 3:    ${\mathbf{q}}_{j+1}=r_j/{\beta }_j$ 4:    $j=j+1$ 5:    ${\alpha }_j={\mathbf{q}}_j^{T}B{\mathbf{q}}_j$ 6:    ${\mathbf{r}}_j=(B-{\alpha }_{j}I){\mathbf{q}}_j-{\beta }_{j-1}{\mathbf{q}}_{j-1}$ 7:    ${\beta }_j=\parallel {\mathbf{r}}_j\parallel$ 8: end while

For a large-scale trust-region sub-problem, an effective solution is to approximately calculate it using the Krylov subspace methods. The Lanczos algorithm, as one of the Kryolv subspace methods, was first introduced in [8] for the trust-region method. Similar to the trust-region method, the Lanczos algorithm is also suitable for solving the cubic regularization sub-problem. By employing Algorithm 1, we find

$${\mathbf{p}}_j^k=Q_j^k{\mathbf{u}}_j^k:=\underset{\mathbf{p}\in {\mathcal{K}}_j(B_k,{\mathbf{g}}_k)}{argmin}{q}_k\left(\mathbf{p}\right)\in {\mathcal{K}}_j(B_k,{\mathbf{g}}_k),$$

(6)

where $q_k\left(\mathbf{p}\right)$ is defined by (3). The original sub-problem (3) is transformed into the following sub-problem

$$min{q}_k\left(\mathbf{u}\right):={\beta }_0{\mathbf{u}}^T{e}_1+\frac{1}{2}{\mathbf{u}}^T{T}_j\mathbf{u}+\frac{1}{3}{\sigma }_k{\parallel \mathbf{u}\parallel }_2^3.$$

(7)

Theorem 1 illustrates that $\mathbf{u}$ is a global minimizer of the above sub-problem, if and only if a pair of $(\mathbf{u},\lambda )$ satisfies

$$(T_j+\lambda I)\mathbf{u}=-{\beta }_0{\mathbf{e}}_1\mathrm{and}{\lambda }^2={\sigma }_k^2{\mathbf{u}}^T\mathbf{u},$$

(8)

where $T_j+\lambda I$ is positive semi-definite. Equation (8) can finally be solved by Newton’s method ([1], Algorithm 6.1). Newton’s method for solving the sub-problem requires the eigenvalue decomposition of $B+\lambda I$ for various $\lambda$. When the scale of the original problem is large, it is very expensive to directly use the iterative method.

In summary, an approximation $\mathbf{p}{}_j^k$ of the solution of the ACR sub-problem (3) can be obtained in the following steps. First, we apply j steps of the Lanczos method to the cubic function appearing in (3) to obtain a tridiagonal matrix $T_j$. Then, we use the Newton’s method for a small-size sub-problem with matrix $T_j$ to compute the Lagrange multiplier ${\lambda }_k$ and ${\mathbf{u}}_j^k$. Finally, the matrix $Q_j$ is used to recover ${\mathbf{p}}_j^k$. Thus, it should be noted that the Lanczos vectors need to be saved. We sketch the algorithm as follows.

In the GLTR algorithm, ([8], Theorem 5.8) discussed a restarting strategy for the degenerate case, which means that multiple global solutions ${\mathbf{p}}_{opt}$ exist. Similar to the GLTR, a restarting strategy also applies to the ACRL, although this is just discussed from a theoretical perspective. Therefore, we mainly consider the nondegenerate case in the following analysis.

4. Convergence Analysis

Theorem 1 shows that we aim to seek a pair of $({\mathbf{p}}_{opt},{\lambda }_{opt})$ satisfying

$$(B_k+{\lambda }_{opt}I){\mathbf{p}}_{opt}=-{\mathbf{g}}_k\mathrm{and}{\lambda }_{opt}={\sigma }_k\parallel {\mathbf{p}}_{opt}\parallel .$$

(9)

Then, we have $\parallel {\mathbf{p}}_{opt}\parallel ={\lambda }_{opt}/{\sigma }_k$. In this section, we will analyze the error between the optimal objective function value of the original sub-problem $q_k\left({\mathbf{p}}_{opt}\right)$ and the the optimal objective function value $q_k\left({\mathbf{p}}_j^k\right)$ of the sub-problem in the subspace ${\mathcal{K}}_j(B_k,{\mathbf{g}}_k)$ generated by the Algorithm 2, as well as the distance between ${\mathbf{p}}_{opt}$ and ${\mathbf{p}}_j^k$ under the assumption ${\sigma }_k>0$ when the Equation (9) was satisfied.

We set

$$B_k^{opt}:=B_k+{\lambda }_{opt}I,$$

(10)

which is positive definite in the nondegenerate case. The spectral condition number of $B_k^{opt}$ is

$$\kappa \left(B_k^{opt}\right)=\frac{{\theta }_n+{\lambda }_{opt}}{{\theta }_1+{\lambda }_{opt}},$$

(11)

where ${\theta }_1\le {\theta }_2\le ...\le {\theta }_n$ are the eigenvalues of $B_k$. We define

$$q_k^{opt}\left(\mathbf{p}\right):=\frac{1}{2}{\mathbf{p}}^T{B}_k^{opt}\mathbf{p}+{\mathbf{p}}^T{\mathbf{g}}_k+\frac{1}{3}\sigma {}_k{\parallel \mathbf{p}\parallel }^3=q_k\left(\mathbf{p}\right)+\frac{1}{2}{\lambda }_{opt}{\parallel \mathbf{p}\parallel }^2,$$

(12)

in which $q_k\left(\mathbf{p}\right)$ is defined by (3).

Next, for the vector ${\mathbf{p}}_j^k$ defined in (6), we analyze the errors

$$\parallel {\mathbf{p}}_j^k-{\mathbf{p}}_{opt}\parallel \mathrm{and}|q{}_k\left(\mathbf{p}{}_j^k\right)-q{}_k\left({\mathbf{p}}_{opt}\right)|.$$

Algorithm 2 The ACRL method

1: for  $j=0\dots$  do 2:    Obtain $T_j$ and $Q_j$ from Algorithm 1 3:    Solve the tridiagonal sub-problem (7) to get $\mathbf{u}{}_j^k$ by Newton’s method 4:    $\mathbf{p}{}_j^k=Q_j\mathbf{u}{}_j^k$ 5:    $j=j+1$ 6: end for

Theorem 2.

Suppose (3) is nondegenerate; $\parallel {\mathbf{p}}_{opt}\parallel ={\lambda }_{opt}/\sigma {}_k$ and $\mathbf{p}{}_j^k$ is the jth approximation of ${\mathbf{p}}_{opt}$ generated by ACRL satisfying $\parallel \mathbf{p}{}_j^k\parallel ={\lambda }_{opt}/\sigma {}_k$, then for any nonzero $\tilde{\mathbf{p}}\in {\mathcal{K}}_j(B_k,{\mathbf{g}}_k)$, we have

$$0\le q{}_k\left(\mathbf{p}{}_j^k\right)-q{}_k\left({\mathbf{p}}_{opt}\right)\le 2\parallel B_k^{opt}\parallel \parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}{\parallel }^2$$

(13)

and

$$\parallel \mathbf{p}{}_j^k-{\mathbf{p}}_{opt}\parallel \le 2\kappa \left(B_k^{opt}\right)\parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}\parallel .$$

(14)

Proof. 

It can be seen that $|\parallel \tilde{\mathbf{p}}\parallel -\frac{{\lambda }_{opt}}{\sigma {}_k}|=|\parallel \tilde{\mathbf{p}}\parallel -\parallel {\mathbf{p}}_{opt}\parallel |\le \parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}\parallel$. Then, we obtain

$$|1-\frac{{\lambda }_{opt}}{\sigma {}_k\parallel \tilde{\mathbf{p}}\parallel }|\le \frac{\parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}\parallel }{\parallel \tilde{\mathbf{p}}\parallel }.$$

(15)

Let $\mathbf{s}=\mathbf{v}-{\mathbf{p}}_{opt}$, where

$$\mathbf{v}=\frac{{\lambda }_{opt}}{\sigma {}_k}·\frac{\tilde{\mathbf{p}}}{\parallel \tilde{\mathbf{p}}\parallel }.$$

(16)

Based on (16), we obtain

$$\parallel \mathbf{v}\parallel =\parallel {\mathbf{p}}_{opt}\parallel =\frac{{\lambda }_{opt}}{\sigma {}_k}.$$

(17)

We immediately have

$$\begin{array}{cc}\hfill \parallel \mathbf{s}\parallel =\parallel {\mathbf{p}}_{opt}-\mathbf{v}\parallel & \le \parallel {\mathbf{p}}_{opt}-\tilde{\mathbf{p}}\parallel +\parallel \tilde{\mathbf{p}}-\mathbf{v}\parallel \hfill \\ \hfill & =\parallel {\mathbf{p}}_{opt}-\tilde{\mathbf{p}}\parallel +\parallel \tilde{\mathbf{p}}-\frac{{\lambda }_{opt}}{\sigma {}_k}·\frac{\tilde{\mathbf{p}}}{\parallel \tilde{\mathbf{p}}\parallel }\parallel \hfill \\ \hfill & \le \parallel {\mathbf{p}}_{opt}-\tilde{\mathbf{p}}\parallel +\parallel \tilde{\mathbf{p}}\parallel \left|1-\frac{{\lambda }_{opt}}{\sigma {}_k\parallel \tilde{\mathbf{p}}\parallel }\right|\hfill \\ \hfill & \le 2\parallel {\mathbf{p}}_{opt}-\tilde{\mathbf{p}}\parallel ,\hfill \end{array}$$

(18)

where the last equality follows from (15).

Furthermore, for any $0\le i\le j_{max}-1$,

$$q{}_k\left({\mathbf{p}}_i^k\right)=\underset{\mathbf{p}\in {\mathcal{K}}_i(B_k,{\mathbf{g}}_k)}{min}q{}_k\left(\mathbf{p}\right)\ge q{}_k\left({\mathbf{p}}_{i+1}^k\right)=\underset{\mathbf{p}\in {\mathcal{K}}_{i+1}(B_k,{\mathbf{g}}_k)}{min}q{}_k\left(\mathbf{p}\right)\ge q{}_k\left({\mathbf{p}}_{opt}\right)=minq{}_k\left(\mathbf{p}\right).$$

Therefore, we have

$$\begin{array}{cc}\hfill 0& \le q{}_k\left(\mathbf{p}{}_j^k\right)-q{}_k\left({\mathbf{p}}_{opt}\right)\le q{}_k\left(\mathbf{v}\right)-q{}_k\left({\mathbf{p}}_{opt}\right)=q_k(\mathbf{s}+{\mathbf{p}}_{opt})-q_k\left({\mathbf{p}}_{opt}\right)\hfill \\ \hfill & =\frac{1}{2}{\mathbf{s}}^T{B}_k\mathbf{s}+{\mathbf{s}}^T(B_k{\mathbf{p}}_{opt}+\mathbf{g}{}_k)+\frac{1}{3}\sigma {}_k{(\parallel \mathbf{v}\parallel }^3-\parallel {\mathbf{p}}_{opt}{\parallel }^3)\hfill \\ \hfill & =\frac{1}{2}{\mathbf{s}}^T{B}_k\mathbf{s}-{\lambda }_{opt}{\mathbf{s}}^T{\mathbf{p}}_{opt}\left(\mathrm{by}\left(17\right)\mathrm{and}\left(9\right)\right)\hfill \\ \hfill & =\frac{1}{2}{\mathbf{s}}^T(B_k+{\lambda }_{opt}I)\mathbf{s}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \le \frac{\parallel B_k^{opt}\parallel }{2}{\parallel \mathbf{s}\parallel }^2\le 2\parallel B_k^{opt}\parallel \parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}{\parallel }^2\left(\mathrm{by}\left(18\right)\right).\hfill \end{array}$$

(20)

From

$${\left(\frac{{\lambda }_{opt}}{\sigma {}_k}\right)}^2={\parallel \mathbf{v}\parallel }^2={\parallel \mathbf{s}\parallel }^2+{\parallel {\mathbf{p}}_{opt}\parallel }^2+2{\mathbf{s}}^T{\mathbf{p}}_{opt}$$

and (17), we get ${\mathbf{s}}^T{\mathbf{p}}_{opt}=-{\parallel \mathbf{s}\parallel }^2/2=-{\mathbf{s}}^T\mathbf{s}/2.$ Then, the equality (19) holds. The conclusion in (13) is given based on the above analysis.

Next, we prove the inequality (14). From the definition of $q_k^{opt}$ in (12), for any $\mathbf{p}{}_j^k$, by $\parallel {\mathbf{p}}_{opt}\parallel =\parallel \mathbf{p}{}_j^k\parallel$, we have

$$\begin{array}{cc}\hfill q_k^{opt}\left(\mathbf{p}{}_j^k\right)-q_k^{opt}\left({\mathbf{p}}_{opt}\right)& =\left(q{}_k\left(\mathbf{p}{}_j^k\right)+\frac{1}{2}{\lambda }_{opt}{\parallel \mathbf{p}{}_j^k\parallel }^2\right)-\left(q{}_k\left({\mathbf{p}}_{opt}\right)+\frac{1}{2}{\lambda }_{opt}{\parallel {\mathbf{p}}_{opt}\parallel }^2\right)\hfill \\ \hfill & =q{}_k\left(\mathbf{p}{}_j^k\right)-q{}_k\left({\mathbf{p}}_{opt}\right).\hfill \end{array}$$

(21)

Furthermore, we obtain

$$\begin{array}{cc}\hfill q_k^{opt}\left(\mathbf{p}{}_j^k\right)-q_k^{opt}\left({\mathbf{p}}_{opt}\right)& =\frac{1}{2}{\left(\mathbf{p}{}_j^k\right)}^T{B}_k^{opt}\mathbf{p}{}_j^k+{\left(\mathbf{p}{}_j^k\right)}^T\mathbf{g}{}_k-\frac{1}{2}{\mathbf{p}}_{opt}^T{B}_k^{opt}{\mathbf{p}}_{opt}-{\mathbf{p}}_{opt}^T\mathbf{g}{}_k\hfill \\ \hfill & =\frac{1}{2}{(\mathbf{p}{}_j^k-{\mathbf{p}}_{opt})}^T{B}_k^{opt}(\mathbf{p}{}_j^k-{\mathbf{p}}_{opt}),\hfill \end{array}$$

where the last equality follows from (9) and (10). Then,

$$q_k^{opt}\left(\mathbf{p}{}_j^k\right)-q_k^{opt}\left({\mathbf{p}}_{opt}\right)\ge \frac{1}{2}({\theta }_1+{\lambda }_{opt}){\parallel \mathbf{p}{}_j^k-{\mathbf{p}}_{opt}\parallel }^2.$$

(22)

Combining (13), (21), and (22), we get

$$\frac{1}{2}({\theta }_1+{\lambda }_{opt})\parallel \mathbf{p}{}_j^k-{\mathbf{p}}_{opt}{\parallel }^2\le q{}_k\left(\mathbf{p}{}_j^k\right)-q{}_k\left({\mathbf{p}}_{opt}\right)\le 2\parallel B_k^{opt}\parallel \parallel \tilde{\mathbf{p}}-{\mathbf{p}}_{opt}{\parallel }^2.$$

The inequality (14) holds. □

5. Numerical Experiments

In order to show the efficiency of the Lanczos for improving the adaptive cubic regularization algorithm, we perform the following two numerical experiments. In this section, we compare the numerical performances of the adaptive cubic regularization algorithm when using the Lanczos approximation method (ACRL) and the adaptive cubic regularization algorithm by just using Newton’s method (ACRN) for unconstrained optimization problems.

The ACRL and ACRN algorithms are implemented with the following parameters

$${\eta }_1=0.1,{\eta }_2=0.8,{\gamma }_1=0.25,{\gamma }_2=1.2,\mathrm{and}{\gamma }_3=2.$$

Convergence in both algorithms for the sub-problem occurs as soon as

$$\parallel \nabla q_k\left({\mathbf{p}}_j^k\right)\parallel \le min\left(0.0001,\frac{\parallel {\mathbf{p}}_j^k\parallel }{max(1,{\sigma }_k)}\right)\parallel \nabla q_k\left(0\right)\parallel$$

or if more than the maximum number of iterations has been performed, which we set to 2000. All numerical experiments in this paper were performed on a laptop with i5-10210U CPU at 1.60 GHz and 16.0 GB of RAM.

Example 1

(Generalized Rosenbrock function [21]). The Generalized Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is defined as follows:

$$f\left(\mathbf{x}\right)=\sum _{i=1}^{n-1}c{({\mathbf{x}}_{i+1}-{\mathbf{x}}_i^2)}^2+{(1-{\mathbf{x}}_i)}^2,c=100.$$

(23)

From the (23), the solution ${\mathbf{x}}^{★}$ is obviously ${(1,1,...,1)}^T$, and the minimum $f\left({\mathbf{x}}^{★}\right)=0$.

In Table 1, we show the results of the ACRL and the ACRN for computing the minima of the Generalized Rosenbrock function, with variables from 10 to 2000. In addition to the dimensions of the Generalized Rosenbrock function, we give the number of iterations (“Iter.”), the total CPU time required in seconds and the relative error between the computational result and the exact minimum (“Err.”). It can be seen that, using the Lanczos method to solve the adaptive cubic regularization sub-problem of Generalized Rosenbrock function is much more efficient than not using the Lanczos method. Moreover, it is not only faster, but also more accurate to calculate, especially when the scale is relatively large.

Table 1. Results for computing the minima of the Generalized Rosenbrock function.

n	ACRL			ACRN
	Iter.	Time (s)	Err.	Iter.	Time (s)	Err.
10	11	0.01	4.05 $\times {10}^{-14}$	8	0.01	4.85 $\times {10}^{-11}$
500	17	0.05	8.33 $\times {10}^{-13}$	12	0.88	1.10 $\times {10}^{-13}$
1000	21	0.27	7.35 $\times {10}^{-13}$	12	4.56	5.53 $\times {10}^{-11}$
5000	23	6.24	1.47 $\times {10}^{-15}$	9	191.95	1.41 $\times {10}^{-12}$
10,000	21	20.33	2.42 $\times {10}^{-15}$	11	1524.88	6.29 $\times {10}^{-13}$
20,000	21	77.8	6.90 $\times {10}^{-13}$	14	16,166.62	3.03 $\times {10}^{-11}$

Example 2

(Eigenvalues of tensors arising from hypergraphs). Next, we consider the problem of computing extreme eigenvalues of sparse tensors arising from a hypergraph. An adaptive cubic regularization method on a Stiefel manifold named ACRCET is proposed to solve the eigenvalues of tensors [22]. We compare the numerical performances of the ACRL and the ACRN method when applying to the sub-problem of ACRCET. Before going to the experiment part, we first introduce the concepts of tensor eigenvalues and hypergraphs.

A real mth order n-dimensional tensor $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$ has $n^m$ entries:

$$\left\{a_{i_1{i}_2\cdots i_m}\right\}$$

for $i_j\in \{1,2,\cdots ,n\}\mathrm{and}j\in \{1,2,\cdots ,m\}.$ If the value of $\left\{a_{i_1{i}_2\cdots i_m}\right\}$ is invariable under any permutation of its indices, $\mathcal{A}$ is a symmetric tensor.

Qi [23] defined a scalar $\Lambda \in \mathbb{R}$ as a Z-eigenvalue of $\mathcal{A}$ and a nonzero vector $\mathbf{x}\in {\mathbb{R}}^n$ as its associated Z-eigenvector if they satisfy

$$\mathcal{A}{\mathbf{x}}^{m-1}=\Lambda \mathbf{x}\mathrm{and}{\mathbf{x}}^T\mathbf{x}=1.$$

Definition 1

(Hypergraph). A hypergraph is defined as $G=(V,E)$, where $V=\{1,2,\cdots ,n\}$ is the vertex set and $E=\{e_1,e_2,\cdots ,e_m\}$ is the edge set for $e_p\subset V,p=1,2,\cdots ,m.$ If $|e_p|=r\ge 2$ for $p=1,2,\cdots ,m$ and $e_i\ne e_j$ when $i\ne j$, we call G an r-uniform hypergraph.

For each vertex $i\in V$, the degree $d\left(i\right)$ is defined as

$$d\left(i\right)=|\{e_p:i\in e_p,e_p\in E\}|.$$

Definition 2

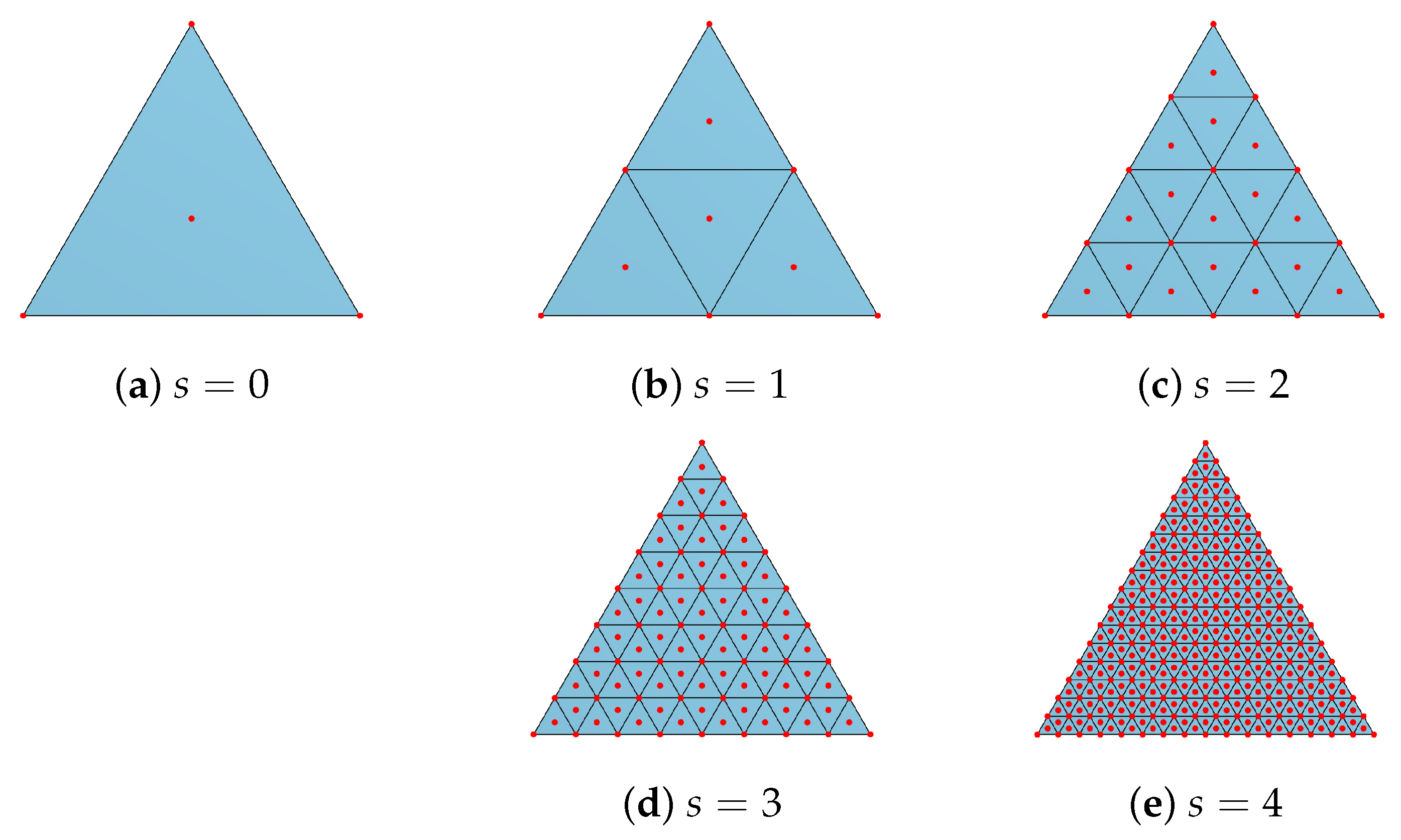
(adjacency tensor and Laplacian tensor). The adjacency tensor $\mathcal{A}\in {\mathbb{R}}^{[m,n]}$ of a m-uniform hypergraph G is a symmetric tensor with entries

$$a_{i_1\cdots i_m}=\left\{\begin{array}{cc}\frac{1}{(m-1)!}\hfill & if\{i_1,\cdots ,i_m\}\in E,\hfill \\ 0\hfill & otherwise.\hfill \end{array}\right.$$

For an m-uniform hypergraph G, the degree tensor $\mathcal{D}$ is a diagonal tensor whose ith diagonal element is $d\left(i\right)$. Then, the Laplacian tensor $\mathcal{L}$ is defined as

$$\mathcal{L}=\mathcal{D}-\mathcal{A}.$$

A triangle has three vertices and three edges. In this example, we subdivide the triangles by connecting the midpoints of each edge of the triangles. Then, the s-order subdivision of a triangle has $4^s$ faces, and each face is a triangle. As shown in Figure 1, three vertices as well as the center of the triangles are regarded as an edge of a 4-uniform graph $G_T^s$.

Figure 1. Four-uniform hypergraphs: subdivision of a triangle.

We compute the largest Z-eigenvalue of the Laplacian tensor $\mathcal{L}\left(G_T^s\right)$ via the ACRCET method, using ACRL and ACRN, respectively. In each run, 10 points on the unit sphere are randomly chosen, and 10 estimated eigenvalues are calculated. Then, we take the best one as the estimated largest eigenvalue. For different subdivision order $s,$ the computation results, including the estimated largest Z-eigenvalue, the total number of iterations, and the total CPU time (in seconds) of the 10 runs are reported in Table 2.

Table 2. Results for finding the largest Z-eigenvalues of $\mathcal{L}\left(G_T^s\right)$.

			ACRL			ACRN
s	m	n	Iter.	Time (s)	${\mathit{\lambda }}_{max}^{\mathit{Z}}\left(\mathcal{L}\left({\mathit{G}}_{\mathit{T}}^{\mathit{s}}\right)\right)$	Iter.	Time (s)	${\mathit{\lambda }}_{max}^{\mathit{Z}}\left(\mathcal{L}\left({\mathit{G}}_{\mathit{T}}^{\mathit{s}}\right)\right)$
1	10	4	53	0.04	3	53	0.05	3
2	31	16	57	0.05	6	56	0.17	6
3	109	64	55	0.08	6	54	0.79	6
4	409	256	56	0.78	6	54	13.05	6
5	1585	1024	67	13.02	6	66	727.77	6
6	6241	4096	81	236.35	6	85	103,900	6

It can be seen that both the ACRL and the ACRN find all the largest eigenvalues. However, the ACRL takes almost no time compared to the ACRN. When $s=6$, the ACRL method only costs 236 s, while the ACRN needs 103,900 s. The numerical comparison between the ACRL and the ACRN verifies that the Lanczos method dramatically accelerates the running speed when solving the ACR sub-problem (3), and is powerful for large-scale problems.

6. Conclusions

In this paper, we have used the Lanczos method to solve the adaptive cubic regularization method sub-problem (ACRL). The ACRL method first projects a large-scale ACR sub-problem (3) into a much smaller sub-problem (7) using the Lanczos method, and then solves the smaller sub-problem (7) using the Newton’s method. For the convergence analysis, we also established prior error bounds on the differences between the approximate objective value $q{}_k\left({\mathbf{p}}_j^k\right)$ and the approximate solution ${\mathbf{p}}_j^k$ with its corresponding optimal ones. Numerical experiments illustrate that the ACRL method greatly improves the computing efficiency and performs well, even for large-scale problems.