Approximate Closed-Form Solutions for the Rabinovich System via the Optimal Auxiliary Functions Method

Abstract

Based on some geometrical properties (symmetries and global analytic first integrals) of the Rabinovich system the closed-form solutions of the equations have been established. The chaotic behaviors are excepted. Moreover, the Rabinovich system is reduced to a nonlinear differential equation depending on an auxiliary unknown function. The approximate analytical solutions are built using the Optimal Auxiliary Functions Method (OAFM). The advantage of this method is to obtain accurate solutions for special cases, with only an analytic first integral. An important output is the existence of complex eigenvalues, depending on the initial conditions and physical parameters of the system. This approach was not still analytically emphasized from our knowledge. A good agreement between the analytical and corresponding numerical results has been performed. The accuracy of the obtained results emphasizes that this procedure could be successfully applied to more dynamic systems with these geometrical properties.

1. Introduction

The Rabinovich system was first studied in [1] with the analysis of a concrete realization in a magnetoactive non-isothermal plasma. This system is a dynamical system of three resonantly coupled waves, parametrically excited [2].

There are some previous papers where are pointed out the relevance for engineering applications of the Rabinovich system, such as: in [3] is reported the existence of hidden attractors and applied to coupled Chua circuits; the integrals of motion were characterized by using the method of characteristic curves in [4]; some relevant dynamical and geometrical properties [5]; the Darboux polynomials [6]. Numerical simulations were investigated in [7] showing that the Rabinovich chaotic system can be regulated to its equilibrium points in the state space.

The synchronization or optimization of nonlinear system performance, secure communications, and other applications in electrical engineering or medicine are based on the study of dynamical systems. Ref. [8] explored the stabilization of the T system via linear controls, and [9] studied the Rikitake two-disk dynamic system and applied it in modeling the reversals of the Earth’s magnetic field [10,11]. Some geometrical properties of the dynamical systems: the integral deformations, the equilibria points, Hamiltonian realization was analyzed in [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39].

The symmetry represents an important geometrical property of the dynamical system. As it is well known, a dynamic system admits symmetry with respect to the origin point $O(0,0,0)$ or with the $Oz-$ axis or the plan $z=0$ if it is invariant under the transformation $(x,y,z)\to (-x,-y,-z)$, respectively $(x,y,z)\to (-x,-y,z)$ and $(x,y,z)\to (x,y,-z)$.

The paper is organized as follows: Section 2 provides a brief description of the geometrical properties and the closed-form solutions of the Rabinovich system. Section 3 is dedicated to building approximate analytic solutions using the OAFM technique. The presented analysis and the corresponding numerical results are discussed in the Numerical results and Discussions sections. Here, we observe the importance and precision of the method by means of the convergence-control parameters. The accuracy and the good agreement between the results are highlighted in the Conclusion section.

2. The Rabinovich System

2.1. Global Analytic First Integrals and Hamilton-Poisson Realization

The Rabinovich system has the form (see [3,4,5,6,7,12,28,29,40]):

$$\left\{\begin{array}{c}\dot{x}=yz-{\alpha }_{1}x+\beta y\hfill \\ \dot{y}=-x·z-{\alpha }_{2}y+\beta x\hfill \\ \dot{z}=x·y-{\alpha }_{3}z\hfill \end{array}\right.,$$

(1)

where the unknown functions x, y and z depend on $t>0$, $(\beta ,{\alpha }_1,{\alpha }_2,{\alpha }_3)\in {\mathbf{R}}^4$ and $\dot{x}$ denotes the derivative of the function x with respect to t.

Remark 1.

Is easy to see that the considered system admits a symmetry with respect to $Oz$- axis, for $\beta \ne 0$ and symmetries with respect to $Oz$, $Ox$, $Oy$ axes, for $\beta =0$, respectively.

In this section, we also recall some geometrical properties of the system (1) [12].

The global analytic first integrals of the Rabinovich system are obtained in [40].

The considered system has a Hamilton-Poisson realization with the Hamiltonian and the Casimir given by $H(x,y,z)=\frac{1}{4}(x^2-z^2)$ and $C(x,y,z)=\frac{1}{4}(x^2+2y^2+z^2)$, respectively, for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$; $H(x,y,z)=-\frac{\beta }{2}{x}^2+\frac{\beta }{2}{y}^2+\beta z^2$ and $C(x,y,z)=-\frac{1}{4\beta }{x}^2-\frac{1}{4\beta }{y}^2+z$, for $\beta \ne 0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$.

There exist three isolated cases:

$H(x,y,z)=x^2-z^2-2\beta z$, for $\beta \in \mathbf{R}$, ${\alpha }_1=0$, ${\alpha }_2\ne 0$, ${\alpha }_3=0$;

$H(x,y,z)=y^2+z^2-2\beta z$, for $\beta \in \mathbf{R}$, ${\alpha }_1\ne 0$, ${\alpha }_2=0$, ${\alpha }_3=0$;

$H(x,y,z)=x^2+y^2$, for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3\ne 0$.

Remark 2.

For the initial conditions

$$x\left(0\right)=x_0,y\left(0\right)=y_0,z\left(0\right)=z_0,$$

(2)

the phase curves of dynamics (1) are the intersections of the surfaces $-\frac{\beta }{2}{x}^2+\frac{\beta }{2}{y}^2+\beta z^2=-\frac{\beta }{2}{x}_0^2+\frac{\beta }{2}{y}_0^2+\beta z_0^2\mathrm{and}-\frac{1}{4\beta }{x}^2-\frac{1}{4\beta }{y}^2+z=-\frac{1}{4\beta }{x}_0^2-\frac{1}{4\beta }{y}_0^2+z_0,\mathrm{for}\beta \ne 0,{\alpha }_1=0,{\alpha }_2=0,{\alpha }_3=0$;

$x^2-z^2=x_0^2-z_0^2\mathrm{and}{x}^2+2y^2+z^2=x_0^2+2y_0^2+z_0^2,\mathrm{for}\beta =0,{\alpha }_1=0,{\alpha }_2=0,{\alpha }_3=0$, respectively.

2.2. Closed-Form Solutions

In this section, we establish the closed-form solutions of the system Equation (1) using previous results, considering the real values for the physical parameters as $\beta$, $a_1$, $a_2$, $a_3$.

(i) 

$\beta \ne 0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$.

Using the transformations:

$$\left\{\begin{array}{c}y\left(t\right)=\frac{R}{4\beta }·\frac{2v\left(t\right)}{1+v^2\left(t\right)}\hfill \\ z\left(t\right)=\beta +\frac{R}{4\beta }·\frac{1-v^2\left(t\right)}{1+v^2\left(t\right)}\hfill \end{array}\right.,$$

(3)

where $R=4\sqrt{\beta ·(H_{\beta }-2{\beta }^2·C_{\beta }+{\beta }^3)}$, $H_{\beta }=-\frac{\beta }{2}{x}_0^2+\frac{\beta }{2}{y}_0^2+\beta z_0^2$, $C_{\beta }=-\frac{1}{4\beta }{x}_0^2-\frac{1}{4\beta }{y}_0^2+z_0$, $v\left(t\right)$ is an unknown smooth function.

The third equation from Equation (1) yields to

$$x\left(t\right)=-\frac{2\dot{v}\left(t\right)}{1+v^2\left(t\right)}.$$

(4)

Now, using the first equation from Equation (1) we obtain:

$$\ddot{v}\left(t\right)·(1+v^2\left(t\right))-2v\left(t\right)·{\left(\dot{v}\left(t\right)\right)}^2+\frac{R^2}{16{\beta }^2}·v\left(t\right)·(1-v^2\left(t\right))+\frac{R}{2}·v\left(t\right)·(1+v^2\left(t\right))=0.$$

(5)

Using the initial conditions Equation (2) and the relations Equations (3) and (4) the initial conditions $v\left(0\right)$ and $\dot{v}\left(0\right)$ become:

$$v\left(0\right)=\sqrt{\frac{1-\frac{4\beta }{R}·(z_0-\beta )}{1+\frac{4\beta }{R}·(z_0-\beta )}},\dot{v}\left(0\right)=-\frac{x_0}{2}·\left(1+\frac{1-\frac{4\beta }{R}·(z_0-\beta )}{1+\frac{4\beta }{R}·(z_0-\beta )}\right).$$

(6)

Remark 3.

If the function $v\left(t\right)$ is the exact solution of the problem given by Equations (5) and (6), then the relations Equations (3) and (4) give closed-form solution of the system Equation (1). If the function $v\left(t\right)$ is an analytic approximate solution of the problem given by Equations (5) and (6), then the relations Equations (3) and (4) give approximate closed-form solution of the system Equation (1).

(ii) 

$\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$.

For this particular case, the system (1) reduces to

$$\left\{\begin{array}{c}\dot{x}=yz\hfill \\ \dot{y}=-x·z\hfill \\ \dot{z}=x·y\hfill \end{array}\right..$$

(7)

Making the transformations:

$$\left\{\begin{array}{c}x\left(t\right)=sign\left(x_0\right)·R·\frac{1}{\sqrt{1+u^2\left(t\right)}}\hfill \\ y\left(t\right)=sign\left(y_0\right)·R·\frac{u\left(t\right)}{\sqrt{1+u^2\left(t\right)}}\hfill \end{array}\right.,$$

(8)

where $R=\sqrt{x_0^2+y_0^2}$ and $u\left(t\right)$ is an unknown smooth function, then the second equation from Equation (7) yields to

$$z\left(t\right)=-\frac{sign\left(y_0\right)}{sign\left(x_0\right)}·\frac{\dot{u}\left(t\right)}{1+u^2\left(t\right)}.$$

(9)

Now, using the third equation from Equation (7) we obtain:

$$\ddot{u}\left(t\right)-\frac{2u\left(t\right)}{1+u^2\left(t\right)}·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)=0.$$

(10)

Using the initial conditions Equation (2) and the relations Equations (3) and (4) the initial conditions $u\left(0\right)$ and $\dot{u}\left(0\right)$ become:

$$u\left(0\right)=\frac{sign\left(y_0\right)}{sign\left(x_0\right)}·\frac{y_0}{x_0},\dot{u}\left(0\right)=-sign\left(z_0\right)·z_0·\left(1+u^2\left(0\right)\right).$$

(11)

Remark 4.

If the function $u\left(t\right)$ is the exact solution of the problem given by Equations (10) and (11), then the relations Equations (8) and (9) give closed-form solution of the system Equation (7). If the function $v\left(t\right)$ is an analytic approximate solution of the problem given by Equations (5) and (6), then the relations Equations (3) and (4) give approximate closed-form solution of the system Equation (7).

(iii) 

$\beta \in \mathbf{R}$, ${\alpha }_1=0$, ${\alpha }_2\ne 0$, ${\alpha }_3=0$.

The closed-form solutions can be put in the following form:

$$\left\{\begin{array}{c}x\left(t\right)=R·\frac{2·u\left(t\right)}{1-u^2\left(t\right)}\hfill \\ z\left(t\right)=-\beta +R·\frac{1+u^2\left(t\right)}{1-u^2\left(t\right)}\hfill \end{array}\right.,$$

(12)

where $R=\sqrt{{(z_0+\beta )}^2-x_0^2}$, for ${(z_0+\beta )}^2-x_0^2>0$, and

$$\left\{\begin{array}{c}x\left(t\right)=R·\frac{1+u^2\left(t\right)}{1-u^2\left(t\right)}\hfill \\ z\left(t\right)=-\beta +R·\frac{2·u\left(t\right)}{1-u^2\left(t\right)}\hfill \end{array}\right.,$$

(13)

where $R=\sqrt{x_0^2-{(z_0+\beta )}^2}$, for $x_0^2-{(z_0+\beta )}^2>0$, respectively.

Then the third equation from Equation (1) yields to

$$y\left(t\right)=\frac{2\dot{u}\left(t\right)}{1-u^2\left(t\right)}.$$

(14)

The unknown smooth function $u\left(t\right)$ is the solution of the nonlinear problem:

$$\left\{\begin{array}{c}\ddot{u}\left(t\right)·(1-u^2\left(t\right))+2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1+u^2\left(t\right))-\hfill \\ -2\beta ·R·u\left(t\right)·(1-u^2\left(t\right))+{\alpha }_2·(1-u^2\left(t\right))·\dot{u}\left(t\right)=0\hfill \\ u\left(0\right)=sign\left(x_0\right)·\frac{x_0}{z_0+\beta +R},\dot{u}\left(0\right)=\frac{y_0}{2}·\left(1-u^2\left(0\right)\right).\hfill \end{array}\right.$$

(15)

(iv) 

$\beta \in \mathbf{R}$, ${\alpha }_1\ne 0$, ${\alpha }_2=0$, ${\alpha }_3=0$.

The closed-form solutions can be put in the following form:

$$\left\{\begin{array}{c}y\left(t\right)=R·\frac{2·u\left(t\right)}{1+u^2\left(t\right)}\hfill \\ z\left(t\right)=\beta +R·\frac{1-u^2\left(t\right)}{1+u^2\left(t\right)}\hfill \end{array}\right.,$$

(16)

where $R=\sqrt{{(z_0-\beta )}^2+y_0^2}$. Then the third equation from Equation (1) yields to

$$x\left(t\right)=-\frac{2\dot{u}\left(t\right)}{1+u^2\left(t\right)}.$$

(17)

The unknown smooth function $u\left(t\right)$ is the solution of the nonlinear problem:

$$\left\{\begin{array}{c}\ddot{u}\left(t\right)·(1+u^2\left(t\right))-2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1-u^2\left(t\right))+\hfill \\ +2\beta ·R·u\left(t\right)·(1+u^2\left(t\right))+{\alpha }_1·(1+u^2\left(t\right))·\dot{u}\left(t\right)=0\hfill \\ u\left(0\right)=\sqrt{\frac{R-(z_0-\beta )}{R+(z_0-\beta )}},\dot{u}\left(0\right)=-\frac{x_0}{2}·\left(1+u^2\left(0\right)\right).\hfill \end{array}\right.$$

(18)

(v) 

$\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3\ne 0$.

The closed-form solutions can be put in the following form:

$$\left\{\begin{array}{c}x\left(t\right)=R·cos\left(u\right(t\left)\right)\hfill \\ y\left(t\right)=R·sin\left(u\right(t\left)\right)\hfill \end{array}\right.,$$

(19)

where $R=\sqrt{x_0^2+y_0^2}$. Then the first equation from Equation (1) yields to

$$z\left(t\right)=-\dot{u}\left(t\right).$$

(20)

The unknown smooth function $u\left(t\right)$ is the solution of the nonlinear problem:

$$\left\{\begin{array}{c}\ddot{u}\left(t\right)+{\alpha }_3·\dot{u}\left(t\right)+\frac{R^2}{2}·sin(2·u\left(t\right))=0\hfill \\ u\left(0\right)=arctan\frac{y_0}{x_0},\dot{u}\left(0\right)=-z_0.\hfill \end{array}\right.$$

(21)

In the literature, there are several analytical methods for solving the nonlinear differential problem is given by Equations (5), (6), (10), (11), (15), (18) and (21) such as: the Optimal Homotopy Asymptotic Method (OHAM) [41,42,43], the Optimal Homotopy Perturbation Method (OHPM) [44,45], the Optimal Variational Iteration Method (OVIM) [46], the Optimal Iteration Parametrization Method (OIPM) [47], the Polynomial Least Squares Method [48], the Least Squares Differential Quadrature Method [49], the Multiple Scales Technique [50], the Function Method [51], the Homotopy Perturbation Method (HPM) and the Homotopy Analysis Method (HAM) [52], the Variational Iteration Method (VIM) [53].

In this work the approximate analytic solutions of the nonlinear differential problem given by Equations (5), (6), (10), (11), (15), (18) and (21) are analytically solved using the Optimal Auxiliary Functions Method (OAFM).

3. Approximate Analytic Solutions via OAFM

We introduce the basic ideas of the OAFM by considering Equation (5) with the initial conditions given by Equation (6) in general form as in [43,54]:

$${\displaystyle \mathcal{L}\left[\overline{v}\left(t\right)\right]+g\left(t\right)+\mathcal{N}\left[\overline{v}\left(t\right)\right]=0,}$$

(22)

where $\mathcal{L}$ is a linear operator, g is a known function and $\mathcal{N}$ is a given nonlinear operator, t denotes the independent variable and the approximate solution $\overline{v}\left(t\right)$ is written with just two components in the form:

$${\displaystyle \overline{v}\left(t\right)=v_0\left(t\right)+v_1(t,C_i),i=1,2,\dots ,s.}$$

(23)

The initial approximation $v_0\left(t\right)$ and the first approximation $v_1(t,C_i)$ will be determined as follows.

Firstly, the Equation (22) becomes

$$\begin{array}{c}{\displaystyle \mathcal{L}\left[v_0\left(t\right)\right]+\mathcal{L}\left[v_1(t,C_i)\right]+g\left(t\right)+\mathcal{N}\left[v_0\left(t\right)+v_1(t,C_i)\right]=0.}\hfill \end{array}$$

(24)

The linear operator $\mathcal{L}$ could be chosen by the form [54]:

$${\displaystyle \mathcal{L}\left(v\left(t\right)\right)=\ddot{v}\left(t\right)+{\omega }_0^{2}v\left(t\right),}$$

(25)

where ${\omega }_0>0$ is an unknown parameter.

From Equation (24) using Equation (25) and initial conditions Equation (6), the initial approximation $v_0\left(t\right)$ is solution of the problem ($g\left(t\right)=0$):

$$\begin{array}{c}{\displaystyle \ddot{v}\left(t\right)+{\omega }_0^{2}v\left(t\right)=0,v\left(0\right)=\sqrt{\frac{1-\frac{4\beta }{R}·(z_0-\beta )}{1+\frac{4\beta }{R}·(z_0-\beta )}},}\hfill \\ {\displaystyle \dot{v}\left(0\right)=-\frac{x_0}{2}·\left(1+\frac{1-\frac{4\beta }{R}·(z_0-\beta )}{1+\frac{4\beta }{R}·(z_0-\beta )}\right),}\hfill \end{array}$$

(26)

namely:

$${\displaystyle v_0\left(t\right)=v\left(0\right)·cos{\omega }_{0}t+\frac{\dot{v}\left(0\right)}{{\omega }_0}·sin{\omega }_{0}t.}$$

(27)

The nonlinear operator $\mathcal{N}\left(v\left(t\right)\right)$ is obtained from Equations (5) and (25):

$${\displaystyle \mathcal{N}\left(v\left(t\right)\right)=-{\omega }_0^{2}v\left(t\right)+\ddot{v}\left(t\right)·v^2\left(t\right)-2v\left(t\right)·{\left(\dot{v}\left(t\right)\right)}^2+\frac{R^2}{16{\beta }^2}·v\left(t\right)·(1-v^2\left(t\right))+\frac{R}{2}·v\left(t\right)·(1+v^2\left(t\right)),}$$

(28)

and can be expanded in the form

$$\begin{array}{c}{\displaystyle \mathcal{N}\left[v_0\left(t\right)+v_1(t,C_i)\right]=}\hfill \\ {\displaystyle =\mathcal{N}\left[v_0\left(t\right)\right]+\sum _{k=1}^{\infty }\frac{v_1^k(t,C_i)}{k!}{\mathcal{N}}^{\left(k\right)}\left[v_0\left(t\right)\right].}\hfill \end{array}$$

(29)

By means of the Equations (27) and (28) it is obtain

$${\displaystyle \mathcal{N}\left(v_0\left(t\right)\right)=M_1·cos{\omega }_{0}t+N_1·sin{\omega }_{0}t+M_2·cos3{\omega }_{0}t+N_2·sin3{\omega }_{0}t,}$$

(30)

where

$$\begin{array}{c}{\displaystyle M_1=-{\omega }_0^{2}M-\frac{5M{\omega }_0^2}{4}(M^2+N^2)+\frac{R^{2}M}{64{\beta }^2}(4-3M^2-3N^2)+\frac{RM}{8}(4+3M^2+3N^2),}\hfill \\ {\displaystyle N_1=-{\omega }_0^{2}N-\frac{5N{\omega }_0^2}{4}(M^2+N^2)+\frac{R^{2}N}{64{\beta }^2}(4-3M^2-3N^2)+\frac{RM}{8}(4-3M^2+3N^2),}\hfill \\ {\displaystyle M_2=-\frac{M{\omega }_0^2}{4}(3N^2-M^2)+\frac{R^{2}M}{64{\beta }^2}(3N^2-M^2)+\frac{RM}{8}(M^2-3N^2),}\hfill \\ {\displaystyle N_2=-\frac{N{\omega }_0^2}{4}(N^2-3M^2)+\frac{R^{2}N}{64{\beta }^2}(N^2-3M^2)+\frac{RN}{8}(3M^2-N^2),}\hfill \\ {\displaystyle M=v\left(0\right),N=\frac{\dot{v}\left(0\right)}{{\omega }_0}.}\hfill \end{array}$$

(31)

Using Equations (24), (25) and (27)–(29), the first approximation $v_1\left(t\right)$ is solution of the problem:

$$\begin{array}{c}{\displaystyle \mathcal{L}\left[v_1(t,C_i)\right]+A_1\left[v_0\left(t\right),C_i\right]\mathcal{N}\left[v_0\left(t\right)\right]+}\hfill \\ {\displaystyle +A_2\left[v_0\left(t\right),C_j\right]=0,}\hfill \end{array}$$

(32)

$${\displaystyle v_1(0,C_i)=0,{\dot{v}}_1(0,C_i)=0,}$$

(33)

where $A_1$ and $A_2$ are two arbitrary auxiliary functions depending on the initial approximation $v_0\left(t\right)$ and several unknown parameters $C_i$ and $C_j$, $i=1,2,\dots ,p$, $j=p+1,p+2,\dots ,s$.

Taking into account of the Equations (32), (25) and (30), the first approximation is obtained from the equation:

$$\begin{array}{c}{\displaystyle {\ddot{v}}_1+{\omega }_0^2{v}_1+A_2(cos{\omega }_{0}t,sin{\omega }_{0}t,cos3{\omega }_{0}t,sin3{\omega }_{0}t,C_j)+A_1(cos{\omega }_{0}t,sin{\omega }_{0}t,cos3{\omega }_{0}t,sin3{\omega }_{0}t,C_i)\times }\hfill \\ {\displaystyle \times (M_1·cos{\omega }_{0}t+N_1·sin{\omega }_{0}t+M_2·cos3{\omega }_{0}t+N_2·sin3{\omega }_{0}t)=0,}\hfill \end{array}$$

(34)

with the initial conditions

$${\displaystyle v_1\left(0\right)=0,{\dot{v}}_1\left(0\right)=0.}$$

(35)

There is an opportunity to choose the optimal auxiliary functions $A_1$ and $A_2$ in the following forms:

$${\displaystyle A_1\left[v_0\left(t\right),C_i\right]=\sum _{k=1}^{N_{max}-1}{a}_k^{\left(1\right)}·cos(2k+1){\omega }_{0}t+b_k^{\left(1\right)}·sin(2k+1){\omega }_{0}t,}$$

(36)

$$\begin{array}{c}{\displaystyle A_2\left[v_0\left(t\right),D_j\right]=\sum _{k=1}^{N_{max}}{a}_k^{\left(2\right)}·cos(2k+1){\omega }_{0}t+b_k^{\left(2\right)}·sin(2k+1){\omega }_{0}t,}\hfill \end{array}$$

(37)

where the convergence-control parameters $C_i\in \left\{a_k^{\left(1\right)}\right|k=\overline{1,N_{max}-1}\}\cup \left\{b_k^{\left(1\right)}\right|k=\overline{1,N_{max}-1}\}$,

$D_j\in \left\{a_k^{\left(2\right)}\right|k=\overline{1,N_{max}}\}\cup \left\{b_k^{\left(2\right)}\right|k=\overline{1,N_{max}}\}$, $N_{max}>2$ is an arbitrary fixed integer number,

or

$${\displaystyle A_1\left[v_0\left(t\right),C_i\right]=0,}$$

$$\begin{array}{c}{\displaystyle A_2\left[v_0\left(t\right),D_j\right]=A_2\left[v_0\left(t\right),D_j\right]=\sum _{k=1}^{N_{max}}{a}_k^{\left(2\right)}·cos(2k+1){\omega }_{0}t+b_k^{\left(2\right)}·sin(2k+1){\omega }_{0}t,}\hfill \end{array}$$

where the convergence-control parameters $D_j\in \left\{a_k^{\left(2\right)}\right|k=\overline{1,N_{max}}\}\cup \left\{b_k^{\left(2\right)}\right|k=\overline{1,N_{max}}\}$,

or yet

$${\displaystyle A_1\left[v_0\left(t\right),C_i\right]=C_{1}cos{\omega }_{0}t+C_{2}sin{\omega }_{0}t,}$$

$$\begin{array}{c}{\displaystyle A_2\left[v_0\left(t\right),C_j\right]=C_{3}cos3{\omega }_{0}t+C_{4}sin3{\omega }_{0}t,}\hfill \end{array}$$

and so on.

If the auxiliary functions $A_1$ and $A_2$ are given by Equations (36) and (37) then Equation (32) becomes:

$$\begin{array}{c}{\displaystyle {\ddot{v}}_1+{\omega }_0^2{v}_1=\sum _{k=1}^{N_{max}}{a}_k^{\left(3\right)}·cos(2k+1){\omega }_{0}t+b_k^{\left(3\right)}·sin(2k+1){\omega }_{0}t,}\hfill \end{array}$$

(38)

with the initial conditions given in Equation (35), whose solution is:

$$\begin{array}{c}{v}_1(t,C_i)=a_{0}cos{\omega }_{0}t+b_{0}sin{\omega }_{0}t+{\displaystyle \sum _{k=1}^{N_{max}}}{a}_k^{\left(4\right)}·cos(2k+1){\omega }_{0}t+b_k^{\left(4\right)}·sin(2k+1){\omega }_{0}t,\hfill \end{array}$$

(39)

where

$$a_0=-\sum _{k=1}^{N_{max}}{a}_k^{\left(4\right)},b_0=-\sum _{k=1}^{N_{max}}(2k+1)b_k^{\left(4\right)},$$

with the unknown parameters $a_k^{\left(3\right)}$, $b_k^{\left(3\right)}$, $a_k^{\left(4\right)}$, $b_k^{\left(4\right)}$ depending on the convergence-control parameters $a_k^{\left(1\right)}$, $b_k^{\left(1\right)}$, $a_k^{\left(2\right)}$, $b_k^{\left(2\right)}$, so will be optimally identified.

Finally, the approximate analytic solution is obtained from the Equation (23) in the form:

$${\displaystyle \overline{v}\left(t\right)=v_0\left(t\right)+v_1(t,C_i),i=1,2,\dots ,s,}$$

(40)

with $v_0\left(t\right)$ and $v_1(t,C_i)$ given by Equations (27) and (39), respectively.

Analogue, in the particular case $\beta =0$, ${\alpha }_1={\alpha }_2={\alpha }_3=0$, the Equation (10) could be rewrite in the following form:

$$\ddot{u}\left(t\right)·(1+u^2\left(t\right))-2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1+u^2\left(t\right))=0.$$

So, choosing the linear operator ${\displaystyle \mathcal{L}\left(u\left(t\right)\right)=\ddot{u}\left(t\right)+{\omega }_0^{2}u\left(t\right)}$ and the nonlinear operator ${\displaystyle \mathcal{N}\left(u\left(t\right)\right)=-{\omega }_0^{2}u\left(t\right)+\ddot{u}\left(t\right)·u^2\left(t\right)-2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1+u^2\left(t\right))}$, the approximate analytic solution $\overline{u}\left(t\right)$ of the Equation (10) with the initial conditions given by Equation (11) can be obtained via OAFM technique in the form:

$$\begin{array}{c}{\displaystyle \overline{u}\left(t\right)=u\left(0\right)·cos{\omega }_{0}t+\frac{\dot{u}\left(0\right)}{{\omega }_0}·sin{\omega }_{0}t+{\tilde{a}}_{0}cos{\omega }_{0}t+{\tilde{b}}_{0}sin{\omega }_{0}t+}\hfill \\ +{\displaystyle \sum _{k=1}^{N_{max}}}{\tilde{a}}_k^{\left(4\right)}·cos(2k+1){\omega }_{0}t+{\tilde{b}}_k^{\left(4\right)}·sin(2k+1){\omega }_{0}t,\hfill \end{array}$$

(41)

where the convergence-control parameters ${\omega }_0$, ${\tilde{a}}_0$, ${\tilde{b}}_0$, ${\tilde{a}}_k^{\left(4\right)}$, ${\tilde{b}}_k^{\left(4\right)}$ will be optimally identified.

Similarly, for the cases ${\alpha }_1\ne 0$, ${\alpha }_2={\alpha }_3=0$ or ${\alpha }_2\ne 0$, ${\alpha }_1={\alpha }_3=0$ respectively, the linear operator can be

$$\mathcal{L}\left(u\left(t\right)\right)=\ddot{u}+{\omega }_0^2·u\left(t\right).$$

Then, the corresponding nonlinear operator $\mathcal{N}\left(u\right(t\left)\right)$ is obtained from Equations (15) and (18), respectively, as:

$$\mathcal{N}\left(u\left(t\right)\right)=-{\omega }_0^2·u\left(t\right)-\ddot{u}\left(t\right)·u^2\left(t\right)+2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1+u^2\left(t\right))-$$

$$-2\beta ·R·u\left(t\right)·(1-u^2\left(t\right))+{\alpha }_2·(1-u^2\left(t\right))·\dot{u}\left(t\right)$$

and

$$\mathcal{N}\left(u\left(t\right)\right)=-{\omega }_0^2·u\left(t\right)+\ddot{u}\left(t\right)·u^2\left(t\right)-2u\left(t\right)·{\left(\dot{u}\left(t\right)\right)}^2+R^2·u\left(t\right)·(1-u^2\left(t\right))+$$

$$+2\beta ·R·u\left(t\right)·(1+u^2\left(t\right))+{\alpha }_1·(1+u^2\left(t\right))·\dot{u}\left(t\right),$$

respectively.

Therefore, by applying the same procedure it obtains that the expression $\mathcal{N}\left(u_0\left(t\right)\right)$ is a combination of the elementary functions $cos\left({\omega }_{0}t\right)$, $sin\left({\omega }_{0}t\right)$, $cos\left(3{\omega }_{0}t\right)$, $sin\left(3{\omega }_{0}t\right)$ in the both cases. So, the first approximation $u_1\left(t\right)$ has the form by Equation (39) and the first-order approximate analytic solution $\overline{u}\left(t\right)$ has the form by Equation (40).

In the case ${\alpha }_3\ne 0$, $\beta ={\alpha }_1={\alpha }_2=0$, the linear operator is ${\displaystyle \mathcal{L}\left(u\left(t\right)\right)=\ddot{u}\left(t\right)+{\omega }_0^{2}u\left(t\right)}$ and the nonlinear operator is deduced from Equation (21) as ${\displaystyle \mathcal{N}\left(u\left(t\right)\right)=-{\omega }_0^{2}u\left(t\right)+{\alpha }_3·\dot{u}\left(t\right)+\frac{R^2}{2}·sin(2·u\left(t\right))}$. The initial approximation is $u_0\left(t\right)=u\left(0\right)·cos\left({\omega }_{0}t\right)+\frac{\dot{u}\left(0\right)}{{\omega }_0}·sin\left({\omega }_{0}t\right)$, solution of the equation ${\displaystyle \mathcal{L}\left(u\left(t\right)\right)=0}$, with initial conditions given by Equation (21). Then, the expression ${\displaystyle \mathcal{N}\left(u_0\left(t\right)\right)}$ contain a combination of the elementary functions $cos\left(2{\omega }_{0}t\right)$, $sin\left(2{\omega }_{0}t\right)$, $cos\left(4{\omega }_{0}t\right)$, $sin\left(4{\omega }_{0}t\right)$. So, the first approximation $u_1\left(t\right)$ has the form by

$$\begin{array}{c}{\displaystyle \overline{u}\left(t\right)=u\left(0\right)·cos{\omega }_{0}t+\frac{\dot{u}\left(0\right)}{{\omega }_0}·sin{\omega }_{0}t+{\tilde{a}}_{0}cos{\omega }_{0}t+{\tilde{b}}_{0}sin{\omega }_{0}t+}\hfill \\ +{\displaystyle \sum _{k=1}^{N_{max}}}{\tilde{a}}_k^{\left(5\right)}·cos\left(2k{\omega }_{0}t\right)+{\tilde{b}}_k^{\left(5\right)}·sin\left(2k{\omega }_{0}t\right),\hfill \end{array}$$

(42)

where the convergence-control parameters ${\omega }_0$, ${\tilde{a}}_0$, ${\tilde{b}}_0$, ${\tilde{a}}_k^{\left(5\right)}$, ${\tilde{b}}_k^{\left(5\right)}$ will be optimally identified.

In this way the approximate analytic solutions of the nonlinear problems Equations (15), (18), (21), can be constructed, via the OAFM method.

4. Numerical Results and Discussions

In this section, we discuss the accuracy of the OAFM method by taking into consideration the first order approximate solutions given by Equations (40) and (41), where the index $N_{max}\in \{10,15,25,35\}$ is an arbitrary fixed positive integer number.

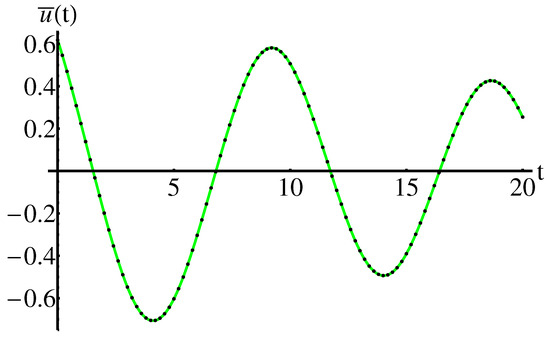
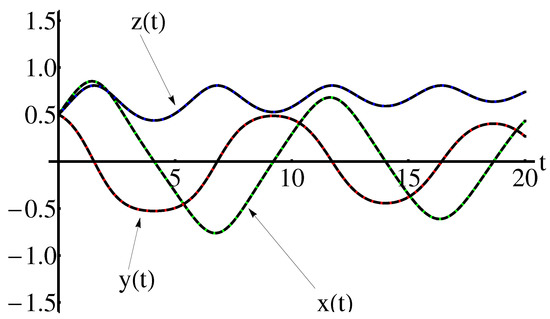
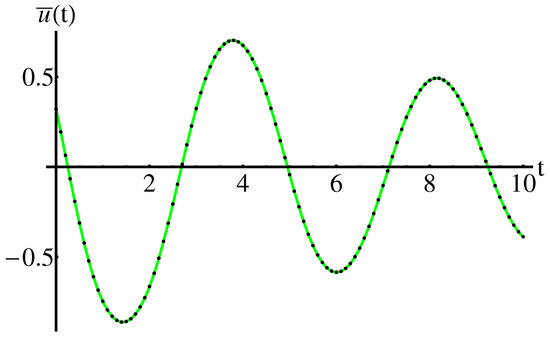
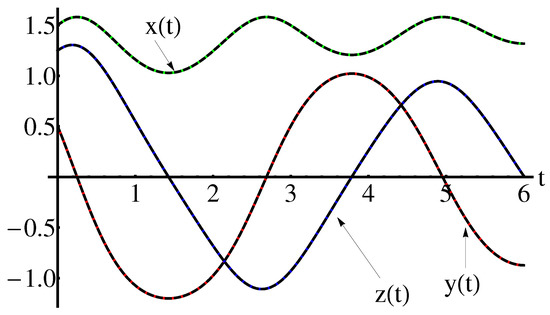
By means of the Equations (3), (4), (40), for $\beta \ne 0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, the Equations (8), (9), (41), for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, the Equations (12), (14), (40), for ${\alpha }_1=0$, ${\alpha }_2\ne 0$, ${\alpha }_3=0$, the Equations (16), (17), (40), for ${\alpha }_1\ne 0$, ${\alpha }_2=0$, ${\alpha }_3=0$, and the Equations (19), (20), (42), for ${\alpha }_1=0$, $\beta =0$, ${\alpha }_2=0$, ${\alpha }_3\ne 0$, respectively, the approximate closed-form solutions of the Rabinovich system are well-determined, via the OAFM technique.

The accuracy of the obtained results is shown in the Figure 1 and Figure 2 (for $\beta =0.25\ne 0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$), the Figure 3 and Figure 4 (for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$) respectively, by comparison of the above obtained approximate solutions with the corresponding numerical integration results, computed by means of the fourth-order Runge-Kutta method using Wolfram Mathematica 9.0 software. On the other hand, the cases ${\alpha }_1\ne 0$, ${\alpha }_2\ne 0$, ${\alpha }_3\ne 0$ are depicted in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The convergence-control parameters $C_1=a_0+v\left(0\right)$, $C_i=a_{k-1}^{\left(4\right)}$, $B_1=b_0+\frac{\dot{v}\left(0\right)}{{\omega }_0}$, $B_i=b_{k-1}^{\left(4\right)}$, $i=2,3,\cdots N_{max}$, which appear in Equations (40)–(42) are optimally identified by the least square method for different values of the known parameter $N_{max}$. As could be observed in the figures there are the symmetry with respect to the $Oz$- axis, for $\beta \ne 0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$ and are the symmetry with respect to the all coordinate axes, for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$. The Figure 11 and Figure 12 highlight the symmetry of the 3D trajectory.

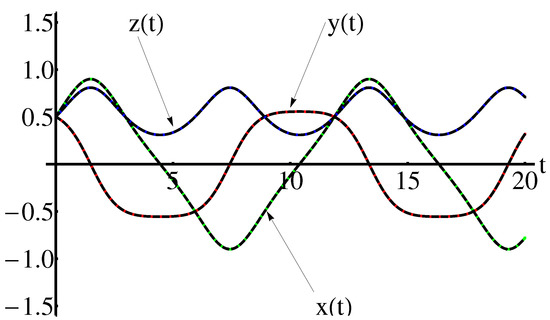
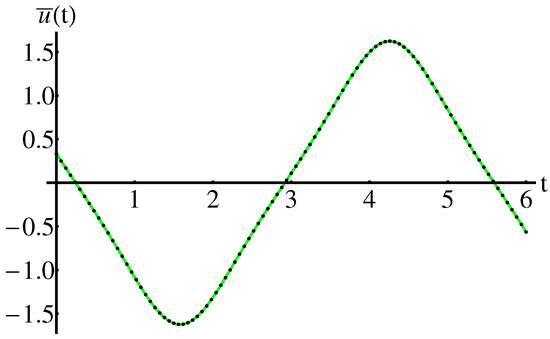
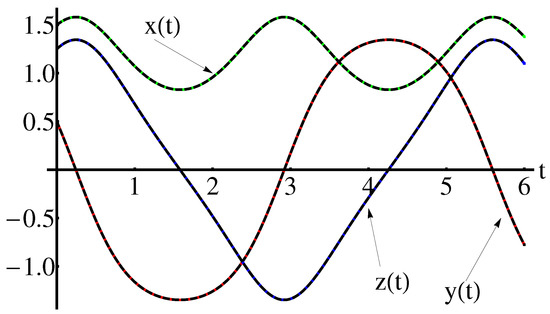
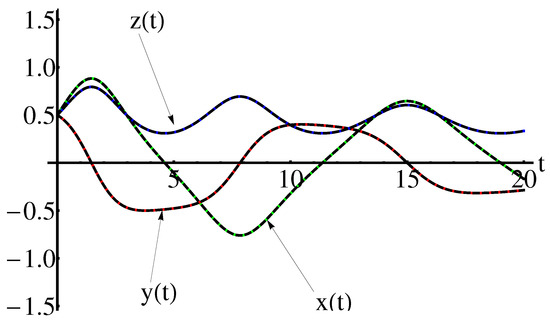
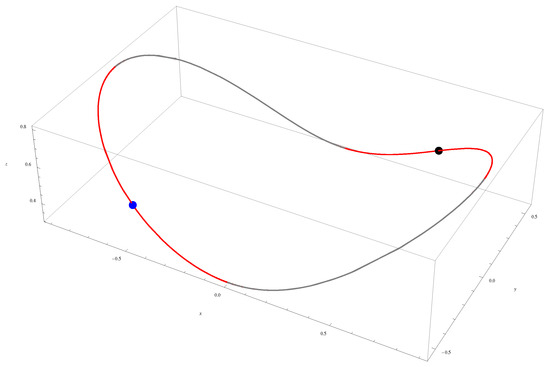
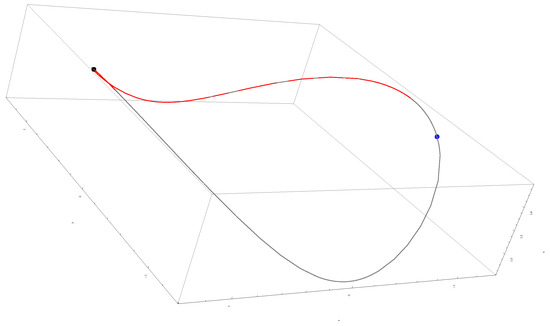
The convergence-control parameters are presented in the section Appendix A.

The influence of the index number $N_{max}$ on the values of the relative errors is examined in

Table 1. Comparison between the relative errors: ${ϵ}_v=|v_{numerical}-{\overline{v}}_{OAFM}|$ for $\beta =0.25$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, $x_0=0.5$, $y_0=0.5$, $z_0=0.5$ and different values of the index $N_{max}$; ${\overline{v}}_{OAFM}$ obtained from Equations (40) and (A1)–(A3).

t	${\mathit{N}}_{\mathbf{max}}=10$	${\mathit{N}}_{\mathbf{max}}=15$	${\mathit{N}}_{\mathbf{max}}=25$
0	1.332267 $\times {10}^{-15}$	4.440892 $\times {10}^{-16}$	2.646771 $\times {10}^{-13}$
7/5	0.0002311701	9.690649 $\times {10}^{-7}$	5.424820 $\times {10}^{-10}$
14/5	0.0001494743	9.806902 $\times {10}^{-7}$	3.389437 $\times {10}^{-10}$
21/5	0.0001987102	1.243573 $\times {10}^{-6}$	1.842952 $\times {10}^{-10}$
28/5	0.0000961699	5.341956 $\times {10}^{-8}$	6.126734 $\times {10}^{-10}$
7	0.0001210484	2.545193 $\times {10}^{-6}$	4.273881 $\times {10}^{-10}$
42/5	0.0000661653	1.815027 $\times {10}^{-6}$	2.335903 $\times {10}^{-10}$
49/5	9.306109 $\times {10}^{-6}$	2.151637 $\times {10}^{-6}$	5.521745 $\times {10}^{-10}$
56/5	0.0000211790	2.055369 $\times {10}^{-6}$	4.816658 $\times {10}^{-10}$
63/5	0.0001510944	2.318730 $\times {10}^{-7}$	7.166223 $\times {10}^{-11}$
14	0.0001919623	1.595892 $\times {10}^{-6}$	1.900378 $\times {10}^{-10}$

and

Table 2. Comparison between the relative errors: ${ϵ}_u=|u_{numerical}-{\overline{u}}_{OAFM}|$ for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, $x_0=1.5$, $y_0=0.5$, $z_0=1.25$ and different values of the index $N_{max}$; ${\overline{u}}_{OAFM}$ obtained from Equations (41) and (A4)–(A6).

t	${\mathit{N}}_{\mathbf{max}}=15$	${\mathit{N}}_{\mathbf{max}}=25$	${\mathit{N}}_{\mathbf{max}}=35$
0	9.475753 $\times {10}^{-14}$	1.587063 $\times {10}^{-13}$	7.716050 $\times {10}^{-15}$
3/5	3.504900 $\times {10}^{-4}$	3.316779 $\times {10}^{-5}$	8.194535 $\times {10}^{-8}$
6/5	2.914220 $\times {10}^{-4}$	2.904368 $\times {10}^{-5}$	7.775160 $\times {10}^{-8}$
9/5	4.067788 $\times {10}^{-4}$	3.306752 $\times {10}^{-5}$	1.002242 $\times {10}^{-7}$
12/5	5.020959 $\times {10}^{-4}$	3.350227 $\times {10}^{-5}$	1.013316 $\times {10}^{-7}$
3	2.399299 $\times {10}^{-4}$	3.095774 $\times {10}^{-5}$	6.350594 $\times {10}^{-8}$
18/5	7.499806 $\times {10}^{-5}$	3.033164 $\times {10}^{-5}$	9.363366 $\times {10}^{-8}$
21/5	2.634217 $\times {10}^{-4}$	3.698857 $\times {10}^{-5}$	7.855941 $\times {10}^{-8}$
24/5	1.023441 $\times {10}^{-4}$	3.459891 $\times {10}^{-5}$	2.951037 $\times {10}^{-8}$
27/5	1.061241 $\times {10}^{-4}$	3.200782 $\times {10}^{-5}$	4.558553 $\times {10}^{-8}$
6	1.528191 $\times {10}^{-4}$	3.492756 $\times {10}^{-5}$	5.671638 $\times {10}^{-8}$

. The better approximate analytical solution corresponds to the value $N_{max}=25$ for $\beta =0.25$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, and $N_{max}=35$ for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0$, respectively. These values were chosen for the efficiency of the solutions shown in

Table 3. Comparison between the approximate analytic solutions ${\overline{u}}_{OAFM}$ given by Equation (40) and corresponding numerical solution for $\beta =0.25$, ${\alpha }_1=0$, ${\alpha }_2=0.05$, ${\alpha }_3=0$, $x_0=0.5$, $y_0=0.5$, $z_0=0.5$ and the index $N_{max}=25$; (relative errors: ${ϵ}_u=|u_{numerical}-{\overline{u}}_{OAFM}|$).

t	${\mathit{u}}_{\mathbf{numerical}}$	${\overline{\mathit{u}}}_{\mathbf{OAFM}}$	${\mathit{ϵ}}_{\mathit{u}}$
0	0.3819660112	0.3819660112	6.566969 $\times {10}^{-14}$
8/5	0.5487198876	0.5487198871	4.569626 $\times {10}^{-10}$
16/5	0.3347566620	0.3347566624	4.373337 $\times {10}^{-10}$
24/5	−0.0474300084	−0.0474300074	9.474402 $\times {10}^{-10}$
32/5	−0.3828045448	−0.3828045450	2.316530 $\times {10}^{-10}$
8	−0.5042437854	−0.5042437838	1.624801 $\times {10}^{-9}$
48/5	−0.3375790298	−0.3375790299	8.105455 $\times {10}^{-11}$
56/5	−0.0332606638	−0.0332606646	8.140353 $\times {10}^{-10}$
64/5	0.2599740718	0.2599740722	3.694533 $\times {10}^{-10}$
72/5	0.4407383794	0.4407383798	4.701539 $\times {10}^{-10}$
16	0.4140215615	0.4140215610	5.571915 $\times {10}^{-10}$

,

Table 4. Comparison between the approximate analytic solutions ${\overline{u}}_{OAFM}$ given by Equation (40) and corresponding numerical solution for $\beta =0.25$, ${\alpha }_1=0.05$, ${\alpha }_2=0$, ${\alpha }_3=0$, $x_0=0.5$, $y_0=0.5$, $z_0=0.5$ and the index $N_{max}=25$; (relative errors: ${ϵ}_u=|u_{numerical}-{\overline{u}}_{OAFM}|$).

t	${\mathit{u}}_{\mathbf{numerical}}$	${\overline{\mathit{u}}}_{\mathbf{OAFM}}$	${\mathit{ϵ}}_{\mathit{u}}$
0	0.6180339887	0.6180339887	8.881784 $\times {10}^{-16}$
8/5	−0.0321978118	−0.0321978110	7.381383 $\times {10}^{-10}$
16/5	−0.5983010647	−0.5983010645	2.040423 $\times {10}^{-10}$
24/5	−0.6430063264	−0.6430063265	1.829493 $\times {10}^{-10}$
32/5	−0.1556677170	−0.1556677166	3.093710 $\times {10}^{-10}$
8	0.4057018841	0.4057018832	9.304779 $\times {10}^{-10}$
48/5	0.5626679938	0.5626679941	3.481130 $\times {10}^{-10}$
56/5	0.1791865300	0.1791865294	6.380252 $\times {10}^{-10}$
64/5	−0.3292856584	−0.3292856577	6.622721 $\times {10}^{-10}$
72/5	−0.4774573136	−0.4774573135	1.349091 $\times {10}^{-10}$
16	−0.1296948250	−0.1296948251	8.001704 $\times {10}^{-11}$

and

Table 5. Comparison between the approximate analytic solutions ${\overline{u}}_{OAFM}$ given by Equation (42) and corresponding numerical solution for $\beta =0$, ${\alpha }_1=0$, ${\alpha }_2=0$, ${\alpha }_3=0.15$, $x_0=1.5$, $y_0=0.5$, $z_0=1.25$ and the index $N_{max}=35$; (relative errors: ${ϵ}_u=|u_{numerical}-{\overline{u}}_{OAFM}|$).

t	${\mathit{u}}_{\mathbf{numerical}}=15$	${\overline{\mathit{u}}}_{\mathbf{OAFM}}$	${\mathit{ϵ}}_{\mathit{u}}$
0	0.3217505543	0.3217505543	1.665334 $\times {10}^{-16}$
3/5	−0.4222547682	−0.4222561402	1.371977 $\times {10}^{-6}$
6/5	−0.8296437373	−0.8296451162	1.378897 $\times {10}^{-6}$
9/5	−0.7776543854	−0.7776557673	1.381888 $\times {10}^{-6}$
12/5	−0.3129872607	−0.3129886423	1.381552 $\times {10}^{-6}$
3	0.3239044822	0.3239031031	1.379085 $\times {10}^{-6}$
18/5	0.6815903593	0.6815889752	1.384109 $\times {10}^{-6}$
21/5	0.5989387285	0.5989373473	1.381160 $\times {10}^{-6}$
24/5	0.1453366672	0.1453352855	1.381609 $\times {10}^{-6}$
27/5	−0.3742949616	−0.3742963398	1.378268 $\times {10}^{-6}$
6	−0.5850269138	−0.5850282851	1.371267 $\times {10}^{-6}$

.

5. Conclusions

In the present paper, some geometrical properties of the Rabinovich system are emphasized and the approximate analytic solutions were established. These analytic solutions depend on some convergence-control parameters. A good agreement between the approximate analytic solutions (using OAFM) and corresponding numerical solutions (using the fourth-order Runge-Kutta method) was found for symmetric solutions with respect to the coordinate axes. The performance of the method is characterized by suitable values of the parameter $N_{max}$ as shown in the Tables and Figures. These obtained solutions can be used in many applications of technological interest. The advantage is to obtain accurate solutions for special cases, with just an analytic first integral known, but the unknown exact solution (as the intersection of the surfaces).