First and Second Sound in Two-Dimensional Bosonic and Fermionic Superfluids

Abstract

We review our theoretical results of the sound propagation in two-dimensional (2D) systems of ultracold fermionic and bosonic atoms. In the superfluid phase, characterized by the spontaneous symmetry breaking of the $U\left(1\right)$ symmetry, there is the coexistence of first and second sound. In the case of weakly-interacting repulsive bosons, we model the recent measurements of the sound velocities of ${}^{39}$K atoms in 2D obtained in the weakly-interacting regime and around the Berezinskii–Kosterlitz–Thouless (BKT) superfluid-to-normal transition temperature. In particular, we perform a quite accurate computation of the superfluid density and show that it is reasonably consistent with the experimental results. For superfluid attractive fermions, we calculate the first and second sound velocities across the whole BCS-BEC crossover. In the low-temperature regime, we reproduce the recent measurements of first-sound speed with ${}^6$Li atoms. We also predict that there is mixing between sound modes only in the finite-temperature BEC regime.

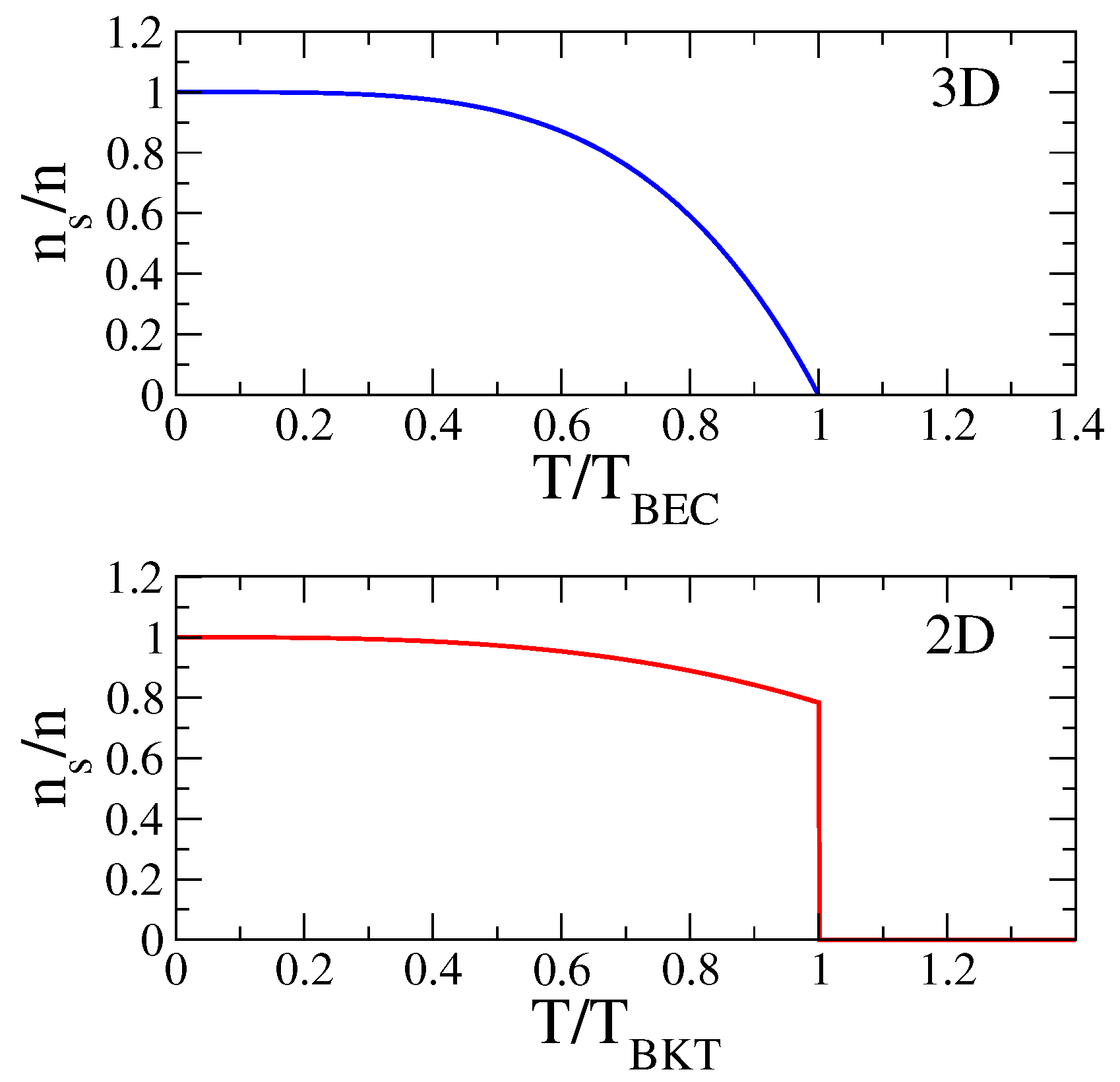
1. Introduction

In this review paper, the propagation of the first and second sound in two-dimensional (2D) systems of ultracold fermionic and bosonic atoms is examined in light of our current theoretical findings. As is well known, the second sound exists only in the $U\left(1\right)$ symmetry-broken superfluid phase. We discuss a quite accurate determination of the superfluid density in the case of weakly-interacting repulsive bosons, finding a good agreement with the experiment to model the recent measurements [1] of the sound velocities of ${}^{39}$K atoms in 2D obtained in the weakly-interacting regime and around the Berezinskii–Kosterlitz–Thouless (BKT) superfluid-to-normal transition temperature [2]. We also analyze the first and second sound velocities across the whole BCS-BEC crossover for superfluid attractive fermions. By considering ${}^6$Li atoms, we simulate and analyze the most recent measurements [3] of the first sound velocity in the low-temperature regime. This velocity is the only one triggered by a density probe because the decoupling of the density and entropy fluctuations makes it possible [4]. The main results discussed here were presented at the International Workshop “Quantum Transport with ultracold atoms” (Dresden, 2022).

According to Landau’s two-fluid theory [5] of superfluids, the total number density n of a system in the superfluid phase can be written as

$$n=n_{\mathrm{s}}+n_{\mathrm{n}},$$

(1)

where $n_{\mathrm{s}}$ is the superfluid density, and $n_{\mathrm{n}}$ is the normal density. At the critical temperature $T_c$, $n_{\mathrm{n}}=n$, and correspondingly, $n_{\mathrm{s}}=0$. Following Landau, in a superfluid, a local perturbation excites two wave-like modes—first and second sound—which propagate with velocities $u_1$ and $u_2$. These velocities are determined by the positive solutions of the algebraic biquadratic equation

$$u^4-(c_{10}^2+c_{20}^2)u^2+c_T^2{c}_{20}^2=0.$$

(2)

The first sound $u_1$ is the largest of the two positive roots of Equation (2), while the second sound $u_2$ is the smallest positive one. In the biquadratic Equation (2), there is the adiabatic sound velocity

$$c_{10}=\sqrt{\frac{1}{m}{\left(\frac{\partial P}{\partial n}\right)}_{\overline{S},V}},$$

(3)

where $\overline{S}=S/N$, as the entropy per particle, $V=L^2$, as the 2D volume (area) of a square of size L, and N is the total number of identical particles. There is also the entropic sound (or Landau) velocity

$$c_{20}=\sqrt{\frac{1}{m}\frac{{\overline{S}}^2}{{\left(\frac{\partial \overline{S}}{\partial T}\right)}_{N,V}}\frac{n_{\mathrm{s}}}{n_{\mathrm{n}}}},$$

(4)

where $n_{\mathrm{s}}/n_{\mathrm{n}}$ is the ratio between the superfluid and normal density, m is the mass of each particle, and the isothermal sound velocity is

$$c_T=\sqrt{\frac{1}{m}{\left(\frac{\partial P}{\partial n}\right)}_{T,V}},$$

(5)

where P is the pressure, and T is the temperature. Thus, having the equation of state and the superfluid fraction of the system under investigation, one can determine the first sound velocity $u_1$ and the second sound velocity $u_2$ by solving Equation (2), namely

$$u_{1,2}=\sqrt{\frac{1}{2}(c_{10}^2+c_{20}^2)\pm \frac{1}{2}\sqrt{{(c_{10}^2+c_{20}^2)}^2-4c_T^2{c}_{20}^2}}.$$

(6)

2. Weakly-Interacting 2D Bose Gas

The Helmholtz free energy [4] of a weakly-interacting two-dimensional gas of purely repulsive identical bosons of mass m can be written as ($\hslash =k_{\mathrm{B}}=1$)

$$F=F_0+F_{\mathrm{Q}}+F_T=\frac{g}{2}\frac{N^2}{L^2}+\frac{1}{2}\sum _{\mathbf{p}}{E}_p+T\sum _{\mathbf{p}}ln\left[1-e^{-E_p/T}\right],$$

(7)

where $F_0$ is the mean-field zero-temperature free energy, and $g>0$ is the Bose–Bose interaction strength. $F_T$ is the low-temperature free energy, and

$$E_p=\sqrt{\frac{p^2}{2m}\left(\frac{p^2}{2m}+2gn\right)}$$

(8)

is the familiar Bogoliubov spectrum of elementary excitations. For the sake of completeness, we emphasize some formal analogy [6] between this Bogoliubov spectrum of bosonic particles, which can be derived from the Gross–Pitaevskii equation [7,8], and the neural spectrum, which can be deduced from the Amari equation of the brain [9]. Indeed, the neural field equation of Amari resembles an imaginary-time Gross–Pitaevskii equation with a nonlocal term. The elementary (linearized) excitations of the Amari equation around a uniform configuration are the analog of the Bologlibov spectrum of the Gross–Pitaevskii equation. The quantum correction $F_{\mathrm{Q}}$ in the free energy is obviously ultraviolet divergent and requires a regularization procedure. Dimensional regularization [10] leads to

$$F_{\mathrm{Q}}=-L^2\frac{m}{8\pi }\left[ln\left(\frac{{ϵ}_{\mathrm{\Lambda }}}{gn}\right)-\frac{2}{\eta }\right]{\left(gn\right)}^2,$$

(9)

where ${ϵ}_{\mathrm{\Lambda }}=4e^{-2\gamma -1/2}/\left(m{a}_{2\mathrm{D}}^2\right)$ is a cutoff energy, $\gamma =0.577$ is the Euler–Mascheroni constant, $a_{2\mathrm{D}}$ is the 2D s-wave scattering length, and

$$\eta =\frac{mg}{2\pi }$$

(10)

is the adimensional gas parameter [2]. Moreover, one also finds

$$\frac{{ϵ}_{\mathrm{\Lambda }}}{gn}=\frac{2\pi }{N}\frac{e^{-2\gamma -1/2+2/\eta }}{\eta }.$$

(11)

All the thermodynamic quantities can be obtained from the Helmholtz free energy of Equation (7). For instance, the pressure P is given by

$$P=-{\left(\frac{\partial F}{\partial L^2}\right)}_{N,T},$$

(12)

while the the entropy reads

$$S={\left(\frac{\partial }{\partial T}\frac{F}{N}\right)}_{N,L^2}.$$

(13)

Instead, the normal density $n_{\mathrm{n}}$ can be extracted from the Landau formula

$$n_{\mathrm{n}}=-\int \frac{d^2\mathbf{p}}{{\left(2\pi \right)}^2}\frac{p^2}{2m}\frac{d{f}_{\mathrm{B}}\left(E_p\right)}{d{E}_p},$$

(14)

where $f_{\mathrm{B}}\left(E\right)=1/\left(e^{E/T}-1\right)$ is the Bose–Einstein distribution.

Actually, the Landau formula for the normal density does not take into account the formation of quantized vortices and antivortices by increasing the temperature. These quantized vortices are crucial for the 2D Bose gas to obtain the phenomenology predicted by Berezinskii [11] and Kosterlitz–Thouless [12]. The presence of quantized vortices renormalizes the superfluid density, $n_{\mathrm{s}}=n-n_{\mathrm{n}}$. The renormalized superfluid density $n_{\mathrm{s}}(t=+\infty )$ is obtained by solving the Nelson–Kosterlitz renormalization group equations [13]

$$\begin{array}{ccc}\hfill {\partial }_t{K}^{-1}\left(t\right)& =& 4{\pi }^3{y}^2\left(t\right)\hfill \\ \hfill {\partial }_{t}y\left(t\right)& =& [2-\pi K(t\left)\right]y\left(t\right)\hfill \end{array}$$

(15)

where $K\left(t\right)=n_{\mathrm{s}}\left(t\right)/T$, with $n_{\mathrm{s}}\left(t\right)$ as the superfluid density at the adimensional fictitious time t, and $y\left(t\right)=exp\left[-{\mu }_{\mathrm{c}}\left(t\right)/T\right]$, which is the fugacity, where ${\mu }_{\mathrm{c}}\left(t\right)$ is the vortex chemical potential at the fictitious time t. In particular, the initial superfluid density $n_{\mathrm{s}}\left(0\right)$ of the flow is the one obtained from $n_{\mathrm{n}}$ of Equation (14) as $n_{\mathrm{s}}\left(0\right)=n-n_{\mathrm{n}}$. The initial vortex chemical potential is instead given by the expression ${\mu }_{\mathrm{s}}\left(0\right)={\pi }^2{n}_{\mathrm{s}}\left(0\right)/\left(2m\right)$. We emphasize that, in the determination of pressure and entropy, one should also take into account the vortex contribution. However, in order to make the theoretical scheme more tractable, we have included the quantized vortices only for the renormalized superfluid density. Another relevant issue is the fact that, in the experiments, the superfluids have a finite size. To describe consistently the finite size of the system, we solve Equation (15) up to a maximum value $t_{max}=ln(A^{1/2}/\xi )$ of the adimensional fictitious time t, where A is the area of the system, and $\xi$ is the healing length, which is practically the size of the vortex core.

For 3D superfluids, the transition to the normal state is a BEC phase transition, while in 2D superfluids the transition to the normal state is something different: a topological phase transition. An important prediction of the Kosterlitz–Thouless transition is that, contrary to the 3D case, in 2D, the superfluid fraction $n_{\mathrm{s}}/n$ jumps to zero above the Berezinskii–Kosterlitz–Thouless critical temperature $T_{BKT}$. See Figure 1.

Figure 1. Typical behavior of a superfluid fraction $n_{\mathrm{s}}/n$ vs. adimensional temperature $T/T_c$ in three-dimensional (3D) and two-dimensional (2D) superfluid systems. Notice that only in the 2D case is there a jump of the superfluid fraction at the Berezinskii–Kosterlitz–Thouless critical temperature $T_{BKT}$ in the superfluid-to-normal phase trasition.

In Figure 2, we report our theoretical first and second sound velocities as a function of the adimensional temperature in comparison with recent experimental data near $T_{BKT}$ [1]. As shown by the figure, the agreement between our theory and the experimental results is quite good.

Figure 2. Sound velocities vs. adimensional temperature. Here, $v_B=gn$ provides the Bogoliubov velocity, $N=2178$ is the number of atoms, and $\eta =0.102$. The blue line is our first sound velocity $u_1$, while the green line is our second sound velocity $u_2$. The dots with error bars are the experimental data obtained by Christodoulou et al. [1]. Figure adapted from Ref. [2].

Another relevant phenomenon is the hybridization with quasi-crossing of the first sound $u_1$ and second sound $u_2$, which appears at a characteristic temperature $T_{hyb}$. In particular, when the hybridization temperature $T_{hyb}$ is crossed, there is an inversion of the role of the density and entropy oscillations in the propagation of sounds. As discussed in detail in Ref. [2], a density perturbation excites mainly $u_1$ below the $T_{hyb}$ and instead probes mainly $u_2$ above $T_{hyb}$. The opposite occurs by imposing a temperature gradient in the superfluid. Numerically, we found that $T_{hyb}$ grows by increasing the repulsive Bose–Bose interaction strength, and eventually, $T_{hyb}$ coincides with $T_{BKT}$ [2].

3. 2D Fermi Gas in the BCS-BEC Crossover

In 2004, the 3D BCS-BEC crossover was observed with ultracold gases made of two-component attractive fermionic ${}^{40}$K or ${}^6$Li atoms [14,15,16]. This crossover was obtained using a Fano–Feshbach resonance to change the 3D s-wave scattering length $a_F$ of the interatomic potential. More recently, the 2D BEC-BEC crossover was achieved experimentally [17,18] with a Fermi gas of two-component ${}^6$Li atoms.

Two-dimensional realistic interatomic attractive potentials always have a bound state, in contrast to the 3D situation. In particular [19], the binding energy ${ϵ}_B>0$ of two fermions is related to the 2D scattering length $a_F$ by

$${ϵ}_B=\frac{4}{e^{2\gamma }}\frac{1}{m{a}_F^2},$$

(16)

where $\gamma =0.577$ is the Euler–Mascheroni constant. Moreover, the attractive interaction of strength $g>0$ of the s-wave pairing is related to the binding energy by the expression [20]

$$\frac{1}{g}=\frac{1}{2L^2}\sum _{\mathbf{k}}\frac{1}{\frac{k^2}{2m}+\frac{1}{2}{ϵ}_B}.$$

(17)

To study the 2D BCS-BEC crossover, we adopt the formalism of functional integration [21]. The partition function $\mathcal{Z}$ of the uniform system with fermionic fields ${\psi }_s(\mathbf{r},\tau )$ at temperature T, in a two-dimensional volume $V=L^2$, with chemical potential $\mu$, reads

$$\mathcal{Z}=\int \mathcal{D}[{\psi }_s,{\overline{\psi }}_s]exp\left\{-S\right\},$$

(18)

where $\beta \equiv 1/T$, and

$$S={\int }_0^{\beta }d\tau {\int }_{L^2}{d}^2\mathbf{r}\mathcal{L}$$

(19)

is the Euclidean action functional with Lagrangian density

$$\mathcal{L}={\overline{\psi }}_s\left[{\partial }_{\tau }-\frac{1}{2m}{\nabla }^2-\mu \right]{\psi }_s-g{\overline{\psi }}_{\uparrow }{\overline{\psi }}_{\downarrow }{\psi }_{\downarrow }{\psi }_{\uparrow },$$

(20)

where $g>0$ is the strength of the attractive s-wave coupling between fermions with opposite spin.

In particular, we are interested in the grand potential $\mathrm{\Omega }$, given by

$$\mathrm{\Omega }=-\frac{1}{\beta }ln\left(\mathcal{Z}\right)\simeq -\frac{1}{\beta }ln\left({\mathcal{Z}}_{mf}{\mathcal{Z}}_g\right)={\mathrm{\Omega }}_{mf}+{\mathrm{\Omega }}_g,$$

(21)

where

$${\mathcal{Z}}_{mf}=\int \mathcal{D}[{\psi }_s,{\overline{\psi }}_s]exp\left\{-S_e({\psi }_s,\overline{{\psi }_s},{\Delta }_0)\right\}$$

(22)

is the mean-field partition function, and

$${\mathcal{Z}}_g=\int \mathcal{D}[{\psi }_s,{\overline{\psi }}_s]\mathcal{D}[\eta ,\overline{\eta }]exp\left\{-S_g({\psi }_s,\overline{{\psi }_s},\eta ,\overline{\eta },{\Delta }_0)\right\}$$

(23)

is the partition function of Gaussian pairing fluctuations.

After functional integration over quadratic fields, one finds that the mean-field grand potential reads [22]

$${\mathrm{\Omega }}_{mf}=\frac{{\Delta }_0^2}{g}{L}^2+\sum _{\mathbf{k}}\left(\frac{k^2}{2m}-\mu -E_{sp}\left(\mathbf{k}\right)-\frac{2}{\beta }ln(1+e^{-\beta E_{sp}\left(\mathbf{k}\right)})\right),$$

(24)

where

$$E_{sp}\left(\mathbf{k}\right)=\sqrt{{\left(\frac{k^2}{2m}-\mu \right)}^2+{\Delta }_0^2}$$

(25)

is the spectrum of fermionic single-particle excitations.

Instead, the Gaussian grand potential is given by

$${\mathrm{\Omega }}_g=\frac{1}{2\beta }\sum _{Q}ln\det \left(\mathbf{M}\right(Q\left)\right),$$

(26)

where $\mathbf{M}\left(Q\right)$ is the inverse propagator of the Gaussian fluctuations of pairs, and $Q=(\mathbf{q},i{\mathrm{\Omega }}_m)$ represents the 4D wavevector, where ${\mathrm{\Omega }}_m=2\pi m/\beta$ are the Matsubara frequencies, and $\mathbf{q}$ is the 3D wavevector [23].

The sum over the Matsubara frequencies is quite complicated, and it does not give a simple expression. An approximate formula [24] is

$${\mathrm{\Omega }}_g\simeq \frac{1}{2}\sum _{\mathbf{q}}{E}_{col}\left(\mathbf{q}\right)+\frac{1}{\beta }\sum _{\mathbf{q}}ln(1-e^{-\beta E_{col}\left(\mathbf{q}\right)}),$$

(27)

where

$$E_{col}\left(\mathbf{q}\right)=\omega \left(\mathbf{q}\right)$$

(28)

is the spectrum of bosonic collective excitations with $\omega \left(\mathbf{q}\right)$ derived from

$$\det \left(\mathbf{M}\right(\mathbf{q},\omega \left)\right)=0.$$

(29)

It is important to stress that the zero-point energy of the collective excitations is divergent. However, by using the convergence factor renormalization procedure (see Ref. [10] for a review of renormalization methods for the zero-point energy of ultracold atoms), one extracts a reliable finite contribution. In Figure 3, we plot the pressure $P=-\mathrm{\Omega }/L^2$ of the 2D Fermi gas in the BCS-BEC crossover comparing our zero-temperature theoretical results [25] with the available experimental data [17]. The agreement between theory and experiment is extremely good including the Gaussian fluctuations. For the specific investigation of the Gaussian fluctuations in the BEC regime of the 2D crossover with analytical and numerical techniques, see also Refs. [26,27]. Quite remarkably, our $T=0$ results with Gaussian fluctuations are also in good agreement with the auxiliary-field path integral calculations [28] and diffusion Monte Carlo simulations [29].

Figure 3. Zero-temperature scaled pressure $P/P_{id}$ vs. scaled binding energy ${ϵ}_B/{ϵ}_F$. Filled squares with error bars: experimental data of Makhalov et al. [17]. Solid line: our regularized Gaussian pair fluctuation (GPF) theory. Figure adapted from Ref. [30].

We are now interested in the temperature dependence of the superfluid density $n_{\mathrm{s}}\left(T\right)$ of the system. At the Gaussian level, $n_{\mathrm{s}}\left(T\right)$ depends only on fermionic single-particle excitations $E_{sp}\left(k\right)$ [31]. Beyond the Gaussian level, bosonic collective excitations $E_{col}\left(q\right)$ also contribute [32]. Thus, we assume the following Landau-type formula for the superfluid density [25]

$$n_{\mathrm{s}}\left(T\right)=n-\beta \int \frac{{\mathrm{d}}^{2}k}{{\left(2\pi \right)}^2}{k}^2\frac{e^{\beta E_{sp}\left(k\right)}}{{(e^{\beta E_{sp}\left(k\right)}+1)}^2}-\frac{\beta }{2}\int \frac{{\mathrm{d}}^{2}q}{{\left(2\pi \right)}^2}{q}^2\frac{e^{\beta E_{col}\left(q\right)}}{{(e^{\beta E_{col}\left(q\right)}-1)}^2}.$$

(30)

This bare superfluid density can be renormalized by using the flow Equations (15) of Kosterlitz–Thouless–Nelson, which take into account the effect of quantized vortices and antivortices [12,13], by using Equation (30) as the initial condition. In Figure 4, we plot the BKT critical temperature obtained by using the Nelson–Kosterlitz criterion [13]:

$$T_{BKT}=\frac{\pi }{8m}{n}_s\left(T_{BKT}\right).$$

(31)

Figure 4. Our theoretical predictions [25] for the Berezinskii–Kosterlitz–Thouless critical temperature $T_{BKT}$ compared to the experimental observation [33] (filled circles with error bars). Figure adapted from Ref. [25].

The figure clearly shows that the mean-field prediction (dashed line) is meaningful only in the deep BCS regime of the 2D crossover. Instead our beyond-mean-field results (solid line), which include Gaussian fluctuations, are in reasonably good agreement with the available experimental data [33] (filled circles). In Refs. [30,34], we found that $T_{BKT}$ derived with the Nelson–Kosterlitz criterion slightly overestimated the critical temperature calculated by solving the renormalization group of Equations (15).

Having the equation of state and the superfluid density at finite temperature, we calculated the first sound velocity $u_1$ and the second sound velocity $u_2$ in the 2D BCS-BEC crossover by using Equation (6). We also analyzed the amplitude modes $W_1$ and $W_2$ of the response to a density perturbation [35], i.e.,

$$\delta n(x,t)=W_1\delta n_1(x\pm u_{1}t)+W_2\delta n_2(x\pm u_{2}t)$$

(32)

where

$$\frac{W_1}{W_1+W_2}=\frac{(u_1^2-c_{20}^2)u_2^2}{(u_1^2-u_2^2)c_{20}^2}$$

(33)

and

$$\frac{W_2}{W_1+W_2}=\frac{(c_{20}^2-u_2^2)u_1^2}{(u_1^2-u_2^2)c_{20}^2}.$$

(34)

In Figure 5, we show our theoretical determination of the sound velocities and density responses (insets) as a function of the interaction strength (actually the logarithm of the adimensional binding energy ${ϵ}_B/{ϵ}_F$) at quite low temperature T. The comparison with the experimental measurements of the first sound velocity (filled diamonds) suggest that our theoretical framework is quite good. It is important to stress that in the BCS regime the speed of second sound is rapidly approaching zero.

Figure 5. First sound velocity $u_1$ (red solid line) and second sound velocity $u_2$ (blue dashed line) along the BCS-BEC crossover, at temperature $T/T_F=0.01$, with $T_F={ϵ}_F$, and $v_F=\sqrt{2{ϵ}_F/m}$. Green diamonds: recent measurements of the first sound [3] Right inset: relative contribution to the density response of $u_1$ (red solid line) and $u_2$ (blue dashed line). Figure adapted from Ref. [4].

In Figure 6, we report instead the sound velocities as a function of the temperature T for three values of the interaction strength (the three panels correspond to increasing values of the adimensional binding energy ${ϵ}_B/{ϵ}_F$). The density responses shown in the insets strongly suggest that a mixing between the first sound and second sound occurred only in the finite-temperature BEC regime. Notice that taking into account Equations (3)–(6), (33) and (34), the presence of mixing means that the adiabatic sound velocity $c_{10}$ was quite different with respect to the isothermal sound velocity $c_T$. Conversely, if $c_{10}\simeq c_T$, then $u_1\simeq c_{10}$, $u_2\simeq c_{20}$, and consequently, $W_2\simeq 0$. For comparison, for the 3D unitary Fermi gas we recently showed [36] that, in contrast to 3D liquid helium, near the critical temperature, the mixing of the first and second sound was quite strong.

Figure 6. Adimensional first sound velocity $u_1/v_F$ (red solid line) and adimensional second sound velocity $u_2/v_F$ (blue dashed line) plotted in terms of the rescaled temperature $T/T_F$, for three different values of the crossover parameter: $ln({ϵ}_B/{ϵ}_F)=-5$ (BCS regime), $ln({ϵ}_B/{ϵ}_F)=0$ (unitary regime), and $ln({ϵ}_B/{ϵ}_F)=5$ (BEC regime). Insets: relative contribution to the density responses $W_{1,2}/(W_1+W_2)$ of $u_1$ and $u_2$. Figure adapted from Ref. [4].

4. Conclusions

We showed that the first and second sound of bosonic and fermionic superfluids could be derived adopting Landau’s two-fluid theory, which required the equation of state and the superfluid fraction of the system under investigation. In the case of a 2D weakly-interacting Bose gas, we found that the comparison of our theory with recent measurements near $T_{BKT}$ was quite good. In the BCS-BEC crossover of the 2D Fermi gas, we proved that to obtain a good agreement with the experimental data for the equation of state, the critical temperature $T_{BKT}$, and the sound modes, both fermionic single-particle excitations and bosonic collective excitations were needed. In conclusion, it is important to stress that all the results discussed here are valid in the collisional regime, where $\omega \tau \ll 1$, with $\omega$ as the frequency of the sound mode and $\tau$ as the collision time of quasiparticles. However, in the collisionless regime ($\omega \tau \gg 1$), the role of the superfluidity in 2D systems of ultracold atoms has not been fully clarified. In Ref. [37], we found that the experimental results of sound and sound damping in a two-dimensional collisionless Bose gas of ${}^{87}$Rb atoms [38] were better reproduced below the critical temperature of the superfluid-to-normal phase transition by the Andreev–Khalatnikov equations of a collisionless superfluid with respect to the finding of the Vlasov–Landau equation [39,40]. Finally, for the sake of completeness, we suggest reading the very recent review paper of Hu, Yao, and Liu [41], which contains a detailed historical account of the second sound in ultracold atoms.